Abstract
During embryonic development, epithelial sheets fold into complex structures required for tissue and organ functions. Although substantial efforts have been devoted to identifying molecular mechanisms underlying epithelial folding, far less is understood about how forces deform individual cells to sculpt the overall sheet morphology. Here we describe a simple and general theoretical model for the autonomous folding of monolayered epithelial sheets. We show that active modulation of intracellular mechanics along the basal-lateral as well as the apical surfaces is capable of inducing fold formation in the absence of buckling instability. Apical modulation sculpts epithelia into shallow and V-shaped folds, whereas basal-lateral modulation generates deep and U-shaped folds. These characteristic tissue shapes remain unchanged when subject to mechanical perturbations from the surroundings, illustrating that the autonomous folding is robust against environmental variabilities. At the cellular scale, how cells change shape depends on their initial aspect ratios and the modulation mechanisms. Such cell deformation characteristics are verified via experimental measurements for a canonical folding process driven by apical modulation, indicating that our theory could be used to infer the underlying folding mechanisms based on experimental data. The mechanical principles revealed in our model could potentially guide future studies on epithelial folding in diverse systems.
Introduction
The epithelial cells cover outer body surfaces and line internal organs, vessels, and cavities, representing the most common type of animal cells (1). The epithelial cells are typically polarized along their apical-basal axis and adhere to one another to form a physically contiguous sheet that serves as a barrier to protect underlying tissues and regulate material exchange between internal and external environments. During embryonic development and organ formation, simple epithelia fold into complex structures, leading to the formation of neural tubes, guts, optic cups, branches of lungs, etc. (2). These folding events require highly coordinated processes of cell shape changes, contact rearrangements, and cell divisions, producing exquisite morphology necessary for the normal functions of tissues and organs.
The folding of epithelial tissues could in principle involve two types of mechanical processes: 1) active deformation caused by intrinsic forces generated within the tissues, and 2) passive buckling due to stresses exerted from the surrounding cellular and acellular environments (3). Although much of the experimental work on the mechanisms underlying epithelial folding focuses primarily on the generation of intrinsic forces and their effect on tissue deformation, mathematical models that aimed at recapitulating the folding processes often included boundary conditions that could imply mechanical influences external to the tissues (4, 5, 6, 7, 8). Based on these theoretical frameworks, it is not possible to evaluate whether or to what extent intrinsic forces acting within the tissues are capable of inducing folding via a nonbuckling process. For example, fold formation in cylindrical or spherical tissues (5, 6, 8, 9) may result from buckling instability induced by an increase in the relative compressive stresses due to tissue expansion in a localized area. Such a folded area will not maintain its shape when isolated from the epithelia because the necessary mechanical support from the surrounding tissue no longer exists (see Fig. S1 for a pictorial illustration). To address the issue of whether epithelial tissues can fold via nonbuckling mechanisms, we seek to build a simple and generalizable theoretical framework for epithelial folding without boundary constraints. Our objectives are to systematically explore potential tissue-autonomous mechanisms for epithelial folding that are not caused by buckling instability, evaluate the robustness of these mechanisms, and examine the effect of boundary conditions on the morphology of epithelial folds from a theoretical point of view.
In a variety of the epithelial folding events that have been examined thus far, myosin-dependent contraction at the apical cell cortex has been thought of as the predominant mode of an active, autonomous process that bends a tissue (10, 11). During a typical myosin-dependent folding event, shrinkage of the apical surface of a cell causes the cell to adopt a wedgelike shape. The forces and the resulting deformation propagate via interconnected cell-cell adhesion to generate tissue-scale deformation. Although myosin-dependent apical constriction represents a powerful paradigm of tissue folding, it is conceivable that there could be other ways to bend a tissue. For example, recent work (12) showed that intercalation-driven contraction of an overlying cell layer causes bending of the underlying epithelium in the invaginating ectodermal placodes, a process that is topologically analogous to apical constriction of cells in an epithelial monolayer, but involves mechanical coupling between cell layers. Furthermore, mounting experimental evidence suggests that epithelial folds can be generated via remodeling of basal or lateral surfaces (13, 14, 15, 16, 17). However, how basal-lateral modulation induces fold formation remains less understood compared to apical modulation. Moreover, a systematic comparison of epithelial fold formation driven by apical and basal-lateral modulations has not been examined.
Measuring mechanical forces that act within a cell or tissue during a morphogenetic process could be challenging. As such, theoretical methods can provide crucial insights into mechanical mechanisms responsible for the shaping of epithelial sheets. The framework of vertex modeling, in particular, has been used to bridge the gap between experimentally observed cellular behaviors and the mechanical understanding of tissue-scale deformation. In such models, individual cells within a sheet are represented by polygons or polyhedral prisms with vertices and edges in two (5, 6, 7, 18, 19, 20, 21) or three dimensions (8, 9, 22). Each vertex changes its position in response to forces resulting from growth, interfacial tension, and pressure within the cell. In this study, we construct a simple vertex model to examine whether alteration of mechanical properties at apical, basal, or lateral surfaces of individual cells is sufficient to induce folding. We show that without imposing constraints at the sheet boundaries, an epithelial sheet can autonomously fold via a nonbuckling process upon mechanical modulation at the apical surface, as well as the basal and lateral surfaces. The characteristics of the folded tissue shapes depend on the modes of modulation, and the correspondence between the modes of modulation and the resultant folded shape is robust against changes in the boundary conditions. The theoretical insights thus revealed allow us to develop a method that could be used to infer the mechanical modulations underlying tissue deformation based on measurements of cell geometry.
Materials and Methods
Mathematical modeling
We consider the cross section along the apical-basal axis of a monolayered epithelial sheet as depicted in Fig. 1 A. The sheet consists of N cells, which are represented by polygons with vertices as well as edges corresponding to apical, basal, and lateral sides. The forces acting on the vertices are derived from the derivative of a potential function, which describes the mechanical properties of the entire sheet (19) and is given by the following:
| (1) |
The first term defines the area elasticity of the cell with the cross-sectional cell area Ai, the elastic modulus , and the preferred area for the ith cell. The area elasticity likely arises from contribution of the hydrostatic pressure of cytoplasm and the intracellular cytoskeleton. The second term is the elasticity of the apical surface with the elastic modulus , the length of apical surface ai, and the preferred apical length . The apical surface elasticity is contributed from the actin cables along the cell junctions and the cytoskeletal meshwork beneath the apical membrane (1). The third and fourth terms correspond to the lowest-order contribution from the tension at the basal and the lateral surfaces with the line tension and the length bi for the basal surface, and the line tension and the length ℓk for the lateral surface. The index k runs across all lateral surfaces. This model setting deliberately breaks the symmetry between the apical and basal sides of the tissue using qualitatively distinct mechanical terms. Such a setting reflects the general feature of epithelial apical-basal polarization and takes into account the contribution from the elasticity of the actin cytoskeleton that is specifically enriched in the apical area (1) (see the Results below, however, for specific and detailed comparisons between this and an alternative setting where the tension term is used to model both the apical and basal mechanics). Hereafter, we choose the units of length and force such that the elastic modulus and the preferred cell area are unity, i.e., and .
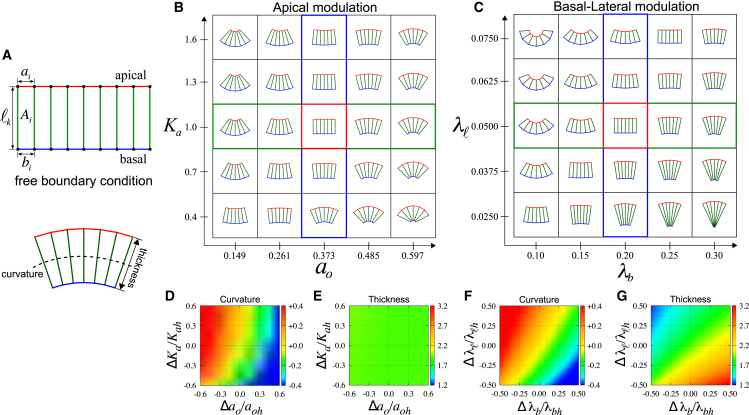
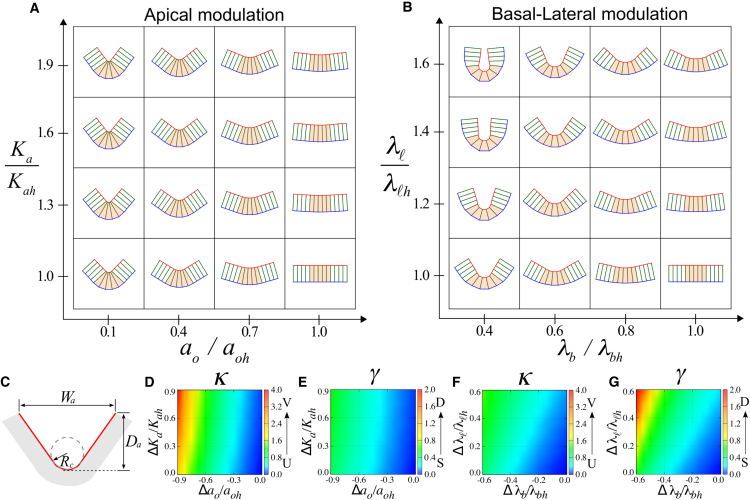
Figure 1.
Morphogenesis of epithelial tissues in the absence of boundary constraints. (A) Model of an epithelial cell sheet. Each cell is represented by a polygon with four vertices denoted by solid circles. The shape of the cells is defined by the lengths of apical ai (red), basal bi (blue), and lateral ℓk (green) surfaces. Ai is the cross-sectional cell area. (B and C) Tissue shape changes under global modulation of the apical (B) or basal-lateral (C) mechanics. The epithelial sheet at the center (red box) is a flat sheet of columnar cells (N = 6) with an aspect ratio g = a/ℓ = 0.25 and an area A ≈ 0.89. The green and blue boxes highlight the morphological transitions resulting from changes of a given mechanical parameter. (D–G) Quantification of two morphological features of epithelial sheets. The curvature of the midplane (D and F) (see Appendix B for details) and the sheet thickness (E and G) are shown. The values aoh, Kah, λbh, and λℓh are the mechanical parameters of the flat sheet, whereas Δq = q − qh with q = ao, Ka, λb, and λℓ. To see this figure in color, go online.
The relaxation time to reach mechanical equilibrium is typically less than a few tens of seconds (18), which is generally faster than the remodeling of cell mechanics that requires alterations such as the reorganization of the cytoskeleton and cell-cell adhesion complexes. Thus, the temporal evolution of fold formation can be described as a series of changes in the mechanical parameters , during which the sheet is under stable force balance with a minimal value of U.
Results
Nonbuckling epithelial folding without boundary constraints
We first studied the morphological changes of a homogeneous sheet that comprises cells with identical shape. To explore cell-autonomous mechanisms that can shape the sheet, we considered a freely deformable sheet without mechanical constraints. According to Eq. 1, the mechanical condition of a flat sheet is for all lateral surfaces except the ones at the boundaries where . The other mechanical parameters , , and are uniform across the sheet. A flat sheet is mechanically stable when the intracellular pressure is positive, which corresponds to a compressed sheet (see Appendix A for details).
For a typical choice of parameter values, we numerically minimized Eq. 1 using Mathematica (Wolfram Research, Champaign, IL). The resulting morphology of a homogeneous sheet is shown in Fig. 1, B and C. For sufficiently large apical elasticity Ka, a reduction in the preferred apical length ao induces apical constriction, as cells adopt an uptrapezoidal shape, resulting in the formation of concave sheets. In contrast, the apical surface undergoes expansion as ao increases, deforming cells into downtrapezoids and producing convex sheets (Fig. 1 B). Such shape changes can be observed quantitatively by measuring the sheet curvature (Fig. 1 D), where concavity is characterized by positive curvature (red), whereas convexity displays negative curvature (blue).
The tension modulation at the basal (λb) and the lateral (λℓ) surfaces can also generate concave and convex sheet structures (Fig. 1 C). A decrease in λb induces expansion of the basal surface, whereas an increase in λℓ causes shrinkage of the lateral surface, resulting in epithelial sheets of concave shapes with uptrapezoidal cells. Conversely, convex morphology with downtrapezoidal cells is formed when λb increases or λℓ decreases. The resulting changes of sheet curvature are presented in Fig. 1 F. Note that the change of λℓ alone is sufficient to induce folding in our model. This is due to the contribution of the elastic term prescribed for the apical surface (the second term in Eq. 1), reflecting the apical-basal polarity of epithelial cells (see also the Materials and Methods). When the apical mechanics is described by a linear tension term instead of a quadratic elastic term (i.e., when the contribution from the elasticity of apical cytoskeleton can be negligible), lateral modulation alone cannot induce fold formation. These results illustrate that folding due to lateral modulation is an emergent property that arises from mechanical symmetry breaking, owing to the apical-basal polarization of epithelial cells. From this point of view, the effect is similar to the generation of nonzero curvature of bilayered materials, where the mechanical differential between the two layers induces the fold formation (see, for example, (23)).
The sheet thickness exhibits distinct behaviors in response to the different modes of modulation. Under apical modulation, the sheet thickness appears constant (Fig. 1 E). In contrast, a significant change in the sheet thickness was observed for basal-lateral modulation (Fig. 1 G). Thinning occurs as the sheets become concave, whereas thickening is associated with the formation of convex sheets. Because cells in a homogeneous sheet have identical shape, below we systematically analyzed these tissue shape changes at the level of individual cells.
Cell deformation pattern depends on initial cell aspect ratio
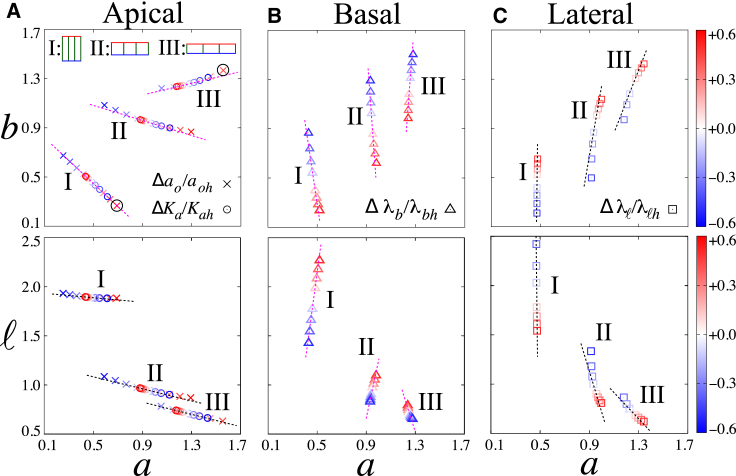
Epithelial cells are conventionally categorized into three types: columnar (I), cuboidal (II), and squamous cells (III) (Fig. 2), based on the cell aspect ratio g = a/ℓ. We examined the characteristic pattern of cell deformation for these three types of epithelial cells in a scattergram for the lengths of any two sides of a cell (e.g., apical versus basal).
Figure 2.
Cell deformation is shown in response to (A) apical, (B) basal, and (C) lateral modulations. The relationship between the changes in apical length and the changes in basal (top) and lateral (bottom) lengths was analyzed for columnar (I; g = 0.25), cuboidal (II; g = 1.00), and squamous (III; g = 1.75) cells. The data points were obtained from the sheets shown in the blue and green boxes in Fig. 1. The dashed lines were obtained from the theoretical analysis of cell deformation (see (A10), (A11), (A9) in the Appendix A) and were highlighted in magenta (otherwise black) when the slope changes sign with varying cell aspect ratio g. The color bars indicate the relative deviation of parameter values from those of the flat sheet. The characteristic deformation of type-I and type-III cells (the circled crosses) are displayed in Fig. 3. To see this figure in color, go online.
We first considered the apical modulation that changes ao and Ka (depicted as cross and circle symbols in Fig. 2). In the columnar and cuboidal epithelia, the changes in the apical and basal lengths, a and b, are negatively correlated (I and II in Fig. 2 A). This negative correlation is due to the cell area elasticity, as the basal surface expands in response to the constriction of apical surface, and vice versa. In contrast, in the squamous epithelia (III in Fig. 2 A), the correlation between the changes in the apical and basal lengths becomes positive, indicating that both surfaces show expansion or contraction as the apical surface undergoes modulation. Note also that the lateral length ℓ varies only slightly in all cases (Fig. 2 A, bottom).
We next considered the modulation of basal and lateral properties (depicted as triangle and square symbols in Fig. 2, respectively). The changes in the length of basal and lateral surfaces, b and ℓ, are much larger than the changes in the apical length a, and the changes in b and ℓ are always negatively correlated.
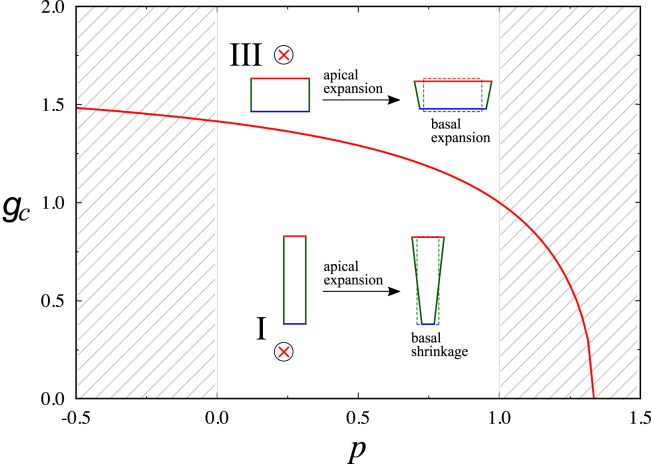
In both apical and basal modulation, the positive or negative correlations for a given pair of lengths depend on the initial cell shape. In the apical modulation, the sign of the correlation between changes of a and b are different between the squamous epithelia (III) and the others (I and II) (Fig. 2 A). Similarly, when the basal mechanics is modulated, the a–b and a–ℓ correlations in the squamous epithelia are opposite to those of the other (I and II) types of epithelial cells (Fig. 2 B). We then analyzed the effect of the cell aspect ratio g on the cell shape changes (see Appendix A for details) and found that the sign inflection point occurs when g satisfies g = gc, as given by the following:
| (2) |
The boundary according to Eq. 2 is plotted in Fig. 3. In the regime above the boundary, the cell is more squamous with g > 1, and the apical length increases with an increase in the basal length. Below the boundary, in contrast, the cell shapes are columnar (g < 1) or cuboidal (g = 1), and the apical length increases as the basal length decreases. As such, near the boundary where the inflection occurs, the basal length is nearly constant under apical modulation, and vice versa. These results illustrate a previously unknown effect of cell aspect ratio on changes of cell shape in response to mechanical modulations.
Figure 3.
Threshold values of cell aspect ratio gc, as a function of pressure p, for changes in the correlation pattern between variations of different surfaces. As demonstrated by the shapes in the insets, below the boundary (the red line), changes in the apical and basal lengths show a negative correlation; above the boundary, the changes of apical and basal lengths display a positive correlation. The ⊗ symbols denote the g and p values for the cells analyzed in Fig. 2. The sheets are unstable in the hatched region. To see this figure in color, go online.
Theoretical prediction of mechanical modulation underlying epithelial folding
Besides the distinct pattern of cell deformation with respect to cell geometry, Fig. 2 also indicates that epithelial cells change their shape in a distinct manner in response to the modulation at different surfaces. For the columnar cells (Fig. 2; I), for example, apical constriction induced by apical modulation is accompanied by basal and lateral expansion (cross and circle). For basal modulation, the basal expansion and lateral shrinkage are observed (triangle), whereas for lateral modulation, the opposite behaviors occur (basal shrinkage and lateral expansion) (square). Such distinct pattern of cell deformation suggests that experimental measurements of cell shape changes could be used to infer the underlying mechanical mechanisms for an epithelial folding event.
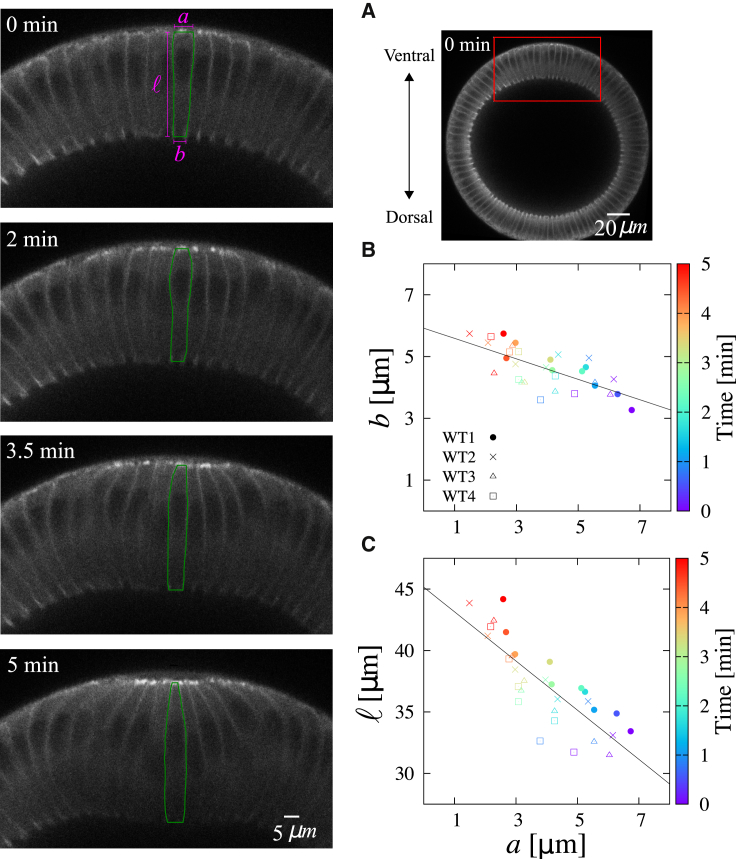
To examine this idea, we performed time-lapse imaging and measured cell shape changes for ventral furrow formation in the Drosophila embryo. The initial stage of this process is considered to be driven by myosin-dependent apical modulation (24). We traced the cell shape at the center of the ventral furrow formation (Fig. 4; left) and plotted the measured lengths b and ℓ versus a in Fig. 4, B and C, respectively. Whereas the apical length reduces with time, both basal and lateral lengths increase during the fold formation, showing the negative correlations between the changes in the basal-lateral and the apical lengths. In our theoretical analyses on the columnar cells, such a correlation pattern was found only in the case of apical modulation (see Fig. 2; I). Thus, our theoretical prediction of cell deformation pattern could serve as a guide for inferring the mechanical modulations that shape epithelia. Note that during furrow formation, the increment in the lateral length ℓ appears to be larger than prediction (Fig. 2 A, bottom, and Fig. 4 C). The difference could be due to the physical constraints present in the in vivo system, such as the vitelline membrane that surrounds the embryo, the yolk sac internal to the cell layer, and the presence of neighboring cells. Alternatively, the concurrent cell lengthening process called “cellularization” may contribute to the difference (Fig. S2). The agreement of the general trend of cell shape changes, however, indicates that the forces resulting from modulation of intracellular mechanics can robustly shape cell geometry against the influence of surrounding environments.
Figure 4.
Analysis of cell shape changes in the early stage of Drosophila ventral furrow formation. (Left) Representative time-lapse images (red box in (A)) showing deformation of mesoderm cells during apical modulation. The cell shape outlined in green is analyzed in (B) and (C), where each symbol denotes the measurements obtained from an embryo. The colors of the symbols indicate the time frame, and the lines are the fitting curves, obtained by using the nonlinear least-squares Marquardt-Levenberg algorithm, which serve as visual guides. The initial time point is chosen arbitrarily before the onset of apical constriction of the mesoderm cells. The details of the experimental setup are provided in Appendix D. To see this figure in color, go online.
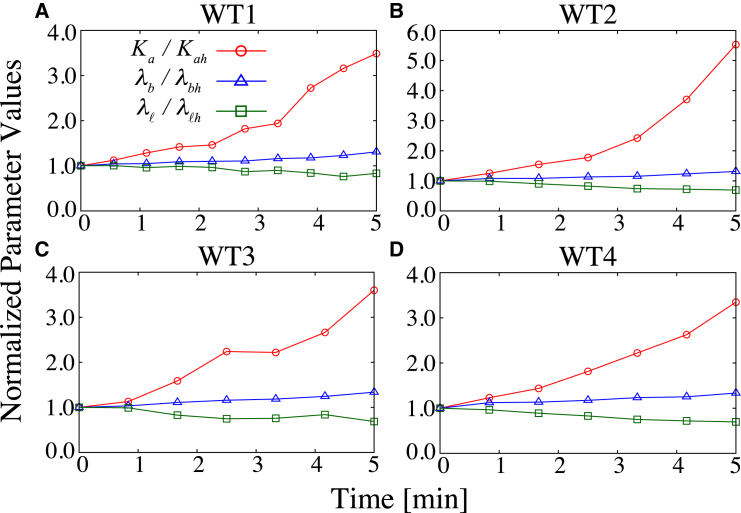
Our theoretical framework can also aid in the quantitative estimation of mechanical parameters in experimental systems. As documented in Appendix A, for a given set of values of cell shape (a, b, ℓ), intracellular pressure p, and preferred apical length ao, one can calculate the values of mechanical parameters (Ka, λb, λℓ) according to Eq. A3. To estimate the changes in parameter values associated with Drosophila ventral furrow formation, we considered the normalized mechanical parameters Q = q/qh with q = ka, λb, λℓ relative to the mechanics qh of some reference point (which we choose as the initial point of observation t = 0). Because the cell volume during ventral furrow formation has been shown to be conserved despite shape changes (6, 25), in our cross-sectional model we thus assumed that the cell area A undergoes negligible fluctuations such that p = 2(1−A) is near constant. We validated such approximation in Fig. S3, which has been obtained by analyzing the cross-sectional cell area from the time-lapse images, where the cell area exhibits <10% fluctuations during the initial stage of furrow formation. Furthermore, we found that the qualitative behaviors of the mechanical parameter prediction appear insensitive to the choice of ao (data not shown), so we simply used a constant ratio αa = ao/a for the estimation. We then calculated the temporal evolution of Q from the time-lapse measurements of cell shapes. As shown in Fig. 5, estimated apical elasticity Ka increases over time, whereas the basal and the lateral mechanics, λb and λℓ, remain relatively constant, thus supporting this view (6, 24) that the initial phase of ventral furrow formation is driven primarily by the forces resulting from the remodeling of apical mechanics.
Figure 5.
(A–D) Parameter estimation for the early stage of Drosophila ventral furrow formation. The data points, which are normalized by the initial point t = 0, are analyzed from the same embryos as those used in Fig. 4, B and C. The decreasing lateral line tension λℓ observed in all embryos may result from the concurrent morphological event of cellularization (as shown in Fig. S2). To see this figure in color, go online.
Basal-lateral modulation induces deep U-shaped folds, whereas apical modulation leads to shallow V-shaped folds
A typical folding process is initiated by mechanical modulation in a localized area within a tissue. As a result, the folded structure exhibits nonuniform curvature, reflecting the heterogeneities of cell shape. We further investigated the effect that distinct modes of local mechanical modulation have on the morphology of epithelial folds. We first simulated apical constriction via alteration of the apical elasticity Ka and the preferred apical length ao in the Nc cells at the center of the columnar sheet comprising N cells, while keeping the original mechanical properties constant for the surrounding cells (Fig. 6). As shown in Fig. 6 A, apical constriction caused either by the decrement of ao or by the increment of Ka in the central cells deforms the cells into trapezoidal shapes or triangles, as is the case for the sheets with global mechanical manipulation described above. Due to the shared lateral boundaries, the active deformation of central cells alters the shapes of their neighbors. The relaxation of the resulting stresses causes the surrounding cells to passively adapt to a folded morphology. Because cells at the peripheries are not constrained physically by the surrounding environment, the stresses induced by apical constriction in the central area dissipate toward the peripheries, producing straight arms at the ends of the sheets. These analyses thus indicate that apical modulation in a localized area is sufficient to fold an epithelial sheet.
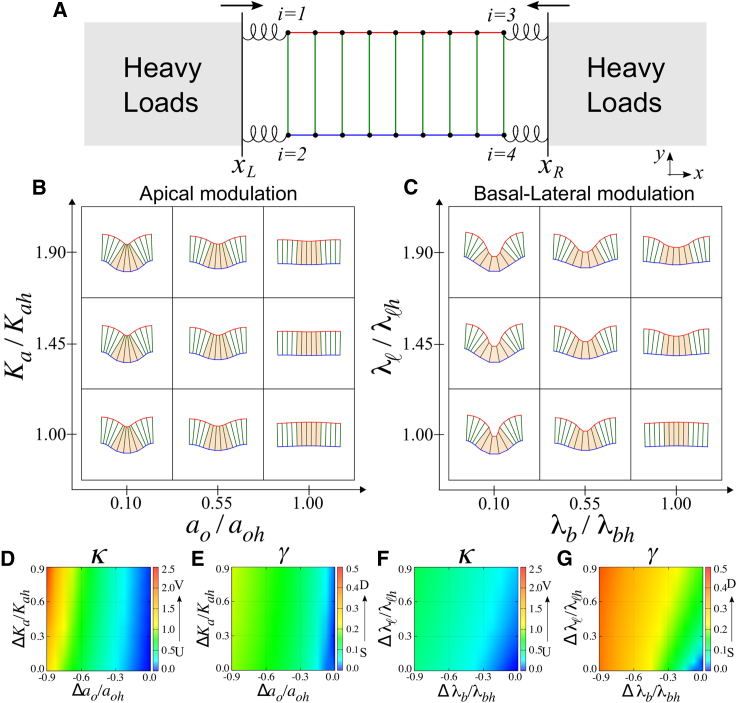
Figure 6.
Localized mechanical modulations at distinct surfaces induce characteristic folds of shallow V-shape or deep U-shape. The cells at the center (Nc = 5, orange) of the sheet (N = 13) are modulated at the apical (A) or basal-lateral (B) surfaces. The flat sheet at the lower-right corner is generated with same parameter values as those in Fig. 1. (C) Quantification of epithelial fold morphology (gray) by the geometry of apical surface (red). (D and F) The local geometry, such as the V- and U-shapes, is characterized by the curvature κ = 1/Rc. (E and G) The deep (D) and shallow (S) global fold morphology is quantified by the aspect ratio γ = Da/Wa. The value Δq with q = ao, Ka, λb, and λℓ measures the mechanical differential between the central and the surrounding cells. Results for the cuboidal and squamous sheets are provided in Fig. S5. To see this figure in color, go online.
We next examined the effect of local modulation of the basal and the lateral surface mechanics. As shown in Fig. 6 B, a decrease in the basal line tension λb allows expansion of the basal surface of the central cells, whereas an increase in the lateral line tension λℓ shrinks the lateral surface at the sheet center. Each of these changes causes the central cells to deform into trapezoidal shapes, thereby initiating the folding of the epithelial sheet. Thus, basal-lateral modulation in a localized area is also sufficient to induce epithelial folding.
The modulation of apical and basal-lateral surfaces appears to produce distinct fold morphologies (Fig. 6, A and B). To quantify these differences, we introduce two morphological descriptors: 1) the curvature , given by the inverse of the radius of curvature Rc at the apical surface formed by the deforming central cells; and 2) the aspect ratio of the folded area , given by the depth Da and the width Wa of the folds (Fig. 6 C). Of these two descriptors, the curvature κ characterizes the local property of the actively deforming central area. In particular, the folded shape resembles the letter “V” (V-shape), when the value of κ is high, whereas the shape resembles the letter “U” (U-shape) for low values of κ. The measurement of γ, on the other hand, reflects the global feature of the sheet morphology. In a flat epithelium, γ = 0, whereas a deep fold is characterized by a large value of γ.
As shown in Fig. 6, D and F, strong apical constriction (top-left corner of Fig. 6 D) produces a sharp V-shape at the apical surface of the deforming central cells. In contrast, basal expansion and lateral shrinkage produce U-shaped folds with moderate values of κ (Fig. 6 F). With regard to the overall depth of the folded sheets, apical constriction induces only shallow folds with low values of γ (Fig. 6 E). In contrast, basal expansion and lateral shrinkage result in the formation of folds that have high values of γ (Fig. 6 G), indicating deep folds.
Taken together, local apical constriction tends to induce shallow and V-shaped folds, whereas basal expansion and lateral shrinkage in a restricted area preferentially generate deep and U-shaped folds. When the apical mechanics is modeled with a line tension term rather than an elastic term, the distinct fold morphology associated with either apical or basal-lateral modulation is still observed (Fig. S4). In addition to these numerical analyses, the morphological differences can be understood analytically, for which the detailed analyses are provided in the Appendix C.
For the cuboidal and squamous cell sheets, both local apical constriction and basal-lateral remodeling can induce autonomous folding (Fig. S5). The V- and U-shaped distinction, however, is less pronounced, as compared to the folding of the columnar cell sheets.
Autonomous folding is robust against boundary constraints
So far we have shown that epithelial folding induced by cell mechanical remodeling does not require external forces. We also showed that, at least in the case of columnar epithelia, the folded morphology contrasts sharply between different modes of mechanical modulation. These conclusions raise the question whether boundary constraints, such as the presence of neighboring tissues or acellular spatial confinements, could alter the folding characteristics that were shown above. To address this question, we considered the presence of neighboring tissues at the edges of the folding sheet. Such scenarios were simulated by supplementing Eq. 1 with the following potential function resulting from the interaction at the sheet boundaries,
| (3) |
where Δxi = xi – xbi with xb1 = xb2 = xL and xb3 = xb4 = xR. The variables x1, x2 and x3, x4 are the horizontal position of the vertices at the left and the right boundaries, respectively (Fig. 7 A). Ks is the elastic modulus that characterizes the interaction between the sheet and the neighboring tissues located at the positions xL and xR. The neighboring tissues can be passively attached to the sheet, comoving with it as it folds when F = 0. Alternatively, they can actively exert either compression (F < 0) or stretching forces (F > 0) for xR > xL.
Figure 7.
Effect of boundary constraints on autonomous folding. (A) An epithelial sheet under horizontal compression by the surrounding tissues (gray). (B and C) Tissue deformation under compression (Nc = 5, N = 13) for local apical (left) or basal-lateral modulation (right). The values for curvature κ and the aspect ratio γ of the folded area are measured in (D) and (F), and (E) and (G), respectively. The parameter values are Ks = 1.0, F = −0.17, and others are given in Fig. 6. To see this figure in color, go online.
Fig. 7, B and C, shows that epithelial sheets compressed by adjacent tissues undergo foldings that do not qualitatively differ from those without boundary constraints. Specifically, the resulting folds are shallow and V-shaped when apical constriction occurs in a localized region (Fig. 7 B), whereas deep and U-shaped if local basal expansion and lateral shrinkage drive the fold formation (Fig. 7 C). Similar results were obtained in the case where a stretching force from the adjacent tissues was applied (F > 0) or when the adjacent tissues were passively attached to the folding sheet (F = 0) (data not shown). These results suggest that the autonomous folding mechanisms are robust against varying mechanical conditions at the tissue surroundings.
Discussion
In this study, we showed unequivocally that both global and local changes of either the apical or basal-lateral mechanics can cause nonbuckling, active folding of epithelial sheets (Figs. 1 and 6). The distinct features of the resulting folds, namely the U- and V-like shapes, are also found in the presence of external forces (Fig. 7), suggesting that these nonbuckling, autonomous folding mechanisms can work robustly under various boundary conditions. Such an autonomous folding process has been observed previously in the mammalian optic-cup organoids (26). The folded structure in the optic cup was maintained even when it was excised from the surrounding tissues, suggesting that the structure is maintained by an intrinsic mechanism, independent of external forces.
We also found that cell shape changes reveal distinct characteristics depending on the initial cell aspect ratios and the surfaces at which the mechanical modulations take place (Figs. 2 and 3). Cell shape measurements for the initial stage of Drosophila ventral furrow formation are in agreement with our theoretical prediction (Fig. 4). The evolution of mechanical parameters estimated from the time-lapse experimental data supports the current understanding of apically driven Drosophila ventral furrow formation (Fig. 5), where accumulation of nonmuscle Myosin II at the medial apical cortex induces contraction of apical actin networks that initiates the furrow formation (27). The resulting furrow shape in this initial phase is a shallow fold (6), which is also consistent with our theory.
We accounted for the apical-basal polarity of epithelial cells by breaking the symmetry between apical and basal mechanics in Eq. 1. Such intrinsic polarity gives epithelial tissues the ability to change their apical and basal surfaces differently in response to modulation at lateral surfaces such as the redistribution of cell-adhesion molecules (14). When the epithelial polarity is impaired, the tissues fail to establish folds under lateral modulation. Thus, the efficacy and versatility of epithelial fold formation are related to the polarization of apical-basal axis within individual cells, which endows the cells with distinct cell surface mechanics.
Given that apical modulation makes shallower folds than basal-lateral modulation, to reach the same degree of fold depth, a higher number of cells would be required if the fold is induced by apical remodeling, as shown in the upper-left regime of Fig. 1, B and C. This is because a reduction in the apical length is limited, whereas the basal side can expand without the length restriction. Note also that apical constriction produces a smaller extracellular luminal space (Fig. 1 B, upper-left), implying a need to control the lateral (cell height) and basal sides to produce an apical lumen of appropriate size (28).
In the case of ventral furrow formation in Drosophila, after the initial shallow fold formation, a subsequent expansion at the basal surface, presumably due to myosin disassembly, allows the furrow to undergo deep folding (6). A recent study showed that interference of the initial apical constriction via a perturbation of myosin pulsatile contraction resulted in the formation of a U-shaped ventral furrow, presumably because the basal expansion at the later stage was intact (29). Our model lends a theoretical support to this interpretation.
We envision that our model could aid in the formulation and assessment of mechanical hypotheses for folding processes for which mechanical mechanisms remain elusive, such as dorsal fold formation in the Drosophila gastrula, proposed to be induced by basal shifts of the cell-cell junctions along the lateral side (14). Other events involving changes of multiple sides of cells for which the canonical apical modulation alone cannot account, would also be of particular interest. For example, the neural tube formation in Xenopus laevis was suggested to be driven by a combination of cell height change, basal remodeling, and apical constriction (30, 31), whereas the inner ear development in chick was reported to involve basal expansion of the otic epithelium, followed by contraction of the apical surface (32). Using the approach demonstrated in Figs. 2 and 4, one may first measure the time-dependent changes of the length of each cell surface and subsequently perform estimation of mechanical parameters using Eq. A3 to infer the cell surface mechanics (see Fig. 5). The evolution of parameter values thus derived could suggest which membrane surface(s) undergo active mechanical modulation. These endeavors could provide mechanical insights into epithelial folding events for which performing mechanical manipulations is challenging and attest the generalizability of our model.
Author Contributions
F.-L.W., Y.-C.W., and T.S. designed research. F.-L.W. performed research. F.-L.W., Y.-C.W., and T.S. analyzed data. F.-L.W., Y.-C.W., and T.S. wrote the article.
Acknowledgments
We thank M. Takeichi and S. Hayashi for valuable comments on this article.
This work was supported by core funding at RIKEN Quantitative Biology Center and RIKEN Center for Developmental Biology, Takeda Science Foundation to T.S., and Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research (KAKENHI) grants 15H04373 to Y.-C.W. and 15KT0086 to T.S.
Editor: Stanislav Shvartsman.
Footnotes
Five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30519-2.
Contributor Information
Fu-Lai Wen, Email: fulai@cdb.riken.jp.
Tatsuo Shibata, Email: tatsuo.shibata@riken.jp.
Appendix A: Mechanical Analysis of a Single Cell
Because cells in a homogeneous sheet possess identical shape, the overall sheet morphology can be derived from the geometric features of the individual cells. The behavior of a homogeneous sheet can be understood from the single cell properties (9). Here we perform a series of analyses to probe the mechanical properties of a single cell.
Force and Torque Balance
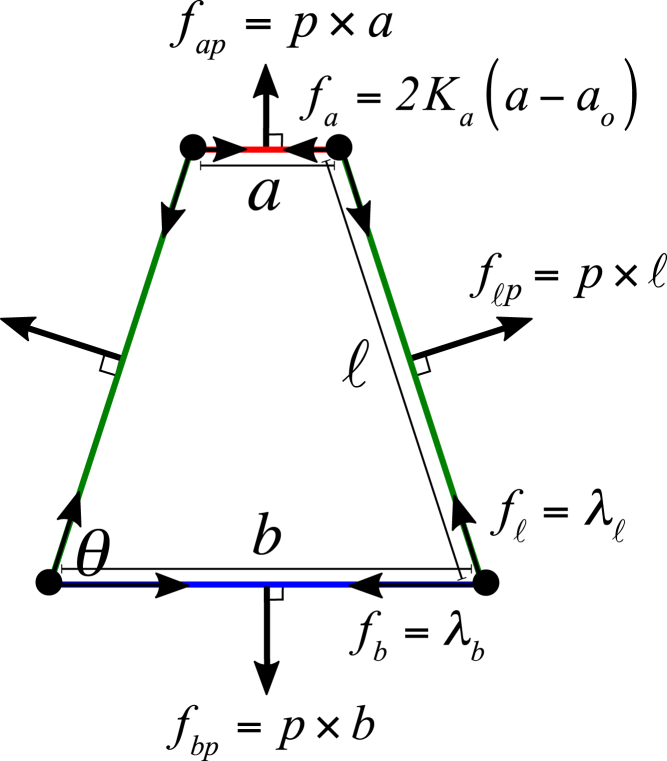
We considered the mechanical balance of a cell with a trapezoidal shape. Based on the potential function of Eq. 1, the forces acting on each cell surface can be depicted as in Fig. 8, from which it is straightforward to derive the condition of force balance as follows:
| (A1) |
Figure 8.
Schematic illustration of forces acting on a cell according to the potential function given by Eq. 1. The force on each cell surface has two components: one parallel and the other perpendicular to the surface. The angle θ defines the rectangular, up-, or downtrapezoidal shape. The mathematical expression of the parallel and the perpendicular components of forces are explicitly shown and illustrated in the text. To see this figure in color, go online.
where p = 2(1 – A) is the pressure pushing outward against the surface when p > 0, or inward compression from outside when p < 0. To prevent cell rotation, we further consider the condition of torque balance as the following:
| (A2) |
According to Eqs. A1 and A2, the mechanical parameters that give rise to a balanced cell shape read as
| (A3) |
For a rectangular cell (a = b), the above formula simplifies to the following:
| (A4) |
In agreement with our intuition, Eq. A4 shows that the apical surface a relaxes to its preferred length ao when Ka increases. Furthermore, the ratio between the lateral line tension λℓ and the basal line tension λb is equal to the aspect ratio a/ℓ. This indicates that λb is greater than λℓ for a columnar cell, whereas λb < λℓ for a squamous cell.
Stability Analysis
It is worthwhile analyzing the stability of a rectangular cell, which displays the same shape as those within a flat cell sheet. For simplicity, we assume that the cell area is conserved so that the lateral surface is related to the apical and the basal surfaces as follows:
| (A5) |
Substituting Eq. A5 into Eq. 1 for a single cell N = 1, the stability of a rectangular shape can be determined straightforwardly from the Hessian matrix M of U, as follows:
| (A6) |
where as and ℓs are the apical and the lateral surfaces of a rectangular cell under force and torque balance, respectively. By analyzing the Hessian matrix, the cell is mechanically stable when the determinant and the trace of M are positive, which gives the stable conditions as follows:
| (A7) |
and
| (A8) |
where x = 1 – αa with αa = ao/as and g = as/ℓs. Note that λℓ is replaced by Ka according to Eq. A4. Because the elastic constant of the apical surface Ka should be positive for the stability, according to Eqs. A7 and A8, the cell is stable when x > 0, which corresponds to a cell under compression. When x becomes negative for a stretched cell, the cell shape is mechanically unstable. Such an instability can be understood from the fact that the expansion (shrinkage) of a cell surface (e.g. the lateral surface ℓ), resulting from environmental perturbations, will enhance (reduce) the inward force produced by the pressure (i.e., flp = p × ℓ). The increasing (decreasing) inward force further expands (shrinks) the cell surface (ℓ) because of the conservation of cell area (or cell area elasticity in a weak constraint), forming a positive feedback that drives the cell to deform away from its original shape.
Linear Response of Cell Deformation to Mechanical Modulation
For a mechanically stable cell, the cell shape is robust against environmental perturbations. A cell can change its shape, however, by modulating the mechanical properties of its surfaces. Here, we further study how a cell is deformed when the mechanics of each cell surface is changed. Taking into account a small deformation around a rectangular shape, the parameters of surface mechanics can be calculated by expanding Eq. A3 around (a,b,ℓ) = (as, as, ℓs) to linear order. From the ensuing equations, the variation of each mechanical parameter (Ka, λb, λℓ) gives rise to the following conditions:
| (A9) |
| (A10) |
| (A11) |
where
| (A12) |
(A10), (A11), (A9) indicate the relation between the active deformation of apical, basal, and lateral surfaces due to the modulation of Ka, λb, and λℓ, respectively, and the passive response of the other surfaces.
Because for a mechanically stable shape p > 0 and αa < 1 according to the previous section, from (A10), (A11), (A9) it is straightforward to derive that the correlation between each surface deformation changes qualitatively when:
| (A13) |
Appendix B: Curvature of a Homogeneous Sheet
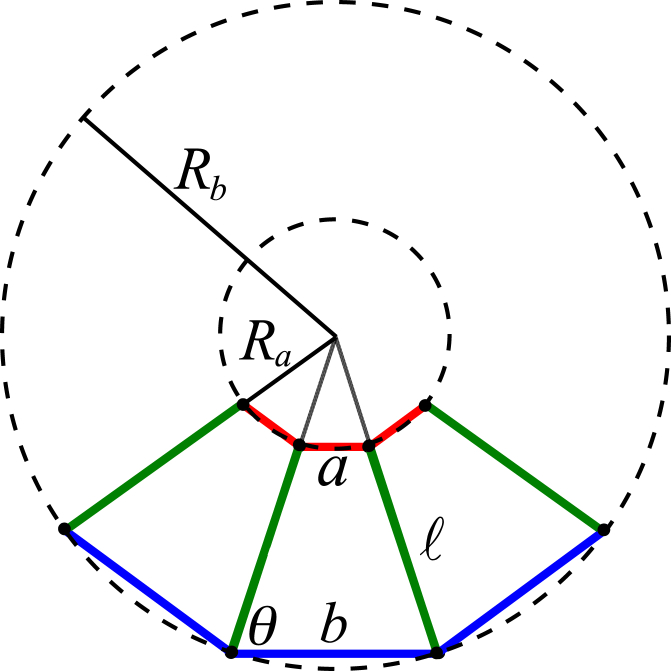
The sheet consists of interconnected cells. When cells deform into trapezoids, the sheet becomes curved. Here we discuss the relation between the individual cell shape and the overall sheet morphology. Specifically, we consider a homogeneous sheet comprising cells with identical shape. Without loss of generality, the sheet can be parameterized, as shown in Fig. 9, where θ follows that
| (B1) |
Figure 9.
Schematic of a homogeneous curved sheet. For clarity, only three cells are shown. See text for details. To see this figure in color, go online.
The radius of curvature of the apical surface (Ra) and the basal surface (Rb) read as follows:
| (B2) |
According to Eq. B2, the curvature C at the midplane of a sheet can be calculated as the following:
| (B3) |
As a result, the shape of cells gives rise to the midplane curvature of a homogeneous sheet according to Eq. B3. When the cell deformation around a rectangular shape is small (θ ≈ π/2), Eq. B3 approximately equals the following:
| (B4) |
Appendix C: Formation of U-/V-Shaped and Shallow/Deep Folds
The distinct morphology of folds generated by local apical and basal-lateral modulation can be understood by noting that because of cell area elasticity, the apical constriction deforms cells into longer lateral surfaces, whereas the basal expansion and lateral shrinkage shorten lateral surfaces. As a result, a thin and tall cell is formed by apical constriction, whereas a wide and short cell is generated by basal expansion and lateral shrinkage (see upper-left corner of Fig. 6, A and B). An epithelial sheet is folded deeply when the change of angle of vectors perpendicular to the lateral surface along central cells is large. Specifically, this angular variation can be calculated as follows:
| (C1) |
where
| (C2) |
is the angle that characterizes rectangular, up- and downtrapezoidal cell shapes (see Fig. 9). The quantities ac, bc, and lc are the apical, basal, and lateral surfaces averaged over central cells, respectively. As folding proceeds via deforming cells into uptrapezoids, (bc – ac) increases for both apical and basal-lateral modulation. In the region of strong cell deformation (the upper-left corner of Fig. 6, A and B), (bc – ac)/lc ≈ bc/lc, which is small for the apical constriction, but is large for the basal expansion and lateral shrinkage. Therefore, the apical constriction preferentially develops an epithelial sheet into a shallow fold with smaller ΔΘ, whereas a deep fold with larger ΔΘ is generated by the basal expansion and lateral shrinkage.
On the other hand, the sharpness of folds is described by the curvature at the center of the sheet, which approximately equals the following:
| (C3) |
Because the apical surface of central cells substantially reduces during apical modulation, but is restricted by its elasticity for basal-lateral modulation, the apical constriction has much smaller ac than that of basal expansion and lateral shrinkage in the region of strong cell deformation. Consequently, a V-shaped fold with larger C is generated by the apical constriction, whereas a U-shaped fold with smaller C is formed by the basal expansion and lateral shrinkage.
The above analyses suggest that the local apical constriction tends to sculpt a sheet into a shallow and V-shaped fold. In contrast, a deep and U-shaped fold is generated by the local basal expansion and lateral shrinkage.
Appendix D: Imaging and Measurements for Drosophila Ventral Furrow Formation
Embryos expressing both a membrane marker Resille-GFP (33) and a marker for myosin (Sqh-GFP) were used in imaging experiments that measured the cell shape changes during Drosophila ventral furrow formation (34). The localization of Sqh-GFP at the base of the cellularizing cells improves the visualization of basal surfaces, whereas the accumulation of Sqh-GFP at the apical surface marks the onset of ventral furrow formation. A two-photon excitation scanning system, a Fluoview FVMPE-RS (Olympus, Melville, NY) equipped with an InSight DeepSee pulsed IR Dual-Line laser system (Spectra-Physics, Santa Clara, CA) tuned at 930 nm, was used for the time-lapse imaging. Embryos were first dechorionated in bleach and then mounted vertically with the posterior pole pointing up in the glass-bottom dish using double-sided tapes. The mounted embryos were immersed in water for imaging with a 25× water immersion objective (numerical aperture = 1.05). A single focal plane, ∼200–250 μm from the posterior pole, was scanned at a frame rate of 10 s/frame. The resultant image datasets were processed in the software ImageJ (National Institutes of Health, Bethesda, MD). Measurements of cell geometry were performed as the following: based on the fluorescent signals of membrane and myosin markers, the shapes of individual cells were traced manually for every three to five frames with the total observation period at ∼5 min (a longer period is used for the analyses in Fig. S2). The initial time frame was chosen arbitrarily before the onset of apical constriction of ventral furrow cells. The length of each cell surface was measured using a straight line with image-processing package of ImageJ. Due to the small deformation around a rectangular shape, the lateral length was simply derived as the distance between the apical and the basal surfaces.
Supporting Material
References
- 1.Alberts B., Johnson A., Walter P. 6th Ed. Garland Science; New York: 2014. Molecular Biology of the Cell. [Google Scholar]
- 2.Gilbert S.F. 10th Ed. Sinauer Associates; Sunderland, MA: 2013. Developmental Biology. [Google Scholar]
- 3.Mao Y., Baum B. Tug of war—the influence of opposing physical forces on epithelial cell morphology. Dev. Biol. 2015;401:92–102. doi: 10.1016/j.ydbio.2014.12.030. [DOI] [PubMed] [Google Scholar]
- 4.Hannezo E., Prost J., Joanny J.F. Instabilities of monolayered epithelia: shape and structure of villi and crypts. Phys. Rev. Lett. 2011;107:078104. doi: 10.1103/PhysRevLett.107.078104. [DOI] [PubMed] [Google Scholar]
- 5.Hočevar Brezavšček A., Rauzi M., Ziherl P. A model of epithelial invagination driven by collective mechanics of identical cells. Biophys. J. 2012;103:1069–1077. doi: 10.1016/j.bpj.2012.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Polyakov O., He B., Wieschaus E. Passive mechanical forces control cell-shape change during Drosophila ventral furrow formation. Biophys. J. 2014;107:998–1010. doi: 10.1016/j.bpj.2014.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Štorgel N., Krajnc M., Ziherl P. Quantitative morphology of epithelial folds. Biophys. J. 2016;110:269–277. doi: 10.1016/j.bpj.2015.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Misra M., Audoly B., Shvartsman S.Y. Shape transformations of epithelial shells. Biophys. J. 2016;110:1670–1678. doi: 10.1016/j.bpj.2016.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hannezo E., Prost J., Joanny J.F. Theory of epithelial sheet morphology in three dimensions. Proc. Natl. Acad. Sci. USA. 2014;111:27–32. doi: 10.1073/pnas.1312076111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Munjal A., Lecuit T. Actomyosin networks and tissue morphogenesis. Development. 2014;141:1789–1793. doi: 10.1242/dev.091645. [DOI] [PubMed] [Google Scholar]
- 11.Sawyer J.M., Harrell J.R., Goldstein B. Apical constriction: a cell shape change that can drive morphogenesis. Dev. Biol. 2010;341:5–19. doi: 10.1016/j.ydbio.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Panousopoulou E., Green J.B.A. Invagination of ectodermal placodes is driven by cell intercalation-mediated contraction of the suprabasal tissue canopy. PLoS Biol. 2016;14:e1002405. doi: 10.1371/journal.pbio.1002405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sherrard K., Robin F., Munro E. Sequential activation of apical and basolateral contractility drives ascidian endoderm invagination. Curr. Biol. 2010;20:1499–1510. doi: 10.1016/j.cub.2010.06.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang Y.C., Khan Z., Wieschaus E.F. Differential positioning of adherens junctions is associated with initiation of epithelial folding. Nature. 2012;484:390–393. doi: 10.1038/nature10938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gutzman J.H., Graeden E.G., Sive H. Formation of the zebrafish midbrain-hindbrain boundary constriction requires laminin-dependent basal constriction. Mech. Dev. 2008;125:974–983. doi: 10.1016/j.mod.2008.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nicolás-Pérez M., Kuchling F., Martínez-Morales J.R. Analysis of cellular behavior and cytoskeletal dynamics reveal a constriction mechanism driving optic cup morphogenesis. eLife. 2016;5:e15797. doi: 10.7554/eLife.15797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bielmeier C., Alt S., Classen A.K. Interface contractility between differently fated cells drives cell elimination and cyst formation. Curr. Biol. 2016;26:563–574. doi: 10.1016/j.cub.2015.12.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Farhadifar R., Röper J.C., Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- 19.Fletcher A.G., Osterfield M., Shvartsman S.Y. Vertex models of epithelial morphogenesis. Biophys. J. 2014;106:2291–2304. doi: 10.1016/j.bpj.2013.11.4498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ishimoto Y., Morishita Y. Bubbly vertex dynamics: a dynamical and geometrical model for epithelial tissues with curved cell shapes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014;90:052711. doi: 10.1103/PhysRevE.90.052711. [DOI] [PubMed] [Google Scholar]
- 21.Xu G.K., Liu Y., Li B. How do changes at the cell level affect the mechanical properties of epithelial monolayers? Soft Matter. 2015;11:8782–8788. doi: 10.1039/c5sm01966d. [DOI] [PubMed] [Google Scholar]
- 22.Okuda S., Inoue Y., Adachi T. Three-dimensional vertex model for simulating multicellular morphogenesis. Biophys Physicobiol. 2015;12:13–20. doi: 10.2142/biophysico.12.0_13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Savin T., Kurpios N.A., Tabin C.J. On the growth and form of the gut. Nature. 2011;476:57–62. doi: 10.1038/nature10277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.He B., Doubrovinski K., Wieschaus E. Apical constriction drives tissue-scale hydrodynamic flow to mediate cell elongation. Nature. 2014;508:392–396. doi: 10.1038/nature13070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gelbart M.A., He B., Kaschube M. Volume conservation principle involved in cell lengthening and nucleus movement during tissue morphogenesis. Proc. Natl. Acad. Sci. USA. 2012;109:19298–19303. doi: 10.1073/pnas.1205258109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Eiraku M., Takata N., Sasai Y. Self-organizing optic-cup morphogenesis in three-dimensional culture. Nature. 2011;472:51–56. doi: 10.1038/nature09941. [DOI] [PubMed] [Google Scholar]
- 27.Martin A.C., Kaschube M., Wieschaus E.F. Pulsed contractions of an actin-myosin network drive apical constriction. Nature. 2009;457:495–499. doi: 10.1038/nature07522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kondo T., Hayashi S. Mechanisms of cell height changes that mediate epithelial invagination. Dev. Growth Differ. 2015;57:313–323. doi: 10.1111/dgd.12224. [DOI] [PubMed] [Google Scholar]
- 29.Mason F.M., Xie S., Martin A.C. RhoA GTPase inhibition organizes contraction during epithelial morphogenesis. J. Cell Biol. 2016;214:603–617. doi: 10.1083/jcb.201603077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schroeder T.E. Neurulation in Xenopus laevis. An analysis and model based upon light and electron microscopy. J. Embryol. Exp. Morphol. 1970;23:427–462. [PubMed] [Google Scholar]
- 31.Suzuki M., Hara Y., Ueno N. MID1 and MID2 are required for Xenopus neural tube closure through the regulation of microtubule organization. Development. 2010;137:2329–2339. doi: 10.1242/dev.048769. [DOI] [PubMed] [Google Scholar]
- 32.Sai X., Ladher R.K. Early steps in inner ear development: induction and morphogenesis of the otic placode. Front. Pharmacol. 2015;6:19. doi: 10.3389/fphar.2015.00019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Morin X., Daneman R., Chia W. A protein trap strategy to detect GFP-tagged proteins expressed from their endogenous loci in Drosophila. Proc. Natl. Acad. Sci. USA. 2001;98:15050–15055. doi: 10.1073/pnas.261408198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Royou A., Sullivan W., Karess R. Cortical recruitment of nonmuscle myosin II in early syncytial Drosophila embryos: its role in nuclear axial expansion and its regulation by Cdc2 activity. J. Cell Biol. 2002;158:127–137. doi: 10.1083/jcb.200203148. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.