Two degrees of freedom quasi-static EMG-force at the wrist using a minimum number of electrodes

Abstract

Surface electromyogram-controlled powered hand/wrist prostheses return partial upper-limb function to limb-absent persons. Typically, one degree of freedom (DoF) is controlled at a time, with mode switching between DoFs. Recent research has explored using large-channel EMG systems to provide simultaneous, independent and proportional (SIP) control of two joints—but such systems are not practical in current commercial prostheses. Thus, we investigated site selection of a minimum number of conventional EMG electrodes in an EMG-force task, targeting four sites for a two DoF controller. In a laboratory experiment with 10 able-bodied subjects and three limb-absent subjects, 16 electrodes were placed about the proximal forearm. Subjects produced 1-DoF and 2-DoF slowly force-varying contractions up to 30% maximum voluntary contraction (MVC). EMG standard deviation was related to forces via regularized regression. Backward stepwise selection was used to retain those progressively fewer electrodes that exhibited minimum error. For 1-DoF models using two retained electrodes (which mimics the current state of the art), subjects had average RMS errors of (depending on the DoF): 7.1–9.5 %MVC for able-bodied and 13.7–17.1 %MVC for limb-absent subjects. For 2-DoF models, subjects using four electrodes had errors on 1-DoF trials of 6.7–8.5 %MVC for able-bodied and 11.9–14.0 %MVC for limb-absent; and errors on 2-DoF trials of 9.9–11.2 %MVC for able-bodied and 15.8–16.7 %MVC for limb-absent subjects. For each model, retaining more electrodes did not statistically improve performance. The able-bodied results suggest that backward selection is a viable method for minimum error selection of as few as four electrode sites for these EMG-force tasks. Performance evaluation in a prosthesis control task is a necessary and logical next step for this site selection method.

1. Introduction

Most upper-limb absence is transradial or more distal (Dillingham et al., 2002). Typical commercial myoelectric hand-wrist prostheses return partial function by using residual forearm muscle surface electromyogram (EMG) signals to control hand closing/opening. Additional degrees of freedom (DoF), e.g. wrist rotation, are not controlled simultaneously; rather, mode switching activates additional DoFs sequentially (Parker et al., 2006). This limitation is problematic (Atkins et al., 1996; Pezzin et al., 2004), as many basic daily tasks require the simultaneous activation and control of two or more joints.

Three notable techniques to provide multi-DoF control have been emerging. First, Kuiken and colleagues (Kuiken et al., 2004; Kuiken et al., 2009) pioneered “targeted muscle reinnervation” surgery in which certain muscles (e.g., pectoralis) or sub-regions within muscles are denervated, and then nerves which formerly innervated absent upper limb muscles are grafted to them. EMGs from the grafted muscles provide simultaneous, independent and proportional (SIP) control. The invasive and costly surgery and long recovery period (3–6 months) likely make this technique most attractive to those with bilateral and proximal limb-absence.

Second, multifunction pattern recognition (recently commercialized (Coapt, Chicago, IL)) uses forearm EMGs to select between a small set of predefined movements (Boostani and Moradi, 2003; Englehart and Hudgins, 2003; Graupe and Cline, 1975; Hudgins et al., 1993; Parker, Englehart, 2006; Powell et al., 2014). All functions are comprised of one DoF of movement at a time—although this degree can be multi-joint.

Third, studies have related forearm surface EMG to multiple DoF finger (Liu et al., 2013; Smith et al., 2009; Smith et al., 2008) and/or hand-wrist (Ameri et al., 2014a; Ameri et al., 2014b; Jiang et al., 2009; Jiang et al., 2012b; Muceli and Farina, 2012; Muceli et al., 2014; Nielsen et al., 2011) forces or kinematics, primarily in able-bodied subjects. Preliminary studies utilized high-density electrode arrays (32–64⁺ channels) (Liu, Brown, 2013; Muceli and Farina, 2012; Muceli, Jiang, 2014) or indwelling electrodes (Kamavuako et al., 2012; Kamavuako et al., 2014; Smith and Hargrove, 2014). These studies demonstrated that intact forearm EMG encodes multiple DoFs of SIP information—but the high-density EMG arrays/indwelling electrodes are not viable in commercial prosthetic systems. Recently, conventional (bipolar) surface EMG systems with as few as 7–8 electrodes have been reported—an electrode quantity that is still high for most practical prosthesis systems. The electrodes are generally equally-spaced about the circumference of the forearm. Jang et al. (Jiang, Englehart, 2009) related eight electrodes to wrist forces of 11 able-bodied subjects, achieving a multivariate R² index of 77.5 ± 10.9% for two DoF tasks utilizing extension-flexion (Ext-Flx) and radial-ulnar deviation (Rad-Uln). Nielson et al. (Nielsen, Holmgaard, 2011) related multiple EMG features from seven electrodes to wrist Ext-Flx with Rad-Uln forces, achieving R² values that exceeded 90% in 10 able-bodied subjects and averaged 72% in their one subject with congenital malformation. Jiang et al. (Jiang, Vest-Nielsen, 2012b) related seven electrodes to the kinematics of all three wrist DoFs. Three amputees with a long residual limb (≥20 cm) achieved a R² performance of 62.5 ± 8.50%, while five able-bodied subjects achieved a R² performance of 72.0 ± 8.29%. Ameri et al. (Ameri, Kamavuako, 2014a) related eight EMG signals to 1- and 2-DoF target displacements. Ten able-bodied subjects achieved average R² values from 82–90% and two limb-deficient subjects from 76–84%, depending on the DoF. Fougner et al. (Fougner et al., 2014) applied only five electrodes over selected anatomical locations, and implemented a form of hybrid control between multi-level control and proportional control. Two able-bodied subjects could actuate a hand, a wrist or simultaneously activate both at a fixed-ratio co-active rate. This approach does not provide independent proportional control, but does provide simultaneous control and represents an improvement step that may be easier for the user to control. Amsuess et al. (Amsuess et al., 2016) used eight electrodes and combined sequential-simultaneous control to improve activity of daily living performance tasks in five able-bodied subjects and two amputees.

Throughout all of this work, many different modeling techniques were evaluated (e.g., regression, regularized regression, neural networks, support vector machines), and studies used a wide selection of force or kinematic trajectories as the model output variable (Ameri et al. (Ameri, Scheme, 2014b) contrasted force vs. kinematic outputs; Jiang, Muceli and colleagues (Jiang et al., 2014; Muceli, Jiang, 2014) developed models requiring minimal supervision). Recent studies have even combined EMG inputs with other modalities, such as kinematic signals (Blana et al., 2016). Most studies found that performance is inversely related to the number of DoFs/classes modeled and positively correlated to the number of EMG channels and the use of nonlinear models.

No study has specifically targeted two DoFs of SIP control from a minimum number of conventional surface electrodes. In particular, if as few as four electrodes could be used to provide 2-DoF control, this number of conventional electrodes is already within the capability of commercial prostheses. Of course, determining the optimal location of a limited number of electrodes a priori is difficult (Cavanaugh et al., 1983) for two DoF control. Hence, our research applied 16 electrodes packed tightly about the circumference of the proximal forearm and then used backward stepwise selection (off-line) to progressively reduce the number of electrodes—removing the least useful electrode at each step. This proximal location was selected since it is applicable to the broadest range of residual forearm lengths. Clinically, we foresee a procedure in which selection of four of 16 electrode sites is determined via our technique during the fitting stage by a prosthetist; then these four sites are fixed into the final prosthesis socket. Herein, we studied 2-DoF combinations of the three possible wrist DoFs: Ext-Flx, Rad-Uln and pronation-supination (Pro-Sup). We did so because the literature is unclear as to which DoF pair is best for prosthesis control in terms of accuracy and intuitiveness. We elicited slowly force/moment-varying contractions (“quasi-static”) for this initial exploration, so as to avoid the additional complexity of dynamical system modeling.

2. Methods

2.1. Experimental apparatus and procedures

Experiments were approved and supervised by the New England IRB (Newton, MA). Each subject provided written informed consent. Ten able-bodied subjects (6 female, 4 male; aged 22–61 years) and three subjects with transradial limb absence and no prior experimental experience (60 year old male, 8 years amputated, uses myocontrolled hand-wrist; 24 year old male, congenital, uses myocontrolled hand; 50 year old male, congenital, uses myocontrolled hand) each successfully completed one experiment lasting 3–4 hours. Data from two additional limb-absent subjects were excluded, one due to unusable MVC values and one due to poor EMG quality.

Able-Bodied Subjects, Setup

Skin about the proximal forearm of the dominant arm was scrubbed vigorously with an alcohol wipe and a bead of electrode gel was applied. Sixteen bipolar EMG electrodes were placed equidistant in a row, transversely about the forearm, each centered 5 cm distal from the crease of the elbow, with one electrode aligned at the most dorsal aspect. Each electrode pair consisted of 5 mm diameter, stainless steel, hemispherical contacts separated 1 cm edge-to-edge, oriented along the forearm’s long axis. The average transverse spacing between bipolar electrodes was 1.6 ± 0.24 cm. A reference electrode was gelled and secured on the ventral forearm, just distal to the row of bipolar electrodes. The EMG signals from each bipolar electrode were cabled to a differential amplifier circuit (Liberating Technologies, Inc. BE328 amplifier; pass band from 30–500 Hz, CMRR > 100 dB over the pass band) and then selectable gain was applied to maximize ADC resolution without signal saturation. The RMS EMG signal level at rest (representing equipment and electrode-skin interface noise plus ambient physiological activity) averaged 7.1 ± 6.4% (median of 3.8%) of the RMS EMG at 50% maximum voluntary contraction (MVC). This rest level is marginally higher than that of our previous laboratory work (Clancy et al., 2005; Clancy and Farry, 2000; Liu et al., 2015), perhaps due to cabling the EMG pre-amplifiers 16 cm from the electrode contacts in a standard “remote” prosthesis configuration (as opposed to using cased electrodes with embedded pre-amplifiers in past work).

Able-bodied subjects sat at the experimental apparatus, as shown in Fig. 1 (top). A thermo-formable plastic hand splint was rigidly attached to a load cell (AMTI, Watertown, MA; model MC3A-100 transducer, Gen 5 signal conditioner). The metacarpal region of the dominant hand was tightly secured to the hand splint using Velcro straps, while leaving the phalanges free. The palm of the hand was perpendicular with the plane of the floor, the hand was in a neutral position with respect to the wrist, the forearm was parallel to the plane of the floor and the shoulder was flexed 45° forward from the anatomical position along the sagittal plane. The elbow was supported just distal to the olecranon process. The load cell measured three DoFs, which were displayed on a computer screen in front of the subject via an arrowhead in which wrist Ext-Flx force specified its x-axis location, Rad-Uln force its y-axis location and Pro-Sup moment its rotation. A second computer-generated target arrowhead could also be displayed. The three load cell signals and the 16 EMG channels were each sampled at 2048 Hz with 16-bit resolution.

Fig. 1.

Experimental apparatus. Dominant/able hand was tightly secured via thermo-formable plastic and Velcro to six-axis load cell. Sixteen electrodes (not visible) were secured about the proximal aspect of the dominant/limb-absent forearm. Top: Able-bodied configuration. Wrist was maintained in a neutral position by a padded restraint. Bottom: Limb-absent configuration. Mirrored display screen at right.

Able-Bodied Subjects, Contractions

Contractions were constant-posture about the wrist. Subjects were instructed to relax all muscles not involved in the task (including their phalanges). Trials were conducted at an interval of at least two minutes, to avoid accumulated fatigue. Subjects were released from the hand cuff for rest between experiment stages. Initially, subjects practiced the contraction tasks for 10–20 minutes to become familiar with the apparatus and experimental protocol. Next, subjects performed MVCs in each of wrist extension, flexion, radial deviation, ulnar deviation, pronation and supination. Subjects increased force to their maximum over 2–3 s, then maintained maximum for 5 s. Verbal encouragement was provided. The average load cell value during the contraction plateau was the MVC.

One-DoF quasi-static trials were then conducted separately for each DoF (Fig. 2). These trials were intended to assess the existing state of the art in proportional control, as well as to provide insight into the ability of subjects to control independent DoFs. For Ext-Flx, subjects followed the target arrowhead as it took 30 s to linearly ramp from zero force, to Peak force level in flexion, to Peak force level in extension, back to Peak force level in flexion and then back to zero force. This Peak force, in N, equaled half the 30 %MVC Ext-Flx force range: Peak = (|30 %MVC Flx| + |30 %MVC Ext|)/2. This trajectory provided a consistent, subject-scaled force range and a constant rate of change of force (within subject) in physical units. The subject-controlled arrowhead was only permitted to move along the active DoF, to avoid distraction from unused DoFs. Analogous ramp trajectories were used for Rad-Uln and Pro-Sup trials, four trials per DoF (12 trials total, block randomized by DoF).

Fig. 2.

Example time-series plots of 1-degree-of-freedom models, able-bodied subject. Solid lines are actual forces/moment, dashed lines are estimated using two EMG channels.

Next, 2-DoF quasi-static ramp trials were conducted (Fig. 4). Two DoFs were active and their target effort levels were coincident. Thus, both active DoFs had their effort levels rise and fall simultaneously. The same “quasi-static” 30 s ramp trajectory was used. Two sets of six (block randomized) trials were conducted (12 trials total), the trials being identified by the contraction directions associated with the first effort direction during the ramp (Flx coincident with Uln, Flx with Rad, Flx with Pro, Flx with Sup, Uln with Pro, Uln with Sup). The subject-controlled arrowhead was only permitted to move/rotate along the two active DoFs.

Fig. 4.

Example time-series plots of 2-degree-of-freedom models applied to co-contraction trials from able-bodied subject. Key: solid lines=actual forces, dashed=estimated using four EMG channels; blue=Ext-Flx, red=Rad-Uln. Positive %MVC corresponds to Ext-Rad. Four EMG channels and training from both 1- and 2-DoF trials.

Limb-Absent Subjects

The same general procedure was used, with a few differences. For warm-up, subjects practiced mirrored movements for the three DoFs using a mirror box (Mirror Box Therapy, Stockport, England; Hand/Wrist model) prior to more extensive practice of constant-posture tasks in the experimental apparatus. Their sound-side wrist was secured to the load cell that was re-positioned such that their elbow angle was reduced to 100° (Fig. 1, bottom). A cupped support contacted the proximal edge of the olecranon process and distal portion of the upper arm, securing the upper arm via taught-fitting Velcro. This posture facilitated bilateral symmetry, since the arm on their limb-absent side was similarly supported and secured, and the 16 electrodes placed on this forearm. Limb-absent subjects completed mirrored contractions, using forces/moment on their sound side for feedback (Ameri, Scheme, 2014b; Clancy et al., 2015; Hahne et al., 2014; Jiang, Vest-Nielsen, 2012b; Muceli and Farina, 2012; Nielsen, Holmgaard, 2011). Additionally, a mirrored screen display showed two graphs, one showing the subject-controlled and target arrowheads for the sound side, and a second which mirrored this display for the limb-absent side. Subjects were instructed to use the muscles in the forearm on their limb-absent side to mirror the forces/moment actually generated on their sound side. EMG from their limb-absent side was related to forces generated on their sound side.

2.2. Methods of analysis

Pre-Processing

Analysis was performed offline in MATLAB (The MathWorks, Inc., Natick, MA) and used causal processing, appropriate for future real-time implementation. Each EMG channel was highpass filtered (fifth-order Butterworth, cut-off at 15 Hz) and notch filtered at the power line frequency (second-order IIR filter at 60 Hz, notch bandwidth of 1 Hz). The narrow notch bandwidth greatly attenuated power line interference, with limited loss of signal power. An estimate of EMG standard deviation (EMGσ) was formed as the mean absolute value of the notched signal followed by decimation to 4.096 Hz. Decimation, (MATLAB “decimate” function) incorporated lowpass filtering at 1.6 Hz (Chebyshev Type 1 filter, ninth-order, 0.05 dB peak-to-peak passband ripple). This lowpass filter served the same function as a smoothing window. Ext-Flx force was normalized to the Ext-Flx MVC ranges. Rad-Uln force and Pro-Sup moment were similarly normalized. Each force/moment signal was then decimated to 4.096 Hz. Thus, the complete input-output data set for EMG-force modeling was sampled at 4.096 Hz—approximately ten times the bandwidth of the output force/moment signal (which is preferred for system identification (Clancy et al., 2006; Ljung, 1999)).

One-DoF Models

For comparison to existing prosthesis control, 1-DoF linear models were fit for each subject, using the 1-DoF trials. For Ext-Flx, EMGσs were least squares fit to Ext-Flx force (the remaining force and moment were ignored), initially using all 16 electrodes. Dynamics were not included in the model due to the slow rate of change of forces. The pseudo-inverse technique was used to regularize the least squares fit, in which singular values were removed if the ratio of that singular value to the largest singular value in the design matrix was less than a tolerance value. Via preliminary analysis, a tolerance value of 0.01 was selected, consistent with prior work (Clancy et al., 2012; Press et al., 1994). Two 1-DoF trials for Ext-Flx were used for model training, with training performance taken as the RMS error between the known force and the EMG-estimated force, averaged across these two training trials. This error was expressed in %MVC. Previous research has shown lower test error when combining multiple training trials into one longer training set (Clancy, Liu, 2012). Backward stepwise selection was then used to progressively reduce the number of EMG channels (i.e., leaving out the channel whose absence resulted in the lowest error), making all decisions only on the training data. In this manner, the complete training operation—including electrode selection—is conducted with the training data. The two remaining 1-DoF trials were used for testing at each step (normalized RMS error, average of the two trials). The entire process was repeated after switching training and testing data, with the average RMS error from this two-fold cross validation used as the overall error. Note that the four remaining cross validation folds would necessarily yield correlated models (which are less statistically efficient), thus this two-fold cross validation was selected for computational efficiency in lieu of exhaustive cross validation. For comparison, a selection of summary results was also reported for able-bodied subjects (the sample size for limb-absent subjects was deemed too small for a robust comparison) using the multivariate R² index (Jiang, Englehart, 2009), limiting per-assessment worst-case error to R² ≥ 0 to express error as a percent of total signal variance of the known force. The analogous process was used for 1-DoF models relating EMG to Rad-Uln force and Pro-Sup moment.

Two-DoF Models

Next, 2-DoF linear models were fit. The EMG-force model and backward stepwise selection were applied identically, except that the model always simultaneously estimated two mechanical DoFs (the third, unused force/moment was ignored). Each model fit produced two sets of coefficients, one per DoF. The model training data either consisted of two 1-DoF trials from each of the two DoFs (representing the simplest method by which a prosthesis controller might be trained), or two 2-DoF trials from each of the two DoF pairs, or both of these trial groupings (representing the most exhaustive method by which a prosthesis controller might be trained). During backward selection, RMS error was assessed on the training data (both DoFs). For testing, RMS error was assessed on the remaining trials, separately for 1-DoF trials (four trials) and 2-DoF trials (four trials). In either case, error was always assessed across the two available DoFs. (When assessing 1-DoF trials for these 2-DoF models, the second mechanical dimension would be expected to remain near a zero value throughout the trial.) The 1-DoF assessments were useful to compare vs. typical prostheses, which only control 1-DoF at a time; and to assess the degree to which independent control had been achieved. Ideally, the implementation of 2-DoF control would supplement and not serve as a detriment to 1-DoF tasks. The trial data were switched and the overall error assigned as the average of the two-fold cross validation. Again, a selection of summary results was also reported for able-bodied subjects using the multivariate R² index.

Statistics

Primary statistical evaluation used multivariate ANOVA, with post hoc pair-wise comparisons conducted using Tukey’s honestly significant difference test (which adjusts for multiple comparisons). A significance level of p = 0.05 was used.

3. Results

Our analysis and models evaluated three 1-DoF contractions (Ext-Flx, Rad-Uln, Pro-Sup), their three 2-DoF co-contraction combinations (with different training conditions) and the number of electrodes used (1–16). Results are reported separately for able-bodied and amputee subjects.

3.1. One-DoF models, able-bodied subjects

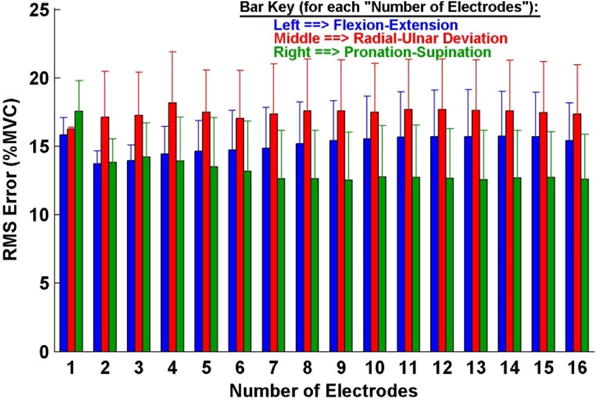
Fig. 2 shows sample time-series EMG-force test results for the 1-DoF models (i.e., separate models formed for each DoF from trials that only excited each respective DoF) for an able-bodied subject. Table 1 (left-most three result columns) and Fig. 3 show summary RMS error results. A two-way ANOVA was computed (factors: DoF and number of electrodes). Both main effects were significant (p<10⁻⁶), with no interaction. Tukey post hoc comparisons found that Pro-Sup errors were significantly higher than the other two DoFs (p<0.01), and that the only statistical differences between number of channels was when comparing one channel (highest error) to each other number of channels (p<10⁻⁶ for each pair). In addition, Table 1 (row 1) shows these RMS errors for two electrodes—typical in a commercial 1-DoF prosthesis controller. Two-channel results for 1-DoF represent the state-of-the art for this contraction task. The rightmost three columns of Table 1, for comparison, show the R² index values corresponding to the RMS errors.

Table 1.

Mean ± std. dev. RMS errors (%MVC, left) and corresponding R² index (right), ten able-bodied subjects.

Condition	DoF(s), RMS Errors (%MVC)			DoFs, R2 Errors (%)
1-DoF Models (2 electrodes)	Ext-Flx	Rad-Uln	Pro-Sup	Ext-Flx	Rad-Uln	Pro-Sup
Assessed on 1-DoF trials	7.3 ± 2.4	7.1 ± 1.8	9.5 ± 3.6	79 ± 13	80 ± 11	64 ± 23
2-DoF Models (4 electrodes)	Ext-Flx & Rad-Uln	Ext-Flx & Pro-Sup	Rad-Uln & Pro-Sup	Ext-Flx & Rad-Uln	Ext-Flx & Pro-Sup	Rad-Uln & Pro-Sup
Assessed on 1-DoF trials:
Train with 1-DoF trials	6.7 ± 2.0	8.5 ± 2.2	7.4 ± 1.5	68 ± 17	57 ± 16	61 ± 14
Train with 2- DoF trials	12.5 ± 5.2	14.0 ± 2.7	11.0 ± 1.0	36 ± 22	23 ± 13	28 ± 7
Train with 1-, 2- DoF trials	7.1 ± 2.0	8.8 ± 2.0	7.6 ± 1.4	65 ± 17	54 ± 16	60 ± 12
Assessed on 2-DoF trials:
Train with 1-DoF trials	13.1 ± 5.4	15.5 ± 4.0	15.7 ± 7.2	46 ± 26	37 ± 15	36 ± 23
Train with 2-DoF trials	11.7 ± 5.4	11.3 ± 3.0	10.6 ± 2.1	59 ± 20	55 ± 19	57 ± 15
Train with 1-, 2-DoF trials	9.9 ± 2.9	10.5 ± 1.6	11.2 ± 2.1	64 ± 18	59 ± 14	52 ± 16

Fig. 3.

Summary results: 1-degree-of-freedom models, ten able-bodied subjects. Error lines show one standard deviation above the mean.

3.2 Two-DoF models, able-bodied subjects

Two-DoF models always estimated both DoFs simultaneously. Fig. 4 shows sample time-series EMG-force test results during 2-DoF (co-contraction) trials from an able-bodied subject. Table 1 (left) and Fig. 5 show summary RMS error results. For comparison, Table 1 (right) also shows the corresponding R² index values.

Fig. 5.

Summary results: 2-degree-of-freedom (DoF) models, ten able-bodied subjects, training from both 1- and 2-DoF models. Top: tested on 1-DoF trials. Bottom: tested on 2-DoF trials. Error lines show one standard deviation above the mean.

For 2-DOF model errors assessed on the 1-DoF trials, a three-way ANOVA (factors: DoF, number of electrodes and training condition—either 1-DoF trials, 2-DoF trials or both) found that training condition interacted with number of electrodes. Thus, separate two-way ANOVAs were computed with each of the training conditions fixed. Results when training with 2-DoF trials were inconclusive, due to interaction. Results when training with 1-DoF trials or both (Fig. 5, top) were similar. Both main factors (DoF and number of electrodes) were significant (p<10⁻⁶), without interaction. Tukey post hoc analysis of DoF found Ext-Flx with Pro-Sup to have higher errors than either of the other two DoF combinations (p<10⁻⁶). For number of electrodes, one electrode always exhibited higher error than more than one (p<10⁻⁶); and two electrodes exhibited higher error than either three or more (when training with 1-DoF trials, p<0.02), or four or more (when training with 1- and 2-DoF trials, p<0.002) electrodes. Thus, performance improved as the selected number of channels increased from one channel, with performance stabilizing (statistically) at 3–4 channels. In addition, Table 1 (row 2) shows these RMS errors for four electrodes (the goal minimum number of electrodes for a commercial 2-DoF prosthesis controller). Lastly, we also computed a two-way ANOVA with number of electrodes fixed at the preferred value of four. Both main factors (DoF, training condition) were significant (p≤0.01), without interaction. Tukey post hoc analysis found Ext-Flx with Pro-Sup DoF to have higher errors than either of the other two DoF combinations (p≤0.03) and training with only 2-DoF trials to have higher errors than either of the other two training conditions (p<10⁻⁶).

Additional results for 2-DoF models assessed on 1-DoF trials are shown in Table 2. The RMS error was computed separately for the “active” DoF (the DoF performing the tracking task) and for the “inactive” DoF (the DoF that was inactive with no feedback provided, but still recorded). Results focus on training with both 1- and 2-DoF trials and selecting four electrodes. Results of paired t-tests, with Bonferroni correction, between each of the active-inactive combinations are shown. The active DoF always had equal or higher RMS error. This result needs to be interpreted cautiously, since the range of forces was much greater for the active DoF (forces ramping to 30 %MVC) than the inactive DoF (forces near zero). Said another way, the two DoFs experienced distinct tasks. As further described in the Discussion section, direct comparison of distinct tasks using RMS error (or R² index values) is difficult and must be done with care. In our task set, if equivalent objective error performance existed in the active and inactive DoFs, larger RMS errors would be expected for the active DoF since its range of forces is much larger. But, the performance differences necessary to demonstrate independent control in a future prosthesis controller is not known.

Table 2.

Test errors (%MVC) from 2-DoF models assessed on the active and inactive DoFs in 1-DoF trials. Training from both 1- and 2-DoF trials for ten able-bodied subjects using four electrodes; ten subjects × four trials per cell. Asterisk denotes statistical significance (p<0.001) between active and inactive error pairs.

		DoF “A” is Active			DoF “B” is Active
DoF “A”	DoF “B”	DoF “A” Error		DoF “B” Error	DoF “A” Error		DoF “B” Error
Ext-Flx	Rad-Uln	7.9 ± 4.2		6.3 ± 2.6	5.8 ± 3.4		7.4 ± 2.1
Ext-Flx	Pro-Sup	8.7 ± 4.0		8.3 ± 3.5	6.3 ± 2.9	*	10.6 ± 3.3
Rad-Uln	Pro-Sup	8.0 ± 2.4	*	5.9 ± 1.9	6.2 ± 1.8	*	9.2 ± 3.6

For 2-DoF model errors assessed on the 2-DoF trials, a three-way ANOVA (factors: DoF, number of electrodes and training condition) found that training condition interacted with DoF and number of electrodes. Thus, separate two-way ANOVAs were computed with each of the training conditions fixed. Results found no interactions. When training with 1-DoF trials, only the main effect of DoF was significant, with Tukey post hoc analysis finding Ext-Flx with Rad-Uln to have lower errors than either of the other two DoF combinations (p<10⁻³). When training with either 2-DoF trials or both 1- and 2-DoF trials (Fig. 5, bottom), only the main effect of number of electrodes was significant. In both ANOVAs, Tukey post hoc analysis found that selection down to one electrode gave higher error than three or more electrodes (p<10⁻⁵) and selection down to two electrodes gave higher error than six or more electrodes (p≤0.03). Errors when selecting down to three electrodes did not differ from when selecting four or more electrodes. In addition, Table 1 (rows 3–4) shows these RMS errors for four electrodes. Overall, performance improved when increasing from one electrode to approximately 3–6. Lastly we also computed a two-way ANOVA with number of electrodes fixed at the preferred value of four (factors: DoF and training condition). Only the main effect of training condition was significant (p<10⁻³), without interaction. Tukey post hoc analysis found that training with only 1-DoF trials had higher errors than either of the other two training conditions (p<0.004).

3.3. Electrodes selected, able-bodied subjects

It is also useful to summarize the extent to which the algorithm is selecting electrodes from diverse locations about the forearm. For 1-DoF models with two electrodes, there are two distances between the selected electrodes, measured in number of interposing electrodes. The average interposing distance must equal 8 electrodes (out of 16 total). The left plot of Fig. 6 shows the distribution of the minimum interposing distances, aggregating the separate results from electrode selection from the three DoFs, two cross validations and ten subjects. The mean ± std. dev. distance was 31 ± 14% of forearm circumference. For 2-DoF models, we considered the case of training with both 1- and 2-DoF trials and selection to four electrodes. Thus, there are four interposing distances whose average must equal 4 electrodes. The right plot of Fig. 6 shows the distribution from each such interposing distance, aggregating the separate results from electrode selection from the three DoFs, two cross validations and ten subjects. The mean ± std. dev. distance was 25 ± 14% of forearm circumference. Note that when an interposing space of, for example, 11 electrodes is found, the remaining three interposing spaces from that model must be small, such that the sum of the four interposing spaces from that model equals 16. Overall, the selected electrodes tended not to be adjacent, but were also not necessarily equally-spaced about the forearm.

Fig. 6.

Distribution of interposing distances, all degrees-of-freedom (DoFs). Left shows proportion of minimum distances for the 1-DoF models using two electrodes. Right shows the proportion of each of the four interposing distances for the 2-DoF models, trained using both 1- and 2-DoF trials, using four electrodes. Total of 16 electrodes/subject.

A more detailed presentation of electrode site selection for each subject is shown in Fig. 7 for 2-DoF, four-channel models, trained using both 1- and 2-DoF trials, for Ext-Flx & Rad-Uln. Corresponding plots for the other two DoF pairs are provided in the online “Supplementary Data” provided by the publisher of this article. Fig. 7 shows, for each subject, the order in which electrodes were eliminated, as well as the final four retained electrodes. This information is provided for the two distinct training folds used in our cross validation approach. Overall, the selected sites were spread rather evenly around the circumference of the forearm. Comparing the four selected sites between the two (cross validated) training sets, on average 2.2 ± 0.92 sites were identically selected by both cross validation folds, 3.0 ± 0.94 selected sites were within one electrode distance of each other, and 3.7 ± 0.48 of the four selected sites were within two electrode distances of each other. Hence, there was a modest amount of consistency between selected electrodes when comparing between training sets.

Fig. 7.

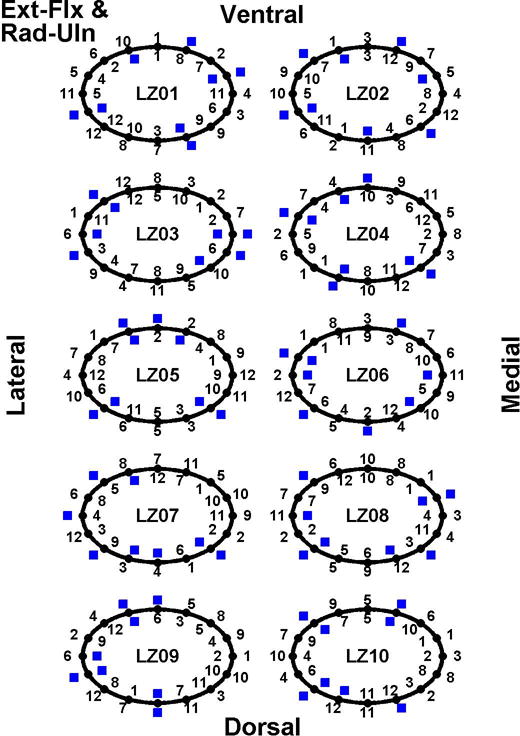
Electrodes selected for 2-DoF, four-channel models, trained using both 1- and 2-DoF trials, for Ext-Flx & Rad-Uln. Results shown for each able-bodied subject, with subject code shown at the center of each result “circle.” Numbers along circle exteriors list the order of electrode elimination for the first cross validation set (e.g., “1” corresponds to first electrode eliminated); while numbers along circle interiors list elimination order for the second cross validation set. Twelve of 16 electrode sites were eliminated for each model. Number locations correspond to electrode locations, as labeled (i.e., lateral, medial, dorsal, ventral forearm). Blue boxes denote the four selected electrodes.

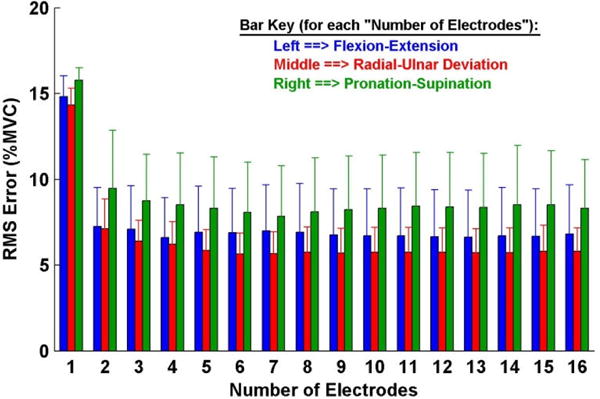
3.4. One-DoF models, limb-absent subjects

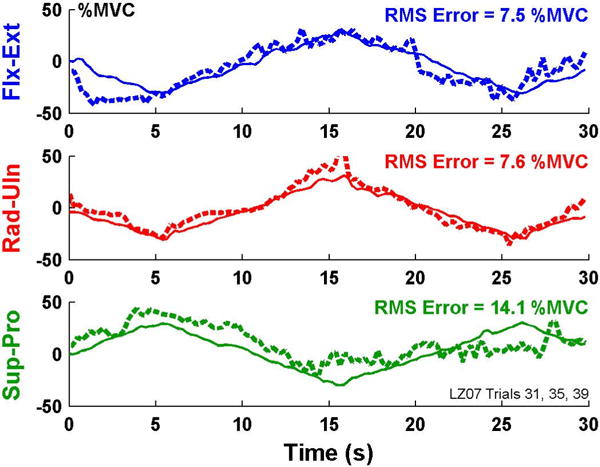
Fig. 8 shows sample time-series EMG-force test results for the 1-DoF models (i.e., separate models formed for each DoF from trials that only excited each respective DoF) from a limb-absent subject. Fig. 9 shows summary results. Table 3 shows RMS error for 1-DoF models using two electrodes. All of the errors were large compared to those of the able-bodied subjects. A two-way ANOVA (factors: DoF and number of electrodes) found the main effect of DoF was significant (p <10⁻⁶), with no interaction. Tukey post hoc analysis found Rad-Uln to have higher error then either of Ext-Flx or Pro-Sup (p<0.02).

Fig. 8.

Example time-series plots of 1-degree-of-freedom models, limb-absent subject. Solid lines are actual forces/moment from sound side, dashed lines are estimated using two EMG channels of limb-absent side.

Fig. 9.

Summary results: 1-degree-of-freedom models, three limb-absent subjects. Error lines show one standard deviation above the mean. Note y-axis scale differs from that of other bar plot result figures.

Table 3.

Mean ± std. dev. RMS errors (%MVC), three limb-absent subjects.

Condition	DoF(s)
1-DoF Models (2 electrodes)	Ext-Flx	Rad-Uln	Pro-Sup
Assessed on 1-DoF trials	13.7 ± 1.2	17.1 ± 4.1	13.8 ± 2.1
2-DoF Models (4 electrodes)	Ext-Flx & Rad-Uln	Ext-Flx & Pro-Sup	Rad-Uln & Pro-Sup
Assessed on 1-DoF trials:
Train with 1-DoF trials	11.9 ± 1.3	14.0 ± 2.7	12.5 ± 2.5
Train with 2- DoF trials	38.4 ± 7.2	35.9 ± 18.6	19.5 ± 3.4
Train with 1-, 2- DoF trials	12.3 ± 1.4	13.9 ± 2.4	11.9 ± 2.1
Assessed on 2-DoF trials:
Train with 1-DoF trials	20.2 ± 2.5	21.0 ± 5.4	17.9 ± 3.9
Train with 2-DoF trials	24.2 ± 2.2	20.0 ± 3.2	16.6 ± 1.8
Train with 1-, 2-DoF trials	16.3 ± 1.0	16.7 ± 2.8	15.8 ± 0.4

3.5. Two-DoF models, limb-absent subjects

Fig. 10 shows sample time-series test results of simultaneous EMG-based estimation of Ext-Flx forces with Pro-Sup moments during 2-DoF (co-contraction) trials from a limb-absent subject. Table 3 and Fig. 11 show summary results. All errors were large when compared to the able-bodied subjects.

Fig. 10.

Example time-series plots of 2-degree-of-freedom (DoF) models applied to co-contraction trials from limb-absent subject. Key: solid lines=actual forces from sound side, dashed=estimated from four EMG channels of limb-absent side; blue=Ext-Flx, green=Pro-Sup. Positive %MVC corresponds to Ext/Pro. Four EMG channels, training from both 1- and 2-DoF trials.

Fig. 11.

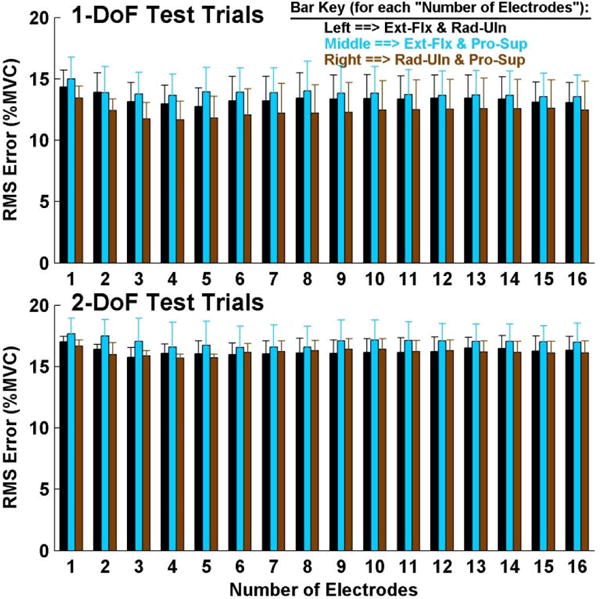
Summary results: 2-degree-of-freedom models, three limb-absent subjects, training from both 1- and 2-DoF trials. Top: tested on 1-DoF trials. Bottom: tested on 2-DoF trials. Error lines show one standard deviation above the mean.

For 2-DoF model errors assessed with the 1-DoF trials, a three-way ANOVA (factors: DoF, number of electrodes and training condition) found that training condition interacted with DoF and number of electrodes. Thus, separate two-way ANOVAs were computed with each of the training conditions fixed. These three ANOVAs each found a significant difference only for the main effect of DoF (p<0.01), without interactions. Tukey post hoc analysis found Ext-Flx with Pro-Sup to have higher errors than either of the other two DoF combinations when training with 1-DoF, or 1- and 2-DoF trials (p<0.03; Fig. 11, top); and for Rad-Uln with Pro-Sup to have lower errors than either of the other two DoF combinations when training with 2-DoF trials (p<0.03) Lastly, we also computed a two-way ANOVA with number of electrodes fixed at the preferred value of four (factors: DoF and training condition). This comparison was only significant for training condition (p<10⁻⁶), with no interaction. Tukey post hoc analysis showed that training with only the 2-DoF trials had higher error than both of the other training conditions (p<10⁻⁴).

For 2-DoF model errors assessed with the 2-DoF trials, a three-way ANOVA (factors: DoF, number of electrodes and training condition) found an interaction between DoF and training condition. Thus, separate two-way ANOVAs were computed with each of the training conditions fixed. None found interactions. When training with 1-DoF trials, no main effects were found. When training with 2-DoF trials, the main effect of DoF was significant (p<10⁻⁶); and Tukey post hoc analysis found Ext-Flx with Rad-Uln to have higher errors than either of the other two DoF combinations (p<10⁻⁶). When training with 1- and 2-DoF trials (Fig. 11, bottom), the main effect of DoF was significant (p=0.01); and Tukey post hoc analysis found Ext-Flx with Pro-Sup to have higher errors than Rad-Uln with Pro-Sup (p=0.01). Lastly we also computed a two-way ANOVA with number of electrodes fixed at the preferred value of four (factors: DoF and training condition). Only the main effect of training condition was significant (p=0.02), without interaction. Tukey post hoc analysis found that training with only 2-DoF trials had higher error than training with both 1- and 2-DoF trials (p=0.02)

3.6. Electrodes selected, limb-absent subjects

Due to the small sample size, only summary interposing distance results are presented. Methods identical to those for the able-subjects were used to produce these results. Distribution plots were not developed, since the samples size is much smaller for limb-absent subjects. For 1-DoF models with two electrodes, the mean ± std. dev. of the minimum distances between selected electrodes was 28 ± 14% of forearm circumference. For 2-DoF models, trained with both 1- and 2-DoF trials and selection to four electrodes, the mean ± std. dev. of each distance was 25 ± 15% of forearm circumference. These results are similar to those of the able-bodied subjects.

4. Discussion

4.1. Able-bodied RMS error results

An existing prosthesis control strategy is the use of two electrodes to provide proportional control of one DoF. When our 1-DoF tasks were used to produce 1-DoF models, Table 1 shows average EMG-force RMS errors for able-bodied subjects of 7.1–9.5 %MVC, depending on the DoF. Our interest was in electrode site selection of EMG-based controllers using as few as four electrodes that could perform comparably in two DoFs. The second row of Table 1 shows that SIP estimation of two DoFs assessed with the same 1-DoF tasks exhibited average RMS errors between 6.7–8.5 %MVC, depending on the DoFs. (Ideally, we desire that 2-DoF control retains low error even when operated on only 1-DoF tasks.) Direct comparison of these RMS values is not appropriate—during 1-DoF tasks, our 2-DoF models simultaneously assess errors in both DoFs, however only one DoF is active while the second DoF has forces near zero. Nonetheless, low errors were achieved in the 2-DoF models with four electrodes; additional electrodes provided no statistically significant advantage. Table 2 shows a more detailed error assessment of the active vs. inactive DoFs, when models were trained from both 1- and 2-DoFs and four electrodes were selected. The active DoF had equal or higher error—consistent with the fact that the active DoF utilized a wider range of forces (ramp to 30 %MVC) than the inactive DoF (forces near zero). This trend is consistent with expectation, but absolute levels of “acceptable” performance that might facilitate independent control in a prosthesis-related application are difficult to infer. It is, nonetheless, encouraging that errors from our 2-DoF models assessed on 1-DoF tasks are competitive with errors from our 1-DoF models assessed on 1-DoF tasks—these 1-DoF models represent the current state of the art in 1-DoF prosthesis control.

When a 2-DoF task was used for assessment, the errors grew. This increase is again consistent with an increase in the average effort level—both DoFs were active. Four-channel versions of these 2-DoF models performed poorest when trained from only 1-DoF trials (bottom row of Table 1). This result is unfortunate, as training from 1-DoF trials would be simpler. Lower errors when including 2-DoF trials may be due to the wider range of the model space explored, or simply due to the noise averaging effect of a larger training set when using both 1- and 2-DoF trials (Clancy, Liu, 2012). These overall results are consistent with much of the developing EMG-force research related to the wrist, extending acceptable 2-DoF performance to a minimum number of electrodes (e.g., four). In particular, for 1-DoF models (Fig. 3), the able-bodied results show that using two electrodes sited via backward stepwise selection is significantly better than one, and additional electrodes beyond two provide limited benefit. For 2-DoF models (Fig. 5), errors generally decreased progressively as the number of selected electrodes increased from one to four, with little additional improvement thereafter. Of the three possible DoF combinations that could be utilized for control, our results suggested some (limited) preference for Ext-Flx paired with Rad-Uln and against Ext-Flx paired with Pro-Sup.

4.2. Comparison of RMS errors to R² errors and prior literature, able-bodied subjects

Table 1, which lists summary error results of both RMS and R² index errors at preferred numbers of electrodes, shows that the relative changes in error values for each metric are very similar within each of the three tasks (1-DoF models, 2-DoF models assessed on 1-DoF trials and 2-DoF models assessed on 2-DoF trials). Some of our prior work relating biceps-triceps EMG to elbow torque (Clancy, Bida, 2006) provides additional comparison of %MVC error vs. variance accounted for (VAF)—a metric similar to R² index; these results also show a very tight relative correspondence between these metrics. Hence, these metrics seem to be tracking relative error within a task in a very similar manner, albeit on distinct scales. Error measures based on %MVC error are common in much of the EMG-force literature (Dai et al., in press; Hashemi et al., 2015; Staudenmann et al., 2006); although correlation-based metrics (such as the R² index) have also been used (Kearney et al., 1997), particularly recently within the context of EMG-based prosthesis control (Ameri, Kamavuako, 2014a; Jiang, Englehart, 2009; Jiang, Vest-Nielsen, 2012b; Nielsen, Holmgaard, 2011).

There are, however, differences between the measures when comparing across tasks. For example, Table 1 lists identical average RMS errors of 7.1 %MVC for Rad-Uln 1-DoF models and Ext-Flx & Rad-Uln 2-DoF models assessed on 1-DoF trials; however, the respective average R² values vary considerably as 0.80 and 0.65. The “better” measure of performance is unclear, as there are strengths and weaknesses to each. RMS error metrics are based on physical units (often normalized to maximum strength), which can be directly understandable and more easily related to physical systems and their interaction with physical devices. For example, an error of 1 %MVC is intuitively small while an error of 50 %MVC is large, for most tasks. But, tasks which exhibit higher average effort levels are biased towards higher errors. Correlation-based metrics normalize the error based on the variance of the known force, which has some ability to normalize across effort levels. But, Altman and Bland (Altman and Bland, 1983; Bland and Altman, 1986) have shown that correlation-based error metrics can be biased towards higher (i.e., better) values if the range of measures is large. They showed, for example, that a few large force contractions combined with a corpus of medium/low force contractions can inflate correlation-based error values. Most importantly, each error metric is clearly a function of the contraction task. Hence, relative comparison of either error metric is quite useful within a task, but always difficult to interpret across tasks or across metrics.

Compared to the prior 2-DoF EMG-force studies cited above, our R² measures in Table 1 (best average performance of 64% on 2-DoF Ext-Flx & Rad-Uln) are noticeably poorer than those found in the literature by 10–20 percentage values. These differences could reflect actual performance, perhaps due to differences in methods, electrode type and placement details, etc. For example, some of the prior studies used non-linear EMG-force relationships, which commonly were more accurate compared to linear relationships (Clancy and Hogan, 1997; Clancy, Liu, 2012; Dai, Bardizbanian, in press; Hashemi et al., 2012; Nielsen, Holmgaard, 2011; Vredenbregt and Rau, 1973). We chose not to utilize non-linear models, because quasi-static contractions at/below 30% MVC tend not to elicit much nonlinearity in the EMG-force relationship (Clancy and Hogan, 1997; Vredenbregt and Rau, 1973). Further, any small improvement in EMG-force performance provided would not necessarily transfer to improved prosthesis control (c.f. (Jiang et al., 2012a; Ortiz-Catalan et al., 2015)).

More likely, the observed R² differences are due to differences in the contraction profiles studied. Several of the prior studies used sinusoidal force contractions at a frequency of 0.5–1 Hz. Thus, we simulated a 1-DoF, 0.5 Hz sinusoid in MATLAB, treating this signal as the “known” force. We then added noise (uncorrelated, Gaussian) with a standard deviation equal to 30% of the force value at each sample, and treated this signal as the estimated force. The R² index comparing them was 91%. (The R² value was not a function of the sine wave amplitude.) We then simulated a ramp contraction extending to a normalize 30% MVC (similar to our study), with the same noise model forming the estimated force. The R² index for the ramp protocol was the considerably lower value of 64%—just as we found lower R² values (compared to the sinusoid contractions found in the literature) in our experimental results. The actual performances in these distinct simulation trials was objectively the same (the errors were each due to additive noise, whose sample-by-sample intensity was identically scaled by the known force), but the R² index values were noticeably different. This simple example helps to demonstrate the difficulty in absolute comparison of error metrics across distinct contraction tasks. Nonetheless, we conclude that our 2-DoF wrist EMG-force methods seem competitive with those previously described in the literature—even when utilizing as few as four backward selected electrodes—if we take into account the expected performance differences between our ramp task vs. the sinusoidal tasks found in the previous literature.

It may well be the case that either error metric is entirely acceptable. Each method, in and of itself, is not directly indicative of acceptable or intuitive performance of these algorithms within an EMG-controlled prosthesis—nor are they intended to be. Rather, they are intended largely as a development tool to refine algorithms and help in decisions to discard unworthy candidate methods for future testing within a prosthesis. In this regard, the common relative performance of each metric serves the same assessment purpose. Of course, these EMG-force algorithms have impact beyond prosthesis control, for example in biomechanical or ergonomic assessment of wrist forces. Nonetheless, such applications also likely benefit from either error metric.

4.3. Limb-absent results

As found in prior studies (Ameri, Kamavuako, 2014a; Jiang, Vest-Nielsen, 2012b; Nielsen, Holmgaard, 2011), force estimation errors for the limb-absent subjects were universally much higher than those from the able-bodied subjects. However, our average errors above 15 %MVC are particularly problematic, as they are more than half the experimental force range. Such errors suggest quite poor EMG-force performance. Further, increasing the number of electrodes did not statistically improve performance. For 1-DoF models, Rad-Uln and Ext-Flx results in Fig. 9 even suggest that higher numbers of electrodes might have led to a statistically significant increase in error, if sufficient statistical power existed. Such contrary results could exist since models with higher numbers of electrodes require retaining electrodes in the model’s training set, even if their corresponding EMG signals have no useful relation to the output forces. (Such a situation is not uncommon due to the altered anatomy of limb-absent subjects.) Once retained, results from the independent test trials (shown in Fig. 9) would demonstrate the poor performance of such models. Nonetheless, the totality of the limb-absent resents, combined with our own anecdotal observations during the experiments, suggest that these subjects may have had great difficulty in their target tracking. Each of our subjects was new to lab-based EMG-force experimentation (thus, had no prior experience with 2-DoF experimental contractions), limited practice was made available in our single-session study and two of our subjects had congenital limb absence (a condition in which phantom limb sensation may be limited, thus impairing the mirrored-contraction protocol). Hence, significant subject training may need to be included in future work with limb-absent subjects (Hahne et al., 2015; Powell, Kaliki, 2014).

Our models require an output signal (force/moment) in order to estimate the model parameters; but, limb-absent subjects cannot directly provide this information. We, therefore, utilized bilateral mirrored contractions. An alternative approach is for the subject to only use their phantom limb on their affected side to match the effort associated with the location and/or orientation of the computer screen target (Ameri, Kamavuako, 2014a; Ameri, Scheme, 2014b). In neither case does a limb-absent subject benefit from afferent feedback. Hence, less accurate muscular activation and measurement is likely, leading to higher EMG-force errors. A better understanding of the limitations imposed by these surrogate force measures might lead to better EMG-force performance.

4.4. Limitations and extensions

Direct comparison of absolute error performance to prior studies can be misleading due to differences in the types of contractions produced (e.g., more forceful contractions will necessarily produce higher errors, measured either in physical units or %MVC; dynamic contractions are generally more challenging to model than static contractions; slow ramp contractions seem more challenging than slow sinusoidal contractions), the measure of error, the subject population, the experimental conditions and numerous other factors. Nonetheless, relative error performance within a task should be a more consistent metric for inter-study comparison. In that regard, it is most useful to observe in able-bodied subjects that 1-DoF models (Fig. 3) experienced no statistically significant benefit when using more than two backward selected electrodes and 2-DoF models (Fig. 5) saw little or no benefit when using more than four backward selected electrodes. Given that EMGσ is a non-negative measure, it is not expected that fewer than four electrode sites could successfully provide 2-DoFs of SIP control. The prior literature has related progressively fewer EMG signals to 2-DoF forces at the wrist; our results help set a lower limit.

Several limitations should be noted. First, the successful results were primarily observed in able-bodied subjects, with much poorer results in limb-absent subjects. Multi-session training could lead to lower errors in limb-absent subjects (Hahne, Dahne, 2015; Powell, Kaliki, 2014). Second, low EMG-force (Jiang, Dosen, 2012a) or EMG-classification (Ortiz-Catalan, Rouhani, 2015) errors in the laboratory do not necessarily transfer to improved prosthesis usability. We utilized the controlled (and inexpensive) laboratory setting—a common paradigm in this field—to demonstrate performance of electrode site selection via the backward stepwise selection method. Future work should investigate its performance by limb-absent subjects performing more functional tasks. Third, the relative merits of bilateral mirrored contractions vs. screen tracking in limb-absent subjects are not well understood. Fourth, we examined a single fixed posture, but Jiang et al. (Jiang et al., 2013) showed that arm pose influences performance of a simultaneous and proportional myoelectric control algorithm. Fifth, our results were from within a single session. If electrodes are re-applied, the effect of subtle shifts in electrode locations is unclear (Muceli, Jiang, 2014; Simon et al., 2012). Sixth, the backward selected electrodes (from the available 16) may not uniquely find the optimal sites. In fact, the two distinct training sets from our two cross validation folds exhibited some variation in their selection of electrodes. Alternative electrode site selection schemes are possible (including simply selecting four equally-spaced electrodes), as well as anatomically-based schemes (e.g., (Fougner, Stavdahl, 2014)). Further, our selected sites do not provide globally optimal electrode site selection; they only provide a locally optimal solution that is limited to the initial positioning of the 16 electrodes, the choice to utilize a bipolar electrode configuration and the use of the backward selection method. And, it could be the case that sub-optimal sites still provide excellent performance. Anecdotally, we made preliminary evaluation of forward stepwise selection of electrode sites, finding rather similar performance to the backward stepwise selection results shown herein. Seventh, our contractions were limited to slowly force-varying (quasi-static— thus narrow band), so that we could concentrate on backward selection of electrode sites providing minimum error. Additionally, our 2-DoF contractions were coupled in effort. Now that the basis of this technique is demonstrated (at least in able-bodied subjects), future work should study wider band, dynamic contractions across a range of frequencies and force levels, which are independent across the 2-DoFs (Clancy, Dai, 2015; Clancy, Liu, 2012; Hashemi, Morin, 2012; Thelen et al., 1994). In our own research, we prefer dynamic target contractions that are random, uniformly distributed and band-limited white. Such targets have equal power across the range of selected frequencies and an equal distribution of effort across the effort range. For such force-varying contractions, models might benefit from including nonlinear behavior, as it has been shown to be beneficial in dynamic EMG-force models used in prosthetics (Nielsen, Holmgaard, 2011). And, this research will clearly need to progress to implementation and testing in prosthetic devices.

5. Conclusions

This initial study is encouraging for the use of backward stepwise selection to site as few as four conventional electrodes for 2-DoF of SIP prosthesis control at the wrist. Two-DoF EMG-force models using four electrodes, trained from both 1- and 2-DoF trials, had average RMS errors of 9.9–11.2 %MVC on able-bodied subjects and 15.8–16.7 %MVC on limb-absent subjects, depending on the DoF. Additional electrodes, up to a total of 16, provided no statistically significant benefit. Electrodes were automatically selected over a reasonably diverse (generally non-adjacent) extent of the forearm. In able-bodied subjects, there was some preference for lower errors when utilizing Ext-Flx, and higher errors when utilizing Pro-Sup. Transition of these results beyond a laboratory task and into prosthesis testing and implementation is necessary, and may require substantive training in limb-absent subjects.

Biographies

Edward (Ted) A. Clancy received the B.S. degree from Worcester Polytechnic Institute (WPI), and the S.M. and Ph.D. degrees from Massachusetts Institute of Technology (MIT), all in Electrical Engineering.

He has worked in industry for medical instrumentation and analysis companies interested in EMG, EEG, ECG and blood pressure, and the defense industry (aircraft instruments and radar). He is Professor of Electrical and Computer Engineering, and of Biomedical Engineering at WPI. He is interested in signal processing, stochastic estimation and system identification, particularly as applied to problems in medical engineering and human rehabilitation.

Carlos Martinez-Luna is a Research Engineer at Liberating Technologies, Inc. (LTI) and has a BSc. in biomedical engineering with a concentration in biomechanics from Worcester Polytechnic Institute (WPI). He has worked with designing, prototyping, and testing electro-mechanical systems through projects at WPI and in contributions to LTI’s federally funded projects working with orthotic and prosthetic technologies. His research interests include novel prosthetic actuators and technologies to train users in myoelectric control.

Marek Wartenberg received the B.S. degree in biomedical engineering from The University of Connecticut and dual M.S. degrees from The University of Connecticut and Politecnico di Milano in biomedical engineering and automation & control engineering, respectively. He is a Ph.D. candidate in robotics engineering at Worcester Polytechnic Institute and his research interests include feedback control systems, MRI compatible robots and image-guided therapy.

Chenyun Dai received the B.S. degree in electrical engineering from Nanjing University of Aeronautics and Astronautics, Nanjing, China and the M.S. and Ph.D. degrees in electrical and computer engineering from Worcester Polytechnic Institute (WPI), Worcester, MA. He is a Post-Doctoral Fellow in the Joint Department of Biomedical Engineering, University of North Carolina-Chapel Hill and North Carolina State University. His research interests include biomedical signal processing, system identification and modeling.

Todd R. Farrell received his B.B.E. degree from the Catholic University of America and his M.S. and Ph.D. degrees in Biomedical Engineering from Northwestern University. He is currently employed by Liberating Technologies, a College Park Company, as their Director of Research. His research interests span across rehabilitation engineering and human-machine interfaces, with a particular focus on prosthetics and orthotics.