Abstract
Soft solids with tunable mechanical response are at the core of new material technologies, but a crucial limit for applications is their progressive aging over time, which dramatically affects their functionalities. The generally accepted paradigm is that such aging is gradual and its origin is in slower than exponential microscopic dynamics, akin to the ones in supercooled liquids or glasses. Nevertheless, time- and space-resolved measurements have provided contrasting evidence: dynamics faster than exponential, intermittency and abrupt structural changes. Here we use 3D computer simulations of a microscopic model to reveal that the timescales governing stress relaxation, respectively, through thermal fluctuations and elastic recovery are key for the aging dynamics. When thermal fluctuations are too weak, stress heterogeneities frozen-in upon solidification can still partially relax through elastically driven fluctuations. Such fluctuations are intermittent, because of strong correlations that persist over the timescale of experiments or simulations, leading to faster than exponential dynamics.
Soft solids have important applications in industry but their material properties can be compromised by aging. Here Bouzid et al. present a large-scale study of a model gel to investigate the aging of soft matter which can help unravel the microscopic dynamics in a range of soft solids.
Soft condensed matter (proteins, colloids or polymers) easily self-assembles into gels or amorphous soft solids with diverse structure and mechanics1,2,3,4,5. The nanoscale size of particles or aggregates makes these solids sensitive to thermal fluctuations, with spontaneous and thermally activated processes leading to rich microscopic dynamics. Besides affecting the time evolution, or aging, of the material properties at rest, such dynamics interplay with an imposed deformation and are hence crucial also for the mechanical response6,7,8,9,10. In the material at rest, thermal fluctuations can trigger ruptures of parts of the microscopic structure that are under tension or can promote coarsening and compaction of initially loosely packed domains, depending on the conditions under which the material initially solidified. The diffusion of particles or aggregates following such local reorganizations (often referred to as ‘micro-collapses’) is governed by a wide distribution of relaxation times, due to the disordered tortuous environment in which it takes place, that is, the microstructure of a soft solid, be it a thin fractal gel or a densely packed emulsion11,12. Therefore, localization, caging and larger-scale cooperative rearrangements in such complex environment will lead to slow, subdiffusive dynamics, similar to the microscopic dynamics close to a glass transition13,14.
Several quasi-elastic scattering experiments or numerical simulations that can access micro- and nanoscale rearrangements in soft matter have indeed confirmed that the dynamics in aging soft solids are slower than exponential. Measuring the time decay of the correlations of the density fluctuations or of the local displacements of particles or aggregates, the experiments find that time correlations follow a stretched exponential decay 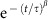 with β<1, akin to the slow cooperative dynamics of supercooled liquids and glasses, in a wide range of gels and other soft solids15,16,17,18,19. Nevertheless, in the past few years there has been emerging evidence, through a growing body of similar experiments, that microscopic dynamics in the aging of soft materials can be instead faster than exponential. In a wide range of soft amorphous solids including colloidal gels, biopolymer networks, foams and densely packed microgels, time correlations measured via quasi-elastic scattering or other time-resolved spectroscopy techniques appear to decay as
with β<1, akin to the slow cooperative dynamics of supercooled liquids and glasses, in a wide range of gels and other soft solids15,16,17,18,19. Nevertheless, in the past few years there has been emerging evidence, through a growing body of similar experiments, that microscopic dynamics in the aging of soft materials can be instead faster than exponential. In a wide range of soft amorphous solids including colloidal gels, biopolymer networks, foams and densely packed microgels, time correlations measured via quasi-elastic scattering or other time-resolved spectroscopy techniques appear to decay as 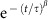 with β>1 (and in most cases 1.3≤β≤1.5)20,21,22,23,24,25,26,27,28,29,30. When analysing the dependence of the relaxation time on the lengthscales probed, the data highlight the presence of super-diffusive rather than subdiffusive microscopic processes, with the relaxation time τ increasing with decreasing the scattering wave vector q (and hence increasing the lengthscale being probed) as τ∝1/q rather than τ∝1/q2. Moreover, experiments specifically designed to quantify the fluctuations in time and space of the microscopic dynamics have revealed strong intermittency and pointed to the possibility of an abrupt and coherent reorganization of relatively large domains. Hence it has been suggested that the elastic rebound of parts of the material, after micro-collapses occur in its structure, should be, instead, the stress relaxation mechanism underlying the aging of soft solids31,32,33. As a matter of fact, viewing the soft glassy material as an elastic continuum and considering that the micro-collapses occur randomly in space (both strong assumptions in most of the materials of interest), the related disruption of the elastic strain field does lead to a compressed exponential relaxation regime, in relatively good agreement with experiments33,34,35,36. Understanding (and controlling) the nature of dynamical processes in aging soft solids is crucial to a wide range of technologies, from those involved in material processing to those relying on stable material properties. Moreover, the contrasting experimental findings also raise the very fundamental question of which microscopic mechanism should be prevalent in which material and under which conditions.
with β>1 (and in most cases 1.3≤β≤1.5)20,21,22,23,24,25,26,27,28,29,30. When analysing the dependence of the relaxation time on the lengthscales probed, the data highlight the presence of super-diffusive rather than subdiffusive microscopic processes, with the relaxation time τ increasing with decreasing the scattering wave vector q (and hence increasing the lengthscale being probed) as τ∝1/q rather than τ∝1/q2. Moreover, experiments specifically designed to quantify the fluctuations in time and space of the microscopic dynamics have revealed strong intermittency and pointed to the possibility of an abrupt and coherent reorganization of relatively large domains. Hence it has been suggested that the elastic rebound of parts of the material, after micro-collapses occur in its structure, should be, instead, the stress relaxation mechanism underlying the aging of soft solids31,32,33. As a matter of fact, viewing the soft glassy material as an elastic continuum and considering that the micro-collapses occur randomly in space (both strong assumptions in most of the materials of interest), the related disruption of the elastic strain field does lead to a compressed exponential relaxation regime, in relatively good agreement with experiments33,34,35,36. Understanding (and controlling) the nature of dynamical processes in aging soft solids is crucial to a wide range of technologies, from those involved in material processing to those relying on stable material properties. Moreover, the contrasting experimental findings also raise the very fundamental question of which microscopic mechanism should be prevalent in which material and under which conditions.
Here we use numerical simulations and a model particle gel which, during aging, undergoes structural changes by means of rupture of particle connections. Such ruptures are prototypical of the micro-collapses in the aging of such materials, occurring in regions where higher than average tensile stresses have been frozen-in during the solidification. By quantifying the consequences of the microscopic ruptures, we unravel that the origin of the different relaxation dynamics is in the dramatically different strain transmission if the stress heterogeneities are significantly larger than Brownian stresses. In those conditions, the characteristic timescale for stress relaxation through thermal fluctuations grows well beyond the duration of typical experiments or simulations, but the stress released in microscopic ruptures can still partially relax through elastically induced fluctuations, that are strongly correlated over time and through the structure. The emergent displacement distribution becomes scale-free, featuring a power law tail that points to the long-range elastic strain field in the gel as the main source of structural rearrangements. Thermal fluctuations and Brownian motion disrupt instead the spatial distributions of the local stresses, as well as the persistence of their correlations in time, which leads to the screening of the strain transmission over the structure. Our results provide a unifying framework to rationalize microscopic dynamical processes in a wide variety of soft solids, crucial to their mechanical performance.
Results
Model
We consider a minimal 3D model for a gel composed of N=62,500 colloidal particles of diameter σ and mass m, with their motion described by a Langevin dynamics in the overdamped limit, at low volume fractions (≃7%) (see ‘Methods’ section). The particles spontaneously self-assemble into a disordered interconnected network thanks to a short range attractive well U2 (combined with a repulsive core) and an additional short range repulsion U3, which depends on the angle between bonds departing from the same particle and imparts an angular rigidity to the gel branches, as expected in such open structures37,38,39,40. Starting from the same gel configuration, we analyse the dynamics relevant to highly cohesive gels (where significant frozen-in stresses can be developed during solidification), by using different temperatures at fixed interaction strength ∈, to vary the ratio kBT/∈ of the Brownian stresses to stress heterogeneities frozen-in during solidification.
In spite of its simplicity, our model captures important physical features of real particle gels and can be used as a prototypical soft amorphous solid. The structural heterogeneities developed during the gel formation entail mechanical inhomogeneities and the simulations reveal the coexistence of stiffer regions (where tensile stresses tend to accumulate) with softer domains, where most of the relaxation occurs41. Hence aging is likely to occur via sudden ruptures of particle connections in the regions where the local tensile stresses are higher, as indeed suggested for the ultraslow aging observed in experiments21. In the simulations, they are quite rare even at the highest temperatures of interest here (roughly only a few over ≃106 MD steps at kBT/∈ = 0.05 (ref. 39)) and become hardly observable on a reasonable simulation time window as we consider even smaller kBT/∈. To investigate the consequences of the ruptures on a timescale computationally affordable, we periodically scan the local stresses in the gel structure and remove particle bonds where the local stress is the highest, with a fixed rate Γ (see ‘Methods’ section). Recombinations of the gel branches are possible but just not observed at the volume fractions and for the time window explored here.
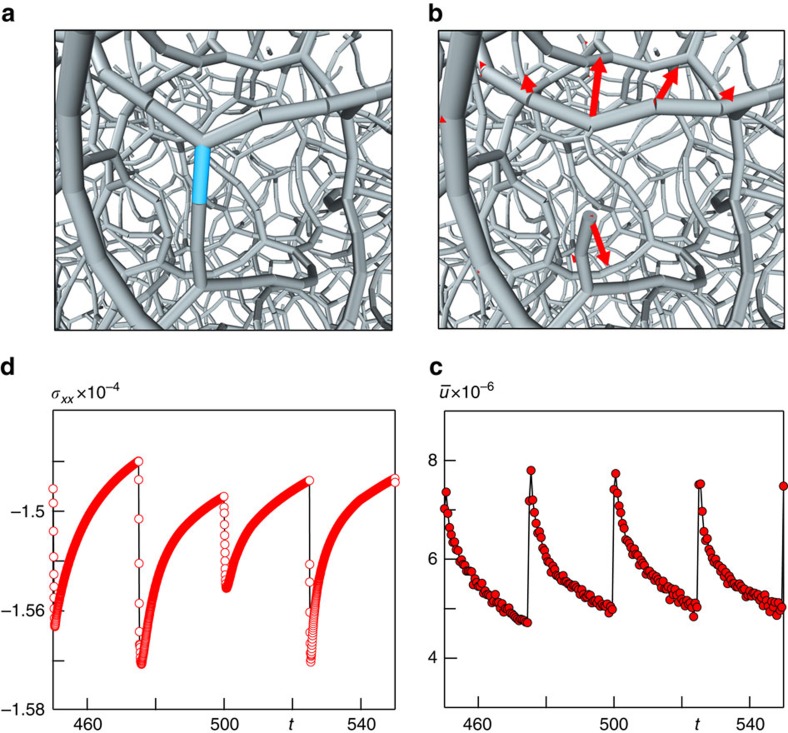
In a rupture event, illustrated in Fig. 1a,b using two subsequent simulation snapshots, the particles depart from each other and move following the part of the network to which they are attached. The topological and elastic constraints exerted by the network, coupled to the local dissipation, result in a progressive slowing down of such motion. The average displacement 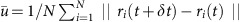 (δt is the integration timestep in the simulations) decreases exponentially between two rupture events, as shown in Fig. 1c for kBT/∈ = 0. After each event, interparticle forces and/or thermal fluctuations drive the redistribution of the stresses over the structure, with the stress relaxation shown in Fig. 1d using the component σxx of the virial stress tensor (that is, the stress computed from the microscopic particle configurations42, see ‘Methods’ section) plotted as a function of the time. All data shown in the following refer to a removal (or cutting) rate
(δt is the integration timestep in the simulations) decreases exponentially between two rupture events, as shown in Fig. 1c for kBT/∈ = 0. After each event, interparticle forces and/or thermal fluctuations drive the redistribution of the stresses over the structure, with the stress relaxation shown in Fig. 1d using the component σxx of the virial stress tensor (that is, the stress computed from the microscopic particle configurations42, see ‘Methods’ section) plotted as a function of the time. All data shown in the following refer to a removal (or cutting) rate 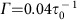 , where
, where 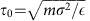 is the MD time unit, and correspond to breaking ≃5% of the initial bonds in total over the simulation time window of 105τ0 considered here. We have carefully investigated how the choice of Γ affects the results discussed below and determined that they do not significantly change as long as the removal rate is high enough to collect enough statistics (of the ruptures and their consequences) but slow enough to allow for a partial stress relaxation between two rupture events (Fig. 1d) (see ‘Methods’ section).
is the MD time unit, and correspond to breaking ≃5% of the initial bonds in total over the simulation time window of 105τ0 considered here. We have carefully investigated how the choice of Γ affects the results discussed below and determined that they do not significantly change as long as the removal rate is high enough to collect enough statistics (of the ruptures and their consequences) but slow enough to allow for a partial stress relaxation between two rupture events (Fig. 1d) (see ‘Methods’ section).
Figure 1. Rupture of gel connections.
Snapshots of the colloidal gel network showing the interparticle bonds before (a) and after (b) a bond rupture, each bond is represented by a segment, when the distance dij between two particles i and j is ≤1.3σ. In a, the bond that will break is highlighted, in b, the arrows indicate the displacement after the rupture. (c) The average displacement 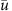 as a function of the time for four consecutive ruptures. (d) The corresponding stress component σxx as a function of the time.
as a function of the time for four consecutive ruptures. (d) The corresponding stress component σxx as a function of the time.
Internal stresses
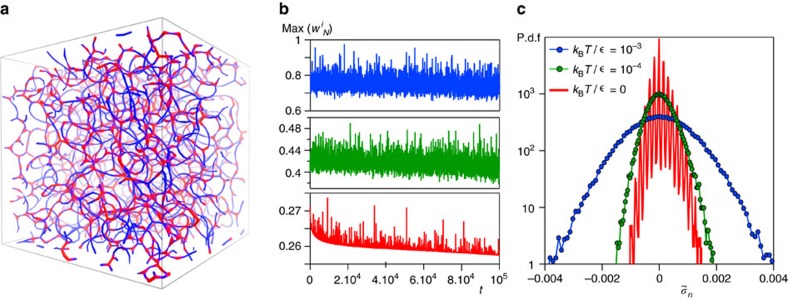
The analysis of the stress heterogeneities in the network helps disentangle how the stress reorganization and the presence of thermal fluctuations contribute to the relaxation dynamics. Because of the topological constraints produced in the network on its formation, in the initial configuration local stresses have significant spatial correlations. Particles located in the nodes of the gel network, in fact, contribute to the local stresses mostly in terms of tensions, as shown in Fig. 2a, where the gel is coloured according to the value of the local normal stress 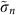 (that is, the normal virial stress computed over a small volume around each particle and containing ∼10 particles, see ‘Methods’ section). Analyzing the evolution over time of the largest among the contributions
(that is, the normal virial stress computed over a small volume around each particle and containing ∼10 particles, see ‘Methods’ section). Analyzing the evolution over time of the largest among the contributions 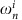 of each particle i to the total normal stress σn, we find that it progressively decreases in all cases, but its fluctuations are clearly different in nature depending on the relative strength of thermal fluctuations (see Fig. 2b). The decrease rate of
of each particle i to the total normal stress σn, we find that it progressively decreases in all cases, but its fluctuations are clearly different in nature depending on the relative strength of thermal fluctuations (see Fig. 2b). The decrease rate of 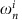 clearly depends on kBT/∈ and is much slower than the cutting rate, indicating that the aging of the material corresponds to a slower, large-scale stress redistribution, which emerges over much longer timescales. In the athermal case, this slow evolution of the structure is found to be logarithmic in time. The final distribution of local stresses
clearly depends on kBT/∈ and is much slower than the cutting rate, indicating that the aging of the material corresponds to a slower, large-scale stress redistribution, which emerges over much longer timescales. In the athermal case, this slow evolution of the structure is found to be logarithmic in time. The final distribution of local stresses 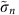 (Fig. 2c) still features a few of the pronounced peaks present in the initial one, pointing to the persistence, during the aging, of the spatial correlations of the local stresses. Thermal fluctuations, instead, clearly disrupt such correlations and help redistribute the local stresses much more homogeneously over the gel structure.
(Fig. 2c) still features a few of the pronounced peaks present in the initial one, pointing to the persistence, during the aging, of the spatial correlations of the local stresses. Thermal fluctuations, instead, clearly disrupt such correlations and help redistribute the local stresses much more homogeneously over the gel structure.
Figure 2. Local stresses.
(a) A snapshot of the initial colloidal gel network for kBT/∈ = 0 and at low volume fraction ϕ=7%, showing the interparticle bonds represented by a segment when the distance dij between two particles i and j is less than 1.3σ. The colours indicate the local normal stress 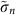 , using red for tension and blue for compression. (b) Time evolution of the maximum contribution (per particle)
, using red for tension and blue for compression. (b) Time evolution of the maximum contribution (per particle) 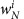 to the normal component of the stresses tensor for the athermal network (red), kBT/∈ = 10−4 (green) and kBT/∈ = 10−3 (blue). (c) The final probability distribution function of
to the normal component of the stresses tensor for the athermal network (red), kBT/∈ = 10−4 (green) and kBT/∈ = 10−3 (blue). (c) The final probability distribution function of 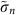 corresponding to the initial configuration shown in a. P.d.f, probability distribution function.
corresponding to the initial configuration shown in a. P.d.f, probability distribution function.
Microscopic dynamics
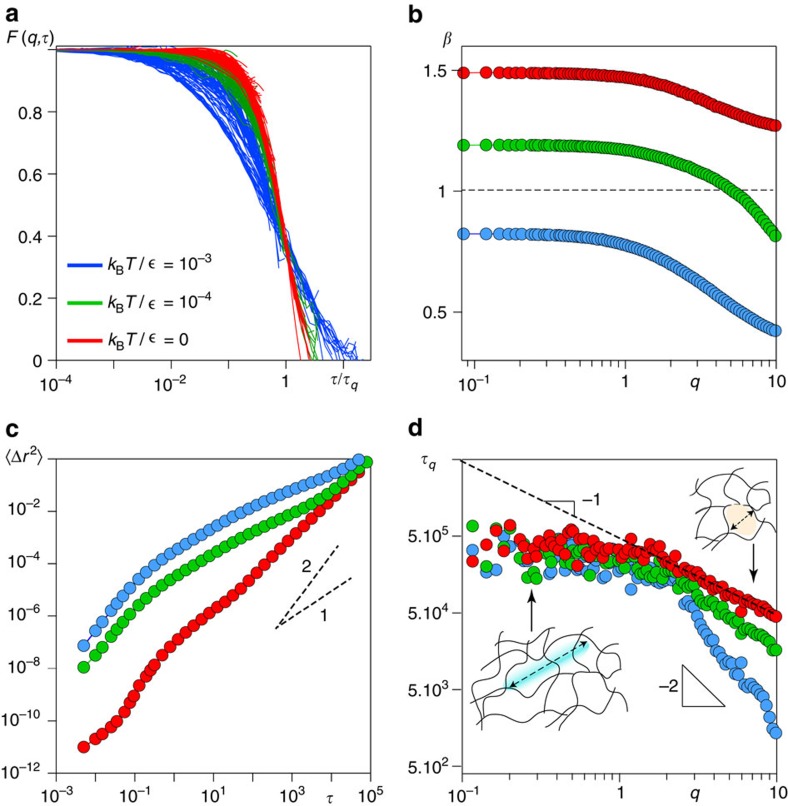
The mechanical heterogeneities and their time evolution during the aging have an impact on the relaxation dynamics. To quantify it, we use the same observables measured in quasi-elastic scattering experiments. From the particle coordinates, we compute the coherent scattering function:
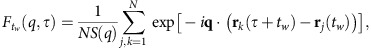 |
where S(q) is the structure factor of the gel and tw the time at which the measurement starts (here tw=0 for all data sets). From the long time decay of F(q,τ) 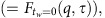 we extract the relaxation time τ(q) for different wave vectors (see ‘Methods’ section) and in Fig. 3a we plot F(q,τ) as a function of τ/τ(q), for q varying between 0.1 and 10 (in units of σ−1), at three different temperatures: kBT/∈ = 10−3 (blue), kBT/∈ = 10−4 (green) and for the athermal network (red). The data indicate that the form of the time decay is sensitive not only to q (as a consequence of the structure heterogeneities)31,43,44, but also to kBT/∈. In all cases, the final part of F(q,τ) is well fitted by a decay
we extract the relaxation time τ(q) for different wave vectors (see ‘Methods’ section) and in Fig. 3a we plot F(q,τ) as a function of τ/τ(q), for q varying between 0.1 and 10 (in units of σ−1), at three different temperatures: kBT/∈ = 10−3 (blue), kBT/∈ = 10−4 (green) and for the athermal network (red). The data indicate that the form of the time decay is sensitive not only to q (as a consequence of the structure heterogeneities)31,43,44, but also to kBT/∈. In all cases, the final part of F(q,τ) is well fitted by a decay 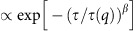 . The exponent β, extracted from the best fit of the past decade of F(q,τ), indicate a transition from a stretched to a compressed exponential decay upon decreasing the ratio kBT/∈ (see Fig. 3b). The dependence of β on kBT/∈ found here is consistent with experimental observations in refs 25, 26. The dependence on q is the same as typically observed in several experiments22,28,31, with the β decreasing rapidly with increasing q over lengthscales typically ranging between a few and several particle diameters, up to roughly the order of the mesh size of the gel network (the mean distance between two network nodes along a gel branch is 2π/q≃5σ at this volume fraction39). For much larger distances, β does not change much with q. The particle mean squared displacement (MSD) is shown in Fig. 3c as a function of the time for the different values of kBT/∈. After a localization process at intermediate times, the MSD displays a change in the time dependence at long times, from subdiffusive to super-diffusive, on decreasing kBT/∈. The wave vector dependence of the relaxation time τ(q) is reported, for different kBT/∈, in Fig. 3d. For q corresponding to distances up to ≃5σ, τ(q) is strongly dependent on q and on kBT/∈ and, as long as kBT/∈≃10−3, it follows the scaling ∝1/q2 typically expected when diffusive processes are at play. Reducing kBT/∈ leads to a different scaling τ(q)∝1/q, which is consistent with the super-diffusive microscopic motion detected in Fig. 3c. The results obtained for kBT/∈<10−3 are consistent with several experiments, finding a compressed exponential dynamics and a 1/q scaling of the relaxation time. Such dependence was ascribed to a super-diffusive, quasi-ballistic particle motion in refs 21, 31, 45, a hypothesis not directly testable in experiments but proven in Fig. 3c. The ballistic motion reported here and in experiments persists over timescales corresponding to a large number of events. This feature points to the fact that the origin of the ballistic motion is not the single breaking event but the elastic relaxation accumulated in the network over many events.
. The exponent β, extracted from the best fit of the past decade of F(q,τ), indicate a transition from a stretched to a compressed exponential decay upon decreasing the ratio kBT/∈ (see Fig. 3b). The dependence of β on kBT/∈ found here is consistent with experimental observations in refs 25, 26. The dependence on q is the same as typically observed in several experiments22,28,31, with the β decreasing rapidly with increasing q over lengthscales typically ranging between a few and several particle diameters, up to roughly the order of the mesh size of the gel network (the mean distance between two network nodes along a gel branch is 2π/q≃5σ at this volume fraction39). For much larger distances, β does not change much with q. The particle mean squared displacement (MSD) is shown in Fig. 3c as a function of the time for the different values of kBT/∈. After a localization process at intermediate times, the MSD displays a change in the time dependence at long times, from subdiffusive to super-diffusive, on decreasing kBT/∈. The wave vector dependence of the relaxation time τ(q) is reported, for different kBT/∈, in Fig. 3d. For q corresponding to distances up to ≃5σ, τ(q) is strongly dependent on q and on kBT/∈ and, as long as kBT/∈≃10−3, it follows the scaling ∝1/q2 typically expected when diffusive processes are at play. Reducing kBT/∈ leads to a different scaling τ(q)∝1/q, which is consistent with the super-diffusive microscopic motion detected in Fig. 3c. The results obtained for kBT/∈<10−3 are consistent with several experiments, finding a compressed exponential dynamics and a 1/q scaling of the relaxation time. Such dependence was ascribed to a super-diffusive, quasi-ballistic particle motion in refs 21, 31, 45, a hypothesis not directly testable in experiments but proven in Fig. 3c. The ballistic motion reported here and in experiments persists over timescales corresponding to a large number of events. This feature points to the fact that the origin of the ballistic motion is not the single breaking event but the elastic relaxation accumulated in the network over many events.
Figure 3. Relaxation dynamics.
(a) The decay of the coherent scattering function as a function of the time rescaled by the relaxation time τq for a wave vector ranging from q=0.1 to 10 and for three different ratios of kBT/∈. (b) The exponent β as a function of the wave vector q, showing a transition from a compressed to a stretched dynamics. (c) The particle MSD as a function of time t for the same kBT/∈ ratios as in a. (d) The relaxation time τ(q) as a function of the wave vector q for the three systems: the scaling goes from τ∼q−1 for the fully athermal regime to diffusive τ∼q−2 when the thermal fluctuations dominate; a plateau emerges at low wave vectors corresponding to distances beyond the mesh size of the network, as sketched in the cartoons.
The agreement between our scenario for small enough kBT/∈ and the experiments support the idea that frozen-in stresses control the microscopic dynamics also in the experimental samples23,46. The relaxation time τ(q) from the simulations becomes less sensitive to the wave vector over distances beyond the mesh size of the network, as indeed observed in experiments20 (see Fig. 3d). Whereas such finding could be interpreted as a loss of dynamical correlations over large distances, we have verified through mechanical tests that the gels are prevalently elastic for all values of kBT/∈ considered here, supporting the presence of long-range spatial correlations of the dynamics. Moreover, the relaxation time extracted from the incoherent scattering keeps instead increasing on decreasing q and also indicate long-range spatial correlations in the dynamics (see Supplementary Fig. 1). Hence the data in Fig. 3d can be better understood by considering that, although local rearrangements are possible, over larger distances the material is solid and elastically connected in spite of being structurally heterogeneous and sparse, and the time correlations of the density fluctuations over those lengthscales are therefore locked-in.
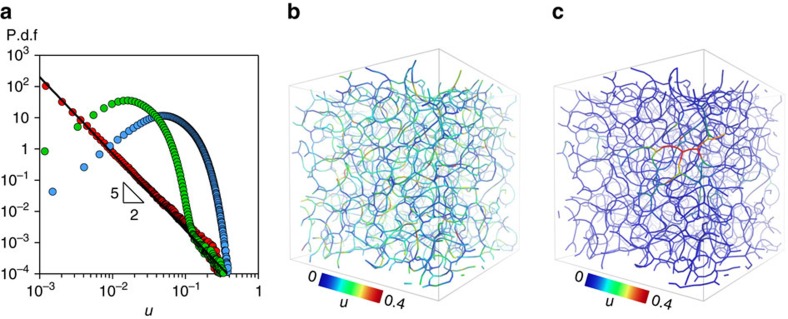
Beyond the capability of experiments, the simulations give us direct access to the distribution of the displacements over a lag time in between two rupture events, which, for kBT/∈>10−3, is a bell-shaped curve with exponential tails (Fig. 4a), similar to those typically seen in supercooled liquids38,47,48. However, on decreasing kBT/∈→0, the probability distribution function becomes instead progressively scale-free. Such findings support our interpretation of Fig. 3d and the idea that the dynamics are spatially correlated and cooperative over extended domains for all kBT/∈. We visualize the displacement field in two representative snapshots of the gel network (Fig. 4b,c) where the colour code indicates the amplitude of the displacements measured along the network after a rupture event, for kBT/∈ = 10−3 and kBT/∈ = 0, respectively. The visualizations highlight how the long-range elastic response of the network dominates the displacement pattern in the athermal limit, where it extends indeed over several network meshes, and it is instead screened by the small displacements induced by thermal fluctuations for larger kBT/∈ (see Supplementary Movies).
Figure 4. Microscopic particle displacements.
(a) The probability distribution function of the particle displacements calculated with a lag time equal to 40τ0 for three ratios of kBT/∈, blue circles represent the fully thermal regime kBT/∈ = 10−3, green circles refer to the intermediate regime kBT/∈ = 10−4 and red circles correspond to the configuration at kBT/∈ = 0, the solid black line represents the MF prediction u−5/2, a deviation from this purely elastic effects is seen when thermal fluctuations act on the small displacements. Snapshots of the colloidal gel network for kBT/∈ = 10−3 (b) and kBT/∈ = 0 (c), showing the interparticle bonds and the amplitude of the displacements after a rupture event.
For a homogeneous elastic material, the amplitude of the strain u induced at a distance r from the rupture event decreases as u(r)∝1/r2 (ref. 50). Given the probability P(r) of having a rupture event at a distance r and if, in a mean field (MF) approximation, rupture events occur anywhere with the same probability, the probability distribution function for a displacement (or strain) of amplitude u can be estimated as 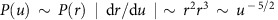 . In the athermal limit kBT/∈ = 0, we clearly recover the MF prediction with the power law u−5/2 (Fig. 4a), which is in fact compatible with a compressed exponential decay of the scattering functions with β=3/2 (refs 33, 35), as shown in Fig. 3b. The agreement with the MF prediction may suggest that structural disorder and correlations between rupture events are in the end negligible. Nevertheless, here (as well as in many experiments) the structure is heterogeneous, the correlations of events are crucial and the MF assumptions are unlikely to truly hold35. We propose therefore a different explanation, that is, structural disorder and correlations between rupture events, in spite of being present, do not disrupt the elastic connectivity of the material because, when kBT/∈∼0, the relaxation of the stresses through elastic fluctuations does not weaken their spatio-temporal correlations. As a matter of fact, in addition to the spatial correlations discussed above, the total stress also features large fluctuations in time, that depend on kBT/∈ and become strongly correlated as kBT/∈→0 (Fig. 5).
. In the athermal limit kBT/∈ = 0, we clearly recover the MF prediction with the power law u−5/2 (Fig. 4a), which is in fact compatible with a compressed exponential decay of the scattering functions with β=3/2 (refs 33, 35), as shown in Fig. 3b. The agreement with the MF prediction may suggest that structural disorder and correlations between rupture events are in the end negligible. Nevertheless, here (as well as in many experiments) the structure is heterogeneous, the correlations of events are crucial and the MF assumptions are unlikely to truly hold35. We propose therefore a different explanation, that is, structural disorder and correlations between rupture events, in spite of being present, do not disrupt the elastic connectivity of the material because, when kBT/∈∼0, the relaxation of the stresses through elastic fluctuations does not weaken their spatio-temporal correlations. As a matter of fact, in addition to the spatial correlations discussed above, the total stress also features large fluctuations in time, that depend on kBT/∈ and become strongly correlated as kBT/∈→0 (Fig. 5).
Figure 5. Stress fluctuations.
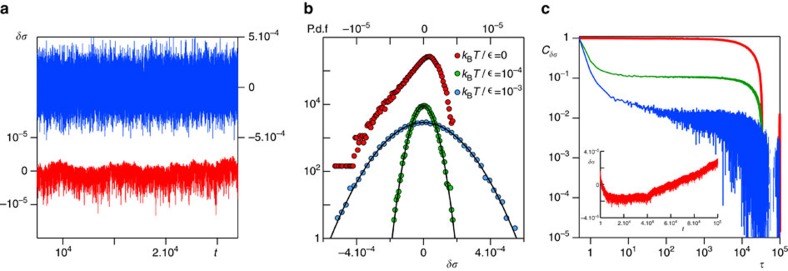
(a) Time series of the normal stress fluctuations 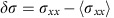 measured over a time interval involving 800 ruptures for the athermal network (red) and for kBT/∈ = 10−3 (blue). The corresponding probability distribution function (b): in the regime dominated by frozen-in stresses (red), the stress fluctuations are elastically driven and intermittent in nature. (c) Main frame: The stress fluctuations autocorrelation function measured over the whole simulation for the fully thermal regime kBT/∈ = 10−3 (blue), the intermediate kBT/∈ = 10−4 (green) and the for kBT/∈ = 0 (red). Inset: Time series of the normal stress fluctuations δσ over all the simulation for the athermal sample showing the aging of the structure. P.d.f, probability distribution function.
measured over a time interval involving 800 ruptures for the athermal network (red) and for kBT/∈ = 10−3 (blue). The corresponding probability distribution function (b): in the regime dominated by frozen-in stresses (red), the stress fluctuations are elastically driven and intermittent in nature. (c) Main frame: The stress fluctuations autocorrelation function measured over the whole simulation for the fully thermal regime kBT/∈ = 10−3 (blue), the intermediate kBT/∈ = 10−4 (green) and the for kBT/∈ = 0 (red). Inset: Time series of the normal stress fluctuations δσ over all the simulation for the athermal sample showing the aging of the structure. P.d.f, probability distribution function.
Stress fluctuations and stress relaxation
The fluctuations of one component of the total stress 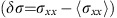 , measured over a time window significantly larger than the time interval between two rupture events, are plotted in Fig. 5a for kBT/∈=10−3 and kBT/∈ = 0. When Brownian stresses become negligible with respect to the stress heterogeneities, such fluctuations clearly deviates from randomly fluctuating values, even after many ruptures have occurred. Their probability distribution function is Gaussian for larger kBT/∈, whereas it develops non-Gaussian tails as kBT/∈→0 (Fig. 5b). The non-Gaussian processes and the intermittent fluctuations measured over the same time window correspond indeed to persistent time correlations (see Supplementary Fig.2).
, measured over a time window significantly larger than the time interval between two rupture events, are plotted in Fig. 5a for kBT/∈=10−3 and kBT/∈ = 0. When Brownian stresses become negligible with respect to the stress heterogeneities, such fluctuations clearly deviates from randomly fluctuating values, even after many ruptures have occurred. Their probability distribution function is Gaussian for larger kBT/∈, whereas it develops non-Gaussian tails as kBT/∈→0 (Fig. 5b). The non-Gaussian processes and the intermittent fluctuations measured over the same time window correspond indeed to persistent time correlations (see Supplementary Fig.2).
When monitoring the stress fluctuations over the whole duration of the simulations, we find evidence of the progressive aging of the structure that eventually emerges from the correlated stress redistribution (see Fig. 5c, inset for kBT/∈ = 0 data). Accordingly, the time correlations of the fluctuations of the total stress over these longer timescales develop a pronounced plateau on decreasing kBT/∈ and eventually extend to the whole duration of the simulation in the athermal limit (Fig. 5c, main frame).
Time- and space-resolved scattering experiments have indeed found evidence of highly intermittent dynamical processes43, hence Fig. 5a,b and the intermittency in the stress fluctuations detected here provide a first coherent physical picture also for these observations, beyond the aspects that can be captured by MF approaches. Our analysis reveals that indeed the spatio-temporal correlation patterns detected in the microscopic displacements and in the density fluctuations (Figs 3a–c and 4a) stem from the way thermal fluctuations, on increasing kBT/∈, help redistribute elastic stresses (and strains) in the material. When thermal fluctuations are weak, the microscopic dynamics emerge instead from elastically driven stress fluctuations that remain strongly correlated in space and time.
Discussion
Our analysis provides a vivid microscopic picture for the hypothesis underlying recent theories of aging in soft solids34,35 and has implications for a potentially wider range of materials.
The control parameter kBT/∈ simply reflects the ratio between the timescales governing stress relaxation, respectively, through thermal fluctuations (η σ3/kBT) and elastic recovery (η σ3/∈) in the material (η being the viscous damping). Hence it helps identify the conditions for which the elastically driven intermittent dynamics emerge in different jammed solids. First, we note that while we have considered here only one type of micro-collapses, the distruption of the elastic strain field due to the rupture of a branch of the gel is basically the same, in a first approximation, as the one induced by a recombination of the gel branches (or by other types of possible microscopic events that help relax frozen-in stresses)33. Therefore, we expect our general picture to have a much wider relevance. Second, the physical mechanisms we propose help rationalize several experimental observations in very different materials, ranging from biologically relevant soft solids to metallic glasses31,45,46,50. In a quasi-equilibrium scenario, enthalpic and thermal degrees of freedom may still couple and stress correlations decay relatively fast. When the material is deeply quenched and jammed, instead, recovering the coupling between the distinct degrees of freedom and restoring equilibrium will require timescales well beyond the ones accessible in typical experiments or simulations. The result will be intermittent dynamics and compressed exponential relaxations. The competition between Brownian motion and elastic effects through the relaxation of internal stresses illustrated in this work suggests different scenarios for the energy landscape underlying the aging of soft jammed materials. When thermal fluctuations screen the long-range elastic strain transmission, microscopic rearrangements may open paths to deeper and deeper local minima in a rugged energy landscape. Compressed exponential dynamics, instead, evoke the presence of flat regions and huge barriers, with the possibility of intermittent dynamics, abrupt rearrangements and avalanches34,35. Investigating how such different dynamical processes couple with imposed deformations will provide a new rationale, and have important implications, for designing mechanics, rheology and material performances.
Methods
Numerical model and viscoelastic parameters
The particles in the model gel interact through a potential composed of two terms. The first force contribution derives from a Lennard–Jones-like potential of the form:
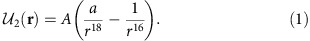 |
The second contribution confers an angular rigidity to the inter particles bonds and takes the form:
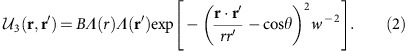 |
The strength of the interaction is controlled by Λ(r) and vanishes over two particles diameters:
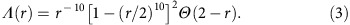 |
where Θ denotes the Heaviside function. The evolution of the gel over time is obtained by solving the following Langevin equation for each particle:
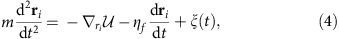 |
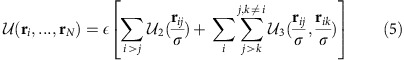 |
where σ is the particle diameter, ξ(t) is a random white noise that models the thermal fluctuations and is related to the friction coefficient ηf by means of its variance 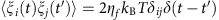 . To be in the overdamped limit of the dynamics ηf is set to 10, and the timestep δt used for the numerical integration is δt=0.005. The parameters of the potential are chosen such that the disordered thin percolating network starts to self assemble at kBT/∈ = 0.05. One convenient choice to achieve this configuration is given by this set of parameters: A=6.27, a=0.85, B=67.27, θ=65° and w=0.3. The system is composed of N=62,500 particles in a cubic simulation box of a size L=76.43σ with periodic boundary conditions, the number density N/L3 is fixed at 0.14, which corresponds approximatively to a volume fraction of 7%. All initial gel configurations are the same, prepared with the protocol described in ref. 40, which consists in starting from a gas configuration (kBT/∈ = 0.5) and letting the gel self-assemble upon slow cooling down to kBT/∈ = 0.05. We then quench this gel configuration by running a simulation with the dissipative dynamics
. To be in the overdamped limit of the dynamics ηf is set to 10, and the timestep δt used for the numerical integration is δt=0.005. The parameters of the potential are chosen such that the disordered thin percolating network starts to self assemble at kBT/∈ = 0.05. One convenient choice to achieve this configuration is given by this set of parameters: A=6.27, a=0.85, B=67.27, θ=65° and w=0.3. The system is composed of N=62,500 particles in a cubic simulation box of a size L=76.43σ with periodic boundary conditions, the number density N/L3 is fixed at 0.14, which corresponds approximatively to a volume fraction of 7%. All initial gel configurations are the same, prepared with the protocol described in ref. 40, which consists in starting from a gas configuration (kBT/∈ = 0.5) and letting the gel self-assemble upon slow cooling down to kBT/∈ = 0.05. We then quench this gel configuration by running a simulation with the dissipative dynamics 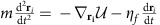 until the kinetic energy drops to zero(10−24). All simulations have been performed using a version of LAMMPS suitably modified by us52.
until the kinetic energy drops to zero(10−24). All simulations have been performed using a version of LAMMPS suitably modified by us52.
Stress calculation and cutting strategy
We let the initial gel configuration evolve with equation (4) for each of the different values of kBT/∈ considered here, while using the following procedure to cut network connections. At each timestep, we characterize the state of stress of a gel configuration by computing the virial stresses as 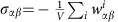 , where the Greek subscripts stand for the Cartesian components x, y, z and
, where the Greek subscripts stand for the Cartesian components x, y, z and 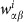 represents the contribution to the stress tensor of all the interactions involving the particle i and V is the total volume of the simulation box52.
represents the contribution to the stress tensor of all the interactions involving the particle i and V is the total volume of the simulation box52. 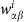 contains, for each particle, the contributions of the two-body and the three-body forces evenly distributed among the particles that participate in them:
contains, for each particle, the contributions of the two-body and the three-body forces evenly distributed among the particles that participate in them:
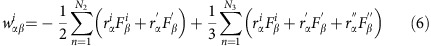 |
The first term on the RHS denotes the contribution of the two-body interaction, where the sum runs over all the N2 pair of interactions that involve the particle i. (ri, F i) and (r′, F′) denote, respectively, the position and the forces on the two interacting particles. The second term indicates the three-body interactions involving the particle i. We consider a coarse-graining volume Ωcg centered around the point of interest r and containing around 9–10 particles on average, and define the local coarse-grained stress based on the per-particle virial contribution as 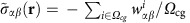 . For a typical starting configuration of the gel, the local normal stress
. For a typical starting configuration of the gel, the local normal stress 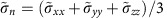 reflect the heterogeneity of the structure and tend to be higher around the nodes, due to the topological frustration of the network. We consider that breaking of network connections underlying the aging of the gel is more prone to happen in the regions where local stresses tend to be higher, as found also in refs 40, 41. Hence, to mimic the aging in the molecular dynamics simulations we scan the whole structure of the gel and remove one of the bonds (by turning off the well in
reflect the heterogeneity of the structure and tend to be higher around the nodes, due to the topological frustration of the network. We consider that breaking of network connections underlying the aging of the gel is more prone to happen in the regions where local stresses tend to be higher, as found also in refs 40, 41. Hence, to mimic the aging in the molecular dynamics simulations we scan the whole structure of the gel and remove one of the bonds (by turning off the well in 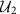 ) whose contribution to the local normal stress
) whose contribution to the local normal stress 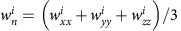 is the largest (prevalently bonds between particles belonging to the network nodes). As the simulation proceeds, local internal stresses redistribute in the aging structure of the gel and the locations of more probable connection rupture (as well as their number) change over time. All simulations discussed here have been performed with a rate
is the largest (prevalently bonds between particles belonging to the network nodes). As the simulation proceeds, local internal stresses redistribute in the aging structure of the gel and the locations of more probable connection rupture (as well as their number) change over time. All simulations discussed here have been performed with a rate 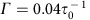 , corresponding to removing only ∼5% of the total network connections over the whole simulation time window. We have run several tests varying the removal rate in order to verify that changing the rate (having kept all other parameters constant) does not modify our outcomes and the emerging physical picture. Overall, varying Γ over nearly two orders of magnitudes, we recover the same results, as long as the τr=1/Γ between two rupture events allows for at least partial stress relaxation (see Fig. 1).
, corresponding to removing only ∼5% of the total network connections over the whole simulation time window. We have run several tests varying the removal rate in order to verify that changing the rate (having kept all other parameters constant) does not modify our outcomes and the emerging physical picture. Overall, varying Γ over nearly two orders of magnitudes, we recover the same results, as long as the τr=1/Γ between two rupture events allows for at least partial stress relaxation (see Fig. 1).
Stress autocorrelation function
The autocorrelation function of the stress fluctuations 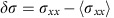 is computed as follows:
is computed as follows: 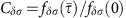 , where fδσ is the auto-covariance and takes the form
, where fδσ is the auto-covariance and takes the form 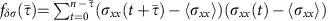 and
and 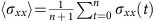 . We have computed the autocorrelation function of the stress fluctuations over partial time series and over the whole duration of the simulations (see Fig. 5 and Supplementary Fig. 2).
. We have computed the autocorrelation function of the stress fluctuations over partial time series and over the whole duration of the simulations (see Fig. 5 and Supplementary Fig. 2).
Fitting procedure for the intermediate scattering functions
To extract the β exponent and the structural relaxation time τq, we fit the last decay of the coherent scattering function F(q,t)tw=0 simultaneously with the incoherent scattering function 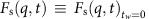 , defined as
, defined as 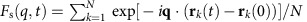 . This observable is less noisy and has the same exponent as the coherent scattering function shown in Fig. 3 (see also Supplementary Fig. 3). Having fitted Fs(q,t) with a stretched exponential type of the form
. This observable is less noisy and has the same exponent as the coherent scattering function shown in Fig. 3 (see also Supplementary Fig. 3). Having fitted Fs(q,t) with a stretched exponential type of the form 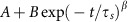 and having extracted the exponent β, such exponent is used to initiate the fit of F(q,t) by locking this parameter and letting all the others free. This procedure helps us to improve the quality of the fit used to extract the relaxation time τq from the coherent scattering.
and having extracted the exponent β, such exponent is used to initiate the fit of F(q,t) by locking this parameter and letting all the others free. This procedure helps us to improve the quality of the fit used to extract the relaxation time τq from the coherent scattering.
Data availability
The authors declare that all data supporting the findings of this study are available within the article and its Supplementary Information Files. All raw data can be accessed on request to the authors.
Additional information
How to cite this article: Bouzid, M. et al. Elastically driven intermittent microscopic dynamics in soft solids. Nat. Commun. 8, 15846 doi: 10.1038/ncomms15846 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Acknowledgments
The authors thank Jean-Louis Barrat, Ludovic Berthier, Luca Cipelletti, Thibaut Divoux, Ezequiel Ferrero, Kirsten Martens, Peter D. Olmsted and Veronique Trappe for insightful discussions. L.V.B. was supported from CAPES Foundation, Ministry of Education of Brazil (Proc. N 88888.059093/2013-00). E.D.G. acknowledges support from the Swiss National Science Foundation (Grant No. PP00P2 150738), the National Science Foundation (Grant No. NSF PHY11-25915). All authors thank Georgetown University.
Footnotes
The authors declare no competing financial interests.
Author contributions M.B., J.C. and E.D.G. designed the research; M.B. performed the research and analysed the data; J.C. and M.B. developed analytical tools; L.V.B. developed visualization tools. M.B. and E.D.G. wrote the paper.
References
- Trappe V. et al. Jamming phase diagram for attractive particles. Nature 411, 772 (2001). [DOI] [PubMed] [Google Scholar]
- Storm C. et al. Nonlinear elasticity in biological gels. Nature 435, 191–194 (2005). [DOI] [PubMed] [Google Scholar]
- Helgeson M. E., Moran S. E., An H. Z. & Doyle P. S. Mesoporous organohydrogels from thermogelling photocrosslinkable nanoemulsions. Nat. Mater. 11, 344–352 (2012). [DOI] [PubMed] [Google Scholar]
- Peter J. et al. Gelation of particles with short-range attraction. Nature 453, 499 (2008). [DOI] [PubMed] [Google Scholar]
- Gibaud T. et al. Unexpected decoupling of stretching and bending modes in protein gels. Phys. Rev. Lett. 110, 058303 (2013). [DOI] [PubMed] [Google Scholar]
- Perge C., Taberlet N., Gibaud T. & Manneville S. Time dependence in large amplitude oscillatory shear: a rheo-ultrasonic study of fatigue dynamics in a colloidal gel. J. Rheol. 58, 1331–1357 (2014). [Google Scholar]
- Hsiao L. C., Newman R. S., Glotzer S. C. & Solomon M. J. Role of isostaticity and load-bearing microstructure in the elasticity of yielded colloidal gels. Proc. Natl Acad. Sci. 109, 16029–16034 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conrad J. C. et al. Arrested fluid-fluid phase separation in depletion systems: Implications of the characteristic length on gel formation and rheology. J. Rheol. 54, 421–438 (2010). [Google Scholar]
- Rajaram B. & Mohraz A. Microstructural response of dilute colloidal gels to nonlinear shear deformation. Soft Matter 6, 2246–2259 (2010). [Google Scholar]
- Manley S. et al. Time-dependent strength of colloidal gels. Phys. Rev. Lett. 95, 048302 (2005). [DOI] [PubMed] [Google Scholar]
- de Gennes P. G. La percolation: un concept unificateur. Recherche 7, 919–927 (1976). [Google Scholar]
- Bouchaud J.-P. & Georges A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195, 127–293 (1990). [Google Scholar]
- Binder K. & Kob. W. Glassy Materials and Disordered Solids: An Introduction to Their Statistical Mechanics World Scientific (2005). [Google Scholar]
- Berthier L. et al. Dynamical Heterogeneities in Glasses, Colloids, and Granular Media Oxford University Press (2011). [Google Scholar]
- Segrè P. N., Prasad V., Schofield A. B. & Weitz D. A. Glasslike kinetic arrest at the colloidal-gelation transition. Phys. Rev. Lett. 86, 6042–6045 (2001). [DOI] [PubMed] [Google Scholar]
- Manley S. et al. Glasslike arrest in spinodal decomposition as a route to colloidal gelation. Phys. Rev. Lett. 95, 238302 (2005). [DOI] [PubMed] [Google Scholar]
- Bandyopadhyay R. et al. Evolution of particle-scale dynamics in an aging clay suspension. Phys. Rev. Lett. 93, 228302 (2004). [DOI] [PubMed] [Google Scholar]
- Jabbari-Farouji S., Wegdam G. H. & Bonn D. Gels and glasses in a single system: evidence for an intricate free-energy landscape of glassy materials. Phys. Rev. Lett. 99, 065701 (2007). [DOI] [PubMed] [Google Scholar]
- Krall A. H. & Weitz D. A. Internal dynamics and elasticity of fractal colloidal gels. Phys. Rev. Lett. 80, 778 (1998). [Google Scholar]
- Cipelletti L., Manley S., Ball R. C. & Weitz D. A. Universal aging features in the restructuring of fractal colloidal gels. Phys. Rev. Lett. 84, 2275–2278 (2000). [DOI] [PubMed] [Google Scholar]
- Ramos L. & Cipelletti L. Ultraslow dynamics and stress relaxation in the aging of a soft glassy system. Phys. Rev. Lett. 87, 245503 (2001). [DOI] [PubMed] [Google Scholar]
- Bellour M. et al. Aging processes and scale dependence in soft glassy colloidal suspensions. Phys. Rev. E 67, 031405 (2003). [DOI] [PubMed] [Google Scholar]
- Angelini R. et al. Dichotomic aging behaviour in a colloidal glass. Soft Matter 9, 10955–10959 (2013). [Google Scholar]
- Mansel B. W. & Williams M. A. K. Internal stress drives slow glassy dynamics and quake-like behaviour in ionotropic pectin gels. Soft Matter 11, 7016–7023 (2015). [DOI] [PubMed] [Google Scholar]
- Conrad H. et al. Correlated heterogeneous dynamics in glass-forming polymers. Phys. Rev. E 91, 042309 (2015). [DOI] [PubMed] [Google Scholar]
- Ruta B. et al. Silica nanoparticles as tracers of the gelation dynamics of a natural biopolymer physical gel. Soft Matter 10, 4547–4554 (2014). [DOI] [PubMed] [Google Scholar]
- Schosseler F., Kaloun S., Skouri M. & Munch J. P. Diagram of the aging dynamics in laponite suspensions at low ionic strength. Phys. Rev. E 73, 021401 (2006). [DOI] [PubMed] [Google Scholar]
- Guo H., Ramakrishnan S., Harden J. L. & Leheny R. L. Gel formation and aging in weakly attractive nanocolloid suspensions at intermediate concentrations. J. Chem. Phys. 135, 154903 (2011). [DOI] [PubMed] [Google Scholar]
- Chung B. et al. Microscopic dynamics of recovery in sheared depletion gels. Phys. Rev. Lett. 96, 228301 (2006). [DOI] [PubMed] [Google Scholar]
- Chaudhuri P. & Berthier L. Ultra-long-range dynamic correlations in a microscopic model for aging gels. arXiv:1605.09770. [DOI] [PubMed]
- Duri A. & Cipelletti L. Length scale dependence of dynamical heterogeneity in a colloidal fractal gel. Europhys. Lett. 76, 972 (2006). [Google Scholar]
- Cipelletti L. et al. Universal non-diffusive slow dynamics in aging soft matter. Faraday Discuss. 123, 237 (2003). [DOI] [PubMed] [Google Scholar]
- Bouchaud J. P. & Pitard E. Anomalous dynamical light scattering in soft glassy gels. Eur. Phys. J. E 6, 231–236 (2001). [DOI] [PubMed] [Google Scholar]
- Bouchaud J.-P. Anomalous relaxation in complex systems: from stretched to compressed exponentials anomalous transport: foundations and applications, 327–345 (2008).
- Ferrero E. E., Martens K. & Barrat J.-L. Relaxation in yield stress systems through elastically interacting activated events. Phys. Rev. Lett. 113, 248301 (2014). [DOI] [PubMed] [Google Scholar]
- Godec A., Bauer M. & Metzler R. Collective dynamics effect transient subdiffusion of inert tracers in flexible gel networks. New J. Phys. 16, 092002 (2014). [Google Scholar]
- Dinsmore A. D., Prasad V., Wong I. Y. & Weitz D. A. Microscopic structure and elasticity of weakly aggregated colloidal gels. Phys. Rev. Lett. 96, 185502 (2006). [DOI] [PubMed] [Google Scholar]
- Dibble C. J., Kogan M. & Solomon M. J. Structural origins of dynamical heterogeneity in colloidal gels. Phys. Rev. E 77, 050401 (2008). [DOI] [PubMed] [Google Scholar]
- Colombo J. & Del Gado E. Self-assembly and cooperative dynamics of a model colloidal gel network. Soft Matter 10, 4003–4015 (2014). [DOI] [PubMed] [Google Scholar]
- Colombo J. & Del Gado E. Stress localization, stiffening, and yielding in a model colloidal gel. J. Rheol. 58, 1089–1116 (2014). [Google Scholar]
- Colombo J., Widmer-Cooper A. & Del Gado E. Microscopic picture of cooperative processes in restructuring gel networks. Phys. Rev. Lett. 110, 198301 (2013). [DOI] [PubMed] [Google Scholar]
- Irving J. H. & Kirkwood J. G. The statistical mechanical theory of transport processes. iv. the equations of hydrodynamics. J. Chem. Phys. 18, 817–829 (1950). [Google Scholar]
- Del Gado E. & Kob W. Length-scale-dependent relaxation in colloidal gels. Phys. Rev. Lett. 98, 28303 (2007). [DOI] [PubMed] [Google Scholar]
- Saw S., Ellegaard N. L., Kob W. & Sastry S. Structural relaxation of a gel modeled by three body interactions. Phys. Rev. Lett. 103, 248305 (2009). [DOI] [PubMed] [Google Scholar]
- Lieleg O. et al. Slow dynamics and internal stress relaxation in bundled cytoskeletal networks. Nat. Mater. 10, 236 (2011). [DOI] [PubMed] [Google Scholar]
- Maccarrone S. et al. Ultra-long range correlations of the dynamics of jammed soft matter. Soft Matter 6, 5514–5522 (2010). [Google Scholar]
- Chaudhuri P., Berthier L. & Kob W. Universal nature of particle displacements close to glass and jamming transitions. Phys. Rev. Lett. 99, 060604 (2007). [DOI] [PubMed] [Google Scholar]
- Ciamarra M. P., Pastore R. & Coniglio A. Particle jumps in structural glasses. Soft Matter 12, 358–366 (2015). [DOI] [PubMed] [Google Scholar]
- Landau Lev D & Lifshitz E. M. in Theory of Elasticity (Course of Theoretical Physics) 3rd edn, Vol. 7, 109 (Butterworth-Heinemann, 1986).
- Ruta B. et al. Atomic-scale relaxation dynamics and aging in a metallic glass probed by x-ray photon correlation spectroscopy. Phys. Rev. Lett. 109, 165701 (2012). [DOI] [PubMed] [Google Scholar]
- Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19 (1995). [Google Scholar]
- Thompson A. P., Plimpton S. J. & Mattson W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 131, 154107 (2009). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors declare that all data supporting the findings of this study are available within the article and its Supplementary Information Files. All raw data can be accessed on request to the authors.