Electronic structure of aqueous solutions: Bridging the gap between theory and experiments

A predictive and efficient computational framework for describing the electronic properties of aqueous solutions is presented.

Abstract

Predicting the electronic properties of aqueous liquids has been a long-standing challenge for quantum mechanical methods. However, it is a crucial step in understanding and predicting the key role played by aqueous solutions and electrolytes in a wide variety of emerging energy and environmental technologies, including battery and photoelectrochemical cell design. We propose an efficient and accurate approach to predict the electronic properties of aqueous solutions, on the basis of the combination of first-principles methods and experimental validation using state-of-the-art spectroscopic measurements. We present results of the photoelectron spectra of a broad range of solvated ions, showing that first-principles molecular dynamics simulations and electronic structure calculations using dielectric hybrid functionals provide a quantitative description of the electronic properties of the solvent and solutes, including excitation energies. The proposed computational framework is general and applicable to other liquids, thereby offering great promise in understanding and engineering solutions and liquid electrolytes for a variety of important energy technologies.

INTRODUCTION

Liquid electrolytes are essential components of important devices used in a wide variety of emerging technologies, including solar water splitting, batteries, and supercapacitors, for energy conversion and storage (1–3). One of the essential prerequisites to predict and optimize the performance of these devices is the detailed understanding of the electronic properties of electrolytes, including their ionization potentials (IPs) and electron affinities (EAs). For example, a proper energy alignment at the electrode-electrolyte interface of photoelectrochemical (PEC) cells is key to achieving efficient hydrogen production (4–6). In addition, IPs and EAs of electrolytes determine their electrochemical windows and thereby the electrochemical stability of the electrode-electrolyte interface in lithium-ion batteries (7, 8). Establishing a predictive theory of the electronic properties of electrolytes, particularly aqueous solutions, that can be used to complement and guide experiments is therefore an important task.

Quantum mechanical methods that do not rely on a priori assumptions on the interatomic forces are excellently suited for this task. However, in practice, predicting the electronic structure of electrolytes based on quantum mechanics remains a great challenge because of the high computational complexity involved in the modeling of their finite temperature properties. In particular, first-principles molecular dynamics (MD) simulations of models consisting of at least hundreds of atoms are required to properly account for the structure of a liquid environment. In addition, an accurate and simultaneously efficient computational framework is desired for describing the electronic properties of the liquid.

Applications of highly accurate quantum chemistry methods, such as coupled-cluster theory, to liquid phases have not been possible because of the prohibitive computational cost and the difficulty of coupling these methods with MD. On the other hand, semilocal density functional theory (DFT) widely used for the simulations of condensed phases often fails to provide a quantitative description of the electronic properties of electrolytes, including simple salt solutions (9). Alternative approaches included the integration of quantum chemistry methods with solvation models, such as polarizable continuum models (10–12) and the effective fragment potential method (13); the former treat the electronic properties of the species of interest in a quantum mechanical region that is embedded in a dielectric continuum described by solvation models. It has been shown that the inclusion of a large quantum mechanical region may be important to account for the properties of complex solutions (12), and the results may significantly depend on the choice of the solvation models (13).

At variance with liquid electrolytes, a systematic hierarchy of approximate yet highly successful first-principles techniques has been established to describe the electronic properties of both pristine and defective semiconductors and insulators in the solid state. Of particular interest are recent developments of hybrid exchange-correlation functionals that contain a fraction of exact exchange (α) proportional to the inverse of the electronic dielectric constant (ε_∞) of the material [hereafter referred to as dielectric-dependent hybrid (DDH) functionals] (14–16). This class of functionals has been shown to provide a good description of the electronic properties not only of bulk materials but also of more complex systems, including band offsets of heterogeneous interfaces and defect charge transition levels in doped semiconductors (17–19). In addition, significant progress has been made in the past decade on post-DFT methods, including the development of efficient approaches for calculating the electronic properties of semiconductors in the framework of many-body perturbation theory (MBPT) (20). Owing to algorithmic advances (21, 22) and progress in high-performance computing, it has now become within reach to combine first-principles MD with hybrid functionals and MBPT to study liquid phases. Encouraging applications have been recently reported (23–27); however, the predictive power of these combined techniques has not been fully explored and systematically investigated.

Here, we present a predictive and efficient first-principles approach to describing the electronic properties of aqueous solutions. We extended first-principles techniques originally developed in solid-state physics for the study of defects to investigate the photoelectron (PE) spectra of aqueous solutions, particularly of solvated anions, and we validated our theoretical results by direct comparison with state-of-the-art liquid-jet PE experiments. We show that a combination of first-principles MD and electronic structure calculations using DDH functionals yields an excellent description of the PE spectra for a broad range of aqueous solutions, providing electronic energy levels of liquid water and solvated anions in quantitative agreement with experiments. In addition, the DDH functionals show comparable performance to the more sophisticated but computationally more expensive MBPT methods. Finally, we demonstrate how these theoretical techniques can be coupled with liquid-jet experiments to provide a detailed interpretation of experimental PE spectra and a direct mapping of chemical species to specific features of the spectra. We note that the experimental technique used here only provides information on the occupied electronic energy levels of aqueous solutions. Unoccupied electronic states can be accessed using other techniques, such as near-edge x-ray absorption fine structure spectroscopy (NEXAFS), which probes the excitation of atomic core electrons to unoccupied molecular orbitals. Because these orbitals are sensitive to the local chemical environment, NEXAFS is more sensitive to the structure and bonding of solutions than x-ray PE spectroscopy, and it has been used to determine the solvation environments of several of the molecules studied here, such as CO₃²⁻, HCO₃⁻, and NO₃⁻ (28, 29).

RESULTS AND DISCUSSION

Accuracy of the computational approach

We first address the performance of different electronic structure theories for a specific, representative ion in water, that is, NO₃⁻, which is commonly used in aqueous electrolytes for high-voltage supercapacitors (30) and solar-to-fuel conversion (31). We focus on anions because their frontier electronic energy levels are usually either close to the band edges of liquid water or within its bandgap and hence directly influence the chemical reactivity of species in solutions. We note that liquid water can be considered as a wide bandgap insulator, and simple anions/cations in water play the same role as defects in insulators and semiconductors (32, 33).

In Fig. 1, we show the PE spectrum (red line) of a 1.0 M NaNO₃ aqueous solution measured by liquid microjet techniques (see Materials and Methods), compared to the results obtained at different levels of theory. Several bands are present, corresponding to the binding energies (BEs) of valence electrons excited into vacuum. The bands are labeled (see bottom panel) according to the symmetry of single-particle states from which the emission occurs. Three peaks (1b₂, 3a₁, and 1b₁) are due to electrons ejected from water molecules; the peak corresponding to the NO₃⁻ highest occupied molecular orbital (HOMO) level is located at 9.42 eV (the full spectrum that includes the cation signal is reported in fig. S1).

Fig. 1. PE spectra of the NO₃⁻ solution.

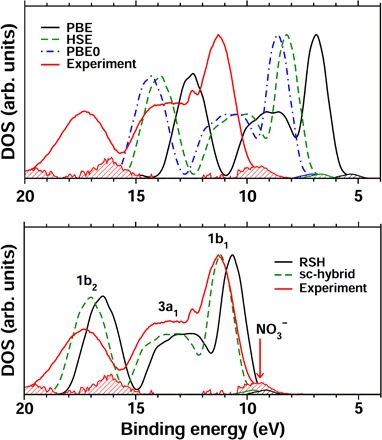
The theoretical results were obtained with DFT using several functionals: PBE, HSE, and PBE0 (top panel), as well as RSH and sc-hybrid functionals (bottom panel). The experimental PE spectrum is indicated by the red solid line. The corresponding shaded areas represent the differential valence PE spectra obtained by subtracting the water spectrum from raw experimental NaNO₃ spectra, and theoretical density of state (DOS) contributions from the NO₃⁻ HOMO. All energy levels are relative to vacuum. Experimental and theoretical DOS intensities were rescaled with respect to the 1b₁ peak of water at 11.31 eV. The differential spectra and theoretical HOMO DOS intensity were magnified (three times) for clarity.

The calculated valence PE spectra shown in Fig. 1 were obtained as DFT Kohn-Sham energies with semilocal [Perdew, Burke, and Ernzerhof (PBE)] and hybrid [Heyd, Scuseria, and Ernzerhof (HSE) and PBE0] functionals (top panel); the latter are commonly used for examining the electronic properties of semiconductors (14, 34). In addition, we considered newly developed range-separated hybrid (RSH) and self-consistent hybrid (sc-hybrid) functionals (bottom panel), which have been shown to provide accurate results for excited-state properties of extended and finite systems (15, 16). The sc-hybrid and RSH functionals include a fraction of exact exchange equal to the inverse macroscopic dielectric constant of water, determined self-consistently from first-principles to be 0.6098. The attenuation parameter in the RSH functional was determined nonempirically and set to the Thomas-Fermi screening length of liquid water, that is, 0.58 bohr⁻¹ (15, 16). We note that calculations of semiconductor bandgaps and vertical IPs of gas-phase molecules have shown a weak dependence of the results on the choice of the attenuation parameter entering the RSH functional (16).

As expected, the PBE functional severely underestimates experimental results, and the HSE and PBE0 improve the agreement with experiments; however, significant errors remain. On the other hand, RSH and sc-hybrid reproduce the main features of the PE spectrum well, providing the water valence band maximum (VBM) and BEs in agreement with experiments to within about 5%, and the NO₃⁻ IP to within 0.3 eV as compared to experimental data. The overall performance of different DFT calculations is summarized in Fig. 2 using the mean absolute percentage error (MAPE) of the theoretical NO₃⁻ IP, water BEs, and water VBM with respect to the corresponding experimental values. It is shown that the RSH and sc-hybrid functionals exhibit the best performance, yielding errors of 3.9 and 2.3% compared to experiments, respectively. We also note that the relative difference between the ion IP and the water VBM is weakly sensitive to the choice of the density functional, indicating that the error of the ion IP obtained at the conventional PBE level of theory is largely due to the underestimation of the water VBM, as already pointed out in other studies (35, 36).

Fig. 2. Accuracy of theoretical approaches.

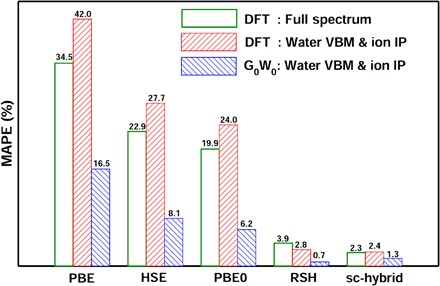
The green boxes represent MAPEs between experiments and DFT calculations, as computed for the NO₃⁻ IP, water VBM, and all water BEs. The red and blue boxes correspond to the MAPEs computed only for the NO₃⁻ IP and water VBM, as obtained with DFT and G₀W₀ calculations, respectively. Theoretical calculations include DFT and G₀W₀ with several exchange-correlation functionals: PBE, HSE, PBE0, RSH, and sc-hybrid functionals (see text).

In addition to DFT calculations, electronic properties of aqueous solutions were investigated using MBPT. Quasi-particle energies, which correspond directly to excitation energies measured in PE spectroscopy, were determined at the G₀W₀ level of theory using DFT wave functions. The G₀W₀ calculations were carried out using the scheme recently proposed by Govoni and Galli (22), Nguyen et al. (37), and Pham et al. (38), which allows for controlled convergence of quasi-particle energies. Only the water VBM and NO₃⁻ IP were computed due to the high computational cost of MBPT calculations (see Table 1).

Table 1. Electronic structure of the NO₃⁻ solution.

The water VBM and BEs (1b₁, 3a₁, 1b₂, and 2a₁) and the NO₃⁻ IP were computed using DFT and MBPT at the G₀W₀ level with different exchange-correlation functionals (see text). All electronic energies (eV) are referred to vacuum using the average potential computed at the same level of theory for water surface models (see Materials and Methods).

Method	2a1	1b2	3a1	1b1	Water VBM	NO3− IP
DFT@PBE	24.35	12.44	9.11	6.89	5.83	5.37
DFT@HSE	27.20	13.94	10.61	8.27	7.16	6.81
DFT@PBE0	27.59	14.36	11.00	8.69	7.53	7.15
DFT@RSH	30.41	16.49	13.04	10.66	9.57	9.21
DFT@sc-hybrid	32.16	17.01	13.61	11.15	10.08	9.70
G0W0@PBE	—	—	—	—	8.42	7.72
G0W0@HSE	—	—	—	—	9.23	8.54
G0W0@PBE0	—	—	—	—	9.40	8.73
G0W0@RSH	—	—	—	—	10.02	9.40
G0W0@sc-hybrid	—	—	—	—	10.10	9.48
Experiment	30.9030	17.4131	13.7831	11.3131	9.9030	9.42

Results presented in Table 1 and Fig. 2 show that G₀W₀ definitely outperforms DFT when PBE, HSE, and PBE0 wave functions are used. On the other hand, G₀W₀ calculations based on RSH and sc-hybrid wave functions show only modest improvement compared to DFT. Specifically, the MAPEs with respect to the experiment of NO₃⁻ IP and water VBM are 0.7 and 1.3% for G₀W₀@RSH and G₀W₀@sc-hybrid, respectively, as compared to values of 2.8 and 2.4% obtained with DFT@RSH and DFT@sc-hybrid. Overall, these results indicate that RSH and sc-hybrid functionals provide an accurate and robust description of the electronic properties of liquid water and the NO₃⁻ ion within a DFT framework while requiring a much lower computational cost than G₀W₀ calculations. This conclusion is consistent with a previous study of aqueous solutions with simple ions, that is, Na⁺ and Cl⁻ (26).

Theoretical predictions

Having established the level of theory capable of providing a proper description of the electronic properties of the representative NO₃⁻ solution, we extended our study to other aqueous solutions to examine the predictive power of first-principles MD coupled with DDH functionals. The moderate computational cost of the hybrid functional calculations allowed us to investigate a relatively large set of ions. In particular, we considered 15 additional solutions containing solvated ions with different atomic species and charge states, which are of interest in studies of electrochemical energy conversion and storage, including NO₂⁻, SO₄²⁻, SO₃²⁻, HCO₃⁻, CO₃²⁻, PO₄³⁻, HPO₄²⁻, ClO₄⁻, ClO₃⁻, ClO₂⁻, and ClO⁻ (30, 39–42) and CN⁻, OCN⁻, SCN⁻, and SeCN⁻ (43, 44). The structural models of the solutions were generated using the same simulation protocol used for NO₃⁻. The IPs of solvated ions were computed using DFT with RSH and sc-hybrid functionals, and we compared the theoretical results to PE liquid-jet experiments (see table S1 for details).

Comparison between RSH and sc-hybrid functional calculations and liquid-jet experiments for the IPs of 16 solvated ions is reported in Fig. 3. The overall agreement between theory and experiment is very good, yielding a mean absolute error of 0.14 and 0.11 eV when using RSH and sc-hybrid functionals, respectively. In addition, we found that the discrepancy between theory and experiment is less than 0.5 eV for all ions in a wide energy range of IPs. Compared to RSH, the sc-hybrid functional systematically predicts larger IPs by 0.15 to 0.50 eV, leading to a slightly better overall agreement with experiments. These results provide robust evidence for the predictive power of the DDH functionals in describing the electronic properties of aqueous solutions.

Fig. 3. Theoretical predictions.

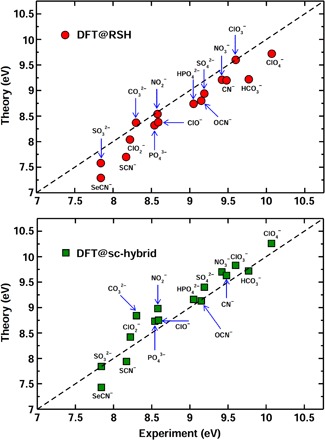
The IPs of 16 solvated anions computed with DFT and the RSH (circles, top panel) and sc-hybrid (squares, bottom panel) functionals compared with liquid-jet experimental measurements.

Our study of a wide variety of aqueous solutions also allowed for investigating the ion effects on the electronic properties of liquid water. The latter appears to be slightly perturbed in the presence of ions at the concentration considered here, that is, the water 1b₁ BE and VBM computed for different aqueous solutions show small variations on the order of 0.3 eV. However, we emphasize that ion effects may be more significant for solutions with higher salt concentrations.

To further corroborate the predictive capability of our theoretical framework, we investigated the sensitivity of the results to the details of the simulation protocol. We find that the ion IP is not sensitive to the level of theory used in the MD simulation when comparing semilocal and hybrid functionals at similar temperatures. For example, using simulation trajectories generated with PBE and PBE0, we found that the IP of CO₃²⁻ shows a small variation on the order of 0.2 eV (Supplementary Materials). In addition, the use of a fraction of exact exchange α determined from the electronic dielectric constant ε_∞ of aqueous solutions instead of that of liquid water does not significantly affect the reported IPs. This is due to a weak dependence of the refractive index on ion concentration and composition (45), which results in a small change of ε_∞. Taking the 1.5 M Na₂CO₃ solution as an example, we found that using α determined from the experimental value of ε_∞ = 1.85 for the solution (ε_∞ = 1.78 for liquid water) resulted in a variation within 0.2 eV of the IP of CO₃²⁻. We also considered finite-size errors in the calculation of ion IPs, which stem from the interaction between periodic images of the ion and the neutralizing background (19). Although accounting for finite-size errors in simulations of aqueous liquids remains a topic of active research (46), finite-size corrections can be estimated reasonably well by following the scheme used for charged defects in semiconductors. Specifically, the leading contribution to the error in defect electronic energy levels is proportional to ε⁻¹V^−1/3, where ε and V are the dielectric constant of the semiconductor and the volume of the simulation cell, respectively (19, 47–49). Here, the use of the static dielectric constant of liquid water (ε₀ = 78) (50) is appropriate because in our computational framework, we only compute the electronic structure of solvated ions in their ground-state atomic configuration, which is obtained with MD and is thus in thermal equilibrium with the solvent (51). That is, we deduce the ion IPs from the electronic structure of the unperturbed ions in their ground state, instead of computing the IPs as total energy differences between two different oxidation states of the ions. This results in a small finite-size error in the calculated IPs, for example, on the order of 0.1 eV for NO₃⁻ for the supercell used here, indicating that finite-size errors in aqueous solutions are largely mitigated by the high static dielectric constant, unlike most solid semiconductors that exhibit much smaller dielectric constants. We note that the second-order correction to the finite-size effects is proportional to V⁻¹; this is discussed in more detail by Ayala and Sprik (52) and in the Supplementary Materials.

Finally, we emphasize that at variance with calculations using solvation models (53, 54), DFT with the DDH functionals represents a fully quantum mechanical approach that treats the solutes and solvent on an equal footing. Although the use of solvation models has successfully reproduced experimental IPs for several ions (10, 11, 13), there is growing evidence that a large number of explicit water molecules are needed for a proper description of complex ions (12, 55). To highlight the importance of a quantum mechanical treatment for the liquid environment, we discuss in detail the solvated PO₄³⁻ ion that has been theoretically investigated using a hybrid model consisting of a solvated ion cluster and a dielectric continuum (12). In particular, we report in Fig. 4 the PO₄³⁻ spectrum obtained from the measurement of a 0.4 M Na₃PO₄ solution, which exhibits two peaks at 8.5 and 9.9 eV. Calculations by Pluhařová et al. (12) showed that at least two solvation shells of explicit water are required to recover the peak at 8.5 eV that corresponds to the anion HOMO level; however, the higher BE peak in the experimental spectrum was not successfully reproduced. We found that DFT with the sc-hybrid functional not only recovers the double-peak feature in the experimental spectrum but also yields the peak positions in good agreement with experiment (within 0.4 eV) while allowing for identifying the peak at 9.9 eV as the (HOMO-1) level of PO₄³⁻. This finding underscores the need for a fully quantum mechanical approach to obtain a proper description of the electronic properties of complex solvated ions.

Fig. 4. PE spectra of the PO₄³⁻ solution.

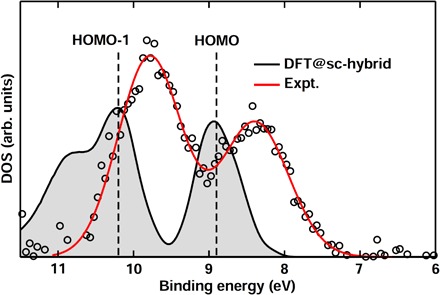
Differential valence PE spectra, measured by liquid-jet techniques, of a 0.4 M Na₃PO₄ solution, obtained by subtracting the water spectrum from the raw Na₃PO₄ spectrum. The decompose fit of the experimental spectral (open circles) is indicated by the red line. DOS computed with DFT and the sc-hybrid functional for the solvated PO₄³⁻ ion is indicated by the gray areas. The anion HOMO and HOMO-1 levels identified from calculations are indicated by the dashed lines. Experimental and theoretical DOS intensities were rescaled with respect to the lower BE peak.

Interpretation of experiments

When coupled with experiments, particularly the liquid-jet technique, the theoretical method presented here offers great promise for a detailed investigation of complex aqueous solutions, beyond the determination of the ion IPs. In particular, it can be used to interpret the origin of experimental features and elucidate the relationship between chemistry and electronic properties. We present below an example of the K₂CO₃ and KHCO₃ solutions, and we focus our discussion on the results obtained with sc-hybrid functional because it exhibits a slightly better overall performance than the RSH for the ion set presented in the previous section.

The liquid-jet PE spectrum of the K₂CO₃ solution (Fig. 5A) exhibits two distinct peaks at 9.77 and 8.3 eV, which may be simply assigned based on the comparison with the KHCO₃ spectrum (Fig. 5B). In particular, the latter shows a broad peak around 10 eV while lacking one at 8.3 eV. This suggests that the lower BE peak in the K₂CO₃ spectrum might be assigned to electrons ejected from CO₃²⁻ only, whereas the higher one may arise from the HCO₃⁻ presence in the K₂CO₃ solution because of the protonation of CO₃²⁻.

Fig. 5. PE spectra of the HCO₃⁻ and CO₃²⁻ solutions.

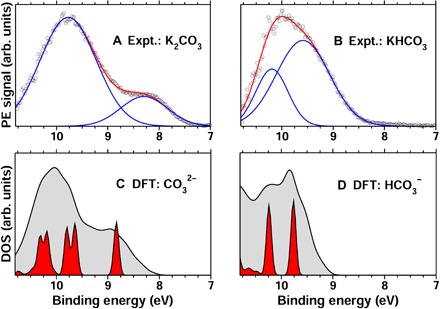
(A and B) Differential valence PE spectra, measured by liquid-jet techniques, of 1 M K₂CO₃ (A) and KHCO₃ (B) aqueous solutions, obtained by subtracting the water spectrum from the raw 1 M KHCO₃ and K₂CO₃ spectra, respectively. The experimental spectra (open circles, Expt.) are decomposed into two Gaussians (blue), with the composite fit shown in red. (C and D) DOS computed with DFT and the sc-hybrid functional for solvated CO₃²⁻ and HCO₃⁻ ions are indicated by the gray areas in (C) and (D), respectively. Projected DOS of a representative snapshot [red areas in (C) and (D)] is also presented, showing the positions of different molecular orbitals for each ion [in increasing order of BE, from HOMO to HOMO-4 in (C) and from HOMO to HOMO-1 in (D)].

Theoretical calculations provide a more complete and complex interpretation of the PE spectra. Consistent with experiments, the DOS computed for the solvated HCO₃⁻ shows a broad peak around 10 eV (Fig. 5D), thereby supporting the abovementioned interpretation. However, we found that CO₃²⁻ also exhibits large DOS in this energy range, which stems from molecular orbitals with higher BEs than the HOMO (Fig. 5C). We therefore conclude that the peak at 8.3 eV in the K₂CO₃ spectrum corresponds to the CO₃²⁻ HOMO, whereas the one at 9.77 eV has two contributions, that is, from CO₃²⁻ molecular orbitals higher in BE than the HOMO and from HCO₃⁻ molecular orbitals. The latter were found to be the HOMO and HOMO-1 levels of HCO₃⁻ based on our theoretical calculations. This example demonstrates that the combined use of first-principles simulations and liquid-jet experiments provides a powerful tool that allows for the identification of chemical species in the solutions and a direct mapping between chemical species and PE signals.

CONCLUSIONS

In summary, we reported a joint theoretical and experimental study of the electronic properties of aqueous solutions, focused on solvated anions, whose frontier electronic energy levels often play a key role in determining the chemical reactivity of the solutions. We showed that DFT calculations with DDH functionals provide a predictive approach for the study of the electronic properties of aqueous solutions, allowing for a quantitative description of both the solvent PE spectra and the solute electronic energy positions. This level of theory shows similar performance compared to more sophisticated, yet computationally more expensive, MBPT calculations. In addition, we demonstrated that the proposed theoretical technique provides a powerful tool for the interpretation of experimental spectra, allowing for detailed mapping between specific photoemission signals and chemical species. The functionals used here were derived from first-principles methods that treat the solutes and solvents on an equal footing and can be applied to any nonmetallic liquid. Our computational framework paves the way to understanding and engineering the electronic properties of liquid electrolytes for important technologies, such as PEC cells for hydrogen production and ionic liquid for batteries.

MATERIALS AND METHODS

MD simulations

All aqueous solutions were simulated using cubic cells consisting of one anion and 63 water molecules with the cell size chosen to yield the experimental water density under ambient conditions, corresponding to a 0.87 M concentration. Counterions were not included, and a positive uniform background charge was used to obtain a neutral system. Born-Oppenheimer molecular dynamics (BOMD) simulations were carried out in the microcanonical ensemble using the Qbox code (http://qboxcode.org/) (56), with interatomic forces derived from DFT using the PBE approximation for the exchange and correlation energy functional (57). The interaction between valence electrons and ionic cores was represented by norm-conserving pseudopotentials (58, 59), and the electronic wave functions were expanded in a plane-wave basis set truncated at a cutoff energy of 85 rydberg (Ry). Hydrogen atoms were replaced with deuterium to increase the allowable time step, which was chosen to be 10 atomic units in all simulations. An elevated temperature of 400 K was used to recover the experimental water structure at T = 300 K (60–62). Analyses of electronic properties were carried out for trajectories collected over 40 ps after a 15-ps equilibration.

The PBE0 simulation of the CO₃²⁻ ion was carried out using the same protocol as described above for PBE simulations. The recursive subspace bisection algorithm with a threshold of 0.02 was used (63); this value was chosen based on a previous study of a NaCl solution, showing that the use of the bisection algorithm with a threshold of 0.02 was an excellent approximation to obtain both structural and electronic properties of the solution while allowing for up to a 10-fold acceleration of BOMD simulations with hybrid functionals (64). Electronic structure calculations were performed using a 20-ps NVT (canonical ensemble) trajectory after a 5-ps equilibration run.

Electronic structure calculations

Calculations of the electronic properties with hybrid functionals were carried out using the Quantum-ESPRESSO (65) and WEST (http://west-code.org/) (22) codes. The DOS of each solution was computed using a Gaussian smearing of 0.14 eV and averaged over 100 equally spaced snapshots along the simulation trajectory of 40 ps. The water VBM and ion IPs were computed based on the projected DOS.

MBPT calculations were carried out using the WEST code. The quasi-particle energies E_n^qp were computed within the G₀W₀ approximation as a first-order correction to the Kohn-Sham (KS) energies ε_n

$${{\mathit{E}}_{\mathit{n}}}^{\text{qp}}={\mathrm{\epsilon }}_{\mathit{n}}+<{\mathrm{\psi }}_{\mathit{n}}|{\mathrm{\Sigma }}_{{\mathrm{G}}_0{\mathrm{W}}_0}({{\mathit{E}}_{\mathit{n}}}^{\text{qp}})|{\mathrm{\psi }}_{\mathit{n}}>-<{\mathrm{\psi }}_{\mathit{n}}|{{\mathit{V}}_{\text{xc}}}^{\text{GKS}}|{\mathrm{\psi }}_{\mathit{n}}>$$

where V_xc^GKS is the exchange-correction potential in the generalized KS Hamiltonian and Σ_G0W0 is the self-energy operator computed from the one particle Green’s function (G₀) and the screened Coulomb interaction (W₀). (20). G₀W₀ calculations based on PBE wave functions and eigenvalues were carried out for 20 equally spaced snapshots along the simulation trajectory, whereas those started from hybrid functionals were performed for a single representative snapshot because of their high computational cost compared to semilocal functionals.

Direct comparison between theoretical calculations and liquid-jet experiments requires the evaluation of energy levels relative to vacuum. Absolute DFT and G₀W₀ single-particle energies were determined using the average electrostatic potential computed for water surface models, as discussed in detail in our previous studies (23, 26). This computational scheme is similar to the one used in solid-state physics for the determination of metal work functions and semiconductor band positions (66). It has also been demonstrated to provide electronic band positions of liquid water and simple ions, consistent with those derived from thermodynamic integration techniques (24, 25).

Liquid-jet experiments

PE measurements were performed at the U41-PGM undulator beamline at the synchrotron radiation facility BESSY II in Berlin, Germany. The liquid microjet with a diameter of 24 μm was injected into the vacuum chamber from a fused silica nozzle. The jet velocity was approximately 40 ms⁻¹, and the temperature was 6°, except for NaH₂PO₄, Na₂HPO₄, and Na₃PO₄ salt measurements, where we used 20° for solubility reasons. Details of the liquid microjet technique and of the experimental setup have been described previously (67–69). The energy resolution of the U41-PGM beamline was better than 60 meV at a 200-eV photon energy used for the liquid water valence PE measurements. The resolution of the hemispherical energy analyzer, 100 meV at a 10-eV pass energy, was constant with kinetic energy. The small focal size (23 μm × 12 μm) of the incident x-ray beam matches the diameter of the liquid jet that leads to a minimal (5%) PE signal contribution from gas-phase water surrounding the jet.

All salt solutions were freshly prepared and immediately injected into the vacuum. Salts were purchased from Sigma-Aldrich (purity, >98%) and not further purified. The counterion in each case was sodium or potassium. All solutions were measured at different concentrations, usually 0.25, 0.5, 1, and 2 M; exceptions are the abovementioned phosphate salts (measured at 0.4 M) and Na₂SO₄ (only at 1 M). Valence PE spectra were energy-calibrated against the 1b₁ level of water, which is 11.31 eV (70). Note that a pressure-driven liquid stream in the discharging capillary disrupts an electric double layer created at the interface between the inner wall of the liquid-jet nozzle and the liquid (68, 70, 71). This leads to a streaming potential, Ф_str, caused by the charge that is transported by the mobile region of the stream. At a particular electrolyte (salt) concentration (20 to 100 mM), Ф_str exactly disappears (70). Studies on halide aqueous solutions, where these Ф_str values have been determined, show that previous determinations of solute BEs from several electrolytes and water were typically off by 0.1 to 0.3 eV (70).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/6/e1603210/DC1

Photoelectron spectra of the NaNO₃ solution

Calculated CO₃²⁻ IPs for different simulation trajectories

IPs of solvated ions

Finite-size effects

fig. S1. Photoelectron spectra of a 1.0 M NaNO₃ solution measured by the liquid-jet technique.

fig. S2. Radial distribution functions of water molecules computed for CO₃²⁻ solutions generated using PBE at 380 K (black) and 400 K (red) and using PBE0 at 380 K (blue).

fig. S3. Radial distribution functions of carbon-water oxygen and carbon-water hydrogen computed for CO₃²⁻ solutions generated using PBE at 380 K (black) and 400 K (red) and using PBE0 at 380 K (blue).

fig. S4. DOS computed with DFT and the PBE functional for CO₃²⁻ solutions generated with PBE at 400 K (red), PBE at 380 K (blue), and PBE0 at 380 K (green).

table S1. IPs (eV) of selected solvated ions computed using DFT with RSH and sc-hybrid density functionals, compared with PE liquid-jet measurements.