Effect of Binding Pose and Modeled Structures on SVMGen and GlideScore Enrichment of Chemical Libraries

Abstract

Virtual screening consists of docking libraries of small molecules to a target protein followed by rank-ordering of the resulting structures using scoring functions. The ability of scoring methods to distinguish between actives and inactives depends on several factors that include the accuracy of the binding pose during the docking step and the quality of the three-dimensional structure of the target. Here, we build on our previous work to introduce a new scoring approach (SVMGen) that uses machine learning trained with features from statistical pair potentials obtained from three-dimensional crystal structures. We use SVMGen and GlideScore to explore how enrichment or rank-ordering is affected by binding pose accuracy. To that end, we create a validation set that consists strictly of proteins whose crystal structure was solved in complex with their inhibitors. For the rank-ordering studies, we use crystal structures from PDBbind along with corresponding binding affinity data provided in the database. In addition to binding pose, we investigate the effect of using modeled structures for the target on the enrichment performance of SVMGen and GlideScore. To accomplish this, we generated homology models for protein kinases in DUD-E for which crystal structures are available to enable comparison of enrichment between modeled and crystal structure. We also generate homology models for kinases in SARfari for which there are many known small-molecule inhibitors but no known crystal structure. These models are used to assess the ability of SVMGen and GlideScore to distinguish between actives and decoys. We focus our work on protein kinases considering the wealth of structural and binding affinity data that exists for this family of proteins.

Graphical abstract

INTRODUCTION

Structure-based virtual screening is commonly used to enrich chemical libraries to identify active compounds that can serve as tools in chemical biology or as leads for drug discovery.¹ A library of small molecules is first docked to a binding site on the structure of a protein followed by the re-scoring and rank-ordering of the resulting protein-compound structures in a process known as scoring. Several docking methods have been implemented in widely-used computer programs such as AutoDock,^{2, 3} Glide,^{4, 5} and Gold.⁶ Algorithms and scoring methods to predict the binding mode of small molecules have matured significantly, but there is a need for better scoring methods to rank-order protein-compound structures.⁷ The performance of scoring methods is often target-specific. This has led to a constant need to develop better scoring methods. Several scoring approaches have been developed ranging from empirical,^{5, 8} force field,^{6, 9} and knowledge-based.^{10, 11} Increasingly, scoring methods are using machine learning techniques to improve database enrichment and rank-ordering.^{12, 13}

The performance of scoring approaches in enriching compound libraries is often explored using validation sets such as DUD-E,¹⁴ DEKOIS,¹⁵ and others.^{16, 17} These datasets provide a set of actives and matching decoys that are used to test the ability of scoring methods to distinguish actives from decoys. Both actives and decoys are docked to their corresponding target, and the resulting complexes are re-scored. Performance is evaluated using enrichment or receiver operating characteristic (ROC) plots. One limitation of these datasets is that there is generally no crystal structure of the active compounds bound to their corresponding targets. Molecular docking is used to predict the binding mode of active compounds. Considering that docking results in high-quality binding modes in only a fraction of binding sites, it is difficult to determine whether limitations in re-scoring methods are due to lack of accuracy in the binding mode, or inherent limitations in the re-scoring method. The lack of accuracy in docking can also impact the re-scoring of compounds during virtual screening. Ideally, a re-scoring method should favor compounds with correct binding poses.

Despite the exponentially-growing list of crystal structures, a majority of proteins of the human proteome have yet to be solved. For example, among the 518 kinases of the human kinome, less than half have been solved by crystallography. This poses a significant impediment to the rational design of selective small-molecule kinase inhibitors. Recent studies have shown that even FDA-approved drugs often have a large number of additional targets.^18–20 These off-targets may be responsible for the failure of the majority of kinase inhibitors in the clinic, despite the often overwhelming evidence to support a role of their target in the disease of interest. To address this limitation, recent efforts have concentrated on building homology models for all unsolved kinases of the human kinome.²¹ A question of interest is how these modeled structures affect scoring and re-scoring performance during virtual screening. Understanding how homology models affect rank-ordering could help to develop better ranking methods for these modeled structures. This will enable the use of all structures of a protein family during virtual screening, which could enhance our ability to identify selective kinase ATP-competitive inhibitors and reduce the failure of drugs in the clinic.

Recently, we introduced an innovative approach for re-scoring protein-compound structures. The method combines knowledge-based potentials with machine learning.²² We called the scoring method SVMSP to highlight the fact that information from the target of interest is used to derive the scoring function. The approach consisted of training Support Vector Machine (SVM) using knowledge-based potentials as features. These potentials were determined using three-dimensional co-crystal structures from the Protein Databank (PDB) for the positive set. This was, to the best of our knowledge, the first attempt to develop a re-scoring method using machine learning trained on three-dimensional structures of proteins and small molecules. The negative set consisted of randomly-selected small molecules docked to the target of interest.¹² Generally, SVMSP performed well in database enrichment, particularly among proteins for which a large number of structural data is available, such as protein kinases.¹³ Since SVMSP is target-specific, a scoring approach must be developed for every target. While this feature resulted in rank-ordering that was consistently high even among different protein families, a scoring method has to be developed separately for each target.

Here, we report a general scoring approach, namely Support Vector Machine General (SVMGen), a significant departure from previous work since it can be used in virtual screening to any binding site. We investigate how the accuracy of the binding pose of compounds affect the enrichment power and rank-ordering ability of SVMGen and GlideScore. To explore how sensitive the scoring methods are to the binding mode, we create a validation set that consists of proteins whose structure was solved with all the actives of the set. To investigate the effect of using homology models in enrichment, we create validation sets using SARfari, which is a repository that includes known kinase compounds with screening data. Throughout, SVMGen is compared to GlideScore, and both Vina and Glide are used for docking. We focus this work on protein kinases, which are ideal for developing and testing scoring methods considering the wealth of binding and inhibition data as well as the large number of structures that are available.

METHODS

Generation of Scoring Approach

SVMGen uses pairwise potentials of docked protein-ligand pairs for classification and rank-ordering. The previously described knowledge-based potentials ^{12, 23} were derived from crystal structures of protein-ligand complexes using SYBYL atom types. Pairs between these atom types are used to generate the 76 features of the SVM model. Like the previously-described SVMSP model,²² SVMGen uses 763 kinase structures from the sc-PDB database (v2012)²⁴ for the positive training set. The main innovation in SVMGen is that the scoring approach is trained on potentials of 5000 randomly selected receptor-ligand pairs.^{22, 25} Unlike the previous SVMSP models, which featured a negative training set of ligands docked to the pocket of interest, SVMGen uses a generalized approach, which can be applied to any pocket without regenerating the SVM model for each target. Features in the training set were normalized using LIBSVM²⁶ onto a 0 to 1 scale. The generalized model was generated using the computer program SVM^light27 using a radial basis function kernel and a cost function of 1. Other parameters were set to default values.

Docking and Rescoring

Kinase structures were retrieved from the Protein Data Bank (PDB)²⁸ and solvent molecules and bound ligands were removed. Selenomethonine residues were converted to methionine using the Protein Preparation Wizard²⁹ workflow in Schrödinger (Schrödinger LLC, New York, NY, 2014). Missing sidechains and loops were added with the Prime³⁰ module in Schrödinger. Disulfide bonds were added and each crystal structure was protonated using PROPKA³¹ at pH 7.0. The prepared structures were saved as Sybyl Mol2 files and PDB formatted-files for further analysis.

Structures were docked with AutoDock Vina³ and Glide.³² Gasteiger charges were added to the PDB structures using the MGLTools package.² A 21 Å box centered on the ATP binding pocket or co-crystallized inhibitor was used for both docking methods. In addition, a 14 Å inner box was used for the Glide grids. All other parameters were set to default values. The GlideSP method was used for all Glide-related docking with the exception of the crystal structures and high-quality homology models for the DUD-E targets, which used GlideHTVS. The binding pose of protein-ligand complexes obtained either from co-crystallized structures or from docked complexes were assessed using a combination of GlideScore³³ and SVMGen. Structures re-scored using Glide were minimized in place from the original binding pose to allow for slight variations in the docking functions between the different approaches.

Co-crystallized Kinase Complexes

A set of well-characterized kinase-compound complexes was retrieved from both the PDBbind refined and general sets (v2014).³⁴ Kinase structures were identified using Enzyme Commission (EC) codes and were limited to protein-tyrosine kinases (EC 2.7.10), protein-serine/threonine kinases (EC 2.7.11), and dual-specificity kinases (EC 2.7.12). Structures that featured short peptides or that were part of the SVMGen training set were discarded. In addition, small molecules that did not bind within the conserved ATP binding site were discarded. A set of 1000 potentially redundant binding poses was generated for each structure by iterating over a series of 50 runs generating 20 poses each in AutoDock Vina.³ In these runs, exhaustiveness was set to 16, the energy range to 10, and the number of modes to 20. The root-mean-squared deviation (RMSD) of heavy atoms in the ligand between each of the 1000 binding poses was determined to form a distance matrix between each pose. These distances were hierarchically clustered to 20 clusters using average linkage. The pose corresponding to the cluster center was used as the representative structure for each cluster and was retained for docking and rescoring.

Homology Modeling

Kinases for homology modeling were retrieved from two sources: DUD-E¹⁴ and SARfari.³⁵ All 26 targets from the kinase subset of DUD-E were collected and mapped to their respective UniProt entries in UniProtKB. Kinases from SARfari were selected based on the number of known inhibitors with activity (IC₅₀, K_d, or K_i) of 1 μM or better. Those with available human crystal structures or that were present in DUD-E were discarded. The top 20 kinases were used to generate the SARfari kinase set. The FASTA sequence of the protein kinase domain was retrieved from UniProt and used as the initial query template for homology modeling in Prime.³⁰

Two strategies were used to select the template for constructing the homology models. The first strategy uses the highest scoring crystal structure of a different kinase from the BLAST search as the template for the subsequent modeling. The second strategy identifies a template with low sequence identity, i.e. between 20 and 50%. The ClustalW³⁶ alignment method was used to calculate the alignment between the query and template. The homology models were built using knowledge-based models. In this approach, insertions and gaps are added using segments from existing structures. All other parameters were kept to default values during the modeling process. Following the modeling process, hydrogen atoms on the protein were removed and reintroduced using the Protein Preparation Wizard tool in the Schrödinger package. In addition, bond orders were assigned, disulfide bonds were created, and missing side chains were added.

For each of the DUD-E kinases, the structures of compounds and matched decoys were retrieved from DUD-E. For each of the selected SARfari kinases, bioactivity data for kinase inhibitors was retrieved and filtered for human biochemical data reporting activities in IC₅₀, K_d, or K_i. SMILES strings for compounds with inhibition at 1 μM or better were collected. Selected compounds were prepared using Canvas. For each of the SARfari kinases, compounds were clustered using Tanimoto similarity and the Leader-Follower algorithm. Only compounds representing cluster centers were used to generate decoys for each kinase using the DUD-E webserver.

Statistical analysis

Values are expressed as mean ± 95% confidence intervals, unless otherwise specified. ANOVA and t-test analyses were performed in R.³⁷ Correlation analysis and ROC analyses was performed using the SciPy³⁸ and scikit-learn³⁹ packages in Python, respectively.

RESULTS

Enrichment Power using Crystal Structures in the Validation Set

We first assess the ability of SVMGen and GlideScore to distinguish between known inhibitors and decoys from the DUD-E validation set. Performance of a scoring function can be evaluated with ROC plots.⁴⁰ A ROC curve is constructed by ranking the docked complexes, selecting a set of compounds starting from the highest scoring compounds, and counting the number of active compounds. In a ROC plot, the farther away the curve is from the diagonal, the better the performance of the scoring function. The area under the ROC curve, which we refer to as ROC-AUC, can also be used as a representation of the performance of the scoring function. A perfect scoring function will result in an area under the curve of 1, while a random classification will have an ROC-AUC of 0.5.

A commonly used validation set is DUD-E, which provides a set of actives and decoys for a large number of proteins. One limitation of validation sets like DUD-E is that the binding mode of most actives has not been solved by crystallography. Considering that molecular docking often does not lead to correct binding poses, it is often challenging to evaluate enrichment performance of the rank-ordering method. This is due to inherent approximations in the method. First, molecular docking is often carried out on a fixed structure of the target. However, molecular recognition is a dynamic process that leads to conformational changes in both receptor and small molecule.^41–43 Second, the scoring methods that are used to drive the docking process do not capture the complexity of the intermolecular interaction between small molecule and receptor. Third, it is often the case that water molecules play a role in the binding process, while most docking methods ignore explicit solvent molecules.⁴⁴ Finally, while the algorithms that are used to drive the molecular process have become very sophisticated, they often can get trapped in local minima that correspond to binding poses that are different than the true binding pose of the small molecule. Collectively, these factors can often lead to binding poses that may not be accurate.

To overcome this challenge, we resorted to creating a validation set that consists strictly of active compounds whose structure was solved by X-ray crystallography. We confined our analysis to protein kinases, a family of 518 proteins that have been the focus on intense drug discovery efforts considering their role in normal and pathological processes. The large number of kinase small-molecule inhibitors along with the substantial number of three-dimensional structures makes this family of proteins ideal for developing and testing computational methods. First, we identified a set of 940 co-crystallized inhibitors across 26 unique kinase targets from the PDBbind general set that bind to the conserved ATP binding pocket of kinases. A set of 50 decoys was generated for each inhibitor using DUD-E’s Web server. The decoys were docked against the kinase binding pocket with either AutoDock Vina or GlideSP to compare the two methods. The binding poses from each docking method were rescored using either GlideScore or SVMGen. The ability of each scoring method to distinguish between the known inhibitor and the decoys was assessed using ROC-AUC (Table 1). To calculate the ROC-AUC for each kinase, we pooled together all corresponding n actives and 50 × n decoys for that kinase. GlideScore re-scoring of GlideSP- and Vina-docked poses achieved mean ROC-AUCs of 0.88 ± 0.02 and 0.89 ± 0.02, respectively. SVMGen re-scored Vina and GlideScore poses led to ROC-AUCs of 0.82 ± 0.04 and 0.83 ± 0.04, respectively. Poses scored with GlideScore performed slightly better overall than those scored with SVMGen for both GlideSP docked (paired t-test, p = 0.01) and Vina docked (paired t-test, p = 0.01) methods. Despite this, both scoring methods are complementary in their performance. There are several examples where SVMGen performs better than GlideScore such as for BRAF, EGFR, and SRC. There are also examples where GlideScore performs better than SVMGen, such as for CHEK1, CHEK2, and MAP2K1.

Table 1.

Enrichment of Select Kinase Targets in PDBBind’s General Set

Kinase	GlideSP		Vina
	GlideScore	SVMGen	GlideScore	SVMGen
AURKA	0.90	0.81	0.90	0.82
BRAF	0.84	0.96	0.84	0.96
CDK2	0.90	0.78	0.91	0.82
CDPK1	0.98	0.98	0.99	0.99
CHEK1	0.91	0.73	0.94	0.79
CHEK2	0.86	0.62	0.90	0.64
CSNK2A1	0.97	0.88	0.98	0.91
EGFR	0.81	0.95	0.78	0.97
GSK3B	0.89	0.82	0.91	0.83
ITK	0.78	0.75	0.77	0.74
JAK2	0.84	0.81	0.86	0.83
KDR	0.93	0.91	0.93	0.91
LCK	0.92	0.92	0.92	0.91
MAP2K1	0.85	0.60	0.89	0.61
MAPK10	0.82	0.84	0.82	0.85
MAPK14	0.81	0.70	0.82	0.69
MET	0.92	0.76	0.92	0.76
NEK2	0.92	0.83	0.93	0.77
PDPK1	0.89	0.80	0.91	0.83
PIM1	0.88	0.63	0.91	0.68
PLK1	0.92	0.96	0.90	0.96
PRKACA	0.93	0.77	0.95	0.80
PTK2	0.91	0.90	0.91	0.90
SRC	0.77	0.92	0.74	0.90
SYK	0.89	0.77	0.91	0.77
TTK	0.93	0.86	0.93	0.86
Mean	0.88	0.82	0.89	0.83
95% CI	0.02	0.04	0.02	0.04

It is worth noting that generally, studies that evaluate enrichment power of scoring methods dock compounds to multiple crystal structures of the target protein, a process that is known as cross-docking. We did not perform cross-docking to ensure that the active set used in the training did not include any docked poses but rather consisted strictly of crystal structures. It is possible that the lack of cross-docking may have resulted in higher ROC-AUC values for both SVMGen and GlideScore.

Binding Pose Sensitivity

We next explored how SVMGen and GlideScore enrichment performance is affected by binding pose accuracy. Generally, it is desirable that a scoring function assigns the most favorable scores to compounds with a correct binding pose. To explore whether this is the case for GlideScore and SVMGen, we investigated how their scores change as the accuracy binding mode of a small molecule becomes progressively worse. Binding mode accuracy is measured using the root-mean-squared deviation (RMSD) of compounds to the crystal structure. We make use of the same set of actives and decoys that we used to evaluate enrichment performance above shown in Table 1. To produce binding poses with a range of pose accuracy, we re-docked all actives from Table 1 to their corresponding target 50 times using AutoDock Vina. For each run, we collected 20 unique binding poses for each active resulting in in 50 × 20 = 1000 poses. The RMSD between each of the 1000 poses was used to hierarchically cluster the poses into 20 clusters. A representative member of each cluster was selected and the RMSD to the crystal pose was determined and scored with both SVMGen and GlideScore.

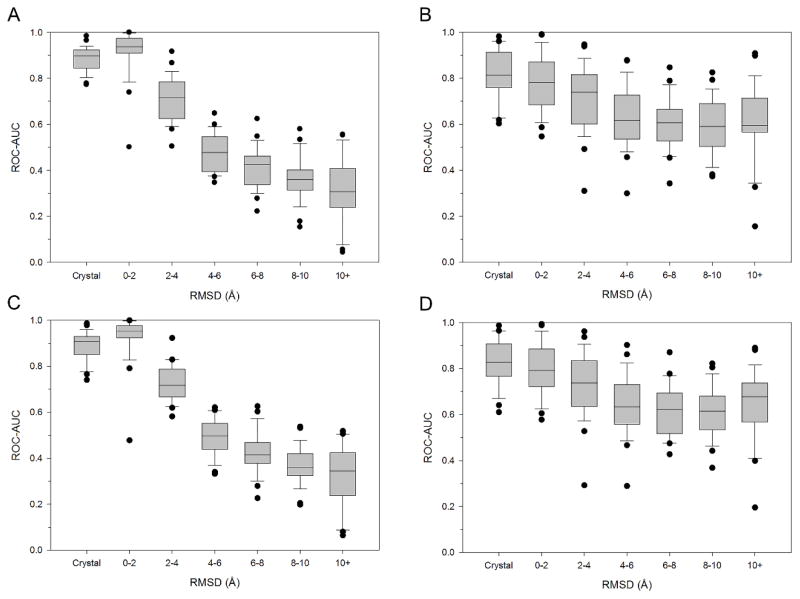
We first explored the effect of pose accuracy on enrichment power. For each of the 26 kinases in Table 1, we divided the binding poses collected above into 6 different bins based on their RMSD to the crystal structure: 0–2, 2–4, 4–6, 6–8, 8–10, and greater than 10 Å. The enrichment performance across the 26 kinases was calculated for each bin (Fig. 1). For the poses scored with GlideScore (Fig. 1A and 1C), the mean ROC-AUC for near native pose (RMSD < 2 Å) was 0.92 ± 0.04 in Glide and 0.93 ± 0.04 in Vina, which was higher than the 0.88 ± 0.02 and 0.89 ± 0.02 that was obtained for the set of actives with binding poses from crystal structure. Enrichment became progressively worse for the subsequent sets as evidenced by a decrease of the ROC-AUC from 0.92 (Glide, RMSD < 2 Å) and 0.93 (Vina, RMSD < 2 Å) to 0.31 ± 0.06 (Glide and Vina, RMSD > 10 Å). For SVMGen (Fig. 1B and 1D), the mean ROC-AUC for the bin of actives with 0–2 Å RMSDs was 0.79 ± 0.05 and 0.80 ± 0.04 for Glide and Vina, respectively. Like GlideScore, the mean ROC-AUC decreased with increasing RMSD to 0.61 ± 0.07 and 0.63 ± 0.06. The decrease in performance for SVMGen was not as substantial as that observed for GlideScore. These results show that both SVMGen and GlideScore are sensitive to the accuracy of the binding pose, but GlideScore shows greater sensitivity.

Figure 1. Enrichment power versus binding pose accuracy across 26 kinase targets.

A set of 20 unique binding poses was generated for 940 co-crystallized inhibitors across 26 kinase targets in PDBBind’s general set. The RMSD to the native crystal pose was used to separate the binding poses into the following bins: <2, 2–4, 4–6, 6–8, and >10 Å. ROC-AUC performance are shown in a box-and-whisker plot for each of the docking method and scoring function combinations: (A) Glide/GlideScore; (B) Glide/SVMGen; (C) Vina/GlideScore; (D) Vina/SVMGen.

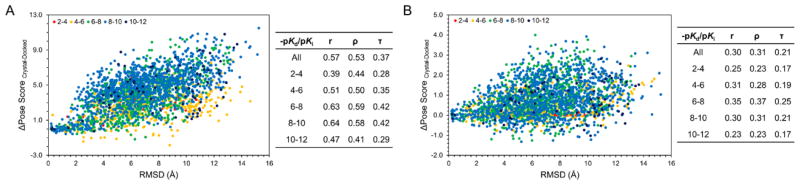
Next, we explored how binding pose accuracy affects SVMGen and GlideScore rank-ordering by binding affinity. To that end, we used the crystal structure of 123 small-molecule kinase inhibitors bound to their target from the refined set of PDBBind. We generated 20 clustered poses for each of the 123 inhibitors using a similar approach described above. We then determined whether there was any correlation between the binding pose accuracy as measured by RMSD and SVMGen and GlideScore scores. We used three measures of correlation: Pearson’s r, Spearman’s ρ, and Kendall’s τ. For poses that were scored with GlideScore (Fig. 2A), there is a positive correlation between RMSD and score (r = 0.57, ρ = 0.53, τ = 0.37). Similar but weaker correlation is observed between SVMGen scores and RMSDs as illustrated in Fig. 2B (r = 0.30, ρ = 0.31, τ = 0.21). It is worth noting that the scores in Fig. 2 are not absolute scores provided by each scoring function, but rather the difference in the scores of the crystal pose and the randomly docked pose.

Figure 2. Binding pose accuracy versus deviation in predicted scores.

A set of 20 unique binding poses was generated for 123 co-crystallized kinase inhibitors from PDBBind’s refined set. For each pose, the difference between the crystal and docked scores was plotted against the RMSD between the docked and crystal poses. Compounds were binned based on their experimental binding affinities into ranges of 2–4, 4–6, 6–8, 8–10, and 10+. Pearson, Spearman, and Kendall correlations were calculated overall and for each bin for (A) GlideScore and (B) SVMGen.

The funnel-like behavior observed in Fig. 2 is expected for a scoring function that can differentiate between a correct versus incorrect binding pose. An increase in the difference in score between the crystal poses and randomly docked poses versus RMSD indicates that a scoring function is favoring more accurate binding modes. A positive correlation indicates that as less accurate binding poses are sampled, a more accurate scoring function assigns these poses a worse score than the native crystal pose, and the difference in score between the crystal pose and docked pose increases. The lower correlations of SVMGen indicates the scoring function does not perform as well as GlideScore for high quality binding poses. However, SVMGen is less sensitive than GlideScore for non-native poses, which may be an advantage in virtual screening campaigns where docked structures may not be native-like.

We further explored how these correlations may change with binding affinity of the compounds. The co-crystallized compounds were binned by their experimental binding affinities. For GlideScore, compounds with −pK_d or −pK_i values between 6–8 or 8–10, show stronger correlation between score and RMSD (6–8: r = 0.63, ρ = 0.59, τ = 0.42; 8–10: r = 0.64, ρ = 0.58, τ = 0.42). For SVMGen, compounds that fall in the 6–8 range exhibit the highest correlations (r = 0.35, ρ = 0.37, τ = 0.25). Interestingly, there are docked poses that score better than the crystal structure pose in both scoring methods. In GlideScore, most of these structures are concentrated to those with RMSD that are less than 2 Å of the crystal pose as well as poses with RMSDs greater than 2 Å with binding affinities (−pK_d or −pK_i) in the 4–6 and 6–8 range. In SVMGen, 17% of the generated poses scored better than the crystal pose compared to 4% in GlideScore.

Exploring the Effect of Target Structure Accuracy on Enrichment Using Homology Models

Despite the exponentially growing list of crystal structures at the PDB, the structure of the majority of proteins has yet to be solved. For many of these proteins, homology modeling can be used to predict a three-dimensional structure using the structure of other proteins with high sequence identity as a template. Homology models can potentially be used in virtual screening efforts to identify small-molecule inhibitors or activators of the target. This has been successfully done on several occasions.^45–49 However, considering that homology models can generally reproduce the overall fold but lack accuracy in the position of sidechains, we wondered whether reasonable enrichment could be achieved with these models using either SVMGen or GlideScore. To explore this question, we resort again to protein kinases, considering the wealth of structural information. Although a large number of crystal structures exist, more than half of the 518 protein kinases do not have a crystal structure of the protein kinase domain.²¹ For those whose structure has not been solved, the conserved nature of the protein kinase domain makes it possible to explore the effect of model quality on enrichment.

Here, we generate two sets of homology models for kinases with known inhibitors using different approaches for selecting the template. The first approach uses the template with the highest sequence identity of a different kinase or a non-human structure. For example, although many crystal structures are available for ABL1, the template that was selected was from ABL2, a closely related protein in the same family. Similarly, for PLK1, the crystal structure comes from a PLK1 homolog in zebrafish. The second approach uses a randomly selected template with a sequence identity between 20 and 50%. The first set of kinases were selected from DUD-E (Table 2), which features 26 kinases with existing crystal structures. Among these kinases, nearly half belong to the tyrosine kinase subfamily. The second set of kinases were selected from SARfari, a database of known kinase inhibitors and their targets. We selected kinases whose kinase domain was not solved by X-ray crystallography, were not in the DUD-E dataset, and had a large number of small-molecule inhibitors (Table 3). In total, 20 kinases were selected with the majority belonging to the AGC serine/threonine family.

Table 2.

Kinase Targets in DUD-E

DUD-E	Symbol	Name	PDB	Family	Total Ligands	Clustered Ligands	Experimental Decoys	Matched Decoys	Resolution (Å)
AKT1	AKT1	RAC-alpha serine/threonine-protein kinase	3CQW	AGC	585	293	53	16450	2.00
AKT2	AKT2	RAC-beta serine/threonine-protein kinase	3D0E	AGC	234	117	23	6900	2.00
KPCB	PRKCB	Protein kinase C beta type	2I0E	AGC	331	135	153	8700	2.60
ROCK1	ROCK1	Rho-associated protein kinase 1	2ETR	AGC	216	100	15	6300	2.60
MAPK2	MAPKAPK2	MAP kinase-activated protein kinase 2	3M2W	CAMK	184	101	81	6150	2.41
CDK2	CDK2	Cyclin-dependent kinase 2	1H00	CMGC	1310	474	136	27850	1.60
MK01	MAPK1	Mitogen-activated protein kinase 1	2OJG	CMGC	79	79	35	4550	2.00
MK10	MAPK10	Mitogen-activated protein kinase 10	2ZDT	CMGC	199	104	23	6600	2.00
MK14	MAPK14	Mitogen-activated protein kinase 14	2QD9	CMGC	2205	578	73	35850	1.70
MP2K1	MAP2K1	Dual specificity mitogen-activated protein kinase kinase 1	3EQH	STE	308	121	12	8150	2.00
BRAF	BRAF	Serine/threonine-protein kinase B-raf	3D4Q	TKL	317	152	28	9950	2.80
TGFR1	TGFBR1	TGF-beta receptor type-1	3HMM	TKL	235	133	7	8500	1.70
ABL1	ABL1	Tyrosine-protein kinase ABL1	2HZI	Tyr	409	182	84	10750	1.70
CSF1R	CSF1R	Macrophage colony-stimulating factor 1 receptor	3KRJ	Tyr	385	166	5	12150	2.10
EGFR	EGFR	Epidermal growth factor receptor	2RGP	Tyr	1612	542	407	35050	2.00
FAK1	PTK2	Focal adhesion kinase 1	3BZ3	Tyr	101	100	11	5350	2.20
FGFR1	FGFR1	Fibroblast growth factor receptor 1	3C4F	Tyr	327	139	146	8700	2.07
SRC	SRC	Proto-oncogene tyrosine-protein kinase Src	3EL8	Tyr	1269	524	287	34500	2.30
VGFR2	KDR	Vascular endothelial growth factor receptor 2	2P2I	Tyr	2320	409	142	24950	2.40
IGF1R	IGF1R	Insulin-like growth factor 1 receptor	2OJ9	Tyr	370	148	75	9300	2.00
JAK2	JAK2	Tyrosine-protein kinase JAK2	3LPB	Tyr	246	130	6	6500	2.00
KIT	KIT	Mast/stem cell growth factor receptor Kit	3G0E	Tyr	378	166	8	10450	1.60
LCK	LCK	Tyrosine-protein kinase Lck	2OF2	Tyr	916	420	148	27400	2.00
MET	MET	Hepatocyte growth factor receptor	3LQ8	Tyr	333	166	17	11250	2.02
PLK1	PLK1	Serine/threonine-protein kinase PLK1	2OWB	Other	227	107	46	6800	2.10
WEE1	WEE1	Wee1-like protein kinase	3BIZ	Other	221	102	15	6150	2.20

Table 3.

Kinase Targets in SARfari

Symbol	Name	Family	SARfari Compounds	Clustered Compounds
AKT3	RAC-gamma serine/threonine-protein kinase	AGC	91	32
CDK1	Cyclin-dependent kinase 1	CMGC	797	383
CHUK	Inhibitor of nuclear factor kappa-B kinase subunit alpha	Other	92	49
CLK4	Dual specificity protein kinase CL4	CMGC	70	32
FLT4	Vascular endothelial growth factor receptor 3	Tyr	102	68
GSK3A	Glycogen synthase kinase-3 alpha	CMGC	269	126
LIMK2	LIM domain kinase 2	TKL	43	15
MAP3K8	Mitogen-activated protein kinase kinase kinase 8	STE	122	47
PDGFRA	Platelet-derived growth factor receptor alpha	Tyr	287	136
PDGFRB	Platelet-derived growth factor receptor beta	Tyr	523	218
PHKG1	Serine/threonine-protein kinase PHKG1	CAMK	43	9
PRKACG	cAMP-dependent protein kinase catalytic subunit gamma	AGC	89	38
PRKCD	Protein kinase C delta type	AGC	452	132
PRKCE	Protein kinase C epsilon type	AGC	223	82
PRKCG	Protein kinase C gamma type	AGC	204	64
PRKCZ	Protein kinase C zeta type	AGC	104	34
PRKD1	Serine/threonine-protein kinase D1	CAMK	104	40
PRKD3	Serine/threonine-protein kinase D3	CAMK	101	38
RAF1	RAF proto-oncogene serine/threonine-protein kinase	TKL	269	129
YES1	Tyrosine-protein kinase Yes	Tyr	50	33

Homology models were constructed using the Prime workflow in the Schrödinger package. Only the sequence of the protein kinase domain was used to identify a suitable template. The high and low identity homology models from the DUD-E set used templates from a variety of kinases (Table 4). Among the respective models that were constructed using the two strategies, there is a significant difference between the RMSDs of the high identity and low identity models (paired t-test, p = 5.1×10⁻⁷). Similarly, the RMSD of the heavy atoms within 8 Å of the ATP binding pocket center is significantly different (paired t-test, p = 1.3×10⁻⁴). In some targets, members of the same subfamily are used for both the high and low identity models. For example, the MAPK1, MAPK10, and MAPK14 models all use members of the MAPK family as templates for homology models, but they have 30 to 40% difference in sequence identity. Similarly, we built high and low identity models for the SARfari kinases (Table 5). In some instances, the sequence identity of the best available structure does not differ much from the template used in the low identity model. For example, the templates used in the PRKD1 and PRKD3 models only have sequence identities of 38 and 39% compared to the 35 and 34% identities of their low identity models.

Table 4.

Kinase Targets in DUD-E and Parameters for Building Homology Models

	High Identity Homology Model								Low Identity Homology Model
Symbol	Template PDB	Template Symbol	Scorea	Identitiesb	Positivesc	Gapsd	Pocket RMSD (Å)	RMSD (Å)	Template PDB	Template Symbol	Scorea	Identitiesb	Positivesc	Gapsd	Pocket RMSD (Å)	RMSD (Å)
AKT1	1O6L	AKT2	569.3	87%	94%	0%	1.26	0.97	3NAX	PDPK1	195.7	37%	60%	2%	2.46	2.44
AKT2	4GV1	AKT1	600.5	85%	92%	3%	1.96	1.05	2ACX	GRK6	211.1	39%	57%	2%	3.77	2.26
PRKCB	2I0E	PRKCA	598.6	85%	93%	0%	1.05	1.28	2ACX	GRK6	193.0	38%	59%	2%	3.85	1.87
ROCK1	4L6Q	ROCK2	712.6	85%	94%	0%	0.77	0.98	3A62	RPS6KB1	186.0	34%	56%	5%	3.44	2.41
MAPKAPK2	3FHR	MAPKAPK3	449.5	69%	81%	8%	1.43	1.29	3NX8	PRKACA	114.0	29%	49%	17%	1.94	2.32
CDK2	3O0G	CDK5	305.8	55%	69%	8%	1.84	2.21	4FV7	MAPK1	185.7	36%	53%	10%	1.31	2.19
MAPK1	2ZOQ	MAPK3	631.3	78%	93%	0%	2.66	1.01	1CM8	MAPK12	286.2	41%	62%	3%	2.21	1.84
MAPK10	3O2M	MAPK8	665.6	90%	92%	3%	1.06	1.63	3GCQ	MAPK14	311.6	47%	63%	7%	2.41	2.38
MAPK14	3GP0	MAPK11	525.0	71%	84%	5%	5.90	1.76	4AWI	MAPK8	302.8	45%	62%	9%	1.86	1.91
MAP2K1	1S9I	MAP2K2	550.4	80%	85%	9%	1.29	1.30	3HA6	AURKA	117.5	26%	49%	7%	3.74	2.73
BRAF	3OMV	CRAF	447.2	77%	86%	4%	1.22	0.90	2VWX	EPHB4	135.2	29%	53%	11%	3.59	2.14
TGFBR1	3MDY	BMPR1B	426.4	66%	81%	1%	1.19	1.36	2G2H	ABL1	80.1	23%	44%	18%	3.62	2.54
ABL1	3HMI	ABL2	528.1	92%	96%	0%	1.78	1.07	3SXS	BMX	232.6	41%	63%	0%	5.24	1.50
CSF1R	4HVS	KIT	457.2	67%	79%	5%	2.26	1.48	3HMI	ABL2	215.3	40%	62%	3%	4.43	1.95
EGFR	3PP0	ERBB2	449.5	74%	84%	7%	0.96	1.49	2QOB	EPHA3	183.7	36%	56%	6%	3.19	2.82
PTK2	3FZS	PTK2B	316.2	57%	71%	7%	2.71	1.72	3BKB	FES	207.2	38%	58%	6%	4.16	2.22
FGFR1	2PVY	FGFR2	548.5	85%	91%	3%	3.15	1.20	3EKK	INSR	222.6	39%	62%	3%	3.77	1.84
SRC	2DQ7	FYN	466.8	79%	88%	4%	2.93	1.02	3PIX	BTK	211.5	40%	60%	5%	3.09	1.57
KDR	2PVY	FGFR2	310.5	52%	68%	9%	4.79	2.00	1FVR	TEK	190.7	37%	56%	6%	6.59	2.13
IGF1R	1P14	INSR	510.0	78%	89%	2%	5.34	1.84	2PVY	FGFR2	231.5	39%	61%	5%	8.93	2.36
JAK2	4HVD	JAK3	357.5	61%	76%	3%	1.32	1.12	3W33	EGFR	171.0	34%	56%	6%	1.95	2.26
KIT	2I1M	CSF1R	479.6	67%	79%	1%	3.15	1.82	3BU3	INSR	212.6	36%	56%	3%	6.74	2.35
LCK	2C0T	HCK	449.5	76%	89%	0%	1.21	1.84	4HCT	ITK	245.7	42%	66%	0%	1.21	2.24
MET	3PLS	MST1R	342.8	58%	71%	7%	4.57	2.36	3KUL	EHPA8	182.6	35%	54%	7%	5.34	1.89
PLK1	3D5U	PLK1	513.8	80%	93%	0%	1.29	0.65	3A8X	PRKCI	141.4	30%	52%	3%	3.74	1.81
WEE1	3P1A	PKMYT1	142.9	35%	50%	13%	6.65	2.47	2J0I	PAK4	61.2	23%	45%	9%	8.53	2.19
Mean			475.2	73%	83%	4%	2.45	1.45			193.4	36%	57%	6%	3.89	2.16

^aBLAST bit score;

^bPercentage of residues that are identical between the sequences;

^cPercentage of residues that are positive matches according to the similarity matrix;

^dPercentage of gaps in both query and homolog as returned by BLAST.

Table 5.

Kinase Targets in SARfari and Parameters for Building Homology Models

	High Identity Homology Model						Low Identity Homology Model
Symbol	Template PDB	Template Symbol	Scorea	Identitiesb	Positivesc	Gapsd	Template PDB	Template Symbol	Scorea	Identitiesb	Positivesc	Gapsd
AKT3	1GZN	AKT2	485.3	87%	95%	0%	1UU9	PDPK1	186.4	39%	60%	0%
CDK1	4EK4	CDK2	406.8	64%	78%	3%	4G6O	MAPK1	184.1	36%	53%	5%
CHUK	4KIK	IKBKB	386.7	64%	77%	1%	4B9D	NEK1	103.6	31%	52%	5%
CLK4	1Z57	CLK1	584.7	86%	92%	0%	1UKI	MAPK8	108.6	29%	46%	15%
FLT4	3VID	KDR	454.9	69%	79%	0%	4FOB	ALK	165.2	33%	47%	19%
GSK3A	1J1B	GSK3B	607.1	86%	93%	0%	3R71	CDK2	177.9	36%	58%	10%
LIMK2	3S95	LIMK1	408.3	69%	83%	2%	2J0L	PTK2	105.1	27%	47%	15%
MAP3K8	3GGF	STK26	145.2	34%	56%	5%	4FZA	STK26	141.8	34%	56%	5%
PDGFRA	3HNG	VEGFR1	340.1	47%	65%	9%	2RFN	MET	43.5	31%	45%	9%
PDGFRB	1Y6A	VEGFR2	323.6	46%	61%	10%	4F64	FGFR1	104.0	45%	61%	1%
PHKG1	2Y7J	PHKG2	421.8	70%	85%	0%	3R2B	MAPKAPK2	150.6	33%	52%	11%
PRKACG	2F7E	PRKACA	473.4	86%	94%	0%	4EL9	RPS6KA3	200.3	37%	63%	2%
PRKCD	1XJD	PRKCQ	512.3	72%	84%	0%	3NX8	PRKACA	191.0	40%	60%	1%
PRKCE	3TXO	PRKCH	525.8	69%	82%	0%	3AMB	PRKACA	203.8	40%	60%	2%
PRKCG	3IW4	PRKCA	559.7	75%	87%	1%	4L45	RPS6KB1	223.8	41%	63%	3%
PRKCZ	3ZH8	PRKCI	497.7	88%	94%	0%	3OTU	PDPK1	162.9	33%	54%	4%
PRKD1	2W0J	CHEK2	193.4	38%	60%	6%	4AE9	PRKACA	146.4	35%	57%	7%
PRKD3	2W0J	CHEK2	194.1	39%	61%	6%	2GNL	PRKACA	141.7	34%	55%	7%
RAF1	3D4Q	BRAF	496.5	77%	89%	0%	2Y4I	KSR2	162.9	35%	56%	5%
YES1	2H8H	SRC	485.0	89%	95%	0%	3K54	BTK	218.8	40%	64%	0%
Mean			425.1	68%	81%	2%			156.1	35%	55%	6%

^aBLAST bit score;

^bPercentage of residues that are identical between the sequences;

^cPercentage of residues that are positive matches according to the similarity matrix;

^dPercentage of gaps in both query and homolog as returned by BLAST.

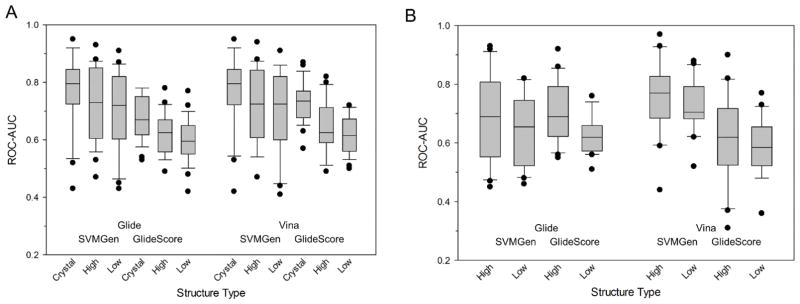
We assessed the performance of the rank-ordering methods in enriching chemical libraries docked to the DUD-E set of homology models for 26 kinases. Both actives and matched decoys were docked to their corresponding models using either Vina or Glide and scored using SVMGen (Fig. 3A) and GlideScore (Fig. 3B). For the DUD-E kinases, the mean ROC-AUCs for SVMGen were 0.77 ± 0.05, 0.72 ± 0.05, and 0.70 ± 0.05 for crystal, high identity homology models, and low identity homology models, respectively (Table 6). In Glide docked poses, GlideScore resulted in mean ROC-AUCs of 0.67 ± 0.03, 0.62 ± 0.03, and 0.60 ± 0.03 for crystal, high homology, and low homology structures. Vina docked poses that were scored with GlideScore resulted in ROC-AUCs of 0.73 ± 0.03, 0.65 ± 0.04, and 0.62 ± 0.03. For the GlideScore scored models, the Vina docked poses resulted in significantly higher enrichment than the Glide docked poses in both the crystal structures (ANOVA, p = 0.002) and high identity model (ANOVA, p = 0.02), but not in the low identity models (ANOVA, p = 0.35). The average scores of the SVMGen poses were higher than their GlideScore counterparts (ANOVA, p = 5.4×10⁻¹¹). Similarly, the quality of the kinase structure significantly impacts the overall enrichment (ANOVA, p = 1.7×10⁻⁷), with the native crystal structure resulting in better rank-ordering both the high and low identities models. Similar to the enrichment of the PDBBind dataset, SVMGen excels at specific targets such as AKT1, MAPK14, and EGFR, while GlideScore does better in kinases such as MAPK1, MAP2K1, and PLK1.

Figure 3. Enrichment of structures generated through homology modeling.

Box-and-whisker plots of ROC-AUC scores for different quality homology models docked using Glide and Vina, and scored using GlideScore and SVMGen for kinases from (A) DUD-E and (B) SARfari.

Table 6.

Scoring Functions Enrichment Performance for DUD-E Kinases

Symbol	Glide						Vina
	SVMGen			GlideScore			SVMGen			GlideScore
	Crystal	High	Low	Crystal	High	Low	Crystal	High	Low	Crystal	High	Low
AKT1	0.84	0.86	0.81	0.65	0.68	0.60	0.84	0.85	0.80	0.70	0.79	0.71
AKT2	0.79	0.79	0.82	0.63	0.64	0.63	0.79	0.79	0.82	0.72	0.66	0.64
PRKCB	0.78	0.77	0.71	0.68	0.64	0.61	0.78	0.76	0.71	0.68	0.65	0.50
ROCK1	0.69	0.70	0.61	0.70	0.66	0.69	0.69	0.70	0.61	0.74	0.80	0.71
MAPKAPK2	0.61	0.59	0.45	0.78	0.78	0.51	0.62	0.59	0.45	0.75	0.77	0.63
CDK2	0.73	0.61	0.58	0.75	0.55	0.55	0.73	0.61	0.57	0.78	0.61	0.61
MAPK1	0.52	0.47	0.43	0.77	0.63	0.55	0.53	0.47	0.41	0.73	0.70	0.68
MAPK10	0.79	0.69	0.72	0.72	0.69	0.42	0.79	0.69	0.72	0.68	0.63	0.62
MAPK14	0.80	0.71	0.76	0.59	0.58	0.65	0.80	0.70	0.76	0.66	0.55	0.58
MAP2K1	0.43	0.61	0.65	0.69	0.53	0.55	0.42	0.62	0.64	0.67	0.61	0.56
BRAF	0.88	0.87	0.65	0.78	0.67	0.69	0.88	0.87	0.65	0.81	0.72	0.56
TGFBR1	0.92	0.88	0.91	0.73	0.73	0.51	0.92	0.88	0.91	0.86	0.82	0.51
ABL1	0.84	0.85	0.82	0.63	0.64	0.62	0.83	0.84	0.82	0.76	0.74	0.72
CSF1R	0.71	0.62	0.68	0.53	0.56	0.65	0.70	0.61	0.68	0.66	0.60	0.54
EGFR	0.80	0.75	0.86	0.68	0.56	0.58	0.80	0.75	0.86	0.57	0.61	0.72
PTK2	0.95	0.93	0.87	0.64	0.49	0.62	0.95	0.94	0.86	0.83	0.52	0.70
FGFR1	0.83	0.77	0.75	0.61	0.62	0.63	0.83	0.77	0.76	0.67	0.67	0.64
SRC	0.88	0.85	0.86	0.60	0.59	0.57	0.88	0.85	0.86	0.75	0.59	0.59
KDR	0.81	0.57	0.69	0.62	0.57	0.59	0.82	0.54	0.69	0.68	0.60	0.56
IGF1R	0.74	0.69	0.72	0.64	0.54	0.53	0.75	0.69	0.73	0.74	0.62	0.62
JAK2	0.86	0.86	0.85	0.78	0.72	0.72	0.86	0.86	0.86	0.77	0.71	0.64
KIT	0.76	0.80	0.74	0.59	0.58	0.56	0.75	0.80	0.73	0.63	0.49	0.58
LCK	0.82	0.80	0.76	0.75	0.67	0.57	0.81	0.79	0.76	0.75	0.59	0.59
MET	0.92	0.59	0.49	0.66	0.55	0.77	0.92	0.58	0.48	0.87	0.57	0.54
PLK1	0.54	0.53	0.53	0.78	0.66	0.67	0.55	0.54	0.53	0.77	0.68	0.67
WEE1	0.76	0.59	0.47	0.54	0.53	0.48	0.75	0.60	0.44	0.70	0.49	0.57
Mean	0.77	0.72	0.70	0.67	0.62	0.60	0.77	0.72	0.70	0.73	0.65	0.62
95% CI	0.05	0.05	0.05	0.03	0.03	0.03	0.05	0.05	0.06	0.03	0.04	0.03

For the SARfari set of kinases, we docked both active compounds and matched decoys to each model using Glide and Vina and rescored using GlideScore and SVMGen (Table 7). In the structures that were generated using Glide, the high and low identity models of the SVMGen scored poses had ROC-AUCs of 0.68 ± 0.07 and 0.63 ± 0.05, respectively. This shows that the quality of the structure has generally no impact on performance (paired t-test, p = 0.35). For GlideScore, the ROC-AUCs were 0.70 ± 0.05 and 0.63 ± 0.03, with slightly better enrichment for the high quality models (paired t-test, p = 0.02). Similarly in the Vina docked structures, the SVMGen ROC-AUCs were 0.75 ± 0.06 and 0.72 ± 0.04 and the GlideScore ROC-AUCs were 0.61 ± 0.06 and 0.59 ± 0.06. Interestingly, SVMGen showed significantly better performance with compounds docked with Vina than with Glide (ANOVA, p = 2.5×10⁻⁴). Similarly, high identity models performed better overall than low identity models (ANOVA, p = 0.01). In some cases, the low identity model outperformed its high identity model counterpart, such as, for example, for MAP3K8, PDGFRB, and PRKD1.

Table 7.

Scoring Functions Enrichment Performance for SARfari Kinases

Symbol	Glide				Vina
	SVMGen		GlideScore		SVMGen		GlideScore
	High	Low	High	Low	High	Low	High	Low
AKT3	0.75	0.53	0.55	0.57	0.72	0.71	0.52	0.55
CDK1	0.64	0.73	0.70	0.60	0.78	0.74	0.65	0.56
CHUK	0.93	0.48	0.86	0.51	0.91	0.52	0.82	0.66
CLK4	0.80	0.50	0.80	0.66	0.79	0.88	0.64	0.52
FLT4	0.67	0.51	0.56	0.66	0.68	0.69	0.43	0.61
GSK3A	0.55	0.64	0.68	0.57	0.79	0.62	0.61	0.58
LIMK2	0.81	0.53	0.62	0.58	0.93	0.75	0.37	0.36
MAP3K8	0.45	0.82	0.65	0.65	0.59	0.87	0.63	0.73
PDGFRA	0.64	0.69	0.69	0.56	0.78	0.77	0.65	0.48
PDGFRB	0.54	0.82	0.63	0.74	0.73	0.84	0.54	0.77
PHKG1	0.83	0.67	0.68	0.62	0.97	0.70	0.90	0.53
PRKACG	0.92	0.46	0.92	0.65	0.84	0.80	0.79	0.63
PRKCD	0.67	0.71	0.81	0.66	0.76	0.69	0.74	0.59
PRKCE	0.51	0.77	0.62	0.60	0.62	0.70	0.51	0.51
PRKCG	0.78	0.70	0.77	0.57	0.73	0.64	0.57	0.48
PRKCZ	0.77	0.57	0.81	0.62	0.70	0.68	0.59	0.67
PRKD1	0.47	0.75	0.62	0.74	0.44	0.70	0.31	0.62
PRKD3	0.71	0.52	0.69	0.73	0.64	0.67	0.60	0.64
RAF1	0.56	0.78	0.69	0.60	0.83	0.74	0.68	0.56
YES1	0.84	0.58	0.77	0.76	0.82	0.82	0.73	0.68
Mean	0.68	0.63	0.70	0.63	0.75	0.72	0.61	0.59
95% CI	0.07	0.05	0.05	0.03	0.06	0.04	0.06	0.04

Early Enrichment

The AUC under the ROC curve is a measure of the fraction of actives discovered over the fraction of inactives. However, only the top targets are further evaluated in virtual screening. One measure to evaluate early enrichment is ROC enrichment, which can be defined at any point on the ROC curve.⁵⁰ At a given false positive rate, it is the fraction of discovered actives divided by the fraction of discovered inactives. Table 8 lists the mean ROC enrichment at various false positive rates in both the DUD-E and SARfari datasets. At a 0.5% false positive rate (FPR), SVMGen performs better or similarly to GlideScore at identifying actives compounds among inactives. Only in the Glide docked SARfari kinases does GlideScore perform better than SVMGen at each FPR. This general trend is similarly reflected in the overall ROC-AUCs of each combination of docking and scoring methods.

Table 8.

Mean ROC Enrichment at Various False Positive Rates

Kinase Set	Docking Method	Scoring Function	Structure Type	Mean ROC-AUC	95% CI	Mean ROC Enrichments
						0.5%	1.0%	2.0%	5.0%	10.0%
DUD-E	Glide	SVMGen	Crystal	0.77	0.72 – 0.82	27.8	20.2	13.8	7.9	5.0
			High	0.72	0.67 – 0.77	20.6	15.2	10.6	6.3	4.1
			Low	0.70	0.65 – 0.75	19.2	13.7	9.6	5.5	3.7
		GlideScore	Crystal	0.67	0.64 – 0.70	16.5	11.4	8.0	4.8	3.3
			High	0.62	0.59 – 0.65	15.3	10.4	7.0	4.1	2.9
			Low	0.60	0.57 – 0.63	14.0	8.8	5.5	3.6	2.4
	Vina	SVMGen	Crystal	0.77	0.72 – 0.82	27.6	20.3	13.8	7.8	5.0
			High	0.72	0.67 – 0.77	21.4	15.3	10.8	6.3	4.1
			Low	0.70	0.64 – 0.76	18.5	13.2	9.6	5.7	3.7
		GlideScore	Crystal	0.73	0.70 – 0.76	28.6	17.4	11.2	6.1	4.0
			High	0.65	0.61 – 0.69	11.5	8.2	5.8	3.8	2.7
			Low	0.62	0.65 – 0.68	4.0	3.2	2.6	2.2	2.0
SARfari	Glide	SVMGen	High	0.68	0.61 – 0.75	17.0	10.8	7.7	4.7	3.4
			Low	0.63	0.58 – 0.68	10.1	7.4	6.1	3.8	2.7
		GlideScore	High	0.70	0.65 – 0.75	20.9	15.5	9.5	5.4	3.6
			Low	0.63	0.60 – 0.66	8.3	5.9	4.7	2.8	2.3
	Vina	SVMGen	High	0.75	0.69 – 0.81	17.0	13.9	8.8	6.2	4.3
			Low	0.72	0.68 – 0.76	10.8	9.5	7.6	5.2	3.5
		GlideScore	High	0.61	0.55 – 0.67	10.2	7.3	5.3	3.5	2.5
			Low	0.59	0.55 – 0.63	7.6	5.7	3.8	2.5	2.0

DISCUSSION

Recently, we introduced an approach for rank-ordering protein-compound structures in virtual screening.¹² The method known as SVMSP used a combination of machine learning and statistical pair potentials to develop a model for rank-ordering protein-compound structures. The results were promising, such that enrichment compared well with other well-established methods such as Glide. However, SVMSP is a target-specific approach and a model must be developed for individual targets. Here, we report a general approach (SVMGen) using the same strategy as SVMSP except that the negative set consists of a collection of randomly selected compounds docked to a diverse set of protein structures. We use SVMGen and GlideScore to explore the sensitivity of these scoring methods to the quality of binding pose or the three-dimensional structure of the target used during virtual screening. We find that SVMGen is sensitive to the quality of the binding pose as evidenced by progressively poorer enrichments with decreasing quality (high RMSDs) of the active compounds. GlideScore was more sensitive, showing a more substantial decrease in performance with increasing RMSDs. The fact that GlideScore is more sensitive may be attributed to the fact that the scoring function was developed strictly with crystal structures of protein-compound complexes, while SVMGen uses both crystal structures (positive set) as well as docked structures (negative set) to represent the negative set used in the training. GlideScore is expected to therefore perform better in situations where the test set contains high-quality docked poses. SVMGen may not perform as well as GlideScore with the highest quality structures, but its lower sensitivity to the quality of binding pose may actually be an asset in virtual screening campaigns where the docking pose of active compounds are not always highly accurate.

In addition to the binding pose, we investigated how the quality of the target structure affects enrichment using both SVMGen and GlideScore. Just like in the above studies, we focused our attention on protein kinases. Nearly half of the kinases in the human kinome do not possess a crystal structure. The use of homology models for these kinases could not only help in identifying novel inhibitors, but could also be used to predict the selectivity of compounds considering that most kinase inhibitors fail due to off-target effects. We selected targets from two datasets: DUD-E and SARfari. Targets from DUD-E featured kinase targets with solved structures, while targets from SARfari consisted of kinases with no crystal structure. Consistent with the above studies evaluating the effects of binding pose, we find that model quality has significant impact on enrichment. For both SVMGen and GlideScore, enrichment was better for high sequence identify homology models compared with homology models obtained with low sequence identity templates. These results are consistent with our studies evaluating the effect of binding mode accuracy on enrichment. The lower sensitivity for SVMGen may be useful in screening campaigns that use homology models, which will likely result in a larger number of less accurate binding poses for actives.