Evaluating flow cytometer performance with weighted quadratic least squares analysis of LED and multi-level bead data

Abstract

We developed a fully automated procedure for analyzing data from LED pulses and multi-level bead sets to evaluate backgrounds and photoelectron scales of cytometer fluorescence channels.

The method improves on previous formulations by fitting a full quadratic model with appropriate weighting and by providing standard errors and peak residuals as well as the fitted parameters themselves. Here we describe the details of the methods and procedures involved and present a set of illustrations and test cases that demonstrate the consistency and reliability of the results.

The automated analysis and fitting procedure is generally quite successful in providing good estimates of the Spe (statistical photoelectron) scales and backgrounds for all of the fluorescence channels on instruments with good linearity. The precision of the results obtained from LED data is almost always better than for multi-level bead data, but the bead procedure is easy to carry out and provides results good enough for most purposes. Including standard errors on the fitted parameters is important for understanding the uncertainty in the values of interest. The weighted residuals give information about how well the data fits the model, and particularly high residuals indicate bad data points.

Known photoelectron scales and measurement channel backgrounds make it possible to estimate the precision of measurements at different signal levels and the effects of compensated spectral overlap on measurement quality. Combining this information with measurements of standard samples carrying dyes of biological interest, we can make accurate comparisons of dye sensitivity among different instruments.

Our method is freely available through the R/Bioconductor package flowQB.

Introduction

The basic capabilities of a fluorescence cytometer measurement channel can be estimated by knowing just two values: Q, the statistical number of photoelectrons (Spe) generated per unit of dye in the sample, and B, the background light in dye equivalents that sets the minimum variance that underlies all measurements (1,2). From these the minimum detectable amount of dye and the precision of measurements at different signal levels can be calculated. Therefore, measurements of Q and B are the key to making valid comparisons between different instruments and among different channels on an instrument. This information can be very useful in identifying problems on an instrument and can be critical in situations like multi-site trials where good comparability of data taken on different instruments is necessary.

High Q values are useful in improving the quality of cytometer measurements both in relation to single channel signal versus background (illustrated in (3) Figres 5 and 7 and in (1) Figures 7, 8 and 9) and in spectral overlap correction (compensation) where high Q values contribute to improved discrimination of signals-of-interest relative to the measurement variance effects of spectral overlaps ((4), including calculations in the Appendix).

We can achieve full specification of Q and B in two steps by evaluating photoelectron scales and backgrounds for the measurement channels of interest and relating those to measurements on dye reference samples. There are problems and challenges in implementing each step in a way that is convenient and accurate in routine use. Here we address the photoelectron scale aspect by providing reliable automated software for obtaining the needed information from LED or multi-level, multi-dye bead data. The automated procedure avoids the effort and inconsistencies involved in manual analysis of cytometry data and requires only specification of the appropriate data files and some specific information like identification of fluorescence and light scatter channels. Since problems, including some outside the range of those encountered in testing, will inevitably occur, we have included several kinds of quality checking outputs designed to alert users to suspect conditions or questionable results.

Signal production in fluorescence cytometers

When a cell or particle moves through a sensing area on a flow cytometer, a focused laser beam excites fluorescent dyes that emit a pulse of light in all directions. The optical system collects some of this light and passes it through optical filters to the cathodes of one or more PMT detectors where a fraction of the photons generate photoelectrons. The photoelectrons are amplified through a series of dynodes to produce an output current pulse. Photoelectron production is a Poisson process, so the variance of signals at a particular level is proportional to the signal level itself (5). Since the amplification process through the dynodes results in some additional variance, we introduce the term “statistical photoelectrons” or Spe to denote the effective Poisson number relating signal levels and their variances. Spe values should be approximately (g-1)/g times actual photoelectrons where g is the dynode step gain (5). For the currently typical 9-dynode PMTs with maximum gain of about 10⁷, g can be as high as 6, but usual PMT voltages give g in the range of 4 leading to Spe values about (g-1)/g = ¾ of the actual photoelectron count.

One instrument used in the study uses avalanche photodiodes (APDs) rather than PMTs, and the analysis of additional noise due to amplification is more complex than in the case of a PMT. The concept of Spe is still appropriate for APDs since there is a direct relationship of Spe to photon generated events.

Background signal includes electronic noise from the detector and the signal processing electronics and optical background from light not associated with a cell or particle transit. Electronic baseline restoration keeps background signal from offsetting the pulse measurements, but the background does introduce corresponding additional variance in the results.

Some instruments measure signal Height rather than, or in addition to, Area. If the shapes of pulses at different signal levels are the same, the Height and Area measurements will be closely proportional except at low signal levels where Heights are elevated by peak detection on noise fluctuations.

Estimating Q and B

Since it is difficult to measure photoelectron counts directly, the usual method for estimating photoelectron scales has been to measure uniform light signals at various levels and fit the measured means and variances to a statistical model involving the Poisson distribution expectations for the relation between them. Historically, two kinds of signal source have been used for this kind of evaluation: an LED light source producing very uniform pulses at adjustable signal levels or a mixture of populations of microspheres (also called “beads”) labeled with several different concentrations of a mixture of fluorescent dyes (or, in some cases, measurements of a single population of bright microspheres with a sequence of neutral density (ND) filters). The model can be expressed as a second-degree (quadratic) polynomial relating the observed signal means and variances to Q, B and CV₀, a source of variability in the measurements that is assumed to be the same among the several microsphere populations (or LED pulse levels).

Summary of previous methods for estimating Q and B from LED or bead measurements

Although not referred to as Q and B, Steen (5) used LED pulses to characterize the ability to convert fluorophore molecules detected in a flow cytometer into photoelectrons in a PMT. Steen also recognized the contributions of both the detection efficiency of signal photons and the background photons that were continuously present. Chase and Hoffman (1) adapted Steen’s basic approach to one that could be done on any flow cytometer using a set of fluorescent beads that spanned the signal range from dim to bright. The results with beads were compared to results with LED pulses to demonstrate that at least qualified beads could substitute for LED pulses to measure Q and B. For bead evaluations, the observed CV of the brightest bead population in the set was used as an estimate of the combined intrinsic CV and flow path variation effect for all of the populations. This fixed the second order term in an otherwise quadratic model allowing results to be obtained by fitting a linear model.

The quadratic mean and variance model and equation

For measurements on a population of similar particles like one of the populations in a multi-level bead set, the observed variance should be the sum of several components, specifically, electronic noise, background light not associated with the particles, Poisson variance related to the signal levels of the particles, the variation in dye amount among the particles and illumination variations due to particles taking different flow paths through the laser beam. The electronic noise and background light combine into a variance contribution that is not dependent on the signal level. The Poisson variance is proportional to the signal level, and the dye and illumination variations combine to form CV₀ whose contribution to the observed variance goes with the square of the signal level. Therefore, the general equation for the observed variance and its components can be expressed as

$$V(M_I)=c0+c1M_I+c2{M_I}^2$$ (Eq. 1a)

where M_I is the mean signal of the population in measurement intensity units, and V(M_I) is the observed variance of a population with mean M_I. We will fit sets of mean and variance data points with this equation to obtain the parameters c0, c1 and c2.

If we scale the signal levels in Spe, we can define B_Spe as the effective background level in Spe and M_Spe as the mean signal in Spe. B_Spe and M_Spe are Poisson distributed variables, so their contribution to the variance equals their value. Since CV₀ is not unit dependent, its contribution to the total variance will be CV₀²M² for any scaling of M, and the equation becomes

$$V(M_{\mathrm{Spe}})=B_{\mathrm{Spe}}+M_{\mathrm{Spe}}+C{V_0}^2{M_{\mathrm{Spe}}}^2.$$ (Eq. 1b)

Considering that the overall CV is also not unit dependent, it can be expressed as

$$C{V}^2=V(M_I)/{M_I}^2=V(M_{\mathrm{Spe}})/{M_{\mathrm{Spe}}}^2.$$ (Eq. 1c)

Defining Q_I as the Spe per intensity unit, Q_I = M_Spe/M_I or M_Spe = M_IQ_I and, from Eq. 1c, V(M_Spe) = V(M_I)Q_I². Rewriting Eq. 1b with these relations, we obtain

$$V\left(M_I\right){Q_I}^2=B_{\mathrm{Spe}}+M_I{Q}_I+C{V_0}^2{M_I}^2{Q_I}^2.$$ (Eq. 1d)

Dividing by Q_I² we obtain

$$V(M_I)=B_{\mathrm{Spe}/}{Q_I}^2+M_{I/}{Q}_I+C{V_0}^2{M_I}^2.$$ (Eq. 1e)

Comparing Eq. 1a and Eq. 1e, we see that c0 = B_Spe/Q_I², c1 = 1/Q_I and c2 = CV₀² or, alternatively, B_Spe = c0/c1², Q_I = 1/c1 and CV₀² = c2. These relations provide the physical interpretation of the fit parameters.

Improved and automated evaluation of Q and B

In the interest of creating a very reliable fully automated computational procedure for evaluating Q and B, we have made five important improvements over previous work:

1. We have implemented a set of methods that eliminate all subjective gating in evaluating multi-peak microsphere samples thereby providing consistent results in a fully automated mode. These include automated FSC-SSC peak finding and gating, K-means segmentation to assign data events to the appropriate peaks, and Gaussian peak fitting to minimize the influence of outlier events and peak shape distortions derived from the samples themselves and from flow conditions in the cytometer.

2. Most previous methods have tried to estimate CV₀ separately and then fit the data to a linear model for Q and B. We fit all three parameters of the quadratic model at once.

3. We have implemented appropriate weighting in carrying out the least squares fitting. Since the variances of the different points are quite variable, this is important for obtaining accurate results and has not been done in much of the previous work.

4. We provide standard errors for all of the fitted parameters so that uncertainties in the Q and B estimates can be taken into account.

5. We provide weighted residuals for the populations in each fit. These reveal any data points that are seriously out of line and act as an important quality control monitor.

Materials and Methods

Multi-level, multi-dye particle sets

We tested an 8-level multi-dye particle set (Sph8) from Spherotech (Lake Forest, IL 64005), Lot AE01, and a 6-level set (TF6) from Thermo Fisher (Fremont, CA 94538), item FC3MV, Batch2. More-or-less uniform bead populations are commonly referred to as “peaks”, particularly when in a multi-level series. Both types consist of polystyrene microspheres about 3 μm in diameter dyed internally with different dilutions of a mixture of 5 (Sph8) or 4 (TF6) fluorescent dyes with a range of spectra to provide signals in all fluorescence channels of multi-laser cytometers. The average signal step ratio between the Sph8 peaks is about 2.7 while the average step ratio between TF6 peaks is about 3.9. In addition to the dyed populations, each set includes a population of “blanks” with no added dye. The base microsphere lots include a main population of single microspheres with some aggregates and some particles of different sizes. The samples are provided as a mixture of the different populations which all have the same light scatter properties, so a combination of FSC-SSC light scatter gating to isolate the main population and a method for assigning events to the appropriate fluorescence populations is required to specify the individual peaks for statistical analysis. Ideally, the dyes will be uniformly distributed in the particles so that the distribution of dye amounts reflects the volume distribution of the particles in the main peak of the sample. In that case, the intrinsic CV of the dye distributions will be the same at all dye concentrations and peak brightness levels. The fitting procedure assumes that a single intrinsic CV is applicable to all of the bead peaks in a set, but, since the populations labeled with different concentrations of the dye mixture are processed separately, the intrinsic CVs may not be truly identical. Also, at very low dye concentration, the limited number of dye molecules per particle may produce a detectable Poisson variation in itself.

LED signal generation, attenuation and coupling into cytometers

Two LED signal generators were used in this work. For most of the work we used a battery-powered device designed and constructed by James Wood. It produces light pulses at a repetition rate of 1300/sec with a total pulse width of 2.0 μsec and a width at half maximum (FWHM) of 1.3 μsec. A current amplifier drives the LED producing light pulses with amplitude CVs of less than 0.2%. This device provides variable electronic attenuation over a signal level range of about 1600:1. In some cases it was used at maximum output with an optical fiber attenuation device that produces about 10,000:1 signal range by varying the distance between the LED and the fiber input. A second constant-level LED output provides an independent threshold signal. For the tests involving different LED pulse widths, we used a device consisting of an Agilent 33120A Function/Arbitrary Waveform Generator producing truncated Sinc function ((sin x)/x) pulses with adjustable width coupled to a Hewlett Packard 8013B Pulse Generator that provided threshold signals with variable delay relative to the Sinc function pulses. Signal level adjustments on this system were made with the optical fiber attenuation device.

On most of the instruments we tested, it was possible to mount a white 3 mm LED (NTE30044 Super Bright white LED) or the 2 mm fiber optic output of the attenuator close to the laser-sample stream intersection facing the collection optics so that all fluorescence detectors could be illuminated at once. Instruments used here that required more customized LED signal introduction are noted in the next section.

Instrument setup and data acquisition

As part of a larger instrument evaluation and comparison study, we collected LED series and multi-level bead data on 23 different cytometers. The instruments were set up for ordinary cell data collection conditions, generally what would be used for immunophenotyping work on lymphoid cells. Each instrument was equipped with its usual optical filters. On most instruments, LED data was taken with lasers off. In addition, a series of additional conditions and variations were investigated on one LSR-II instrument (designated LSR-IIF in the larger study, BD Biosciences, Milpitas, CA USA). These included data sets taken at different times, tests at several different PMT voltages, LED data with different pulse widths and bead data at different sample flow rates. Other instruments providing data reported here include other LSR-IIs (LSR-IIB, LSR-IIC, LSR-IIE, LSR-IIH), a two FACSArias (Aria-B and Aria-C), a FACSCanto (Canto), a Fortessa (Fortessa-A), a BD Influx (Influx-A) (all manufactured by BD Biosciences, Milpitas, CA USA) and a Xitogen XTG1600 prototype instrument (Xitogen was acquired by Beckman Coulter Life Sciences, Indianapolis, IN USA, and the test instrument was the precursor to the Beckman Coulter CytoFLEX.). On the Influx, the LED was mounted at the usual nozzle tip position. On the Xitogen XTG1600, the optical fiber output was coupled successively into the input of each detector set.

LED data files with 20,000 events were collected at approximate 2x intervals across the attenuation range of the LED system. The white LEDs provide some signal at all visible wavelengths (nominally 425nm to 750nm), but the far-red emission is weak. A given LED pulse level will generate quite different photoelectron signals on different detectors, so it is important to collect data over a wide range of LED levels to assure that the measurement series on each detector will include the low, middle and high level signals needed for optimal results in the fitting procedure. For the multi-level bead sets, 100,000 events were collected to assure that each defined peak would include about 10,000 events.

Peak evaluation for LED data files

LED data were acquired as a separate file for each LED level. All of the events in each file should represent valid LED signals. However, for consistency and to minimize problems due to possible stray events or imperfect linearity, we fit a Gaussian to the data and use its mean and variance as the Mean and Variance estimates.

Automated peak analysis of multi-level bead data files

The multi-level bead samples consist of a mixture of subsamples with different dye levels that are all based on the same original undyed bead lot. Therefore, the FSC and SSC distributions are all the same. The data events consist of a main population with at least 80% of the events, other low-frequency populations, bead doubles and aggregates and some small particles and debris.

The identification of event populations at the different dye levels and the estimation of their means and variances proceeds in three steps:

1. To isolate the core of the main population, we employ a peak finding routine in the log-FSC and log-SSC dimensions separately. The data values are sorted, and the width of each region containing 10% of events is evaluated across the data range to find the narrowest, and thus densest, region. Then, on each side, the 10% zone is moved away from the peak until the width is twice what it was at the densest region. The medians of the data in each of these two zones are taken as the upper and lower bounds of the interval where the estimated density is greater than half the maximum. The midpoint, which is half of the sum, is taken as the center and half the difference is taken as the radius. Finally, the data are gated by an ellipse in log-FSC versus log-SSC centered at the midpoints with a radius in each dimension equal to twice the radius estimated from the half width in that dimension.

2. We employ a standard K-means clustering algorithm from the ‘stats’ R package (6) to assign each data event in the FSC-SSC main peak gate to one of 6 (TF6) or 8 (Sph8) clusters. The data in each fluorescence dimension is presented to the K-means procedure in a logicle transformation (7,8) so that assigning events to the “nearest” cluster reliably gives correct assignments. The K-means procedure is applied to all of the fluorescence dimensions at once so that, as long as the peaks are well separated in at least some dimensions, the correct segmentation is achieved for all of the peaks in all dimensions.

3. In each of the fluorescence dimensions, we carry out a Gaussian fit for each cluster using the 'getOutliers' function from the 'extremevalues' R package, and we take the mean and variance of the best fit Gaussian as the Mean and Variance for the population. The fitting procedure strongly discounts outlier events and is relatively insensitive to peak distortion due to sample flow rate effects.

Peak validity criteria for Area and Height measurements

Once we have Mean and Variance values for the LED or bead peaks, we need to exclude any peaks that do not comply with the requirements of the data model. On some instruments, the blank bead population or the lowest LED peaks may be cut off at a data baseline so that the peak statistics will not be valid. Therefore, peaks too close to the baseline are excluded from the quadratic fitting. Many instruments do not maintain good linearity to the full top of scale, so it is important to specify a maximum level for good linearity and, on each fluorescence channel, exclude any peak that is above that maximum. We tested a sample of different instruments for linearity by measuring a single-level, multi-dye bead sample at a series of PMT voltages and tracking the ratio of signal medians between double and single bead peaks (ideally, a constant ratio of about 2.0). On Becton Dickinson instruments that utilize CS&T, the Baseline procedure evaluates linearity. The method is somewhat different from the double-single ratio procedure, but the results are similar when both procedures are run in parallel.

Area measurements are generally usable to down to zero signal level as long as the data acquisition system allows the negative side of the distribution to be recorded. For Height measurements at low signal levels, however, peak detection on noise+signal fluctuations results in higher means and lower variances than would be expected for the actual signal levels. To minimize distortion in the Height fitting, we have excluded peaks with Means less than ten times minimum peak height or with CVs > 65%.

Fitting the LED and multi-level bead data, assigning appropriate weights to the data and evaluating standard errors and individual peak weighted residuals

For a given detector and LED data file or isolated bead peak i we have N_i observations X_ij. The sample mean $M_i=\frac{1}{N_i}{\displaystyle {\sum }_{j=1}^{N_i}{X}_{ij}}$ and variance $V_i=\frac{1}{N_i-1}{\displaystyle {\sum }_{j=1}^{N_i}{\left(X_{ij}-M_i\right)}^2}$ are then also statistics with their own errors and distribution. We used unbiased estimators so that E[M_i] = E[X_i] and E[X_i] = Var[X_i], where E[X_i] and Var[X_i] are the true (but unknown) values of M_i and V_i respectively. For normal X_i, the M_i are also normally distributed with $\mathit{Var}[M_i]=\frac{\mathit{Var}[X_i]}{N_i}$ while V_i has a rescaled chi squared distribution, which will be very close to normal for large N_i and with $\mathit{Var}[V_i]=2\frac{\mathit{Var}{\left[X_i\right]}^2}{N_i-1}$. Technically, since both coordinates are subject to random errors, this is an error in variables model, which is, in general, hard to solve exactly. However, these two statistics are known to be independent so the errors are at least uncorrelated. In the ideal case (e.g., LED signals where electronic noise and light background are negligible) and in Spe coordinates, we have E[X_i] = Var[X_i] = Spe, so that $\frac{\mathit{Var}\left[V_i\right]}{\mathit{Var}\left[M_i\right]}=2\frac{\mathit{Var}{\left[X_i\right]}^2}{\mathit{Var}\left[X_i\right]}\frac{N_i}{N_i-1}\approx 2\mathit{Var}\left[X_i\right]=2\mathit{Spe}$, and, for large samples, the ratio of the errors is $\sqrt{2\mathit{Spe}}$. for a pulse of 100 Spe this ratio is more than fourteen to one and rising with pulse amplitude. The intrinsic CV₀ of the beads complicates this but, in the range of a few percent, does not change the conclusion that the variance in the V_i dimension dominates for all but the very smallest signals. Therefore, we can ignore the errors in M_i altogether and use the method of weighted least squares (9), where the weights are conventionally given as the inverses of the Var[V_i]. The least squares solution is not affected by a linear scale change of the data, so it doesn’t matter if we don’t actually know the Spe scale when doing the computation. The error estimated by least squares for the c₀ coefficient is likely to be systematically low on channels with very low background because of the neglected errors, but the c₀ error is not something that we rely on for making detailed comparisons.

To put this into a more descriptive form and describe the actual methods employed, the peaks in the multi-level bead samples and the LED data series have a wide range of variances, so unweighted least squares fitting is not appropriate, and we need to apply appropriate weights in the fitting procedure. In particular, the populations with lower variances get more weight since having the fit miss them by any particular amount is worse than missing a high variance population by the same amount. The weights are typically supplied to the statistics package as one divided by the expected variance and, using the formula above, we could express them in terms of the true variance Var[X_i] if we knew it. We have taken two approaches in carrying out the fitting procedure. The simpler one is to derive the estimate from the value we already have in hand, namely Vi. In the second approach, the coefficients of the fit polynomial are first estimated using weights for each point computed directly from the sample variance of each peak as in the first method. These results are then refined iteratively by computing new weights based on the variance predicted by the fit polynomial, evaluated at the mean of each peak and refitting. This process is repeated until all the coefficients have converged to four significant figures, i.e., the absolute value of the relative change in the coefficients was less than the round off error of 5×10⁻⁵. This occurs quickly, usually in about 4 iterations.

When the uncertainty in estimates of peak means and variances are due to limited sample size and related statistical variability, the iterative method has theoretical advantages and should improve the accuracy of the results. However, with sample sizes in the range of 10,000 events per sample population, statistical error should be small, and improvements using the iterative method should be minimal. For multi-level beads, the main sources of error in the fitting are likely to be differences in the effective CV₀ of the different bead populations leading to data that contains systematic deviations from the assumptions of the quadratic model. The multi-level bead samples start with a single undyed lot of polymer beads, and aliquots of that are stained with different concentrations of a mixture of several dyes. In our experience, optimal uniformity of the staining may not be achieved in all of the separately dyed populations in a multi-level sample, and any production problems will tend to give one or more populations with effective CV₀ higher than the others. One population with high CV₀ will shift the initial fit parameters somewhat away from what would be obtained with all equal CV₀s, but, in the presence of one bad data point, the single step method, while degraded, generally produces a sensible result from the remaining points.

When the initial fitting procedure is applied with its assumption of a single CV₀ for all populations, any population with higher CV₀ can be expected to have an observed variance greater than that predicted by the fit. Applying the iterative procedure in this situation will increase the weights of any bad points and shift the fit parameters away from those corresponding to the actual Spe scale and Background values that are the objective of the whole procedure. The iterative method can be driven quite far from the single step result by trying to accommodate an inopportunely placed bad point. Therefore, it should not be used blindly but only after quality control of the first step result. Our results discussed below in the section “Are there differences in intrinsic CV …” demonstrate that this is a relevant issue, so in this work we have relied on the results of the single fitting procedure.

The fitting routine provides estimates for the three quadratic parameters (c0, c1 and c2) and their standard errors. A weighted residual is evaluated for each data peak as the difference between the observed variance and the fit parameters estimate of that variance multiplied by the square root of the weight for that peak.

In the data processing and fitting we use the R packages flowCore (10), flowViz (11), xlsx and extremevalues. The first two are available from BioConductor http://www.bioconductor.org/ and the remaining two are available from any CRAN mirror. Package flowCore is used to read and write FCS files, flowViz is used for visualization and debugging, xlsx lets us read the Excel spreadsheets that we use in order to organize files and capture metadata essential for the automated calculations, and the function getOutliers in extremevalues returns as part of its output the estimated mean and standard deviation obtained by fitting a Gaussian distribution. The quadratic model is fit using the 'lm' (linear model) function from the 'stats' library in R. We are able to use the 'lm' function since our quadratic model is essentially a linear model in two variables, one of which is the square of the other. For some work we used the equivalent platform in JMP 10 (SAS Institute, Cary, NC, USA).

LED fitting includes both quadratic and linear fits

For LED analysis, results are reported for both quadratic fitting and linear fitting (effectively fixing CV₀ = 0). Since the uniformity of LED signal outputs is likely to be better than the ability of the cytometer electronics to evaluate it, the c2 term in a quadratic fit should be very close to zero with a small standard error. If the results of the quadratic fit are consistent with CV₀ = 0, we can rely on the linear fit results whose standard errors on c1 will generally be smaller than the c1 standard errors of the quadratic fit.

Information needed to carry through the otherwise fully automated procedure

The scripted analysis procedure requires some information to process the sample data correctly:

1. A folder or file name and designation as LED or multi-level bead data.

2. For different populations in a single file, the number of peaks to be identified.

3. Fluorescence channels to be used in the fitting must be identified and designated as Area or Height. Also, for bead data, channel names for light scatter gating dimensions are needed.

4. The highest measurement level that is expected to maintain good linearity.

Note that no subjective processing or gating decisions are involved.

Monte Carlo modeling for the effect of CV₀ differences in fitting

When the weighted residuals in the fits are good for both LED signals and multi-level beads on the same instrument, we usually see good correspondence among the c1 fit parameters, but the relative standard errors are almost always larger for the bead fits than for the corresponding LED fits. In order to clarify whether this is due to imperfections in the beads themselves or because the presence of a positive quadratic term in itself reduces the sensitivity of the model, we conducted a series of Monte Carlo simulations of the procedure. Given a number of peaks, a fixed ratio between the successive peaks and a signal value for the top bead, we calculate a defined set of peak means Mi. Then, for a given choice of the parameters (c0, c1 and c2=CV₀²), we can form a suitable set of variances Vi using a chi-squared distribution pseudo random number generator and then fit these data to the model. For each trial the predicted relative error of c1 and the actual relative error are recorded. After 1000 trials the average predicted relative error and standard deviation of the actual relative error are saved.

We extended the modeling to include the effect of differences in effective CV₀ among the different bead peaks by multiplying each Vi by a pseudo random factor, log normally distributed with a mean of one and 5% CV thereby simulating random errors in the uniformity of the beads themselves.

FlowJo and JMP data analysis for data illustrations

FlowJo 9.7.6 and FlowJo VX0.7 (FlowJo LLC, Ashland, OR USA) were used for additional analysis of fcs data files and for production of some data illustrations. JMP 10 software was used to produce illustrations of the quadratic fitting results and weighted residuals.

Results

In this section we illustrate the results of the gating and fitting procedures on 11 different instruments and then focus on confirming the validity of the analytical methods used, the consistency of the results over variations in the measurement conditions and comparison of the results obtained from LED data with those from multi-level bead sets. The validity tests include results on the normality of the LED data and the distortion of low-level Height measurements. We carried out a series of consistency tests investigating the stability of the Spe scaling results with data sets taken at different times, at different PMT voltages, at different pulse widths (LED data only) and at different sample flow rates (multi-level bead data only). These consistency tests were all conducted on one LSR-II (LSRII-F) in the Stanford Shared FACS Facility.

Gating results for multi-level beads

Figure 1 illustrates the measurements on the Sph8 and TF6 bead sets and the results of the FSC-SSC gating on the main bead peak. Panel A shows the FSC-SSC pattern of Sph8 beads, and panel B shows the events in the automated elliptical gate on the main peak region. Panel C shows all events in two fluorescence dimensions, and panel D shows the same plot for just the events in the main peak gate. Panels E, F, G and H show the parallel plots for TF6 beads. The Sph8 sample shows more events and low frequency populations outside the main FSC-SSC peak than the TF6 sample (compare panels A and E), but, within the main peak gated population, the Sph8 fluorescence populations are well defined with few events outside the peaks while the FSC-SSC gated TF6 fluorescence populations show more outliers (compare panels D and H). In the 23 instrument comparison series, the FSC-SSC gating procedure identified the main single bead FSC-SSC peak in all cases.

Figure 1.

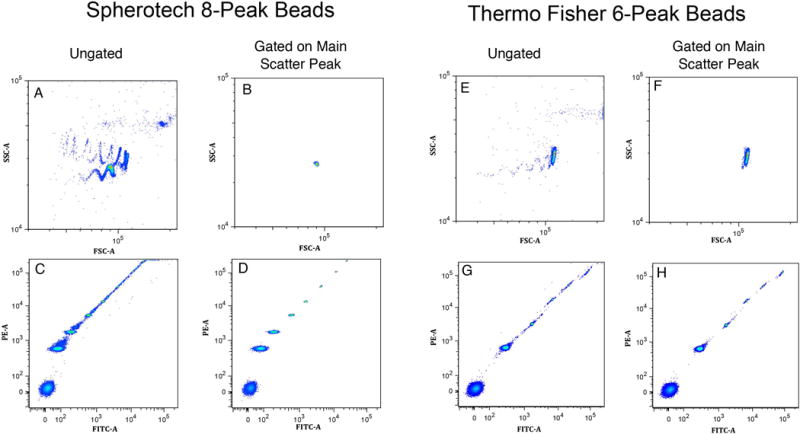
Light scatter gating on the main single particle population in Sph8 and TF6 bead samples. Panels A and E show the FSC-A vs. SSC-A light scatter patterns for Spherotech 8-peak (Sph8) and Thermo Fisher 6-peak (TF6) beads. After peak detection in each dimension and gating on the main single particle peak, the gated FSC vs. SSC distributions are shown in Panels B and F. The ungated distributions for FITC-A vs. PE-A signals are shown in Panels C and G, and the corresponding gated distributions are in Panels D and H. Note that Panels A, B, E and F show an enlarged view of the FSC-A and SSC-A dimensions starting at a signal level of 10⁴.

K-means segmentation results for multi-level beads and setting the logicle Width for reliably accurate peak assignments

The K-means assignment of the events to the appropriate bead peaks depends on having each bead peak resolved from the others in at least one fluorescence dimension. Both the Sph8 and TF6 samples showed good resolution of all peaks in at least one fluorescence dimension on each of the 23 instruments tested, and correct peak segmentation was achieved in all cases. Rather than attempting to identify dimensions with good peak separations, the automated method uses all fluorescence dimensions in the K-means procedure, and the dimensions in which peaks are well resolved dominate the results.

The K-means procedure assigns each data point to the cluster center closest to it, but, in cases where the lowest population is spread too widely, K-means may divide it into two clusters and combine two other peaks as a single cluster. Since the Sph8 and TF6 bead sets have nearly equal frequencies of the different populations, this kind of clustering error results in two half-frequency clusters and one double-frequency cluster. Finding this pattern indicates that the Width must be increased. In the 23 instrument data series the initial logicle Width setting of 0.5 led to correct K-means segmentation of the Sph8 and TF6 bead peaks for all but one instrument (see (5) for an explanation of the logicle Width parameter). Increasing the logicle Width parameter to 1.0 gave accurate peak segmentation on all of the instruments. If necessary, an appropriate logicle Width could be determined for each measurement channel individually as described in (5).

Fitting results for multi-level beads

The upper and middle parts of Figure 2 illustrate the results of fitting Sph8 and TF6 bead peaks with the quadratic model, showing examples of two fluorescence channels (FITC and PE) for each bead set. To obtain graphical illustrations, we used a fitting procedure in JMP that is equivalent to the one we used in R for the main analysis. In the JMP results illustrated here, the fit parameters labeled Intercept, M and Mˆ2 correspond to c0, c1 and c2, respectively. The four fits are all reasonably good with no extreme residuals and relative standard errors on the linear term (M ⇔ c1) in the range of 3–8%. As long as there are at least 4 valid peaks in a data set, the fitting procedure provides estimates of the three fitting parameters (c0, c1 and c2) with standard errors for each of them. If there are only 3 valid peaks, the fitting parameters are evaluated, but no error estimates can be made. The weighted residuals indicate how much the fitted curve misses each point relative to the weighting for that point. For data that match the model perfectly with only the expected statistical variations, the weighted residuals should have a Gaussian distribution with mean of zero and standard deviation of 1. For real measurement samples under good conditions, the weighted residuals spread somewhat more than the theoretical expectation without any obvious pattern, but in some situations high residuals point to deviations from instrument linearity or to problems in particular samples or particular data collections.

Figure 2.

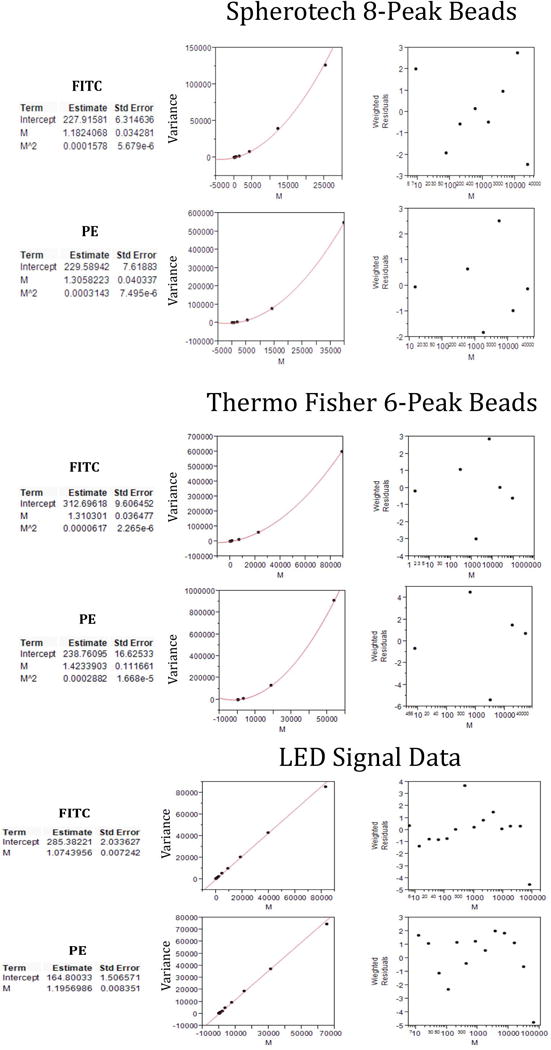
Examples of fitting procedure outputs for fit parameters, fit curves and weighted residuals on multi-level bead and LED data. The upper, middle and lower sections each show results in FITC and PE measurement channels for Spherotech 8-peak (Sph8), Thermo Fisher 6-peak (TF6) and LED measurements, respectively. These results were produced in JMP, and the fit parameters Intercept, M and M^2 correspond to c0, c1 and c2, respectively, in the R analysis. The population means M are in instrument measurement units. Linear fitting was used for the LED data, so there is no M^2 parameter in the results. The left plots show the fit curve in relation to the fitted data points. The right plots show the weighted residuals for each of the data points.

Analysis of LED data – normality of the data distributions and uniformity of LED signals

For LED data, although we evaluate the Mean and Variance of each population by Gaussian fitting, we expect that the LED peaks will be normally distributed since the pulses are very uniform, and measurement variation should be dominated by the Poisson process of photoelectron production. We confirmed this expectation by testing some of the measured distributions for normality. Sample results are illustrated in Supplementary Material Figure S1 where the plots show that the data distributions are virtually identical to the theoretical expected distributions.

We tested the uniformity of the LED pulses by placing the LED directly in front of a PMT operating at a low 265V to allow signals producing high photoelectron counts to be on scale. With the electronic attenuation system, we measured signals at the minimum setting and compared them to signals with the LED at maximum level but with 1000× optical attenuation to achieve the same signal level on the PMT. The optically attenuated maximum level signals were measured at 0.13% CV including Spe variance, indicating that they are as uniform as the system can reasonably measure. The LED signals with electronic attenuation were measured at 0.8% CV indicating some measurable variability but not enough to be a problem since, in the normal configuration, the observed CVs at minimum setting were much greater than this on all measurement channels.

Fitting results for LED data

An example of linear fitting to LED data (with lasers on) is shown in the bottom part of Figure 2 for the same instrument and measurement channels that were illustrated for the quadratic bead fits. In the JMP output, Intercept and M correspond to c0 and c1, respectively, and c2 is effectively set to zero. In both channels the linear fit is good with no excessive residuals, and the relative standard errors on the linear terms (M ⬄ c1) are very good at about 0.7% (compared to 3–8% for bead fits on the same channels).

Measurement distortion with low Height signals

As described above in the Methods section “Peak validity criteria for Area and Height measurements”, both Means and Variances of low-signal populations in Height measurements are distorted by selection of the highest point in a signal pulse as the Height value for the pulse. At high signal levels, we observe, as expected, that the ratios of Height to Area means and the ratios of Height to Area variances or standard deviations are constant over a range of signal levels. At lower signal levels, Me-H/Me-A rises, and SD-H/SD-A decreases, indicating that the Height evaluations are being affected by noise fluctuations around the peak. Figure 3 shows an example in which Me-H/Me-A is up by about 4% and SD-H/SD-A is down by about 6% in the region where the measured Height is 10 times the lowest Height value (with zero actual signal) compared to the plateau values at high signal levels. This suggests that peaks with Means less than about 10 times the minimum Height value should be excluded to avoid distorting the fit by including data that does not comply with the linearity expectations of the data model. For the current work, we use a 10x cutoff.

Figure 3.

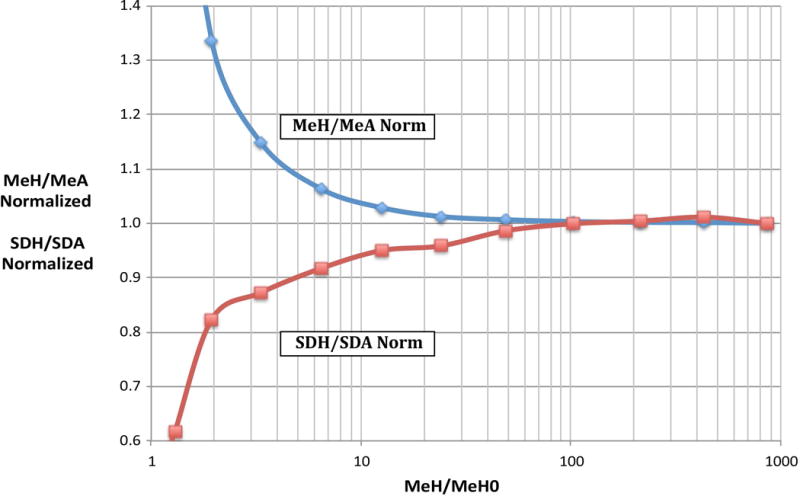
Distortion of Height Mean and SD measurements at low signal levels relative to Area Means and SDs. LED measurements on the FITC channel of LSR-IIF were evaluated for both Area and Height Means and SDs. For each LED level, the Mean Height was divided by the Mean Height for a data set with zero LED signal (MeH/MeH0) to obtain the value displayed on the horizontal axis. The ratio of the Height Mean to Area Mean (MeH/MeA) and Height SD to Area SD (SDH/SDA) were evaluated for each LED level and normalized to the value at about MeH/MeH0 = 850.

Examples of fitting procedure outputs and comparison of LED and bead results

The flowQB package produces a number of tables and other outputs that contain the primary fitting results and multiple types of other results that are useful for quality assurance and troubleshooting. An example of tables showing input Means, Variances and weights for LED fitting on one fluorescence channel and the weighted residuals for the resulting fit is in Supplementary Material Table S1. Table 1 shows an example of the primary results from LED and bead fits on 8 channels of one LSR-II instrument (LSR-IIF, later run). The upper part of the table is the direct output from the fitting procedure for LED quadratic, LED linear, Sph8 Beads and TF6 Beads. The lower part shows ratios among the components of the fit results and some results expressed in terms of CV₀, Q_I and B_Spe. The quadratic fit results include the c0, c1 and c2 parameters and their standard errors. The LED quadratic fit includes a c2 P-value line. In this example, the P values are all non-significant except for a 0.001 for FITC and a 0.002 for PE, but the corresponding c2 values which represent CV₀² are both negative and cannot represent a real positive CV₀. Therefore, we rely on the linear fit results for the LED data noting that the LED linear values for “c1 Relative StdErr (%)” in the lower section are all smaller than the LED quadratic values except for FITC and PE, and, even for these the fitted c1 values differ by no more than 2%.

Table 1.

The results of the fitting procedure for LED quadratic and linear fits and for Sph8 and TF6 bead fits. The upper part shows flowQB output results for c0, c1 and c2 and their standard errors on 8 channels of one LSR-II instrument (LSR-IIF, later run). The c2 P-value is included for the LED-quadratic fit. The lower section shows the ratio of standard errors to fit parameter values as percent (%). The “Bead CV₀ Estimates” are the square roots of the corresponding c2 values expressed as percent (%). The “LED linear fit results expressed in terms of Spe units” section shows LED linear results expresses as B_Spe and Q_I. The “ Q_I estimates for other methods relative to the LED linear Q_I” section at the bottom shows the similarity of the different estimators of the Spe scale.

LSR-IIF, later run Primary Fit Output		Dye	APC	APC-Cy7	FITC	PE	PE-Cy7	PerCP-Cy55	V450	V500-C
	LED quadratic	c0	129	1047	284	164	152	284	1437	343
		c0 StdErr	0.9	5.5	1.4	1.1	0.8	3.0	9.8	9.0
		c1	4.09	11.23	1.09	1.21	3.03	5.35	1.59	2.67
		c1 StdErr	0.0171	0.0659	0.0064	0.0074	0.0205	0.0459	0.0194	0.0679
		c2	9.60E-7	8.19E-7	7.08E-7	10.1E-7	8.14E-7	1.21E-7	10.9E-7	17.8E-7
		c2 StdErr	8.56E-7	41.17E-7	1.71E-7	2.60E-7	43.3E-7	22.7E-7	7.62E-7	24.4E-7
		c2 P value	0.284	0.847	0.001	0.002	0.854	0.958	0.179	0.481
	LED linear	c0	129	1047	285	165	152	284	1441	344
		c0 StdErr	0.9	5.2	2.0	1.5	0.7	2.8	10.0	8.7
		c1	4.10	11.22	1.07	1.20	3.02	5.35	1.56	2.64
		c1 StdErr	0.0143	0.0501	0.0072	0.0084	0.0150	0.0359	0.0134	0.0525
	Sph8	c0	84	729	180	156	119	153	1055	237
		c0 StdErr	67.2	176.1	6.1	4.7	5.3	8.8	291.0	33.8
		c1	4.28	12.47	1.15	1.31	3.11	5.46	2.21	2.79
		c1 StdErr	0.4519	1.5455	0.0398	0.0300	0.0805	0.1268	0.4043	0.1359
		c2	42.062E-5	22.465E-5	22.862E-5	17.7E-5	19.714E-5	22.06E-5	7.20E-5	5.52E-5
		c2 StdErr	50.8E-6	91.0E-6	8.39E-6	4.38E-6	12.8E-6	12.0E-6	17.5E-6	7.16E-6
	TF6	c0	70	913	278	193	131	187	1361	293
		c0 StdErr	41.3	28.9	9.0	7.9	4.2	8.8	238.3	34.9
		c1	4.65	11.10	1.25	1.42	2.97	5.29	1.91	2.78
		c1 StdErr	0.2988	0.2386	0.0386	0.0565	0.0850	0.1619	0.5809	0.3017
		c2	8.81E-5	17.696E-5	8.48E-5	16.875E-5	25.717E-5	18.084E-5	50.003E-5	59.019E-5
		c2 StdErr	16.6E-6	12.3E-6	2.93E-6	6.41E-6	18.0E-6	11.5E-6	68.9E-6	70.1E-6
RelStdErr for the fit parameters			APC	APC-Cy7	FITC	PE	PE-Cy7 P	PerCP-Cy55	V450	V500-C
	LED quadratic	c0 Relative StdErr (%)	0.66	0.52	0.49	0.65	0.51	1.05	0.68	2.62
	LED linear	c0 Relative StdErr (%)	0.66	0.50	0.71	0.91	0.48	1.00	0.69	2.53
	Sph8	c0 Relative StdErr (%)	80.04	24.15	3.38	2.99	4.45	5.79	27.57	14.24
	TF6	c0 Relative StdErr (%)	59.01	3.17	3.25	4.11	3.22	4.68	17.51	11.91
	LED quadratic	c1 Relative StdErr (%)	0.42	0.59	0.59	0.61	0.68	0.86	1.23	2.55
	LED linear	c1 Relative StdErr (%)	0.35	0.45	0.67	0.70	0.50	0.67	0.86	1.99
	Sph8	c1 Relative StdErr (%)	10.55	12.39	3.45	2.28	2.59	2.32	18.28	4.86
	TF6	c1 Relative StdErr (%)	6.43	2.15	3.09	3.98	2.86	3.06	30.38	10.84
	LED quadratic	c2 Relative StdErr (%)	89.20	−509.22	−24.22	−25.68	−532.18	−1876.62	−69.69	−137.56
	LED linear	c2 Relative StdErr (%)
	Sph8	c2 Relative StdErr (%)	12.07	40.51	3.67	2.48	6.49	5.45	24.27	12.98
	TF6	c2 Relative StdErr (%)	18.84	6.95	3.46	3.80	7.00	6.36	13.78	11.88
Bead CVo Estimates			APC	APC-Cy7	FITC	PE	PE-Cy7	PerCP-Cy55	V450	V500-C
	Sph8	c2 CVo (%)=100*sqrt(c2)	2.05	1.50	1.51	1.33	1.40	1.49	0.85	0.74
	TF6	c2 CVo (%)=100*sqrt(c2)	0.94	1.33	0.92	1.30	1.60	1.34	2.24	2.43
LED linear fit results expressed in terms of Spe units
	BSpe for LED lin	(=c0/c12)	8	8	247	115	17	10	588	49
	QI for LED Iin	(=1/c, or Spe/Signal Unit)	0.24	0.09	0.93	0.84	0.33	0.19	0.64	0.38
QI estimates for other methods relative to the LED linear QI
Other QI/LED [in QI(=LED Iin c1/Other c1)		LED quadratic	1.00	1.00	0.98	0.99	1.00	1.00	0.99	0.99
		Sph8 AE01	0.96	0.90	0.93	0.91	0.97	0.98	0.71	0.94
		TF6 FC3MV	0.88	1.01	0.86	0.84	1.02	1.01	0.82	0.95

For the bead fits the CV₀ estimates corresponding to the fitted c2 values are shown in the lower section where the CV₀ values are all in the 1–2% range. The c0 and c1 relative errors for the bead fits are all higher than for the LED fits with some c1 relative standard errors close to 2% but with several over 10%. In the bottom section of the table, 11 of the 16 Sph8 and TF6 bead fit c1 values are within 10% of the corresponding linear LED c1 values, and only one differs by more than 20%.

Comparison of c1 values and c1 standard errors between LED and bead fits on several instruments

Figure 4 shows the c1 parameter values and their standard errors relative to the LED c1 for 8 measurement channels on a number of different instruments. Panels A and B show Area results for two runs on the same LSR-II (LSR-IIF) taken 8 months apart. The patterns are very similar indicating that both the measurements and their errors were stable over that period. Panel C shows Height fit results from the same run as Panel B. This is generally similar, but some bead evaluations show more deviation from the LED values and larger standard errors due to the need to omit some low signal beads in the Height fitting as described above in “Measurement distortion with low Height signals”. Figure 2 is based on FITC and PE channel data from the original run on this instrument (Figure 4, Panel A), and Table 1 is based on the run 8 months later (Figure 4, Panel B), leading to similar but not quite identical fitting results in the FITC and PE columns.

Figure 4.

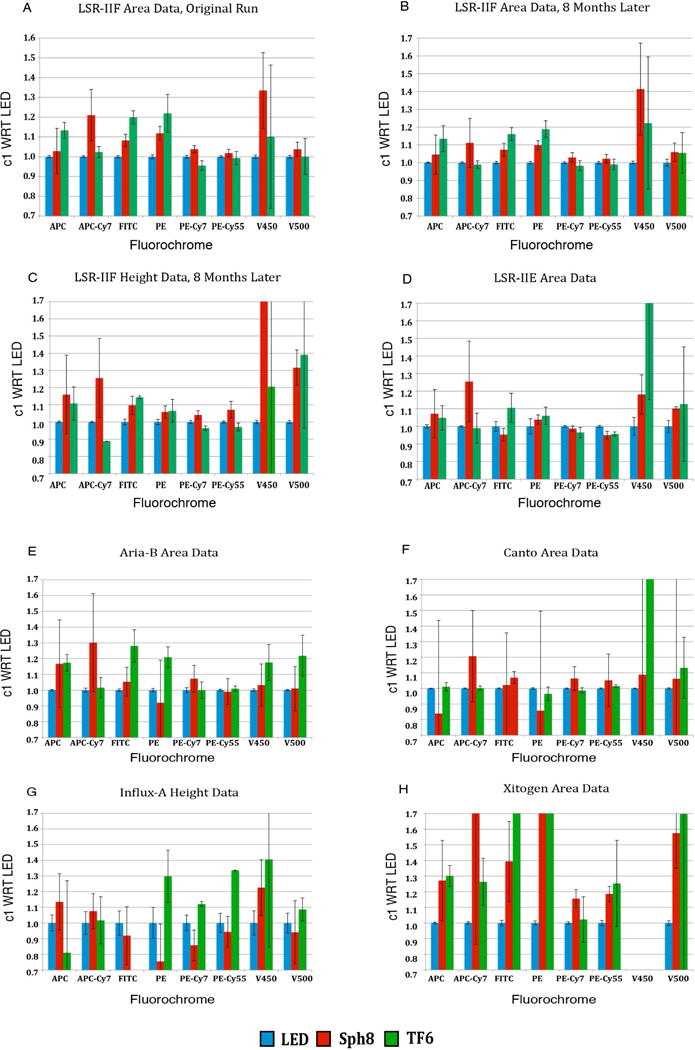
Relative c1 values and relative standard errors on c1 for LED, Sph8 and TF6 fits. Values for c1 and its relative standard error for LED signals, Sph8 beads and TF6 beads on several instruments and measurement channels were normalized to the corresponding LED c1 value. Panels A and B show results for the same instrument takes 8 months apart. Panel C shows Height data corresponding to the Area data in Panel B. Panels D, E, F, G and H show parallel results for 5 other instruments. Since 1/c1 = Q_I = Spe/signal unit, bead values greater than 1.0 correspond to Spe scale estimates lower than the LED estimates. In some cases the c1 ratio for beads to LED is greater than the 1.7 maximum of the plot scale. In these cases, the bead fit had failed to produce a reasonable correspondence with the LED result, and the exact value is not relevant.

Panels D, E and F show data from a different LSR-II, a FACSAria and a Canto. The patterns show some similarities to the first LSR-II and some differences. Overall, the LED fits give much smaller standard errors than the bead fits. Most of the bead derived c1 parameters are within 20% of the LED values except for the V450 channel. Panel G shows results for an Influx system with analog logamps that show periodic irregularities in their signal evaluations. These irregularities generate shifts in peak positions and variances that increase the uncertainties in the fit results leading to high variability in the bead fits and to much higher relative standard errors on the LED evaluations of c1 than are seen on the other instruments.

Panel H shows results for the Xitogen prototype instrument. This cytometer uses solid-state detectors and novel optics to achieve much higher Q values (as Spe per unit of dye) than any of the PMT detector instruments tested. The solid-state detectors do, however, have relatively high noise/background. The fitting works well on LED data and gives low relative errors on c1, but the bead fits give erratic values and large error estimates. It turns out that almost all of the observed variance in the bead peaks is accounted for by the background and CV₀ (c0 and c2) components so that the c1 contribution is small and difficult to estimate. In this case where even the lower bead peaks are measured at relatively high Spe levels, differences among the intrinsic CVs of the bead peaks will produce anomalous contributions to the observed peak variances so that the assumption of equal intrinsic CVs for all stained beads in the set fails to be an acceptable approximation. Comparison of the CVs from LED pulses and from beads at similar signal levels on a Xitogen instrument showed the dimmest beads in both bead sets to have higher intrinsic CV’s than the brightest beads in the set. This causes inaccurate estimation of c1 in bead fitting evaluations.

Monte Carlo modeling for the effect of CVo differences in fitting

We investigated the possibility that bead CV₀ values in the 2% range in themselves lead to higher c1 relative standard errors compared to LED results. Monte Carlo modeling confirmed that this is the case. The test emulated TF6 bead data on an LSR-II with 6 peaks each containing 10,000 events at peak mean levels starting at 100,000 signal units and going down by a factor of 3.5 for each step. The procedure systematically probed the parameter space covering the actual range of results on the LSR-II instruments. An example of the results, presented as the relative error as a function of Spe per signal unit and CV_0, is shown in the upper panels of Supplementary Material S2. The plots demonstrate that, in bead fits with relatively low error estimates, virtually all the additional error over the LED results can be accounted for by the loss of sensitivity due to CV₀ > 0 and that, for both bead data with no special problems and for the LED data, the performance is close to the theoretical limit.

We also investigated the sensitivity of the fitting procedure to small deviations in the peak variances by multiplying each peak variance by a 5% CV pseudo-random factor to simulate random errors in the beads themselves with results illustrated in the lower panels of Supplementary Material Figure S2. The additional variation did increase the error as expected but did not appear to destabilize the model. Even if it were possible to measure these effects for real beads and correct the data to account for them, the accuracy would not be substantially improved as long as CV₀ itself can't be reduced. This, of course, does not address the problems that any systematic errors would introduce. We also looked at models with a few different background levels and found that the results are not sensitive to this for realistic values (data not shown).

Are there differences in intrinsic CV among the populations in a multi-level bead sample?

In some cases the bead fit results are much worse than the Monte Carlo results can explain, so we analyzed some of the data for indications of substantial differences in the intrinsic CVs of the different bead peaks in a set. Such a violation of the assumptions of the quadratic model could cause the kind of consistently high standard errors seen in the V450 channel data on most instruments illustrated in Figure 4, especially among the TF6 results. We tested the data from 9 instruments on three spectrally separated measurement channels (APC, FITC and V450). We obtained a residual variance by subtracting the background variance contribution (c0) and a linear term variance (estimated from the LED linear fit c1′ value) from the observed total variance. Dividing this residual variance by the square of the mean signal level for each peak gives an effective c2 value for that peak. We subtracted the effective c2 for the highest peak used in the fit from the values for the other peaks leading to the results for “Excess c2” shown in Figure 5. Here positive values indicate excess variance in the particular peak relative to the highest one. In the left panels for Sph8 beads, peaks 2 and, to a lesser extent, 3 show erratic differences between instruments and measurement channels, and the values for the higher beads are all small with no obvious pattern. Since the Sph8 peaks 2 and 3 are not very bright, the residual variance estimates are probably not very accurate and small differences in the effective CV will not have much effect on the c1 estimate. In the right panels TF6 peak 2, which is relatively brighter than the low Sph8 peaks, stands out with high c2 increments in all three channels on all instruments. The average value in the range of 0.002 for peak 2 in the V450 channel would correspond to an intrinsic CV in the range of 5% when the other peaks are in the range of 2% or less. This is probably the reason for the poor V450 fits on most instruments. Interestingly, the smaller but detectable deviations for TF6 peak 2 in the APC and FITC channels are not associated with consistently bad fits, presumably because the measured CVs of peak 2 in those channels are higher than the peak 2 CVs in the V450 channel.

Figure 5.

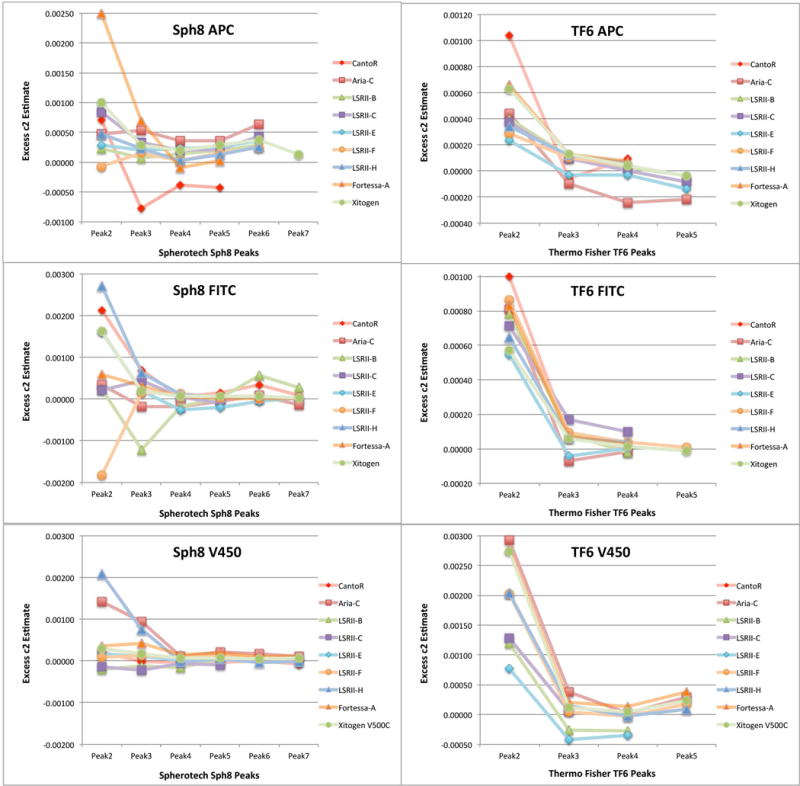
“Excess c2” among lower signal bead peaks in Sph8 and TF6 is an indicator of differences in intrinsic CV among the bead populations. For each bead peak between the unstained and the brightest used in the fitting procedure, we calculated a residual variance by subtracting the expected background variance (c0) and the expected linear term variance using the c1′ value of the corresponding LED fit from the observed total variance. Dividing this by the square of the peak mean gives an effective c2 residual and subtracting the effective c2 for the highest peak in the fit from the others gives “Excess c2” values for the intermediate peaks that can be compared among different peaks and instruments. The figure illustrates results for three measurements (APC, FITC and V450 dye channels) on nine instruments.

Under favorable conditions Bead fit estimates of c1 have relative standard errors of less than 10% and c1 values within 20% of the LED-based estimates

We evaluated the c1 (= 1/Q_I) values and their relative standard errors for selected instruments with good linearity to determine how well we can expect the bead fitting to work in general. Figure 6 shows the distribution of the LED c1/Bead c1 (= Bead Q_I/LED Q_I = Bead Spe/LED Spe) ratio in relation to the Bead c1 relative standard error for 7 measurement channels of 10 instruments that should have good linearity and for which usable LED, Sph8 and TF6 data and fits are available. We consider points in the highlighted region with LEDc1/Beadc1 between 0.8 and 1.2 and Bead fit c1 relative standard errors no more than 10% to represent good results for the Bead fitting. Among the 140 data points, only 4 (3%) represent bead c1 values more than 25% above or below the LED c1 value. Overall, 89% of the points fall between 0.8 and 1.2, although some of these have relative standard errors greater than 10% so that we would not have high confidence in the c1 values. The “good” points in the 0.8 to 1.2 range with relative standard errors less than 10% constitute 78% of the total. The center of the LED c1/Bead c1 distribution is at about 0.95 indicating that the bead fit Spe estimates average about 5% lower than the LED-based estimates.

Figure 6.

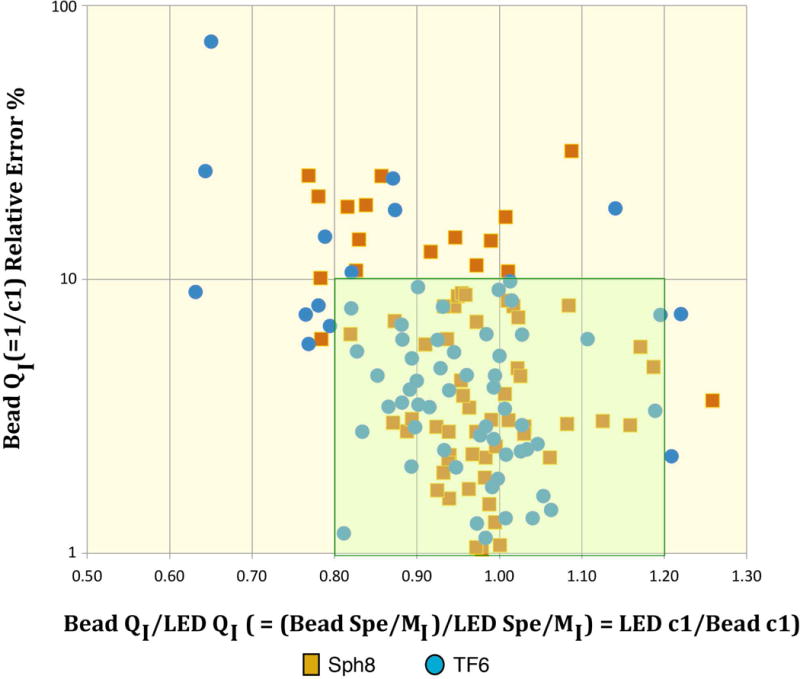
LED c1/Bead c1 estimates (= Bead Spe/LED Spe) in relation to relative standard errors for Bead c1. The figure includes data on 7 measurement channels of 10 instruments that should have good linearity and for which usable LED, Sph8 and TF6 data and fits are available. We consider points in the highlighted region with LEDc1/Beadc1 between 0.8 and 1.2 and Bead fit c1 relative standard errors no more than 10% to represent good results for the Bead fitting.

We ran a series of 5 consistency tests to confirm that the fitting results and parameter values behave appropriately under various differences in measurement conditions. Besides the main investigation involving acquisition and analysis of parallel LED and multi-level bead data on a series of cytometers, we tested the same instrument at different times, at different PMT voltages, at different bead flow rates (2 types of tests) and with different LED pulse widths.

Test 1: Consistent Spe scales were found on a single instrument over 8 months

The evaluation panel of LED and bead analyses was run again on LSR-IIF 8 months after the original multi-instrument program (see the c1 parameter results in Figure 4, Panels A and B). For each data source (LED, Sph8 and TF6) the ratio between the later and earlier Spe/Intensity values across 8 dye channels averaged close to 1.01 with a standard deviation among channels of about 4%.

Test 2: Spe scales measured at different PMT voltages show the expected gain proportional changes

LED data series and Sph8 and TF6 samples were recorded at three different PMT voltage levels on one instrument. The voltages were the standard starting voltages for the instrument and voltages 10% and 20% above that to give signal gains of about 2 and 4 times the standard gain, respectively. The resulting data sets were analyzed by the usual fitting method, and the resulting c1 estimates were adjusted with the reference particle signal levels to give Spe values that would ideally be the same for the different PMT voltages. Averaging over 7 dye channels and LED, Sph8 and TF6 data, the Spe scale at +10% voltage averaged 1.043 times that at the standard voltage with an SD of 0.043. The Spe scale at +20% voltage averaged 1.020 times that at +10% with an SD of 0.034. These results show that the estimated Spe scales shift appropriately with gain changes. The background or c0 term scaled in Spe decreased with increasing PMT voltages as expected. The adjusted background at +10% voltage was 74% of that at the standard voltage and decreased further to 60% at the +20% voltage indicating that the background at the standard setting included a substantial electronic noise contribution whose relative contribution decreased at higher gain.

Test 3: Higher sample flow rates increase c2=CV₀² estimates but have little effect on c1=1/Q_I for Sph8 and TF6 analyses

Multi-level bead samples were run on LSR-IIF at three different sample flow rates with volume ratios close to 1:3:5. Over 18 fluorescence channels each for Sph8 and TF6 beads, the corresponding average ratios for c1 were 1:1.011:1.015 while the c2 averages were 1:1.85:2.89. This shows that the c1 estimates were quite stable while the c2 values increased with flow rate as expected.

Test 4: Comparison of methods for estimating bead peak Mean and Variance

In the Sph8 and TF6 data collected at different flow rates, the narrower peaks are clearly unsymmetrical with low-side tails (skew) that are more prominent at higher flow rates. The automated procedure does a Gaussian fit for each bead peak in each fluorescence dimension, and the resulting SD estimates are lower than directly calculated SDs or robust SDs as shown in Supplementary Material Figure S3. The different methods all project to the same SD at zero flow rate, but the Gaussian fitted estimates are less affected by flow rate differences than the other estimators, so we consider them to be preferable for use in the quadratic fitting procedure.

Test 5: Comparison of Area and Height Spe values for different pulse widths

On instruments that offer both Area and Height measurements from the same signal inputs, differences in the Spe scales reveal differences in the relative efficiency with which the Area and Height evaluations use the available signal. To investigate this directly, we used the Agilent LED driver to generate pulses with different widths on LSR-IIF. Differences in laser focusing resulted in different bead pulse widths on different fluorescence channels, so we adjusted the LED driver to approximate the bead pulse widths with FWHM (Full Width at Half Maximum) 0.9 μsec (matching the 405 nm laser), FWHM 2.0 μsec (532 nm laser) and FWHM 2.7 μsec (488 nm and 640 nm lasers). The values of SpeH/SpeA were 0.88 at 0.9 μsec, 0.58 at 2.0 μsec and 0.46 at 2.7 μsec. The Area processing should utilize the whole photoelectron pulse, so at 2.7 μsec pulse width the Height measurements utilize less than half of the available light. An example of parallel fitting of Area and Height measurements on the same set of signals is shown in Supplementary Materials Table S1.

Discussion

Advantages and disadvantages of LED versus Bead-based estimation of background and Spe scales

The automated analysis method that we have developed works reliably for both LED and bead data. The LED method has the advantages of providing considerably more precise estimates for Spe scales and yielding good results on all measurement channels of almost any instrument that allows a path for the LED signals to reach the detectors (with rare exceptions like the Accuri noted below). The intrinsic CVs of the LED signal peaks should be essentially zero at all levels, and closely spaced peaks covering a wide range of signal levels can be used since the data collections are separate. This leads to results with very low relative standard errors unless the instrument electronics do not provide good linearity or something is actually wrong with the instrument. On most of the instruments we tested, the LED signal introduction does not block the normal light path, and background measurements can be made with lasers on (electronic noise plus continuous laser background) or off (electronic noise only). Knowing both of these backgrounds is valuable for selecting PMT voltages that optimize sensitivity for samples with minimal autofluorescence and can be useful in detecting light scatter leakage and Raman scatter contributions to background.

A special device is required to produce the LED signals, but a suitable signal generator is now commercially available as quantiFlash™ from A·P·E Angewandte Physik & Elektronik GmbH, Berlin, Germany. Use of LED pulses also requires access to light paths leading to the cytometer’s detectors both for threshold signals (usually the FSC or SSC channel) and for the fluorescence channel signals. Such signal introduction may be difficult or require unacceptable disassembly in some instruments. Also some measurement systems are incompatible with simple LED pulse inputs. In testing an Accuri instrument, we were able to deliver signals to each of the detectors individually, but the Area processing gave high variability on the blue laser channels, and the LED signals were fundamentally incompatible with the modulated red laser system. Some instruments offer no reasonable way to introduce LED signals in the light path unless the manufacturer were to build them in.

The multi-dye, multi-level bead sets are easy and convenient to run and require no skills beyond those needed to run typical test particles. Successful automated analysis relies on having good FSC-SSC data to obtain clean populations, and the instrument must show adequate separation of the different bead peaks on at least one measurement channel. The operator must exercise reasonable care in running the bead samples. We have observed some problems with excessive carryover of one sample into the next and with samples run at high flow rates spread out both the light scatter and fluorescence peaks. Fitting the three quadratic parameters requires three valid points to obtain a fit at all, and 4 or more points are needed to obtain error estimates. More points in the middle range where photoelectron statistical variation is usually the dominant source of variance is better for obtaining Spe estimates with low standard errors. The current 6 or 8 level bead sets are minimal in this regard since, for a given measurement channel, one or more peaks may be outside the good linearity range, and for Height data one or more peaks may have to be excluded at the low end. With 6 or 8 peak beads, we often find some channels with too few valid points for fitting with error estimates and occasionally for Height measurements even the minimum of 3 points is not maintained. The number of peaks in a mixed set is limited by the need to be able to resolve all of the peaks accurately, but separating alternate peak levels into two different samples might allow for more peaks with closer spacing.

Even if all aspects of the bead measurements are optimal, the fitting results show relative standard errors that are consistently higher than for good LED data with some errors above useful levels. Our Monte Carlo results indicate that the presence of a non-zero intrinsic CV limits the quality of the fits, and whatever differences in intrinsic CV exist among the bead populations in a set will make this worse. In the case of the second peak in the TF6 set we found clear evidence that it has a much higher intrinsic CV than the other members of the set. This was particularly clear for the V450 channel, and almost all instruments showed poor fits with the TF6 set on this channel. Manufacturers of the bead sets may find it useful to evaluate bead peak data in comparison to LED data as a quality control measure to identify any problems in consistency of different bead peaks in a set. We noted a similar problem on multiple channels of the Xitogen instrument where the dimmest beads were measured with low enough CVs for discrepancies in peak uniformity to degrade the estimates of fitting parameters.

Data acceptance and troubleshooting

The current flowQB output includes several kinds of analysis results that are useful in quality assurance and troubleshooting. We expect to develop warning flags to highlight any results that indicate problems in the data or unreliability in the results, but we have not yet settled on the appropriate trigger levels for issuing such warnings. The initial features to check are the relative standard errors on the c1 (=signal units/Spe) parameter that are usually below 3% for LED data (<10% for analog logamp systems) and less than 10% for most bead data (but 20–25% may be as good as the bead samples support in some measurement channels. For LED data, quadratic fit c2 parameters highly significantly different from zero indicate some sort of problem may result from inadequate instrument linearity or, if c2 is clearly positive, possible noise in the LED signals. When we see discrepancies in LED relative standard errors or c2 values, we go to the individual peak residuals to see if any are particularly high pointing to a problem in instrument linearity or, if c2 is clearly positive, possible noise in the LED signals. Table S1 shows an example of the input data points and weighted residuals in the resulting fit.

For bead fits, large relative standard errors in c1 and data peaks with high residuals on a few channels point to inconsistencies in the production of the bead populations at different levels. If these occur on most or all channels, the K-means peak segmentation may be incorrect. The outputs of the flowQB package include a color dot plot showing the events allocated to each of the K-means populations. Any problems in the segmentation will be clearly visible in this display, and, for well-balanced multi-level bead sets, large differences in number of events per population indicate allocation errors. Increasing the logicle transform Width parameter corrected the allocations of data events to bead populations in the one case where we observed this problem. Excessive c2 values may point to a flow problem or excessive flow rate in the data collection.

Alternative methods for estimating population weights in the quadratic fitting

The evaluations presented here use the single pass weighting and fitting method described above in the section on “Fitting the LED and multi-level bead data”. We have also used an alternative method described there and included in the flowQB package that re-evaluates the weights after initial fitting and refits until the results to reach convergence. With LED data and with most bead data we have not seen substantial differences between the results of the two methods. We attribute the significant differences we have seen with some bead data to imperfect matching of the bead populations in the multi-level sample. Since the iterative method has different degrees of freedom than the single estimation method, it’s possible that the iterative method is overfitting or customizing the fit to imperfections in the bead samples. More investigation is warranted in this area, and different sets of multi-level beads might give different results, but, for the current evaluations, we have relied on the single pass method.

Availability and details of the flowQB R/BioConductor package

The flowQB - Automated Quadratic Characterization of Flow Cytometer Instrument Sensitivity R/BioConductor is available from http://bioconductor.org/packages/flowQB. Please see the package Vignette (http://bioconductor.org/packages/release/bioc/vignettes/flowQB/inst/doc/flowQBVignettes.pdf) and manual (http://bioconductor.org/packages/release/bioc/manuals/flowQB/man/flowQB.pdf) for a detailed description. The Vignette includes examples of the tables and other outputs produced by flowQB.

Data and fitting results are available in the FlowRepository

All of the cytometer data used in this work, as well as the fitting procedure results, is available in the FlowRepository at http://flow.org/id/FR-FCM-ZZTF.

Closing summary

We have demonstrated an automated analysis for evaluating backgrounds and Spe scales on fluorescence cytometers and applied it to a series of instruments using both LED signals and multi-level, multi-dye bead sets. The method has proved to be reliable and robust. Even in situations where high noise levels or poor linearity resulted in large errors of estimate, the computations worked properly, and the results were useful in identifying the problems.

On instruments with good linearity and reasonable noise levels, the LED method yields both Background and Spe scale estimates with standard errors usually under 1%. The results using multi-level, multi-dye bead sets give standard errors that are considerably higher and more variable. However, considering that individual PMTs can show efficiency differences up to a factor of 2, our finding that bead-derived Spe scale values are usually within 20% of those from LED data if the relative standard error estimates are not much over 10% confirms that the bead method can provide quite adequate accuracy for most instrument evaluation purposes.

In order to make comparisons of sensitivity for particular dyes and effective backgrounds, we need to evaluate samples carrying these dyes of interest and, if possible, use samples with calibrated amounts of dye so that measurements taken at different times and in different places can be aligned. Combining such results with the Spe scale and background evaluations presented here gives Q values in Spe per dye unit and backgrounds in dye units. These values provide valid and useful comparisons of the capabilities of different instruments. We have tested promising samples of beads carrying specified dye levels of antibody reagents in lyophilized form. Having something like this generally available for a variety of common dyes would complement the work we report here to make high quality instrument evaluations routinely available.