Numerical Approximation of Elasticity Tensor Associated With Green-Naghdi Rate

Abstract

Objective stress rates are often used in commercial finite element (FE) programs. However, deriving a consistent tangent modulus tensor (also known as elasticity tensor or material Jacobian) associated with the objective stress rates is challenging when complex material models are utilized. In this paper, an approximation method for the tangent modulus tensor associated with the Green-Naghdi rate of the Kirchhoff stress is employed to simplify the evaluation process. The effectiveness of the approach is demonstrated through the implementation of two user-defined fiber-reinforced hyperelastic material models. Comparisons between the approximation method and the closed-form analytical method demonstrate that the former can simplify the material Jacobian evaluation with satisfactory accuracy while retaining its computational efficiency. Moreover, since the approximation method is independent of material models, it can facilitate the implementation of complex material models in FE analysis using shell/membrane elements in abaqus.

1. Introduction

With an ever increasing use of finite element (FE) analysis to study biomechanics involved in biomedical applications, many constitutive models have been developed to simulate a variety of biomaterial behaviors. These models not only have nonlinear, hyperelastic properties, undergoing finite deformation, such as the Holzapfel–Gasser–Ogden (HGO) model [1], but can also incorporate microstructural [2], viscoelastic [3], growth and remodeling [4,5], active contraction [6], or fatigue damage characteristics [7]. Consequently, these models vary in functional forms and sometimes involve time series and complex integrations. The implementation of such experimentally derived, user-defined material models in commercial FE packages such as abaqus (Simulia, Providence, RI) can be challenging, which may pose a barrier for the widespread use of these material models.

To implement a user-defined material model, the user must explicitly specify, in the user-defined material subroutine (UMAT), the Cauchy stress and the tangent modulus tensor (also known as elasticity tensor or material Jacobian) associated with the material model. Correct derivation and coding of these two quantities in the user material subroutine are important to obtain converged simulation results. While the Cauchy stress derived from a constitutive model is relatively easy to obtain, the tangent modulus tensor is often problematic especially when multidecomposition of the constitutive model into volumetric and distortional parts is required. Tangent modulus tensor is the power-conjugate between a specific form of the objective stress rate and the deformation rate tensor. Objective stress rates, referring to the intrinsic requirement for the constitutive law to be frame-independent, can be expressed in different forms, including the Jaumann rate and Green-Naghdi rate of Kirchhoff or Cauchy stresses in commercial FE packages, such as abaqus.

Shell/membrane elements are often preferred in finite element analyses of thin membrane structures such as heart valves [7–12]. Shell and membrane elements possess significant advantages over 3D solid elements in simulating thin structures due to the simplification in topology and reduced demand for computational resources. Unfortunately, the tangent modulus tensor based on the Green-Naghdi rate of Kirchhoff stress, which is used for abaqus shell/membrane elements [13], is rather complex to evaluate analytically. Details on the analytical calculation of the elasticity tensor associated with Green-Naghdi rate of Kirchhoff stress can be found in Simo and Hughes [14], Prot et al. [15], and also Sec. 2.4 of this paper.

Since the tangent moduli serve as an iterative operator in solving boundary value problems using Newton's method, the exact analytical solution is preferred to provide quadratic rate of convergence [16], but not mandatory. This critical property of the tangent moduli in computational mechanics gives rise to an alternative method—approximation approaches of the tangent modulus tensor, which can be easy to implement without substantially compromising the convergence rate. Miehe [17] reported an approximation to the elasticity tensor which was based on the convective rate of Kirchhoff stress. Sun et al. [18] presented a method that approximated the elasticity tensor associated with the Jaumann rate of Kirchhoff stress tensor, which is used in 3D solid elements in abaqus. Liu and Sun [19] conducted an accuracy analysis and computational efficiency study of the method proposed in Ref. [18] and confirmed that the approximation was able to achieve reasonably good accuracy and comparable computational efficiency to the closed-form solution. Recently, Tanaka and Fujikawa [20] suggested an approximation method for tangent moduli based on Green-Naghdi rate of Kirchhoff stress and implemented the method using hyperelastic material models. However, to rigorously evaluate the accuracy and efficiency of the approximation method, a side-by-side comparison of the approximation and the closed-form solution is needed. In this paper, we present a detailed description of both methods for the evaluation of elasticity tensor associated with the Green-Naghdi rate of Kirchhoff stress. By comparing the approximation results with the closed-form solution using a popular hyperelastic material model in the biomechanics community, the accuracy and computational efficiency of the approximation method are evaluated. Finally, a more complex material model, involving the integration of a fiber distribution function, is incorporated to demonstrate the effectiveness of the method.

2. Continuum Mechanics Framework

2.1. Kinematics.

Deformation of a body is described by mapping $\chi$ from a material point $\mathbf{X}$ at its undeformed (referential) configuration ${\Omega }_0$ to its position $\mathbf{x}=\chi (\mathbf{X},t)$ at deformed (current) configuration $\Omega$ at time t. The deformation can be described by the deformation gradient F, defined as $\mathbf{F}=(\partial \mathbf{x}/\partial \mathbf{X})$, with Jacobian $J=\text{det}(\mathbf{F})$. $\mathbf{C}={\mathbf{F}}^{\mathrm{T}}\mathbf{F}$ and $\mathbf{B}=\mathbf{F}{\mathbf{F}}^{\mathrm{T}}$ are the right and left Cauchy–Green tensors, respectively. The Green–Lagrange strain tensor in material description is expressed as $\mathbf{E}=(1/2)(\mathbf{C}-\mathbf{I})$.

The deformation gradient can also be expressed as $\mathbf{F}=\mathbf{R}\mathbf{U}=\mathbf{V}\mathbf{R}$ via Polar decomposition, where R is the rotation tensor, representing local rotation of a referential orientation. U and V denote the right and left stretch tensors, respectively. Due to the requirement of objectivity (i.e., frame indifference), the mechanical responses of materials are frequently addressed in corotational systems. A corotational system is defined so that the coordinate system is embedded in the material and rotates with it. Hence, the deformation gradient tensor in the corotational system can be expressed as: $\widehat{\mathbf{F}}={\mathbf{R}}^{\mathrm{T}}\mathbf{F}$, where the hats “ $^$ ” are used to denote parameters in the corotational frame throughout the paper. It should be noted that the deformation gradient tensor F is a two-point tensor; therefore, only the first part of it describing the spatial coordinates is rotated back to counter the local rotation.

The rate of deformation can be defined as velocity (v) gradient: $\mathbf{L}=\text{grad}(\mathbf{v})=\dot{\mathbf{F}}{\mathbf{F}}^{-1}$. It can be further decomposed into a symmetric and asymmetric part

$$\mathbf{L}=\mathbf{D}+\mathbf{W},\hspace{1em}\mathbf{D}=\text{sym}\left(\mathbf{L}\right)=\frac{1}{2}\left(\mathbf{L}+{\mathbf{L}}^{\mathrm{T}}\right),\hspace{1em}\mathbf{W}=\text{skew}\left(\mathbf{L}\right)=\frac{1}{2}\left(\mathbf{L}-{\mathbf{L}}^{\mathrm{T}}\right)$$ (1)

where D and W are known as the rate of deformation tensor and the rate of rotation tensor, respectively. A spin tensor $\mathbf{\Omega }:=\dot{\mathbf{R}}{\mathbf{R}}^{\mathbf{T}}$ stands for the spin of the current orientation.

2.2. Hyperelastic Stress Response.

Among various measures of stress, three of them are employed in this paper. They are (1) the second Piola-Kirchhoff stress, S, defined in the reference configuration, (2) the Kirchhoff stress, $\mathit{\tau }$, which is a push-forward of the second Piola-Kirchhoff stress, and (3) the Cauchy stress $\mathit{\sigma }$. These three measures of stress are expressed as [21]

$$\mathbf{S}=2\frac{\partial W\left(\mathbf{C}\right)}{\partial \mathbf{C}},\hspace{1em}\mathit{\tau }=\mathbf{F}\mathbf{S}{\mathbf{F}}^{\mathrm{T}},\hspace{1em}\mathit{\sigma }=J^{-1}\mathit{\tau }$$ (2)

where W denotes a scalar valued strain-energy function postulated to exist for hyperelastic materials.

2.3. Tangent Modulus Tensor.

Implementation of a user-defined material model in abaqus/umat usually involves the evaluation of (a) Cauchy stress $\mathit{\sigma }$ and (b) the tangent modulus tensor $\mathbf{C}$ that is derived from a rate-form constitutive equation. There are various forms of elasticity tensors with respect to different forms of objective rate of stress. The following objective rates, namely, the Jaumann rate of the Kirchhoff stress ${\mathit{\tau }}^{\nabla J}$, the convective rate of the Kirchhoff stress ${\mathit{\tau }}^{\nabla c}$, and the Green-Naghdi rate of the Kirchhoff stress ${\mathit{\tau }}^{\nabla G}$ are frequently used in the literature and adopted in abaqus

$${\mathit{\tau }}^{\nabla \mathbf{J}}=\dot{\mathit{\tau }}-\mathbf{W}\mathit{\tau }-\mathit{\tau }{\mathbf{W}}^{\mathrm{T}}={\mathrm{c}}^{\tau \mathbf{J}}:\mathbf{D}$$ (3)

$${\mathcal{L}}_v(\mathit{\tau })={\mathit{\tau }}^{\nabla c}=\dot{\mathit{\tau }}-\mathbf{L}\mathit{\tau }-\mathit{\tau }{\mathbf{L}}^{\mathrm{T}}={\mathrm{c}}^{\tau c}:\mathbf{D}$$ (4)

$${\mathit{\tau }}^{\nabla G}=\dot{\mathit{\tau }}-\mathbf{\Omega }\mathit{\tau }-\mathit{\tau }{\mathbf{\Omega }}^{\mathrm{T}}={\mathrm{c}}^{\tau G}:\mathbf{D}$$ (5)

where the notation $\nabla$ in the superscript denotes objective derivative, while the notation “$\cdot$” stands for material time derivative, ${\mathrm{c}}^{\tau \mathbf{J}}$ (or ${\mathrm{c}}^{\tau c}$, ${\mathrm{c}}^{\tau G}$) denotes the fourth-order elasticity tensor, with the superscripts representing the form of stress and stress rate utilized in the equation, i.e., $\tau \mathbf{J}$ indicates the Jaumann rate of the Kirchhoff stress, $\tau c$ is the convective rate of the Kirchhoff stress, $\tau G$ is the Green-Naghdi rate of the Kirchhoff stress, and ${\mathcal{L}}_v(*)$ is the Lie time derivative of *. For 3D continuum elements, abaqus uses the elasticity tensor associated with the Jaumann rate of the Kirchhoff stress. For structural elements, abaqus uses the one associated with the Green-Naghdi rate of the Kirchhoff stress ${\mathrm{c}}^{\tau G}$. It is also worth noting that we represent the elasticity tensors in the current configuration with the lowercase $\mathrm{c}$, whereas the elasticity tensor in the referential configuration is denoted using the uppercase $\mathrm{C}$.

In Secs. 2.4 and 2.5, the elasticity tensor ${\mathrm{c}}^{\tau G}$ is calculated with both analytical and approximation approaches.

2.4. Analytical Method.

The elasticity tensor in the referential configuration is expressed as [14]

$$\mathrm{C}=\frac{\partial \mathbf{S}\left(\mathbf{C}\right)}{\partial \mathbf{C}}=4\frac{{\partial }^{2}W\left(\mathbf{C}\right)}{\partial \mathbf{C}\partial \mathbf{C}}$$ (6)

The elasticity tensor ${\mathrm{c}}^{\tau c}$ defined in the current configuration is then obtainable after a push-forward operation [15,21]

$${\mathrm{c}}^{\tau c}={\mathit{\chi }}_{*}(\mathrm{C}),\hspace{1em}{({\mathrm{c}}^{\tau c})}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}=F_{\mathit{a}\mathit{A}}{F}_{\mathit{b}\mathit{B}}{F}_{\mathit{c}\mathit{C}}{F}_{\mathit{d}\mathit{D}}{(\mathrm{C})}_{\mathit{A}\mathit{B}\mathit{C}\mathit{D}}$$ (7)

By comparing Eq. (3) with Eq. (4) and using the split $\mathbf{L}=\mathbf{D}+\mathbf{W}$ in Eq. (1), the tangent moduli for the Jaumann rate of the Kirchhoff stress can be shown as

$$\begin{array}{c}{\mathrm{c}}^{\tau \mathbf{J}}:\mathbf{D}={\mathrm{c}}^{\tau c}:\mathbf{D}+\mathbf{D}\mathit{\tau }+\mathit{\tau }{\mathbf{D}}^{\mathrm{T}} \\ {\left({\mathrm{c}}^{\tau \mathbf{J}}\right)}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}={\left({\mathrm{c}}^{\tau c}\right)}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}+\frac{1}{2}\left({\delta }_{\mathit{a}\mathit{c}}{\tau }_{\mathit{b}\mathit{d}}+{\delta }_{\mathit{b}\mathit{d}}{\tau }_{\mathit{a}\mathit{c}}+{\delta }_{\mathit{a}\mathit{d}}{\tau }_{\mathit{b}\mathit{c}}+{\delta }_{\mathit{b}\mathit{c}}{\tau }_{\mathit{a}\mathit{d}}\right)\end{array}$$ (8)

Finally, the elasticity tensor for the Green-Naghdi rate of the Kirchhoff stress ${\mathbf{C}}^{\tau G}$ is expressible as

$${\mathrm{c}}^{\tau G}={\mathrm{c}}^{\tau \mathbf{J}}+{\mathrm{c}}^{\text{spin}}$$ (9)

where ${\mathbf{C}}^{\text{spin}}$ is obtained by

$${\mathrm{c}}^{\text{spin}}:\mathbf{D}=(\mathbf{W}-\mathbf{\Omega })\mathbf{\tau }-\mathbf{\tau }(\mathbf{W}-\mathbf{\Omega })$$ (10)

Upon adopting the definition and notation in Simo and Hughes [14], we have

$$\mathbf{W}-\mathbf{\Omega }=\mathbf{\Lambda }:\mathbf{D}$$ (11)

where

$${\Lambda }_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}=c_1(V_{\mathit{a}\mathit{c}}{\delta }_{\mathit{b}\mathit{d}}+V_{\mathit{a}\mathit{d}}{\delta }_{\mathit{b}\mathit{c}}-V_{\mathit{b}\mathit{d}}{\delta }_{\mathit{a}\mathit{c}}-V_{\mathit{b}\mathit{c}}{\delta }_{\mathit{a}\mathit{d}})-c_2(B_{\mathit{a}\mathit{c}}{\delta }_{\mathit{b}\mathit{d}}+B_{\mathit{a}\mathit{d}}{\delta }_{\mathit{b}\mathit{c}}-B_{\mathit{b}\mathit{d}}{\delta }_{\mathit{a}\mathit{c}}-B_{\mathit{b}\mathit{c}}{\delta }_{\mathit{a}\mathit{d}})+c_3(B_{\mathit{a}\mathit{c}}{V}_{\mathit{b}\mathit{d}}+B_{\mathit{a}\mathit{d}}{V}_{\mathit{b}\mathit{c}}-V_{\mathit{a}\mathit{c}}{B}_{\mathit{b}\mathit{d}}-V_{\mathit{a}\mathit{d}}{B}_{\mathit{b}\mathit{c}})$$ (12)

with

$$c_1=\frac{{{\mathrm{I}}_V}^2}{2\left({\mathrm{I}}_V{\text{II}}_V-{\text{III}}_V\right)},\hspace{1em}{c}_2=\frac{{\mathrm{I}}_V}{2\left({\mathrm{I}}_V{\text{II}}_V-{\text{III}}_V\right)},\hspace{1em}{c}_3=\frac{1}{2\left({\mathrm{I}}_V{\text{II}}_V-{\text{III}}_V\right)}$$ (13)

and ${\mathrm{I}}_V:=\text{tr}(\mathbf{V})$, ${\text{II}}_V:=(1/2)(\text{tr}{(\mathbf{V})}^2-\text{tr}(\mathbf{V}\cdot \mathbf{V}))$, and ${\text{III}}_V:=\text{det}(\mathbf{V})$ are the invariants of the left stretch tensor V, respectively.

${\mathrm{c}}^{\tau \mathrm{G}}$ can thus be represented in its index form as

$${({\mathrm{c}}^{\tau G})}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}={({\mathrm{c}}^{\tau \mathbf{J}})}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}+{\Lambda }_{\mathit{a}\mathit{k}\mathit{c}\mathit{d}}{\tau }_{\mathit{k}\mathit{b}}-{\tau }_{\mathit{a}\mathit{k}}{\Lambda }_{\mathit{k}\mathit{b}\mathit{c}\mathit{d}}$$ (14)

It is noted from Eqs. (6)–(8), (12), and (14) that while ${\mathrm{c}}^{\tau \mathbf{J}}$ possesses full symmetry (not only major symmetry but also minor symmetries), ${\mathrm{c}}^{\tau \mathrm{G}}$, on the other hand, loses its major symmetry while retaining minor symmetries. It is also noted that the UMAT implementation of the Green-Naghdi rate of the Kirchhoff stress ${\mathit{\tau }}^{\nabla G}$ in abaqus requires all the equations from Eqs. (6)–(14). The implementation procedure is thus complex, lengthy, and prone to coding errors, especially when the constitutive equations have complex functional forms.

2.5. Approximation Method.

Alternatively, Sun et al. [18] and Tanaka and Fujikawa [20] showed that numerical approximation of a rate form of elasticity tensors can make such evaluation much simpler to implement and the approach is independent of material models.

It is known that rotations taking place in the deformation are compensated in the corotational configuration, and the material stress rate in the configuration is objective. Therefore, the Green-Naghdi rate of the Kirchhoff stress, in the corotational configuration, is defined as

$${\widehat{\mathbf{\tau }}}^{\nabla G}=\dot{\widehat{\mathbf{\tau }}}-\widehat{\mathbf{\Omega }}\widehat{\mathit{\tau }}-\widehat{\mathit{\tau }}{\widehat{\mathbf{\Omega }}}^{\mathrm{T}}={\widehat{\mathrm{c}}}^{\tau G}:\widehat{\mathbf{D}}$$ (15)

where $\widehat{\mathit{\tau }}={\mathbf{R}}^{\mathbf{T}}\mathit{\tau }\mathbf{R}$.

Due to the fact that the rotation R goes to identity in the corotational configuration, the spin tensor $\mathbf{\Omega }=\dot{\mathbf{R}}{\mathbf{R}}^{\mathbf{T}}$ goes to zero, thus, Eq. (15) reduces to

$${\widehat{\mathbf{\tau }}}^{\nabla \mathrm{G}}=\dot{\widehat{\mathbf{\tau }}}={\widehat{\mathrm{c}}}^{\tau G}:\widehat{\mathbf{D}}$$ (16)

Equation (16) can then be linearized as

$$\Delta \widehat{\mathbf{\tau }}={\widehat{\mathrm{c}}}^{\tau G}:\Delta \widehat{\mathbf{D}}$$ (17)

Following Miehe [17], Sun et al. [18], Liu and Sun [19], the perturbation to the rate of deformation can be further written as

$$\Delta {\widehat{\mathbf{D}}}^{\left(\widehat{i}\widehat{j}\right)}=\frac{1}{2}\left(\Delta \widehat{\mathbf{L}}+\Delta {\widehat{\mathbf{L}}}^{\mathrm{T}}\right)=\frac{1}{2}\left(\Delta {\widehat{\mathbf{F}}}^{\left(\widehat{i}\widehat{j}\right)}{\widehat{\mathbf{F}}}^{-1}+{\left(\Delta {\widehat{\mathbf{F}}}^{\left(\widehat{i}\widehat{j}\right)}{\widehat{\mathbf{F}}}^{-1}\right)}^{\mathrm{T}}\right)$$ (18)

with the perturbation to the deformation gradient $\Delta \widehat{\mathbf{F}}$ defined in the following form:

$$\Delta {\widehat{\mathbf{F}}}^{\left(\widehat{i}\widehat{j}\right)}=\frac{\epsilon }{2}\left[\left({\widehat{\mathbf{e}}}_{\widehat{i}}\otimes {\widehat{\mathbf{e}}}_{\widehat{j}}\right)\widehat{\mathbf{F}}+\left({\widehat{\mathbf{e}}}_{\widehat{j}}\otimes {\widehat{\mathbf{e}}}_{\widehat{i}}\right)\widehat{\mathbf{F}}\right]$$ (19)

where $\epsilon$ is the perturbation parameter, and ${\{{\widehat{\mathbf{e}}}_{\widehat{i}}\}}_{\widehat{i}=1,2,3}$ represents the basis vectors in the corotational frame.

Therefore,

$$\Delta {\widehat{\mathbf{D}}}^{\left(\widehat{i}\widehat{j}\right)}=\frac{\epsilon }{2}\left({\widehat{\mathbf{e}}}_{\widehat{i}}\otimes {\widehat{\mathbf{e}}}_{\widehat{j}}+{\widehat{\mathbf{e}}}_{\widehat{j}}\otimes {\widehat{\mathbf{e}}}_{\widehat{i}}\right)$$ (20)

The increment of the Kirchhoff stress $\widehat{\mathbf{\tau }}$ is taken as

$$\Delta \widehat{\mathbf{\tau }}\cong \widehat{\mathbf{\tau }}(\widehat{\mathbf{F}}+\Delta {\widehat{\mathbf{F}}}^{(\mathit{i}\mathit{j})})-\widehat{\mathbf{\tau }}(\widehat{\mathbf{F}})$$ (21)

Combining Eqs. (17), (20), and (21) and utilizing the (minor) symmetric feature of ${\mathrm{c}}^{\tau G}$, the forward Euler approximation of ${\mathrm{c}}^{\tau G}$ in the corotational frame has its index form

$${\left({\widehat{\mathrm{c}}}^{\tau G}\right)}_{\widehat{a}\widehat{b}\widehat{i}\widehat{j}}\cong \frac{1}{\epsilon }\left[\widehat{\mathrm{\tau }}{\left(\widehat{\mathbf{F}}+\Delta {\widehat{\mathbf{F}}}^{\left(\widehat{i}\widehat{j}\right)}\right)}_{\widehat{a}\widehat{b}}-\widehat{\mathrm{\tau }}{\left(\widehat{\mathbf{F}}\right)}_{\widehat{a}\widehat{b}}\right]$$ (22)

The tangent moduli for the Green-Naghdi rate of the Kirchhoff stress in the current configuration can be recovered via

$${({\widehat{\mathrm{c}}}^{\tau G})}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}={\mathrm{R}}_{a\widehat{a}}{\mathrm{R}}_{b\widehat{b}}{\mathrm{R}}_{c\widehat{c}}{\mathrm{R}}_{d\widehat{d}}{({\widehat{\mathrm{c}}}^{\tau G})}_{\widehat{a}\widehat{b}\widehat{c}\widehat{d}}$$ (23)

By converting the Green-Naghdi rates (obtained from either analytical or approximate evaluation) to the form that is accepted by abaqus, we get the material Jacobian

$${\mathrm{c}}^{\text{MJ}}=\frac{1}{J}{\mathrm{c}}^{\tau \mathrm{G}}$$ (24)

3. Numerical Examples

In this section, we demonstrate the implementation of the approximation method with two constitutive models: (1) a modified version of the Holzapfel–Gasser–Ogden (HGO) model [1]. The HGO model (and its derivatives) is a fiber structural-based hyperelastic model that is commonly used to describe soft tissue material properties in biomedical applications [22–24]. (2) A fiber structural-based model that employs a continuous fiber distribution function [25]. This model [25] has an integral function for which the analytical form of the tangent moduli is difficult to obtain. We use these two examples to demonstrate the effectiveness of the approximation method in abaqus.

3.1. Numeric Example 1—Modified HGO Model.

The HGO model [1] is modified as

$$W\left(\mathbf{C},\mathbf{M},\mathbf{N},J\right)=c_{10}\left(\text{exp}\left[c_{01}\left({\mathrm{I}}_1-3\right)\right]-1\right)+\frac{k_1}{2k_2}\left[\text{exp}\left(k_2{\epsilon }_1^2\right)-1\right]+\frac{k_1}{2k_2}\left[\text{exp}\left(k_2{\epsilon }_2^2\right)-1\right]-p\left(J-1\right)$$ (25)

where

$${\epsilon }_1=\kappa (I_1-3)+(1-3\kappa )(I_4-1)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\epsilon }_2=\kappa (I_1-3)+(1-3\kappa )(I_6-1)$$ (26)

$c_{01}\hspace{0.17em}\text{and}\hspace{0.17em}{c}_{10}$ are the material parameters characterizing extracellular matrix and $k_1\hspace{0.17em}\text{and}\hspace{0.17em}{k}_2$ are the material parameters for embedded collagen fibers. $\kappa$, ranging from 0 to 1/3, determines the dispersion of fibers; the invariants $I_1:=\text{tr}(\mathbf{C})$, $I_4:=\mathbf{C}:(\mathbf{M}\mathrm{\otimes }\mathbf{M})$, and $I_6:=\mathbf{C}:(\mathbf{N}\mathrm{\otimes }\mathbf{N})$, where M $(\mathbf{M}=\left[\begin{array}{c}\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \\ \hspace{0.17em}\text{sin}\hspace{0.17em}\alpha \\ 0\end{array}\right])$ and N $(\mathbf{N}=\left[\begin{array}{c}\hspace{0.17em}\text{cos}\hspace{0.17em}\beta \\ \hspace{0.17em}\text{sin}\hspace{0.17em}\beta \\ 0\end{array}\right])$ represent the referential fiber orientations, with $\alpha$ and $\beta$ representing the angles between the orientations of the fibers in the undeformed state and the material axis; $J=1$ for incompressible material; and p is an indeterminate Lagrangian multiplier. The analytical calculations of stress tensor S, elasticity tensor $\mathrm{C}$, and the determination of p for the modified HGO model are shown in the Appendix.

3.1.1. Finite Element Model Using the Modified HGO Model.

In this study, material parameters of the modified HGO model were obtained by means of data fitting to match the previously published planar biaxial mechanical testing [26] (resultant parameters: $c_{01}$ = 14.87, $c_{10}$ = 1.16 kPa, $k_1$ = 4.48 kPa, $k_2$ = 62.20, $\kappa$ = 0, $\alpha$ = 32.64 deg, and $\beta$ = 56.02 deg). The modified HGO model was implemented for abaqus membrane elements via UMAT. The effectiveness of the implementation was examined by simulating the biaxial experiment under experimental loading condition. Detailed descriptions of the biaxial testing on soft tissue can be found in Sacks [27] and Sacks et al. [28].

The FE model was then set up in accordance with the specimen (glutaraldehyde-treated bovine pericardium (GLBP)) with the dimension of 25 mm × 25 mm × 0.4 mm. Four evenly spaced nodal forces, with 5 mm apart from each other and 2.5 mm inside the specimen edge (Fig. 1(a)), were imposed on each side. Each nodal force was 2.5 N, which produced 1 MPa Lagrangian stress on each edge. The geometry domain (Fig. 1(a)) was discretized with 20 × 20 eight-node membrane elements (M3D8). Especially, the 4 × 4 elements (5 mm × 5 mm) in the central region (enclosed by the frame in Fig. 1(a)) were selected to represent the square region enclosed by the markers in the biaxial testing. Within this region, the averaged strain and stress from the numerical simulation were compared with those taken from the biaxial test. In the material model implementation, elasticity tensors were calculated with both approximate and analytical methods described in Secs. 2.4 and 2.5. The simulations were performed on a Windows 64-bit desktop computer equipped with Intel Core i7-3770 processor (3.40 GHz) and 16 GB RAM. The predicted stress contour at end loading is shown in Fig. 1(b).

Fig. 1.

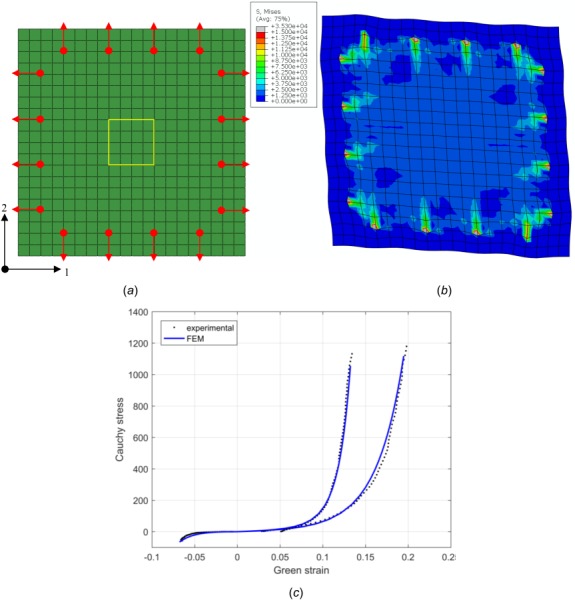
FE meshes used in the biaxial test simulation: the arrows denote the loading directions with their round roots showing the sites of loading, the box enclosed region in the center represents the area delineated by the four markers in the biaxial test (a), Von Mises stress contour in the deformed configuration (b), and curves of Cauchy stress versus Green strain resulted from experiment (dashed line) and numerical simulation (solid line) (c)

Figure 1(c) shows that the stress–strain relations obtained from experiment and numerical simulation are in good agreement, highlighting the effectiveness of the material model in capturing the key features of the soft tissue property.

3.1.2. Accuracy Analysis of Approximation.

The accuracy of the approximation can be quantified using the relative error of the approximated tangent. The relative error $\text{Er}$ was defined as follows [29]:

$$\text{Er}={\left(\sum _{a,b,c,d}{(c_{abcd}^{\mathit{M}\mathit{J}}-c_{abcd}^{MJ,\text{apm}})}^2\right)}^{1/2}/{\left(\sum _{a,b,c,d}{(c_{abcd}^{\mathit{M}\mathit{J}})}^2\right)}^{1/2}$$ (27)

where the superscript “apm” represents the approximated values.

The relative error obtained using the approximation method was plotted against a range of perturbation parameter values of $\epsilon$ in Fig. 2(a). As shown in Tanaka and Fujikawa [20], the approximation errors are of the same order as $\epsilon$, which suggests a preference for a small value of $\epsilon$. However, when $\epsilon$ becomes too small, the evaluation is prone to numerical truncation errors. There exists an optimal value for $\epsilon$. It is shown in Fig. 2(a) that the approximation achieved its optimal accuracy when $\epsilon$ was selected to be ${\epsilon }_{\mathrm{o}}=$ 1.0 × 10⁻⁸.

Fig. 2.

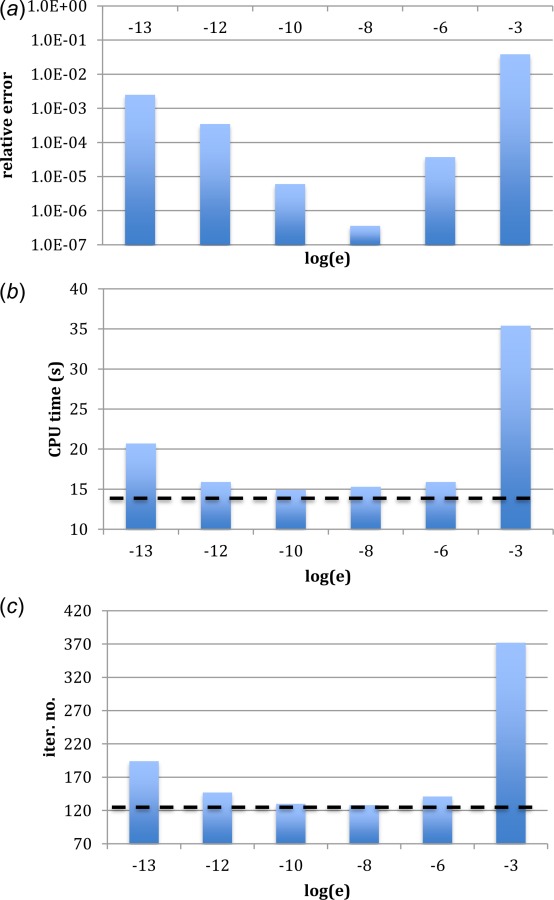
Relative error of the Jacobian approximation at different logarithmic perturbations (a), the CPU time (b), and the iteration number (c) at different logarithmic perturbations using themodified HGO model in the biaxial testing simulation. Dashed lines (—) represent the level achieved using UHYPER subroutine.

3.1.3. Computational Efficiency Analysis.

The total iteration number and the CPU time used to achieve convergence were plotted against varying values of perturbation parameter, as shown in Figs. 2(b) and 2(c). For comparison purposes, UHYPER, the abaqus subroutine officially recommended for user-defined hyperelastic material, is utilized as a benchmark for performance. In general, the computational efficiency follows the approximation accuracy of the tangent, that is, the more accurate the approximation is, the less iteration number (the shorter CPU time) is taken to converge the simulation. To take a closer look at the computational efficiency, the residual norms of the largest force at each iteration are listed in Table 1 for all the tested schemes. A typical load step was selected to do the comparison. It is shown that the approximation achieves quadratic rate of convergence when ${\epsilon }_{\mathrm{o}}$ is selected for perturbation. It is observed that the performance of approximation is similar to that of UHYPER in terms of CPU time and convergence rate when optimal value is chosen for perturbation.

Table 1.

Norm of the largest force residual at each iteration (taken at the load step #32 of the simulation)

		$\epsilon$
Iteration #	UHYPER	10−13	10−12	10−10	10−8	10−6	10−3
1	1.54 × 101	1.54 × 101	1.54 × 101	1.54 × 101	1.54 × 101	1.54 × 101	1.42 × 101
2	3.98 × 10 − 1	4.17 × 10−1	3.99 × 10−1	3.98 × 10−1	3.98 × 10−1	3.98 × 10−1	4.16 × 10−1
3	2.91 × 10−4	1.38 × 10−3	3.66 × 10−4	2.91 × 10−4	2.91 × 10−4	2.95 × 10−4	2.53 × 10−2
4	3.89 × 10−10	6.97 × 10−6	2.38 × 10−7	9.41 × 10−10	4.85 × 10−10	8.48 × 10−9	2.10 × 10−3
5		2.14 × 10−8	3.09 × 10−10				1.69 × 10−4
6		3.21 × 10−10					1.37 × 10−5
7							1.09 × 10−6
8							8.72 × 10−8
9							6.86 × 10−9

It is worth noting that the CPU time per iteration of an implicit FE simulation would be dominated by the factoring time of stiffness matrix when the simulation scale becomes sufficiently large [29]. Therefore, the closed-form solution should in general have better computational efficiency for large-scale simulation, due to the intrinsic slower convergence of the approximation method. However, given the severe stress concentration taking place in this simulation and that the approximation takes almost the same number of iterations as the UHYPER, the overall performance of the approximation is similar to that of the closed-form solution. Combining its feature of simple to use and material model independency, the approximation method remains attractive.

3.2. Numeric Example 2—The Material Model With Continuous Fiber Distribution Function.

Sun et al. [25] proposed a structural model for arterial tissue. It takes the form as

$$W\left(\mathbf{C},\mathbf{M},\mathbf{N},J\right)=\left(1-d_f\right)d_0\left(I_1-3\right)+{\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{d}_f\left(R_1(\theta )W_{f1}\left(I_4\right)+R_2(\theta )W_{f2}\left(I_6\right)\right)\mathrm{d}\theta -p\left(J-1\right)$$ (28)

where

$$\begin{array}{c}{W}_{f1}(I_4)=d_1(e^{d_2{(\sqrt{I_4}-1)}^2}-1),\hspace{1em}{I}_4>1\\ W_{f2}(I_6)=d_1(e^{d_2{(\sqrt{I_6}-1)}^2}-1),\hspace{1em}{I}_6>1\end{array}$$ (29)

$d_f$ is the fiber volume fraction; $d_0$, $d_1$, and $d_2$ are the material constants; and $R_1(\theta )$ and $R_2(\theta )$ are the fiber distribution functions which are normal distributions with standard deviation (SD) and mean angle between fiber and circumferential direction, $\overline{\mathrm{\Theta }}$. Since this model has an integral function, it is relatively complicated to obtain the analytical form of the tangent moduli. Thus, the approximation method is used.

3.2.1. Finite Element Model Using the Distributed Fiber Model.

Following Sun et al. [25], we construct an FE model of rat carotid artery segment based on the geometry described by Zulliger et al. [30]. The vessel is fixed at both ends in the axial direction and is inflated up to 25 kPa with pressure acting on the inner surface. The computational model is comprised of 1056 M3D4 elements. The material parameters are determined so as to match the experimental data (Figs. 3(c) and 3(d)). The baseline group of parameters are $d_f=0.5, d_0=35.24\hspace{0.17em}\text{kPa}, d_1=0.2\hspace{0.17em}\text{kPa}, d_2=11.35, \overline{\mathrm{\Theta }}=39.76\hspace{0.17em}\text{deg}, \text{and}\hspace{0.17em}\text{SD}=1\hspace{0.17em}\mathrm{deg}.$ Figures 3(a) and 3(b), show the initial meshes and deformed meshes after inflation.

Fig. 3.

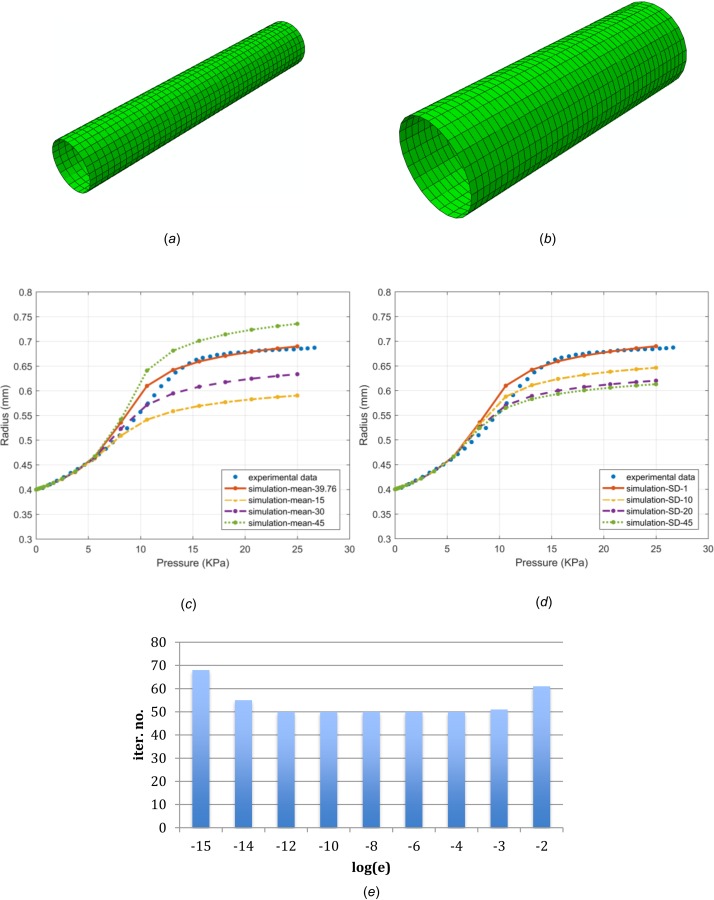
FE meshes used in the vessel inflation simulation, before (a) and after (b) deformation; loading pressure versus the outermost radius of the deformed vessel, observed in experiment (dotted line) and numerical simulations. Material models with various mean fiber directions while the other parameters are kept the same as baseline values (c); material models with various standard deviations while the other parameters are kept the same as baseline values (d); and the iteration number at different logarithmic perturbations using the distributed fiber model in the rat carotid artery simulation (e).

Figures 3(c) and 3(d) show the change of the outermost radius as the vessel is pressurized in experiment [30] and numerical simulations, with varying $\overline{\mathrm{\Theta }}$ and SD. It demonstrates that when fibers were oriented more in the circumferential direction, with $\overline{\mathrm{\Theta }}$ from 45 deg to 15 deg, the artery is less compliant, whereas as the fiber dispersion increases, SD from 1 to 45, the vessel becomes stiffer, which are in agreement with Sun et al. [25].

3.2.2. Computational Efficiency Analysis.

Figure 3(e) shows the iteration number taken by the simulations for different perturbation parameters. When the perturbation parameter is in the range of 10⁻¹² and 10⁻⁴, the iteration number required is unchanged. The effect of perturbation parameter becomes obvious only when the perturbation is chosen outside this range, and the iteration number increases substantially until no convergence is obtained. CPU time follows the same trend.

From these two numerical examples, we have demonstrated that the approximation method simplifies the evaluation of ${\mathrm{c}}^{\tau G}$. One only needs to calculate the stresses and their transformation between frames. In addition, a major advantage of the approximation method lies in its feature of material model independence, i.e., a UMAT code written for a particular material model can be easily adapted for another material model with minimum effort on coding—by simply updating the stress calculations of the new model. It enables the implementation of complex constitutive models in abaqus.

4. Conclusion

This paper presents a detailed description of an approximation method to evaluate the tangent moduli associated with the Green-Naghdi rate of the Kirchhoff stress. By means of implementing a user-defined fiber-reinforced hyperelastic material model in abaqus/Standard via user-defined subroutine UMAT, the aforementioned method was successfully applied and its performance was examined. Upon a proper selection of the perturbation parameter, the approximation method achieved good accuracy and its computational efficiency was similar to UHYPER in terms of the total number of iterations. We believe the method presented here will facilitate the implementation of user-defined material models due to the fact that calculating and coding stress and rotation of frame are much easier than directly evaluating the tangent moduli based on Green-Naghdi rate of Kirchhoff stress itself, especially as material models are becoming more complicated in biomedical engineering applications.

Appendix

The analytical derivation of the second P-K stress along with that of the Lagrangian multiplier p and the elasticity tensor can be presented as below:

The second Piola-Kirchhoff stress can be expressed as

$$\mathbf{S}=2\frac{\partial W\left(I_1,I_4,I_6,J\right)}{\partial \mathbf{C}}=2\left(W_1\mathbf{I}+W_4\mathbf{M}\mathrm{\otimes }\mathbf{M}+W_6\mathbf{N}\mathrm{\otimes }\mathbf{N}\right)-p{\mathbf{C}}^{-1}$$ (A1)

where

$$\begin{array}{c}{W}_1=\frac{\partial W\left(I_1,I_4,I_6,J\right)}{\partial I_1}=c_{10}{c}_{01}\left(\text{exp}\left[c_{01}\left(I_1-3\right)\right]-1\right)+k_1\kappa \left[{\epsilon }_1\hspace{0.17em}\text{exp}\left(k_2{\epsilon }_1^2\right)+{\epsilon }_2\hspace{0.17em}\text{exp}\left(k_2{\epsilon }_2^2\right)\right]\\ W_4=\frac{\partial W\left(I_1,I_4,I_6,J\right)}{\partial I_4}=k_1\left(1-3\kappa \right){\epsilon }_1\hspace{0.17em}\text{exp}\left(k_2{\epsilon }_1^2\right)\\ W_6=\frac{\partial W\left(I_1,I_4,I_6,J\right)}{\partial I_6}=k_1\left(1-3\kappa \right){\epsilon }_2\hspace{0.17em}\text{exp}\left(k_2{\epsilon }_2^2\right)\end{array}$$ (A2)

According to the plane stress condition, the out of plane stress S₃₃ is zero, so that we get $p=2W_1{C}_{33}$ and

$$\mathbf{S}=2(W_1\mathbf{I}+W_4\mathbf{M}\mathrm{\otimes }\mathbf{M}+W_6\mathbf{N}\mathrm{\otimes }\mathbf{N})-2W_1{C}_{33}{\mathbf{C}}^{-1}$$ (A3)

To calculate the elasticity tensor associated with Green-Naghdi rate, we start with the calculation of the referential elasticity tensor $\mathrm{C}$

$$\begin{array}{c}\mathrm{C}=2\frac{\partial \mathbf{S}\left(\mathbf{C}\right)}{\partial \mathbf{C}}=4\left(W_{11}\mathbf{I}\mathrm{\otimes }\frac{\partial I_1}{\partial \mathbf{C}}+W_{14}\mathbf{I}\mathrm{\otimes }\frac{\partial I_4}{\partial \mathbf{C}}+W_{16}\mathbf{I}\mathrm{\otimes }\frac{\partial I_6}{\partial \mathbf{C}}+W_{41}\mathbf{M}\mathrm{\otimes }\mathbf{M}\mathrm{\otimes }\frac{\partial I_1}{\partial \mathbf{C}}+W_{44}\mathbf{M}\mathrm{\otimes }\mathbf{M}\mathrm{\otimes }\frac{\partial I_4}{\partial \mathbf{C}}+W_{61}\mathbf{N}\mathrm{\otimes }\mathbf{N}\mathrm{\otimes }\frac{\partial I_1}{\partial \mathbf{C}}+W_{66}\mathbf{N}\mathrm{\otimes }\mathbf{N}\mathrm{\otimes }\frac{\partial I_6}{\partial \mathbf{C}}\right)-4{\mathrm{C}}_{33}{\mathbf{C}}^{-1}\mathrm{\otimes }\left(W_{11}\frac{\partial I_1}{\partial \mathbf{C}}+W_{14}\frac{\partial I_4}{\partial \mathbf{C}}+W_{16}\frac{\partial I_6}{\partial \mathbf{C}}\right)-4W_1{\mathbf{C}}^{-1}\mathrm{\otimes }\frac{\partial {\mathrm{C}}_{33}}{\partial \mathbf{C}}-4W_1{C}_{33}\frac{\partial {\mathbf{C}}^{-1}}{\partial \mathbf{C}}\end{array}$$ (A4)

where

$$\begin{array}{c}{W}_{11}=\frac{{\partial }^{2}W\left(I_1,I_4,I_6,J\right)}{\partial {I_1}^2}=c_{10}{c}_{01}^2\hspace{0.17em}\text{exp}\left[c_{01}\left(I_1-3\right)\right]+k_1{\kappa }^2\left[\left(1+2k_2{\epsilon }_1^2\right)\text{exp}\left(k_2{\epsilon }_1^2\right)+\left(1+2k_2{\epsilon }_2^2\right)\text{exp}\left(k_2{\epsilon }_2^2\right)\right]\\ W_{44}=\frac{{\partial }^{2}W\left(I_1,I_4,I_6,J\right)}{\partial {I_4}^2}=k_1{\left(1-3\kappa \right)}^2\left(1+2k_2{\epsilon }_1^2\right)\text{exp}\left(k_2{\epsilon }_1^2\right)\\ W_{66}=\frac{{\partial }^{2}W\left(I_1,I_4,I_6,J\right)}{\partial {I_6}^2}=k_1{\left(1-3\kappa \right)}^2\left(1+2k_2{\epsilon }_2^2\right)\text{exp}\left(k_2{\epsilon }_2^2\right)\\ W_{14}=\frac{{\partial }^{2}W\left(I_1,I_4,I_6,J\right)}{\partial I_1\partial I_4}=k_1\kappa \left(1-3\kappa \right)\left(1+2k_2{\epsilon }_1^2\right)\text{exp}\left(k_2{\epsilon }_1^2\right)\\ W_{16}=\frac{{\partial }^{2}W\left(I_1,I_4,I_6,J\right)}{\partial I_1\partial I_6}=k_1\kappa \left(1-3\kappa \right)\left(1+2k_2{\epsilon }_2^2\right)\text{exp}\left(k_2{\epsilon }_2^2\right)\\ W_{41}=W_{14}\\ W_{61}=W_{16}\end{array}$$ (A5)

It should be noted that the incompressibility condition in planar biaxial experiment implies ${\mathrm{C}}_{33}=1/({\mathrm{C}}_{11}{\mathrm{C}}_{22}-{\mathrm{C}}_{12}^2)$. This condition should apply in all the evaluations involved in Eq. (A4). It follows:

$$\begin{array}{l}\frac{\partial C_{33}}{\partial C_{11}}=-C_{22}{C}_{33}^2\\ \frac{\partial C_{33}}{\partial C_{22}}=-C_{11}{C}_{33}^2\\ \frac{\partial C_{33}}{\partial C_{12}}=\frac{\partial C_{33}}{\partial C_{21}}=C_{12}{C}_{33}^2\\ \frac{\partial I_1\left(\mathbf{C}\right)}{\partial C_{11}}=\frac{\partial I_1}{\partial C_{11}}+\frac{\partial I_1}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{11}}=1-C_{22}{C}_{33}^2\\ \frac{\partial I_1\left(\mathbf{C}\right)}{\partial C_{22}}=\frac{\partial I_1}{\partial C_{22}}+\frac{\partial I_1}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{22}}=1-C_{11}{C}_{33}^2\\ \frac{\partial I_1\left(\mathbf{C}\right)}{\partial C_{12}}=\frac{\partial I_1\left(\mathbf{C}\right)}{\partial C_{21}}=\frac{\partial I_1}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{12}}=C_{12}{C}_{33}^2\\ \frac{\partial I_4\left(\mathbf{C},\mathbf{M}\right)}{\partial C_{11}}=\frac{\partial I_4}{\partial C_{11}}+\frac{\partial I_4}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{11}}=M_1^2\\ \frac{\partial I_4\left(\mathbf{C},\mathbf{M}\right)}{\partial C_{22}}=\frac{\partial I_4}{\partial C_{22}}+\frac{\partial I_4}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{22}}=M_2^2\\ \frac{\partial I_4\left(\mathbf{C},\mathbf{M}\right)}{\partial C_{12}}=\frac{\partial I_4\left(\mathbf{C},\mathbf{M}\right)}{\partial C_{21}}=\frac{\partial I_4}{\partial C_{12}}+\frac{\partial I_4}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{12}}=M_1{M}_2\\ \frac{\partial I_6\left(\mathbf{C},\mathbf{N}\right)}{\partial C_{11}}=\frac{\partial I_6}{\partial C_{11}}+\frac{\partial I_6}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{11}}=N_1^2\\ \frac{\partial I_6\left(\mathbf{C},\mathbf{N}\right)}{\partial C_{22}}=\frac{\partial I_6}{\partial C_{22}}+\frac{\partial I_6}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{22}}=N_2^2\\ \frac{\partial I_6\left(\mathbf{C},\mathbf{N}\right)}{\partial C_{12}}=\frac{\partial I_6\left(\mathbf{C},\mathbf{N}\right)}{\partial C_{21}}=\frac{\partial I_6}{\partial C_{12}}+\frac{\partial I_6}{\partial C_{33}}\frac{\partial C_{33}}{\partial C_{12}}=N_1{N}_2\\ {\left(\frac{\partial {\mathbf{C}}^{-1}}{\partial \mathbf{C}}\right)}_{\mathit{a}\mathit{b}\mathit{c}\mathit{d}}=-{\left({\mathbf{C}}^{-1}\right)}_{\mathit{a}\mathit{m}}\frac{\partial C_{\mathit{m}\mathit{n}}}{\partial C_{\mathit{c}\mathit{d}}}{\left({\mathbf{C}}^{-1}\right)}_{\mathit{n}\mathit{b}}\end{array}$$ (A6)