Testing a single regression coefficient in high dimensional linear models

Abstract

In linear regression models with high dimensional data, the classical z-test (or t-test) for testing the significance of each single regression coefficient is no longer applicable. This is mainly because the number of covariates exceeds the sample size. In this paper, we propose a simple and novel alternative by introducing the Correlated Predictors Screening (CPS) method to control for predictors that are highly correlated with the target covariate. Accordingly, the classical ordinary least squares approach can be employed to estimate the regression coefficient associated with the target covariate. In addition, we demonstrate that the resulting estimator is consistent and asymptotically normal even if the random errors are heteroscedastic. This enables us to apply the z-test to assess the significance of each covariate. Based on the p-value obtained from testing the significance of each covariate, we further conduct multiple hypothesis testing by controlling the false discovery rate at the nominal level. Then, we show that the multiple hypothesis testing achieves consistent model selection. Simulation studies and empirical examples are presented to illustrate the finite sample performance and the usefulness of the proposed method, respectively.

1. Introduction

In linear regression models, it is a common practice to employ the z-test (or t-test) to assess whether an individual predictor (or covariate) is significant when the number of covariates (p) is smaller than the sample size (n). This test has been widely applied across various fields (e.g., economics, finance and marketing) and is available in most statistical software. One usually applies the ordinary least squares (OLS) approach to estimate regression coefficients and standard errors for constructing a z-test (or t-test); see, for example, Draper and Smith (1998) and Wooldridge (2002). However, in a high dimensional linear model with p exceeding n, the classical z-test (or t-test) is not applicable because it is infeasible to compute the OLS estimators of p regression coefficients. This motivates us to modify the classical z-test (or t-test) to accommodate high dimensional data.

In high dimensional regression analysis, hypothesis testing has attracted considerable attention (Goeman et al., 2006, 2011; Zhong and Chen, 2011). Since these papers mainly focus on testing a large set of coefficients against a high dimensional alternative, their approaches are not applicable for testing the significance of a single coefficient. Hence, Bühlmann (2013) recently applied the ridge estimation approach and obtained a test statistic to examine the significance of an individual coefficient. His proposed test involves a bias correction, which is different from the classical z-test (or t-test) via the OLS approach. In the meantime, Zhang and Zhang (2014) proposed a low dimensional projection procedure to construct the confidence intervals for a linear combination of a small subset of regression coefficients. The key assumption behind their procedure is the existence of good initial estimators for the unknown regression coefficients and the unknown standard deviation of random errors. To this end, the penalty function with a tuning parameter is required to implement Zhang and Zhang’s (2014) procedure. Later, van de Geer et al. (2014) extended the results of Zhang and Zhang’s (2014) to broad models and general loss functions.

Instead of the ridge estimation and low dimensional projection, Fan and Lv (2008) and Fan et al. (2011) used the correlation approach to screen out those covariates that have weak correlations with the response variable. As a result, the total number of predictors that are highly correlated with the response variable is smaller than the sample size. However, Cho and Fryzlewicz (2012) found out that such a screening process via the marginal correlation procedure may not be reliable when the predictors are highly correlated. To this end, they proposed a tilting correlation screening (TCS) procedure to measure the contribution of the target variable to the response. Motivated by the TCS idea of Cho and Fryzlewicz (2012), we develop a new testing procedure that can lead to accurate inferences. Specifically, we adopt the TCS idea and introduce the Correlated Predictors Screening (CPS) method to control for predictors that are highly correlated with the target covariate before a hypothesis test is conducted. It is worth noting that Cho and Fryzlewicz (2012) mainly focus on variable selection, while we aim at hypothesis testing.

If the total number of highly correlated predictors resulting from the CPS procedure is smaller than the sample size, their effects can be profiled out from both the response and the target predictor via projections. Based on the profiled response and the profiled predictor, we are able to employ a classical simple regression model to obtain the OLS estimate of the target regression coefficient. We then demonstrate that the resulting estimator is $\sqrt{n}$-consistent and asymptotically normal, even if the random errors are heteroskedastic as considered by Belloni et al. (2012, 2014). Accordingly, a z-test statistic can be constructed for testing the target coefficient. Under some mild conditions, we show that the p-values obtained by the asymptotic normal distribution satisfy the weak dependence assumption of Storey et al. (2004). As a result, the multiple hypothesis testing procedure of Storey et al. (2004) can be directly applied to control the false discovery rate (FDR). Finally, we demonstrate that the proposed multiple testing procedure achieves model selection consistency.

The rest of the article is organized as follows. Section 2 introduces model notation and proposes the CPS method. The theoretical properties of hypothesis tests via the CPS as well as the FDR procedures are obtained. Section 3 presents simulation studies, while Section 4 provides real data analyses. Some concluding remarks are given in Section 5. All technical details are relegated to Appendix.

2. The methodology

2.1. The CPS method

Let (Y_i, X_i) be a random vector collected from the ith subject (1 ≤ i ≤ n), where Y_i ∈ ℝ¹ is the response variable and X_i = (X_i1, …, X_ip)^⊤ ∈ ℝ^p is the associated p-dimensional predictor vector with E(X_i) = 0 and cov(X_i) = Σ = (σ_j1j2 ) ∈ ℝ^p×p. In addition, the response variable has been centralized such that E(Y_i) = 0. Unless explicitly stated otherwise, we hereafter assume that p ≫ n and n tends to infinity for asymptotic behavior. Then, consider the linear regression model,

$$Y_i=X_i^{\top }\beta +{\epsilon }_i,$$ (2.1)

where β = (β₁, …, β_p)^⊤ ∈ ℝ^p is an unknown regression coefficient vector. Motivated by Belloni et al. (2012, 2014), we assume that the error terms ε_i are independently distributed with E(ε_i|X_i) = 0 and finite variance $var({\epsilon }_i)={\sigma }_i^2$ for i = 1, …, n. In addition, define the average of error variances as ${\overline{\sigma }}_n^2=n^{-1}{\sum }_i{\sigma }_i^2$, and assume that ${\overline{\sigma }}_n^2\to {\overline{\sigma }}^2$ as n → ∞ for some finite positive constant σ̄². To assess the significance of a single coefficient, we test the null hypothesis H₀ : β_j = 0 for any given j. Without loss of generality, we focus on testing the first regression coefficient. That is,

$$H_0:{\beta }_1=0\text{vs.}{H}_1:{\beta }_1\ne 0,$$ (2.2)

and the same testing procedure is applicable to the rest of the individual regression coefficients.

For the sake of convenience, let 𝕐 = (Y₁, …, Y_n)^⊤ ∈ ℝⁿ be the vector of responses, 𝕏 = (X₁, …, X_n)^⊤ ∈ ℝ^n×p be the design matrix with the jth column 𝕏_j ∈ ℝⁿ, and ℰ = (ε₁, …, ε_n)^⊤ ∈ ℝⁿ. In addition, let ℓ be an arbitrary index set with cardinality |ℓ|. Then, define X_iℓ = (X_ij : j ∈ ℓ)^⊤ ∈ ℝ^|ℓ|, 𝕏_ℓ = (X_1ℓ, …, X_nℓ)^⊤ = (𝕏_j : j ∈ ℓ) ∈ ℝ^n×|ℓ|, Σ_ℓ = (σ_j1j2 : j₁ ∈ ℓ, j₂ ∈ ℓ) ∈ ℝ^|ℓ|×|ℓ|, and ${\mathit{\sum }}_{\ell j}={\mathit{\sum }}_{j\ell }^{\top }=({\sigma }_{j_1{j}_2}:j_1\in \ell ,j_2=j)\in {ℝ}^{\mid \ell \mid }$. Moreover, define Σ_ℓaℓb = (σ_j1j2 : j₁ ∈ ℓ_a, j₂ ∈ ℓ_b) ∈ ℝ^{|ℓ_a|×|ℓ_b|} for any two arbitrary index sets ℓ_a and ℓ_b, which implies Σ_ℓℓ = Σ_ℓ.

Before constructing the test statistic, we first control those predictors that are highly correlated with X_i1. Otherwise, they can generate a confounding effect, due to multicollinearity and yield an incorrect estimator of β₁. Specifically, the marginal regression coefficient ${({\mathbb{X}}_1^{\top }{\mathbb{X}}_1^{\top })}^{-1}{\mathbb{X}}_1^{\top }\mathbb{Y}={\beta }_1+{({\mathbb{X}}_1^{\top }{\mathbb{X}}_1^{\top })}^{-1}{\mathbb{X}}_1^{\top }(\mathbb{Y}-{\mathbb{X}}_1{\beta }_1)$ is not a consistent estimator of β₁ when 𝕐 − 𝕏₁β₁ and 𝕏₁ have a strong linear relationship. To remove the confounding effect, define ρ_1j = corr(X_i1, X_ij) as the correlation coefficient of X_i1 and X_ij for j = 2, …, p, and ${\rho }_1^{\ast }={(\mid {\rho }_{12}\mid ,\dots ,\mid {\rho }_{1p}\mid )}^{\top }\in {ℝ}^{p-1}$. We also assume that |ρ_1j| are distinct. Then, let 𝒮_k be the set of k indices whose associated predictors have the largest absolute correlations with X_i1:

$${\mathcal{S}}_k=\{2\le j\le p:\mid {\rho }_{1j}\mid \text{is}\text{among}\text{the}\text{first}k\text{largest}\text{absolute}\text{correlation}\text{in}{\rho }_1^{\ast }\}.$$ (2.3)

The choice of k (i.e., 𝒮_k) will be discussed in Remark 2. With a slight abuse of notation, we sometimes denote 𝒮_k by 𝒮 in the rest of the paper for the sake of convenience. To remove the confounding effect due to X_i𝒮, we construct the profiled response and predictor as 𝕐̃ = 𝒬_𝒮𝕐 and 𝕏̃₁ = 𝒬_𝒮𝕏₁, respectively, where ${\mathcal{Q}}_{\mathcal{S}}=I_n-{\mathbb{X}}_{\mathcal{S}}{({\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_{\mathcal{S}})}^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }\in {ℝ}^{n\times n}$ and I_n ∈ ℝ^n×n is the n×n identity matrix. We next follow the OLS approach and obtain the estimate of the target coefficient β₁,

$${\widehat{\beta }}_1={({\stackrel{\sim }{\mathbb{X}}}_1^{\top }{\stackrel{\sim }{\mathbb{X}}}_1)}^{-1}({\stackrel{\sim }{\mathbb{X}}}_1^{\top }\stackrel{\sim }{\mathbb{Y}})={({\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1)}^{-1}({\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}\mathbb{Y}).$$

We refer to the above procedure as the Correlated Predictors Screening (CPS) method, β̂₁ as the CPS estimator of β₁, and 𝒮 as the CPS set of X_i1.

It is of interest to note that the proposed CPS estimator β̂₁ is closely related to the estimator obtained via the “added-variable plot” approach (e.g., see Cook and Weisberg, 1998). To illustrate their relationship, let 𝕏₋₁ be the collection of all covariates in 𝕏 except for 𝕏₁. Then the method of “added-variable plot” essentially takes the residuals from regressing 𝕐 against 𝕏₋₁ as the response and the residuals from regressing 𝕏₁ against 𝕏₋₁ as covariates. Although both approaches can be used to assess the effect of 𝕏₋₁ on the estimation of β₁, they are different. Specifically, the “added-variable plot” approach requires regressing 𝕏₁ on all remaining covariates, which is not computable when the dimension p is larger than n. By contrast, CPS only considers those predictors in 𝒮 that are highly correlated with 𝕏₁, which is applicable in high dimensional settings.

Making inferences about β₁ in high dimensional models is challenging because these inferences can depend on the accuracy of estimating the whole vector β; see Belloni et al. (2014), van de Geer et al. (2014) and Zhang and Zhang (2014). The main contribution of our proposed CPS method is employing a simple marginal regression approach to estimate β₁ after controlling for the predictors that are highly correlated with 𝕏₁. As a result, the profiled predictor, 𝕏̃₁, is approximately independent of the remaining covariates. This allows us to not only directly estimate β₁, but also make inferences about β₁. The theoretical properties of the CPS estimator and associated test statistic are presented below.

2.2. Asymptotic normality of the CPS estimator and test statistic

To make inferences, we study the asymptotic properties of the CPS estimator β̂₁. Define ${\mathrm{\varrho }}_{j_1{j}_2}(\mathcal{S})={\sigma }_{j_1{j}_2}-{\mathit{\sum }}_{\mathcal{S}{j}_1}^{\top }{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}{j}_2}\in {ℝ}^1$, which measures the partial covariance of X_ij1 and X_ij2, after controlling for the effect of X_i𝒮 = (X_ij : j ∈ 𝒮)^⊤ ∈ ℝ^|𝒮|. Then, we make the following assumptions to facilitate the technical proofs, while admittedly not the weakest possible assumptions.

• (C1)Gaussian condition. Assume that the X_is are independent and normally distributed with mean 0 and covariance matrix Σ.
• (C2)Bounded diagonal elements. There exist two finite constants c_max and $c_{max}^{\ast }$ such that the diagonal components of Σ and Σ⁻¹ are bounded above by c_max and $c_{max}^{\ast }$ , respectively.
• (C3)Predictor dimension. There exist two positive constants ħ < 1 and ν > 0 such that log p ≤ νn^ħ for every n > 0.
• (C4)Partial covariance. There exists a constant ξ > 3/2 such that max_j∉𝒮 |ϱ_1j(𝒮)| = O(|𝒮|^−ξ ) as |𝒮| → ∞.
• (C5)Dimension of the CPS set. There exist a CPS set |𝒮| and two positive constants C_a and C_b such that C_an^ν₁ ≤ |𝒮| ≤ C_bn^ν₂, where ν₁ and ν₂ are two positive constants with 1/(2ξ) < ν₁ ≤ ν₂ < 1/3 and ħ + 3ν₂ < 1, where ħ is defined in Condition (C3).
• (C6)Regression coefficients. Assume that $\mid \beta \mid ={\sum }_{j=1}^p\mid {\beta }_j\mid <C_{max}{n}^{\varpi }$ for some constant C_max > 0 and ϖ < min(1/4, ξν₁ − 1/2), where ξ and ν₁ are defined in (C4) and (C5), respectively.

Condition (C1) is a common condition used for high dimensional data to simplify theoretical proofs; see for example, Wang (2009) and Zhang and Zhang (2014). This condition can be relaxed to the sub-Gaussian random variables (Wang, 2012; Li et al., 2012) and our theoretical results still hold. Condition (C2) is a mild condition that has been well discussed in Liu (2013). Condition (C3) allows the dimension of predictors p to diverge exponentially with the sample size n, so that p can be much larger than n. Condition (C4) is a technical condition for simplifying the proofs of our theory, and it requires that the partial covariance between the target covariate and any other predictor that does not belong to 𝒮, after controlling for the effect of X_i𝒮 (i.e., key confounders), and that it converges towards 0 at a fast speed as |𝒮| → ∞. This condition is satisfied for many typical covariance structures, e.g., diagonal and autoregressive structures. It is worth noting that, according to (C1), the conditional distribution of X_i1 given X_i,−1 = (X_i2, …, X_ip)^⊤ ∈ ℝ^p−1 remains normal. As a result, there exists a coefficient vector θ₍₁₎ = (θ_(1),1, …, θ_(1),p−1)^⊤ ∈ ℝ^p−1 such that $X_{i1}=X_{i,-1}^{\top }{\theta }_{(1)}+e_{i1}$, where e_i1 is a random error that is independent of X_i,−1. Furthermore, if 𝒮 ⊂ 𝒮_θ = {j : θ_(1),j ≠ 0}, then it implies that max_j∉𝒮 |ϱ_1j(𝒮)| = 0. Hence, Condition (C4) is satisfied. Furthermore, this condition is closely related to the assumption given in Theorem 5 of Zhang and Zhang (2014). Moreover, Condition (C5), together with Condition (C4), ensures that the size of the CPS set is much smaller than the sample size, but it does not imply that the number of regressors highly correlated with 𝕏₁ is bounded. Condition (C5) is used to guarantee that max_j∉𝒮 |ϱ_1j(𝒮)| is of order o(n^−1/2), so that the bias of β̂₁ vanishes. Note that the size of the CPS set in Condition (C5) depends on the rate of max_j∉𝒮 |ϱ_1j(𝒮)| → 0. Thus, Condition (C5) can be dropped if θ₍₁₎ has finite non-zero elements or Σ follows an autoregressive structure so that max_j∉𝒮 |ϱ_1j(𝒮)| = O{exp(−ζ̄ |𝒮|^η̄)} for some positive constants ζ̄ and η̄. Lastly, Condition (C6) is satisfied when β is sparse with only a finite number of nonzero coefficients. Under the above conditions, we obtain the following result.

Theorem 1

Assume that Conditions (C1)–(C6) hold. We then have $n^{1/2}({\widehat{\beta }}_1-{\beta }_1)\stackrel{d}{\to }N(0,{\sigma }_{{\beta }_1}^2)$, where ${\sigma }_{{\beta }_1}^2={\tau }_{{\beta }_1}^2{({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})}^{-1},{\tau }_{{\beta }_1}^2={\beta }_{{\mathcal{S}}^{\ast }}^{\top }({\mathit{\sum }}_{{\mathcal{S}}^{\ast }}-{\mathit{\sum }}_{{\mathcal{S}}^{\ast }{\mathcal{S}}^{+}}{\mathit{\sum }}_{{\mathcal{S}}^{+}}^{-1}{\mathit{\sum }}_{{\mathcal{S}}^{+}{\mathcal{S}}^{\ast }}){\beta }_{{\mathcal{S}}^{\ast }}+{\stackrel{\sim }{\sigma }}^2$, 𝒮⁺ = {1}∪ 𝒮, and 𝒮^* = {j : j ∉ 𝒮⁺}.

Using the results of two lemmas in Appendix A, we are able to prove the above theorem; see the detailed proofs in Appendix B. By Theorem 1, we construct the test statistic,

$$Z_1=n^{1/2}{\widehat{\beta }}_1/{\widehat{\sigma }}_{{\beta }_1},$$ (2.4)

where ${\widehat{\sigma }}_{{\beta }_1}^2={\widehat{\tau }}_{{\beta }_1}^2{(n^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1)}^{-1},{\widehat{\tau }}_{{\beta }_1}^2={(n-\mid {\mathcal{S}}^{+}\mid )}^{-1}{\widehat{\mathcal{E}}}_{{\mathcal{S}}^{+}}^{\top }{\widehat{\mathcal{E}}}_{{\mathcal{S}}^{+}}$,ℰ̂_𝒮⁺ is the residual vector obtained by regressing Y_i on X_i𝒮⁺, and X_i𝒮⁺ = (X_ij : j ∈ 𝒮⁺)^⊤. Applying similar techniques to those used in the proof of Theorem 1 under Conditions (C1)–(C6), together with Slutsky’s theorem and the result that $c_{max}^{\ast -1}\le n^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1\le c_{max}$ obtained from Lemma 3 and Condition (C2), we can verify that ${\widehat{\sigma }}_{{\beta }_1}^2$ is the consistent estimator of ${\sigma }_{{\beta }_1}^2$. As a result, Z₁ is asymptotically standard normal under H₀, and one can reject the null hypothesis if |Z₁| > z_1−α/2, where z_α stands for the αth quantile of the standard normal distribution. Note that if p < n and 𝒮 = {j : j ≠ 1}, the test statistic Z₁ is the same as the classical z-test statistic.

To make the testing procedure practically useful, one needs to select the CPS set 𝒮 among the sets 𝒮_k for k ≥ 1. Since 𝒮_k in (2.3) is unknown in practice, we consider its estimator

$${\widehat{\mathcal{S}}}_k=\left\{2\le j\le p:\mid {\widehat{\rho }}_{1j}\mid \text{is}\text{among}\text{the}k\text{largest}\text{elements}\text{of}{\widehat{\rho }}_1^{\ast }\right\},$$ (2.5)

where ρ̂_1j is the sample correlation coefficient of X_i1 and X_ij and ${\widehat{\rho }}_1^{\ast }={(\mid {\widehat{\rho }}_{12}\mid ,\dots ,\mid {\widehat{\rho }}_{1p}\mid )}^T\in {ℝ}^{p-1}$. The connection between 𝒮_k and its sample counterpart 𝒮̂_k is established in the following proposition.

Proposition 1

Let |ρ_1ji | be the ith largest absolute value of {ρ_1j : 2 ≤ j ≤ p}. For any 1 ≤ k ≤ C_bn^ν₂ with C_b and ν₂ being defined in Condition (C5), min_{i≥dmaxn^ν2}/₂(|ρ_1jk| − |ρ_1jk+i |) > d_min/n^ν₂ for some positive constants d_min and d_max. Then, under Conditions (C1) and (C3), for any CPS set 𝒮_k0 satisfying k₀ ≤ C_bn^ν₂, there exists k^* ≤ k₀ + d_maxn^ν₂ such that P(𝒮̂_k^* ⊂ 𝒮_k0 ) → 1.

The proof is given in Appendix C. The condition min_{i≥dmaxn^ν2}/₂(|ρ_1jk | − |ρ_1jk+i |) > d_min/n^ν₂ for some finite positive constants d_min and d_max is quite mild, and it ensures that the difference between |ρ_1jl | and |ρ_1jm| cannot be too small when |j_l − j_m| is large enough. By Condition (C5), there exists a positive integer k₀ ∈ (C_an^ν₁, C_bn^ν₂ ) such that 𝒮_k0 is the CPS set. According to Proposition 1, we can then find k^* ≤ k₀ + d_maxn^ν₂ = O(n^ν₂ ) satisfying P(𝒮̂_k^* ⊂ 𝒮_k0 ) → 1. This indicates that there exists a set among the paths 𝒮̂_k that contains the CPS set. By Condition (C4), we further have that ${max}_{j\notin {\widehat{\mathcal{S}}}_{k^{\ast }}^{+}}\mid {\mathrm{\varrho }}_{1j}({\widehat{\mathcal{S}}}_{k^{\ast }})\mid =O({\mid {\mathcal{S}}_{k_0}\mid }^{-\xi })=o(n^{-1/2})$. Using this result, one can verify that Theorem 1 holds by replacing 𝒮_k0 with 𝒮̂_k^*.

Proposition 1 indicates that the sequential selection of the CPS set along the paths 𝒮̂_k (k = 1, …, p − 1) is attainable. In practice, however, k is unknown and needs to be selected effectively. By the results of Corollary 1 of Kalisch and Bühlmann (2007), we have that |ϱ̂_1j(𝒮̄) − ϱ_1j(𝒮̄)| = O_p(n^−1/2) uniformly for any conditional set with size |𝒮̄| = O(n^ν₂ ), which leads to ${max}_{j\notin {\widehat{\mathcal{S}}}_k^{+}}\mid {\widehat{\mathrm{\varrho }}}_{1j}({\widehat{\mathcal{S}}}_k)-{\mathrm{\varrho }}_{1j}({\widehat{\mathcal{S}}}_k)\mid =O_p(n^{-1/2})$ for any k = O(n^ν₂ ). This indicates that the sample partial correlation is close to its true partial correlation as the sample size gets large. Motivated by this finding, we propose choosing the CPS set among the paths 𝒮̂_k by sequentially testing the partial correlations. Specifically, for any k ≥ 1, ${\widehat{\mathrm{\varrho }}}_{1j}({\widehat{\mathcal{S}}}_k)={\mathbb{X}}_1^{\top }{\mathcal{Q}}_{{\widehat{\mathcal{S}}}_k}{\mathbb{X}}_j/n$ be the sample counterpart of ϱ_1j(𝒮_k) and define F̂_1j(𝒮̂_k) = 2⁻¹ log[{1 + ϱ̂_1j(𝒮̂_k)}/{1 − ϱ̂_1j(𝒮̂_k)}], which is in the spirit of Fisher’s Z-transformation for the purpose of identifying nodes (variables) that have edges connected to the variable X_i1 in a Gaussian graph (see Kalisch and Bühlmann, 2007). Then, we select the smallest size of k sequentially such that ${(n-\mid {\widehat{\mathcal{S}}}_k\mid -3)}^{1/2}{max}_{j\notin {\widehat{\mathcal{S}}}_k^{+}}\mid {\widehat{F}}_{1j}({\widehat{\mathcal{S}}}_k)\mid <z_{1-\gamma /2}$ (denoted as k̂), for every $j\notin {\widehat{\mathcal{S}}}_k^{+}$, where γ is a pre-specified significance level and ${\widehat{\mathcal{S}}}_k^{+}=\{1\}\cup {\widehat{\mathcal{S}}}_k$. Employing Lemma 3 in Kalisch and Bühlmann (2007) that |F̂_1j(𝒮̄)−F_1j(𝒮̄)| = O_p(n^−1/2) uniformly for any conditional set with size |𝒮̄| = O(n^ν₂ ), we then have ${max}_{j\notin {\widehat{\mathcal{S}}}_k^{+}}\mid F_{1j}({\widehat{\mathcal{S}}}_{\widehat{k}})\mid =O(n^{-1/2})$, which immediately leads to ${max}_{j\notin {\widehat{\mathcal{S}}}_k^{+}}\mid {\mathrm{\varrho }}_{1j}({\widehat{\mathcal{S}}}_{\widehat{k}})\mid =O(n^{-1/2})$. Using the result of Proposition 1 and Condition (C4), we further obtain |𝒮̂_k̂| ≤ (C_b + d_max)n^ν₂. Hence, the k̂ selected via the sequential testing procedure is of order O(n^ν₂ ), which is directly related to the assumption imposed on 𝒮_k in Condition (C5).

Remark 1

It is worth noting that the proposed CPS method is based on the same idea as the tilting method of Cho and Fryzlewicz (2012), namely controlling the effect of the predictors that could generate a confounding effect. However, there is a difference between these two methods in one of their scaling factors. Specifically, our proposed test statistic is

$$\frac{{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}\mathbb{Y}{(1-\mid {\mathcal{S}}^{+}\mid /n)}^{1/2}}{{({\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1)}^{1/2}{\{{\mathbb{Y}}^{\top }{\mathcal{Q}}_{{\mathcal{S}}^{+}}\mathbb{Y}\}}^{1/2}}$$

and the tilted correlation of Cho and Fryzlewicz (2012) is

$$\frac{{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}\mathbb{Y}}{{({\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1)}^{1/2}{({\mathbb{Y}}^{\top }{\mathcal{Q}}_{\mathcal{S}}\mathbb{Y})}^{1/2}}.$$

Note that 𝒮⁺ = 𝒮 ∪ {1}. The asymptotic properties of these two quantities above can be quite different when β₁ ≠ 0 because the difference between 𝕐^⊤ 𝒬_𝒮⁺𝕐 and 𝕐^⊤𝒬_𝒮𝕐 can be large. This indicates that the tilted correlation approach designed for variable selection may not be appropriate for hypothesis testing.

Remark 2

Based on partial correlation, we construct the CPS set. An alternative approach is via the correlation approach proposed by Cho and Fryzlewicz (2012, Section 3.4), who focused on testing correlations between covariates by controlling the false discovery rate. Although their method is quite useful for variable selection, it raises the following two concerns for our testing procedure. First, Theorem 1 may not be valid via the correlation approach. The reason is that Theorem 1 requires the partial covariance, max_j |ϱ_1j(𝒮)|, to converge to 0 at a fast rate so that the bias of β̂₁ is asymptotically negligible; see the proof of Theorem 1 in Appendix B for details. However, the correlation approach only ensures the convergence of max_j |ρ_1j|, but not max_j |ϱ_1j(𝒮)|. Hence, β̂₁ may yield a nontrivial bias by using the correlation approach. Second, their method requires that only a small proportion of the ρ_j1j2 s are nonzero. Accordingly, it may not be applicable for our proposed test when correlations among predictors are either non-sparse or less sparse (see the covariance structure with the polynomial decay setting above Example 4).

Remark 3

We use a single screening approach to obtain the CPS set of the target covariate, which yields the CPS estimator of the target regression coefficient. On the other hand, Zhang and Zhang (2014) employed the scaled lasso procedure of Sun and Zhang (2012) to obtain the initial estimators of all regression coefficients and the scale parameter estimator. Then, they apply the classical lasso procedure to find the low dimensional projection vector. In sum, Zhang and Zhang (2014) applied the lasso approach to find the low dimensional projection estimator (LDPE) for the target regression coefficient. When 𝕏 has orthogonal columns and p < n, both approaches lead to the same parameter estimator as that obtained from the marginal univariate regression (MUR). However, these two approaches are quite different, and it seems nearly impossible to find the exact relationship between the CPS estimator and LDPE when the columns of 𝕏 are not orthogonal.

2.3. Controlling the False Discovery Rate (FDR)

In identifying significant coefficients among the high dimensional regression coefficients β_j (j = 1, …, p), a multiple testing procedure can be considered by testing H_0j : β_j = 0 simultaneously. Denote the p-value obtained by testing each individual null hypothesis, H_0j, as p_j = 2{1 − Φ(|Z_j|)}, where Z_j is the test statistic and can be constructed similarly to that in Eq. (2.4). To guard against false discoveries, we next develop a procedure to control the false discovery rate (Benjamini and Hochberg, 1995).

Let 𝒩₀ = {j : β_j = 0} be the set of variables whose associated coefficients are truly zero and 𝒩₁ = {j : β_j ≠ 0} be the set of variables whose associated coefficients are truly nonzero. For any significance level t ∈ [0, 1], let V(t) = #{j ∈ 𝒩₀ : p_j ≤ t} be the number of falsely rejected hypotheses, S(t) = #{j ∈ 𝒩₁ : p_j ≤ t} be the number of correctly rejected hypotheses, and R(t) = #{j : p_j ≤ t} be the total number of rejected hypotheses. We adopt the approach of Storey et al. (2004) to implement the multiple testing procedure, which is less conservative than the method of Benjamini and Hochberg (1995) and is applicable under a weak dependence structure (Storey et al., 2004). To this end, define FDP(t) = V(t)/[R(t)∨1] and FDR(t) = E{V(t)/[R(t)∨1]}, where R(t) ∨ 1 = max{R(t), 1}. Then, the estimator proposed by Storey (2002) is

$${\widehat{\text{FDR}}}_{\lambda }(t)=\frac{{\widehat{\pi }}_0(\lambda )t}{\{R(t)\vee 1\}/p},$$ (2.6)

where π̂₀(λ) = {(1−λ)p}⁻¹{p−R(λ)} is an estimate of π₀ = p₀/p, p₀ = |𝒩₀| is the number of true null hypotheses, and λ ∈ [0, 1) is a tuning parameter. Then, for any pre-specified significance level q and a fixed λ, consider the cutoff point chosen by the thresholding rule, $t_q({\widehat{\text{FDR}}}_{\lambda })=sup\{0\le t\le 1:{\widehat{\text{FDR}}}_{\lambda }(t)\le q\}$. We reject the null hypotheses for those p-values that are less than or equal to $t_q({\widehat{\text{FDR}}}_{\lambda })$.

To study the theoretical property of ${\widehat{\text{FDR}}}_{\lambda }(t)$, we begin by introducing two notations. Let $T_{1,n}(t)=p^{-1}{\sum }_{j=1}^{p}P(p_j\le t)$ be the average probability of all rejected hypotheses and 𝒮_j be the CPS set of covariates X_ij. We next demonstrate that $t_q({\widehat{\text{FDR}}}_{\lambda })$asymptotically provides strong control of FDR at the pre-specified nominal level q.

Theorem 2

Assume that p₀/p → 1 as p goes to infinity, lim_n→∞ T_1,n(t) = T₁(t) and, for any k ∈ 𝒩₀, ${\sum }_{j\in {\mathcal{N}}_0}{\sum }_{l\in {\mathcal{S}}_j}{\sigma }_{lk}^2=o(p/{\mathit{\Lambda }}_0^2)$, where T₁(t) is a continuous function and Λ₀ = max{max_j∈𝒩0 |𝒮_j|, |𝒩₁|}. Under Conditions (C1)–(C6), we have that $lim{sup}_{n\to \infty }\text{FDR}\{t_q({\widehat{\text{FDR}}}_{\lambda })\}\le q$.

The proof is given in Appendix D. In general, the dependences among the test statistics Z_j become stronger as the overlap among the CPS sets increases. To control the dependences, they must have weaker dependence among covariates as the size of overlap increases. Accordingly, the condition ${\sum }_{j\in {\mathcal{N}}_0}{\sum }_{l\in {\mathcal{S}}_j}{\sigma }_{lk}^2=o(p/{\mathit{\Lambda }}_0^2)$ for any k ∈ 𝒩₀, in Theorem 2, controls the overall dependence between the covariates in the union of the CPS sets ∪_l∈𝒩0 𝒮_l for any fixed k ∈ 𝒩₀; see Fan et al. (2012) for a similar condition on dependence. In addition, Λ₀ provides an upper bound on the size of the overlap among the CPS sets. Assume that Σ follows an autoregressive structure such that the |𝒮_j|s are small compared with n and ${\sum }_j{\sigma }_{jk}^2<\infty$ for any 1 ≤ k ≤ p. Hence, the above condition is satisfied. In sum, ${\widehat{\text{FDR}}}_{\lambda }$ in (2.6) is applicable under weak dependence. For a more general dependence structure, one might apply the FDP estimation procedure proposed by Fan et al. (2012).

2.4. Model selection consistency

According to Theorem 2, for any given significance level q > 0, the FDR can be controlled asymptotically by setting the threshold at $t=t_q({\widehat{\text{FDR}}}_{\lambda })$. This result motivates us to further investigate the model selection consistency by letting q → 0. In fact, the model selection consistency in high dimensional linear models has been intensively studied in the variable selection literature. There is a large body of papers discussing the model selection consistency via the penalized likelihood approach (e.g., Meinshausen and Bühlmann, 2006; Zhao and Yu, 2006; Huang et al., 2007). However, the use of p-values for model selection has not received considerable attention. Some exceptions include Bunea et al. (2006) who considered variable selection consistency using p-values under the condition p = o(n^1/2), and Meinshausen et al. (2009) who investigated the consistency of a two-step procedure involving screening and then a multiple test procedure. It is worth noting that the p-value obtained in Meinshausen et al. (2009) is not designed for assessing the significance of a single coefficient. The aim of this section in our paper is to study the model selection consistency using p-values obtained from the test proposed in Section 2.2.

For any given nominal levels α_n, let ${\widehat{\mathcal{N}}}_1^{{\alpha }_n}=\{j:p_j\le {\alpha }_n\}$ be an estimate of 𝒩₁, the set containing all the variables whose associated coefficients are truly nonzero. Assume that α_n → 0 as n → ∞. By Theorem 2, the probability of obtaining false discoveries is $P\{\mid {\widehat{\mathcal{N}}}_1^{{\alpha }_n}\cap {\mathcal{N}}_0\mid \ge 1\}\le {\alpha }_n\to 0$, which implies that $P\{{\widehat{\mathcal{N}}}_1^{{\alpha }_n}\subset {\mathcal{N}}_1\}\to 1$. Thus, this procedure requires a sure screening property $P\{{\mathcal{N}}_1\subset {\widehat{\mathcal{N}}}_1^{{\alpha }_n}\}\to 1$ to obtain model selection consistency. Before demonstrating this property, two additional assumptions are given below.

• (C7)There exist two positive constants κ and C_κ such that min_{j∈𝒩 1} |β_j| > C_κn^−κ for κ + ħ < 1/2, where ħ is defined in (C3).
• (C8)There exists some positive constant C_e such that for any ℓ > 0 and 1 ≤ j ≤ p, $P\left(n^{-1}\mid X_j^{\top }\mathcal{E}\mid >\ell \right)\le exp(-C_{e}n{\ell }^2)$.

Condition (C7) is a minimum signal assumption, and similar conditions are commonly considered in the variable screening literature (Fan and Lv, 2008; Wang, 2009). We further assume that the random errors ε_i are independent and normally distributed. Using the fact that n⁻¹||𝕏_j||² → 1 and that $n^{-1/2}{\mathbb{X}}_j^{\top }\mathcal{E}$ follows a normal distribution with finite variance for j = 1, …, p, Condition (C8) is satisfied. The above conditions, together with Conditions (C1)–(C6), lead to the following result.

Theorem 3

Under Conditions (C1)–(C8), there exists a sequence of significance levels α_n → 0 such that $P({\widehat{\mathcal{N}}}_1^{{\alpha }_n}={\mathcal{N}}_1)\to 1$.

The proof of Theorem 3 is given in Appendix E. According to the proof of Theorem 3, one can select α_n at the level of α_n = 2{1 − Φ(n^j)} with ħ < j < 1/2 − κ. This selection implies that pα_n/log(p) → 0 as n → ∞, which is similar to the assumption (C_q) in Bunea et al. (2006). Compared with the penalized likelihood method, the proposed testing procedure is able to control the false discovery rate and the family-wise error rate for the given α_n. This is important especially in the finite sample case; see Meinshausen et al. (2009) for a detailed discussion.

3. Simulation studies

To demonstrate the finite sample performance of the proposed methods, we consider four simulation studies with different covariance patterns and distributions among predictors. Each simulation includes three different sample sizes (n = 100, 200, 500) and two different dimensions of predictors (p = 1000 and 2000). All simulation results presented in this section were based on 1000 realizations. The nominal level α of the CPS test and the significance level q of FDR are both set to 5%. Moreover, to determine the CPS set for each predictor, three different significance levels were considered (α = 0.01, 0.05, and 0.10). Since the results were similar, we only report the case with the nominal level α = 0.05.

To study the significance of each individual regression coefficient, consider the proposed test statistic Z_rj for testing the jth coefficient in the rth simulation, where j = 1, …, p and r = 1, …, 1000. Then, define an indicator measure I_rj = I(|Z_rj| > z_1−α/2) and compute the empirical rejection probability (ERP) for the jth coefficient test, ${\text{ERP}}_j={1000}^{-1}{\sum }_{r=1}^{1000}{I}_{rj}$. As a result, ERP_j is the empirical size under the null hypothesis H_0j : β_j = 0, while it is the empirical power under the alternative hypothesis. Subsequently, define the average empirical size (ES) and the average empirical power (EP) as ES = |𝒩₀|⁻¹Σ_{j∈𝒩 0} ERP_j and EP = |𝒩₁|⁻¹Σ_{j∈𝒩 1} ERP_j, respectively. Accordingly, ES and EP provide overall measures for assessing the performance of the single coefficient test. Based on the p-values of the Z_rj tests, we next employ the multiple testing procedure of Storey et al. (2004) to study the performance of multiple tests via the empirical FDR discussed in Section 2.3. It is worth noting that we adopt the commonly used tuning parameter λ = 1/2 in the first two examples, and its robustness is evaluated in Example 3. To assess the effect of model selection consistency, we examine the average true rate $\text{TR}=\mid {\widehat{\mathcal{N}}}_1^{\alpha }\cap {\mathcal{N}}_1\mid /\mid {\mathcal{N}}_1\mid$ and the average false rate $\text{FR}=\mid {\widehat{\mathcal{N}}}_1^{\alpha }\cap {\mathcal{N}}_0\mid /\mid {\mathcal{N}}_0\mid$. When the true model can be identified consistently, TR and FR should approach 1 and 0, respectively, as the sample size gets large. For the sake of comparison, we also examine the marginal univariate regression (MUR) test (i.e., the classical t-test obtained from the marginal univariate regression model) and the low dimensional projection estimator (LDPE) proposed by Zhang and Zhang (2014) and van de Geer et al. (2014) in Monte Carlo studies. The tuning parameter of the LDPE method is set to {2 log p/n}^1/2, as suggested by Zhang and Zhang (2014). It is noteworthy that we do not include the method of Bühlmann (2013) for comparison since it is not optimal, as shown by van de Geer et al. (2014).

Example 1: Autocorrelated predictors

Consider a linear regression model with autocorrelated predictors X_i generated from a multivariate normal distribution with mean 0 and covariance Σ = (σ_j1j2) ∈ ℝ^p×p with σ_j1j2 = 0.5^{|j₁−j₂|}. Although different predictors are correlated with each other, the correlation decreases to 0 as the distance |j₁ − j₂| between X_ij1 and X_ij2 increases. The regression coefficient vector β is such that β_3j+1 = 1 for any 0 ≤ j ≤ d₀, and β_j = 0 otherwise. Note that d₀ = |𝒩₁| represents the number of non-zero regression coefficients. In this example, we consider three different values of d₀ (d₀ = 10, 50, 100) to investigate the performance of the proposed test under sparse (i.e., d₀ = 10) and less sparse (i.e., d₀ = 50 and 100) scenarios. In addition, the average variance of ε_i (i.e., σ̄²) is chosen to generate a theoretical $R^2=var(X_i^{\top }\beta )/\{var(X_i^{\top }\beta )+{\overline{\sigma }}^2\}=0.5$. Moreover, the variance of ${\epsilon }_i({\sigma }_i^2)$ is independently generated from a uniform distribution with the lower and upper endpoints σ̄²/2 and 3 σ̄²/2, respectively. Accordingly, we generate the heteroscedastic linear regression model.

The results for d₀ = 10 are presented in Table 1. Since the results for d₀ = 50 and 100 yield a similar pattern to those in Table 1, we provide them in the supplementary material to save space. Table 1 shows that both CPS and MUR control the size well, while MUR has a larger power than CPS. After closely examining MUR’s performance, however, we find that its ES can be misleading. For example, X_i2 ∈ 𝒩₀ is moderately correlated with a nonzero predictor X_i1 ∈ 𝒩₁. As a result, the empirical size for testing H₀ : β₂ = 0 obtained from MUR could be as large as 0.90 in almost all realizations. On the other hand, most predictors in𝒩₀ are nearly independent of the predictors in 𝒩₁ and the response variable. Accordingly, MUR can have a reasonable average empirical size and a high average true rate (TR). This misleading result can be detected by the empirical false discovery rate (FDR) being much greater than the nominal level. In addition, the average false rate (FR) becomes larger as the sample size increases. Therefore, the MUR approach should be used with caution when testing a single coefficient, conducting multiple hypothesis tests, or selecting variables.

Table 1.

Simulation results for Example 1 with α = 5%, q = 5% and d₀ = 10.

p	n	Methods	ES	EP	FDR	TR	FR
1000	100	MUR	0.055	0.981	0.753	0.812	0.004
		LDPE	0.071	0.882	0.396	0.808	0.028
		CPS	0.056	0.495	0.127	0.451	0.000
	200	MUR	0.054	1.000	0.726	1.000	0.007
		LDPE	0.059	0.980	0.354	0.901	0.014
		CPS	0.053	0.792	0.073	0.762	0.000
	500	MUR	0.054	1.000	0.691	1.000	0.011
		LDPE	0.055	1.000	0.201	1.000	0.006
		CPS	0.053	0.982	0.053	0.958	0.000
2000	100	MUR	0.057	0.884	0.717	0.731	0.014
		LDPE	0.078	0.731	0.429	0.690	0.035
		CPS	0.055	0.442	0.128	0.362	0.000
	200	MUR	0.053	1.000	0.793	0.951	0.020
		LDPE	0.059	0.941	0.390	0.892	0.009
		CPS	0.053	0.712	0.078	0.668	0.000
	500	MUR	0.052	1.000	0.826	1.000	0.023
		LDPE	0.055	1.000	0.229	1.000	0.006
		CPS	0.052	0.979	0.056	0.971	0.000

We next study the performance of LDPE. Table 1 indicates that, although LDPE can control the size well at a reasonable level, it fails to control the FDR at the nominal level, particularly in small samples. For instance, when the sample size n = 100, the FDR values are 0.396 and 0.429 for p = 1000 and p = 2000, respectively. In contrast to MUR and LDPE, the CPS approach not only controls the size well, but also leads to FDR converging to the nominal level as the sample size increases. Furthermore, the average TR increases towards 1 and the average FR decreases to 0, both of which are consistent with theoretical findings.

In addition to d₀ = 10, the results for d₀ = 50 and 100 in Tables S1 and S2 of the supplementary material indicate that CPS is still superior to MUR and LDPE under the less sparse scenario. It is of interest to note that LDPE does not control the size well under less sparse regression models. This finding is not surprising since LDPE depends heavily on the accuracy of estimating the whole vector β. In sum, CPS performs well for testing a single coefficient, and the resulting p-values are reliable for multiple hypothesis tests and model selection.

Example 2: Moving average predictors

In this example, we generate data from a linear regression model with predictors following the moving average model with order 1: X_i = u_i + 0.5u_i−1 for i = 2, …, n and X₁ = u₁, where u_i are independently generated from a multivariate normal distribution with mean 0 and covariance 0.8I_p for i = 1, …, n. Accordingly, the covariance matrix of X_i can be written as Σ = (σ_j1j2) ∈ ℝ^p×p with σ_j1j2 = 1 if j₁ = j₂, σ_j1j2 = 0.4 if |j₁ − j₂| = 1, and σ_j1j2 = 0 otherwise. The regression coefficients β, the number of non-zero coefficients d₀, and the variance of ${\epsilon }_i({\sigma }_i^2)$, are the same as those in Example 1.

Table 2 reports the results for d₀ = 10, and similar findings for d₀ = 50 and 100 can be found in Tables S3 and S4, respectively, of the supplementary material. Table 2 shows that both CPS and MUR control the size well. However, MUR fails to control FDR at the nominal level. In fact, its FDR is much greater than the nominal level. In addition, its average false rate (FR) becomes larger as the sample size increases. We next study the performance of LDPE. Table 2 indicates that LDPE fails to control the FDR at the nominal level, particularly in small samples, although it can control the size well at a reasonable level. In addition, LDPE fails to control the size well for less sparse regression models (see Tables S3 and S4 for d₀ = 50 and 100, respectively, in the supplementary material). This finding is not surprising since LDPE depends heavily on the accuracy of estimating the whole vector β. In contrast to MUR and LDPE, the resulting p-values obtained by CPS are reliable for multiple hypothesis tests and model selections. Furthermore, CPS performs well even under less sparse models (see Tables S3 and S4 in the supplementary material), and this nice property is not enjoyed by MUR and LDPE.

Table 2.

Simulation results for Example 2 with α = 5%, q = 5% and d₀ = 10.

p	n	Methods	ES	EP	FDR	TR	FR
1000	100	MUR	0.054	0.929	0.289	0.787	0.005
		LDPE	0.070	0.793	0.179	0.765	0.021
		CPS	0.057	0.386	0.120	0.398	0.000
	200	MUR	0.053	1.000	0.236	1.000	0.009
		LDPE	0.061	0.998	0.147	1.000	0.015
		CPS	0.053	0.947	0.068	0.952	0.000
	500	MUR	0.052	1.000	0.186	1.000	0.011
		LDPE	0.054	1.000	0.098	1.000	0.002
		CPS	0.051	1.000	0.051	1.000	0.000
2000	100	MUR	0.054	0.882	0.282	0.716	0.009
		LDPE	0.074	0.737	0.169	0.724	0.027
		CPS	0.058	0.329	0.126	0.325	0.000
	200	MUR	0.053	1.000	0.229	1.000	0.012
		LDPE	0.060	0.968	0.128	0.954	0.015
		CPS	0.054	0.874	0.071	0.901	0.000
	500	MUR	0.051	1.000	0.156	1.000	0.015
		LDPE	0.056	1.000	0.093	1.000	0.006
		CPS	0.051	1.000	0.055	1.000	0.000

Example 3: Equally correlated predictors

Consider a model with equally correlated predictors, X_i, generated from a multivariate normal distribution with mean 0 and a compound symmetric covariance matrix Σ = (σ_j1j2) ∈ ℝ^p×p, where σ_j1j2 = 1 if j₁ = j₂ and σ_j1j2 = 0.5 for any j₁ ≠ j₂. In addition, the regression coefficients are set as follows: β_j = 5 for 1 ≤ j ≤ d₀, and β_j = 0 for j > d₀. The number of non-zero regression coefficients d₀ and the variance of ${\epsilon }_i({\sigma }_i^2)$ are the same as those in Example 1.

To save space, we only present the results for d₀ = 10 in Table 3, and the results for d₀ = 50 and 100 are in Tables S5 and S6, respectively, of the supplementary material. Table 3 indicates that MUR performs poorly in terms of both ES and FDR measures. This finding is not surprising because every predictor in 𝒩₀ is equally correlated with those predictors in 𝒩₁. As a result, the marginal correlation between any predictor in 𝒩₀ and the response variable is bounded well away from 0. Thus, MUR’s empirical rejection probability is close to 100%, which leads to highly inflated ES and FDR. Furthermore, FR equals 1 at all sample sizes, which implies that MUR tends to over reject the null hypothesis. Moreover, the results of LDPE are similar to those in Tables 1–2. On the other hand, the ES and FDR of CPS are close to the nominal level, except for the case of CPS with n = 100. Moreover, TR and EP increase towards 1 as the sample size gets large, and FR equals 0 at all sample sizes.

Table 3.

Simulation results for Example 3 with α = 5%, q = 5% and d₀ = 10.

p	n	Test	ES	EP	FDR	TR	FR
1000	100	MUR	1.000	1.000	0.997	1.000	1.000
		LDPE	0.054	0.528	0.349	0.477	0.009
		CPS	0.058	0.449	0.141	0.418	0.000
	200	MUR	1.000	1.000	0.998	1.000	1.000
		LDPE	0.054	0.832	0.207	0.719	0.005
		CPS	0.049	0.747	0.051	0.701	0.000
	500	MUR	1.000	1.000	0.998	1.000	1.000
		LDPE	0.051	1.000	0.162	0.981	0.004
		CPS	0.049	0.987	0.048	0.965	0.000
2000	100	MUR	1.000	1.000	0.996	1.000	1.000
		LDPE	0.050	0.465	0.402	0.428	0.008
		CPS	0.055	0.398	0.138	0.366	0.000
	200	MUR	1.000	1.000	0.997	1.000	1.000
		LDPE	0.049	0.776	0.232	0.713	0.005
		CPS	0.051	0.689	0.055	0.664	0.000
	500	MUR	1.000	1.000	0.995	1.000	1.000
		LDPE	0.050	1.000	0.144	0.962	0.002
		CPS	0.050	0.937	0.050	0.915	0.000

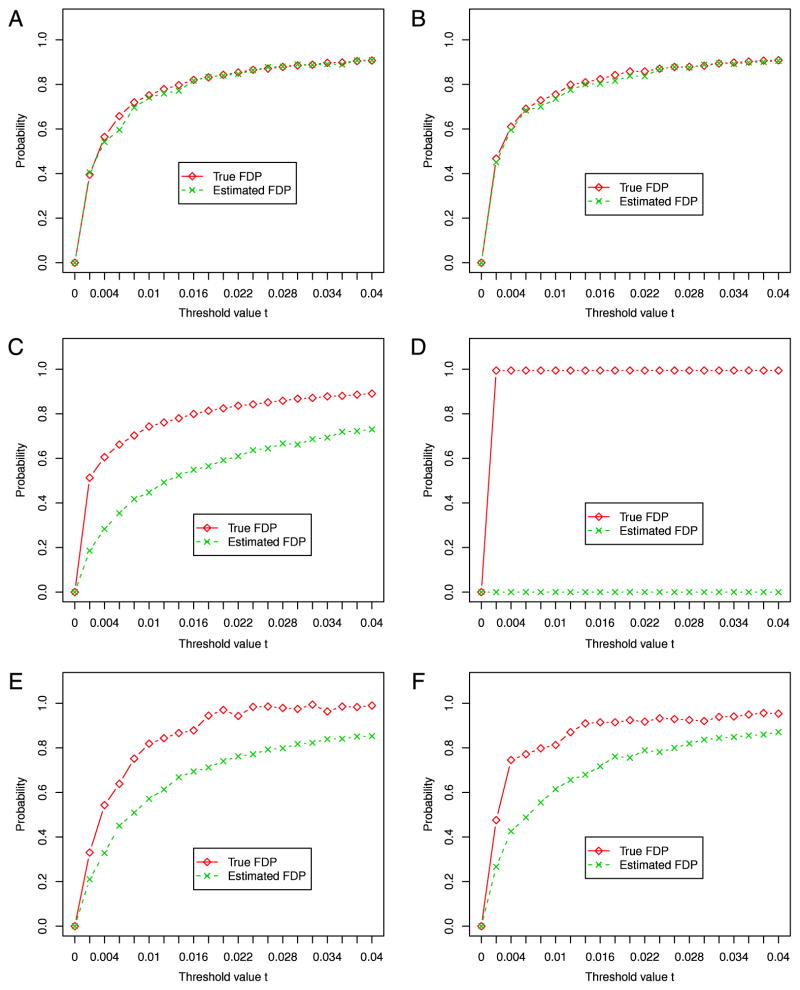
From the above simulation studies, we find that FDR plays an important role for examining the reliability of test statistics. Hence, we next study the accuracy for the estimation of FDR discussed in Section 2.3. Since we are interested in the statistical behavior of the number of false discoveries V(t), we follow Fan et al.’s (2012) suggestion and compare $\widehat{{\text{FDR}}_{\lambda }}(t)$ in (2.6), with λ = 1/2, to FDP(t) calculated via V(t)/[R(t) ∨ 1]. For the sake of illustration, we consider the same simulation settings as given in Examples 1 and 3 with n = 100, p = 1000 and d₀ = 10. Panels A and B in Fig. 1 depict $\widehat{{\text{FDR}}_{\lambda }}(t)$ and FDP(t), obtained via the CPS method for Examples 1 and 3, respectively, across various t values. In contrast, Panels C and D are calculated via the MUR approach and Panels E and F are calculated via the LDPE method. Fig. 1 clearly shows that $\widehat{{\text{FDR}}_{\lambda }}(t)$ calculated from the p-values of CPS is reliable and consistent with the theoretical finding in Theorem 2. However, MUR and LDPE do not provide accurate estimates of FDP, and they should be used with caution in high dimensional data analysis.

Fig. 1.

Panels A and B depict the estimated FDP value (i.e., $\widehat{{\text{FDR}}_{0.5}}(t)$) compared with the true FDP value obtained via the CPS method for Examples 1 and 3, respectively. Panels C and D are obtained via the MUR approach, and Panels E and F are obtained via the LDPE method.

The above three examples have demonstrated that CPS performs well across three commonly used covariance structures. It is worth noting that Conditions (C4) and (C5) hold in the first two examples, while these conditions are invalid in the third example. However, CPS still performs well in Example 3, which shows its robustness. Motivated by an anonymous referee’s comments, we present an additional study with the covariance structure Σ = I_p+uu^⊤, where u = (u₁, …, u_p)^⊤ ∈ ℝ^p, u_j = δj⁻² for j = 1, …, p, and δ is a finite constant. Accordingly, cov(X_i1, X_ij) = (δ/j)² so that covariates exhibit polynomial decay and ρ_1j = (δ/j)²/{(1+δ²)(1+ δ²/j⁴)}^0.5. Hence, there are quite a number of predictors that are highly correlated with X_i1 when δ is large enough. One can also verify that max_j∉∈𝒮 |ϱ_1j(𝒮)| = O(|𝒮|⁻²) as |𝒮| → ∞, and then both Conditions (C4) and (C5) hold. Our simulation results indicate that CPS performs well; see Table S7 in the supplementary material.

Example 4: Robustness of covariate distribution and λ parameter

In the first three examples, the covariate vector X_is were generated from a multivariate normal distribution and the tuning parameter λ was set to be 1/2. To assess the robustness of CPS against the covariate distribution and λ, we conduct simulation studies for various λs and three distributions of X_i = Σ^1/2Z_i, where each element of Z_i is randomly generated from the standard normal distribution, the standardized exponential distribution exp(1), and the normal mixture distribution 0.1N(0, 3²) + 0.9N(0, 1), respectively, for i = 1, …, n, and the Σs are correspondingly defined in Examples 1–3. Since all results are qualitatively similar, we only report the case when λ = 0.1, d₀ = |𝒩₁| = 10 and Z_i follows a standardized exponential distribution. The results in Tables 4–6 show similar findings to those in Tables 1–3, respectively. Hence, Monte Carlo studies indicate that the CPS approach is robust against the covariate distribution and the threshold parameter λ.

Table 4.

Simulation results for Example 4 with α = 5%, q = 5%, d₀ = 10, Σ as given in Example 1, λ = 0.1, and X_is being generated from a standardized exponential distribution.

p	n	Methods	ES	EP	FDR	TR	FR
1000	100	MUR	0.055	0.962	0.728	0.833	0.008
		LDPE	0.068	0.881	0.407	0.816	0.021
		CPS	0.057	0.518	0.129	0.492	0.000
	200	MUR	0.055	1.000	0.721	0.975	0.012
		LDPE	0.058	0.995	0.349	0.912	0.014
		CPS	0.052	0.775	0.067	0.744	0.000
	500	MUR	0.052	1.000	0.722	1.000	0.016
		LDPE	0.055	1.000	0.174	1.000	0.006
		CPS	0.052	0.991	0.053	0.971	0.000
2000	100	MUR	0.056	0.882	0.723	0.711	0.015
		LDPE	0.069	0.731	0.441	0.704	0.022
		CPS	0.058	0.449	0.130	0.401	0.000
	200	MUR	0.056	1.000	0.744	0.922	0.018
		LDPE	0.063	0.943	0.386	0.915	0.016
		CPS	0.054	0.738	0.076	0.703	0.000
	500	MUR	0.052	1.000	0.782	1.000	0.022
		LDPE	0.053	1.000	0.196	1.000	0.005
		CPS	0.053	0.988	0.057	0.981	0.000

Table 6.

Simulation results for Example 4 with α = 5%, q = 5%, d₀ = 10, Σ as given in Example 3, λ = 0.1, and X_is being generated from a standardized exponential distribution.

p	n	Test	ES	EP	FDR	TR	FR
1000	100	MUR	1.000	1.000	0.998	1.000	1.000
		LDPE	0.054	0.521	0.374	0.496	0.005
		CPS	0.059	0.449	0.126	0.433	0.000
	200	MUR	1.000	1.000	0.998	1.000	1.000
		LDPE	0.054	0.832	0.211	0.743	0.002
		CPS	0.049	0.743	0.052	0.683	0.000
	500	MUR	1.000	1.000	0.998	1.000	1.000
		LDPE	0.050	1.000	0.127	0.982	0.001
		CPS	0.049	0.982	0.051	0.970	0.000
2000	100	MUR	1.000	1.000	0.996	1.000	1.000
		LDPE	0.052	0.471	0.412	0.451	0.012
		CPS	0.054	0.429	0.143	0.352	0.000
	200	MUR	1.000	1.000	0.996	1.000	1.000
		LDPE	0.052	0.772	0.217	0.717	0.005
		CPS	0.051	0.712	0.058	0.686	0.000
	500	MUR	1.000	1.000	0.997	1.000	1.000
		LDPE	0.050	1.000	0.143	0.981	0.002
		CPS	0.052	0.952	0.050	0.937	0.000

4. Real data analysis

To illustrate the usefulness of the proposed method, we consider two empirical examples. The first example analyzes financial data and the second example studies supermarket data.

4.1. Index fund data

The data set consists of a total of n = 155 observations, in which the response Y_i is the weekly return of the Shanghai composite index. Explanatory variables X_i are p = 382 stock returns that traded on the Shanghai stock exchange during the period from Oct. 9, 2010 to Sep. 28, 2013, with i = 1, …, 155. We assume that there is a linear relationship between Y_i and X_i, which is $Y_i=X_i^{\top }\beta +{\epsilon }_i$, as given in Eq. (2.1). In addition, both the response and predictors are standardized so that they have zero mean and unit variance. The task of this study is identifying a small number of relevant stocks that financial managers can use to establish a portfolio that tracks the return of the Shanghai composite index.

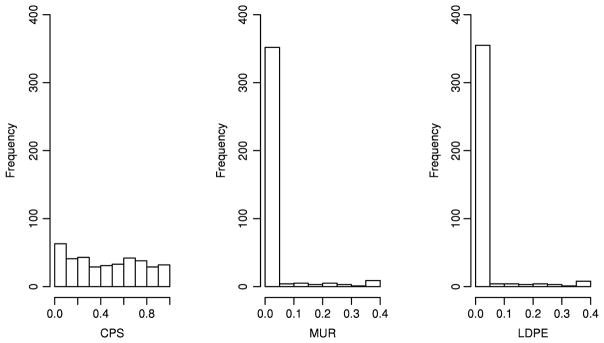
To identify important stocks (predictors) that are associated with Y_i, we employ the CPS, MUR, and LDPE methods and test the significance of each individual regression coefficient, namely, testing H_0j : β_j = 0 vs. H_1j : β_j ≠ 0 for j = 1, …, 382. Here, the tuning parameter of the LDPE method is set to {2 log p/n}^1/2, as suggested by Zhang and Zhang (2014). Since the asymptotic distribution of the p-values obtained from the above test statistics is uniform [0, 1], we use the histogram to effectively illustrate their performances. Fig. 2 depicts the histograms of the p-values for testing H_0j (j = 1, …, 382) via three tests. Based on the CPS test, we find 32 p-values that are less than the significance level α = 5%. After controlling the false discoveries rate via the method of Storey et al. (2004) at the level of q = 5%, the number of hypotheses H_0j being rejected is 12. As a result, we have identified the 12 most important stocks that can be used for index tracking.

Fig. 2.

Index fund data. The histograms of the p-values for the CPS, MUR, and LDPE tests.

In contrast, the histogram of the p-values calculated from the MUR tests is heavily skewed with very thin tails. This suggests that most of its p-values are very small. Consequently, it rejected a total of 161 hypotheses H_0j after controlling the FDR at the level of q = 5%. This finding is not surprising since the covariates in the model are highly correlated due to the existence of latent factors, as observed by Fama and French (1993). Analogous results can be found in the histogram of the p-values generated from LDPE. In sum, CPS is able to identify the most relevant stocks from high dimensional data, while MUR and LDPE cannot.

4.2. Supermarket data

This data set contains a total of n = 464 daily records. For each record, the response variable (Y_i) is the number of customers and the predictors (X_i1, …, X_ip) are the sales volumes of p = 6398 products. Consider a linear relationship between Y_i and X_i = (X_i1, …, X_ip)^⊤ ∈ ℝ^p, given by $Y_i=X_i^{\top }\beta +{\epsilon }_i$, where both the response and predictors are standardized so that they have zero mean and unit variance. The purpose of this study is to determine a small number of products that attract the most customers.

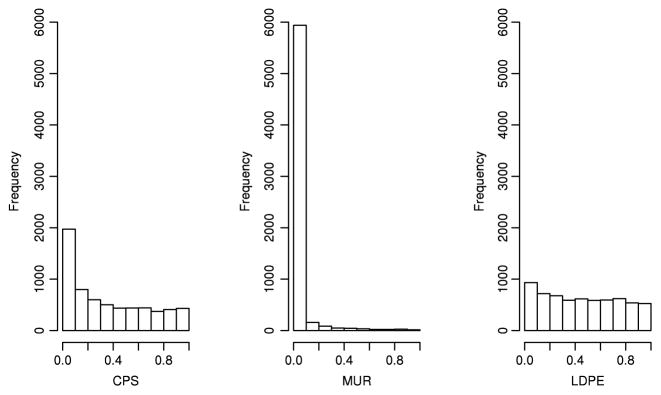
We apply the proposed CPS, MUR, and LDPE methods to test the significance of each regression coefficient, namely H_0j : β_j = 0 vs. H_1j: β_j ≠ 0. Fig. 3 depicts the three histograms of the p-values computed via the CPS, MUR, and LDPE methods, respectively. As one can observe from the histogram, for the CPS method, the pattern indicates that most of the H_0j are true and the p-values are asymptotically valid. There were 1426 p-values that are less than the significance level α = 5%. After controlling the false discoveries rate via the method of Storey et al. (2004) at the level of q = 5%, the number of hypotheses H_0j being rejected is 132. In other words, we have identified 132 most important products on which the supermarket decision maker (or manager) might perform further analysis. In contrast, for the MUR method, the histogram of the p-values are extremely skewed with very thin tails. It rejected a total of 5648 hypotheses H_0j after controlling the FDR at the level of q = 5%. In addition, the histogram of the p-values generated from the LDPE tests in Fig. 3 shows a flat pattern within the entire interval [0, 1]. As a result, it is not surprising to find that there were a total of 535 p-values that are less than the significance level α = 5%, while none of them were significant after controlling the false discoveries rate at the level of q = 5%.

Fig. 3.

Supermarket data. The histograms of the p-values for the CPS, MUR, and LDPE tests.

The above two above examples indicate that the CPS method not only practically provides a simple and efficient approach to compute the p-value for testing a single coefficient in a high dimensional linear model, but also results in reliable p-values for multiple hypothesis testing.

5. Discussion

In linear regression models with high dimensional data, we propose a single screening procedure, Correlated Predictors Screening (CPS), to control for predictors that are highly correlated with the target covariate. This allows us to employ the classical ordinary least squares approach to obtain the parameter estimator. We then demonstrate that the resulting estimator is asymptotically normal. Accordingly, we extend the classical t-test (or z-test) for testing a single coefficient to the high dimensional setting. Based on the p-value obtained from testing the significance of each covariate, the multiple hypothesis testing is established by controlling the false discovery rate at the nominal level. In addition, we show that multiple hypothesis test leads to consistent model selection. Accordingly, the main focus of this paper is on statistical inference rather than variable selection and parameter estimation, which are often the aims of regularization methods such as LASSO (Tibshirani, 1996) and SCAD (Fan and Li, 2001).

The proposed CPS method can be extended for testing a small subset of regression coefficients. Consider the hypothesis:

$$H_0:{\beta }_{\mathcal{M}}=0\text{vs.}{H}_1:{\beta }_{\mathcal{M}}\ne 0,$$ (5.1)

where ℳ is a pre-specified index set with a fixed size and β_ℳ = (β_j: j ∈ ℳ)^⊤ ∈ ℝ^|ℳ| is the subvector of β corresponding to ℳ. Without loss of generality, we assume that ℳ = {j: 1 ≤ j ≤ |ℳ|} and 1 < |ℳ| ≪ n. Then, define an overall CPS set of ℳ as 𝒮_ℳ = ⋃_j∈ℳ 𝒮_j, where 𝒮_j is the CPS set for the jth predictor in ℳ. Accordingly, the target parameter estimator β_ℳ = (β_j: j ∈ ℳ) ^⊤ ∈ ℝ^|ℳ| can be estimated by ${\widehat{\beta }}_{\mathcal{M}}={({\mathbb{X}}_{\mathcal{M}}^{\top }{\mathcal{Q}}_{{\mathcal{S}}_{\mathcal{M}}}{\mathbb{X}}_{\mathcal{M}})}^{-1}({\mathbb{X}}_{\mathcal{M}}^{\top }{\mathcal{Q}}_{{\mathcal{S}}_{\mathcal{M}}}\mathbb{Y})$, where 𝕏_ℳ = (𝕏_j: j ∈ ℳ) ∈ ℝ^n×|ℳ|. Applying similar techniques to those used in the proof of Theorem 1, we can show that n^1/2(β̂_ℳ −β_ℳ)→_d N(0,Σ_β), where ${\mathit{\sum }}_{\beta }={\sigma }_{\mathcal{M}}^2{({\mathit{\sum }}_{\mathcal{M}}-{\mathit{\sum }}_{\mathcal{S},\mathcal{M}}^{\top }{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}\mathcal{M}})}^{-1}$ with ${\sigma }_{\mathcal{M}}^2={\beta }_{{\mathcal{S}}_{\mathcal{M}}^{\ast }}^T({\mathit{\sum }}_{{\mathcal{S}}_{\mathcal{M}}^{\ast }}-{\mathit{\sum }}_{{\mathcal{S}}_{\mathcal{M}}^{\ast }{\mathcal{S}}_{\mathcal{M}}^{+}}{\mathit{\sum }}_{{\mathcal{S}}_{\mathcal{M}}^{+}}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{\mathcal{M}}^{+}{\mathcal{S}}_{\mathcal{M}}^{\ast }}){\beta }_{{\mathcal{S}}_{\mathcal{M}}^{\ast }}+{\overline{\sigma }}^2,{\mathcal{S}}_{\mathcal{M}}^{+}={\cup }_{j\in \mathcal{M}}{\mathcal{S}}_j^{+}$ and ${\mathcal{S}}_{\mathcal{M}}^{\ast }=\{j:j\notin {\mathcal{S}}_{\mathcal{M}}^{+}\}$. Consequently, an F-type test statistic can be constructed to test (5.1).

To broaden the usefulness of the proposed method, we conclude the article by discussing three possible research avenues. Firstly, from the model aspect, it would be practically useful to extend the CPS method to generalized linear models, single index models, partial linear models, and survival models. Secondly, from the data aspect, it is important to generalize the proposed CPS method to accommodate category explanatory variables, repeated measurements, and missing observations. Lastly, to control the FDR at the nominal level, we have imposed a weak dependence assumption in Theorem 2. Hence, it would be useful to employ the method of Fan et al. (2012) to adjust for the arbitrary covariance dependence among test statistics Z_j. We believe these extensions would enhance the usefulness of CPS in high dimensional data analysis.

Table 5.

Simulation results for Example 4 with α = 5%, q = 5%, d₀ = 10, Σ as given in Example 2, λ = 0.1, and X_is being generated from a standardized exponential distribution.

p	n	Test	ES	EP	FDR	TR	FR
1000	100	MUR	0.055	0.938	0.296	0.792	0.009
		LDPE	0.071	0.802	0.185	0.772	0.022
		CPS	0.056	0.404	0.132	0.401	0.000
	200	MUR	0.055	1.000	0.228	1.000	0.012
		LDPE	0.064	1.000	0.152	1.000	0.013
		CPS	0.052	0.943	0.070	0.947	0.000
	500	MUR	0.053	1.000	0.190	1.000	0.017
		LDPE	0.054	1.000	0.103	1.000	0.004
		CPS	0.052	1.000	0.052	1.000	0.000
2000	100	MUR	0.053	0.891	0.290	0.725	0.009
		LDPE	0.072	0.744	0.181	0.731	0.030
		CPS	0.059	0.352	0.133	0.332	0.000
	200	MUR	0.053	1.000	0.242	1.000	0.013
		LDPE	0.059	0.977	0.153	0.973	0.018
		CPS	0.054	0.853	0.069	0.911	0.000
	500	MUR	0.054	1.000	0.134	1.000	0.015
		LDPE	0.053	1.000	0.097	1.000	0.009
		CPS	0.052	1.000	0.058	1.000	0.000

Appendix A. Four useful lemmas

Before proving the theoretical results, we present the following four lemmas which are needed in the proofs. The first lemma is directly borrowed from Lemma A.3 of Bickel and Levina (2008), and the second lemma can be found in Bendat and Piersol (1966). As a result, we only verify the third and fourth lemmas.

Lemma 1

Let σ̂_j1j2 = n⁻¹Σ_i X_ij1X_ij2 and ρ̂_j1j2 = σ̂_j1j2/{σ̂_j1j1 σ̂_j2j2}^1/2, and assume that Condition (C1) holds. Then, there exist three positive constants ζ₀ > 0, C₁ > 0, and C₂ > 0, such that (i) P(|σ̂_j1j2 − σ_j1j2| > ζ) ≤ C₁ exp(−C₂nζ²) and (ii) P(|ρ̂_j1j2 − ρ̂_j1j2 | > ζ) ≤ C₁ exp(−C₂nζ²) for any 0 < ζ < ζ₀ and every 1 ≤ j₁, j₂ ≤ p.

Lemma 2

Let (U₁, U₂, U₃, U₄)^⊤ ∈ ℝ⁴ be a 4-dimensional normal random vector with E(U_j) = 0 and var(U_j) = 1 for 1 ≤ j ≤ 4. We then have E(U₁U₂U₃U₄) = δ₁₂δ₃₄ + δ₁₃δ₂₄ + δ₁₄δ₂₃, where δ_ij = E(U_iU_j).

Lemma 3

Assume that Conditions (C1)–(C3) hold, and m = O(n^ν₂) for some positive constant ν₂ which satisfies 3ν₂ + ħ < 1, where ħ is given in (C3). Then, ${max}_{\mid \mathcal{S}\mid \le m}\mid n^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1-({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})\mid {\to }_{p}0$.

Proof

Since $n^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1=n^{-1}{\mathbb{X}}_1^{\top }{\mathbb{X}}_1-(n^{-1}{\mathbb{X}}_1^{\top }{\mathbb{X}}_{\mathcal{S}}){(n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_{\mathcal{S}})}^{-1}(n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_1)$ and $n^{-1}{\mathbb{X}}_1^{\top }{\mathbb{X}}_1{\to }_p{\sigma }_{11}$, it suffices to show that

$$\underset{\mid \mathcal{S}\mid \le m}{max}\left|(n^{-1}{\mathbb{X}}_1^{\top }{\mathbb{X}}_{\mathcal{S}}){(n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_{\mathcal{S}})}^{-1}(n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_1)-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1}\right|{\to }_{p}0.$$ (A.1)

Denote ||A|| = {tr(AA^⊤)}^1/2 for any arbitrary matrix A. Since ${\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1}$ is the conditional variance of X₁ given X_𝒮, ${\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1}\ge 0$. Then by Condition (C2), we have ${\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1}\le {\sigma }_{11}\le c_{max}<\infty$. Then, we obtain (A.1) if the following two uniform convergence results hold:

$$\underset{\mid \mathcal{S}\mid \le m}{max}\Vert n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_1-{\mathit{\sum }}_{\mathcal{S}1}\Vert =o_p(1),$$ (A.2)

$$\text{and}\underset{\mid \mathcal{S}\mid \le m}{max}\Vert n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_{\mathcal{S}}-{\mathit{\sum }}_{\mathcal{S}}\Vert =o_p(1).$$ (A.3)

Accordingly, it suffices to demonstrate (A.2) and (A.3).

It is noteworthy that, for any 𝒮 satisfying |𝒮| ≤ m, we have

$$\begin{array}{l}\Vert n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_1-{\mathit{\sum }}_{\mathcal{S}1}\Vert ={\left\{\sum _{j\in \mathcal{S}}{({\widehat{\sigma }}_{1j}-{\sigma }_{1j})}^2\right\}}^{1/2}\\ \le m^{1/2}\underset{j\in \mathcal{S}}{max}\mid {\widehat{\sigma }}_{1j}-{\sigma }_{1j}\mid .\end{array}$$

This, together with the Bonferroni inequality, Condition (C1), Lemma 1(i), and the fact that #{𝒮 ⊂ {1, …, p}: |𝒮| ≤ m} ≤ p^m, implies

$$\begin{array}{l}P\left(\underset{\mid \mathcal{S}\mid \le m}{max}\Vert n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_1-{\mathit{\sum }}_{\mathcal{S}1}\Vert >\epsilon \right)\le \sum _{\mid \mathcal{S}\mid \le m}P\left(\Vert n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_1-{\mathit{\sum }}_{\mathcal{S}1}\Vert >\epsilon \right)\\ \le \sum _{\mid \mathcal{S}\mid \le m}P\left(\underset{j\in \mathcal{S}}{max}\mid {\widehat{\sigma }}_{1j}-{\sigma }_{1j}\mid >\epsilon /m^{1/2}\right)\\ \le \sum _{\mid \mathcal{S}\mid \le m}\sum _{j\in \mathcal{S}}P\left(\mid {\widehat{\sigma }}_{1j}-{\sigma }_{1j}\mid >\epsilon /m^{1/2}\right)\\ \le p^{m}m{C}_{1}exp(-C_{2}n{m}^{-1}{\epsilon }^2)\\ =C_{1}exp\left(-C_{2}n{m}^{-1}{\epsilon }^2+logm+\mathit{m}logp\right).\end{array}$$ (A.4)

Furthermore, by the assumptions in Lemma 3 (m = O(n^ν₂)) and Condition (C3) (log p ≤ νn^ħ), we have that m log p = O(n^ν₂+ħ). Moreover, using the assumptions in Lemma 3 again (3ν₂ + ħ < 1), the right-hand side of (A.4) converges towards 0 as n → ∞. Hence, we have proved (A.2). Applying similar techniques to those used in the proof of (A.2), we can also demonstrate (A.3). This completes the entire proof.

Lemma 4

Assume that (a) lim_p→∞ V(t)/p₀ = G₀(t) and lim_p→∞ S(t)/(p − p₀) = G₁(t), where G₀(t) and G₁(t) are continuous functions; (b) 0 < G₀(t) ≤ t for t ∈ (0, 1]; (c) lim_p→∞ p₀/p = 1. Then, we have $lim{sup}_{p\to \infty }\text{FDR}\{t_{\alpha }({\widehat{\text{FDR}}}_{\lambda })\}\le \alpha$.

Proof

By slightly modifying the proof of Theorem 4 in Storey et al. (2004), we can demonstrate the result. The detailed proof can be obtained from the authors upon request.

Appendix B. Proof of Theorem 1

Let $T_1={({\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}\mathcal{E}$ and $T_2={({\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_{{\mathcal{S}}^{\ast }}{\beta }_{{\mathcal{S}}^{\ast }}$. Then, β̂₁ − β₁ = T₁ + T₂. Using the fact that E(ε_i|X_i) = 0, one can show that cov(T₁, T₂) = E(T₁T₂) − E(T₁)E(T₂) = 0. Therefore, T₁ and T₂ are uncorrelated. To prove the theorem, hence, it suffices to show that ${(\sqrt{n}{T}_1,\sqrt{n}{T}_2)}^{\top }$ is asymptotically bivariate normal. By Conditions (C1)–(C3) and Lemma 2, we obtain that $\Vert n^{-1}{\mathbb{X}}_1^{\top }{\mathbb{X}}_{\mathcal{S}}-{\mathit{\sum }}_{1\mathcal{S}}\Vert {\to }_{p}0,\Vert n^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }{\mathbb{X}}_{\mathcal{S}}-{\mathit{\sum }}_{\mathcal{S}}\Vert {\to }_{p}0$, and ${max}_{\mathcal{S}}\mid n^{-1}{\mathbb{X}}_1^{\top }{\mathcal{Q}}_{\mathcal{S}}{\mathbb{X}}_1-({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})\mid {\to }_{p}0$. Accordingly, we have

$$\begin{array}{l}\sqrt{n}{T}_1=\{1+o_p(1)\}{({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})}^{-1}\times (n^{-1/2}{\mathbb{X}}_1^{\top }\mathcal{E}-n^{-1/2}{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathbb{X}}_{\mathcal{S}}^{\top }\mathcal{E})\\ =\{1+o_p(1)\}{({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})}^{-1}\times \left\{n^{-1/2}\sum _{i=1}^n(X_{i1}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{X}_{i\mathcal{S}}){\epsilon }_i\right\}.\end{array}$$

Applying the same arguments as those given above, we also obtain that

$$\sqrt{n}{T}_2=\{1+o_p(1)\}{({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})}^{-1}\times \left\{n^{-1/2}\sum _{i=1}^n(X_{i1}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{X}_{i\mathcal{S}})X_{i{\mathcal{S}}^{\ast }}{\beta }_{{\mathcal{S}}^{\ast }}\right\}.$$

Let ${\xi }_{i1}=(X_{i1}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{X}_{i\mathcal{S}}){\epsilon }_i$ and ${\delta }_{i1}=(X_{i1}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{X}_{i\mathcal{S}})X_{i{\mathcal{S}}^{\ast }}{\beta }_{{\mathcal{S}}^{\ast }}$. Then, it can be shown that E(ξ_i1) = 0, $var({\xi }_{i1})={\sigma }_i^2({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})$, and $E({\delta }_{i1})=({\mathit{\sum }}_{1{\mathcal{S}}^{\ast }}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}{\mathcal{S}}^{\ast }}){\beta }_{{\mathcal{S}}^{\ast }}$. Using Conditions (C4)–(C6), we further obtain that $\sqrt{n}\mid ({\mathit{\sum }}_{1{\mathcal{S}}^{\ast }}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}{\mathcal{S}}^{\ast }}){\beta }_{{\mathcal{S}}^{\ast }}\mid <C_{max}\times n^{1/2+\varpi }{max}_{j\notin {\mathcal{S}}^{+}}\mid {\mathrm{\varrho }}_{1j}(\mathcal{S})\mid \to 0$. Moreover,

$$\begin{array}{l}var({\delta }_{i1})\to E({\delta }_{i1}^2)=E\left\{{(X_{i1}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{X}_{i\mathcal{S}})}^2{\beta }_{{\mathcal{S}}^{\ast }}^{\top }{X}_{i{\mathcal{S}}^{\ast }}{X}_{i{\mathcal{S}}^{\ast }}^{\top }{\beta }_{{\mathcal{S}}^{\ast }}\right\}\\ =E\left[{(X_{i1}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{X}_{i\mathcal{S}})}^2{\beta }_{{\mathcal{S}}^{\ast }}^{\top }E\left\{X_{i{\mathcal{S}}^{\ast }}{X}_{i{\mathcal{S}}^{\ast }}^{\top }\mid X_{i{\mathcal{S}}^{+}}\right\}{\beta }_{{\mathcal{S}}^{\ast }}\right]\\ \to \left({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1}\right){\beta }_{{\mathcal{S}}^{\ast }}^{\top }\left({\mathit{\sum }}_{{\mathcal{S}}^{\ast }}-{\mathit{\sum }}_{{\mathcal{S}}^{\ast }{\mathcal{S}}^{+}}{\mathit{\sum }}_{{\mathcal{S}}^{+}}^{-1}{\mathit{\sum }}_{{\mathcal{S}}^{+}{\mathcal{S}}^{\ast }}\right){\beta }_{{\mathcal{S}}^{\ast }}.\end{array}$$

The bivariate Central Limit Theorem, together with the above results, implies that

$${\left(\sqrt{n}{T}_1,\sqrt{n}{T}_2\right)}^{\top }=\left(1+o_p(1)\right){\left({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1}\right)}^{-1}\times \left\{n^{-1/2}\sum _{i=1}{({\xi }_{i1},{\delta }_{i1})}^{\top }\right\}$$

is asymptotically bivariate normal with mean zero and diagonal covariance matrix V = Diag(V_ii). In addition, $V_{11}={\overline{\sigma }}^2{({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})}^{-1}$ and $V_{22}={({\sigma }_{11}-{\mathit{\sum }}_{1\mathcal{S}}{\mathit{\sum }}_{\mathcal{S}}^{-1}{\mathit{\sum }}_{\mathcal{S}1})}^{-1}{\beta }_{{\mathcal{S}}^{\ast }}^{\top }({\mathit{\sum }}_{{\mathcal{S}}^{\ast }}-{\mathit{\sum }}_{{\mathcal{S}}^{\ast }{\mathcal{S}}^{+}}{\mathit{\sum }}_{{\mathcal{S}}^{+}}^{-1}{\mathit{\sum }}_{{\mathcal{S}}^{+}{\mathcal{S}}^{\ast }}){\beta }_{{\mathcal{S}}^{\ast }}$. Consequently, $\sqrt{n}(T_1+T_2)$ is asymptotically normal with mean zero and variance V₁₁ + V₂₂, which completes the proof.

Appendix C. Proof of Proposition 1

As defined in (2.3), 𝒮_k0 = {j₁, …, j_k0} contains the indices whose associated predictors have the k₀ largest absolute correlations with X_i1. For a given k̄, 𝒮̂_k̄ is defined as in (2.5). In addition, the event {𝒮̂_k̄ ⊅ 𝒮_k0} indicates that there exists at least one index, say j_i1 ∈ 𝒮_k0 (i₁ ≤ k₀), but j_i1 ∉ 𝒮̂_k̄. Then, for any k̄ satisfying k₀ + d_maxn^ν₂/2 < k̄ < k₀ + d_maxn^ν₂ with 1 ≤ k₀ ≤ C_bn^ν₂, we have {𝒮̂_k̄ ⊅ 𝒮_k0} ⊂ {There exist indices i₁ ≤ k₀ and i₂ > k̄ that satisfy |ρ̂_1ji2| > |ρ̂_1ji1|}. The reasoning is as follows. When j_i1 ∉ 𝒮̂_k̄, it implies that there exists some index, say j_i2 with i₂ > k̄, such that j_i2 ∈ 𝒮̂_k̄. Otherwise, all indices j_k in 𝒮̂_k̄ satisfy k ≤ k̄₀, which implies that 𝒮̂_k̄ = {j₁, …, j_k̄} contains 𝒮_k0 as a subset. This yields a contradiction. As a result, we have P(𝒮̂_k̄ ⊅ 𝒮_k0) ≤ P(There exist indices i₁ ≤ k₀ and i₂ > k̄ that satisfy |ρ̂_1ji2 | > |ρ̂_1ji1|). Thus,

$$\begin{array}{l}P\left({\widehat{\mathcal{S}}}_{\overline{k}}\supset {\mathcal{S}}_{k_0}\right)=1-P\left({\widehat{\mathcal{S}}}_{\overline{k}}\not\supset {\mathcal{S}}_{k_0}\right)\\ \ge 1-P(\text{There}\text{exist}\text{indices}{i}_1\le k_0\text{and}{i}_2>\overline{k}\text{that}\text{satisfy}\mid {\widehat{\rho }}_{1j_{i_2}}\mid >\mid {\widehat{\rho }}_{1j_{i_1}}\mid ).\end{array}$$

After simple calculation, we obtain that

$$\begin{array}{l}\mid {\widehat{\rho }}_{1j_{i_2}}\mid -\mid {\widehat{\rho }}_{1j_{i_1}}\mid =\mid {\rho }_{1j_{i_2}}\mid -\mid {\rho }_{1j_{i_1}}\mid +(\mid {\widehat{\rho }}_{1j_{i_2}}\mid -\mid {\rho }_{1j_{i_2}}\mid )-(\mid {\widehat{\rho }}_{1j_{i_1}}\mid -\mid {\rho }_{1j_{i_1}}\mid )\\ \le \mid {\rho }_{1j_{i_2}}\mid -\mid {\rho }_{1j_{i_1}}\mid +\mid {\widehat{\rho }}_{1j_{i_1}}-{\rho }_{1j_{i_1}}\mid +\mid {\widehat{\rho }}_{1j_{i_2}}-{\rho }_{1j_{i_2}}\mid \\ \le \mid {\rho }_{1j_{i_2}}\mid -\mid {\rho }_{1j_{i_1}}\mid +2\underset{j}{max}\mid {\widehat{\rho }}_{1j}-{\rho }_{1j}\mid .\end{array}$$

This, together with Lemma 1(ii) and the assumption in Proposition 1 that |ρ_1ji1| − |ρ_1ji2| > d_minn^−ν₂ for any i₂ − i₁ > d_maxn^ν₂/2, leads to

$$\begin{array}{l}P(\text{There}\text{exist}\text{indices}{i}_1<k_0\text{and}{i}_2>\overline{k}\text{that}\text{satisfy}\mid {\widehat{\rho }}_{1j_{i_2}}\mid >\mid {\widehat{\rho }}_{1j_{i_1}}\mid )\\ \le P(\text{There}\text{exist}\text{indices}{i}_1<k_0\text{and}{i}_2>\overline{k}\text{that}\text{satisfy}\mid {\rho }_{1j_{i_2}}\mid -\mid {\rho }_{1j_{i_1}}\mid +2\underset{j}{max}\mid {\widehat{\rho }}_{1j}-{\rho }_{1j}\mid >0)\\ \le P(\underset{j}{max}\mid {\widehat{\rho }}_{1j}-{\rho }_{1j}\mid >d_{min}{n}^{-{\nu }_2}/2)\\ \le pP(\mid {\widehat{\rho }}_{1j}-{\rho }_{1j}\mid >d_{min}{n}^{-{\nu }_2}/2)\\ \le C_{1}exp(-C_2{n}^{1-2{\nu }_2}{d}_{min}^2/4+logp).\end{array}$$

By Condition (C3), the negative sign of the first term on the right-hand side of the above equation, $C_2{n}^{1-2{\nu }_2}{d}_{min}^2/4$, dominates the second term log p. As a result,

$$P(\text{There}\text{exist}\text{indices}{i}_1<k_0\text{and}{i}_2>\overline{k}\text{that}\text{satisfy}\mid {\widehat{\rho }}_{1j_{i_2}}\mid >\mid {\widehat{\rho }}_{1j_{i_1}}\mid )\to 0,$$

which completes the proof.

Appendix D. Proof of Theorem 2

We mainly apply Lemma 4 to prove Theorem 2. To this end, we need to show the following two results,

$$\frac{1}{p}\sum _{j=1}^{p}I(p_j\le t)-T_{1,n}(t)\to 0\text{a.s.}\text{and}$$ (D.1)

$$\frac{1}{p_0}\sum _{j\in {\mathcal{N}}_0}I(p_j\le t)-G_{0,n}(t)\to 0\text{a.s.},$$ (D.2)

as p → ∞, where $G_{0,n}(t)=p_0^{-1}{\sum }_{j\in {\mathcal{N}}_0}P(p_j\le t)$. Since the proofs for (D.1) and (D.2) are quite similar, we only verify (D.1). By the law of large numbers, it is enough to show that

$$var\left\{\frac{1}{p}\sum _{j=1}^{p}I(p_j\le t)\right\}=O(p^{-\delta })\text{for}\text{any}\delta >0.$$ (D.3)

It is worth noting that the left-hand side of (D.3) is equivalent to

$$\begin{array}{l}var\left\{\frac{1}{p}\sum _{j=1}^{p}I(\mid Z_j\mid \ge z_{1-t/2})\right\}\\ =var\left\{\frac{1}{p}\sum _{j\in {\mathcal{N}}_0}I(\mid Z_j\mid \ge z_{1-t/2})\right\}+var\left\{\frac{1}{p}\sum _{j\in {\mathcal{N}}_1}I(\mid Z_j\mid \ge z_{1-t/2})\right\}\\ +\frac{2}{p^2}\sum _{j_1\in {\mathcal{N}}_0}\sum _{j_2\in {\mathcal{N}}_1}cov\left\{I(\mid Z_{j_1}\mid \ge z_{1-t/2}),I(\mid Z_{j_2}\mid \ge z_{1-t/2})\right\}\\ :=J_1+J_2+2J_3.\end{array}$$ (D.4)

Using the fact that var{I(|Z_j| ≥ z_1−t/2)} ≤ E{I(|Z_j| ≥ z_1−t/2)} ≤ 1 and the assumption that p₀/p → 1, together with the Cauchy–Schwarz inequality, we have that J₂ ≤ p⁻²|𝒩₁| Σ_j∈𝒩1 var{I(|Z_j| ≥ z_1−t/2)} ≤ (p − p₀)²/p² → 0. In addition, applying the Cauchy–Schwarz inequality, we obtain

$$\begin{array}{l}{J}_3^2\le var\left\{\frac{1}{p}\sum _{j\in {\mathcal{N}}_0}I(\mid Z_j\mid \ge z_{1-t/2})\right\}\text{var}\left\{\frac{1}{p}\sum _{j\in {\mathcal{N}}_1}I(\mid Z_j\mid \ge z_{1-t/2})\right\}\\ \le {(p-p_0)}^2{p}_0^2/p^4\to 0.\end{array}$$

Accordingly, to prove (D.3), we only need to show that J₁ = O(p^−δ) for some δ > 0. It can be seen that

$$\begin{array}{l}{J}_1=\frac{1}{p^2}\sum _{j\in {\mathcal{N}}_0}var\left\{I(\mid Z_j\mid \ge z_{1-t/2})\right\}+\frac{1}{p^2}\sum _{j_1\ne j_2,j_1,j_2\in {\mathcal{N}}_0}cov\left\{I(\mid Z_{j_1}\mid \ge z_{1-t/2}),I(\mid Z_{j_2}\mid \ge z_{1-t/2})\right\}\\ :=J_{11}+J_{12}.\end{array}$$

Since J₁₁ ≤ p₀/p² → 0 as p → ∞, it suffices to show that J₁₂ = O(p^−δ) for some δ > 0. Note that

$$cov\left\{I(\mid Z_{j_1}\mid \ge z_{1-t/2}),I(\mid Z_{j_2}\mid \ge z_{1-t/2})\right\}:=I_1+I_2+I_3+I_4,$$

where I₁ = E{I(Z_j1≥ z_1−t/2)I(Z_j2 ≥ z_1−t/2)} − E{I(Z_j1 ≥ z_1−t/2)}E{I(Z_j2 ≥ z_1−t/2)}, I₂ = E{I(Z_j1 ≥ z_1−t/2)I(Z_j2 ≤ −z_1−t/2)} − E{I(Z_j1 ≥ z_1−t/2)}E{I(Z_j2 ≤ −z_1−t/2)}, I₃ = E{I(Z_j1 ≤ −z_1−t/2)I(Z_j2 ≥ z_1−t/2)} − E{I(Z_j1 ≤ −z_1−t/2)}E{I(Z_j2 ≥ z_1−t/2)} and I₄ = E{I(Z_j1 ≤ −z_1−t/2)I(Z_j2 ≤ −z_1−t/2)} − E{I(Z_j1 ≤ −z_1−t/2)}E{I(Z_j2 ≤ −z_1−t/2)}. Since the proofs for I₁ to I₄ are essentially the same, we only focus on I₁.

Applying the asymptotic expansion of Z_j given in the proof of Theorem 1, we have

$$Z_j=\frac{\sqrt{n}{\widehat{\beta }}_j}{{\widehat{\sigma }}_{{\beta }_j}}=\frac{\sqrt{n}{\beta }_j}{{\sigma }_{{\beta }_j}}+n^{-1/2}\sum _{i=1}^n{u}_{ij}+o_p(1),$$ (D.5)

where $u_{ij}={\sigma }_{{\beta }_j}^{-1}({\delta }_{ij}+{\xi }_{ij}),{\delta }_{ij}=(X_{ij}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{X}_{i{\mathcal{S}}_j})X_{i{\mathcal{S}}_j^{\ast }}^{\top }{\beta }_{{\mathcal{S}}_j^{\ast }},{\xi }_{ij}=(X_{ij}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{X}_{i{\mathcal{S}}_j}){\epsilon }_i$, and ${\sigma }_{{\beta }_j}^2=({\sigma }_{jj}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j})\{{\beta }_{{\mathcal{S}}_j^{\ast }}^{\top }({\mathit{\sum }}_{{\mathcal{S}}_j^{\ast }}-{\mathit{\sum }}_{{\mathcal{S}}_j^{\ast }{\mathcal{S}}_j^{+}}{\mathit{\sum }}_{{\mathcal{S}}_j^{+}}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_j^{+}{\mathcal{S}}_j^{\ast }}){\beta }_{{\mathcal{S}}_j^{\ast }}+{\sigma }^2\}$. As a result, for any j ∈ 𝒩₀, $Z_j=n^{-1/2}{\sum }_{i=1}^n{u}_{ij}+o_p(1)$ and Z_j can be expressed as a summation of independent and identically distributed (i.i.d.) random variables u_ij. In addition, Condition (C1) implies that u_ij has an exponential tail. This, together with the bivariate large deviation result (Zhong et al., 2013), leads to

$$E\left\{I(Z_{j_1}\ge z_{1-t/2})I(Z_{j_2}\ge z_{1-t/2})\right\}=U(z_{1-t/2},z_{1-t/2};{\rho }_{j_1{j}_2})\{1+o(1)\},$$

where ρ_j1j2 = corr(u_ij1, u_ij2) and

$$U(a,b;\rho )={\left\{2\pi {(1-{\rho }^2)}^{1/2}\right\}}^{-1}\times {\int }_a^{\infty }{\int }_b^{\infty }exp\left\{-\frac{1}{2(1-{\rho }^2)}(y_1^2+y_2^2-2\rho y_1{y}_2)\right\}d{y}_{1}d{y}_2.$$

Without loss of generality, we assume that ρ_j1j2 = corr(u_ij1, u_ij2) > 0 and z_1−t/2 > 0. Then, by using the inequality in Willink (2004), we have

$$\begin{array}{l}\mathit{\Phi }(z_{1-t/2})\mathit{\Phi }(\zeta z_{1-t/2})\le U(z_{1-t/2},z_{1-t/2};{\rho }_{j_1{j}_2})\\ \le \mathit{\Phi }(z_{1-t/2})\mathit{\Phi }(\zeta z_{1-t/2})(1+{\rho }_{j_1{j}_2}),\end{array}$$ (D.6)

where ζ = {(1−ρ_j1j2)/(1+ρ_j1j2)}^1/2. Accordingly, we obtain that

$$\mathit{\Phi }(z_{1-t/2})\left\{\mathit{\Phi }(\zeta z_{1-t/2})-\mathit{\Phi }(z_{1-t/2})\right\}\le I_1\le \mathit{\Phi }(z_{1-t/2})\left\{\mathit{\Phi }(\zeta z_{1-t/2})(1+{\rho }_{j_1{j}_2})-\mathit{\Phi }(z_{1-t/2})\right\}.$$

After algebraic simplification, (1 − ζ)/ρ_j1j2 → 1 as ρ_j1j2 → 0. Hence, I₁/(C_Iρ_j1j2) → 1 for a positive constant C_I, which implies that cov{I(|Z_j1 | ≥ z_1−t/2), I(|Z_j2 | ≥ z_1−t/2)} ≈ C_I |ρ_j1j2 |. Consequently, if Σ_j∈𝒩0 |ρ_jk| = o(p) for any k ∈ 𝒩₀, then J₁₂ = O(p^−δ) for some δ > 0.

To complete the proof, we next verify the above condition Σ_j∈𝒩0 |ρ_jk| = o(p) for any k ∈ 𝒩₀. By the Cauchy–Schwarz inequality, we need to show that ${\sum }_{j\in {\mathcal{N}}_0}{\rho }_{jk}^2=o(p)$. Since ${\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j}$ is the conditional variance of X_j given X_𝒮j, ${\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j}\ge 0$. Therefore, ${\sigma }_{jj}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j}\le {\sigma }_{jj}<c_{max}<\infty$ uniformly by Condition (C2) and ${\beta }_{{\mathcal{S}}_j^{\ast }}^{\top }({\mathit{\sum }}_{{\mathcal{S}}_j^{\ast }}-{\mathit{\sum }}_{{\mathcal{S}}_j^{\ast }{\mathcal{S}}_j^{+}}{\mathit{\sum }}_{{\mathcal{S}}_j^{+}}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_j^{+}{\mathcal{S}}_j^{\ast }}){\beta }_{{\mathcal{S}}_j^{\ast }}$ is bounded, respectively, for any j ∈ 𝒩₀. Hence, max_j ${\sigma }_{{\beta }_j}^2<\infty$. In addition, (D.5) implies var(u_ij) = 1. As a result, we only need to demonstrate that ${\sum }_{j\in {\mathcal{N}}_0}{v}_{jk}^2=o(p)$, where υ_jk = cov(u_ij, u_ik).

It can be shown that υ_jk = υ_jk,1+υ_jk,2, where υ_jk,1 = cov(ξ_ij, ξ_ik), υ_jk,2 = cov(δ_ij, δ_ik), and ξ_ij and δ_ij are defined after Eq. (D.5). Hence, to complete the proof, it suffices to show the following results:

$$p^{-1}\sum _{j\in {\mathcal{N}}_0}{v}_{jk,1}^2=o(1)\text{and}{p}^{-1}\sum _{j\in {\mathcal{N}}_0}{v}_{jk,2}^2=o(1).$$ (D.7)

We begin with proving the first equation of (D.7). Applying the Cauchy–Schwarz inequality, it can be shown that

$$\begin{array}{l}{v}_{jk,1}^2={\sigma }^4{\left({\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k}-{\mathit{\sum }}_{j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}j}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}k}\right)}^2\\ \le 3{\sigma }^4\left\{{({\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k})}^2+{({\mathit{\sum }}_{j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}j})}^2+{({\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}k})}^2\right\}.\end{array}$$

We then study the above three components separately.

By definition, we have ${\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k}={\mathrm{\varrho }}_{jk}({\mathcal{S}}_j)\le {max}_{k\notin {\mathcal{S}}_j}{\mathrm{\varrho }}_{jk}({\mathcal{S}}_j)=O({\mid {\mathcal{S}}_j\mid }^{-\xi })$ uniformly for any j = 1, … , p. This, together with Condition (C5), implies that ${\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k}=O(n^{-1/2})$ uniformly for any j. As a result, we have

$$\begin{array}{l}\sum _{j\in {\mathcal{N}}_0}{({\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k})}^2=\left(\sum _{\begin{array}{c}j\in {\mathcal{N}}_0,\\ k\notin {\mathcal{S}}_j\end{array}}+\sum _{\begin{array}{c}j\in {\mathcal{N}}_0,\\ k\in {\mathcal{S}}_j\end{array}}\right){({\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k})}^2\\ =O(n^{-1/2}p)=o(p),\end{array}$$

where the second summation on the right-hand side of the above equation is 0 since, for k ∈ 𝒮_j, ${\sigma }_{jk}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}k}$ is one of the component of the vector ${\mathit{\sum }}_{j{\mathcal{S}}_j}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_j}=0$. We next consider the second term ${({\mathit{\sum }}_{j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}j})}^2$. Using the fact that the conditional variance of X_ij is non-negative and then applying Condition (C2), we have ${\mathit{\sum }}_{j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}j}\le {\sigma }_{jj}<C_{max}$. This, together with the assumption in Theorem 2, Condition (C2), and the fact that |𝒮_k| ≤ Λ₀, leads to

$$\begin{array}{l}{p}^{-1}\sum _{j\in {\mathcal{N}}_0}{({\mathit{\sum }}_{j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}j})}^2\le c_{max}{p}^{-1}\sum _{j\in {\mathcal{N}}_0}tr({\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}){\Vert {\mathit{\sum }}_{j{\mathcal{S}}_k}\Vert }^2\\ \le (c_{max}{c}_{max}^{\ast })\mid {\mathcal{S}}_k\mid p^{-1}\sum _{j\in {\mathcal{S}}_0}{\Vert {\mathit{\sum }}_{j{\mathcal{S}}_k}\Vert }^2\\ =(c_{max}{c}_{max}^{\ast })\mid {\mathcal{S}}_k\mid p^{-1}\sum _{j\in {\mathcal{N}}_0}\sum _{l\in {\mathcal{S}}_k}{\sigma }_{jl}^2=o(1).\end{array}$$

Employing similar techniques, we can show that $p^{-1}{\sum }_j{({\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_j{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{k}k})}^2=o(1)$. The above results complete the proof of the first equation in (D.7).

Subsequently, we will verify the second equation of (D.7). According to the result in the proof of Theorem 1, $E({\delta }_{ij})\le C_{\delta }{max}_{l\in {\mathcal{S}}_j^{+}}\mid {\rho }_{jl}({\mathcal{S}}_j)\mid =o(1)$ for some positive constant C_δ. It follows that p⁻¹Σ_j∈𝒩0^E2(δ_ij)E²(δ_ik) = o(1); hence, we only need to show that p⁻¹Σ_j∈𝒩0E²(δ_ijδ_ik) = o(1). After algebraic simplification, we obtain that

$$\begin{array}{l}E({\delta }_{ij}{\delta }_{ik})=E\{(X_{ij}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{X}_{i{\mathcal{S}}_j})X_{i{\mathcal{S}}_j^{\ast }}^{\top }{\beta }_{{\mathcal{S}}_j^{\ast }}{X}_{ik}{X}_{i{\mathcal{S}}_k^{\ast }}^{\top }{\beta }_{{\mathcal{S}}_k^{\ast }}\}-E\{(X_{ij}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{X}_{i{\mathcal{S}}_j})X_{i{\mathcal{S}}_j^{\ast }}^{\top }{\beta }_{{\mathcal{S}}_j^{\ast }}{\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{X}_{i{\mathcal{S}}_k}{X}_{i{\mathcal{S}}_k^{\ast }}^{\top }{\beta }_{{\mathcal{S}}_k^{\ast }}\}\\ :=Q_{1j}-Q_{2j}.\end{array}$$

For the sake of simplicity, we suppress the subscript i in the rest of the proof.

We first demonstrate Q_1j = o(1) for each j ∈ 𝒩₀. By Lemma 2 with some tedious calculations, we obtain that

$$\begin{array}{l}{Q}_{1j}=\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_3\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j_2}{\beta }_{j_3}{\sigma }_{j_2{j}_3}{\mathrm{\varrho }}_{jk}({\mathcal{S}}_j)\\ +\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_3\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j_2}{\beta }_{j_3}{\sigma }_{k{j}_3}{\mathrm{\varrho }}_{j{j}_2}({\mathcal{S}}_j)\\ +\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_3\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j_2}{\beta }_{j_3}{\sigma }_{j_{2}k}{\mathrm{\varrho }}_{j{j}_3}({\mathcal{S}}_j):=Q_{1j}^{(1)}+Q_{1j}^{(2)}+Q_{1j}^{(3)}.\end{array}$$

By Condition (C2), we have |σ_j2j3| ≤ c_max. As a result.

$$\begin{array}{l}{Q}_{1j}^{(1)}=\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_3\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j2}{\beta }_{j3}{\sigma }_{j_2{j}_3}{\mathrm{\varrho }}_{jk}({\mathcal{S}}_j)\\ \le c_{max}\underset{k\notin {\mathcal{S}}_j}{max}\mid {\mathrm{\varrho }}_{jk}({\mathcal{S}}_j)\mid \sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_3\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}\mid {\beta }_{j_2}\mid \mid {\beta }_{j_3}\mid \\ \le c_{max}\underset{k\notin {\mathcal{S}}_j}{max}\mid {\mathrm{\varrho }}_{jk}({\mathcal{S}}_j)\mid {(\sum _j\mid {\beta }_j\mid )}^2.\end{array}$$

Then employing Condition (C6), we obtain Σ_j |β_j| = O(n^ϖ). In addition, Conditions (C4) and (C5) imply that ϱ_jk(𝒮_j) = O(n^−1/2). The above results lead to

$$Q_{1j}^{(1)}=O(n^{2\varpi })\times O(n^{-1/2})=O(n^{1/2-2\varpi })=o(1)$$

uniformly for any j. Applying similar techniques, we can also show that $Q_{2j}^{(1)}=o(1)$ and $Q_{3j}^{(2)}=o(1)$, which complete the proof of Q_1j = o(1).

We next verify Q_2j = o(1) for each j ∈ 𝒩₀. After algebraic calculation, we obtain that

$$\begin{array}{l}{Q}_{2j}=\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_4\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j_2}{\beta }_{j_4}{\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_k{j}_4}{\mathrm{\varrho }}_{j{j}_2}({\mathcal{S}}_j)\\ +\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_4\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j_2}{\beta }_{j_4}{\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_k{j}_2}{\mathrm{\varrho }}_{j{j}_4}({\mathcal{S}}_j)\\ +\sum _{j_2\in {\mathcal{S}}_j^{\ast }\cap {\mathcal{N}}_1}\sum _{j_3\in {\mathcal{S}}_k\cap {\mathcal{N}}_1}\sum _{j_4\in {\mathcal{S}}_k^{\ast }\cap {\mathcal{N}}_1}{\beta }_{j_2}{\beta }_{j_4}{\sigma }_{j_2{j}_4}{({\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1})}_{j_3}{\mathrm{\varrho }}_{j{j}_3}({\mathcal{S}}_j)\\ :=Q_{2j}^{(1)}+Q_{2j}^{(2)}+Q_{2j}^{(3)},\end{array}$$

where ${({\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1})}_{j_3}$ represents for the j₃th elements of ${\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}$. By Conditions (C2), (C4) and (C5), we have that $\mid {\mathit{\sum }}_{k{\mathcal{S}}_k}{\mathit{\sum }}_{{\mathcal{S}}_k}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_k{j}_4}\mid =\mid {\sigma }_{k{j}_4}-{\mathrm{\varrho }}_{k{j}_4}({\mathcal{S}}_k)\mid \le \mid {\sigma }_{k{j}_4}\mid +{max}_{j_4\notin {\mathcal{S}}_k}{\mathrm{\varrho }}_{k{j}_4}({\mathcal{S}}_k)\le c_{max}+O(n^{-1/2})$ and ϱ_jj2 (𝒮_j) ≤ max_{j2∉𝒮jϱjj2}(𝒮_j) = O(n^−1/2). These results, in conjunction with Condition (C6), yield

$$Q_{2j}^{(1)}\le O(n^{-1/2}){\left(\sum _j\mid {\beta }_j\mid \right)}^2=o(1).$$

Employing similar techniques, we can also demonstrate that $Q_{2j}^{(2)}=o(1)$ and $Q_{3j}^{(3)}=o(1)$, which lead to Q_2j = o(1). This, together with Q_1j = o(1), implies that

$$p^{-1}\sum _{j\in {\mathcal{N}}_0}{E}^2({\delta }_{ij}{\delta }_{ik})=p^{-1}\sum _{j\in {\mathcal{N}}_0}{(Q_{1j}-Q_{2j})}^2=o(1),$$

which completes the proof of (D.1).

It is worth noting that G_0,n(t) → t. This, in conjunction with (D.1), (D.2), and the assumptions T_1,n → T₁(t) with T₁(t) continuous and p₀/p → 1 as p→∞, indicates that Conditions (a), (b), and (c) in Lemma 4 hold. Accordingly, the proof of Theorem 2 is complete.

Appendix E. Proof of Theorem 3

Let Z_j = n^1/2β̂_j/σ̂_βj be the test statistic and p_j be the corresponding p-value for j = 1, … , p. Define α_n = 2{1 − Φ(n^j)} for some ħ < j < 1/2 − κ, where ħ and κ are given in Condition (C7); hence, α_n → 0 as n → ∞. To prove the theorem, it suffices to show that

$$\begin{array}{l}\underset{n\to \infty }{lim}P\left\{V({\alpha }_n)>0\right\}\to 0\text{and}\\ \underset{n\to \infty }{lim}P\left\{S({\alpha }_n)/(p-p_0)=1\right\}\to 1.\end{array}$$

It is worth noting that n → ∞ implicitly implies p → ∞. We demonstrate the above equations in the following two steps accordingly.

STEP I

We show that P{V(α_n) > 0} → 0. Using the fact that ${\tau }_{{\beta }_j}^2\ge {\overline{\sigma }}^2$ for 1 ≤ j ≤ p, we have

$$\begin{array}{l}\mid Z_j\mid =\left\{\left|{(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}+{(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_{{\mathcal{S}}_j^{\ast }}{\beta }_{{\mathcal{S}}_j^{\ast }}\right|\right\}/(n^{-1/2}{\widehat{\sigma }}_{{\beta }_j})\\ \le {\overline{\sigma }}^{-1}\left|{(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}\right|+{\overline{\sigma }}^{-1}\left|{(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_{{\mathcal{S}}_j^{\ast }}{\beta }_{{\mathcal{S}}_j^{\ast }}\right|.\end{array}$$

This, together with Bonferroni’s inequality, leads to

$$\begin{array}{l}P\left\{V({\alpha }_n)>0\right\}=P\left(\underset{j\in {\mathcal{N}}_0}{max}\mid Z_j\mid >z_{1-{\alpha }_n/2}\right)\\ \le P\left(\underset{j\in {\mathcal{N}}_0}{max}\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}/\overline{\sigma }\mid >n^j/2\right)\\ +P\left(\underset{j\in {\mathcal{N}}_0}{max}\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_{{\mathcal{S}}_j^{\ast }}{\beta }_{{\mathcal{S}}_j^{\ast }}\mid >\overline{\sigma }{n}^j/2\right).\end{array}$$ (E.1)

Consider the quantity $\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}/\overline{\sigma }\mid$, which is in the first term of the right-hand side of the above equation. Employing the same technique as used in the proof of Lemma 3, we obtain that ${max}_j\mid n^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j-({\sigma }_{jj}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j})\mid =o_p(1)$. By Condition (C2), one can easily verify that ${\sigma }_{jj}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j}\ge c_{max}^{\ast -1}$. The above two results lead to $n^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j\ge c_{max}^{\ast -1}$ uniformly for any j. Accordingly, there exists some constant C₃ such that

$$\underset{j\in {\mathcal{N}}_0}{max}\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}/\overline{\sigma }\mid \le C_3\underset{j\in {\mathcal{N}}_0}{max}{n}^{-1/2}\mid X_j^{\top }\mathcal{E}\mid .$$

This, in conjunction with Bonferroni’s inequality and Condition (C8), yields

$$\begin{array}{l}P\left(\underset{j\in {\mathcal{N}}_0}{max}\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}/\overline{\sigma }\mid >n^j/2\right)\\ \le \sum _{j\in {\mathcal{N}}_0}P\left(n^{-1}\mid X_j^{\top }\mathcal{E}\mid >C_3^{-1}{n}^{j-1/2}/2\right)\\ \le 2pexp\{-C_4{n}^{2j}\}\le 2exp\{-C_4{n}^{2j}+\nu n^{\hslash }\}\end{array}$$

for some positive constant C₄. By definition, ħ < 2j. Thus, the first term on the right-hand side of the above equation, −C_ℰn^2j/4, dominates the second term νn^ħ, which immediately leads to

$$\underset{n\to \infty }{lim}P\left(\underset{j\in {\mathcal{N}}_0}{max}\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}\mathcal{E}/\overline{\sigma }\mid >n^j/2\right)\to 0.$$

We next consider the quantity ${(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_{{\mathcal{S}}_j^{\ast }}{\beta }_{{\mathcal{S}}_j^{\ast }}$, which is in the second term of the right-hand side of Eq. (E.1). It is worth noting that

$$\begin{array}{l}{(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1/2}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_{{\mathcal{S}}_j^{\ast }}{\beta }_{{\mathcal{S}}_j^{\ast }}={(X_j^{\top }{Q}_{{\mathcal{S}}_j}{X}_j/n)}^{-1/2}{n}^{1/2}\sum _{j^{\ast }\in {\mathcal{S}}_j^{\ast }}{\widehat{\mathrm{\varrho }}}_{jj\ast }({\mathcal{S}}_j){\beta }_{j^{\ast }}\\ \le C_5{\left\{\underset{j}{min}{n}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j\right\}}^{-1/2}\underset{j^{\ast }\in {\mathcal{S}}_j^{\ast }}{max}\mid n^{1/2}{\widehat{\mathrm{\varrho }}}_{j{j}^{\ast }}({\mathcal{S}}_j)\mid \end{array}$$

for some finite positive constant C₅.

Using the results of ${max}_j\mid n^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j-({\sigma }_{jj}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j})\mid =o_p(1)$ and ${\sigma }_{jj}-{\mathit{\sum }}_{j{\mathcal{S}}_j}{\mathit{\sum }}_{{\mathcal{S}}_j}^{-1}{\mathit{\sum }}_{{\mathcal{S}}_{j}j}\ge c_{max}^{\ast -1}$ discussed after (E.1), we have that ${\{{min}_j{n}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j\}}^{-1/2}=O_p(1)$. In addition, Condition (C4), together with the fact that 𝒮_j satisfies Condition (C5), leads to ${max}_{j^{\ast }\in {\mathcal{S}}_j^{\ast }}\mid n^{1/2}{\mathrm{\varrho }}_{j{j}^{\ast }}({\mathcal{S}}_j)\mid =o(1)$. By Corollary 1 of Kalisch and Bühlmann (2007), we immediately obtain

$$\underset{j,{\mathcal{S}}_j^{\ast }}{max}P\left\{\underset{j^{\ast }\in {\mathcal{S}}_j^{\ast }}{max}\mid n^{1/2}{\widehat{\mathrm{\varrho }}}_{jj\ast }({\mathcal{S}}_j)\mid >O(n^{b/2})\right\}\to 0$$

for every ħ < b < 1. Taking b = (ħ + j)/2, we then have ${max}_{j^{\ast }\in {\mathcal{S}}_j^{\ast }}\mid n^{1/2}{\widehat{\mathrm{\varrho }}}_{j{j}^{\ast }}({\mathcal{S}}_j)\mid =o(n^{b/2})=o(n^j)$. This, in conjunction with the above result ${\{{min}_j{n}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j\}}^{-1/2}=O_p(1)$, results in

$$P\left(\underset{j\in {\mathcal{N}}_0}{max}\mid {(X_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_j)}^{-1}{X}_j^{\top }{\mathcal{Q}}_{{\mathcal{S}}_j}{X}_{{\mathcal{S}}_j^{\ast }}{\beta }_{{\mathcal{S}}_j^{\ast }}\mid >\sigma n^j/2\right)\to 0.$$

In sum, we have shown the asymptotic behavior of the first component on the right-hand side of (E.1).

STEP II

We prove that lim_n→∞ P{S(α_n)/(p − p₀) = 1} → 1. By definition, we have

$${(p-p_0)}^{-1}S({\alpha }_n)={(p-p_0)}^{-1}\sum _{j\in {\mathcal{N}}_1}I\left(\mid n^{1/2}{\widehat{\beta }}_j/{\widehat{\sigma }}_{{\beta }_j}\mid >n^j\right).$$

Applying the asymptotic result of the first component on the right-hand side of (E.1), we have max_j |n^1/2( β̂_j−β_j)/σ̂_βj| = o(n^j). Then by Condition (C7) that min_j∈𝒩1|β_j| ≥ C_κn_−κ for some constants C_κ > 0 and κ > 0, we can further obtain that min_j∈𝒩1|n^1/2β_j/σ̂_βj| = O(n^1/2−κ). Moreover, by Bonferroni’s inequality and the fact that j +κ < 1/2, we have

$$\begin{array}{l}P\left({(p-p_0)}^{-1}S({\alpha }_n)=1\right)=P\left(\underset{j\in {\mathcal{N}}_1}{min}\mid n^{1/2}{\widehat{\beta }}_j/{\widehat{\sigma }}_{{\beta }_j}\mid >n^j\right)\\ \ge P\left(\underset{j\in {\mathcal{N}}_1}{min}\mid n^{1/2}{\beta }_j/{\widehat{\sigma }}_{{\beta }_j}\mid >n^j\right)\\ -P\left(\underset{j\in {\mathcal{N}}_1}{max}\mid n^{1/2}({\widehat{\beta }}_j-{\beta }_j)/{\widehat{\sigma }}_{{\beta }_j}\mid >2n^j\right)\to 1,\end{array}$$

which completes the proof of Step II. Consequently, the entire proof is complete.

Appendix F. Supplementary data

Supplementary material related to this article can be found online at http://dx.doi.org/10.1016/j.jeconom.2016.05.016.