A general framework for the regression analysis of pooled biomarker assessments

Abstract

As a cost efficient data collection mechanism, the process of assaying pooled biospecimens is becoming increasingly common in epidemiological research; e.g. pooling has been proposed for the purpose of evaluating the diagnostic efficacy of biological markers (biomarkers). To this end, several authors have proposed techniques that allow for the analysis of continuous pooled biomarker assessments. Regretfully, most of these techniques proceed under restrictive assumptions, are unable to account for the effects of measurement error, and fail to control for confounding variables. These limitations are understandably attributable to the complex structure that is inherent to measurements taken on pooled specimens. Consequently, in order to provide practitioners with the tools necessary to accurately and efficiently analyze pooled biomarker assessments, herein a general Monte Carlo maximum likelihood based procedure is presented. The proposed approach allows for the regression analysis of pooled data under practically all parametric models and can be used to directly account for the effects of measurement error. Through simulation, it is shown that the proposed approach can accurately and efficiently estimate all unknown parameters and is more computational efficient than existing techniques. This new methodology is further illustrated using monocyte chemotactic protein-1 data collected by the Collaborative Perinatal Project in an effort to assess the relationship between this chemokine and the risk of miscarriage.

1. Introduction

In resource limited environments, the process of assaying pooled biospecimens (i.e., a sample comprised of several individual specimens) has become a cost effective alternative to assaying specimens one-by-one. The origins of group (or pool) testing are commonly attributed to [1], where it was proposed as a means to reduce the cost of screening military inductees for syphilis during the Second World War. Since its advent, pool testing has been adopted for the purposes of screening for various infectious diseases [2, 3, 4, 5] and the incidence of bioterrorism [6], identifying lead compounds in drug discovery [7], and detecting rare mutations in genetics [8]. The general advantages of collecting data on pools are three-fold: a reduction in the cost associated with measuring the outcome of interest, the ability to preserve irreplaceable specimens, and the means to collect information in a more timely fashion. Further, these advantages persist when the outcome of interest is continuous. For example, [9] reports that the 2005–2006 National Health and Nutrition survey reduced the number of analytical measurements required to characterize the distribution of polychlorinated and polybrominated compounds within the population of the United States from 2201 to 228 by pooling, which translated to a savings of $2.78 million in testing cost.

[10] was the first to consider modeling outcomes obtained from assaying pooled specimens in order to estimate population level characteristics; i.e., binary outcomes, measured on pools, were used to estimate the proportion of individuals within a population who possessed a characteristic of interest. In this context, the process of pooling offers a cost effective data collection mechanism, and for this reason has received a great deal of attention among the statistical literature; e.g., see [11, 12] and the references therein. Extending this earlier work, [13] proposed a regression framework which relates binary outcomes measured on pools to covariate information. The work of [13] has since seen numerous generalizations; to include allowing for random pooling and imperfect testing [14], confirmatory testing [15], random effects [16], and covariate measurement error [17], as well as the development of techniques that allow for a nonparametric [18, 19] and semiparametric [20, 21] regression analysis of group testing data. Note, all of the aforementioned techniques were specifically developed for binary outcomes measured on pools.

Broadening the utilitarian nature of pooling as a cost effective data collection mechanism, techniques for analyzing continuous outcomes obtained from assaying pooled specimens have been proposed. For example, in an effort to reduce cost, several authors have proposed methods of analyzing pooled measurements in order to evaluate the efficacy of a biological marker (biomarker) as a diagnostic tool; e.g., see [22, 23, 24, 25, 26, 27, 28]. More recently, this research area has shifted to consider the regression analysis of continuous biomarker measurements taken on pools; e.g., see [29] and Malinovsky et al. (2012). It is worthwhile to point out that the aforementioned regression techniques were developed under the rather stringent assumption that the biomarker levels of the individuals, and hence the pools, are conditionally Gaussian, given the covariate information. In most practical applications, biomarker levels tend to follow a right-skewed continuous distributions with positive support. Consequently, [30] proposed an Monte Carlo expectation maximization (MCEM) algorithm which could be used to conduct the regression analysis of pooled biomarker assessments under the assumption that the individual biomarker levels conditionally, given the covariates, follow a log-normal distribution. Further, these authors investigated several pooling strategies with respect to estimation efficiency, with their findings resounding the work of [31] in the binary regression group testing literature; i.e., measurements taken on pools that are formed homogeneously, with respect to covariate information, can be used to construct estimators that are nearly as efficient as the analogous estimators based on individual level data. Regretfully, the technique proposed by these authors allows for the regression analysis under a single parametric model and does not account for measurement error, which is omnipresent in biomarker evaluation studies.

The regression analysis of continuous outcomes measured on pools is fraught with many complexities, thus the potential benefits from using pooling as a cost efficient data collection mechanism has been largely untapped when the response variable of interest is continuous. To circumvent this hurdle, herein a general regression methodology for continuous pooled biomarker assessments is proposed. Unlike previously proposed techniques, this methodology allows for the regression analysis under many common parametric models, to include distributions belonging to the class of generalized linear models, and can easily account for measurement error in the response variable, when it is present. Further, the proposed technique is more computationally efficient than other existing methods; e.g., MCEM algorithm of [30]. The asymptotic properties of the proposed approach are established, and through simulation studies the new methodology is shown to accurately and efficiently analyze pool response data, both subject to and free of measurement error, under several different parametric models.

The remainder of this article is organized as follows. Section 2 presents the general modeling framework which can be used to perform a regression analysis of continuous outcomes measured on pooled specimens. The asymptotic properties of the proposed approach are provided in Section 3, and Section 4 provides a simulation study which investigates the finite sample performance of the new methodology. In Section 5 the proposed approach is used to analyze monocyte chemotactic protein-1 data collected by the Collaborative Prenatal Project (CPP). Section 6 concludes with a summary discussion. All of the theoretical proofs and additional technical details are provided in the Web Appendix.

2. Methodology

In what follows a general methodology is proposed for the regression analysis of continuous outcomes measured on pooled specimens. In this context the observed data consists of J measurements taken on pools, where the jth pool is formed by amalgamating c_j specimens collected from individuals. Let Ỹ_ij denote the biomarker level of the ith individual in the jth pool, for i = 1, …, c_j and j = 1, …, J. When assessments are being made on pools the Ỹ_ij are latent, and the observed data consists of either the biomarker level of the pool, which is denoted by Ỹ_pj, or an error contaminated measurement of Ỹ_pj, which is denoted by Y_pj. In order to relate the Ỹ_ij to the Ỹ_pj, herein it is assumed that the biomarker level of the jth pool is the arithmetic average of the biomarker levels of the individuals of which the jth pool is comprised; i.e., ${\stackrel{\sim }{Y}}_{p_j}=c_j^{-1}{\sum }_{i=1}^{c_j}{\stackrel{\sim }{Y}}_{ij}$ This assumption is common among the literature [26, 27, 30] and is reasonable as long as pools are formed from specimens of equal volume.

For modeling purposes, it is assumed that x_ij = (1, x_ij1, …, x_ijp)′, a (p + 1) × 1 vector of covariates, is available for each individual. Given the covariate information, it is assumed that the biomarker levels of the individuals are (conditionally) independent and follow a continuous distribution with probability density function f(·|x_ij, θ₀); i.e., ${\stackrel{\sim }{Y}}_{ij}\stackrel{\mathit{ind}.}{\sim }f(·\mid {\mathbf{x}}_{ij},{\mathit{\theta }}_0)$, for i = 1, …, c_j and j = 1, …, J, where ${\mathit{\theta }}_0={({\mathit{\beta }}_0^{\prime },{\mathit{\gamma }}_0^{\prime })}^{\prime }$ denotes the collection of model parameters, β₀ = (β₀₀, …, β_0p)′ is a vector of regression coefficients, and γ₀ is a set of nuisance parameters. The generality in the assumed parametric model for Ỹ_ij is meant to illustrate the broad applicability of the proposed approach; e.g., f(·|x_ij, θ₀) could belong to the class of generalized linear models, with Ỹ_ij being related to x_ij in the usual fashion [32], or the regression analysis could be performed under other common parametric models for biomarker data, such as the Weibull and log-normal distributions; e.g., see [30].

If the individual biomarker levels were observed, the maximum likelihood estimator (MLE) of θ₀ could be obtained through traditional techniques once the parametric model is assumed. However, when pooled assessments are being made, the Ỹ_ij are latent and the observed data consists of either Ỹ_pj or Y_pj, depending on whether or not the measured biomarker levels are subject to measurement error. Under the aforementioned assumptions, the probability density function of Ỹ_pj, for a given value of θ = (β′, γ′)′, can be expressed as

$$f_j({\stackrel{\sim }{y}}_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta })=\int \cdots \int c_{j}f\left(c_j{\stackrel{\sim }{y}}_{p_j}-\sum _{i=2}^{c_j}{\stackrel{\sim }{y}}_{ij}|{\mathbf{x}}_{1j},\mathit{\theta }\right)\prod _{i=2}^{c_j}f({\stackrel{\sim }{y}}_{ij}\mid {\mathbf{x}}_{ij},\mathit{\theta })d{\stackrel{\sim }{\mathit{y}}}_{(-1)j},$$ (1)

where ỹ _(−1)j = (ỹ_2j, …, ỹ_cjj) and x_j = (x_1j, …, x_cjj). In the presence of measurement error, it is common to assume that the conditional distribution of the observed measurement, given the true level, is known; cf., [33]. Let f_ε(·|Ỹ_pj ) denote the conditional probability density function of Y_pj, given Ỹ_pj. Thus, the density of Y_pj can be expressed as

$$g_j(y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta })=\int \cdots \int f_{\epsilon }\left(y_{p_j}\mid {\stackrel{\sim }{y}}_{p_j}\right)\prod _{i=1}^{c_j}f({\stackrel{\sim }{y}}_{ij}\mid {\mathbf{x}}_{ij},\mathit{\theta })d{\stackrel{\sim }{\mathit{y}}}_j,$$ (2)

where ỹ_j = (ỹ_1j, …, ỹ_cjj)′ and ${\stackrel{\sim }{y}}_{p_j}=c_j^{-1}{\sum }_{i=1}^{c_j}{\stackrel{\sim }{y}}_{ij}$. Note, under most of the common parametric models for biomarker data, expressions for f_j(·|x_j, θ) and g_j(·|x_j, θ) do not exist in closed form, but they can be evaluated through the use of numerical integration.

For ease of exposition, herein the proposed method is presented under the assumption that the observed pooled assessments are subject to measurement error. Although, it is worthwhile to point out that this approach is still applicable when the true biomarker levels are observed, as is demonstrated in Sections 4 and 5. Under the aforementioned modeling assumptions, the log of the observed data likelihood is given by

$$l(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x})=\sum _{j=1}^{J}log\{g_j(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta })\},$$ (3)

where Y_p = (Y_p1, …, Y_pJ)′ and x = (x₁, …, x_J ). By maximizing (3) one can obtain the MLE of θ₀, which is denoted by θ̂; i.e., θ̂ = arg max_θ∈Θ l(θ|Y_p, x). If g_j(·|x_j, θ) could be expressed in closed form, obtaining the MLE of θ₀ would be relatively straightforward. Alternatively, if g_j(·|x_j, θ) does not exist in closed form, numerical integration techniques (e.g., adaptive Gaussian quadrature) could be used to evaluate g_j(·|x_j, θ) at Y_pj, and thus facilitate the maximization of (3). However, it is well known [34] that the computational burden associated with implementing these numerical techniques rapidly increases with the dimension of the integral, making this approach infeasible for c_j > 2; for further discussion see [30]. Further, numerical integration techniques, like the adaptive Gaussian quadrature, may perform poorly for peaked-integrand distribution functions [35]. Consequently, it is not recommended that these techniques be used to facilitate the maximization of (3).

To overcome the drawbacks of implementing numerical integration methods, such as adaptive Gaussian quadrature, the proposed approach uses a Monte Carlo technique to approximate the value of g_j(·|x_j, θ) when evaluated at Y_pj. Note, the value of g_j(Y_pj |x_j, θ) can be viewed as the expected value of f_ε(Y_pj |Ỹ_pj ) with respect to Ỹ_j = (Ỹ_1j, …, Ỹ_cjj)′; i.e.

$$g_j(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta })=E\{f_{\epsilon }(Y_{p_j}\mid {\stackrel{\sim }{Y}}_{p_j})\}=\int \cdots \int f_{\epsilon }(Y_{p_j}\mid {\stackrel{\sim }{y}}_{p_j})h_j({\stackrel{\sim }{\mathit{y}}}_j\mid {\mathbf{x}}_j,\mathit{\theta })d{\stackrel{\sim }{\mathit{y}}}_j,$$ (4)

where $h_j({\stackrel{\sim }{\mathit{y}}}_j\mid {\mathbf{x}}_j,\mathit{\theta })={\prod }_{i=1}^{c_j}f({\stackrel{\sim }{y}}_{ij}\mid {\mathbf{x}}_{ij},\mathit{\theta })$ is the joint density of Ỹ_j. Let ${\stackrel{\sim }{\mathit{Y}}}_j^1,\dots ,{\stackrel{\sim }{\mathit{Y}}}_j^M$ be a random sample from h_j(·|x_j, θ), where ${\stackrel{\sim }{\mathit{Y}}}_j^m={({\stackrel{\sim }{Y}}_{1j}^m,\dots ,{\stackrel{\sim }{Y}}_{c_{j}j}^m)}^{\prime }$, and define ${\stackrel{\sim }{Y}}_{p_j}^m=c_j^{-1}{\sum }_{i=1}^{c_j}{\stackrel{\sim }{Y}}_{ij}^m$. A Monte Carlo estimate of g_j(Y_pj |x_j, θ) can then be obtained as

$$g_j^M(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta })=\frac{1}{M}\sum _{m=1}^M{f}_{\epsilon }(Y_{p_j}\mid {\stackrel{\sim }{Y}}_{p_j}^m).$$ (5)

Consequently, a Monte Carlo approximation of the log-likelihood, when evaluated at a specific value of θ, can be obtained as

$$l_M(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x})=\sum _{j=1}^{J}log\{g_j^M(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta })\}.$$ (6)

By numerically maximizing (6), one can obtain the Monte Carlo Maximum Likelihood Estimator (MCMLE) of θ₀, which is denoted by θ̂_M; i.e., θ̂_M = arg max_θ∈Θ l_M(θ|Y_p, x). Further, under mild regularity conditions, see Section 3, it can be shown that ${\widehat{\mathit{\theta }}}_M\stackrel{p}{\to }\widehat{\mathit{\theta }}$, as M → ∞.

Regretfully, for the purposes of maximizing (6), when (5) is being used to approximate g_j(Y_pj |x_j, θ), numerical optimization algorithms can often be unreliable; i.e., these algorithms have the propensity to converge before reaching θ̂_M. This is a byproduct of the fact that these algorithms require that the Monte Carlo log-likelihood be evaluated at multiple values of θ, and at each value of θ a new random sample from h_j(Ỹ_j |x_j, θ), for j = 1, …, J, has to be taken in order to evaluate (6). Due to the inherent variability in each of the random samples, this process results in a coarse (non-smooth) objective function which is difficult to numerically optimize; for further discussion see [36]. To circumvent this issue, [36] suggests that a single random sample, for each j, be drawn from a predetermined importance distribution $h_j^{\ast }(·\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$, where θ^* is a known set of parameters. This random sample would then be used to evaluate (6) for each value of θ, thus insuring that the Monte Carlo log-likelihood is a smooth function and that optimization algorithms can be used reliably to obtain θ̂_M.

Proceeding in this fashion, let ${\stackrel{\sim }{\mathit{Y}}}_j^1,\dots ,{\stackrel{\sim }{\mathit{Y}}}_j^M$ be a random sample from $h_j^{\ast }(·\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$, and based on this sample a Monte Carlo estimate of g_j(Y_pj |x_j, θ) can be obtained as

$$g_j^M(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })=\frac{1}{M}\sum _{m=1}^M{f}_{\epsilon }(Y_{p_j}\mid {\stackrel{\sim }{Y}}_{p_j}^m)w_j({\stackrel{\sim }{\mathit{Y}}}_j^m,{\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })$$ (7)

where $w_j({\stackrel{\sim }{\mathit{Y}}}_j^m,{\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })=h_j({\stackrel{\sim }{\mathit{Y}}}_j^m\mid {\mathbf{x}}_j,\mathit{\theta })/h_j^{\ast }({\stackrel{\sim }{\mathit{Y}}}_j^m\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$. The corresponding Monte Carlo log-likelihood is given by

$$l_M(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x},{\mathit{\theta }}^{\ast })=\sum _{j=1}^{J}log\{g_j^M(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })\},$$ (8)

and the MCMLE of θ₀ can be obtained as θ̂_M = arg max_θ∈Θ l_M(θ|Y_p, x, θ^*). Note, this process is identical to the approach described above, with the exception of the distributions from which the Monte Carlo samples were drawn.

Theoretically, there are very few restrictions on the choice of the importance distribution $h_j^{\ast }(·\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$, but its specification can dramatically impact the computational efficiency of the proposed approach. In general, the computational burden associated with the proposed approach is due to the size of the Monte Carlo sample being drawn to construct the estimator in (7). That is, obtaining the MCMLE can be computationally inefficient if M is too large, and alternatively imprecise if M is to small. In Section 3, guidance is provided on how to choose the value of M in order to insure that a specified level of precision is attained, under a specific importance distribution. Note, the Monte Carlo sample size required to attain the specified level of precision is inherently tied to the choice of the importance distribution; i.e., a well specified importance distribution results in a smaller value of M, and vice versa. In general, $h_j^{\ast }(·\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$ should have the same support as h_j(·|x_j, θ₀), and the two densities should be similar in shape and center. Further, $h_j^{\ast }(·\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$ should be easy to sample from. In Sections 4 and 5, the importance distributions were selected according to the strategies considered in [37] and [30]; for further discussion see Web Appendix A. Note, under specific types of measurement error (e.g., additive) other more computationally efficient estimators akin to (7) can be derived; for further details see Web Appendix A.2.

3. Asymptotic properties

It is important to note that the Monte Carlo log-likelihood l_M(θ|Y_p, x, θ^*) is evaluated using a random sample from the importance distribution and, as such, different random samples will yield different values of θ̂_M. Therefore, θ̂_M is a non-deterministic approximation of θ̂ whose variability is referred to as Monte Carlo error [38]. As was previously mentioned, the Monte Carlo sample size M plays a significant role with respect to determining the precision of θ̂_M; i.e., the Monte Carlo error decreases as M is increased, and vice versa. By quantifying the Monte Carlo error, one can determine a value of M which will ensure that the approximation of θ̂ attains a specified level of precision. To this end, the asymptotic properties of θ̂_M, as M → ∞, are presented and are further used to develop a method of identifying M which controls the Monte Carlo error at a specified level.

Throughout the remainder of this article, it is assumed that θ consists of k components and that the parameter space Θ is a compact subset of ℝ^k. From Kolmogorov’s Strong Law of Large Numbers (SLLN), under standard regularity conditions, it is easy to establish that ∀ θ ∈ Θ, the Monte Carlo log-likelihood function (8) converges, as M → ∞, to the true log-likelihood function with probability 1 (w.p.1). However, this point-wise convergence does not guarantee the consistency of θ̂_M; i.e., it does not establish that ${\widehat{\mathit{\theta }}}_M\stackrel{p}{\to }\widehat{\mathit{\theta }}$. A sufficient condition under which consistency can be established is the uniform convergence of (8), i.e.

$$\underset{M\to \infty }{lim}\underset{\mathit{\theta }\in \mathbf{\Theta }}{sup}\mid l_M(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x},{\mathit{\theta }}^{\ast })-l(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x})\mid =0,\text{w.p.}1,$$

and Theorem 1 provides this result.

Theorem 1

Under regularity conditions i)–iii) provided in Web Appendix B, it can be shown that

$$\underset{M\to \infty }{lim}\underset{\mathit{\theta }\in \mathbf{\Theta }}{sup}\mid l_M(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x},{\mathit{\theta }}^{\ast })-l(\mathit{\theta }\mid {\mathit{Y}}_p,\mathbf{x})\mid =0,\text{w.p}\mathrm{.1.}$$

For a proof of Theorem 1 see [39]. Given the uniform convergence established in Theorem 1, the following result provides the consistency of θ̂_M.

Corollary 1

Let θ̂ denote the unique element Θ, such that θ̂ = arg max_θ∈Θ l(θ|Y_p, x), and let {θ̂_M}_M be a sequence of maximizers of {l_M(θ|Y_p, x, θ^*)}_M, then ${\widehat{\mathit{\theta }}}_M\stackrel{p}{\to }\widehat{\mathit{\theta }}$, as M → ∞.

For a proof of Corollary 1 see [39]. Given the consistency of θ̂_M, the asymptotic normality is established.

Theorem 2

Under regularity conditions iv)–viii) provided in Web Appendix B, as M → ∞, then

$$\begin{array}{lll}\hfill \sqrt{M}\nabla l_M(\widehat{\mathit{\theta }}\mid {\mathit{Y}}_p,\mathbf{x},{\mathit{\theta }}^{\ast })& \stackrel{d}{\to }\hfill & N(\mathbf{0},\mathbf{A}),\hfill \\ \hfill -{\nabla }^2{l}_M({\widehat{\mathit{\theta }}}_M\mid {\mathit{Y}}_p,\mathbf{x},{\mathit{\theta }}^{\ast })& \stackrel{p}{\to }\hfill & \mathbf{B},\hfill \\ \hfill \sqrt{M}({\widehat{\mathit{\theta }}}_M-\widehat{\mathit{\theta }}\mid {\mathit{\theta }}^{\ast })& \stackrel{d}{\to }\hfill & N(\mathbf{0},\mathbf{\sum }),\hfill \end{array}$$

where Σ = B⁻¹AB⁻¹ and B = −∇²l(θ̂|Y_p, x).

The proof of Theorem 2 is classical [40] and a sketch is provided in Web Appendix C. Further, it is worthwhile to point out that it relatively easy to show that all of the parametric models considered herein adhere to the regularity conditions provided in Web Appendix C.

Establishing Theorem 2 provides two primary benefits; i.e., a means to identify the Monte Carlo sample size that maintains a specified level of precision and it allows one to perform typical large sample inference. Using the covariance matrix Σ, an asymptotic approximation of the Monte Carlo error associated with estimating θ̂ can be obtained. Consequently, a natural strategy for choosing the Monte Carlo sample size would be to specify M so that the Monte Carlo error is bounded by a predetermined value, say d²; i.e., choose M such that ${\sigma }_{max}^2{M}^{-1}\le d^2$, where ${\sigma }_{max}^2$ is the maximum diagonal element of Σ. Regretfully, in general a closed form expression for Σ does not exist, but it can be estimated. Under the regularity condition provided in Web Appendix B, a consistent estimator of B is given by B̂(θ̂_M|θ^*) = −∇²l_M(θ̂_M|Y_p, x, θ^*), and in Web Appendix C an estimator of A, which is denoted by  (θ̂_M|θ^*), is developed. Thus, an estimator of the covariance matrix Σ is given by

$$\widehat{\mathbf{\sum }}({\widehat{\mathit{\theta }}}_M\mid {\mathit{\theta }}^{\ast })=\widehat{\mathbf{B}}{({\widehat{\mathit{\theta }}}_M\mid {\mathit{\theta }}^{\ast })}^{-1}\widehat{\mathbf{A}}({\widehat{\mathit{\theta }}}_M\mid {\mathit{\theta }}^{\ast })\widehat{\mathbf{B}}{({\widehat{\mathit{\theta }}}_M\mid {\mathit{\theta }}^{\ast })}^{-1}.$$ (9)

Using this estimator, M can be chosen such that ${\widehat{\sigma }}_{max}^2{M}^{-1}\le d^2$, where ${\widehat{\sigma }}_{max}^2$ is the maximum diagonal element of Σ̂ (θ̂_M|θ^*). Further, B̂ (θ̂_M|θ^*)⁻¹ is a consistent estimator of the observed Fisher information matrix; i.e., $\widehat{\mathbf{B}}{({\widehat{\mathit{\theta }}}_M\mid {\mathit{\theta }}^{\ast })}^{-1}\stackrel{p}{\to }{\mathbf{B}}^{-1}$, where B = −∇²l(θ̂|Y_p, x). Using this estimator, one can conduct typical Wald type inference.

One will note that the process of estimating Σ relies on obtaining θ̂_M, which in turn depends on M. Consequently, for determining the appropriate Monte Carlo sample size, it is suggested that the following approach be implemented to ensure that a specified level of precision is attained.

• Step 1: Choose a value of d², the initial Monte Carlo sample size M₀, and θ^*.

• Step 2: Find the MCMLE, θ̂_M0, and calculate Σ̂(θ̂_M0 |θ^*).

• Step 3: Based on ${\widehat{\sigma }}_{max}^2$, the maximum diagonal element of Σ̂(θ̂_M0 |θ^*):

  1. Accept θ̂_M0 as the final estimate of θ̂, if ${\widehat{\sigma }}_{max}^2{M}_0^{-1}\le d^2$.

  2. Proceed to Step 4, if ${\widehat{\sigma }}_{max}^2{M}_0^{-1}>d^2$.

• Step 4: Reselect θ^* based on θ̂_M0 and recompute Σ̂(θ̂_M0 |θ^*).

• Step 5: Choose M such that ${\widehat{\sigma }}_{max}^2{M}^{-1}\le d^2$ and find θ̂_M, the MCMLE of θ̂.

Note, depending on the goals of the study, one could use this procedure either to control the precision of the whole parameter vector, or a subset of interest.

4. Simulation study

A simulation study was conducted in order to assess the finite sample performance of the proposed methodology. In this study, the following models for the biomarker levels of the individuals were considered:

$$\begin{array}{l}\mathrm{M}1:{\stackrel{\sim }{Y}}_{ij}\mid {\mathbf{x}}_{ij}~\mathrm{N}({\mu }_{ij},{\sigma }^2),{\mu }_{ij}={\mathbf{x}}_{ij}^{\prime }\mathit{\beta },\text{and}\mathit{\beta }={({\beta }_0,{\beta }_1,{\beta }_2)}^{\prime }={(4,1,2)}^{\prime };\\ \mathrm{M}2:log({\stackrel{\sim }{Y}}_{ij})\mid {\mathbf{x}}_{ij}~\mathrm{N}\{{\mu }_{ij},{\sigma }^2\},{\mu }_{ij}={\mathbf{x}}_{ij}^{\prime }\mathit{\beta },\text{and}\mathit{\beta }={({\beta }_0,{\beta }_1,{\beta }_2)}^{\prime }={(-1,1,2)}^{\prime };\\ \mathrm{M}3:{\stackrel{\sim }{Y}}_{ij}\mid {\mathbf{x}}_{ij}~\text{ST}({\mu }_{ij},\nu ),{\mu }_{ij}={\mathbf{x}}_{ij}^{\prime }\mathit{\beta },\text{and}\mathit{\beta }={({\beta }_0,{\beta }_1,{\beta }_2)}^{\prime }={(4,1,2)}^{\prime };\\ {\mathrm{M}}_4:{\stackrel{\sim }{Y}}_{ij}\mid {\mathbf{x}}_{ij}~\text{Gamma}\{1/{\sigma }^2,{({\sigma }^2{\mu }_{ij})}^{-1}\},{\mu }_{ij}={\eta }_1^{-1}({\mathbf{x}}_{ij}^{\prime }\mathit{\beta }),\text{and}\mathit{\beta }={({\beta }_0,{\beta }_1,{\beta }_2)}^{\prime }={(-1,1,2)}^{\prime };\\ {\mathrm{M}}_5:{\stackrel{\sim }{Y}}_{ij}\mid {\mathbf{x}}_{ij}~\text{Gamma}\{1/{\sigma }^2,{({\sigma }^2{\mu }_{ij})}^{-1}\},{\mu }_{ij}={\eta }_2^{-1}({\mathbf{x}}_{ij}^{\prime }\mathit{\beta }),\text{and}\mathit{\beta }={({\beta }_0,{\beta }_1,{\beta }_2)}^{\prime }={(0.5,0.1,0.2)}^{\prime };\end{array}$$

for i = 1, …, c_j and j = 1, …, J, where η₁(·) and η₂(·) are the inverse and log links, respectively, x_ij = (1, x_ij1, x_ij2)′, σ = 0.5, and ν = 4. Note, ST(μ, ν) denotes the shifted t-distribution, which has mean μ and degrees of freedom ν. The two covariates were independently sampled: one, x_ij1, from a standard normal distribution (which was supposed to emulate a standardized age effect) and the other, x_ij2, from a Bernoulli distribution having success probability 0.5 (which was supposed to correspond to a gender effect). For the purposes of this study, a common pool size c was specified, where c ∈ {1, …, 5}; i.e., c_j = c, for j = 1, …, J, where J ∈ {50, 100, 200, 500}. These choices were made to investigate the performance of the proposed approach across a broad spectrum of characteristics which could be encountered when modeling pooled biomarker data. In particular, the simulation configurations consider models both within (M1, M4, and M5) and outside (M2 and M3) of the class of generalized linear models which are commonly used to analyze biomarker data. Further, the different combinations of (c, J) provide an assessment of the impact of the pool and sample size on estimation and inference.

In both the binary group testing [31] and the pooled biomarker regression [30] literature it has been shown that pool composition, with respect to the covariates, has the potential to influence estimation efficiency. That is, randomly assigning subjects to pools, so that pools are heterogeneous with respect to covariate composition, can result in a loss in efficiency, while homogeneous pooling strategies (i.e., strategies which specify the pooling of subjects with similar covariates) maintain a high level of efficiency. For this reason, herein homogeneous pooling was used to assign subjects to pools. Once pool assignment was complete, the biomarker levels of the pools were determined as ${\stackrel{\sim }{Y}}_{p_j}=c^{-1}{\sum }_{i=1}^c{\stackrel{\sim }{Y}}_{ij}$, for j = 1, …, J. To investigate the effect of measurement error, an error contaminated measurement of Ỹ_pj was obtained as Y_pj |Ỹ_pj ~ N(Ỹ_pj, τ₂), for j = 1, …, J and τ ∈ {0.05, 0.10, 0.20}. Combining these simulated values two separate pooled data sets were created: {(Ỹ_pj, x_j), j = 1, …, J} and {(Y_pj, x_j), j = 1, …, J}. This process was repeated 500 times for each model and configuration of (c, J, τ ), resulting in 200,000 simulated data sets.

The methodology proposed in Section 2 was then implemented to analyze each of the aforementioned data sets. Throughout, the importance distributions for models M1–M5 were selected according to the strategies outlined in [37] and [30]; see Web Appendix A for their explicit forms and further discussion. To implement the model fitting approach described in Section (3), an initial Monte Carlo sample size of M₀ = 2000 was used and the tolerance was specified to be d² = 0.01. Note: to model the non-error contaminated data, minor alterations to the proposed approach are necessary. In particular, the density of Ỹ_pj, which is given in (1), was approximated by

$$f_j^M({\stackrel{\sim }{Y}}_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })=\frac{1}{M}\sum _{m=1}^M{c}_{j}f\left(c_j{\stackrel{\sim }{Y}}_{p_j}-\sum _{i=2}^{c_j}{\stackrel{\sim }{Y}}_{ij}^m|{\mathbf{x}}_{1j},\mathit{\theta }\right)\frac{h_j({\stackrel{\sim }{\mathit{Y}}}_{(-1)j}^m\mid {\mathbf{x}}_j,\mathit{\theta })}{h_j^{\ast }({\stackrel{\sim }{\mathit{Y}}}_{(-1)j}^m\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })},$$

where ${\stackrel{\sim }{\mathit{Y}}}_{(-1)j}^m={({\stackrel{\sim }{Y}}_{2j}^m,\dots ,{\stackrel{\sim }{Y}}_{c_{j}j}^m)}^{\prime }$, for m = 1, …, M, is a random sample from the importance distribution $h_j^{\ast }(·\mid {\mathbf{x}}_j,{\mathit{\theta }}^{\ast })$. Replacing $g_j^M(Y_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })$ in (8) by $f_j^M({\stackrel{\sim }{Y}}_{p_j}\mid {\mathbf{x}}_j,\mathit{\theta },{\mathit{\theta }}^{\ast })$ and maximizing with respect to θ results in obtaining an MCMLE of θ₀ when the pooled assessments are non-error laden. To complete model fitting for the error contaminated data it was assumed, as is common in the literature [22, 27], that the distribution of the measurement error was known. In practice this assumption may not be reasonable, but the true form of this distribution could be replaced by an estimate, which can be obtained through standard techniques; e.g., see [33]. Further, this approach is implemented in Section 5. Note, since additive measurement error is assumed the alternate formulation of (4), which is presented in Web Appendix A.2, is implemented herein.

In order to assess the performance of the proposed approach, it is first noted that when c = 1 and the Ỹ_pj are observed (i.e., the individual level data is observed without measurement error), standard regression techniques are applicable, and were implemented. This was done in order to provide a baseline by which comparisons could be made. Further, under the considered simulation configurations for model M1 it is possible to obtain an analytical expression for the MLE of θ₀ based on either {(Ỹ_pj, x_j), j = 1, …, J} or {(Y_pj, x_j), j = 1, …, J}, for c = 1, …, 5; see Web Appendix D for further details. Consequently, both the proposed approach and the aforementioned analytical techniques were used to analyze the simulated data created under model M1. Comparisons between the results obtained from these two techniques allows one to assess the error that is introduced into the analysis by stochastically estimating the MLE through the proposed methodology. Lastly, the MCEM algorithm proposed in [30] was used to analyze the non-error contaminated data under model M2; i.e., {(Ỹ_pj, x_j), j = 1, …, J}. This competing approach was specifically designed for analyzing data of this form and this comparison allows one to assess the performance of the proposed methodology with respect to an existing technique.

Table 1 summarizes the estimates of the regression coefficients (i.e., β) that were obtained from analyzing the non-error contaminated pooled observations via the proposed approach and the alternate techniques, for all considered models and values of c, when J = 100. In particular, Table 1 summarizes the empirical bias and the sample standard deviation of the 500 point estimates of the regression coefficients stratified by model and pool size. The average of the 500 estimated standard errors, and the estimated coverage probability associated with 95% Wald confidence intervals are also included. Web Tables 1 and 2 in the Web Appendix provide the analogous results for J = 50 and 200, respectively. From these results, one will first notice that the point estimates obtained by the proposed approach exhibit little if any evidence of bias. Secondly, the sample standard deviation and the average standard error of the 500 estimates are predominantly in agreement. Further, the estimated coverage probabilities are all at their nominal level. These finding suggest that the approach proposed in Section 3 for estimating the asymptotic variance performs well for finite samples, and could subsequently be used to reliably conduct Wald-type inference.

Table 1.

Presented results include the empirical bias (Bias) of the 500 estimated regression coefficients and there sample standard deviation (SD) obtained from analyzing data generated according to models M1–M5, for all considered pool sizes when J = 100 in the absence of measurement error. Also included are the average estimated standard errors (SE) and the empirical coverage probabilities (Cov) associated with 95% Wald confidence intervals. Three model fitting procedures were implemented, the proposed methodology (MCMLE), the analytical approach described in Section 4 (MLE), and the MCEM algorithm, with the latter two techniques only being applicable for models M1 and M2, respectively.

Model		Measure	c = 1	c = 2	c = 3	c = 4	c = 5
M1(MCMLE)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.03)
		Cov(SE)	0.96(0.07)	0.94(0.05)	0.94(0.04)	0.95(0.03)	0.92(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.03)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.96(0.05)	0.95(0.04)	0.93(0.03)	0.94(0.02)	0.94(0.02)
	β2	Bias(SD)	0.00(0.10)	0.00(0.07)	0.00(0.06)	0.00(0.05)	0.00(0.05)
		Cov(SE)	0.94(0.10)	0.94(0.07)	0.94(0.06)	0.94(0.05)	0.93(0.04)
M1(MLE)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.03)
		Cov(SE)	0.96(0.07)	0.95(0.05)	0.94(0.04)	0.95(0.04)	0.92(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.03)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.96(0.05)	0.96(0.04)	0.94(0.03)	0.95(0.03)	0.94(0.02)
	β2	Bias(SD)	0.00(0.10)	0.00(0.07)	0.00(0.06)	0.00(0.05)	0.00(0.05)
		Cov(SE)	0.94(0.10)	0.95(0.07)	0.94(0.06)	0.94(0.05)	0.93(0.04)
M2(MCMLE)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.04)
		Cov(SE)	0.94(0.07)	0.95(0.05)	0.95(0.04)	0.94(0.04)	0.94(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.04)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.95(0.05)	0.94(0.04)	0.95(0.03)	0.94(0.03)	0.94(0.02)
	β2	Bias(SD)	0.01(0.10)	0.00(0.08)	0.00(0.06)	0.00(0.05)	0.00(0.05)
		Cov(SE)	0.95(0.10)	0.93(0.07)	0.96(0.06)	0.97(0.05)	0.96(0.05)
M2(MCEM)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.04)
		Cov(SE)	0.94(0.07)	0.95(0.05)	0.95(0.04)	0.93(0.04)	0.94(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.04)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.95(0.05)	0.94(0.04)	0.94(0.03)	0.94(0.03)	0.94(0.02)
	β2	Bias(SD)	0.01(0.10)	0.00(0.08)	0.00(0.06)	0.00(0.05)	0.00(0.05)
		Cov(SE)	0.95(0.10)	0.92(0.07)	0.96(0.06)	0.97(0.05)	0.96(0.05)
M3(MCMLE)	β0	Bias(SD)	0.00(0.16)	−0.01(0.12)	0.00(0.11)	0.00(0.10)	0.00(0.09)
		Cov(SE)	0.96(0.16)	0.95(0.13)	0.94(0.11)	0.95(0.09)	0.94(0.08)
	β1	Bias(SD)	0.00(0.12)	0.00(0.09)	0.00(0.08)	0.00(0.06)	0.00(0.06)
		Cov(SE)	0.94(0.12)	0.94(0.09)	0.96(0.08)	0.95(0.07)	0.94(0.06)
	β2	Bias(SD)	0.01(0.24)	0.01(0.18)	0.00(0.16)	0.00(0.14)	0.00(0.13)
		Cov(SE)	0.94(0.23)	0.93(0.18)	0.93(0.15)	0.95(0.13)	0.95(0.12)
M4(MCMLE)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.03)
		Cov(SE)	0.96(0.07)	0.94(0.05)	0.94(0.04)	0.94(0.03)	0.94(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.03)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.96(0.05)	0.98(0.04)	0.93(0.03)	0.95(0.03)	0.93(0.02)
	β2	Bias(SD)	0.00(0.10)	0.00(0.07)	0.00(0.06)	0.00(0.05)	0.00(0.04)
		Cov(SE)	0.95(0.10)	0.95(0.07)	0.95(0.06)	0.95(0.05)	0.95(0.04)
M5(MCMLE)	β0	Bias(SD)	0.01(0.04)	0.00(0.03)	0.00(0.02)	0.00(0.02)	0.00(0.02)
		Cov(SE)	0.94(0.04)	0.94(0.02)	0.95(0.02)	0.92(0.02)	0.96(0.02)
	β1	Bias(SD)	0.00(0.03)	0.00(0.02)	0.00(0.01)	0.00(0.01)	0.00(0.01)
		Cov(SE)	0.94(0.03)	0.94(0.02)	0.95(0.01)	0.96(0.01)	0.97(0.01)
	β2	Bias(SD)	0.00(0.06)	0.00(0.04)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.95(0.06)	0.95(0.04)	0.94(0.03)	0.93(0.03)	0.97(0.03)

To assess the effect that pooling has on parameter estimation and inference, one may compare the parameter estimates obtained from the individual level data (i.e., when c = 1) to those obtained from the pooled data (i.e., when c > 1). These comparisons reveal two striking features of the proposed methodology. First, the estimates of the regression coefficients based on the pooled data are more efficient (i.e., have a smaller sample standard deviation and average standard error) than the estimates obtained from analyzing the individual level data. Moreover, the efficiency of the estimators tends to increase with the pool size c. This finding suggests that the process of analyzing biomarker assessments made on pools, rather than individuals, will result in more precise estimation and inference, when a fixed number of assessments J is mandated. Secondly, this comparison also suggests that the error that is introduced by approximating the observed data likelihood through the expression in (8), is appropriately controlled by the approach presented in Section 3. This assertion is reinforced when one considers the comparison between the estimates obtained from the proposed methodology and the analytical form of the MLE under model M1. In particular, the summary measures of the estimated regression coefficients obtained from these two techniques are practically identical. This finding provides evidence that the approach developed in Section 3 can be used to appropriately control the precision of the MCMLE.

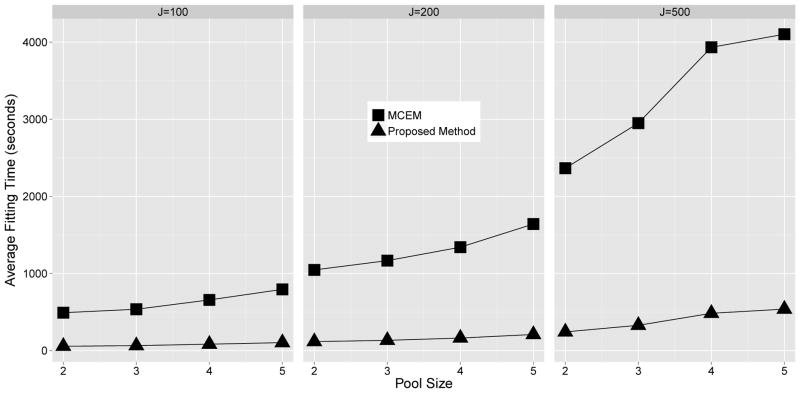
Table 1 also provides a summary of the estimated regression coefficients obtained from the MCEM algorithm proposed by [30], for model M2. In comparing these results to the those obtained from the proposed methodology one will note that the two procedures are practically identical in terms of estimation and inference. Though similar in terms of estimation and inference, an advantage of the proposed methodology over that of the MCEM algorithm arises in the computational time required to complete model fitting. Figure 1 provides the average model fitting time for both the proposed approach and the MCEM algorithm, for all considered combinations of (c, J) under model M2. From these results one will note that the proposed approach is able to complete model fitting roughly 5 to 8 times faster than the MCEM algorithm, on average. Moreover, it appears that the average model fitting time for the MCEM algorithm increases more rapidly with both the sample size (J) and pool size (c). Note, the aforementioned comparisons between the proposed approach and the MCEM algorithm were implemented using code written solely in R, which used no advanced computing techniques (e.g., interfacing R with C++, parallel processing, etc.), and was run on a Optiplex 790 desktop running Windows 7 with an Intel i7-2600 3.40 GHz CPU and 16GB of RAM. Further, these comparisons are for data that are not subject to measurement error, as the MCEM algorithm was not designed to correct for the effect of error laden measurements.

Figure 1.

Simulation study: Average model fitting times required by the proposed methodology and the MCEM algorithm developed in Mitchell et al. (2014) for data generated under model M2 which is not subject to measurement error. Presented results are stratified by pool size (c) and the number of pools (J).

Table 2 summarizes the estimates of the regression coefficients that were obtained from analyzing the error contaminated pooled observations via the proposed approach, for all considered models and values of c, when J = 100 and τ = 0.05. Web Tables 3–10 in the Web Appendix provides the analogous results for the other considered values of J and τ. The results from this study reinforce all of the main findings discussed above; i.e., the proposed approach can be used to accurately and efficiently analyze pooled biomarker data, while correcting for the effects of measurement error. In summary, the results of this study highlight the three definitive advantages of the proposed methodology, when compared to other existing techniques: first, the proposed technique can account for data subject to measurement error; second, the methodology outlined in Section 2 can be implemented under many different parametric models to conduct the regression analysis of measurements taken on pools; and third, the proposed methodology is far less computationally burdensome when compared to existing techniques.

Table 2.

Simulation study: Presented results include the empirical bias (Bias) of the 500 estimated regression coefficients and there sample standard deviation (SD) obtained from analyzing data generated according to models M1–M5, for all considered pool sizes when J = 100 in the presence of measurement error (τ = 0.05). Also included are the average estimated standard errors (SE) and the empirical coverage probabilities (Cov) associated with 95% Wald confidence intervals. Two model fitting procedures were implemented, the proposed methodology (MCMLE) and the analytical approach described in Section 4 (MLE), with the latter technique only being applicable for model M1.

Model		Measure	c = 1	c = 2	c = 3	c = 4	c = 5
M1(MCMLE)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.03)
		Cov(SE)	0.93(0.07)	0.96(0.05)	0.94(0.04)	0.91(0.04)	0.94(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.04)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.95(0.05)	0.94(0.04)	0.97(0.03)	0.93(0.03)	0.94(0.02)
	β2	Bias(SD)	0.00(0.10)	0.00(0.07)	0.00(0.06)	0.00(0.05)	0.00(0.05)
		Cov(SE)	0.94(0.10)	0.96(0.07)	0.94(0.06)	0.93(0.05)	0.92(0.05)
M1(MLE)	β0	Bias(SD)	0.00(0.07)	0.00(0.05)	0.00(0.04)	0.00(0.04)	0.00(0.03)
		Cov(SE)	0.94(0.07)	0.96(0.05)	0.94(0.04)	0.92(0.04)	0.95(0.03)
	β1	Bias(SD)	0.00(0.05)	0.00(0.04)	0.00(0.03)	0.00(0.03)	0.00(0.02)
		Cov(SE)	0.95(0.05)	0.95(0.04)	0.97(0.03)	0.93(0.03)	0.95(0.02)
	β2	Bias(SD)	0.00(0.10)	0.00(0.07)	0.00(0.06)	0.00(0.05)	0.00(0.05)
		Cov(SE)	0.94(0.10)	0.96(0.07)	0.95(0.06)	0.93(0.05)	0.93(0.05)
M2(MCMLE)	β0	Bias(SD)	0.02(0.08)	0.00(0.06)	0.01(0.05)	0.01(0.05)	0.01(0.04)
		Cov(SE)	0.94(0.08)	0.94(0.06)	0.94(0.05)	0.93(0.05)	0.94(0.04)
	β1	Bias(SD)	−0.01(0.05)	0.00(0.04)	0.00(0.03)	0.00(0.03)	0.00(0.03)
		Cov(SE)	0.96(0.06)	0.93(0.04)	0.96(0.03)	0.94(0.03)	0.94(0.03)
	β2	Bias(SD)	−0.01(0.10)	0.00(0.08)	0.00(0.06)	−0.01(0.06)	0.00(0.05)
		Cov(SE)	0.95(0.10)	0.94(0.08)	0.94(0.07)	0.94(0.06)	0.94(0.05)
M3(MCMLE)	β0	Bias(SD)	0.00(0.17)	−0.01(0.13)	0.00(0.11)	0.00(0.09)	0.00(0.09)
		Cov(SE)	0.93(0.17)	0.94(0.13)	0.94(0.11)	0.94(0.09)	0.94(0.08)
	β1	Bias(SD)	0.00(0.12)	0.00(0.09)	−0.01(0.08)	0.00(0.07)	0.00(0.06)
		Cov(SE)	0.95(0.12)	0.94(0.09)	0.95(0.08)	0.93(0.07)	0.94(0.06)
	β2	Bias(SD)	−0.01(0.24)	0.01(0.19)	0.00(0.15)	0.00(0.13)	0.00(0.12)
		Cov(SE)	0.95(0.24)	0.94(0.18)	0.95(0.15)	0.95(0.13)	0.95(0.12)
M4(MCMLE)	β0	Bias(SD)	0.00(0.08)	0.00(0.06)	0.00(0.05)	0.00(0.05)	0.00(0.04)
		Cov(SE)	0.95(0.08)	0.97(0.06)	0.95(0.05)	0.93(0.04)	0.96(0.04)
	β1	Bias(SD)	−0.01(0.06)	−0.01(0.04)	−0.01(0.04)	0.00(0.03)	0.00(0.03)
		Cov(SE)	0.95(0.05)	0.95(0.04)	0.93(0.03)	0.92(0.03)	0.95(0.03)
	β2	Bias(SD)	−0.01(0.11)	0.00(0.08)	0.00(0.06)	−0.01(0.06)	0.00(0.05)
		Cov(SE)	0.92(0.10)	0.95(0.08)	0.94(0.06)	0.94(0.06)	0.94(0.05)
M5(MCMLE)	β0	Bias(SD)	0.00(0.04)	0.00(0.03)	0.00(0.02)	0.00(0.02)	0.00(0.02)
		Cov(SE)	0.96(0.04)	0.94(0.02)	0.94(0.02)	0.94(0.02)	0.93(0.02)
	β1	Bias(SD)	0.00(0.03)	0.00(0.02)	0.00(0.01)	0.00(0.01)	0.00(0.01)
		Cov(SE)	0.96(0.03)	0.96(0.02)	0.96(0.02)	0.94(0.01)	0.95(0.01)
	β2	Bias(SD)	0.00(0.06)	0.00(0.04)	0.00(0.04)	0.00(0.03)	0.00(0.03)
		Cov(SE)	0.95(0.06)	0.95(0.04)	0.93(0.03)	0.95(0.03)	0.94(0.03)

5. Data application

The Collaborative Perinatal Project (CPP) was a longitudinal study, conducted from 1957 to 1974, which was aimed at assessing multiple hypotheses regarding varying aspects of maternal and child health [41]. The data collected by this study constitutes an important resource for biomedical research in many areas of perinatology and pediatrics. In 2007 data from the CPP was used in a nested case-control study which examined whether circulating levels of chemokines are related to miscarriage risk; for further details see [42]. In particular, this study considered measuring cytokine levels, to include monocyte chemotactic protein-1 (MCP1), on stored serum samples from CPP participants who had experienced a miscarriage (cases) and those who had not (controls), where cases and controls were matched based on gestational age. This analysis focuses on the MCP1 measurements obtained in the aforementioned study and considers only the participants for which full covariate information was available, where the selected explanatory variables consist of age (standardized; denoted by x₁), race (1=Africa American/0=otherwise; denoted by x₂), and miscarriage status (1=yes/0=no; denoted by x₃).

This data set possess two unique features which are of particular interest; i.e., MCP1 measurements were taken on both individual and pooled specimens, in duplicate. Consequently, the data available from this study can be divided into two separate data sets: the pooled data (PD) which consists of 81 and 350 MCP1 measurements taken on individual and pooled (with c_j = 2 for all j) specimens, respectively, and the individual data (ID) which consists of 752 measurements taken on individual specimens. This feature allows one to asses the effect of pooling on parameter estimation, a characteristics that could not be examined if only pooled data was considered. Further, within the PD and ID the MCP1 measurements were taken in duplicate for most of the specimens (pooled and individual), which allowed for the detection and subsequently the estimation of the measurement error [33]. In particular, through differencing the replicated MCP1 measurements it was found that it was reasonable to assume that additive measurement error was present, and that the error terms followed a normal distribution with mean 0 and variance τ². From these differences, τ² was estimated to be 0.044² and 0.050² based on the ID and PD, respectively.

As with many cytokines, the MCP1 measurements are positive and seem to follow a right-skewed distribution. For this reason, three parametric models were considered for the MCP1 levels: a log-normal regression model and a gamma regression model under two different link functions, namely the log and inverse links. The linear predictor of the full model was specified to be

$$\eta ={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_4{x}_1^2+{\beta }_5{x}_1{x}_2+{\beta }_6{x}_1{x}_3+{\beta }_7{x}_2{x}_3,$$

where β = (β₀, …, β₇)′ are the regression coefficients. To identify the final model, best subsets regression, driven by the Akaike information criterion, was implemented to evaluate each of the 2⁷ = 128 submodels. In order to assess the effect of measurement error, this process, for each parametric model, was completed both acknowledging and ignoring measurement error for both data sets (i.e., ID and PD). Consequently, this analysis considers 12 different scenarios, each of which required the fitting of 128 models. For all of these analyses, the proposed methodology was implemented in the same fashion as was discussed in Section 4.

Table 3 provides the top 5 models (ranked according to their AIC values) within each scenario. From these results, it can be seen that under all considered parametric models, both for the ID and PD, the collection of predictor variables most frequently selected include age (x₁), miscarriage status (x₃), and the interaction between miscarriage status and race (x₂x₃). For this reason, the final model under all scenarios was chosen to possess these predictor variables. For comparative purposes, the MCEM algorithm proposed by [30] was also implemented to perform model fitting and evaluation for the PD under the log-normal regression model, assuming that the observed outcomes were non-error laden. The model estimates, and consequently the AIC values, obtained by both the MCEM algorithm and the proposed methodology were practically identical. The marked difference between these two competing techniques arose in the computational time required to complete best subsets regression. In particular, the MCEM algorithm required 74 hours to complete this process, while the proposed approach took only 7. Consequently, based on these findings it is conjectured that the proposed methodology would likely be preferred in practice due to its computational efficiency, especially for the purposes of completing model selection via automated search algorithms.

Table 3.

Data application: The top five models according to their AIC values for all 12 considered scenarios, where a ✓ denotes that a particular predictor was included in the model. The predictor variables x₁, x₂, and x₃ represent the participant’s age, race, and miscarriage status, respectively. Note, the presence (absence) of “ ^*” indicates that the MCMLE accounted for (ignored) the effect of measurement error.

Model	Data set	x1	x2	x3	$x_1^2$	x1x2	x1x3	x2x3
Log-normal		✓	✓	✓				✓
	ID	✓		✓				✓
		✓	✓	✓
		✓	✓	✓		✓		✓
		✓	✓	✓	✓			✓
		✓		✓				✓
	ID*	✓	✓	✓				✓
		✓		✓			✓	✓
		✓		✓		✓		✓
		✓	✓
				✓				✓
	PD	✓		✓				✓
		✓		✓			✓	✓
		✓		✓		✓		✓
				✓	✓			✓
		✓		✓				✓
	PD*	✓	✓	✓				✓
		✓		✓			✓	✓
		✓	✓	✓			✓	✓
		✓	✓	✓		✓		✓
Gamma(log link)		✓		✓				✓
	ID	✓	✓	✓				✓
		✓		✓			✓	✓
		✓		✓	✓			✓
		✓		✓		✓		✓
		✓		✓				✓
	ID*	✓	✓	✓				✓
		✓		✓			✓	✓
		✓		✓		✓		✓
		✓		✓	✓			✓
		✓	✓	✓				✓
	PD	✓	✓	✓			✓	✓
		✓	✓	✓		✓		✓
		✓	✓	✓	✓			✓
		✓	✓	✓		✓	✓	✓
		✓	✓	✓				✓
	PD*	✓	✓	✓		✓		✓
		✓	✓	✓			✓	✓
			✓	✓		✓		✓
Gamma(inverse link)		✓	✓	✓	✓	✓		✓
		✓		✓				✓
	ID	✓	✓	✓				✓
		✓		✓			✓	✓
		✓		✓		✓		✓
		✓		✓	✓			✓
		✓		✓				✓
	ID*	✓		✓			✓	✓
		✓		✓		✓		✓
		✓	✓	✓				✓
		✓		✓	✓			✓
		✓	✓	✓				✓
	PD	✓	✓	✓			✓	✓
		✓	✓	✓		✓		✓
		✓	✓	✓	✓			✓
			✓	✓		✓	✓	✓
		✓	✓	✓				✓
	PD*	✓	✓	✓			✓	✓
		✓	✓	✓		✓		✓
		✓	✓	✓	✓			✓
			✓	✓		✓	✓	✓

Table 4 provides the estimates of the regression coefficient along with their estimated standard errors and p-values for the final model, across the 12 different scenarios. These results warrant several comments, first one will note that ignoring measurement error in this application impacted both estimation and inference, for both the ID and PD; i.e., there were 4 (1) cases for the ID (PD) in which a regression coefficient was deemed to be significant (at the α = 0.05 significance level) when measurement error was accounted for but were found to be insignificant when it was ignored. Secondly, the estimates obtained from the PD are in general agreement with the estimates resulting from the ID, across all of the considered configurations. Although, in some instances discrepancies were observed; e.g., under the gamma regression model with the inverse link, the estimates of the regression coefficient associated with the interaction term obtained from the ID and PD were 1.972 and 7.002, respectively.

Table 4.

Data application: Presented results include the regression parameter estimates (Est.), the estimated standard errors (SE), and the corresponding p-values (P-value), under all 12 considered scenarios. Also included are the analogous results obtained from the artificial constructed homogeneous pooling data (HPD). Note, the presence (absence) of “ ^*” indicates that the MCMLE accounted for (ignored) the effect of measurement error.

Model	Data set		Intercept	Age	Miscarriage	Race*Miscarriage
Lognormal	ID	Est.(SE)	−2.130(0.055)	0.111(0.039)	0.271(0.087)	−0.508(0.122)
		P-value	0.000	0.005	0.002	0.000
	ID*	Est(SE)	−2.091(0.053)	0.117(0.037)	0.220(0.082)	−0.409(0.119)
		P-value	0.000	0.002	0.007	0.001
	PD	Est.(SE)	−2.438(0.070)	0.105(0.066)	0.314(0.116)	−0.822(0.225)
		P-value	0.000	0.112	0.007	0.000
	PD*	Est.(SE)	−2.365(0.077)	0.155(0.065)	0.262(0.115)	−0.681(0.246)
		P-value	0.000	0.018	0.023	0.006
	HPD*	Est.(SE)	−2.116(0.059)	0.110(0.041)	0.220(0.089)	−0.360(0.128)
		P-value	0.000	0.007	0.014	0.005
Gamma (log link)	ID	Est.(SE)	−1.592(0.075)	0.099(0.054)	0.227(0.119)	−0.406(0.167)
		P-value	0.000	0.066	0.056	0.015
	ID*	Est.(SE)	−1.615(0.053)	0.100(0.038)	0.232(0.084)	−0.403(0.119)
		P-value	0.000	0.008	0.006	0.000
	PD	Est.(SE)	−1.680(0.061)	0.171(0.058)	0.305(0.099)	−0.976(0.207)
		P-value	0.000	0.003	0.002	0.000
	PD*	Est.(SE)	−1.708(0.067)	0.176(0.063)	0.311(0.109)	−1.033(0.249)
		P-value	0.000	0.005	0.004	0.000
	HPD*	Est.(SE)	−1.601(0.058)	0.097(0.042)	0.230(0.091)	−0.407(0.130)
		P-value	0.000	0.020	0.012	0.002
Gamma (inverse link)	ID	Est.(SE)	4.922(0.365)	−0.424(0.227)	−0.959(0.511)	1.947(0.892)
		P-value	0.000	0.062	0.061	0.029
	ID*	Est.(SE)	5.033(0.265)	−0.437(0.163)	−0.989(0.369)	1.972(0.647)
		P-value	0.000	0.008	0.007	0.002
	PD	Est.(SE)	5.365(0.322)	−0.667(0.228)	−1.301(0.447)	6.429(1.915)
		P-value	0.000	0.003	0.004	0.001
	PD*	Est.(SE)	5.518(0.368)	−0.703(0.253)	−1.350(0.503)	7.002(2.507)
		P-value	0.000	0.006	0.007	0.005
	HPD*	Est.(SE)	4.964(0.286)	−0.418(0.177)	−0.977(0.398)	1.973(0.705)
		P-value	0.000	0.018	0.014	0.005

One plausible explanation for these deviations involves the pooling strategy considered in the original study; i.e. cases were randomly pooled with cases and controls with controls. In order to investigate this assertion, a second pooled data (HPD) set was artificially constructed using the ID, where pools, of size 2, were formed homogeneously with respect to the participants covariate information and the MCP1 measurement for each pool was taken to be the average of the MCP1 measurements for the individuals of which it was comprised. Table 4 provides the parameter estimates obtained from the analysis of the HPD, and from these results one will note that the use of homogeneous pooling has practically resolved all of the aforementioned discrepancies; i.e., the regression parameter estimates based on ID and HPD are practically identical. Further, the regression parameter estimates obtained from the HPD were generally more accurate and efficient than those based on the PD which contains 80 more observations.

The aforementioned analysis illustrates the primary strengths of the proposed approach; i.e., this new methodology can be used to conduct the regression analysis of pooled data under a variety of parametric models, it can be used to directly account for the effects of measurement error, and it is computationally efficient. Further, this study also illustrates that in order to obtain the most accurate estimation and inference homogeneous pooling should be implemented in practice. Similar findings were reported in [30].

6. Discussion

In this work, a general framework for the regression analysis of assessments taken on pools has been developed. The proposed approach allows for the regression analysis under practically all parametric models, can be used to account for the effects of measurement error if present, and is computationally efficient. The asymptotic properties of the proposed technique have been established. Through simulation studies the proposed approach was shown to obtain precise estimates and accurate inference under several common parametric models, as well as to be superior, with respect to computational efficiency, to existing techniques. Further, the simulation study indicated that the regression analysis of pooled data can result in parameter estimates that are more efficient than those which are based on individual level data, if pools are formed homogeneously and a fixed number of assessments, J, are to be made. Similarly, from the data application one will observe that for a fixed population size, there is practically no loss in estimation efficiency when analyzing homogeneously pooled outcomes. In order to further disseminate this work, software, programmed in R, which implements the proposed methodology has been developed and is available upon request.

The primary focus of the work presented in this manuscript was placed on developing a general methodology for conducting the regression analysis of pooled assessments, based on an assumed parametric model for the latent individual level data. A topic for future research could involve developing techniques which can be used to evaluate the selected parametric model; e.g., goodness-of-fit tests. Further, similar to [29], future research in this area could focus on developing pooling algorithms which attempt to minimize the loss in estimation efficiency that is incurred due to pooling.