High‐Pressure NiAs‐Type Modification of FeN

Abstract

The combination of laser‐heated diamond anvil cells and synchrotron Mössbauer source spectroscopy were used to investigate high‐temperature high‐pressure chemical reactions of iron and iron nitride Fe₂N with nitrogen. At pressures between 10 and 45 GPa, significant magnetic hyperfine splitting indicated compound formation after annealing at 1300 K. Subsequent in situ X‐ray diffraction reveals a new modification of FeN with NiAs‐type crystal structure, as also rationalized by first‐principles total‐energy and chemical‐bonding studies.

Since the pioneering research into binary nitrides,1 this field of chemistry has grown into a rich diversity of sub‐classes.2, 3, 4, 5, 6, 7, 8, 9 One of the families that has been investigated more intensely is that of iron nitrides. Several different phases are already known,10 which range from the most iron‐rich phases, such as α′′‐Fe₁₆N₂ or α′‐Fe₈N through γ′‐Fe₄N, ϵ‐Fe₃N_1±x and ζ‐Fe₂N to γ′′′‐FeN,11 which represents the most nitrogen‐rich phase to date. However, in 2011, the existence of nitrogen‐richer FeN₂ was predicted.12 Iron nitrides are used as coatings for steel‐based materials combining hardening with protection against corrosion. More recent studies have shown that iron nitrides can be used as catalysts for the production of hydrocarbons13 and as a potential treatment of cancer cells.14 Moreover, iron nitrides are of relevance for the geosciences as they may be an important constituent of the Earth's core. Since the interaction of iron and nitrogen at higher pressures has seen little attention, there remains much to be investigated with regard to properties and phase relations.15, 16, 17

In 1993, the much debated cubic FeN was reported.11, 18, 19, 20 The published data supports either the rock salt structure,21, 22, 23, 24 or the zinc blende arrangement.25, 26 An independent prediction stated that cubic FeN would actually prefer the zinc blende type, while FeN_x (x=0.5–0.7) would adopt a rock salt arrangement,25 but results remain controversial. Single‐phase thin films of γ′′′‐FeN adopt a zinc blende pattern.20 Herein, we report on synthesis, magnetic properties, and electronic structure of NiAs‐type bulk FeN. For synthesis at elevated temperatures and pressures, we chose the diamond anvil cell technique combined with laser heating. Phase transformations were probed with synchrotron source Mössbauer spectroscopy which serves as an ideal tool to investigate electronic configuration and chemical state of iron.27, 28, 29

Two different types of experiments were carried out, one using ⁵⁷Fe and the other using ζ‐⁵⁷Fe₂N, both with N₂ as reactant and pressure medium. Samples heated up to 1300 K at pressures below 10 GPa form an iron nitride with a composition close to ζ‐Fe₂N/ϵ‐Fe₃N_1.4.30 At pressures higher than 10 GPa, a new phase was observed after annealing, which gave moderate magnetic hyperfine splitting, as shown in Figure 1 (green curve). The magnetic splitting remains essentially up to 45 GPa, suggesting a quite robust magnetic order. Upon heating at a pressure below 10 GPa, the new phase transforms back into ζ‐Fe₂N/ϵ‐Fe₃N_1.4.

Figure 1.

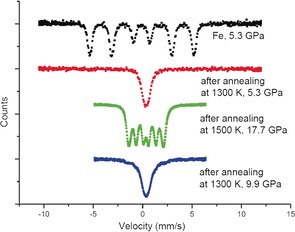
⁵⁷Fe‐Mössbauer spectra at various pressures before and after heat treatment of iron–nitrogen mixtures. Black: Initial ⁵⁷Fe in N₂ pressure medium at 5.3 GPa prior to laser heating. Red: After laser heating at 5.3 GPa the spectrum indicates formation of ζ‐⁵⁷Fe₂N/ϵ‐⁵⁷Fe₃N_1+x 30 Green: Multiplet of the new phase after laser heating. Blue: Spectrum indicating the reformation of ζ‐⁵⁷Fe₂N/ϵ‐⁵⁷Fe₃N_1+x after laser heating at pressures below 10 GPa.

There are a distinct major and a minor component observed by comparing the ⁵⁷Fe‐Mössbauer spectra from all samples annealed above 1000 K and 10 GPa (Figure 2 and Figure S1 in the Supporting Information). The major component of all spectra consists of a magnetic sextet, while the minor component represents a non‐magnetic singlet (Table 1). After annealing, magnetic components have similar hyperfine parameters: a small magnetic hyperfine field (ca. 11 T) and a moderate center shift (ca. 0.35 mm s⁻¹), suggesting the presence of a new phase. The minor component singlet with a center shift of 0.4 mm s⁻¹ corresponds to the center shift of ζ‐Fe₂N.30

Figure 2.

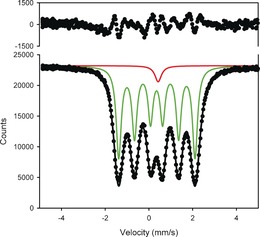
⁵⁷Fe‐Mössbauer spectra of ζ‐⁵⁷Fe₂N in N₂ pressure medium, after annealing, at 17.7 GPa.

Table 1.

Refined ⁵⁷Fe‐Mössbauer spectra parameters before annealing and of the major component after annealing.[a]

Sample	δ [mm s−1]	ΔE Q [mm s−1]	ΔE M (T)
57Fe in N2 (0.1 MPa, not annealed)	−0.073±0.005	0.011±0.009	32.645±0.037
57Fe in N2 (11.9 GPa, annealed)	0.305±0.012	0.015±0.019	11.553±0.063
ζ‐57Fe2N in N2 (0.1 MPa, not annealed)	0.441±0.023	–	–
ζ‐57Fe2N in N2 (17.7 GPa, annealed)	0.356±0.002	0.012±0.003	10.814±0.014

[a] δ represents the center shift, ΔE_Q the quadrupole splitting, and ΔE _M the hyperfine field. Spectra were fit using MossA software.32

X‐ray diffraction patterns were obtained at pressures of 13.3 GPa, 4.4 GPa, and 0.1 MPa using synchrotron radiation. Patterns of the new phase were indexed on basis of a hexagonal unit cell, and Rietveld refinements indicate a NiAs‐type arrangement (Figure 3 a, b and Table S1).31 Most patterns contain extra reflections, which are mainly attributed to N₂ or residual ζ‐Fe₂N. Despite the small number of experiments for pressure–volume correlation, a least squares fit of a Murnaghan‐type equation of state to the experimental data results in the reasonable values V ₀=33.78(3) ų and B ₀=198(8) GPa with B₀′ fixed to 4.

Figure 3.

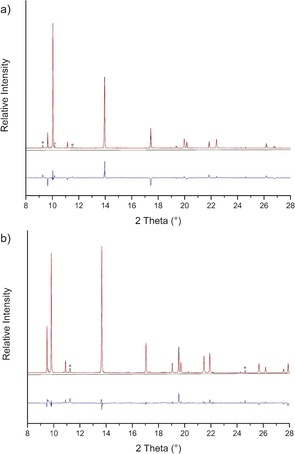
Crystal‐structure refinements of NiAs‐type FeN based on full diffraction profiles at a) 13.3 GPa and b) 0.1 MPa. The observed pattern is shown in black, the calculated one in red, and the difference in blue. The marked reflections (*) are attributed to secondary phases (see text).

Crystal structure refinements based on full diffraction profiles measured at various pressures and sample positions indicate a broad homogeneity range for the new phase Fe_xN with x in the estimated range of between 0.60(5) and 1.0(1). In the following we will denote the phase as FeN.

NiAs‐type FeN consists of a hexagonal closed packing of nitrogen, with the iron occupying all octahedral voids for x=1. These FeN₆ octahedra form infinite chains by face sharing along the c direction (Figure 4). To our knowledge, this is not only the first face‐sharing arrangement of FeN₆ octahedra in a nitride, but also the single NiAs‐type 3d transition‐metal nitride. Although some have been predicted, such as VN33 and MoN,34 they remain elusive and only heavier homologues, such as δ‐NbN35 and TaN,36 have been successfully synthesized. Comparison of the interatomic iron distances of NiAs‐type FeN and ϵ‐iron with the same iron arrangement reveals37 that d(Fe–Fe) along the c axis varies only slightly (2.467 Å versus 2.442 Å) whereas along the a axis there is a larger difference: In the nitride, the Fe–Fe distance is significantly larger than in ϵ‐iron (2.737 Å versus 2.473 Å). Typical Fe–N distances range from 1.8 Å to 2.0 Å, but in NiAs‐type FeN this distance is at the upper limit of 2.0 Å and hardly changes with pressure. FeN shows a large c/a ratio of about 1.80 (Table 2) which is typical for NiAs‐type compounds of transition metals with Group V or VI elements.

Figure 4.

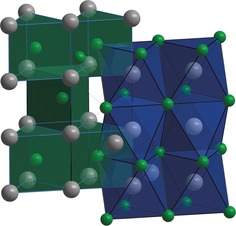
Crystal structure of NiAs‐type FeN, showing the face‐sharing condensation of the iron‐centered octahedra (blue), as well as the trigonal‐prismatic coordination environment of the nitride ions (green).

Table 2.

The c/a ratios of NiAs‐type FeN, under pressure and ambient pressure, with related NiAs‐type compounds.

NiAs‐Type Compound	c/a ratio
NiAs	1.392041
FeN (0.1 MPa)	1.7911
FeN (13.3 GPa)	1.8015
δ‐NbN	1.866535
TiS	1.951542
VP	1.956043

An insight into the electronic structure of NiAs‐type Fe_xN for x=1 was gained by examining band structure and density of states (DOS), while a bonding analysis used the projected crystal orbital Hamilton populations (−pCOHP), a variant of the COHP technique38 and their integrated values (−IpCOHP; Computational Details are provided in the Supporting Information). Features at the Fermi level, E _F, in the non‐spin‐polarized DOS and −pCOHP curves (Figure 5 c,d) indicate an electronically unfavorable situation as E _F falls into a maximum of the DOS curves39 with strongly antibonding Fe–N interactions; such attributes at E _F, however, may also suggest that the material alleviates this unfavorable situation by approaching a magnetic state,40 as indicated by Mössbauer spectroscopy.

Figure 5.

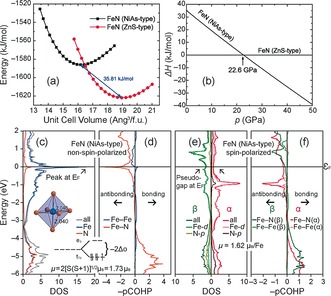
a) Energy–volume curves and b) relative enthalpies as functions of pressure for NiAs‐type as well as ZnS‐type FeN at 0 K; c), d) non‐spin‐polarized DOS and −pCOHP curves; e), f): spin‐polarized DOS and −pCOHP curves of NiAs‐type FeN.

A comparison of the total energies between various magnetic models reveals that the antiferromagnetic NiAs‐type FeN model is just 0.6 kJ mol⁻¹ higher in energy than the ferromagnetic model, which, accordingly, tends to be preferred. Because the Fermi level falls into a pseudogap of the spin‐polarized DOS curves (Figure 5 e and Figure S2), an electronically favorable situation is inferred for magnetic NiAs‐type FeN. This outcome is in good agreement with the Mössbauer spectra in which the magnetic sextet clearly denotes the presence of a magnetic ground state (Figure 2). The theoretical magnetic moment of 1.62 μ_B/Fe follows a spin‐only rule‐derived value for low‐spin Fe³⁺ (${\mathrm{t}}_{2\mathrm{g}}^5{\mathrm{e}}_{\mathrm{g}}$ configuration), for which the ligand‐field stabilization energy is maximized (Figure 5 c). The presence of such a low‐spin‐configuration for the iron atoms corresponds well to the observed Fe–N distances of approximately 2.01 Å, which is expected based on the covalent radii of nitrogen (0.71 Å) and low‐spin iron (1.32 Å).44 An alternative calculus using Shannon's ionic radii of N³⁻ (1.54 Å) and low‐spin Fe³⁺ (0.55 Å) yields a similar Fe–N distance of 2.09 Å.45 The states near and below the Fermi level stem primarily from Fe d as well as N p atomic orbitals (Figure 5 e). Although antibonding Fe–N interactions are evident below E _F in the spin‐polarized −pCOHP curves of both magnetic models (Figure 5 f and Figure S3), the integrated values (Table S2) of the Fe–N −pCOHP (−IpCOHP) are indicative of a net bonding character for these contacts.

Previous research on the electronic and vibrational properties revealed that the zinc blende‐type structure of FeN maintains dynamically stable.25, 46 To evaluate the stability of NiAs‐type iron nitride, we determined the energy–volume curves and pressure‐dependent relative enthalpies at absolute zero (Figure 5 a,b). Because crystal structure data, Mössbauer spectra and electronic structure calculations suggest a ferromagnetic ground state for NiAs‐type FeN while an antiferromagnetic ground state is proposed for ZnS‐type iron nitride,11 spin‐polarized band structure computations were used. A comparison reveals that the total energy of the ZnS modification is lower by almost 36 kJ mol⁻¹. At the atomic scale, the preference to adopt the ZnS‐type rather than NiAs‐type modification originates from shorter Fe–N contacts corresponding to larger −IpCOHP values in ZnS‐type FeN, that is, the modification is favored owing to a larger number of strong heteroatomic contacts. However, the values of the pressure‐dependent relative enthalpies imply a phase transition from the ZnS‐type to the NiAs‐type for pressures ≥22.6 GPa. Additionally, investigations of the vibrational properties for NiAs‐type FeN (Figure S4) point to dynamic stability.

In summary, a new high‐pressure phase has been discovered in the Fe–N system by combining diamond anvil cell laser heating techniques with synchrotron‐source Mössbauer spectroscopy and in situ X‐ray diffraction. Theoretical investigations confirm that NiAs‐type FeN exhibits a magnetic ground state. Although the modification is less stable than the ZnS‐type form at ambient conditions, the application of pressure provides access to this modification at elevated temperatures.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

W. P. Clark, S. Steinberg, R. Dronskowski, C. McCammon, I. Kupenko, M. Bykov, L. Dubrovinsky, L. G. Akselrud, U. Schwarz, R. Niewa, Angew. Chem. Int. Ed. 2017, 56, 7302.