Modeling gene regulation from paired expression and chromatin accessibility data

Significance

Chromatin plays a critical role in the regulation of gene expression. Interactions among chromatin regulators, sequence-specific transcription factors, and cis-regulatory sequence elements are the main driving forces shaping context-specific chromatin structure and gene expression. However, because of the large number of such interactions, direct data on them are often missing in most cellular contexts. The purpose of the present work is to show that, by modeling matched expression and accessibility data across diverse cellular contexts, it is possible to recover a significant portion of the information in the missing data on binding locations and chromatin states and to achieve accurate inference of gene regulatory relations.

Abstract

The rapid increase of genome-wide datasets on gene expression, chromatin states, and transcription factor (TF) binding locations offers an exciting opportunity to interpret the information encoded in genomes and epigenomes. This task can be challenging as it requires joint modeling of context-specific activation of cis-regulatory elements (REs) and the effects on transcription of associated regulatory factors. To meet this challenge, we propose a statistical approach based on paired expression and chromatin accessibility (PECA) data across diverse cellular contexts. In our approach, we model (i) the localization to REs of chromatin regulators (CRs) based on their interaction with sequence-specific TFs, (ii) the activation of REs due to CRs that are localized to them, and (iii) the effect of TFs bound to activated REs on the transcription of target genes (TGs). The transcriptional regulatory network inferred by PECA provides a detailed view of how trans- and cis-regulatory elements work together to affect gene expression in a context-specific manner. We illustrate the feasibility of this approach by analyzing paired expression and accessibility data from the mouse Encyclopedia of DNA Elements (ENCODE) and explore various applications of the resulting model.

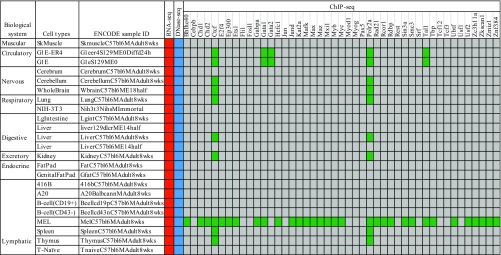
Ever since the emergence of high-throughput gene expression experiments (1), computational biologists have been interested in the inference of gene regulatory relationships from gene expression data across diverse cellular contexts corresponding to diverse cell types and experimental conditions (Fig. 1, red boxes). However, progress has been hindered by the fact that gene expression measurements provide little information on underlying regulatory mechanisms such as transcription factor binding and chromatin modification. To fill this gap, chromatin immunoprecipitation-based methods (2, 3) have been developed for the genome-wide mapping of transcriptional regulator binding locations and the detection of epigenetic marks characteristic of specific chromatin states. For example, by performing thousands of ChIP-seq experiments, the Encyclopedia of DNA Elements (ENCODE) consortium has generated such data for many chromatin marks and transcriptional regulators on a small number of cell lines (Fig. 1, green boxes). However, because a large number of transcriptional regulators and chromatin marks have to be analyzed one by one, it is unlikely that such comprehensive data will become available for many other cell lines. For most cellular contexts, the desired data will remain missing in the foreseeable future (Fig. 1, gray boxes).

Fig. 1.

Genome-wide data for gene-regulatory inference. Each row represents a particular cellular context under which multiple types of genome-wide data may be available. In this paper we illustrate our method by analyzing data from 25 contexts studied in the mouse ENCODE project covering a variety of mouse cell types and developmental stages. Expression data (from RNA-seq, red boxes) and chromatin accessibility data (from DNase-seq or ATAC-seq, blue boxes) are available for each context, but most of the location data (from ChIP-seq data, green boxes) for transcriptional regulators are missing. We expect that the number of contexts (i.e., number of rows) with expression and accessibility data will increase rapidly in the future, but corresponding location data will be sparse; i.e., gray boxes indicating missing data will remain numerous as the number of rows in the table grows.

On the other hand, it is known that many of the protein–DNA interactions important for gene regulation occur in regulatory elements (REs) such as enhancers and insulators, which compose only a small portion of the noncoding sequences in a genome. The REs active in gene regulation in a given cellular state tend to have an open chromatin structure so that they are accessible for binding by relevant transcriptional regulators. This suggests that many of the relevant regulatory relations may be revealed by analyzing the accessible REs. Fortunately, genome-wide measurement of chromatin accessibility is now straightforward by recent methods such as DNase-seq (4) or ATAC-seq (5). Similar to gene expression data, accessibility data are available for a diverse set of cellular contexts (Fig. 1, blue boxes). In fact, we expect the amount of matched expression and accessibility data (i.e., measured on the same sample) will increase very rapidly in the near future.

The purpose of the present work is to show that, by using matched expression and accessibility data across diverse cellular contexts, it is possible to recover a significant portion of the information in the missing data on binding location and chromatin state and to achieve accurate inference of the gene regulatory relations. In our approach, key events in the regulatory process, such as recruitment of chromatin remodeling factors to a regulatory element, activation of regulatory elements, etc., are regarded as latent unobserved variables in a statistical model that describes the relations among these variables and the gene expression variables, conditional on accessibility data on the regulatory elements. By fitting this model to expression and accessibility data across a large number of cellular contexts, we can infer many details of the gene regulatory system helpful in the interpretation of new data or the generation of new hypotheses.

We end this Introduction with comments on related works. Several methods have recently been proposed to detect transcription factor (TF) binding sites by “footprinting” in which the presence of a bound TF is reflected by the shape of the DNase-seq (or ATAC-seq) profile around its binding site (6–8). These works focus on the effect of TF binding on the frequency of cleavage near the site and do not attempt to model gene regulatory relations. Blatti et al. (9) integrate motif, DNA accessibility, and gene expression data to build regulatory maps in Drosophila. They use RNA in situ images from the Berkeley Drosophila Genome Project to define “expression domains” (conceptually similar to our “cellular contexts”) and use DNase-seq accessibility from four developmental stages to filter out motif sites. Their expression and accessibility data are not paired as in our approach. Furthermore, their model parameters are domain specific. In contrast, the parameters in our model are not context specific, which allows the use of the model to predict regulatory relations in contexts not represented in the training data. Despite these important differences, Blatti et al. (9) should be regarded as a forerunner of the present work.

Approach

We assume that a good genome annotation is available that contains the coordinates of all transcriptional units (genes) and most regulatory elements in the genome. In this paper, a RE is defined as a short region in the chromosome, typically a few hundred base pairs in size, on which sequence-specific TFs and other related proteins may assemble to exert control on the transcription of nearby genes. During the past decade, large-scale projects such as ENCODE have mapped more than 100,000 REs in the genomes of humans and mice. Although this set of REs (Methods, Definition of cis-Regulatory Elements) is still incomplete, especially for cellular contexts far from those analyzed in ENCODE, we do not further study the annotation of REs in this work. Instead, our goal is to infer, from the observed expression and accessibility data in any cellular context, how each known RE may interact with relevant transcriptional regulators to affect the expression of its target genes.

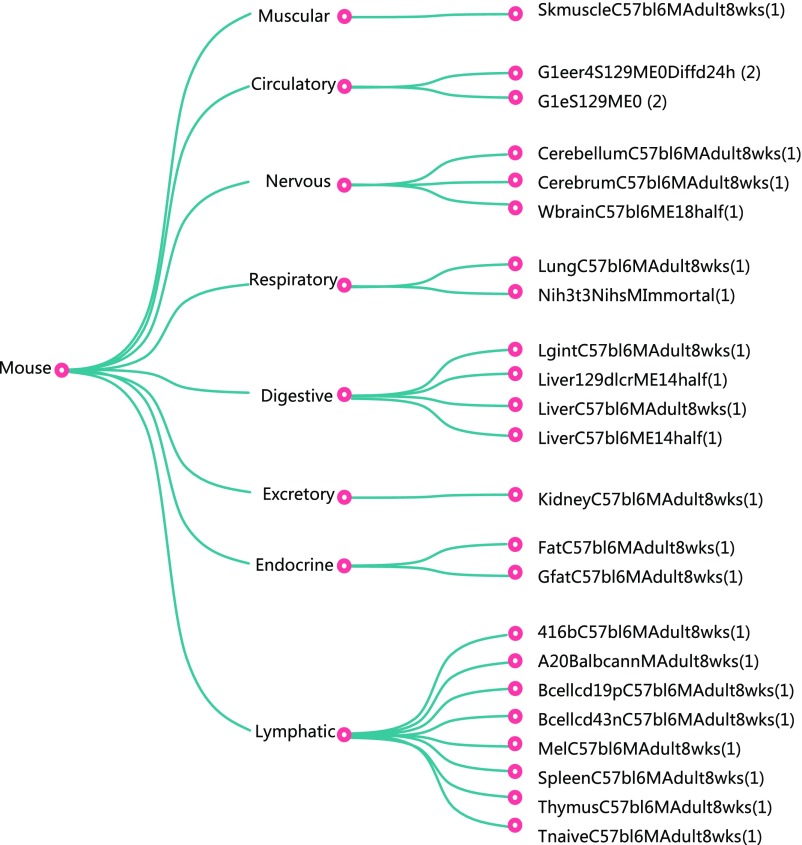
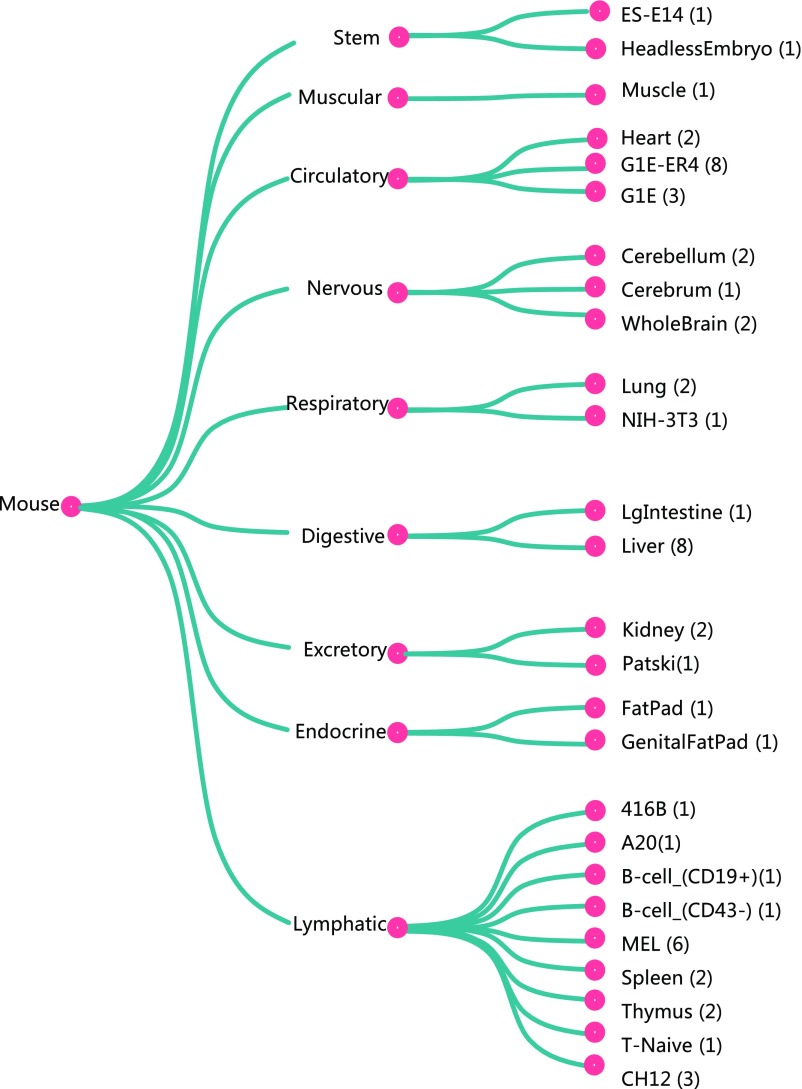
Fig. 1 summarizes the types of data to be analyzed or incorporated in our model of gene regulation. Context-dependent data, such as those on gene expression, chromatin accessibility, and TF-binding location, can show significant variation across cellular contexts, for example, across different cell types or across different treatments on the same cell type. There are hundreds of assays measuring different types of context-dependent data. In this paper we focus on gene expression and chromatin accessibility. These two types of data are already available for many contexts and respectively provide strong information on the result and the mechanism of regulation. For example, Fig. S1 lists the 25 cellular contexts for which matched expression and accessibility data are available from the mouse ENCODE project, when matching is done at the sample level, and Fig. S2 lists the 56 cellular contexts for which matched expression and accessibility data are available from the mouse ENCODE project, when matching is done at the cell type level. Most of the results below are based on the model trained on the sample-matched data.

Fig. S1.

The 25 ENCODE samples with matched RNA-seq and DNase-seq data at bio-sample level. These matched samples are used in PECA model training. More detailed information on these samples is in Dataset S5.

Fig. S2.

The 56 ENCODE samples with matched RNA-seq and DNase-seq data at cell-type level. These matched samples are used in out-sample gene expression prediction in RA-induced mESC differentiation data. More detailed information of these samples is in Dataset S5.

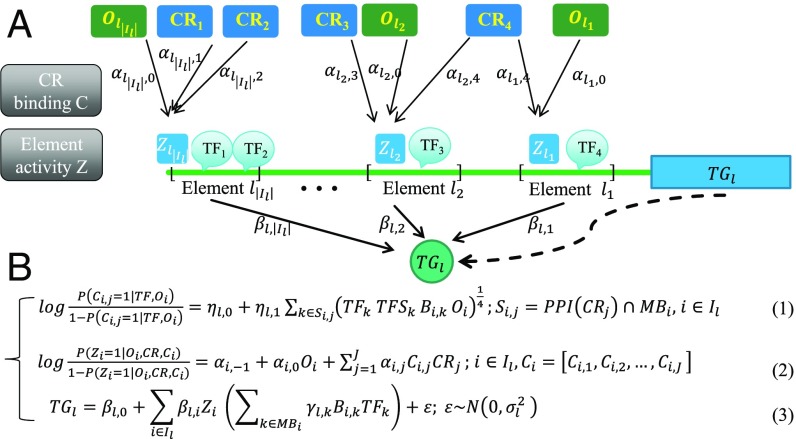
Our analytical approach for learning from these data is to model the distribution of the expression of target genes (TGs) conditional on the accessibility of regulatory elements and the expression of TFs and chromatin regulators (CRs). Note that by a target gene we mean a gene that is not a TF or a CR. Our model, depicted in Fig. 2, has three components designed to model, respectively, (i) control of target gene expression, (ii) activity status of the regulatory element, and (iii) recruitment of the chromatin regulator to the regulatory element. Definitions of the variables in Fig. 2 are given in Table 1.

Fig. 2.

Schematic overview of PECA model. (A) PECA is a model for transcriptional regulation that integrates matched gene expression and chromatin accessibility data with well-defined cis-REs (promoter of lth TG is denoted as element l₁ and enhancers are denoted as elements l₂, l₃,…, etc. The set of REs associated with the lth TG is denoted as I_l = {l₁,l₂,…}). The input of PECA includes the expression of TF genes, CR genes, and TGs; the openness of Res; the motif binding in the elements for TFs, and protein–protein interactions (PPI) among CRs and TFs. (B) The three components of PECA are described in Eqs. 1–3 (Table 1 for definitions of notations): (i) CR localization prediction in Eq. 1 models how a CR is recruited to a RE by its interacting sequence-specific TFs. C (C_i,j = 0,1) is introduced as a hidden variable to indicate whether the jth CR has been recruited to the ith RE. (ii) RE activity prediction in Eq. 2 models how the activation status of a RE is modulated by the expressions of recruited CRs and the RE’s openness. Z (Z_i = 0, 1) is introduced as a hidden variable to denote the activity of the ith RE. (iii) TG expression prediction in Eq. 3 models how the activities of REs and the expressions of binding TFs together explain TG expression. Based on this model and the observed expression and accessibility data, we can estimate the model parameters and the hidden variables (C, Z).

Table 1.

Model components

Description of data and variables	Notation	Example
Context-dependent data
Expression of TF	TFk := expression of kth TF	TFJun = 94.9 in lung
Expression of CR	CRj := expression of jth CR	CREp300 = 19.4 in lung
Expression of TG, not TF/CR	TGl := expression of lth TG	TGKrt8 = 86.1 in lung
Accessibility of RE	Oi := degree of openness of ith RE	Ochr4:94,821,700–94,824,600 = 5.45 in lung
Context-dependent latent variable
Activity status of RE	Zi := indicator for whether ith RE is active	RE at chr4:94,821,700–94,824,600 is active in lung
Binding status of CR in RE	Ci,j := indicator for whether jth CR is recruited to ith RE	Hdac2 binds RE at Chr4:94,821,700–94,824,600 in lung
Non–context-dependent data
Interacting TFs for a CR	PPI(CRj) := set of TFs known to interact with jth CR	PPI(Hdac2) contains Creb3l1
TFs with motif match in a RE	MBi := set of TFs with significant motif match in ith RE	Pou4f1 has motif match at RE chr4:94,567,400–94,568,400
Motif matching strength of TF on RE	Bi,k := sum of −log(P value) of kth TF's motif on ith RE	Bchr4:94,821,700–94,824,600, Sox8 = 12.61

Expression of a TG.

We assume that the rate of transcription of a TG in a cellular context is affected by TFs bound to regulatory elements that are active in that cellular context. For each RE we construct a variable (parenthesized term in Eq. 3 of Fig. 2) that represents the combined effect of TFs that are expressed in that context and have significant motif matches on that RE. TG expression is modeled by a regression with these variables as potential predictors. However, only active REs associated with a TG will be included in the regression model for that TG (Fig. 2, Eq. 3). The association of RE to TG was done before model building, based on the distance between them and the degree of correlation between the accessibility of the RE with promoter accessibility and expression of the TG (Methods).

Activity Status of RE.

The activity status of a RE (say the ith RE) is represented by a context-dependent binary variable Z_i, with Z_i = 1 indicating that the ith RE is in an active state. Testing whether a RE is active in a cellular context, say by editing the RE in a cell line, is time consuming experimentally. As an alternative, genome-wide inference of active REs is usually done based on ChIP-seq signals for selected chromatin regulators (e.g., P300), histone modification marks (e.g., H3K4me3, H3K27ac) (10), and local methylation signal (11). Thus, the knowledge of which CRs have been recruited to a RE is informative on the activity status of that RE. To incorporate this into our model, we denote the recruitment status of a CR to a RE by a binary variable C, i.e., C_i,j = 1 indicates that the jth CR has been recruited to the ith RE. These variables are used together with the expression of CRs and the accessibility of the RE to define predictive variables in our model for the activity status of the RE (Fig. 2, Eq. 2).

Recruitment of the CR to the RE.

Generally CRs do not have sequence specificity. We assume a CR is likely to be recruited to a RE if the RE is open and is bound by TFs that have protein interaction propensity with the CR. For each pair of CR and RE, we consider any TF that (i) is a protein interaction partner with the CR and (ii) has significant motif match on the RE and use it to construct a predictor variable for the modeling of the recruitment status of the CR on the RE. This predictor variable is defined as the geometric mean of the openness of the RE, the binding potential of the TF to the RE, the expression of the TF, and the expression specificity score of the TF. The specificity score (denoted as TFS), defined as geometric mean of maximum TF expression and max/(min + 0.5) where max and min are, respectively, maximum and minimum expression over a panel of cellular contexts, measures the tissue specificity of the expression of the TF. Including it in the definition of the predictor variable has the desirable effect of down-weighting any TF whose expression is nonvarying across cellular contexts. The resulting model for CR recruitment is given in Eq. 1 of Fig. 2.

To infer the unknown parameters $\alpha ,\beta ,\gamma ,\eta$ and latent variables (C, Z) based on the observed expression data (TG, TF, CR) and accessibility data (O), we consider the conditional density of TG given TF, CR, and O:

$$\begin{array}{l}P\left(TG|TF,CR,O\right)={\displaystyle \sum _{C,Z}P\left(C|TF,O\right)P\left(Z|CR,C,\hspace{0.17em}O\right)P\left(TG|TF,Z\right)}\\ ={\displaystyle \sum _{C,Z}\left({\displaystyle {\prod }_i{\displaystyle {\prod }_{j}P\left(C_{i,j}|TF,O_i\right)}}\right)}\left({\displaystyle {\prod }_{i}P\left(Z_i|CR,C_i,\hspace{0.17em}{O}_i\right)}\right)\times \left({\displaystyle {\prod }_{l}P\left({TG}_l|TF,Z\right)}\right).\end{array}$$

The term $P\left(C_{i,j}|TF,O_i\right)$ represents the conditional density of the recruitment status of the jth CRs on the ith RE, as specified in Eq. 1 of Fig. 2. Similarly the terms $P\left(Z_i|CR,C_i,O_i\right)$ and $P\left({TG}_l|TF,Z\right)$ are specified by Eqs. 2 and 3 of Fig. 2 (Methods for details). Note that these terms involve different components of the parameter vector: η appears in the first term, $\alpha$ appears in the second term, and ($\beta ,$ $\gamma$) appears in the third term. This conditional experiment (TG|TF, CR, O) provides a valid basis for the inference of the unknown parameters $\alpha ,\beta ,\gamma ,\eta$ and latent variables (C, Z). To induce sparsity, we use Laplacian priors for the parameters α and $\beta .$ We use an iterated conditional modes algorithm for this inference. The resulting model and inference methodology is called paired expression and chromatin accessibility (PECA) modeling (Methods for details of PECA).

Note that in the above analysis, the response variables TG include only the expression for non-TFs and non-CRs. Thus, this initial analysis provides inference for only those parameters that correspond to non-TF REs. TF-associated REs, namely those REs whose closest associated target gene is a TF or a CR, were excluded in the initial analysis. The inference of parameters specific to these TF-associated REs is accomplished by a second-stage analysis (Methods for details). Briefly, fixing the values α_i learned from the initial analysis, we infer the $\beta ,$ $\gamma ,$ and $\eta$ and those α_is corresponding to TF-associated REs based the model in Fig. 2, with the response variables TG replaced by TF and CR in Eq. 3 and with any parameter and hidden variables already learned from the initial analysis regarded as known.

To test feasibility of this approach, we constructed a training set consisting 25 sample-matched pairs of expression and accessibility data from the mouse ENCODE project. Based on these data, we learn the parameters of the model using the above procedure. Evaluation and applications of the resulting model are discussed in Results below.

As seen in Table 1 and Fig. 2, a large amount of non–context-dependent data have been incorporated into our model. These include the locations of REs in the genome, protein interactions between CRs and TFs, and motif-matching strengths of TFs on REs. Although most of these data are also derived from high-throughput experiments (Methods, Data Collection), they reflect propensities of interactions and have interpretations largely independent of cellular context. For example, if a TF and CR pair has been shown to interact in yeast two-hybrid experiments, then they are likely to have interacting domains that would allow them to interact if both are expressed. Likewise, if a RE contains sites matching strongly to the motif of a TF, then we would expect TF binding if the TF is expressed and the RE is accessible. The incorporation of these non–context-dependent data into our model has allowed us to greatly reduce the complexity of the model. The caveat is that knowledge of such protein–protein interactions and protein–DNA interactions is currently incomplete and this may cause modeling bias. The validation results reported below show that despite this, our method is already useful for many types of inferences and predictions. We expect that the bias associated with the use of non–context-dependent data will be further minimized as these data become more complete in the future.

Results

Inference of the Recruitment Status of Chromatin Regulators.

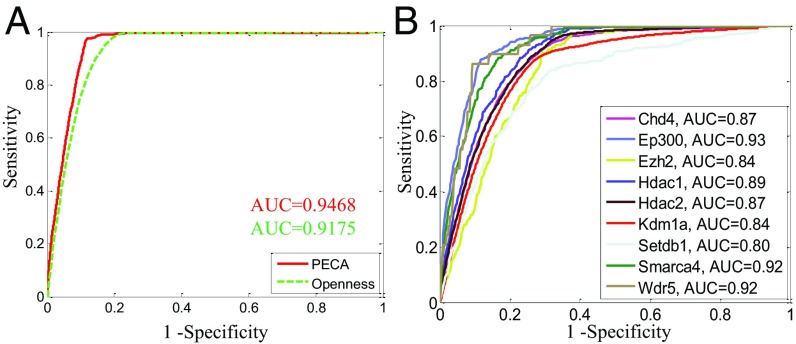
To assess whether the models can be used to infer CR recruitment status, we first consider a cell line (MEL) within the training set for which ChIP-seq data for the CR Ep300 are available. The ChIP-seq data are used to define ground truths for the recruitment status C_i,js of Ep300 to the REs. Using Eq. 1 of Fig. 2 with parameters learned from training data, we can infer Ep300 recruitment status conditional on the expression of TFs and CRs in the MEL context (Methods). Fig. 3A shows the receiver operating characteristic (ROC) curve for our predictions, where each point on the curve corresponds to a different cutoff value for P(C_i,j = 1|TF, O). As a comparison, we also show the ROC curve for the default prediction based on thresholding the accessibility of the RE. The curve shows that prediction based on our model is significantly better than that based on accessibility alone. Superiority of the PECA approach is also demonstrated in comparisons with several other methods based on various ways of using information on CR–TF interactions data, TF-motif occurrences, etc. (Fig. S3).

Fig. 3.

PECA accurately predicts CR binding/recruitment status. (A) Comparison of PECA-based prediction of Ep300 binding status on MEL with accessibility-based prediction. (B) ROC curves of PECA prediction of binding status for nine CRs on mESC.

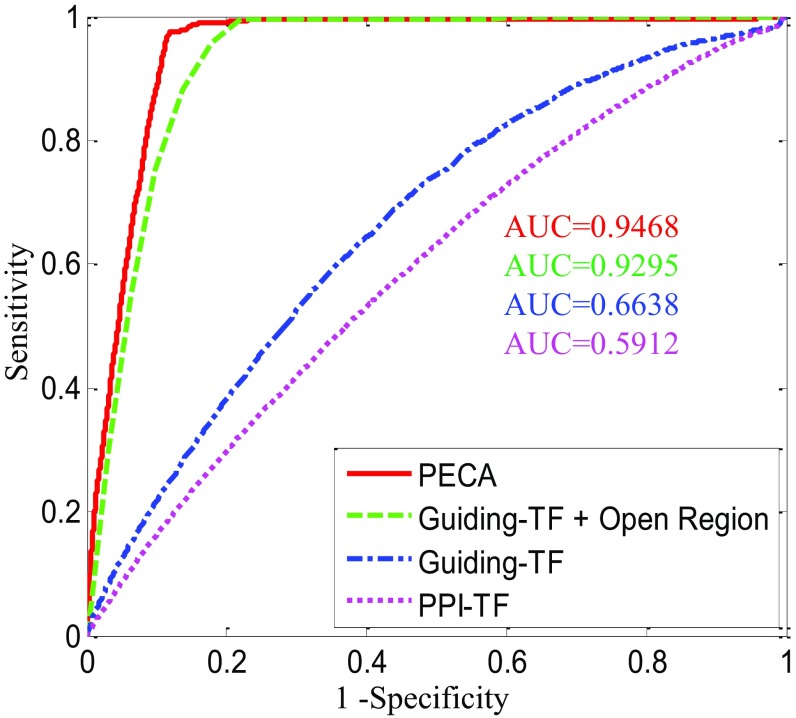
Fig. S3.

PECA outperforms three alternative methods, PPI-TF motif occurrence, guiding-TF motif occurrence, and combination of guiding TFs with open regions, in predicting Ep300 binding sites in MEL. In total there are 419,299 candidate cis-REs and 18,998 ChIP-seq peaks as a gold standard in MEL. Given a CR and tissue context, guiding TFs are defined as TFs that satisfy the following three conditions: (i) interact with the CR in a protein–protein interaction network, (ii) are dynamically expressed across tissues, and (iii) are highly expressed in a given tissue. For PPI-TF and guiding-TF motif occurrence, the motif binding strength on element (${\displaystyle {\sum }_j-\log \left(P\hspace{0.5em}{\text{value}}_j\right)}$) is used as the prediction score. In a combination of guiding-TF motif occurrence with the open region, the product of the overlapping fraction with the open region and motif binding strength are the prediction scores for the elements. PECA uses the posterior probability of CR binding $\left(C_{i,j}\right)$ to score the elements. We slide these scores and plot the ROC curves and the y axis is sensitivity and the x axis is 1 − specificity. The ROC curves show that the open region can dramatically improve the AUC and PECA reaches the highest AUC at 0.9465.

Next we ask whether our model has predictive power in a cellular context not covered by the training set. ChIP-seq datasets for nine CRs are available in mouse embryonic stem cells (mESCs), which are not part of the training set. We evaluate our predictions of the recruitment status of these nine CRs in mESCs by comparing them to ChIP-seq–based ground truths. Fig. 3B shows the ROC curves of the prediction on these nine CRs. It is seen that very good performances [80–93% area under the curve (AUC)] have been achieved for a diverse set of CRs, in a cellular context not covered by the training sets (Fig. S4). The strong performance in out-sample prediction suggests that the PECA approach is capable of learning regulatory relations useful in understanding new cellular contexts.

Fig. S4.

Comparison of PECA-based prediction of AUC of nine CRs binding status on mESC with accessibility-based prediction.

Prediction of the Activation Status of Regulatory Elements.

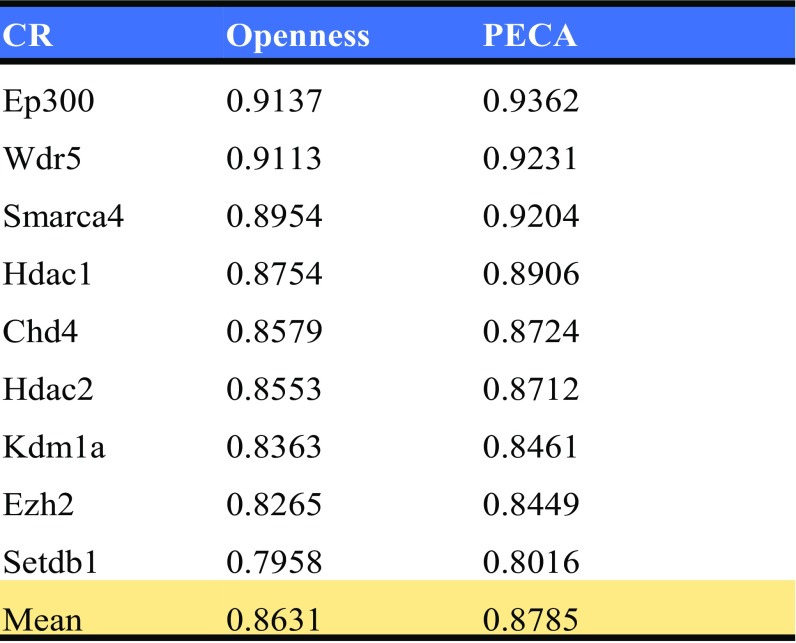
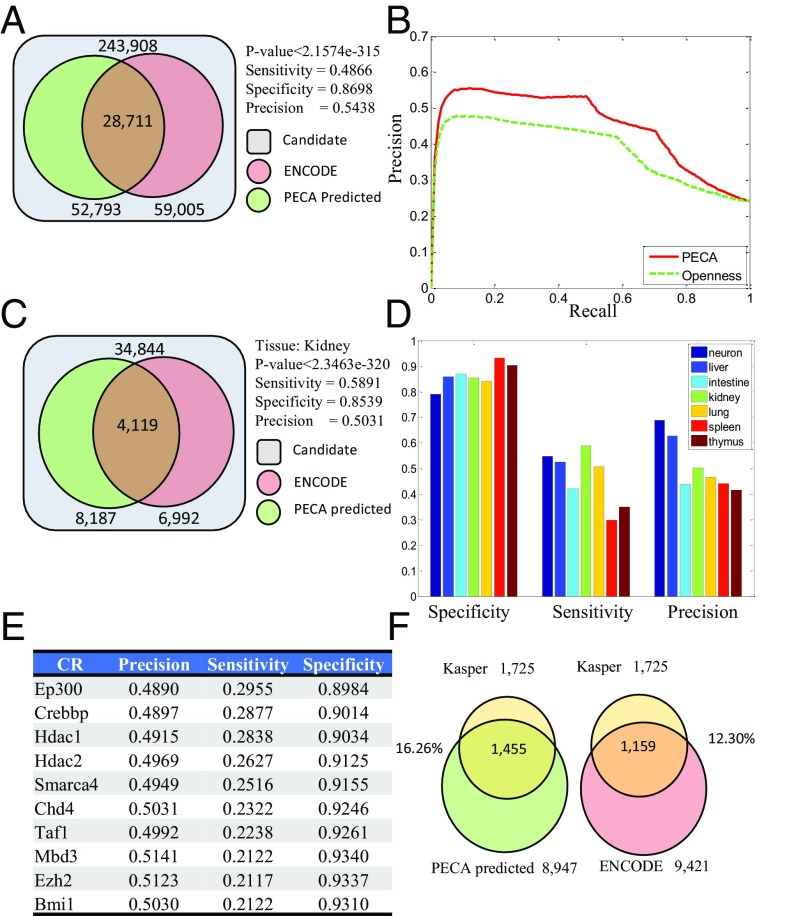
A key aspect of the PECA model is the introduction of the latent variable z_i to indicate whether the ith RE is active in a cellular context. Once the model has been trained, prediction on the activation status of a RE in a new cellular context can be made based on P(z_i = 1|O_i, TF, CR), where O_i, TF, and CR are measured in the cellular context of interest. To validate this aspect of the model, we evaluate the predictions in several cellular contexts where annotation of active REs is available. Traditionally, the genome-wide mapping of active REs in a given cellular context is accomplished by examining multiple types of location data for CR binding or for chromatin modification. For example, ENCODE tissue-specific enhancers are defined by five types of ChIP-seq data: RNA polymerase II (polII), CCCTC-binding factor (CTCF), histone H3 lysine 4 trimethylation (H3K4me3), histone H3 lysine 4 monomethylation (H3K4me1), and H3 lysine 27 acetylation (H3K27ac) in each tissue (12). We examine a set of 34,844 REs that (i) are associated with 419 core TFs and (ii) overlap with an ENCODE active enhancer in at least one of the following seven cellular contexts: neuron (cerebellum, e14.5-brain, and olfactory bulb), liver (e14.5-liver, liver), intestine, kidney, lung, spleen, and thymus. The set of core TFs was studied in ref. 13, and details of enhancer mapping by ENCODE on various tissues are given in ref. 12. We choose to focus on these seven contexts because paired expression and chromatin accessibility data are available for them. Based on ENCODE annotation, we define a 34,888 by seven matrix of ground truth values for the indicator z of activation status, with each entry of the matrix corresponding to a different combination of RE and cellular context. For each cell in this matrix, we predict the value of z based on whether P(z_i = 1|O_i, TF, CR) is larger than 1/2 or not. The comparison of our prediction to ENCODE annotation is given in Fig. 4A. Of the 243,908 entries of the matrix, 59,005 should be active (z = 1) according to ENCODE annotation. PECA predicted 52,793 active entries, of which 28,711 are consistent with ENCODE annotation. This gives a sensitivity of 0.4866 and a precision of 0.5438. As a comparison, if we use accessibility as the basis for prediction (i.e., a RE is regarded as active if its openness level is more than twofold that of background), the sensitivity is 0.5370 and precision is 0.4300. Thus, PECA provides a large gain in precision at a slight cost of sensitivity. Fig. 4B shows the full precision- recall curves. It is seen that PECA-based predictions achieve a considerably higher AUC than accessibility-based predictions. PECA-based prediction of active status of REs on each of the individual tissues are shown in Fig. 4 C and D.

Fig. 4.

PECA accurately predicts the activation status of REs. (A) Significant overlap of PECA predicted enhancer with ENCODE enhancers (P value <2.1574e-315). We examine the activation status of 34,844 enhancers in seven tissues (see text for criteria for choice of tissues and enhancers). The activation status of these enhancers has been annotated by ENCODE based on ChIP-seq data. In total we need to predict a binary matrix of size 34,844 × 7 = 243,908. (B) Precision-recall curve of PECA-based prediction using ENCODE annotation as gold standard. (C) Significant overlap of PECA predicted active enhancers with ENCODE active enhancers in kidney (P value <2.3463e-320). (D) Performance of enhancer activity prediction by PECA in each of seven tissues, using ENCODE enhancers as gold standard positives. (E) List of CRs with high predictive power. The results are based on the contribution of each CR in predicting enhancer activity, using ENCODE enhancers as gold standard positives. (F) Comparison of ENCODE enhancers and PECA predicted enhancers with a set of enhancers independently discovered by Kasper et al. (17) in MEF.

Based on consistency of each of the individual CR’s binding status with the RE’s activity, our model also identifies the CRs most predictive for active enhancer. We list the top 10 CRs in predicting enhancer activity in Fig. 4E. The top CRs are largely associated with histone acetylation, which is consistent with the fact that active enhancer is enriched in histone acetylation H3K27ac. We find the p300-CBP coactivator family (Ep300 and Crebbp) can predict enhancers; these two CRs contain a protein or histone acetyltransferase (PAT/HAT) domain and a bromodomain that binds acetylated lysines and is reported to play a major key role in the active enhancer (14). Histone deacetylase 1 and 2 (Hdac1 and Hdac2) (15) and BAF complex member Smarca4, which contain a bromodomain (16), also have good performance in predicting active enhancers.

In the above analysis we used tissue-specific active enhancer lists from ENCODE to define ground truths. Because those lists may be incomplete or may contain false positives, it is of interest to compare PECA-predicted active enhancers and ENCODE-predicted active enhancers to a set of enhancers from an independent source. Kasper et al. (17) defined active enhancers in mouse MEF by comparing CBP ChIP-seq data in wild type and CBP/p300 double-knockout data. Because there are no paired expression and accessibility data for MEF in mouse ENCODE, we analyzed the most similar cellular context (NIH 3T3) with paired data available and obtained PECA-predicted and ENCODE-predicted active enhancers in that context. We found that 1,455 of 8,947 (16.26%) PECA-predicted enhancers and 1,159 of 9,421 (12.30%) ENCODE-predicted enhancers are consistent with the active enhancer set in Kasper et al. (17) (Fig. 4F). This result suggests that, in this cellular context, PECA analysis may identify active enhancers with an accuracy matching or exceeding that of ENCODE annotations.

Prediction of Gene Expression.

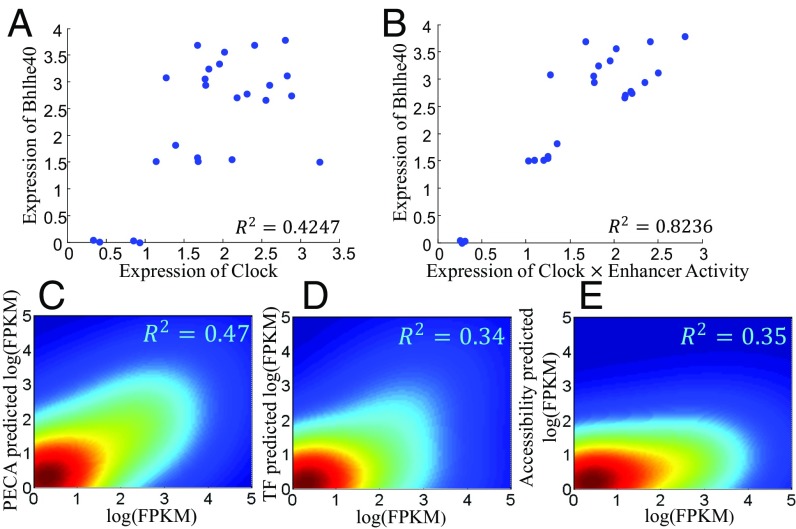
In our approach, we use a variable x_i (defined as the parenthesized term in Eq. 3 of Fig. 2) to represent the integrated effect of TFs bound on the ith RE and model the expression of the target gene by a linear regression with predictors (z_ix_i). To illustrate the importance of the activation status indicator z_i, consider for example the regulation of Bhlhe40 by the circadian rhythm-associated TF, Clock. Although this regulatory relation is well known (18), Bhlhe40 and Clock expressions are not strongly correlated (R² = 0.4247 in log scale, Fig. 5A). In contrast, Bhlhe40 expression is strongly correlated (R² = 0.8236 in log scale, Fig. 5B) with the product of Clock expression and the activation status of the RE (chr6:108,658,100–108,660,100), which is predicted to regulate Bhlhe40.

Fig. 5.

PECA accurately predicts expressions of TGs. Taking the Clock-Bhehl40 pair as an example (A), TF expression (Clock) has a clear but moderate correlation with TG expression (Bhehl40). The R² is 0.42. (B) The product of Clock expression and the activation status of an RE (chr6:108,658,100–108,660,100) have a much higher correlation (R² = 0.82) with Bhehl40 expression. This example illustrates the usefulness of RE accessibility in the prediction. (C–E) Out-sample comparison of gene expression prediction by PECA with those by TF expression or by RE accessibility. Matched expression and accessibility data were generated in a new cellular context (RA-induced differentiation of mESC) different from those used to train the PECA model. In this example, the model is trained from 56 cell types with matched expression and accessibility data. Fig. S2 provides details on these cell types.

To assess this component of our model systematically, we generated paired expression and accessibility data in a new cellular context quite different from those in the training sets. Mouse ESC was induced to differentiate by treatment with retinoic acid (RA). After 6 d, samples are collected for RNA-seq and ATAC-seq (Methods). Based on the PECA model learned from training data, we predicted the expression of all genes based on the accessibility data and the TF and CR expression data in this context. As comparisons, we also performed (i) accessibility-based predictions, where the predictor variables are the degree of openness (O_i) of the REs associated with the target gene, and (ii) TF-binding–based predictions, where the predictor variables are the integrated TF effect variable (x_i) for the REs associated with the target gene (Fig. 5 C–E). The results show that PECA-based prediction is significantly more accurate ($R^2=0.47$) than accessibility-based prediction ($R^2=0.35$) or TF-binding–based prediction ($R^2=0.34$).

Extraction of Regulatory Relations.

Our model provides a means to extract regulatory relations among REs, CRs, TFs, and TGs. Given a TG, the TFs and active REs that correspond to the nonzero β and γ are inferred to be regulators of this TG. To control the false discovery rate, we select highly active REs by requiring the posterior probability for z = 1 to be 0.9 or higher in at least one cellular context and use only these REs to extract the regulatory relations. Pooling all these regulatory relations together, we assemble a gene regulatory network consisting of four types of nodes (RE, CR, TF, and TG) and three types of edges (CR recruitment to RE, TF binding to RE, and RE regulation of TG). This network (Dataset S1) contains 18,463 TGs, 168,883 REs, 357 TFs, and 83 CRs.

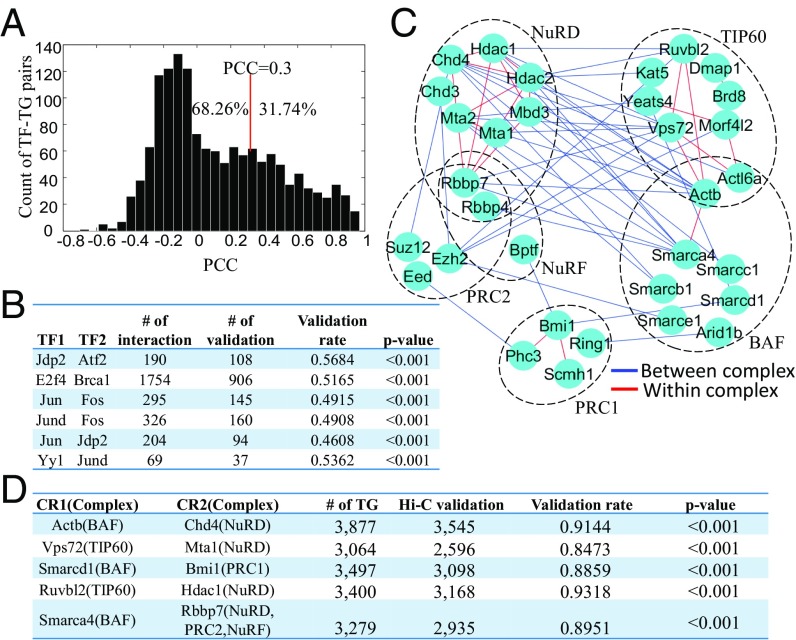
This network contains a large number of TF–TG relations (i.e., TF and TG connected through a RE) not detectable from expression data alone. To illustrate this, we examine 1,465 TF–TG relations in our network that are supported by prior experimental data (19) and compute the Pearson correlation coefficient (PCC) between the TF and TG in our training set (Fig. 6A). We found that for most of these pairs (68.26%), the TF and TG do not have highly correlated expressions (PCC < 0.3). This confirms the value of having RE accessibility in the model even if we are interested only in TF–TG relations.

Fig. 6.

PECA extracts regulatory relations. (A) Distribution of PCCs of validated TF–TG pairs detected by PECA. It is clear that PECA can recover many TF–TG pairs with low PCCs that cannot be detected by the traditional correlation-based method. (B) Candidate chromatin loop is inferred as a promoter and enhancer pair (associated with the same TG) on which two TFs with known protein–protein interaction are binding, respectively; i.e., one TF is promoter binding and the other is enhancer binding. For each interacting TF pair in the table, we compare the inferred chromatin loops to Hi-C data. Significant fractions of the predicted chromatin loops are validated by Hi-C experimental data. (C) Cooperating CR–CR pairs are further classified according to whether the two CRs in the pair tend to bind to the same element (red edge) or to different elements (blue edge). (D) A candidate chromatin loop is inferred as a pair of different REs bound, respectively, by two different CRs with protein–protein interaction and belonging to two different complexes. Most of the chromatin loops are validated by Hi-C experimental data (all validation percentages are larger than 80%). We also performed the permutation test and all of the predicted CR pairs are significantly validated by Hi-C data (all P values <0.001).

We identify cooperating TF–TF pairs based on whether they share common targets and whether they are protein–protein interaction partners (Methods). If two cooperating TFs regulate the same target gene but one binds to the promoter and the other to an enhancer, then this suggests a candidate protein–protein interaction that may mediate DNA looping to facilitate enhancer–promoter cooperation. In this way, we detected 53 such TF–TF pairs at a false discovery rate of 0.05. Indeed, some TF–TF pairs detected this way, such as Jdp2-Atf2, E2f4-Brca1, Jun-Fos, Jund-Fos, Jun-Jdp2, and Yy1-Jund, have been reported to show chromatin looping structure (20). We checked our chromatin looping predictions against Hi-C data in mESC and cortex (12) (Methods for details of Hi-C validation) and found that they are highly consistent (TF–TF pairs validated both in Hi-C and in the literature are shown in Fig. 6B, and all of the 53 TF–TF pairs’ results are in Dataset S2). For example, 108 of 190 loopings of Jdp2-Atf2 are validated.

We also examined CR–CR cooperation. We depict the CR–CR cooperation among six CR complexes including the BAF complex, TIP60 complex, NuRD complex, NuRF complex, PRC1, and PRC2 in Fig. 6C. Results show that TIP60, NuRD, and PRC1 complexes tend to cooperate within complexes whereas the BAF complex, NuRF complex, and PRC2 complex tend to cooperate between complexes. Much of the CR–CR cooperation is regulating target genes by binding to the same element. But we find that BAF complex member Actb and NuRD complex member Chd4 cooperate and tend to regulate the TG by using different elements that may result in chromatin looping. All of the CR–CR pairs from different complexes that tend to regulate the TG by different REs are shown in Fig. 6D. Actb and Chd4 regulate 3,877 TGs by different elements and 3,545 (91.44%) of them are validated by Hi-C data. This suggests that CRs from different complexes may lead to chromatin looping as well.

Inference of Context-Specific Regulatory Network.

For any cellular context, a regulatory network may be inferred by selecting the REs predicted to be active in the cellular context of interest and connecting the CRs, specifically expressed TFs [fragment per kilobase million (FPKM) > 10, TFS > 10], and expressed TGs (FPKM > 10) through regulatory relations involving these REs. The examination of this network may reveal details of the regulatory mechanism. For example, in the network specific to brain samples in our training set (Dataset S3), the target gene Snapc5 is regulated by two enhancers. One enhancer is regulated by TF Hbp1, and the other one is regulated by CR Ep300. Ep300 and Hbp1 are reported to have protein–protein interaction and may mediate contact of the two enhancers, which is consistent with evidence from ChIA-PET data (20).

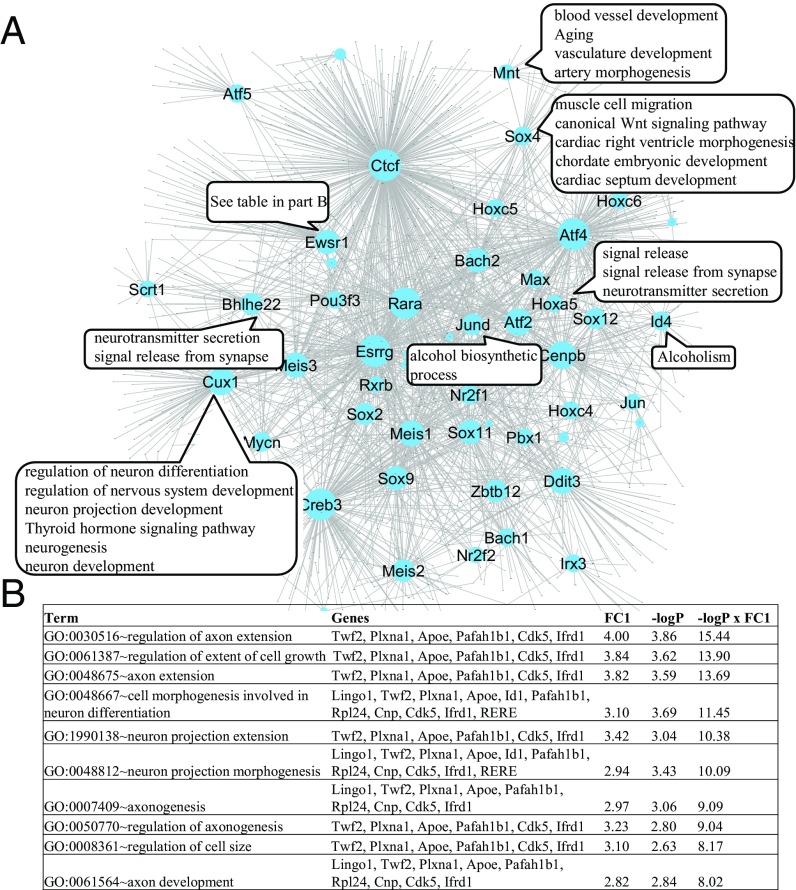
We can also infer the regulatory network in a new cellular context different from those used in training the model. To assess the utility of this approach, we apply the model learned from the training set to expression and accessibility data from the mESC differentiation sample (6 d after RA treatment). We infer the context-specific regulatory network by selecting active REs and specifically expressed TFs and expressed TGs in this context. For each of the 34 highly expressed TFs (FPKM ≥ 20) with a sufficient number (≥20) of downstream genes, we perform Gene Ontology (GO) enrichment analysis on these genes to gain insight on the role of the TF in this context (Dataset S4). Fig. 7A presents the results for some of the TFs. It is seen that the targets of Ewsr1, Bhlhe22, Cux1, Hoxa5, Id4, and Jund are enriched for various neuronal associated functions, which is consistent with the fact that RA induces neuron differentiation. Fig. 7B gives details for Ewsr1. The results suggest enrichment in axon genesis and neuron projection morphogenesis, which is consistent with the previous report that differentially expressed genes after Ewsr1/Fli1 knockdown are enriched in cell morphogenesis involved in differentiation and neuron projection morphogenesis (21). It is also interesting that cardiovascular development-related GO terms are highly enriched among the downstream genes of Sox4 and Mnt. The results for all TFs are given in Dataset S4.

Fig. 7.

PECA reveals a context-specific network in mESC differentiation (6 d after RA-induced differentiation). (A) Node size of each TF is proportional to the number of target genes. For some highly expressed TFs, enriched GO terms of their target genes are noted in the associated text boxes. (B) Enriched GO terms of Ewsr1’s target genes, where FC1 means fold change defined as count/(expected count + 1). Only those GO terms with ranking score (last column) greater than 8 are shown.

Interpretation of Genetic Variants Relevant to Traits and Diseases.

The regulatory model inferred from accessibility and expression data in diverse contexts may provide new tools for interpretation of genetic variants. We use this approach to examine QTL mapping results based on two mouse strains: A/J and C57BL/6J. There are a total of 17 long QTL regions (>0.5 Mb) mapped using these two strains (Bhr1, Bhr2, Bhr3, Char4, Hpi1, Hpi2, Aod1a, Vacq1, Nilac10, Dbm1, Dbm2, Ssrq1, Ssrq2, Ssrq8, Obrq13, Obrq14, and Obrq15). We focus on a subset of 7 QTL regions that have clearly relevant tissue contexts (Table 2). The sizes of these regions range from 3 Mb to 48 Mb.

Table 2.

QTL statistics

QTL symbol	QTL study name	QTL length	No. SNPs	No. SNPs in TFBS in active REs	No. nonsynonymous SNPs on expressed gene	No. deleterious SNPs on expressed gene	Tissue contexts
Bhr1	Bronchial hyperresponsiveness	35,958,073	84,720	169	77	10	Lung, Immune
Hpi2	Hepatic PMN infiltration	27,225,093	52,957	9	6	0	Liver
Hpi1	Hepatic PMN infiltration	48,679,702	50,787	44	13	1	Liver
Bhr2	Bronchial hyperresponsiveness	39,081,857	69,497	186	107	15	Lung, Immune
Bhr3	Bronchial hyperresponsiveness	44,773,774	99,128	263	176	22	Lung, Immune
Vacq1	Voluntary alcohol consumption QTL	3,072,943	5,173	18	12	1	Neuron
Nilac10	Nicotine-induced locomotor activity	22,087,605	12,543	29	3	0	Neuron, Immune

We consider strain-specific SNPs (i.e., single-nucleotide variants with different alleles in A/J and C57BL/6J). Among the thousands of strain-specific SNPs located in the QTL regions, the majority of them (>99%) are in noncoding regions. To further prioritize these noncoding SNPs, we consider only the subset located on relevant motif-binding site on REs that are (i) active in the phenotype-related tissue context and (ii) regulating one or more expressed TGs (FPKM > 5). Here a relevant motif means a motif associated with a TF that is inferred (by PECA analysis) to be using this RE in the phenotype-related tissue context. Table 2 presents the results of this analysis. It is seen that dozens of candidate causal loci are detected in each QTL region.

Some QTL regions, such as Hpi1, Hpi2, Vacq1, and Nilac10, have very few or even no deleterious SNPs [i.e., SNPs predicted to affect protein function by SIFT (22)]. So on these QTL regions, SNPs from a noncoding region may play important roles. We examine two examples.

Example 1.

The regions Hpi1 (chr13:4,363,272–53,042,973) and Hpi2 (chr5:37,815,383–65,040,475) are QTL for the lipopolysaccharide (LPS)-induced hepatic polymorphonuclear (PMN) infiltration phenotype. It has been reported that these two QTL have an epistatic interaction (23). A crucial aspect of the inflammatory response is the recruitment of activated neutrophils (PMNs) to the site of damage. Lytic enzymes and oxygen radicals released by PMNs are important in clearing an infection or cellular debris, but can also produce host tissue damage (24). Hpi1 contains a deleterious SNP on Slc17a3. Hpi2 has no deleterious SNPs but has nine noncoding region SNPs in binding sites of expressed TFs in active REs that regulate seven genes: Cd38, Klf3, Lyar, Mir574, Rell1, Sepsecs, and Sod3. Three of the nine SNPs are located in REs upstream of Sod3. Slc17a3 encodes a voltage-driven transporter that excretes intracellular urate uric acid that may be a maker of oxidative stress. The major function of Sod3 is to protect the tissues from oxidative stress. Thus, our analysis suggests the possibility that Slc17a3 and Sod3 may be the causal genes underlying Hpi1 and Hpi2, respectively, and may account for the epistatic interaction between these QTL. This possibility remains to be validated by further investigations.

Example 2.

The region Vacq1 (chr2:178,535,250–181,608,192) is a QTL for voluntary alcohol consumption. It contains a deleterious SNP on the coding region of Ppdpf but we did not find evidence for Ppdpf in the literature. On the other hand, there are some noncoding SNPs on this region with good evidence from the literature. In total there are 18 noncoding region SNPs affecting the motif-binding sites of expressed TFs on active REs. These REs are associated with 11 target genes, including Chrna4 and Oprl1. Chrna4, a nicotinic acetylcholine receptor, is regulated by Spi1, and A/J-specific SNP rs27680347 is located in a motif-binding site of Spi1. Neuronal nicotinic acetylcholine receptors are important targets for alcohol reward and dependence (25). Oprl1, an opioid-related nociceptin receptor, is regulated by Sox4, Fli1, and Esrrg, and A/J-specific SNPs rs27688371, rs29586730, and rs27702497 are located in the motif-binding site of these three TFs, respectively. Activation of this receptor system has been shown to reduce alcohol drinking in rats (26).

Overall, we find the number of candidate causal loci in the noncoding region is of the same order of magnitude as the number of nonsynonymous SNPs in the coding region (Table 2). This suggests that variants in noncoding regions contribute substantially to phenotypic variation and deserve serious attention in genome interpretation.

Discussion and Conclusions

In this paper, we propose a method, named PECA, to infer gene regulatory networks by jointly modeling paired gene expression and chromatin accessibility data. Building on the recent advances in identifying candidate REs (enhancers) in the genome, PECA tries to answer a number of questions on the regulatory roles of these elements. How is the RE’s activity spatiotemporally regulated by CRs? How do colocalized TFs and CRs on a RE regulate target genes and achieve context-specific gene expression? Answers to these questions are key to understanding the functions of the annotated REs and will enable effective interpretation of sequence variants that may be relevant to physiological traits and disease risks. We choose to focus on paired accessibility and expression data as such data are easy to measure and will be obtained in the near future for the majority of definable cell types in different tissues and developmental stages, as well as for many abnormal cell types arising from diseases. The utility and reliability of the model will increase rapidly as these data become available for more cellular states.

Methods

Data Collection.

We collected 25 bio-sample–matched and 56 cell-type–matched RNA-seq and DNase-seq data from the mouse ENCODE project. We used these data to train our PECA model (Figs. S1 and S2 and Dataset S5). Both human and mouse protein–protein interaction data are from the BIOGRID database (https://thebiogrid.org). We collected 557 TFs’ motif data from JASPAR, TRANSFAC, UniPROBE, and Taipale. We also collected 120 CRs from GO annotation, which consist of 5 ATP-dependent chromatin-remodeling complexes (BAF complex, PBAF complex, NuRD complex, NuRF complex, and Tip60 complex), 2 chromatin-modifying complexes (polycomb complex and trithorax complex), and 3 chromatin-modifying enzyme families [K-demethylase family enzymes (Kdm), K-acetyltransferase family enzymes (Kat), and K-methyltransferase family enzymes (Kmt)] (Dataset S6).

Definition of cis-Regulatory Elements.

The promoter is defined as the 2-kb region upstream of the TG’s transcription start site (TSS). Enhancers are obtained from the mouse ENCODE defined via five ChIP-seq datasets in 19 tissues and length is set to be 1 kb centered on the predictions in ref. 12. This gives 931,427 enhancers in total. The annotated enhancers add up to 11% of the mouse genome and include more than 70% of conserved noncoding sequences (12). Overlapping enhancers regulating the same target gene are merged into one enhancer. The resulting 419,299 enhancers are used in our model training.

Statistical Model to Define Openness.

We propose a score to quantify the openness (i.e., accessibility) for the cis-REs and make it comparable across different conditions. Given a certain region of length L, we treat this region as foreground and denote by X the count of reads in the region. To remove the sequencing depth effect, we choose a background region with length $L_0$ and denote by Y the count of reads in this background window. The openness score is formally defined as the fold change of read numbers per base pair and can be simply calculated as

$$O=\frac{\left(X+\delta \right)/L}{\left(Y+\delta \right)/L_0},$$

where δ is a pseudocount (the default value of δ is 5 in our implementation).

Enhancer–Target Prediction via Crossing Tissue Correlation.

We obtain and pool enhancer–TG associations from three sources: ENCODE annotations, inferred from ChIA-PET data, and inferred from accessibility correlations. Enhancer–target associations are available for 19 tissues from ENCODE. Associations based on ChIA-PET data are available for mESC, NPCs, and NSC (27). Additionally, enhancer–target associations are also inferred from accessibility and expression data by the method described below.

Given an enhancer, we first list all of the potential TGs within a certain distance (default is 1 million bp upstream or downstream from the TSS). Then, for each potential target gene in this list, we compute a conditional fold change of expression (CFC-e) to quantify the correlation across tissues between the expression of the gene and the accessibility of the RE, as follows. Given the RE’s openness X = [x₁,…x_n], apply Jenk’s method (28) to divide the samples (denoted by G) into two groups ${\text{G}}_{\text{h}}$ and ${\text{G}}_{\text{l}}$ with high and low openness, respectively, and define CFC-e as the ratio of the mean expression in G_h to that of a comparison group G_m of the same size selected from G. Specifically, if the expression values of the target gene in the n tissues are Y = [y₁,…y_n], then

$$\text{CFC}=\frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left|{\text{G}}_{\text{h}}\right|$}\right.{{\displaystyle \sum }}_{\text{k}\in {\text{G}}_{\text{h}}}{\text{y}}_{\text{k}}}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\left|{\text{G}}_{\text{m}}\right|$}\right.{{\displaystyle \sum }}_{\text{k}\in {\text{G}}_{\text{m}}}{\text{y}}_{\text{k}}},$$

where ${\text{G}}_{\text{m}}\subseteq \text{G},$ $\left|{\text{G}}_{\text{m}}\right|=\left|{\text{G}}_{\text{h}}\right|,$ ${\text{y}}_{\text{i}}>{\text{y}}_{\text{j}},\hspace{0.17em}\forall \hspace{0.17em}\text{j}\in {\text{G}}_{\text{m}},$ $\text{i}\in \text{G}\backslash {\text{G}}_{\text{m}}.$ We note that the RE’s target is specific for samples in ${\text{G}}_{\text{h}}$ and this allows us to achieve tissue-specific enhancer target prediction. Jenk’s method is a way to threshold a set of values into two classes, where we minimize each class’s average deviation from the class mean, while maximizing each class’s deviation from the means of the other class. In our implementation, a small constant 0.05 is added to the denominator to avoid division by very small values. Similarly, using promoter openness, we also compute a conditional fold change of openness (CFC-o) to represent the correlation between enhancer accessibility and promoter accessibility. We pick out the RE and TG association by requiring both CFC-e and CFC-o to be larger than 2. In addition to the local correlation quantitated by CFC-e and CFC-o, we also adopt the PCC to assess the global correlation across conditions between RE and TG. Similarly we propose a PCC of openness (PCC-o) to represent the correlation between the RE’s accessibility and the gene’s promoter accessibility. We also compute a PCC of expression (PCC-e) to quantify the correlation across tissues between the expression of the gene and the accessibility of the RE. We pick out the RE and TG association by requiring both PCC-e and PCC-o to be larger than 0.5.

Finally we take the union of four sources of RE and gene associations: ENCODE annotations, inferred from ChIA-PET data, inferred from local accessibility correlations by CFC, and inferred from global accessibility correlations by PCC. We get 39,006 enhancer–TG associations from ChIA-PET data, 395,031 from ENCODE, and 3,332,931 from our correlation-based method. This method improves the coverage about 10-fold.

TF Localization by Motif Scan.

We collected 557 TF position weight matrix (PWM) matrices for the known motifs from widely used databases, including JASPAR, TRANSFAC, UniPROBE, and Taipale. We identified these TF binding sites by a whole-genome motif scan, using Homer with a P-value cutoff of 1.0e-4.

PECA Model.

We formally introduce the notations for variables in PECA’s statistical model as follows:

• i)$T{F}_k(k=\mathrm{1,2},\dots ,K),$ $T{G}_l(l=\mathrm{1,2},\dots ,L),$ and $C{R}_j(j=\mathrm{1,2},\dots ,J)$ are the expression levels for TFs, TGs, and CRs and can be obtained from expression data for S samples.
• ii)Cis-regulatory elements of $T{G}_l:$ $e_i,$ where $i\in I_l.\hspace{0.17em}{I}_l=\{l_1,l_2,\dots \}$ is subset of REs that connected to $T{G}_l.$
• iii)Openness of the cis-regulatory elements $e_i :$ $O_i,$ obtained from accessibility data for S samples.
• iv)$T{F}_k$ binding strength on cis-regulatory elements $e_i :$ $B_{i,k}(k=\mathrm{1,2},\dots K),$ which is defined as the sum of binding strength of all of the binding sites on this element:

$$B_{i,k}={\displaystyle \sum _m}-\log \left(P\hspace{0.5em}{\text{value}}_m\right).$$

• v)Set of TFs with significant motif match in cis-regulatory elements $e_i :$ $M{B}_i.$
• vi)Set of TFs known to interact with jth CR: $PPI\left(C{R}_j\right).$

Model of CR binding to REs.

We model the CR binding to REs by a logistic regression, and recruitment status of the jth CRs on the ith RE is denoted as $C_{i,j}\in \left\{\mathrm{0,1}\right\}.$ The features are geometric mean of TF expression, TF specificity expression (TFS), TF motif-binding strength on RE, and openness of RE,

$$\log \frac{P\left(C_{i,j}=1|TF,O_i\right)}{1-P\left(C_{i,j}=1|TF,O_i\right)}={\eta }_{l,0}+{\eta }_{l,1}\hspace{0.17em}{\displaystyle \sum _{k\in S_{i,j}}{\left(T{F}_{k}TF{S}_k{B}_{i,k}{O}_i\right)}^{\frac{1}{4}}}$$

$$P\left(C_{i,j}=1|TF,O_i\right)=\frac{\exp \left({\eta }_{l,0}+{\eta }_{l,1}{\displaystyle {\sum }_{k\in S_{i,j}}{\left(T{F}_{k}TF{S}_k{B}_{i,k}{O}_i\right)}^{\frac{1}{4}}}\right)}{1+\exp \left({\eta }_{l,0}+{\eta }_{l,1}{\displaystyle {\sum }_{k\in S_{i,j}}{\left(T{F}_{k}TF{S}_k{B}_{i,k}{O}_i\right)}^{\frac{1}{4}}}\right)},$$

where $S_{i,j}=PPI\left(C{R}_j\right)\cap M{B}_i,i\in I_l,j\in \{\mathrm{1,2},\dots J\},$ $l\in \{\mathrm{1,2},\dots L\};$ and $TF{S}_k$ represents TF expression specificity score and is defined as

$$TF{S}_k=\sqrt{\text{max}\left(T{F}_k\right)\times \frac{\text{max}\left(T{F}_k\right)}{\text{min}\left(T{F}_k\right)+0.5}}.$$

Parameters to be estimated are ${\eta }_k\left(k=\mathrm{1,2},\dots K\right).$

Model of RE activity.

We model the activation status of a RE by a logistic regression, and activation status of the ith RE is denoted as $Z_i\in \left\{\mathrm{0,1}\right\}.$ The features are the REs’ openness and the expressions of binding CRs,

$$\log \left(\frac{P\left(Z_i=1|O_i,CR,C_i\right)}{1-P\left(Z_i=1|O_i,CR,C_i\right)}\right)={\alpha }_{i,-1}+{\alpha }_{i,0}{O}_i+{\displaystyle \sum _{j=1}^J{\alpha }_{ij}{C}_{i,j}C{R}_j}$$

$$P\left(Z_i=1|O_i,CR,C_i\right)=\frac{\exp \left({\alpha }_{i,-1}+{\alpha }_{i,0}{O}_i+{\displaystyle {\sum }_{j=1}^J{\alpha }_{ij}{C}_{i,j}C{R}_j}\right)}{1+\exp \left({\alpha }_{i,-1}+{\alpha }_{i,0}{O}_i+{\displaystyle {\sum }_{j=1}^J{\alpha }_{ij}{C}_{i,j}C{R}_j}\right)},$$

where $C_i=\left[C_{i,1},C_{i,2},\dots ,C_{i,J}\right],\hspace{0.17em}i\in I_l,l\in \left\{\mathrm{1,2},\dots L\right\}.$ Parameters to be estimated are ${\alpha }_{i,j}\left(i=-\mathrm{1,0,1},\dots J\right).$

Model of TG expression.

We model the expression of a TG as a Gaussian variable with mean $\mu$ and SD $\sigma ,$ where $\mu$ is a linear combination of the effects of associated REs. The effect of each RE is modeled as a product of the RE’s activity and the expression of its binding TF complex. To reduce the number of parameters, we assume that the effect of the TF complex is a weighted sum of its binding TFs’ expression values:

$$T{G}_l|TF,Z\sim N\left({\beta }_{l,0}+{\displaystyle \sum _{i\in I_l}{\beta }_{l,i}{Z}_i\left({\displaystyle \sum _{k\in M{B}_i}\hspace{0.17em}{\gamma }_{l,k}{B}_{i,k}T{F}_k}\right)},{\sigma }_l^2\right);l\in \left\{\mathrm{1,2},\dots L\right\}.$$

N($\mu ,{\sigma }^2$) denotes a Gaussian distribution with mean $\mu$ and SD $\sigma .$ $\beta ,\hspace{0.17em}\gamma ,\hspace{0.17em}\text{and}\hspace{0.17em}{\sigma }^2$ are the parameters to be estimated.

Likelihood function and inference.

The complete likelihood function for PECA’s hierarchical model for matched chromatin accessibility and gene expression data is

$$\begin{array}{l}P\left(TG|TF,CR,O\right)\\ ={\displaystyle \sum _{C,Z}P\left(C|TF,O\right)P\left(Z|CR,C,\hspace{0.17em}O\right)P\left(TG|TF,Z\right)}\\ ={\displaystyle {\sum }_{C,Z}\hspace{0.17em}\left({\displaystyle {\prod }_i{\displaystyle {\prod }_{j}P\left(C_{i,j}|TF,O_i\right)}}\right)\left({\displaystyle {\prod }_i\text{P}\left(Z_i|\text{CR},C_i,\hspace{0.17em}{O}_i\right)}\right)\left({\displaystyle {\prod }_l\text{P}\left(T{G}_l|\text{TF},\text{Z}\right)}\right)},\end{array}$$

where C and Z are hidden variables. They are estimated together with parameters $\alpha ,\beta ,\gamma ,\eta$ from the input data by maximizing the likelihood function,

$$\underset{\alpha ,\beta ,\gamma ,\eta }{\max }P\left(TG|TF,CR,O,\alpha ,\beta ,\gamma ,\eta ,{\sigma }^2\right),$$ [4]

where $TG,TF,\text{and}CR$ denote the observed expression of target gene (except TF and CR), transcription factor, and chromatin regulator. $O$ is the observed openness of the REs (Fig. 2C). $P\left(C\right|TF,\hspace{0.17em}O,\eta ),$ $P\left(Z\right|CR,O,C,\alpha ),$ and $P\left(TG|TF,Z,\beta ,\gamma \right)$ are the conditional probabilities derived from Eqs. 1, 2, and 3, respectively.

We impose sparsity on $\alpha$ and $\beta$ by l₁ penalization. Given a TG, all of the nonzero β and γ corresponding to TFs and REs are inferred as regulators of this TG. We regard an RE as highly active in a cellular context only if the posterior probability for it to be active is at least 0.9 [i.e., P(Z_i = 1 | data) ≥ 0.9]. If an RE is highly active in any context, then the TFs binding to it are regarded as regulators of associated target genes. Pooling all of the regulatory relations together, we assemble a gene regulatory network consisting of four types of nodes (RE, CR, TF, and TG) and three types of edges (CR recruitment to RE, TF binding to RE, and RE regulation of TG). This network provides high-level annotations for the REs.

Inference algorithm.

For the TGs (not TF or CR), we estimate parameters $\alpha ,\beta ,\gamma ,\hspace{0.17em}\text{and}\hspace{0.17em}\eta$ and hidden variables C and Z by maximizing Eq. 4. For the genes that are TF or CR, we model them one by one, using Eqs. 1–3 to estimate the parameters and hidden variables. Whereas parameters and hidden variables that are estimated from Eq. 4 are regarded as fixed and no longer variables. We have implemented PECA in MATLAB in three steps:

• i)We maximize $P\left(T{G}_l|TF,CR,O_{I_l},\alpha ,\beta ,\gamma ,\eta \right)$ to estimate $\alpha ,\beta ,\gamma ,\eta$ and hidden variables ($C_{I_l},$ $Z_{I_l}$) on each TG, where $I_l$ represents the set of REs associated with $T{G}_l.$ For the REs associated with multiple TGs, we average C and Z over the TGs to estimate C and Z, respectively.
• ii)We iterate steps iia and iib to estimate $\alpha ,\beta ,\gamma ,\eta$ and hidden variables ($C_i,$ $Z_i$) on each $T{G}_l$ ($i\in I_l$):
• iia)We fix C and Z of shared REs and estimate $\alpha ,\beta ,\gamma ,\eta$ and ($C_i,$ $Z_i$) of a specific RE (which is associated with only one TG) by maximizing $P\left(T{G}_l|TF,CR,O_{I_l},\alpha ,\beta ,\gamma ,\eta \right)$ on each TG.
• iib)We fix C and Z of a specific RE and estimate $\alpha ,\beta ,\gamma ,\eta$ and ($C_i,$ $Z_i$) of shared REs by maximizing $P\left(T{G}_l|TF,CR,O_{I_l},\alpha ,\beta ,\gamma ,\eta \right)$ on each $T{G}_l.$ The value of any shared C (or Z) variable is then set to be the average of its value estimated from each of the associated TGs.
• iii)Finally, we estimate the parameters on REs specifically associated with TFs or CRs (i.e., not associated with TGs) in a similar manner, but with the hidden variables C and Z on REs shared with any TGs fixed at their estimated values from step ii.

The maximizations of the likelihood function in these steps are carried out using an EM-like algorithm. For each given TG, iterate the E and M steps below to estimate parameters $\alpha ,\beta ,\gamma ,\hspace{0.17em}\text{and}\hspace{0.17em}\eta$ and hidden variables C and Z.

E step: estimating $\text{C}\hspace{0.17em}\text{and}\hspace{0.17em}\text{Z}$ with fixed $\mathit{\alpha },\beta ,\gamma ,$ and $\eta .$

• i)Estimate $P\left(C_{i,j}=1|TF,O_i\right)$ on the condition of given $\eta :$

$$\log \frac{P\left(C_{i,j}=1|TF,O_i\right)}{1-P\left(C_{i,j}=1|TF,O_i\right)}={\eta }_{l,0}+{\eta }_{l,1}{\displaystyle \sum _{k\in S_{i,j}}{\left(T{F}_{k}TF{S}_k{B}_{i,k}{O}_i\right)}^{\frac{1}{4}}};\hspace{1em}{S}_{i,j}=PPI\left(C{R}_j\right)\cap M{B}_i.$$

• ii)Estimate $P\left(Z_i=1|O_i,CR\right)$ on the condition of given $\gamma ,\hspace{0.17em}\alpha ,\hspace{0.17em}\beta ,$ and $P\left(C_{i,j}=1|TF,O_i\right):$

$$\log \left(\frac{P\left(Z_i=1|O_i,CR,C_i\right)}{1-P\left(Z_i=1|O_i,CR,C_i\right)}\right)={\alpha }_{i,-1}+{\alpha }_{i,0}{O}_i+{\displaystyle \sum _{j=1}^J}{\alpha }_{ij}P\left(C_{i,j}=1|TF,O_i\right)C{R}_j$$

$$T{G}_l={\beta }_{l,0}+{\displaystyle \sum _{i\in I_l}}{\beta }_{l,i}P\left(Z_i=1|O_i,CR,C_i\right)\left({\displaystyle \sum _{k=1}^K}{\gamma }_{l,k}{B}_{i,k}T{F}_k\right).$$

We use the least-squares estimation to estimate $P\left(Z_i=1|O_i,CR\right).$

M step: estimating the parameters $\alpha ,\beta ,\hspace{0.17em}\gamma ,$ and $\eta$ on the condition of given $P\left(Z_i=1|O_i,CR\right)$ and $P\left(C_{i,j}=1|TF,O_i\right).$

• i)The parameters $\alpha$ are estimated by the following optimization:

$$\underset{\alpha }{\min }{\displaystyle \sum _{i\in I_l}}\Vert \log \left(\frac{P\left(Z_i=1|O_i,CR,C_i\right)}{1-P\left(Z_i=1|O_i,CR,C_i\right)}\right)-{\alpha }_{i,-1}-{\alpha }_{i,0}{O}_i-{\displaystyle \sum _{j=1}^J}{\alpha }_{ij}P\left(C_{i,j}=1|TF,O_i\right)C{R}_j{\Vert }_2^2+{\lambda }_1\Vert \alpha {\Vert }_1.$$

• ii)The parameters $\beta$ are estimated by minimizing the following optimization on the condition of given $\gamma :$

$$\underset{\mathrm{\beta }}{\min }\Vert T{G}_l-\left[{\beta }_{l,0}+{\displaystyle \sum _{i\in I_l}}{\beta }_{l,i}P\left(Z_i=1|O_i,CR,C_i\right)\left({\displaystyle \sum _{k=1}^K}{\gamma }_{l,k}{B}_{i,k}T{F}_k\right)\right]{\Vert }_2^2+{\lambda }_2\Vert \beta {\Vert }_1.$$

• iii)The parameters $\gamma$ are estimated by minimizing the following optimization on the condition of given $\beta :$

$$\underset{\mathrm{\gamma }}{\min }{\Vert T{G}_l-\left[{\beta }_{l,0}+{\displaystyle \sum _{i\in I_l}}{\beta }_{l,i}P\left(Z_i=1|O_i,CR,C_i\right)\left({\displaystyle \sum _{k=1}^K}{\gamma }_{l,k}{B}_{i,k}T{F}_k\right)\right]\Vert }_2^2.$$

• iv)The parameters $\eta$ are estimated by least-squares solution of the following equations:

$$\log \frac{P\left(C_{i,j}=1|TF,O_i\right)}{1-P\left(C_{i,j}=1|TF,O_i\right)}={\eta }_{l,0}+{\eta }_{l,1}{\displaystyle \sum _{k\in S_{i,j}}{\left(T{F}_{k}TF{S}_k{B}_{i,k}{O}_i\right)}^{\frac{1}{4}}};\hspace{1em}{S}_{i,j}=PPI\left(C{R}_j\right)\cap M{B}_i.$$

In our model, both ${\lambda }_1$ and ${\lambda }_2$ are chosen as 0.01.

TF–TF Cooperation Network.

Given two TFs, we count the number of coregulating TGs. By coregulating TG we mean one TF binds to the promoter and one binds to the enhancer of the TG. Then, we randomly generate 1,000 TF–TG networks that have the same degree distribution as the original TF–TG network. We count the number of coregulated TGs of the two TFs in the 1,000 random networks. Comparing the number of coregulated TGs with background distribution generated from the random networks, we get the significantly cooperating TF–TF pairs by thresholding the P value at 0.05. We then overlap this network with the protein–protein interaction (PPI) network and get the TF–TF cooperation network.

Validation of Chromatin Looping by Hi-C.

We use the Hi-C data on mESC and cortex that have resolution 40 kb (dividing each chromosome into bins of size 40 kb). Only the regions associated with expressed genes (FPKM > 10 on mESC and cortex) are considered in Hi-C validation. Given a chromosome and two regions (two bins) on this chromosome, a Hi-C score is denoted as $I\left(A,B\right),$ where A and B are the bin indexes of the two regions. We define the interaction between A and B in Hi-C data if $I\left(A,B\right)>\text{max}\left(I\left(A-1,B\right),I\left(A+1,B\right),I\left(A,B-1\right),I\left(A,B+1\right)\right).$

Given an interacting TF–TF pair may result in region–region chromatin looping, we perform a permutation test to find whether they are significantly validated by Hi-C data or not. We randomly select a region–region pair from the whole genome 1,000 times (same distance distribution with the original region–region pairs) and then count the number of validated pairs in each permutation to generate the background distribution. Comparing the count of validated pairs with the background distribution, we calculate the P value of the Hi-C data validation.

Experimental Design of Retinoic Acid-Induced mESC Differentiation.

Cell culture.

Mouse ES cell lines R1 were obtained from ATCC. The mESCs were first expanded on an mouse embryonic fibroblasts (MEF) feeder layer previously irradiated. Then, subculturing was carried out on 0.1% bovine gelatin-coated tissue culture plates. Cells were propagated in mESC medium consisting of knockout DMEM supplemented with 15% knockout serum replacement, 100 μM nonessential amino acids, 0.5 mM beta-mercaptoethanol, 2 mM GlutaMax, and 100 units/mL penicillin–streptomycin with the addition of 1,000 units/mL of LIF (ESGRO; Millipore).

Cell differentiation.

mESCs were differentiated using the hanging-drop method (29). Trypsinized cells were suspended in differentiation medium (mESC medium without LIF) to a concentration of 50,000 cells/mL. Twenty-microliter drops (∼1,000 cells) were then placed on the lid of a bacterial plate and the lid was placed upside down. After 48 h incubation, embryoid bodies (EBs) formed at the bottom of the drops were collected and placed in the well of a six-well ultralow attachment plate with fresh differentiation medium containing 0.5 μM RA for up to 6 d, with the medium changed daily.

ATAC-seq.

We followed the ATAC-seq protocol published by Buenrostro et al. (5) with the following modifications. The EBs were first treated with 0.25% Trypsin + EDTA at 37 °C for 10–15 min with pipetting. The pellet was then resuspended in the transposase reaction mix (25 μL 2× TD buffer, 2.5 μL transposase, and 22.5 μL nuclease-free water) and incubated at 37 °C for 30 min. After purification, DNA fragments were amplified using 1:30 dilution of 25 μM Nextera Universal PCR primer and Index primer (for details see ATAC-seq PCR Primer) under the following conditions: 72 °C for 5 min; 98 °C for 30 s; and a total of 10 cycles of 98 °C for 10 s, 63 °C for 30 s, and 72 °C for 1 min. The library was sequenced on Illumina HiSeq with 50-bp paired-end reads.

RNA-seq.

Total RNA was extracted using a Qiagen RNeasy mini kit. Libraries were constructed using the NEBNext Ultra RNA Library Prep Kit for Illumina (New England Biolabs) with the following modifications: mRNA was first isolated from 1 μg of total RNA, using the NEBNext Poly(A) mRNA Magnetic Isolation Module. Then it was fragmented at 94 °C for 12 min before first-strand and second-strand cDNA synthesis. The double-stranded cDNA was then end repaired and ligated with NEBNext adaptor, followed by AMPure XP beads purification (Beckman Coulter). Each library was amplified using NEBNext Universal PCR primer and Index primer (for details see NEBNext Multiplex Oligo for Illumina) under the following conditions: 98 °C for 30 s and a total of six cycles of 98 °C for 10 s, 65 °C for 30 s, and 72 °C for 30 s, with a final extension at 72 °C for 5 min. Additional PCRs (four to six cycles) were necessary to obtain enough DNA for sequencing. Finally, equal amounts of DNA from each library were pooled together and a 400-bp fragment was selected by 2% E-Gel SizeSelect Gels (Thermo Fisher Scientific) and purified with AMPure XP beads. The library was sequenced on Illumina HiSeq with 100-bp paired-end reads.

Software and Data.

PECA software and training data are available at web.stanford.edu/∼zduren/PECA/. Gene expression data and chromatin accessibility data of RA induction have been deposited in the GEO database under accession no. GSE98479.

ATAC-seq PCR Primer

Nextera Universal PCR primer:

• AATGATACGGCGACCACCGAGATCTACACTCGTCGGCAGCGTCAGATGTG

Index 1:

• CAAGCAGAAGACGGCATACGAGATTCGCCTTAGTCTCGTGGGCTCGGAGATGT

Index 2:

• CAAGCAGAAGACGGCATACGAGATCTAGTACGGTCTCGTGGGCTCGGAGATGT

Index 3:

• CAAGCAGAAGACGGCATACGAGATTTCTGCCTGTCTCGTGGGCTCGGAGATGT

Index 4:

• CAAGCAGAAGACGGCATACGAGATGCTCAGGAGTCTCGTGGGCTCGGAGATGT

Index 5:

• CAAGCAGAAGACGGCATACGAGATAGGAGTCCGTCTCGTGGGCTCGGAGATGT

Index 6:

• CAAGCAGAAGACGGCATACGAGATCATGCCTAGTCTCGTGGGCTCGGAGATGT

Index 7:

• CAAGCAGAAGACGGCATACGAGATGTAGAGAGGTCTCGTGGGCTCGGAGATGT

Index 8:

• CAAGCAGAAGACGGCATACGAGATCCTCTCTGGTCTCGTGGGCTCGGAGATGT

Index 9:

• CAAGCAGAAGACGGCATACGAGATAGCGTAGCGTCTCGTGGGCTCGGAGATGT

Index 10:

• CAAGCAGAAGACGGCATACGAGATCAGCCTCGGTCTCGTGGGCTCGGAGATGT

Index 11:

• CAAGCAGAAGACGGCATACGAGATTGCCTCTTGTCTCGTGGGCTCGGAGATGT

Index 12:

• CAAGCAGAAGACGGCATACGAGATTCCTCTACGTCTCGTGGGCTCGGAGATGT

NEBNext Multiplex Oligo for Illumina

NEBNext Universal PCR primer:

• AATGATACGGCGACCACCGAGATCTACACTCTTTCCCTACACGACGCTCTTCCGATCT

Index 1:

• CAAGCAGAAGACGGCATACGAGATCGTGATGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 2:

• CAAGCAGAAGACGGCATACGAGATACATCGGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 3:

• CAAGCAGAAGACGGCATACGAGATGCCTAAGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 4:

• CAAGCAGAAGACGGCATACGAGATTGGTCAGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 5:

• CAAGCAGAAGACGGCATACGAGATCACTGTGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 6:

• CAAGCAGAAGACGGCATACGAGATATTGGCGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 7:

• CAAGCAGAAGACGGCATACGAGATGATCTGGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 8:

• CAAGCAGAAGACGGCATACGAGATTCAAGTGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 9:

• CAAGCAGAAGACGGCATACGAGATCTGATCGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 10:

• CAAGCAGAAGACGGCATACGAGATAAGCTAGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 11:

• CAAGCAGAAGACGGCATACGAGATGTAGCCGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT

Index 12:

• CAAGCAGAAGACGGCATACGAGATTACAAGGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT