Abstract
The complexity of neural dynamics stems in part from the complexity of the underlying anatomy. Yet how white matter structure constrains how the brain transitions from one cognitive state to another remains unknown. Here we address this question by drawing on recent advances in network control theory to model the underlying mechanisms of brain state transitions as elicited by the collective control of region sets. We find that previously identified attention and executive control systems are poised to affect a broad array of state transitions that cannot easily be classified by traditional engineering-based notions of control. This theoretical versatility comes with a vulnerability to injury. In patients with mild traumatic brain injury, we observe a loss of specificity in putative control processes, suggesting greater susceptibility to neurophysiological noise. These results offer fundamental insights into the mechanisms driving brain state transitions in healthy cognition and their alteration following injury.
Keywords: Network neuroscience, Control theory, Traumatic brain injury, Cognitive control, Diffusion imaging
Introduction
The human brain is a complex dynamical system that transitions smoothly and continuously through states that directly support cognitive function (Deco et al., 2011). Intuitively, these trajectories can map out the mental states that our brain may pass through as we go about the activities of daily living. In a mathematical sense, these transitions can be thought of as trajectories through an underlying state space (Shenoy et al., 2011; Freeman, 1994; Gu et al., 2016). While an understanding of these trajectories is critical for our understanding of cognition and its alteration following brain injury, fundamental and therefore generalizable mechanisms explaining how the brain moves through states have remained elusive.
One key challenge hampering progress is the complexity of these trajectories, which stems in part from the architectural complexity of the underlying anatomy (Hermundstad et al., 2011, 2013, 2014). Different components (neurons, cortical columns, and brain areas) are linked with one another in complex spatial patterns that enable diverse neural functions (Rajan et al., 2016; Fiete et al., 2010; Levy et al., 2001). These structural interactions can be represented as a graph or network, where component parts form the nodes of the network, and where anatomical links form the edges between nodes (Bullmore and Sporns, 2009). The architecture of these networks displays heterogenous features that play a role in neural function (Medaglia et al., 2015), development (Di Martino et al., 2014), disease (Braun et al., 2015), and sensitivity to rehabilitation (Weiss et al., 2011). Despite these recent discoveries, how architectural features constrain neural dynamics in any of these phenomena is far from understood.
One simple and intuitive way to formulate questions about how neural dynamics are constrained by brain network architecture is to define a state of the brain by the 1 ×N vector representing magnitudes of neural activity across N brain regions, and to further define brain network architecture by the N × N adjacency matrix representing the number of white matter streamlines linking brain regions (Gu et al., 2015). Building on these two definitions, we can ask how the organization of the white matter architecture constrains the possible states in which the brain can or does exist (Durstewitz and Deco, 2008; Hansen et al., 2015). Moreover, building on decades of cognitive neuroscience research that have carefully delineated the role of regional activation in cognitive functions (Gazzaniga, 2013; Szameitat et al., 2011; Alavash et al., 2015), we can then map brain states to cognitive processes, and extend our question to: how does the organization of white matter architecture constrain cognitive states (Hermundstad et al., 2013, 2014), and the processes that enable us to move between those cognitive states (Cocchi et al., 2013)?
To address these questions, we draw on recent advances in network control theory (Pasqualetti et al., 2014) to develop a biologically informed mathematical model of brain dynamics from which we can infer how the topology of white matter architecture constrains how the brain may affect (or control) transitions between brain states. Within this model, we examine finite-time transitions (from initial to target state) that are elicited via the collective control of many regions, consistent with the collective dynamics observed to support cognition (Salvador et al., 2005; Meunier et al., 2009; Power et al., 2011; Yeo et al., 2011) and action (Bassett et al., 2011b, 2013, 2015). A natural choice for an initial state is the brain’s well-known baseline condition, a state characterized by high activity in the precuneus, posterior cingulate, medial and lateral temporal, and superior frontal cortex (Raichle, 2015; Raichle and Snyder, 2007; Raichle et al., 2001). While potential transitions from this default mode are myriad, we focus this first study on examining transitions into target states of high activity in sensor-imotor cortex: specifically the extended visual, auditory, and motor cortices. These states represent the simplest and most fundamental targets to transition from the default mode: for example, transitioning from the default mode to visual states might represent an immediate response to a surprising stimulus. Similarly, the transition from the default mode to motor states might represent the simple transition from rest to action. Moreover, these transitions are of particular interest in many clinical disorders including stroke (Carter et al., 2012) and traumatic brain injury (Nudo, 2006; Lee et al., 2011) where the cognitive functions performed by these target areas are often altered, significantly effecting quality of life (Kalpinski et al., 2013).
Using network control theory, we examine the optimal trajectories from an initial state (composed of high activity in the default mode system) to target states (composed of high activity in sensorimotor systems) with finite time and limited energy. In this optimal control context, we investigate the role of white matter connectivity between brain regions in constraining dynamic state transitions by asking three interrelated questions. First, we ask which brain regions are theoretically predicted to be most energetically efficient in eliciting state transitions. Second, we ask whether these state transitions are best elicited by one of three well-known control strategies commonly utilized in mechanical systems (Gu et al., 2015). Third, we ask how specific each region’s role is in these state transitions, and we compare this specificity between a group of healthy adults and a group of patients with mild traumatic brain injury. In particular, the inclusion of this clinical cohort enables us to determine whether widespread injury leads to a decrement in the healthy network control profiles, thus requiring greater energy for the same functions, or an enhancement of the healthy network control profiles at the cost of a more fragile system, overly sensitive to external perturbations. Together, these studies offer initial insights into how structural network characteristics constrain transitions between brain states, and predict their alteration following brain injury.
To address these questions, we build structural brain networks from diffusion spectrum imaging (DSI) data acquired from 48 healthy adults and 11 individuals with mild traumatic brain injury (Fig. 1A). We perform diffusion tractography on these images to estimate the quantitative anisotropy along the streamlines linking N=234 large-scale cortical and subcortical regions extracted from the Lausanne atlas (Cammoun et al., 2012; Daducci et al., 2012). We summarize these estimates in a weighted adjacency matrix whose entries reflect the number of streamlines connecting different regions (Fig. 1B). We then define a model of brain state dynamics informed by the weighted adjacency matrix, and we use this model to perform a systematic study of the controllability of the system. This construction enables us to examine how structural network differences between brain regions impact their putative roles in controlling transitions between cognitive states (Fig. 1C).
Fig. 1.
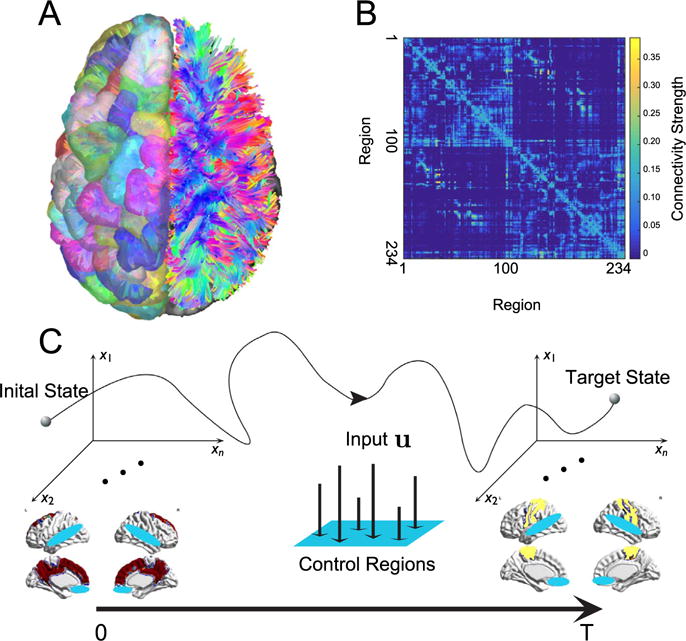
Conceptual schematic. (A) Diffusion imaging data can be used to estimate connectivity from one voxel to any other voxel via diffusion tractography algorithms. (B) From the tractography, we construct a weighted network in which N=234 brain regions are connected by the quantitative anisotropy along the tracts linking them (see Methods). (C) We study the optimal control problem in which the brain starts from an initial state (red) at time t=0 and uses multi-point control (control of multiple regions; blue) to arrive at a target state (yellow) at time t = T.
Materials and methods
Data acquisition and brain network construction
Diffusion spectrum images (DSI) were acquired from 59 human adults with 72 scans in total, among which 61 scans were acquired from 48 healthy subjects (mean age 22.6 ± 5.1 years, 24 female, 2 left handed) and 11 were acquired from individuals with mild traumatic brain injury (Cieslak and Grafton, 2014) (mean age 33.8 ± 13.3 years, 4 female, handedness unclear). All participants volunteered with in-formed written consent in accordance with the Institutional Review Board/Human Subjects Committee, University of California, Santa Barbara. Deterministic fiber tracking using a modified FACT algorithm was performed until 100,000 streamlines were reconstructed for each individual. Consistent with previous work (Bassett et al., 2010, 2011a, Hermundstad et al., 2013, 2014; Klimm et al., 2014; Gu et al., 2015, Muldoon et al., 2016a,b, Sizemore et al., 2015), we defined structural brain networks from the streamlines linking N = 234 large-scale cortical and subcortical regions extracted from the Lausanne atlas (Hagmann et al., 2008). We summarize these estimates in a weighted adjacency matrix A whose entries Aij reflect the structural connectivity (quantitative anisotropy) between region i and region j (Fig. 1A). See SI for further details.
Network control theory
Next, we consider the general question of how the brain moves between different states, where a state is defined as a pattern of activity across brain regions or voxels. In particular, we are interested in studying how the activity in individual brain regions affects the trajectory of the brain as it transitions between states; here, we define a trajectory as a set of states ordered in time. To address this question, we follow Gu et al. (2015), Muldoon et al. (2016a), and Betzel et al. (2016) by adopting notions from the emerging field of network control theory, which offers a theoretical framework for describing the role of network nodes in the control of a dynamical networked system.
Network control theory is predicated on the choice of both a structural network representation for the system, and a prescribed model of node dynamics. In the context of the human brain, a natural choice for the structural network representation is the graph on N brain regions whose ijth edge represents the QA between node i and node j. The choice for the model of node dynamics is perhaps less constrained, as many models are available to the investigator. These models range in complexity from simple linear models of neural dynamics with few parameters to nonlinear neural mass models with hundreds of parameters (Gu et al., 2015; Muldoon et al., 2016a).
In choosing a model of neural dynamics to employ, we consider multiple factors. First, although the evolution of neural activity acts as a collection of nonlinear dynamic processes, prior studies have demonstrated the possibility of predicting a significant amount of variance in neural dynamics as measured by fMRI through simplified linear models (Galán, 2008; Honey et al., 2009; Gu et al., 2015). On the basis of this literature, we employ a simplified noise-free linear continuous-time and time-invariant network model
| (1) |
where x: ℝ≥0⟶ ℝN describes the state of brain regions over time, and A ∈ ℝN×N is a symmetric and weighted adjacency matrix. The diagonal elements of the matrix A satisfy Aii =0. The input matrix identifies the control nodes in the brain, where and
| (2) |
and ei denotes the i-th canonical vector of dimension N. The input denotes the control strategy. Intuitively, this model enables us to frame questions related to brain state trajectories in formal mathematics. Moreover, it allows us to capitalize on recent advances in network control theory (Pasqualetti et al., 2014) to inform our understanding of internal cognitive control (Gu et al., 2015; Betzel et al., 2016) and to inform the development of optimal external neuromodulation using brain stimulation (Muldoon et al., 2016b).
Optimal control trajectories
Given the above-defined model of neural dynamics, as well as the structural network representation extracted from diffusion imaging data, we can now formally address the question of how the activity in individual brain regions affects the trajectory of the brain as it transitions between states.
We begin by defining an optimization problem to identify the trajectory between a specified pair of brain states that minimizes a given cost function. We define a cost function by the weighted sum of the energy cost of the transition and the integrated squared distance between the transition states and the target state. We choose this dual-term cost function for two reasons. First, theoretically, the energy cost term constrains the range of the time-dependent control energy u(t). In practice, this means that the brain cannot use an infinite amount of energy to perform the task (i.e., elicit the state transition), a constraint that is consistent with the natural energetic restrictions implicit in the nature of all biological systems but particularly neural systems (Niven and Laughlin, 2008; Laughlin et al., 1998; Attwell and Laughlin, 2001; Laughlin, 2001). Second, the integrated distance term provides a direct constraint on the trajectory. Mathematically, this constraint penalizes trajectories that traverse states that are far away from the target state, based on the intuition that optimal transitions between states should possess reasonable lengths rather than being characterized by a random walk in state space. Together, these two terms in the cost function enable us to define an optimal control model from which we expect to find trajectories (from a given initial state to a specified target state) characterized by a balance between energy cost and trajectory length.
In the context of the optimization problem defined above, we wish to determine the trajectory from an initial state x0 to a target state xT. To do so, it suffices to solve the variational problem with the constraints from Eq. (1) and the boundary conditions for x(t), i.e., x(0) is the initial state and x(T) is the target state. Note that here, the variational problem does not refer toBayesian variational inference, which tries to approximate an intractable posterior distribution. Instead, we use the term in the more traditional sense, and address the variational problem to infer a control input function u(t) to minimize the cost functional defined in Eq. (4) with the boundary constraints. Mathematically, the variational problem is formulated as
| (3) |
where T is the control horizon, ρ ∈ ℝ > 0, and (xT − x (t)) is the distance between the state at time t and the target state.
To compute an optimal control u* that induces a transition from the initial state x0 to the target state x0 to the target state xT, we define the Hamiltonian as
| (4) |
From the Pontryagin minimum principle (Boltyanskii et al., 1960), if u* is an optimal solution to the minimization problem with corresponding state trajectory x*, then there exists p* such that
| (5) |
| (6) |
which reduces to
| (7) |
Next, we denote
| (8) |
| (9) |
| (10) |
then Eq. (7) can be written as
| (11) |
from which we can derive that
| (12) |
where is a constant to be fixed from the boundary conditions. Let , and plug in t = 0, T with the corresponding x0 and xT, we have
| (13) |
| (14) |
Note that from Eq. (13), we can solve for , where
| (15) |
Finally, with on hand from Eq. (14), we can compute p(T), where
| (16) |
with which we can finally get , where
| (17) |
and further u(t) and x(t) from Eq. (12).
Note that the formulae we derive here are the closed form solutions to the optimization objective, and therefore a numerical solver is not needed.
Statistics of optimal control trajectories
After calculating the optimal trajectories between initial and final states, we next sought to address the question of whether these trajectories differed in their energetic and spatial requirements for different choices of control strategies, and between individual’s whose brains were healthy and normally functioning, and individuals who had experienced a mild traumatic brain injury and had presented with complaints of mild cognitive impairment. To address this question, we computed the energy cost of a trajectory, integrated over time T, as
| (18) |
and the spatial cost of a trajectory, integrated over time T, as
| (19) |
where is the associated control input and is the controlled trajectory with the given control set , initial state x0 and the target state xT. We treat this energy as a simple statistic that can be compared across trajectories and subject groups, as an indirect measure from which we may infer optimality of cognitive function.
Control efficiency
The control efficiency is defined for each region to quantify its efficiency in affecting the transition from the default mode state to the three target states. Mathematically, suppose we have N randomly chosen control sets, each indexed by , for the target states , j = 1, 2, 3, we calculate the corresponding optimal trajectory with respect to and denote the energy cost of the trajectory as . The tiered value of the control set for target is then defined as
| (20) |
where lower energy costs imply higher tiered values. The control efficiency for node i in task j is then
| (21) |
or intuitively, the average of these tiered values.
Network communicability to the target state
For a given weighted network A, the network communicability G quantifies the extent of indirect connectivity among nodes. Here we adopt the generalized definition in Crofts and Higham (2009) and define the network communicability as G = exp(D−1/2AD−1/2), where D is the diagonal matrix with the diagonal element Dii = Σi Aij. For a given target state xT, denote the set of active regions as communicability to the target states (GTi) is then defined as the sum of communicability to all of the target regions, i.e., . Further, the normalized network communicability to the target regions is then defined as
| (22) |
All results reported in this study are based on the normalized network communicability.
Energetic impact of brain regions on control trajectories
To quantify the robustness of controllability of a node when it is removed from the control set consisting of all nodes, we iteratively remove nodes from the network and compute the energetic impact of each region on the optimal trajectory as the resulting increase in the log value of the energy cost. Intuitively, regions with high energetic impact are those whose removal from the network causes the greatest increase in the energy required for the state transition. Mathematically, denote as the control set of all nodes and as the control set without node , the energetic impact of node i for target is defined as
| (23) |
which intuitively measures robustness controllability.
Results
To begin, we set the initial state of the brain to be an activation pattern consistent with those empirically observed in the brain’s baseline condition. More specifically, we set the initial state such that the regions of the default mode network had activity magnitudes equal to 1 (on), while all other regions had activity magnitudes equal to 0 (off). Furthermore, we examined 3 distinct target states such that regions of the (i) auditory, (ii) extended visual, or (iii) motor systems had activity magnitudes equal to 1 (on), while all other regions had activity magnitudes equal to 0 (off). In this context, we sought to understand characteristics of the transitions between initial and target states that could be performed with minimal energy, minimal time, and along short trajectories in state space by multiple control regions (multi-point control; see Fig. 1C and Methods). We note that mathematically, we measure time in arbitrary units, at each of which control energy can be utilized by a brain region. Intuitively, we operationalize time as consistent with the temporal scale at which brain regions can alter their activity magnitudes to affect state transitions.
Characteristics of optimal control trajectories
We first study the three state transitions from the default mode to (i) auditory, (ii) extended visual, and (iii) motor states (Fig. 2A). We take a hypothesis-driven approach and define the “control set” to be composed of dorsal and ventral attention (Posner and Petersen, 1989), fronto-parietal, and cingulo-opercular cognitive control regions (Gu et al., 2015). That is, this set of 87 regions will utilize control energy using a multi-point control strategy, thereby changing the time-varying activity magnitudes of all brain regions (Fig. 2B). The optimal trajectories display multiple peaks in the distance from the target state as a function of time, and are altered very little by whether the target state is the auditory, extended visual, or motor system (Fig. 2C). Because the optimal trajectory is determined via a balance of control energy and trajectory distance (see Methods), it stands to reason that the time-dependent energy utilized by the control set is inversely related to the distance between the current state and the target state. When little control energy is utilized, the current state can drift far from the target state, while when a larger magnitude of control energy is utilized, the current state moves closer to the target state (Fig. 2D).
Fig. 2.
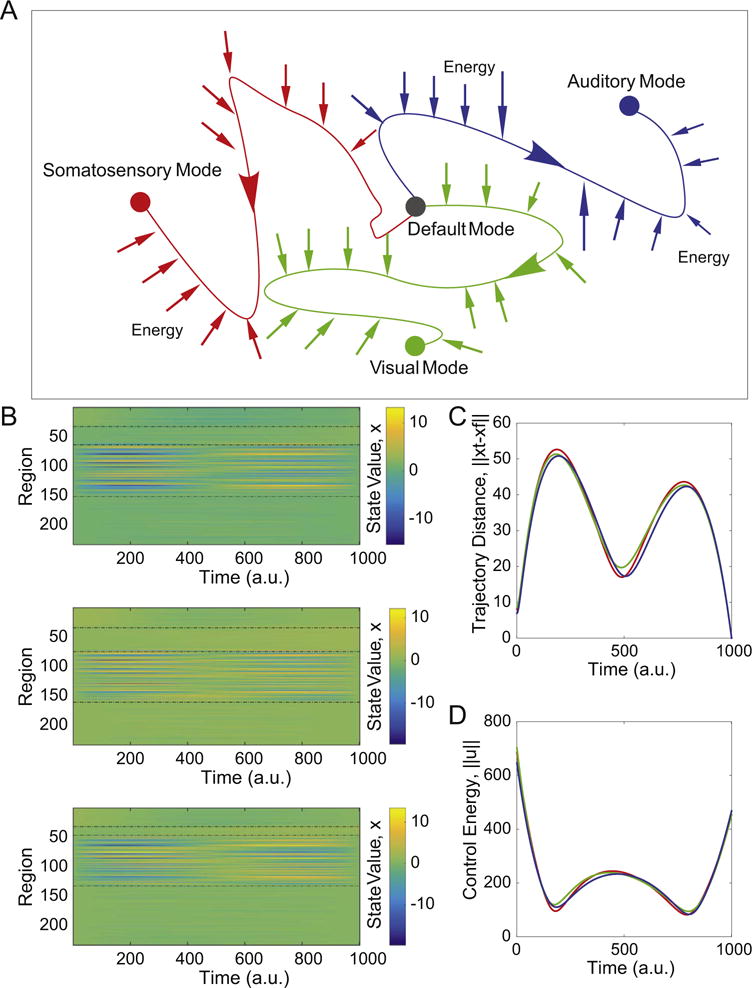
Optimal control trajectories. (A) We study 3 distinct types of state transitions in which the initial state is characterized by high activity in the default mode system, and the target states are characterized by high activity in auditory (blue), extended visual (green), or motor (red) systems. (B) The activation profiles of all N=234 brain regions as a function of time along the optimal control trajectory, illustrating that activity magnitudes vary by region and by time. Activation can be either positive or negative, and the exact range of values will depend on the initial state, the target state, and the control set. Regions are listed in the following order: initial state, target state, controllers, and others. (C) The average distance from the current state x(t) to the target state x(T) as a function of time for the trajectories from the default mode system to the auditory, visual, and motor systems, illustrating behavior in the large state space. (D) The average control energy utilized by the control set as a function of time for the trajectories from the default mode system to the auditory, visual, and motor systems. The similarity of the curves observed in panels (C) and (D) is driven largely by the fact that they share the same control set. See Fig. S2(B) for additional information on the range of these control energy values along the trajectories. Colors representing target states are identical in panels (A), (C), and (D).
It is important to note that these general characteristics of the optimal control trajectories are dependent on our choice of the control set (which here we guide with biologically motivated hypotheses), as well as on a penalty on the time required for the transition (ρ in Eq. (3); see Methods). In the supplement, we examine the effect of alternative choices for both the control set and ρ. First, we find that when the control set includes every node in the network, the distance to the target state decreases monotonically to zero along the trajectory (Fig. S1A). Second, we consider the effect of the penalty term on control energy, ρ. For the results presented here, we fix ρ to be equal to 1. However, in the supplement, we explore a wide range of ρ values, and show that when ρ is small, the optimal control trajectory is largely driven by a minimization of the integrated squared distance to the target. In contrast, when ρ is large, the optimal control trajectory is predominantly driven by the magnitude of the utilized energy (Fig. S1B). Importantly, we did not perform a full sweep of ρ from 0 to infinity because very small values of ρ cause numeric instabilities in the calculations.
Structurally driven task preference for control regions
We next ask whether certain brain regions are located at specific points in the structural network that make them predisposed to play consistent and important roles in driving optimal control trajectories. To answer this question, we choose control sets of the same size as the brain’s hypothesized cognitive control set; recall that in the previous section, we defined the brain’s cognitive control set to consist of the 87 nodes of the dorsal and ventral attention, fronto-parietal, and cingulo-opercular systems following Gu et al. (2015). Here, we choose the 87 regions of these new control sets uniformly at random from the set of all nodes. Using these “random” control sets, we computed the optimal control trajectory for each of the three state transitions and for each subject separately. Then, we rank the random control sets in descending order according to the energy cost of the trajectory and we assign every region participating in an r-ranked control set with rank-value r. Next, we define the control efficiency of a brain region to be the sum of its rank values in all of the random control sets it belongs to divided by the total number of sets it belongs to. Intuitively, a region with a high control efficiency is one that exerts control with little energy utilization. Importantly, it must decrease activation in the initial state, and increase activation in the target state, a pair of capabilities that depends on the pattern of connections emanating from the region.
In general, we observe that a region’s preference for being an optimal controller (exerting control with little energy utilization) is positively correlated with its network communicability to the regions of high activity in the target state (Spearman correlation r = 0.27, p < 4.8 × 10−4; see Fig. 3A). We recall that network communicability is a measurement of the strength of a connection from one region to another that accounts for walks of all lengths (see Methods). Interestingly, we observed this same correlation between control efficiency and network communicability across optimal control trajectories for all three state transitions, from the default mode to the auditory (r=0.36, p = 1.4 × 10−8), extended visual (r=0.51, p = 1.1 × 10−16), or motor (r=0.42, p = 2.1 × 10−11) systems (Fig. 3B–D). Together, these results indicate that regions that are close (in terms of walk lengths) to regions of high activity in the target state are efficient controllers for that specific state transition. Note that these regions are not purely target areas, likely due to the fact that they must also decrease activation in the initial state.
Fig. 3.
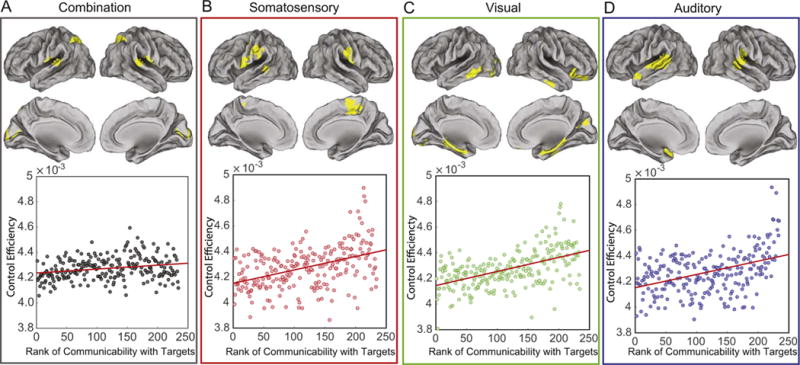
Structurally driven task preference for control regions. (A) Top: Regions with high control efficiency (see Eq. (21)) across all 3 state transitions: from the default mode to auditory, extended visual, and motor systems. Bottom: Scatterplot of the control efficiency with the average network communicability to all 3 target regions (Spearman correlation r = 0.27, p < 4.8 × 10−4). (B–D) Top: Regions with high control efficiency for the transition from default mode to (B) motor, (C) extended visual, and (D) auditory (r=0.36, p = 1.4 × 10−8) targets (top). Bottom: Scatter plot of control efficiency versus normalized network communicability with regions that are active in the target state: motor (r=0.42, p = 2.1 × 10−11), extended visual (r=0.51, p = 1.1 × 10−16), and auditory (r=0.36, p = 1.4 × 10−8). Values of control efficiency in all four panels are averaged over subjects.
The general role that network proximity to the target state plays for control regions ensures that regions that are proximate to all three target states (auditory, extended visual, and motor) will be task-general controllers, while regions that are proximate to only one of the target states will be task-specific controllers. To better understand the anatomy of efficient controllers, we transformed control efficiency values to z-scores and defined an efficient control hub to be any region whose associated p-value was less than 0.025. Across all three state transitions, we found that the supramarginal gyrus specifically, and the inferior parietal lobule more generally, consistently acted as an efficient control hub. The consistent control role of these regions is likely due to the fact that these areas are structurally interconnected with ventral premotor cortex, a key input to primary sensorimotor areas (Kandel et al., 2000). The areas that are more specific to the three state transitions include medial parietal cortex (motor transition), orbitofrontal and inferior temporal cortex (visual transition), and superior temporal cortex (auditory transition).
Regional roles in control tasks
The analyses outlined above are built on the assumption that the brain uses fronto-parietal, cingulo-opercular, and attention systems to affect cognitive control, which we define as the ability to move the brain from an initial state (e.g., the default mode system) to a specified final state (e.g., activation of extended visual, auditory, or motor cortex). However, one might naturally ask whether these regions of the brain could have been predicted a priori to be effective controllers based on traditional engineering-based notions of control. In the control theory literature, particularly the literature devoted to the subfield of network controllability, there exist several controllability notions, including average, modal, and boundary control (Pasqualetti et al., 2014). Average controllability identifies brain areas that can theoretically steer the system into many different states, or patterns of neurophysiological activity magnitudes across brain regions. Modal controll-ability identifies brain areas that can theoretically steer the system into difficult-to-reach states. Boundary controllability identifies brain areas that can theoretically steer the system into states where different cognitive systems are either coupled or decoupled. See the SI for mathematical definitions and Gu et al. (2015) for prior studies in human neuroimaging.
We calculated average, modal, and boundary control values for each node in the network. We observe that while cognitive control regions cover a broad swath of frontal and parietal cortex, including medial frontal cortex and anterior cingulate (Fig. 4A), the number of these regions that intersect with the strongest 87 average, modal, or boundary control hubs was on average approximately 50 (Fig. 4B). These results suggest that the control capabilities of the human brain’s cognitive control regions may not be perfectly aligned with control notions previously developed in the field of mechanical engineering, provided that the model assumptions and data quality are appropriate (see Methodological Considerations). Instead, cognitive control regions in the human brain may have distinct capabilities necessary for the specific transitions required by the brain under the constraints imposed by neuroanatomy and neurophysiology.
Fig. 4.
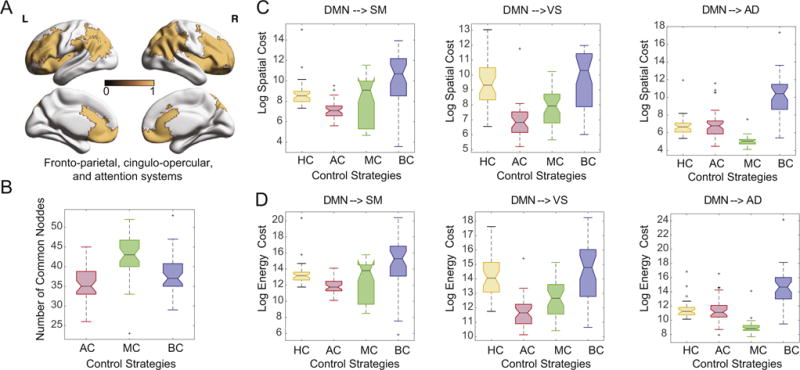
Regional roles in control tasks. (A) Cognitive control regions cover a broad swath of frontal and parietal cortex, including medial frontal cortex and anterior cingulate, and are defined as regions included in fronto-parietal, cingulo-opercular, and attention systems (Gu et al., 2015). (B) The number of these regions overlapping with the strongest 87 average, modal and boundary control hubs is approximately 50. Different choices of control strategies result in variation in both (C) trajectory cost and (D) energy cost. Here, HC refers to cognitive control regions, AC refers to average control hubs, MC refers to modal control hubs, and BC refers to boundary control hubs.
To more directly test this possibility, we examined the average distance (Fig. 4C) and energy (Fig. 4D) for transitions from the default mode to the auditory, extended visual, and sensorimotor states that are driven by average, modal, and boundary control hubs, or by regions of fronto-parietal, cingulo-opercular, and attention systems. We observed that both the trajectory cost and the energy cost differ by control strategy and by target state. We quantify this observation using a 2-way ANOVA with both the control strategy and the target state as categorical factors. Using the trajectory cost as the dependent variable, we observed a significant main effect of control strategy (F=78.74, p = 4.65 × 10−41), a significant main effect of target state (F=29.24, p = 1.12 × 10−12), and a significant interaction between control strategy and target state (F=11.36, p = 7.6 × 10−12). Similarly, using the energy cost as the dependent variable, we observed a significant main effect of control strategy (F=67.94, p = 2.48 × 10−36), a significant main effect of target state (F=39.18, p = 1.99 × 10−16), and a significant interaction between control strategy and target state (F=10.93, p = 2.18 × 10−11). Collapsing over target states and performing post hoc testing, we observed that cognitive control regions displayed a similar average trajectory cost to average control hubs, but a lower average trajectory cost than modal and boundary control hubs (p < 0.05 uncorrected). Furthermore, cognitive control regions possessed a higher average energy cost than the average and modal control hubs, but a lower average energy cost than the boundary control hubs. These results interestingly suggest that the human’s cognitive control regions, as defined by decades of research in cognitive neuroscience, may affect state transitions using neither the shortest distances nor the lowest energies possible, provided that the model assumptions and data quality are appropriate (see Methodological Considerations). This is likely due to the fact that cognitive control regions must affect a broad array of state transitions that cannot easily be classified into average, modal, and boundary control strategies.
Specificity of control in health and following injury
The unique role of brain regions in affecting control strategies may bring with it vulnerability to injury. When a brain network is injured, regional control roles may be significantly altered, potentially increasing susceptibility to underlying abnormalities in neuronal dynamics. To characterize this vulnerability, we determine the degree to which a single brain region impacts putative control processes and we ask whether that specificity is maintained or altered following brain injury. We measure specificity by iteratively removing nodes from the control set, and we compute the energetic impact of each region on the optimal trajectory as the resulting increase in the log value of the energy cost (see Fig. 5A and Eq. (23) in Methods). Intuitively, regions with high energetic impact are those whose removal from the network causes the greatest increase in the energy required for the state transition. Across all subjects and all tasks, we observe that the regions with the highest energy impact are the supramarginal gyrus specifically, and the inferior parietal lobule more generally, the same regions that emerged as consistent and efficient controllers in Fig. 2A.
Fig. 5.
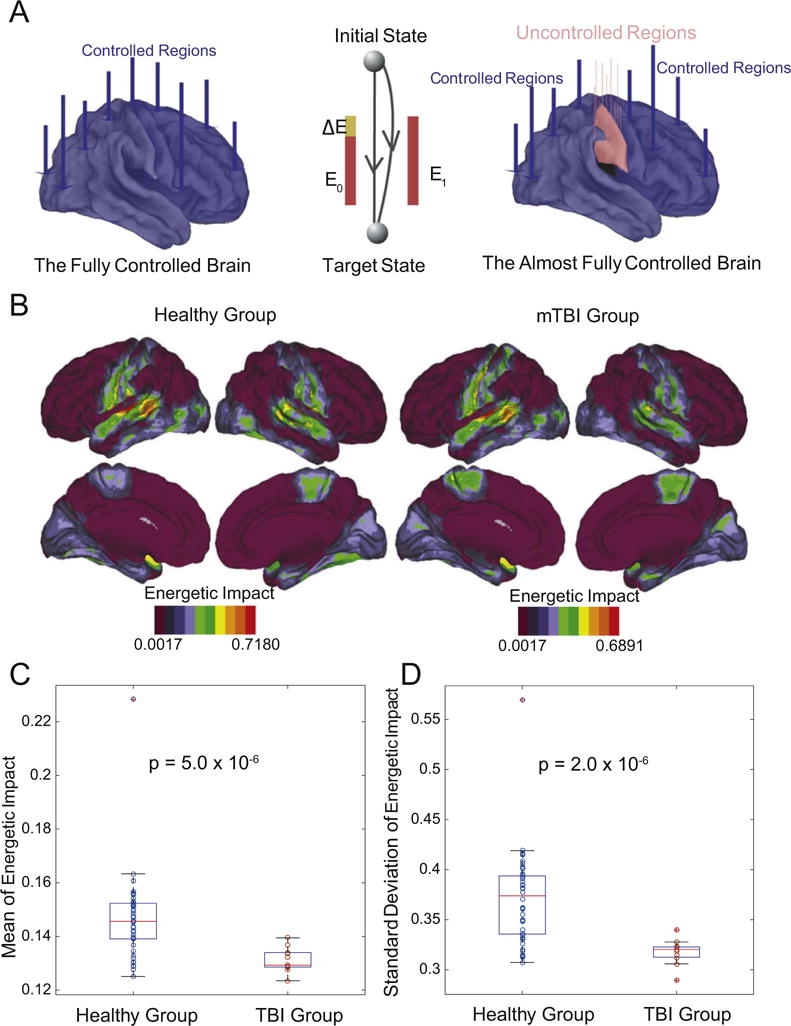
Specificity of control in health and following injury. (A) Theoretically, the brain is fully controllable when every region is a control point, but may not be fully controllable when fewer regions are used to affect control. (B) The regions with the highest values of energetic impact on control trajectories upon removal from the network, on average across subjects and tasks, were the supramarginal gyrus specifically, and the inferior parietal lobule more generally. In general, the healthy group and the mTBI group displayed similar anatomical patterns of energetic impact. (C) Magnitude and standard deviation of energetic impact averaged over regions and tasks; boxplots indicate variation over subjects. Even after removing the single outlier in the healthy group, patients with mTBI displayed significantly lower values of average magnitude of energetic impact (permutation test: p = 1.1 × 10−5) and lower values of the average standard deviation of energetic impact (p = 2.0 × 10−6) than healthy controls.
Next we determined whether energetic impact – our proxy for regional specificity of control roles – is altered in individuals with mild traumatic brain injury (mTBI). Intuitively, if all regions of a brain have high energetic impact, this indicates that each region is performing a different control role which is destroyed by removal of the node. By contrast, if all regions of a brain have low average energetic impact, this indicates that each region is performing a similar control role that is not destroyed by removal of a node. We observed that individuals with mTBI displayed anatomically similar patterns of energetic impact on control trajectories as regions are removed from the network (Fig. 5B). However, the average magnitude and variability of the energetic impact differed significantly between the two groups, with individuals having experienced mTBI displaying significantly lower values of average magnitude of energetic impact (permutation test: p = 5.0 × 10−6) and lower values of the average standard deviation of energetic impact (p = 2.0 × 10−6). We note that common graph metrics including the degree, path length, clustering coefficient, modularity, local efficiency, global efficiency, and density were not significantly different between the two groups, suggesting that this effect is specific to control (see Supplement). These results indicate that mTBI patients display a loss of specificity in the putative control roles of brain regions, suggesting greater susceptibility to damage-induced noise in neurophysiological processes, or to external drivers in the form of stimulation.
Discussion
Here we ask whether structural connectivity forms a fundamental constraint on how the brain may move between diverse cognitive states. To address this question, we capitalize on recent advances in network control theory to identify and characterize optimal trajectories from an initial state (composed of high activity in the default mode system) to target states (composed of high activity in sensorimotor systems) with finite time, limited energy, and multi-point control. Using structural brain networks estimated from diffusion imaging data acquired in a large cohort of 48 healthy individuals and 11 patients with mild traumatic brain injury, we show that these optimal control trajectories are characterized by continuous changes in regional activity across the brain. We show that the regions critical for eliciting these state transitions differ depending on the target state, but that hetero-modal association hubs – predominantly in the supramarginal gyrus specifically, and the inferior parietal lobule more generally – are consistently recruited for all three transitions. Finally, we study the sensitivity of optimal control trajectories to the removal of nodes from the network, and we demonstrate that brain networks from individuals with mTBI display maladaptive control capabilities suggestive of a limited dynamic range of states available to the system. Together, these results offer initial insights into how structural network differences between individuals impact their potential to control transitions between cognitive states.
Role of structural connectivity in shaping brain functional patterns
A growing body of literature on the relationship between brain structure and function has demonstrated that the brain’s network of anatomical connections constrains the range of spontaneous (Deco et al., 2011) and task-related (Hermundstad et al., 2013) fluctuations in brain activity. Evidence for such structural underpinnings comes from two distinct lines of research. On one hand, empirical studies have demonstrated that structural insults in the form of lesions result in acute reorganization of the brain’s pattern of functional coupling (Johnston et al., 2008; O’Reilly et al., 2013). These observations are further buttressed by simulation studies in which structural connectivity has been used to constrain interactions among dynamic elements in biophysical models of brain activity (Honey et al., 2007, 2009; Adachi et al., 2011) and models of network communication (Goñi et al., 2014; Abdelnour et al., 2014; Mišić et al., 2015). Though this forward modeling approach has proven fruitful in predicting observed patterns of functional connectivity, the precise mapping of brain structure to function remains unclear.
The present study builds on this body of work, using a dynamical model of how brain activity propagates over a network in order to gain insight into what features of that network facilitate easy transitions from a baseline (default mode) state to states where the brain’s primary sensorimotor systems are activated. In contrast to previous simulation studies that have focused on network features that influence the passive spread of activity over time, this present study directly engages the question of how those same features enable the state of the system to be controlled. We use this model to demonstrate that brain regions are differentially suited for particular control tasks, roles that can be predicted on the basis of how well-connected they are to regions in the target state. Regions that are close (in terms of walk lengths) to regions of high activity in the target state are efficient controllers for that specific state transition. It follows, then, that a brain region’s capacity to dynamically influence a network depends not only on its pattern of connectivity, but also on the repertoire of states that the system visits. In other words, a region that maintains many connections (both direct and indirect), but never to regions that are “active” in target states, may exert less influence than a region that maintains few connections, but whose connections are distributed among regions that are “active” in many target states. We further demonstrate that this mapping of brain structure to specific functions is altered in individuals with mTBI, suggesting that injury may alter control profiles of individual brain regions.
Our finding that the inferior parietal lobule forms a consistently effective control region, across all three target states, is particularly interesting when considered in the context of prior literature on this region’s structural and functional roles. In particular, the inferior parietal lobule represents the superior portion of the temporoparietal junction, a multimodal area associated with functions as wide ranging as calculation, finger gnosis, left/right orientation, and writing (Rusconi et al., 2009). Focal damage to this area leads to wide-spread cognitive dysfunction (e.g., Gerstmann syndrome) as a consequence of the unique confluence of white matter pathways underlying this region (Rushworth et al., 2006). The diverse white matter projections emanating from this area may support its putative role in effectively controlling brain function. Indeed, recent evidence suggests that the right temporoparietal junction links two antagonistic brain networks processing external versus internal information: a midcingulate–motor–insular network associated with attention, and a parietal net-work associated with social cognition and memory retrieval (Bzdok et al., 2013). These data support the notion that the right temporoparietal junction controls our attention to salient external events (Corbetta and Shulman, 2002), perhaps with early input from the right fronto-insular cortex thought to drive switching between central-executive and default-mode networks (Sridharan et al., 2008).
Single versus multipoint control
An important feature of our model lies in the delineation of a control set, a group of brain regions that can affect distributed control. The focus on multiple points of control throughout the system is one that has important theoretical motivations and empirical correlates. Prior computational models demonstrate that while the brain is theoretically controllable via input to a single control point, the energy and time required for that control is such that the brain is practically uncontrollable (Gu et al., 2015). These data argue for an assessment of multi-point control as a better proxy of control strategies that the brain might utilize. Indeed, such an argument is consistent with empirical observations that stimulation (or even drug manipulations) focused on single brain regions are less effective in treating psychiatric disease than interventions that target multiple brain regions (Sommer et al., 2012; Tortella et al., 2014). A prime empirical example of multi-point control is cognitive behavioral therapy, which offers a spatio-temporal pattern of activations that enhances cognitive function and decreases psychiatric symptoms across diagnostic categories (Lett et al., 2014; Radhu et al., 2012; Cima et al., 2014). Other potential multi-point control mechanisms include grid stimulation across multiple electrodes, suggested in the control of medically refractory epilepsy (Ching et al., 2012).
Diversity in human brain control strategies
By studying multi-point control, we were able to directly assess whether the optimal control trajectories elicited from fronto-parietal, cingulo-opercular, and attention systems displayed similar distance and energy trajectories to those obtained using regions selected for engineering-based notions of control (Pasqualetti et al., 2014). Specifically, we compare and contrast the performance of human cognitive control regions to average, modal, and boundary controllers (Gu et al., 2015). One might naturally ask whether and how each of these engineering-based notions of controllers is an appropriate theoretical quantity to consider in the context of neurobiology. Average controllers are those theoretically able to push the system from any arbitrary initial state to any easily reachable state, nearby on the energy landscape. Modal controllers are those that are optimally placed to move the system from any arbitrary initial state to any difficult-to-reach state, far away on the energy landscape. Boundary controllers are those that are optimally placed to integrate or segregate network communities in the system. Common assumptions that underlie each of these control strategies are that (i) controllers can be identified independently from the initial and final states, and (ii) all states in the energy landscape are accessible to the system. The common constraint on each of these strategies is that expended energy must be minimized for a region to be referred to as a controller. In the human brain, it is not well-known whether these assumptions are met, or whether the energetic constraint is sufficient to predict control functions.
Interestingly, we observe that the optimal trajectories elicited by canonically defined cognitive control regions do not show similar energy requirements or trajectory distances to any of these previously described control types. There are several potential reasons for this observation: (i) false negatives in the diffusion imaging data impacting on the observed network profiles, (ii) assumptions of the linear model, and (iii) bona fide differences between mechanical controllers and biological controllers. Prior work demonstrating robustness of controllability profiles across large cohorts and different diffusion imaging acquisition protocols provide initial evidence that the first explanation is unlikely to fully explain our findings (Gu et al., 2015). Regarding the second explanation – assumptions of the linear model – it is interesting to note that recent evidence suggests that the average, modal, and boundary controllability profiles identified by the linear model provide excellent predictions for the behavior of nonlinear models (Muldoon et al., 2016b). Evidence supporting the third interpretation – that these observed differences are bona fide differences between mechanical controllers and biological controllers – is provided by the fact that cognitive control regions must affect a broad array of state transitions that do not easily fit into prior classifications. These transitions include switching behavior (Hansen et al., 2015), inter-state competition (Cocchi et al., 2013), distributed rather than centralized control (Eisenreich et al., 2016), and push–pull control (Khambhati et al., 2016), which may each offer differential advantages for neural computations (Durstewitz and Deco, 2008).
Maladaptive control in traumatic brain injury
Finally, our assessment of patients with mild traumatic brain injury enabled us to determine whether widespread injury leads to a decrement in the healthy network control profiles, thus theoretically requiring greater energy for the same functions, or an enhancement of the healthy network control profiles at the cost of expected sensitivity to external perturbations. Our data provide initial evidence for maladaptive control of the latter sort in patients with mild traumatic brain injury. Understanding the impact of brain injury on cognitive processes, including the ability to switch between cognitive states, is a major goal in clinical neuroscience. Indeed, traumatic brain injury is a common source of brain dysfunction, affecting more than 200,000 individuals per year in the United States alone. Injuries – often caused by motor vehicle and sports accidents – result in damage to neuronal axons, including long-distance white matter fiber bundles (Johnson et al., 2013) as well as u-fibers and deep white matter tracks with multiple crossings. The pattern of injury can be multi-focal and variable across individuals (Kinnunen et al., 2011; Sidaros et al., 2008; Hellyer et al., 2013), challenging comprehensive predictors and generalizable interventions.
Recent evidence suggests that injury-induced, widespread damage to white matter tracts critically impacts large-scale network organization in the human brain, as measured by diffusion imaging tractography (Kinnunen et al., 2011; Fagerholm et al., 2015). Moreover, this damage is associated with fundamental changes in cognitive function (Sharp et al., 2014), including information processing speed, executive function, and associative memory (Fagerholm et al., 2015). Each of these cognitive deficits intuitively depends on the ability to transition from one cognitive state to another; yet an understanding of structural drivers of these transitions and their potential alteration in mTBI has remained elusive. Here we demonstrate a loss of specificity in putative control processes in mTBI, suggesting that the unique roles of individual brain regions in supporting cognitive state transitions are damaged. It is intuitively plausible that this decrement in regional specificity of control leads to broad changes in functional dynamics, particularly in the system’s susceptibility to damage-induced noise in neurophysiological processes (Garrett et al., 2013). Indeed, the observed decrements in energetic impact might further provide a direct structural mechanism for the decreased signal variability observed in mTBI using electrophysiological imaging (Raja Beharelle et al., 2012; Nenadovic et al., 2008). More generally, these findings highlight the fact that the healthy brain might display a degree of controllability that is either decremented or enhanced in injury and disease, suggesting the possibility of a U-shaped curve reminiscent of similar curves observed in other brain network phenotypes (Collin and van den Heuvel, 2013; Cools and D’Esposito, 2011).
Methodological considerations
A few methodological points are worthy of additional consideration. First, in this study we examined structural brain networks derived from diffusion imaging data and associated tractography algorithms. These algorithms remain in their relative infancy, and can still report spurious tracts or fail to report existing tracts (Thomas et al., 2014; Reveley et al., 2015; Pestilli et al., 2014). Despite the evolving nature of diffusion protocols and tractography algorithms, preliminary data provide initial evidence that consistent controllability profiles can be robustly observed across large cohorts and different diffusion imaging acquisition protocols (Gu et al., 2015). Formal validation in axonal tracing studies in monkeys and other mammals (Jbabdi et al., 2013) remains the gold standard for these types of data. However, it is important to note that initial work supports the notion that much of the structure present in DSI connectivity matrices recapitulates known projections observed in tract tracing studies of the macaque (Hagmann et al., 2008).
Second, following Gu et al. (2015), Betzel et al. (2016), and Muldoon et al. (2016b), we employ a linear dynamical model, consistent with prior empirical studies demonstrating their ability to predict features of resting state fMRI data (Galán, 2008; Honey et al., 2009). This choice is to some degree predicated on the well-developed theoretical and analytical results in the engineering and physics literatures examining the relationship between control and network topology (Liu et al., 2011; Müller and Schuppert, 2011; Yan et al., 2012). Moreover, it is plausible that even these results using simple linear models may offer important intuitions for controlling nonlinear models of brain function. Indeed, theoretical work over the last several decades has demonstrated the utility of describing non-linear systems in terms of a linear approximation in the neighborhood of the system’s equilibrium points (Luenberger, 1979). Very recent evidence has extended these intuitions to neuroimaging data, demonstrating that the average and modal controllability profiles identified by the linear model can be used to predict the behavior of nonlinear models in the form of Wilson–Cowan oscillators, which are commonly used to understand the dynamics of cortical columns (Muldoon et al., 2016b).
Future directions
An interesting hypothesis generated by the current framework is that control capabilities may be altered dimensionally across traditionally separated diagnostic groups that display dysconnectivity in network hubs, as measured by regions of high eigenvector centrality. Such a hypothesis builds on the now seminal dysconnection hypothesis in schizophrenia (Stephan et al., 2009), and expands it to include an explicit dynamical control component. Indeed, mounting evidence suggests that the overload or failure of brain network hubs may be a common neurophysiological mechanism of a range of neurological disorders including Alzheimer’s disease, multiple sclerosis, traumatic brain injury, and epilepsy (Stam, 2014). Alterations in these hubs can also be used to predict the progression of psychiatric disorders such as schizophrenia (Collin et al., 2016). In both neurological and psychiatric disorders, these changes to network hubs may alter the control capabilities of the individual, challenging the normal executive functions required for daily living. It is also intuitively plausible that normal variation in hub architecture may play a role in individual differences in control capabilities in healthy individuals, impacting on the speed with which they transition between cognitive states. These topics will form important provender for future work.
Supplementary Material
Acknowledgments
D.S.B., S.G., and R.F.B. acknowledge support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the Army Research Laboratory and the Army Research Office through Contract numbers W911NF-10-2-0022 and W911NF-14-1-0679,the National Institute of Mental Health (2-R01-DC-009209-11), the National Institute of Child Health and Human Development (1R01HD086888-01), the Office of Naval Research, and the National Science Foundation (BCS-1441502, BCS-1430087, and CAREER PHY-1554488). S.T.G. and P.R.D. acknowledge support from a Head Health Challenge grant from General Electric and the National Football League (SB140165). F.P. acknowledges support from the National Science Foundation award #BCS 1430280. The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies.
Appendix A. Supplementary data
Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.neuroimage.2017.01.003.
Footnotes
Author contributions
S.G. performed the analysis. M.C. preprocessed the data. S.T.G. and P.R.D. acquired the data. S.G., R.F.B., F.P., D.S.B. developed the project. S.G., R.F.B., F.P., D.S.B. wrote the paper.
Conflict of interest
None declared.
References
- Abdelnour F, Voss HU, Raj A. Network diffusion accurately models the relationship between structural and functional brain connectivity networks. Neuroimage. 2014;90:335–347. doi: 10.1016/j.neuroimage.2013.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adachi Y, Osada T, Sporns O, Watanabe T, Matsui T, Miyamoto K, Miyashita Y. Functional connectivity between anatomically unconnected areas is shaped by collective network-level effects in the macaque cortex. Cerebral cortex. 2011 doi: 10.1093/cercor/bhr234. [DOI] [PubMed]
- Alavash M, Hilgetag CC, Thiel CM, Gießing C. Persistency and flexibility of complex brain networks underlie dual-task interference. Hum Brain Mapp. 2015;36:3542–3562. doi: 10.1002/hbm.22861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Brown JA, Deshpande V, Carlson JM, Grafton ST. Conserved and variable architecture of human white matter connectivity. Neuroimage. 2011a;54:1262–1279. doi: 10.1016/j.neuroimage.2010.09.006. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Greenfield DL, Meyer-Lindenberg A, Weinberger DR, Moore SW, Bullmore ET. Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput Biol. 2010;6:e1000748. doi: 10.1371/journal.pcbi.1000748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Wymbs NF, Porter MA, Mucha PJ, Carlson JM, Grafton ST. Dynamic reconfiguration of human brain networks during learning. Proc Natl Acad Sci USA. 2011b;108:7641–7646. doi: 10.1073/pnas.1018985108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Wymbs NF, Rombach MP, Porter MA, Mucha PJ, Grafton ST. Task-based core-periphery organization of human brain dynamics. PLoS Comput Biol. 2013;9:e1003171. doi: 10.1371/journal.pcbi.1003171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Yang M, Wymbs NF, Grafton ST. Learning-induced autonomy of sensorimotor systems. Nat Neurosci. 2015;18:744–751. doi: 10.1038/nn.3993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betzel RF, Gu S, Medaglia JD, Pasqualetti F, Bassett DS. Optimally controlling the human connectome: the role of network topology. 2016 doi: 10.1038/srep30770. arXiv:1603.05261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boltyanskii VG, Gamkrelidze RV, Pontryagin LS. The Theory of Optimal Processes. I. The Maximum Principle. Technical Report DTIC Document 1960 [Google Scholar]
- Braun U, Muldoon SF, Bassett DS. eLS. John Wiley & Sons; Chichester: 2015. On Human Brain Networks in Health and Disease. [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Bzdok D, Langner R, Schilbach L, Jakobs O, Roski C, Caspers S, Laird AR, Fox PT, Zilles K, Eickhoff SB. Characterization of the temporo-parietal junction by combining data-driven parcellation, complementary connectivity analyses, and functional decoding. Neuroimage. 2013;81:381–392. doi: 10.1016/j.neuroimage.2013.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cammoun L, Gigandet X, Meskaldji D, Thiran JP, Sporns O, Do KQ, Maeder P, Meuli R, Hagmann P. Mapping the human connectome at multiple scales with diffusion spectrum MRI. J Neurosci Methods. 2012;203:386–397. doi: 10.1016/j.jneumeth.2011.09.031. [DOI] [PubMed] [Google Scholar]
- Carter AR, Patel KR, Astafiev SV, Snyder AZ, Rengachary J, Strube MJ, Pope A, Shimony JS, Lang CE, Shulman GL, Corbetta M. Upstream dysfunction of somatomotor functional connectivity after corticospinal damage in stroke. Neurorehabil Neural Repair. 2012;26:7–19. doi: 10.1177/1545968311411054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ching S, Brown EN, Kramer MA. Distributed control in a mean-field cortical network model: implications for seizure suppression. Phys Rev E Stat Nonlinear Soft Matter Phys. 2012;86:021920. doi: 10.1103/PhysRevE.86.021920. [DOI] [PubMed] [Google Scholar]
- Cieslak M, Grafton S. Local termination pattern analysis: a tool for comparing white matter morphology. Brain Imaging Behav. 2014;8:292–299. doi: 10.1007/s11682-013-9254-z. [DOI] [PubMed] [Google Scholar]
- Cima RF, Andersson G, Schmidt CJ, Henry JA. Cognitive-behavioral treatments for tinnitus: a review of the literature. J Am Acad Audiol. 2014;25:29–61. doi: 10.3766/jaaa.25.1.4. [DOI] [PubMed] [Google Scholar]
- Cocchi L, Zalesky A, Fornito A, Mattingley JB. Dynamic cooperation and competition between brain systems during cognitive control. Trends Cogn Sci. 2013;17:493–501. doi: 10.1016/j.tics.2013.08.006. [DOI] [PubMed] [Google Scholar]
- Collin G, van den Heuvel MP. The ontogeny of the human connectome: development and dynamic changes of brain connectivity across the life span. Neuroscientist. 2013;19:616–628. doi: 10.1177/1073858413503712. [DOI] [PubMed] [Google Scholar]
- Collin G, de Nijs J, Hulshoff Pol HE, Cahn W, van den Heuvel MP. Connectome organization is related to longitudinal changes in general functioning, symptoms and IQ in chronic schizophrenia. Schizophr Res. 2016;173:166–173. doi: 10.1016/j.schres.2015.03.012. [DOI] [PubMed] [Google Scholar]
- Cools R, D’Esposito M. Inverted-U-shaped dopamine actions on human working memory and cognitive control. Biol Psychiatry. 2011;69:e113–e125. doi: 10.1016/j.biopsych.2011.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M, Shulman GL. Control of goal-directed and stimulus-driven attention in the brain. Nat Rev Neurosci. 2002;3:201–215. doi: 10.1038/nrn755. [DOI] [PubMed] [Google Scholar]
- Crofts JJ, Higham DJ. A weighted communicability measure applied to complex brain networks. J R Soc Interface. 2009 doi: 10.1098/rsif.2008.0484. [DOI] [PMC free article] [PubMed]
- Daducci A, Gerhard S, Griffa A, Lemkaddem A, Cammoun L, Gigandet X, Meuli R, Hagmann P, Thiran JP. The connectome mapper: an open-source processing pipeline to map connectomes with MRI. PLoS One. 2012;7:e48121. doi: 10.1371/journal.pone.0048121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G, Jirsa VK, McIntosh AR. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat Rev Neurosci. 2011;12:43–56. doi: 10.1038/nrn2961. [DOI] [PubMed] [Google Scholar]
- Di Martino A, Fair DA, Kelly C, Satterthwaite TD, Castellanos FX, Thomason ME, Craddock RC, Luna B, Leventhal BL, Zuo XN, et al. Unraveling the miswired connectome: a developmental perspective. Neuron. 2014;83:1335–1353. doi: 10.1016/j.neuron.2014.08.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durstewitz D, Deco G. Computational significance of transient dynamics in cortical networks. Eur J Neurosci. 2008;27:217–227. doi: 10.1111/j.1460-9568.2007.05976.x. [DOI] [PubMed] [Google Scholar]
- Eisenreich B, Akaishi R, Hayden B. Control Without Controllers: Towards a Distributed Neuroscience of Executive Control. 2016 doi: 10.1162/jocn_a_01139. 〈 www.biorxiv.org/content/early/2016/09/26/077685〉. [DOI] [PMC free article] [PubMed]
- Fagerholm ED, Hellyer PJ, Scott G, Leech R, Sharp DJ. Disconnection of network hubs and cognitive impairment after traumatic brain injury. Brain. 2015;138:1696–1709. doi: 10.1093/brain/awv075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiete IR, Senn W, Wang CZ, Hahnloser RHR. Spike-time-dependent plasticity and heterosynaptic competition organize networks to produce long scale-free sequences of neural activity. Neuron. 2010;65:563–576. doi: 10.1016/j.neuron.2010.02.003. [DOI] [PubMed] [Google Scholar]
- Freeman WJ. Characterization of state transitions in spatially distributed, chaotic, nonlinear, dynamical systems in cerebral cortex. Integr Physiol Behav Sci. 1994;29:294–306. doi: 10.1007/BF02691333. [DOI] [PubMed] [Google Scholar]
- Galán RF. On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS One. 2008;3:e2148. doi: 10.1371/journal.pone.0002148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrett DD, Samanez-Larkin GR, MacDonald SW, Lindenberger U, McIntosh AR, Grady CL. Moment-to-moment brain signal variability: a next frontier in human brain mapping? Neurosci Biobehav Rev. 2013;37:610–624. doi: 10.1016/j.neubiorev.2013.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazzaniga MS, editor. The Cognitive Neurosciences. MIT Press; Cambridge, MA: 2013. [Google Scholar]
- Goñi J, van den Heuvel MP, Avena-Koenigsberger A, de Mendizabal NV, Betzel RF, Griffa A, Hagmann P, Corominas-Murtra B, Thiran JP, Sporns O. Resting-brain functional connectivity predicted by analytic measures of network communication. Proc Natl Acad Sci. 2014;111:833–838. doi: 10.1073/pnas.1315529111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu S, Cieslak M, Baird B, Muldoon SF, Grafton ST, Pasqualetti F, Bassett DS. The energy landscape of neurophysiological activity implicit in brain network structure, submitted for publication. 2016 doi: 10.1038/s41598-018-20123-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu S, Pasqualetti F, Cieslak M, Telesford QK, Alfred BY, Kahn AE, Medaglia JD, Vettel JM, Miller MB, Grafton ST, et al. Controllability of structural brain networks. Nat Commun. 2015;6 doi: 10.1038/ncomms9414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008;6:e159. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen EC, Battaglia D, Spiegler A, Deco G, Jirsa VK. Functional connectivity dynamics: modeling the switching behavior of the resting state. Neuroimage. 2015;105:525–535. doi: 10.1016/j.neuroimage.2014.11.001. [DOI] [PubMed] [Google Scholar]
- Hellyer PJ, Leech R, Ham TE, Bonnelle V, Sharp DJ. Individual prediction of white matter injury following traumatic brain injury. Ann Neurol. 2013;73:489–499. doi: 10.1002/ana.23824. [DOI] [PubMed] [Google Scholar]
- Hermundstad AM, Bassett DS, Brown KS, Aminoff EM, Clewett D, Freeman S, Frithsen A, Johnson A, Tipper CM, Miller MB, et al. Structural foundations of resting-state and task-based functional connectivity in the human brain. Proc Natl Acad Sci. 2013;110:6169–6174. doi: 10.1073/pnas.1219562110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermundstad AM, Brown KS, Bassett DS, Aminoff EM, Frithsen A, Johnson A, Tipper CM, Miller MB, Grafton ST, Carlson JM. Structurally-constrained relationships between cognitive states in the human brain. PLoS Comput Biol. 2014;10:e1003591. doi: 10.1371/journal.pcbi.1003591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermundstad AM, Brown KS, Bassett DS, Carlson JM. Learning, memory, and the role of neural network architecture. PLoS Comput Biol. 2011;7:e1002063. doi: 10.1371/journal.pcbi.1002063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey C, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci. 2009;106:2035–2040. doi: 10.1073/pnas.0811168106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Kötter R, Breakspear M, Sporns O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc Natl Acad Sci. 2007;104:10240–10245. doi: 10.1073/pnas.0701519104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Behrens TE. The topographic connectome. Curr Opin Neurobiol. 2013;23:207–215. doi: 10.1016/j.conb.2012.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson VE, Stewart W, Smith DH. Axonal pathology in traumatic brain injury. Exp Neurol. 2013;246:35–43. doi: 10.1016/j.expneurol.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston JM, Vaishnavi SN, Smyth MD, Zhang D, He BJ, Zempel JM, Shimony JS, Snyder AZ, Raichle ME. Loss of resting interhemispheric functional connectivity after complete section of the corpus callosum. J Neurosci. 2008;28:6453–6458. doi: 10.1523/JNEUROSCI.0573-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalpinski RJ, Williamson ML, Elliott TR, Berry JW, Underhill AT, Fine PR. Modeling the prospective relationships of impairment, injury severity, and participation to quality of life following traumatic brain injury. Biomed Res Int. 2013;2013:102570. doi: 10.1155/2013/102570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandel ER, Schwartz JH, Jessell TM, et al. Principles of Neural Science. Vol. 4. McGraw-Hill; New York: 2000. [Google Scholar]
- Khambhati A, Davis K, Lucas T, Litt B, Bassett DS. Virtual cortical resection reveals push–pull network control preceding seizure evolution, submitted for publication. 2016 doi: 10.1016/j.neuron.2016.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinnunen KM, Greenwood R, Powell JH, Leech R, Hawkins PC, Bonnelle V, Patel MC, Counsell SJ, Sharp DJ. White matter damage and cognitive impairment after traumatic brain injury. Brain. 2011;134:449–463. doi: 10.1093/brain/awq347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klimm F, Bassett DS, Carlson JM, Mucha PJ. Resolving structural variability in network models and the brain. PLOS Comput Biol. 2014;10:e1003491. doi: 10.1371/journal.pcbi.1003491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laughlin SB. Efficiency and complexity in neural coding. Novartis Found Symp. 2001;239:177–187. doi: 10.1002/0470846674.ch14. [DOI] [PubMed] [Google Scholar]
- Laughlin SB, de Ruyter van Steveninck RR, Anderson JC. The metabolic cost of neural information. Nat Neurosci. 1998;1:36–41. doi: 10.1038/236. [DOI] [PubMed] [Google Scholar]
- Lee S, Ueno M, Yamashita T. Axonal remodeling for motor recovery after traumatic brain injury requires downregulation of gamma-aminobutyric acid signaling. Cell Death Dis. 2011;2:e133. doi: 10.1038/cddis.2011.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lett TA, Voineskos AN, Kennedy JL, Levine B, Daskalakis ZJ. Treating working memory deficits in schizophrenia: a review of the neurobiology. Biol Psychiatry. 2014;75:361–370. doi: 10.1016/j.biopsych.2013.07.026. [DOI] [PubMed] [Google Scholar]
- Levy N, Horn D, Meilijson I, Ruppin E. Distributed synchrony in a cell assembly of spiking neurons. Neural Netw. 2001;14:815–824. doi: 10.1016/s0893-6080(01)00044-2. [DOI] [PubMed] [Google Scholar]
- Liu YY, Slotine JJ, Barabási AL. Controllability of complex networks. Nature. 2011;473:167–173. doi: 10.1038/nature10011. [DOI] [PubMed] [Google Scholar]
- Luenberger D. Introduction to Dynamic Systems: Theory, Models, and Applications 1979 [Google Scholar]
- Medaglia JD, Lynall ME, Bassett DS. Cognitive network neuroscience. J Cogn Neurosci. 2015;27:1471–1491. doi: 10.1162/jocn_a_00810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier D, Achard S, Morcom A, Bullmore E. Age-related changes in modular organization of human brain functional networks. Neuroimage. 2009;44:715–723. doi: 10.1016/j.neuroimage.2008.09.062. [DOI] [PubMed] [Google Scholar]
- Mišić B, Betzel RF, Nematzadeh A, Goñi J, Griffa A, Hagmann P, Flammini A, Ahn YY, Sporns O. Cooperative and competitive spreading dynamics on the human connectome. Neuron. 2015;86:1518–1529. doi: 10.1016/j.neuron.2015.05.035. [DOI] [PubMed] [Google Scholar]
- Muldoon SF, Bridgeford EW, Bassett DS. Small-world propensity and weighted brain networks. Sci Rep. 2016a;6 doi: 10.1038/srep22057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muldoon SF, Pasqualetti F, Gu S, Cieslak M, Grafton ST, Vettel JM, Bassett DS. Stimulation-based control of dynamic brain networks. 2016b doi: 10.1371/journal.pcbi.1005076. arXiv:1601.00987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller FJ, Schuppert A. Few inputs can reprogram biological networks. Nature. 2011;478:E4. doi: 10.1038/nature10543. [DOI] [PubMed] [Google Scholar]
- Nenadovic V, Hutchison JS, Dominguez LG, Otsubo H, Gray MP, Sharma R, Belkas J, Perez Velazquez JL. Fluctuations in cortical synchronization in pediatric traumatic brain injury. J Neurotrauma. 2008;25:615–627. doi: 10.1089/neu.2007.0474. [DOI] [PubMed] [Google Scholar]
- Niven JE, Laughlin SB. Energy limitation as a selective pressure on the evolution of sensory systems. J Exp Biol. 2008;211:1792–1804. doi: 10.1242/jeb.017574. [DOI] [PubMed] [Google Scholar]
- Nudo RJ. Mechanisms for recovery of motor function following cortical damage. Curr Opin Neurobiol. 2006;16:638–644. doi: 10.1016/j.conb.2006.10.004. [DOI] [PubMed] [Google Scholar]
- O’Reilly JX, Croxson PL, Jbabdi S, Sallet J, Noonan MP, Mars RB, Browning PG, Wilson CR, Mitchell AS, Miller KL, et al. Causal effect of disconnection lesions on interhemispheric functional connectivity in rhesus monkeys. Proc Natl Acad Sci. 2013;110:13982–13987. doi: 10.1073/pnas.1305062110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasqualetti F, Zampieri S, Bullo F. Controllability metrics, limitations and algorithms for complex networks. IEEE Trans Control Netw Syst. 2014;1:40–52. [Google Scholar]
- Pestilli F, Yeatman JD, Rokem A, Kay KN, Wandell BA. Evaluation and statistical inference for human connectomes. Nat Methods. 2014;11:1058–1063. doi: 10.1038/nmeth.3098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posner MI, Petersen SE. The Attention System of the Human Brain. Technical Report DTIC Document 1989 [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE. Functional network organization of the human brain. Neuron. 2011;72:665–678. doi: 10.1016/j.neuron.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radhu N, Daskalakis ZJ, Guglietti CL, Farzan F, Barr MS, Arpin-Cribbie CA, Fitzgerald PB, Ritvo P. Cognitive behavioral therapy-related increases in cortical inhibition in problematic perfectionists. Brain Stimul. 2012;5:44–54. doi: 10.1016/j.brs.2011.01.006. [DOI] [PubMed] [Google Scholar]
- Raichle ME. The brain’s default mode network. Annu Rev Neurosci. 2015;38:433–447. doi: 10.1146/annurev-neuro-071013-014030. [DOI] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME, Snyder AZ. A default mode of brain function: a brief history of an evolving idea. Neuroimage. 2007;37:1083–1090. doi: 10.1016/j.neuroimage.2007.02.041. [DOI] [PubMed] [Google Scholar]
- Raja Beharelle A, Kovacevic N, McIntosh AR, Levine B. Brain signal variability relates to stability of behavior after recovery from diffuse brain injury. Neuroimage. 2012;60:1528–1537. doi: 10.1016/j.neuroimage.2012.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajan K, Harvey CD, Tank DW. Recurrent network models of sequence generation and memory. Neuron. 2016;90:128–142. doi: 10.1016/j.neuron.2016.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reveley C, Seth AK, Pierpaoli C, Silva AC, Yu D, Saunders RC, Leopold DA, Frank QY. Superficial white matter fiber systems impede detection of long-range cortical connections in diffusion MR tractography. Proc Natl Acad Sci. 2015;112:E2820–E2828. doi: 10.1073/pnas.1418198112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rusconi E, Pinel P, Eger E, LeBihan D, Thirion B, Dehaene S, Kleinschmidt A. A disconnection account of Gerstmann syndrome: functional neuroanatomy evidence. Ann Neurol. 2009;66:654–662. doi: 10.1002/ana.21776. [DOI] [PubMed] [Google Scholar]
- Rushworth MF, Behrens TE, Johansen-Berg H. Connection patterns distinguish 3 regions of human parietal cortex. Cereb Cortex. 2006;16:1418–1430. doi: 10.1093/cercor/bhj079. [DOI] [PubMed] [Google Scholar]
- Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philos Trans R Soc Lond B Biol Sci. 2005;360:937–946. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp DJ, Scott G, Leech R. Network dysfunction after traumatic brain injury. Nat Rev Neurol. 2014;10:156–166. doi: 10.1038/nrneurol.2014.15. [DOI] [PubMed] [Google Scholar]
- Shenoy KV, Kaufman MT, Sahani M, Churchland MM. A dynamical systems view of motor preparation: implications for neural prosthetic system design. Prog Brain Res. 2011;192:33–58. doi: 10.1016/B978-0-444-53355-5.00003-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidaros A, Engberg AW, Sidaros K, Liptrot MG, Herning M, Petersen P, Paulson OB, Jernigan TL, Rostrup E. Diffusion tensor imaging during recovery from severe traumatic brain injury and relation to clinical outcome: a longitudinal study. 2008 doi: 10.1093/brain/awm294. [DOI] [PubMed] [Google Scholar]
- Sizemore A, Giusti C, Bassett D. Classification of weighted networks through mesoscale homological features. 2015 arXiv:1512.06457. [Google Scholar]
- Sommer IE, Slotema CW, Daskalakis ZJ, Derks EM, Blom JD, van der Gaag M. The treatment of hallucinations in schizophrenia spectrum disorders. Schizophr Bull. 2012;38:704–714. doi: 10.1093/schbul/sbs034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan D, Levitin DJ, Menon V. A critical role for the right fronto-insular cortex in switching between central-executive and default-mode networks. Proc Natl Acad Sci USA. 2008;105:12569–125674. doi: 10.1073/pnas.0800005105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ. Modern network science of neurological disorders. Nat Rev Neurosci. 2014;15:683–695. doi: 10.1038/nrn3801. [DOI] [PubMed] [Google Scholar]
- Stephan KE, Friston KJ, Frith CD. Dysconnection in schizophrenia: from abnormal synaptic plasticity to failures of self-monitoring. Schizophr Bull. 2009;35:509–527. doi: 10.1093/schbul/sbn176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szameitat AJ, Schubert T, Müller HJ. How to test for dual-task-specific effects in brain imaging studies—an evaluation of potential analysis methods. Neuroimage. 2011;54:1765–1773. doi: 10.1016/j.neuroimage.2010.07.069. [DOI] [PubMed] [Google Scholar]
- Thomas C, Frank QY, Irfanoglu MO, Modi P, Saleem KS, Leopold DA, Pierpaoli C. Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proc Natl Acad Sci. 2014;111:16574–16579. doi: 10.1073/pnas.1405672111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tortella G, Selingardi PM, Moreno ML, Veronezi BP, Brunoni AR. Does non-invasive brain stimulation improve cognition in major depressive disorder? A systematic review CNS Neurol Disord Drug Targets. 2014;13:1759–1769. doi: 10.2174/1871527313666141130224431. [DOI] [PubMed] [Google Scholar]
- Weiss SA, Bassett DS, Rubinstein D, Holroyd T, Apud J, Dickinson D, Coppola R. Functional brain network characterization and adaptivity during task practice in healthy volunteers and people with schizophrenia. Front Hum Neurosci. 2011;5:81. doi: 10.3389/fnhum.2011.00081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan G, Ren J, Lai YC, Lai CH, Li B. Controlling complex networks: how much energy is needed? Phys Rev Lett. 2012;108:218703. doi: 10.1103/PhysRevLett.108.218703. [DOI] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zollei L, Polimeni JR, Fischl B, Liu H, Buckner RL. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


