Stochastic amplification and signaling in enzymatic futile cycles through noise-induced bistability with oscillations

Abstract

Stochastic effects in biomolecular systems have now been recognized as a major physiologically and evolutionarily important factor in the development and function of many living organisms. Nevertheless, they are often thought of as providing only moderate refinements to the behaviors otherwise predicted by the classical deterministic system description. In this work we show by using both analytical and numerical investigation that at least in one ubiquitous class of (bio)chemical-reaction mechanisms, enzymatic futile cycles, the external noise may induce a bistable oscillatory (dynamic switching) behavior that is both quantitatively and qualitatively different from what is predicted or possible deterministically. We further demonstrate that the noise required to produce these distinct properties can itself be caused by a set of auxiliary chemical reactions, making it feasible for biological systems of sufficient complexity to generate such behavior internally. This new stochastic dynamics then serves to confer additional functional modalities on the enzymatic futile cycle mechanism that include stochastic amplification and signaling, the characteristics of which could be controlled by both the type and parameters of the driving noise. Hence, such noise-induced phenomena may, among other roles, potentially offer a novel type of control mechanism in pathways that contain these cycles and the like units. In particular, observations of endogenous or externally driven noise-induced dynamics in regulatory networks may thus provide additional insight into their topology, structure, and kinetics.

Enzymatic futile cycles and cycle cascades†† represent a recurring control motif in biological molecular networks, appearing in a wide variety of processes from energy metabolism to signal transduction (1). In particular, it has been experimentally observed that bimodalities in chemical activity that naturally occur in a number of biochemical systems often include those containing various types of enzymatic cycles (refs. 2–4; see Supporting Text, which is published as supporting information on the PNAS web site). However, because classical Michaelis–Menten (MM)-type kinetics that are often used to model these systems typically do not directly result in bifurcations, oscillations, and other complex behavioral patterns, authors with few exceptions have tended, often with experimental support, to introduce additional mechanisms such as positive/negative feedback among the species to explain their onset whether in deterministic or nondeterministic systems (refs. 5–7, 31 and Supporting Text). These added structures are indeed necessary in the deterministic case (8, 9, 32) to describe such complex network dynamics. In this work, however, we demonstrate that, at least in systems containing enzymatic futile cycles, an alternative explanation is possible, whereby the observed bifurcation and the induced bistability are caused solely by the influence of the external unimodal noise on the underlying reaction system rather than any explicit feedback or such other additional mechanism in the system.

As has been demonstrated earlier (both numerically and experimentally), stochastic noise plays an important role in determining the characteristic behavior of biological processes (10), including metabolism, signal transduction, and gene expression (11, 33). Here we examine the effect of noise on the behavior of a simple enzymatic futile cycle (Fig. 1). This mechanism is indeed ubiquitous throughout biological systems and is encountered as a recurrent control motif in such diverse regulatory processes as metabolism, GTPase cycles, mitogen-activated protein kinase (MAPK) cascades, glucose mobilization, cell division/apoptosis, checkpoint control, actin treadmilling, and membrane transport as well as two-component systems and phosphorelays in microbial stress-response signaling pathways (12) (to name a few; see Supporting Text) and recognized for its ability to display a (possibly) sharp sigmoidal change in substrate/product concentration in response to variation in enzyme activity (13).

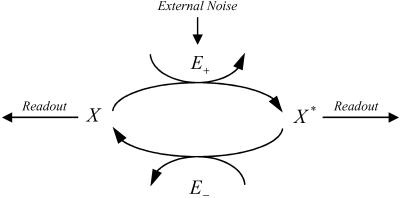
Fig. 1.

The enzymatic futile cycle reaction mechanism.

The main evolutionary design objectives thought to select for these cycles and cycle cascades are considered to be the need for switch-like elements that convert graded increases in an input to a more binary output and the demand for signal amplification, which may be necessary because the primary messengers are often present in extremely low concentrations (12). However, these objectives lead to an important dichotomy intrinsic to the problem: as the signal gets substantially amplified by one or more of these nonlinear mechanisms, so do the small external noise-driven fluctuations in its level. As will be shown below, such noise in primary messenger concentrations can qualitatively change the dynamics of even the simple futile cycle motifs, thus profoundly influencing how these objectives are met by the biological systems at large.

In this article we demonstrate that signals of sufficient complexity, the ones that can be modeled as input of noise into the enzymatic futile cycle, can have significant impact on the types of signal processing and response that networks containing these cycle mechanisms can perform. Specifically, such noise input can result in qualitatively novel behavior modalities within the system as compared to strictly deterministic analysis predictions (under any set of parameters), including a bifurcation and the appearance of a bistability that exhibits dynamic switching between low- and high-activity states. These features, among other things, act to substantially enhance the amplification properties of the cycle mechanism and potentially allow it to function as a more versatile signal transducer, including being able to filter and checkpoint noisy or transient upstream signals better than could be done by the corresponding deterministic system or other such mechanisms previously considered and offer new modalities for transmitting the onset and turn-off of these signals to the downstream targets (14).

We further find that the behavior of the stochastically driven enzymatic cycle can be very sensitive not only to the strength of the external driving noise but also to its exact distribution. This powerful control mechanism may account for a potential plethora of response profiles, because “noise” origins in biological systems could themselves be very diverse. For instance, they may include some fundamentally stochastic mechanisms such as thermal fluctuations in chemical reaction rates and their subsequent effects propagated through the downstream pathways or result from other intrinsically random processes such as the opening/closing of membrane channels and radiation-induced DNA damage. Alternatively, the apparent noise could be a temporally complex upstream signal such as the quasirandom chaotic processes reported in cardiac or neural tissue (15) or the multifarious variability in calcium spiking dynamics in response to the multiplexing of one or more external agonist signals together such as that observed in immune cells (16, 34). Finally, they could simply be the result of signals traversing long pathways and accumulating static or temporal heterogeneities en route (such as those an endocrine messenger might encounter because of perturbations in blood or lymphatic flows, temperature and pH gradients, and other variations in the local environmental conditions on the way from a gland to its final target; see Supporting Text). As shown here, driven mechanisms can then filter and shape these noise inputs in a variety of unconventional ways, which opens up the possibility that such “filtering” regulation might be exploited for control in and of assorted biological systems (14, 24, 35). Furthermore, because the external driving noise is itself the output of yet another stochastic chemical or physical process, the form of its distribution is then determined by the exact identity of that mechanism. Thus, given that each specific external perturbation type can be generated only by a certain range of processes, it may prove possible to use this noise-filtering information to deduce the structure and study the function of the larger reaction networks in which such systems are embedded (17, 36, 37).

To study the enzymatic futile cycle mechanism subject to noise we apply a two-pronged approach. On one hand, the stochastic dynamics of (bio)chemical-reaction networks is accurately described by the chemical master equation formalism (18, 19); however, this technique is, in general, not tractable analytically. On the other hand, it is possible to solve a Langevin (20, 21) stochastic differential equation model of the system governed by MM kinetics and driven by the noise on the enzyme concentration in the stationary limit, which we do first. Using this approach we show that introduction of external noise into such mechanisms' description may lead to quantifiable qualitative changes in their characteristic behaviors as well as identify the key parameters and relationships that control these effects. We then test and confirm the validity of our results from this (approximate) stochastic differential equation model by demonstrating the predicted effects in the direct simulations of the system's master equation representation at the elementary reaction level by means of the Gillespie algorithm (22) and showing that the relevant noise profile could be generated in a biochemically meaningful way by a simple set of auxiliary reactions using parameters inferred with the help of our analytical model.

Enzymatic Futile Cycle

For the purposes of our analysis we consider a model of the enzymatic futile cycle, diagrammed in Fig. 1, subject to external noise in the forward enzyme concentration. Here {E₊, E_-} denote the forward and reverse (e.g., activating and deactivating) enzymes, and {X, X^*} stand for the concentrations of the forward substrate and product, respectively. Our goal is to determine the stationary response curve (nullcline) relationship, 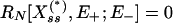, between the strength of the input (control) signal (in this case, E₊) and the response (signal) produced by the system (X or X^*) with (stochastic) and without (deterministic) external noise, N_t, on the input concentration at the stationary steady state while the total amount of E_- is held constant. The classical deterministic model of this system predicts a (possibly strong) sigmoidal behavior for the stationary response curve (Fig. 6, which is published as supporting information on the PNAS web site), 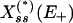, which is the reason it is often referred to as a “switch”: in a certain parameter range the steady state of the system flips from the “high X_ss, low 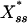” state to its opposite in an almost binary way as E₊ is increased. In its extreme, this effect is commonly known as zero-order ultrasensitivity, whereby small percentage changes in the concentration of the enzyme can give much larger percentage changes in the amount of modified protein (13). When, however, there is noise on E₊, we show that this sigmoidal stationary response curve can evolve further to become multivalued in 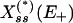, which indicates the emergence of an underlying bistability in the system that is not accounted for by the deterministic treatment (including zero-order ultrasensitivity).

Analytical Approach

The classical description of the system in Fig. 1 has zero noise input and is typically analyzed in the MM limit (13), E_+/- << X₀ + K_+/- (where X₀ is the total amount of X and X^*), from which the steady-state response equation may be derived:

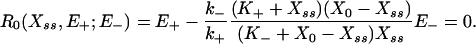[1]

This equation has a unique positive root, X_ss(E₊), satisfying X_ss ≤ X₀. Thus, deterministically, given a set of initial conditions, the system approaches a unique predetermined stable steady state, which lies on the response curve at E₊ and, having reached it, stays there “indefinitely.” (Notice that this expression is of the second order in X_ss, i.e., the deterministic description of this system is intrinsically monostable and incapable of supporting bistable solutions for any set of parameters.)

We now consider what happens if the system is subjected to external noise on E₊, looking to determine the new stationary response curve and study its properties. For a broad range of noise sources (such as those driven by the basic protein synthesis and degradation mechanisms) the stochastic version of cycle dynamics yields a compact Langevin equation for the level of the signal molecule X^*,

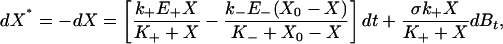[2]

(that could be similarly extended to include the potential contribution of internal noise as well as noise in E_- and/or other system parameters; see Supporting Text). Here 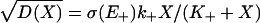is the external driver-induced noise intensity that depends on the substrate concentration, σ is the forward enzyme noise strength (which may depend on E₊), E₊ is its “basal” level, and B_t is the standard Brownian process. In our model this expression can be considered a stochastic analogue to the deterministic MM chemical kinetic ordinary differential equation.

From Eq. 2 one can immediately obtain a Fokker–Planck equation for the probability density of X_t, which in turn yields the stationary-state response curve:

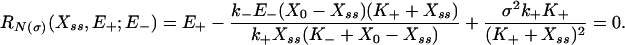[3]

[The Fokker–Planck equation can be further solved for the explicit form of the stationary distribution useful for some applications (see Supporting Text).] Comparing the stochastic Eq. 3 and deterministic Eq. 1, we immediately see that the effect of noise is compactly summarized by the addition of a correction (diffusion) term to the classical result. Note that the effect of the additional term is, among other things, to raise this expression to fourth order in X_ss, thus allowing for the appearance of a bistable solution (which is oscillatory; see Figs. 2 and 3). Eqs. 2 and 3 [which incorporate the effects of the multiplicative noise on the position and number of the stationary states of the system and are different from, but in the zero noise case reduce to the classical deterministic limits (e.g., Eq. 1)] also form the basis for our subsequent analysis of stochastic cycle function.

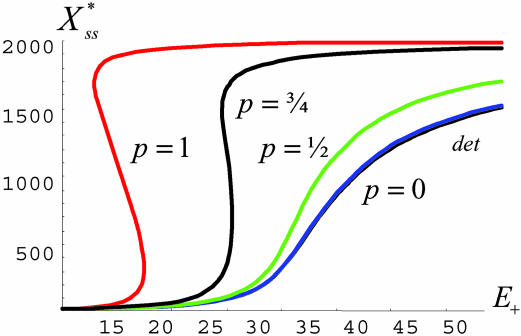
Fig. 2.

The analytical stationary-state response curves, R_N(p), for the enzymatic futile cycle (Fig. 1 with parameters of Fig. 3), obtained by using Eqs. 1, 3, and 6 with σ₊ = 0.2 and various values of p (includes the deterministic curve, which largely overlaps).

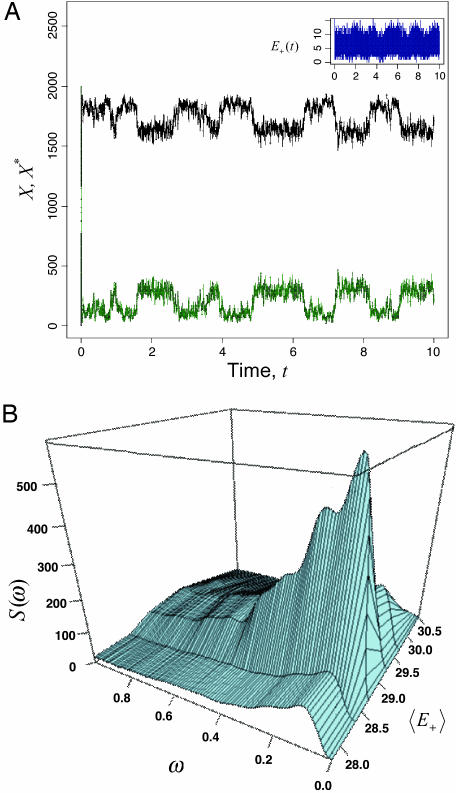
Fig. 3.

Temporal and frequency characteristics of the cycle dynamics. (A) Sample time-evolution courses for the enzymatic cycle signal and response molecular counts, X_t and 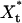, obtained by using exact numerical simulation of the reaction mechanism given in Expressions 7 and 8. (Inset) Forward enzyme, E₊(t). (B) Spectral density, S(ω), of the process 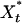vs. frequency ω and 〈E₊〉 (arbitrary scale). Cycle reaction parameters (Expression 7) are: E₊(t = 0) = 20; X(t = 0) = 0; X^* (t = 0) = 2,000; C₊(t = 0) = 0; C_-(t = 0) = 0; E_-(t = 0) = 50; k₊₁ = 40; k₊₂ = 10⁴; k₊₃ = 10⁴; k_-1 = 200; k_-2 = 100; and k_-3 = 5·10³ given in terms of the number of molecules. Driver reaction (Expression 8) parameters: N(t = 0) = 10 with k₂₁ = 10, k_-21 = 5, k₂₂ = 10, and k_-22 = 0.2.

Signal Amplification. It was noted earlier that because the noise term is explicitly present in the stationary-state condition, Eq. 3, we should expect it to not only affect the dynamic behavior of the system but to also alter its concentration levels relative to the deterministic case. In fact, it turns out that in our treatment the stochastic stationary-state levels, 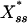, are always greater than the corresponding deterministic one, thus resulting in signal amplification. From the signal-transduction point of view, this property of the mechanism is typically quantified as signal gain (23), which in our case may be written as

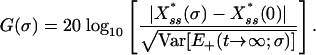[4]

The ratio in Eq. 4 represents the strength of the output signal over the input, which in our case corresponds to the driving noise level itself.

Note that for sufficiently strong noise G(σ) becomes a decreasing function regardless of the explicit form of Eq. 4. (As noise intensity increases, signal amplification stays upper-bounded by the limit on the number of substrate/product molecules: 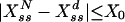.) Then if G(σ) is anywhere increasing (as is the case here for small noise intensities), it will have at least one maxima and, as such, a nonzero resonant noise intensity level. That is, an enzymatic futile cycle can act not only as a signal transducer but also as a stochastic amplifier, quite apart from its otherwise deterministic amplification properties. In fact, as will be seen shortly, there are circumstances in which the system is not expected to have any significant amplification deterministically (an enzyme level below the sigmoidal threshold) but nevertheless shows substantial signal gain stochastically.

Stochastic Signaling. In this system, the presence of noise not only can introduce multistability (as described above) but also noise-driven dynamic switching between the stationary states. However, although amplitude modulation could be handled relatively easily within the framework of the previous sections, analytically quantifying the frequency response profile of such processes is substantially more difficult. Whereas oscillation amplitude basically depends on the relative position of the stable states, its frequency is generally dictated by the overall shape of the probability distribution of the process, which significantly complicates the analysis. For example, a general expression for the mean oscillation period of a dynamically bistable process can be extracted from the formula for mean transition time (22) and made more explicit through asymptotic expansion,

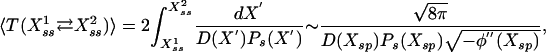[5]

where X_sp is the saddle point, ϕ(X) is the potential, D(X) is the diffusion function, and P_s(X) is the stationary probability distribution of the process as discussed and more explicitly given in the Supporting Text.

Signal Processing. Eq. 5 shows that the transition rate between the two stable states is a (complex) function of other system parameters. This fact, combined with our earlier results regarding the stable state location and oscillation amplitude control, evinces how modulation of these properties can allow enzymatic futile cycles to serve as flexible stochastic signaling mechanisms within larger biomolecular networks. That is, this motif can transform the signal from an enzymatic input (for example, a kinase) by amplification, bistable switching, and induction or changing frequencies of oscillations. The resultant dynamic variation in substrate/product concentration serves as a rich signal carrier among the various biochemical modules that can filter and be differentially responsive to such modes of transmission (14, 24).

Noise Regulation and Inference. In our Langevin model, the dependence of stochastic properties of the driving process on system parameters is determined by means of σ(·). This relationship is essentially defined by the nature of the external noise sources and offers a mode of control over the behavior of the system as discussed earlier. A general power-law model (Fig. 2),

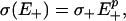[6]

provides sufficient basis for our subsequent analysis.

Summary of Analysis. We can now make more concrete the notions of noise-based system regulation and structure inference. On the one hand, the ability to control the external stochastic driver and vary some of its parameters, e.g., σ₊, allows one to practically regulate such noise-induced properties of the mechanism as onset or demise of the bistability by using Eq. 3, the degree of signal amplification following Eq. 4, and the characteristic signal oscillation frequency as evinced through Eq. 5. Alternatively, if the source of external perturbations is not well understood but we can observe, vary, and measure the underlying parameters of the cycle mechanism, then the above formulas allow one to deduce the intensity profile of the stochastic driver such as that given in Eq. 6 by, for example, measuring the response curve R_N and fitting it to Eq. 3. Because different external mechanisms generate distinctive noise distributions, this information might allow us to infer much about the structure of the larger external system in which this mechanism is included.

Numerical Analysis

The above analytical model of the noise-driven enzymatic futile cycle mechanism is based on a set of simplifying assumptions (MM dynamics, the form of external driver, lack of internal noise, etc.), which has allowed us to make several interesting predictions about the underlying system behavior that arises only in the stochastic case. However, in natural biomolecular systems, the situation is substantially more complicated. For instance, the specific type of external noise is dictated, in general, by the characteristics of the larger biomolecular network in which the system is embedded, resulting in potentially far more complex noise patterns than considered above. The mechanism is further subject to other effects, which include discrete molecular dynamics, internal noise generated within the mechanism itself, etc. These factors impose very strong constraints on the types of stochastic drivers one may consider “biochemically meaningful.” They cannot be arbitrary but have to belong to a class of processes that do not violate the in situ (bio)molecular system properties such as being comprised of proper (bio)chemical reactions, not sampling the negative state space, etc. As noted, these conditions greatly complicate the task of meaningfully specifying a particular biomolecular stochastic driver by (among other things) requiring that a proper “external” set of reactions with the desired noise profile characteristics be identified, which is made particularly challenging by the difficulties in a priori predicting the exact type of distribution that these reactions would impart on the target system.

In this section we numerically validate the general conclusions of the analytical results discussed above by using a direct chemical master equation approach in which both the external and internal noise are explicitly generated by proper (bio)chemical processes and exactly simulated by using the Gillespie algorithm.

Cycle Mechanism. We look at a model of the futile cycle that uses only elementary chemical reactions as appropriate for direct master equation molecular dynamics simulations that do not rely on MM approximations. Specifically, we consider a detailed version of the enzymatic futile cycle mechanism (Fig. 1) at the individual reactions level given by

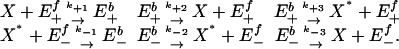[7]

External Noise. As noted before, to introduce a particular type of external noise into the system in a manner consistent with the master equation and Gillespie-algorithm formulation, we cannot simply add an arbitrary stochastic process of choice to the quantity of interest but instead are restricted to augmenting the set of reactions shown in Expression 7 with an external driver of E₊ that itself must consist of proper chemical reactions. An external reaction set closely satisfying the constraints of the analytical model could be specified by using a relatively simple form,

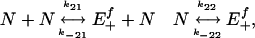[8]

which is an example of auto(de)activating enzyme dynamics. Here, species N provides an example of external interactions that add noise to [E₊] in a chemically permissible manner consistent with Fig. 1. Although the reactions' properties do not exactly match those of the driving processes considered in the analytical model above, the correspondence is strong enough to allow for a broadly accurate description of the induced behavior.

A specific instantiation of the systems in Expressions 7 and 8 is given in Fig. 3. This simple system deterministically behaves as a stable node (see Supporting Text), although stochastically it is overtly bistable. The substrates are not at low concentrations, yet stochastic effects on their dynamics are quite evident and driven with something close to p = 1 noise (Eq. 6) on the concentration of E₊(t) (see below).

Analytical Predictions. Based on Eqs. 3 and 6, we expect the given Expressions 7 and 8 to exhibit the onset of bistability [the point at which 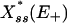becomes multivalued] at 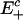between 20 and 30 for an external noise driver of power p > 0.75 and intensity parameter σ₊ ≈ 20%. [Drivers of lower powers were not expected to be in the bistable range for these conditions (see Fig. 2).]

Numerical Simulation. The results of the numerical simulations shown in Fig. 3A confirm that the concentrations of X and X^* are transiting between two states. This dynamical bistable behavior and stochastic oscillatory response are not possible based on a classical deterministic description or without the prescribed external noise added to the forward enzyme, as was discussed earlier (Fig. 2). The effect disappears with the removal of the external driver (Expression 8), thus confirming that it is indeed external noise-induced (Fig. 7, which is published as supporting information on the PNAS web site). The switching effect also disappears if a weaker p is used (data not shown). The oscillations seen in Fig. 3A have a well defined characteristic switching frequency distribution in the bistable regime, as is evidenced by the spectral density plot (Fig. 3B) and product histogram (Fig. 4A), and exhibit the expected signal amplification (Fig. 8, which is published as supporting information on the PNAS web site).

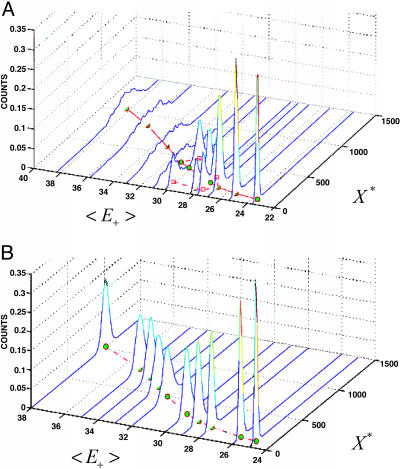
Fig. 4.

Signal response histograms for the simulated futile cycle (Expressions 7 and 8)(• represents positions of the average, whereas □ represents positions of the stationary states where different). (A) Molecular count histogram of X^* vs. different values of the average enzyme input, 〈E₊(t)〉, generated by the noise driver given in Expression 8. The evolution of the probability distributions of X^* with increase in 〈E₊(t)〉 demonstrates the noise-induced bistability effect. (B) If no external driver is applied, bistable behavior is not observed (uncertainty is due purely to the internal noise).

Fig. 4A demonstrates the split in the stationary distribution of X^* within a limited range of 〈E₊(t)〉 given that it is subject to the noisy dynamics driven by Expression 8. In contrast, Fig. 4B is obtained when the process (Expression 8) is not present. For the noise-driven case in the bistable region of 〈E₊(t)〉, a single measurement of a population of cells by, for example, flow cytometry would reveal that each cell is expressing a different level of X^* according to the distribution shown in Fig. 4A. However, as described above, this is not the whole story. A single cell, if measured over time, will dynamically express X^* in an oscillatory manner, as shown in Fig. 3A, so that the histogram of the measured concentration in an individual cell is the same as that shown in Fig. 4A, i.e., the same as for the whole population. [This situation could be contrasted with the one in which each cell expresses a different but fixed amount of X^*. In this case, a single measurement of a population of cells would also reveal that each cell is expressing a different level of X^* according to the distribution shown in Fig. 4A; however, measuring X^* over time in an individual cell would yield a constant baseline that looks similar to what is shown in Fig. 7 and result in a single-peaked individual-cell histogram similar to that shown in Fig. 4B and not Fig. 4A (i.e., different from the whole population, with the bimodal distribution across the population thus arising solely from cell–cell heterogeneity and not individual cell dynamics).]

Stochastic Signaling. As Fig. 4A shows, the oscillations seen in Fig. 3A subside some distance before the deterministic (sigmoidal) switch point, with the amplitude and frequency distribution of the oscillations changing in between. This transient switching is also a type of information that can be used in cellular signal processing. For instance, information about cycle state, such as distance away from the deterministic threshold, the nature of external perturbations, etc., is encoded (along with other system attributes) in its stochastic oscillatory dynamics. This frequency-domain content of the signal could then be used differentially by the downstream systems through some of the frequency-filtering mechanisms reported in ref. 14.

Signal Amplification. By altering the coupling to the external driving reaction or changing the external species concentration, we can effectively vary the strength of the input signal and thus measure the signal-to-noise ratio for this mechanism (Fig. 9, which is published as supporting information on the PNAS web site). The results match our analytical predictions of signal amplification reasonably well. They also further and more explicitly confirm our earlier predictions of the ability of the enzymatic futile cycle to work not only as a signal transducer but as a stochastic amplifier as well.

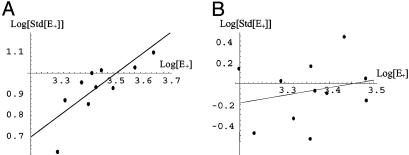
Noise Regulation and Inference. As is evident from Fig. 2, of all noise types modeled only those with p ≳ 0.75 are predicted to induce some form of bifurcation in this system for the given set of parameters. This prediction is indeed born out in the analysis of the direct numerical simulations, whereby a power law is fit to the scatter plot of std(E₊) vs. E₊ per Eq. 6. Application of the full mechanism given in Expression 8 results in an exponent close to one (shown in Fig. 5A) and generates the bistable behavior for the system as a whole (Fig. 4A); however, applying only the linear component of that driver, which has p ≈ 0.7 (Fig. 5B), does not (data not shown), which is consistent with our analytical predictions.

Fig. 5.

Scatter plot of standard deviation vs. average generated during the numerical simulations with varied cycle-driver coupling. (A) Full system given in Expressions 7 and 8, which results in the noise fit slope (power) p = 0.96 and bistability. (B) Only the linear driver in Expression 8, which results in the fit slope of p = 0.71 and no bistability.

Discussion

In this article we demonstrate that stochastic effects could lead to substantial qualitative differences from the deterministic predictions in the characteristic behaviors of biological and chemical systems. As an example, we specifically addressed this issue in the context of a common biomolecular network motif: the enzymatic futile cycle. We have shown that driving just one enzyme with a member of a wide class of external noise distributions is sufficient to create a stochastically switching (dynamic) bistability in the system in which none existed before. In particular, this result suggests that in some instances the switching behavior and other functions in biomolecular circuits can be a byproduct of external noise induction rather than feedback or other deterministic mechanisms as is frequently assumed. This, in turn, may explain why (among other things) futile cycles seem to be an evolutionarily favorable choice as a flexible signal-transduction motif and extend the utility of such mechanism for de novo bioengineering and similar applications.

Additionally and of potentially greater interest might be the global systemic effects that such noise-induced phenomena could have on our understanding of the overall structure and function of extra- or intracellular biochemical networks. Because noise is pervasive in our environment, it is possible that organisms have had to evolve not only to adapt but also to use the additional uniquely stochastic functional choices afforded to them, because (among other things) they come at low or no additional cost (entropic or otherwise) as compared to the deterministic ones. Two such simple examples of noise-induced functional options were considered in this article: stochastic amplification and stochastic signaling.

In the first case, additional amplification in the stationary level of system response is generated solely through an external noise driver. The implication of this is that futile cycles are intrinsically more sophisticated as signal transducers and amplifiers than would otherwise be expected solely on the basis of the deterministic analysis.

In the second case, as the external signal increases and begins to approach the sigmoidal region, the response level becomes bistable and begins to transiently switch between two states with a characteristic amplitude/frequency distribution. This dynamic switching may be viewed as an extra information channel through which more (accurate) signals can be passed to the downstream processes. The extra channel is obtained simply through the stochastic nature of the chemistry and without adding extra network features such as feedback/forward loops [or, conversely, the potential reason for the presence of such feedback might be to suppress this type of unwanted switching ingrained in the system (25)]. This result might be of further interest because, although it has been previously understood that various biochemical and biophysical processes can filter and shape oscillatory signals in a variety of unconventional ways (14, 26), the example considered herein opens up a possibility that such noise-filtering regulation and network inference techniques might be exploited in stochastic biological control systems as well.

The implications of the existence of such mechanisms for the robust design and functional control of biomolecular systems are complex: on the one hand, the need for chemistry and species otherwise involved in forming functional features (such as feedback loops) of classical deterministic designs can sometimes be obviated, thus removing some points of failure and possible energetic costs for the production of proteins or other constitutive molecules; on the other hand, new fragilities are introduced, such as dependence on the stochastic switching dynamics. It thus is possible that there are some evolutionary conditions that favor the stochastic design over the deterministic one or vice versa.

Because the theory and simulation we develop in this article demonstrate that a simple mechanism such as an enzymatic futile cycle can generate complex behavioral patterns under the influence of noise-driven stochastic effects, the question naturally arises of how one would experimentally identify and study these phenomena. While there are observations of noise-induced bistabilities in other physical and engineering systems (27, 28), there is little such conclusive experimental evidence in biomolecular structures to date, although it might be difficult to deconvolve the herein-predicted effects from the measurement noise. Furthermore, single-cell measurements of protein activity and gene expression are (although increasing) few, and of those, fewer still follow single-cell expression temporally at sufficient resolution. To complicate matters, additional mechanisms such as feedback loops often appear in biochemical pathways alongside the futile cycles and can also obscure or purposefully suppress the elucidated effects. Finally, the creation and control of noise-induced bistable switches in the laboratory is experimentally more challenging than that of the standard deterministic feedback-based architecture with a continuous switching parameter (29, 30). Nevertheless, given the pervasiveness of this signal-transduction motif and the simplicity of the mechanism that generates the effects described in this article, it is reasonable to assume that such a behavior is exploited in at least some cellular systems. Conversely, if it is never observed, that is interesting as well, because it would imply a certain evolutionary selection against this effect, and it is unclear why such a selection should exist. At least, all other things being equal, now that it is shown and characterized how noise can induce qualitatively novel dynamical behaviors and behavioral changes in biomolecular systems as simple as enzymatic futile cycles, perhaps it will make such effects easier to recognize when and if they are indeed observed.