Abstract
The Y22W/Q33Y/G46,48A mutant of the protein λ6–85 folds in a few microseconds at room temperature. We find that its folding kinetics are probe-dependent under a strong bias toward the native state, a new signature for downhill folding. The IR- and fluorescence-detected relaxation time scales converge when the native bias is removed by raising the temperature, recovering activated two-state folding. Langevin dynamics simulations on one- and 2D free energy surfaces tunable from two-state to downhill folding reproduce the difference between the IR and fluorescence experiments, as well as the temperature and viscosity trends. In addition, the 2D surface reproduces the stretched exponential dynamics that we fit to the glucose solution experimental data at short times. Nonexponential dynamics at <10 μs is a signature either for local free energy minima along the reaction coordinate (“longitudinal roughness”), or for folding on a higher-dimensional free energy surface (“transverse roughness”).
Keywords: fluorescence, infrared, helix bundle, amide band, landscape roughness
The possibility of downhill (type 0) folding is one of the central but least expected predictions of the energy landscape theory. As discussed by Bryngelson et al. (1), folding could proceed downhill in free energy when there is a sufficiently strong bias toward the native state. When the bias is reduced by heat denaturation, activated folding over a barrier (the type 1 scenario) is recovered (1). This switch corresponds to a transition from potentially nonexponential diffusion on a rough free energy surface to activated kinetics with a single rate coefficient, ka. Type 1 folding seems to be the norm among natural proteins, but type 0 folding remains a possibility for proteins with an unusually strong native bias.
Significant experimental progress has been made in the search for downhill folding kinetics (2). With the advent of fast laser initiation techniques (3), including laser T-jumps (4–6), the necessary nano- to microsecond time scales have become accessible. In 1999, Sabelko et al. (7) reported downhill formation of a phosphoglycerate kinase (PGK) folding intermediate. The nonexponential dynamics could be tuned toward a single exponential by cold or heat denaturing the protein, decreasing the bias toward the native state. The C-terminal domain of PGK was later shown to be responsible for this behavior (8). Kinetic evidence indicating downhill folding to the native state has also been reported. Activated kinetics of the engineered λ6–85 protein were preceded by a fast (km ≈ 1 μs-1) “molecular phase” (9). This new phase was attributed to a substantial population en route between the native and denatured states and accounted for nearly the entire signal in stabilizing glucose solution (10). The experimental downhill folding “speed limit” is in agreement with the preexponential factor calculated by Portman et al. (11). Estimates based on diffusion of denatured proteins (12, 13), on generic folding models (14), and on molecular dynamics studies of the free energy surface (15) also agree with the data.
Here, we provide new evidence for downhill folding kinetics of engineered λ6–85 in aqueous and glucose solutions: Downhill folding manifests itself as a probe-dependence (IR absorption vs. fluorescence) of the kinetics, as shown in Fig. 1. Such probe-dependence during microsecond folding was previously observed only for a peptide with a rough free energy surface (16). We further show that when the native bias is decreased by raising the temperature, the different probes converge and the type 0 scenario shifts toward a type 1 scenario (Fig. 1B). A 1D Langevin model fit accounts for much of the data, whereas the classic “intermediate” mechanism does not. A rough 1D free energy surface, or a 2D free energy surface, is required to account fully for the nonexponential molecular phase now resolved with excellent signal-to-noise ratio in fluorescence experiments.
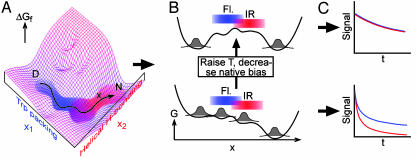
Fig. 1.
Relationship between free energy surface, folding probes, and observed kinetics. (A) Change in spectroscopic signatures projected along two reaction coordinates. x1 (blue; collapse/packing) correlates with a change in fluorescence, and x2 (red; helix formation) correlates with a change in the IR spectrum. (B) Projection along a single global reaction coordinate. The barrier region where signatures switch is not probed by two-state folders (Lower), it is probed by large populations during downhill folding/uphill unfolding (Upper). (C) The resulting time-dependence of the spectroscopic signatures during unfolding is identical for two-state folders, and different for downhill folding in the absence of a barrier.
Methods
The Engineered Protein. λ6–85 is an 80-residue, 5-helix globular protein. A fast-folding mutant, hereafter abbreviated as “λQ33Y,” is studied here. The mutations are Glu-33 → Tyr, Tyr-22 → Trp (to allow fluorescence detection), Gly-46 → Ala, and Gly-48 → Ala (10, 17–19). The protein was expressed and purified as described in ref. 10. Protein purity was confirmed by low-resolution electrospray ionization mass spectrometry and electrophoresis.
Thermal Titrations. Thermal denaturation was monitored by integrated fluorescence, near- and far-UV CD, and Fourier transform IR (FTIR) spectroscopy. To shift the water absorption peak away from the protein amide I band, 50 mM phosphate buffer in D2O was used for all FTIR measurements. Thermal denaturations were fitted within experimental uncertainty to two-state transitions with arbitrarily adjustable linear native and unfolded baselines, yielding free energy data in agreement with our previous work (10). A linear free energy relationship, ΔG = ΔG1(T - Tm), was sufficient to account for all of the data near the heat denaturation transition, where the present experiments were carried out to obtain the best signal-to-noise ratio.
Laser T-Jump Kinetics. Folding/unfolding kinetics are initiated by an 8° laser temperature jump, which changes the equilibrium constant of the protein, followed by fast relaxation. IR absorption spectroscopy, in 32 channels from 1,550–1,750 cm-1 (amide I′ band) with a 200-ns time resolution, is sensitive to helix formation during protein folding. Fluorescence decays pumped at 287 nm, with a 500-ps time resolution and 14 ns between successive decays, are sensitive to tryptophan solvent exposure and packing. For this study, the IR and fluorescence instruments were merged, so that both kinetic probes are detected simultaneously by using the same sample on the same temperature jump. To provide an objective measure of the kinetic decays, the folding-induced changes of the IR spectra and fluorescence decays with time were analyzed by singular value decomposition, as detailed in refs. 20 and 21. For the highest signal-to-noise ratio fluorescence transients, χ analysis (linear decomposition) was also used (22).
IR and fluorescence measurements were performed by using a 75-μm film of 50 mM deuterated phosphate buffer over a 50–360 μM protein concentration range at pD 7. Glucose at 1 M was added in some measurements as a viscogen and to decrease the free energy barrier further. Measurements were taken at a fresh sample position every 10 shots, and a new sample was loaded every 50 shots. Control experiments showed that the kinetics of the sample were not changed by repetitive pulse heating on the same spot with 50 shots, leaving a factor 5 safety margin.
Data Fitting. The protein folding kinetics monitored by IR and fluorescence were fitted by least squares to single, double, and single+stretched exponential models of the type
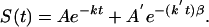 |
[1] |
A single exponential accounted for the lower signal-to-noise ratio IR data by itself, but neither for the fluorescence data below Tm, nor for the IR/fluorescence data simultaneously below Tm. The double and single+stretched exponential models are physically motivated by including an exponential decay for the slow activated phase with rate coefficient k = ka, and a second single (β = 1) or stretched (β < 1) exponential function with rate coefficient k′ = km for the molecular phase coming from diffusion of proteins on the free energy surface en route to/from the native state (10).
Kinetic rate equations cannot be used to simulate low barrier/downhill folding. Instead, we carried out Langevin dynamics modeling in the high friction limit on one- and 2D free energy surfaces using a fourth-order Runge–Kutta integrator:
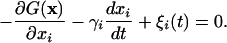 |
[2] |
G(x) denotes a 1D or 2D free energy surface along reaction coordinate(s) x (x1 or x1 and x2). γi = kT/Di denotes the velocity relaxation rate, and ξi is Gaussian white noise with zero mean to account for solvent fluctuations. The scale of the reaction coordinate was chosen so distances could be interpreted roughly in nm and diffusion constants roughly in nm2/ns. The diffusion constant in aqueous solution at 63°C was scaled to match the average of the IR and fluorescence time scales. The diffusion constant was also adjusted to track the known glucose- and temperature-dependence of the bulk solvent viscosity of different measurements. T-jumps were simulated by first equilibrating the population on a surface corresponding to pre-T-jump thermodynamic conditions, then switching the surface and allowing the population to relax. The biases induced by temperature and glucose were approximated by bilinear potentials:
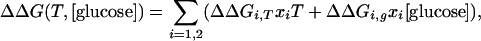 |
[3] |
with the ΔΔGi parameters chosen to match the known thermodynamic data (e.g., the Tm of 71°C, the 2°C increase of Tm upon addition of 1 M glucose, and the lowering of the activation barrier by 0.6 kT upon addition of 1 M glucose) (10). Folded populations as a function of time were obtained by partitioning the populations along the reaction coordinate(s) or equally well by using more gradual sigmoidal switching functions. In addition to the smooth free energy surfaces discussed in the text, we also computed dynamics on multiwell potentials. We previously showed that such surfaces, as long as the traps still tend downhill toward the native state, can reproduce the molecular phase without a rescaling of the diffusion coefficient to smaller values (9, 10).
Results
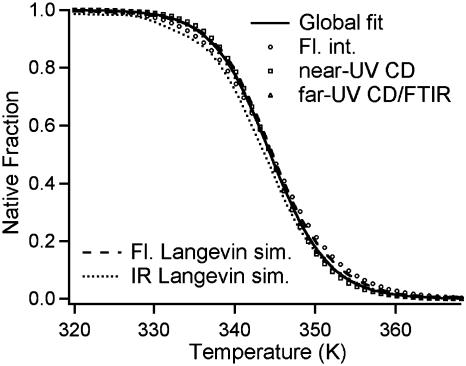
Unfolding Thermodynamics Are Nearly “Type 1” at the Midpoint. The thermodynamic data from near-UV CD-detected, far-UV CD/FTIR-detected, and integrated fluorescence intensity-detected thermal denaturation of λQ33Y can be fitted globally by a two-state sigmoidal unfolding transition, provided arbitrarily adjustable baselines are allowed for each measurement (Fig. 2, Table 1, and supporting information, which is published on the PNAS web site). The fitted melting temperature (Tm = 71.4 ± 0.5°C) agrees with the value reported by Yang and Gruebele for λQ33Y (10).
Fig. 2.
The heat denaturation populations (1 = native, 0 = denatured) of λQ33Y monitored by several spectroscopic probes can be described by a cooperative (type 1) scenario with Tm = 71.4 ± 0.5°C, if the native and denatured baselines are fitted. The model free energy surfaces shown in Fig. 5A show a similar spread as the experimental data; IR and fluorescence populations using the same dividing surfaces in Fig. 5A as for the kinetics differ by ΔTm = 1°C, nearly but not quite a type 1 scenario.
Table 1.
Thermodynamic parameters of λQ33Y using different probes and a fit with arbitrarily adjustable linear baselines (first three rows), as well as the Tms obtained from the Langevin model in Fig. 5 (last two rows)
| Probe | Tm, K | ΔΔG1, kJ/mole |
|---|---|---|
| Far-UV CD and FTIR | 344.4 (1) | 0.79 (1) |
| Near-UV CD | 344.4 (7) | 0.86 (2) |
| Fl. intensity | 344.6 (1) | 0.68 (1) |
| Fl. lifetime (Langevin) | 344.7 (5) | See Fig. 5 |
| IR (Langevin) | 343.7 (5) | See Fig. 5 |
Fl., fluorescence.
*Uncertainties are 1σ precision of the fit. The accuracy of temperature measurements was ±0.5°C.
The thermodynamic melts could also be fitted by the type-0-to-type-1 model discussed in detail later, yielding slightly different melting temperatures (Fig. 2, ΔTm ≈ 1°C). The thermal denaturation midpoint of λQ33Y is, thus, near the type 1 limit by either fitting method. The two-state and downhill model fits illustrate the danger of inferring two-state folding far below Tm from the observation of a sigmoidal transition with a small spread in Tm near the midpoint. As discussed in refs 1, 7, and 23, the very act of heat, chaotropic, or cold denaturation can turn a downhill folder into a two-state folder at the transition midpoint.
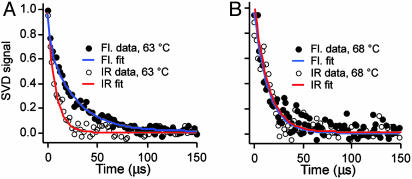
IR and Fluorescence Probes Differ at Strong Native Bias. We previously showed that the IR and fluorescence kinetic transients of a slow-folding λ6–85 mutant nearly coincide and that they are nearly single exponential (21). This finding contrasts with our key result here that the IR-detected relaxation of λQ33Y is ≈2.5 times faster than the fluorescence-detected process below the denaturation midpoint (Fig. 3A).
Fig. 3.
Transition from downhill to activated folding as the temperature is increased. (A) Folding kinetics of 260 μM λQ33Y in 50 mM phosphate buffer at 63°C, comparing IR and fluorescence singular value decomposition (SVD) signals; the IR decay is significantly faster, and the fluorescence decay requires a second fast phase to fit within uncertainty (Table 2). (B) Folding kinetics of 260 μM λQ33Y at 68°C, comparing IR and fluorescence SVD signals. The IR- and fluorescence-detected kinetics become more similar, as predicted by a type 0 → type 1 folding transition.
Although a single-exponential model suffices for the IR data by itself (Table 2), a double-exponential model is minimally required to fit both kinetic probes simultaneously or to fit the higher signal-to-noise ratio fluorescence kinetics individually (Table 2).
Table 2. Minimal kinetic parameters for λQ33Y in aqueous buffer for 260 M protein.
| T, K | Probe | A (A′ = 1 - A) | k, μs-1 | k′, μs-1 |
|---|---|---|---|---|
| 336 | Fl. | 0.67 (3) | 0.036 (5) | 0.5 (2) |
| IR | 1 | 0.12 (1) | — | |
| 341 | Fl. | 1 | 0.069 (3) | — |
| IR | 1 | 0.070 (5) | — | |
| 348 | Fl. | 1 | 0.37 (13) | — |
| IR | 1 | 0.45 (8) | — |
Fl., fluorescence.
*The uncertainties are 1σ precisions of the fit.
IR and Fluorescence Probes Converge at Higher Temperature. Another important result comes from decreasing the native bias by T-jumping close to or above the heat denaturation midpoint. At higher temperatures (68°C, 75°C), the difference between the kinetics detected by IR and fluorescence becomes negligible, allowing a reasonably accurate fit by a single exponential (Fig. 3B and Table 2). A full account of the unusual temperature dependence of the folding rate of λQ33Y is given in ref. 23.
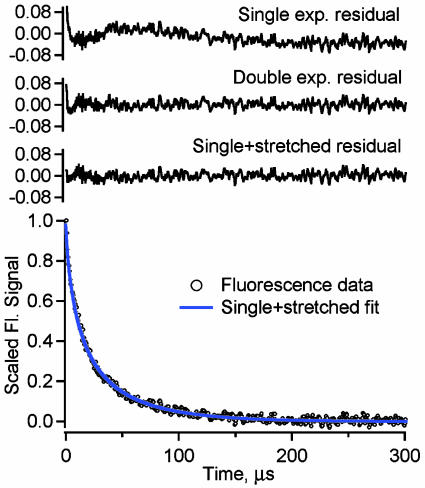
The Molecular Phase Deviates from Exponential Decay Under Highly Stabilizing Conditions. We also examined the unfolding kinetics of λQ33Y in buffer containing 1 M glucose, which we previously showed increases the native bias of λ6–85 by another 0.6 kT toward downhill folding (10). The very high signal-to-noise ratio of the fluorescence-detected data under the most stabilizing conditions cannot be accounted for by a single- or double-exponential fit. Fig. 4 shows the observed kinetics in 1 M glucose and single-, double-, and stretched+single-exponential residuals. Only the stretched+single-exponential model of Eq. 1 fits the observed kinetics over the whole dynamic range (300 ns to 300 μs) within uncertainty with a stretching factor β = 0.70 ± 0.03, in agreement with the previous lower limit β ≥ 0.7 (9).
Fig. 4.
Fluorescence kinetics and residuals in 1 M glucose at 68°C (by linear decomposition or “χ-analysis” of the tryptophan fluorescence decays; see ref 20). Single-, double-, and stretched+single-exponential residuals are shown. (Only the stretched+single model reproduces the data within uncertainty over the full dynamic range from 0.3 to 300 μs, with k = ka = 0.019(1) μs-1, A′ = Am = 0.71(3), k′ = km = 0.104(4) μs-1, and β = 0.70(3).
Discussion
During strict two-state folding, only a single rate coefficient ka is detected (24). When the native bias is increased sufficiently so the free energy barrier decreases below 2–3 kT, diffusion of the population in the “activated region” also contributes to the signal (25) (Fig. 1). The resulting additional fast phase is not necessarily exponential but under certain conditions may be described by an exponential with rate coefficient km (26).
In a multiprobe measurement, different probes switch from the native to the unfolded signal at different positions along the reaction coordinate(s) and, hence, at different free energies (27) (Fig. 1). Therefore, different probes sample different parts of the protein population that contribute to the two observed groups of rate eigenvalues ka and km. Such heterogeneous sampling changes the relative amplitudes of the activated and molecular contributions to the observed signal and, hence, the apparent rate. In our experiments, we compare two probes: IR is more sensitive to local secondary structural changes (primarily helical hydrogen bond formation in λQ33Y), whereas fluorescence is more sensitive to side-chain contacts and local collapse around the tryptophan. At low temperatures, the IR probe is faster (has a larger molecular-phase amplitude) than the fluorescence probe. Therefore, at native bias IR switches from the native to the unfolded signal at a lower free energy than fluorescence. This experimental observation is reflected in the schematic surfaces in Fig. 1 and in the fitting models discussed below and in Figs. 5 and 6.
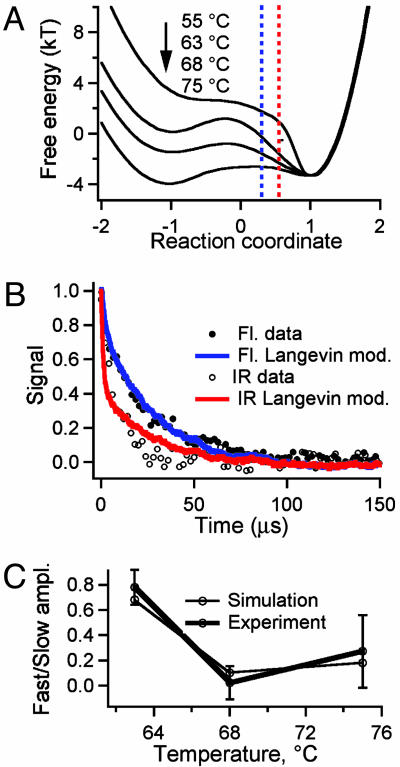
Fig. 5.
Langevin folding dynamics using smoothed 1D free energy profiles and a reduced diffusion coefficient. (A) Free energy profiles at temperatures relevant for the thermodynamics in Fig. 2 and kinetics in Fig. 3; different partitions of the reaction coordinated into “reactant” and “product” according to IR (red) and fluorescence (blue) are shown as vertical dotted lines. (B) Simulated (red, IR; blue, fluorescence) downhill folding signals compared with the experimental data at 63°C. (C) The simulation also reproduces the smaller difference in IR/fluorescence decays when the native bias is removed by raising the temperature to 68°C and 75°C. The y axis is 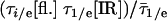 , where τ1/e indicates the 1/e decay time and
, where τ1/e indicates the 1/e decay time and 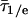 indicates the average for IR and fluorescence.
indicates the average for IR and fluorescence.
Fig. 6.
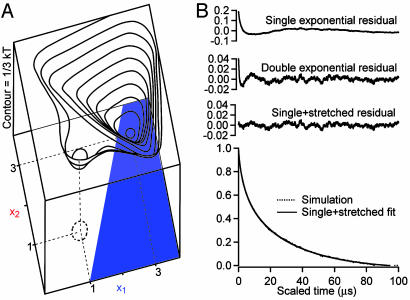
A 2D surface recovers a stretched downhill phase. (A) Two-dimensional model free energy surface, with a switch between unfolded and native fluorescence (blue) at x2 = 2x1 - 2, reproduces the results of the 1D surface but also reproduces the nonexponential molecular phase found experimentally in Fig. 4 (B). The computed stretching factor is β = 0.72 ± 0.01.
As the temperature approaches the transition midpoint, the native bias decreases, and the landscape theory predicts a more two-state-like (type 1) folding process (1). Our experiments support this with two observations: As the temperature is increased above the midpoint, the activated folding rate, ka, accounts for most of the folding kinetics, and the kinetics observed by two probes becomes more similar (Figs. 3B and 5C and Table 2). Secondly, the heat denaturation of λQ33Y observed by several probes can be fitted by a two-state model near the transition midpoint (Fig. 2); with only a small discrepancy (1°C) between melting temperatures, the model described below and in the supporting information (Fig. 2) also works. Thus, λQ33Y switches from downhill to two-state folding at elevated temperature, unlike the purely downhill thermodynamics proposed for the small protein BBL (28).
The 1D surface in Fig. 5A coupled with Langevin dynamics provides a simple and robust model for the temperature dependence and different time scales of multiprobe kinetics illustrated in Fig. 3. The barrier height is determined by matching the discrepancy between IR- and fluorescence-detected kinetics at 63°C. The barriers are 0 kT before the T-jump and 0.9 kT at 63°C. To match the average IR/fluorescence time scale, a diffusion constant, D ≈ 3 × 10-5, was used. The small diffusion constant accounts for longitudinal roughness (small traps along the reaction coordinate) as well as transverse roughness (along other coordinates), which are not included explicitly in our smooth 1D model. The supporting information describes several other free energy surfaces we tested numerically, including those with explicit traps and larger diffusion constants. As detailed in the supporting information and in ref. 10, the classic “intermediate” model proposed in the literature for other fast folders (29) fails to account for our kinetics and thermodynamics data, but a cascade of small traps following the main barrier (30) is equivalent to our smoothed surface when the main barrier becomes low or nonexistent.
Using a “sudden” switch between the unfolded and native signals along the reaction coordinate (Fig. 5A, dotted lines), the calculated relaxation kinetics after the temperature perturbation reproduces the observed discrepancy between the IR and fluorescence probes at 63°C (Fig. 5B). More realistic sigmoidal dividing curves produce similar results (data not shown). The model also correctly predicts the merging of the IR and fluorescence kinetic time scales when the temperature is tuned from 63°C to 68°C to 75°C (Fig. 5C). At low temperatures, the simulation yields a large type 0 downhill phase and a large difference between the IR- and fluorescence-detected kinetics, whereas at higher temperatures, the downhill phase diminishes and the IR and fluorescence signals merge toward a type 1 scenario with equally fast exponential decays (Figs. 3B and 5C and Table 2). The scenario by Bryngelson et al. actually predicts a turnaround to type 0 (now downhill unfolding) above the transition midpoint. The uncertainty of the data in Fig. 5C is too large to deduce whether the small turnaround in the experiment at 75°C is real, although it was modeled by the 1D free energy surfaces in Fig. 5A.
The precise shape of the decays cannot be accounted for by the smooth 1D surfaces in Fig. 5A. For example, the observed fluorescence-detected kinetics in Fig. 4 is not perfectly fitted by a double exponential (β = 0.70 ± 0.03 is needed when fitting to Eq. 1). The kinetics on the faster molecular timescale are affected by nonexponential diffusive dynamics on a rough free energy landscape, whereas our 1D Langevin simulation with the free energy in Fig. 5A yields β ≈ 1. One possible explanation is the existence of small longitudinal traps, which contribute additional time scales, although this assumption by itself does not yield a very robust model fit (parameters must be carefully fine-tuned; see the supporting information).
Diffusion along additional reaction coordinates provided a more robust model for a nonexponential early phase of the folding dynamics. To test whether downhill diffusion on a higher-dimensional free energy surface could account for the observed stretching of the molecular time scale, a 2D free energy surface with a weak coupling of the reaction coordinate to the second coordinate was generated (Fig. 6A and supporting information). On such a surface, the protein does not have to fold through a single route (31–34), resulting in a spread of time scales (35–38). Fig. 6B shows the computed 2D kinetics together with a fit to the single+stretched-exponential model. Similar to the experimental data, the molecular phase from the 2D Langevin simulation can only be fully accounted for by a distribution of molecular rate coefficients, km. The calculated stretching factor for the model in the supporting information is β = 0.72 ± 0.01, in very good agreement with the data. However, the current experimental data do not allow us to distinguish how much either a higher dimensionality of the surface, or coordinate-dependent Di(x) and γi(x) (equivalently, different-sized longitudinal traps) contribute to the stretching.
In summary, downhill folding causes the IR- and fluorescence-detected kinetics to differ from one another at strong native bias. They converge toward activated kinetics with one time scale at higher temperature because thermal denaturation destabilizes the native state and transition region, creating a barrier (1). A fast molecular phase is observed as previously reported; at strong native bias, the molecular phase is no longer described by a single rate coefficient but requires a stretched exponential with β = 0.70 ± 0.03, a signature of multiscale diffusion on a rough free-energy surface. One-dimensional Langevin simulations on a smooth free energy surface can account for the first two observations, and explicit traps (see the supporting information) or a 2D free energy surface also can account for the third observation.
Supplementary Material
Acknowledgments
This work was supported by National Science Foundation Grant MCB 0316925.
Author contributions: M.G. designed research; H.M. performed research; H.M. and M.G. analyzed data; and H.M. and M.G. wrote the paper.
Abbreviation: FTIR, Fourier transform IR.
References
- 1.Bryngelson, J. D., Onuchic, J. N., Socci, N. D. & Wolynes, P. G. (1995) Proteins Struct. Funct. Genet. 21, 167-195. [DOI] [PubMed] [Google Scholar]
- 2.Kubelka, J., Hofrichter, J. & Eaton, W. A. (2004) Curr. Opinion. Struct. Biol. 14, 76-88. [DOI] [PubMed] [Google Scholar]
- 3.Jones, C. M., Henry, E. R., Hu, Y., Chan, C., Luck, S. D., Bhuyan, A., Roder, H., Hofrichter, J. & Eaton, W. A. (1993) Proc. Natl. Acad. Sci. USA 90, 11860-11864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Phillips, C. M., Mizutani, Y. & Hochstrasser, R. M. (1995) Proc. Natl. Acad. Sci. USA 92, 7292-7296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Williams, S., Causgrove, T. P., Gilmanshin, R., Fang, K. S., Callender, R. H., Woodruff, W. H. & Dyer, R. B. (1996) Biochemistry 35, 691-697. [DOI] [PubMed] [Google Scholar]
- 6.Ballew, R. M., Sabelko, J. & Gruebele, M. (1996) Proc. Natl. Acad. Sci. USA 93, 5759-5764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sabelko, J., Ervin, J. & Gruebele, M. (1999) Proc. Natl. Acad. Sci. USA 96, 6031-6036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Osváth, S., Sabelko, J. & Gruebele, M. (2003) J. Mol. Biol. 333, 187-199. [DOI] [PubMed] [Google Scholar]
- 9.Yang, W. Y. & Gruebele, M. (2003) Nature 423, 193-197. [DOI] [PubMed] [Google Scholar]
- 10.Yang, W. & Gruebele, M. (2004) Biophys. J. 87, 596-608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Portman, J. J., Takada, S. & Wolynes, P. G. (1998) Phys. Rev. Lett. 81, 5237-5240. [Google Scholar]
- 12.Hagen, S. J., Hofrichter, J., Szabo, A. & Eaton, W. A. (1996) Proc. Natl. Acad. Sci. USA 93, 11615-11617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chang, I. J., Lee, J. C., Winkler, J. R. & Gray, H. B. (2003) Proc. Natl. Acad. Sci. USA 100, 3838-3840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Camacho, C. J. & Thirumalai, D. (1995) J. Physique I 5, 1457-1467. [Google Scholar]
- 15.Pogorelov, T. V. & Luthey-Schulten, Z. (2004) Biophys. J. 87, 207-214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yang, W. Y. & Gruebele, M. (2004) J. Am. Chem. Soc. 126, 7758-7759. [DOI] [PubMed] [Google Scholar]
- 17.Burton, R. E., Huang, G. S., Daugherty, M. A., Calderone, T. L. & Oas, T. G. (1997) Nat. Struct. Biol. 4, 305-310. [DOI] [PubMed] [Google Scholar]
- 18.Ghaemmaghami, S., Word, J. M., Burton, R. E., Richardson, J. S. & Oas, T. G. (1998) Biochemistry 37, 9179-9185. [DOI] [PubMed] [Google Scholar]
- 19.Myers, J. M. & Oas, T. G. (1999) Biochemistry 38, 6761-6768. [DOI] [PubMed] [Google Scholar]
- 20.Ervin, J., Sabelko, J. & Gruebele, M. (2000) J. Photochem. Photobiol. B54, 1-15. [DOI] [PubMed] [Google Scholar]
- 21.Ma, H., Ervin, J. & Gruebele, M. (2003) Rev. Sci. Instrum. 75, 486-491. [Google Scholar]
- 22.Ballew, R. M., Sabelko, J., Reiner, C. & Gruebele, M. (1996) Rev. Sci. Instrum. 67, 3694-3699. [Google Scholar]
- 23.Yang, W. Y. & Gruebele, M. (2004) Biochemistry 43, 13018-13025. [DOI] [PubMed] [Google Scholar]
- 24.Jackson, S. E. & Fersht, A. R. (1991) Biochemistry 30, 10428-10435. [DOI] [PubMed] [Google Scholar]
- 25.Berne, B. J. (1993) in Activated Barrier Crossing: Applications in Physics, Chemistry, and Biology, eds. Hänggi, P. & Fleming, G. R. (World Scientific, Singapore), pp. 82-119.
- 26.Zwanzig, R. (1988) Proc. Natl. Acad. Sci. USA 85, 2029-2030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Klimov, D. K. & Thirumalai, D. (2002) J. Comput. Chem. 23, 161-165. [DOI] [PubMed] [Google Scholar]
- 28.Garcia-Mira, M. M., Sadqi, M., Fischer, N., Sanchez-Ruiz, G. M. & Muñoz, V. (2002) Science 298, 2191-2195. [DOI] [PubMed] [Google Scholar]
- 29.Mayor, U., Guydosh, N. R., Johnson, C. M., Grossmann, J. G., Sato, S., Jas, G. S., Freund, S. M., Alonso, D. O., Daggett, V. & Fersht, A. R. (2003) Nature 421, 863-867. [DOI] [PubMed] [Google Scholar]
- 30.Bai, Y. W. (2003) Biochem. Biophys. Res. Comm. 305, 785-788. [DOI] [PubMed] [Google Scholar]
- 31.Onuchic, J. N., Nymeyer, H., Garcia, A. E., Chahine, J. & Socci, N. D. (2000) Adv. Protein Chem. 53, 87-152. [DOI] [PubMed] [Google Scholar]
- 32.Bryngelson, J. D. & Wolynes, P. G. (1987) Proc. Natl. Acad. Sci. USA 84, 7524-7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shea, J. & Brooks, C. L. (2001) Annu. Rev. Phys. Chem. 52, 499-535. [DOI] [PubMed] [Google Scholar]
- 34.Cheung, M. S., Chavez, L. L. & Onuchic, J. N. (2003) Polymer 45, 547-555. [Google Scholar]
- 35.Skorobogatiy, M., Guo, H. & Zuckerman, M. (1998) J. Chem. Phys. 109, 2528-2535. [Google Scholar]
- 36.Nymeyer, H., García, A. E. & Onuchic, J. N. (1998) Proc. Natl. Acad. Sci. USA 95, 5921-5928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Metzler, R., Klafter, J. & Jortner, J. (1999) Proc. Natl. Acad. Sci. USA 96, 11085-11089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Volk, M., Kholodenko, Y., Lu, H. S. M., Gooding, E. A., DeGrado, W. F. & Hochstrasser, R. M. (1997) J. Phys. Chem. 101, 8607-8616. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.