The kinetics of conformational fluctuations in an unfolded protein measured by fluorescence methods

Abstract

The simplest dynamic model for an unfolded protein is a statistical coil that continually undergoes substantial conformational fluctuations. A growing number of studies indicate that the unfolded protein is not a simple random coil but rather forms transient structures. We have directly measured the rate of conformational fluctuations of unfolded intestinal fatty acid binding protein (131 aa, 15 kDa) by using fluorescence self-quenching in combination with fluorescence correlation spectroscopy. The conformational fluctuations in this state have an apparent relaxation time, τ_R, of 1.6 μsec in 3 M guanidine-HCl at pH 7 and 20°C. The value of τ_R increases with increasing solution viscosity, suggesting a diffusive process. In the molten globule state at pH 2, τ_R is 2.5 μsec, increasing further with the formation of salt-induced secondary structure. These measurements, which should be widely applicable to other systems, can provide important information about the still incompletely understood conformational properties of unfolded proteins and the mechanism of protein folding.

Alarge number of theoretical and experimental studies have recently been devoted to understanding the structure of the unfolded state of a protein. These studies suggest the presence of transient, if not stable, structural elements (e.g., refs. 1 and 2). Little is known, however, about the dynamics between different conformers in the unfolded state. Probing these conformational transitions is not trivial for two reasons. First, the dynamics are expected to be rapid (μsec) and inaccessible to NMR and other commonly used experimental techniques. Second, the difference in spectroscopic signatures between two conformational states is small or even absent, thus making it difficult to find a suitable probe. In this study, we have used fluorescence self-quenching of tetramethyl rhodamine (TMR) as analyzed by fluorescence correlation spectroscopy (FCS) to study the dynamics of the unfolded state under different solution conditions.

To perform these experiments we have incorporated a fluorescent probe in two positions of the intestinal fatty acid binding protein (IFABP), 48 residues apart, and have directly measured both the rate of diffusion of the whole molecule and the rate of internal dynamics of the chain in the unfolded state. IFABP consists of two β-sheets enclosing a large cavity into which the fatty acid binds (3). The protein (131 residues, 15 kDa) does not contain either cysteine or proline residues, but numerous mutations of residues to cysteine, to which fluorescence probes have been covalently attached (4) have been made with few deleterious effects. Thus, this protein provides an excellent model system for these studies. The persistence of structure in the unfolded state of IFABP was observed by Hodsdon and Frieden (5). In the present study two polar residues, in the two different β-sheets, have been mutated to cysteine (D59C/E107C) and then modified with TMR-5-maleimide. Two other mutants were generated, each with only one residue replaced by cysteine and modified by TMR (D59C-TMR and E107C-TMR). Relative to the labeled single mutants, the doubly labeled mutant is significantly quenched in the presence of 2 M guanidine-HCl (Gdm·HCl). We conclude that this quenching (fluorescence self-quenching) is a consequence of transient close proximity of the two fluoroprobes in the unfolded state, similar to that reported by Zhuang et al. (6) in single-molecule studies. In effect, the quenching results from transient closure of a loop in the polypeptide chain caused by the close approach of the two rhodamine moieties. We use that observation of fluorescence self-quenching in conjunction with FCS to measure the dynamics of segmental motion, manifested by loop closure, in the unfolded protein.

Materials and Methods

Mutagenic primers were obtained from Integrated DNA Technologies (Coralville, IA), and the QuikChange site-directed mutagenesis kit was obtained from Stratagene. TMR-5-maleimide was purchased from Molecular Probes. Guanidium hydrochloride was obtained from ICN Biochemicals. All other reagents used were analytical grade.

Site-directed mutagenesis and expression and purification of the WT and mutant proteins of IFABP was carried out as described (7). The reaction with TMR-5-maleimide was carried out by using a previously published procedure (8). For experiments as a function of Gdm·HCl, a series of protein solutions at different denaturant concentrations were prepared in 20 mM phosphate buffer at pH 7.3, and the solutions were equilibrated for 30 min before the measurements.

Steady-state fluorescence experiments were performed at 20°C by using a PTI Alphascan fluorometer (Photon Technology International, South Brunswick, NJ) with protein concentrations of ≈1 μM. For TMR-modified proteins the excitation wavelength was 546 nm, and emission spectra were recorded between 550 and 650 nm. CD experiments were performed on a Jasco (Tokyo) J-715 by using a 0.1-cm path length cell.

The procedure for FCS experiments using two-photon excitation has been described (8, 9), and the same experimental procedure has been used here. Data analyses were performed with origin 7.0 (OriginLab, Northampton, MA).

For a single species with a diffusion time, τ_D, a correlation function of the form of Eq. 1 can be obtained:

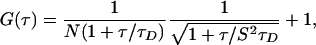[1]

where N is the number of particles in the observation volume, and S is the depth-to-diameter ratio of the 3D Gaussian volume element. If the diffusing species (with the diffusion time of τ_D) undergoes a chemical reaction or conformational change with a relaxation time of τ_R, the correlation function of the system can be represented by Eq. 2:

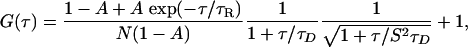[2]

where A is the magnitude (or extent) of the process defined by τ_R.

The radius, W, of the focal volume of the system can be calculated by using Eq. 3

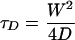[3]

where D is the diffusion coefficient. For this purpose, FCS experiments were performed with rhodamine 6G for which the diffusion coefficient (D) is known so that W can be calculated from the measured τ_D value.

Results and Discussion

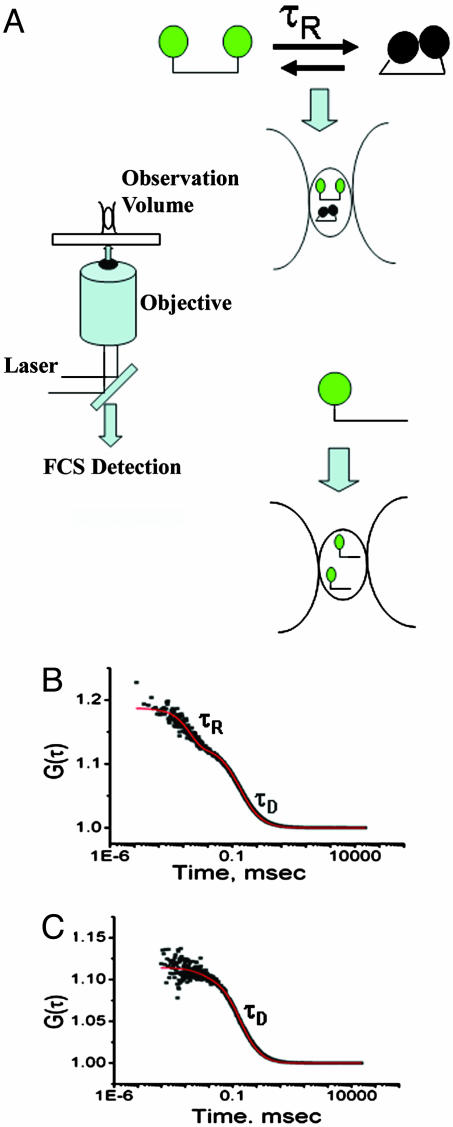
The basic principles of the FCS measurements are shown in Fig. 1A. Some of the salient features are (i) the molecules are free to diffuse, thus avoiding the possible effects of tethering the molecule to a solid surface, (ii) the autocorrelation function can be used to determine the translational diffusion time (τ_D) of the protein, (iii) any fluorescence fluctuation arising from conformational dynamics of the protein can be analyzed from the correlation function provided the rate of conformational fluctuation (τ_R) is faster than the diffusion (τ_R << τ_D), and (iv) the measurements are carried out at a low concentration with only a few molecules in the observation volume, thus avoiding aggregation problems.

Fig. 1.

The principles of an FCS experiments are outlined. (A) A laser beam at 810 nm from a Ti-sapphire laser is focused for two-photon excitation through a microscope objective lens of high aperture (Olympus, ×60 water immersion), resulting in a small observation radius of 260 nm. Fluorescence fluctuations arising from a dilute solution (10–50 nM) of TMR-labeled proteins are monitored by using two avalanche photo diode detectors. (B) Autocorrelation plot for D59C/E107C-(TMR)₂ showing a diffusion component (τ_D) and an exponential component (τ_R) with the fit shown in red. (C) Autocorrelation plot of E107C-TMR fit to a model containing only the diffusion component (τ_D) (shown in red). Experiments were carried out at pH 7.3 with 20 mM phosphate buffer at room temperature and in the presence of 2 M Gdm·HCl. An experimental complication arising from the refractive index mismatch between the immersion medium of the objective (water) and the Gdm·HCl solution was corrected by using the correction collar of the objective and changing the distance between the objective and the coverslip (9).

Fig. 1B shows the autocorrelation function obtained for the double mutant [D59C/E107C-(TMR)₂] in the presence of 2 M Gdm·HCl. Corrections for refractive index changes are described elsewhere (9). The data shown in Fig. 1B clearly show two distinct phases and so could not be fit by Eq. 1 but required an additional exponential relaxation term. From Eq. 2 τ_R was calculated to be 1.8 ± 0.1 μsec at 2 M Gdm·HCl and 1.6 ± 0.1 μsec at 3 M Gdm·HCl. These values reflect the relaxation time of segmental motion in the unfolded protein as a consequence of quenching of the TMR fluoroprobes.

To show that τ_R is not an artifact of the triplet-state photo-physics, the experiments were repeated by using three different laser powers (2.5, 5, and 7 mW). No variation of τ_R or its amplitude with laser power was observed. FCS experiments were also performed with two mutants containing only a single fluoroprobe (either E107C-TMR and D59C-TMR). Because these two mutants are singly labeled they should not show fluorescence self-quenching. Fig. 1C shows the autocorrelation function observed for the single mutant E107C-TMR of IFABP labeled with TMR in the presence of 2 M Gdm·HCl, an amount sufficient to denature the protein. The data of Fig. 1C are well fit to a simple diffusion model (Eq. 1) with a diffusion time (τ_D) of 180 μsec, which is similar to the value of τ_D observed for the double-labeled protein (193 μsec in the presence of 3 M Gdm·HCl). The same result was also obtained for the other singly labeled mutant (D59C-TMR).

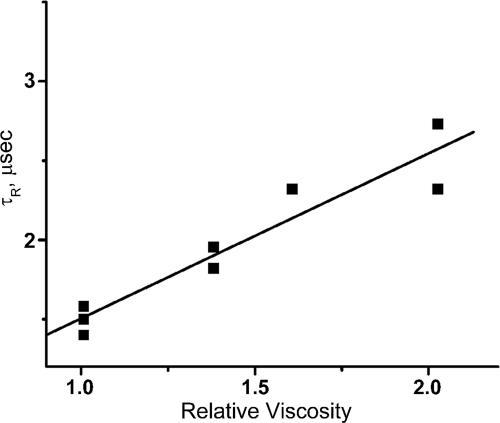
To test whether the process characterized by τ_R is diffusion-controlled experiments were performed in the presence of either sucrose or glycerol in 3 M Gdm·HCl. Fig. 2 shows that τ_R is directly proportional to the bulk viscosity, showing that the motion defined by τ_R is a diffusional process.

Fig. 2.

Viscosity dependence of τ_R. The viscosity of 3 M Gdm·HCl solutions was changed by the addition of glycerol. The experiments were performed in 20 mM potassium phosphate buffer at pH 7.3 at room temperature.

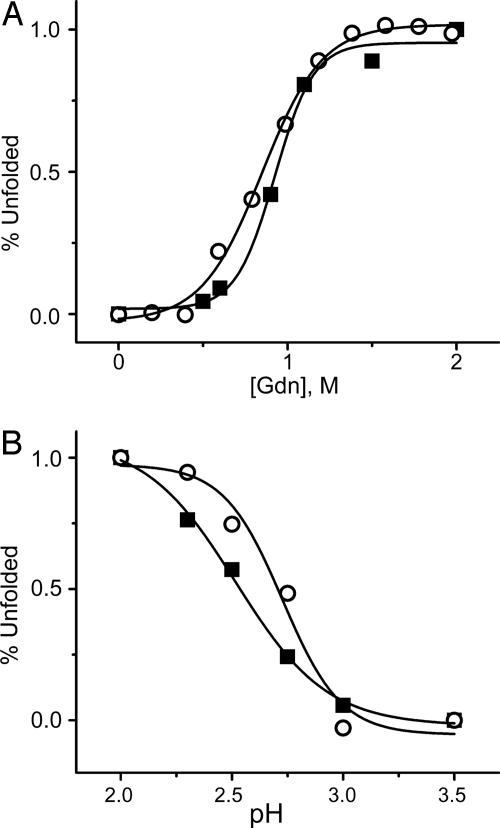
The effects of Gdm·HCl and low pH were also examined by using the D59C/E107C-(TMR)₂ protein. Fig. 3A shows the variation of the amplitude of the τ_R component as a function of Gdm·HCl concentration. The amplitude of τ_R has been normalized to the percentage of unfolded protein. The Gdm·HCl data follow the same unfolding transition as D59C/E107C-(TMR)₂ IFABP monitored by steady-state fluorescence experiments (excitation = 541 nm, emission = 575 nm). Examination of the native protein at pH 7 in the absence of Gdm·HCl yields only the diffusion component (τ_D = 120 μsec), supporting the idea that the structure is too rigid to allow the probes to come in contact.

Fig. 3.

Variation of the amplitude of τ_R (▪) as a function of Gdm·HCl concentrations (A) and pH (B). The Gdm·HCl- and pH-induced unfolding of D59C/E107C-(TMR)₂ monitored by steady-state fluorescence is also shown (○). In both cases, the experimental parameters are converted in terms of percentage unfolding. Gdm·HCl unfolding experiments were performed in 20 mM potassium phosphate buffer at pH 7.3. pH unfolding experiments were performed by using 2 mM citrate buffer. All of the experiments were carried out at room temperature.

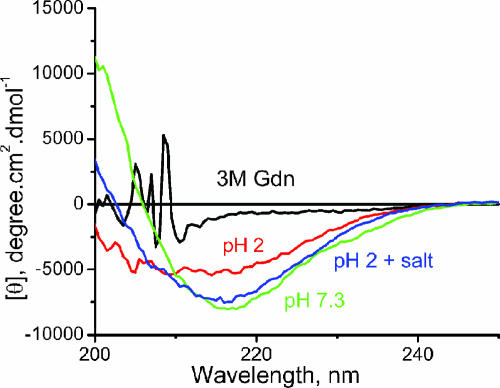
At low pH values proteins are believed to be molten globules having disordered tertiary structure and some secondary structure. Far UV CD measurements show that the unfolded state of IFABP at low pH (pH 2) contains a significant amount of secondary structure compared with that in 3 M Gdm·HCl (Fig. 4). Determination of the Stokes radius from the measured diffusion time, τ_D, at pH 2, indicates that the protein is compact (22 Å), whereas in the presence of 2–3 M Gdm·HCl, it is close to a random coil (46 Å) (9). The far UV CD data also show that the addition of salt (100 mM KCl) at pH 2 induces more structure with the spectrum resembling that of the native state. To examine the effect of such structure on τ_R we have carried out experiments at pH 2 in the absence and presence of salt. In the absence of 100 mM KCl the autocorrelation function of D59C/E107C-(TMR)₂ IFABP could not be fit to a simple diffusion model but required an isomerization step with τ_R of 2.5 μsec, which is significantly larger than that in the presence of Gdm·HCl (1.6 μsec in 3 M Gdm·HCl). The value of τ_R in the presence of 100 mM KCl at pH 2 is found to be 8 μsec. Table 1 shows that the value of τ_R is related to the extent of preexisting secondary structure in that the more structured the protein the slower the rate of segmental interaction.

Fig. 4.

Far UV CD of WT IFABP under different conditions. The salt concentration was 100 mM KCl. Experiments at pH 7.3 were carried out in 20 mM phosphate buffer. Low-pH experiments were carried out in 2 mM citrate buffer. All of the experiments were carried out at room temperature.

Table 1. Structural parameters of IFABP under different conditions.

Experimental condition	τR, sec	Radius,† Å	Ellipticity at 216 nm,‡ degree·cm2·dmol-1	Secondary structure,§ %
pH 7.3	35*	17	-7,962	100
3 M Gdm·HCl	1.6	38	-963	12
pH 2	2.5	22	-5,025	63
In the presence of 100 mM KCl at pH 2¶	8		-7,545	95

^*τ_R at pH 7.3 has been reported (8) by using fluorescein-labeled IFABP and represents a different conformational fluctuation in the native state

^†The radius of the protein has been determined from the diffusion coefficient obtained from the FCS data by using Stoke's Einstein approximation (assuming that the protein molecule is spherical). In the presence of 3 M Gdm·HCl, the value for the radius was divided by 0.66 to account for the shape factor (33). Values are taken from Chattopadhyay et al. (9)

^‡Experiments using WT IFABP. Experiments at pH 7.3 were carried out in 20 mM phosphate buffer. Low pH experiments were carried out in 2 mM citrate buffer. All the experiments were carried out at room temperature

^§Percentage of secondary structure has been determined by using CD at 216 nm taking the pH 7.3 value as 100%

^¶At low pH and particularly in the presence of salt, there might be a very fast exponential term in addition to τ_R that could not be characterized

What determines the rates of motion that we have measured? Assuming that the process is controlled by the rate of diffusion of the two rhodamine moieties to form an encounter complex and that the quenching rate within this complex is very fast [in the range of ns (10)] then the encounter rate of the fluoroprobes will depend on the structure and mobility of the polypeptide chain. Although the mechanism of self-quenching is still unknown, the viscosity data indicate that we are measuring the encounter rate rather than the rate of any electronic quenching process.

The rate of formation of internal contacts of small polypeptides has been measured by using various methods, including the quenching of the triplet state of a tryptophan residue by cysteine (11, 12), triplet-triplet energy transfer between donor and acceptor chromophores (13, 14), and fluorescence quenching (10, 15). Krieger et al. (14), for example, using small, highly flexible, synthetic peptides, have measured rates considerably faster than 1 μs even for a peptide as long as 60 residues. These and other measurements also demonstrate that the encounter times depend on the amino acid composition and the solution conditions as well as the number of peptide bonds separating the spectroscopically interacting partners (16).

For larger proteins, we can use a statistical (random) coil to provide a minimal baseline model for a structural interpretation of our results. Assuming that mutual diffusion of polypeptide chain segments in a large protein determines the correlation time for interaction, it is reasonable to cast the problem in terms of the mean first passage time for the interaction of the spectroscopic indicator groups. For a Gaussian chain the correlation time for encounter is given by (17, 18)

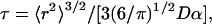[4]

where 〈r²〉, the mean square distance between probes is proportional to the number of residues separating the spectroscopic indicator pair, D is the relative diffusion rate, and α is the contact distance between the indicator groups that allows their spectroscopic interaction. Although none of these parameters is known with certainty, τ should vary as n^3/2 [or n^3/2+ε, where ε is a correction for excluded volume effects (14, 19)]. This prediction is approximately borne out for n > ≈10 (11, 14). The value of α can be approximated as a van der Waals contact distance (14, 20), whereas the value of D is more difficult to assign. Approximating the chain as a free draining polymer in which each of the amino acids has approximately the same diffusion coefficient D₀, then D ≈ 2D₀ (21, 22). Assuming that the diffusion coefficient of an amino acid is D₀ ≈ 5 × 10^-6 cm²·s^-1, α ≈ 4 × 10^-8 cm, and 〈r²〉 ≈ 2.8 × 10^-13 cm² (23), then τ ≈ 200 ns. Although the uncertainties in this calculation render quantitative conclusions tentative, experimental findings on small peptide systems show similar values. For example, if we extrapolate the results of Krieger et al. (14) to a 48-residue-long sequence, we can obtain a time constant of ≈0.12 μsec for the poly(glycine-serine) and ≈0.35 μsec for the polyserine homopolymer peptides in water. Our measured value of 1.6 μs for the fluctuation correlation time suggests that conformational mobility of the unfolded IFABP in 3 M Gdm·HCl is retarded relative to its expected minimum for a freely mobile Gaussian chain.

Earlier studies of intramolecular contact formation in cytochrome c have obtained times for the diffusion-dependent encounter of Met-80 with the heme group attached to His-18 in the range of 10–40 μs in the presence of ≈3 M Gdm·HCl (24, 25). This time would be reduced by (48/62)^1.5 = 0.68 to ≈7–30 μs for closure of a loop comparable in size to that in IFABP. Similar measurements carried out on a small cold shock protein from Thermotoga maritima have given a value of ≈10 μs for the encounter time of a loop of 38 residues in 3 M Gdm·HCl (26). All of these observations report time constants significantly larger than values observed for small peptide systems (typically 100–300 nsec extrapolated to 48 residues) and values expected for a Gaussian chain (200 nsec). From the experiments of Krieger et al. (14), the presence of 3 M Gdm·HCl might be expected to increase the time constant but only by a factor of ≈2. In contrast to the data of Krieger et al., the time constants for IFABP decrease at higher Gdm·HCl concentrations. The longer times observed for IFABP, cytochrome c (25), and the cold shock protein from T. maritima (26) lead us to believe that for a large protein system the chain is stiffer than for a Gaussian random coil polypeptide. The slight discrepancy between our results and the data from cytochrome c may be a consequence of the presence of the bulky heme group, which might interfere with polypeptide chain mobility.

Similarly, the relaxation time for IFABP increases under conditions in which the polypeptide chain would be expected to have more ordered structure (2.5 μs at pH 2 at low salt and 8 μs in the presence of 100 mM KCl). The observed increase in the relaxation time, τ_R, at low pH may reflect a change in the equilibrium between transiently structured and unfolded forms. Transient substructures or molecular domains could briefly form and then dissolve. If these domains prevented rhodamine self-quenching, then the rate of fluorescence fluctuation would depend on the rate of formation and dissolution of the ordered substructures. Alternatively, ordered structures with lifetimes long compared with the measured conformational relaxation time could influence the conformational fluctuation rate of the still mobile portions of the polypeptide chain. Finally, the slowing may arise from a general stiffening of the disordered polypeptide chain without the formation of specifically ordered regions.

How do these results relate to protein folding? The structures that form in the unfolded chain could accelerate or retard protein folding. Preformation in the unfolded state of transiently ordered structures on the folding pathway could accelerate the process by providing a nucleus for folding. On the other hand, structure that deviated from that in the native protein could retard folding by requiring dissolution of the misfolded structure before correct folding could begin.

As summarized by Kubelka et al. (16), and exemplified by the data of Myers and Oas (27), the fastest folding times for selected small proteins are in the range of μs. It is possible that polypeptide chain dynamics in the range of μs will be significant for folding of many proteins, either those characterized as two-state proteins that fold rapidly or those that show more complex folding kinetics, including a fast process usually referred to as the “burst phase” in refolding. A multitude of more or less equivalent faster steps such as the observed conformational fluctuations in the μs range could limit the folding rate. For IFABP there is an initial fast step (>10,000 s^-1) in the folding process (28, 29), which may represent an initial collapse.

The “new view” of protein folding proposed by Dill and coworkers (30–32) suggests that the landscape of an unfolded protein is smooth, i.e., that there are no barriers between multiple conformational forms. The method presented here can examine that question by placing the fluorescent probes either at the same number of residues apart at different regions of the polypeptide chain or by changing the number of residues between the probes. It is, of course, also possible that the type of conformational fluctuations we observe have nothing to do with the rate-limiting steps of folding or that an initial collapse in a specific region does not determine the rate of folding. Future experiments in which conformational fluctuations in different regions of the protein chain are measured as well as studies of IFABP mutants with specifically altered structures will be required to determine the possible contributions of the observed conformational fluctuations to folding the protein.