Weighted win loss approach for analyzing prioritized outcomes

Abstract

To analyze prioritized outcomes, Buyse [1] and Pocock et al. [2] proposed the win loss approach. In this paper, we first study the relationship between the win loss approach and the traditional survival analysis on the time to the first event. We then propose the weighted win loss statistics to improve the efficiency of the un-weighted methods. A closed-form variance estimator of the weighted win loss statistics is derived to facilitate hypothesis testing and study design. We also calculated the contribution index to better interpret the results of the weighted win loss approach. Simulation studies and real data analysis demonstrated the characteristics of the proposed statistics.

1. Introduction

In cardiovascular (CV) trials, the term MACE, i.e. Major Adverse Cardiac Events, is a commonly used endpoint. By definition, MACE is a composite of clinical events and usually includes CV death, myocardial infarction, stroke, coronary revascularization, hospitalization for angina, and etc. The use of composite endpoints will increase event rate and effect size therefore reduce sample size and the duration of study. On the other hand, it is often difficult to interpret the findings if the composite is driven by one or two components or some components are going in the opposite direction of the composite, which may weaken the trial’s ability to reach reliable conclusion.

There are two ways to define and compare composite endpoints. The traditional way, which we call “first combine then compare”, is to first combine the multiple outcomes into a single composite endpoint and then compare the composite between the treatment group and the control group. Recently, Buyse [1] and Pocock et al. [2] proposed another approach, which we call “first compare then combine”, that is to first compare each endpoint between the treatment group and the control group and then combine the results from all the endpoints of interest.

This latter approach was proposed to meet the challenges of analyzing prioritized outcomes. In CV trials, it is common that different outcomes may have different clinical importance, and trialists and patients may have different opinions on the order of importance. This phenomenon has been quantified by a recent survey [3], which concludes that equal weights in a composite clinical endpoint do not accurately reflect the preferences of either patients or trialists. If the components of a composite endpoint have different priorities, the traditional time-to-first-event analysis may not be suitable. Only the first event is used in the time-to-first-event analysis and the subsequent, oftentimes more important, events such as CV death are ignored. The “first compare then combine” approach, or more commonly called the win ratio approach, can account for the event hierarchy in a natural way: the most important endpoint is compared first, if tied, then the next important outcome will be compared. This layered comparison procedure will continue until a winner or loser has been determined or the ultimate tie is resulted. Clearly, the order of comparisons aligns with the pre-specified event priorities.

To implement the win loss approach, subjects from the treatment group and the control group are first paired, then a “winner” or “loser” per pair is determined by comparing the endpoints following the hierarchical rule as above. The win ratio and the win difference (also named “proportion in favor of treatment” by Buyse [1]) comparing the total wins and losses per treatment group can then be computed, with large values (win ratio greater than one or win difference greater than zero) indicating the treatment effect. This approach can be applied to all types of endpoints including continuous, categorical and survival [4], even though it was first named by Pocock et al. [2] when analyzing survival endpoints. It can also be coupled with matched [2] and stratified [5] analyses to reduce heterogeneity in the pairwise comparison.

To facilitate hypothesis testing, Luo et al. [6] established a statistical framework for the win loss approach under survival setting. A closed-form variance estimator for the win loss statistics is obtained through an approximation of U-statistics [6]. Later on, Bebu and Lachin [7] generalized this framework to other settings and derived variance estimator based on large sample distribution of multivariate multi-sample U-statistics.

As indicated by Luo et al. [6], the win ratio will depend on the potential follow-up times in the trial. Thus there may be some limitations when applying it to certain trials or populations. To reduce the impact of censoring, Oakes [8] proposed to use a common time horizon for the calculation of the win ratio statistic.

Despite many developments on the win loss approach, there still appears a need of more transparent comparison between the win loss approach and the traditional time-to-first-event analysis. Other than saying that “we first compare the more important endpoint and then the less important endpoint”, it would be more interesting to delineate how the order of importance plays its role in defining the test statistics and how the change of order results in different types of statistics (i.e. win loss vs first-event). We will present this comparison in Section 2 under the survival data setting, in particular, the semi-competing risks data setting where there are a non-terminal event and a terminal event. This setting is very common in CV trials where for instance CV death is the terminal event and the non-fatal stroke or MI is the non-terminal event. We will examine two opposite scenarios with either the terminal event or the non-terminal event as the prioritized outcome. We will show in Section 2 that, when the terminal event has higher priority, the layered comparison procedure will result in the win loss statistics, otherwise, it will end up with the Gehan statistic derived from the first-event analysis. Therefore, different from the common belief, the first-event analysis in fact emphasizes the non-terminal event instead of considering both events of equal importance. Because the non-terminal event always occurs before the terminal event if both events are observed, this analysis assigns the order of importance according to the time course of event occurrence.

In many studies, the log-rank or weighted log-rank statistics are preferred to the Gehan statistic in first-event analysis. From the comparison between the win loss approach and the first-event analysis, it is natural to weigh the win loss statistics similarly to achieve better efficiency and interpretability. The weighted win ratio statistics are proposed in Section 3. In the sequel, weighting is specific to the time that events occur, not the type of events. To facilitate the use of the weighted win loss statistics, we derive a closed-form variance estimator under the null hypothesis and provide some optimality results for weight selection. In order to improve the interpretability of the win loss composite endpoint, the weighted win loss approach is coupled with the contribution index analysis where the proportion of each component event contributing to the overall win/loss is computed. Thus the driving force of the overall win/loss can be identified. The weighted win loss approach is illustrated and compared with the traditional method through real data examples and simulation studies.

2. Comparison between the win loss approach and the first-event analysis

Let T₁ and T₂ be two random variables denoting the time to the non-terminal event and the time to the terminal event, respectively. These two variables are usually correlated. T₂ may right-censor T₁ but not vice versa. Let Z = 1 denote the treatment group and Z = 0 the control group. In addition, C is the time to censoring, which is assumed to be independent of (T₁, T₂) given Z. For simplicity, we assume that in both groups the distribution of (T₁, T₂) is absolutely continuous, whereas the censoring distribution can have jump points.

Due to censoring, we can only observe Y₁ = T₁ ∧ T₂ ∧ C and Y₂ = T₂ ∧ C and the event indicators δ₁ = I(Y₁ = T₁) and δ₂ = I(Y₂ = T₂). Here and in the sequel a ∧ b = min(a, b) for any real values a and b. The observed data {(Y_1i, Y_2i, δ_1i, δ_2i, Z_i) : i = 1, . . . , n} are the independently identically distributed samples of (Y₁, Y₂, δ₁, δ₂, Z).

For two subjects i and j, the win (i over j) indicators based on the terminal event and the non-terminal event are W_2ij = δ_2jI(Y_2i ≥ Y_2j) and W_1ij = δ_1jI(Y_1i ≥ Y_1j) respectively. Correspondingly, the loss (i against j) indicators are L_2ij = δ_2iI(Y_2j ≥ Y_2i) and L_1ij = δ_1iI(Y_1j ≥ Y_1i). The other scenarios are undecidable therefore we define the tie indicators based on the terminal event and the non-terminal event as Ω_2ij = (1 − W_2ij)(1 − L_2ij) and Ω_1ij = (1 − W_1ij)(1 − L_1ij), respectively.

Because the pairwise comparison based on each event results in three categories (win, loss and tie), the pairwise comparison based on two events has nine possible scenarios (see Table 1). Naturally, a win for subject i can be claimed if the three scenarios W_2ijW_1ij, W_2ijΩ_1ij and Ω_2ijW_1ij occur, which indicate subject i wins on one event and at least ties on the other. Similarly, a loss for subject i is claimed if the scenarios L_2ijL_1ij, L_2ijΩ_1ij and Ω_2ijL_1ij occur, meaning subject i losses on one event and does not win on the other. However, rules are needed to classify the two conflicting scenarios W_2ijL_1ij and L_2ijW_1ij when subject i wins on one event but loses on the other.

Table 1.

The nine possible outcomes of the pairwise comparison between subjects i and j

		Non-terminal
		Win	Tie	Loss
Terminal	Win	W2ijW1ij	W2ijΩ1ij	W2ijL1ij
	Tie	Ω2ijW1ij	Ω2ijΩ1ij	Ω2ijL1ij
	Loss	L2ijW1ij	L2ijΩ1ij	L2ijL1ij

If the terminal event is more important, the scenario W_2ijL_1ij will be considered as a win for subject i and the scenario L_2ijW_1ij will be a loss. The difference of total wins and losses in the treatment group is

$$\begin{array}{l}\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{(W_{2ij}{W}_{1ij}+W_{2ij}{\mathrm{\Omega }}_{1ij}+{\mathrm{\Omega }}_{2ij}{W}_{1ij}+W_{2ij}{L}_{1ij})-(L_{2ij}{L}_{1ij}+L_{2ij}{\mathrm{\Omega }}_{1ij}+{\mathrm{\Omega }}_{2ij}{L}_{1ij}+L_{2ij}{W}_{1ij})\right\}\\ =\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{(W_{2ij}-L_{2ij}+{\mathrm{\Omega }}_{2ij}(W_{1ij}-L_{1ij})\right\},\end{array}$$

which is the win difference statistic [2, 6]. This statistic compares the more important terminal event first (W_2ij − L_2ij), if tied (i.e. Ω_2ij = 1), then proceeds to compare the non-terminal event (W_1ij − L_1ij).

On the contrary, if the non-terminal event ranks higher, scenario W_2ijL_1ij will be classified as a loss for subject i and L_2ijW_1ij will be a win. Thus the difference of total wins and total losses in the treatment group is

$$\begin{array}{l}\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{(W_{2ij}{W}_{1ij}+W_{2ij}{\mathrm{\Omega }}_{1ij}+{\mathrm{\Omega }}_{2ij}{W}_{1ij}+L_{2ij}{W}_{1ij})-(L_{2ij}{L}_{1ij}+L_{2ij}{\mathrm{\Omega }}_{1ij}+{\mathrm{\Omega }}_{2ij}{L}_{1ij}+W_{2ij}{L}_{1ij})\right\}\\ =\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{(W_{1ij}-L_{1ij})+{\mathrm{\Omega }}_{1ij}(W_{2ij}-L_{2ij})\right\}\\ =\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{{\delta }_{j}I(Y_{1i}\ge Y_{1j})-{\delta }_{i}I(Y_{1j}\ge Y_{1i})\right\},\end{array}$$ (1)

which is the Gehan statistic based on the first-event time T₁ ∧ T₂. The equality (1) holds with probability one. This is due to the facts that the first-event indicator δ_i = δ_1i + (1 − δ_1i)δ_2i, and that, when T₂ is continuous, W_2ijΩ_1ij = (1 − δ_1j)δ_2jI(Y_1i ≥ Y_1j) and L_2ijΩ_1ij = (1 − δ_1i)δ_2iI(Y_1j ≥ Y_1i) with probability one. The proof of the latter fact is provided in the Appendix. As compared to the win difference statistic, the Gehan statistic compares the non-terminal event first (W_1ij − L_1ij), if tied (i.e. Ω_1ij = 1), then compares the terminal event (W_2ij − L_2ij).

Apparently, both the win difference statistic and the Gehan statistic bear a layered comparison structure: to decide a winner or loser, the most important event is compared first, if tied, the second important event will be compared. The difference lies in which event has higher priority. Higher priority in the non-terminal event results in the Gehan statistic and higher order in the terminal event leads to the win difference statistic. The flipping positions in placing W_2ijL_1ij and L_2ijW_1ij therefore reflect the fundamental view of the event priorities. The Gehan statistic from the first-event analysis puts more emphasis on the non-terminal event, which is contrary to the common belief that both events are considered equally important. More importantly, we can now delineate the weighting scheme the traditional method entails. This motivates us to explore weighting schemes for the win difference/ratio statistics in next section.

3. Weighted win loss statistics

In practice, weighted log-rank statistics are often preferred to the Gehan statistic because the latter may be less efficient due to equally weighting the wins regardless of when they occurred and heavily depending on the censoring distributions. From equation (1), the weighted log-rank statistics from the first-event analysis can be written as

$$\begin{array}{l}\sum _{i=1}^n\sum _{j=1}^n\frac{Z_i(1-Z_j)}{\stackrel{\sim }{G}(Y_{1i}\wedge Y_{1j})}\left\{{\delta }_{j}I(Y_{1i}\ge Y_{1j})-{\delta }_{i}I(Y_{1j}\ge Y_{1i})\right\}\\ =\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{\frac{W_{1ij}-L_{1ij}}{\stackrel{\sim }{G}(Y_{1i}\wedge Y_{1j})}+\frac{{\mathrm{\Omega }}_{1ij}(W_{2ij}-L_{2ij})}{\stackrel{\sim }{G}(Y_{1i}\wedge Y_{1j})}\right\}\end{array}$$

where G̃(·) is an arbitrary and possibly data-dependent positive function. For example, G̃ = 1 will result in the Gehan statistic, $\stackrel{\sim }{G}(y_1)=R_3(y_1)=n^{-1}{\sum }_{i=1}^{n}I(Y_{1i}\ge y_1)$ will result in the log-rank statistic, and $\stackrel{\sim }{G}(y_1)=R_3(y_1)/{\widehat{S}}_3^{\rho }(y_1)$ with ρ ≥ 0 will result in the G^ρ family of weighted log-rank statistics proposed by Fleming and Harrington [9], where Ŝ₃ is the Kaplan-Meier estimate of the survival function of T₁ ∧ T₂.

It is straightforward to generalize the weighted log-rank statistics to a more general form

$$\sum _{i=1}^n\sum _{j=1}^n{Z}_i(1-Z_j)\left\{\frac{W_{1ij}-L_{1ij}}{{\stackrel{\sim }{G}}_1(Y_{1i}\wedge Y_{1j})}+\frac{{\mathrm{\Omega }}_{1ij}(W_{2ij}-L_{2ij})}{{\stackrel{\sim }{G}}_2(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})}\right\},$$ (2)

where G̃₁(·) and G̃₂(·, ·) are arbitrary positive univariate and bivariate functions respectively. Clearly, the statistic (2) is a weighted version of the Gehan statistic, which compares the non-terminal event first. The use of a bivariate weight function in the second part is because the strength of win or loss may depend on both observed times Y₁ and Y₂.

In view of (2), when the terminal event has higher priority, the win ratio and win difference statistics [2, 6] can be generalized as follows. Suppose we have two weight functions G₂(·) and G₁(·, ·), we can define the total numbers of weighted wins and weighted losses based on the terminal event as

$$W_2(G_2)=\sum _{i=1}^n\sum _{j=1}^n\frac{Z_i(1-Z_j)W_{2ij}}{G_2(Y_{2i}\wedge Y_{2j})},L_2(G_2)=\sum _{i=1}^n\sum _{j=1}^n\frac{Z_i(1-Z_j)L_{2ij}}{G_2(Y_{2i}\wedge Y_{2j})}$$

and the total numbers of weighted wins and weighted losses based on the non-terminal event as

$$W_1(G_1)=\sum _{i=1}^n\sum _{j=1}^n\frac{Z_i(1-Z_j){\mathrm{\Omega }}_{2ij}{W}_{1ij}}{G_1(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})},L_1(G_1)=\sum _{i=1}^n\sum _{j=1}^n\frac{Z_i(1-Z_j){\mathrm{\Omega }}_{2ij}{L}_{1ij}}{G_1(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})}.$$

The weighted win difference is

$$\begin{array}{l}{W}_D(G_1,G_2)=\{W_2(G_2)+W_1(G_1)\}-\{L_2(G_2)+L_1(G_1)\}\\ =\sum _{i=1}^n\sum _{j=1}^n{Z}_j(1-Z_j)\left\{\frac{W_{2ij}-L_{2ij}}{G_2(Y_{2i}\wedge Y_{2j})}+\frac{{\mathrm{\Omega }}_{2ij}(W_{1ij}-L_{1ij})}{G_1(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})}\right\}\end{array}$$

and the weighted win ratio is W_R(G₁, G₂) = {W₂(G₂) + W₁(G₁)}/{L₂(G₂) + L₁(G₁)}. These statistics bear the same idea of the un-weighted ones as they all first compare the terminal event, if tied, non-terminal event is compared. The weighted statistics, however, weight the wins and losses according to when they occur so that for example a win occurring later may be weighted more than a win occurring earlier. To evaluate how much each event will contribute to the final win and loss determination, we calculate the contribution indexes as

$$\frac{CE}{W_2(G_2)+L_2(G_2)+W_1(G_1)+L_1(G_1)}\times 100\%,$$

where CE = W₂(G₂), L₂(G₂), W₁(G₁) or L₁(G₁), corresponding to each win or loss situation.

Now we explore some weighting schemes for these win loss statistics. Let $R_{2k}(y)=n^{-1}{\sum }_{i=1}^{n}I(Y_{2i}\ge y,Z_i=k)$ for k = 0, 1 and R₂(y) = R₂₀(y) + R₂₁(y) with a lower case r being the corresponding expectations, i.e. r₂₀(y) = E{R₂₀(y)}, etc.. If we set the weight function G₂(y) = R₂(y), then it is easy to show that

$$L_2(G_2)-W_2(G_2)=n\sum _{j=1}^n{\delta }_{2j}\left\{Z_j-\frac{R_{21}(Y_{2j})}{R_2(Y_{2j})}\right\},$$

which is the log-rank statistic for the terminal event. For a general weight function G₂,

$$L_2(G_2)-W_2(G_2)=n\sum _{j=1}^n{\delta }_{2j}\frac{R_2(Y_{2j})}{G_2(Y_{2j})}\left\{Z_j-\frac{R_{21}(Y_{2j})}{R_2(Y_{2j})}\right\},$$

which is a weighted log-rank statistic. In addition, if G₂ converges to a deterministic function g₂ > 0, then n⁻²{L₂(G₂) − W₂(G₂)} will converge to

$$\int \frac{r_2(y_2)}{g_2(y_2)}\frac{r_{20}(y_2)r_{21}(y_2)}{r_2(y_2)}\{{\lambda }_{21}(y_2)-{\lambda }_{20}(y_2)\}d{y}_2,$$ (3)

where, for k = 0, 1, λ_2k(·) is the hazard function of T₂ in group k. Therefore, for any given weight function G₂, the weighted difference L₂(G₂) − W₂(G₂) can be used to test the hypothesis

$$H_2^0:{\lambda }_{21}(y_2)={\lambda }_{20}(y_2)\text{for}\text{all}{y}_2>0.$$

For the non-terminal event, suppose the possibly data-dependent bivariate weight function G₁(y₁, y₂) converges to some deterministic function g₁ > 0. Let $R_{1k}(y_1,y_2)=n^{-1}{\sum }_{i=1}^{n}I(Y_{1i}\ge y_1,Y_{2i}\ge y_2,Z_i=k)$ for k = 0, 1 and R₁(y₁, y₂) = R₁₀(y₁, y₂) + R₁₁(y₁, y₂) with a lower case r denoting the corresponding expectations, i.e. r₁₀(y₁, y₂) = E{R₁₀(y₁, y₂)}, etc. We show in the Appendix that n⁻²{L₁(G₁) − W₁(G₁)} converges to

$${\int }_{y_1\le y_2}\frac{r_1(y_1,y_2)}{g_1(y_1,y_2)}\frac{r_{11}(y_1,y_2)r_{10}(y_1,y_2)}{r_1(y_1,y_2)}\{{\lambda }_{11}(y_1\mid y_2)-{\lambda }_{10}(y_1\mid y_2)\}d{y}_1{\mathrm{\Lambda }}_a(d{y}_2),$$ (4)

where, for k = 0, 1, λ_1k(y₁ | y₂) = pr(T₁ = y₁ | T₁ ≥ y₁, T₂ ≥ y₂, Z = k), Λ_ck is the cumulative hazard function for the censoring time in group k with the differential increment

$${\mathrm{\Lambda }}_{ck}(dt)=\{\begin{array}{ll}{\mathrm{\Lambda }}_{ck}(t)-{\mathrm{\Lambda }}_{ck}(t^{-}),\hfill & \text{if}t\text{is}\mathrm{a}\text{jump}\text{point}\text{of}{\mathrm{\Lambda }}_{ck}\hfill \\ {\lambda }_{ck}(t)dt,\hfill & \text{otherwise},\hfill \end{array}$$

and Λ_a(dt) = Λ_c0(dt) + Λ_c1(dt) − Λ_c0(dt) Λ_c1(dt). Here and in the sequel, for any function f, f (t⁻) is the left limit at point t. The limit (4) is reasonable because when G₁ = 1 and both Λ_c1 and Λ_c0 are absolutely continuous, the un-weighted difference does converge to it [6]. Thus, similar to the un-weighted version, the weighted difference L₁(G₁) − W₁(G₁) can be used to test the hypothesis

$$H_1^0:{\lambda }_{11}(y_1\mid y_2)={\lambda }_{10}(y_1\mid y_2)\text{for}\text{all}0<y_1\le y_2.$$

Overall, the weighted win difference and win ratio can be used to test the hypothesis $H_2^0\cap H_1^0$.

4. Properties of the weighted win loss statistics

4.1. Weight selection

To construct weighted log-rank statistics for the terminal event, various weights can be used, for example,

1. fG₂(y) = 1, i.e. Gehan weight;

2. G₂(y) = R₂(y), i.e. log-rank weight.

Several choices of G₁ are apparent:

1. G₁(y₁, y₂) = 1, this is the same as the un-weighted win loss endpoints;

2. G₁(y₁, y₂) = R₁(y₁, y₂), this is similar to the log-rank test for the terminal event;

3. G₁(y₁, y₂) = R₂(y₂), this is essentially giving a log-rank weight as the terminal event;

4. $G_1(y_1,y_2)=R_3(y_1)=n^{-1}{\sum }_{i=1}^{n}I(Y_{1i}\ge y_1)$, this is the log-rank weight for the first event analysis.

In general we may choose G₁ and G₂ to satisfy the following conditions, under which the asymptotic results in next section hold.

Condition 1

G₁ converges to a bounded function g₁ in the sense that sup_0<y1≤y2|G₁(y₁, y₂) − g₁(y₁, y₂)| = o(n^−1/4) almost surely and the difference G₁ − g₁ can be approximated in the sense that ${sup}_{0<y_1\le y_2}\mid G_1(y_1,y_2)-g_1(y_1,y_2)-n^{-1}{\sum }_{k=1}^n{V}_{1k}(y_1,y_2)\mid =o(n^{-1/2})$ almost surely, where V_1k(y₁, y₂) is a bounded random function depending only on the observed data O_k = (Y_1k, Y_2k, δ_1k, δ_2k, Z_k) from the kth subject such that E{V_1k(y₁, y₂)} = 0 for any 0 < y₁ ≤ y₂, k = 1, . . . , n;

Condition 2

G₂ converges to a bounded function g₂ in the sense that sup_y |G₂(y) − g₂(y)| = o(n^−1/4) almost surely and the difference G₂ − g₂ can be approximated in the sense that ${sup}_y\mid G_2(y)-g_2(y)-n^{-1}{\sum }_{k=1}^n{V}_{2k}(y)\mid =o(n^{-1/2})$ almost surely, where V_2k(y) is a bounded random function depending on O_k such that E{V_2k(y)} = 0 for any y, k = 1, . . . , n.

These conditions are clearly satisfied by the above choices of the weight functions. In fact, they are applicable to a wide range of selections. For example, one may choose the weight $G_2(y)=R_2(y)/{\widehat{S}}_2^{\rho }(y)$ which is the Fleming-Harrington family of weights [9], where Ŝ₂ is the Kaplan-Meier estimate of the survival function S₂ for T₂ and ρ = 0 is a fixed constant. In this case, the convergence rate of sup_y |G₂(y) − g₂(y)| will be o(n^−1/2+ε) for any ε > 0, which is o(n^−1/4) when choosing ε ≤ 1/4. The asymptotic approximation of G₂(y) − g₂(y) by $n^{-1}{\sum }_{k=1}^n{V}_{2k}(y)$ follows from the Taylor’s series expansion of ${\widehat{S}}_2^{\rho }(y)$ around the true S₂(y) and the approximation of the Kaplan-Meier estimator.

4.2. Variance estimation

It can be shown that, under $H_0=H_2^0\cap H_1^0$ and Conditions 1 and 2, W_D(G₁, G₂) = W_D(g₁, g₂) + o_p(n^3/2). This indicates that using the estimated weights G₁ and G₂ does not change the asymptotic distribution of W_D(g₁, g₂). A detailed proof can be found in the supporting web materials. We therefore need to find the variance of W_D(g₁, g₂) under H₀.

By definition, for any i, j = 1, . . . , n and k = 1, 2, W_kji = L_kij and Ω_2ij = Ω_2ji, therefore Z_i(1 − Z_j)(W_2ij − L_2ij) + Z_j(1 − Z_i)(W_2ji − L_2ji) = (Z_i − Z_j)(W_2ij − L_2ij) and Z_i(1 − Z_j)Ω_2ij(W_1ij − L_1ij) + Z_j(1 − Z_i)Ω_2ij(W_1ji − L_1ji) = (Z_i − Z_j)Ω_2ji(W_1ij − L_1ij). With these, noting that W_D(g₁, g₂) is a U-statistic, we can use the the exponential inequalities for U-statistics [10, 11] to approximate W_D(g₁, g₂) as

$$n^{-1}{W}_D(g_1,g_2)=\sum _{i=1}^{n}E\left[(Z_i-Z_j)\left\{\frac{W_{2ij}-L_{2ij}}{g_2(Y_{2i}\wedge Y_{2j})}+\frac{{\mathrm{\Omega }}_{2ij}(W_{1ij}-L_{1ij})}{g_1(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})}\right\}|O_i\right]+o(n^{1/2})$$ (5)

almost surely, where O_i = (Y_1i, Y_2i, δ_1i, δ_2i, Z_i), i = 1, . . . , n. A detailed proof can be found in the supporting web materials. The approximation (5) provides an explicit variance estimator when we substitute (g₁, g₂) with its empirical counterpart. In particular, under H₀, n^−3/2W_D(G₁, G₂) converges in distribution to a normal distribution $N(0,{\sigma }_D^2)$, where the variance ${\sigma }_D^2$ can be consistently estimated by ${\widehat{\sigma }}_D^2=n^{-1}{\sum }_{i=1}^n{\{{\sigma }_{2i}(G_2)+{\sigma }_{1i}(G_1)\}}^2$ with

$${\sigma }_{2i}(G_2)=\frac{1}{n}\sum _{j=1}^n\frac{(Z_i-Z_j)(W_{2ij}-L_{2ij})}{G_2(Y_{2i}\wedge Y_{2j})},{\sigma }_{1i}(G_1)=\frac{1}{n}\sum _{j=1}^n\frac{(Z_i-Z_j){\mathrm{\Omega }}_{2ij}(W_{1ij}-L_{1ij})}{G_1(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})}.$$

Furthermore, for the weighted win ratio W_R(G₁, G₂), n^1/2{W_R(G₁, G₂) − 1} converges in distribution to $N(0,{\sigma }_R^2)$, where the variance ${\sigma }_R^2$ can be consistently estimated by

$${\widehat{\sigma }}_R^2={\widehat{\sigma }}_D^2{\{L_2(G_2)/n^2+L_1(G_1)/n^2\}}^{-2}.$$

Therefore, the 100 × (1 − α)% confidence intervals for the win difference and win ratio are, respectively, n⁻²W_D(G₁, G₂) ± q_αn^−1/2σ̂_D and exp{W_R(G₁, G₂) ± q_αn^−1/2σ̂_R/W_R(G₁, G₂)}, where q_α is the 100 × (1 − α/2)-th percentile of the standard normal distribution. A R package “WWR”, available in CRAN, has been developed to facilitate the above calculations.

In the supporting web materials, we also discuss some optimality results to guide the selection of the best weights for different alternative hypotheses. However, because the variance ${\sigma }_D^2$ usually does not yield a simple form and the equation for calculating the optimal weights is very difficult to solve, these results are of less practical value. We will use simulation to evaluate the performance of the weighted win/loss statistics and their variance estimators.

5. Simulation

5.1. Simulation Setup

We evaluated the performance of the proposed weighted win loss statistics via simulation. The simulation scenarios are the same as [6], which cover three different bivariate exponential distributions with the Gumbel-Hougaard copula, the bivariate normal copula and the Marshall-Olkin distribution.

Let λ_Hz = λ_H exp(−β_Hz) be the hazard rate for the non-terminal event hospitalization, where z = 1 if a subject is on the new treatment and z = 0 if on the standard treatment. Similarly, let λ_Dz = λ_D exp(−β_Dz) be the hazard rate for the terminal event death. The first joint distribution of (T_H, T_D) is a bivariate exponential distribution with Gumbel-Hougaard copula

$$\text{pr}(T_H>y_1,T_D>y_2\mid Z=z)=exp\{-{[{({\lambda }_{Hz}{y}_1)}^{\rho }+{({\lambda }_{Dz}{y}_2)}^{\rho }]}^{1/\rho }\},$$

where ρ ≥ 1 is the parameter controlling the correlation between T_H and T_D (Kendall’s concordance τ equals to 1 − 1/ρ). The second distribution is a bivariate exponential distribution with bivariate normal copula

$$\text{pr}(T_H\le y_1,T_D\le y_2\mid Z=z)={\mathrm{\Phi }}_2\{{\mathrm{\Phi }}^{-1}(1-e^{-{\lambda }_{Hz}{y}_1}),{\mathrm{\Phi }}^{-1}(1-e^{-{\lambda }_{Dz}{y}_2});\rho \}$$

where Φ is the distribution function of the standardized univariate normal distribution with Φ⁻¹ being its inverse and Φ₂(u, v; ρ) is the distribution function of the standardized bivariate normal distribution with correlation coefficient ρ. The third distribution is the Marshall-Oklin bivariate distribution

$$\text{pr}(T_H>y_1,T_D>y_2\mid Z=z)=exp\{-{\lambda }_{Hz}{y}_1-{\lambda }_{Dz}{y}_2-\rho max(y_1,y_2)\},$$

where ρ modulates the correlation between T_H and T_D.

Independent of (T_H, T_D) given Z = z, the censoring variable T_C has an exponential distribution with rate λ_Cz = λ_C exp(−β_Cz).

Throughout the simulation, we fixed parameters λ_H = 0.1, λ_D = 0.08, λ_C = 0.09, β_C = 0.1. We then varied β_H, β_D and ρ in each distribution. We simulated a two-arm parallel trial with 300 subjects per treatment group, so the sample size n = 600. The number of replications was 1, 000 for each setting. The Gumbel-Hougaard bivariate exponential distribution was generated using the R package “Gumbel” [12, 13].

The proposed statistics were evaluated in terms of power in detecting treatment effect and controlling Type I error under the null hypothesis. We also compared the proposed approach with the log-rank test based on the terminal event and the first event. In addition, the impact of weights assigned to the terminal and non-terminal events on the performance of the proposed approach was also investigated. The power and Type I error are calculated as proportions of |T_x|/SE(T_x) greater than q_α in the 1,000 simulations, where T_x is the test statistic (win loss, log-rank based on the first event and log-rank based on death) and SE(T_x) is the corresponding estimated standard error and q_α is the 100 × (1 − α/2)-th percentile of the standard normal distribution and α = 0.05.

5.2. Simulation Results

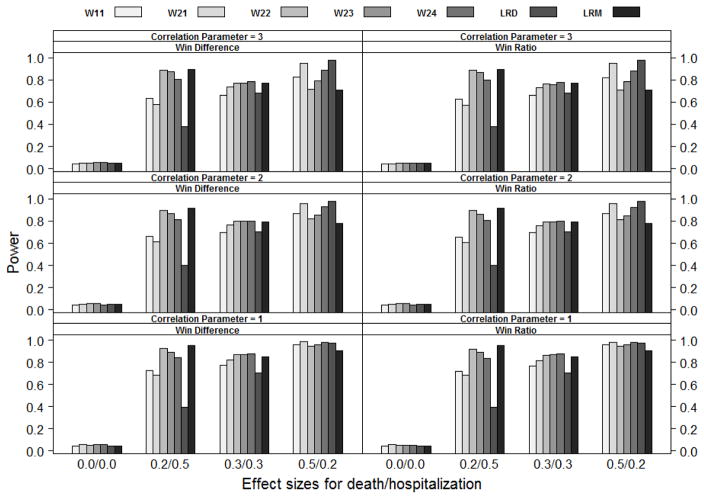
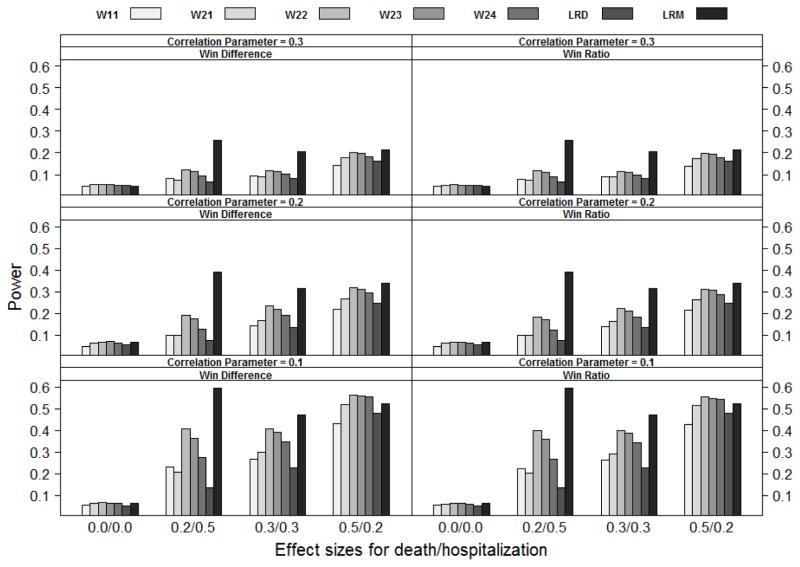
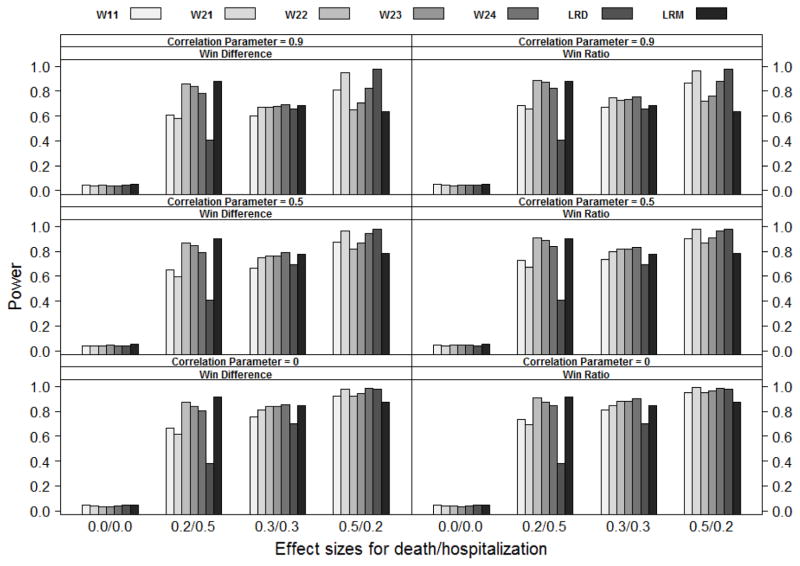
The simulation results are summarized in Figures 1 to 3. As shown in the figures, all the methods listed can control Type I error under different settings. The weighted win loss statistics can improve the efficiency of the un-weighted ones, with the biggest improvements seen when the effect size on hospitalization (β_H) is larger than the effect size on death (β_D).

Figure 1.

Power comparison of statistics W11, W21, W22, W23, W24, LRD and LRM (from left to right) under the Gumbel-Hougaard bivariate exponential distribution (GH), where Wij is the weighted win loss statistics using weight (i) for the terminal event and weight (j) for the non-terminal event in Section 4.1, LRD are the log-rank statistics based on the terminal event and LRM are the log-rank statistics based on the first event. Effect sizes for death/hospitalization are the log hazard ratios β_D and β_H respectively. The correlation parameter is ρ. Not all weighted win loss statistics are reported due to the space limit.

Figure 3.

Power comparison of statistics W11, W21, W22, W23, W24, LRD and LRM (from left to right) under the Marshall-Olkin bivariate exponential distribution (MO), where Wij is the weighted win loss statistics using weight (i) for the terminal event and weight (j) for the non-terminal event in Section 4.1, LRD are the log-rank statistics based on the terminal event and LRM are the log-rank statistics based on the first event. Effect sizes for death/hospitalization are the log hazard ratios β_D and β_H respectively. The correlation parameter is ρ. Not all weighted win loss statistics are reported due to the space limit.

The traditional log-rank test based on the time-to-first-event analysis (LRM) has better power than the other methods when the effect size on hospitalization (β_H ) is larger than that on death (β_D). The traditional log-rank test based on the time-to-death analysis (LRD) has better power when β_D is larger than β_H. In terms of power, the win loss approach falls between and lands closer to the better of the traditional methods. Please note that the win loss statistics, LRM and LRD are actually testing completely different null hypotheses albeit we compare them side-by-side here.

The weighted win-ratio approach with optimal weights (optimal within the listed weights) shows comparable power to the best performed traditional method for all scenarios except when the death effect size is not larger than the hospitalization effect size under Marshall-Oklin distribution, see Figure 3 when (β_D, β_H ) = (0.2, 0.5) and (0.3, 0.3). In these cases, LRM dominates the others. This is understandable as the hazard for T_H ∧ T_D given Z = z is λ_Hz + λ_Dz + ρ under the Marshall-Oklin distribution, which has the largest effect size as compared to other methods.

In summary, the weighted win loss statistics improve the efficiency of the un-weighted ones. The weighted win loss approach with optimal weights can have a power that is comparable to or better than that of the traditional analyses.

6. Applications

6.1. The PEACE study

In the Prevention of Events with Angiotensin Converting Enzyme (ACE) Inhibition (PEACE) Trial [14], the investigators tested whether ACE inhibitor therapy, when added to modern conventional therapy, reduces cardiovascular death (CVD), myocardial infarction (MI), or coronary revascularization in low-risk, stable coronary artery disease (CAD) in patients with normal or mildly reduced left ventricular function. The trial was a double-blind, placebo-controlled study in which 8290 patients were randomly assigned to receive either trandolapril at a target dose of 4mg per day (4158 patients) or matching placebo (4132 patients). The pre-specified primary endpoint is the composite including MI, CVD, CABG (coronary-artery bypass grafti) and PCTA (percutaneous coronary Coronary Angioplasty). The primary efficacy analysis based on the intent-to-treat principal has shown no benefit among patients who were assigned to trandolapril compared to the patients who were assigned to placebo. In our analysis, the CVD is the prioritized outcome and the minimum of non-terminal MI, CABG and PTCA is the secondary outcome. The analysis results are summarized in Tables 2–3. The weighted win ratio approach with the weight assigned to the non-terminal event results in higher contribution from the non-terminal events (increased from 40.7–42.2% to 47.9–48.7%) and yields the smaller p-values in testing the treatment effect compared to other scenarios. The log-rank test based on time to death analysis has the biggest p-value. Assigning a weight on the prioritized outcome CVD alone does increase the power relative to the traditional approaches, although the improvement is nominal. The log-rank test based on time to first event analysis yields a smaller p-value than the log-rank test based on time to death analysis, but the p-value is far larger than the ones from the weighted win ratio approach with the non-terminal event suitably weighted.

Table 2.

Analysis of PEACE Data using the traditional methods

	Tran	Placebo	HR and 95% CI	log-rank	Gehan
No. of patients	4158	4132
No. of patients having either MI, CABG, PTCA or CVD	909	929	0.96(0.88, 1.06)
			p = 0.43*	p = 0.51	p = 0.52
No. of patients having CVD after MI, CABG or PTCA	47	47
No. of CVD	146	152	0.95(0.76, 1.19)
			p = 0.67*	p = 0.66	p = 0.55

^*p-values are based on Wald tests.

Table 3.

Analysis of PEACE Data using the weighted win ratio approach

	W11+	W21	W12	W22
a: CVD on Tran first	487,795 (8.1%)#	602,055.8 (9.6%)	487,795 (3.3%)	602,055.8 (4.0%)
b: CVD on Placebo first	524,382 (8.6%)	633,075.2 (10.1%)	524,382 (3.6%)	633,075.2 (4.2%)
c: MI, CABG or PTCA on Tran first	2,492,674 (41.1%)	2,492,674 (39.6%)	6,551,555 (44.5%)	6,551,555 (43.8%)
d: MI, CABG or PTCA on Placebo first	2,561,374 (42.2%)	2,561,374 (40.7%)	7,167,545 (48.7%)	7,167,545 (47.9%)
Total: a + b + c + d	6,067,225	6,289,179	14,732,277	14,954,231
Win ratio: (b + d)/(a + c)	1.04	1.03	1.09	1.09
Reciprocal of Win ratio	0.96	0.97	0.92	0.92
95% CI	(0.88, 1.06)	(0.88, 1.06)	(0.83, 1.01)	(0.83, 1.01)
p-value *	0.46	0.50	0.083	0.088

⁺Wij is the weighted win loss statistics using weight (i) for the terminal event and weight (j) for the non-terminal event listed in Section 4.1;

^#the percentages in the parentheses are the contribution indexes as, for example, a/(a + b + c + d) × 100%;

^*p-values are from the tests based on the weighted win difference.

6.2. The ATLAS study

ATLAS ACS 2 TIMI 51 was a double-blind, placebo controlled, randomized trial to investigate the effect of Rivaroxaban in preventing cardiovascular outcomes in patients with acute coronary syndrome [15]. For illustration purpose, we reanalyzed the events of MI, Stroke and Death occurred during the first 90 days after randomization among subjects in Rivaroxaban 2.5mg and placebo treatment arms with intention to use Asprin and Thienopyridine at baseline.

Table 4 presents the results using the traditional analyses including Cox proportional hazards model, log-rank test and Gehan test for the time to death and the time to the first occurrence of MI, Stroke or Death. The composite event occurred in 2.77%(132/4765) and 3.57%(170/4760) of Rivaroxaban and placebo subjects respectively. The hazard ratio is 0.78 with 95% confidence interval (0.62, 0.97). The hazard ratio can be interpreted as the hazard of experiencing the composite endpoint for an individual on the Rivaroxaban arm relative to an individual on the placebo arm. Hazard ratio of 0.78 with the upper 95% confidence limit less than 1 demonstrates that Rivaroxaban reduced the risks of experiencing MI, Stroke or Death.

Table 4.

Analysis of ATLAS First 90 Days Data using the traditional methods

	Riva	Placebo	HR and 95% CI	log-rank	Gehan
No. of patients	4765	4760
No. of patients having either MI, Stroke or Death	132	170	0.78(0.62, 0.97)
			p = 0.028*	p = 0.028	p = 0.026
No. of patients having Death after MI or Stroke	7	14
No. of Death	44	64	0.69(0.47, 1.01)
			p = 0.056*	p = 0.055	p = 0.061

^*p-values are based on Wald tests.

Table 5 presents the win ratio results where death is considered of higher priority than MI and Stroke. Every subject in Rivaroxaban arm was compared to every subject in placebo arm, which resulted in a total of 22, 681, 400(= 4765 × 4760) patient pairs. Among such pairs, we reported the weighted wins and losses of Rivaroxaban in preventing Death and MI and Stroke respectively. Please note that, due to a slight change in handling the ties, the reported counts in the first column are slightly different from the ones in [6]. Also, we used the variance under the null here as compared to the variance under the alternative in [6], therefore the resulting confidence intervals are slightly different.

Table 5.

Analysis of ATLAS First 90 Days Data using the win ratio approach

	W11+	W21	W12	W22
a: Death on Riva first	202,868 (14.8%)#	209,585.8 (15.1%)	202,868 (13.8%)	209,585.8 (14.0%)
b: Death on Placebo first	292,132 (21.4%)	304,607.4 (22.0%)	292,132 (19.8%)	304,607.4 (20.4%)
c: MI or Stroke on Riva first	392,876 (28.7%)	392,876 (28.3%)	440,620.4 (29.9%)	440,620.4 (29.5%)
d: MI or Stroke on Placebo first	480,285 (35.1%)	480,285 (34.6%)	536,990.6 (36.5%)	536,990.6 (36.0%)
Total: a + b + c + d	1,368,161	1,387,354	1,472,611	1,491,804
Win ratio: (b + d)/(a + c)	1.30	1.30	1.29	1.29
Reciprocal of Win ratio	0.77	0.77	0.78	0.78
95% CI	(0.63, 0.94)	(0.63, 0.93)	(0.64, 0.95)	(0.63, 0.94)
p-value*	0.025	0.022	0.029	0.026

⁺Wij is the weighted win loss statistics using weight (i) for the terminal event and weight (j) for the non-terminal event listed in Section 4.1;

^#the percentages in the parentheses are the contribution indexes as, for example, a/(a + b + c + d) × 100%;

^*p-values are from the tests based on the weighted win difference.

The four methods resulted in that the (weighted) win ratios of Rivaroxaban are around 1.30, which are calculated as the total number of (weighted) wins divided by the total number of (weighted) losses. In order to compare with the traditional methods, we also calculated the reciprocals of the win ratios and their 95% confidence intervals. The reciprocals of the win ratios with values around 0.78 and the upper 95% confidence limits less than 1 show that Rivaroxaban was effective in delaying the occurrence of MI, Stroke or Death. Both the traditional analyses and the (weighted) win loss analysis provide evidence that Rivaroxaban is efficacious in preventing MI, Stroke or Death within first 90 days of randomization. Even though the four weighted win loss analysis produce roughly the same results, weighting applied to the terminal event appears to marginally improve the overall significance. Please note that we reported the p-values in Table 5 based on the weighted win differences as they are more closely related to the log-rank and Gehan test statistics in the traditional analyses.

7. Discussion

Motivated by delineating the relationship between the win ratio approach and the first-event analysis, this paper proposes the weighted win loss statistics to analyze prioritized outcomes in order to improve efficiency of the un-weighted statistics. We derive a closed-form variance estimator under the null hypothesis to facilitate hypothesis testing and study design. The calculated contribution index further compliments the win loss approach to better interpret the results.

As illustrated in Section 2, the choice between the weighted win ratio approach and the weighted log-rank approach based on the first event depends on the relative importance of the two events. If the power is of concern, according to our simulation, when the effect size on non-terminal event is larger than that on the terminal event, the traditional method based on the first event analysis is preferred, vice versa, the win ratio approach is the choice. However, it is important to note that these two approaches are testing completely different null hypotheses.

Within the weighted win loss statistics, one may want to first suitably weight the terminal event (i.e. for example, if the proportional hazards assumption holds, the log-rank test is preferred). It appears that a weight equal to one is good enough for the non-terminal event. More research is needed along this line.

The weighted win ratio with the discussed weight functions still seems to rely on the censoring distributions. In viewing of (3) and (4), we may use some suitable weights to get rid of the censoring distributions so that the win ratio will only depend on the hazard functions λ_2k(y) and λ_1k(y₁ | y₂), k = 0, 1. However, it may still be hard to interpret such result as the resulting win ratio will be

$$\frac{{\int }_0^{\tau }{\lambda }_{21}(y)dy+{\int }_{y_1\le y_2\le \tau }{\lambda }_{11}(y_1\mid y_2)d{y}_{1}d{y}_2}{{\int }_0^{\tau }{\lambda }_{20}(y)dy+{\int }_{y_1\le y_2\le \tau }{\lambda }_{10}(y_1\mid y_2)d{y}_{1}d{y}_2}.$$

Note that a suitable weight for the non-terminal event involves density estimate of the overall hazard rate of the censoring time C.

Further improvement may be achieved by differentially weighting the nine scenarios in Table 1 according to the strength of wins, because double wins might be weighted more than one win and one tie. The proposed weighting method and its improvement can be applied to other types of endpoints or recurrent events, with careful adaptation. We shall study this in future papers.

Figure 2.

Power comparison of statistics W11, W21, W22, W23, W24, LRD and LRM (from left to right) under the bivariate exponential distribution with bivariate normal copula (BN), where Wij is the weighted win loss statistics using weight (i) for the terminal event and weight (j) for the non-terminal event in Section 4.1, LRD are the log-rank statistics based on the terminal event and LRM are the log-rank statistics based on the first event. Effect sizes for death/hospitalization are the log hazard ratios β_D and β_H respectively. The correlation parameter is ρ. Not all weighted win loss statistics are reported due to the space limit.

Appendix

Proof of (1)

Because 1 = I(Y_1i ≥ Y_1j) + I(Y_1j ≥ Y_1i) − I(Y_1j = Y_1i), the tie indicator for the non-terminal event

$$\begin{array}{l}{\mathrm{\Omega }}_{1ij}=1-W_{1ij}-L_{1ij}+W_{1ij}{L}_{1ij}\\ =(1-{\delta }_{1j})I(Y_{1i}\ge Y_{1j})+(1-{\delta }_{1i})I(Y_{1j}\ge Y_{1i})-(1-{\delta }_{1i}{\delta }_{1j})I(Y_{1j}=Y_{1i}).\end{array}$$

Because T₂ is continuous, the event δ_2iI(Y_2i = x) will have probability zero for any real number x and i = 1, . . . , n. By definition, Y_2i ≥ Y_1i and Y_2i = Y_1i when δ_1i = 0, i = 1, . . . , n. With these facts, notice that 1 − δ_1iδ_1j = (1 − δ_1i)δ_1j + (1 − δ_1j), we have, for i ≠ j,

$$\begin{array}{l}(1-{\delta }_{1j})I(Y_{1i}\ge Y_{1j})W_{2ij}=(1-{\delta }_{1j}){\delta }_{2j}I(Y_{1i}\ge Y_{1j},Y_{2i}\ge Y_{2j})=(1-{\delta }_{1j}){\delta }_{2j}I(Y_{1i}\ge Y_{1j}),\\ (1-{\delta }_{1i})I(Y_{1j}\ge Y_{1i})W_{2ij}=(1-{\delta }_{1i}){\delta }_{2j}I(Y_{2i}\ge Y_{2j}\ge Y_{1j}\ge Y_{1i}=Y_{2i})\le {\delta }_{2j}I(Y_{2j}=Y_{1i}),\\ (1-{\delta }_{1i}){\delta }_{1j}I(Y_{1j}=Y_{1i})W_{2ij}=(1-{\delta }_{1i}){\delta }_{1j}{\delta }_{2j}I(Y_{2i}\ge Y_{2j}\ge Y_{1j}=Y_{1i}=Y_{2i})\le {\delta }_{2j}I(Y_{2j}=Y_{1i}),\\ (1-{\delta }_{1j})I(Y_{1j}=Y_{1i})W_{2ij}=(1-{\delta }_{1j}){\delta }_{2j}I(Y_{2i}\ge Y_{2j}=Y_{1j}=Y_{1i})\le {\delta }_{2j}I(Y_{2j}=Y_{1i}),\end{array}$$

from which we conclude that Ω_1ijW_2ij = (1 − δ_1j)δ_2jI(Y_1i ≥ Y_1j) with probability one. If we write 1 − δ_1iδ_1j = (1 − δ_1j)δ_1i + (1 − δ_1i), a similar technique will show Ω_1ijW_2ij = (1 − δ_1i)δ_2iI(Y_1j ≥ Y_1i) with probability one.

Proof of (4)

If T₂ has an absolutely distribution, then the tie indicator for the terminal event

$${\mathrm{\Omega }}_{2ij}=I({\delta }_{2j}=0,Y_{2i}\ge Y_{2j})+I({\delta }_{2i}=0,Y_{2j}\ge Y_{2i})-(1-{\delta }_{2i})(1-{\delta }_{2j})I(Y_{2i}=Y_{2j}),$$

with which, we can write

$$\begin{array}{l}\frac{Z_i(1-Z_j){\mathrm{\Omega }}_{2ij}{W}_{1ij}}{g_1(Y_{1i}\wedge Y_{1j},Y_{2i}\wedge Y_{2j})}\\ =I(Z_i=1,Z_j=0,{\delta }_{2j}=0,Y_{2i}\ge Y_{2j},{\delta }_{1j}=1,Y_{1i}\ge Y_{1j})/g_1(Y_{1j},Y_{2j})\\ +I(Z_i=1,Z_j=0,{\delta }_{2i}=0,Y_{2j}\ge Y_{2i},{\delta }_{1j}=1,Y_{1i}\ge Y_{1j})/g_1(Y_{1j},Y_{2i})\\ -I(Z_i=1,Z_j=0,{\delta }_{2i}=0,{\delta }_{2j}=0,Y_{2i}=Y_{2j},{\delta }_{1j}=1,Y_{1i}\ge Y_{1j})/g_1(Y_{1j},Y_{2j})\\ =A_1+A_2-A_3,\text{say.}\end{array}$$

We calculate

$$\begin{array}{lll}E{A}_1\hfill & =\hfill & {\int }_{y_1\le y_2}\frac{r_1(y_1,y_2)}{g_1(y_1,y_2)}\frac{r_{11}(y_1,y_2)r_{10}(y_1,y_2)}{r_1(y_1,y_2)}{\lambda }_{10}(y_1\mid y_2)d{y}_1{\mathrm{\Lambda }}_{c0}(d{y}_2),\hfill \\ E{A}_2\hfill & =\hfill & {\int }_{y_1\le y_2}\frac{r_1(y_1,y_2)}{g_1(y_1,y_2)}\frac{r_{11}(y_1,y_2)r_{10}(y_1,y_2)}{r_1(y_1,y_2)}{\lambda }_{10}(y_1\mid y_2)d{y}_1{\mathrm{\Lambda }}_{c1}(d{y}_2),\hfill \\ E{A}_3\hfill & =\hfill & {\int }_{y_1\le y_2}\frac{r_1(y_1,y_2)}{g_1(y_1,y_2)}\frac{r_{11}(y_1,y_2)r_{10}(y_1,y_2)}{r_1(y_1,y_2)}{\lambda }_{10}(y_1\mid y_2)d{y}_1{\mathrm{\Lambda }}_{c0}(d{y}_2){\mathrm{\Lambda }}_{c1}(d{y}_2).\hfill \end{array}$$

Therefore n⁻²W₁(G₁) converges to

$${\int }_{y_1\le y_2}\frac{r_1(y_1,y_2)}{g_1(y_1,y_2)}\frac{r_{11}(y_1,y_2)r_{10}(y_1,y_2)}{r_1(y_1,y_2)}{\lambda }_{10}(y_1\mid y_2)d{y}_1{\mathrm{\Lambda }}_a(d{y}_2),$$

similarly, n⁻²L₁(G₁) converges to

$${\int }_{y_1\le y_2}\frac{r_1(y_1,y_2)}{g_1(y_1,y_2)}\frac{r_{11}(y_1,y_2)r_{10}(y_1,y_2)}{r_1(y_1,y_2)}{\lambda }_{11}(y_1\mid y_2)d{y}_1{\mathrm{\Lambda }}_a(d{y}_2),$$

which completes the proof of (4).