Recognition of the spliceosomal branch site RNA helix on the basis of surface and electrostatic features

Darui Xu; Nancy L Greenbaum; Marcia O Fenley

doi:10.1093/nar/gki249

. 2005 Feb 23;33(4):1154–1161. doi: 10.1093/nar/gki249

Recognition of the spliceosomal branch site RNA helix on the basis of surface and electrostatic features

Darui Xu ¹, Nancy L Greenbaum ^1,^2,^*, Marcia O Fenley ²

PMCID: PMC549433 PMID: 15728744

Abstract

We have investigated electrostatic and surface features of an essential region of the catalytic core of the spliceosome, the eukaryotic precursor messenger (pre-m)RNA splicing apparatus. The nucleophile for the first of two splicing reactions is the 2′-hydroxyl (OH) of the ribose of a specific adenosine within the intron. During assembly of the spliceosome's catalytic core, this adenosine is positioned by pairing with a short region of the U2 small nuclear (sn)RNA to form the pre-mRNA branch site helix. The solution structure of the spliceosomal pre-mRNA branch site [Newby,M.I. and Greenbaum,N.L. (2002) Nature Struct. Biol., 9, 958–965] showed that a phylogenetically conserved pseudouridine (ψ) residue in the segment of U2 snRNA that pairs with the intron induces a markedly different structure compared with that of its unmodified counterpart. In order to achieve a more detailed understanding of the factors that contribute to recognition of the spliceosome's branch site helix and activation of the nucleophile for the first step of pre-mRNA splicing, we have calculated surface areas and electrostatic potentials of ψ-modified and unmodified branch site duplexes. There was no significant difference between the total accessible area or ratio of total polar:nonpolar groups between modified and unmodified duplexes. However, there was substantially greater exposure of nonpolar area of the adenine base, and less exposure of the 2′-OH, in the ψ-modified structure. Electrostatic potentials computed using a hybrid boundary element and finite difference nonlinear Poisson–Boltzmann approach [Boschitsch, A.H. and Fenley, M.O. (2004) J. Comput. Chem., 25, 935–955] revealed a region of exceptionally negative potential in the major groove surrounding the 2′-OH of the branch site adenosine. These surface and electrostatic features may contribute to the overall recognition of the pre-mRNA branch site region by other components of the splicing reaction.

INTRODUCTION

Nucleic acids are highly charged, and their structure–function relationships and molecular recognition events are strongly influenced by electrostatic interactions (1,2). Therefore, the ability to model the electrostatic properties of RNA accurately is particularly critical. The irregular molecular surface resulting from unique structural motifs (3), noncanonical base pairing (4,5), bulged bases and base triples, all of which distort the backbone, creates unique electrostatic potential patterns. The different three-dimensional (3D) RNA structural motifs create more intricate backbone geometries than seen in the more regular RNA and DNA double helical stem regions. Some folds are comparable in complexity to protein structures, and generate spots with intense negativity due to altered backbone charge distribution. Regions of intense negative potential in some structures have been identified as recognition sites for cations (4,6).

Assembly of the precursor messenger (pre-m)RNA splicing machinery, the cellular (or organellar) ribonucleoprotein complex that catalyzes the removal of noncoding regions (introns) from RNA and ligates the flanking coding regions (exons), is an important problem in structural biology. In some cases, such as Group I and Group II introns, the catalytic power resides entirely within the RNA component. By comparison, the spliceosome, the supramolecular splicing apparatus found in the nuclei of eukaryotic cells, utilizes the same chemical mechanism as the Group II intron, yet requires both RNA and protein components for complete function. The five small nuclear (sn)RNA and numerous associated protein components comprising the spliceosome undergo a cycle of assembly and dissociation with the catalysis of each pre-mRNA substrate. The dynamic and highly specific nature of spliceosome activity makes its assembly a particularly fascinating and challenging target of study.

Phylogenetic, mutational and biochemical studies have demonstrated the role of specific and highly conserved RNA interactions in the assembly of the catalytic core of the spliceosome (7). A critical RNA–RNA interaction is formed by pairing of a consensus sequence of the intron with a short region of the U2 snRNA forming a complementary helix of 7 bp with a single unpaired adenosine (called the branch site adenosine). The 2′-OH of this adenosine initiates a nucleophilic attack on the phosphodiester linkage at the 5′ splice site during the first step of splicing.

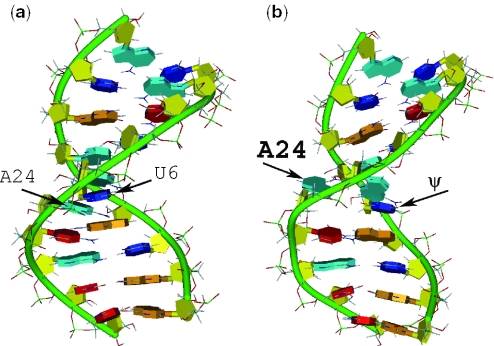
The structure of an RNA duplex representing the U2 snRNA-intron pre-mRNA branch site helix from the yeast Saccharomyces cerevisiae was recently solved by Newby and Greenbaum using solution NMR techniques (8). In their study, the structural role of a phylogenetically conserved pseudouridine (ψ) residue within the segment of U2 snRNA directly opposite the AA dinucleotide at the intron's branch site region was investigated by exploring the architectural features of a ψ-modified duplex (ψBP) and its unmodified counterpart (uBP). Duplex sequences were shown in Figure 1. Pseudouridine, a post-transcriptional modification of the canonical uridine (U) residue, is prevalent in structural RNAs such as tRNA, rRNA and snRNA of all eukaryotes. In particular, ψ residues in certain conserved locations in U2 snRNA, including the branch site pairing region, have been found to be important for spliceosome assembly and function (9–11). Structural models reveal that the conserved ψ induces a dramatically different structure from that seen in its unmodified counterpart (8). The structure of uBP adopts a continuous A-type helical RNA geometry, with the branch site adenosine stacked in the helix. ψBP, on the other hand, features a pronounced kink in the backbone of the intron part in the branch site region, resulting in the extrusion of the branch site adenosine from the helix (Figure 2). In contrast with the 2′-OH of the ribose in A-type RNA helical structures, the 2′-OH of this adenosine, the nucleophile in the first cleavage step of splicing, is oriented toward the major groove. As strong evidence that this structural change correlates with activity, Valadkhan and Manley (12) found that the presence of this pseudouridine greatly enhances the splicing reaction by protein-free U2/U6 complex.

Sequences of the uBP (a) and ψBP (b) used in the calculations. The sequences and numbering are the same as those in Ref. (2). In both cases, the top strand corresponds to the U2 snRNA fragment, and the bottom strand is that of the intron.

A schematic view of uBP (a) and ψBP (b) from structures solved by Newby and Greenbaum (8; uBP PDB:1LMV; ψBP PDB: 1LPW. Model #1 from both duplexes was used). RNA helices were rendered using the DINO (http://www.dino3d.org) visualization program. The color schemes are as follows: the backbone is green; the sugar is yellow; base A is cyan; base C is red; base G is orange and base U and ψ are blue. Note that uBP adopts a typical A-helical pattern, whereas ψBP is characterized by an extrahelical branch site adenosine.

In an attempt to achieve a detailed understanding of the interactions that stabilize the unusual structure of the branch site helix, and the features by which the 2′-OH of the branch site adenosine may be recognized by other RNA molecules, proteins or metal ions in the process of spliceosome assembly and activity, we calculated surface accessible areas and the surface and site electrostatic potentials of the ψ-modified branch helix and its unmodified counterpart. This information will help provide insight into the structure–function relationships in pre-mRNA splicing. Our calculations showed that in addition to the structural features associated with the ψBP, marked differences were found for the exposure of the polar and nonpolar surface areas around the branch site region and there is a region of significant negative electrostatic potential in the major groove, localized around the 2′-OH of the branch site adenosine. These features may contribute to the recognition of the branch site adenosine by other components and the activity in the first step of splicing.

METHODS

Structures

The branch site structural models used in this paper were the solution NMR structures solved by Newby and Greenbaum (8). Nine lowest energy structures for ψBP and ten lowest energy structures for uBP have been deposited in the Protein Data Bank (13) (PDB accession codes 1LMV and 1LPW for uBP and ψBP, respectively). The calculations in this paper were applied to all models of both structures. Here, we presented the results from model one of both structures. However, there were no significant differences among the results from other models. The NMR structures were not subjected to energy minimization prior to the calculations.

Calculation of solvent accessible surface areas

The overall polar and nonpolar solvent accessible surface area (SASA) of each RNA helix was modeled with NACCESS (14) and MSMS (15) programs. For the van der Waals radii of each atom, we used both the values of Alden and Kim (16) and the default values of the NACCESS program. The solvent probe radius was set to 1.4 Å and the triangulation density was 1.4 vertex/Å² in the MSMS program. The slice size parameter that controls the level of accuracy in NACCESS was taken as 0.05 Å. Essentially, identical areas were obtained with parameters that provide a finer resolution surface mesh. The polar atoms were oxygen and nitrogen, and the nonpolar atoms were carbon and phosphorus. Hydrogen atoms were treated implicitly during the calculation by increasing the heteroatom van der Waals radius by a small amount. The solvent accessible surfaces provide information about the degree of solvent exposure of polar/nonpolar and charged atoms or residues of nucleic acids or other biomolecules.

Solutions to the nonlinear Poisson–Boltzmann equation

Because of the high charge density of nucleic acids generated by the sugar–phosphate backbone, and the irregular surface of RNA in particular, it is necessary to solve the complete nonlinear Poisson–Boltzmann (NLPB) equation (17). Numerical solutions to the NLPB equation used here were obtained with a hybrid boundary element (BE) and finite difference (FD) PBE algorithm (25). The NLPB equation for a biopolyelectrolyte immersed in a 1:1 salt solution, given below, was solved numerically subject to the appropriate boundary conditions (e.g. continuity of the electrostatic potential at the dielectric interface and zero potential when infinitely apart from the molecule):

\nabla \cdot [ε (\overset{\to︀}{R}) \nabla Φ (\overset{\to︀}{R})] - κ^{2} (\overset{\to︀}{R}) sinh (Φ (\overset{\to︀}{R})) + \frac{4 π e}{k_{B} T} ρ^{f} (\overset{\to︀}{R}) = 0,

where ε is the dielectric constant, e represents the protonic charge, k_B denotes the Boltzmann constant and T is the absolute temperature of the solution, ∇ is the divergence operator, Φ is the electrostatic potential, ρ^f is the solute charge density and κ is the Debye–Hückel screening parameter. The quantities ε, Φ, ρ^f and κ are all functions of the position vector $\overset{\to︀}{R}$ . It is through the Debye–Hückel parameter that the effects of mobile ions on the electrostatic potential are captured. The second term in Equation (1) represents the charge density of the mobile ions in solution, which are treated in a ‘mean field’ way as a continuous Boltzmann distribution. The dielectric interface that separates the regions of different polarizability was here represented by the solvent excluded molecular surface. The ionic solution, which contains 0.1 M added NaCl [close to the NMR experimental condition (19)], was treated as the region of high dielectric, here taken as 80 (25°C), and the solute interior had a low dielectric constant of 2 in order to account for electronic polarization (20). The magnitude of the electrostatic potential is sensitive to the interior dielectric constant. The assignment of the interior dielectric constant of biomolecules is controversial (21). However, the assumed interior dielectric constant value does not affect the trend of the conclusions of this work. The atomic partial charge and radii were taken from the AMBER94 (22) and the Discover (http://pylelab.org/) force fields. Formal RNA charges, with a −0.5e charge assigned to each nonbridging phosphate oxygen atom, were also employed to examine sequence-independent electrostatic features. When formal RNA charges were employed, the atomic radii were assigned based on the AMBER94 parameter set. The solvent-excluded molecular surface was panelized into at least 50 000 triangular elements using the MSMS program and a grid size of 129³ was employed in the FD-based calculation of the nonlinear correction term. The total extent of the 3D grid was at least two times the largest dimension of the molecule in order to minimize outer boundary errors. Comparative calculations with and without the ion exclusion region resulted in similar trends. Thus, the ion exclusion region was not included in the PBE calculations.

Visualization

The molecular surfaces, which were color-coded according to electrostatic potential derived from the nonlinear PBE, were viewed using the virtual reality modeling language (VRML) (23). The 3D structures of the RNA helices were displayed using the ViewerPro program (Accelrys, Inc.) and saved in the VRML file format. The 3D structure was then incorporated into the electrostatic potential maps for easy identification. In order to facilitate visual inspection, color mapping of the electrostatic potential was finely scaled as follows: green (most positive), followed by blue, white (neutral), red and yellow (most negative).

Calculations of site electrostatic potentials

The electrostatic potentials surrounding specific atom sites were calculated by taking the average electrostatic potential of sampled grid points outside the molecule around a particular atom. The grid points were sampled by generating two layers of spheres 0.5 and 1.0 Å away from the van der Waals surface of the atom. The electrostatic potentials of the grid points were obtained by NLPB calculations using the hybrid PBE approach with Amber94 atomic radii and charge parameters.

RESULTS

Surface areas of the duplexes

We calculated the surface accessible area of the two branch site RNA structural models. The SASA determined by NACCESS, which is based on the method of Lee and Richards (24) with the atomic radii published by Alden and Kim (16), is shown in Table 1. Repetition of the calculations with the MSMS algorithm and with default NACCESS atomic radii indicated that the results did not vary significantly with the choice of surface method or atomic radii.

Table 1.

Surface area calculations of the branch site RNA helices are as described in the Methods

	Total SASA (Å²)	Polar/nonpolar SASA	Nonpolar SASA of branch site adenosine (Å²)	SASA of 2′-OH branch site adenosine (Å²)
ψψBP	3770 ± 168	1.95	110 ± 30	0.4 ± 1.8
uBP	3670 ± 39	1.9	56 ± 6	18 ± 3.9

Open in a new tab

The calculations are averaged over the ensembles of all NMR models for both modified and unmodified RNA structures. Values were calculated by NACCESS using the radii published by Alden and Kim (16).

The total SASA for uBP is 3670 ± 39 Å² and that for ψBP is 3770 ± 168 Å². The two duplexes exhibit, at most, a 2% difference in the total solvent accessible area (well within SD). The ratio of polar/nonpolar exposure level is also similar for the two duplexes. Because the stable form of any polyanionic system such as RNA in solution may be the one with maximal polar exposure and minimal nonpolar part exposure, this result is in accord with the thermal denaturation experiment results (19), which showed that ψBP has only a slightly smaller free energy than uBP (−0.7 kcal/mol).

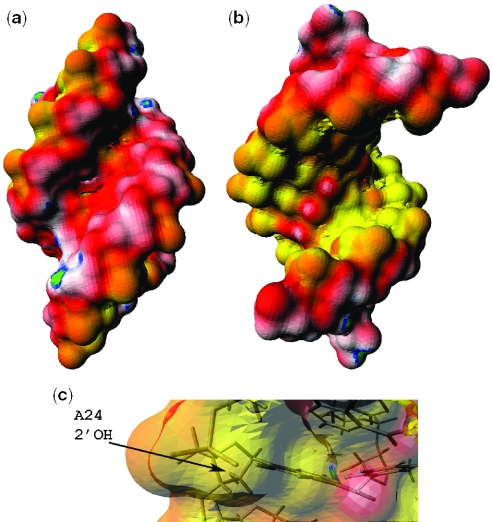
Our data revealed significant differences in the vicinity of the branch site base, however. The nonpolar SASA of the branch site adenosine in ψBP is 110 ± 30 Å², a much greater value than that for the same base in the unmodified helix (56 ± 6 Å²). Since adenine has the most nonpolar atoms among all bases, this is consistent with the structural model of the branch site adenine of ψBP extruding into the solvent instead of stacking in the helix, as is the analogous adenine of uBP. We speculate that the cost of nonpolar exposure is compensated by the formation of the base triple and an additional water-mediated hydrogen bond formed by ψBP in the major groove.

The most surprising result was the finding that the SASA of the 2′-OH of ψBP's branch site adenosine is much smaller than that of its counterpart in uBP or any other 2′-OH in either duplex (0.4 ± 1.8 Å² versus 18 ± 3.9 Å²). These data imply that the 2′-OH of ψBP branch site adenosine does not protrude into solvent in the major groove, but is level with the lower dielectric environment of the groove itself.

Surface electrostatic potentials of the RNA branch site

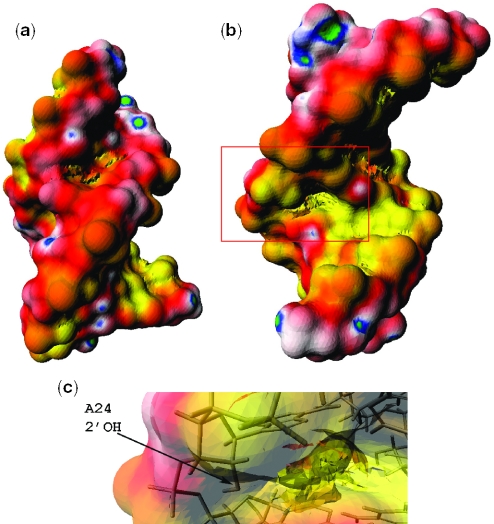
The surface electrostatic potentials of uBP and ψBP were calculated using the hybrid PBE approach with the atomic partial charges and radii taken from the AMBER94 force field, except for the atomic partial charges for ψ, which were obtained by quantum chemical calculations using the Gaussian98 program (http://www.gaussian.com) (Prof. Maria Nagan, Truman State University, unpublished results). The electrostatic potential mapped on the surface of the unmodified branch site has similar features to that of a typical A-form RNA helix. As expected, the backbones have mostly negative electrostatic potential as a result of the negatively charged phosphate groups, although the grooves display some patches of positive potential, reflecting the presence of electropositive base atoms (Figure 3a–c). The overall surface potential of the major groove is considerably more negative than that of the minor groove, typical of the A-form RNA helix. As shown in Figure 3a and b, and reported in prior studies (6,25), this feature of A-form helices is independent of base sequence (26). Presence of the additional adenosine stacked in the helix does not impact the electrostatic surface.

Surface electrostatic potential maps of uBP. The atomic charge and radii are those from the AMBER94 molecular mechanical force field. The color scheme used in this map is as follows: yellow is the most negative (−3 kcal/mol/e) and green is the most positive (1 kcal/mol/e). White is neutral. Red and blue represent negative and positive potentials, respectively. The calculation was performed using the hybrid nonlinear PBE approach as described in the Methods. (a) The surface electrostatic potential map of the minor groove, (b) the surface electrostatic potential map of the major groove and (c) the surface electrostatic potential map of the branch site region combined with a ball-and-stick model of the molecule.

The results of the electrostatic surface potential calculation of the ψ-modified helix highlight an intriguing difference between the two duplexes that is likely to play an important role in recognition. The backbone region and the grooves of the regions several base pairs away from the branch site have similar features to uBP, but there is a distinct and exceptionally negative region in the major groove (Figure 4b and c) corresponding to the region of the branch site adenosine, the 2′-OH of which is the nucleophile in the cleavage reaction at the pre-mRNA 5′ splice site. Since the electrostatic properties calculated with continuum PBE models are sensitive to the atomic radii and partial charges used, we repeated the electrostatic potential calculations with the atomic charge and radii for every atom including the pseudouridine taken from the Discover force field parameter set. A comparison of the electrostatic potentials generated using each force field revealed no visible difference between the two sets of data (data not shown). The electrostatic potential in the minor groove was not significantly different from that of the minor groove of uBP (Figures 3a and 4a).

Surface electrostatic potential maps of ψBP. The atomic charge and radii are those from the AMBER94 molecular mechanical force field. The color scheme used in this map is the same as in Figure 3. The calculation was performed using the hybrid nonlinear PBE approach as described in the Methods. (a) The surface electrostatic potential map of the minor groove, (b) the surface electrostatic potential map of the major groove and (c) the surface electrostatic potential map of the branch site region combined with a ball-and-stick structure of the molecule. The yellow region within the major groove of ψBP suggests a region of significant electronegative potential surrounding the 2′-OH of the branch site nucleophile.

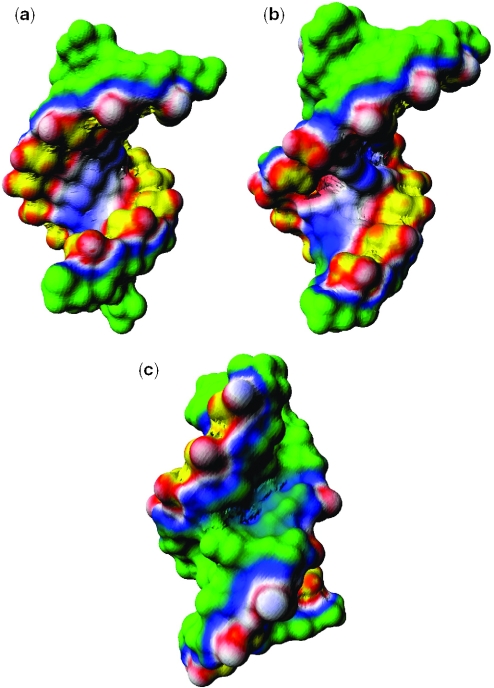
In order to determine if the negative potential region in ψBP is sequence dependent, we performed calculations in which a −0.5e charge placed on each nonbridging phosphate oxygen atom was considered (i.e. no partial charges on the nucleotides). As shown in Figure 5, the backbone charges are responsible for the overall enhanced negativity of the electrostatic potential in the major groove as opposed to the minor groove in both uBP and ψBP. Thus, this electrostatic trademark, which is characteristic of both A-DNA and A-RNA, is largely due to the sugar–phosphate backbone charges. Furthermore, the negative potential region in the major groove is still present in the ψBP, albeit less pronounced than when all the partial charges of the RNA were included. This finding supports a model in which both the kinked backbone and the bases are each partially responsible for creating the exceptionally negative electrostatic potential region. However, according to more quantitative results discussed below, the backbone still makes the largest contribution to the total potential in this pocket of enhanced negative electrostatic potential.

Surface electrostatic potential of (a) uBP, (b) ψBP major groove (c) ψBP minor groove in which only a −0.5e charge was placed on each nonbridging phosphate oxygen. The atomic radii were taken from the AMBER94 force field. Here, the electrostatic potential is negative over the whole molecular surface with yellow (−3 kcal/mol/e), red, white, blue and green (−1 kcal/mol/e) going from most negative to least negative potential. The calculation was carried out using the hybrid PBE approach as described in the Methods.

Electrostatic potentials at 2′-OH of nonterminal residues

Although the images of the surface potential of the ψBP RNA duplex indicate some interesting electrostatic features associated with its major groove, such results are at most qualitative. Thus, to quantify the electrostatic potential around the branch site adenosine, we calculated the electrostatic potentials at the 2′-OH of each nonterminal residue. The results for uBP are shown in Table 2 and those for ψBP are shown in Table 3. For uBP, the electrostatic potential at the 2′-OH of each nonterminal residue is approximately −1.3 kcal/mol/e. The electrostatic potential at the 2′-OH of the branch site adenosine is similar to that of the other 2′-OH. This is consistent with the surface electrostatic potential depiction.

Table 2.

Electrostatic potentials at 2′-OH of each nonterminal residue of the unmodified branch helix

Atom	Electrostatic potential (kcal/mol/e)	Distance (Å)	SASA (Å²)
G3	−0.92 ± 0.36	18.62	15.49
U4	−0.92 ± 0.69	17.95	24.83
G5	−1.42 ± 0.28	14.84	21.88
U6	−1.28 ± 0.42	10.59	26.35
A7	−1.69 ± 0.29	8.38	17.36
G8	−1.47 ± 0.55	10.90	22.62
U9	−1.04 ± 0.42	15.97	23.49
A20	−1.19 ± 0.44	21.70	19.04
C21	−1.15 ± 0.49	17.52	22.48
U22	−1.45 ± 0.52	11.40	14.72
A23	−1.5 ± 0.27	5.83	17.04
A24^*	−1.45 ± 0.24	0.00	16.98
C25	−1.28 ± 0.37	5.98	17.82
A26	−0.92 ± 0.76	11.70	21.52
C27	−1.19 ± 0.4	16.54	18.82

Open in a new tab

The distance is from the specific atom to the 2′-OH of the branch site adenosine (denoted by ^*). The surface is the solvent accessible surface of the specific atom calculated by the NACCESS program.

Table 3.

Electrostatic potentials at 2′-OH of each nonterminal residue of the modified branch helix

Atom	Electrostatic potential (kcal/mol/e)	Distance (Å)	SASA (Å²)
G3	−1.3 ± 0.31	16.58	16.8
U4	−1.42 ± 0.36	15.51	16.1
G5	−1.29 ± 0.45	14.49	25.77
U6	−1.72 ± 0.73	12.17	15.32
A7	−2.69 ± 0.48	9.45	10.61
G8	−2.27 ± 0.66	9.98	24.36
U9	−1.11 ± 0.5	15.49	20.54
A20	−0.84 ± 0.62	22.74	22.48
C21	−0.92 ± 0.5	17.46	19.1
U22	−3.52 ± 0.42	11.58	5.32
A23	−2.85 ± 0.58	5.89	8.67
A24^**	−3.7 ± 0.4	0.00	0.65
C25	−1.59 ± 0.37	5.73	27.35
A26	−1.45 ± 0.3	10.17	18.43
C27	−1.11 ± 0.65	14.29	20.74

Open in a new tab

The results for the ψ-modified helix show markedly different values for the branch site adenosine and neighboring residues than for the rest of the duplex. The 2′-OH of the branch site adenosine has a very strong negative electrostatic potential (−3.7 kcal/mol/e) compared with that of the unmodified branch site adenosine, which may steer cationic species into this potential binding pocket. Because the branch site adenosine's 2′-OH of ψBP is located in the widened major groove, one might expect a lesser negative electrostatic potential due to the sugar–phosphate backbone, as compared with the narrower major groove of uBP (5). However, based only on the backbone charges, we observed the opposite trend, with a potential of −3.9 and −0.84 kcal/mol/e at the 2′-OH of the branch site adenosine in ψBP and uBP, respectively. Thus, the localized kink and overall distortion of the backbone in the modified RNA helix has a profound influence on the electrostatic potential at this local site and surroundings.

Interestingly, because the 2′-OH of the branch site adenosine of ψBP is embedded in the environment of the molecule (as opposed to exposure to solvent only), the electrostatic potential of the 2′-OH was less negative when calculated with increasing interior dielectric constant, whereas the opposite was found for the solvent-exposed 2′-OH in uBP. The electrostatic potential at specific atom sites became less negative as distance from the branch site adenosine increased.

DISCUSSION

The development of improved nonlinear PB solvers (25,27–29) and molecular visualization algorithms (30,31) now allows the routine calculation and display of contour and surface electrostatic potential maps of highly charged biomolecules such as nucleic acids at the qualitative level. The early quantum mechanics and vacuum-based Coulombic potential profiles (32) mapped on the surface and the modern color-coded PB-based surface potential images of nucleic acids (6,25) have revealed some insightful and unique sequence- and structure-dependent electrostatic patterns that have helped understand electrostatic-mediated recognition principles employed during binding processes of cationic drugs and proteins to a variety of nucleic acid structures (33,34). The classical work of Pullman and co-workers (32,35) was the first to show the concerted role of electrostatics and solvent accessibilities in governing the recognition and binding events in nucleic acids.

The regions or pockets of intense negative potential in RNA structures, such as found in loops or major grooves, are potential binding or recognition sites for cationic species such as metal ions (e.g. Mg²⁺), cationic drugs, and amino acid side chains. Such regions have been identified using surface electrostatic potential calculations or Brownian dynamics simulations, both of which are based on the nonlinear PBE (3,36–38). In fact, many crystallographically observed metal ions are found to be located in regions of high negative potential in a variety of RNA structures such as the P4–P6 domain from the Tetrahymena Group I intron, the loop E fragment of 5s rRNA, the hammerhead ribozyme, tRNA, Escherichia coli 58 nt 23S rRNA and the P5b stem loop of the Group I intron (3,6,37,38).

The very high negative charge density of nucleic acids requires the complete nonlinear form of the PBE for a rigorous calculation of electrostatic potentials. However, the full PBE does not possess an analytical solution for anything beyond very simple symmetrical geometries such as infinite planar and cylinder cases in certain limits. In the 1980s, several numerical approaches were developed in order to solve the PBE for any arbitrary 3D shape and charge distribution (39–41). The algorithms most widely used (DelPhi, UHBD) fall in the category of finite difference solutions to the PBE (29,42). However, these and newer nonlinear PBE implementations (43) still suffer two main deficiencies: convergence issues and inadequate treatment of outer boundary conditions, especially in the limits of low salt and high charge. This is a big limitation since many macromolecular assemblies such as nucleosomes and ribosomes are highly charged.

Boschitsch and Fenley (25) recently developed a novel hybrid PBE approach that employs both the boundary element and finite difference methods. It combines the intrinsic advantages of a BE and finite difference scheme to solve the nonlinear PBE for complicated molecular geometries by decomposing the electrostatic potential into a linear component satisfying the linear PBE solved by a fast multipole-accelerated BEM (18) and a correction term to account for the nonlinear effects. One of the main advantages of the hybrid PBE approach lies in its robust and superior treatment of outer boundary conditions and solution convergence, with the latter being accelerated by multigrid techniques [for a more detailed discussion of this novel PBE approach, see (25)]. The hybrid BE/FD PBE approach predicts surface and site (at specified locations) electrostatic potentials and electrostatic solvation free energies for realistic nucleic acid structures with high accuracy and efficiency.

The calculation of solvent accessible surface area, first introduced by Lee and Richards (24) to quantify the molecular surface, provides information about the interaction of a biomolecule's functional groups with other solute and solvent molecules. Measurement of the curvature, surface area and precise geometrical shape of a molecular surface are routinely used by the structural biology and biophysics communities when predicting intra- and intermolecular interaction and associated conformational change.

Here, we compared results of solvent accessible surface areas and nonlinear PBE calculations of the ψ-modified and unmodified U2 snRNA-intron branch site sequence in order to evaluate the molecular basis of stability and recognition. Although the ψ-modified RNA branch helix and its unmodified counterpart have similar global values for total surface area and polar/nonpolar exposure, the two helices have marked differences in the polar/nonpolar exposure in the region of the branch site. We also found that ψBP exhibits a region of profound electrostatic negativity in the more accessible widened major groove in the vicinity of the 2′-OH of the branch site adenosine. This finding indicates that the presence of ψ not only affects the structure of this biochemically important region of the spliceosome, but also impacts on other properties of the molecule not readily seen from the structure.

We propose that this heterogeneity contributes to molecular recognition of the branch site adenosine by other components of the spliceosome in order to facilitate splicing activity. Biochemical studies in which individual functional groups of the branch site adenosine were modified imply an extrahelical orientation of the adenine base and recognition of its topology by other components of splicing (44); this conclusion was supported by NMR structural studies (8,19). Apparently, the energetic cost of exposure of the nonpolar groups is balanced by formation of a base triple including the branch site adenine base (8) and by a water-mediated hydrogen bond involving ψNH1 (45).

Unusual electronegative pockets sometimes correspond to metal ion binding sites (6). Unusual electrostatic negativity surrounding the branch site adenosine in the ψ-modified duplex, largely due to the distortions created in sugar–phosphate backbone analogous to those observed in RNA bulges and K-turn motifs, suggests it might represent a cation binding site. NMR studies by Newby and Greenbaum found no evidence of a site-bound magnesium ion in the U2 snRNA–intron duplex (19). However, because the duplex they studied is only one component of the catalytic core, it is possible that this region may attract a hydrated metal ion or other cation in the context of other components. It may also help to minimize electrostatic repulsion between the components of the spliceosome during the first step splicing interactions. In addition to topological features associated with ψ-dependent structure, there are also marked electrostatic features that may contribute to recognition and activity.

In summary, we have calculated surface areas and electrostatic potentials of the ψ-modified and unmodified branch site RNA helices. We have found unusually small 2′-OH exposure and have identified a region of exceptionally negative electrostatic potential surrounding the 2′-OH of the branch site adenosine in the major groove of the ψ-modified duplex. In addition to structural features associated with the presence of this highly conserved ψ residue, surface area and electrostatic features may contribute prominently to the recognition, and perhaps indirectly to the activation, of the branch site nucleophile of the spliceosome's catalytic core.

Acknowledgments

This work was supported by NSF grant CHE-0137961 (to M.O.F.) and NIH grant R01 GM54008 (to N.L.G.). D.X. is a recipient of AHA prodoctoral fellowship (041511DB). We thank Dr Maria Nagan for providing the charges for pseudouridine. Funding to pay the Open Access publication charges for this article was provided by NSF grant CHE-0137961 (to M.O.F.) and NIH grant R01 GM54008 (to N.L.G.).

REFERENCES

1.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Quart. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
2.Record M.T.J., Anderson C.F., Lohman T.M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening and ion effects on water activity. Quart. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
3.Hermann T., Westhof E. Exploration of metal ion binding sites in RNA folds by Brownian-dynamics simulations. Structure. 1998;6:1303–1314. doi: 10.1016/s0969-2126(98)00130-0. [DOI] [PubMed] [Google Scholar]
4.Westhof E., Fritsch V. RNA folding: beyond Watson–Crick pairs. Structure Fold. Des. 2000;8:R55–R65. doi: 10.1016/s0969-2126(00)00112-x. [DOI] [PubMed] [Google Scholar]
5.Leontis N.B., Stombaugh J., Westhof E. The non-Watson–Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002;30:3497–3531. doi: 10.1093/nar/gkf481. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Chin K., Sharp K.A., Honig B., Pyle A.M. Calculating the electrostatic properties of RNA provides new insights into molecular interactions and function. Nature Struct. Biol. 1999;6:1055–1061. doi: 10.1038/14940. [DOI] [PubMed] [Google Scholar]
7.Moore M., Query C., Sharp P. Splicing of precursor to mRNA by the spliceosome. In: Gesteland R.F., Atkins J.F., editors. The RNA World. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1993. pp. 303–357. [Google Scholar]
8.Newby M.I., Greenbaum N.L. Sculpting the spliceosomal branch site recognition motif by a conserved pseudouridine. Nature Struct. Biol. 2002;9:958–965. doi: 10.1038/nsb873. [DOI] [PubMed] [Google Scholar]
9.Reddy R., Busch H. Small nuclear RNAs: RNA sequences, structure and modifications. In: Birnstiel M.L., editor. Structure and Function of Major and Minor Small Nuclear Ribonucleoprotein Particles. Berlin: Springer-Verlag Press; 1988. pp. 1–37. [Google Scholar]
10.Gu J., Patton J., Shimba S., Reddy R. Location of modified nucleotides in Schizosaccharomyces pombe spliceosomal small nuclear RNAs: modified nucleotides are clustered in functionally important regions. RNA. 1996;2:909–918. [PMC free article] [PubMed] [Google Scholar]
11.Patton J., Jacobsen M., Pederson T. Pseudouridine formation in small nuclear RNA. Proc. Natl Acad. Sci. USA. 1994;91:3324–3328. doi: 10.1073/pnas.91.8.3324. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Valadkhan S., Manley J.L. Characterization of the catalytic activity of U2 and U6 snRNAs. RNA. 2003;9:892–904. doi: 10.1261/rna.5440303. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Berman H.M., Westbrook J., Feng Z., Gilliland G., Bhat T.N., Weissig J., Shindyalov I.N., Bourne P.E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Hubbard S.J., Thornton J.M. UK: Department of Biochemistry and Molecular Biology, University College London; 1993. NACCESS. [Google Scholar]
15.Sanner M.F., Olson A.J., Spehner J.-C. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
16.Alden C.J., Kim S.-H. Solvent-accessible surfaces of nucleic acids. J. Mol. Biol. 1979;132:411–434. doi: 10.1016/0022-2836(79)90268-7. [DOI] [PubMed] [Google Scholar]
17.Hecht J.L., Honig B., Shin Y.-K., Hubbell W.L. Electrostatic potential near the surface of DNA: comparing theory and experiment. J. Phys. Chem. 1995;99:7782–7786. [Google Scholar]
18.Boschitsch A.H., Fenley M.O., Zhou H.-X. Fast boundary element method for the linear Poisson–Boltzmann equation. J. Phys. Chem. B. 2002;106:2741–2754. [Google Scholar]
19.Newby M.I., Greenbaum N.L. A conserved pseudouridine modification in eukaryotic U2 snRNA induces a change in branch- site architecture. RNA. 2001;7:833–845. doi: 10.1017/s1355838201002308. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Honig B., Sharp K.A., Yang A.-S. Macroscopic models of aqueous solutions: biological and chemical applications. J. Phys. Chem. 1993;97:1101–1109. [Google Scholar]
21.Schutz C.N., Warshel A. What are the dielectric ‘constants’ of proteins and how to validate electrostatic models? Proteins Struct. Funct. Genet. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
22.Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
23.Ames A.L., Nadeau D.R., Moreland J.L. VRML 2.0 Source Book. 2nd edn. NY: John Wiley & Sons, Inc; 1996. [Google Scholar]
24.Lee B., Richards F.M. The interpretation of protein structures: estimation of static accessibility. J. Mol. Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
25.Boschitsch A.H., Fenley M.O. Hybrid boundary element and finite difference method for solving the nonlinear Poisson–Boltzmann equation. J. Comput. Chem. 2004;25:935–955. doi: 10.1002/jcc.20000. [DOI] [PubMed] [Google Scholar]
26.Lavery R., Pullman B. The molecular electrostatic potential and steric accessibility of A-DNA. Nucleic Acids Res. 1981;9:4677–4688. doi: 10.1093/nar/9.18.4677. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Sayyed-Ahmad A., Tuncay K., Ortoleva P.J. Efficient solution technique for solving the Poisson–Boltzmann equation. J. Comput. Chem. 2004;25:1068–1074. doi: 10.1002/jcc.20039. [DOI] [PubMed] [Google Scholar]
28.Baker N.A., Sept D., Joseph S., Holst M.J., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Rocchia W., Alexov E., Honig B. Extending the applicability of the nonlinear Poisson–Boltzmann equation: multiple dielectric constants and multivalent ions. J. Phys. Chem. B. 2001;105:6507–6514. [Google Scholar]
30.Petrey D., Honig B. GRASP2: visualization, surface properties, and electrostatics of macromolecular structures and sequences. Meth. Enzymol. 2003;374:492–509. doi: 10.1016/S0076-6879(03)74021-X. [DOI] [PubMed] [Google Scholar]
31.Nicholls A., Sharp K.A., Honig B. Protein folding and association: insights form the interfacial and thermodynamic properties of hydrocarbons. Proteins Struct. Funct. Genet. 1991;11:281–296. doi: 10.1002/prot.340110407. [DOI] [PubMed] [Google Scholar]
32.Pullman A., Pullman B. Molecular electrostatic potential of the nucleic acids. Quart. Rev. Biophys. 1981;14:289–380. doi: 10.1017/s0033583500002341. [DOI] [PubMed] [Google Scholar]
33.Hermann T. Strategies for the design of drugs targeting RNA and RNA–protein complexes. Angew. Chem. Int. Ed. 2000;39:1890–1905. doi: 10.1002/1521-3773(20000602)39:11<1890::aid-anie1890>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
34.Hermann T., Westhof E. Docking of cationic antibiotics to negatively charged pockets in RNA folds. J. Med. Chem. 1999;42:1250–1261. doi: 10.1021/jm981108g. [DOI] [PubMed] [Google Scholar]
35.Pullman B., Lavery R., Pullman A. Two aspects of DNA polymorphism and microheterogeneity: molecular electrostatic potential and steric accessibility. Eur. J. Biochem. 1982;124:229–238. doi: 10.1111/j.1432-1033.1982.tb06582.x. [DOI] [PubMed] [Google Scholar]
36.Misra V.K., Draper D.E. Mg2+ binding to tRNA revisited: the nonlinear Poisson–Boltzmann model. J. Mol. Biol. 2000;299:813–825. doi: 10.1006/jmbi.2000.3769. [DOI] [PubMed] [Google Scholar]
37.Banatao D.R., Altman R.B., Klein T.E. Microenvironment analysis and identification of magnesium binding sites in RNA. Nucleic Acids Res. 2003;31:4450–4460. doi: 10.1093/nar/gkg471. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Misra V.K., Draper D.E. A thermodynamic framework for Mg2+ binding to RNA. Proc. Natl Acad. Sci. USA. 2001;98:12456–12461. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Gilson M.K., Sharp K.A., Honig B. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comput. Chem. 1987;9:327–335. [Google Scholar]
40.Warwicker J., Watson H.C. Calculation of the electric potential in the active site cleft due to α-helix dipoles. J. Mol. Biol. 1982;157:671–679. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]
41.Zauhar R.J., Morgan R.S. The rigorous computation of the molecular electric potential. J. Comput. Chem. 1988;9:171–187. [Google Scholar]
42.Davis M.E., Madura J.D., Luty B.A., McCammon J.A. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian Dynamics Program. Comput. Phys. Commun. 1991;62:187–197. [Google Scholar]
43.Rocchia W., Sridharan S., Nicholls A., Alexov E., Chiabrera A., Honig B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: applications to the molecular systems and geometric objects. J. Comput. Chem. 2002;23:128–137. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
44.Query C.C., Strobel S.A., Sharp P.A. Three recognition events at the branch-site adenine. EMBO J. 1996;15:1392–1402. [PMC free article] [PubMed] [Google Scholar]
45.Newby M.I., Greenbaum N.L. Investigation of Overhauser effects between pseudouridine and water protons in RNA helices. Proc. Natl Acad. Sci. USA. 2002;99:12697–12702. doi: 10.1073/pnas.202477199. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b1] 1.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Quart. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]

[b2] 2.Record M.T.J., Anderson C.F., Lohman T.M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening and ion effects on water activity. Quart. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]

[b3] 3.Hermann T., Westhof E. Exploration of metal ion binding sites in RNA folds by Brownian-dynamics simulations. Structure. 1998;6:1303–1314. doi: 10.1016/s0969-2126(98)00130-0. [DOI] [PubMed] [Google Scholar]

[b4] 4.Westhof E., Fritsch V. RNA folding: beyond Watson–Crick pairs. Structure Fold. Des. 2000;8:R55–R65. doi: 10.1016/s0969-2126(00)00112-x. [DOI] [PubMed] [Google Scholar]

[b5] 5.Leontis N.B., Stombaugh J., Westhof E. The non-Watson–Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002;30:3497–3531. doi: 10.1093/nar/gkf481. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b6] 6.Chin K., Sharp K.A., Honig B., Pyle A.M. Calculating the electrostatic properties of RNA provides new insights into molecular interactions and function. Nature Struct. Biol. 1999;6:1055–1061. doi: 10.1038/14940. [DOI] [PubMed] [Google Scholar]

[b7] 7.Moore M., Query C., Sharp P. Splicing of precursor to mRNA by the spliceosome. In: Gesteland R.F., Atkins J.F., editors. The RNA World. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1993. pp. 303–357. [Google Scholar]

[b8] 8.Newby M.I., Greenbaum N.L. Sculpting the spliceosomal branch site recognition motif by a conserved pseudouridine. Nature Struct. Biol. 2002;9:958–965. doi: 10.1038/nsb873. [DOI] [PubMed] [Google Scholar]

[b9] 9.Reddy R., Busch H. Small nuclear RNAs: RNA sequences, structure and modifications. In: Birnstiel M.L., editor. Structure and Function of Major and Minor Small Nuclear Ribonucleoprotein Particles. Berlin: Springer-Verlag Press; 1988. pp. 1–37. [Google Scholar]

[b10] 10.Gu J., Patton J., Shimba S., Reddy R. Location of modified nucleotides in Schizosaccharomyces pombe spliceosomal small nuclear RNAs: modified nucleotides are clustered in functionally important regions. RNA. 1996;2:909–918. [PMC free article] [PubMed] [Google Scholar]

[b11] 11.Patton J., Jacobsen M., Pederson T. Pseudouridine formation in small nuclear RNA. Proc. Natl Acad. Sci. USA. 1994;91:3324–3328. doi: 10.1073/pnas.91.8.3324. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b12] 12.Valadkhan S., Manley J.L. Characterization of the catalytic activity of U2 and U6 snRNAs. RNA. 2003;9:892–904. doi: 10.1261/rna.5440303. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b13] 13.Berman H.M., Westbrook J., Feng Z., Gilliland G., Bhat T.N., Weissig J., Shindyalov I.N., Bourne P.E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b14] 14.Hubbard S.J., Thornton J.M. UK: Department of Biochemistry and Molecular Biology, University College London; 1993. NACCESS. [Google Scholar]

[b15] 15.Sanner M.F., Olson A.J., Spehner J.-C. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]

[b16] 16.Alden C.J., Kim S.-H. Solvent-accessible surfaces of nucleic acids. J. Mol. Biol. 1979;132:411–434. doi: 10.1016/0022-2836(79)90268-7. [DOI] [PubMed] [Google Scholar]

[b17] 17.Hecht J.L., Honig B., Shin Y.-K., Hubbell W.L. Electrostatic potential near the surface of DNA: comparing theory and experiment. J. Phys. Chem. 1995;99:7782–7786. [Google Scholar]

[b18] 18.Boschitsch A.H., Fenley M.O., Zhou H.-X. Fast boundary element method for the linear Poisson–Boltzmann equation. J. Phys. Chem. B. 2002;106:2741–2754. [Google Scholar]

[b19] 19.Newby M.I., Greenbaum N.L. A conserved pseudouridine modification in eukaryotic U2 snRNA induces a change in branch- site architecture. RNA. 2001;7:833–845. doi: 10.1017/s1355838201002308. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b20] 20.Honig B., Sharp K.A., Yang A.-S. Macroscopic models of aqueous solutions: biological and chemical applications. J. Phys. Chem. 1993;97:1101–1109. [Google Scholar]

[b21] 21.Schutz C.N., Warshel A. What are the dielectric ‘constants’ of proteins and how to validate electrostatic models? Proteins Struct. Funct. Genet. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]

[b22] 22.Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]

[b23] 23.Ames A.L., Nadeau D.R., Moreland J.L. VRML 2.0 Source Book. 2nd edn. NY: John Wiley & Sons, Inc; 1996. [Google Scholar]

[b24] 24.Lee B., Richards F.M. The interpretation of protein structures: estimation of static accessibility. J. Mol. Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]

[b25] 25.Boschitsch A.H., Fenley M.O. Hybrid boundary element and finite difference method for solving the nonlinear Poisson–Boltzmann equation. J. Comput. Chem. 2004;25:935–955. doi: 10.1002/jcc.20000. [DOI] [PubMed] [Google Scholar]

[b26] 26.Lavery R., Pullman B. The molecular electrostatic potential and steric accessibility of A-DNA. Nucleic Acids Res. 1981;9:4677–4688. doi: 10.1093/nar/9.18.4677. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b27] 27.Sayyed-Ahmad A., Tuncay K., Ortoleva P.J. Efficient solution technique for solving the Poisson–Boltzmann equation. J. Comput. Chem. 2004;25:1068–1074. doi: 10.1002/jcc.20039. [DOI] [PubMed] [Google Scholar]

[b28] 28.Baker N.A., Sept D., Joseph S., Holst M.J., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b29] 29.Rocchia W., Alexov E., Honig B. Extending the applicability of the nonlinear Poisson–Boltzmann equation: multiple dielectric constants and multivalent ions. J. Phys. Chem. B. 2001;105:6507–6514. [Google Scholar]

[b30] 30.Petrey D., Honig B. GRASP2: visualization, surface properties, and electrostatics of macromolecular structures and sequences. Meth. Enzymol. 2003;374:492–509. doi: 10.1016/S0076-6879(03)74021-X. [DOI] [PubMed] [Google Scholar]

[b31] 31.Nicholls A., Sharp K.A., Honig B. Protein folding and association: insights form the interfacial and thermodynamic properties of hydrocarbons. Proteins Struct. Funct. Genet. 1991;11:281–296. doi: 10.1002/prot.340110407. [DOI] [PubMed] [Google Scholar]

[b32] 32.Pullman A., Pullman B. Molecular electrostatic potential of the nucleic acids. Quart. Rev. Biophys. 1981;14:289–380. doi: 10.1017/s0033583500002341. [DOI] [PubMed] [Google Scholar]

[b33] 33.Hermann T. Strategies for the design of drugs targeting RNA and RNA–protein complexes. Angew. Chem. Int. Ed. 2000;39:1890–1905. doi: 10.1002/1521-3773(20000602)39:11<1890::aid-anie1890>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]

[b34] 34.Hermann T., Westhof E. Docking of cationic antibiotics to negatively charged pockets in RNA folds. J. Med. Chem. 1999;42:1250–1261. doi: 10.1021/jm981108g. [DOI] [PubMed] [Google Scholar]

[b35] 35.Pullman B., Lavery R., Pullman A. Two aspects of DNA polymorphism and microheterogeneity: molecular electrostatic potential and steric accessibility. Eur. J. Biochem. 1982;124:229–238. doi: 10.1111/j.1432-1033.1982.tb06582.x. [DOI] [PubMed] [Google Scholar]

[b36] 36.Misra V.K., Draper D.E. Mg2+ binding to tRNA revisited: the nonlinear Poisson–Boltzmann model. J. Mol. Biol. 2000;299:813–825. doi: 10.1006/jmbi.2000.3769. [DOI] [PubMed] [Google Scholar]

[b37] 37.Banatao D.R., Altman R.B., Klein T.E. Microenvironment analysis and identification of magnesium binding sites in RNA. Nucleic Acids Res. 2003;31:4450–4460. doi: 10.1093/nar/gkg471. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b38] 38.Misra V.K., Draper D.E. A thermodynamic framework for Mg2+ binding to RNA. Proc. Natl Acad. Sci. USA. 2001;98:12456–12461. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b39] 39.Gilson M.K., Sharp K.A., Honig B. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comput. Chem. 1987;9:327–335. [Google Scholar]

[b40] 40.Warwicker J., Watson H.C. Calculation of the electric potential in the active site cleft due to α-helix dipoles. J. Mol. Biol. 1982;157:671–679. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]

[b41] 41.Zauhar R.J., Morgan R.S. The rigorous computation of the molecular electric potential. J. Comput. Chem. 1988;9:171–187. [Google Scholar]

[b42] 42.Davis M.E., Madura J.D., Luty B.A., McCammon J.A. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian Dynamics Program. Comput. Phys. Commun. 1991;62:187–197. [Google Scholar]

[b43] 43.Rocchia W., Sridharan S., Nicholls A., Alexov E., Chiabrera A., Honig B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: applications to the molecular systems and geometric objects. J. Comput. Chem. 2002;23:128–137. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]

[b44] 44.Query C.C., Strobel S.A., Sharp P.A. Three recognition events at the branch-site adenine. EMBO J. 1996;15:1392–1402. [PMC free article] [PubMed] [Google Scholar]

[b45] 45.Newby M.I., Greenbaum N.L. Investigation of Overhauser effects between pseudouridine and water protons in RNA helices. Proc. Natl Acad. Sci. USA. 2002;99:12697–12702. doi: 10.1073/pnas.202477199. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Recognition of the spliceosomal branch site RNA helix on the basis of surface and electrostatic features

Darui Xu

Nancy L Greenbaum

Marcia O Fenley

Abstract

INTRODUCTION

Figure 1.

Figure 2.