Shared and specific muscle synergies in natural motor behaviors

Abstract

Selecting the appropriate muscle pattern to achieve a given goal is an extremely complex task because of the dimensionality of the search space and because of the nonlinear and dynamical nature of the transformation between muscle activity and movement. To investigate whether the central nervous system uses a modular architecture to achieve motor coordination we characterized the motor output over a large set of movements. We recorded electromyographic activity from 13 muscles of the hind limb of intact and freely moving frogs during jumping, swimming, and walking in naturalistic conditions. We used multidimensional factorization techniques to extract invariant amplitude and timing relationships among the muscle activations. A decomposition of the instantaneous muscle activations as combinations of nonnegative vectors, synchronous muscle synergies, revealed a spatial organization in the muscle patterns. A decomposition of the same activations as a combination of temporal sequences of nonnegative vectors, time-varying muscle synergies, further uncovered specific characteristics in the muscle activation waveforms. A mixture of synergies shared across behaviors and synergies for specific behaviors captured the invariances across the entire dataset. These results support the hypothesis that the motor controller has a modular organization.

To generate purposeful behavior the central nervous system (CNS) has to coordinate the many degrees of freedom of the musculoskeletal system, taking into account the nonlinear characteristics of the muscles and the dynamic interactions among the articulated segments of the body and between the body and the environment (1). Moreover, the same motor apparatus is used to achieve different goals in a variety of natural behaviors. This complex task of mapping goals to muscle patterns might be simplified by organizing a modular and hierarchical control architecture (2–4). In the last few years, a number of studies on the organization of the spinal cord (5–12) have led to the hypothesis that the CNS uses a set of muscle synergies, the coherent activation in space or time of a group of muscles, as output modules. According to this hypothesis, supraspinal and afferent signals flexibly combine a few muscle synergies to generate a variety of muscle patterns.

In this article, we have investigated whether the CNS uses muscle synergies as output modules by studying different natural motor behaviors. We have recorded the muscle patterns of intact freely moving frogs during jumping, swimming, and walking. Rather than characterizing the average muscle activation waveforms corresponding to particular movements, we have used multidimensional factorization techniques to identify muscle synergies as the invariant amplitude and timing relationships among the muscle activations underlying a variety of different movements. We have considered two models for the generation of muscle patterns as synergy combinations: synchronous and time-varying. In our formulation, a synchronous muscle synergy is a vector of real numbers, each component of which represents the activation of a particular muscle. A muscle activation waveform is generated by scaling each component of this vector by the same time-varying coefficient. A muscle pattern is then constructed by summing the muscle activation waveforms generated by different synergies. Thus a synchronous muscle synergy captures a set of fixed amplitude relationships among the muscle activations, i.e., an invariant spatial organization of the muscle patterns. In contrast, a time-varying synergy is a time sequence of vectors representing a collection of muscle activation waveforms. A muscle pattern is constructed by scaling different synergies, each sequence multiplied by a single amplitude coefficient, shifting the synergy onset in time, each sequence shifted by a single timing coefficient, and finally summing them muscle by muscle. If the vectors in the sequence that define a time-varying synergy are all in the same direction, the time-varying model essentially reduces to the synchronous model. In general, though, the sequence of vectors may represent a collection of asynchronous muscle activation waveforms, and hence a time-varying synergy captures spatiotemporal invariants in the muscle patterns.

We used a nonnegative matrix factorization algorithm (13) to identify synchronous synergies and an extension of an optimization algorithm that we recently developed (14) to identify time-varying synergies. We found that a small number of synergies could explain a large fraction of the variation in the muscle patterns and that the synergies extracted from the same behavior in different frogs were in most cases similar. When we compared five synergies extracted from jumping, swimming, and walking data simultaneously from all frogs, we found that at least three synergies were similar in all pairs of behaviors, suggesting that some synergies are shared across behaviors whereas others are behavior-specific. We also found that the spatial structure revealed by the synchronous synergies matched closely the spatial structure of the time-varying synergies, but the latter also unveiled a specific temporal organization within the muscle patterns. These results support the hypothesis that the motor output has a modular organization and indicate that some, but not all, output modules are shared across behaviors.

Methods

Three adult bullfrogs (Rana catesbeiana) were used in the experiments. All surgical and experimental procedures were approved by the Committee on Animal Care at the Massachusetts Institute of Technology.

Electrode Implantation. In each frog, 13 hind-limb muscles were implanted with bipolar intramuscular electrodes. The animals were anesthetized by injection of 1 ml of tricaine (5%, MS-222, Sigma) in the dorsal lymph sac and they were kept on ice during the surgical procedure. Pairs of multistranded Teflon-coated stainless steel wires (A-M Systems, Carlsborg, WA), with the insulation removed for a length of 1.5 mm on each wire, were implanted in the following muscles: rectus internus major (RI), adductor magnus (AD), semimembranosus (SM), vastus internus (VI), vastus externus (VE), peroneus (PE), gastrocnemius (GA), rectus anterior (RA), ventral head of semitendinosus (ST), sartorius (SA), biceps (or iliofibularis, BI), iliopsoas (IP), and tibialis anterior (TA). After insertion, the wires were led s.c. to the back and, through a skin incision, connected to a multipin miniature connector.

Data Collection and Preprocessing. During the experimental sessions a lightweight miniature flat cable was attached to the connector on the back of the frogs, and electromyographic (EMG) activity was recorded. During swimming sessions the connector was insulated by using a removable fast-setting polymer (Permlastic; Kerr, Romulus, MI). The EMG signals were differentially amplified (gain 5,000), band-pass filtered (10–1,000 Hz), digitized (1 kHz), and stored on a computer hard drive. All behavioral episodes were videotaped by using a video camera (29.97 frames per second, Sony TRV-9) synchronized with the EMG recordings. Data analysis was performed by using in-house software written in Matlab (Mathworks, Natick, MA). Using the video, we first segmented the EMG records into different continuous behavioral episodes (e.g., one jump or a sequence of swimming cycles). The raw EMG data for each segment were then digitally rectified and low-pass filtered (20-Hz cutoff frequency with a finite impulse response filter) and integrated over 25-ms intervals. The resulting samples were then normalized for each animal and each muscle to the amplitude of the maximum sample of integrated EMG activity in that muscle over all episodes of all behaviors.

Synergy Extraction Algorithms. Synchronous synergies. We used a nonnegative matrix factorization algorithm (13, 15) to extract synchronous synergies from the data. Briefly, the algorithm starts with random nonnegative synergies and coefficients and proceeds to minimize the total reconstruction error by iterating a coefficient update step and a synergy update step based on multiplicative update rules (see Supporting Text, which is published as supporting information on the PNAS web site). We used a convergence criterion of five consecutive iterations for which the increase of the reconstruction R² was <10^-4. To minimize the probability of finding local minima we repeated the optimization five times and selected the solution with the highest R².

Time-varying synergies. To extract a set of time-varying synergies we used an optimization algorithm that extends the one we recently introduced (14) by allowing the reconstruction of each EMG segment by combinations of an arbitrary number of synergy instances (as in Eq. 3 in Supporting Text). Thus for repetitive, rhythmical behaviors such as swimming and walking the algorithm automatically identifies cyclical components in the muscle patterns as repeated instances of the extracted synergies.

The algorithm starts by initializing N synergies with random nonnegative values, and it proceeds to minimize the total reconstruction error by iterating three steps (see Supporting Text). First, for each EMG segment a variable number of synergy instances, each corresponding to one of the N synergies shifted to some onset time in the segment, are selected to best match the data by using a procedure based on the matching pursuits algorithm (16). Second, for each segment and given the set of N synergies, the scaling coefficients of the n instances selected in the first step that best reconstruct the data are determined by back-projection (16). Third, once the instances and their scaling coefficients have been determined for all episodes, the synergies are updated by an multiplicative update rule similar to the one used in the nonnegative matrix factorization algorithm (see Eq. 6 in Supporting Text). These three steps are repeated until the algorithm converges on a set of synergies. In this algorithm we used the same convergence criterion and run selection procedure used for the extraction of synchronous synergies.

Shared and specific synergies. We extracted a mixture of synergies common to all behaviors and synergies specific to a subset of behaviors by modifying the extraction algorithms presented above. For synchronous synergies, following the procedure proposed by Cheung and collaborators (V. C. K. Cheung, A.dA., M. C. Tresch, and E.B., unpublished work), we initialized the amplitude coefficients for a number of behavior-specific synergies to zero over all EMG segments not belonging to the selected behaviors. Because of the multiplicative update rules used in the algorithm, these coefficients are bound to zero throughout the iterations. For the time-varying synergies, we restricted the matching pursuits procedure for each EMG segment to the instances of the shared synergies and to the instances of the synergies specific for the behavior to which the segment belonged.

Significance of Extracted Synergies. We verified that the particular synergies extracted by our algorithms were not selected as a result of any bias built into the method by comparing the R² value for the reconstruction of the real data with the extracted synergies and the R² value for the reconstruction of structureless simulated data with synergies extracted from those simulated data. For synchronous synergies, we generated structureless data by randomly reshuffling the samples for each muscle independently. In this way the simulated data had the same muscle amplitude distribution as the real data but each muscle amplitude was uncorrelated with all the others. For time-varying synergies, after reshuffling the samples for each muscle over the entire dataset and assigning them to episodes of the same duration as in the real data, we also low-pass filtered the reshuffled waveforms (10-Hz cutoff) to maintain a frequency composition of the simulated data similar to that of the real data. For each simulated dataset we repeated 100 synergy extraction runs with the same procedure used for the real data and we computed the 95th percentile of the R² distribution. In the case of time-varying synergies, we used a random subset of reshuffled episodes containing at least 2,000 samples.

Synergy Similarity. The cosine of the angle between two synergies was used as a measure of their similarity. For the synchronous synergies we simply computed the scalar product between the two normalized vectors w₁ and w₂ representing the two synergies. For the time-varying synergies we used the maximum of the normalized scalar products between the two time-varying synergies shifted by k₁ and k₂ samples over all possible relative delays (k₁ - k₂) (see ref. 14 for more details).

Synergy Set Comparison. We compared two sets of synergies (e.g., extracted from different frogs or behaviors) by computing the similarities between their best matching pairs and by counting the number of pairs with a similarity above chance. We matched pairs of synergies starting with the pair with the highest similarity, removing the synergies of the selected pair from their respective sets, and then matching the remaining elements. We estimated the number of pairs with a similarity significantly above chance with a simulation. For synchronous synergies, we generated random synergies by sampling the empirical distribution of the activation amplitudes of each muscle in the dataset from which the synergies were extracted. We then compared the similarity between the best-matching pairs among 1,000 sets of random synergies and computed the 95th percentile of the chance similarity for each pair. For time-varying synergies, we generated sequences of random data of the same length as the synergy duration and we then low-pass filtered the sequences (10-Hz cutoff) to match the smoothness in the actual synergies.

Results

Muscle Patterns During Natural Behaviors in Intact Frogs. To examine the variability in the muscle patterns typical of natural behaviors we recorded EMGs from frogs that were unrestrained and freely jumping or walking in a large cage, or swimming in a tank. A large number of behavioral episodes were either produced spontaneously or elicited by gentle cutaneous stimulation (Table 1). We observed a great variability in the expression of the different forms of locomotion. Each frog naturally performed jumps in a range of directions and distances. Swimming occurred with two different forms of bilateral coordination (in-phase and out-of-phase), at different speeds, and at different depths in the water. Natural speed variations were also observed in walking and, in one frog (F17), walking was also performed over a surface inclined at different slopes.

Table 1. Summary of data collected from three frogs (F10, F11, and F17).

	No. of episodes			No. of samples
Behavior	F10	F11	F17	F10	F11	F17
Jumping	218	117	133	11,674	6,188	5,183
Swimming	135	40	35	42,068	15,750	23,234
Walking	166	36	166	12,028	2,474	16,912

Spatial Structure Captured by Synchronous Synergies. We first characterized the invariant relationships among the muscle activation amplitudes, i.e., their spatial structure, by using nonnegative matrix factorization (13). We extracted sets of synchronous synergies from individual behaviors of each frog with the number of synergies in each set ranging from 2 to 8. The fraction of the total variation in the data explained by the combination of the synergies in each set increased with the number of synergies, ranging from an average 0.67 with two synergies to an average of 0.96 with eight synergies (Table 2). The fact that a large fraction of the total variation could be explained with a number of synergies much smaller than the dimensionality of the patterns (13, equal to the number of muscles) indicated that the model provided an adequate characterization of the spatial structure of the data.

Table 2. Fraction of the total data variation explained by synchronous synergy combinations extracted from each frog and behavior.

		Fraction for each no. of synergies
Frog	Behavior	2	3	4	5	6	7	8
F10	Jumping	0.75	0.82	0.86	0.90	0.92	0.94	0.95
F11	Jumping	0.71	0.85	0.89	0.91	0.93	0.95	0.96
F17	Jumping	0.71	0.80	0.86	0.90	0.92	0.94	0.96
F10	Swimming	0.78	0.84	0.89	0.91	0.93	0.95	0.96
F11	Swimming	0.68	0.77	0.82	0.88	0.91	0.94	0.95
F17	Swimming	0.59	0.69	0.76	0.81	0.86	0.90	0.94
F10	Walking	0.56	0.72	0.85	0.89	0.92	0.94	0.96
F11	Walking	0.68	0.79	0.89	0.91	0.94	0.95	0.97
F17	Walking	0.55	0.73	0.80	0.87	0.91	0.93	0.95

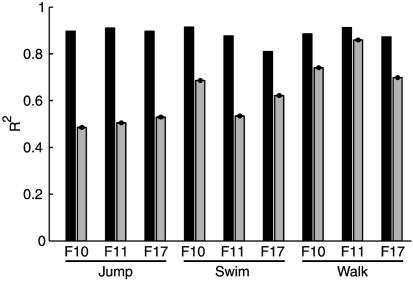
Only the sets with five synergies were considered for further analysis. For these sets R² was on average 0.89, thus representing a compromise between a parsimonious (small N) and accurate (large R²) characterization of the different datasets. To verify that the extracted synergies captured real structure and did not result from a bias in the method, we compared the reconstruction error for the synergies extracted from the data with the reconstruction error obtained with synergies extracted from structureless simulated data (see Methods). This comparison (Fig. 1) showed that for all nine datasets the R² value for five synergies extracted from the real data was significantly higher than the R² value for the five synergies extracted from simulated data. Hence, the synergy extraction algorithm captures the amplitude relationships among the muscle activations, i.e., their spatial structure, and not simply the amplitude distribution for each individual muscle (which was identical in the real and simulated data).

Fig. 1.

Significance of synchronous synergy extraction. The fraction of the total variation of each dataset explained by the combination of five synergies (black bars) is compared with the fraction of the total variation of simulated structureless datasets explained by five synergies extracted from the simulated data with the same procedure used for the real data (gray bars, mean ± SD over 100 runs).

We then compared sets of five synergies extracted from the same behavior in different frogs. We computed the similarities between the best-matching pairs of synergies for each pair of datasets and we compared these values with the similarities expected from randomly generated synergies. We found that the synergies extracted from the same behavior in different frogs were in most cases significantly similar (Table 3). For jumping, all five synergies were similar across individuals. For swimming and walking, all five pairs of synergies were similar for two frogs (F10 and F11), whereas there were a few dissimilar synergy pairs for the third frog (F17). Hence, the spatial structure captured by the synchronous synergies appeared essentially invariant across individuals. Given this result, we then pooled the data from different frogs to investigate the similarities across behaviors. The R² values for the sets of five synergies extracted from the pooled data (0.87 for jumping, 0.87 for swimming, and 0.84 for walking) were very close to the R² values for the synergies extracted from individual animals (see Table 2). Hence a single set of synergies well characterized the spatial structure characteristic of each behavior.

Table 3. Number of pairs of synchronous synergies with similarity above chance between the sets with five elements extracted from the same behavior in different frogs.

	No. of pairs
Behavior	F10–F11	F10–F17	F11–F17
Jumping	5	5	5
Swimming	5	2	3
Walking	5	3	3

Shared and Specific Synchronous Synergies. While it is reasonable that the CNS organizes specific synergies to cope with the kinematics and biomechanical requirements of the movements involved in individual behaviors, some synergies might be shared across behaviors. To investigate this possibility, we first compared the sets of five synergies extracted from each individual behavior. We found that three pairs of synergies for jumping and swimming, four pairs for jumping and walking, and three pairs for swimming and walking had similarities that were significantly higher than the corresponding similarities of pairs of random synergies. To test whether these similarities across pairs of behaviors derived from the existence of a common set of shared synergies, we extracted a mixture of synergies shared across behaviors and behavior-specific synergies from the data pooled from all behaviors. Because there were three pairs of similar synergies in each comparison between behaviors and one extra pair in the comparison between jumping and walking, we extracted three synergies shared across all behaviors and one synergy shared between jumping and walking. We also extracted one synergy restricted to jumping, two synergies restricted to swimming, and one synergy restricted to walking so that each behavior was reconstructed by five synergies. The R² value for the reconstruction of the entire dataset with this set of shared and specific synergies was 0.87, whereas the R² values for the reconstruction of all of the episodes of each individual behavior were 0.86 for jumping, 0.86 for swimming, and 0.81 for walking. Thus a single set consisting of a mixture of shared and specific synergies could reconstruct the patterns of individual behaviors with essentially the same accuracy as the synergies extracted independently from the individual datasets.

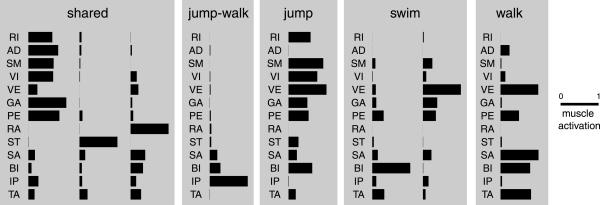
The three synergies shared across jumping, swimming, and walking, the synergy shared between jumping and walking, and the remaining four behavior-specific synergies (Fig. 2) all show specific features in their muscle composition and balance. The first of the three shared synergies shows a strong recruitment of all muscles with an extensor action on the hip, knee, and ankle joints. The second and third shared synergies as well as the synergy shared between jumping and walking and the first of the two swim-specific synergies are instead characterized by a recruitment of muscles with mainly a flexor action. Each synergy has a specific balance in the activation of flexor muscles. The jump-specific synergy, like the first shared synergy, has a strong activation of hip (RI and SM) and knee (VI) extensors but, in contrast to the shared synergy, also comprises a strong activation of VE (knee extensor with a hip abduction action) and BI (knee flexor with hip abduction action) and no activation of the hip adductor AD. The walking-specific synergy shows a strong activation of VE combined with a strong activation of the knee flexors BI and SA and the ankle flexor TA, whereas there is almost no activation of hip extensors. Finally, the second swim-specific synergy combines a strong activation of VE with slightly weaker activation of GA and PE.

Fig. 2.

Behavior-independent and behavior-specific synchronous synergies. The three shared synergies are extracted from the entire dataset of muscle patterns recorded during jumping, swimming, and walking in three frogs. One synergy (jump-walk) is extracted from only jumping and walking episodes. The other behavior-specific synergies (jump, swim, and walk) are extracted from only the muscle patterns of individual behaviors. Each synergy is normalized to the maximum over all muscles.

In summary, the decomposition of the muscle patterns for jumping, swimming, and walking as combinations of shared and specific synergies indicates that the muscle patterns for a large repertoire of movements can be constructed from a small set of building blocks and that some, but not all, of these building blocks are shared across behaviors.

Spatiotemporal Structure Revealed by Time-Varying Synergy Decomposition. The synchronous synergies presented above capture the spatial structure of the patterns but they do not characterize their spatiotemporal structure. We therefore also investigated whether there were invariant relationships among the muscle activation time courses across different episodes and conditions, i.e., whether the patterns could be reconstructed by scaling in amplitude, shifting in time, and combining a number of time-varying muscle synergies. As with the synchronous synergies, we extracted sets of time-varying synergies (20 samples for a total duration of 500 ms) from individual behaviors of each frog with the number of elements ranging from 2 to 8. The fraction of the total variation in the data explained by the combination of the synergies in each set increased with the number of synergies, ranging from an average R² value of 0.65 with two synergies to an average R² value of 0.83 with eight synergies (Table 4).

Table 4. Fraction of the total data variation explained by time-varying synergy combinations extracted from each frog and behavior.

		Fraction for each no. of synergies
Frog	Behavior	2	3	4	5	6	7	8
F10	Jumping	0.78	0.81	0.82	0.84	0.85	0.86	0.87
F11	Jumping	0.79	0.82	0.84	0.85	0.87	0.87	0.88
F17	Jumping	0.75	0.79	0.81	0.83	0.84	0.85	0.85
F10	Swimming	0.74	0.80	0.83	0.85	0.86	0.86	0.87
F11	Swimming	0.64	0.71	0.76	0.79	0.81	0.81	0.84
F17	Swimming	0.53	0.60	0.67	0.71	0.74	0.76	0.78
F10	Walking	0.52	0.64	0.71	0.74	0.75	0.78	0.78
F11	Walking	0.59	0.72	0.78	0.81	0.83	0.85	0.86
F17	Walking	0.53	0.65	0.71	0.74	0.75	0.77	0.78

We selected the sets composed of five time-varying synergies for further analysis. In terms of their spatial structure, given by the synergy activations averaged across time, in most cases the time-varying synergies closely matched the synchronous synergies. The R² value for the reconstruction of each data set by combinations of five synergies was on average 0.80. This value is considerably lower than the value for the same number of synchronous synergies (0.89); however, if we consider that the number of parameters in the synchronous model (one amplitude coefficient for each synergy and each sample) was on average 19.8 times larger than the number of parameters in the time-varying model (one amplitude and one timing coefficient per synergy instance), such a difference is not surprising. On the contrary, it is remarkable that the time-varying synergy model can explain 80% of the data variation despite the fact that, given the sets of synergies, the only temporal parameters used to explain the muscle waveforms are the synergy onset times.

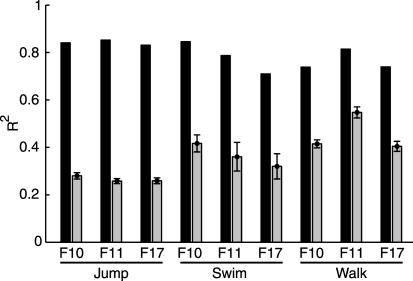
We verified that the extracted synergies captured real structure and did not result from a bias in the extraction method by comparing the reconstruction error for the synergies extracted from the data with the reconstruction error for synergies extracted from structureless simulated data (see Methods). For all nine datasets, the R² value for the real data was significantly higher than that for the corresponding simulated data (Fig. 3), indicating that the extraction algorithm recovers the invariant spatiotemporal relationships in the muscle waveforms and does not simply fit the waveforms of individual muscles.

Fig. 3.

Significance of time-varying synergy extraction. A much larger fraction of the total variation of the data is explained by the combination of five synergies (black bars) than by five synergies extracted from simulated structureless data (gray bars, mean ± SD over 100 runs).

We then compared the synergies extracted from the same behavior in different animals. We found that at least three of the five synergies extracted for each behavior in different frogs were significantly similar across frogs (Table 5), indicating that the spatiotemporal structure of the patterns revealed by the synergies was to a large extent the same for all individuals. This result allowed us to then compare different behaviors by using the data pooled from all of the frogs. We found that the R² values for the sets of five synergies extracted from the pooled data (0.81 for jumping, 0.80 for swimming, and 0.70 for walking) were comparable to the R² values for the synergies extracted from individual animals. Thus a single set of synergies adequately characterized the spatiotemporal structure in the patterns of each behavior.

Table 5. Number of pairs of time-varying synergies with similarity above chance between the sets with five elements extracted from the same behavior in different frogs.

	No. of pairs
Behavior	F10–F11	F10–F17	F11–F17
Jumping	5	4	4
Swimming	4	3	3
Walking	5	3	4

Shared and Specific Time-Varying Synergies. We compared the synergies extracted from individual behaviors and we found that four pairs of synergies were significantly similar between jumping and swimming, three pairs were significantly similar between jumping and walking, and three pairs were significantly similar between swimming and walking. As with the synchronous synergies, we extracted a mixture of shared and specific synergies and we found that they explained the data as well as the synergies extracted from individual behaviors. We extracted three synergies shared across all behaviors, one synergy restricted to jumping and swimming, one restricted to jumping and walking, one restricted to swimming, and one restricted to walking. With this set of synergies every episode of each behavior was reconstructed by five synergies. The R² value for the reconstruction of the entire dataset set was 0.79, whereas it was 0.81 for the jumping episodes, 0.75 for the swimming episodes, and 0.66 for the walking episodes.

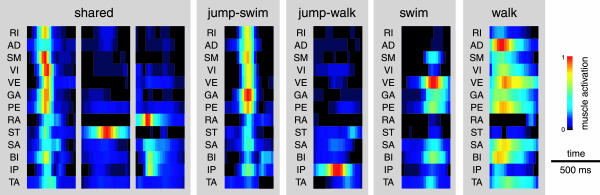
The shared and specific time-varying synergies extracted from the entire dataset (Fig. 4) show specific muscle activation balances and waveforms. Each of the three shared time-varying synergies has a spatial organization similar to one of the three synchronous shared synergies (Fig. 2) while, in addition, possessing distinctive temporal characteristics. In the first synergy, where RI, SM, VI, VE, GA, PE, and BI are vigorously recruited, the duration of muscle activation bursts is very short. Moreover, the peak times of the activation waveforms of different muscles are close but the waveforms are not exactly synchronous. The third shared synergy shows asynchronous activation waveforms for flexor muscles. The synergy shared between jumping and swimming is similar to the first synergy shared across all behaviors but has a strong activation of AD, a stronger activation of GA, and a weaker activation of BI. The synergy shared between jumping and walking has a strong activation of IP and a spatial structure matching the synchronous synergy shared between the same two behaviors. The swim-specific synergy has a strong and prolonged activation of VE, GA, PE, and BI. Finally, the walk-specific synergy shows even longer bursts in a set of muscles (AD, VE, PE, SA, and BI) and its spatial structure is very close to that of the synchronous walk-specific synergy.

Fig. 4.

Behavior-independent and behavior-specific time-varying synergies. Each synergy represents the activation of the 13 muscles with specific activation waveforms (20 samples for a total duration of 500 ms; amplitude is color coded) and it is normalized to the maximum over all samples of all muscles. Three shared synergies are extracted from the entire dataset, whereas the other behavior-specific synergies are extracted from only the muscle patterns from two behaviors (jump–swim and jump–walk) or a single behavior (swim and walk).

In summary, the time-varying synergy decomposition of the muscle patterns observed in different behaviors reinforces the finding obtained with the synchronous synergies that a large repertoire of movements can be constructed by combining a small number of building blocks, some shared across behaviors and some behavior-specific. The extracted time-varying synergies further provide a characterization of the spatiotemporal structure of these building blocks.

Discussion

We developed and used an approach to investigate how the CNS achieves motor coordination. Using multidimensional factorization techniques, we exploited the variability of natural motor behaviors to characterize the invariant spatial and spatiotemporal structure of the muscle patterns underlying a large movement repertoire. We found that combinations of a small number of synchronous and time-varying muscle synergies accounted for a large fraction of the variation in the muscle patterns observed during jumping, swimming, and walking in intact freely moving frogs. When we compared the synergies extracted from individual behaviors, we found a large degree of similarity, indicating the existence of substantial amount of shared structure in the control of different tasks. However, there were also some differences between behaviors, supporting the existence of behavior-specific synergies.

While there is a growing amount of evidence for a modular organization of the motor output in the frog (6, 9–11, 14, 17) and in other vertebrates (8, 12, 18), we know of no other work in which such evidence arises from the analysis of the muscle patterns observed in a large set of movements from three different natural behaviors in the same intact individual. Because our claim for a modular organization is based on the assumption that the invariances in the output of the system correspond to structural features of the system, the larger the set of conditions over which the invariances are observed, the stronger the inference on the organization of the controller can be.

While the idea of shared modules for the control of different behaviors is a longstanding one (19–21), our approach is distinctive not only for the extent of the behavioral repertoire that we have investigated but especially because it is based on a quantitative analysis of the spatiotemporal characteristics of the activations of most of the hind-limb muscles. This analysis allowed us to identify both behavior-independent and behavior-specific modules. Similar observations have recently come from the analysis of three types of behaviors of an invertebrate (22), suggesting that mixing behavior-independent and behavior-specific modules might be a general strategy to flexibly yet efficiently construct complex behaviors. Behavior-independent synergies might implement some basic biomechanical functions of the whole limb involved in the control of all behaviors, whereas behavior-specific synergies might instead meet the unique biomechanical requirements of individual behaviors.

The generation of muscle patterns as combinations of muscle synergies is compatible with both an open-loop and a feedback control architecture and, more generally, might be a way to implement an optimal feedback controller (23, 24). For fast, ballistic movements such as kicking (14) the CNS might recruit the appropriate synergy combination by relying mainly on an internal model of the limb and body dynamics. When feedback plays a larger role, as in wiping (25), sensory afferents might modulate the centrally organized synergy recruitment to allow for feedback error correction. Although the role of sensory feedback in the activation of muscle synergies during natural behaviors of the frog still needs to be fully characterized, one would expect that, if the synergies implement whole-limb biomechanical functions, the appropriate sensory signal used for their modulation would also encode global limb parameters. Interestingly, in the dorsal spinocerebellar tract of the cat there is evidence of such an encoding scheme (26).

In the time-varying synergy reconstruction, the observed muscle activation waveforms are captured simply by scaling fixed-duration synergies in amplitude and shifting them in time, indicating that there are characteristic burst durations in the muscle patterns. Similarly, Hart and Giszter (17) found a common burst duration for several independent synchronous premotor drives identified with independent component analysis in decerebrated frogs. In contrast, the results of Ivanenko and colleagues (27) do not support the existence of a single time scale in the muscle activity pattern for human locomotion: they instead found that five basic muscle activation waveforms were preserved at different walking speeds, indicating that the corresponding burst durations scale with the cycle period. Their approach, which is based on factor analysis, focused separately on the spatial structure on the muscle patterns (factor loadings, i.e., synchronous synergies) and on their activation time course (factor scores), but it would be interesting to directly identify spatiotemporal invariants in human locomotion EMG patterns.

The approach we pursued allowed us to make inferences about the functional organization of the motor controller. However, in the frog, there is already evidence of physiological mechanisms from microstimulation studies (6, 11) and during reflexive behavior (9, 10). In addition, the identification of muscle synergies during natural motor behaviors presented here may provide a powerful tool to help in decoding the activity of spinal interneurons recorded in behaving frogs as well as the activity of neurons involved in the production of motor behaviors in other animals.