Significance
Deterministic lateral displacement (DLD) is a technique for size fractionation of particles in continuous flow that has shown great potential for biological and clinical applications. Several theoretical models have been proposed to explain the trajectories of different-sized particles in relation to the geometry of the pillar array, but experimental evidence has demonstrated that a rich class of intermediate migration behavior exists, which is not predicted by models. In this work, we present a unified theoretical framework to infer the trajectory of particles in the whole array on the basis of trajectories in the unit cell. This framework explains many of the unexpected particle trajectories reported in literature and can be used to design arrays for the fractionation of particles, even at the smallest scales reaching the molecular realm. We also performed experiments that verified our predictions, even at the nanoscales. Using our model as a set of design rules, we developed a condenser structure that achieves full particle separation with a single fluidic input.
Keywords: nanofluidics, deterministic ratchet, particle tracking
Abstract
Deterministic lateral displacement (DLD) is a technique for size fractionation of particles in continuous flow that has shown great potential for biological applications. Several theoretical models have been proposed, but experimental evidence has demonstrated that a rich class of intermediate migration behavior exists, which is not predicted. We present a unified theoretical framework to infer the path of particles in the whole array on the basis of trajectories in a unit cell. This framework explains many of the unexpected particle trajectories reported and can be used to design arrays for even nanoscale particle fractionation. We performed experiments that verify these predictions and used our model to develop a condenser array that achieves full particle separation with a single fluidic input.
Deterministic lateral displacement (DLD) is an efficient technology used to sort and purify small particles (1). Since their introduction (2), DLD pillar arrays have been used in applications from cell sorting (3) to biosensors (4) and can efficiently sort, separate, and enrich a broad range of particles, including parasites (5), bacteria (6), blood cells (7–9), circulating tumor cells (10), and exosomes (11). The original theory (12) predicts that particle trajectories fall into one of two modes, bumping or zigzag, as determined by the critical diameter defined by the array geometry (2, 12). However, experimental evidence is clear that a rich class of intermediate migration behavior exists between these modes (13, 14). Although a few theoretical models (15–17) have been proposed to explain this behavior, a general framework to study how geometric symmetry caused by pillar array influences particle trajectories is still missing.
The symmetry of the pillar array can be explained in a specifically chosen unit cell. A typical DLD pillar array and associated unit cell are schematically represented in Fig. 1 A and B. Rows of pillars with diameter are located along the y direction, with the pillars separated by a distance , leaving a gap in between pillars in the y direction. Adjacent rows of pillars are separated by a distance in the x direction and shifted a distance in the y direction. The shift between one row and the -th nearest row is then . If this shift is chosen to coincide with , then the array is periodic, and invariant to a translation of in the x direction. Therefore, the array geometry has a built-in angle (smallest angle in the red triangle in Fig. 1B), such that when . Note that two types of array designs have been studied in the literature: the row-shifted parallelogram array (or stretched array) and the rotated square lattice (18, 19). Here, we only studied the stretched DLD array design as shown in Fig. 1A. Our results do not extend to the rotated square array layout.
Fig. 1.
Definition of geometric parameters of a DLD array and streamlines in a unit cell. (A) Diagram of the DLD array unit cell used in our simulations. Here, and . (B) The 3D diagram of a DLD pillar array. The unit cell is indicated by a blue dotted box and the array periodicity and angle is shown by the red triangle. (C–F) Flow streamlines in the unit cell of a pillar array for different geometries, with decreasing pillar diameters , respectively. In all cases, . 100 streamlines are shown, with initial positions uniformly distributed along the inlet HA.
Because of the invariance of translational transformation, the fluid streamlines are assumed to have the same symmetry. When a pressure gradient is applied in the x direction to a body of fluid in the array, and assuming point-like pillars where , the fluid streamlines will be parallel to the x axis. Each pillar would have a stagnation point in its upstream side and one in its downstream side (Fig. 1F). The streamlines that start at a stagnation point of one pillar and end at the pillar that is exactly rows downstream, which we will refer to as “separatrix streamlines,” play a special role. The fluid in between two adjacent separatrices will not be in contact with the pillars and will flow basically unobstructed. In the gap between two neighboring pillars on the same row, there will be exactly flow “lanes” separated by separatrices.
The original theory of operation for DLD devices (2, 12) is based on the assumption that, for pillars of finite size, the fluid streamlines are a smoothly deformed version of the streamlines, corresponding to an array of point-like pillars, inheriting the periodicity of the pillar array. Any sufficiently small passively advected particle starting at a position (not on a separatrix) would be carried unobstructed to a position , without any lateral displacement in the y direction, making a zigzag motion around the pillars. Particles larger than the critical diameter [estimated to be twice the width of the lane closest to the pillars (12)] would eventually bump with the pillars (bumping mode), leading to trajectories that follow the angle . In other words, particles in DLD arrays would exhibit two types of trajectories: zigzag or bumping mode. However, several DLD experiments (2, 11, 15) have shown trajectories that deviate from the original theory in that particles migrated laterally in the array with angles that were neither zero (zigzag mode) nor (bumping mode).
A handful of theoretical models (15–17) (summarized in SI Appendix) were developed to account for the nondichotomous particle trajectories in DLD arrays (Table 1). In their explanation, previous models relied either on array geometries with restricted conditions (e.g., ) or on the flow structure proposed in the original theory. Questions regarding whether pillar arrays with periodicity always have exactly flow lanes in between gaps, or how the nature of particle trajectories (zigzag, bumping, or other types) depend on the array geometry, have never been systematically studied.
Table 1.
Models on the migration angle of DLD devices
| Source | Pillar diameter() | Modes | Mode transition | Diffusion | ||||
| Inglis et al. (2006) (12) | Point | 1 | Integer | Z, B | Binary | No | ||
| Heller and Bruus (2008) (16) | Point | 1 | Integer | Z, B | Continuous | Yes | ||
| Long et al. (2008) (17) | Point | 1 | Noninteger | Z, MD, B | Discrete, dependence | No | ||
| Kulrattanarak et al. (2011) (15) | Physical | 1,2,3 | Integer | Z, M, B | Continuous | No | ||
| Cerbelli (2012) (20) | Physical | 1 | Noninteger | Z, MD, B | Discrete, dependence | No | ||
| Present work | Physical | All | All | AZ, B | Binary, dependence | No |
AZ, altered zigzag mode; B, bumping mode; M, mixed mode; MD, multidirectional mode; Z, zigzag mode; , migration angle of zigzag mode; , migration angle of bumping mode; , structural angle of pillar array; ε, row-shift fraction.
We present a theoretical framework to more universally determine the dependence of the migration angle of particles in terms of DLD array geometry parameters. Our model aims at capturing the deterministic nature of the trajectories, as applied to high Pèclet number systems. We observed that the pillar array geometry distorts the fluid flow such that particle trajectories do not necessarily follow the periodicity or symmetry of the array, generating trajectories with migration angles that can have values between 0 and . Finally, we provide experimental verification of the model predictions using nanoscale DLD (nanoDLD) arrays of varying geometry. The model explains and the experimental data demonstrate that intermediate migration angles can occur in the purely deterministic regime.
Results
Fluid Dynamics in the Unit Cell.
We first study the velocity field in the unit cell of a 2D pillar array. Because the Reynolds number in typical DLD experiments is <, we can model the fluid dynamics in our system using the stationary Stoke’s equations
where u and are the local velocity and pressure fields, and is the dynamic viscosity of the solvent. We use nonslip boundary conditions on the surface of the pillars (arcs AB, CD, EF, and GH in Fig. 1A), where the component of the pressure gradient in the direction normal to the pillar surface is zero. Periodic boundary conditions require that the velocity and pressure fields on the lines BC and FG are identical. At the inlet (HA) and outlet (DE), we used normal velocity gradient () and constant pressure, with the pressure at the inlet being larger than the pressure at the outlet. Here, we applied Pa (Fig. 1C). Note that we imposed no boundary conditions associated to the enclosing walls and treated our system as an unbounded infinite array.
The resulting fluid streamlines for different pillar diameters are shown in Fig. 1 C–F (Materials and Methods). It will be convenient to categorize the streamlines starting at the inlet line into two types: (i) “veering flow” and (ii) “direct flow,” colored red and green, respectively, in Fig. 1D. We also define the “separatrix line” as a streamline dividing the veering and direct streamlines, which ends at a stagnation point on the bottom right pillar surface (Fig. 1F). Direct streamlines exit through the outlet of the same unit cell. In a unit cell, veering red streamlines below the separatrix line exit through the bottom segment BC to reenter through the top segment FG as the blue streamlines in the adjacent unit cell beneath, after which they proceed to exit at some point on the outlet line DE.
Recurrence Map.
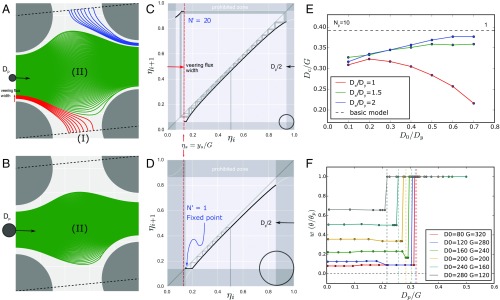
Every streamline represents the trajectory of a point-like, passively advected particle that enters the unit cell at some point on the inlet line and exits the unit cell at some other point on the outlet line (Fig. 1E). The distances and are measured as a ratio of along the inlet and outlet lines respectively, starting from the respective points A and D of the bottom pillars, and therefore . We will denote . This normalized coordinate defines a mapping that uniquely assigns a point at the inlet line to a point on the outlet line, and that depends on the geometric parameters and . Because the outlet of a unit cell is the input of the next unit cell, the map determines the position of a particle at the inlet of the next cell, given its position at the outlet of the previous cell.
This mapping is known in the theory of dynamical systems as a Poincare first recurrence map, or recurrence map for short. Fig. 2A shows one instance of the map for a given geometry. The shape of the recurrence map determines the characteristics of the particle trajectory. The point of discontinuity on the x axis corresponds to the position , where the separatrix crosses the inlet line. All of the inlet points between 0 and correspond to veering streamlines and, because of the imposed periodic boundary conditions, map to the upper-left branch of the recurrence map. The direct streamlines (green) corresponding to inlet points between and map to the lower-right branch of the map. The recurrence map is not a straight line, but has curvature. In the point-like pillar array, the recurrence map is a straight line (SI Appendix).
Fig. 2.
The recurrence map of a particle trajectory and corresponding traces in a unit cell and over the length of the array. (A) Ten iterations of the recurrence map starting at . Here, and . (B) A particle trajectory across the 10 rows of the DLD array superimposed on the unit cell, showing how the ending of one trajectory segment maps back to the starting position of the next. The numbers on the left side indicate the initial positions (), and the numbers on the right side show the corresponding final positions (). (C) A particle trajectory in the pillar array, crossing 10 rows of pillars. The direct and zigzag transitions are represented in green and red, respectively.
The map can be iterated to track the trajectory of small particles over consecutive unit cells in the array for any system geometry. Fig. 2 A and B shows a particle originally at position 0 being transported to position 1 in the outlet line. Identifying the outlet line of this cell with the inlet line of the next cell, we identify the equivalent point 1 on the inlet line. Iterating this procedure, the particle ultimately lands at position 9 on the inlet line, which corresponds to a veering streamline. The particle now follows the red streamline and moves to the cell below, which is represented as reentering the cell from the top (blue streamline) to end up at position 10. This process simulates a single trajectory over multiple consecutive cells as shown in Fig. 2C, where the 10 streamline segments described above as entering and exiting from the same unit cell are now unfolded as they exist in the actual array. Because the trajectories of Fig. 2C are equivalent to the trajectories of Fig. 2A, the recurrence map can therefore be used to represent any single trajectory over multiple cells as the composition of a single function.
We will call the span of a particle trajectory a “cycle,” which starts when the particle enters the unit cell after having zigzagged the previous pillar (i.e., right before entering the unit cell, the particle trajectory was a blue veering streamline in the previous cell), continues while the trajectory corresponds to direct streamlines, and completing the cycle when the particle escapes the unit cell as a red veering streamline. For example, the trace in Fig. 2C shows one cycle starting at position 0, corresponding to a trajectory that in the previous iteration had escaped the unit cell as a veering streamline (blue) and continued for 9 iterations as direct segments (green). In the next iteration, the trajectory exited the cell as a veering streamline (red) and started again as a direct segment (green).
These 10 segments constitute a cycle. We will call the number of segments in one cycle the “local periodicity” and denote it by , as shown in Fig. 2C. This cycle can be written as follows:
where . If the system had perfect symmetry, the local periodicity should be the same as the structural periodicity of the pillar array, as defined in the original model (12), and . In reality, the hydrodynamics in the unit cell are distorted such that the local periodicity may be different from , as shown in Fig. 2 A and B, where the last point (10) does not match with the position.
Because of this mismatch between the and positions, the local periodicity of a trajectory changes intermittently between two consecutive integers and . An illustration of this intermittency over multiple cycles is shown in detail in SI Appendix. We defined the pseudoperiodicity from the average of local periodicities ().
Although we write the formula as , the number of cycles can be finite if the particle stops at a stagnation point. The value of is typically a noninteger number between and .
We calculated the recurrence map of pillar arrays with different geometries, as well as the local periodicity over multiple cycles (SI Appendix, Fig. S2 A–D). As the pillar diameter increases, approaches the line, and as a result, the local periodicity of each cycle increases, even though the structural periodicity is the same. As , the map approaches a tangent bifurcation, which is one of the known routes to chaos through intermittency.
Geometric Effects on the Migration Angle.
The pseudoperiodicity is the average of the local periodicity of a particle trajectory over multiple cycles. Therefore, the migration angle of a trajectory can be calculated from its pseudoperiodicity. If the pseudoperiodicity is larger than , the average trajectory direction does not fall in line with the x axis of the array (Fig. 3, red and blue line). In this case, we define the trajectory as in an “altered zigzag mode,” and a nonzero migration angle is given by
The structural periodicity of the array can be computed as
Therefore, the ratio between the altered zigzag mode migration angle and the pillar structural angle, assuming small angles, becomes:
As , the altered zigzag migration angle can be greater than zero.
Fig. 3.
The migration modes of a particle trajectory in a DLD array and the corresponding angles. The bumping, altered zigzag, and zigzag modes are represented in red, blue, and green lines, respectively. Here, the structural periodicity is 5, and the pseudoperiodicity of the particle trajectory is 8.
We computed the particle trajectories over multiple pillar arrays with the same structural periodicity, but different pillar diameters (SI Appendix, Fig. S2). As the pillar diameter increases, the pseudoperiodicity increases regardless of the initial position (SI Appendix, Fig. S3 A–D) and a corresponding increase in the migration angle results. This nonzero altered zigzag migration angle is solely the result of the geometry of the pillar array modifying the fluid flow, and not the interactions of the particle with the pillars.
In Fig. 4A, we plot the normalized migration angle as a function of the ratio between the pillar diameter and the lateral pitch distance . We can see that there is no dependence of with for arrays with , and as in the original theory. For , we can see a mild dependence of with the normalized pillar diameter. However, at , there is a dramatic increase of with , where the larger pillar diameters and closer pillar row spacing enhance the normalized migration angle closer to bumping mode.
Fig. 4.
Experimental validation of our predictions using nanoDLD arrays. (A) Normalized migration angle as a function of the pillar-to-pitch ratio for both simulations and experiments. B–D and F–G points represent the corresponding experiments in A–C, F, and G. (B–D) Fluorescent microscope images of the array outlet of nanoDLD devices with increasing and . The bright regions are fluorescent bead () fluxes, which have been deflected by different degrees to the right-hand wall. The experimental details are presented in Materials and Methods. (E) The microscope image of the nanoDLD array with a heterogeneous structure ( and ). (F) The fluorescent image of a 50-nm particle migrating through two regions of a channel. The deflected particle trajectory lays between the bumping and zigzag modes (green and red lines). F, Inset provides a SEM image showing heterogeneous nanoDLD structure at the boundary of two regions. (G) A heterogeneous structure for highly efficient separation. The diagram shows the full-width injection trajectory of the and particle. The fluorescent images are composites of separate particle measurements aligned with the representative diagram.
To test these predictions, we experimentally measured the migration angle of fluorescent polystyrene beads in a series of nanoDLD arrays of varying (Materials and Methods). These experiments used full-width injection, in which particles are introduced across the entire width of the array inlet, and the migration angle is measured based on how much the particle flux is deflected (11). Beads were run at velocities (toward the maximum obtainable with our experimental setup) to reduce the influence of diffusion (Pe 200). Importantly, for all gap sizes used, the original theory (12) would predict a critical diameter around , and, therefore, according to this theory, 50-nm particles should follow a zigzag mode. Fig. 4 B–D shows fluorescent microscope images of deflected bead flux for different , showing how the geometry of the array is influencing the lateral displacement of the beads. Fig. 4A plots the experimental results along with our model predictions.
Although there is considerable agreement between theory and experiment, the agreement is not perfect. Potential reasons for this discrepancy include the fact that the pillar array in any real device is not infinitely periodic, so that boundary effects could influence , as well as effects of the 3D nature of the flow, and the inability to completely nullify particle diffusion with high-velocity flow.
To verify the predicted dependence of the migration angle with , we fabricated and tested a nanoDLD device with two sequential pillar arrays with ratios of 1 and 2, and nm, and nm (Fig. 4E). Fig. 4F shows a fluorescence microscope image mosaic of 50-nm beads injected into the full width of the device with a first array of and 250- length, and a second array of and 500- length. Beads entering the first array follow the altered zigzag mode and deflect laterally to the upper wall (migration angle , normalized migration angle ). When the deflected flux reaches the second array, the increased axial pitch reduces the altered zigzag mode, and the bead flux no longer deflects significantly (migration angle, ; normalized migration angle, ). This phenomena is in contrast with the original theory (12), according to which the critical particle diameter should be , and therefore beads should be in zigzag mode for both regions of the array.
Our model predicts an important phenomenon—the deflection of small particles with high ratio that should operate in zigzag mode according to the original theory, a feature with practical utility. The structure in Fig. 4G exploits this concept to achieve high-efficiency separation from a single fluidic input. In the first part of the device, which we refer to as a condenser, and both and particles are deflected without the requirement of smaller gaps to bump the particles. In the second part or sorter region, and the array fractionates the particle mixture in the opposite direction. Together, the condenser and sorter arrays in series greatly simplify the fluidic input, while still allowing complete separation of particle populations by using a full-width injection layout.
Pillar-Size Effect on the Critical Diameter.
We can use the recurrence map to model the trajectories of finite-size particles and study the dependence of the critical diameter on pillar geometry. As in Inglis et al. (12), our model uses two simplifying assumptions: (i) Flow is not modified due to the particle’s presence; and (ii) the hard walls and our finite size particles interact with perfect inelastic collision.
We simulated the trajectories of the particles’ center of mass with different diameters within a unit cell. As the particle size increases, only the trajectories starting between and are allowed at the inlet line due to the hard-wall repulsion. When the particle is close to the pillar surface, several trajectories starting at different positions collapse to one trajectory [a phenomenon known as directional mode locking (21)], as shown in Fig. 5 A and B. When the particle diameter is less than the critical diameter , there exist veering streamlines (red lines in Fig. 5A), but with larger particles, only direct streamlines remain (green line in Fig. 5B). In this case, all trajectories collapse, leaving only direct streamlines, meaning that only a bump mode remains.
Fig. 5.
The trajectory of particles with different diameters and corresponding recurrence maps. (A and B) Particle trajectories inside a unit cell with different particle diameters. Here, the particle diameters are , respectively, and , and . A black circle represents the particle with a given radius. (C and D) Corresponding recurrence maps for a particle starting at the midpoint (). The dark gray regions represent a forbidden region by the particle–wall interaction as directional locking. The black circle shows the particle radius with a scale of gap size. (E) The critical diameter dependence on the pillar geometry (). (F) The effect of DLD array geometry on the transition from altered zigzag to bumping mode. The plot shows the normalized migration angle as a function of particle size for different pillar diameter (). The simulated particle diameters range from 1 to 110 nm, and the pillar diameters are . The dotted lines represent the critical diameter calculated from E.
Fig. 5 C and D show the recurrence maps for particles with different diameters. With increasing particle size, the allowed region in the map (bright gray) shrinks due to geometric constraints of the particle and pillars. When the starting position is close to the streamline that leads to the stagnation point (), the mapping function becomes constant because the collapsed trajectories give the same final position. When a particle has a larger radius than the distance to the streamline that leads to the stagnation point (), the map will have a fixed point, and all trajectories will collapse into the bumping-mode streamline (Movie S1). Therefore, the recurrence map gives the critical diameter of the system.
Note that this corresponds to the width of the flux stream in the original theory (12).
The critical diameter dependence on the geometry is shown in Fig. 5E for various systems. Unlike the original theory (dashed line), the critical diameter in our model depends on the ratio . We observe two different behaviors depending on the ratio . When the , the ratio decreases as the pillar size increase (red line), meaning that will be smaller than suggested by the original theory. When and 2 (green and blue lines), the critical diameter increases as the pillar size increases. These results can be understood based on the particle trajectory’s pseudoperiodicity. The inlet flow is divided by lanes separated by streamlines that will end in a stagnation point downstream. The critical diameter can be calculated as twice the width of first lane, which carries of the total flux through the inlet. In the original DLD model, the periodicity is the structural periodicity of the array, whereas in our model, increases substantially with the pillar diameter when . Therefore, the first stream width decreases with large pseudoperiodicity , and, as a result, the critical diameter decreases. A similar argument can be used to explain the critical diameter dependence on the pillar size in the case of and , whereas .
Fig. 5F shows the transition between the altered zigzag mode and bumping mode for diameters ranging from to and for different pillar diameter and gap size . The migration angle shows a binary transition between a zigzag and bump mode in all cases, as expected when diffusion is not present. Consistent with our earlier observations, the migration angle of small particles increases as the pillar diameter increases, and the critical diameter decreases as the pillar diameter increases. Interestingly, the migration angle for particle diameters has subtle transitions for . These transitions may be related to the intermittency of the local periodicity similar to a devil’s-staircase-like structure in a phase-locking system. (22).
Conclusions
The original theory explaining the principles of operation of DLD arrays was formulated under the assumption that the symmetry of the fluid streamlines would match the symmetry of the pillar array. Our work shows that this assumption does not provide a complete picture of the underlying physics. By reformulating the principle of operation of DLD arrays, we have shown that particle trajectory dependencies on array geometry are stronger than in the original theory and that the particle trajectory behavior is considerably richer than originally thought. The nonzero migration angle of small particles discussed in this work stems from the anisotropic permeability of row-shifted parallelogram DLD array layouts, as has been discussed by other authors (15, 23). Indeed, we confirmed that the velocity field averaged over a unit cell has a nonzero lateral component and that the angle between the average velocity vector and the pressure gradient direction is almost identical to the migration angle of small particle trajectories calculated by using the recurrence map. (SI Appendix, Fig. S1).
Despite the remarkable agreement between theory and experiment shown in Fig. 4A, we should note the assumptions and limitations of our theory. First, we assume an infinite lattice and neglect the effect of the array-bounding walls. Second, the fact that the mean direction of the streamlines follows an angle not in the direction of the pressure gradient imposes an anisotropic permeability on the fluid flow. In finite arrays, this off-axis flow would create a depletion of fluid from one wall and a buildup of fluid on the other wall, modifying the pressure boundary conditions assumed in our model. Both of these limitations will be less severe if the array is sufficiently extended. A third limitation is the assumption that the unit cell has constant pressure at the input and output. Simulations done in systems of two or more unit cells show that this assumption is approximately correct. Finally, we assume that the particle presence does not affect the streamlines and that the particle–pillar interaction can be reduced to a hard-wall repulsion. These assumptions can be justified by using Maxey–Riley equations and the fact that the Reynolds number in the system is small (supplement in ref. 11). (Note that some of these approximations are also made in the original theory.)
Our theory provides rules on how to modify the pillar array geometry to tune not only the critical diameter, but also the migration angle of small particles in the altered zigzag mode. These results can be used as guiding principles for DLD design to control the separation of particles and biocolloids from the microscale to the nanoscale. The condenser adaptation of these design rules also provides a path toward simplified DLD systems that can achieve full separation of particles by using a single fluidic inlet.
Materials and Methods
Continuum Simulation.
We calculated the 2D velocity and pressure fields in a unit cell by solving the Navier–Stokes equation using the finite volume method. Several techniques, such as the finite element method (COMSOL) and the Boltzmann lattice method have been used to simulate particle motion in a pillar array (15, 24). In this work, we used OpenFOAM together with its Lagrangian particle tracking library (25). In addition, gmsh was used for a mesh generation tool. By using it, the geometric components () were parameterized, and different designs were simulated in a systematic way (26). The simulations presented in the work were run with an unstructured mesh with a total of mesh cells. We explored different mesh sizes as well as different residual resolutions, confirming the consistency of the simulation results. The residual resolution for the simulations shown in the work was set as .
A discrete element method was used to calculate the particle trajectories in the fluid, taking into account the necessary particle–pillar interaction. For the latter, we used a simple hard-wall repulsion model with homemade code modifying OpenFOAM’s Lagrangian particle library. Other particle–pillar interactions such as soft-wall models are available, but the simplified model can grab the essence of the dynamics (21). We calculated and mapped the trajectories of a diameter particle as a streamline tracer at 1,000 starting positions along the inlet (segment AC in Fig. 1). These particle traces are almost identical to the flow streamlines. An average fluid velocity of was used, and different time steps were tested to confirm the consistency of the simulated trajectories. The recurrence map was generated by using Python as the programing language. The continuous line in the map was constructed by linear interpolation between 1,000 data points. We also confirmed that the results of the recurrence map with >1,000 points were consistent with the simulations using 1,000 points at the inlet.
Chip Fabrication.
The nanoDLD device arrays were fabricated on 40- ×40-mm chips on wafers to permit fluorescence imaging of nanoscale polymer beads as described in ref. 11. Briefly, lithographic definition of fluidic features were first etched into an -thick hard mask (HM) by using a two-stage process: (i) optical contact lithography was used to define the microchannel features followed by a reactive-ion etch (RIE) to transfer these features into the HM; (ii) after stripping the resist from (i), a combination of electron-beam (e-beam) and deep-ultraviolet (DUV) lithography were used sequentially to pattern the nanoDLD pillar array features by adjoining the microchannels, transferring these features into the same HM by using a similar RIE process. With both sets of patterns etched into the HM down to bulk Si, all open features were simultaneously etched into into the silicon by using an DPSII ICP etch chamber (Applied Materials). This double-stage lithographic process permitted predefinition of microchannels, and subsequent use of e-beam/DUV lithography provided a robust platform for rapid and flexible prototyping of various nanoDLD arrays used within this study. Final chip preparation required stripping the HM oxide in 10:1 dilute hydrofluoric acid and regrowing a thin thermal oxide layer ranging from 10 to 50 nm, depending on the desired gap size.
The 40- × 40-mm chips were bonded with -thick borosilicate coverslips, micromachined with a custom array of holes (Mark Optics Inc.) for making fluidic connection between the chip and an external connector. Chips were sequentially cleaned with acetone and then isopropanol and jet-dried. To prepare a hydrophilic bonding surface, chips were run in plasma RIE for 20 min, and then both the chips and coverslip were run in Piranha solution [1:1 (vol:vol) sulfuric acid:nitric acid, 90 °C for 60 min]. Chips and coverslips were then washed sequentially with deionized water, acetone, and then isopropanol and immediately jet-dried. The coverslip was then immediately aligned and contacted to the chip surface. Pressure, applied by a tweezer tip, was used to make a tacking bond between the coverslip and chip, in which pockets of air were pushed out of the interface. Bonded chips were then annealed at 550 °C for 8 h.
Priming Chip.
To wet the chips a 100-mL solution of 2% (vol/vol) Tween 20 (Sigma-Aldrich) in deionized water was prepared in a 500-mL beaker. A custom glass holder was used to position the chips vertically, with the inlet ports down, in the Tween 20 solution to allow capillary wetting of the fluidic channels. Typical wetting times were h for the liquid to reach the outlet ports. The chip was then fully submerged in Tween 20 solution for 16–24 h to allow any residual bubbles to clear from the device. Chips were then rinsed thoroughly with deionized water and jet-dried. Immediately, the chip was transferred to a custom-built flow cell, and the inlet ports were filled with Tween 20 solution to prevent drying out of the fluid channels. For small gap sizes (e.g., ), some bubbles would remain in the fluid channel near the array and would have to be purged before running experiments. For purging method, the flow cell was connected to the drive pump (vida infra) and run at bar for , during which time all remaining bubbles collapsed.
Bead Displacement Experiments.
NanoDLD device chips with gap sizes ranging from were prepared as described above. Fluorescence-dyed polystyrene beads with carboxylate groups (Bangs Laboratories Inc.) were used as the testing sample, having particle diameter particles per mL, with excitation at 488 nm and emission at . The 1:100 (vol:vol) dilutions of as-supplied bead stock to 2% (vol/vol) Tween 20 solution were prepared and used for all experiments. Diluted bead solution was loaded into the fluid cell (), injected at 10 bars, and watched via a microscope/camera until the beads arrived. For driving the fluid, a syringe pump and pressure sensor (QMixx, Cetoni GmBH) was connected to the inlet port of the fluid cell. Imaging was carried out on a Zeiss Scope.A1 upright fluorescence microscope coupled with an Andor iXon Ultra 897 (Andor Technology Ltd., Oxford Instruments) EMCCD camera connected to a computer, where both imaging and pump pressure were controlled. Exposure time was 17.9 ms per frame and 200 frames per video. A LED was used for excitation, with the Zeiss filter set 38 HE (470/40 excitation, 495 beam splitters, 525/50 emission). Once bead flow across the entire array width was established, the pressure was increased to 18 bars (the maximum permitted by our system), and the bead fluorescence was imaged along the length of the array. The bead velocity was estimated from extrapolation of the speed measured from particle traces as a function of applied pressure, . The fluorescence profile at the outlet of the array was measured by using custom software, using the average intensity of video of the bead flow. From the fluorescence intensity profile, the displacement of the bead flow, , was estimated from the inflection point at the onset transition from no fluorescence (depleted region) to fluorescence (bead flux region). The bead migration angle was then calculated from the displacement by , with the length of array, .
Supplementary Material
Acknowledgments
We thank Stacey Gifford, Navneet Dorgra, and Pablo Meyer from the IBM Nanobiotechnology program, and Prof. Howard A. Stone from Princeton University for fruitful discussions. We also thank the IBM Microelectronics Research Laboratory staff for processing the microfluidic chips used in this study, with special thanks to Simon Dawes and Markus Brink for e-beam lithography assistance.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1706645114/-/DCSupplemental.
References
- 1.McGrath J, Jimenez M, Bridle H. Deterministic lateral displacement for particle separation: A review. Lab Chip. 2014;14(21):4139–4158. doi: 10.1039/c4lc00939h. [DOI] [PubMed] [Google Scholar]
- 2.Huang LR. Continuous particle separation through deterministic lateral displacement. Science. 2004;304(5673):987–990. doi: 10.1126/science.1094567. [DOI] [PubMed] [Google Scholar]
- 3.Morton KJ, et al. Crossing microfluidic streamlines to lyse, label and wash cells. Lab Chip. 2008;8(9):1448–1453. doi: 10.1039/b805614e. [DOI] [PubMed] [Google Scholar]
- 4.D’Silva J, Austin RH, Sturm JC. Inhibition of clot formation in deterministic lateral displacement arrays for processing large volumes of blood for rare cell capture. Lab Chip. 2015;15(10):2240–2247. doi: 10.1039/c4lc01409j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Holm SH, Beech JP, Barrett MP, Tegenfeldt JO. Separation of parasites from human blood using deterministic lateral displacement. Lab Chip. 2011;11(7):1326–1332. doi: 10.1039/c0lc00560f. [DOI] [PubMed] [Google Scholar]
- 6.Inglis DW, Herman N, Vesey G. Highly accurate deterministic lateral displacement device and its application to purification of fungal spores. Biomicrofluidics. 2010;4(2):024109. doi: 10.1063/1.3430553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Davis JA, et al. Deterministic hydrodynamics: Taking blood apart. Proc Natl Acad Sci USA. 2006;103(40):14779–14784. doi: 10.1073/pnas.0605967103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Inglis DW, et al. Determining blood cell size using microfluidic hydrodynamics. J Immunol Methods. 2008;329(1-2):151–156. doi: 10.1016/j.jim.2007.10.004. [DOI] [PubMed] [Google Scholar]
- 9.Inglis DW, Lord M, Nordon RE. Scaling deterministic lateral displacement arrays for high throughput and dilution-free enrichment of leukocytes. J Micromech Microeng. 2011;21(5):054024–054028. [Google Scholar]
- 10.Okano H, et al. Enrichment of circulating tumor cells in tumor-bearing mouse blood by a deterministic lateral displacement microfluidic device. Biomed Microdevices. 2015;17(3):9964. doi: 10.1007/s10544-015-9964-7. [DOI] [PubMed] [Google Scholar]
- 11.Wunsch BH, et al. Nanoscale lateral displacement arrays for the separation of exosomes and colloids down to 20 nm. Nat Nanotechnol. 2016;11:936–940. doi: 10.1038/nnano.2016.134. [DOI] [PubMed] [Google Scholar]
- 12.Inglis DW, Davis JA, Austin RH, Sturm JC. Critical particle size for fractionation by deterministic lateral displacement. Lab Chip. 2006;6(5):655–658. doi: 10.1039/b515371a. [DOI] [PubMed] [Google Scholar]
- 13.Kulrattanarak T, van der Sman RGM, Schroën CGPH, Boom RM. Analysis of mixed motion in deterministic ratchets via experiment and particle simulation. Microfluid Nanofluidics. 2010;10(4):843–853. [Google Scholar]
- 14.Zeming KK, Salafi T, Chen CH, Zhang Y. Asymmetrical deterministic lateral displacement gaps for dual functions of enhanced separation and throughput of red blood cells. Sci Rep. 2016;6:22934. doi: 10.1038/srep22934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kulrattanarak T, et al. Mixed motion in deterministic ratchets due to anisotropic permeability. J Colloid Interface Sci. 2011;354(1):7–14. doi: 10.1016/j.jcis.2010.10.020. [DOI] [PubMed] [Google Scholar]
- 16.Heller M, Bruus H. A theoretical analysis of the resolution due to diffusion and size dispersion of particles in deterministic lateral displacement devices. J Micromech Microeng. 2008;18(7):075030–075037. [Google Scholar]
- 17.Long BR, et al. Multidirectional sorting modes in deterministic lateral displacement devices. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;78(4):046304–046309. doi: 10.1103/PhysRevE.78.046304. [DOI] [PubMed] [Google Scholar]
- 18.Cerbelli S, Giona M, Garofalo F. Quantifying dispersion of finite-sized particles in deterministic lateral displacement microflow separators through Brenner’s macrotransport paradigm. Microfluid Nanofluidics. 2013;15(4):431–449. [Google Scholar]
- 19.Vernekar R, Krüger T, Loutherback K, Morton K. 2016. Anisotropic permeability in deterministic lateral displacement arrays. arXiv:1610.08427. [DOI] [PubMed]
- 20.Cerbelli S. Separation of polydisperse particle mixtures by deterministic lateral displacement. The impact of particle diffusivity on separation efficiency. Asia-Pacific J Chem Eng. 2012;7:S356–S371. [Google Scholar]
- 21.Frechette J, Drazer G. Directional locking and deterministic separation in periodic arrays. J Fluid Mech. 2009;627:379–23. [Google Scholar]
- 22.Bak P. Commensurate phases, incommensurate phases and the devil’s staircase. Rep Prog Phys. 1982;45(6):587–629. [Google Scholar]
- 23.Alshare AA, Strykowski PJ, Simon TW. Modeling of unsteady and steady fluid flow, heat transfer and dispersion in porous media using unit cell scale. Int J Heat Mass Transf. 2010;53(9-10):2294–2310. [Google Scholar]
- 24.Cerbelli S, Garofalo F, Giona M. Effective dispersion and separation resolution in continuous particle fractionation. Microfluid Nanofluidics. 2015;19(5):1035–1046. [Google Scholar]
- 25.Weller HG, Tabor G, Jasak H, Fureby C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput Phys. 1998;12(6):620–13. [Google Scholar]
- 26.Geuzaine C, Remacle JF. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int J Numer Method Eng. 2009;79(11):1309–1331. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.