The Na/K pump exports cytoplasmic Na ions while importing K ions, and its activity is thought to be affected by restricted intracellular Na diffusion in cardiac myocytes. Lu and Hilgemann find instead that the pump can enter an inactivated state and that inactivation can be relieved by cytoplasmic Na.
Abstract
Decades ago, it was proposed that Na transport in cardiac myocytes is modulated by large changes in cytoplasmic Na concentration within restricted subsarcolemmal spaces. Here, we probe this hypothesis for Na/K pumps by generating constitutive transsarcolemmal Na flux with the Na channel opener veratridine in whole-cell patch-clamp recordings. Using 25 mM Na in the patch pipette, pump currents decay strongly during continuous activation by extracellular K (τ, ∼2 s). In contradiction to depletion hypotheses, the decay becomes stronger when pump currents are decreased by hyperpolarization. Na channel currents are nearly unchanged by pump activity in these conditions, and conversely, continuous Na currents up to 0.5 nA in magnitude have negligible effects on pump currents. These outcomes are even more pronounced using 50 mM Li as a cytoplasmic Na congener. Thus, the Na/K pump current decay reflects mostly an inactivation mechanism that immobilizes Na/K pump charge movements, not cytoplasmic Na depletion. When channel currents are increased beyond 1 nA, models with unrestricted subsarcolemmal diffusion accurately predict current decay (τ ∼15 s) and reversal potential shifts observed for Na, Li, and K currents through Na channels opened by veratridine, as well as for Na, K, Cs, Li, and Cl currents recorded in nystatin-permeabilized myocytes. Ion concentrations in the pipette tip (i.e., access conductance) track without appreciable delay the current changes caused by sarcolemmal ion flux. Importantly, cytoplasmic mixing volumes, calculated from current decay kinetics, increase and decrease as expected with osmolarity changes (τ >30 s). Na/K pump current run-down over 20 min reflects a failure of pumps to recover from inactivation. Simulations reveal that pump inactivation coupled with Na-activated recovery enhances the rapidity and effectivity of Na homeostasis in cardiac myocytes. In conclusion, an autoregulatory mechanism enhances cardiac Na/K pump activity when cytoplasmic Na rises and suppresses pump activity when cytoplasmic Na declines.
Introduction
How diffusion is influenced by the molecular constituents of living cells remains an important and sometimes controversial biological problem. Diffusion of Na ions in cardiac myocytes was proposed in the 1970s to be restricted to such an extent that subsarcolemmal Na concentrations would increase by several millimolar during each excitation–contraction cycle (Akera et al., 1976). This idea was revived in 1990 with the suggestion that Na influx through Na channels could drive Ca influx via Na/Ca exchangers in a restricted subsarcolemmal space (Leblanc and Hume, 1990) that was dubbed “fuzzy space” (Lederer et al., 1990). Direct support for this idea emerged later when ion microprobe studies reportedly revealed large, activity-dependent Na gradients over subsarcolemmal distances of 30 nm with dissipation times of ∼10 s (Wendt-Gallitelli et al., 1993). That Na diffusion in cardiac myocytes is indeed peculiar and highly constrained appeared to be verified by one further study using Na-sensitive dyes (Despa et al., 2004). In that study, Na diffusion coefficients were estimated to be 50 times smaller in the cytoplasm of myocytes than in free water. A more recent Na dye study reportedly identified Na “hot spots” in smooth muscle cells (Poburko et al., 2007).
Apart from these measurements, numerous functional studies suggest that subsarcolemmal Na gradients exist in one form or another. Action potential and Na reversal potential measurements suggested the existence of modest subsarcolemmal Na gradients in one recent study (Hegyi et al., 2016). However, most studies follow a paradigm that Na transport activity of one transport system causes larger functional changes of Na transport by another transport system than would be expected if there were no local, cytoplasmic Na gradients. Besides activating reverse Na/Ca exchange (Leblanc and Hume, 1990), the opening of Na channels was reported to locally activate Na-dependent K channels (Wendt-Gallitelli et al., 1993). Furthermore, Na pump activity was suggested to excessively depress reverse Na/Ca exchange activity (Bielen et al., 1991; Fujioka et al., 1998; Su et al., 1998), and the decay of Na/K pump currents during their activation by extracellular K has been widely interpreted to reflect depletion of subsarcolemmal Na (for reviews, see Carmeliet, 1992; Verdonck et al., 2004).
To place these suggestions in a quantitative context, the Na influx needed to depolarize a typical cardiac myocyte by 100 mV, assuming a cytoplasmic volume of 15 pL and ∼20 × 103 μm2 of surface area, increases the mean cytoplasmic Na concentration by only ∼8 μM, and Na diffusion across 30 nm of free water takes place in a microsecond. For Ca channels, located at junctions between the sarcoplasmic reticulum and cell surface, nanoscale subsarcolemmal Ca gradients are expected to develop and decay on a millisecond timescale in parallel with the opening and closing of Ca channels (Shang et al., 2014). This same physical arrangement might support small subsarcolemmal Na accumulations that promote reverse Na/Ca exchange (Leblanc and Hume, 1990). However, most results mentioned require the existence of long-lived Na gradients over short distances. How such gradients would be supported (Carmeliet, 1992) remains enigmatic, and whether they exist remains unsubstantiated. A more recent ion microprobe study did not verify the existence of activity-dependent Na gradients in cardiac myocytes (Silverman et al., 2003), and a more recent Na dye study indicates that Na diffusion in cardiac myocytes takes place only twofold slower than in free water (Swietach et al., 2015), consistent with classical studies of ion diffusion in skeletal muscle (Kushmerick and Podolsky, 1969) and geometrical tortuosities of the cardiac cytoplasmic space (Swietach et al., 2015). For mouse myocytes, used here, mitochondria contribute with good certainty to this tortuosity (Agarwal et al., 2016; Richards et al., 2016), constituting ∼35% of the cytoplasmic space (Bossen et al., 1978; Eisele et al., 2008). In addition to myofilaments and sarcoplasmic reticulum, transverse tubules, which constitute 40% of membrane surface area, will also contribute significantly (Bossen et al., 1978).
Recently, we have examined whether Na/K pump current decay during continuous activation by saturating extracellular K concentrations indeed reflects cytoplasmic Na depletion or might rather reflect an inactivation mechanism (Lu et al., 2016). Most of our results support the idea that Na/K pumps inactivate in “E1” configurations and recover from inactivation in a Na-dependent manner. Furthermore, our results suggest that Na/K pump conformational changes can significantly affect physical properties of the cardiac sarcolemma, as monitored via the permeation of hydrophobic cations. Accordingly, Na/K pumps might modulate the function of transporters in their vicinity by mechanisms other than depletion of Na. To further address these issues, we now differentiate more rigorously the roles of Na depletion and inactivation in Na/K pump current decay transients. To do so, we have analyzed the kinetics of ion turnover in patch-clamped cardiac myocytes by using veratridine (Shanes et al., 1953) to generate persistent conductances for monovalent cations in the cardiac sarcolemma (Sperelakis and Pappano, 1969; Brill and Wasserstrom, 1986; Zong et al., 1992) and by using the ionophore channel nystatin to generate sarcolemmal conductances for all monovalent ions (Marty and Finkelstein, 1975). Analysis of current decay kinetics, reversal potential changes, and access resistance changes associated with ion accumulation suggest that all monovalent ions equilibrate with similar, unrestricted kinetics. Although Na/K pump inactivation and cytoplasmic Na depletion can both occur and can overlap kinetically, inactivation is usually faster than cytoplasmic Na depletion, and subsarcolemmal Na changes are usually not larger than expected from the total ionic mixing space of the cytoplasm.
Materials and methods
Electrical methods and cardiac myocytes
Patch clamp, myocyte preparation, and recording conditions were as described previously (Wang and Hilgemann, 2008; Yaradanakul et al., 2008; Lariccia et al., 2011; Lu et al., 2016). The UT Southwestern Medical Center Animal Care and Use Committee approved all animal studies. Highly polished pipette tips with diameters of >3 µm were used, and access resistances during recordings with standard experimental solutions ranged from 1.5 to 4 MΩ. Experiments were performed at 0 mV and 37°C, except as indicated. The mathematical routine used to quantify capacitance determines all charge moved in the transient components of current during voltage steps (Wang and Hilgemann, 2008). Voltage steps were 10 to 20 mV, and step durations were 2 to 5 ms. Electrical time constants were 150 to 500 µs. Current–voltage relations were determined by applying alternating positive and negative voltage steps of increasing magnitude away from and back to the 0 mV holding potential for 100 ms. Data points are mean current values during the voltage pulse with omission of the first 5 ms that contained the capacitance transient. Best exponential fits of transient currents were determined by a least squares method, and the fitted exponential functions are given in many figures as faint lines.
Solutions
Standard solutions used (Lu et al., 2016) minimize currents besides Na/K pump currents and were designed to be isosmotic (290 mosM/liter). The standard extracellular solution contained 110 mM NMDG, 4 mM MgCl2 ±2 mM CaCl2, 0.5 mM EGTA, 20 mM TEA-OH, 7 mM NaCl or KCl, and 10 mM HEPES, set to pH 7.0 with aspartate. The standard cytoplasmic solution contained 90 mM KOH or 90 mM NMDG, 20 mM TEA-OH, 25 mM Na-OH, 15 mM HEPES, 0.5 mM MgCl2, 0.5 mM EGTA, and 0.25 mM CaCl2, set to pH 7.4 with aspartate. Unless stated otherwise, 6 mM MgATP, 1.5 mM TrisATP, and 0.2 mM GTP were used in cytoplasmic solutions, generating a free Mg2+ of ∼0.5 mM. When NMDG was replaced by other monovalent cations, the cations were added as hydroxides. All cytoplasmic and extracellular solutions contained 20 mM TEA. Solutions using 10 and 60 mM EGTA were prepared by first dissolving EGTA with the hydroxides used to give a neutral pH, followed by heating to 80°C for 20 min with the required amounts of CaCO3.
Reagents and chemicals
All salts were from Sigma-Aldrich and were the highest available grade.
Simulations of ion turnover ion kinetics
For orientation to the experiments, we describe here simulations of ion turnover kinetics in simple whole-cell patch-clamp models, and we describe subsequently a Na/K pump model used to simulate Na/K pump function both separately from and combined with simulations of ion turnover. All simulations were developed in MATLAB, and integration was performed with accuracy control equivalent to the width of the lines plotted in figures.
Analysis of ion kinetics in patch-clamp experiments
We describe first results for diffusion in one dimension and second results for simulations with instantaneous ion mixing. In the diffusion model, we recreate the geometry of the patch pipette and the myocyte as shown in Fig. 1 A. Concentrations are simulated in millimolar units, dimensions are in microns, and ion fluxes are calculated in picoampere equivalents. For the results presented, a discretization step of 7.14 μm was used. The myocyte was assumed to be a tapered cylinder 100 μm long with a minimum radius (rmin) of 1.2 μm, equal to the radius of the myocyte opening into the patch pipette tip. The maximal myocyte radius is 6.6 μm, giving a cytoplasmic mixing volume of 9.4 pL. This volume is ∼40% of the measured mean total volume of murine myocytes (Bensley et al., 2016), and this choice will be discussed in relation to experimental results. The radius of the myocyte (rmyo) at length, λmyo, is:
| (1) |
As illustrated in Fig. 1 A, the contour of the pipette tip was approximated by a rectangular hyperbola that entirely hides the outline of the pipette wall in the micrograph. As shown in the figure, we assumed for simplicity that the pipette tip was attached to the tip of the myocyte. The radius of the pipette (rpip) at length, λpip, is:
| (2) |
Although we normally perform patch clamp near the center of myocytes, we noted no significant differences for results using terminal attachment versus mid-cell attachment (n > 15), and our simulations support that longitudinal diffusion is at most a small determinant of experimental results.
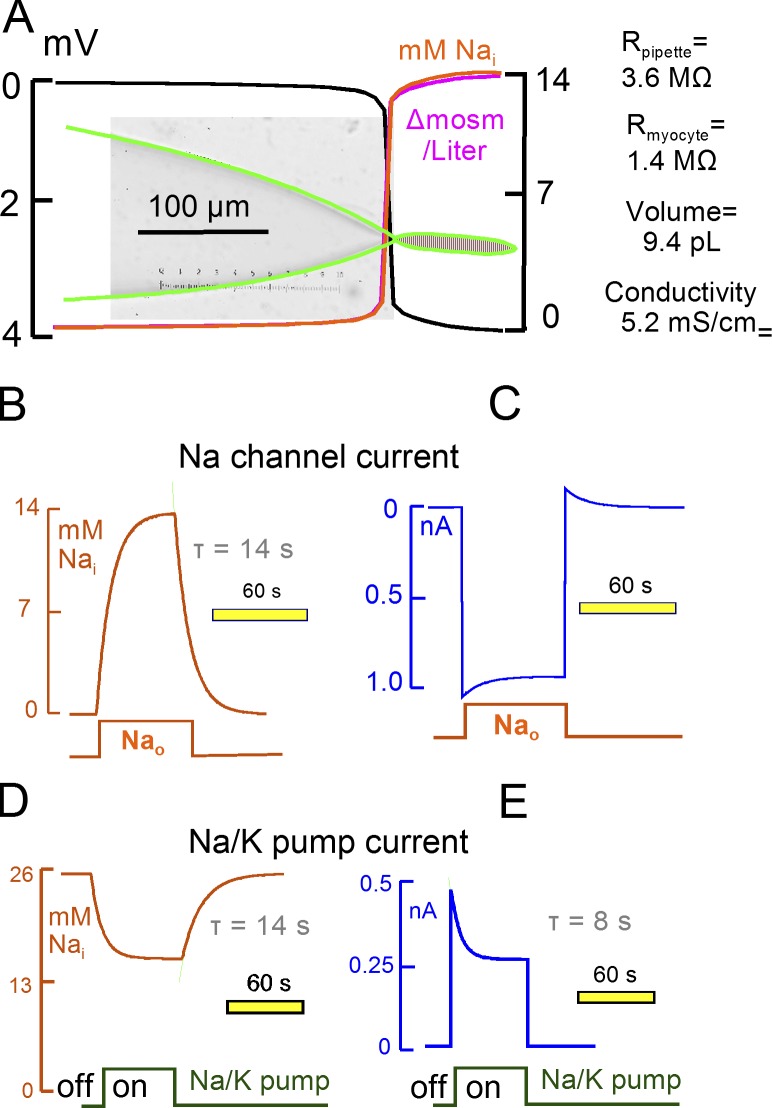
Figure 1.
Simulation of Na diffusion and turnover in a patch-clamped cardiac myocyte. The pipette resistance is 3.6 MΩ when using the standard low-conductance (5.2 mS/cm) NMDG-Asp–containing pipette solution. Myocyte volume is 9.4 pL, and the longitudinal myocyte resistance is 1.4 MΩ. (A) The micrograph of the pipette includes the microscope reticule (15 µm/large divisions). The pipette dimensions are accurately duplicated by a rectangular hyperbola (green lines). Diffusion of three ions was simulated as described in Materials and methods. The predicted electrical potential, Na concentration, and osmolarity gradients are shown during a 1 nA Na current at a 40-s time point. (B) Time dependence of Na concentration changes in the middle of the myocyte during activation of a 1 nM Na current for 60 s with 0 mM Na in the pipette. Here and in subsequent figures, we superimpose individual records with the best-fit exponential functions used to estimate time constants as faint lines, here in green. (C) Time dependence of membrane current during the responses in C. (D) Time dependence of cytoplasmic Na concentration changes with a 25 mM pipette Na concentration, during and after activation of enough Na/K pumps to generate a 0.5 nA pump current. Na/K pumps do not inactivate and the simulation includes no other conductance. (E) Time dependence of membrane current during the responses simulated in D.
We simulated the diffusion of three electrolytes, aspartate (Asp), NMDG, and Na, with diffusion coefficients (DAs, DNm, and DN) of 640, 490, and 1,300 µm2/s, respectively. Values for Na and Cl were assumed from the literature. Then, values for Asp and NMDG were forced by comparing the conductances of NaCl solutions (10.2 mS/cm at 100 mM), Na-Asp solutions (6.7 mS/cm at 100 mM), and NMDG-Asp (4.1 mS/cm at 100 mM) solutions, assuming that
| (3) |
To simulate the concentration gradient-dependent diffusion component in picoampere equivalents from millimolar and micrometer dimensions, we calculated a flux scalor (α) for each discretization step ([i]) of length, dλ:
| (4) |
The gradient-related ion fluxes were then calculated for each discretization step with electroneutrality enforced by an electrochemical coupling factor, Ke:
| (5) |
| (6) |
| (7) |
where
| (8) |
Inward and outward Na currents were assumed to be proportional to extra- and intracellular Na concentrations at 0 mV. Both Na currents (Ina) and Na/K pump currents (Ipump) were assumed to be proportional to membrane area with the density constants Kina (pA/mM/µm2) and Kpump (pA/µm2):
| (9) |
where Nout and Nin are the extracellular and intracellular Na concentrations. Na/K pump currents were proportional to a Hill equation with a slope of 2.3. This equation describes well the Na dependence of pump current under the conditions of the experiments (Lu et al., 2016):
| (10) |
To simulate 3:2 Na/K pump stoichiometry, Na pump activity was simulated to extrude three times more Na than the monovalent current equivalent, and a simultaneous influx of monovalent cations was simulated to be twice larger than the current equivalent. For simplicity, the influx component (representing K transport) was simulated to contribute NMDG to the cytoplasm. Current was then integrated laterally from the myocyte tip to the pipette tip. The electrogenic component of diffusion (FΨ) was assumed to be equal to the current integral from the tip to each discretization point in the myocyte, and it was assumed to be equal to the total myocyte current along the length of the pipette. Accordingly,
| (11) |
| (12) |
| (13) |
The potential profile (mV) was calculated from the current integral (pA) and local resistance (R[i]) in MΩ:
| (14) |
| (15) |
Finally, the discretized concentration changes were calculated from the total ion fluxes (FT):
| (16) |
| (17) |
| (18) |
Converting picoampere equivalents and picoliters with millimolar concentration changes,
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where V[i] is the discretized volume in pL (i.e., μm3/1,000).
Fig. 1 shows results, relevant to this study, for Na channels that generate ∼1 nA of continuous inward current and for Na/K pumps that generate initially ∼0.5 nA outward current. As orientation to the magnitudes of ion movements occurring over time, 1 nA of inward Na current corresponds to 1 mM/liter Na concentration change per second in a 10 pL cell, and 0.5 nA of pump current corresponds to 1.5 mM/liter Na depletion per second in a 10 pL cell. Similar to the experiments to be described, we simulate that Na channels are open continuously and that Na flux is manipulated by changing the extracellular Na concentration (120 mM). Fig. 1 A illustrates the voltage and ion gradients that develop from Na current when the pipette solution contains no Na. With the low conductance solutions used, pipette resistance amounts to 3.6 MΩ, longitudinal resistance of the myocyte is 1.4 MΩ, and the total voltage gradient amounts to 4 mV. Approximately 85% of the voltage gradient occurs within 10 μm in the narrowest part of the pipette tip, and ion gradients occur similarly. The Na gradient becomes matched by an osmotic gradient, and electroneutrality occurs equally by depletion of NMDG and accumulation of Asp in the cell and pipette tip (not depicted). As shown in Fig. 1 (B and C), cytoplasmic Na accumulates and inward current decreases with a time constant (τ) of 14 s to a steady-state Na concentration of 14 mM. With 120 mM extracellular Na, current decay amounts to 11.7%, and an equivalent reverse Na current develops when extracellular Na is removed. Fig. 1 (D and E) presents results for Na/K pump activity with a pipette solution containing 25 mM Na, with no Na channel flux, and with the same pipette parameters as in Fig. 1 (B and C). Activation of pump activity, corresponding to a 0.5 nA peak current, in the presence of 25 mM cytoplasmic Na results in depletion of 44% of total cytoplasmic Na. Depletion occurs with a smaller τ than Na accumulation/depletion during channel activity, owing to the steep dependence of Na/K pump current on the cytoplasmic Na concentration. We point out that diffusion coefficients can be decreased by factors of three to four with very little change of simulation results described in Fig. 1. Furthermore, simulations of diffusion in two dimensions (not depicted) generated results that were essentially identical to those presented in Fig. 1.
Fig. 2 presents simulation results for a model cell with instantaneous ion mixing. All results are very similar to those just presented. For instantaneous cytoplasmic ion mixing, we assume that ion concentrations in the pipette are constant and that Na contributes a larger fraction (FD) of the pipette ion flux than other components of the cytoplasmic solution in proportion to its larger diffusion coefficient (FD = Dn/(Dn + Dnm + Das)⋅3 = 1.70). In the absence of Na in the pipette, it can be estimated that
| (25) |
In the steady-state,
| (26) |
| (27) |
| (28) |
For cases in which the steady-state current is known but peak current is unknown, the solution for Ni is a quadratic equation with a = FD/Raccess ⋅ 100, b = −a ⋅ 120 − Isteady state, and c = Isteady state∙120. Then,
| (29) |
The time constant (τ) with which Na turns over from the cytoplasm is
| (30) |
and when cell conductance is small in relation to the pipette tip conductance,
| (31) |
For results presented in Fig. 2 A, ion concentrations, cell volumes, and access resistance were similar to values used in Fig. 1. As shown in Fig. 2 A, a Na current that is 1 nA in magnitude decays by ∼12% as cytoplasmic Na accumulates to 14 mM with a time constant of 15 s. Outward current activated upon removing extracellular Na decays with nearly the same time constant. Asp and NMDG accumulate and decrease in the cytoplasm as dictated by the tip potential of 3.4 mV. Fig. 2 B shows the predicted model function in dependence on the peak Na current from 0 to 6 nA. From top to bottom, the pipette tip potential increases linearly with Na current up to 18 mV, the τ of current decay decreases from 16 to 9 s, Na accumulation increases from 14 mM at 1 nA to 50 mM at 6 nA, Asp and NMDG concentration changes increase to one half of their concentrations in the absence of Na current, and osmolarity doubles with 6 nA of current. For the most part, these results reiterate a previous analysis of ion exchange in patch-clamped myocytes (Mogul et al., 1989). As described later, most of our results for ion flux and concentration changes during experiments conform to these simple predictions.
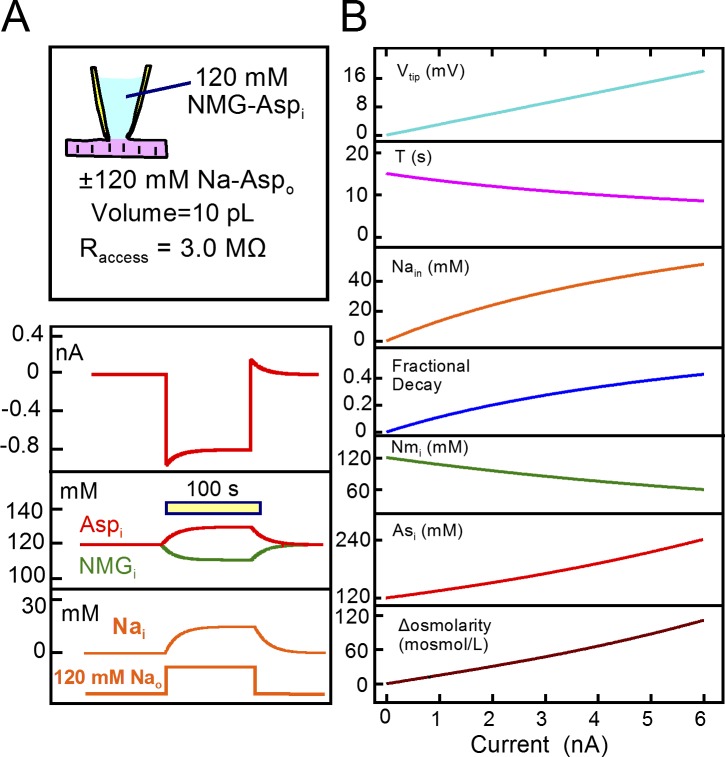
Figure 2.
Simulation of Na turnover in a patch-clamped cardiac myocyte with instantaneous ion mixing. Cell volume is 10 pL, access resistance is 3 MΩ, the patch pipette contains no Na, and the cell membrane has a Na conductance of 38 nS Na in the presence of 120 mM extracellular Na. The cytoplasm is assumed to contain initially 120 mM Asp and NMDG. (A) Application of 120 mM extracellular Na supports a 0.95 nA Na current that decays by ∼12% with a τ of 14 s. Cytoplasmic Na accumulates by 14 mM, and NMDG and Asp decrease and increase, respectively, to maintain electroneutrality. Upon removing extracellular Na, an outward Na current develops with a magnitude equal to the decaying inward current. The reverse Na current decays with nearly the same time constant as the forward current decays. (B) Complete description of the simple model in dependence on the peak Na current activated from 0 to 6 nA. From top to bottom, the tip potential increases linearly from 0 to 18 mV, the τ with which current decays decreases from 16 to 9 s, cytoplasmic Na increases from 0 to 50 mM, the fractional decay of Na current increases from 0 to 0.5, cytoplasmic NMDG decreases from 120 to 60 mM, cytoplasmic Asp increases from 120 to 240 mM, and osmolarity increases from baseline (290 mosM/liter) to 120 mosM/liter over baseline.
Simulation of Na/K pump function
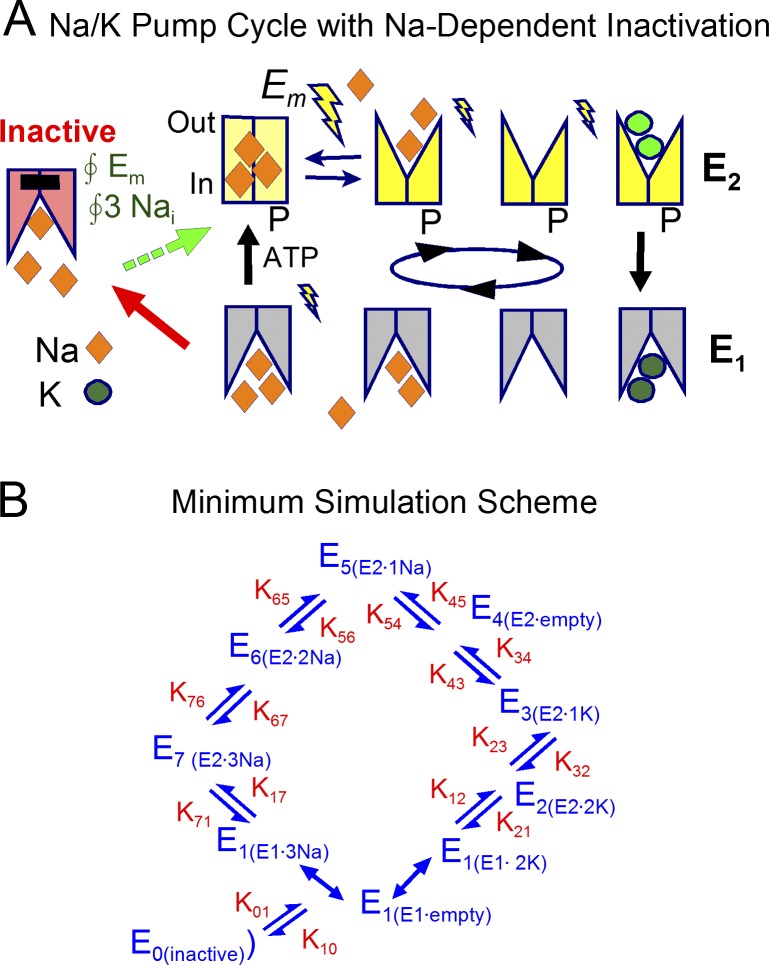
To quantitatively evaluate predictions for the Na/K pump inactivation hypothesis we require simulations of pump function that include the major electrogenic reactions (Heyse et al., 1994; Hilgemann, 1994; Gadsby et al., 2012) and that can predict the contribution of Na/K pumps to membrane capacitance. Fig. 3 A illustrates the Na/K pump cycle as it is presently proposed to occur (De Weer et al., 1988; Nakao and Gadsby, 1989; Apell et al., 1998), together with our hypothesis concerning Na/K pump inactivation (Lu et al., 2016). Fig. 3 B depicts the state diagram derived from the cartoon and simulated. In brief, the normal pump cycle occurs in clockwise fashion with strict 3Na/2K transport coupling (i.e., moving one charge per cycle). E1 states represent pumps with binding sites open to the cytoplasmic side, whereas E2 states are oriented with binding sites opening to the extracellular side. When three Na ions and ATP are bound on the cytoplasmic side (i.e., in E1 states), pumps are phosphorylated and they occlude the three Na ions in a weakly voltage-dependent step (i.e., small lightning bolt). As indicated by a large lightning bolt in Fig. 3 A, the major electrogenic reaction of the pump occurs with the deocclusion of a single Na ion to the outside, followed by release of two further Na ions and binding of two potassium ions. All of the latter steps are weakly electrogenic and voltage dependent, as indicated by small lightning bolts. We lump K occlusion by the E2 state and the opening of pumps to the cytoplasmic side (i.e., as E1 states) in a single, irreversible reaction, assuming that cytoplasmic ADP and Pi concentrations are negligible. As already indicated, we include a minor voltage dependence in the step that occludes 3Na bound from the cytoplasmic side in association with phosphorylation. This accounts for the weak voltage dependence of pump currents that persists in the absence of extracellular Na. The simulations assume that all pumps in E1 states can undergo an inactivation reaction, generating a long-lived inactive state that cannot be phosphorylated and/or cannot deocclude Na to the outside. Recovery from inactivation is assumed to occur with the same cytoplasmic Na and voltage dependence as pump phosphorylation. Accordingly, inactive pumps might to a greater or lesser extent be able to hydrolyze ATP in an uncoupled fashion.
Figure 3.
Na/K pump model with Na-dependent inactivation from E1 states. (A) Cartoon of Na/K pump function with electrogenic steps marked by lightning bolts. Binding sites open to the cytoplasmic side in E1 states and to the extracellular side in E2 states. Translocation of three Na outwardly with ATP hydrolysis and 2K inwardly with dephosphorylation are irreversible reactions under the assumption that cytoplasmic ADP and Pi are negligible. Release of the first Na ion moves 0.75 charges through membrane field, binding/release reactions of the other ions within E2 states moves 0.3 charges, and occlusion of Na from E1 states moves 0.25 charges. Inactivation occurs from all E1 states and recovery has the same Na and voltage dependence as the occlusion of cytoplasmic Na. (B) State diagram used to model Na/K pump function. The normal cycle occurs clockwise. Kinetically defined states are numbered from 0 to 7, and their ion occupancy is indicated. Reaction rates are designated by the numbering of states. E1 states bind 3Na and 2K instantaneously. Reaction rates K12 and K71 are assumed to be zero.
In simulations presented, E1 states can bind three Na ions or two K ions instantaneously in sequential, mutually exclusive reactions. To simulate accurately the voltage (Em) dependencies of pump currents and capacitive signals, we find it essential to subdivide the E2 state into six substates with time- and ion concentration–dependent transitions that correspond to binding/dissociation of each ion. The simulation begins by calculating three modifiers for the voltage-dependent reactions, assuming that voltage dependence can be asymmetrical in the forward versus backward transitions of each reaction: Na occlusion from the cytoplasmic side moves 0.15 e, the major electrogenic Na binding reaction moves 0.85 e, and the binding of the other Na ions and K ions from the extracellular side each move 0.3 e. With these assignments, the reaction cycle moves one charge per complete cycle. With F/RT = 26 mV,
| (32) |
| (33) |
| (34) |
Next, we calculate occupation of the E1 binding sites by three Na ions (F3Ni) or two K ions (F2Ki) using a sequential binding sequence. For the purposes of this presentation, it is adequate to roughly reproduce the concentration dependencies of currents (Lu et al., 2016) by using 15 mM dissociation constants for all three cytoplasmic Na sites and 30 mM dissociation constants for the two cytoplasmic K sites:
| (35) |
| (36) |
We then calculate the rate constants for the E1–E2 transitions and the transitions within E2 states, relative to a value of 1 mM−1⋅s−1 for Na binding in the major charge moving step (reaction 42, K67). ADP and Pi concentrations are assumed to be negligible, and therefore, K12 and K71 are 0:
| (37) |
| (38) |
| (39) |
| (40) |
| (41) |
| (42) |
| (43) |
| (44) |
| (45) |
| (46) |
| (47) |
| (48) |
Because the transport cycle is rapid with respect to the inactivation reaction, the fraction of inactive pumps in steady state can be approximated as
| (49) |
These reactions are then integrated with accuracy control, pump turnover is calculated by summing the rates of electrogenic reactions multiplied by their corresponding fractional charge movements (i.e., 0.15 for cytoplasmic Na occlusion, 0.85 for release of the first Na to the outside, and 0.3 for binding/dissociation of each of the other extracellular ions), and the capacitance generated by the pump is calculated from the integral of transient current components generated during 20-mV voltage steps. The rate constants used generate a pump turnover rate of 18 s−1 at 0 mV with 25 mM Nai, 7 mM Ko, and 120 mM Nao. With ∼400 pumps/µm2, as estimated in Fig. 4 from charge movements, the maximal pump turnover rate is ∼150 s−1.
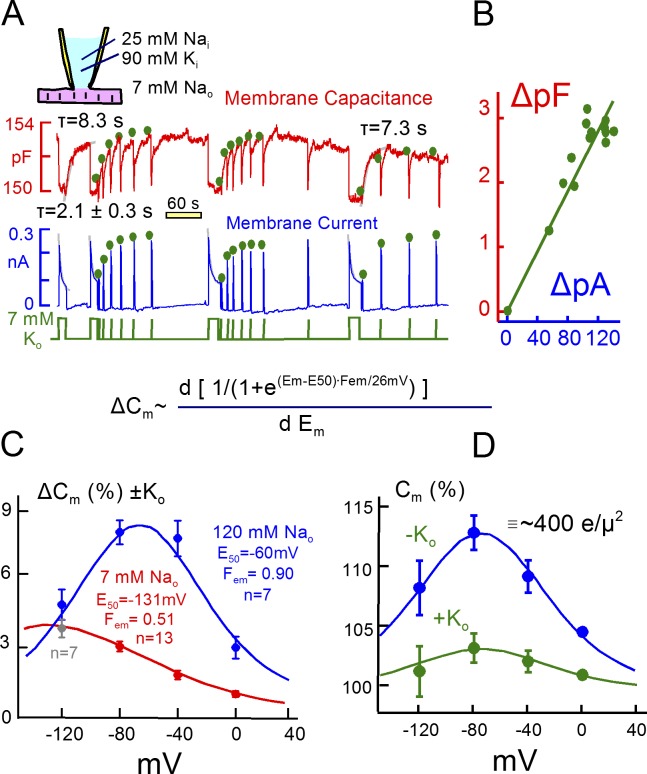
Figure 4.
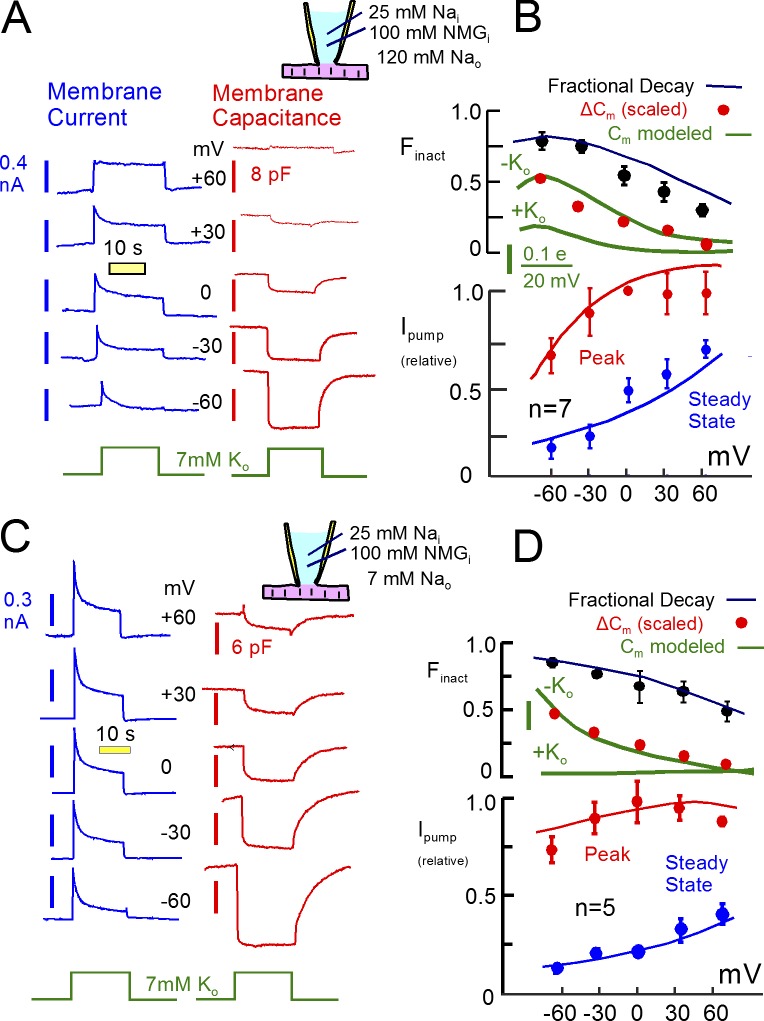
Representative Na/K pump currents and capacitance transients in the presence of 25 mM Na and 90 mM K on the cytoplasmic side. (A) Pump currents are activated by substituting 7 mM Na for 7 mM K on the extracellular side. Outward pump current decays by 70% with a τ of ∼2 s and recovers with a τ of ∼8 s. Membrane capacitance falls immediately upon pump activation by 1 to 2% and recovers with a time course that matches the recovery of pump currents. Dots above the current and capacitance records are scaled to one another to illustrate the close temporal correlation between recovery of pump current and membrane capacitance. (B) Plot of Na/K pump current changes versus capacitance changes during pump current recovery. (C) Voltage dependence of K-induced capacitance changes in the presence of 120 mM extracellular Na (blue, n = 7) and for the substitution of 7 mM Na for 7 mM K (red, n = 13, except for −120 mV, where n = 7). The bell shaped capacitance curve with 120 mM Na reflects the major charge movement of the pump with a Boltzmann slope of 29 mV and a midpoint of −60 mV. (D) Voltage dependence of capacitance in the presence of 120 mM Na in the absence (blue) and the presence (green) of 7 mM K. Note that the midpoint of the bell shifts at most 10 mV to more negative potentials. Assuming that Na and K binding are mutually exclusive, this result requires that time-dependent steps separate Na and K binding.
Choice of experimental conditions and models
In cardiac myocytes, inward rectifier K channels localize to transverse tubules where their activity can cause significant extracellular K changes (Clark et al., 2001), and in skeletal muscle, K accumulation in T-tubules can cause large changes of Na/K pump activity in response to muscle activity (DiFranco et al., 2015). To avoid an influence of extracellular K concentration changes, we activated Na/K pump currents routinely with 7 mM extracellular K. In the absence of extracellular Na, this is more than 10 times greater than the K concentration required to activate half-maximal Na/K pump currents in cardiac myocytes (Nakao and Gadsby, 1989). Based on apparent Kd’s for extracellular K determined in cardiac myocytes (Nakao and Gadsby, 1989; Han et al., 2009), this K concentration activates more than 90% of maximal pump current in the presence of 120 mM extracellular Na. Upon removing extracellular K, pump currents decayed routinely from 90% to 10% of peak values within less than 0.2 s, and time constants for current decay from 75% of maximum to complete deactivation were routinely less than 0.1 s (usually ∼50 ms). Accordingly, it is unlikely that extracellular K accumulation or depletion plays any role in the results presented.
Na/Ca exchange current cannot be used to assay Na concentration changes
Two previous studies used Na/Ca exchange currents to define subsarcolemmal Na changes during Na/K pump current transients. As described in Figs. S1, S2, and S3, we cannot justify equivalent experiments in mouse myocytes. The first of the two studies defined Na/Ca exchange currents in mouse myocytes by the substitution of extracellular Na for Li in the presence of extracellular Ca (Su et al., 1998). As described previously (Hermans et al., 1997) and confirmed in supplemental data (Fig. S1 A), extracellular Li at a concentration of 120 mM substitutes for extracellular K in activating Na/K pumps and activates nearly the maximal ouabain-sensitive pump current that can be activated with K (Hermans et al., 1997). Thus, currents interpreted as Na/Ca currents included the Na/K(Li) pump current in addition to any component of Na/Ca exchange current that may have been activated. According to that study, Tris ions could also be substituted for Na with similar results. As described in Fig. S2 B, we find that Na substitution with Tris causes an outward current shift by decreasing Na flux through the leak (patch seal) pathway (Fig. S1 B) and potentially also via nonselective cation channels that appear to exist in murine myocytes at a significant density (Fig. S3).
The second study analyzed Na/Ca exchange reversal potentials to assess Na concentration changes in response Na/K pump activity (Fujioka et al., 1998). Depending on details of the protocol, different results were obtained. Reversal potentials defined by blocking Na/Ca exchange currents with extracellular nickel in some cases suggested that Na pump activity depleted cytoplasmic Na, but in other cases decreased Na/Ca exchange activity without a change of Na concentration. As verified in Fig. S3, activation of Na/K pump activity indeed causes a substantive, time-dependent decrease of membrane conductance under conditions that support reversing Na/Ca exchange currents. However, we find it impossible to define Na/Ca exchange current reliably. As outlined in Fig. S3, application of 4 mM nickel generates a substantial inward current that is independent of the Na gradient and therefore is not related to Na/Ca exchange. Rather, murine myocytes seem to possess cation channels that conduct Ni, possibly TRPM6 and TRM7 channels (Gwanyanya et al., 2004; Li et al., 2006). We mention in this connection that we could not confirm the expected inhibition by polyamines, and lastly, we point out that Na/Ca exchangers themselves appear to transport nickel in myocytes (Egger et al., 1999). For now, therefore, Na/Ca exchangers cannot be used to define subsarcolemmal Na changes. For this reason, we proceeded to analyze cardiac monovalent cation currents activated by the Na channel opener veratridine (Sperelakis and Pappano, 1969; Zong et al., 1992) in relation to subsarcolemmal Na gradients.
Online supplemental material
Fig. S1 shows extracellular Na substitution cannot be used to define outward Na/Ca exchange current. Fig. S2 shows Na/K pump activity modifies membrane conductance for prolonged times under conditions that enable reversible Na/Ca exchange function (i.e., with a highly Ca-buffered cytoplasmic solution, containing 60 mM EGTA with 33 mM Ca, and with 20 mM cytoplasmic Na and 120 mM extracellular Na and 1 mM extracellular Ca). Fig. S3 shows Ni cannot be used to define Na/Ca exchange current-voltage relations in murine myocytes. Fig. S4 shows Na/K pump activity causes significant Na depletion when high cytoplasmic Na concentrations (60 mM) are used and Na/K pump inactivation is attenuated.
Results
We first describe several properties of Na/K pump current decay that appear more consistent with an inactivation mechanism than cytoplasmic Na depletion. Second, we present results that appear inconsistent with Na channels and Na/K pumps influencing one another via restricted subsarcolemmal Na concentration changes. Third, we present results for large currents that allow estimates of ion turnover kinetics and cytoplasmic mixing volumes. Finally, after verifying that current kinetics indeed reflect myocyte volume, we present simulations that demonstrate the role of Na/K pump inactivation in promoting rapid and effective cardiac Na homeostasis.
Immobilization of Na/K charge-moving reactions during pump current decay
Fig. 4 A presents a representative set of Na/K pump current decay records (bottom record), together with parallel measurements of myocyte capacitance (top record), from a murine cardiac myocyte under the standard experimental conditions used previously (Lu et al., 2016). The pipette solution contains 90 mM K and 25 mM cytoplasmic Na, and 20 mM TEA is present on both membrane sides to minimize K channel currents. The pump current activated by 7 mM extracellular K, which is ∼60% of maximal pump current, decays without a delay by ∼65% (Lu et al., 2016). Similar to published records, the mean τ for the four individual pump current decay curves was 2.1 s. Subsequent to the second pump current episode, we applied extracellular K for short 1-s periods to follow the recovery of pump current and repeated the protocol twice.
As illustrated in the upper trace, membrane capacitance routinely decreases by 1% to 2% upon activation of pump current and returns to baseline more slowly. The time constant here is 8.3 s, and it is 7.3 s after the final prolonged application of extracellular K. Importantly, this time course mirrors the time course of Na/K pump current recovery. To illustrate this, the magnitudes of pump current in the test pulses are marked with green dots and scaled to the capacitance responses without changing their relative amplitudes, and the corresponding changes of peak pump current and capacitance are plotted in a linear regression in Fig. 4 B (r2 = 0.96). In each of the three test series, recovery of peak pump current closely parallels recovery of capacitance.
We have suggested previously (Lu et al., 2016) that the decrease of capacitance in these experiments corresponds to a shift of Na/K pumps from E2 configurations (i.e., with binding sites open to the outside) to E1 configurations with binding sites open to the inside (see Fig. 3). When open to the outside, extracellular Na binds to them in an electrogenic fashion, thereby generating capacitive signals. Those signals are lost when pumps shift to the E1 configuration, and the recovery time course reflects the time that pumps remain locked into inactive states. This interpretation was supported by the finding that the capacitive signals are inhibited by ouabain in close parallel with inhibition of pump current (Lu et al., 2016). Furthermore, we have previously analyzed the frequency spectrum of capacitive pump signals, and we could readily detect multiple charge-moving reactions predicted from conventional voltage-clamp studies (Lu et al., 1995). Lastly, capacitive pump signals have characteristic dependencies on extracellular Na and voltage, and we verify next that this is the case for the signals that are suppressed for long times in the present experiments.
Fig. 4 (C and D) document that the long-lived capacitive signals are voltage and Na dependent. Fig. 4 C shows the voltage dependence of K-induced capacitance changes over the range of 0 to −120 mV. One set of experiments used 7 mM extracellular Na (red), and one set used 120 mM extracellular Na (blue). The capacitance changes at 0 to −80 mV, quantified as percent of total cellular capacitance, are three- to fourfold larger with 120 mM versus 7 mM extracellular Na. In the presence of 7 mM Na, the signal decreases monotonically with depolarization, whereas in the presence of 120 mM extracellular Na, the capacitive signal has a characteristic bell shape. This shape reflects the voltage dependence of the underlying charge moving reactions, and it is therefore fit in Fig. 4 C to the derivative of a Boltzmann function, as given within the figure. As expected for the major charge moving reaction of cardiac Na/K pumps (Nakao and Gadsby, 1986; Hilgemann, 1994), the slope factor (Fem; 0.9) corresponds to the movement of nearly one full charge across the entire electrical field, and the midpoint is −60 mV. The same analysis with 7 mM Na generates a shallower slope (0.51), and the midpoint is shifted strongly to negative potentials. This signal likely arises from Na binding to high-affinity sites that generate charge movements with microsecond kinetics (Hilgemann, 1994; Lu et al., 1995; Gadsby et al., 2012). As shown in Fig. 4 D, the bell shape of the capacitive signal with 120 mM Na is readily apparent without subtracting signals. It has nearly the same voltage dependence in the presence of 7 mM extracellular K, as in the absence of K, and this property is well reproduced by simulations of the model from Fig. 3, as described next.
Na/K pump current decay and recovery are voltage dependent
Fig. 5 describes the voltage dependence of pump currents, capacitive signals, and current decay, together with corresponding predictions of the pump model outlined in Fig. 3. K-free cytoplasmic solutions were used to ensure that K channel currents were negligible. They contained 100 mM NMDG, 25 mM Na, and 15 mM TEA as monovalent cations. As shown in Fig. 5 A with 120 mM extracellular Na, 7 mM K was applied and removed, as in Fig. 4, to activate pump currents at different holding potentials. The corresponding current (blue) and capacitance (red) records are plotted next to each other in the figure. The decay of pump current and the magnitudes of capacitive signals are suppressed as membrane potential is increased from −60 mV to +60 mV. Composite results are presented in Fig. 5 B for seven similar experiments. The current–voltage relation of the peak current develops a clear maximum with depolarization. The capacitance signal decreases monotonically, as already described in Fig. 4, and the fractional decay of current decreases from ∼80% to 25%, on average, as voltage is increased from −60 to +60 mV (n = 7). Results for experiments with 7 mM Na, shown in Fig. 4 (C and D), are qualitatively similar. Current decay is somewhat stronger, and the current–voltage relation of the peak current is less steep. Nevertheless, current decay decreases from more than 80% at −60 mV to 55% at +60 mV.
Figure 5.
Voltage dependence of Na/K pump currents and K-induced capacitance changes with 120 and 7 mM extracellular Na. Cytoplasmic K was omitted to ensure minimal K conductance. (A) Na/K pump currents and capacitance changes recorded at five voltages from −60 to +60 mV. K-induced capacitance changes decrease and Na/K pump current decay attenuates progressively with depolarization. (B) Mean peak (blue) and 20 s (red) pump currents plotted against membrane voltage, together with the fractional decay of pump currents (black) and the magnitude of K-induced capacitance changes (red). The voltage range is too narrow to reveal the bell shape of capacitance changes with 120 mM Na. Solid curves are simulation results scaled to the data points. According to the model, capacitance changes reflect primarily the voltage dependence of Na-dependent charge movements. The attenuation of current decay with depolarization reflects a shift of pumps from E1 to E2 configurations. Although the dissociation of Na in E2 conformations is favored by depolarization, thereby promoting a shift to E1, extracellular K binding is progressively hindered and Na occlusion from the cytoplasmic side is progressively favored. With depolarization, these latter influences become dominant and pumps shift on average to E2 from E1. (C and D) Equivalent results for experiments in which 7 mM extracellular Na was replaced with 7 mM K to activate pump currents. Voltage dependence of pump current is reduced in characteristic fashion, whereas other patterns are principally similar.
The solid lines in Fig. 5 (B and D) are predictions of the pump model, scaled to the experimental results. In brief, pump current decay becomes attenuated with depolarization because pumps shift from E1 configurations to E2 configurations, thereby preventing inactivation. The reason for this shift is that K-binding reactions, K43 and K32, become inhibited with progressive depolarization, whereas the Na-occluding reaction from the cytoplasmic side (K71) becomes accelerated. These changes override the influence of the major charge moving reaction at more positive potentials, and the two changes together promote an accumulation of pumps in E2 states. The capacitive signals decrease with depolarization as Na dissociates on average from E2 states, as outlined in relation to Fig. 4. Whether these results could be explained in the context of the Na depletion hypothesis seems questionable. Pump currents are smaller at negative potentials than at positive potentials, and therefore, cytoplasmic Na depletion should decrease, not increase, with hyperpolarization.
Failure to verify a local Na space next to Na channels
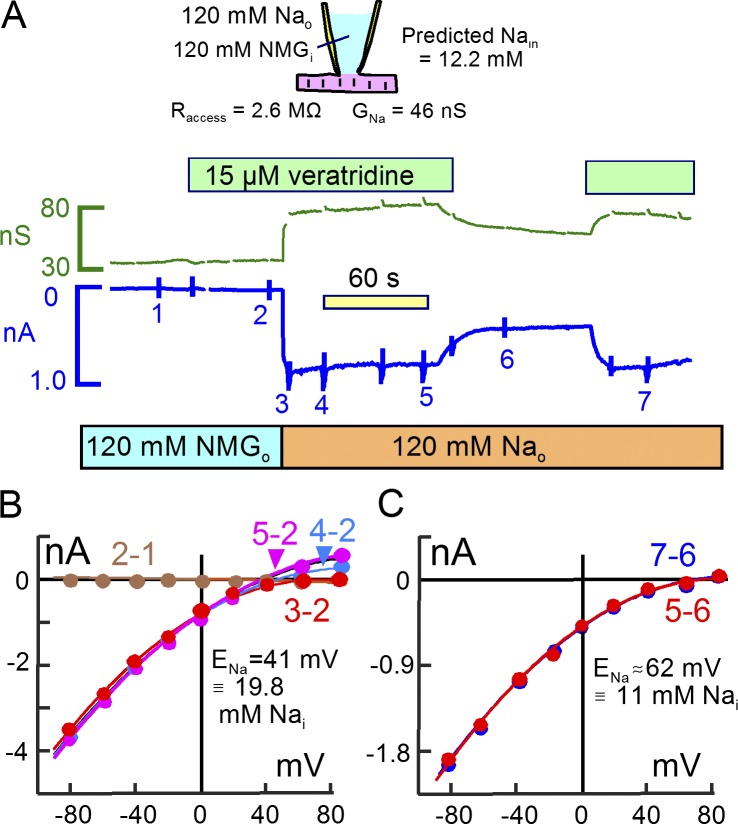
We consider next to what extent “local” Na concentrations change during the activation of Na channels. Fig. 6 presents a representative experiment in which Na channels were opened at 0 mV with 15 µM veratridine in the presence of 120 mM extracellular Na using K-free and Na-free pipette solution. Square wave voltage perturbations for capacitance recording were interrupted at the time points indicated by glitches to acquire current–voltage relations. As indicated above the record in Fig. 6 A, we applied veratridine first in the absence of Na. Similar to five other experiments, veratridine caused no conductance change in solutions lacking Na and K. Upon substituting 120 mM extracellular NMDG for Na, a large inward current ∼0.8 nA in magnitude develops and then decays by ∼15% over 60 s. Membrane conductance increases from 32 to 88 nS and does not decay. The Na conductance amounts to 56 nS, compared with the pipette conductance of 420 nS. From Eqs. 26 and 29 the cytoplasmic Na concentration is expected to increase by 12.2 mM in the simple model.
Figure 6.
Veratridine-activated Na currents cause Na concentration changes that are consistent with unrestricted cytoplasmic Na diffusion. (A) Conductance and membrane current records during application of 15 µM veratridine. As apparent in the records, veratridine activates no conductance in the absence of Na and K. Application of 120 mM Na in replacement for NMDG then activates an inward current that is initially 860 pA in magnitude and that decays by 13% over 90 s. Removal of veratridine reversibly reduces the Na-dependent current and conductance by 55%. Thus, 45% of the Na current may be carried by mechanisms other than veratridine-modified Na channels, and Fig. S3 gives evidence for nonselective cation channels in murine myocytes. (B) Na-defined current–voltage relations obtained by subtracting the records 3, 4, and 5 from record 2. During the 90 s of Na application (3′ to 5′), the Na-defined current–voltage relation shifts from having no clear reversal to having a reversal at +41 mV, indicating a subsarcolemmal Na concentration of 19.8 mM. (C) Veratridine-defined current–voltage relation. The current–voltage relations defined by removing (5–6) and reapplying (7–6) veratridine reverse at +62 mV, corresponding to a subsarcolemmal Na concentration of 11 mM.
After 100 s in Na-containing solution, the myocyte was switched to a solution without veratridine. Currents and conductance decay by ∼60%, and they are restored by reapplication of veratridine. As verified by application and removal of Na in the absence of veratridine (unpublished data), up to 40% of the inward current carried by Na may occur through the seal conductance and/or nonselective cation channels that exist in murine myocytes (see Fig. S3). Fig. 6 (B and C) presents current–voltage relations from these records. Fig. 6 B presents records defined by the Na concentration change, and Fig. 6 C presents records defined by removal of veratridine. As indicated in Fig. 6 B by the “2 − 1” (brown) subtraction, veratridine was without effect in the absence of Na. The “3 − 2” (red) subtraction defines the Na current just after applying Na. The inward current does not reverse at potentials up to 80 mV. Over the course of the next 100 s, the current–voltage relations develop a clear reversal and at 100 s (“5 − 2”, purple) reversal occurs at +41 mV. This corresponds to a subsarcolemmal Na concentration of 19.8 mM, a value that is 56% greater than expected from the simple model. In five similar experiments, the discrepancy was not greater than in this example, and we present next an example in which no Na accumulation was detected. Fig. 6 C presents the current–voltage relations defined by removing (5–6) and reapplying (7–6) veratridine. The current–voltage relations reverse at approximately +70 mV, indicating that cytoplasmic Na sensed by Na channels is not more than 10 mM. This result that is consistent with the simple model.
Failure to verify that Na channel influx locally supports Na/K pump activity
We next tested to what extent Na influx via veratridine-modified Na channels would support Na/K pump activity by promoting subsarcolemmal Na accumulation. As shown in Fig. 7, these experiments were initiated similarly with NMDG, Asp, and TEA on both membrane sides. 15 µM veratridine was applied, and subsequently, NMDG was replaced by Na in the presence of veratridine. The Na-activated current amounted to 400 pA and increased the membrane conductance by 28 nS. When 7 mM K was applied in the presence of Na, pump currents remained negligible, indicating that the subsarcolemmal Na concentration was not greater than expected from the Na current and the pipette resistance (5.6 mM). As shown in Fig. 7 C, the current–voltage relations defined by subtractions with and without Na did not reverse at potentials up to +80 mV, verifying that cytoplasmic Na remained less than 10 mM in subsarcolemmal spaces during continuous Na currents 400 pA in magnitude.
Figure 7.
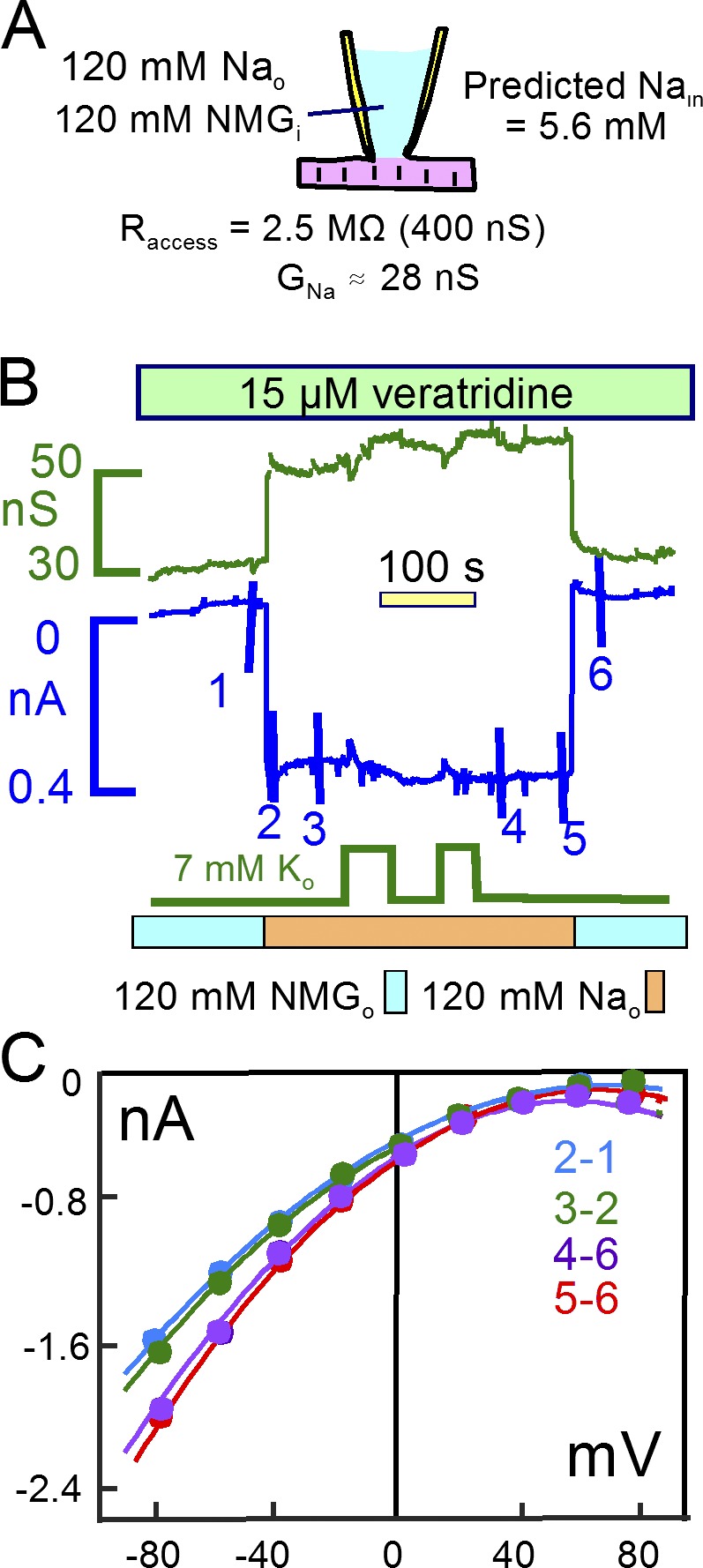
A continuous 400 pA Na current does not cause a detectable rise of subsarcolemmal Na. (A) The cartoon summarizes patch-clamp conditions and the predicted 5.6 mM cytoplasmic Na concentration during a continuous 0.38 nA Na current. (B) Veratridine was applied in the absence of Na, and the subsequent application of 120 mM Na activated a 0.38 nA inward current. Na/K pump currents activated by applying 7 mM K were at the threshold of reliable detection, indicating that subsarcolemmal Na remains with good certainty less than 10 mM. (C) Current–voltage relations given by the indicated subtractions do not reverse up to 80 mV, verifying that subsarcolemmal Na remains <10 mM.
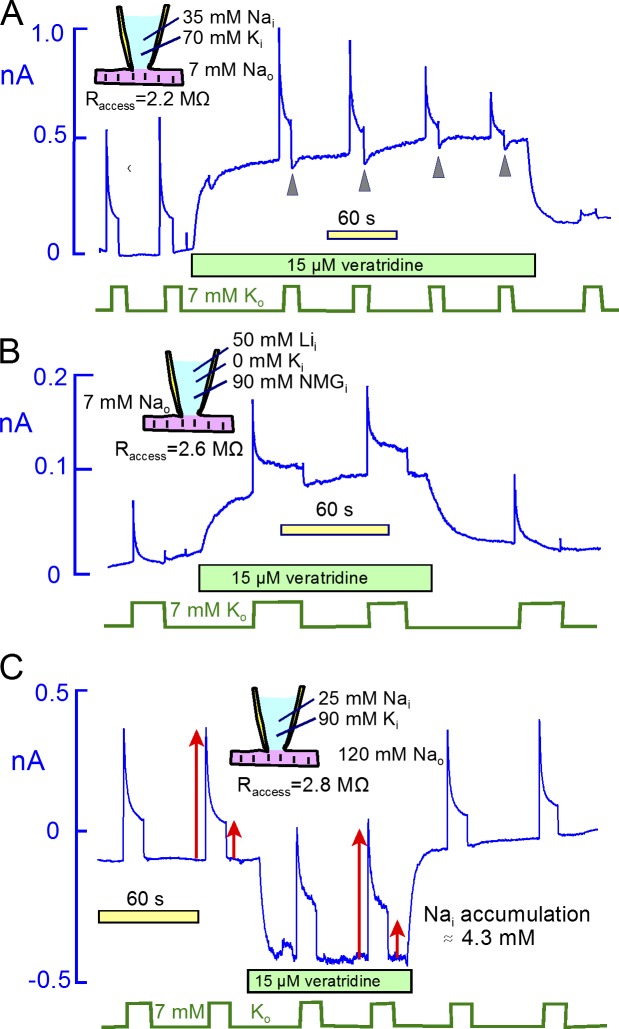
Fig. 8 presents experiments designed to reveal possible bidirectional interactions between veratridine-activated Na channels and Na/K pumps in murine myocytes. We use conditions in which Na channels generate large outward currents (Fig. 8, A and B) or large inward currents (Fig. 8 C). Fig. 8 A, Na/K pump current was activated by 7 mM extracellular K with 35 mM Na and 70 mM K on the cytoplasmic side and with 7 mM Na on the extracellular side. The pump currents are therefore very similar to those of Fig. 4. Application of veratridine generates a large outward current ∼450 pA in magnitude. If subsarcolemmal Na diffusion were restricted, this Na current would significantly deplete subsarcolemmal Na and reduce the Na/K pump current. Furthermore, if pump current decay reflected subsarcolemmal Na depletion, pump activity would markedly decrease outward Na current this protocol. However, the pump current initially does not change after activating Na channels. The subsequent decline of pump current in this example reflects a run-down phenomenon, described again in Fig. 15. This is apparent because the pump current does not recover after removal of veratridine. Concerning the effect of pump activity on Na currents, the membrane current indeed shows small, transient downward deflections upon deactivation of the pump (Fig. 8 A, arrowheads). However, the magnitudes of those (small) downward deflections do not change as pump current runs down. Therefore, the deflections cannot reflect depletion of subsarcolemmal Na. In short, there is no indication that pump activity in this experiment is affecting Na channel activity.
Figure 8.
Continuous veratridine-activated Na currents only weakly affect Na/K pump currents that decay by 70% to 90%. Na/K (or Li/K) pump currents were repeatedly activated for 20 s by applying 7 mM extracellular K. (A) With 35 mM Na and 70 mM K on the cytoplasmic side, 15 µM veratridine activates a 0.4 nA outward current. Small inward current deflections upon deactivating pump currents, marked by arrowheads, are consistent with a 10% depletion of subsarcolemmal Na by pump activity. However, the deflections do not change as current runs down, indicating that they are not caused by pump activity. (B) In the presence of 50 mM Li and no K on the cytoplasmic side, Li/K pump currents decay almost completely in the absence of veratridine and decay by ∼85% in the presence of veratridine. The veratridine-activated outward Li current, upon deactivating pump current, is unaffected by Li/K pump currents. (C) In the presence of 120 mM extracellular Na, 25 mM cytoplasmic Na and 90 mM extracellular K, 15 µM veratridine activates a 0.4 nA inward current that is unaffected by activating and deactivating Na/K pump currents. Arrows indicate the magnitudes of peak and steady-state pump current without veratridine. Peak and steady-state pump currents are increased by 8% and 24%, respectively, in the presence of inward current, consistent with an increase of Na by 4.3 mM (Lu et al., 2016).
Figure 15.
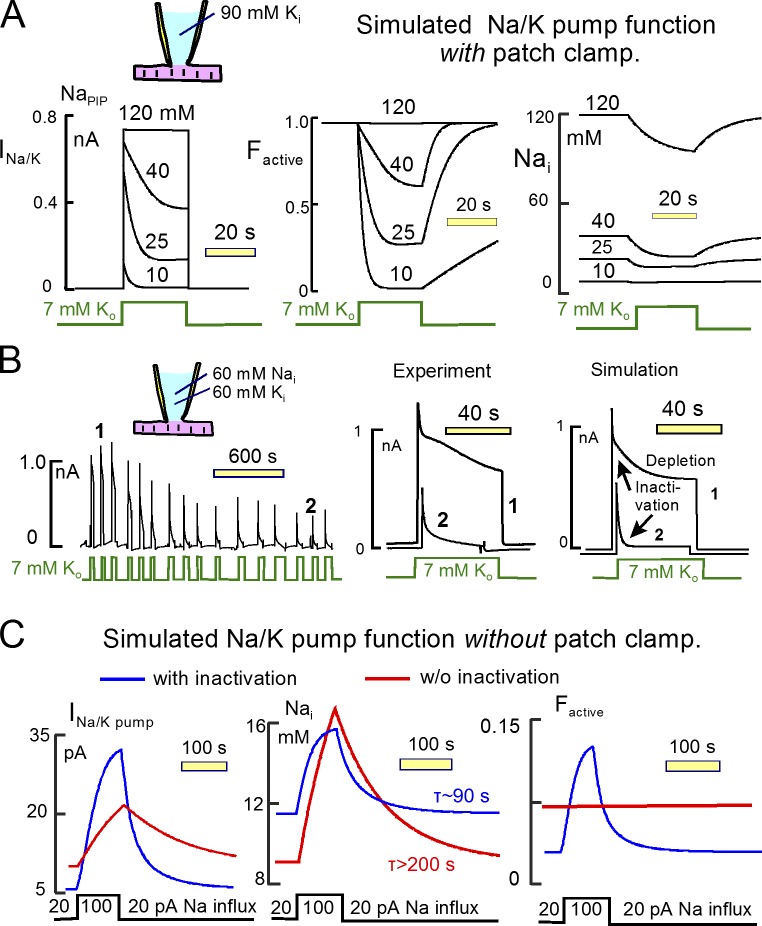
Projected roles of Na depletion and Na/K pump inactivation with (A and B) and without (B) patch clamp. (A) Simulation of Na/K pump currents, the fraction of pumps that are actively pumping (Factive), and cytoplasmic Na concentrations in a cell model with instantaneous ion diffusion (Fig. 2) and Na/K pumps that inactivate (Fig. 3). Inactivation occurs from all E1 conformations, whereas recovery occurs only when three Na ions are bound to inactive states. The simulation reproduces well the corresponding experiments with different cytoplasmic Na concentrations (Lu et al., 2016). Current decay involves both inactivation and Na depletion with the contributions depicted in the central panel for inactivation and in the right panel for Na concentration changes. (B) Representative long-duration experiment with 60 mM cytoplasmic Na. In the central panel, pump current decay records are shown from the initial (1) and late (2) portions of the experiment. Initially (1), pump current decays in a biphasic fashion. The initial phase has a τ of ∼1 s and amounts to 10% to 20% of peak current magnitude. The slow phase develops with a lag, continues over 40 s, and merges with the usual slow run-down of pump current that occurs in these experiments. After 30 min (2), run-down of pump current has progressed so that peak currents are ∼30% of initial peak currents, and current decay amounts to ∼90% during a 20s application of extracellular K. The right panel reproduces these pump current decay records using slightly modified model parameters. The initial fast current decay in record “1” corresponds largely to inactivation, and the latter decay phase in 1 corresponds largely to Na depletion. Because Na depletion promotes inactivation, however, the processes are interdependent, and the model can develop small oscillations via this feedback. (C) Simulated function of the inactivation process when Na load is changed in a cardiac myocyte that is not patch clamped. Using the same simulation parameters as in A, C depicts model function when Na influx is increased and decreased. The initial Na influx is equivalent to a 20 pA current. It is then increased for 100 s to 100 pA and decreased again to 20 pA. From left to right, the three panels show cytoplasmic Na currents with (blue) and without (red) the simulated Na/K pump inactivation mechanism, cytoplasmic Na concentration changes, and changes of the active state probability of the pump. In summary, the inactivation mechanism promotes the pump to minimize, relatively, cytoplasmic Na changes in the face of Na influx changes. Importantly, cytoplasmic Na concentrations approach a steady state markedly faster (τ ∼90 and ∼200 s with and without inactivation) than the actual turnover of the mean cytoplasmic Na ion to the extracellular space (τ ∼700 s).
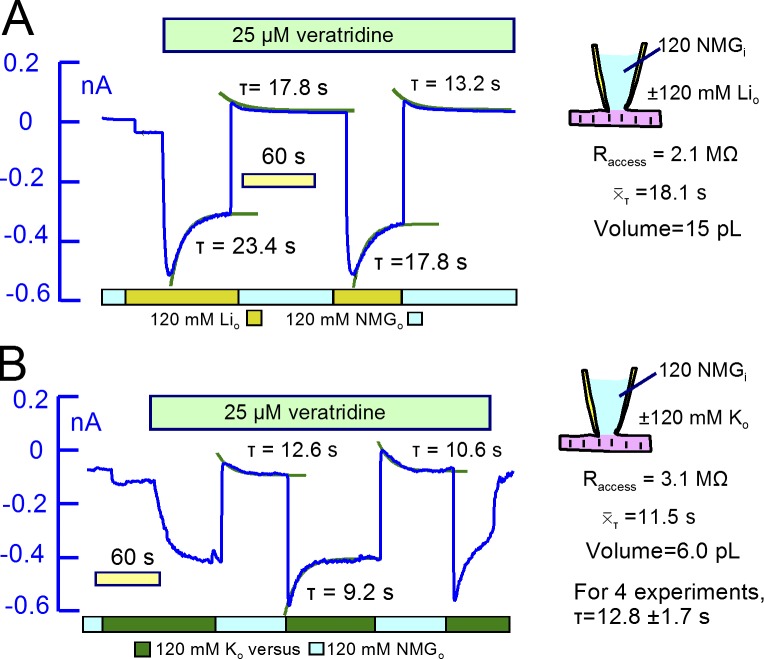
We next used Li as a congener for cytoplasmic Na in equivalent experiments. As described previously (Lu et al., 2016), pump currents carried by cytoplasmic Li are of smaller magnitude than Na/K pump currents and decay more strongly than Na/K pump currents. Should the decay of Li/K pump current reflect subsarcolemmal Li depletion, pump activity would very strongly decrease outward Li-carried channel currents. In Fig. 8 B, therefore, we used 50 mM Li in K-free pipette solution. This choice ensures that outward currents activated by veratridine are carried solely by Li. In this recording and four very similar additional recordings, the veratridine-activated outward Li current was unaffected by activating pump currents, and the Li/K pump currents were not decreased by activating outward Li currents through Na channels. In all of the experiments, pump currents developed a small steady-state component in the presence of veratridine, a result that is opposite to the expectation that outward Li currents might deplete subsarcolemmal Li.
Fig. 8 C presents an experiment using veratridine to generate a large inward Na flux. In the presence of 120 mM extracellular Na and 25 mM cytoplasmic Na, 15 µM veratridine activated a 400 pA inward current. Red arrows mark the magnitudes of the peak and steady-state pump currents in the absence of veratridine, and arrows of the same magnitude were copied into the subsequent record to visualize accurately the small effect of inward Na current on the pump currents. In the presence of Na current, the peak pump current was increased by 8% and the steady-state pump current was increased by 22%. Assuming the Na dependence of pump current to have a Hill slope of 2.4, as determined for this condition (Lu et al., 2016), this enhancement of pump current reflects a subsarcolemmal Na accumulation of only 4.3 mM. This compares to an accumulation of 7 mM predicted by the simple model. Furthermore, the activation of pump currents with peaks of 0.3 nA resulted in no evident change of the veratridine-activated inward current. From the simple model, a 0.3 nA pump current (equivalent to a 0.9 nA monovalent Na flux) should deplete cytoplasmic Na by ∼11 mM. The magnitude of that effect would be readily detected in these experiments. The fact that pump current does not affect Na channel current in these experiments therefore provides a strong argument that pump current decay represents primarily inactivation. If the pump did not inactivate, the inward current through Na channels would have decreased even if diffusion were instantaneous within the cytoplasm.
The final magnitudes of current changes caused by cytoplasmic ion concentration changes are not expected to depend on cytoplasmic volume (see Eqs. 30 and 31). Nevertheless, the experiments raise obvious questions about the size of the cytoplasmic mixing volume and the behavior of other ions in similar experiments. To address these issues, we designed experiments in which the membrane conductance becomes significant with respect to access conductance (250–600 nS). First, we used veratridine at higher concentrations (25 µM) to generate both K and Li conductances in Na channels, and second, we used nystatin at concentrations of 40–80 µM that activate 100 to 200 nS conductances for monovalent cations and for chloride.
Large Na channel and Na/K pump currents generate global Na concentration changes and reveal Na turnover kinetics
Fig. 9 illustrates the kinetics of Na turnover when large current magnitudes are maintained. In Fig. 9 A, 25 µM veratridine was used using NMDG and Asp on the cytoplasmic side. We used Cs as the Na substitute in these experiments, because Cs permeation through the veratridine-modified Na channels was undetectable. With 120 mM Na on the extracellular side, veratridine activated an inward current 0.9 nA in magnitude. When extracellular Na was replaced by Cs, the inward current was immediately suppressed, and a smaller outward current developed and decayed with a τ of 16 s. Na was then reapplied and removed three more times, current–voltage relations were taken before and after removal of veratridine, and the time constants of current decay were evaluated. Assuming that Na currents are proportional to Na concentration differences across the sarcolemma, the decay of inward current and the magnitudes of outward currents indicate that cytoplasmic Na accumulates to 22% of the extracellular concentration (i.e., to 27 mM). This agrees reasonably with the reversal potential of the Na current (40 mV), indicating a subsarcolemmal Na concentration of 21 mM. This value is 29% larger than expected from the simple model. As indicated within Fig. 9 A, the mean τ of current decay for both inward and outward Na currents was 21.2 s. With an access resistance of 3.5 MΩ, this τ projects to a cytoplasmic mixing volume of 10.5 pL.
Figure 9.
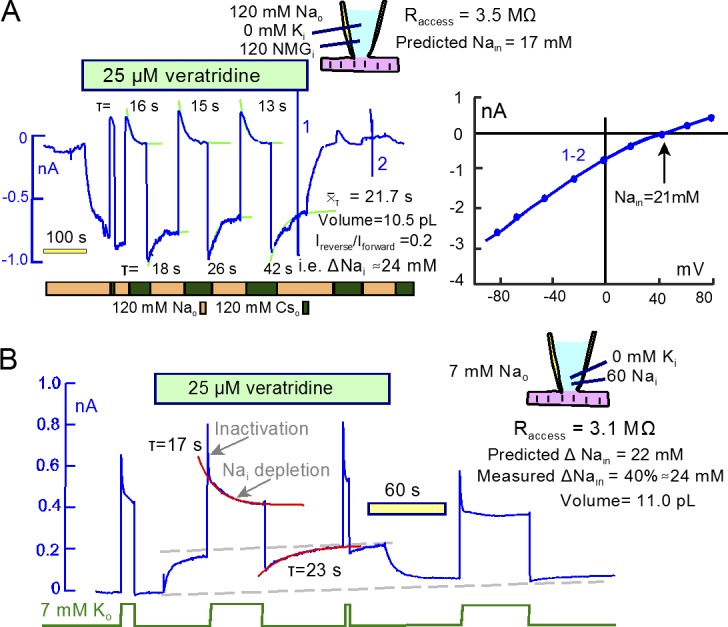
Large Na and Na/K pump currents cause cytoplasmic Na concentration changes with a τ of ∼20 s. (A) A high veratridine concentration (25 µM) activates continuous Na currents of ∼1 nA. The Na-activated currents decay by 22% with an mean τof 28 s. Reverse currents activated upon Na removal decay with a τ of ∼15 s. The mean τ and the access resistance give a mixing volume of 10.5 pL, and the magnitudes of decaying currents in relation to peak current (0.2) indicate that Na accumulated by 24 mM. As indicted in the cartoon, calculations from Eq. 26 give a steady-state cytoplasmic Na concentration of 17 mM. The reversal potential of the veratridine-activated current indicates a steady-state cytoplasmic Na concentration of 21 mM, ∼40% greater than predicted by the simple model. (B) Using 60 mM cytoplasmic Na, Na/K pump currents decay in two distinct phases, a fast phase with a τ of ∼1 s and a slow phase with a τ of ∼17s. The veratridine-activated outward Na current is decreased by ∼40% immediately after deactivation of pump current, and it recovers with a τ of 23 s. These results project to a Na depletion of 24 mM and a mixing volume of 11.0 pL. Using the same protocol as in B, Fig. S4 describes very similar results using current–voltage relations to define the cytoplasmic Na accumulation.
That Na/K pumps can indeed mediate large global cytoplasmic Na concentration changes in murine myocytes is documented in Fig. 9 B. To do so, it is essential that pumps do not inactivate, and this seems to be the case when cytoplasmic Na concentrations are higher than 30 mM. In these experiments, therefore, we used 60 mM Na in pipette solutions. In this setting, the pump current shows a very rapid (<1 s) decay phase that amounts to ∼20% of peak pump current, consistent with high cytoplasmic Na promoting a faster recovery from inactivation and therefore faster decay kinetics (Lu et al., 2016). After the rapid decay phase, pump currents decay more slowly, as expected for Na depletion (τ, 17 s). In contrast to recordings with lower cytoplasmic Na concentrations, the outward veratridine current decreases markedly in response to pump activity. In this case, the outward Na current is decreased by 40% after removing extracellular K, and it recovers with a τ of 23 s. We can estimate from these results that Na decreased by 24 mM. The access resistance, 3.1 MΩ, and the steady-state pump current magnitude (∼0.4 nA, equivalent to a Na current of 1.2 nA) predict that Na depletion should amount to 22 mM according to the simple model. Similar close agreement between the simple model and experimental results is verified with current–voltage relations in Fig. S4.
In our experience, the K conductance of veratridine-modified Na channels in myocytes amounts to ∼30% of their Na conductance. Therefore, we could use veratridine-modified Na channels to perform equivalent experiments for both Li and K. Using 25 µM veratridine in Fig. 10, the fractional decay of Li- and K-carried Na channel currents (Fig. 10, A and B, respectively) was substantially greater than mean equivalent results for Na. Furthermore, the decay phases of both currents were substantially larger than the magnitudes of the outward current that occurred upon removing extracellular Li and K. These outcomes presumably reflect rectification properties of the modified channels. The time constants for Li current decay were on average 60% larger than those for K. From the expected “FD” values (2.1 and 1.1 for K and Li, respectively), τ values, and access resistances, the apparent mixing volumes for K and Li were 15 and 6 pL, respectively. We suspect that the small τ value for Li currents reflects a high Li affinity of cardiac Na channels (Kurata et al., 1999). Given these complexities, we next tested whether nystatin-generated monovalent ion conductances might be more useful for the goals of this project.
Figure 10.
Li and K currents carried by veratridine-modified Na channels. For both Li and K currents, the decaying components of inward currents are substantially larger than the reverse currents that develop upon removing the extracellular cations. (A) NMDG was substituted for 120 mM Li. 25 µM veratridine then rapidly activated a 0.55 nA inward current that decayed with a τ of ∼20 s. The mean for the decay phases was 18.1 s, and the mixing volume is estimated to be 7.5 pL. (B) NMDG was substituted for 120 mM K, and 25 µM veratridine application then activated a 0.30 nA inward current. When activated by applying extracellular K, the current decayed partially with a τ of 9.2 s. The mean τ was 11.1 s, and the mixing volume is estimated to be 6.0 pL.
Nystatin channels reveal similar kinetics for all monovalent ions
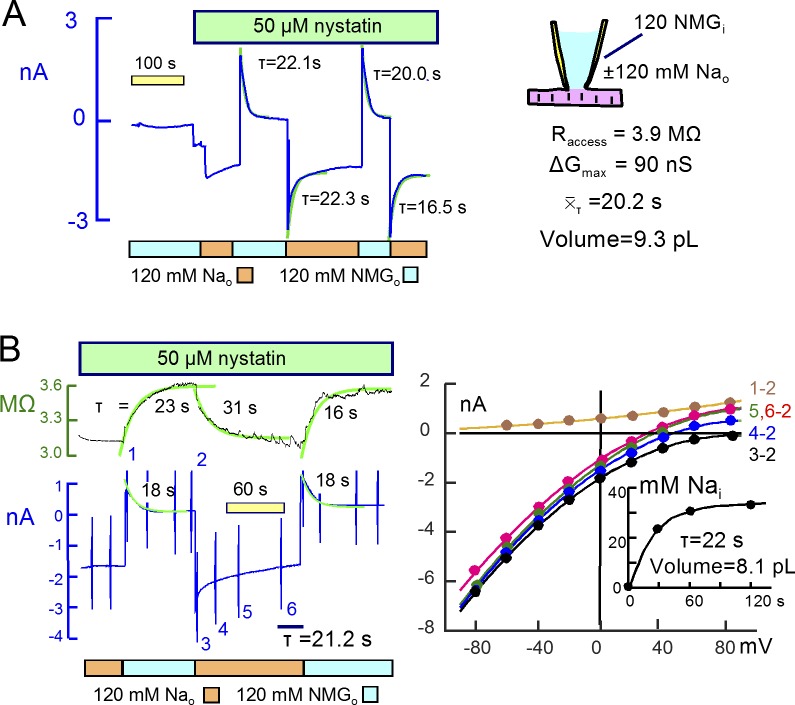
Experiments with nystatin were performed similarly using solutions primarily NMDG and Asp on both membrane sides. Application of nystatin typically caused no conductance change in this condition, whereas the subsequent replacement of NMDG by Na, Li, Cs, and K generated large conductances, as did the replacement of Asp by Cl. Fig. 11 shows results for Na. In Fig. 11 A, 120 mM Na was applied and removed three times, generating a peak conductance of 90 nS. The access resistance was 3.8 MΩ (260 nS), and the Na currents decayed by almost 50%. Reverse outward currents developed on removal of Na with similar decay time courses. The mean τ was 20.2 s for the reverse current decay, corresponding to a mixing volume of 9.3 pL. Fig. 11 B presents an equivalent experiment in which current–voltage relations were determined. The outward currents upon removal of Na decayed with a τ of ∼18s. The inward current activated by Na, however, could not be analyzed accurately because it continued to decay almost linearly over 2 min. Reversal potentials of current–voltage relations, shown in Fig. 11 B (right), shifted to the left and approached asymptotically a value equivalent to a cytoplasmic Na concentration of 32 mM. This value is in good agreement with predictions of the simple model. The access resistance, 3.2 MΩ, and the mean time constant for outward current decay project to a mixing volume of 8.1 pL.
Figure 11.
Large Na currents carried by nystatin channels have similar kinetics to those carried by veratridine-modified Na channels. (A) 50 µM nystatin was applied in the absence of Na, and NMDG was then replaced by Na, generating an initial steady-state current of ∼1 nA. The outward current activated by removing Na amounts to 2 nA, and peak inward current on reapplying Na was 3 nA with current decay amounting to approximately one half of peak current. The mean τ for current decay was 20.2 s, the peak conductance was 90 nS, and the access resistance was 90 nS. We estimate the mixing volume to be 9.3 pL and the steady-state cellular Na concentration to be 43 mM. (B) Current–voltage relations and access resistance changes during the same protocol. Access resistance rises and falls with a time course that is similar to the Na current, therefore revealing no longitudinal diffusion delays. Note that inward current decay is not a simple exponential function, possibly reflecting a change of the nystatin conductance. Reversal potentials (right) shift negatively as Na accumulates, and the calculated cytoplasmic Na concentration (inset) approach a steady state of 32 mM monotonically with a τ of 22 s, similar to the mean τ for outward current decay (21.2 s).
We present in addition the access resistance record for this experiment, which behaved similarly in >50 experiments. In brief, the access resistance decreases and increases during cation influx and efflux, respectively, and the time courses of resistance changes are similar to those of currents. These changes presumably reflect changes of total ion concentrations in the pipette tip, and the magnitudes of the resistance changes are in good agreement with the changes expected from the simple model (see Fig. 2). In this case, resistance increases by ∼20% during the decay of reverse Na current, and decreases correspondingly as Na accumulates by ∼30 mM.
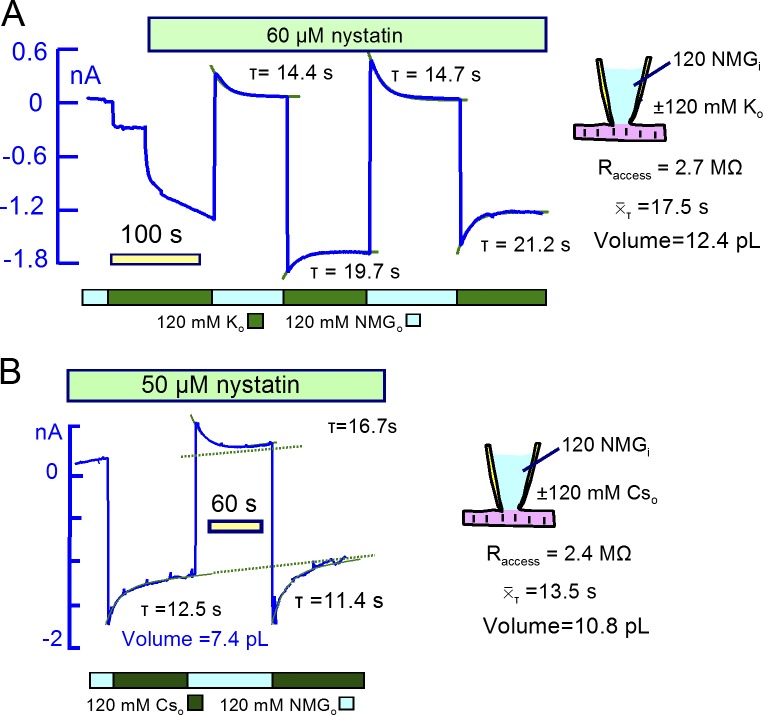
Figs. 12 and 13 present equivalent nystatin results for K, Cs, and Cl. As shown in Fig. 12, decay time constants for Cs and K currents were similar (τ≈13 s), and results for six additional experiments were similar to these. Importantly, the magnitudes of current decay phases for inward and outward currents were similar, as expected if current changes are roughly proportional to ion concentration changes. The calculated mixing volumes were 10.2 ± 2 pL (n = 7). To generate a large conductance for Cl, as, shown in Fig. 13, a larger nystatin concentration (80 µM) was required. On applying 120 mM Cl in exchange for Asp, outward currents then amounted to >2 nA, and large inward currents developed immediately upon removal of Cl. The inward Cl currents decayed with a time constant of ∼10 s. Similar to results for Na, the current induced by reapplying Cl decayed with a complex time course. Therefore, we estimated cytoplasmic Cl concentration changes from current-voltage relations described in Fig. 13 B. The current–voltage relation determined just before applying Cl was used as baseline, and subsarcolemmal Cl concentrations calculated from reversal potentials, plotted in Fig. 13 C, increased monotonically to 47 mM with a τ of 24.5 s. With an access resistance of 2.7 MΩ, these results indicate a cytoplasmic mixing volume for Cl of 11 pL. Results from three other experiments were similar.
Figure 12.
Large K and Cs currents carried by nystatin channels project to similar mixing volumes as results for Na currents. (A) Nystatin-carried K current. Extracellular NMDG was replaced by K and 60 µM nystatin was applied, generating an inward current of ∼1.7 nA. The outward current activated by removing K amounted to 0.3 nA and decayed with a time constant of 14.4 s. The fractional decay of inward current is less than for equivalent Na currents (or for K currents in veratridine-modified Na channels), and the mean τ of current decay is 17.5 s. The projected mixing volume is 10.1 pL. (B) Nystatin-carried Cs current. In the presence of 50 µM nystatin, extracellular NMDG was replaced with Cs multiple times, activating peak inward currents of ∼1.6 nA. Currents decayed with a mean τ of 13.5 s, projecting to a mixing volume of 10.8 pL.
Figure 13.
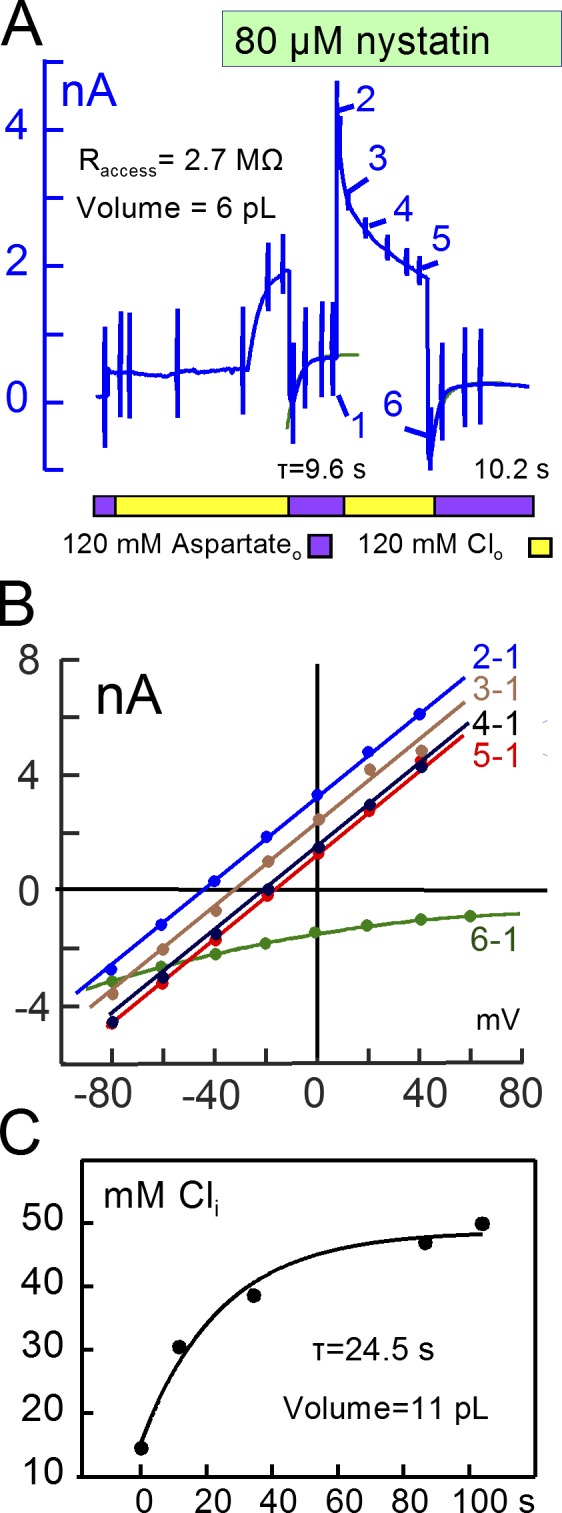
Large Cl currents carried by nystatin channels project to similar mixing volumes as cation currents. (A) Nystatin-carried Cl current. Extracellular aspartate was replaced with Cl, and 80 µM nystatin was applied, generating an outward current of 1.8 nA. Removal of Cl then generated peak inward currents of 0.7 to 1 nA with decay time constants of 9.6 and 10.2 s. The peak Cl−-activated outward current reached 4 nA and, similar to the nystatin-carried Na current, decayed in a nonexponential fashion. (B) Current–voltage relations during decay of outward current and upon reapplying extracellular Cl. (C) Cytoplasmic Cl concentrations calculated from reversal potentials in B. Cl increases monotonically from 21 mM to 48 mM with a τ of 24.5 s, projecting to a mixing volume of 11 pL.
Verification that nystatin current kinetics reflect myocyte mixing volumes
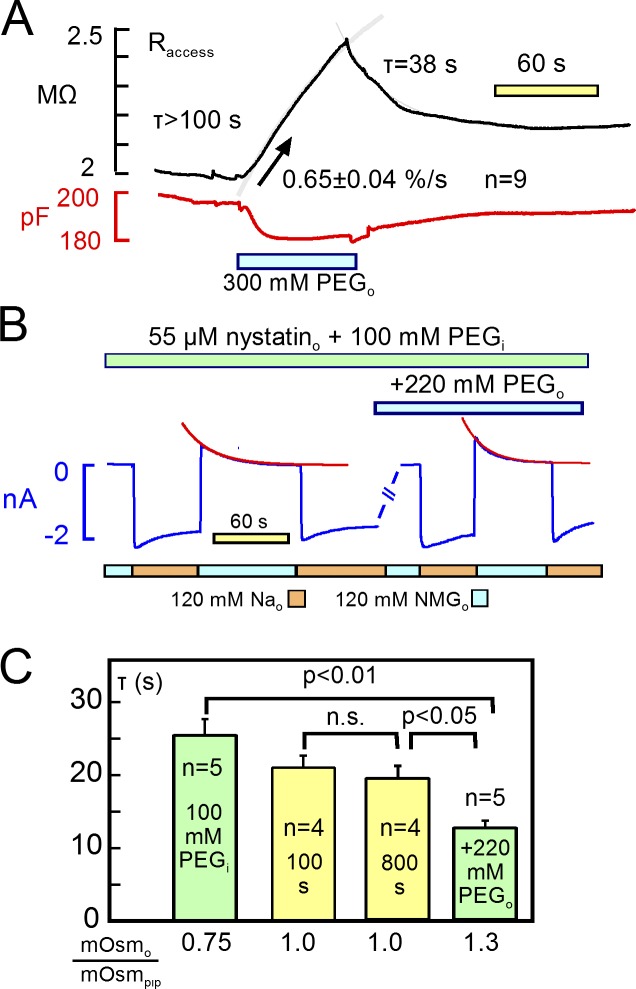
To verify that the decay of ion currents reflect cell mixing volumes in these experiments, we manipulated cell volume by changing the osmolarity of both cytoplasmic and extracellular solutions. Relevant to these results, cardiac myocytes have a rather low water permeability (Ogura et al., 2002). Volume changes occur over 1 to 2 min after changing osmolarity, and regulatory (compensatory) volume responses have not been observed to occur in cardiac myocytes even when observations were extended to >20 min (Drewnowska and Baumgarten, 1991). Given that the longitudinal resistance of myocytes constitutes at least 20%, and possibly 40% of the myocyte access resistance (see Fig. 1), volume changes can be tracked as inverse changes of access resistance. As illustrated in Fig. 14 A, a doubling of extracellular osmolarity with 300 mM polyethylene glycol (PEG; 500 MW) causes access resistance to increase at a rate 0.65 ± 0.04%/s with no indication of saturation after 90 s (n = 9). Typical for nine observations, access resistance returned only partially toward baseline after removing the hyperosmotic solution, presumably because cytoplasmic solutes equilibrate rapidly with solute in the pipette, thereby dissipating the driving force to reswell the cell.
Figure 14.
Mixing volumes determined by nystatin-mediated currents are predictably changed by osmolarity gradients. (A) Representative record of access resistance and capacitance when extracellular osmolarity is doubled for 80 s by 300 mM extracellular polyethylene glycol (PEG; 500 MW). Otherwise, solution compositions were standard, with no Na. Access resistance, which includes longitudinal myocyte resistance, increases as expected for a reduction of the myocyte diameter. Note that resistance does not return to baseline after removing PEG. (B) Membrane current transients in the presence of nystatin when 120 mM NMDG is replaced with 120 mM Na. Osmolarity of the pipette solution was increased to 400 mosM/liter with 100 mM PEG. After recording the initial responses to Na changes, the extracellular solution was switched to a hyperosmotic solution containing 220 mM PEG. Responses to cation substitution were recorded again and compared with the initial currents. (C) With 100 mM hyperosmotic pipette solution, the τ of current decay is 25 ± 2 s (n = 5) versus 12 ± 2 s (n = 5) in the 220 mM hyperosmotic solution. Mean τ values with isosmotic (290 mosM/liter) solutions on both sides amounted to 20 ± 3 s initially and did not change significantly after 800 s of recording time (not depicted, n = 4). Error bars indicate SEM.
To manipulate volume more modestly, as illustrated in Fig. 14 B, we used a cytoplasmic solution with osmolarity increased from 280 to 380 mosM/liter with 100 mM PEG. After a 2-min equilibration period with 55 µM nystatin, we applied and removed 120 mM Na, and we determined the time constant of Na current decay. Then, we applied an extracellular solution with osmolarity increased from 280 to 500 mosM/liter with 220 mM PEG, and we repeated the Na application after ∼2 min. As shown in Fig. 14 B, the time constant of outward Na current decay decreased from 26 s to less than 12 s in the presence of the extracellular hyperosmotic solution. In matched experiments, we determined the time constant of outward current decay in the control solutions without PEG. The control τ was significantly less than that determined with a hyperosmotic cytoplasmic solution, and it was greater than the τ determined with hypertonic extracellular solution. Impressively, the τ of current decay decreased and increased to a greater extent than expected for osmosis-induced volume changes without patch-clamp control of solutions. Furthermore, the time constant of Na current decay in nystatin-treated myocytes was stable over 10s of minutes and, in contrast to Na/K pump currents, the nystatin-mediated Na currents showed no run-down over periods of >20 min (n = 6).
The projected physiological function of Na/K pump inactivation
Fig. 15 provides quantitative predictions about the function of Na/K pump inactivation and its role in cardiac Na homeostasis. In brief, we simulated Na turnover and Na/K pump function with inactivation together in a myocyte model. Simulations in Fig. 15 (A and B) are with patch clamp. The simulation in Fig. 15 B is without patch clamp. We assumed instantaneous ion mixing in a 9 pL cytoplasmic volume. Na pump activity was adjusted to generate a maximal pump current of 0.7 nA, and inactivation was simulated as described in Fig. 3. Fig. 15 A depicts the simulated Na/K pump function when pumps are activated by extracellular K with different cytoplasmic Na concentrations. The left panel presents the pump currents, the central panel presents the function of inactivation, and the right panel presents the expected cytoplasmic Na concentration changes. When cytoplasmic Na concentrations are less than 40 mM, pump current decay is dominated by inactivation. At the lowest Na concentration (10 mM), inactivation occurs rapidly, whereas recovery is slow. Recovery rate increases with increasing Na concentrations, and these results are consistent experimental results (Lu et al., 2016). As documented in Results, cytoplasmic Na depletion can indeed promote current decay at 35 to 60 mM cytoplasmic Na concentrations.
Fig. 15 B demonstrates the enhancement of inactivation that occurs during run-down of pump currents in long recordings. In this case, the cytoplasmic solution contains 60 mM Na with 60 mM K. As shown in the left panel of Fig. 15 B, peak currents decrease over 20 min by ∼70%. Current decay during application of K initially amounts to ∼35%, and the decay increases to 90% over time. Individual records from an early time in the recording and from a late time in the recording are shown in the middle panel of Fig. 15 B, and corresponding simulations are shown in the right panel. In the early record (1), current decay shows clearly separated fast and slow decay components, the fast component presumably reflecting inactivation and the slow component reflecting mostly Na depletion. In the late record (2), the inactivation phase is much stronger. As illustrated by the simulation (right), we find that the changes occurring during run-down can be largely accounted for by a slowing of the recovery from inactivation, whereas the rate of inactivation (i.e., the initial rate of current decline) changes very little.
Fig. 15 C describes the projected function of the inactivation mechanism in a myocyte without patch clamp. For this demonstration, we simulated initially a continuous 20 pA Na influx in the presence of the same pump function simulated in Fig. 15 A. The cytoplasmic Na concentration comes to a steady state of 6 to 8 mM with and without inactivation, respectively. We then increased Na influx to 100 pA for 100 s and reduced it again back to 20 pA. The left panel of Fig. 15 C shows the simulated pump currents, the middle panel shows the simulated Na concentration changes, and the right panel shows the fraction of active pumps. With the chosen Na/K pump densities, pump activity keeps cytoplasmic Na in the range of 8 to 15 mM in both simulations. Approximately 80% of pumps are projected to be inactive in the basal state with 6 mM cytoplasmic Na. In response to an increased Na load, pump currents increase to a substantially greater extent when the inactivation mechanism is operative than when it is not. Accordingly, Na concentration changes (middle panel) are smaller and Na concentrations reach a steady state more rapidly when inactivation is operative than when it is not. We point out that the mean lifetime of a Na ion in the cytoplasm is ∼10 min in this simulation. Owing to the steep dependence of Na/K pump activity on cytoplasmic Na, the cytoplasmic Na concentration comes to a steady state with a smaller time constant of ∼200 s, and that time constant is reduced further by more than twofold when the inactivation mechanism is operative. In summary, the inactivation mechanism effectively minimizes Na concentration changes when Na load changes and effectively accelerates the achievement of Na homeostasis in response to Na load changes.
Discussion
We have analyzed the biophysical basis of Na/K pump current decay when Na/K pumps are activated by saturating concentrations of extracellular K in murine cardiac myocytes. Using multiple approaches to generate graded Na currents in both directions and to estimate subsarcolemmal Na concentration changes, we uncovered no clear evidence that subsarcolemmal Na gradients are involved in this decay or could mediate physiologically significant functional cross talk between Na channels and Na/K pumps. The immobilization of Na/K pump charge movements during pump current decay (Figs. 4 and 5), the voltage dependence of pump current decay (Fig. 5), and the enhancement of current decay in parallel with pump current run-down (Fig. 15) are all readily explained by an inactivation mechanism, but not by subsarcolemmal Na depletion. In addition, our results suggest that cytoplasmic mixing volumes and turnover kinetics for all monovalent ions are similar in murine myocytes. Although pump currents can indeed be large enough to substantively deplete cytoplasmic Na, Na/K pump inactivation minimizes Na decay when cytoplasmic Na is in a physiological range. We discuss the experimental support for our conclusions with an emphasis on their potential physiological significance. We stress in this connection that the experiments were all performed at 37°C so that the magnitudes of transport fluxes are not unphysiologically suppressed.
Failure to verify large subsarcolemmal Na gradients
As sketched in the Introduction, the idea that large subsarcolemmal Na gradients occur in cardiac myocytes has a long history involving Na channels, Na transporters, and Na-dependent K channels. Submembrane Na microdomains have also been suggested to mediate functional cross talk between Ih channels and Na/K pumps in neurons (Kang et al., 2004), as well as between TRP channels and Na/Ca exchangers in arterial smooth muscle where Na hot spots have putatively been identified with a fluorescent Na-sensitive dye (Poburko et al., 2007). In the case of cross talk between Na/K pumps and Na/Ca exchangers, we have noted (Fig. S1) that the procedure used to activate Na/Ca exchange in one supportive study (Su et al., 1998) activates additionally maximal Na/K pump currents. Furthermore, we find that in murine cardiac myocytes nickel cannot be used to define Na/Ca exchange currents because nickel activates substantial inward currents that are unrelated to Na/Ca exchange (Fig. S3). In the future, highly specific Na/Ca exchange inhibitors may allow improved studies. However, the best-characterized inhibitors available at this time do not provide the required specificity (Birinyi et al., 2005). For this reason, we proceeded to consider currents generated by veratridine-modified Na channels. Our protocols should have revealed subsarcolemmal Na accumulation by multiple criteria. Na channel activity should have caused greater than expected inward current decay (Fig. 6), outward Na current upon removing Na (Figs. 7 and 9), and activation of Na/K pumps (Fig. 7). It did not. Na/K pump activity should have caused greater than expected changes of Na and Li currents carried by Na channels (Fig. 8). It did not. In fact, it is essential to assume that pump currents decay as a result of their inactivation to explain the small effects, or indeed lack of effects, of pump current on Na channel current (e.g., Fig. 8 C).
In the most extreme example encountered (Fig. 9 A), the subsarcolemmal Na accumulation, determined from reversal potentials during activation of a 1 nA Na current, amounted to nearly twice that expected from a cell model with instantaneous Na diffusion (Fig. 1). Although this is a significant discrepancy, and may well be indicative of lateral ion inhomogeneity in myocytes, the discrepancy is of small magnitude in relation to subsarcolemmal Na gradients proposed to exist in the articles outlined in the Introduction. The fact is that Na/K pump currents decay substantially with a time constant of ∼2 s (Figs. 4 and 5), even when pump currents are small (Fig. 8 B), and we find no evidence that this current decay reflects subsarcolemmal Na depletion. Na accumulation/depletion can certainly occur in response to transsarcolemmal Na flux, but it occurs with a longer time constant of 14 to 20 s (Figs. 9, 10, and 11).
Potential roles of local nucleotide concentration changes
One alternative to local Na depletion is that pump current decay reflects depletion of ATP and/or accumulation of ADP and Pi. We have found it difficult to address these possibilities, starting with the fact that deletion of ATP from pipette solutions has little effect on pump current recordings over many minutes. The idea that ATP hydrolyzed by cardiac Na/K pumps is locally channeled to pumps from nearby glycolytic enzymes (Chu et al., 2012) is increasingly well supported (Sepp et al., 2014). Given that mean cytoplasmic Na can decrease by ∼20 mM within 30 s with activation of maximal pump activity (Fig. 9 B), it seems not only feasible but also likely that significant nucleotide changes occur, whether locally or globally. In this regard, new optical methods to monitor nucleotide concentration changes (Tantama et al., 2012) hold a great potential to provide relevant insights. For now, however, our central observations seem inconsistent with a causal role of nucleotide changes: (1) Current decay is less pronounced, not more pronounced, as pump currents are increased by increasing cytoplasmic Na (Lu et al., 2016). (2) Nucleotide changes do not explain the capacitance changes that correlate with pump activity changes (Figs. 4 and 5) or the pronounced enhancement of pump current decay that occurs with hyperpolarization (Fig. 5). (3) Cardiac Na/K pumps in excised membrane patches have a very high Ki for inhibition by ADP (>4 mM) and Pi (>10 mM; Hilgemann et al., 2006). (4) Finally, we have no reason to believe that the increased current decay that develops as pump currents run down (Fig. 15 B) reflects a failure of ATP regenerating systems that support pump activity.
Ion mixing volumes and kinetics: Are cytoplasmic mixing volumes for ions smaller than expected?
The time constants with which ions appear to turn over in murine cardiac myocytes (14–20 s; Figs. 9, 10, 11, 12, 13, and 14) are substantially smaller than we had expected from previous estimates of myocyte mixing volumes (Lu et al., 2016). Importantly, results for K, Li, and Cs (Figs. 11, 12, 13, and 14) are not notably different from results for Na, except for Li and K currents carried by veratridine-modified Na channels (Fig. 10). In those two cases, the complexity emerged that inward current decay during cation influx is substantially larger than expected from the simple model and substantially larger than reverse currents that develop upon removing the cations. Clearly, those currents are not proportional to ion concentration differences across the sarcolemma, and it seems likely that complex rectification functions underlie those patterns.
For Cl (Fig. 13), it is potentially surprising that the apparent cytoplasmic mixing space is similar in size to the spaces suggested for monovalent cations. Fixed negative charges of myofilaments are expected to constitute a large fraction of total negative charges in the cytoplasm of myocytes. Accordingly, Donnan potentials would be expected to hinder Cl accumulation during continuous influx via nystatin channels. This might not happen because (1) myofilaments may bind the major unnatural cation used in these experiments, NMDG, thereby suppressing the Donnan phenomenon, and/or (2) Donnan effects are physiologically smaller than expected from experiments with myofilaments (Stephenson et al., 1981).
Our kinetic results indicate that ion mixing volumes are less than 50% of the geometrical cell volume. Surprisingly, there are very few studies to support or contradict this conclusion. The results are highly consistent among different types of experiments (e.g., Na influx versus efflux) and with different monovalent ions. The ion mixing volumes (7–10 pL) can be compared first to total cellular volumes of ∼24 pL for binuclear murine myocytes (Bensley et al., 2016). To our knowledge, fluorescent dyes cannot be used to estimate myocyte mixing volumes, because all dyes interact significantly with cytoplasmic components. Therefore, cytoplasmic mixing spaces of cardiac myocytes have been estimated exclusively from morphometric/ultrastructural analysis up to now. Mitochondria occupy with certainty 30% of the murine myocyte space (Eisele et al., 2008; Hayashi et al., 2009; Jarosz et al., 2017), and proteins occupy at least another 10% of the cytoplasmic space, leaving up to 60% of the cytoplasmic space as immediate ion mixing space.
Previous findings that tend to support smaller cytoplasmic volumes include the following. First, total water volume of cardiac muscle can be as low as 75% in some cardiac muscle preparations (Page and Solomon, 1960). Second, it has long been suggested that hydration water in muscle involves more than 20% of cellular water (Rorschach et al., 1991), and therefore that the effective volume of protein in muscle may be greater than expected from dry weight/wet weight ratios. Third, analysis of volume changes of cardiac myocytes in response to osmotic changes reveals that nearly 40% of the myocyte volume is osmotically inactive (Drewnowska and Baumgarten, 1991; Ogura et al., 2002). It would be of great interest to know whether osmotically inactive spaces involve mostly myofilaments or whether mitochondria and possibly other organelles are involved.
We have verified that the kinetics of current changes thought to reflect myocyte volume are sensitive to changes of osmolarity and therefore changes of myocyte volume (Fig. 14). The time constant of current decay is predictably increased by swelling cells via pipette solutions that are 100 mM hyperosmotic, and the time constant of current decay predictably decreases in response to extracellular solutions that are made 220 mM hyperosmotic. In fact, the responses are larger than expected from the percentual changes of osmolarity. This outcome is readily explained. The establishment of whole-cell patch clamp does not dissipate but in fact supports and maintains the osmotic gradients that drive water movements across the plasmalemma. In the absence of regulatory volume responses and restorative forces, imposition of an osmotic gradient will cause unrelenting volume changes during patch clamp. Because solute exchange to the patch pipette is more rapid than the equilibration of water (Fig. 14), the volume of patch-clamped myocytes need not return to control values after removing an osmotic gradient (Fig. 14 A).
Finally, we stress that our results do not contradict a wide range of studies that indicate significant complexities of diffusion in the myocyte cytoplasm. We, like others, are impressed that monovalent ions evidently enter the myoplasm through patch pipettes in an unimpeded fashion, consistent with recent estimates of Na diffusion coefficients in myocytes (Swietach et al., 2015). On the other hand, diffusion of organic molecules as small as cAMP appears to be hindered much more significantly by the myocyte tortuosity and/or molecular crowding (Agarwal et al., 2016; Richards et al., 2016; Yang et al., 2016). Uncertainties remain impressive, and it might be interesting to attempt to address them for myocytes with some type of molecular simulation. It would also be of interest to perform equivalent experiments in myocytes from different species with a lower mitochondrial content. Ion exchange times and/or Na/K pump inactivation times are substantially longer, for example, in guinea pig myocytes (Fujioka et al., 1998) than described here in mouse myocytes.
Implications of Na/K pump inactivation for cardiac Na/K pump function and Na homeostasis
This study supports the hypothesis that Na/K pump activity in murine myocytes is controlled by autoregulatory reactions that enhance pump activity secondarily when cytoplasmic Na rises and suppress pump activity when cytoplasmic Na declines. The inactivation mechanism is also voltage dependent, being promoted by hyperpolarization when cytoplasmic Na is in a physiological range (Fig. 5). The mechanism may therefore be of substantial physiological importance, and it will be of great interest to determine if the regulatory properties are isoform and/or tissue dependent. Mouse cardiac myocytes contain primarily type 1 and 2 α pump subunits (Dostanic et al., 2004). Because pump currents can inactivate almost completely (e.g., Fig. 5 A at −60 mV or with cytoplasmic Na <15 mM; Lu et al., 2016), it seems likely that both of these isoforms undergo inactivation.
As demonstrated in simulations (Fig. 15), the inactivation mechanism effectively accelerates myocyte Na homeostasis and maintains cytoplasmic Na concentrations more nearly constant than would otherwise be the case. That transporters might use ion binding by their transport sites to regulate their activity is previously documented for Na/Ca exchangers, which inactivate preferentially when all three Na transport sites are occupied (Hilgemann et al., 1992). Na/H exchangers also appear to have a Na-dependent inactivation mechanism that depends on a pertussis toxin-sensitive G-protein (Ishibashi et al., 1999; Hilgemann et al., 2006). In pathological settings, both transporters are thought to become culprits, the former promoting Na influx together with sustained Na channels (Belardinelli et al., 2015; Cardona et al., 2016) and the latter promoting Na-dependent Ca influx (Tang et al., 2012). The time-and Na-dependent recovery from inactivation of Na/K pumps would logically work against the ensuing problem that excess Na load causes excessive Ca load. As a final perspective, we underscore that the Na-dependent inactivation of Na/K pumps in murine myocytes is strongly regulated by cytoplasmic Ca, being attenuated by transient Ca elevations, perhaps with an involvement of lipid signaling mechanisms (Lu et al., 2016). Given the strong dependence of cardiac excitation–contraction cycle on the transsarcolemmal Na gradient (e.g., Brill and Wasserstrom, 1986), this could be a mechanism through which cardiac myocytes regulate their contractile activity by modifying the Na gradient.
Supplementary Material
Acknowledgments
We thank Michael Fine, Mei-Jung Lin, and Christine Deisl (University of Texas Southwestern) for helpful discussions and criticisms.
The work was supported by National Institutes of Health grant HL119843 and the Charles and Jane Pak Center of Mineral Metabolism and Clinical Research.
The authors declare no competing financial interests.
Eduardo Ríos served as editor.
Footnotes
Abbreviation used:
- PEG
- polyethylene glycol
References
- Agarwal S.R., Clancy C.E., and Harvey R.D.. 2016. Mechanisms restricting diffusion of intracellular cAMP. Sci. Rep. 6:19577 10.1038/srep19577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akera T., Bennett R.T., Olgaard M.K., and Brody T.M.. 1976. Cardiac Na+, K+-adenosine triphosphatase inhibition by ouabain and myocardial sodium: A computer simulation. J. Pharmacol. Exp. Ther. 199:287–297. [PubMed] [Google Scholar]
- Apell H.J., Schneeberger A., and Sokolov V.S.. 1998. Partial reactions of the Na,K-ATPase: Kinetic analysis and transport properties. Acta Physiol. Scand. Suppl. 643:235–245. [PubMed] [Google Scholar]
- Belardinelli L., Giles W.R., Rajamani S., Karagueuzian H.S., and Shryock J.C.. 2015. Cardiac late Na+ current: Proarrhythmic effects, roles in long QT syndromes, and pathological relationship to CaMKII and oxidative stress. Heart Rhythm. 12:440–448. 10.1016/j.hrthm.2014.11.009 [DOI] [PubMed] [Google Scholar]
- Bensley J.G., De Matteo R., Harding R., and Black M.J.. 2016. Three-dimensional direct measurement of cardiomyocyte volume, nuclearity, and ploidy in thick histological sections. Sci. Rep. 6:23756 10.1038/srep23756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bielen F.V., Glitsch H.G., and Verdonck F.. 1991. Changes of the subsarcolemmal Na+ concentration in internally perfused cardiac cells. Biochim. Biophys. Acta. 1065:269–271. 10.1016/0005-2736(91)90239-5 [DOI] [PubMed] [Google Scholar]
- Birinyi P., Acsai K., Bányász T., Tóth A., Horváth B., Virág L., Szentandrássy N., Magyar J., Varró A., Fülöp F., and Nánási P.P.. 2005. Effects of SEA0400 and KB-R7943 on Na+/Ca2+ exchange current and L-type Ca2+ current in canine ventricular cardiomyocytes. Naunyn Schmiedebergs Arch. Pharmacol. 372:63–70. 10.1007/s00210-005-1079-x [DOI] [PubMed] [Google Scholar]
- Bossen E.H., Sommer J.R., and Waugh R.A.. 1978. Comparative stereology of the mouse and finch left ventricle. Tissue Cell. 10:773–784. 10.1016/0040-8166(78)90062-9 [DOI] [PubMed] [Google Scholar]
- Brill D.M., and Wasserstrom J.A.. 1986. Intracellular sodium and the positive inotropic effect of veratridine and cardiac glycoside in sheep Purkinje fibers. Circ. Res. 58:109–119. 10.1161/01.RES.58.1.109 [DOI] [PubMed] [Google Scholar]
- Cardona K., Trenor B., and Giles W.R.. 2016. Changes in intracellular Na+ following enhancement of late Na+ current in virtual human ventricular myocytes. PLoS One. 11:e0167060 10.1371/journal.pone.0167060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmeliet E. 1992. A fuzzy subsarcolemmal space for intracellular Na+ in cardiac cells? Cardiovasc. Res. 26:433–442. 10.1093/cvr/26.5.433 [DOI] [PubMed] [Google Scholar]
- Chu H., Puchulu-Campanella E., Galan J.A., Tao W.A., Low P.S., and Hoffman J.F.. 2012. Identification of cytoskeletal elements enclosing the ATP pools that fuel human red blood cell membrane cation pumps. Proc. Natl. Acad. Sci. USA. 109:12794–12799. 10.1073/pnas.1209014109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark R.B., Tremblay A., Melnyk P., Allen B.G., Giles W.R., and Fiset C.. 2001. T-tubule localization of the inward-rectifier K(+) channel in mouse ventricular myocytes: A role in K(+) accumulation. J. Physiol. 537:979–992. 10.1111/j.1469-7793.2001.00979.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Despa S., Kockskämper J., Blatter L.A., and Bers D.M.. 2004. Na/K pump-induced [Na](i) gradients in rat ventricular myocytes measured with two-photon microscopy. Biophys. J. 87:1360–1368. 10.1529/biophysj.103.037895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Weer P., Gadsby D.C., and Rakowski R.F.. 1988. Voltage dependence of the Na-K pump. Annu. Rev. Physiol. 50:225–241. 10.1146/annurev.ph.50.030188.001301 [DOI] [PubMed] [Google Scholar]
- DiFranco M., Hakimjavadi H., Lingrel J.B., and Heiny J.A.. 2015. Na,K-ATPase α2 activity in mammalian skeletal muscle T-tubules is acutely stimulated by extracellular K+. J. Gen. Physiol. 146:281–294. 10.1085/jgp.201511407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dostanic I., Schultz J.J., Lorenz J.N., and Lingrel J.B.. 2004. The alpha 1 isoform of Na,K-ATPase regulates cardiac contractility and functionally interacts and co-localizes with the Na/Ca exchanger in heart. J. Biol. Chem. 279:54053–54061. 10.1074/jbc.M410737200 [DOI] [PubMed] [Google Scholar]
- Drewnowska K., and Baumgarten C.M.. 1991. Regulation of cellular volume in rabbit ventricular myocytes: Bumetanide, chlorothiazide, and ouabain. Am. J. Physiol. 260:C122–C131. [DOI] [PubMed] [Google Scholar]
- Egger M., Ruknudin A., Lipp P., Kofuji P., Lederer W.J., Schulze D.H., and Niggli E.. 1999. Functional expression of the human cardiac Na+/Ca2+ exchanger in Sf9 cells: rapid and specific Ni2+ transport. Cell Calcium. 25:9–17. 10.1054/ceca.1998.0002 [DOI] [PubMed] [Google Scholar]
- Eisele J.C., Schaefer I.M., Randel Nyengaard J., Post H., Liebetanz D., Brüel A., and Mühlfeld C.. 2008. Effect of voluntary exercise on number and volume of cardiomyocytes and their mitochondria in the mouse left ventricle. Basic Res. Cardiol. 103:12–21. 10.1007/s00395-007-0684-x [DOI] [PubMed] [Google Scholar]
- Fujioka Y., Matsuoka S., Ban T., and Noma A.. 1998. Interaction of the Na+-K+ pump and Na+-Ca2+ exchange via [Na+]i in a restricted space of guinea-pig ventricular cells. J. Physiol. 509:457–470. 10.1111/j.1469-7793.1998.457bn.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadsby D.C., Bezanilla F., Rakowski R.F., De Weer P., and Holmgren M.. 2012. The dynamic relationships between the three events that release individual Na+ ions from the Na+/K+-ATPase. Nat. Commun. 3:669 10.1038/ncomms1673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gwanyanya A., Amuzescu B., Zakharov S.I., Macianskiene R., Sipido K.R., Bolotina V.M., Vereecke J., and Mubagwa K.. 2004. Magnesium-inhibited, TRPM6/7-like channel in cardiac myocytes: Permeation of divalent cations and pH-mediated regulation. J. Physiol. 559:761–776. 10.1113/jphysiol.2004.067637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han F., Tucker A.L., Lingrel J.B., Despa S., and Bers D.M.. 2009. Extracellular potassium dependence of the Na+-K+-ATPase in cardiac myocytes: isoform specificity and effect of phospholemman. Am. J. Physiol. Cell Physiol. 297:C699–C705. 10.1152/ajpcell.00063.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi T., Martone M.E., Yu Z., Thor A., Doi M., Holst M.J., Ellisman M.H., and Hoshijima M.. 2009. Three-dimensional electron microscopy reveals new details of membrane systems for Ca2+ signaling in the heart. J. Cell Sci. 122:1005–1013. 10.1242/jcs.028175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegyi B., Bányász T., Shannon T.R., Chen-Izu Y., and Izu L.T.. 2016. Electrophysiological determination of submembrane Na(+) concentration in cardiac myocytes. Biophys. J. 111:1304–1315. 10.1016/j.bpj.2016.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermans A.N., Glitsch H.G., and Verdonck F.. 1997. Activation of the Na+/K+ pump current by intra- and extracellular Li ions in single guinea-pig cardiac cells. Biochim. Biophys. Acta. 1330:83–93. 10.1016/S0005-2736(97)00143-0 [DOI] [PubMed] [Google Scholar]
- Heyse S., Wuddel I., Apell H.J., and Stürmer W.. 1994. Partial reactions of the Na,K-ATPase: Determination of rate constants. J. Gen. Physiol. 104:197–240. 10.1085/jgp.104.2.197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilgemann D.W. 1994. Channel-like function of the Na,K pump probed at microsecond resolution in giant membrane patches. Science. 263:1429–1432. 10.1126/science.8128223 [DOI] [PubMed] [Google Scholar]
- Hilgemann D.W., Matsuoka S., Nagel G.A., and Collins A.. 1992. Steady-state and dynamic properties of cardiac sodium-calcium exchange. Sodium-dependent inactivation. J. Gen. Physiol. 100:905–932. 10.1085/jgp.100.6.905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilgemann D.W., Yaradanakul A., Wang Y., and Fuster D.. 2006. Molecular control of cardiac sodium homeostasis in health and disease. J. Cardiovasc. Electrophysiol. 17(s1, Suppl 1):S47–S56. 10.1111/j.1540-8167.2006.00383.x [DOI] [PubMed] [Google Scholar]
- Ishibashi H., Dinudom A., Harvey K.F., Kumar S., Young J.A., and Cook D.I.. 1999. Na(+)-H(+) exchange in salivary secretory cells is controlled by an intracellular Na(+) receptor. Proc. Natl. Acad. Sci. USA. 96:9949–9953. 10.1073/pnas.96.17.9949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosz J., Ghosh S., Delbridge L.M., Petzer A., Hickey A.J., Crampin E.J., Hanssen E., and Rajagopal V.. 2017. Changes in mitochondrial morphology and organization can enhance energy supply from mitochondrial oxidative phosphorylation in diabetic cardiomyopathy. Am. J. Physiol. Cell Physiol. 312:C190–C197. 10.1152/ajpcell.00298.2016 [DOI] [PubMed] [Google Scholar]
- Kang Y., Notomi T., Saito M., Zhang W., and Shigemoto R.. 2004. Bidirectional interactions between h-channels and Na+-K+ pumps in mesencephalic trigeminal neurons. J. Neurosci. 24:3694–3702. 10.1523/JNEUROSCI.5641-03.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurata Y., Sato R., Hisatome I., and Imanishi S.. 1999. Mechanisms of cation permeation in cardiac sodium channel: Description by dynamic pore model. Biophys. J. 77:1885–1904. 10.1016/S0006-3495(99)77031-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kushmerick M.J., and Podolsky R.J.. 1969. Ionic mobility in muscle cells. Science. 166:1297–1298. 10.1126/science.166.3910.1297 [DOI] [PubMed] [Google Scholar]
- Lariccia V., Fine M., Magi S., Lin M.J., Yaradanakul A., Llaguno M.C., and Hilgemann D.W.. 2011. Massive calcium-activated endocytosis without involvement of classical endocytic proteins. J. Gen. Physiol. 137:111–132. 10.1085/jgp.201010468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leblanc N., and Hume J.R.. 1990. Sodium current-induced release of calcium from cardiac sarcoplasmic reticulum. Science. 248:372–376. 10.1126/science.2158146 [DOI] [PubMed] [Google Scholar]
- Lederer W.J., Niggli E., and Hadley R.W.. 1990. Sodium-calcium exchange in excitable cells: Fuzzy space. Science. 248:283 10.1126/science.2326638 [DOI] [PubMed] [Google Scholar]
- Li M., Jiang J., and Yue L.. 2006. Functional characterization of homo- and heteromeric channel kinases TRPM6 and TRPM7. J. Gen. Physiol. 127:525–537. 10.1085/jgp.200609502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu C.C., Kabakov A., Markin V.S., Mager S., Frazier G.A., and Hilgemann D.W.. 1995. Membrane transport mechanisms probed by capacitance measurements with megahertz voltage clamp. Proc. Natl. Acad. Sci. USA. 92:11220–11224. 10.1073/pnas.92.24.11220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu F.M., Deisl C., and Hilgemann D.W.. 2016. Profound regulation of Na/K pump activity by transient elevations of cytoplasmic calcium in murine cardiac myocytes. eLife. 5:e19267 10.7554/eLife.19267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marty A., and Finkelstein A.. 1975. Pores formed in lipid bilayer membranes by nystatin: Differences in its one-sided and two-sided action. J. Gen. Physiol. 65:515–526. 10.1085/jgp.65.4.515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogul D.J., Singer D.H., and Ten Eick R.E.. 1989. Ionic diffusion in voltage-clamped isolated cardiac myocytes. Implications for Na,K-pump studies. Biophys. J. 56:565–577. 10.1016/S0006-3495(89)82704-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakao M., and Gadsby D.C.. 1986. Voltage dependence of Na translocation by the Na/K pump. Nature. 323:628–630. 10.1038/323628a0 [DOI] [PubMed] [Google Scholar]
- Nakao M., and Gadsby D.C.. 1989. [Na] and [K] dependence of the Na/K pump current-voltage relationship in guinea pig ventricular myocytes. J. Gen. Physiol. 94:539–565. 10.1085/jgp.94.3.539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogura T., Matsuda H., Imanishi S., and Shibamoto T.. 2002. Sarcolemmal hydraulic conductivity of guinea-pig and rat ventricular myocytes. Cardiovasc. Res. 54:590–600. 10.1016/S0008-6363(02)00267-5 [DOI] [PubMed] [Google Scholar]
- Page E., and Solomon A.K.. 1960. Cat heart muscle in vitro. I. Cell volumes and intracellular concentrations in papillary muscle. J. Gen. Physiol. 44:327–344. 10.1085/jgp.44.2.327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poburko D., Liao C.H., Lemos V.S., Lin E., Maruyama Y., Cole W.C., and van Breemen C.. 2007. Transient receptor potential channel 6-mediated, localized cytosolic [Na+] transients drive Na+/Ca2+ exchanger-mediated Ca2+ entry in purinergically stimulated aorta smooth muscle cells. Circ. Res. 101:1030–1038. 10.1161/CIRCRESAHA.107.155531 [DOI] [PubMed] [Google Scholar]
- Richards M., Lomas O., Jalink K., Ford K.L., Vaughan-Jones R.D., Lefkimmiatis K., and Swietach P.. 2016. Intracellular tortuosity underlies slow cAMP diffusion in adult ventricular myocytes. Cardiovasc. Res. 110:395–407. 10.1093/cvr/cvw080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rorschach H.E., Lin C., and Hazlewood C.F.. 1991. Diffusion of water in biological tissues. Scanning Microsc. Suppl. 5:S1–S9, discussion :S9–S10. [PubMed] [Google Scholar]
- Sepp M., Sokolova N., Jugai S., Mandel M., Peterson P., and Vendelin M.. 2014. Tight coupling of Na+/K+-ATPase with glycolysis demonstrated in permeabilized rat cardiomyocytes. PLoS One. 9:e99413 10.1371/journal.pone.0099413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanes A.M., Grundfest H., and Freygang W.. 1953. Low level impedance changes following the spike in the squid giant axon before and after treatment with “veratrine” alkaloids. J. Gen. Physiol. 37:39–51. 10.1085/jgp.37.1.39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shang W., Lu F., Sun T., Xu J., Li L.L., Wang Y., Wang G., Chen L., Wang X., Cannell M.B., et al. 2014. Imaging Ca2+ nanosparks in heart with a new targeted biosensor. Circ. Res. 114:412–420. 10.1161/CIRCRESAHA.114.302938 [DOI] [PubMed] [Google Scholar]
- Silverman B., Warley A., Miller J.I., James A.F., and Shattock M.J.. 2003. Is there a transient rise in sub-sarcolemmal Na and activation of Na/K pump current following activation of I(Na) in ventricular myocardium? Cardiovasc. Res. 57:1025–1034. 10.1016/S0008-6363(02)00645-4 [DOI] [PubMed] [Google Scholar]
- Sperelakis N., and Pappano A.J.. 1969. Increase in PNa and PK of cultured heart cells produced by veratridine. J. Gen. Physiol. 53:97–114. 10.1085/jgp.53.1.97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephenson D.G., Wendt I.R., and Forrest Q.G.. 1981. Non-uniform ion distributions and electrical potentials in sarcoplasmic regions of skeletal muscle fibres. Nature. 289:690–692. 10.1038/289690a0 [DOI] [PubMed] [Google Scholar]
- Su Z., Zou A., Nonaka A., Zubair I., Sanguinetti M.C., and Barry W.H.. 1998. Influence of prior Na+ pump activity on pump and Na+/Ca2+ exchange currents in mouse ventricular myocytes. Am. J. Physiol. 275:H1808–H1817. [DOI] [PubMed] [Google Scholar]
- Swietach P., Spitzer K.W., and Vaughan-Jones R.D.. 2015. Na+ ions as spatial intracellular messengers for co-ordinating Ca2+ signals during pH heterogeneity in cardiomyocytes. Cardiovasc. Res. 105:171–181. 10.1093/cvr/cvu251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang Q., Ma J., Zhang P., Wan W., Kong L., and Wu L.. 2012. Persistent sodium current and Na+/H+ exchange contributes to the augmentation of the reverse Na+/Ca2+ exchange during hypoxia or acute ischemia in ventricular myocytes. Pflugers Arch. 463:513–522. 10.1007/s00424-011-1070-y [DOI] [PubMed] [Google Scholar]
- Tantama M., Hung Y.P., and Yellen G.. 2012. Optogenetic reporters: Fluorescent protein-based genetically encoded indicators of signaling and metabolism in the brain. Prog. Brain Res. 196:235–263. 10.1016/B978-0-444-59426-6.00012-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdonck F., Mubagwa K., and Sipido K.R.. 2004. [Na(+)] in the subsarcolemmal ‘fuzzy’ space and modulation of [Ca(2+)](i) and contraction in cardiac myocytes. Cell Calcium. 35:603–612. 10.1016/j.ceca.2004.01.014 [DOI] [PubMed] [Google Scholar]
- Wang T.M., and Hilgemann D.W.. 2008. Ca-dependent nonsecretory vesicle fusion in a secretory cell. J. Gen. Physiol. 132:51–65. 10.1085/jgp.200709950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wendt-Gallitelli M.F., Voigt T., and Isenberg G.. 1993. Microheterogeneity of subsarcolemmal sodium gradients. Electron probe microanalysis in guinea-pig ventricular myocytes. J. Physiol. 472:33–44. 10.1113/jphysiol.1993.sp019934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang P.C., Boras B.W., Jeng M.T., Docken S.S., Lewis T.J., McCulloch A.D., Harvey R.D., and Clancy C.E.. 2016. A computational modeling and simulation approach to investigate mechanisms of subcellular cAMP compartmentation. PLOS Comput. Biol. 12:e1005005 10.1371/journal.pcbi.1005005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaradanakul A., Wang T.M., Lariccia V., Lin M.J., Shen C., Liu X., and Hilgemann D.W.. 2008. Massive Ca-induced membrane fusion and phospholipid changes triggered by reverse Na/Ca exchange in BHK fibroblasts. J. Gen. Physiol. 132:29–50. 10.1085/jgp.200709865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zong X.G., Dugas M., and Honerjäger P.. 1992. Relation between veratridine reaction dynamics and macroscopic Na current in single cardiac cells. J. Gen. Physiol. 99:683–697. 10.1085/jgp.99.5.683 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.