Species-independent attraction to biofilms through electrical signaling

Summary

Bacteria residing within biofilm communities can coordinate their behavior through cell-to-cell signaling. However, it remains unclear if these signals can also influence the behavior of distant cells that are not part of the community. Using a microfluidic approach, we find that potassium ion channel-mediated electrical signaling generated by a Bacillus subtilis biofilm can attract distant cells. Integration of experiments and mathematical modeling indicates that extracellular potassium emitted from the biofilm alters the membrane potential of distant cells, thereby directing their motility. This electrically-mediated attraction appears to be a generic mechanism that enables cross-species interactions, as Pseudomonas aeruginosa cells also become attracted to the electrical signal released by the B. subtilis biofilm. Cells within a biofilm community can thus not only coordinate their own behavior, but also influence the behavior of diverse bacteria at a distance through long-range electrical signaling.

Introduction

Bacteria within biofilms can coordinate their behavior through distinct forms of communication (Shapiro 1998; Waters & Bassler 2005; Brameyer et al. 2015; Liu et al. 2015). The best characterized cell-to-cell signaling process in bacteria is known as quorum sensing (Miller & Bassler 2001). Recently another cell-to-cell communication mechanism based on ion channel-mediated electrical signaling has also been described (Prindle et al. 2015). This electrical signaling has been shown to facilitate communication within a biofilm community (Liu et al. 2015; Prindle et al. 2015). Specifically, cells within B. subtilis biofilms can actively relay extracellular potassium signals, producing electrical waves that propagate through the biofilm and coordinate metabolic states, thereby increasing collective fitness (Prindle et al. 2015; Liu et al. 2015). These findings provoke the question of whether such extracellular signals could extend beyond the biofilm, resulting in long-range interactions that could affect distant bacteria that are not part of the biofilm. Here we utilized a microfluidic approach to investigate whether electrical signals generated within the biofilm can influence the behavior of other bacteria that share the same aqueous environment. In particular, we hypothesized that electrical signals could direct bacterial motility through altering the membrane potential. Such long-range signaling could provide a generic mechanism for bacterial communities to exert control over the motile behavior of distant cells.

Results

Periodic attraction of distant motile cells to electrically oscillating biofilms

We began by measuring the interaction dynamics between a biofilm and motile cells in a large microfluidic chamber (3 mm × 3 mm × 6 μm) (Fig. S1). Specifically, we grew a biofilm in the microfluidic chamber until it reached the size (over one million cells) at which oscillations emerge (Liu et al. 2015). We then introduced motile cells into the chamber and noticed that they were periodically attracted to the electrically oscillating biofilm (Supplemental Movie 1). To accurately discriminate between biofilm and motile cells, we then introduced fluorescently labeled motile cells (constitutively expressing a fluorescent protein) into the growth chamber, again after biofilm formation (Fig. 1a). To determine the relationship between motile cell attraction and electrical oscillations in the biofilm (Prindle et al. 2015), we quantified the membrane potential of biofilm cells by using the previously characterized fluorescent cationic dye Thioflavin T (ThT) (Fig. 1a) (Prindle et al. 2015). This charged reporter dye diffuses across the membrane according to the membrane potential and thereby acts as a Nernstian voltage indicator of bacterial membrane potential (Plásek & Sigler 1996). This approach revealed that the periodic increase in motile cell density at the biofilm edge accurately tracks the oscillations in biofilm membrane potential (Fig. 1b, c, and Supplemental Movie 2). In particular, the peak accumulation of motile cells at the biofilm edge slightly lags the peak of electrical signaling in the biofilm by 26 ± 9 min (mean ± st. dev., n = 44 pulses Fig. 1c, d). Furthermore, the period of motile cell attraction to the biofilm edge tracks with the natural variation in the period of electrical signaling within biofilms (Fig. 1e). We observed no attraction of motile cells to biofilms that had not yet initiated electrical oscillations (Fig. S2), suggesting that electrical signaling plays a critical role in motile cell attraction. In addition, functional motility machinery in distant cells is also required, as non-motile cells lacking the flagellin gene hag showed no attraction to electrically oscillating biofilms (Fig. 1f). Together, these results show that electrical oscillations generated by the biofilm are correlated in time with periodic attraction of distant motile cells to the biofilm.

Figure 1.

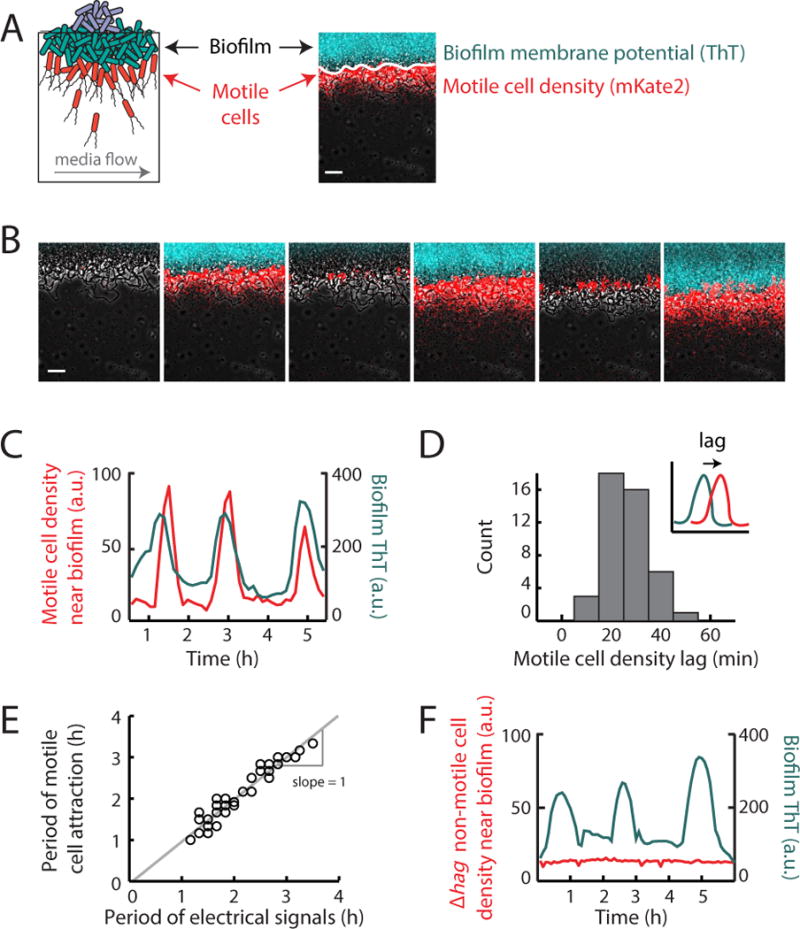
Distant motile cells are periodically attracted to an electrically oscillating biofilm. (a) Illustration of motile cell interaction with a biofilm within a shared microfluidic growth chamber (see Figure S1). Media flows in the direction indicated by the gray arrow, at a rate of 12 μm/s. Membrane potential changes are reported by Thioflavin T (ThT, pseudocolored cyan), a cationic dye that acts as a Nernstian voltage indicator (Prindle et al. 2015). ThT fluorescence increases when the cell becomes more inside-negative, making ThT fluorescence inversely related to the membrane potential. Motile cells (pseudocolored red) express a fluorescent protein mKate2 from the P_hyperspank promoter induced with 1 mM IPTG. Motile cell density is measured using mKate2 fluorescence (only present in motile cells) in the 100 μm region outward from the biofilm edge (indicated as a solid white line, see Quantification and Statistical Analysis). Scale bar, 50 μm. (b) Filmstrip showing the edge of a biofilm which is located on the top of each image. Images depict periodic motile cell attraction to an electrically oscillating biofilm and subsequent passive dispersal away from the biofilm. Gray (phase contrast), cyan (membrane potential), red (motile cells). Scale bar, 50 μm. (c) Time series of motile cell density (red) near the biofilm edge together with membrane potential reporter ThT measured within the biofilm (cyan). Time series shows that motile cell density changes periodically along with electrical oscillations within the biofilm. Time series is representative of 3 independently reproduced experiments. (d) Histogram of the time between peaks in biofilm electrical activity and peaks in motile cell attraction (motile cell density lag). Motile cell peaks occur on average 26.4 ± 8.8 min after the initiation of electrical oscillations within the biofilm (mean ± st. dev., n = 44 pulses, see Quantification and Statistical Analysis). Inset, illustration of the quantification method for motile cell density lag. Motile cell density lag is defined as the time between the electrical pulse (cyan) and the motile cell pulse (red), represented with an arrow (See Quantification and Statistical Analysis). (e) Scatter plot of the periods of electrical oscillations within biofilms (peak to peak) and the periods of co-occurring pulses in motile cell attraction (peak to peak). Periods of motile cell attraction correlate with natural variations in the periods of electrical oscillations within biofilms (see Quantification and Statistical Analysis, Pearson correlation coefficient = 0.96, n = 33 periods). (f) Time series of non-motile (Δhag, red) cell density together with biofilm membrane potential (cyan). Time series shows no periodic attraction of non-motile cells to an oscillating biofilm. Time series is representative of 3 independently reproduced experiments. See also Figure S2.

Sufficiency of extracellular potassium in directing cell motility

We next asked whether the observed attraction of motile cells was due to changes in extracellular potassium generated during biofilm oscillations (Prindle et al. 2015). Utilizing the microfluidic device, we directly tested whether potassium signals were sufficient to influence motile cells. Specifically, we investigated whether we could redirect motile cells away from the biofilm by providing an alternative and stronger source of extracellular potassium. Accordingly, we transiently flowed media supplemented with potassium into the region most distant from the biofilm (Fig. 2a). This alternative potassium source was introduced during a peak in biofilm electrical activity (maximal motile cell attraction) (Fig. 2b). We find that instead of being attracted to the biofilm, motile cells now accumulated at the competing potassium source (Fig. 2b, c). Removal of this alternative potassium source restored motile cell attraction to the biofilm in the subsequent pulse of electrical activity (Fig. 2b). These results demonstrate that changes in extracellular potassium gradients are sufficient to direct motile cell behavior.

Figure 2.

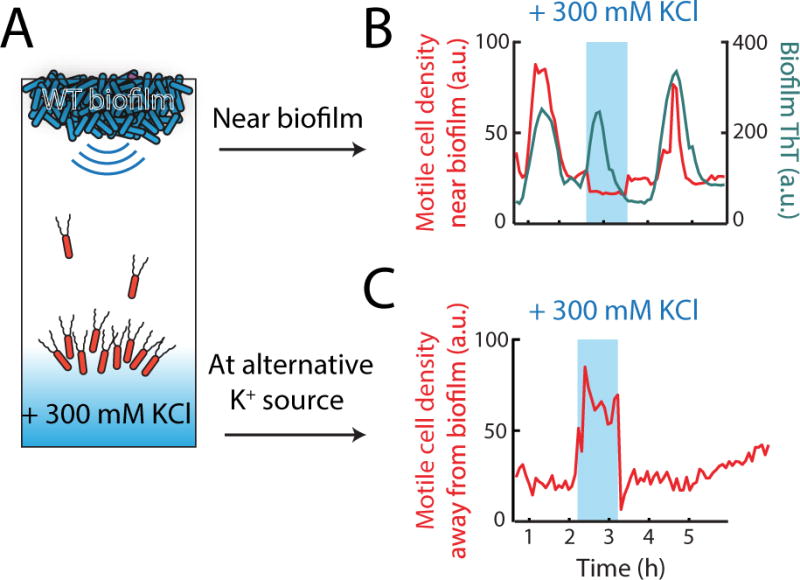
Extracellular potassium is sufficient to direct motility. (a) An alternative potassium source is introduced into the growth chamber (blue shading) to redirect motile cells away from an oscillating biofilm (see Method Details). Arrows indicate the two regions where cell density was evaluated for the time series shown in (b, c). (b, c) Time series showing redirection of motile cells (in red) away from the electrically oscillating biofilm (shown in (b), cyan) and towards the alternative potassium source (MSgg + 300 mM KCl, shown in (c)) which was introduced at a distance from the biofilm edge. The alternative potassium source (indicated by blue shading) was generated for 1 hour during the peak of electrical activity in the biofilm when motile cell attraction is typically maximal. Time series shown are representative of 8 independently reproduced experiments.

We then began to investigate the potential mechanism by which waves of extracellular potassium released by the biofilm could influence the motility of distant cells. It is known that changes in extracellular potassium lead to changes in the cell’s membrane potential and proton motive force (Bakker & Mangerich 1981; Booth 1985; Abee et al. 1988). The proton motive force in turn influences bacterial motility by controlling the frequency of tumbling events that enable a biased random walk along a concentration gradient (Berg & Brown 1972; De Jong et al. 1976; Manson et al. 1977; Miller & Koshland 1980). The relationship between extracellular potassium, membrane potential and tumbling frequency of motile cells suggests a possible mechanism for the observed attraction of motile cells to biofilms.

The role of the potassium ion channel in motile cell attraction

To determine the mechanism of motile cell attraction, we first confirmed that potassium ion channel activity in the biofilm generates the extracellular potassium signal that results in motile cell attraction. Complete deletion of the potassium ion channel YugO interferes with B. subtilis biofilm formation (Lundberg et al. 2013; Prindle et al. 2015). Therefore, we turned to a previously characterized mutant strain (ΔtrkA), which only lacks the TrkA gating domain of the YugO potassium ion channel and exhibits diminished electrical signaling (Prindle et al. 2015) (Fig. 3b). We find that biofilms formed by this mutant strain have a 75% ± 4% (mean ± st. dev., n = 3 experiments for each genotype) lower electrical signaling amplitude when compared to wild type biofilms (Fig. 3a, b). Correspondingly, motile cell attraction to ΔtrkA biofilms is reduced by 70% ± 9% (mean ± st. dev., n = 3 experiments for each genotype) (Fig. 3d). Therefore, we find a direct correlation between the weaker electrical signal generated by ΔtrkA biofilms and the corresponding decrease in motile cell attraction. These results show that potassium ion channels in biofilm cells play an important role in generating the electrical signal that attracts motile cells.

Figure 3.

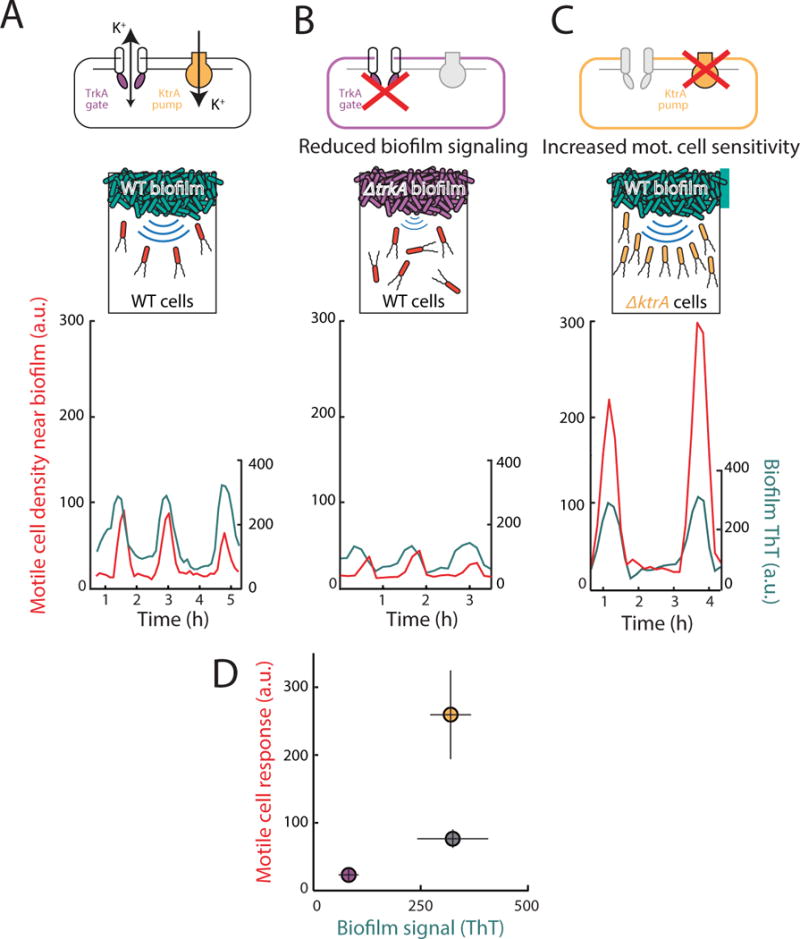
Motile cell attraction depends both on the strength of biofilm electrical signals and the sensitivity of motile cells to these signals. (a) (Top) wild type cells contain a potassium ion channel YugO that is gated by a TrkA domain, and a potassium ion pump KtrA. (Bottom) Wild type (WT) motile cell attraction (in red) to electrical oscillations from a WT biofilm (in cyan, same data as Figure 1, shown here for comparison to (b) and (c)). (b) (top) The TrkA gating domain of YugO was deleted in biofilm cells, resulting in reduced biofilm signaling. (bottom) Time series of WT motile cell response to ΔtrkA biofilm electrical oscillations shows reduced oscillation amplitude (n = 6, p = 2.20×10⁻⁷, two sample t-test), and reduced motile cell attraction compared to a WT biofilm (n = 3, p = 2.24×10⁻⁷, two sample t-test). Time series is representative of 6 independently reproduced experiments. (c) (top) The potassium pump KtrA was deleted in motile cells, which leads to hyperpolarization (See Figure S3) and increased sensitivity to potassium signals. (bottom) Time series of ΔktrA motile cell response to WT biofilm electrical oscillations shows increased attraction (n = 8, p = 6.66 × 10⁻⁶, two sample t-test) compared to WT motile cells responding to a WT biofilm (see (a)). WT biofilms in this experiment had similar oscillation amplitude as in (a) (n = 3, p = 0.906, two sample t-test). Time series is representative of 8 independently reproduced experiments. (d) Plot of average peak biofilm signal vs. average peak motile cell response for WT (gray circle) compared to ΔtrkA (purple circle) and ΔktrA (yellow circle) mutants shows that reducing the amplitude of the potassium signal reduces attraction, while increasing the sensitivity to the potassium signal increases attraction (mean ± st. dev., WT n = 3, ΔtrkA n = 6, ΔktrA n = 8, see Quantification and Statistical Analysis).

Motile cell membrane potential influences attraction to biofilms

We speculated that attraction of motile cells depends not only on the signal emitted by the biofilm, but also the sensitivity of motile cells to the potassium signal. Specifically, the sensitivity to changes in extracellular potassium depends on the resting membrane potential of the cell (Hille 2001). We anticipated that motile cells with a more negative resting membrane potential would be more sensitive to the potassium signals emitted by the biofilm. Accordingly, we deleted the major B. subtilis potassium pump (KtrA) in motile cells. Potassium pumps are responsible for maintaining the high intracellular concentration of potassium ions and thus play a key role in establishing the resting membrane potential (Castañeda-García et al. 2011; Gries et al. 2013). Consequently, ΔktrA motile cells would have a reduced ability to pump in positively charged potassium ions and thus have a relatively more negative membrane potential. Indeed, we find a 57% ± 6% (st. dev., n = 2 experiments) more negative membrane potential in the ΔktrA strain relative to wild type (Figure S3). When exposed to wild type biofilms with nearly identical electrical oscillation amplitudes, we observed more than two-fold (239% ± 25%, st. dev., n = 8 experiments) increase in attraction of ΔktrA motile cells, compared to wild-type motile cells (Fig. 3a, c, d). These results show that attraction also depends on the membrane potential-mediated sensitivity of motile cells to the potassium signals generated by the biofilm.

Membrane potential and tumbling frequency of distant cells depend on biofilm oscillations

Next, we established that electrical activity within the biofilm can alter the membrane potential of distant cells. We confirmed that an electrically active biofilm generates a dynamic potassium gradient, as reported by the potassium specific fluorescent dye Asante Potassium Green 4 (APG-4) (Fig. 4a, S4). We then utilized distant cells that by chance adhered to the microfluidic chamber to measure membrane potential in individual cells over time without having to track their movement (Fig. 4b). This allowed us to precisely measure the membrane potential dynamics of distant cells during an entire period of electrical signaling in the biofilm. We find that the membrane potential of these stationary cells becomes more negative during the peak of electrical oscillations in the biofilm (Fig. 4c, d). Together, these data indicate that potassium waves generated by the biofilm can induce changes in the membrane potential of distant cells.

Figure 4.

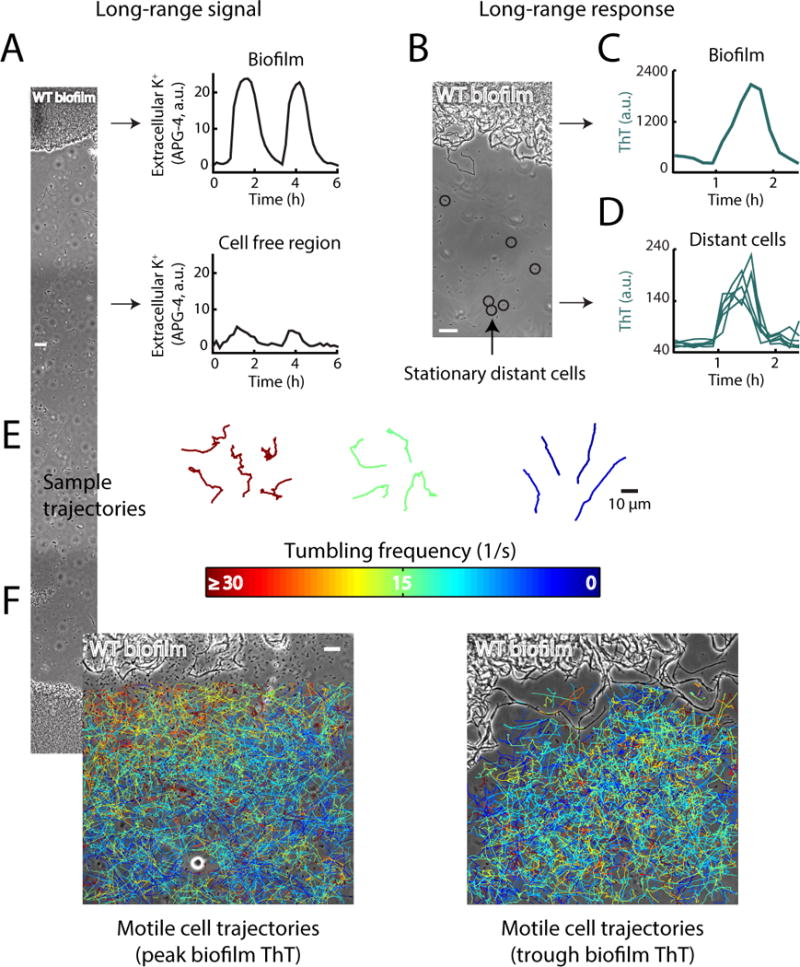
Extracellular potassium is a long range signal that can influence the membrane potential and tumbling frequency of motile cells. (a) The fluorescent chemical dye Asante Potassium Green (APG-4) was used to track the extracellular concentration of potassium between cells in the biofilm and the surrounding cell free region. APG-4 fluorescence was measured over time at the regions shown in the phase image on the left. On the right, time series of APG-4 fluorescence intensity oscillations between cells in the biofilm (top), and in the cell-free region distant from the biofilm (bottom). Scale bar, 50 μm. See also Figure S4. (b) Phase contrast image of a biofilm and distant stationary cells. The membrane potential of cells circled in black was tracked over time to determine the response to long-range signals emitted from the biofilm. Scale bar, 12 μm. (c) Time series of a membrane potential (ThT) pulse in the biofilm. (d) Time series of the co-occurring membrane potential pulse in distant cells shows membrane potential changes that are in phase with biofilm electrical oscillations. (e) Individual motile cells were tracked over time and their motion was compiled into trajectories that trace their movement. To track motile cells, we used high frequency (10 msec interval) phase contrast imaging. Sample trajectories are shown for 3 different average tumbling frequencies and are colored based on their average tumbling frequency (1/s), color scale is the same as in (f). (f) Individual motile cells were tracked near the biofilm at both the peak and trough of electrical activity (n = 2,668 trajectories). Trajectories are colored based on their average tumbling frequency, and overlaid on a phase contrast image of the biofilm. (left) During a peak in electrical activity in the biofilm, motile cell tumbling frequencies are inversely related to distance from the biofilm, consistent with a biased random walk up a potassium concentration gradient. (right) During a trough in biofilm electrical activity, there is no relationship between motile cell tumbling frequency and distance from the biofilm. The biofilm is at the top of each image, scale bar applies to both images. Overlaid trajectories include cells which were tracked for at least 500 ms.

We then asked whether the tumbling frequency of individual motile cells also depends on the electrical activity of the biofilm. Using phase contrast imaging every 10 msec, we compared a total of 2,668 motile cell trajectories obtained specifically during a peak or trough of electrical oscillations in the biofilm (Figure 4e, Supplemental Movie 3). This approach allowed us to determine the relationship between tumbling frequency of motile cells and the electrical signaling generated by the biofilm. During the peak of electrical activity in the biofilm, we observed that the tumbling frequency of motile cells was inversely related to their distance from the biofilm (Figure 4f). In other words, distant motile cells exhibited directional swimming, while cells already near the electrically active biofilm edge tumbled and thus remained at the biofilm edge. In contrast, there was no such spatial organization of tumbling frequencies during the trough in biofilm electrical activity (Figure 4f). These results suggest that the tumbling frequency of motile cells is altered by the spatio-temporal extracellular potassium gradient generated by the biofilm.

Agent-based mathematical modeling confirms that extracellular potassium can direct motility

To integrate the above described multiple lines of experimental evidence into a coherent phenomenological framework, we turned to mathematical modeling. We utilized an electrophysiological model based on the mathematical framework developed by Hodgkin and Huxley to predict changes in membrane potential in response to extracellular potassium (Prindle et al. 2015; Hodgkin & Huxley 1952) (see Supplemental Information for details). This model was constrained by our measurement of membrane potential dynamics observed in distant stationary cells (Fig. 4d). We integrated this electrophysiological model with an agent-based physical model (Mather et al. 2010; Volfson et al. 2008) to simulate the motility of individual cells (see Supplemental Information for details of the agent-based model). In brief, cells were modeled as soft spherocylinders that moved according to Newton’s law under the forces and torques caused by their own motility and contacts with other cells. In a departure from earlier models (Prindle et al. 2015; Mather et al. 2010; Volfson et al. 2008), each cell was endowed with a set of ordinary differential equations coupling its electrophysiological state with its motility (Fig. 5a, Supplemental Information). Using this model, we computed how a change in extracellular potassium altered the cell’s membrane potential and how this in turn affected the tumbling probability of each motile cell (Fig. 5a, Fig. S5) (De Jong et al. 1976; Manson et al. 1977; Miller & Koshland 1980). Furthermore, the simulations contained non-motile biofilm cells that were assumed to alternate between acting as a source or sink of potassium (peak and trough electrical activity respectively) (Fig. 5b, cyan and black cells, respectively). The resulting extracellular potassium dynamics followed the standard diffusion equation (see Supplemental Information for details). Consistent with experimental results, simulations showed periodic attraction of distant motile cells to an electrically oscillating biofilm (Fig. 5b, Supplemental Movie 4). These modeling results demonstrate that an oscillating source (biofilm) of extracellular potassium can periodically attract motile cells by changing their membrane potential.

Figure 5.

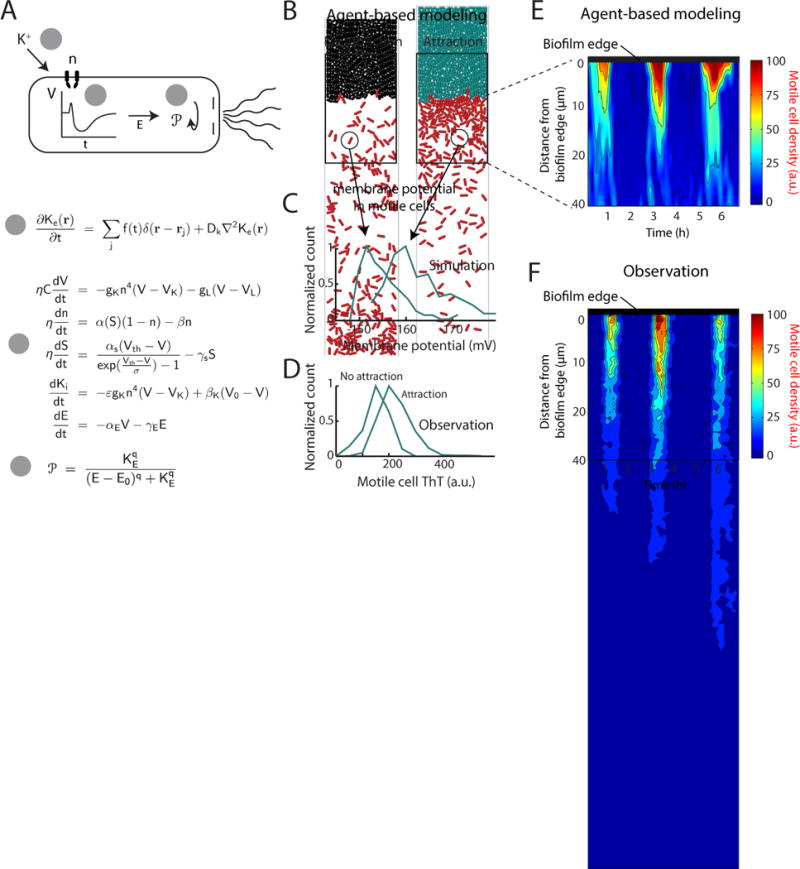
Agent-based modeling of motile cell attraction driven by electrical signaling from biofilms. (a) (top) Schematic illustrating how extracellular potassium alters motility by changing the membrane potential. Step 1: Extracellular potassium depolarizes the cell. Step 2: Depolarization prompts adaptation by the cell leading to hyperpolarization. Step 3: Hyperpolarization increases the proton motive force, thus directing motility by altering the tumbling frequency of the cell. (bottom) The computational model encompassing: (1) spatiotemporal reaction-diffusion model for the extracellular potassium K_e dynamics; (2) intracellular electrophysiological model for the cell membrane potential V, ion channel state n, metabolic stress S, intracellular potassium K_i and energy needed to drive the flagellar motor E (we can think of this energy as PMF or ATP); (3) discrete biomechanical model for individual cell motion influenced by their internal motility and interaction with other cells. The motility of individual cells is affected by the internal cellular state E via the change of the probability of tumbling $\mathcal{P}$. The details of the model and the model parameters are given in the Supplemental Information. See also Figure S5. (b) Two snapshots of the combined agent-based simulation show increased density of motile (red) cells near the biofilm during the peak of the attraction phase to the biofilm. Biofilm cells are colored according to their membrane potential during each time point, where cyan coloring indicates more negative membrane potential relative to black coloring. (c) Distributions of membrane potential in motile cells from the computational model indicate that motile cell membrane potential is more negative during the peak of the attraction phase to the biofilm. (d) Experimental data confirms the modeling prediction that the distribution of motile cell membrane potential (ThT, a.u.) is relatively more negative during attraction to the biofilm compared to the non-attraction phase (See Quantification and Statistical Analysis). (e) Plot of motile cell density in the first 40 μm away from the biofilm edge over time, obtained from agent-based modeling simulations of motile cell attraction. The region closest to the biofilm edge is located at the top of the plots for both e and f, and distance from the biofilm edge increases moving downward. (f) Experimental data shows similar motile cell density dynamics in the first 40 μm away from the biofilm edge.

Our model was predominantly informed by measurements in stationary cells, providing the opportunity to independently validate modeling predictions through additional motile cell measurements. In particular, we tested the modeling prediction that motile cells moving along a spatial potassium gradient are expected to have a similar membrane potential profile as stationary cells responding to temporal changes of potassium (Fig. 5c). In other words, motile cells during peak biofilm electrical activity should on average have a more negative membrane potential. To test this prediction, we measured the distribution of membrane potential in motile cells specifically at the attraction (peak) and non-attraction (trough) phases of the electrical oscillations in the biofilm. As predicted by our model, we find that motile cells have on average a more negative membrane potential in the attraction phase (Fig. 5d). These data show that similar to stationary cells, the membrane potential of motile cells also depends on the electrical activity of the biofilm. In addition, we find that the motile cell density profile as a function of time and distance from the biofilm is consistent with modeling predictions (Fig. 5e, f). Together, these results further validate the mathematical model and allow us to establish a coherent framework to interpret experimental observations.

Electrically mediated attraction applies across distinct bacterial species

The membrane potential plays a general role in bacterial motility (Manson et al. 1977; Meister et al. 1987; Lo et al. 2007), and thus a mechanism of attraction based on inducing changes in membrane potential could apply to other bacterial species as well. To test this hypothesis, we studied the interaction of Pseudomonas aeruginosa cells with a pre-existing B. subtilis biofilm. We chose P. aeruginosa because it is a Gram-negative bacterium that is evolutionarily distant to Gram-positive B. subtilis. As expected, we find that motile P. aeruginosa cells also become periodically attracted to the B. subtilis biofilm during electrical oscillations (Fig. 6a, b, S6). Consistent with observations for B. subtilis, we find that the peak accumulation of P. aeruginosa motile cells at the biofilm edge again lags the peak of electrical activity in the biofilm by 22 ± 13 min (mean ± st. dev., n = 30 pulses) (Fig. 6c). In addition, variations in the period of electrical signaling within the biofilm are directly matched by the period of P. aeruginosa attraction to the biofilm edge (Fig. 6d). These results indicate that the mechanism of electrically-mediated attraction is not limited to B. subtilis cells, and thus enables cross-species interactions.

Figure 6.

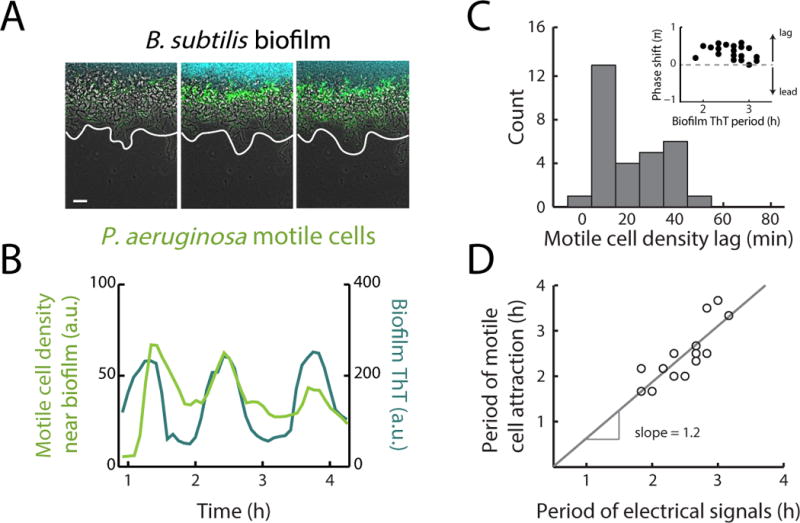
Biofilm electrical signals can also attract other bacterial species. (a) Film strip showing P. aeruginosa motile cell attraction to a pre-existing B. subtilis biofilm. Gray (phase contrast), cyan (membrane potential), green (P. aeruginosa motile cells). White line indicates the edge of the biofilm. Scale bar, 50 μm. (b) Time series of P. aeruginosa motile cell accumulation (in green) near a B. subtilis biofilm, in phase with biofilm electrical oscillations (in cyan). Images and time series are representative of 12 independently reproduced experiments. (c) Histogram of the time between peaks in biofilm electrical activity and peaks in P. aeruginosa motile cell attraction (motile cell density lag). Peaks in P. aeruginosa motile cell density occur on average 21.6 ± 13.4 min after the initiation of electrical oscillations within B. subtilis biofilms (mean ± st. dev., n = 30 pulses, See Quantification and Statistical Analysis). (inset) Plot of the phase shift between peaks in P. aeruginosa attraction and B. subtilis electrical activity relative to the period of biofilm electrical oscillations. Arrows illustrate that a positive phase shift indicates a lag between a peak in P. aeruginosa attraction and biofilm electrical activity. (d) Scatter plot of the periods of electrical oscillations within B. subtilis biofilms (peak to peak), and the periods of co-occurring pulses in P. aeruginosa motile cell attraction (peak to peak). The periods of pulses in motile cell density correlate with natural variations in the periods of electrical oscillations within biofilms (See Quantification and Statistical Analysis, Pearson correlation coefficent = 0.83, n = 16 periods). See also Figure S6.

Strength of electrical attraction modulates incorporation of new members into a biofilm

Attraction of distant cells to the biofilm edge could result in their incorporation into the biofilm, providing an additional opportunity to quantify the strength of electrical attraction (Fig. 7a). We first confirmed that motile B. subtilis cells can become permanently incorporated into a pre-existing B. subtilis biofilm by utilizing the fluorescence labeling of motile cells (Fig. 7b). We then utilized ΔtrkA mutant biofilms that are deficient in electrical attraction to determine if reduced electrical attraction would decrease incorporation of distant cells into the biofilm. As expected, we find less permanent incorporation of B. subtilis cells into ΔtrkA mutant biofilms (Fig. 7c). Importantly, we find that P. aeruginosa cells can also become permanently incorporated into a B. subtilis biofilm. Consistent with B. subtilis motile cell results, we find less incorporation of P. aeruginosa motile cells into ΔtrkA B. subtilis biofilms (Fig. 7d, e). The strong correlation between motile cell attraction and permanent incorporation for both species confirms that incorporation accurately reflects the strength of motile cell attraction (Fig. 7f, g). These data show that the level of permanent incorporation of new members into a pre-existing biofilm depends on the strength of electrical attraction.

Figure 7.

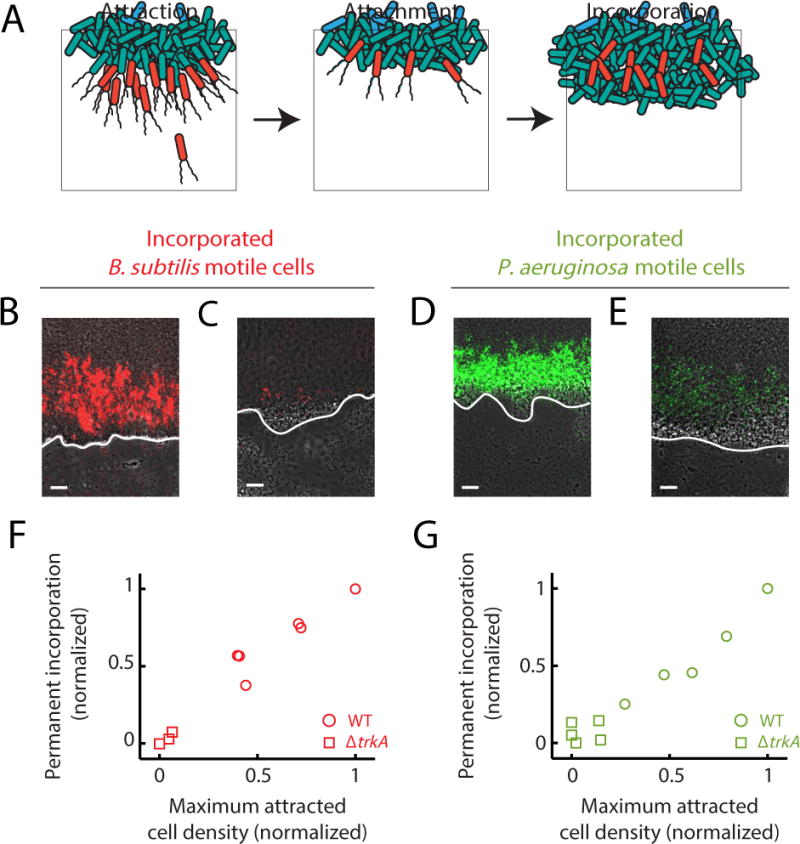
Attraction can lead to incorporation of motile cells into biofilms, depending on the strength of the attraction. (a) Illustration of how attraction can lead to incorporation of new cells into a pre-existing biofilm. Attracted cells (left panel) can remain attached to the biofilm following attraction (middle panel). Subsequent growth of the biofilm leads to capture of attached cells, resulting in permanent incorporation (right panel). (b) Image of previously attracted B. subtilis motile cells (red) that have been incorporated into a pre-existing wild type B. subtilis biofilm. Image representative of 6 independently reproduced experiments. Incorporated cells are surrounded by cells originating from the pre-existing biofilm and are located inside the biofilm. (c) Image of previously attracted B. subtilis motile cells that have been incorporated into a pre-existing ΔtrkA biofilm. Reduced B. subtilis motile cell attraction to ΔtrkA biofilms that are deficient in electrical signaling results in diminished incorporation into the biofilm. Image representative of 6 independently reproduced experiments. (d) Image of previously attracted P. aeruginosa motile cells that also became incorporated into a pre-existing B. subtilis biofilm. Image representative of 12 independently reproduced experiments. (e) Image of previously attracted P. aeruginosa motile cells that have become incorporated into a pre-existing B. subtilis ΔtrkA biofilm. Diminished incorporation of P. aeruginosa motile cells is also observed as a consequence of reduced attraction to ΔtrkA B. subtilis biofilms. Image representative of 5 independently reproduced experiments. (b, c, d, e) White lines indicate each biofilm edge, and biofilms are located at the top of each image. Gray (phase contrast), red (B. subtilis motile cells), green (P. aeruginosa motile cells). Scale bars, 50 μm. (f, g) Scatter plots comparing the average peak motile cell density during attraction to biofilms and the resulting permanent incorporation of these attracted cells into biofilms (See Quantification and Statistical Analysis). The observed direct relationship indicates that the incorporation of attracted motile cells depends on the degree of attraction. (f) Circles, B. subtilis motile cell attraction and incorporation into wild type B. subtilis biofilms (n = 6 independently reproduced experiments); squares, B. subtilis motile cells attraction and incorporation into electrical signaling deficient ΔtrkA B. subtilis biofilms (Pearson correlation coefficient = 0.98, n = 3 independently reproduced experiments). (g) Circles, P. aeruginosa motile cell attraction and incorporation into wild type B. subtilis biofilms (n = 6 independently reproduced experiments); squares, P. aeruginosa motile cell attraction and incorporation into signaling deficient ΔtrkA B. subtilis biofilms (Pearson correlation coefficient = 0.91, n = 5 independently reproduced experiments).

Discussion

Our study shows that electrical signaling mediated by potassium ion channels can extend beyond the boundaries of a biofilm to attract distant cells. This attraction is driven by dynamic gradients of potassium ions, which can alter the membrane potential of distant cells and thereby direct their motile behavior. Our work thus builds on and extends previous studies that emphasize the importance of membrane potential in bacterial motility (Miller & Koshland 1977; Manson et al. 1977; Shioi et al. 1978; Matsuura et al. 1979; Miller & Koshland 1980; Shioi et al. 1980; Meister et al. 1987; Meister et al. 1989; Lo et al. 2007). We find that long-range signaling mediated through potassium ions can generate a rapid response in cell motility, because it does not require biochemical synthesis or complex signaling networks. Given our experimental conditions, bacterial communities can effectively modulate the motility of distant cells through potassium ion channel-mediated electrical signals. These results indicate that bacterial biofilms not only regulate the behavior of cells that reside within the community, but also exert control over distant cells that are not part of the community.

Our findings show that the interaction mechanism between the biofilm and distant cells applies to even evolutionarily distant bacteria and is thus not limited to cells from a single species. In particular, the effect of extracellular potassium on membrane potential is shared among all cells, because the interaction is of physical nature. This suggests a new paradigm for long-range cross-species signaling that is generic, as it does not require specific receptors or signaling pathways. Interestingly, as a result of cross-species attraction, bacteria from a different species can become incorporated into a preexisting biofilm. Therefore, our work raises many new intriguing questions regarding the complex co-existence of biofilm communities and surrounding cells. The pursuit of these questions is likely to provide not only basic insights, but also tools that can be utilized in synthetic biology approaches to control the interaction of single cells and communities.

STAR Methods

Key Resources Table

Contact for Reagent and Resource Sharing

Requests for strains and further information can be directed to the Lead Contact, Gurol M. Suel (gsuel@ucsd.edu).

Experimental Model and Subject Details

Bacterial Strains

All experiments were performed using the Bacillus subtilis strain NCIB 3610 and the Pseudomonas aeruginosa strain PA01. B. subtilis 3610 was a kind gift from W. Winkler (University of Maryland) (Irnov & Winkler 2010). P. aeruginosa PA01 was a kind gift from K. Pogliano (University of California, San Diego) and contained a td-Tomato fluorescent reporter plasmid which was made by J. Aguilar (University of California, San Diego). All strains used in this study can be found in Table S1 and were derived from B. subtilis 3610 or P. aeruginosa PA01. B. subtilis motile cells contained an mKate2 reporter under the control of the inducible P_hyp promoter (1 mM IPTG was used for induction). In addition, the sinI gene (regulator of biofilm formation) was deleted in motile cells in order to reduce clogging in the device. The mKate2 construct was a kind gift from R. Losick. The ΔtrkA and Δhag strains were made by PCR amplifying 1 kb regions upstream and downstream of the gene to be deleted and cloning them into the pER449 vector (gift from W. Winkler) flanking an antibiotic resistance cassette. Constructs were sequence verified and chromosomally integrated using a standard one-step transformation procedure (Jarmer et al. 2002). The ΔktrA strain was made by obtaining the KtrA deletion strain BKE31090 from the Bacillus Genetic Stock Center and using it as a donor to move the ΔktrA::mls construct into strain 3610 via SPP1-mediated phage transduction into the 3610 background (Yasbin & Young, 1974). For ΔktrA and Δhag cells, a constitutive reporter was then chromosomally integrated using the one-step transformation procedure. Integrations were confirmed by colony PCR.

Growth conditions and dye concentrations

Biofilms were grown in MSgg medium: 5 mM potassium phosphate buffer (pH 7.0), 100 mM MOPS buffer (pH 7.0, adjusted with NaOH), 2 mM MgCl₂, 700 μM CaCl₂, 50 μM MnCl₂, 100 μM FeCl₃, 1 μM ZnCl₂, 2 μM thiamine HCl, 0.5% (v/v) glycerol, and 0.5% (w/v) monosodium glutamate. MSgg medium was made fresh from stocks the day of the experiment. Glutamate and iron stocks were made fresh weekly. ThT (Sigma-Aldrich) was used at a final concentration of 10 μM and APG-4 (TEFLabs) was used at 2 μM. The P_hyp reporter used in motile cells was induced using 1 mM IPTG. Biofilms were acclimated for at least 1 hour to any dyes and inducers used in the experiment before addition of motile cells.

Method Details

Microfluidics and motile cell culturing

B. subtilis biofilms were grown to a mature state (~20h of growth), and then a separately grown planktonic cell culture of either B. subtilis or P. aeruginosa was introduced into the growth chamber with the biofilm.

Biofilm growth

For microfluidic culturing, we used a CellASIC ONIX Microfluidic Platform and Y04D microfluidic plates (EMD Millipore). The day before growing biofilms, the strain to be used was streaked out onto LB agar plates from −80 °C glycerol stocks. The following day, a single colony was picked from the biofilm strain plate and inoculated in 3 mL lysogeny broth (LB). After 3h of growth shaking at 37 °C, cells were spun down at 2100 rcf for 1 min, re-suspended in fresh MSgg and loaded into the microfluidic chamber. After loading, cells were incubated at 32.5 °C overnight, then 30 °C for the rest of the experiment. Prior to addition of motile cells, biofilms were grown with media supplied at 1.5 psi from one well.

Motile cell growth

Motile cell strains to be used were streaked out onto LB agar plates from −80 °C glycerol stocks. The same night as biofilms were initially loaded and growing, a single colony of the B. subtilis motile cell strain to be used was inoculated in 3 mL of MSgg + 1 mM IPTG and any fluorescent reporters such as ThT or APG-4 to be used in the experiment. This culture was grown overnight (10–14 h) in a 15 mL culture tube shaking at 37 °C. In the morning, the culture was re-suspended in fresh MSgg and immediately loaded into the microfluidic chamber. Non-motile Δhag B. subtilis cells were cultured and introduced into the microfluidic device in the same manner as motile B. subtilis cells. P. aeruginosa motile cells were cultured in the same way as B. subtilis, except after growth overnight, the culture was diluted 1:30 in fresh MSgg and allowed to grow at 37 °C shaking for 2 hours before re-suspending in fresh MSgg, and loading into the microfluidic chamber.

After the onset of oscillations in the mature biofilm, motile cells were introduced into the microfluidic chamber. The OD of motile cells was measured and normalized to 1 for B. subtilis and 0.5 for P. aeruginosa. Motile cells were passed through a 5 μm filter to remove any cell aggregates, spun down at 2100 rcf for 1 min, and resuspended in fresh MSgg + 1 mM IPTG + fluorescent dyes. Motile cells were allowed to flow into the chamber through a dedicated media inlet well. The flow rate (12 μm/sec) was low enough to supply the growth chamber with fresh media while not being so fast that it prevented motile cells from being able to swim upstream against the flow.

The potassium addition experiment shown in Figure 2 was performed by growing a single biofilm on one side of the growth chamber and introducing an artificial potassium source into the other side of the chamber. In addition to the inlet used to flow in the motile cell suspension, a potassium concentration gradient could be produced by flowing MSgg supplemented with 300 mM KCl from the inlet furthest from the biofilm.

Time-lapse microscopy

Growth of biofilms was tracked using phase contrast microscopy and motile cell behavior was tracked by fluorescence microscopy of the P_hyp-mKate2 reporter (only present in motile cells). The imaging systems used were Olympus IX83 with an X-Cite LED light source from Lumen Dynamics and Olympus IX81 with a Lambda XL light source from Sutter Instruments. Attraction experiments were acquired using a 10× objective and a 40× objective was used to evaluate ThT intensity in motile cells for the experiments shown in Figure 4c, d and Figure 5d. During time lapse experiments, phase and fluorescence images were taken in 10 minute intervals.

Computational model for electrical attraction

Our agent-based model assumes that each motile cell changes its electrophysiological state and motility independently of each other and only in response to changes in extracellular potassium. We describe intracellular potassium-driven dynamics within each cell using a generalization of the electrophysiological model introduced in our earlier paper (Prindle et al. 2015). The membrane potential is governed by the standard Hodgkin-Huxley-type conductance equation

$$\eta C\frac{dV}{dt}=-g_K{n}^4(V-V_K)-g_L(V-V_L)$$ (1)

in which C is the capacitance of the cell membrane. The first term in the right hand side describes the change in membrane potential by potassium ions escaping the cell through potassium ion channels, while the second term describes the leak current. In the standard Hodgkin-Huxley model, the membrane potential dynamics are very fast (milliseconds), much faster than the slow changes in extracellular potassium and corresponding changes in bacterial motility (hours). Since it is very difficult to simulate together processes of such vastly different time scales, we introduced a scaling factor η to slow down the intracellular electrophysiological dynamics. The scaling factor is also applied to Eq. (3) and (4). As long as the electrophysiological processes remain much faster than the slow part of the model, this did not have an appreciable effect on the slow dynamics of the cellular population. We used the value η = 300 and verified that changing this factor to 150 did not appreciably affect the results of our simulations.

The resting potentials V_K and V_L are set by the ion pumps, and generally are dependent on both intra- and extracellular potassium levels, for which we assume a simple linear form,

$$V_K=V_{K0}+{\delta }_K(K_e+K_i);V_L=V_{L0}+{\delta }_L(K_e+K_i)$$ (2)

The fourth power in the first term of (1) stems from the fact (Doyle et al, 1998) that bacterial potassium channels are formed by four subunits, which on average are open during a fraction of time n whose dynamics is given by the following rate equation:

$$\eta \frac{dn}{dt}=\alpha (S)(1-n)-\beta n$$ (3)

where the first term describes channel opening and the second term specifies the rate of channel closing. As in Prindle et al. (2015), the opening rate α of the potassium channel is assumed to depend on metabolic stress, S, according to the Hill function $\alpha (S)=\frac{{\alpha }_0{S}^m}{S_{th}^m+S^m}$. This metabolic stress variable that stands for the concentration of stress-related metabolic products (Cao et al. 2013), such as excess NAD⁺ (Roosild et al. 2002; Schlösser et al. 1993) is itself controlled by the membrane potential according to the equation

$$\eta \frac{dS}{dt}=\frac{{\alpha }_s(V_{th}-V)}{\exp \left(\frac{V_{th}-V}{\sigma }\right)-1}-{\gamma }_{s}S$$ (4)

In departure from our previous model (Prindle et al. 2015) that described time-dependent dynamics of the extracellular potassium in the dense biofilm environment, here we assume that motile cells have sufficiently low density and therefore do not change the extracellular potassium appreciably. Instead, we focus on the concentration of the intracellular potassium K_i,

$$\frac{d{K}_i}{dt}=-\epsilon g_K{n}^4(V-V_K)+{\beta }_K(V_0-V)$$ (5)

where the first term describes the flux of potassium through ion channels and the second term describes the action of potassium pumps which maintain the membrane potential at the resting value V₀. The second term only appears when V₀ > V and is zero otherwise, because the ion pump can only pump the potassium from outside to inside of a cell.

It can be shown that the regulation of the intracellular potassium described by Eq. (5) plays the role of the integral feedback control loop similar to other mechanisms of bacterial chemotaxis (Yi et al. 2000). Indeed, in the absence of stress (S ≈ 0), the ion channels are closed (n ≈ 0), and the membrane potential equilibrates near V = V ₀ independently of the level of extracellular potassium (perfect adaptation). However, a change in extracellular potassium levels may cause complex transient changes in the membrane potential. When extracellular potassium level rises, according to Eq. (1) it slightly depolarizes the cell (increases V). The depolarization causes opening of the ion channels (n > 0), intracellular potassium flushes out according to Eq. (5), and the cell becomes strongly hyperpolarized. Then the channels close, and the ion pumps restore the membrane potential to the resting value. If the level of extracellular potassium continues to rise, the process repeats, and a periodic sequence of depolarization pulses ensues (see Fig. S5). If the level of extracellular potassium slowly decreases, it slightly hyperpolarizes the cell, but the channels remain closed, and the ion pump maintains the membrane potential close to the resting value. These transient changes in the membrane potential lead to changes in intracellular energy levels (we can think of this energy as PMF or ATP) and in turn lead to changes in the bacterial motility. We describe the energy dynamics by the simple relaxation equation

$$\frac{dE}{dt}=-{\alpha }_{E}V-{\gamma }_{E}E$$ (6)

and postulate that the tumbling probability is downregulated by the energy:

$$\mathcal{P}=\frac{K_E^q}{{\left(E-E_0\right)}^q+K_E^q}$$ (7)

The strong anisotropy in the dynamics of the membrane potential for increasing and decreasing extracellular potassium leads to the chemotactic response of motile bacteria to the spatial gradient of potassium. Indeed, if a cell swims up the gradient, it experiences rising levels of potassium and strongly hyperpolarizes, thus increasing the mean proton motive force and the level of energy in the cell. Therefore, its tumbling probability diminishes, and the cell continues to swim in the same direction. However, when the cell swims down the potassium gradient, hyperpolarization does not occur, and the tumbling probability remains high.

To simulate bacterial motion, we adapted the mechanical agent-based model developed in our earlier work (Volfson et al. 2008; Mather et al. 2010). Each cell is modeled as a spherocylinder of unit diameter that grows linearly along its axis and divides equally after reaching a critical length l_d = 4. It can also move along the plane due to forces and torques produced by interactions with other cells and its own flagellae-mediated motility (however, we do not model the flagella dynamics explicitly). The slightly inelastic cell-cell normal contact forces are computed via the standard spring-dashpot model, and the tangential forces are computed as velocity-dependent friction. During periods of directed motion, the cell experiences a self-propelling force directed along its axis. During the periods of tumbling, the self-propelling directional force is switched off, and the cell experiences a strong random torque which quickly turns it in a random new direction. The probability of switching from directed motion to tumbling for each cell is controlled by variable $\mathcal{P}$ that is computed from the electrophysiological cell model. Biofilm-bound cells were assumed to be non-motile (no self-propelling force, no tumbling torque).

The dynamics of extracellular potassium ion field were implemented via a reaction-diffusion model where the biofilm cells played the role of sources and sinks of potassium periodically,

$$\frac{\partial K_e(\mathit{r})}{\partial t}={\displaystyle \sum _{j}f(t)\delta (\mathit{r}-{\mathit{r}}_j)+D_k}{\nabla }^2{K}_e(\mathit{r})$$ (8)

Here K_a is the extracellular potassium concentration and r_j is the location of the j-th cell, f(t) is the periodic function describing periodic excretion (with rate α_k) and absorption (with rate –β_kK_e) cycles of extracellular potassium by the biofilm cells, and D_k is the potassium diffusion constant.

Each simulated motile “cell” carried a set of equations (1)–(7) describing its membrane potential dynamics in response to the local extracellular potassium concentration. The effect of the motile cells on the extracellular potassium concentration was ignored. The parameters of the model are shown in Table S1.

We performed multiple simulations in a narrow channel of length 100 and width 20 (Fig. 5b). The biofilm consisting of approximately 200 cells was initially grown in the back of the open channel (200 × 20 μm²), after which 100 motile cells were introduced into the open space of the channel. Of course, this computational domain represents only a small portion of the microfluidic chamber used in experimental studies, so our computational results only can be interpreted on a semi-quantitative level, as a way to reveal and explore the underlying biophysical mechanism of the potassium-driven chemotaxis. For simplicity, we also neglected growth and division for motile cells and only considered their motion in response to the external potassium changes. We used periodic boundary conditions on the side walls for motile cells: when a motile cell touches the left wall, it disappears and reappears at the right side and vice versa. The non-motile biofilm cells were periodically switched between producing and absorbing potassium.

A typical simulation is shown in Supplemental Movie 4. At each time step we computed the average concentration of potassium and the motile cell density near the biofilm edge. The periodic oscillations of cell density are clearly seen, which indicate the chemotactic response of bacteria to the potassium oscillations. The distribution of the proton motive force shifts between the peak and the trough phases (Fig. 5c), in agreement with experimental findings (Fig. 5d).

Parameters of the model

The aim of the computational model is to reproduce the observed phenomenology semi-quantitatively. Since the electrophysiology of bacterial cells is much less studied than of their mammalian counterparts, the parameters of the electrophysiological equations were taken either from the classical literature (Hodgkin and Huxley, 1952) or our earlier model describing potassium signaling in bacteria (Prindle et al, 2015). Some parameters (such as resting membrane potentials) were deduced from direct measurements. Other model parameters that connect electrophysiology and motility (marked as “fitting”) were chosen by random parameter search within physiologically relevant ranges and then further improved by manual variation to maximize the agreement with experimental observations.

Quantification and Statistical Analysis

FIJI/ImageJ (Schindelin et al. 2012; Preibisch et al. 2009) and MATLAB (MathWorks Inc. 2012) were used for image analysis. Biofilm growth, motile cell density at the biofilm edge, and ThT/APG-4 intensity were obtained using the MATLAB image analysis toolbox.

Statistical Analysis

Statistical analysis was performed using MATLAB. P values of < 0.05 were considered to be statistically significant. To determine whether data met assumptions of the statistical tests used, MATLAB’s skewness and kurtosis functions were used. Data sets did not have excessive skew or kurtosis and thus were assumed to be normally distributed.

Motile cell and biofilm ThT measurements

Phase contrast images were used to determine the coordinates of the biofilm edge. Based on the coordinates of the biofilm edge, a 100 μm wide region was established both inward (towards biofilm interior) and outward from the biofilm edge (See illustration in Figure 1a). The 100 μm region inside the biofilm was used to measure ThT intensity within the biofilm and the 100 μm region outside the biofilm was used to measure motile cell fluorescent reporter intensity in the region immediately surrounding the biofilm. The average intensities obtained from these regions were reported as the biofilm ThT and motile cell density near biofilm time traces. The motile cell density values were normalized to the density of the cell suspension introduced into the device. ThT traces were detrended using MATLAB’s “detrend” function. Specifically, the function fits a least-squares line to the data and subtracts this linear trend from the data.

The motile cell response reported in Figure 3d was obtained by averaging the intensities of motile cell attraction peaks from multiple experiments to obtain a single motile cell response measurement. The biofilm signal average reported in Figure 3d was obtained in a similar way, by averaging the intensities of ThT peaks for multiple experiments into a single maximum biofilm ThT measurement. A similar analysis was done for Figure 7f, g, except the peak intensities of attracted motile cells were averaged for each independent biofilm so that they could be compared to the resulting permanent incorporation of attracted cells for that biofilm. For all these measurements, the exact value of n is presented in the corresponding figure legend and represents the number of independent experiments of each genetic background used.

Motile cell density lag and oscillation period measurements

The motile cell density lag measurements reported in Figure 1d and Figure 6c were obtained using the peak of motile cell attraction and biofilm ThT. Lag was defined as the time between a biofilm ThT peak and the corresponding peak in motile cell attraction. Positive lag times indicate that a peak in motile cell attraction occurred after a peak in biofilm ThT. For Figure 1d and 6c the exact value of n is presented in the corresponding figure legends and represents the number of peaks of ThT and corresponding attraction shown in the histogram. The period comparisons reported in Figure 1e and Figure 6d were obtained by determining the period, peak-to-peak, of oscillations in biofilm ThT and motile cell attraction. The period of motile cell attraction was then plotted versus the period of the corresponding pulse in biofilm ThT. For Figure 1e and 6d, the exact value of n is presented in the corresponding figure legends and represents the number of periods, peak-to-peak, of oscillations and corresponding attraction included in the plot.

Permanent incorporation of attracted cells

The permanent incorporation of attracted cells reported in Figure 7f, g was obtained by measuring the average fluorescence intensity of mKate2 (a reporter only present in motile cells) in the 100 μm region immediately inward from the biofilm edge (towards biofilm interior) and normalizing by the area of the evaluated region and the density of the motile cell suspension flowing into the device. Incorporation measurements were obtained at the conclusion of each experiment. The exact value of n is presented in the corresponding figure legend and represents the number of independent experiments included in each plot.

Membrane potential in motile cells

Data for Figure 5d was obtained by segmenting motile cells and obtaining ThT fluorescence intensity for each cell using the Oufti software (Paintdakhi et al. 2016) and MATLAB.

Motile cell tracking

Single cell trajectories for the evaluation of tumbling frequency in motile cells were obtained by analyzing time lapse phase contrast image stacks taken at 10 ms intervals at 40× magnification. The Python based cell tracking software TrackPy and the Anaconda Python platform (Trackpy authors 2016; Continuum Analytics 2016) were used to track single cell movement over time and compile this movement into trajectories for each tracked cell. We included trajectories for cells that were tracked for 500 ms or longer in Figure 4e, f. The exact value of n is presented in the corresponding figure legend and represents the number of motile cell trajectories obtained during the peak and trough of electrical activity. Trajectories obtained with TrackPy were further analyzed using MATLAB. Tumbling events were determined by finding the angle of rotation between each time point of the trajectory and if this rotational angle was greater than 60 degrees, it was called a tumbling event. Tumbling frequencies are reported as number of tumbling events per second.

KEY RESOURCES TABLE Humphries et al.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Potassium chloride	Sigma-Aldrich	Cat #: P3911, CAS: 7447-40-7
L-glutamic acid monosodium salt hydrate	Sigma-Aldrich	Cat #: G5889, CAS: 142-47-2 (anhydrous)
Glycerol	Sigma-Aldrich	Cat #: G5516, CAS: 56-81-5
Magnesium chloride hexahydrate	Fisher Scientific	Cat #: BP214, CAS: 7786-30-3
Potassium phosphate monobasic	Fisher Scientific	Cat #: BP362, CAS: 7778-77-0
Potassium phosphate dibasic	Fisher Scientific	Cat #: BP363, CAS: 7758-11-4
Thiamine HCl	Fisher Scientific	Cat #: BP892, CAS: 67-03-8
Manganese chloride	Acros Organics	Cat #: AC193451000, CAS: 13446-34-9
Calcium chloride	Fisher Scientific	Cat #: BP510, CAS: 10035-04-8
Iron (III) chloride	Acros Organics	Cat #: AC217090025, CAS10025-77-1
Zinc (II) chloride	Sigma-Aldrich	Cat #: Z0152, CAS: 7646-85-7
Thioflavin T	Acros Organics	Cat #: AC211761000, CAS: 2390-54-7
Isopropyl β-D-1-thiogalactopyranoside	Sigma-Aldrich	Cat #: IPTG-RO, CAS: 367-93-1
Asante Potassium Green (AM)	TEFLabs	Cat #: 3602
MOPS	Sigma-Aldrich	Cat #: M3183, CAS: 1132-61-2
Experimental Models: Organisms/Strains
B. subtilis NCIB 3610	Bacillus Genetic Stock Center	BGSCID: 3A1
B. subtilis NCIB 3610 AmyE::Phyp-mKate2, sinI::neo (motile cells)	This study	N/A
B. subtilis NCIB 3610 AmyE::Phyp-YFP, hag::cat (non-motile cells)	This study	N/A
B. subtilis NCIB 3610 trkA::neo (ΔtrkA)	Prindle et al., 2015)	N/A
B. subtilis NCIB 3610 AmyE::Phyp-mKate2, ktrA::mls (ΔktrA)	This study	N/A
P. aeruginosa PA01/pJA06-miniRK2 PSpac-tdTomato::kan	This study	N/A
Software and Algorithms
MATLAB and Image Processing Toolkit	MathWorks, Inc. 2012	https://www.mathworks.com/products/matlab/
Python (Anaconda)	Continuum Analytics, 2016	https://www.continuum.io/
Trackpy	Trackpy Contributors 2016	http://soft-matter.github.io/trackpy/v0.3.2/#
FIJI and Stitching Plugin	Schindelin, J et al. 2015, Preibisch et al. 2009	https://fiji.sc/
Oufti	Paintdakhi et al. 2016	http://oufti.org/
Other
CellASIC Y04D microfluidic plates	EMD Millipore	Cat #: Y04D-02-5PK
CellASIC ONIX microfluidic platform	EMD Millipore	Cat #: EV262