Effects of the Ordering of Natural Selection and Population Regulation Mechanisms on Wright-Fisher Models

Abstract

We explore the effect of different mechanisms of natural selection on the evolution of populations for one- and two-locus systems. We compare the effect of viability and fecundity selection in the context of the Wright-Fisher model with selection under the assumption of multiplicative fitness. We show that these two modes of natural selection correspond to different orderings of the processes of population regulation and natural selection in the Wright-Fisher model. We find that under the Wright-Fisher model these two different orderings can affect the distribution of trajectories of haplotype frequencies evolving with genetic recombination. However, the difference in the distribution of trajectories is only appreciable when the population is in significant linkage disequilibrium. We find that as linkage disequilibrium decays the trajectories for the two different models rapidly become indistinguishable. We discuss the significance of these findings in terms of biological examples of viability and fecundity selection, and speculate that the effect may be significant when factors such as gene migration maintain a degree of linkage disequilibrium.

In population genetics, one studies the genetic composition of biological populations and the changes in genetic composition that result from the operation of various factors, including natural selection. Bürger (2000), Ewens (2004) and Durrett (2008) provided an excellent theoretical introduction to this field. The most basic, but also most important, model in population genetics is the Wright-Fisher model, developed by Fisher (1922) and Wright (1931), which forms the basis for most theoretical and applied research in population genetics to date, including Kingman’s coalescent (Kingman 1982), Ewens’ sampling formula (Ewens 1972), Kimura’s work on fixation probabilities (Kimura 1955) and techniques for inferring demographic and genetic properties of biological populations [see Tataru et al. (2017), and references therein]. Such widespread application is mainly due to not only the strong universality results for the Wright-Fisher model, e.g., Möhle’s work on the Cannings model (Möhle 2001), but also the fact that the Wright-Fisher model captures the essence of the biology involved and provides an elegant mathematical framework for characterizing the dynamics of gene frequencies, even in complex evolutionary scenarios.

The simplest version of the Wright-Fisher model (Fisher 1922; Wright 1931) is concerned with a finite random-mating population of fixed population size evolving in discrete and nonoverlapping generations at a single biallelic locus, which can be regarded as a simplified version of the life cycle where the next generation is randomly sampled with replacement from an effectively infinite gene pool built from equal contributions of all individuals in the current generation. The Wright-Fisher model can be generalized to incorporate other evolutionary forces such as natural selection (see, for example, Etheridge 2011).

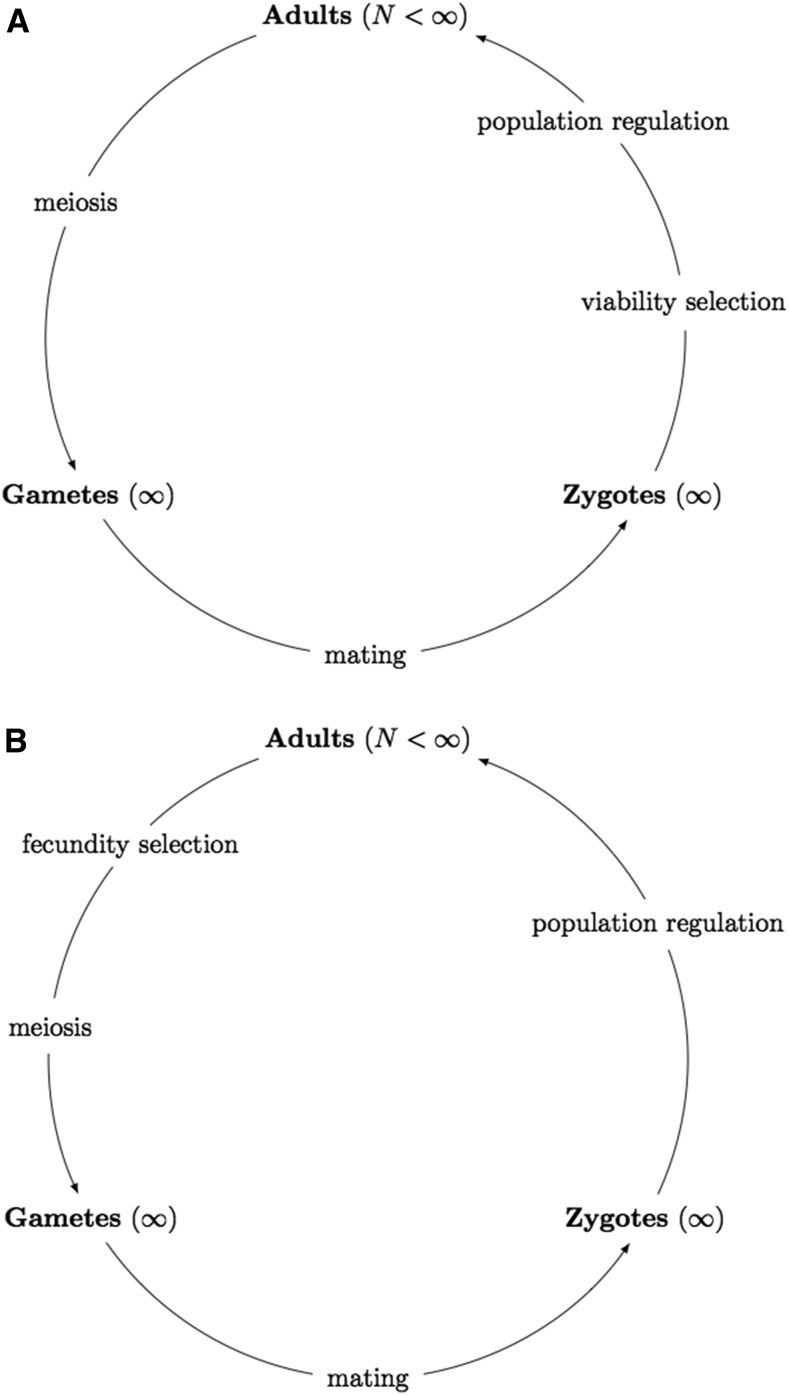
Natural selection is the differential survival and reproduction of individuals due to differences in phenotype, which has long been a topic of interest in population genetics. According to Christiansen (1984), natural selection can be classified according to the stage of an organism’s life cycle at which it acts: viability selection (or survival selection), which acts to improve the rate of zygote survival, and fecundity selection (or reproduction selection), which acts to improve the rate of gamete reproduction, as shown in Figure 1.

Figure 1.

Life cycles of a diploid population incorporated with different types of natural selection. (A) The life cycle is incorporated with viability selection. (B) The life cycle is incorporated with fecundity selection.

Nagylaki (1997) provided different derivations of multinomial-sampling models for genetic drift at a single multiallelic locus in a monoecious or dioecious diploid population for different orders of the evolutionary forces (i.e., mutation, natural selection, and genetic drift) in the life cycle. Prugnolle et al. (2005) found that gene migration occurring before or after asexual reproduction in the life cycle of monoecious trematodes can have different effects on a finite island model, depending on values of the other genetic parameters. A natural question that arises here is whether different stages of an organism’s life cycle at which natural selection acts can cause different population behaviors under the Wright-Fisher model. It is an inevitable choice that we have to make in current statistical inferential frameworks based on the Wright-Fisher model for inferring demographic and genetic properties of biological populations, especially for natural selection, which also affects the performance of these statistical inference methods.

In the present work, we are concerned with a finite random-mating diploid population of fixed population size N (i.e., a population of $2N$ chromosomes), evolving with discrete and nonoverlapping generations under natural selection within the framework of the Wright-Fisher model, especially for the evolution of one- and two-locus systems under natural selection. We carry out diffusion analysis of Wright-Fisher models with selection, and use extensive Monte Carlo simulation studies to address the question of whether different types of natural selection can cause different population behaviors under the Wright-Fisher model, especially when natural selection takes the form of viability or fecundity selection. Our main finding is that the distribution of the trajectories of haplotype frequencies for two recombining loci depends on whether viability or fecundity selection is operating. However, this difference is appreciable only when the haplotype frequencies are in significant linkage disequilibrium, and arises as a consequence of the interplay between genetic recombination and natural selection. Once linkage disequilibrium disappears, the distributions of trajectories under the Wright-Fisher model with either viability or fecundity selection become almost identical fairly quickly.

Materials and Methods

In this section, we provide detailed formulations for a finite random-mating diploid population of fixed population size evolving with discrete and nonoverlapping generations under natural selection (i.e., viability and fecundity selection, respectively) within the framework of the Wright-Fisher model and their diffusion approximations. We also introduce the Hellinger distance to measure the difference in the behavior of the Wright-Fisher model between viability and fecundity selection.

Wright-Fisher models with selection

Consider a monoecious population of N randomly mating diploid individuals evolving with discrete and nonoverlapping generations under natural selection. We assume that there are two alleles segregating at each autosomal locus, and the population size N is fixed. Let $X_i^{\left(N\right)}\left(k\right)$ be the frequency of haplotype i in N adults of generation $k\in \mathrm{\mathbb{N}}\text{,}$ and ${\mathit{X}}^{\left(N\right)}\left(k\right)$ denote the vector with frequencies of all possible haplotypes. We can study the population evolving under natural selection in terms of the changes in haplotype frequencies from generation to generation.

To determine the transition of haplotype frequencies from one generation to the next, we need to investigate how the mechanisms of evolution (e.g., natural selection) alter the genotype frequencies at intermediate stages of the life cycle. Let $Y_{ij}^{\left(N\right)}\left(k\right)$ be the frequency of the ordered genotype made up of haplotypes i and j in N adults of generation k, and ${\mathit{Y}}^{\left(N\right)}\left(k\right)$ designate the vector with frequencies of all possible genotypes. Note that genotypes are regarded as ordered here only for simplicity of notation. Under the assumption of random mating, the genotype frequency is equal to the product of the corresponding haplotype frequencies (Edwards 2000),

$$Y_{ij}^{\left(N\right)}\left(k\right)=X_i^{\left(N\right)}\left(k\right)X_j^{\left(N\right)}\left(k\right)=X_j^{\left(N\right)}\left(k\right)X_i^{\left(N\right)}\left(k\right)=Y_{ji}^{\left(N\right)}\left(k\right).$$ (1)

As illustrated in Figure 1, natural selection takes the form of viability selection and the life cycle moves through a loop of population regulation, meiosis, random mating, viability selection, population regulation, and so forth (see Figure 1A), or natural selection takes the form of fecundity selection and the life cycle moves through a loop of population regulation, fecundity selection, meiosis, random mating, population regulation, and so forth (see Figure 1B). The entrance of the life cycle here is assumed to be with the population reduced to N adults right after a round of population regulation. In the life cycles shown in Figure 1, there are four potential mechanisms of evolutionary change: natural selection, meiosis, random mating, and population regulation. We assume that natural selection, meiosis, and random mating occur in an effectively infinite population so can be treated deterministically (Hamilton 2011). Suppose that population regulation (i.e., genetic drift) acts in a similar manner to the Wright-Fisher sampling introduced by Fisher (1922) and Wright (1931). In other words, population regulation corresponds to randomly drawing N zygotes with replacement from an effectively infinite population to become new adults in the next generation, consequently completing the life cycle shown in Figure 1. Thus, given the genotype frequencies ${\mathit{Y}}^{\left(N\right)}\left(k\right)=\mathit{y}\mathrm{,}$ the genotype frequencies in the next generation satisfy

$${\mathit{Y}}^{\left(N\right)}\left(k+1\right)|{\mathit{Y}}^{\left(N\right)}\left(k\right)=\mathit{y}\sim \frac{1}{N}\text{Multinomial}\left(N,\mathit{q}\right),$$ (2)

where q is a function of the genotype frequencies y, denoting the vector with frequencies of all possible genotypes of an effectively infinite population after the possible mechanisms of evolutionary change (except population regulation) at intermediate stages of the life cycle, such as natural selection, meiosis, and random mating within generation k. The explicit expression of the sampling probabilities q will be given in the following two sections for the evolution of one- and two-locus systems under natural selection, respectively.

To simplify notation, we introduce a function ${\rho }_{uv}^i$ of three variables u, v, and i, defined as

$${\rho }_{uv}^i=\frac{1}{2}\left({\delta }_{ui}+{\delta }_{vi}\right),$$ (3)

where ${\delta }_{ui}$ and ${\delta }_{vi}$ denote the Kronecker delta functions. We can then express the frequency of haplotype i in terms of the corresponding genotype frequencies as

$$X_i^{\left(N\right)}\left(k\right)={\displaystyle \sum _{u,v}{\rho }_{uv}^i{Y}_{uv}^{\left(N\right)}\left(k\right)},$$ (4)

and the transition probabilities of the haplotype frequencies from one generation to the next can be easily obtained from Equations (2)–(4). We refer to the process ${\mathit{X}}^{\left(N\right)}=\left\{{\mathit{X}}^{\left(N\right)}\left(k\right):k\in \mathrm{\mathbb{N}}\right\}$ as the Wright-Fisher model with selection, whose first two conditional moments satisfy

$$E^{\left(k,\mathit{x}\right)}\left(X_i^{\left(N\right)}\left(k+1\right)\right)=p_i$$ (5)

$$E^{\left(k,\mathit{x}\right)}\left(X_i^{\left(N\right)}\left(k+1\right)X_j^{\left(N\right)}\left(k+1\right)\right)=\frac{p_i\left({\delta }_{ij}-p_j\right)}{2N}+p_i{p}_j,$$ (6)

where

$$E^{\left(k,\mathit{x}\right)}\left(\mathrm{·}\right)=E\left(\mathrm{·}|{\mathit{X}}^{\left(N\right)}\left(k\right)=\mathit{x}\right)$$

is the short-hand notation for the conditional expectation of a random variable given the population of the haplotype frequencies x in generation k, and

$$p_i={\displaystyle \sum _{u,v}{\rho }_{uv}^i{q}_{uv}}$$

is the frequency of haplotype i of an effectively infinite population after the possible mechanisms of evolutionary change (except population regulation) at intermediate stages of the life cycle such as natural selection, meiosis, and random mating within generation k, which obviously can be expressed in terms of the haplotype frequencies $\mathit{x}.$

One-locus Wright-Fisher models with selection:

Let us consider a monoecious population of N randomly mating diploid individuals at a single autosomal locus $\mathcal{A},$ segregating into two alleles, ${\mathcal{A}}_1$ and ${\mathcal{A}}_2,$ evolving under natural selection in discrete and nonoverlapping generations. We call the two possible haplotypes ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ haplotypes 1 and 2, respectively. As stated above, we need to formulate the sampling probabilities q for the evolution of one-locus systems under natural selection, which is the vector of frequencies of all possible genotypes of an effectively infinite population after a single generation of natural selection, meiosis (without genetic recombination), and random mating due to the absence of genetic recombination at meiosis in the evolution of one-locus systems.

With a single biallelic locus, there are four possible zygotes (i.e., four ordered genotypes) that result from the random union of two gametes. We denote the fitness of the genotype formed by haplotypes i and j by $w_{ij}$ for $i,j=1,2.$ In the life cycles illustrated in Figure 1, the number of adults is regulated to be of size N, and the gene frequencies in the subsequent generation can be described by multinomial sampling of the normalized frequencies in an effectively infinite pool of zygotes. When natural selection takes different forms, genotype frequencies in the zygotes can be modeled in different ways.

In the case of what can be called “viability selection” shown in Figure 1A, the N adults have an equal chance of forming gametes, which unite at random to form zygotes. This is followed by viability selection on genotypes of zygotes, leading to modified genotype frequencies. The subsequent genotype frequencies are obtained by multinomial sampling. We can express the frequency of the genotype formed by haplotypes i and j of an effectively infinite population after a single generation of meiosis, random mating, and viability selection as

$$q_{ij}^{\left(v\right)}=\hspace{0.17em}\frac{w_{ij}}{\overline{w}}\left({\displaystyle \sum _{u,v=1}^2{\rho }_{uv}^i{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^2{\rho }_{uv}^j{y}_{uv}}\right),$$ (7)

where

$$\overline{w}={\displaystyle \sum _{i,j=1}^2{w}_{ij}}\left({\displaystyle \sum _{u,v=1}^2{\rho }_{uv}^i{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^2{\rho }_{uv}^j{y}_{uv}}\right).$$ (8)

Alternatively, in what can be termed “fecundity selection” illustrated in Figure 1B, the N adults have an unequal chance of forming gametes, depending on their genotypes; the gametes unite at random, and the subsequent genotype frequencies remain unchanged until multinomial sampling. We can express the frequency of the genotype formed by haplotypes i and j of an effectively infinite population after a single generation of fecundity selection, meiosis, and random mating as

$$q_{ij}^{\left(f\right)}=\left({\displaystyle \sum _{u,v=1}^2{\rho }_{uv}^i\frac{w_{uv}}{\overline{w}}{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^2{\rho }_{uv}^j\frac{w_{uv}}{\overline{w}}{y}_{uv}}\right),$$ (9)

where

$$\overline{w}={\displaystyle \sum _{u,v=1}^2{w}_{uv}{y}_{uv}}.$$ (10)

From Equations (7)–(10), we see that the transition probabilities of the genotype frequencies from one generation to the next depend only on the genotype frequencies in the current generation for both viability and fecundity selection, but take on different forms. Combining with Equations (2)–(4), we find that the process ${\mathit{X}}^{\left(N\right)}$ is a time-homogeneous Markov process with respect to the filtration ${\mathcal{F}}^{\left(N\right)}=\left\{{\mathcal{F}}_k^{\left(N\right)}:k\in \mathrm{\mathbb{N}}\right\}$ generated by the process ${\mathit{Y}}^{\left(N\right)}$ evolving in the state space

$${\Omega }_{{\mathit{X}}^{\left(N\right)}}=\left\{\mathit{x}\in {\left\{0,\frac{1}{2N},\dots ,1\right\}}^2:{\displaystyle \sum _{i=1}^2{x}_i}=1\right\},$$

which we call the one-locus Wright-Fisher model with selection.

Two-locus Wright-Fisher models with selection:

Now we turn to the study of a monoecious population of N randomly mating diploid individuals at two linked autosomal loci named $\mathcal{A}$ and $\mathcal{B},$ each segregating into two alleles, ${\mathcal{A}}_1,$ ${\mathcal{A}}_2$ and ${\mathcal{B}}_1,$ ${\mathcal{B}}_2,$ evolving under natural selection with discrete and nonoverlapping generations. We call the four possible haplotypes ${\mathcal{A}}_1{\mathcal{B}}_1,$ ${\mathcal{A}}_1{\mathcal{B}}_2,$ ${\mathcal{A}}_2{\mathcal{B}}_1,$ and ${\mathcal{A}}_2{\mathcal{B}}_2$ haplotypes 1, 2, 3, and 4, respectively. As stated above, we need to formulate the sampling probabilities q for the evolution of two-locus systems under natural selection, which is the vector with frequencies of all possible genotypes of an effectively infinite population after a single generation of natural selection, meiosis (with genetic recombination), and random mating due to the presence of genetic recombination at meiosis in the evolution of two-locus systems.

With two biallelic loci, there are 16 possible zygotes (i.e., 16 ordered genotypes) that result from the random union of four gametes. We denote the fitness of the genotype formed by haplotypes i and j by $w_{ij}$ for $i,j=1,2,3,4,$ and designate the recombination rate between the two loci by r (i.e., the rate at which a recombinant gamete is produced at meiosis). To simplify notation, we introduce a vector of auxiliary variables $\mathit{\eta }=\left({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4\right),$ where ${\eta }_1={\eta }_4=-1$ and ${\eta }_2={\eta }_3=1.$ In the life cycles shown in Figure 1, the number of adults is regulated to be of size N, and the gene frequencies in the subsequent generation can be described by multinomial sampling of the normalized frequencies in an effectively infinite pool of zygotes. When natural selection takes different forms, genotype frequencies in the zygotes can be modeled in different ways.

Following similar reasoning as in the one-locus case, we can express the frequency of the genotype formed by haplotypes i and j of an effectively infinite population after a single generation of meiosis, random mating, and viability selection as

$$q_{ij}^{\left(v\right)}=\frac{w_{ij}}{\overline{w}}\left({\displaystyle \sum _{u\mathrm{,}v=1}^4{\rho }_{uv}^i{y}_{uv}+{\eta }_{i}rD}\right)\left({\displaystyle \sum _{u\mathrm{,}v=1}^4{\rho }_{uv}^j{y}_{uv}+{\eta }_{j}rD}\right),$$ (11)

where

$$\overline{w}={\displaystyle \sum _{i,j=1}^4{w}_{ij}}\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^i{y}_{uv}+{\eta }_{i}rD}\right)\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^j{y}_{uv}+{\eta }_{j}rD}\right)$$ (12)

$$D=\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^1{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^4{y}_{uv}}\right)-\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^2{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^3{y}_{uv}}\right).$$ (13)

Similarly, the frequency of the genotype formed by haplotypes i and j of an effectively infinite population after a single generation of fecundity selection, meiosis, and random mating is

$$q_{ij}^{\left(f\right)}=\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^i\frac{w_{uv}}{\overline{w}}{y}_{uv}+{\eta }_{i}rD}\right)\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^j\frac{w_{uv}}{\overline{w}}{y}_{uv}+{\eta }_{j}rD}\right),$$ (14)

where

$$\overline{w}={\displaystyle \sum _{u,v=1}^4{w}_{uv}{y}_{uv}}$$ (15)

$$D=\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^1\frac{w_{uv}}{\overline{w}}{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^4\frac{w_{uv}}{\overline{w}}{y}_{uv}}\right)-\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^2\frac{w_{uv}}{\overline{w}}{y}_{uv}}\right)\left({\displaystyle \sum _{u,v=1}^4{\rho }_{uv}^3\frac{w_{uv}}{\overline{w}}{y}_{uv}}\right).$$ (16)

From Equations (11)–(16), we see that the transition probabilities of the genotype frequencies from one generation to the next depend only on the genotype frequencies in the current generation for both viability and fecundity selection, but take on different forms. Combining with Equations (2)–(4), we show that the process ${\mathit{X}}^{\left(N\right)}$ is a time-homogeneous Markov process with respect to the filtration ${\mathcal{F}}^{\left(N\right)}=\left\{{\mathcal{F}}_k^{\left(N\right)}:k\in \mathrm{\mathbb{N}}\right\}$ generated by the process ${\mathit{Y}}^{\left(N\right)}$ evolving in the state space

$${\Omega }_{{\mathit{X}}^{\left(N\right)}}=\left\{\mathit{x}\in {\left\{0,\frac{1}{2N},\dots ,1\right\}}^4:{\displaystyle \sum _{i=1}^4{x}_i}=1\right\},$$

which we call the two-locus Wright-Fisher model with selection.

Diffusion approximations

Due to the interplay of stochastic and deterministic forces, the Wright-Fisher model with selection presents analytical challenges beyond the standard Wright-Fisher model for neutral populations. The analysis of the Wright-Fisher model with selection today is greatly facilitated by its diffusion approximation, commonly known as the Wright-Fisher diffusion with selection, which can be traced back to Kimura (1964), and has already been successfully applied in the statistical inference of natural selection [see Malaspinas (2016), and references therein]. Here, we present only the formulation of the Wright-Fisher diffusion with selection, and refer to Durrett (2008) for a rigorous proof, especially for one- and two-locus systems.

The Wright-Fisher diffusion with selection is a limiting process of the Wright-Fisher model with selection characterizing the changes in haplotype frequencies over time in an extremely large population evolving under extremely weak natural selection. More specifically, the selection coefficients (and the recombination rate if there is >1 locus) are assumed to be of order $1/\left(2N\right),$ and the process runs time at rate $2N,$ i.e., $t=k/\left(2N\right).$ The selection coefficient mentioned here represents the difference in fitness between a given genotype and the genotype with the highest fitness. For example, a common category of fitness values for a diploid population at a single locus can be presented as follows: genotypes ${\mathcal{A}}_1{\mathcal{A}}_1,$ ${\mathcal{A}}_1{\mathcal{A}}_2,$ and ${\mathcal{A}}_2{\mathcal{A}}_2$ at a given locus $\mathcal{A}$ have fitness values 1, $1-h_{\mathcal{A}}{s}_{\mathcal{A}},$ and $1-s_{\mathcal{A}},$ respectively, where $s_{\mathcal{A}}$ is the selection coefficient, and $h_{\mathcal{A}}$ is the dominance parameter [see Hamilton (2011), for other categories of fitness values presented in terms of selection coefficients].

Let $\Delta X_i^{\left(N\right)}\left(k\right)$ denote the change in the frequency of haplotype i from generation k to the next. Using Equations (5) and (6), we can obtain its first two conditional moments

$$E^{\left(k\mathrm{,}\mathit{x}\right)}\left(\Delta X_i^{\left(N\right)}\left(k\right)\right)=p_i-x_i$$

$$E^{\left(k,\mathit{x}\right)}\left(\Delta X_i^{\left(N\right)}\left(k\right)\Delta X_j^{\left(N\right)}\left(k\right)\right)=\frac{p_i\left({\delta }_{ij}-p_j\right)}{2N}+\left(p_i-x_i\right)\left(p_j-x_j\right).$$

Considering the limits as the population size N goes to infinity, we can formulate the infinitesimal mean vector $\mathit{\mu }\left(t,\mathit{x}\right)$ as

$$\begin{array}{c}{\mu }_i\left(t,\mathit{x}\right)=\underset{N\to \mathrm{\infty }}{\text{lim}}2N{E}^{\left(\left[2Nt\right],\mathit{x}\right)}\left(\Delta X_i^{\left(N\right)}\left(\left[2Nt\right]\right)\right)\\ =\underset{N\to \mathrm{\infty }}{\text{lim}}2N\left(p_i-x_i\right)\end{array}$$ (17)

and the infinitesimal covariance matrix $\mathbf{\Sigma }\left(t,\mathit{x}\right)$ as

$$\begin{array}{c}{\Sigma }_{ij}\left(t,\mathit{x}\right)=\underset{N\to \mathrm{\infty }}{\text{lim}}2N{E}^{\left(\left[2Nt\right],\mathit{x}\right)}\left(\Delta X_i^{\left(N\right)}\left(\left[2Nt\right]\right)\Delta X_j^{\left(N\right)}\left(\left[2Nt\right]\right)\right)\\ =\underset{N\to \mathrm{\infty }}{\text{lim}}{p}_i\left({\delta }_{ij}-p_j\right)+2N\left(p_i-x_i\right)\left(p_j-x_j\right),\end{array}$$ (18)

where $\left[\mathrm{·}\right]$ is used to denote the integer part of the value in the brackets, according to standard techniques of diffusion theory [see, for example, Karlin and Taylor (1981)].

The process ${\mathit{X}}^{\left(N\right)}$ thereby converges to a diffusion process, denoted by $\mathit{X}=\left\{\mathit{X}\left(t\right),t\ge 0\right\},$ satisfying the stochastic differential equation of the form

$$d\mathit{X}\left(t\right)=\mathit{\mu }\left(t,\mathit{X}\left(t\right)\right)dt+\mathit{\sigma }\left(t,\mathit{X}\left(t\right)\right)d\mathit{W}\left(t\right),$$

where the diffusion coefficient matrix $\mathit{\sigma }\left(\mathit{x}\right)$ satisfies the relation that

$$\mathit{\sigma }\left(t,\mathit{x}\right){\mathit{\sigma }}^T\left(t,\mathit{x}\right)=\mathbf{\Sigma }\left(t,\mathit{x}\right)$$

and $\mathit{W}\left(t\right)$ is a multi-dimensional standard Brownian motion. We refer to the process X as the Wright-Fisher diffusion with selection, which we will use to investigate the difference in the behavior of the Wright-Fisher model between viability and fecundity selection in the section Diffusion analysis of the Wright-Fisher model.

Statistical distances

Given that the Wright-Fisher model with selection is a Markov process, the evolution is completely determined by its transition probabilities. We can, therefore, study the difference in the behavior of the Wright-Fisher model between viability and fecundity selection in terms of their transition probabilities.

We define the conditional probability distribution function of the Wright-Fisher model with selection $X^{\left(N\right)}$ evolving from the population of the initial haplotype frequencies ${\mathit{x}}_0$ over k generations (i.e., k-step transition probabilities) as

$$\pi \left({\mathit{x}}_0,{\mathit{x}}_k\right)=P\left({\mathit{X}}^{\left(N\right)}\left(k\right)={\mathit{x}}_k|{\mathit{X}}^{\left(N\right)}\left(0\right)={\mathit{x}}_0\right).$$ (19)

We use a statistical distance to quantify the difference between two probability distributions for the Wright-Fisher model with viability and fecundity selection (i.e., the difference in the behavior of the Wright-Fisher model between viability and fecundity selection). Rachev et al. (2013) provided an excellent introduction of statistical distances, and here we employ the Hellinger distance, introduced by Hellinger (1909), to quantify the difference in the behavior of the Wright-Fisher model between viability and fecundity selection, defined as

$$H\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right)\left({\mathit{x}}_0,k\right)=\frac{1}{\sqrt{2}}\sqrt{{\displaystyle \sum _{{\mathit{x}}_k}{\left({\pi }^{\left(v\right)}\left({\mathit{x}}_0,{\mathit{x}}_k\right)-{\pi }^{\left(f\right)}\left({\mathit{x}}_0,{\mathit{x}}_k\right)\right)}^2}},$$ (20)

where ${\pi }^{\left(v\right)}$ is the probability distribution for the Wright-Fisher model with viability selection, and ${\pi }^{\left(f\right)}$ is the probability distribution for the Wright-Fisher model with fecundity selection, both of which are given by Equation (19) combined with the Wright-Fisher model with the corresponding type of natural selection.

Given the difficulties in analytically formulating the probability distribution π, especially for the population evolving over a long-time period, we resort to Monte Carlo simulation here, which enables us to get an empirical probability distribution function associated to the probability distribution π, defined as

$$\widehat{\pi }\left({\mathit{x}}_0,{\mathit{x}}_k\right)=\frac{1}{M}{\displaystyle \sum _{m=1}^M{I}_{\left\{{\mathit{\xi }}_k^{\left(m\right)}={\mathit{x}}_k\right\}}},$$ (21)

where I is the indicator function, namely $I_{\left\{{\mathit{\xi }}_k={\mathit{x}}_k\right\}}$ is one if ${\mathit{\xi }}_k={\mathit{x}}_k$ is true and zero otherwise, ${\mathit{\xi }}_k^{\left(m\right)}$ is the m-th realization of the haplotype frequencies simulated under the Wright-Fisher model with selection from the population of the initial haplotype frequencies ${\mathit{x}}_0$ over k generations, and M is the total number of independent realizations in Monte Carlo simulation. Combining Equations (20) and (21), we can formulate the Monte Carlo approximation for the Hellinger distance $H\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right)$ as

$$\widehat{H}\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right)\left({\mathit{x}}_0,k\right)=H\left({\widehat{\pi }}^{\left(v\right)},{\widehat{\pi }}^{\left(f\right)}\right)\left({\mathit{x}}_0,k\right).$$

According to Van der Vaart (2000), the rate of the convergence for the empirical probability distribution $\widehat{\pi }$ to the probability distribution π with respect to the Hellinger distance is of the order $C_1{\left(\left|{\Omega }_{\mathit{X}}\right|-1\right)}^{1/2}/M^{1/2},$ where $C_1$ is a constant, and $\left|{\Omega }_{\mathit{X}}\right|$ is total number of possible states in the state space ${\Omega }_{\mathit{X}}.$ Combining with Le Cam and Yang (2000), we find that the rate of the convergence for the Hellinger distance approximated by Monte Carlo simulation, $\widehat{H}\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right),$ to the Hellinger distance $H\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right)$ is of order $C_2{\left(\left|{\Omega }_{\mathit{X}}\right|-1\right)}^{1/2}/M^{1/2},$ where $C_2$ is a constant. Therefore, in theory, the Monte Carlo approximation for the Hellinger distance $\widehat{H}\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right)$ can be used instead of the Hellinger distance $H\left({\pi }^{\left(v\right)},{\pi }^{\left(f\right)}\right)$ as long as we increase the total number of independent realizations M, which we will apply to measure the difference in the behavior of the Wright-Fisher model between viability and fecundity selection in the section Simulation analysis of the Wright-Fisher model.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. Code used to simulate the Wright-Fisher model with selection, including both viability and fecundity selection, and compute the results is provided in Supplemental Material, File S1.

Results

In this section, we use diffusion analysis of Wright-Fisher models with selection and extensive Monte Carlo simulation studies to investigate whether different types of natural selection can cause different population behaviors under the Wright-Fisher model, especially when natural selection takes the form of viability or fecundity selection.

We employ the category of fitness values presented in terms of selection coefficients given in the section Diffusion approximations, and consider the simple case of directional selection with $0\le s_{\mathcal{A}}\le 1,$ which implies that the ${\mathcal{A}}_1$ allele is the type favored by natural selection. The dominance parameter is assumed to be in the range $0\le h_{\mathcal{A}}\le 1,$ i.e., general dominance. Suppose that fitness values of two-locus genotypes are determined multiplicatively from fitness values at individual loci, e.g., the fitness value of genotype ${\mathcal{A}}_1{\mathcal{B}}_2/{\mathcal{A}}_2{\mathcal{B}}_2$ is $\left(1-h_{\mathcal{A}}{s}_{\mathcal{A}}\right)\left(1-s_{\mathcal{B}}\right),$ which means that there is no position effect, i.e., coupling and repulsion double heterozygotes have the same fitness, $w_{14}=w_{23}=\left(1-h_{\mathcal{A}}{s}_{\mathcal{A}}\right)\left(1-h_{\mathcal{B}}{s}_{\mathcal{B}}\right).$ Moreover, the recombination rate defined in the section Two-locus Wright-Fisher models with selection is in the range $0\le r\le \mathrm{0.5.}$

Diffusion analysis of the Wright-Fisher model

Now we use diffusion analysis of Wright-Fisher models with selection to address the question of whether viability and fecundity selection can cause different population behavior under the Wright-Fisher model, especially for the evolution of one- and two-locus systems under natural selection. From the section Diffusion approximations, we see that the diffusion approximation for the Wright-Fisher model with selection is fully determined from its infinitesimal mean vector $\mu \left(t,\mathit{x}\right)$ in Equation (17) and its infinitesimal covariance matrix $\text{Σ}\left(t,\mathit{x}\right)$ in Equation (18), which implies that we can carry out diffusion analysis of Wright-Fisher models with selection to investigate the difference in the behavior of the Wright-Fisher model between viability and fecundity selection by comparing the difference in the haplotype frequencies of an effectively infinite population after a single generation of natural selection, meiosis, and random mating mentioned in Equations (17) and (18) between viability and fecundity selection.

Under the set of assumptions on fitness values given above, and using Taylor expansions with respect to the selection coefficient $s_{\mathcal{A}},$ we find that for one-locus systems there is no difference in the haplotype frequencies of an effectively infinite population after a single generation of natural selection, meiosis, and random mating between viability and fecundity selection, i.e.,

$$\left|p_i^{\left(v\right)}-p_i^{\left(f\right)}\right|=0,$$

for $i=1,2.$ For two-locus systems with the selection coefficients $s_{\mathcal{A}}$ and $s_{\mathcal{B}}$ and the recombination rate r, File S2 shows that

$$\left|p_i^{\left(v\right)}-p_i^{\left(f\right)}\right|=\mathcal{O}\left(\frac{1}{N^2}\right),$$

for $i=1,2,3,4.$ Combining with Equations (17) and (18), we have

$${\mathit{\mu }}^{\left(v\right)}\left(t,\mathit{x}\right)={\mathit{\mu }}^{\left(f\right)}\left(t,\mathit{x}\right)$$

$${\mathbf{\Sigma }}^{\left(v\right)}\left(t,\mathit{x}\right)={\mathbf{\Sigma }}^{\left(f\right)}\left(t,\mathit{x}\right),$$

which leads to the same stochastic differential equation representation of the Wright-Fisher diffusion with viability and fecundity selection for the evolution of one- and two-locus systems under natural selection, respectively (see File S2 for detailed calculations).

Therefore, we can conclude that viability and fecundity selection bring about the same population behavior under the Wright-Fisher diffusion for the evolution of one- and two-locus systems under natural selection, which implies that there is almost no difference in population behaviors under the Wright-Fisher model between viability and fecundity selection for the evolutionary scenario of an extremely large population evolving under extremely weak natural selection (and genetic recombination if there is >1 locus).

Simulation analysis of the Wright-Fisher model

Diffusion analysis of Wright-Fisher models with selection require assumptions on genetic parameters for tractability, i.e., it is only guaranteed to be a good approximation of the underlying Wright-Fisher model in the case of an extremely large population evolving under extremely weak natural selection (and genetic recombination if there is >1 locus). In this section, we use extensive Monte Carlo simulation studies to investigate the difference in the behavior of the Wright-Fisher model between viability and fecundity selection for other evolutionary scenarios such as a small population evolving under strong natural selection. We illustrate how different types of natural selection affect the behavior of the Wright-Fisher model with haplotype 1 in detail in the following, and expect other haplotypes to behave in a similar manner.

Let us designate the marginal probability distribution of the frequency of haplotype 1 by ${\pi }_1,$ and simulate the dynamics of the Hellinger distance $H\left({\mathit{\pi }}_1^{\left(v\right)},{\mathit{\pi }}_1^{\left(f\right)}\right)$ over time for different evolutionary scenarios to investigate whether viability and fecundity selection can cause different population behaviors under the Wright-Fisher model using Equations (20) and (21) in Equation (19).

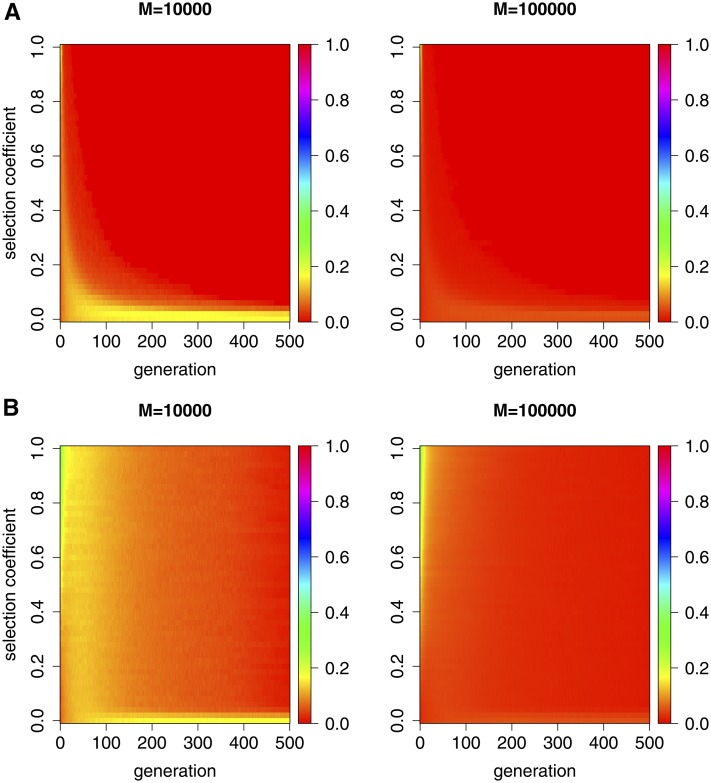
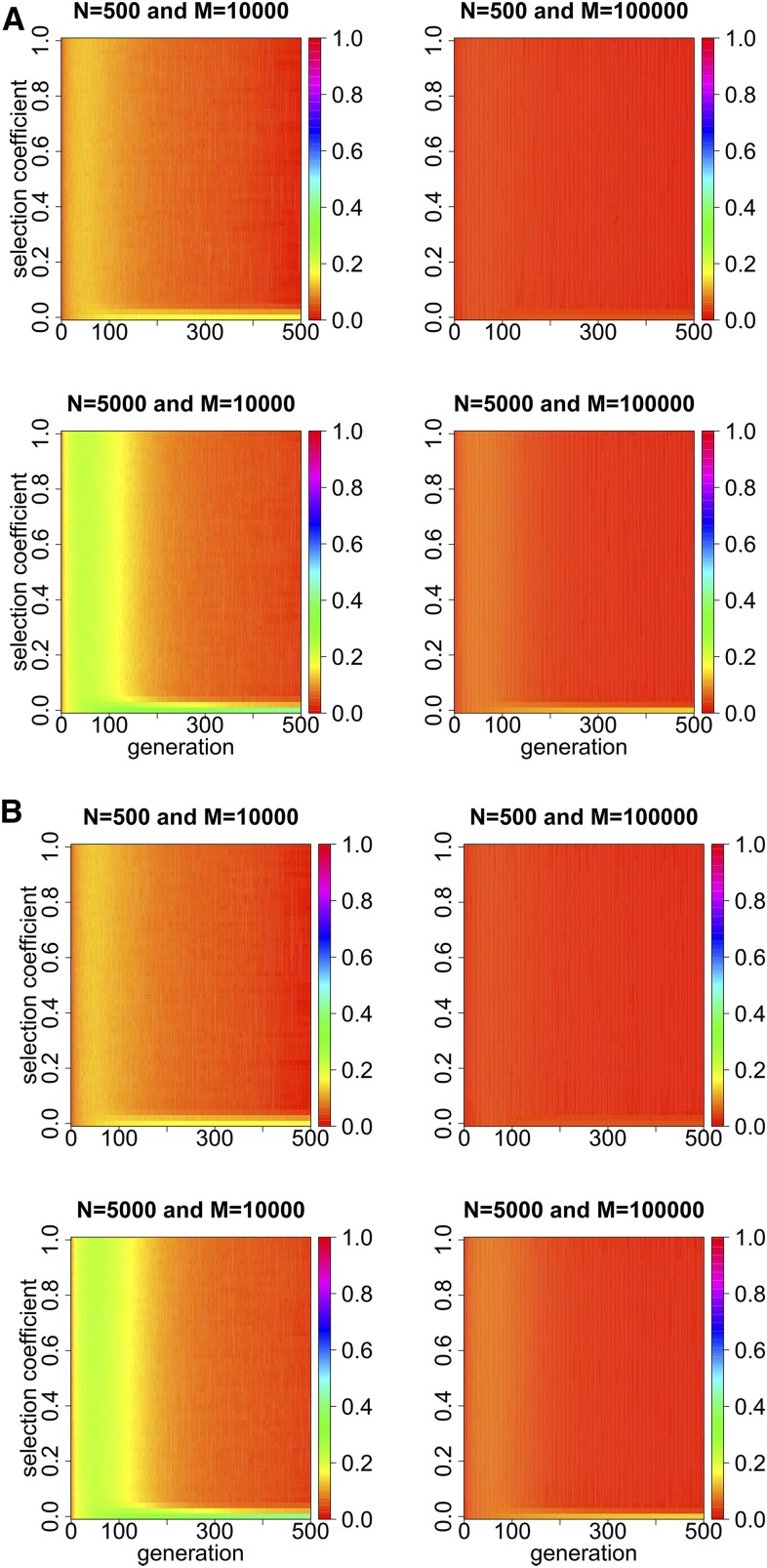
In Figure 2, we show the dynamics of the Hellinger distance $H\left({\mathit{\pi }}_1^{\left(v\right)},{\mathit{\pi }}_1^{\left(f\right)}\right)$ with the varying selection coefficient $s_{\mathcal{A}}$ over 500 generations under the one- and two-locus Wright-Fisher models with selection, respectively, in which the Hellinger distance $H\left({\mathit{\pi }}_1^{\left(v\right)},{\mathit{\pi }}_1^{\left(f\right)}\right)$ is clearly not always close to zero. This may result from the different forms natural selection takes or the statistical noise produced in Monte Carlo simulation. Comparing the left columns of Figure 2, A and B, with their right columns, we find that the Hellinger distance $H\left({\mathit{\pi }}_1^{\left(v\right)},{\mathit{\pi }}_1^{\left(f\right)}\right)$ decreases as the total number of independent realizations M in Monte Carlo simulation increases, especially when the selection coefficient $s_{\mathcal{A}}$ is close to zero. We believe, therefore, that the discrepancy should be caused mainly by the statistical noise produced in Monte Carlo simulation, rather than the different forms natural selection takes when the selection coefficient is close to zero, which otherwise leads to a contradiction to what we have already achieved in the section Diffusion analysis of the Wright-Fisher model. On the contrary, when the selection coefficient is not close to zero, the discrepancy should indeed be caused by the different forms natural selection takes, rather than the statistical noise in Monte Carlo simulation. We will confirm and discuss this point in more detail in the section Robustness of Monte Carlo simulation studies.

Figure 2.

Dynamics of the Hellinger distance $H\left({\pi }_1^{\left(v\right)},{\pi }_1^{\left(f\right)}\right)$ simulated with the varying selection coefficient $s_{\mathcal{A}}$ over 500 generations under the one- and two-locus Wright-Fisher models with selection. (A) We generate M independent realizations from simulating the one-locus Wright-Fisher model with selection, where we adopt $N=500,$ $h_{\mathcal{A}}=0.5,$ and ${\mathit{x}}_0=\left(0.3,0.7\right).$ (B) We generate M independent realizations from simulating the two-locus Wright-Fisher model with selection, where we adopt $N=500,$ $s_{\mathcal{B}}=0.05,$ $h_{\mathcal{A}}=0.5,$ $h_{\mathcal{B}}=0.5,$ $r=0.45,$ and ${\mathit{x}}_0=\left(0.3,0.4,0.2,0.1\right).$

Figure 2 shows that the difference in the behavior of the Wright-Fisher model between viability and fecundity selection does exist, and becomes more significant when the effect of natural selection on the population evolving over time increases. For the population evolving under natural selection at a single locus, the difference in the behavior of the Wright-Fisher model between viability and fecundity selection is almost negligible. However, for the population evolving under natural selection at two linked loci, the difference in the behavior of the Wright-Fisher model between viability and fecundity selection is no longer negligible, especially when natural selection is not extremely weak. Therefore, we assert that viability and fecundity selection can cause different population behaviors under the Wright-Fisher model, especially for the population evolving under natural selection at two linked loci.

For further investigation into the difference in the population evolving over time at two linked loci under the Wright-Fisher model between viability and fecundity selection, we introduce the coefficient of linkage disequilibrium, proposed by Lewontin and Kojima (1960), to quantify the level of linkage disequilibrium between the two loci, which is defined as

$$D^{\left(N\right)}\left(k\right)=X_1^{\left(N\right)}\left(k\right)X_4^{\left(N\right)}\left(k\right)-X_2^{\left(N\right)}\left(k\right)X_3^{\left(N\right)}\left(k\right).$$

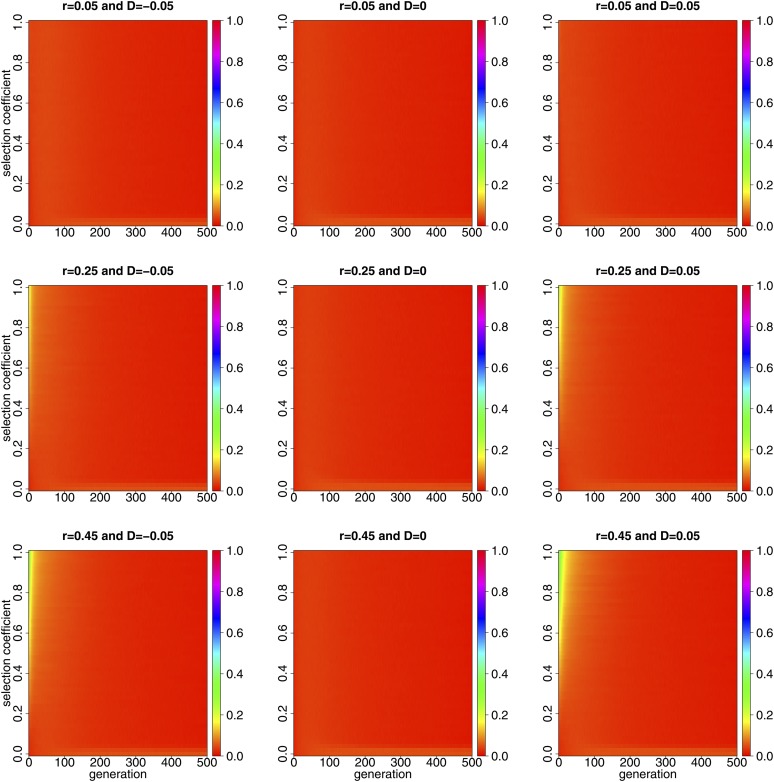
We simulate the dynamics of the Hellinger distance $H\left({\mathit{\pi }}_1^{\left(v\right)},{\mathit{\pi }}_1^{\left(f\right)}\right)$ with the varying selection coefficient $s_{\mathcal{A}}$ and recombination rate r over 500 generations under the two-locus Wright-Fisher model with selection for the population initially at different levels of linkage disequilibrium, in Figure 3.

Figure 3.

Dynamics of the Hellinger distance $H\left({\pi }_1^{\left(v\right)},{\pi }_1^{\left(f\right)}\right)$ simulated with the varying selection coefficient $s_{\mathcal{A}}$ and recombination rate r over 500 generations under the two-locus Wright-Fisher model with selection for the population initially at different levels of linkage disequilibrium. We generate $M={10}^5$ independent realizations in Monte Carlo simulation, and adopt $N=500,$ $s_{\mathcal{B}}=0.05,$ $h_{\mathcal{A}}=0.5,$ and $h_{\mathcal{B}}=\mathrm{0.5.}$

Comparing the middle column of Figure 3 with its left and right columns, we find that the difference in the behavior of the two-locus Wright-Fisher model between viability and fecundity selection becomes negligible when the population is initially in linkage equilibrium (see the middle column of Figure 3), which implies that, whether different types of natural selection can cause different population behaviors under the Wright-Fisher model at two linked loci depends significantly on the level of linkage disequilibrium. We thereby consider the dynamics of linkage disequilibrium over time under the two-locus Wright-Fisher model with viability and fecundity selection, respectively, for the population initially at different levels of linkage disequilibrium.

We define the conditional probability distribution function of linkage disequilibrium $D^{\left(N\right)}$ evolving under the Wright-Fisher model from the population of the initial haplotype frequencies ${\mathit{x}}_0$ over k generations as

$${\pi }_D\left(D_0,D_k\right)=P\left(D^{\left(N\right)}\left(k\right)=D_k|D^{\left(N\right)}\left(0\right)=D_0\right),$$

where

$$D_0=x_{0,1}{x}_{0,4}-x_{0,2}{x}_{0,3}.$$

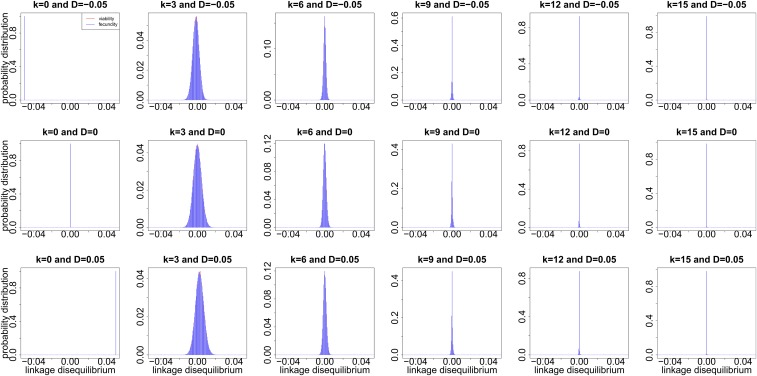
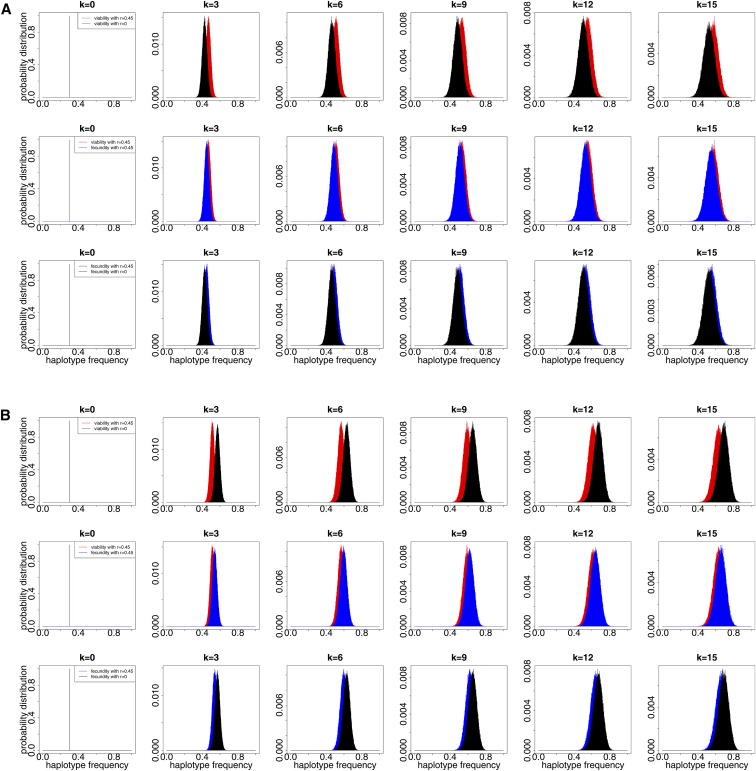
We simulate the dynamics of the probability distribution ${\pi }_D$ over time for the population initially at different levels of linkage disequilibrium in Figure 4. We observe that the probability distribution ${\pi }_D$ becomes concentrated on a narrower and narrower range of possible values centered ∼0 from generation to generation until fixing at 0. The dynamics of the probability distribution ${\pi }_D$ over time seems not to be associated with whether viability or fecundity selection is occurring.

Figure 4.

Dynamics of the probability distributions ${\pi }_D^{\left(v\right)}$ and ${\pi }_D^{\left(f\right)}$ simulated over 15 generations under the two-locus Wright-Fisher model with selection for the population initially at different levels of linkage disequilibrium. We generate $M={10}^5$ independent realizations in Monte Carlo simulation, and adopt $N=500,$ $s_{\mathcal{A}}=0.95,$ $s_{\mathcal{B}}=0.05,$ $h_{\mathcal{A}}=0.5,$ $h_{\mathcal{B}}=0.5,$ and $r=\mathrm{0.45.}$

From Ridley (2004), there are three potential mechanisms of evolutionary change, genetic recombination, natural selection, and population regulation (genetic drift), in the life cycle, which may affect the dynamics of linkage disequilibrium over time. Genetic recombination always works toward linkage equilibrium due to genetic recombination generating new gamete types to break down nonrandom genetic associations (Ridley 2004). Natural selection alone cannot move the population far away from linkage equilibrium under the assumption that fitness values of two-locus genotypes are multiplicative (Slatkin 2008). Genetic drift can destroy linkage equilibrium and create many genetic associations since genetic drift leads to the random change in haplotype frequencies, which, however, can cause persistent linkage disequilibrium only in small enough populations (Ridley 2004). So once linkage equilibrium has been reached, populations usually will not move far away from linkage equilibrium.

From Equations (11)–(16), provided that the population evolving over time is always close to linkage equilibrium, the amount of the change in haplotype frequencies caused by genetic recombination is negligible. The two-locus Wright-Fisher model where each locus segregates into two alleles thereby becomes similar to the one-locus Wright-Fisher model for a single locus segregating four alleles, where each gamete is analogous to a single allele. Therefore, once linkage equilibrium has been reached, populations evolving under natural selection at two linked loci within the framework of the Wright-Fisher model would no longer depend on whether viability or fecundity selection is occurring. That is, viability and fecundity selection can cause different population behaviors under the Wright-Fisher model only when the population is far away from linkage equilibrium, which is confirmed by Figure 3.

Now we discuss why viability and fecundity selection lead to different population behaviors under the two-locus Wright-Fisher model with selection. We simulate the dynamics of the probability distributions ${\pi }_1^{\left(v\right)}$ and ${\pi }_1^{\left(f\right)}$ over time for the population initially at different levels of linkage disequilibrium in Figure 5, from which it is clear that the Wright-Fisher models with different types of natural selection have different rates of change in the frequency of haplotype 1 approaching fixation when the population is initially far away from linkage equilibrium, which leads to the difference in the behavior of the Wright-Fisher model between viability and fecundity selection, as illustrated in the left and right columns of Figure 3.

Figure 5.

Dynamics of the probability distributions ${\pi }_1^{\left(v\right)}$ and ${\pi }_1^{\left(f\right)}$ simulated over 15 generations under the two-locus Wright-Fisher model with selection for the population initially at different levels of linkage disequilibrium. We generate $M={10}^5$ independent realizations in Monte Carlo simulation, and adopt $N=500,$ $s_{\mathcal{A}}=0.95,$ $s_{\mathcal{B}}=0.05,$ $h_{\mathcal{A}}=0.5,$ $h_{\mathcal{B}}=0.5,$ and $r=\mathrm{0.45.}$ (A) The population is initially in negative linkage disequilibrium ($D_0=-0.05$). (B) The population is initially in positive linkage disequilibrium ($D_0=0.05$).

More specifically, as shown in Figure 5A, when the population is in negative linkage disequilibrium, the Wright-Fisher model with selection of two linked loci drives haplotype 1 more rapidly toward fixation than the Wright-Fisher model with selection of two completely linked loci (i.e., $r=0$). This is due to the fact that genetic recombination reinforces the change in haplotype frequencies caused by natural selection for negative linkage disequilibrium (see Hamilton 2011). The middle row of Figure 5A shows that the Wright-Fisher model with viability selection drives haplotype 1 more rapidly toward fixation than the Wright-Fisher model with fecundity selection when the population is in negative linkage disequilibrium, which implies that genetic recombination affecting natural selection at two linked loci is more significant in the Wright-Fisher model with viability selection than that in the Wright-Fisher model with fecundity selection for negative linkage disequilibrium. These results are also confirmed with Figure 5B for the population in positive linkage disequilibrium. Therefore, the difference in the behavior of the two-locus Wright-Fisher model between viability and fecundity selection results from the different effect of genetic recombination on different types of natural selection within the framework of the Wright-Fisher model, i.e., genetic recombination has a more significant effect on natural selection at two linked loci when natural selection takes the form of viability selection than fecundity selection.

Notice that here we employ the Hellinger distance to measure the difference in the behavior of the Wright-Fisher model between viability and fecundity selection, and only simulate the Hellinger distance between two probability distributions for the Wright-Fisher model with viability and fecundity selection in limited evolutionary scenarios such as completely additive gene action ($h=0.5$). In the Supplemental Material, we simulate the Hellinger distance between two probability distributions for the Wright-Fisher model with viability and fecundity selection for completely dominant gene action ($h=0$) and completely recessive gene action ($h=1$), respectively (see File S3). We also provide the dynamics of the difference in the behavior of the Wright-Fisher model between viability and fecundity selection for different population sizes (see File S4). Moreover, we simulate the total variation distance between two probability distributions for the Wright-Fisher model with viability and fecundity selection for different evolutionary scenarios (see File S5). All these simulated results confirm what we have achieved above.

Discussion

In this section, we discuss the robustness of Monte Carlo simulation studies carried out in this study. Moreover, we summarize our main results and discuss the significance of these findings in terms of biological examples of fecundity and viability selection.

Robustness of Monte Carlo simulation studies

We performed a robustness analysis of Monte Carlo simulation studies as described in Results. This was designed mainly to demonstrate that the discrepancy in Monte Carlo simulation studies results from whether viability selection or fecundity selection is occurring is not due to the statistical noise produced in Monte Carlo simulation, and is indeed caused by the different forms natural selection takes.

We simulated the dynamics of the Hellinger distance of the two empirical probability distributions for the two runs of the two-locus Wright-Fisher model with the same type of natural selection here as an illustration, the two-locus Wright-Fisher model with viability selection in Figure 6A and the two-locus Wright-Fisher model with fecundity selection in Figure 6B, respectively. Figure 6 shows that the statistical noise in Monte Carlo simulation is increasing in the population size N, but is deceasing in the total number of independent realizations M. This is confirmed by the rate of convergence for the Hellinger distance approximated by Monte Carlo simulation, as stated in Statistical distances. For the population of $N=500$ individuals in Monte Carlo simulation studies, generating $M={10}^5$ independent realizations in Monte Carlo simulation is large enough to remove most of the statistical noise. In comparison with Figure 6, A and B, the discrepancy in Figure 2B shares the same pattern, except for large selection coefficients, which implies that the difference in the behavior of the Wright-Fisher model between viability and fecundity selection indeed results from the different forms natural selection rather than the statistical noise produced in Monte Carlo simulation when natural selection is not extremely weak.

Figure 6.

Dynamics of the Hellinger distance $H\left({\mathit{\pi }}_1^{\left(\mathrm{·}\right)},{\mathit{\pi }}_1^{\left(\mathrm{·}\right)}\right)$ simulated with the varying selection coefficient $s_{\mathcal{A}}$ over 500 generations under the two-locus Wright-Fisher model with selection for natural selection taking different forms. We adopt $s_{\mathcal{B}}=0.05,$ $h_{\mathcal{A}}=0.5,$ $h_{\mathcal{B}}=0.5,$ $r=0.45,$ and ${\mathit{x}}_0=\left(0.3,0.4,0.2,0.1\right).$ (A) Natural selection takes the form of viability selection. (B) Natural selection takes the form of fecundity selection.

Summary and further perspectives

Our diffusion analysis of Wright-Fisher models with selection and extensive Monte Carlo simulation studies show that, with genetic recombination, the population evolving under natural selection within the framework of the Wright-Fisher model depends significantly on whether viability or fecundity selection is occurring when the population is far away from linkage equilibrium. This is caused mainly by different effects of genetic recombination on different types of natural selection, i.e., genetic recombination has a more significant effect on natural selection at linked loci when natural selection takes the form of viability selection than fecundity selection. The difference in the behavior of the Wright-Fisher model becomes more significant as the effect of natural selection and genetic recombination increases. However, after the population reaches linkage equilibrium, population behaviors under the Wright-Fisher model with viability and fecundity selection become almost identical fairly quickly.

We have shown that, with genetic recombination, the population evolving under natural selection within the framework of the Wright-Fisher model depends significantly on whether viability or fecundity selection is occurring when the population is far away from linkage equilibrium. According to Ridley (2004), most natural populations are probably near linkage equilibrium, which implies that the different behavior of the Wright-Fisher model caused by viability or fecundity selection may not be significant. However, one evolutionary scenario in which it may have significant consequences is that of admixture between two populations. In this case, there is likely to be significant linkage disequilibrium due to the allele frequency differences between populations (Pritchard and Rosenberg 1999), and, also, there is likely to be local natural selection in which alleles that are favored in one population are selected against in the other (Charlesworth et al. 1997), and vice-versa. Therefore, the results presented here may lead to testable predictions about the role of life-history on the natural selection dynamics in populations. For example, we predict that genetic recombination will have a less significant effect on the natural selection dynamics when natural selection acts through fecundity difference between genotypes. It should be noted that, in our formulation, the fecundity selection is associated with a difference among monoecious diploid genotypes in their overall gamete production, and should not be confused with gametic selection, for example, natural selection on sperm binding alleles (Palumbi 1999). Moreover, we do not distinguish between sperm and egg production [i.e., the two haplotype frequencies $X_i$ and $X_j$ in Equation (1) are exchangeable]. The most relevant organisms that may be expected to conform to this assumption may be monoecious plant species, where correlations between pollen and seed production may be induced through genetic variation in flower size (e.g., Galen 2000).

Given that we have developed a Monte Carlo framework for simulating the Wright-Fisher model under either scenario (i.e., viability or fecundity selection), future developments could include the addition of population structure, and it should then be straightforward to develop a statistical inferential framework to allow us to distinguish between viability selection or fecundity selection at candidate loci such as the approximate Bayesian computation (ABC) framework (Liepe et al. 2014), which enables us to compute the posterior probabilities of the Wright-Fisher models with viability and fecundity selection. Once the posterior probabilities of candidate models have been estimated, we can make full use of the techniques of Bayesian model comparison. Furthermore, in the present work, we investigate how different types of natural selection affect the population evolving under the Wright-Fisher model mainly through Monte Carlo simulation studies, which can only demonstrate the qualitative difference in the behavior of the Wright-Fisher model. It would be far more challenging to carry out the analysis of the effect of different types of natural selection on the Wright-Fisher model that can lead to more quantitative comparisons.

Supplementary Material

Supplemental material is available online at www.g3journal.org/lookup/suppl/doi:10.1534/g3.117.041038/-/DC1.