Abstract
The use of RNA-seq as the preferred method for the discovery and validation of small RNA biomarkers has been hindered by high quantitative variability and biased sequence counts. In this paper we develop a statistical model for sequence counts that accounts for ligase bias and stochastic variation in sequence counts. This model implies a linear quadratic relation between the mean and variance of sequence counts. Using a large number of sequencing datasets, we demonstrate how one can use the generalized additive models for location, scale and shape (GAMLSS) distributional regression framework to calculate and apply empirical correction factors for ligase bias. Bias correction could remove more than 40% of the bias for miRNAs. Empirical bias correction factors appear to be nearly constant over at least one and up to four orders of magnitude of total RNA input and independent of sample composition. Using synthetic mixes of known composition, we show that the GAMLSS approach can analyze differential expression with greater accuracy, higher sensitivity and specificity than six existing algorithms (DESeq2, edgeR, EBSeq, limma, DSS, voom) for the analysis of small RNA-seq data.
INTRODUCTION
Technological improvements and rapid reduction in costs have resulted in the increasing adoption of RNA-seq for the discovery of small RNAs as extracellular biomarkers (ex-RNA). The use of RNA-seq as the preferred method for the discovery and validation of small RNA biomarkers can be seriously hindered by high variability (1,2), poor reproducibility and bias (3–8). In this paper we aim to mitigate these issues by developing a statistical model for sequence counts (9–19) that is grounded in the physical processes of the measurement. By analyzing RNA-seq profiles from samples of known composition, we demonstrate the validity of the model. We also show that one can use this modeling framework to explicitly address and account for both systematic factors and random variation in RNA-seq experiments.
We develop this framework in a step-wise manner. First, we describe a conceptual stochastic model for the hierarchy of the distinct steps in an RNA-seq experiment, and the relatively mild assumptions on which it depends. We then use this model to demonstrate that the mean and variance of sequence counts obey a linear quadratic (LQ) relationship. This is a testable prediction, which we validate against numerous public and novel datasets. Second, we derive the parametric form for the distribution of sequence counts that conforms to this LQ relationship. To do so, we consider several distinct processes that account for measurement variation in sequence counts, i.e. sequence-dependent ligase bias, the stochastic nature of library amplification by polymerase chain reaction (PCR) and library depth variation in the sequencing process. We handle these sources of noise and bias, through a combination of analytical approximations, stochastic simulations and exact calculation and determine closed-form expressions for the distribution of counts in an RNA-seq experiment. A major contribution of our work is the derivation of a normal probability model for which the variance is a LQ function of the mean and the negative binomial law (15,20). Both appear to be accurate, numerically robust approximations to the underlying, intractable distribution of RNA-seq counts over a wide range of parameters.
These developments lead us to introduce distributional regression approaches for the analyses of RNA-seq datasets. In particular, our work highlights the generalized additive models for location-scale-shape (GAMLSS) (21) as the optimal regression framework for the analyses of RNA-seq data. GAMLSS allows parametric, flexible and random effects modeling of both the mean and the variance of the underlying distribution. Such a flexible approach is required for the analysis of RNA-seq data, because both the mean and the variance carry important information and are influenced by initial RNA species abundance, the sequence of the RNA species and PCR efficiency. We leverage the flexibility of the GAMLSS to quantify systematic (ligase) bias in the presence of stochastic sources of variation in RNA-seq experiments. We demonstrate that one can use the GAMLSS regression framework to derive empirical correction factors that substantially reduce the bias in RNA-seq measurements. To do so, we undertake an extensive series of cross-validation and out-of-sample model validation analyses in public and novel datasets generated by our group. Finally, we apply our methodology to the problem of assessing differential expression (DE) using libraries of known composition. We demonstrate that the proposed statistical framework performs better than six commonly used alternatives in terms of accuracy of differential expression (assesses as log-fold expression changes), Type I (false positive) and Type II (false negative) errors. Consequently, our proposal achieves the optimal balance between a smaller false discovery rate (FDR) and false omission rate (FOR).
MATERIALS AND METHODS
A multi-step model for RNA-seq experiments
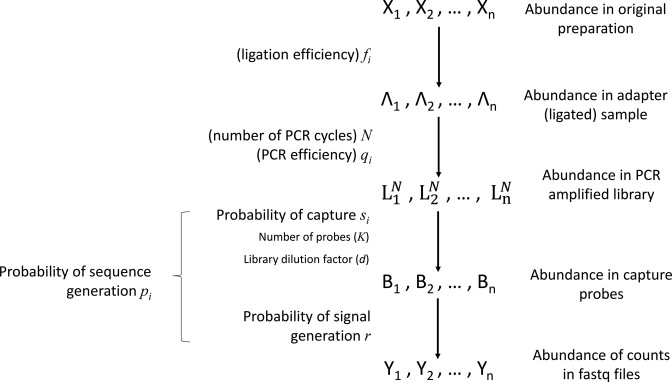
We introduce a conceptual model (Figure 1) for an RNA-seq experiment and use this notation for the remainder of this paper. In this model, each RNA present in the original preparation, whose level is indicated as 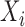 , is transformed, with variable efficiency (
, is transformed, with variable efficiency (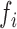 ) into a barcoded DNA sequence by the ligation of adapter sequences and reverse transcription. The abundance of these sequences (Λi) along with the efficiency of the PCR amplification (
) into a barcoded DNA sequence by the ligation of adapter sequences and reverse transcription. The abundance of these sequences (Λi) along with the efficiency of the PCR amplification (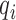 ) and the number of cycles (N) determines the amount of the PCR product (
) and the number of cycles (N) determines the amount of the PCR product (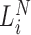 ). After PCR libraries may be size selected and/or diluted d-fold and before ‘loaded’ in capture probes in the sequencing apparatus. We use the term ‘capture probe’ to refer to active sites on the surface of the sequencing chip, or the beads used in emulsion PCR-based technologies. These probes are responsible for generating a signal after a platform-specific signal amplification step; e.g. cluster generation in the Illumina platform or clonal amplification by emulsion PCR in the Ion Torrent workflow. If all the sequences from a single library were loaded onto probes and all probes generated a signal, then the depth of the sequence library would be constant and equal to K0. Allowing for random library depths, leads to additional variation in the total number of reads, represented by
). After PCR libraries may be size selected and/or diluted d-fold and before ‘loaded’ in capture probes in the sequencing apparatus. We use the term ‘capture probe’ to refer to active sites on the surface of the sequencing chip, or the beads used in emulsion PCR-based technologies. These probes are responsible for generating a signal after a platform-specific signal amplification step; e.g. cluster generation in the Illumina platform or clonal amplification by emulsion PCR in the Ion Torrent workflow. If all the sequences from a single library were loaded onto probes and all probes generated a signal, then the depth of the sequence library would be constant and equal to K0. Allowing for random library depths, leads to additional variation in the total number of reads, represented by 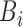 , in Figure 1. This simple model explicitly includes the major factors affecting the sequence counts of RNA-seq experiments: library construction and the associated ligase bias (3–5,7–8,22–23), PCR amplification, library sampling and depth variation. The focus of this paper is to derive quantitative relations for each of these factors and construct a framework for the statistical analysis of variation and remediation of bias in RNA sequencing data.
, in Figure 1. This simple model explicitly includes the major factors affecting the sequence counts of RNA-seq experiments: library construction and the associated ligase bias (3–5,7–8,22–23), PCR amplification, library sampling and depth variation. The focus of this paper is to derive quantitative relations for each of these factors and construct a framework for the statistical analysis of variation and remediation of bias in RNA sequencing data.
Figure 1.
Conceptual model of the steps in an HTS experiment. Each of the n small RNAs present in the original sample (Xi) is ligated with variable efficiency (fi) to generate an adapter ligated sequence (Λi). After reverse transcription, these sequences are PCR amplified, with potentially sequence-dependent efficiency (qi), over N cycles to generate amplified products (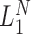 ). PCR products generate capture probes with probability si, after variable dilution. These probes are either immobilized on the clusters in flow-cells or are attached to beads. The abundance of probes that will eventually detect sequences of the ith small RNA kind (Bi) is determined by si, which in turn is determined by the dilution factor (d), the number of probes (K) that are available to capture small RNAs and the relative abundance of the ith species. Upon sequencing by synthesis, each probe may become active to generate a signal with probability r. This signal is converted to a sequence by the software of the experimental apparatus, so that the total number of counts from the ith small RNA species is Yi. The sequence generation probability pi is the probability that a given molecule existing in the PCR amplified library will generate a sequence entry in the output of the sequence. This probability encapsulates signal loss due to many factors, e.g. imperfect capture, signal generation and pre-analytic variability as described in the text.
). PCR products generate capture probes with probability si, after variable dilution. These probes are either immobilized on the clusters in flow-cells or are attached to beads. The abundance of probes that will eventually detect sequences of the ith small RNA kind (Bi) is determined by si, which in turn is determined by the dilution factor (d), the number of probes (K) that are available to capture small RNAs and the relative abundance of the ith species. Upon sequencing by synthesis, each probe may become active to generate a signal with probability r. This signal is converted to a sequence by the software of the experimental apparatus, so that the total number of counts from the ith small RNA species is Yi. The sequence generation probability pi is the probability that a given molecule existing in the PCR amplified library will generate a sequence entry in the output of the sequence. This probability encapsulates signal loss due to many factors, e.g. imperfect capture, signal generation and pre-analytic variability as described in the text.
Modeling the ligase reaction in the RNA-seq pipeline
The most crucial step in the RNA-seq pipeline is the ligation of adapters to create a library suitable for amplification and sequencing. The T4 bacteriophage ligase (24–29) used for this purpose, catalyzes the formation of 3΄-5΄ phosphodiester bonds between a 5΄ monophosphorylated RNA donor sequence and a 3΄ hydroxylated acceptor sequence. This approach for the 5΄ adapter ligation is modified in the case of the 3΄ ligation by using pre-adenylated 5΄ ends for the 3΄ adapters. Irrespective of whether the ligation of 5΄ and 3΄ adapters proceeds in two sequential steps (Illumina) or a single step (Ion Torrent), the variable efficiency of the ligase reaction of 5΄ and 3’ adapters, underlines the bias in RNA sequence experiments. Sequences that are not efficiently ligated will be under-represented in the sequence counts relative to sequences of equal abundance that are ligated more efficiently. Note that even though different sequence species have different ligation efficiencies, if the reactions were driven to completion this sequence-specific bias would disappear.
The overall variation in ligation efficiency over all the sequences present in any given sample will depend not only on the intrinsic affinity of the enzyme for any given sequence and the reaction velocity, but also on the presence of all other sequences competing for the enzyme and reaction cofactors. As we heuristically argue in the Supplement (section on Ligase reaction mechanism and kinetics), the complex, reversible three step (25,30–32) ligation reaction mechanism can be treated as a single step process by considering only the reactant limiting steps. The effects of multiple substrate inhibition may be taken into account by considering a large population of competitive substrates and the relatively poor affinity of the ligase for RNA sequences (reported to be in the micromolar range (30,33–38)). These two considerations and the law of large numbers dictate that the overall reaction efficiency will be effectively constant over the range of concentration of RNA sequences and independent of the presence of other competing RNA species. The quantitative argument for this assertion is made in Supplementary Methods, section on Multiple Substrate Inhibition and Ligation efficiency. We adopt the constancy and sample composition independence of ligation efficiency as working assumptions for our methodology of bias correction. These working assumptions anticipate that sequencing data from an equimolar mix of fixed composition may be used to estimate relative efficiencies that are universally applicable to all datasets created with the same protocol. Consequently, one can use these bias correction factors to adjust the abundance estimates, and thus reduce the bias in other datasets in which these sequences were present in variable amounts.
Modeling polymerase chain reaction (PCR) amplification of libraries
The accumulation of products during the PCR reaction may be stochastically modeled by a Galton-Watson (GW) branching process (39–43). This is a stochastic law that yields a distribution for the amplified ith product after  cycles of PCR (
cycles of PCR ( ) conditioned on the initial abundance; i.e. the output of the ligase-RT reaction
) conditioned on the initial abundance; i.e. the output of the ligase-RT reaction 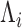 . Despite the analytical intractability of the GW distribution,
. Despite the analytical intractability of the GW distribution, 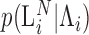 , the relationship between the mean and variance may be explicitly calculated. In particular, (Supplementary Methods—Mean and Variance Relationships in stochastic branching processes for PCR reactions and Supplementary Figure S1), the variance of PCR products at the N cycle (
, the relationship between the mean and variance may be explicitly calculated. In particular, (Supplementary Methods—Mean and Variance Relationships in stochastic branching processes for PCR reactions and Supplementary Figure S1), the variance of PCR products at the N cycle (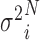 ) is nearly proportional to the square of the mean (
) is nearly proportional to the square of the mean (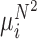 ) with the proportionality constant being a function of the initial abundance (
) with the proportionality constant being a function of the initial abundance (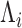 ) and the PCR efficiency (
) and the PCR efficiency (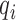 ):
):
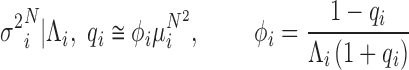 |
(1) |
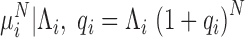 |
(2) |
Martingale arguments (43,44) can be invoked to show that approximations to the GW process do exist, since the latter ultimately converges to a random variable. However, these theoretical results, do not establish the parametric form of these approximations. Furthermore, this convergence is attained only in the limit of infinite PCR cycles, and it is not clear that one could find accurate approximations in the range of amplification rounds, typically used in RNA-seq experiments (between 10 and 16). In particular, stochastic fluctuations have led others to use normal (Gaussian) approximations only after 15–20 cycles of PCR amplification (40,45). Notwithstanding this literature, one cannot dismiss the possibility that other distributions may offer better approximations to the GW distribution relative to the Gaussian law. To explore this further, we used information theoretic criteria (Kullback-Leibler divergence) to calculate the distance (in bits) between the binned histograms from counts of a simulated GW process and a number of candidate distributional approximations (Table 1). In these distributions, the variance is either proportional to the mean or is related to the latter in a LQ fashion.
Table 1. Candidate distributions that approximate the PCR Galton–Watson process for finite reaction cycles.
| Mixing distribution | Parameterization | Probability density function | Mean | Variance | Mixed poisson model |
|---|---|---|---|---|---|
| Gaussian (Normal) |
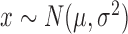
|
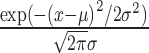
|
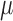
|
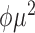
|
Poisson-Gaussian |
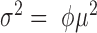
|
|||||
| Gamma |
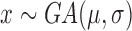
|
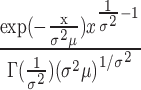
|
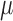
|
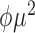
|
Negative Binomial I |
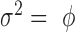
|
|||||
| Inverse Gaussian |
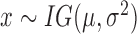
|
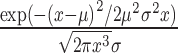
|
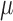
|
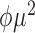
|
Poisson Inverse Gaussian (Sichel) |
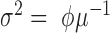
|
|||||
| Log-normal |
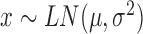
|
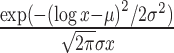
|
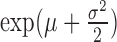
|
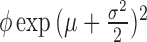
|
Poisson-log-normal |
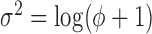
|
|||||
| Negative binomial I |
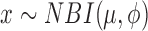
|
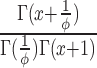
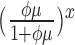
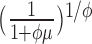
|
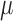
|
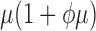
|
Poisson-negative binomial |
These analyses of our simulations are shown in Supplementary Figure S2A for various combinations of PCR efficiencies and initial abundances. Overall the Gaussian, provided the best approximation to the GW process than the other candidates, followed by the Gamma distribution. Of interest, the Negative Binomial, which implements a LQ rather than a proportional relationship between the square of mean and variance, provided a better approximation than the Inverse Gaussian and the Log-Normal distributions which obey the LQ relationship. A regression analysis showed that the higher overall performance of the Gaussian model could be attributed to its ability to approximate the GW for small initial abundances (not shown). Since the normal distribution may assume negative values in this range, we explored whether truncating this distribution in the positive numbers may yield an even better approximation than the normal. Truncating the normal distribution to the non-negative numbers, provided a better approximation to the GW process than the normal one for <1000 copies of starting material (Supplementary Figure S2B). For higher abundances and within the range of efficiencies considered in this work, the difference between the Gaussian distribution and its truncated version falls below the precision limits of floating point arithmetic and thus are indistinguishable as far as computer algorithms are concerned. Based on these investigations, we retained the (truncated) Gaussian with its variance constrained to be proportional to its mean and the Gamma distributions as models for the PCR amplification of adapter ligated RNA libraries.
Modeling library sampling and library depth variation during sequencing
Due to the finite number of RNA molecules in each library, the distribution of the counts, i.e. captured RNA numbers of the ith species is the multivariate hypergeometric distribution. As the typical library contain tens or hundreds of billions of molecules, while the library depth is usually in the millions range, library sampling appears to be essentially without replacement. Hence, the hypergeometric distribution, which corresponds to sampling from a population without replacement, should converge to the multinomial distribution, which corresponds to a sampling mechanism with replacement. The corresponding (capture) probabilities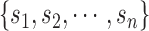 are given by the relative frequency of the amplified library products:
are given by the relative frequency of the amplified library products:
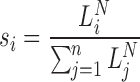 |
(3) |
The multinomial model for library sampling on the surface of the sequencing chip/cell, along with the assumption of a constant ligation efficiency yield a testable hypothesis about the relationship between the mean and variance of sequence counts (next section).
A testable linear quadratic law for the relationship between the variance and mean of counts in RNA-seq experiments
To derive the relation between the mean and the variance of the observed counts, we apply the laws of conditional expectation and variance. In all derivations, we assume we are working with a platform and experimental protocol, so that the theoretical library depth and the combined probability of signal generation/library depth variation are fixed quantities which may be conditioned on. Marginalizing the multinomial sampling model over all other RNA species except the ith one and conditioning on the observed library depth (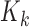 ) and the capture probability, yields a binomial probability model, e.g. see p-32 ref. (46):
) and the capture probability, yields a binomial probability model, e.g. see p-32 ref. (46):
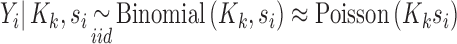 |
(4) |
The Poisson approximation to the binomial is justified when 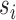 is small. This condition is verified for the vast majority of RNA species which individually account for only a small fraction of all total counts. Application of the laws of iterated expectation and expectation, allows us to relate the mean (
is small. This condition is verified for the vast majority of RNA species which individually account for only a small fraction of all total counts. Application of the laws of iterated expectation and expectation, allows us to relate the mean ( ) and the variance (
) and the variance (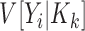 ) of the sequence counts, to the corresponding quantities of the sequence probabilities:
) of the sequence counts, to the corresponding quantities of the sequence probabilities:
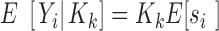 |
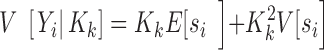 |
A Taylor series argument yields the variance of the sequence counts as a LQ function of the mean (see Appendix A. for the derivation).
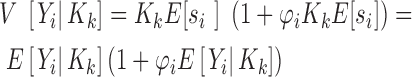 |
(5) |
In this equation, the factors 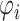 , capture the influences of the PCR reaction (reaction efficiency), the composition of the initial sample and the varying efficiency (bias) step in Figure 1, conditional on the inputs, i.e. the outputs of the previous step in the RNA-seq measurement. The LQ law and thus its underlying assumptions of multinomial sampling and constant ligation efficiency may be explicitly tested in datasets derived from synthetic RNA mixes of known composition. In these datasets, there is no biological variation and thus the relationship between the mean and variance of capture probabilities is determined solely be the effects of ligation and PCR efficiency.
, capture the influences of the PCR reaction (reaction efficiency), the composition of the initial sample and the varying efficiency (bias) step in Figure 1, conditional on the inputs, i.e. the outputs of the previous step in the RNA-seq measurement. The LQ law and thus its underlying assumptions of multinomial sampling and constant ligation efficiency may be explicitly tested in datasets derived from synthetic RNA mixes of known composition. In these datasets, there is no biological variation and thus the relationship between the mean and variance of capture probabilities is determined solely be the effects of ligation and PCR efficiency.
A multinomial law for library depth variation in RNA-seq experiments
Sampling of PCR amplified libraries during RNA sequencing exhibits variability and sequencing runs yield different total numbers of reads. This variation in sequencing depth may arise from a number of physical sources/processes: (i) pre-analytical variation in the library depth e.g. due to pooling of libraries, loading concentrations or due to quality control issues with the sequencing chips used to sequence libraries, and (ii) random failure of the signal (cluster generation in the Illumina platforms or emulsion PCR on the Ion Torrent beads) amplification from each capture probe.
We model pre-analytical variation in the k th library sequencing depth by a binomial probability law
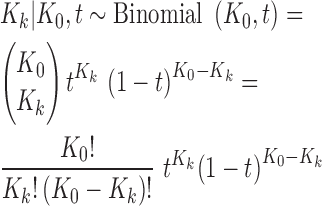 |
(6) |
with 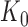 denoting the maximum (theoretical) library depth and the probability
denoting the maximum (theoretical) library depth and the probability 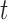 , representing the variation in sequencing depth.
, representing the variation in sequencing depth.
On the other hand, the post-capture failure gives rise to a ‘multi-hit’ model, in which library size is progressively decreased due to multiple modes of failure that operate consecutively and independently of each other. For example, not all active areas in the sequencing chip will capture a sequence (or a bead), while functional probe sites may fail to amplify properly leading to signals that fall below the detection limit of the sequencing apparatus. Such a multi-hit failure model may be statistically represented as a chain of conditionally independent binomial processes. In this model, the number of probes that could potentially fail by a given failure mechanism, is equal to the number of probes that have not failed by all other modes of failure up to that point. As we show in the Appendix to the Supplement (Section B), the statistical distribution describing this multi-hit model, is a binomial law. Therefore, the binomial distribution provides a statistical model for the total variation in library depth due to combined effects of all modes of post-capture failure. The parameters of this binomial distribution are the number of trials in the first node of the chain (e.g. the abundance of Bi probes that have captured the i th small RNA species) while the overall probability of success (r in Figure 1) is equal to the product of the probabilities of not failing from each ‘hit’.
The pre-analytical and post-analytical stages for library size variation may be combined to yield a composite model of library depth variation. This hierarchical multinomial model allows both sources of depth variation to operate in a given experiment:
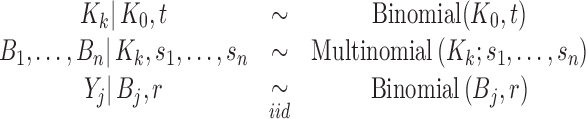 |
(7) |
The marginal distribution of the observed counts 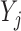 may be proven (see Appendix Section C in Supplement) to also be a multinomial distribution. This multinomial distribution is augmented to include one outcome in addition to the counts of the individual RNA species sequenced during the experiment. In particular, this extra outcome corresponds to the counts that were never observed due to library depth variation. In any given experiment, the number of occurrences of this outcome is equal to the number of ‘missing’ counts i.e., the difference between the theoretical (
may be proven (see Appendix Section C in Supplement) to also be a multinomial distribution. This multinomial distribution is augmented to include one outcome in addition to the counts of the individual RNA species sequenced during the experiment. In particular, this extra outcome corresponds to the counts that were never observed due to library depth variation. In any given experiment, the number of occurrences of this outcome is equal to the number of ‘missing’ counts i.e., the difference between the theoretical (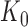 ) and the observed library size (
) and the observed library size (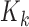 ). This augmented distribution is given by:
). This augmented distribution is given by:
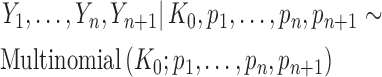 |
(8) |
with 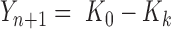 ,
, 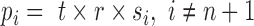 and
and 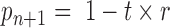 . As the probabilities
. As the probabilities 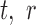 appear in these equations only through their product, we can absorb the former into the latter by redefining the signal generation probabilities in Figure 1 as
appear in these equations only through their product, we can absorb the former into the latter by redefining the signal generation probabilities in Figure 1 as 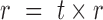 .
.
Mixed Poisson distributions for sequence counts in RNA-seq experiments
To derive a distribution of counts that is not conditioned on the library depth, we marginalize the latter variable (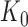 ) out of (Equation 8). It is well known that this marginal distribution is the product of independent Poisson random variables (see page 32 in (46)); the key parameter of each of these distributions is equal to
) out of (Equation 8). It is well known that this marginal distribution is the product of independent Poisson random variables (see page 32 in (46)); the key parameter of each of these distributions is equal to 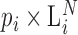 for all RNA species, with
for all RNA species, with 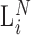 the total size of the PCR amplified products after the Nth PCR cycle. The parameter for the number of ‘missing counts’ is equal to the total size of the PCR amplified library,
the total size of the PCR amplified products after the Nth PCR cycle. The parameter for the number of ‘missing counts’ is equal to the total size of the PCR amplified library, 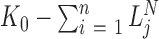 , multiplied by the probability
, multiplied by the probability 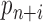 . Marginalizing the ‘product of independent Poisson's’ over the number of unobserved counts, yields the following statistical model for the observed counts:
. Marginalizing the ‘product of independent Poisson's’ over the number of unobserved counts, yields the following statistical model for the observed counts:
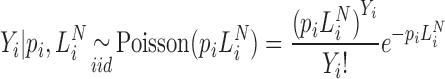 |
(9) |
This equation now defines an exact model for sequence counts that does not depend on the library size and is parameterized by the absolute abundances (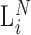 ). On the other hand, the corresponding model that conditions on library depth (Equation 4), is an approximate relation that depends on the capture probabilities. A statistical expression for the observed counts that conditions on the abundances of the various species after the ligation reaction (
). On the other hand, the corresponding model that conditions on library depth (Equation 4), is an approximate relation that depends on the capture probabilities. A statistical expression for the observed counts that conditions on the abundances of the various species after the ligation reaction (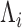 ) may be obtained by using (Equation 9) to marginalize the joint distribution of
) may be obtained by using (Equation 9) to marginalize the joint distribution of 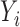 and
and 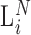 :
:
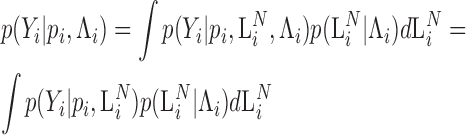 |
(10) |
Integration of this equation using any of the candidate approximate distributions for the GW process, 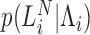 , listed in Table 1 yields a mixed Poisson model (see sections 8.3 and 11.1 of Johnson et al. (47) and the survey by Kalis and Xekalaki (48) for a thorough discussion of mixed Poisson models). Therefore, these distributions (last column in Table 1) define alternative models for analyzing RNA-seq data. In this work we focused on the (truncated) Gaussian model which provided the best approximation to the GW process and the corresponding mixed Poisson model (as determined by simulations).
, listed in Table 1 yields a mixed Poisson model (see sections 8.3 and 11.1 of Johnson et al. (47) and the survey by Kalis and Xekalaki (48) for a thorough discussion of mixed Poisson models). Therefore, these distributions (last column in Table 1) define alternative models for analyzing RNA-seq data. In this work we focused on the (truncated) Gaussian model which provided the best approximation to the GW process and the corresponding mixed Poisson model (as determined by simulations).
A re-interpretation of the Negative Binomial Model and introduction of the LQ normal family for RNA-seq data
As the truncated normal mixed Poisson model is a rather involved distribution to implement in software, we undertook a series of numerical investigations to find accurate approximations within the range of parameters that appear to be relevant for RNA-seq experiments. These investigations (detailed in Supplementary Methods: Numerical Approximation to the truncated Normal mixed Poisson distribution), show that either the NBI (as defined in Table 1) or the LQ Normal family defined as:
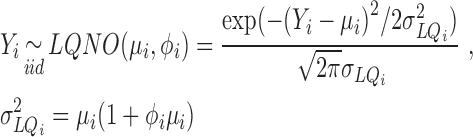 |
(11) |
can provide numerically accurate approximations (within 5–7 decimal digits, Supplementary Figure S3) to the probability mass function of the truncated normal mixed Poisson distribution (47,48). For all practical purposes, truncation of the mixed Poisson does not contribute substantially to the numerical accuracy of calculations involving the distribution of sequence counts, even if one starts with an initial abundance as low as three molecules. The attenuated impact of range truncation on the accuracy of approximation to the distribution of counts (i.e. less than three copies), compared to distribution of PCR products (<1000 copies) is due to the mixing operation in (Equation 10). The advantage of the truncated normal relative to its untruncated version and the Gamma, which lead to the LQNO and the NBI distributions respectively, is effectively lost for abundances <1000 copies because of integration. The NBI distribution appears to yield a numerically superior approximation for smaller signal generation probabilities, while the LQNO will also do so for higher values of this probability (Supplementary Figure S4) and higher mean values. When either distribution is used to analyze sequence data, it should be emphasized that the 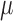 parameters are the means of the GW process in (Equation 2) multiplied by the signal generation probability (
parameters are the means of the GW process in (Equation 2) multiplied by the signal generation probability (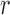 ), while the dispersion parameters are defined as in (Equation 1).
), while the dispersion parameters are defined as in (Equation 1).
Distributional regression frameworks for the analysis of RNA-seq data
Each RNA-seq profile implicitly defines simultaneous models for the mean and the standard deviation of sequence counts through either the NBI or the LQ Normal family. Stated in other terms, these are models for the ‘Location’ (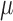 ,, i.e. the average) and the ‘Scale’ (
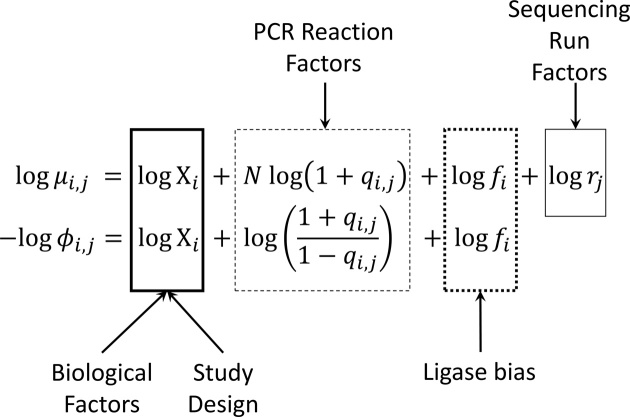
,, i.e. the average) and the ‘Scale’ (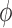 , the dispersion parameter which describes the variation around the average) of the underlying distributions. Both parameters may be directly related to study design, biological and technical factors that operate at the level of the ligase or PCR reaction and the sequencing run (Figure 2). On the logarithmic scale, both location and scale models assume a linear, additive form.
, the dispersion parameter which describes the variation around the average) of the underlying distributions. Both parameters may be directly related to study design, biological and technical factors that operate at the level of the ligase or PCR reaction and the sequencing run (Figure 2). On the logarithmic scale, both location and scale models assume a linear, additive form.
Figure 2.
Structure of regression models for RNA-seq data. Each RNA-seq profile implicitly defines two simultaneous models for the Location (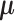 , mean sequence count) and a Scale (
, mean sequence count) and a Scale (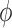 , the dispersion parameter). Each of these two sub-models assumes a modular additive structure in log-space (squares in the figure).
, the dispersion parameter). Each of these two sub-models assumes a modular additive structure in log-space (squares in the figure).
The composite, regression model for both location and scale parameters may be estimated with methods for GAMLSS (21,49). These distributional regression models allow the analyst to specify regression models for all parameters of a given underlying distribution, not just the mean. The distributional GAMLSS regression models for the sequence count of the ith RNA species from the jth sequencing dataset may be expressed as:
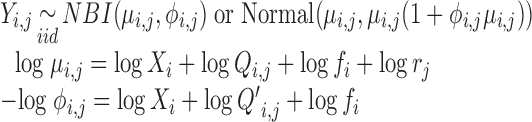 |
(12) |
The 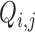 and
and 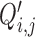 terms appearing in (Equation 12) correspond to the non-linear PCR efficiency functions appearing in Figure 2. An obligatory term for these regression models is the incorporation of run-specific effects to account for global factors that affect the average expression (and the variance) of the counts of all sequences identified in the same library. These factors capture the variation in library depth (the
terms appearing in (Equation 12) correspond to the non-linear PCR efficiency functions appearing in Figure 2. An obligatory term for these regression models is the incorporation of run-specific effects to account for global factors that affect the average expression (and the variance) of the counts of all sequences identified in the same library. These factors capture the variation in library depth (the 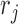 terms), but also the effects of sequence-dependent variations in PCR efficiency. In this work, we constrained parameters that admit a group interpretation (e.g. the
terms), but also the effects of sequence-dependent variations in PCR efficiency. In this work, we constrained parameters that admit a group interpretation (e.g. the 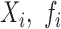 ), to conform to the normal distribution. This constraint allows for shrinkage estimation, a feature of almost all analytic approaches to RNA-seq data to date (16,20). Shrinkage analysis corresponds to the Gaussian random effects model which apriori constrain the estimates to be symmetrically distributed around their mean. Shrinkage estimation allows one to combine information among observations, to estimate parameters with limited number of samples. This is particularly important given the relative small number of observations (number of libraries in an experiment), relative to the number of parameters (expression values of distinct RNA species) that have to be estimated during the analysis of an RNA-seq dataset.
), to conform to the normal distribution. This constraint allows for shrinkage estimation, a feature of almost all analytic approaches to RNA-seq data to date (16,20). Shrinkage analysis corresponds to the Gaussian random effects model which apriori constrain the estimates to be symmetrically distributed around their mean. Shrinkage estimation allows one to combine information among observations, to estimate parameters with limited number of samples. This is particularly important given the relative small number of observations (number of libraries in an experiment), relative to the number of parameters (expression values of distinct RNA species) that have to be estimated during the analysis of an RNA-seq dataset.
The linear additive form (in log-space) of GAMLSS models such as (Equation 12) is not completely identifiable, unless additional, working assumptions are made. Non-identifiability concerns two different sets of parameters in (Equation 12): the PCR amplification factors 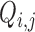 with the signal generation probabilities
with the signal generation probabilities 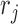 and the initial RNA amounts,
and the initial RNA amounts, 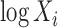 , with the ligase bias,
, with the ligase bias, 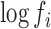 . Non-identifiability implies that one cannot learn the true value of certain parameters, even if one had access to an infinite number of observations (see p523 in (50) for a technical definition of statistical identifiability). Under our working assumption of
. Non-identifiability implies that one cannot learn the true value of certain parameters, even if one had access to an infinite number of observations (see p523 in (50) for a technical definition of statistical identifiability). Under our working assumption of 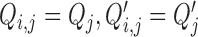 we can address the first source of non-identifiability by re-parameterization; i.e. setting
we can address the first source of non-identifiability by re-parameterization; i.e. setting 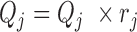 . We assume here that all RNAs sequenced in the same library are amplified with the same efficiency. This leads to an identifiable model, because the product of the two parameters (sum in log-space) is then uniquely identifiable from the data of a given run, as the average expression value of all RNAs sequenced in that library run.
. We assume here that all RNAs sequenced in the same library are amplified with the same efficiency. This leads to an identifiable model, because the product of the two parameters (sum in log-space) is then uniquely identifiable from the data of a given run, as the average expression value of all RNAs sequenced in that library run.
The lack of correspondence, or identifiability, between the RNA abundance and the ligase efficiency is a more serious issue because it cannot be addressed by either re-parameterization or even non-linear modeling. Due to the lack of identifiability, regression modeling based on (Equation 12) (or for that matter any of the existing approaches for the analysis of RNA-seq data), will be estimating the product (or sum in log space) of the initial abundance and the ligase efficiency for any given sequence. This intrinsic lack of identifiability can only be addressed through experimental protocol (e.g. devise a protocol that eliminates bias by driving the ligase reaction to completion for all RNAs) or by bringing additional data into the analyses as we discuss below.
Accounting for sequence-dependent ligase bias in RNA-seq datasets using equimolar mixes of RNAs
A critical application of the distributional GAMLSS regression model is the quantification of sequence-specific ligation biases by analyzing data obtained from equimolar mixes in which the specific sequence was present. In these equimolar mixes the 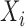 's are all equal (to a close approximation), and their common value may be set to any constant: e.g. to unity so that the logarithms are zero. In such a case, the regression model will be directly estimating the sequence-specific parameters,
's are all equal (to a close approximation), and their common value may be set to any constant: e.g. to unity so that the logarithms are zero. In such a case, the regression model will be directly estimating the sequence-specific parameters, 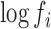 , corresponding to ligase bias. In random effects GAMLSS models, these empirical bias correction terms correspond to variations around an average expression in a sequencing run. Once these empirical bias correction terms have been estimated from a reference RNA dataset, they can be used to correct for the presence of sequence specific bias in other experiments. To do so, one has only to incorporate the values of the
, corresponding to ligase bias. In random effects GAMLSS models, these empirical bias correction terms correspond to variations around an average expression in a sequencing run. Once these empirical bias correction terms have been estimated from a reference RNA dataset, they can be used to correct for the presence of sequence specific bias in other experiments. To do so, one has only to incorporate the values of the 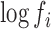 factors estimated from the equimolar mix as known quantities (‘offsets’) prior to fitting the GAMLSS model. By doing so, one forces the resulting regression to estimate the abundance of any given sequence as if the bias was not present. Such an approach statistically corrects for ligase efficiency and sequence dependent bias through an external calibration dataset. This is a direct extension of the idea of sequence dependent correction factors that were previously proposed for the raw sequence count data in RNA-seq (4). Thus, full correction leading to accurate quantitation is possible, but only if one has a reference RNA run with the same protocol so that the values of kinetic parameters in the model for ligase bias apply exactly.
factors estimated from the equimolar mix as known quantities (‘offsets’) prior to fitting the GAMLSS model. By doing so, one forces the resulting regression to estimate the abundance of any given sequence as if the bias was not present. Such an approach statistically corrects for ligase efficiency and sequence dependent bias through an external calibration dataset. This is a direct extension of the idea of sequence dependent correction factors that were previously proposed for the raw sequence count data in RNA-seq (4). Thus, full correction leading to accurate quantitation is possible, but only if one has a reference RNA run with the same protocol so that the values of kinetic parameters in the model for ligase bias apply exactly.
Distributional regression models for the analysis of differential expression
The extension of the proposed framework to the analysis of DE is straightforward. The two regression submodels in (Equation 12), are augmented to account for differences in the abundances between experimental conditions. In this model, the mean parameter of the ith sequence, from the jth experiment in the kth experimental condition, may be written as a function of the fold expression change of that sequence (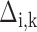 ) in that state relative to the (log-)expression against the referent state (
) in that state relative to the (log-)expression against the referent state (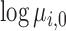 ):
):
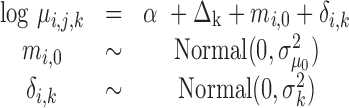 |
(13) |
This is a flexible approach that can readily accommodate global differential changes in expression level (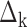 ) that shift the expression level of every sequence by the same amount, while allowing sequence-specific variations (
) that shift the expression level of every sequence by the same amount, while allowing sequence-specific variations (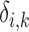 ) around this pattern by random effects modeling. In this model, the intercept term,
) around this pattern by random effects modeling. In this model, the intercept term, 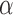 , stands for the mean of the counts in the referent group. Sequence-specific variation in the observed counts of the referent group around the mean is captured by the
, stands for the mean of the counts in the referent group. Sequence-specific variation in the observed counts of the referent group around the mean is captured by the 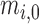 terms. This formulation makes two implicit assumptions, i.e. that the ligase bias is not of primary interest in DE analysis, while technical variation in PCR efficiency and sequence generation probabilities is of substantially smaller magnitude than other sources of variation in expression counts (e.g. ligase bias or even biological variability). The first assumption allows us to absorb the ligase bias factors,
terms. This formulation makes two implicit assumptions, i.e. that the ligase bias is not of primary interest in DE analysis, while technical variation in PCR efficiency and sequence generation probabilities is of substantially smaller magnitude than other sources of variation in expression counts (e.g. ligase bias or even biological variability). The first assumption allows us to absorb the ligase bias factors, 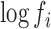 , into the
, into the 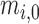 , facilitating the calculation of DE (fold-changes) even for sequences for which these factors are not available from equimolar calibration runs. The second assumption leads to the absorption of an experiment wide factor (the Q in (Equation 12)) into the intercept term. The parameters of (Equation 13) are directly related to those in (Equation 12) and in fact may be derived from them after a suitable re-parameterization as detailed in the Supplement (Section on distributional regression models for the analysis of differential expression). An equivalent expression may be recovered, mutatis mutandis for the sub-model of the
, facilitating the calculation of DE (fold-changes) even for sequences for which these factors are not available from equimolar calibration runs. The second assumption leads to the absorption of an experiment wide factor (the Q in (Equation 12)) into the intercept term. The parameters of (Equation 13) are directly related to those in (Equation 12) and in fact may be derived from them after a suitable re-parameterization as detailed in the Supplement (Section on distributional regression models for the analysis of differential expression). An equivalent expression may be recovered, mutatis mutandis for the sub-model of the 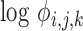 parameter. The use of the logarithmic link simultaneously satisfies the constraints of positivity of sequence counts and their variance, while ensuring compatibility with existing approaches for DE analysis, which also model the relative log-expression. The GAMLSS model comprised of the two sub-models for
parameter. The use of the logarithmic link simultaneously satisfies the constraints of positivity of sequence counts and their variance, while ensuring compatibility with existing approaches for DE analysis, which also model the relative log-expression. The GAMLSS model comprised of the two sub-models for 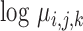
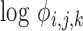 parameters of either the NBI or the LQNO distribution is the cornerstone of our approach to DE analysis. Our model, fits all relevant parameters jointly. As we detail in the ‘Software’ section, model estimation may be accomplished using available software and from different statistical perspectives.
parameters of either the NBI or the LQNO distribution is the cornerstone of our approach to DE analysis. Our model, fits all relevant parameters jointly. As we detail in the ‘Software’ section, model estimation may be accomplished using available software and from different statistical perspectives.
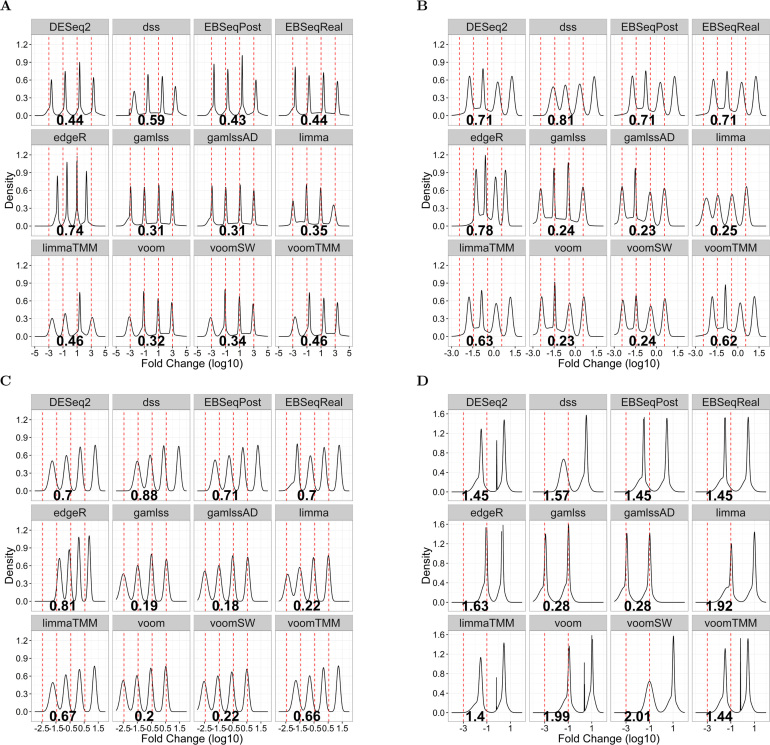
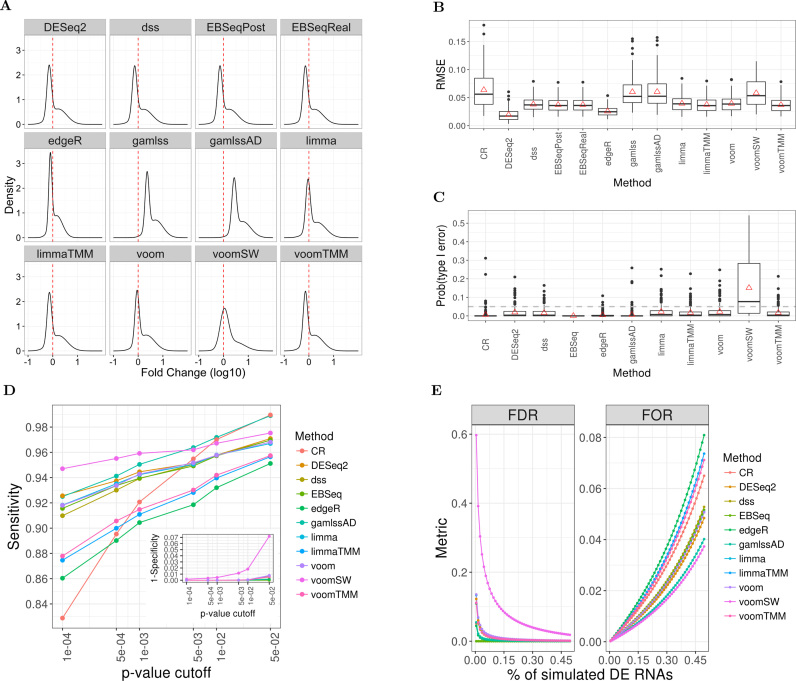
Our approach to DE analysis was compared with six popular algorithms for the analysis of RNA-seq data (DESeq2 (20), edgeR (15,51), EBSeq (52), DSS (10), limma (53) and voom (19)). Similar to our approach, these methods rely on shrinkage and random effects modeling to estimate DE. They also make specific assumptions about the underlying distribution based on either the Negative Binomial or the normal laws. However, they differ from ours with respect to the interpretation of parameters and numerical estimation procedures. We also considered a recently introduced method of DE based on the cubic root (CR) transformation of the raw counts to normality, followed by the t-test (54). Similar to our method, the CR approach works on a (transformed) scale of absolute counts, rather than modeling counts as fractions of the observed library depth. However, the CR method makes a different distributional assumption for the counts, i.e. it assumes they follow a gamma distribution rather than the NBI or the LQNO family we use. Furthermore, it analyzes each short RNA species in isolation, rather than considering the totality of the expression profile via shrinkage estimation. We used our datasets of known composition to compare the algorithms under the following scenarios of DE: (i) clustered symmetric DE (fraction of overexpressed sequences equal to that of underexpressed) without a change in the global expression (one scenario) (ii) clustered asymmetric DE, in which the aggregate DE changes directionally, thus shifting global expression compared to the referent state (three scenarios) (iii) DE in which all RNAs exhibit a variable but consistent directional change in expression (one scenario) (iv) no differential DE at the group level but with variable expression levels in the experiments within each group. The last scenario is composed of a bootstrap of 200 comparisons from the equimolar validation datasets. In each of these comparisons, we employed a stratified re-sampling strategy to ensure that the two artificial groups compared, include an equal number (n = 4) from each of the four equimolar series. In this scenario, there was no overall, inter-group difference in the expression of each of the 286 miRNAs, despite the large intra-group difference (spanning three orders of magnitude) in expression of the sequence counts analyzed.
Datasets
As we are concerned here with the derivation of the simplest statistical model that recapitulates technical sources of variation in RNA-seq experiments, we analyzed data from synthetic RNA samples of known composition. The known composition of these samples provides a ‘ground truth’, within the limits of accuracy of mixing RNA oligonucleotides, against which to assess model predictions. We considered two public datasets of microRNA (miRNA) equimolar mixes from the studies of Hafner et al. (3) and Fuchs et al. (7) and the sequencing experiments utilizing synthetic 21-mer oligos by Sorefan et al. (8). These datasets, totaling 52 sequencing runs of 18 distinct combinations of ligation reaction settings, adapter sequences and sequencing platforms have clarified important quantitative points about the nature of sequence-dependent ligase bias. Consequently, our re-analysis provides an opportunity to quantify bias with the methodologies developed here and provides a benchmark for bias reduction. We supplement these datasets by our own sequencing data of synthetic small RNA mixes based on a protocol that randomizes the sequence of the four nucleotides adjacent to the ligation junction (4N protocol—detailed in Supplementary Methods). These comprise 32 legacy experiments with different amounts of starting material, ranging from 0.1 or 10 fmole, from the same 962 (miRXplore; Miltenyi Biotec) mix used in the report by Fuchs et al. (7). These publicly available and legacy internal development datasets cover a wide range of library protocols and sequencing apparatus. We used these diverse datasets to test predictions about the relationship between mean and variance of sequence counts and to undertake an initial exploration of the performance of the bias correction factors over a limited range of input RNA concentrations. To verify the performance of bias correction factors and the transferability of these factors across datasets of variable total input (over four orders of magnitude) and composition we designed a custom validation dataset with the 4N protocol. For these experiments, RNA inputs were pools of 962 (miRXplore) or 286 custom synthetic RNA oligos (from IDT). These two pools share 197 miRNAs affording us the opportunity of comparing the magnitude of bias reduction when an equimolar mix of different composition than the target sample is used to estimate correction factors (e.g. bias correction in the 286 pool when correction factors are based on the miRXplore and vice versa). The availability of these two pools enables the comparison of expression values for miRNAs that were common to both pools against those that were present in only one of them. This comparison not only served as an internal control of bias correction, but also allowed us to assess the practical implications of incorporating bias correction factors for only a subset of RNAs, i.e. those that have been included in the reference sample. The known composition of the validation libraries, also enabled us to assess the potential of different approaches to generate unbiased measures of DE and their intrinsic FDR (false positives) and FOR (false negative). Each library was prepared using between 0.1 femtomole and 100 femtomoles of total RNA input. Pools were either equimolar or ratiometric mixes as indicated in Supplementary Table S1, yielding a total of 58 sequencing experiments in 7 groups. Libraries construction was done in three batches and the identity of the samples (miRXplore versus 286 and ratiometric versus equimolar) were randomly allocated to each batch so as to ensure that drift in laboratory practice or equipment performance did not bias the data. All 58 libraries were sequenced together. We also assessed the sensitivity of our method for DE analysis to sequencing noise, by resequencing all libraries a second time.
Statistical and numerical analyses
We undertook stochastic and numerical simulations to clarify points that were not amenable to analytical arguments, e.g. the approximation of the distributions of PCR amplified libraries and the distribution of RNA-seq count data by more tractable distributions. We provide the details of these simulations in the Supplementary Methods. We used the means and standard deviations in reporting raw data, while regression model estimates are reported together with each associated 95% confidence intervals. We adopted a Bayesian approach to calculate the Kullback-Leibler distance in bits between the exact (simulated GW process) and the approximate PCR models. This approach takes a flexible, Dirichlet prior on the expected counts in the binned histograms for each distribution prior to calculating the distance (55). Binning was necessary for the comparison of samples from unbounded distributions that are discrete (NBI) or continuous (Gaussian, Log-normal, Gamma) against the discrete, bounded GW process which has a finite range. We assumed a moderate number of bins (50) over the range of values compatible with the GW model for a given efficiency, number of cycles and initial PCR abundance; i.e. 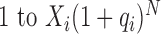 .
.
We applied Monte Carlo Cross Validation (56,57) to assess the effects of bias correction in the publicly available and legacy datasets. In this procedure, we replicated 200 analyses workflows, in which two-thirds of each of these experiments were used for development, while a third were held back for validation. The values of the factors were estimated in the development subset and were used to correct the validation subset. We used empirical measures of variance (58,59) for the assessment of the effects of bias correction using the methods proposed in this paper. The Root Mean Square Error (RMSE), i.e. the square root of the mean squared difference of estimated expression values from their true (expected) value, quantifies the variability of ligase bias for RNAs of known abundance. In the equimolar experiments, analyzed under a shrinkage model that references all expression value to the mean, the true expression value is zero. For the ratiometric series, we used the group average of all RNAs with the same concentration as a proxy of the true expression value. For both equimolar and ratiometric experiments, the RMSE coincides with the sample standard deviation of the squared residuals. For the RMSE calculation, we used the GAMLSS estimates derived from models that incorporated bias correction and compared them against those of models that did not incorporate these terms. Statistical comparison between the RMSE was undertaken via means of non-parametric tests for the equality of these standard deviations (60): the Fligner-Killeen (FK) statistic that tests for equality and the Ansari-Bradley (AB) procedure for testing the hypothesis that the variability of expression values corrected for bias is smaller than that of the uncorrected values. As the RMSE may not be robust in the presence of outliers, we also calculated alternative measures of variability (58) of expression values corrected for bias: the Mean Absolute Deviation (MAD) and the Mean Absolute Deviation from the Sample Median. As a final assessment of bias correction, we constructed empirical, cumulative distribution functions (ECDF) from either bias-corrected or uncorrected values. We compared the ECDF curves for equality using the non-parametric Kolmogorov Smirnov (KS) test. Furthermore, we used the ECDF to compute the probability of observing expression values within 2-fold of the mean (P2F) and the range of values in which 95 and 99% of expression values are expected to lie. These metrics provide a quantitative measure of the order of magnitude of bias reduction afforded by correction factors.
Comparison of bias correction factors estimated from different equimolar samples, or estimates of RNA expression corrected by different reference samples (e.g. correcting the miRXplore via the 286 and vice versa) was undertaken via ‘errors-in-variables’, measurement-error least squares models (61,62). In this statistical procedure, both the ordinate and the abscissa are assumed to be approximately known (“measured with error”) and the best line fit is obtained by estimating the relevant error terms and the correlation between the two quantities.
The RMSE was used to assess the bias of model estimates in the scenarios of DE we considered. Each of these scenarios implies the presence of one to four clusters of differentially expressed short RNAs, with fold-changes spanning between less than one and up to six orders of magnitude. We used unsupervised, model-based clustering techniques (Gaussian mixture models (63)) to visualize the potential of competing methodologies to resolve these clusters. We assessed the Type I and Type 2 error by analyzing P-values of the Wald test generated by each of the competing methodologies in sequencing experiments involving the 286 pool. In these analyses, the outcome was a P-value <0.05 and the estimated proportion of rejecting tests (datasets without DE expression) and non-rejecting tests (datasets with DE expression) was taken as a measure of Type I and Type II error respectively. We applied generalized logistic regression to account for dependencies among statistical tests involving the same datasets. We used these estimates to assess the FDR and FOR implied by the Type I and Type II error in future applications, over a range of probability of truly differentially expressed RNAs and different p-values thresholds of significance by bootstrapping these regression models.
Software
We used the multi-threaded 64-bit Microsoft R Open 3.2.3–3.3.1 for the simulations of the GW PCR process and the fitting of the GAMLSS models described in the text. Calculation of information theoretic measures of distance between the simulated and the approximate PCR models was carried out with the package entropy (64) (v. 1.2-1). Errors-in-variable regression was carried out via the R-package leiv (v. 2.0-7) that implements a Bayesian approach for this problem (65). Flexible parametric, data-driven smoothing of mean-variance scatterplots were performed with the package mgcv (66) (v. 1.8-10). Gaussian mixture modeling was undertaken with the package mclust, v5.2 (63,67).
We provide two implementations of the statistical methodologies, a native R, reference implementation that can be used with the gamlss (49) package and a much faster hybrid C++/R version for the package TMB (68). The former version, takes advantage of the Cole-Green, CG, (69) and Rigby-Stasinopoulos, RS, (21) algorithms to maximize the penalized log-likelihood implied by the regression models for ligase bias estimation (Equation 12) and DE analysis (Equation 13). These are iterative algorithms that maximize the likelihood either jointly (CG) or by alternating between the two submodels (RS) until convergence. The reference implementation is based on a mature approach to distributional regression which supports a wide variety of linear and even non-linear regression models (such as neural networks) but suffers from a major drawback: accurate calculation of standard errors of model estimates, as required for calculation of P-values for DE is extremely slow. The computational bottleneck is rather severe (e.g. the algorithm did not finish even after 15 h of execution on a high end overclocked processor running a multi-threaded version of R). Even though one can obtain approximate answers from this implementation very quickly (a few seconds), the levels of Type I error high FDRs are unclear for these approximations. We therefore, re-implemented the models implied by (Equation 12) and (Equation 13) in C++ and interfaced them with the TMB package. The latter uses the Laplace approximation to integrate the random effects in (Equation 12) and (Equation 13) out of the penalized log-likelihood; algorithmic differentiation (AD) of the C++ source code is used for the fast, accurate calculation of the high-dimensional Hessian function (the second-order partial derivative of the log-likelihood with respect to model parameters) as required to obtain the standard errors and P-values. The estimates produced by the TMB implementation (gamlssAD) are numerically nearly identical to the those produced by the gamlss reference implementation despite the difference in estimation algorithms.
RESULTS
The LQ mean and variance relationship in small RNA-seq datasets
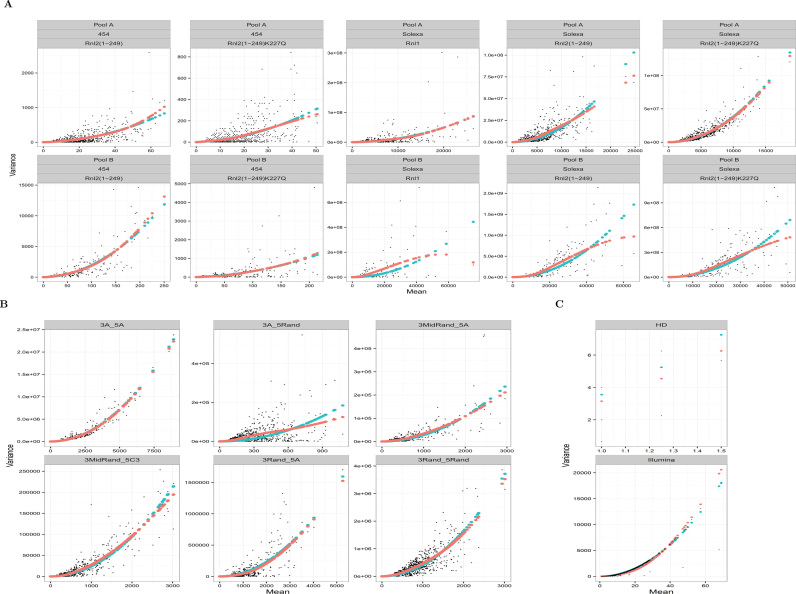
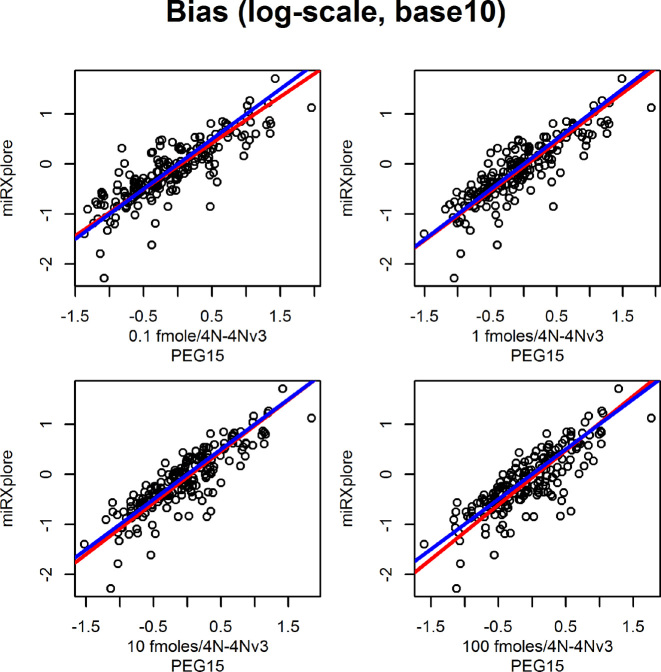
We examined the mean and variance relationship in sequencing experiments involving synthetic oligonucleotide mixes of defined (equimolar) composition. When such mixtures are sequenced and analyzed, the observed count variation is entirely due to technical factors, providing thus an opportunity to empirically validate the LQ relation. The LQ curve implied by (Equation 5) is superimposable (Figure 3) to the curves predicted by smoothing regression models (70,71). The latter, smooth the mean-variance scatterplots in a data-driven fashion without assuming a particular, parametric form for this relationship. There is substantial visual agreement between the model based LQ estimate and the data-driven spline estimates. This agreement was also noted in our internal legacy datasets (Supplementary Figure S5). The degree of agreement is remarkable when one considers the difference in the degrees of freedom of the LQ (one) and the penalized spline fits (estimated as ∼3 by the smoothing process). These analyses strongly support our argument for a LQ relationship between mean and variance of counts, and are compatible with our model of constant ligation efficiency and multinomial sampling of amplified libraries.
Figure 3.
Modeling of mean—variance relationship in 18 different RNA-seq experimental combinations (total of 52 RNA-seq libraries) involving different ligase enzymes, adapter sequences and measurement platforms from three different published series. Blue curve: linear—quadratic fit, Red curve: smoothing regression model fit. These parametric curves are superimposed to flexible smoothing splines that were fit to the same data with smoothing regression models (red). Data from: Hafner et al. (3) (A), Fuchs et al. (7) (B) and Sorefan et al. (8) (C). Refer to the original publications for the abbreviations used in subplots.
GAMLSS and sequence-dependent, ligase bias
Analysis and correction of (sequence-dependent) ligase bias in development datasets
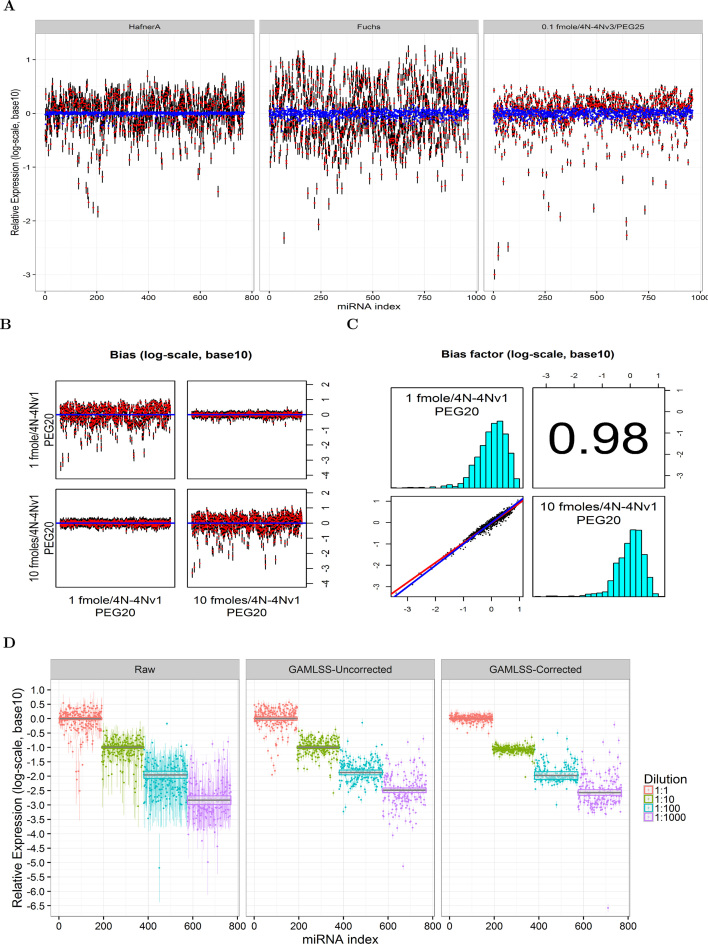
There was considerable bias in the publicly available equimolar datasets of Hafner et al. (3), Fuchs (7) and our legacy, 4N protocol datasets (Figure 4). GAMLSS estimates of abundance (relative to the mean) that were not corrected for bias, were variable and spanned more than three orders of magnitude; this is shown in Figure 4A which graphs the model estimates (red dots) and the associated 95% confidence intervals. Monte Carlo Cross Validation (MCCV) bias corrected values (blue dots) were much more tightly clustered around their expected value of zero, than the uncorrected ones. As shown in Table 2, bias correction reduced variability by more than 81.5% (RMSE) or 73.4% (MAD). Simultaneously, the percentage of miRNAs with expression that varied up to 2-fold from the mean, was increased to more than 99.8%. Furthermore, the range of expression values spanned by 95 and 99% of the short RNAs in these experiments was reduced by more than 1 and up to 2.2 orders of magnitude respectively (Table 2). These quantitatively significant reductions in bias were also highly statistically significant (p-values for the FK, AB and KS statistics were computed as <10−308).
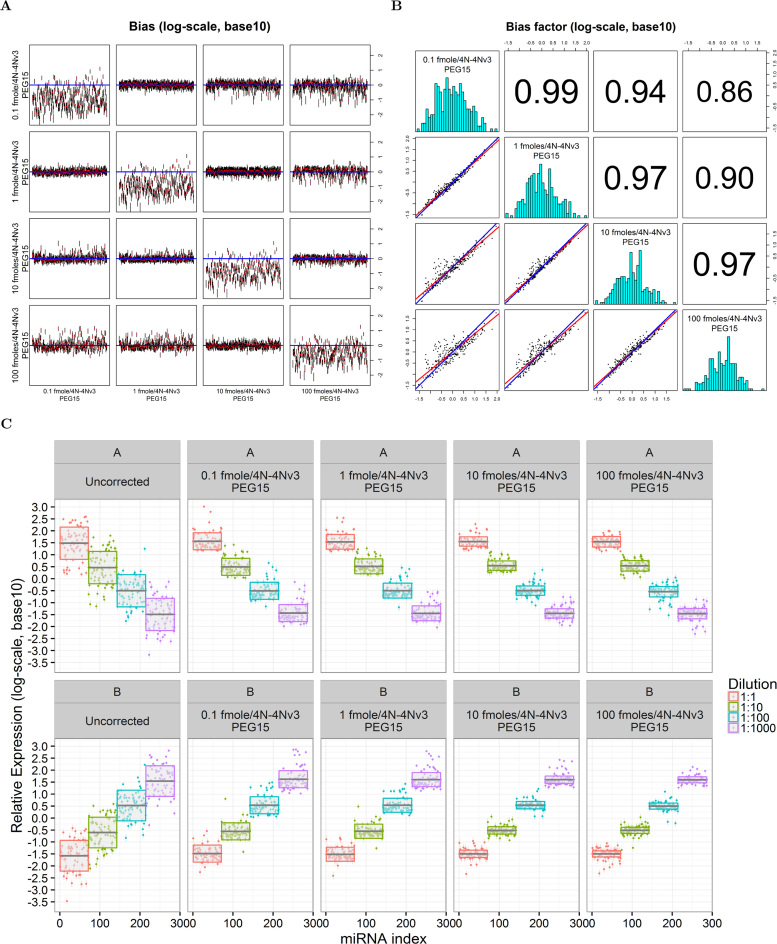
Figure 4.
Effects of bias correction in the publicly available and internal-legacy datasets. (A) GAMLSS estimates for the log expected abundance of each miRNA (red dot) ± prediction standard error (black lines) in the equimolar Hafner (pool A), Fuchs (miRXplore 962 pool) and one of our legacy miRXplore 4N runs. (blue dots—estimated in 200 samples of Monte Carlo Cross-Validation). (B) Effects of bias correction over a 10-fold range of initial abundance in the miRXplore pool. Correction of the 1 fmole run with the bias factors from the 10 fmole one (upper right) and vice versa (bottom left). Uncorrected runs are shown in the top left and bottom right for the 1 fmole and 10 fmoles runs respectively. (C) Histograms (diagonal plots), correlation coefficient (top right) and linear errors-in-variables regression (bottom left) between the correction factors estimated in (B). (D) Effects of bias correction in the ratiometric (Pool B) dataset reported by Hafner et al. (3). Bias correction factors were derived from the equimolar run (Pool A) in the same publication. The figure shows the means and prediction standard deviations of the raw counts (in log 10 space), followed by the GAMLSS estimates without application of a sequence-specific bias correction term (second panel). The third panel shows the effects of bias correction. The solid black line and gray band indicate the average expression and the associated 95% interval calculated by a fixed effects meta-analysis for the group mean.
Table 2. Effects of bias correction in publicly available and legacy 4N development datasets.
| RMSE | MAE | MAD | Prob(2-fold) | 95% Range | 99% Range | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | Correction factor dataset | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. |
| Hafner A | HafnerA† | 0.034 | 0.331 | 0.019 | 0.245 | 0.021 | 0.297 | 1.000 | 0.717 | 0.105 | 1.293 | 0.261 | 2.036 |
| Fuchs | Fuchs† | 0.066 | 0.507 | 0.051 | 0.412 | 0.061 | 0.537 | 0.998 | 0.420 | 0.256 | 1.830 | 0.351 | 2.482 |
| 0.1 fmole/4N-4Nv3/PEG25 | 0.1 fmole/4N-4Nv3/PEG25† | 0.066 | 0.356 | 0.051 | 0.222 | 0.061 | 0.230 | 0.998 | 0.793 | 0.256 | 1.225 | 0.351 | 2.542 |
| 1 fmole/4N-4Nv1/PEG20 | 10 fmoles/4N-4Nv1/PEG20 | 0.098 | 0.558 | 0.069 | 0.418 | 0.077 | 0.524 | 0.989 | 0.423 | 0.405 | 2.136 | 0.643 | 3.570 |
| 10 fmoles/4N-4Nv1/PEG20 | 1 fmole/4N-4Nv1/PEG20 | 0.121 | 0.521 | 0.097 | 0.379 | 0.129 | 0.455 | 0.985 | 0.491 | 0.449 | 1.985 | 0.612 | 3.323 |
| Hafner B | Hafner A | ||||||||||||
| Subpool 1 | 0.113 | 0.412 | 0.081 | 0.292 | 0.092 | 0.333 | 0.979 | 0.646 | 0.451 | 1.649 | 0.689 | 2.334 | |
| Subpool 2 | 0.131 | 0.316 | 0.089 | 0.240 | 0.120 | 0.296 | 0.973 | 0.713 | 0.392 | 1.174 | 0.811 | 1.667 | |
| Subpool 3 | 1.121 | 0.653 | 0.296 | 0.342 | 0.189 | 0.421 | 0.774 | 0.585 | 1.233 | 1.509 | 2.721 | 2.636 | |
| Subpool 4 | 0.762 | 0.603 | 0.464 | 0.450 | 0.530 | 0.791 | 0.405 | 0.441 | 1.957 | 2.296 | 5.909 | 3.278 | |
The column ‘Corr.’ gives the metric for the corrected estimate for each series (column ‘Dataset’) using the correction factor from the series listed under the column ‘Correction factor dataset’. Column ‘Uncor.’ tabulates the uncorrected estimate for each dataset. P-values for the Flinger-Killeen, Ansari and Kolmogorov Smirnov tests for the comparison of variability reduction were all <0.001 with the exception of subpool 4, where values of 0.56, 0.68 and 0.081 were obtained † Correction factors in these datasets were derived by Monte Carlo Cross Validation (MCCV).
We noted similar reductions in bias in our legacy equimolar 4N datasets. These experiments, shown in Figure 4B, demonstrate that bias correction factors may be applied to datasets in which the total RNA input varies by an order of magnitude from the RNA input of the experiment one would like to correct. When the correction factors from the two legacy 4N datasets were examined, it was noted that they were not only highly correlated (Pearson correlation coefficient of 0.98), but they were nearly identical in magnitude (Figure 4C). Similar to the MCCV experiments, the empirical factors resulted in bias correction that exceeded 72%, a proportion of short RNAs that differed up to 2-fold from their mean that was greater than 98% and reduction of the 95 and 99% range of values of more than 1.5 and two orders of magnitude respectively (Table 2).
To assess the performance of empirical bias correction over four orders of magnitude we applied the correction factors from the Hafner A pool to the ratiometric Hafner B pool, in which the miRNAs were mixed in different ratios prior to sequencing. Application of bias correction factors, appear to result in reductions in bias over two (and possibly three) orders of magnitude of initial RNA abundance (Figure 4D). Quantitative analyses of the same data, (Table 2), demonstrated that these initial impressions held across the range of metrics used to assess bias reduction for the two lower dilutions, and for the third higher dilution when robust measures (such as the MAE and MAD) were considered. On other hand, no appreciable reduction in bias was effected for the RNA molecules that were present in the lowest initial amount (higher dilution) in the sample. This was verified statistically by the results of the FK, AB and KS tests (Table 2).
This bias reduction may have implications for downstream analysis: when we analyzed the means and standard errors of the relative expression changes from the miRNAs in each dilution group with a meta-analysis model, we obtained tighter confidence intervals as we shifted from raw sequence counts to model estimates and bias corrected ones (Figure 4D). This indicates that one may use the GAMLSS approach and bias correction factors to gain precision in discerning (group) level differences in expression of small RNAs. Application of bias correction factors, also allow one to recover the underlying expression profile, comprised of four well separated peaks (Supplemental Figure S6A) relative to the raw, uncorrected data or gamlss model estimates without bias correction.
In summary, the analyses of the public and legacy 4N development RNA-seq datasets, demonstrate that empirical correction factors may reduce bias by more than 70% for RNAs with expression levels that are up to two (and possibly three) orders of magnitude less than the most abundant RNAs in the sample. Furthermore, the values of correction factors appear to be constant over one order of magnitude of difference in the RNA input between the equimolar datasets used to estimate them and the equimolar dataset they are applied to.
Analysis and correction of (sequence-dependent) ligase bias in validation datasets
In the validation (4N) dataset, empirical correction factors considerably decreased bias in equimolar experiments over four orders of magnitude of RNA input (Figure 5A). Bias reduction (assessed by any of the metrics) was highest when the dataset used for the calculation factors, differed up to an order of magnitude for the dataset that was corrected (Supplementary Table S2). In particular, RMSE was reduced from 77–90% in these equimolar analysis scenarios. Even when the RNA input in the correction dataset differed from the dataset to be corrected by three orders of magnitude, the percentage reduction in the RMSE was between 54% (correction of the 100 fmoles dataset by the 0.1 fmole) and 67% (correction of the 0.1 fmole dataset by the correction factors estimated from the 100 fmoles dataset). The predicted concentration independence and near constancy, of the bias correction factors were also verified in the validation 4N dataset over four orders of magnitude of RNA input (Figure 5B). Nevertheless, correlation between correction factors estimated from two equimolar series was highest when these differed by no more than one order of magnitude. Correlation was lowest (but still substantial) between correction factors estimated from runs with RNA input that varied over three orders of magnitude (e.g. it was 0.86 between the 0.1 and 100 fmoles groups). There was high numerical agreement between the correction factors estimated in these four series. In particular, correction factors from runs with RNA input that varied over one order of magnitude (first graph in second row, second graph in third row and third graph in fourth row) are nearly identical: the regression line (red) is superimposable to the blue one that has an intercept of zero and a slope of one.
Figure 5.
Effects of bias correction in the 4N miRNA validation dataset (286 pool). (A) Bias (red dot) and 95% prediction confidence intervals of GAMLSS estimates for the uncorrected equimolar series (shown in the diagonal line from top left to bottom right). The remaining graphs are arranged so that the dataset identified by the y label is corrected using the bias correction factors identified by the x axis label. The blue line in each graph is the expected expression level. (B) Histograms (diagonal plots), correlation coefficients (graphs above the diagonal right) and linear errors-in-variables regression (graphs below the diagonal) between the correction factors estimated in (A). (C) Effects of bias correction in the ratio-metric 4N experiments (total RNA input of 100 fmoles): A (descending) and B (ascending) concentration. Each row shows the effects of no-correction as well as correction with the factors estimated from the four equimolar 286 datasets with input ranging from 0.1 to 100 fmoles. The solid black line and gray band indicate the average expression and the associated 95% interval calculated by a fixed effects meta-analysis for the group mean.
The performance of correction factors in the ratiometric series which emulates a scenario of variable expression of short RNAs is shown in Figure 5C. Application of these factors resulted visually in reduction of bias and tight clustering of miRNAs around their group average, and clear separation of the expression profile into four well demarcated peaks (Supplementary Figure S6B). Table 3 summarizes the quantitative analysis of bias reduction for these series. The RMSE was reduced by 56 ± 11.5%, the MAE by 59.9 ± 11.2% and the MAD by 68.8 ± 9.3% over the different combination of correction factors, groups and series. The proportion of miRNAs with an expression level that was within 2-fold of their group mean increased from 34.3 ± 6.3% to 80.4 ± 8.5%. The 95 and 99% range were reduced by 52.9 ± 12.7% and 51.5 ± 11.2% respectively.
Table 3. Effects of bias correction in the ratiometric 4N validation datasets (A: descending concentration, B: ascending concentration).
| Group | Dilution in A | Dilution in B | Correction factor dataset | RMSE | MAE | MAD | Prob(2-fold) | 95% Range | 99% Range | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | A | B | A | B | A | B | A | B | A | B | ||||
| A | 1:1 | 1:1000 | Uncorrected | 0.635 | 0.626 | 0.506 | 0.491 | 0.517 | 0.634 | 0.408 | 0.380 | 2.272 | 2.236 | 2.394 | 2.785 |
| A | 1:1 | 1:1000 | 0.1 fmole | 0.356 | 0.298 | 0.262 | 0.217 | 0.215 | 0.237 | 0.690 | 0.789 | 1.278 | 1.203 | 1.763 | 1.580 |
| A | 1:1 | 1:1000 | 1 fmole | 0.311 | 0.247 | 0.241 | 0.182 | 0.254 | 0.191 | 0.718 | 0.873 | 1.221 | 0.948 | 1.387 | 1.406 |
| A | 1:1 | 1:1000 | 10 fmoles | 0.231 | 0.211 | 0.176 | 0.147 | 0.217 | 0.158 | 0.803 | 0.887 | 0.840 | 0.916 | 1.020 | 1.224 |
| A | 1:1 | 1:1000 | 100 fmoles | 0.195 | 0.226 | 0.155 | 0.167 | 0.171 | 0.163 | 0.873 | 0.859 | 0.789 | 0.913 | 0.853 | 1.169 |
| B | 1:10 | 1:100 | Uncorrected | 0.700 | 0.643 | 0.578 | 0.533 | 0.804 | 0.717 | 0.254 | 0.310 | 2.539 | 2.305 | 2.892 | 2.609 |
| B | 1:10 | 1:100 | 0.1 fmole | 0.319 | 0.296 | 0.251 | 0.203 | 0.267 | 0.199 | 0.704 | 0.803 | 1.156 | 1.047 | 1.365 | 1.806 |
| B | 1:10 | 1:100 | 1 fmole | 0.282 | 0.246 | 0.228 | 0.174 | 0.223 | 0.161 | 0.789 | 0.873 | 0.947 | 0.846 | 1.071 | 1.457 |
| B | 1:10 | 1:100 | 10 fmoles | 0.212 | 0.176 | 0.161 | 0.127 | 0.167 | 0.133 | 0.887 | 0.901 | 0.783 | 0.744 | 0.848 | 0.918 |
| B | 1:10 | 1:100 | 100 fmoles | 0.221 | 0.210 | 0.181 | 0.151 | 0.219 | 0.173 | 0.803 | 0.887 | 0.819 | 0.770 | 0.954 | 1.270 |
| C | 1:100 | 1:10 | Uncorrected | 0.549 | 0.552 | 0.435 | 0.431 | 0.485 | 0.487 | 0.417 | 0.403 | 1.889 | 2.080 | 2.639 | 2.824 |
| C | 1:100 | 1:10 | 0.1 fmole | 0.334 | 0.350 | 0.254 | 0.260 | 0.239 | 0.259 | 0.736 | 0.667 | 1.293 | 1.306 | 1.678 | 1.432 |
| C | 1:100 | 1:10 | 1 fmole | 0.299 | 0.284 | 0.219 | 0.210 | 0.135 | 0.170 | 0.819 | 0.806 | 1.070 | 1.022 | 1.498 | 1.217 |
| C | 1:100 | 1:10 | 10 fmoles | 0.246 | 0.181 | 0.175 | 0.120 | 0.144 | 0.111 | 0.819 | 0.903 | 0.922 | 0.697 | 1.380 | 1.111 |
| C | 1:100 | 1:10 | 100 fmoles | 0.293 | 0.186 | 0.209 | 0.126 | 0.187 | 0.133 | 0.764 | 0.931 | 1.178 | 0.681 | 1.459 | 1.222 |
| D | 1:1000 | 1:1 | Uncorrected | 0.666 | 0.614 | 0.555 | 0.498 | 0.798 | 0.616 | 0.264 | 0.306 | 2.306 | 2.141 | 2.846 | 2.872 |
| D | 1:1000 | 1:1 | 0.1 fmole | 0.368 | 0.446 | 0.267 | 0.335 | 0.256 | 0.266 | 0.694 | 0.583 | 1.484 | 1.708 | 1.768 | 1.832 |
| D | 1:1000 | 1:1 | 1 fmole | 0.313 | 0.382 | 0.233 | 0.292 | 0.184 | 0.236 | 0.778 | 0.653 | 1.199 | 1.410 | 1.399 | 1.590 |
| D | 1:1000 | 1:1 | 10 fmoles | 0.243 | 0.259 | 0.183 | 0.190 | 0.196 | 0.169 | 0.806 | 0.847 | 0.939 | 1.089 | 1.188 | 1.142 |
| D | 1:1000 | 1:1 | 100 fmoles | 0.272 | 0.163 | 0.195 | 0.111 | 0.215 | 0.080 | 0.861 | 0.931 | 1.220 | 0.665 | 1.404 | 0.810 |
Ligase bias metrics were calculated for each uncorrected dataset, and for three corrected analyses, which used the empirical correction factors from equimolar experiments, differing in the amount of total RNA.
Analysis and correction of (sequence-dependent) ligase bias from samples of heterogeneous composition
We analyzed the effects of bias correction when the empirical factors are estimated from samples that differ in composition from the target sample (e.g. use of miRXplore to correct the 286 series experiments and vice versa). Furthermore, this analysis allowed us to assess the robustness of the statistical estimation (GAMLSS fitting) procedure when only a subset of short RNAs are subject to bias correction. Supplementary Table S3 summarizes the effects of bias correction in the equimolar experiments from the 286 and miRXplore pools. In these analyses, RMSE was reduced by 47.2 ± 12.9%, the MAE by 51.3 ± 13.5%, the MAD by 56.2 ± 13.3% for the miRNAs that were common between the target and correction factor datasets. The percentage of miRNAs with expression level within 2-fold of the group mean increased from 23.0 ± 9.5% (uncorrected) to 69.9 ± 3.3%. Simultaneously, the 95 and 99% range were decreased by 36.6 ± 8.8% and 33.8 ± 8.4% respectively. There was no change in the bias metrics for miRNAs, which were not corrected. The effects of bias correction in the ratiometric series are shown in Table 4. RMSE was reduced by 38.5 ± 4.9%, the MAE by 42.5 ± 6.9%, the MAD by 46.8 ± 13.2% for the miRNAs that were shared between the target and correction factor datasets. The percentage of miRNAs with expression level within 2-fold of the group mean increased from 33.4 ± 4.3% (uncorrected) to 63.8 ± 8.5%. Simultaneously, the 95 and 99% range were decreased by 31.5 ± 8.8% and 33.7 ± 9.2% respectively. No changes in bias metrics were observed for the miRNAs that were not subjected to bias correction. P-values for the Flinger-Killeen, Ansari and KS tests for the comparison of variability reduction were all <10–4 for the common subset. To gain a better understanding of what appears a small drop in performance of the correction factors from heterogeneous samples, we plotted the values of these factors for the miRXplore pool against those from the four 286 pools (Figure 6). Regression estimates suggest that on average the values of the correction factors are equal; nevertheless, there is variation around this average pattern, so that regression factors do not cluster as tightly along the regression line, compared to the case of factors derived from series with the same molecular composition (see Figure 5B).
Table 4. Effects of bias correction in the case of empirical factors from samples of heterogeneous composition (ratiometric series).
| Group | Series | Correction factor data | miRNA subset | RMSE | MAE | MAD | Prob(2-fold) | 95% Range | 99% Range | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | Corr. | Uncor. | ||||
| A | A | miRXplore | Common | 0.431 | 0.651 | 0.342 | 0.520 | 0.412 | 0.485 | 0.560 | 0.380 | 1.640 | 2.228 | 1.908 | 2.369 |
| A | A | miRXplore | Unique | 0.531 | 0.531 | 0.403 | 0.403 | 0.463 | 0.463 | 0.524 | 0.524 | 1.845 | 1.845 | 2.051 | 2.051 |
| A | B | miRXplore | Common | 0.390 | 0.649 | 0.293 | 0.514 | 0.336 | 0.634 | 0.600 | 0.360 | 1.394 | 2.277 | 2.047 | 2.863 |
| A | B | miRXplore | Unique | 0.476 | 0.477 | 0.386 | 0.387 | 0.472 | 0.473 | 0.476 | 0.476 | 1.604 | 1.605 | 1.737 | 1.738 |
| B | A | miRXplore | Common | 0.356 | 0.614 | 0.264 | 0.509 | 0.290 | 0.713 | 0.681 | 0.277 | 1.370 | 2.122 | 1.586 | 2.386 |
| B | A | miRXplore | Unique | 0.841 | 0.841 | 0.679 | 0.679 | 0.815 | 0.815 | 0.292 | 0.292 | 2.857 | 2.856 | 2.931 | 2.929 |
| B | B | miRXplore | Common | 0.344 | 0.618 | 0.248 | 0.512 | 0.294 | 0.703 | 0.809 | 0.319 | 1.234 | 1.897 | 1.735 | 2.382 |
| B | B | miRXplore | Unique | 0.695 | 0.696 | 0.534 | 0.534 | 0.534 | 0.534 | 0.292 | 0.292 | 2.407 | 2.408 | 2.575 | 2.577 |
| C | A | miRXplore | Common | 0.373 | 0.577 | 0.249 | 0.463 | 0.251 | 0.498 | 0.725 | 0.333 | 1.685 | 1.883 | 2.005 | 2.744 |
| C | A | miRXplore | Unique | 0.422 | 0.422 | 0.325 | 0.324 | 0.402 | 0.400 | 0.571 | 0.571 | 1.416 | 1.415 | 1.491 | 1.489 |
| C | B | miRXplore | Common | 0.406 | 0.570 | 0.310 | 0.440 | 0.328 | 0.590 | 0.569 | 0.392 | 1.422 | 2.083 | 1.554 | 2.833 |
| C | B | miRXplore | Unique | 0.508 | 0.509 | 0.369 | 0.369 | 0.337 | 0.337 | 0.571 | 0.571 | 1.746 | 1.748 | 2.038 | 2.043 |
| C | A | miRXplore | Common | 0.391 | 0.687 | 0.304 | 0.566 | 0.339 | 0.784 | 0.592 | 0.265 | 1.484 | 2.277 | 1.625 | 2.867 |
| C | A | miRXplore | Unique | 0.551 | 0.551 | 0.454 | 0.454 | 0.615 | 0.617 | 0.304 | 0.304 | 1.794 | 1.796 | 2.188 | 2.191 |
| D | B | miRXplore | Common | 0.386 | 0.652 | 0.307 | 0.520 | 0.357 | 0.638 | 0.571 | 0.347 | 1.396 | 2.300 | 1.604 | 2.937 |
| D | B | miRXplore | Unique | 0.417 | 0.417 | 0.327 | 0.327 | 0.420 | 0.420 | 0.522 | 0.522 | 1.360 | 1.360 | 1.537 | 1.537 |
The column ‘Corr.’ gives the metric for the corrected estimate for each series (column ‘Dataset’) using the correction factor from the series listed under the column ‘Correction factor dataset’. Column ‘Uncor.’ tabulates the uncorrected estimate for each dataset.
Figure 6.
Empirical correction factors from datasets of heterogeneous composition. The figure shows the correction factors estimated from the miRXplore dataset against the values of the correction factors of the shared miRNAs calculated from the four-equimolar series of the 286 pool. On average, the correction factors from the heterogeneous datasets (miRXplore versus any of the 286 series) agree (the errors in variable regression line (red) is superimposable to the blue one that has an intercept of zero and a slope of one. There is however variation around this average pattern, which exceeds that observed when correction factors from datasets with homogeneous composition are compared (see Figure 5B).
Timings of code execution (means and standard deviations of 20 runs) required to derive and apply the correction factors are shown in Supplementary Table S4 for a number of processors, ranging from legacy laptop ones to those used in modern desktops. The reference, native R implementation, required between 119 s (9 year old processor laptop) to 31 s (high end i7 Intel octacore processor) to estimate the correction factors and a similar time to apply them to another dataset. We found that execution time scales linearly with the number of RNA sequences, i.e. the analysis of the miRXplore data with 962 takes almost thrice as long as the 286 experiments. The hybrid C++/R implementation is between four and six times as fast as the native R one. Using the NBI distribution implies 2.6× longer execution time than the LQNO one (this was only tested in the fast hybrid implementation).
Collectively, the analyses from the development and the validation datasets show that bias correction can be effective even when correction factors are estimated from equimolar mixes that differ up to four orders of magnitude from the dataset of interest. Bias correction can remove most of the bias in the absence of DE (equimolar series) and almost 60% of the bias in the presence of variable expression of miRNAs (ratiometric series). When samples of heterogeneous composition are used to derive the values of the correction factors, bias reduction is smaller; i.e. ∼40%. Empirical bias correction factors appear to be nearly constant over a broad range of RNA input and sample composition.
Differential expression analysis with GAMLSS
Under conditions of symmetric DE expression (Figure 7A), the lowest RMSE error was observed for the proposed methods (galmss, galmssAD), limma and voom (with or without sample weights, voomSW). Application of the trimmed mean normalization method (TMM) resulted in a deterioration of performance of both voom (voomTMM and limma (limmaTMM). The remaining methods had intermediate performance, with the highest error observed for the dss method. In all cases, the expected pattern of DE consisting of four well separated peaks at −3, −1, 1 and 3 (in log10 space) was recovered in model based, unsupervised clustering analysis. However, the peaks of these clusters were nearly perfectly aligned with the expected DE values only for the best performing methods.
Figure 7.
Analysis of differential expression (DE), with the NBI distribution, under scenarios of clustered symmetric DE without global changes in expression ratiometric A versus B (A), clustered asymmetric DE which shifts the global expression in one direction: equimolar versus ratiometric series A (B), equimolar versus ratiometric series B (C), ratiometric series A versus B in which the measurements of the overexpressed RNAs (subpools A and B) were omitted from the analyses (D). The dashed red lines are the true DE values, the numbers in bold, the RMSE errors and the histograms are the model based clustering of the DE measures estimated by each method.
Differences between methods were magnified under conditions of asymmetric DE with many more under-expressed than over over-expressed sequences. In these scenarios, shown in Figure 7B and C, the equimolar experiments are compared to the ratiometric series A and B respectively, yielding simulated conditions in which one-fourth of sequences are over expressed and roughly three-fourth are underexpressed. Only the application of gamlss, gamlssAD, limma, voom and voomSW yielded DE profiles, with peaks at the expected locations. The other methods, also yielded the anticipated four peak pattern, but the DE measures were shifted to the right, yielding a symmetric and demonstratively erroneous expression pattern with an equal fraction of over-expressed and under-expressed sequences. Consequently, the associated RMSEs were three times as large as that of the best performing methods.
Out of the generalized linear model methods, only gamlss and gamlssAD were able to recover correctly a clustered DE pattern of directional changes (Figure 7D). We simulated such a pattern by deleting the readings of sequences in groups 1 and 2 from the experiments shown in Figure 7A prior to analysis. The estimated DE measures differed substantially from the true ones for all methods analyzed, except gamlss/gamlssAD. The bias was rather severe (more than two orders of magnitude) and were both quantitative (absolute value of DE) and qualitative, with under-expressed sequences deemed to be over-expressed. This analysis demonstrates that the DE measures generated by existing methods are dependent on the entire complement of sequence counts analyzed. Furthermore, some of the methods generated spurious artifacts in DE profiles, taking the form of measures with the exact same value (spikes seen in DESeq2, limmaTMM, voom, voomSW). Interestingly, limma and voom had the worst RMSE performance out of all methods in this scenario. Similar patterns were observed when we repeated these DE expression analyses after resequencing these libraries (Supplemental Figure S7).
We also examined the performance of the competing methods for input examples showing directional DE behavior. This was simulated by comparing the expression profiles of the 0.1 fmole equimolar dataset versus that of the 100 fmole. Under this scenario, the 1000-fold higher input is offset by amplifying by seven fewer PCR cycles and possibly by changes in PCR efficiency. Hence the expression of every single sequence was higher by an amount that was between 0 and 3 in base 10 logarithmic scale. This analysis is shown in Figure 8A; only the gamlss and gamlssAD methods estimated the expression profile to be shifted to the right in its entirety. The competing methods all yielded qualitatively similar DE profiles in shape to the GAMLSS methods. However, the corresponding profiles were centered to zero suggesting that roughly half of the sequences were under-expressed in direct contradiction to the known quantitative character of the experiment. Application of the CR method to transform raw counts to normality, followed by the inverse transformation (multiplication by the constant factor of 3), of the log ratio of transformed mean counts yielded expression profiles that were in general comparable to our proposal. Nevertheless, this approximate method yielded higher RMSEs for extreme DE ratios relative to the gamlss (Supplementary Figure S8).
Figure 8.
Analysis of DE with the NBI distribution under consistent, but variable directional change in expression (comparison of the two equimolar experiments with total input of 0.1 and 100 fmoles, (A). RMSE (B) and Type I error (C) in the absence of DE (statistics of 200 experiments). In each of these graphs, the red triangle represents the mean over all bootstrap samples. Regression analysis of sensitivity and specificity for different thresholds of statistical significance (D). False discovery (FDR) and false omission (FOR) rates for DE algorithms under variable proportions of truly DE sequences (E), averaging over the values of P-value cutoff considered in D.
A bootstrap analysis was used to quantify the Type I error and the RMSE measures under conditions of no-DE. Overall, RMSE errors were low and the differences noted were of the order of the second significant digit (Figure 8B) for all methods considered. Type I errors (fraction of sequences considered to be DE at the 0.05 significant level) were also very small. With the exception of voomSW, most approaches resulted in conservative testing, with attained (expected error—red triangles in Figure 8C) less than the stated level of 0.05. A regression analysis using the DESeq2 as reference, showed that the least number of false positives was obtained with the EBSeq method, followed by edgeR and gamlssAD. We analyzed sensitivities (DE datasets in Figures 7 and 8A) and specificities (bootstrap datasets) of all methods against the threshold of statistical significance. These analyses shown in Figure 8D, illustrate that the proposed method (along with the CR approach) achieved the highest sensitivity for the P-value cutoff of 0.05. The voomSW followed by the gamlssAD method, were the least sensitive to the selection of the threshold of significance, while the CR method exhibited a substantial drop in sensitivity as the P-value cutoff was varied. With the exception of voomSW, all other methods exhibit high specificity as the threshold for statistical significance was relaxed (Figure 8D, insert). Bootstrap confidence intervals for sensitivities and specificities against the gamlssAD method are shown in Supplementary Figures S9 and S10. To explore the practical implications of these differences, we computed the FDR (false positives) and FOR (false negatives) as functions of the fraction of truly DE sequences, averaging over all P-value cutoffs. These analyses shown in Figure 8E illustrate that gamlssAD offers the optimal balance between FDR and FOR. Execution times for the gamlssAD method were favorable in absolute terms: i.e. a mean of 47.13 ± 6.43 s to analyze DE in two groups with 16 experiments per group for the high end i7-5960X processor, but not in relative terms. In particular, the software was nearly 1000 slower than limma, which executed in 0.008 ± 0.013 s and nearly five times slower than the second slowest method,EBSeq, at 9.48 ± 0.66 s.
In summary, gamlssAD can quantify DE with extremely high accuracy (RMSE), sensitivity (low number of false negatives) and specificity (low number of false positives), under scenarios of clustered symmetric and asymmetric DE, global changes in expression or even in the absence of DE. While other negative binomial regression methods, exhibit similar accuracy in the case of clustered, symmetric DE (equal fraction of overexpressed and underexpressed sequences), their accuracy deteriorates when the patterns of DE deviate from that of a symmetric change. A method based on the CR transformation of raw counts exhibited performance similar to gamlssAD in terms of RMSE for non-extreme signals, but had reduced sensitivity for thresholds of significance smaller than 0.05.
DISCUSSION
Rationale and relation to existing methods
Our impetus for introducing the distributional regression models for RNA-seq data was the need to understand the statistical nature of RNA-seq data. We have endeavored to apply statistical approaches that deal with the multi-step nature of these complex experiments in a more or less realistic fashion. The major complication factors in the experimental pipeline for an RNA-seq process are the ligation reaction, PCR amplification, the library sampling and the library depth variation. We derived a general statistical expression that relates the input of the RNA-seq; i.e. the abundance in the biological samples to the outputs i.e. the sequence counts through heuristics that simplify kinetic modeling and by specifying the relevant probabilistic expressions for the stochastic steps. To our knowledge, this is the first such modeling effort reported for these RNA-seq experiments. The analytical contributions of this work are these: the description of the LQ relation between the mean and variance of the sequence counts in an RNA-seq experiment, and the derivation of the Poisson truncated normal mixture as the underlying probability distribution for RNA-seq data. Our numerical/algorithmic contributions relate to the exploration of distributional, GAMLSS regression frameworks for the analysis RNA-seq data based on numerically robust approximations to these complex models. These in turn are based on familiar NBI distribution and the LQ Normal family we introduce for short RNA-seq measurements. We demonstrate that popular models for the stochastic modeling of RNA-seq datasets (14–15,18,20), may be seen as special cases of GAMLSS. This connection allows for a transparent evaluation of the underlying assumptions of these models, which in turn may inform their use in practical applications.
The relation between the mean and variance of sequence counts is a major underlying, yet under-appreciated feature of existing approaches for analyzing RNA-seq data (9,15,17,19–20). Despite the critical importance of this relationship, existing approaches have assumed its form without any formal justification. Although others have assumed that the mean-variance relationship should be approximately quadratic, this relationship has been attributed to the combined effects of biological and technical sources of variation (51). In this work we show that such a relationship is entirely due to the stochastic steps implicit in an RNA-seq experiment. Stated in other terms, there is no need to invoke underlying properties of the biological systems being studied to explain this relatioship. This is, of course, a testable prediction and we have provided evidence from sequencing of synthetic RNA mixes that this relationship is in fact observed in the absence of any biological variability. By incorporating PCR effects in the statistical formulation, our approach explicitly addresses concerns for both DNA (45) or RNA (72) sequencing applications raised by previous investigators. These reports suggest that library amplification by PCR may be a major source of heterogeneity in the observed distribution of sequence reads (45,72) due to stochasticity (40–43,73–77) and sequence-dependent (e.g. GC bias) variation in reaction efficiency (78–81).
We suggest that the theoretical investigations presented here facilitate a better understanding of recent observations in small RNA-seq applications (54). Those investigators identified the Gamma distribution as model for sequence counts and attributed this feature to the stochastic nature of PCR amplification. Our numerical/analytical investigations indicate that the underlying PCR stochasticity may be approximated with the Gamma model as a reasonable alternative to the truncated normal. However, the resulting counts will exhibit additional variation relative to the Gamma leading to a Negative Binomial Type I or a LQ normal model as highly accurate approximations of a more complex mixed Poisson model.
Modeling and correcting for ligase bias in RNA-seq experiments
The adoption of RNA-seq as a quantitative measurement for biological investigation and biomarker discovery is currently limited by large bias and excessive variation in the observed counts. This sequence (and adapter) specific sequence bias plagues all small RNA sequencing protocols. Despite the encouraging results in reducing the bias by protocol adaptations (4,7–8), no method to date has managed to eliminate it completely. Our kinetic modeling is consistent with this bias being protocol specific. However, the bias can be estimated on a per-sequence and protocol basis with equimolar mixes of small RNAs from the family one is investigating (e.g. miRNAs). In essence, one uses these mixes as calibration samples to derive correction factors that are subsequently applied to the analyses of experimental series of interest. We argued heuristically that these bias correction factors are not only constant over a broad range of concentrations of RNA input, but are also independent from the composition of the sample analyzed. Using a wide range of publicly available and legacy datasets from ur group, we demonstrated that the concentration independence holds over an order of magnitude. Furthermore, our analyses of the validation datasets suggest that concentration independence will definitely extend up to one order and possibly up to four orders of magnitude. We also demonstrated composition independence, using two different reference samples (e.g. the miRXplore and the 286 pools) which only share a subset of small RNAs. Because of these two properties, it is possible to correct RNA-seq profiles for ligase bias, using equimolar series from reference samples to calculate the values of the corresponding correction factors. Due to the concentration independence, imprecisions in the estimation of the RNA input may have little bearing on the results. To our knowledge, this is the first time that this possibility is demonstrated experimentally and its performance in terms of bias (e.g. RMSE reduction) is quantified.
GAMLSS in the analysis of differential expression
The application of the GAMLSS framework to DE analysis is seen to have several key advantages: higher accuracy, sensitivity and specificity compared to the alternatives examined. In sharp contrast to other competing generalized linear model methods, our approach generates DE measures that are robust with respect to the overall direction of the profile of expression changes. Other methods exhibit a behavior of some concern in that they appear to constrain DE estimates to be more or less symmetrically distributed around zero. Extreme forms of this behavior were seen when we filtered out readings from specific groups of miRNAs in our sequencing runs, causing DE estimates to change both magnitude and sign. This leads to spurious errors of both type ‘M’ (DE estimates are of the wrong absolute magnitude) and type ‘S’ (overexpressed sequences are considered underexpressed and vice versa) (82). This hitherto unrecognized shortcoming of existing methods was not observed for our approach and to a smaller extent for the CR transformation, which recovered the true DE changes regardless of sequence filtering.
The factors accounting for this behavior of the comparator methods are not entirely clear to us. Similar to our methodology, DESeq2 (20), edgeR (15,51), EBSeq (52), dss (10), limma (53) and voom (19) model sequence counts by the Negative Binomial distribution or by the normal distribution in which the variance is related to the mean through a smooth regression model (9,53). A unifying feature of all these methods is their explicit reference to the concept of a library depth that scales sequence counts. With the exception of DESeq2 and dss, the remaining approaches appear to analyze counts as relative proportions (counts per million) over the observed library depth (total counts). DESeq2 and dss also normalize to sequence depth, but the latter is estimated through the median of the ratios of counts in a given library to those of a pseudo-reference sample, obtained by taking the geometric mean of counts across samples (10,14,20). Hence all these methods, seem to be analyze sequence counts as proportions of the observed library depth, rather than as absolute counts. If this were the case, then one would expect these models to manifest a ‘zero sum’ behavior, in which the percentage of the over-expressed sequences is equal to that of the under-expressed so that their relative proportions sum to unity. Another possible explanation for this behavior rests with the shrinkage estimation procedures employed by the methods examined. In particular, if the underlying implementation fails to include a freely varying term for the difference of the group level mean from the referent group, or if that term is excessively penalized, then the algorithm would consider the overall group level differences to be zero. This will also result in a zero-sum situation, with an equal number of over-expressed and under-expressed sequences. Nonetheless, the variation around that mean would still be correctly estimated, even though the mean itself would be grossly mis-estimated. Interestingly enough, we have observed such a pattern in the DE experiments we analyzed. This behavior is avoided in our approach and the CR transformation method by modeling sequence abundances directly, i.e. without reference to the concept of a library depth. Our method also includes freely-varying (non-penalized) terms for the differences between group means to avoid excessive penalization of group differences. In summary, the direct modeling of sequence counts, rather their indirect analysis as proportions of a given library depth and the simultaneous estimation of variance parameters (LQ relationship), more than likely accounts for the smaller RMSE error and the optimal tradeoff of sensitivity and specificity of the proposed method. Furthermore, the use of the negative binomial, as justified by our theoretical investigations, rather than the gamma distribution assumption underlying the CR transformation, likely contributes to the more favorable balance between false omission and FDRs exhibited by our proposal.
Irrespective of the particular factors underlying the behavior of these widely-used algorithms, there are grave implications of for the reproducibility of RNA-seq signals against other quantification techniques. In particular, if the measures of DE for a given sequence are dependent on other sequences that were included in the analysis, then one depending on filtering may never recover the DE signal against a technique, e.g. qRT-PCR that does not refer to other sequences. Another implication of this behavior is the de-facto inability of these methods to recover global DE exchanges that are directional in nature, rather than symmetric around a reference expression level. This is particularly relevant for microRNAs in which global downregulation of miRNAs has been observed in a number of states as a result of reduced DICER activity (83–87), DROSHA (88–90) or through yet unidentified mechanisms (91–93). It follows that application of a method that implicitly constraints estimated DE changes to be symmetric in nature, will misclassify the direction of expression changes of up to half of the RNAs species assayed, while misquantifying the magnitude of the expression changes of the remaining 50% of RNAs. This undesirable behavior is clearly avoided by using our proposal.
Limitations
The encouraging results reported with the distributional regression models reported here have several limitations that should be noted. First, the proposed approach has specific data requirements due to the large number of parameters that are estimated (two per each sequence and sequence run). Fitting thousands of parameters requires that one provides the model with the necessary data and we have found that one may not reliably estimate unconstrained models with less than 15 libraries. Shrinkage estimation will in general decrease these requirements so one could use as little as four sequencing runs (libraries). Nevertheless, one will encounter numerical convergence issues for such under-replicated data. Overcoming these problems so as to obtain reliable estimate values, may involve extensive troubleshooting of the values of the tuning parameters of the algorithms and even the initial values of the parameter estimates.
Second, our method for bias reduction using offset variables, ignores the uncertainty in the estimates of these correction factors. A proper adjustment would require the use of techniques from measurement error models (such as regression-calibration, the simulation-extrapolation algorithm or bona fide Bayesian methods) (61) to account for this uncertainty. Such methods may be particularly important when one is working with samples in which the initial abundance varies over more than three orders of magnitude and one is interested in obtaining reliable estimates for low abundance RNA species. We did not attempt to provide results with these methods, as they are straightforward technical modifications that may not be relevant for the majority of applied work that focuses on high to medium strength signals. Nevertheless, these directions should be pursued as extensions of our bias reduction approach in future investigations.
Third, we assumed that the PCR efficiency will be the same for all the RNAs sequenced in the same library. This is a working assumption that allowed us to employ generalized linear modeling to derive correction factors. Due to the co-linearity between the PCR efficiency factors and the ligase bias, removing this assumption will require that non-linear models be applied instead. Non-linear modeling, may lead to more precise quantification of ligase bias and possibly increased performance of the empirical correction factors. These putative benefits should be weighed against the computational complexity of fitting non-linear models. Given the acceptable performance of empirical correction factors, we decided against pursuing this possibility in this report.
Fourth, our validation experiments were undertaken entirely using the Illumina sequencing platform and thus the bias correction factor approach may not translate to other sequencing platforms in use. We consider this somewhat unlikely though, due to the generic nature of the derivations of our approach that do not rely on specifics of any sequencing platforms. Furthermore, the LQ relationship, which provides a testable prediction of our modeling framework, was verified in datasets created by multiple sequencing instruments and approaches.
Fifth, our approach to bias reduction assumes the existence of a calibration dataset in which the sequences under investigation have been measured. This will present a challenge for the immediate future, but we have at least pointed the way forward with a clear picture of what is needed. The availability of commercial mixes of miRNAs ensures that these bias correction factors will be available for sequences that are included in these reference samples. This is rather similar to the previous application of universal references to account for biases related to labeling or hybridization in microarray analyses of microRNAs (94). However, for the vast number of sequence variants that are potentially recovered in biofluid samples, but not included in these reference sets, this approach is not applicable. In this case, correction will by necessity have to be applied only to a subset of RNAs. Our work shows that bias correction will be successful for such RNAs even if the relevant factors are estimated from a universal reference of a different composition and even drastically different total input than the samples of interest.
Last but certainly not least, the sensitivity and specificity metrics reported for our method relative to other approaches, were derived from datasets in which the anticipated changes of clusters of RNA sequences were rather large, i.e. the smallest change was a 64.2% reduction in expression. Furthermore, cluster separation was rather large, i.e. one or two orders of magnitude. It is likely that sensitivity and specificity will be less favorable for smaller DE changes and for sequence profiles which exhibit more tight clustering of DE values. Future studies should examine datasets which simulate both smaller DE changes and more challenging clustering structure, to assess the robustness of the proposed DE algorithm.
Applications and future extensions
The proposed methods for bias correction were developed with the intention to support applications that go beyond the usual goal of assessing DE of short RNAs between experimental conditions. In fact, analysis of DE does not require the use of bias correction factors as long as one is not interested in the absolute expression values of the referent experimental state. On the other hand, the application of bias correction factors is warranted when one is interested in comparing expression across different RNAs within experimental conditions. This could take the form of a pathway analysis, or more sophisticated systems biology modeling (95,96). For such applications, bias correction should eliminate non-biological, technical factors affecting the expression level (count), allowing one to concentrate on inferring biologically relevant influences and the underlying design principles. Last, but certainly not least, bias correction opens the possibility of elevating the status of RNAseq to clinical diagnostic applications. The relevant issues here pertain to analytical validity (recently reviewed by Byron et al. (97)) and ‘resolution of serious standardization prior to general applications’ in personalized medicine as pointed out by Raabe et al. (22). Our present work clearly demonstrates that bias may be substantially eliminated across a wide variety of protocols and sequencing platforms using a combination of calibration (reference) samples and advanced statistical modeling. This should support additional investigations in advanced systems biology modeling across non-clinical and clinical domains. Even if one does not contemplate such applications, one may still take advantage of the higher accuracy, sensitivity and specificity of the proposed methodology to undertake DE analysis.
We consider various extensions of the proposed methods. First, to expand the scope of the method to encompass sequences not included in the reference sets, one may consider performing a small discovery pilot to identify these variant sequences that may be found in a given application. Subsequently, one may include these variants in a commercially available reference sample and generate a custom, equimolar synthetic mix. The latter, is then used to derive correction factors for all sequences that one may potentially encounter in the context of one's application. However, the flexible regression approach we introduced suggests that one may model these correction factors using sequence-dependent features of the RNA species and the adapter. Future studies should thus concentrate on exploring suitable features of sequences that could be used to adjust regression models for counts and thus circumvent the need for calibration samples to estimate the bias correction factors.
A second, potential extension concerns the improvement of execution time of the method. This is currently a minor factor considering that bias corrected expression values and DE measures may be obtained in reasonable time (about 1 min in high end processors available at the time of this writing) relative to the time required to construct and sequence lobraries. However, execution times may become troublesome for larger datasets, involving hundreds of experiments, thousands of sequences, many more groups and correlated expression patterns (e.g. time series experiments). In such a case, faster implementations would be useful. We anticipated these needs, by implementing our methods in software libraries (the TMB framework) that can utilize parallel computation infrastructure (e.g. multicore processors, or even computer clusters).
Third, one should consider extensions of the proposed methodology to long RNA sequencing. The restriction of the scope to microRNAs and other short RNAs largely stems from the context of our applied work in the field of short RNA biomarker discovery and is not an inherent shortcoming of our methodology. However, one should explicitly acknowledge that long and short RNA-seq are different methodologies before attempting such an extension of scope. The most notable difference is that long RNA sequencing includes an additional experimental step to reduce RNAs to smaller fragments that are subsequently amplified and sequenced. This step is rather less characterized in terms of the statistics of its output. e.g. number of fragments and the length of the sequences generated than the other steps in the RNA-seq pipeline. Even though we do not claim to have a definitive answer, we think that the proposed method may be applied very cautiously to long RNA-seq data, since sequence fragmentation functions as a form of signal (pre)amplification. This is a length-dependent form of amplification, as longer sequences would be expected to yield more fragments than shorter ones. Furthermore, there is clearly a branching process at work: fragments generated may themselves be subject to additional rounds of fragmentation upon continuing exposure to the reaction reagents, up until their final reduction to single nucleotides. One can postulate that our framework would still apply in long RNA-seq, by applying theoretical innovations from the theory of length dependent branching processes to characterize both fragmentation and PCR amplification. In such a case, one should expect to forego the interpretation of amplification efficiency factors appearing in our equations as arising only from PCR. Nevertheless, we cannot endorse such an interpretation and this application without reservation, until further theoretical investigations and empirical studies demonstrate that long RNA sequencing obeys the LQ variance mean relationship highlighted by our approach. This appears to be the case by visual inspection of the figures in the papers introducing the competing methodologies (e.g. edgeR, voom or DESeq2). However, it is clearly evident that further theoretical, experimental and metrological studies beyond our subjective assessment are needed in this area.
AVAILABILITY
Source code for the implementation of the LQNO distribution in the gamlss package and for fitting the LQNO/NBI gamlssAD models in the TMB package is included in the bitbucket repository https://bitbucket.org/chrisarg/rnaseqgamlss. The repository also includes examples for the use of both the gamlss and gamlssAD packages as well as the R scripts used to compare approaches to DE analysis.
ACCESSION NUMBER
Read counts for the legacy and the validation datasets are available as Gene Expression Omnibus (GEO) accession GSE93399.
Supplementary Material
ACKNOWLEDGEMENTS
The 286 pool was kindly provided by Dr Kai Wang, Institute for Systems Biology, Seattle, WA, USA.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Institutes of Health, National Center for Advancing Translational Sciences [UL1TR001449 to C.A, in part]; National Institutes of Health Common Fund, Extracellular RNA Communication Consortium (ERCC) [1U01HL126496-01 to D.G., A.E., N.S., in part]; Dialysis Clinic Inc (DCI) [DCI #C-3765 to C.A]. Funding for open access charge: DCI [DCI #C-3765].
Conflict of interest statement. None declared.
REFERENCES
- 1. McIntyre L.M., Lopiano K.K., Morse A.M., Amin V., Oberg A.L., Young L.J., Nuzhdin S.V.. RNA-seq: technical variability and sampling. BMC Genomics. 2011; 12:293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Hansen K.D., Irizarry R.A., Wu Z.. Removing technical variability in RNA-seq data using conditional quantile normalization. Biostatistics. 2012; 13:204–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Hafner M., Renwick N., Brown M., Mihailović A., Holoch D., Lin C., Pena J.T.G., Nusbaum J.D., Morozov P., Ludwig J. et al. RNA-ligase-dependent biases in miRNA representation in deep-sequenced small RNA cDNA libraries. RNA. 2011; 17:1697–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Jayaprakash A.D., Jabado O., Brown B.D., Sachidanandam R.. Identification and remediation of biases in the activity of RNA ligases in small-RNA deep sequencing. Nucleic Acids Res. 2011; 39:e141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Zhuang F., Fuchs R.T., Sun Z., Zheng Y., Robb G.B.. Structural bias in T4 RNA ligase-mediated 3΄-adapter ligation. Nucleic Acids Res. 2012; 40:e54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Baran-Gale J., Kurtz C.L., Erdos M.R., Sison C., Young A., Fannin E.E., Chines P.S., Sethupathy P.. Addressing bias in small RNA library preparation for sequencing: a new protocol recovers microRNAs that evade capture by current methods. Front. Genet. 2015; 6:352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Fuchs R.T., Sun Z., Zhuang F., Robb G.B.. Bias in ligation-based small RNA sequencing library construction is determined by adaptor and RNA structure. PLoS One. 2015; 10:e0126049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Sorefan K., Pais H., Hall A.E., Kozomara A., Griffiths-Jones S., Moulton V., Dalmay T.. Reducing ligation bias of small RNAs in libraries for next generation sequencing. Silence. 2012; 3:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Liu R., Holik A.Z., Su S., Jansz N., Chen K., Leong H.S., Blewitt M.E., Asselin-Labat M.-L., Smyth G.K., Ritchie M.E.. Why weight? Modelling sample and observational level variability improves power in RNA-seq analyses. Nucleic Acids Res. 2015; 43:e97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Wu H., Wang C., Wu Z.. A new shrinkage estimator for dispersion improves differential expression detection in RNA-seq data. Biostatistics. 2013; 14:232–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Zhou Y.-H., Xia K., Wright F.A.. A powerful and flexible approach to the analysis of RNA sequence count data. Bioinformatics. 2011; 27:2672–2678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Srivastava S., Chen L.. A two-parameter generalized Poisson model to improve the analysis of RNA-seq data. Nucleic Acids Res. 2010; 38:e170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Hardcastle T.J., Kelly K.A.. baySeq: empirical Bayesian methods for identifying differential expression in sequence count data. BMC Bioinformatics. 2010; 11:422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Anders S., Huber W.. Differential expression analysis for sequence count data. Genome Biol. 2010; 11:R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Robinson M.D., McCarthy D.J., Smyth G.K.. edgeR: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010; 26:139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Robinson M.D., Smyth G.K.. Moderated statistical tests for assessing differences in tag abundance. Bioinformatics. 2007; 23:2881–2887. [DOI] [PubMed] [Google Scholar]
- 17. Bi Y., Davuluri R.V.. NPEBseq: nonparametric empirical bayesian-based procedure for differential expression analysis of RNA-seq data. BMC Bioinformatics. 2013; 14:262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Robinson M.D., Smyth G.K.. Small-sample estimation of negative binomial dispersion, with applications to SAGE data. Biostatistics. 2008; 9:321–332. [DOI] [PubMed] [Google Scholar]
- 19. Law C.W., Chen Y., Shi W., Smyth G.K.. voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol. 2014; 15:R29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Love M.I., Huber W., Anders S.. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014; 15:550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Rigby R.A., Stasinopoulos D.M.. Generalized additive models for location, scale and shape. J. R. Stat. Soc. 2005; 54:507–554. [Google Scholar]
- 22. Raabe C.A., Tang T.-H., Brosius J., Rozhdestvensky T.S.. Biases in small RNA deep sequencing data. Nucleic Acids Res. 2014; 42:1414–1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Song Y., Liu K.J., Wang T.-H.. Elimination of ligation dependent artifacts in T4 RNA ligase to achieve high efficiency and low bias microRNA capture. PLoS One. 2014; 9:e94619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Silber R., Malathi V.G., Hurwitz J.. Purification and properties of bacteriophage T4-induced RNA ligase*. Proc. Natl. Acad. Sci. U.S.A. 1972; 69:3009–3013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Uhlenbeck O.C. T4 RNA ligase. Trends Biochem. Sci. 1983; 8:94–96. [Google Scholar]
- 26. Yin S., Ho C.K., Shuman S.. Structure-function analysis of T4 RNA ligase 2. J. Biol. Chem. 2003; 278:17601–17608. [DOI] [PubMed] [Google Scholar]
- 27. Yin S., Kiong Ho C., Miller E.S., Shuman S.. Characterization of bacteriophage KVP40 and T4 RNA ligase 2. Virology. 2004; 319:141–151. [DOI] [PubMed] [Google Scholar]
- 28. Ho C.K., Wang L.K., Lima C.D., Shuman S.. Structure and Mechanism of RNA Ligase. Structure. 2004; 12:327–339. [DOI] [PubMed] [Google Scholar]
- 29. Omari K.E., Ren J., Bird L.E., Bona M.K., Klarmann G., LeGrice S.F.J., Stammers D.K.. Molecular architecture and ligand recognition determinants for T4 RNA ligase. J. Biol. Chem. 2006; 281:1573–1579. [DOI] [PubMed] [Google Scholar]
- 30. Raae A.J., Kleppe R.K., Kleppe K.. Kinetics and effect of salts and polyamines on T4 polynucleotide ligase. Eur. J. Biochem. 1975; 60:437–443. [DOI] [PubMed] [Google Scholar]
- 31. Ohtsuka E., Nishikawa S., Sugiura M., Ikehara M.. Joining of ribooligonucleotides with T4 RNA ligase and identification of the oligonucleotide-adenylate intermediate. Nucleic Acids Res. 1976; 3:1613–1624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Higgins N.P., Geballe A.P., Snopek T.J., Sugino A., Cozzarelli N.R.. Bacteriophage T4 RNA ligase: preparation of a physically homogeneous, nuclease-free enzyme from hyperproducing infected cells. Nucleic Acids Res. 1977; 4:3175–3186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Cranston J.W., Silber R., Malathi V.G., Hurwitz J.. Studies on ribonucleic acid ligase characterization of an adenosine triphosphate-inorganic pyrophosphate exchange reaction and demonstration of an enzyme-adenylate complex with T4 bacteriophage-induced enzyme. J. Biol. Chem. 1974; 249:7447–7456. [PubMed] [Google Scholar]
- 34. Kaufmann G., Klein T., Littauer U.Z.. T4 RNA ligase: substrate chain length requirements. FEBS Lett. 1974; 46:271–275. [DOI] [PubMed] [Google Scholar]
- 35. Hinton D.M., Baez J.A., Gumport R.I.. T4 RNA Ligase joins 2΄-deoxyribonucleoside 3΄, 5΄-bisphosphates to oligodeoxyribonucleotides. Biochemistry. 1978; 17:5091–5097. [DOI] [PubMed] [Google Scholar]
- 36. McCoy M.I., Gumport R.I.. T4 ribonucleic acid ligase joins single-strand oligo(deoxyribonucleotides). Biochemistry. 1980; 19:635–642. [DOI] [PubMed] [Google Scholar]
- 37. Walker G.C., Uhlenbeck O.C., Bedows E., Gumport R.I.. T4-induced RNA ligase joins single-stranded oligoribonucleotides. Proc. Natl. Acad. Sci. U.S.A. 1975; 72:122–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Snopek T.J., Sugino A., Agarwal K.L., Cozzarelli N.R.. Catalysis of DNA joining by bacteriophage T4 RNA ligase. Biochem. Biophys. Res. Commun. 1976; 68:417–424. [DOI] [PubMed] [Google Scholar]
- 39. Harris T.E. The Theory of Branching Processes. 1963; Berlin -Göttingen- Heidelberg: Springer-Verlag GmBH. [Google Scholar]
- 40. Hanlon B., Vidyashankar A.N.. Inference for quantitation parameters in polymerase chain reactions via branching processes with random effects. J. Am. Stat. Assoc. 2011; 106:525–533. [Google Scholar]
- 41. Lalam N. A quantitative approach for polymerase chain reactions based on a hidden Markov model. J. Math. Biol. 2009; 59:517–533. [DOI] [PubMed] [Google Scholar]
- 42. Gevertz J.L., Dunn S.M., Roth C.M.. Mathematical model of real-time PCR kinetics. Biotechnol. Bioeng. 2005; 92:346–355. [DOI] [PubMed] [Google Scholar]
- 43. Stolovitzky G., Cecchi G.. Efficiency of DNA replication in the polymerase chain reaction. PNAS. 1996; 93:12947–12952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Jagers P., Klebaner F.. Random variation and concentration effects in PCR. J. Theor. Biol. 2003; 224:299–304. [DOI] [PubMed] [Google Scholar]
- 45. Kebschull J.M., Zador A.M.. Sources of PCR-induced distortions in high-throughput sequencing data sets. Nucleic Acids Res. 2015; 43:e143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Johnson N.L., Kotz S., Balakrishnan N.. Discrete Multivariate Distributions. 1997; 1st edn, NY: Wiley-Interscience. [Google Scholar]
- 47. Johnson N.L., Kemp A.W., Kotz S.. Univariate Discrete Distributions. 2005; Hoboken: John Wiley & Sons. [Google Scholar]
- 48. Karlis D., Xekalaki E.. Mixed poisson distributions. Int. Stat. Rev. 2005; 73:35–58. [Google Scholar]
- 49. Stasinopoulos D., Rigby R.. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007; 23:1–46. [Google Scholar]
- 50. Casella G., Berger R.L.. Statistical Inference. 2001; 2nd edn, Australia; Pacific Grove: Cengage Learning. [Google Scholar]
- 51. McCarthy D.J., Chen Y., Smyth G.K.. Differential expression analysis of multifactor RNA-Seq experiments with respect to biological variation. Nucleic Acids Res. 2012; 40:4288–4297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Leng N., Dawson J.A., Thomson J.A., Ruotti V., Rissman A.I., Smits B.M.G., Haag J.D., Gould M.N., Stewart R.M., Kendziorski C.. EBSeq: an empirical Bayes hierarchical model for inference in RNA-seq experiments. Bioinformatics. 2013; 29:1035–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Ritchie M.E., Phipson B., Wu D., Hu Y., Law C.W., Shi W., Smyth G.K.. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015; 43:e47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Qin L.-X., Tuschl T., Singer S.. Empirical insights into the stochasticity of small RNA sequencing. Sci. Rep. 2016; 6:24061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Agresti A., Hitchcock D.B.. Bayesian inference for categorical data analysis. Stat. Methods Appl. 2005; 14:297–330. [Google Scholar]
- 56. Burman P. A comparative study of ordinary cross-validation, v-fold cross-validation and the repeated learning-testing methods. Biometrika. 1989; 76:503–514. [Google Scholar]
- 57. Burman P. Estimation of optimal transformations using v-fold cross validation and repeated learning-testing methods. Sankhyā. 1990; 52:314–345. [Google Scholar]
- 58. Argyropoulos C., Daskalakis A., Nikiforidis G.C., Sakellaropoulos G.C.. Background adjustment of cDNA microarray images by Maximum Entropy distributions. J. Biomed. Inform. 2010; 43:496–509. [DOI] [PubMed] [Google Scholar]
- 59. Argyropoulos C., Chatziioannou A.A., Nikiforidis G., Moustakas A., Kollias G., Aidinis V.. Operational criteria for selecting a cDNA microarray data normalization algorithm. Oncol. Rep. 2006; 15:983–996. [DOI] [PubMed] [Google Scholar]
- 60. Conover W.J., Johnson M.E., Johnson M.M.. A comparative study of tests for homogeneity of variances, with applications to the outer continental shelf bidding data. Technometrics. 1981; 23:351–361. [Google Scholar]
- 61. Carroll R.J., Ruppert D., Stefanski L.A., Crainiceanu C.M.. Measurement error in nonlinear models: a modern perspective. 2006; 2nd edn, Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- 62. Fuller W.A. Measurement Error Models. 2006; 1st edn, Hoboken: Wiley-Interscience. [Google Scholar]
- 63. Fraley C., Raftery A.E.. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002; 97:611–631. [Google Scholar]
- 64. Hausser J., Strimmer K.. Entropy inference and the james-stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009; 10:1469–1484. [Google Scholar]
- 65. Leonard D. Estimating a bivariate linear relationship. Bayesian Anal. 2011; 6:727–754. [Google Scholar]
- 66. Wood S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. 2011; 73:3–36. [Google Scholar]
- 67. Fraley C., Raftery A.E., Murphy B.M., Scruppa L.. mclust Version 4 for R: Normal Mixture Modeling for Model-Based Clustering, Classification, and Density Estimation. 2012; Seattle: University of Washington. [Google Scholar]
- 68. Kristensen K., Nielsen A., Berg C.W., Skaug H., Bell B.M.. TMB: automatic differentiation and laplace approximation. J. Stat. Softw. 2016; 70:5. [Google Scholar]
- 69. Cole T.J., Green P.J.. Smoothing reference centile curves: the lms method and penalized likelihood. Stat. Med. 1992; 11:1305–1319. [DOI] [PubMed] [Google Scholar]
- 70. Wood S. Generalized Additive Models: an Introduction with R. 2006; Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- 71. Cleveland W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979; 74:829–836. [Google Scholar]
- 72. Best K., Oakes T., Heather J.M., Shawe-Taylor J., Chain B.. Computational analysis of stochastic heterogeneity in PCR amplification efficiency revealed by single molecule barcoding. Sci. Rep. 2015; 5:14629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Lalam N. Statistical inference for quantitative polymerase chain reaction using a Hidden Markov model: a bayesian approach. Stat. Appl. Genet. Mol. Biol. 2007; 6:19–33. [DOI] [PubMed] [Google Scholar]
- 74. Lalam N., Jacob C., Jagers P.. Modelling the PCR amplification process by a size-dependent branching process and estimation of the efficiency. Adv. Appl. Probab. 2004; 36:602–615. [Google Scholar]
- 75. Piau D. Confidence intervals for nonhomogeneous branching processes and polymerase chain reactions. Ann. Probab. 2005; 33:674–702. [Google Scholar]
- 76. Rubin E., Levy A.A.. A mathematical model and a computerized simulation of PCR using complex templates. Nucleic Acids Res. 1996; 24:3538–3545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Cobbs G. Stepwise kinetic equilibrium models of quantitative polymerase chain reaction. BMC Bioinformatics. 2012; 13:203–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Aird D., Ross M.G., Chen W.-S., Danielsson M., Fennell T., Russ C., Jaffe D.B., Nusbaum C., Gnirke A.. Analyzing and minimizing PCR amplification bias in Illumina sequencing libraries. Genome Biol. 2011; 12:R18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Benjamini Y., Speed T.P.. Summarizing and correcting the GC content bias in high-throughput sequencing. Nucleic Acids Res. 2012; 40:e72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Chen Y.-C., Liu T., Yu C.-H., Chiang T.-Y., Hwang C.-C.. Effects of GC bias in next-generation-sequencing data on de novo genome assembly. PLoS One. 2013; 8:e62856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Dabney J., Meyer M.. Length and GC-biases during sequencing library amplification: a comparison of various polymerase-buffer systems with ancient and modern DNA sequencing libraries. Biotechniques. 2012; 52:87–94. [DOI] [PubMed] [Google Scholar]
- 82. Gelman A., Carlin J.. Beyond power calculations: assessing type S (Sign) and type M (Magnitude) errors. Perspect. Psychol. Sci. 2014; 9:641–651. [DOI] [PubMed] [Google Scholar]
- 83. Faggad A., Budczies J., Tchernitsa O., Darb-Esfahani S., Sehouli J., Müller B.M., Wirtz R., Chekerov R., Weichert W., Sinn B. et al. Prognostic significance of Dicer expression in ovarian cancer—link to global microRNA changes and oestrogen receptor expression. J. Pathol. 2010; 220:382–391. [DOI] [PubMed] [Google Scholar]
- 84. Rupaimoole R., Wu S.Y., Pradeep S., Ivan C., Pecot C.V., Gharpure K.M., Nagaraja A.S., Armaiz-Pena G.N., McGuire M., Zand B. et al. Hypoxia-mediated downregulation of miRNA biogenesis promotes tumour progression. Nat. Commun. 2014; 5:5202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Harvey S.J., Jarad G., Cunningham J., Goldberg S., Schermer B., Harfe B.D., McManus M.T., Benzing T., Miner J.H.. Podocyte-specific deletion of dicer alters cytoskeletal dynamics and causes glomerular disease. J. Am. Soc. Nephrol. 2008; 19:2150–2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Shi S., Yu L., Chiu C., Sun Y., Chen J., Khitrov G., Merkenschlager M., Holzman L.B., Zhang W., Mundel P. et al. Podocyte-selective deletion of dicer induces proteinuria and glomerulosclerosis. JASN. 2008; 19:2159–2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Kumar M.S., Lu J., Mercer K.L., Golub T.R., Jacks T.. Impaired microRNA processing enhances cellular transformation and tumorigenesis. Nat. Genet. 2007; 39:673–677. [DOI] [PubMed] [Google Scholar]
- 88. Torrezan G.T., Ferreira E.N., Nakahata A.M., Barros B.D.F., Castro M.T.M., Correa B.R., Krepischi A.C.V., Olivieri E.H.R., Cunha I.W., Tabori U. et al. Recurrent somatic mutation in DROSHA induces microRNA profile changes in Wilms tumour. Nat. Commun. 2014; 5:4039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Shu J., Kren B.T., Xia Z., Wong P.Y.-P., Li L., Hanse E.A., Min M.X., Li B., Albrecht J.H., Zeng Y. et al. Genomewide microRNA down-regulation as a negative feedback mechanism in the early phases of liver regeneration. Hepatology. 2011; 54:609–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Lin R.-J., Lin Y.-C., Chen J., Kuo H.-H., Chen Y.-Y., Diccianni M.B., London W.B., Chang C.-H., Yu A.L.. microRNA signature and expression of Dicer and Drosha can predict prognosis and delineate risk groups in Neuroblastoma. Cancer Res. 2010; 70:7841–7850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Graff J.W., Powers L.S., Dickson A.M., Kim J., Reisetter A.C., Hassan I.H., Kremens K., Gross T.J., Wilson M.E., Monick M.M.. Cigarette smoking decreases global microRNA expression in human alveolar macrophages. PLoS One. 2012; 7:e44066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Neal C.S., Michael M.Z., Pimlott L.K., Yong T.Y., Li J.Y.Z., Gleadle J.M.. Circulating microRNA expression is reduced in chronic kidney disease. Nephrol. Dial. Transplant. 2011; 26:3794–3802. [DOI] [PubMed] [Google Scholar]
- 93. Smalheiser N.R., Lugli G., Rizavi H.S., Torvik V.I., Turecki G., Dwivedi Y.. MicroRNA expression is down-regulated and reorganized in prefrontal cortex of depressed suicide subjects. PLoS One. 2012; 7:e33201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Bissels U., Wild S., Tomiuk S., Holste A., Hafner M., Tuschl T., Bosio A.. Absolute quantification of microRNAs by using a universal reference. RNA. 2009; 15:2375–2384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Chang T.-C., Wentzel E.A., Kent O.A., Ramachandran K., Mullendore M., Lee K.H., Feldmann G., Yamakuchi M., Ferlito M., Lowenstein C.J. et al. Transactivation of miR-34a by p53 broadly influences gene expression and promotes apoptosis. Mol. Cell. 2007; 26:745–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Schwanhäusser B., Busse D., Li N., Dittmar G., Schuchhardt J., Wolf J., Chen W., Selbach M.. Global quantification of mammalian gene expression control. Nature. 2011; 473:337–342. [DOI] [PubMed] [Google Scholar]
- 97. Byron S.A., Van Keuren-Jensen K.R., Engelthaler D.M., Carpten J.D., Craig D.W.. Translating RNA sequencing into clinical diagnostics: opportunities and challenges. Nat. Rev. Genet. 2016; 17:257–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.