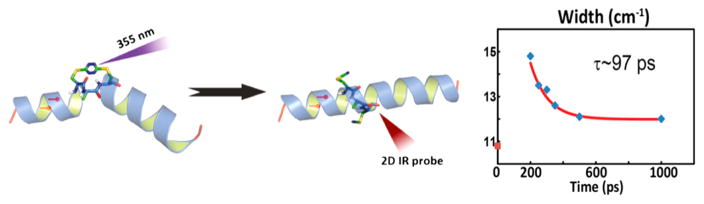
Abstract
Proteins exhibit structural fluctuations over decades of time scales. From the picosecond side chain motions to aggregates that form over the course of minutes, characterizing protein structure over these vast lengths of time is important to understanding their function. In the past 15 years, two-dimensional infrared spectroscopy (2D IR) has been established as a versatile tool that can uniquely probe proteins structures on many time scales. In this review, we present some of the basic principles behind 2D IR and show how they have, and can, impact the field of protein biophysics. We highlight experiments in which 2D IR spectroscopy has provided structural and dynamical data that would be difficult to obtain with more standard structural biology techniques. We also highlight technological developments in 2D IR that continue to expand the scope of scientific problems that can be accessed in the biomedical sciences.
Graphical Abstract
1. INTRODUCTION
The structural evolution of proteins, designed to accomplish precise functions, is at the heart many processes in biology.1–3 Knowledge of the kinetics of the interconversion between members of a structural ensemble can lead to fundamental insights into the mechanisms of these processes.4,5 Of course, for a technique to measure kinetics, the time resolution of the technique needs to be shorter than the time scale of structural change. 2D IR spectroscopy provides the ideal time resolution to measure structural change. With a subpicosecond time resolution, there is essentially no protein or biological structural change that is too fast for it to follow. About the only things that move on a 1 ps time scale are water molecules and ions as they make and break hydrogen bonds; protein backbones are essentially fixed in space, as are side chains, on this picosecond time scale.1,6,7 Thus, a 2D IR spectrum provides a snapshot of water and ion dynamics around static protein structures. Collecting multiple 2D IR spectra as a function of time turns these static snapshots into a movie.
Water and ion dynamics is critical for biological function and many researchers have utilized the picosecond dynamics of 2D IR spectroscopy to measure water structure in liquids and in biological systems.7–10 Hydration can be mapped in membrane proteins and ion channels and other biomolecular assemblies, such as DNA.11–13 Regarding the protein structures themselves, the 2D lineshapes reflect the distribution of protein structures in the ensemble, thereby providing a measure of structural heterogeneity.12,14–17 Structural heterogeneity, by which we mean the populations of protein structures, plays a role in enzymes, since the active sites are very sensitive to geometry.4 Structural heterogeneity is important in stability, such as side chains that stabilize protein structures.18 It is a probable cause of amyloid polymorphs.19
2D IR spectroscopy can also be used to study kinetics longer than the intrinsic picosecond time resolution by triggering a conformational change. Triggers include cis–trans isomerizations, conformational change, temperature or pH jumps, bond breakage, and other methods that induce conformational changes.20–22 Following the trigger, 2D IR spectra can be used to probe the resulting conformational changes to arbitrarily long times. To get statistics for spectra with good signal-to-noise ratio, the experiments either need to be repeated using replenishable triggers or by collecting the 2D IR spectra faster than the kinetics.14,23 Between the intrinsic time scale and the trigger methods, there are few kinetics that cannot be measured with 2D IR spectroscopy.
The excellent time resolution of 2D IR spectroscopy can also be complimented by bond-specific or domain-specific structural resolution by the use of isotope labeling. The intrinsic structural resolution of 2D IR spectroscopy is already much better than FTIR spectroscopy, because of the cross-peaks, 2D line shapes, and the quadratic scaling of signals with transition dipole strengths.24,25 But 13C or 13C=18O isotope labeling creates spectroscopic features for precise portions of the protein. Isotope labeling of individual residues has been used in many protein systems.26–29 More recently, domains of proteins have been labeled to look at global structures,30 and mixtures of labeled and unlabeled proteins provide 2D IR spectra of monomers in protein ensembles. This combination of time and structural resolution is unique among all tools in structural biology.
The focus of this review is to survey the applications of 2D IR spectroscopy toward investigating protein conformations and their evolution, both under equilibrium and nonequilibrium conditions. In addition to proteins and peptides, 2D IR has been successfully used to address a broad range of fundamental questions in physical chemistry,31–35 which are unfortunately outside the scope of this review. We cover the development of the 2D IR technique and emphasize its contribution to measuring the dynamics of structural change in biological systems. Throughout the review, we hope to highlight the important experiments that have impacted protein science. Additionally, we would like the reader to recognize why 2D IR spectroscopy can, and will, impact the fields of biochemistry and protein science. We return to this point in the conclusion, where we present what we believe to be the future of 2D IR spectroscopy in biophysics and biochemistry.
2. THE 2D IR EXPERIMENT
2.1. Overview of Typical 2D IR Spectra
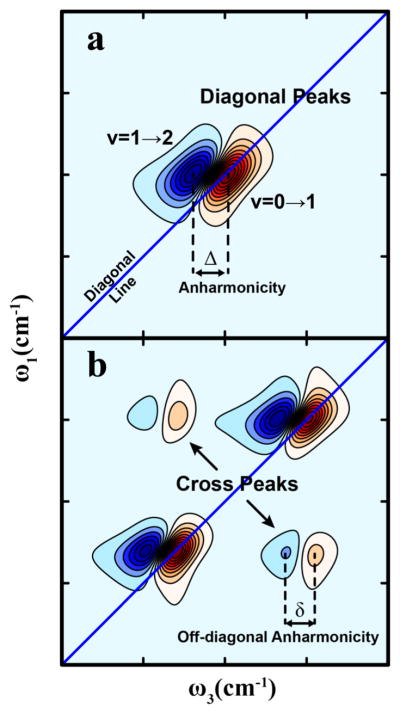
Figure 1a shows a cartoon of a 2D IR spectrum of a single vibrational mode in a molecule. A linear IR (or FTIR or absorption spectrum) of this mode would have a single absorption peak centered at its vibrational frequency. The corresponding 2D IR spectrum contains two out-of-phase transitions. The positive peak (shown in red) corresponds to the v = 0 → 1 transition, where v is the vibrational quantum number for the mode, while the negative peak (shown in blue) corresponds to the v = 1 → 2 transition. The two peaks are separated by the anharmonic shift, Δ. These peaks are typically known as diagonal peaks, as they appear along the diagonal (ω1 = ω3) line with the v = 0 → 1 peak precisely on the diagonal. Both positive and negative peaks will appear elongated along the diagonal if there is inhomogeneous broadening. Each diagonal point can be thought of as a linear IR transition with a characteristic homogeneous width; when there is a distribution of frequencies, there are many diagonal points, leading to spectral elongation along the diagonal. For transitions that are only homogeneously broadened, the 2D peak shapes become nearly circular. As we will discuss in section 3.7, if the inhomogeneous distribution of frequencies are time-dependent, then the 2D contours become circular with increasing waiting time, leading to quantitative evaluations of fluctuations near a vibrator. This separation of homogeneous and inhomogeneous line widths, characteristic of the photon echo, lends 2D IR unique capabilities for investigating vibrational dynamics
Figure 1.
Typical features of a 2D IR spectrum. (a) Diagonal peaks and (b) cross-peaks. The spectra shown were simulated from the third-order response functions described in ref 36.
Figure 1b is a cartoon of a molecule with two vibrational modes. When multiple oscillators are present, such as in a protein, off-diagonal features can appear in 2D spectra, commonly known as cross-peaks. The existence of cross-peaks depends on the vibrational coupling between the two modes concerned. Cross-peaks give the joint frequency distributions of the two coupled vibrators. Similar to diagonal peaks, cross-peaks also appear as out-of-phase pairs that are separated by the off-diagonal or mixed-mode anharmonicity (δ). The off-diagonal anharmonicity depends on the coupling constant between the two modes, which will depend on the molecular geometry and is often simply a function of the angle and distance between the two transition dipoles. Thus, whereas diagonal peaks reveal inhomogeneites of the vibrational frequency distribution, cross-peaks carry structural information. The ability to measure vibrational couplings directly is one of the major strengths of 2D IR. The following sections goes into the details of the pathways that lead to cross-peaks and how they can be used to decipher molecular structure.
Before we end this brief discussion on the basics of 2D IR spectra, it needs to be mentioned that in the literature, 2D IR spectra have been plotted in two different ways. The first approach plots ω1 as the ordinate and ω3 as the abscissa. The alternate approach plots ω3 as the ordinate and ω1 as the abscissa. The spectra thus generated are related through an axis rotation and inversion. Also, the sign convention used for 2D spectra have varied over the years: some prefer the fundamental 0 → 1 transition to have a negative value, similar to pump–probe spectroscopy, while the opposite, where the fundamental peak has a positive value, is also commonly used. Of course, irrespective of the plotting convention, the spectral information remains the same, and thus it is merely a matter of preference in using one style over the other. Additionally, it is important to note that we refer to any functional group that absorbs IR light as a chromophore, in analogy to visible spectroscopy of electronic states.
2.2. Outline of 2D IR Spectroscopy
2D IR spectra can be interpreted in a phenomenological manner following the discussion in the last section (section 2.1). In many cases it is not necessary to understand the mathematical details of how the spectra are generated. For those readers that are interested, this section provides a brief outline of the fundamentals of the 2D IR experiment. The theory of third-order nonlinear spectroscopy has been described in detail on many occasions;36–38 we therefore only introduce the key aspects of 2D IR that are necessary to understand and interpret results that are discussed in the later sections. The technology that makes possible generation of ultrashort mid-IR pulses has come a long way in the past decade and has been described at length.39,40 We therefore skip straight to the experimental implementations of 2D IR. The 2D IR experiment involves successive interaction of a chromophore with three light pulses to produce a third-order material polarization, which generates a signal electric field in directions specified by the wave vectors of the incident light. The signal S(t1, T, t3) obtained in a three-pulse heterodyned echo measurement is a function of the pulse delays t1 (also labeled as τ), T, and t3 (also labeled as t), which are the time intervals between the first and second, between the second and third, and between the third and the detected fields, respectively. These delays are referred to as the coherence time, the waiting time, and the detection time, respectively. Fourier transform of the signal over t1 and t3 yields a 2D spectrum, which is a function of frequencies ω1 and ω3 (or ωτ and ωt). The 2D IR signal is traditionally detected by heterodyning with a reference pulse known as the local oscillator. Heterodyning is necessary to measure the amplitude and the phase of the generated signal. Measuring only the generated field with a square law detector yields the amplitude squared of the generated field, whereas heterodyning yields both the amplitude and phase of the signal as long as the phase of the local oscillator is known:
| (1) |
There are two principal methods of obtaining heterodyned spectra in a 2D IR experiment: time domain and spectral interferometry.36 In time domain interferometry, the delay between the local oscillator and the signal is scanned for every t1 and Fourier transformed over both time dimensions to yield the 2D spectrum. However, this increases data acquisition times significantly, which is why the signal and the local oscillator are often dispersed in a spectrograph and measured using an array detector. The spectrograph, or monochromator, is effectively an experimental Fourier transform over t3, thus reducing data collection times and errors due to laser fluctuations (This is why in some literature the ω3 axis has been labeled as ωm). The first laser pulse creates a coherence, which evolves in time (the coherence time) before the second pulse terminates this evolution by creating a population. After a finite delay (the waiting time), the third pulse regenerates the coherent state, which now evolves again (the detection time). The signals that contribute to the third-order polarization can be categorized into two kinds, rephasing and nonrephasing, that differ with respect to the phase of the coherence during the coherence (t1) and detection (t3) times. Nonrephasing pathways have the same phase for coherences during t1 and t3, whereas for rephasing pathways, the coherence that is created by the third pulse is the complex conjugate of that during t1
| (2) |
where ρij is the i,j-th element of the density operator. The coherences evolving during t3 in the nonrephasing pathways undergo a relaxation similar to free induction decay, while for the rephasing pathways, the coherences “rephase”, returning to have the same macroscopic dipole as at t1 = 0, so it emits a field known as the echo, akin to optical photon echoes observed many years ago.41 The ability of 2D IR to separate homogeneous and inhomogeneous contributions to the spectra arises from this vibrational photon echo. The rephasing and nonrephasing molecular responses can be represented as42
| (3) |
| (4) |
The angular brackets represent an average over a distribution of frequencies. The phase difference of the coherence during t1 for rephasing and nonrephasing signals comes from interactions with components of the electric field that are complex conjugates. Thus, these pathways can be isolated by phase-matching conditions, which means selecting a certain combination of the phases of the incident pulses by choosing a particular direction of the signal field. The phase-matched signal direction for rephasing and nonrephasing pathways is −k1 + k2 + k3 and k1 − k2 + k3, respectively. This is only true for a time ordering of pulses where pulse 1 (with wave vector k1) precedes pulse 2 (with wave vector k2). For a time ordering of pulses where pulse 2 precedes pulse 1, the nonrephasing signal is emitted in the same phase-matched direction as rephasing; thus by switching between pulse orderings (123) and (213), both rephasing and nonrephasing signals can be generated in the −k1 + k2 + k3 phase matched direction. This is used in the boxCARS experimental implementations of 2D IR (vide infra). From the above equations, it is also clear that the rephasing and nonrephasing signals appear in different quadrants of the {ω1, ω3} space: rephasing in the {−, +} and the nonrephasing in the {+, +} quadrants. Both rephasing and nonrephasing spectra have absorptive and dispersive components; a purely absorptive 2D IR spectrum is obtained by summing the rephasing and nonrephasing spectra.36,43 In addition to these pathways, the most commonly measured signals, there are other types of 2D IR spectra that could provide more information about the sample. Another nonrephasing pathway that is usually difficult to measure is the so-called double-quantum version of 2D IR spectroscopy that is emitted in the k1 + k2 − k3 direction. There has been past44 and recent45 interest in this particular implementation of 2D IR due to the ease of measuring vibrational couplings and anharmonicities. This pathway is not usually measured because it further complicates the most common experimental geometries. However, recent collinear implementations of 2D IR46,47 promise to resurrect the use of this particular pathway to further enhance the utility of 2D IR as a structural tool.
2.3. Experimental Implementations of 2D IR Spectroscopy
The two most common optical geometries for 2D IR spectroscopy are the four-wave mixing boxCARS and the pump–probe geometry. In a traditional boxCARS geometry, the three incident pulses are noncollinear; the signal emitted in the phase-matched direction −k1 + k2 + k3 is heterodyned with a local oscillator. The primary advantage of the boxCARS geometry stems from the background-free detection of the third-order signal. Alternatively, the experiment can also be implemented in the so-called pump–probe geometry.14,48 In fact, some of the earliest reported 2D spectra were collected in this experimental scheme, albeit with a hole-burning approach.49 In a pump–probe optical setup, the first two pulses (often called the pump-pulses in analogy to transient absorption spectroscopy) are collinear. It thus follows that both rephasing and nonrephasing signals are emitted in the same direction, which is that of the wave vector of the third (or probe) pulse, k3. The signal is therefore not background free, but this has an advantage: it is automatically heterodyned by k3, thus making a separate local oscillator unnecessary and the experimental design much simpler. Additionally, both rephasing and nonrephasing (and hence the absorptive) spectra are measured simultaneously, leading to faster data acquisition. It is important to note in this context that the pump–probe spectrum is related to the 2D IR spectrum through the projection-slice theorem: it is projection of the heterodyned 2D IR signal on to the ω3 axis.36,50,51
3. THEORY OF 2D IR SPECTROSCOPY
Interpreting 2D IR spectra in terms of protein structures and their environments requires a physical model linking observables like frequencies, cross-peaks, and 2D line shapes with molecular details. The more deeply one understands these models, the more quantitatively 2D IR spectra can be interpreted. But, once again, in many cases 2D IR spectra can be interpreted qualitatively without a deep understanding of these details. This section gives a brief overview of these details, but readers can also skip ahead to section 4 if applications are the end goal.
3.1. Vibrational Coupling
The very existence of a 2D IR spectrum is predicated on the anharmonic character of the chemical bond.36 This means that the usual normal mode description is inadequate to describe 2D IR because normal modes are harmonic. Theoretical developments in 2D IR spectroscopy have thus relied on an anharmonic local mode description of the molecules, especially for systems with a large number of oscillators.52 From the local modes, the delocalized vibrations can be constructed. Here, we borrow terminology from the electronic spectroscopy community and call these delocalized states vibrational excitons.53 2D IR can characterize vibrational excitons, which can be related to the three-dimensional structure of a molecule. To understand how 2D IR is used to determine the structure of proteins, we present a brief synopsis of vibrational coupling.
Although the physical processes of electronic and vibrational excitons differ, the mathematics are formally the same.36 If retaining only quantum-conserving terms, the Hamiltonian can be written down as
| (5) |
where and bj are the raising and lowering operators, respectively, N is the number of oscillators, ħ is Planck’s constant divided by 2π, βij is the coupling between oscillators i and j in units of energy, ωi is the fundamental frequency of oscillator i, Δi is the anharmonicity of oscillator i, and HSB is the system bath Hamiltonian that describes the fluctuations of the local mode energies and their respective couplings. For the moment, we neglect the system bath Hamiltonian, focus on the molecules of interest, and refer to the reader to ref 38 for a complete treatment.38 If only considering the two-exciton Hamiltonian necessary to describe 2D IR, H is a block diagonal matrix in the local mode basis. To calculate a 2D IR spectra, we diagonalize the one and two exciton quadrants. This gives us the frequencies of the observed transitions. The coupling constant β, which depends on the distance and orientation of the individual chromophores, can be related to the three-dimensional molecular structure. The excitonic energies are determined by diagonalizing the local mode Hamiltonian
| (6) |
where Ω is the diagonal matrix of the excitonic vibrational frequencies and U and UT are the matrices used to diagonalize the Hamiltonian. These are the vibrational frequencies measured in an experiment. In addition to the frequencies, we need to know the transition dipoles of the excitonic states. We express the excitonic transition dipoles as a linear combinations of the local modes. That is, we transform the transition dipole matrix by the same unitary transformation used to diagonalize the Hamiltonian.
To illustrate, it is useful to consider two coupled oscillators. In this case, the total Hamiltonian in the local mode basis is as follows.
| (7) |
The factor of √2 comes from the ladder operators operating on the doubly excited states. To calculate the linear absorption signal, we only need the singly excited state energies. The eigenvalues are given by
| (8) |
The eigenvectors are then use to generate the excitonic transition dipoles from linear combinations of the local mode transition dipoles. In the weak coupling limit, β12 ≪ |ħω1 – ħω2| and the excitonic states are primarily localized onto individual chromophores with energies that are approximately given by36
| (9) |
In the strong coupling limit, when β12 ≫ |ħω2 – ħω1|, the excitonic states effectively become completely delocalized.36,38 The excitonic energies are split according to
| (10) |
So far we have only considered the singly excited states. However, to calculate a 2D IR spectrum, we also need to consider the two-exciton Hamiltonian, which contains the anharmonicities of the oscillators. Again, we first consider the strong coupling limit. In this case, the oscillator strength is completely delocalized and therefore the separation between the ground-state bleach and excited-state absorption is Δ/2.36 The cross-peaks, which correspond to sequentially exciting the separated excitons, are separated by Δ. In the weak coupling limit, the diagonal peaks are separated by the local mode anharmonicity, since the excitons are primarily localized on the individual oscillators. The separation between the out-of-phase cross-peaks can be calculated perturbatively to be36,54
| (11) |
3.2. Coupling Models
The key to relating the observed excitonic frequencies, anharmonicities, and peak intensities to molecular structure is measuring the coupling, βij. In a protein, the amide I backbone vibrations couple differently on the basis of the structure.55,56 To relate the measured coupling to a molecular structure, we need to have some model that relates the three-dimensional position of the atoms to the measured excitonic frequencies and transition dipoles.57–62 In principle, one can use use a fully ab initio normal mode calculation to fully account for dipole, electrostatic, and mechanical coupling.63 Most biologically relevant proteins are too large for this to be feasible. In lieu of a fully quantum mechanical calculation, some models must be used to interpret the typical infrared spectrum of a protein. Typically, these models are parametrized with fully quantum mechanical calculations.
The simplest of these models is transition dipole coupling.36,64,65 In this picture, the local mode transition dipoles interact with one another via through-space dipole–dipole interactions. The coupling βij between chromophores is expressed as
| (12) |
This is the most intuitive picture of vibrational coupling, although it neglects the effects of through-bond coupling and, therefore, breaks down at short distances.36 Another coupling model is the transition charge density, which takes into account the electrostatic interaction energy between two coupled local modes.36 A similar approach is the transition point charge model, which replaces the integration in the transition charge density model with a summation, which is more computationally feasible.36 Recently, Lee et al. published a comparison of coupling models for a β-sheet.66 Jansen and Knoester have developed coupling maps based on the effects of local electrostatics on the vibrational frequency.62 All of these models are necessary to provide simple and intuitive interpretations of the vibrational spectra of proteins.
3.3. Transition Dipole Coupling in Common Protein Structural Motifs
Before discussing the general features of vibrational spectra associated with proteins, we briefly discuss the infrared spectra of an infinite chain of coupled oscillators. Generally, the mathematics to determine the eigenstates and their corresponding energies are formally the same as the calculation of band structures in solid-state physics. Borrowing terminology from this field, we consider the so-called “tight binding” model and only consider nearest-neighbor couplings. We consider degenerate site energies (i.e., the local modes are chemically identical oscillators) and we assume that the structure is periodic so all of the nearest-neighbor couplings are identical. The Bloch theorem states that the eigenstates of the system can be expressed as linear combinations of Bloch functions. The Bloch functions are the local mode wave functions modulated by a phase factor. Therefore, the wave function for state k is given by
| (13) |
Here N is the number of oscillators and the summation of j is performed over all oscillators in the chain. In the limit of an infinite chain, there is only an optically allowed state, although fluctuations in the environment and structure can lead to the appearance of other modes.36 The dispersion relation for an infinite chain is given by
| (14) |
For a truly infinite chain, the k = 0 state is the only one that is optically allowed. Whether this is the highest energy state or the lowest depends on the sign of the coupling and, therefore, the orientations of the transition dipoles.
3.3.1. α-Helix Vibrational Excitons
The α-helix is a common secondary structure in proteins and is especially prominent in membrane-bound proteins.12 Since an α-helix is a three-dimensional structure, with ~3.6 amino acid residues per turn, couplings beyond nearest neighbors cannot be neglected.36 There are three major excitonic modes in an α-helix. The first is along the z-axis of the protein, parallel to the helical axis. This is called the A mode. There are two other excitonic states, the E modes, that are degenerate and lie perpendicular to the helical axis. It should be noted that the transition dipole strength and frequencies of the transitions depend on a competition between the negative and positive couplings. This often leads an α-helix to show up at about the same frequency as a random coil. However, if we recall our discussion of the coupled dimer, we will notice that the observed anharmonic shift, that is, the difference between the fundamental and excited-state absorption in a 2D IR spectrum, is significantly smaller than the local mode anharmonicity for strongly coupled oscillators.36 The ability to distinguish between the strong and weak coupling limit makes 2D IR spectroscopy a useful tool for distinguishing between a random coil and an α-helix.67
3.3.2. β-Sheet Vibrational Excitons
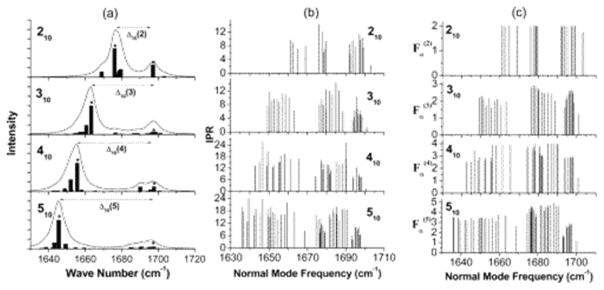
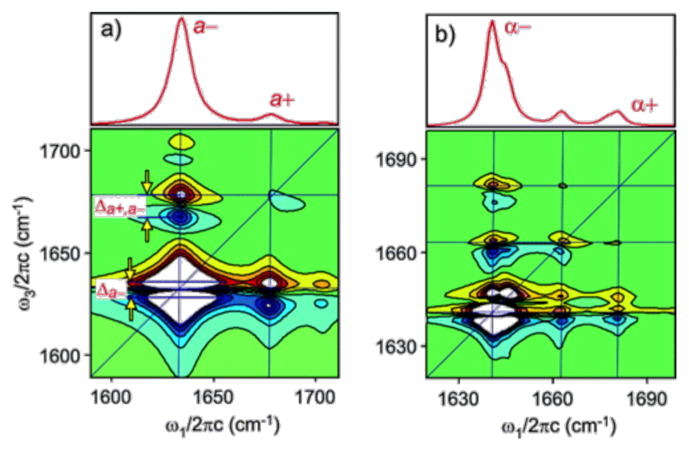
β-Sheets of amino acids effectively form a 2D system of coupled oscillators, with interstrand and intrastrand couplings. There has been significant effort in calculating the couplings in β-sheets and relating them to observables in a 2D IR spectrum.66,68 As shown in Figure 2, the linear FTIR spectrum is dominated by two excitonic modes, referred to as the a+ and a− modes. It can also be seen that the intersheet couplings dominate and lead to the intense, low-frequency mode at about 1620 cm−1. The large frequency shift and increase in transition dipole strength allow 2D IR to better discriminate between random coils and β-sheets.68 In combination with isotope labeling, this makes 2D IR and FTIR spectroscopies powerful tools to monitor changes in protein secondary structure on the time scale of picoseconds to hours.
Figure 2.
(a) Simulated IR absorption spectra of 210–510 β-sheets. (b) The inverse participation ratios of each of the normal modes. (c) The Fα (M) spectrum, which is approximately a measure of the number of strands participating in a given normal mode. Reproduced with permissionfrom ref 66. Copyright 2004 American Chemical Society.
3.4. Effects of Disorder
In realistic systems, there is a distribution of local mode frequencies due to hydrogen bonding and solvent fluctuations. Additionally, structural disorder can lead to a distribution of the vibrational couplings. In this case, to simulate a realistic 2D IR spectrum, one must include some standard deviation of the local mode frequencies and couplings about their mean values. One would then generate many Hamiltonians, diagonalize them individually with some phenomenological homogeneous dephasing time, and sum the resulting spectra.36
A distribution of local mode frequencies is often referred to as “diagonal disorder” because its effects are observed along the diagonal of the Hamiltonian in the local mode basis. These diagonal fluctuations serve to effectively localize the excitons to their local modes because the disorder negates the effect of the coupling. Additionally, the fluctuations in the coupling, β, effectively randomize the effect of the mixing and can make normally forbidden modes become IR-active.36 Fluctuations in the diagonal and off-diagonal elements can also lead to line shape effects, such as disorder-induced localization and exchange narrowing, as observed in electronic and vibrational molecular aggregates.69–71
In a conventional FTIR spectrum, it can be extraordinarily difficult to determine if there is significant structural or local mode disorder. However, Ge et al. noted that 2D IR spectroscopy is exquisitely sensitive to the differences in these two cases.72 When the diagonal disorder dominates, the cross-peaks are elongated parallel to the diagonal, because they maintain the line shape of the fundamental peaks. When experimentally observed, this is often referred to as a positive vibrational frequency correlation. If the standard deviation of the coupling is much greater than the distribution of local mode frequencies, then the cross-peaks are effectively rotated so that the energy levels become negatively correlated, or anticorrelated, as shown in Figure 3.40 In practice, it is difficult to distinguish between these two cases because both environmental and structural disorder are present. Additionally, the peaks of interest need to be sufficiently resolved. However, there have been recent cases where frequency correlations do give a more detailed understanding of the system.73
Figure 3.
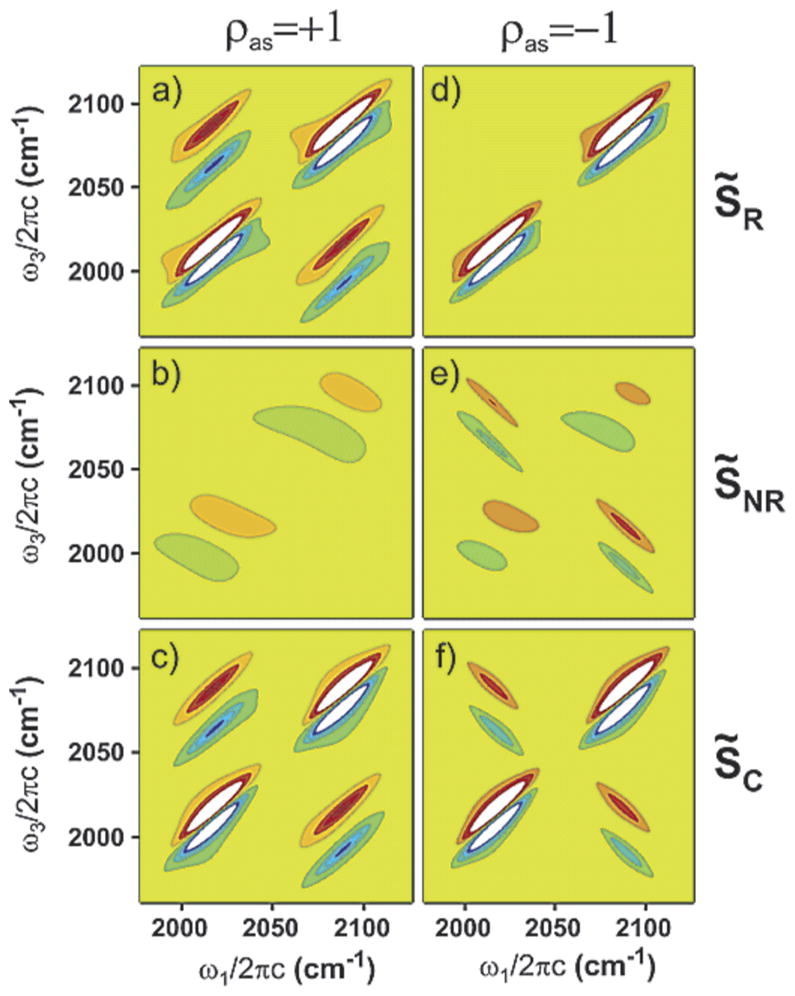
Effects of correlated line broadening on 2D line shapes for fully correlated (ρpq = +1) (a–c) and fully anticorrelated (ρpq = −1) (d–f) cases for rephasing (a, d), nonrephasing (b, e), and 2D correlation spectra (c, f). The simulations are done for the RDC six-level system assuming that the dynamics of system bath interactions are completely separable into fast (Γaa = Γss = Γas = 2 cm−1) and slow (σaa = σss = σas = 10 cm−1) components. Note that in the case of ρpq = +1 cross-peaks are tilted parallel to the diagonal in the rephasing spectrum (a), and the amplitudes of the cross-peaks are suppressed relative to diagonal peaks in the nonrephasing spectrum (b). For ρpq = −1, the cross-peaks are tilted perpendicular to the diagonal, and their amplitudes are enhanced relative to the diagonal peaks in the nonrephasing spectrum (e), whereas the cross-peak amplitudes are suppressed in the rephasing spectrum (d). The difference in the cross-peak intensities in the correlation spectra (c–f) is due to the imbalance in the number of corresponding pathways in the generation of the nonrephasing signal. The contours are plotted at 8% intervals. Reproduced with permission from ref 40. Copyright 2003 American Chemical Society.
In addition to the static distribution of local mode energies and structures (which create a distribution of couplings), these quantities can also be dynamic. That is, as we change the waiting time of the 2D IR spectrum, individual site energies and couplings could be modulated. This leads to a change in line shape in a 2D IR spectrum. This dynamic disorder is best described by a line shape function as opposed to generating many different Hamiltonians and adding some fluctuations about a mean value. We describe this in more detail in section 3.7.
3.5. Polarization Controlled 2D IR To Determine Structure
Since 2D IR is a coherent spectroscopy, all of the interacting fields have polarizations that can be independently controlled. Control of the polarization of the pump and probe fields has long been used to measure reorientation dynamics in electronic transient absorption spectroscopy.74 This is useful because it allows for the precise determinations of transition dipole orientations. The same approach can be extended to 2D IR as well.75–77 As mentioned above, the cross-peaks in a 2D IR spectrum allow for unambiguous measurement of the coupling constant between local vibrational modes. That being said, the cross-peaks are often overlapping with the diagonal peaks. This leads to complex interference, which can complicate spectral interpretation. Zanni et al. were the first to show that by exploiting the polarization dependence of a 2D IR spectrum, one can mathematically combine distinct spectra to eliminate diagonal peaks and retain only the cross-peaks.78 By measuring a 2D spectrum with the pump polarized parallel to the probe pulse and subsequently measuring the spectrum with the pump pulses perpendicular to the probe, the spectra can be mathematically combined according to eq 15, eliminating all contributions to the spectrum from the parallel component of the transition dipoles.
| (15) |
Although, in principle, this eliminates the diagonal peaks, in practice there is always some ambiguity in the data due to longterm laser power fluctuations and fast anisotropy decays due to energy transfer or fast dipole reorientations.35 The Tokmakoff group showed that one can measure the parallel and perpendicular signals simultaneously to help alleviate noise from these power fluctuations.79 Such experimental schemes can now be implemented more easily with the availability of improved infrared detectors, as has recently been demonstrated. 80 Additionally, Zanni et al. showed that the pulses could be polarized according to (−45°,45°,0°,90°) to experimentally eliminate the Feynman pathways contributing to the diagonal peaks.78 Polarization control can also be used to measure the rotational relaxation or only measure population transfer by measuring a 2D spectrum with pump pulses polarized at the so-called “magic angle”.36 However, since the rotational correlation times of most proteins are much longer than the time scale of the 2D IR experiment, we will not explore this in detail.
3.6. Isotope Labeling in 2D IR
For large proteins, the amide I band is often too complicated to directly measure couplings because a protein has many amino acids that a congested line shape is created. Isotope labeling has proven to be powerful tool in FTIR spectroscopy to determine molecular structure.81,82 An isotope label effectively adds static diagonal disorder to a particular local mode. In an uncoupled molecule this can shift a transition away from the broad line shape of natural absorption. In a linear coupled chain, this static diagonal disorder disrupts the coupling and effectively uncouples the amino acid from the rest of the chain. This can be an extremely useful technique to determine couplings between two chromophores in extended excitonic structures. Consider an infinite linear chain of coupled oscillators that, in general, will not have identical couplings. If we want to determine the couplings between oscillator i and i + 2, it is extraordinarily difficult to measure this from the excitonic spectrum. However, we can isotope label both of them, which decouples them from the extended vibrational exciton by changing the energy spacing between the isotope label and natural isotopes in the extended linear chain, but since their local mode energies are still about the same, the band will split due to the coupling between them. The splitting from the local mode frequency can then be used to determine this coupling constant. As mentioned earlier, this would be even easier with a 2D IR spectrum, where the cross-peaks and anharmonicities can be used to determine the couplings between isotope labels. Additionally, environments local to specific residues can also be interrogated using this approach, which is described later.
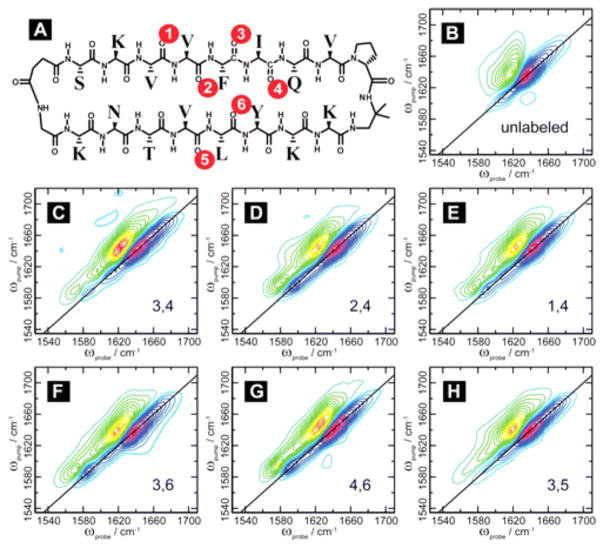
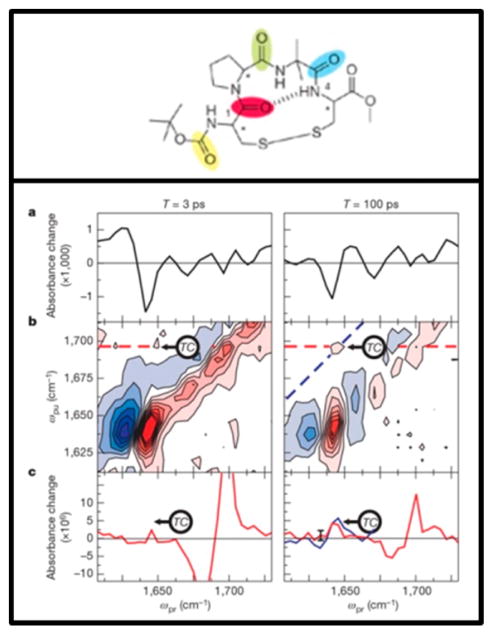
In proteins, we often consider the amide I band, which primarily consists of the C=O stretch with some contribution from the C–N stretch and N–H bends. Labeling with 13C=O gives a small frequency shift of about 15–30 cm−1,83 but it is still largely obscured by the natural amide I line width. Instead, one can label both the carbon and oxygen. Labeling of the 13C=18O leads to a shift of ~60 cm−1.83 This is the most useful method to shift individual amino acid absorptions away from the main amide I band, and there are many methods in the literature with which to incorporate site-specific isotope labels in a peptide synthesis.27,84 Figure 4 shows 2D IR spectra of a model parallel β-sheet with the indicated residues (in Figure 4A) labeled. The authors used this isotope labeling scheme to measure the efficacy of coupling models with the goal of using it to look for spectral signatures of parallel β-sheets in more complicated systems.85
Figure 4.
Structure of the macrocyclic peptide with numbering scheme for isotope-labeled pairs (A). 2D IR data for the unlabeled macrocycle (B) and for the doubly labeled macrocycle (C–H). This figure demonstrates the shift observed upon isotope labeling the amide backbone. Reproduced with permission from ref 85. Copyright 2012 American Chemical Society.
2D IR has several advantages over conventional FTIR when it comes to isotope labeling. The 2D IR signal scales as the fourth power of the transition dipole, whereas linear IR scales as the dipole squared.36–38 This leads to enhanced spectral contrast and often leads to better resolution of the isotope-labeled peak.86,87 Additionally, Woys et al. showed that line shape analysis of a 2D IR spectrum can determine the environment, secondary structure, and orientation of a membrane-bound peptide.88 Moran et al. have shown that segmentally isotope labeled domains of a large protein can determine the secondary structure of the N-terminus and C-terminus separately.30 Recently, Peuker et al. showed that non-natural isotope labels can be included in large proteins using cell-free expression.89 These latter two methods are extremely exciting, as they have opened the door to isotope labeling proteins regardless of size.
3.7. Line Shapes and Dynamics
The frequency of a vibrational probe is sensitive to the motions of nearby atoms, particularly those with net charges. The molecular motions that affect the vibrational frequency and its evolution range from ultrafast time scales, such as hydrogen-bond making and breaking,90,91 to slower structural reorganizations, such as enzyme binding pocket dynamics.6 The vibrations thus represent site specific, minimally perturbative probes of structure and dynamics in a wide range of examples. The vibrational frequency correlation function or its spectral representation carries the essential information regarding the properties of these motions. The frequency correlation function, however, cannot be accurately obtained from linear spectroscopies.92 This makes 2D IR an essential technique for exploring the structural dynamics in biological systems. A full interpretation of the microscopic origins of the factors influencing these frequency correlation functions have stimulated detailed quantum simulations,61,62,91,93–101 but in many cases, the experiments can lead to direct quantitative inferences obtainable through judicious choice and variation of experimental parameters. Certain vibrational modes, such as amide I, carbonyl, and C≡N stretches, that are either inherent to or easily incorporable into proteins serve as noninvasive probes of local dynamics and structure. This is particularly advantageous, as other techniques that are capable of exploring ultrafast structural dynamics, such as time-resolved fluorescence, need incorporation of fluorescent probes that can occasionally be structurally perturbative, leading to limited applicability of the technique. A 2D IR experiment, as mentioned above, involves interaction of the chromophore with a sequence of three ultrashort infrared pulses. The 2D IR echo signal depends on whether the inhomogeneous distribution of frequencies originally present survived during the waiting time. Thus, the evolution of 2D spectra with the waiting time reveals the signatures of fast dynamics that cause the frequency distributions to decay. The decay of the inhomogeneous distribution of frequencies is embedded in the frequency autocorrelation function, which can be modeled by a single or a sum of exponential decays if the frequency fluctuations follow Gaussian statistics.36–38 The frequency correlation appears in the relaxation functions of the third-order molecular response:36–38
| (16) |
| (17) |
The line shape functions g(t) are given as
| (18) |
Here the frequency fluctuations shown in eq 18 are assumed to follow Gaussian statistics. The correlation function can therefore be modeled as a sum of Kubo functions:36–38
| (19) |
where τ denotes the time scale of the decay of the frequency correlations, and Δ represents the standard deviations of the distribution of frequencies that lose correlation over that time scale. Each pair {Δ, τ} represents an independent relaxation process within the total inhomogeneous distribution. In reality, it frequently occurs that there is a homogeneous dephasing that can be incorporated as part of eq 19 by choosing the product Δτ to be very small for one of the terms.92,102 Furthermore, given that vibrational lifetimes limit the actual time window over which the frequency correlation decay can be observed, processes involving large amplitude changes in the backbone or side chain structure are too slow to impact the correlation decay in a significant way and are modeled by setting the correlation time of one of the components to infinity. A simplified and commonly used form for the correlation function thus obtained is103
| (20) |
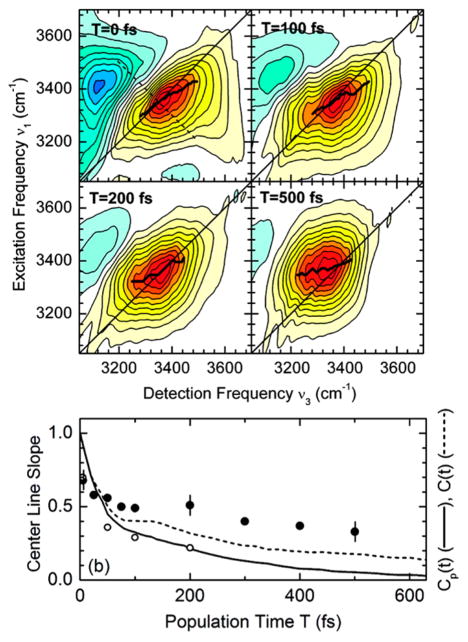
where is known as the pure dephasing time scale. The frequency domain 2D spectrum is directly proportional to the real part of the Fourier transform of the molecular response in eq 17. The inhomogeneity of the frequency distribution is reflected in the 2D line shape as an elongation along the diagonal line. As the waiting time is increased in a 2D IR experiment, the decay of the frequency correlation function causes the 2D line shape to change, becoming more symmetric with increasing loss of correlation, as depicted in Figure 5. The diagonal line width is thus directly related to the inhomogeneous distribution of frequencies. The inhomogeneity, as mentioned before, can arise out a large number of processes that can span a wide range of time scales, from solvent fluctuations to conformational disorder.104 The frequency correlation decay can be quantitatively evaluated by tracking the evolution of the shape of the 2D contours.105–107
Figure 5.
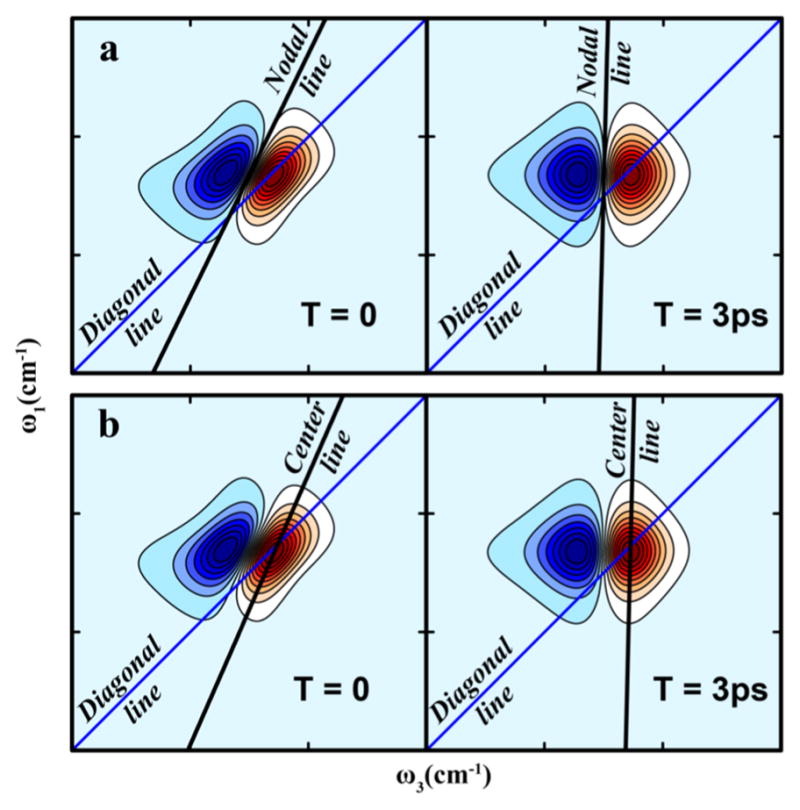
Relaxation of the frequency autocorrelation function (FFCF) is reflected in the waiting time (T) evolution of 2D IR spectra: the spectra are more elongated at early T and become more symmetric at longer T as the FFCF decays. The correlation relaxation can be quantitatively measured through slope of the 2D contours as a function of T. (a) The nodal line slope and (b) the center line slope.
One way to follow this shape change is to record the slope of the nodal line between the positive and negative peaks of the 2D spectrum (Figure 5a). This was first demonstrated by Kwac and Cho and shortly thereafter by Skinner and co-workers for model peptides such as N-methylacetamide (NMA)91,108 and has since been successfully applied to a variety of systems to probe frequency correlation dynamics.109,110 The nodal line slope method, however, depends strongly on the overlap of the fundamental and overtone peaks in a 2D spectrum and is only well-suited to systems with small vibrational anharmonicities. Another approach that circumvents this limitation is the center line slope (CLS), which is defined as the slope of the line joining the 2D fundamental peak maxima (Figure 5b). The CLS method was first demonstrated by Fayer and co-workers and has since been accepted as the method of choice in the field for extracting correlation time scales from 2D IR spectra.105,106 Besides the slope of the 2D contours, other experimental parameters that reflect the spectral evolution can also be utilized, such the ellipticity111 and integrated photon echo peak shift10,112, that have been shown to be accurate measures of the correlation function. A review of many of the popular techniques for extracting correlation dynamics was published by Tokmakoff and co-workers.16
Another experimental quantity that 2D IR makes significantly easier to access is the vibrational lifetime. The vibrational lifetime of an oscillator depends on coupling to the bath modes and thus implicitly reflects the nature of the solvent around a vibrator.36,113 Traditionally, vibrational lifetimes have been estimated through frequency-resolved infrared pump–probe spectroscopy, which is of course related to 2D IR through the projection slice theorem. However, the additional frequency axis in 2D IR helps resolve specific resonances, better allowing for more accurate determination of lifetime relaxation parameters, which can be used to unambiguously access nuanced structural features.114
4. USING 2D IR OF THE AMIDE I VIBRATION TO DETERMINE STATIC PROTEIN STRUCTURE
With the ability to measure vibrational couplings, 2D IR spectroscopy has allowed the determination of the structure of many peptides. NMR and X-ray crystallography are two extraordinarily successful techniques in protein structure determinations.115–118 However, structures of protein ensembles that are kinetically evolving are difficult to study with current NMR and X-ray technologies. Early 2D IR experiments on biomolecules focused on small polypeptides, with the goal of eventually applying 2D IR to more complex scientific problems. In one of the first experimental implementations of 2D IR, Hamm et al. studied three small peptides, apaamin, scyllatoxin, and bovine pancreatic trypsin inhibitor.49 The authors of this study used a simple excitonic model to show that the amide I vibrations are indeed delocalized. They were also the first to note that, in principle, 2D IR can uniquely determine all elements of the coupling matrix and be related to the three-dimensional structure. Another early 2D IR experiment related the cross-peak position and intensities to the three-dimensional structure of a cyclic pentapeptide.54 Comparing the experimental results to 2D IR spectra from density functional theory (DFT) calculations revealed extraordinary agreement between theory and experiment. This study also showed that through-bond mechanical coupling is an important mechanism that must be accounted for in the 2D IR spectrum of small peptides. These first experiments on small peptides have led to extensive application of 2D IR spectroscopy to determine protein structures. Woutersen and Hamm used a coupling map computed with ab initio calculations to determine the dihedral angle of trialanine from couplings measured with polarization-selective 2D IR spectrscopy.119
2D IR spectroscopy has been exceptionally successful in studying the secondary structure of proteins. As stated earlier, excitonic features with delocalized vibrations dominate the infrared spectrum of α-helices and β-sheets. Fang et al. have used 2D IR spectroscopy to precisely measure the couplings in a model α-helix using isotope labeling.120 This experiment established that, with the exception of nearest neighbors, a transition charge coupling model could reproduce observed frequencies and anharmonicities of the isotopically edited α-helix. Nearest-neighbor couplings required consideration of through-bond mechanical coupling. The Hochstrasser group also used isotope labeling in conjunction with line shape measurements to show that selected residues had a broader structural distribution than others.120 Fang et al. also used 2D IR on a transmembrane protein to measure the coupling between separate tertiary helices.121
Ge and co-workers have made significant progress in using 2D IR spectroscopy to study helical peptides. This review, and most 2D IR studies, have focused on the amide I stretch because of its structural sensitivity. Peptides also exhibit the so-called amide II stretch, which consists of the in-plane bend of the NH group and the CN stretching.56 Maekawa et al. have shown that cross-peaks between the amide I and amide II modes, in conjunction with isotope labeling, could be used to determine a single helical turn in a 310-helical peptide.122–125 They additionally showed that local mode frequency maps could be used to improve the structural sensitivity of 2D IR.126
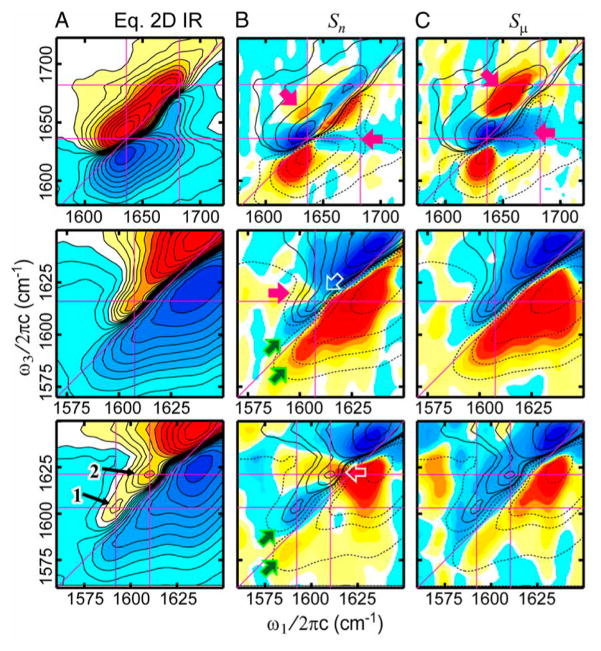
Many experiments have focused on understanding the 2D IR spectra of β-sheets. β-Sheets are interesting because they are a common structural motif in amyloid diseases that include Alzheimer’s disease, type II diabetes, and cataracts. Demirdöven et al. first used 2D IR to measure the couplings of an antiparallel β-sheet.68 In this work, the authors showed that 2D IR could be sensitive to both high- and low-frequency modes of β-sheets, even if the high-frequency one was not visible in the conventional FTIR spectra. Figure 6 shows simulated 2D and FTIR spectra and illustrate that through the cross-peaks 2D IR can detect the coupling between the a+ and a− modes indicative of a β-sheet. Kim et al. have used isotopic dilution in conjunction with 2D IR to determine the distance between selected residues in amyloid fibers of Aβ40.127 Woys et al. studied the coupling in a parallel β-sheet macrocycle. They found that there was significant environmental disorder in the peptide that led to negligible frequency shifts. However, because couplings redistribute oscillator strengths, small changes in coupling can be determined by differences in peak intensities.85
Figure 6.
Calculated infrared (top) and 2D IR spectra (bottom) for an idealized extended β-sheet composed of a 3 × 3 lattice of the unit cells. Calculations are for (a) periodic boundary conditions and (b) open boundary conditions. The 2D IR calculations assumed a crossed polarization (XXYY) condition. Lorentzian line shapes are used with a width of (a) γ = 4 cm−1 and (b) γ = 2.5 cm−1. Positive features are shown in red, and negative features are shown in blue. Equally spaced contours are plotted between −10% and 10% of the a-diagonal peak maximum. Reproduced from ref 68. with permission. Copyright 2004 American Chemical Society.
In the past 10 years, there has been significant progress in using 2D IR to study the static structures of protein aggregates.86,128 Moran et al. have used 2D IR to study the structure of γD-crystallin protein, which is implicated in cataract formation.30 The authors were able to individually label distinct domains of the protein, which allowed them to identify that the C-terminal domain forms extended β-sheets. Lam et al. used a combined molecular dynamics and spectroscopic approach to generated incredible agreement between simulation and theory for such a large protein.129 Moran et al. also showed that UV-B radiation could induce aggregation in the γD-crystallin protein.130 These experiments are very exciting, as 2D IR spectroscopy is now being used to impact understanding outside of the specialized field.
Currently, there has been significant interest in understanding the three-dimensional arrangement of proteins, beyond measuring the secondary structure. One of the most exciting applications of 2D IR was the work of Remorino et al.86 The authors used isotope dilution strategies to measure the couplings in a transmembrane protein. Measured coupling constants, as determined by the experiment, were then used as constraints in simulations to determine the three-dimensional structure. Baiz et al. have used Markov state models in conjunction with isotope labeling to study the structural disorder in a folded protein.131 The simulations and site-specific spectral probes of the isotope labels helped to identify ordered and disordered states in a β-loop. This study also showed that the isotope labels can be used to measure solvent exposure. This work helped show that 2D IR spectroscopy can be used to help parametrize and improve existing force fields to help simulations capture the entire range of equilibrium structures in a folded protein.
2D IR spectroscopic studies have progressively addressed more sophisticated problems. With advances in laser technology, 2D IR spectrometers are now significantly easier to design27,132,133 and even commercially available. The past decade has also seen integration of theoretical predictions, such as molecular dynamics, into 2D IR studies, and these combined approaches have furthered the scope of 2D IR as a tool in structural biology.94,134 Although 2D IR spectroscopy has not yet achieved the wide applicability of X-ray crystallography and NMR in structure determination, in our opinion, there are many problems in biochemistry and biophysics that 2D IR is uniquely suited to study. All of the examples given thus far have focused on the characterization of static structures. As we describe below, the true success of 2D IR spectroscopy is the characterization of structural heterogeneity and fluctuations over a wide range of time scales.
5. PICOSECOND STRUCTURAL DYNAMICS
5.1. Dynamics Assessed Using Protein Backbone Vibrations
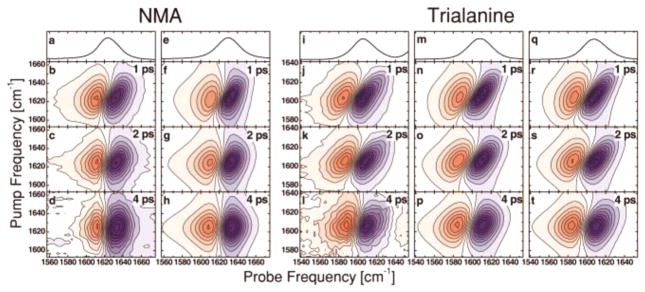
The amide stretches of the protein backbone serve as simple and nonperturbative probes of solvent and protein dynamics. In 2001, Zanni, Hochstrasser, and their co-worker measured the spectral diffusion time scales of N-methylacetamide (NMA) in deuterated water.135 The measurements found a pure dephasing time scale of 1.12 ps for NMA. Shortly after, Woutersen and Hamm used 2D IR to compare the conformational heterogeneity of the amide I band of trialanine to that of NMA.119 As shown in Figure 7, in contrast to NMA, the amide I band of trialanine exhibits significantly more inhomogeneous broadening, even up to waiting times of 4 ps, which was attributed to conformational transitions of the backbone. Interestingly, both trialanine and NMA showed a correlation decay time scale of 1.6 ps, which points to the fact that the correlation decay is dominated by solvent fluctuations and should be interpreted as characteristic of solvents. Kim and Hochstrasser136 investigated the spectral dynamics observed in aqueous solutions of alanine dipeptide and observed spectral diffusion time scales of 0.8 ps for all the amide modes, further demonstrating that the correlation time scale is predominantly a solvent property. These early results were of fundamental importance, as they established the parameters necessary for understanding amide dynamics in more complex environments like proteins. The spectral dynamics of NMA has since been revisited by other researchers, notably by DeCamp and coworkers, 137 and more recently by Ghosh and Hochstrasser.103 Both studies reproduce the ~1 ps correlation time scale in water (D2O). DeCamp et al. further showed that in polar solvents other than water, the frequency relaxation is significantly slower, reinforcing the idea that the FFCF and its decay are directly associated with the local environment of a vibrational mode.137 It should be noted that the FFCF actually decays on two time scales: one is approximately 1 ps, as mentioned above. The other is below 100 fs and is therefore difficult to accurately determine with ~100 fs pulses typically used in 2D IR experiments and hence is often approximated by a pure dephasing component.
Figure 7.
Linear IR and waiting-time-dependent 2D IR spectra of N-methylacetamide (NMA) (a–d) and trialanine (i–l) in D2O. The 2D spectra of alanine look more elongated along the diagonal, even at waiting times at long as 4 ps, compared to those of NMA, indicating more inhomogeneous broadening. The FFCF relaxation parameters were obtained through fitting the experimental data with simulated spectra, which are shown in panels e–h and m–t. Reproduced with permission from ref 104. Copyright 2002 AIP Publishing.
The 2D IR experimental observations have been brought into relation with molecular level pictures through detailed theoretical models.91,94,138 MD simulations and so-called empirical frequency maps developed through electronic structure calculations now allow for calculating vibrational frequency distributions and the associated correlation function. The theoretical results are consistent with the bimodal decay observed in experiments91 and go on to reveal that the slower ~1 ps time scale is caused by hydrogen bond making and breaking between both the carbonyl and N–H group of the amide moiety and adjacent water molecules. The fast components of the FFCF are caused by the librational motions of water molecules not always H-bonded to the amide.
The preceding discussion considers a single, isolated oscillator. Spectral evolution of vibrators whose frequency distributions are coupled can be significantly more complex to interpret and can exhibit oscillatory correlation decay.139,140 Investigating site-specific, spectrally isolated vibrations in a protein can be accomplished by isotope labeling or incorporating unnatural vibrational probes. The latter is discussed in detail in a later section; we start with the first by surveying 2D IR reports of ultrafast dynamics using isotopic substitution of amides (12C=16O to 13C=18O) in proteins. Taking advantage of the spectral isolation provided by isotope labeling, there have been many reports of the correlation time scale for amide modes in a variety of systems ranging from small peptides to large proteins. Fang and Hochstrasser reported 2D IR spectra of isotopically edited amide modes of a 25-residue alanine-rich α-helix.141 The fast component in the FFCF was evaluated to estimate the dynamics of these amide frequency distributions using the nodal line slope approach and calculating the first moment of the integrated photon echo peak shift. Both approaches showed good agreement, providing evidence that these metrics can be used interchangeably. Furthermore, wider line widths were observed for residues 14 and 11 compared to 12 and 13, and this was attributed to effects of nearby lysine residues on the intrahelical hydrogen-bond network. This work was the first among many that correlated 2D IR diagonal line widths to inhomogeneity caused by hydrogen bonding. Shortly after, Mukherjee, Zanni, and their co-workers used 2D IR spectroscopy with isotope labeling to measure the vibrational dynamics of amide I modes in the transmembrane domain of the CD3ζ protein.12 The human CD3ζ is a 163-residue-long α-helical membrane protein essential for T cell receptor expression.142,143 Transmembrane proteins are vital components of cells, transporting ions and water across the cell membrane.144,145 The water structures present in these protein cavities can be drastically different from the bulk, from structured clusters to single file.144–146 In most transmembrane proteins, the water structures form by interactions of water molecules with the polar peptide units that line the interior of the channel and therefore mirror the structural conformations of the backbone.147–149
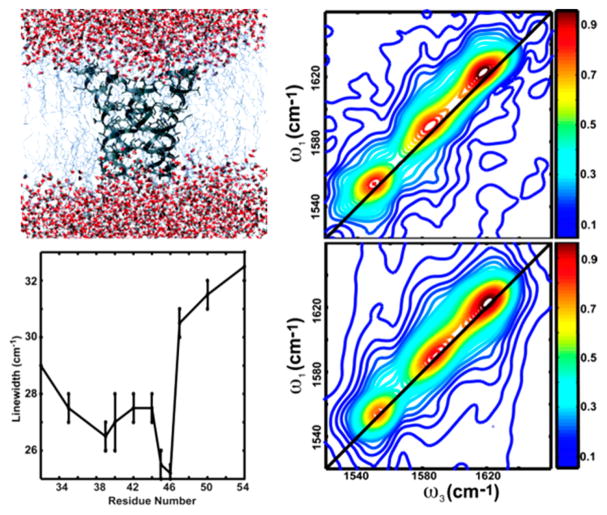
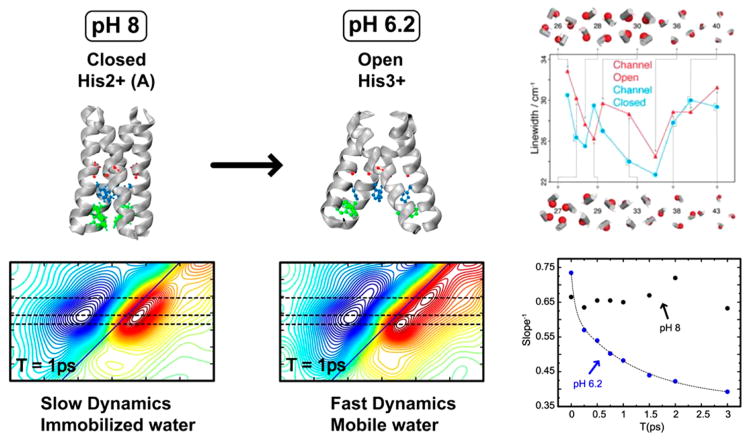
One of the very first applications of 2D IR to transmembrane proteins, the work by Mukherjee and co-workers, demonstrated that the 2D IR diagonal line widths can be used to track residue-specific hydration in a complex biomolecule (Figure 8). While this work did not have any explicit structural implications, the authors subsequently expanded this approach to investigate gating mechanisms and structural transitions in another transmembrane protein: the M2 channel. M2 is a homotetrameric transmembrane protein found in influenza viruses.11,150 The channel is gated to transport protons across the membrane to acidify the viral interior only at low pH.151 The channel activation is associated with protonation of histidine residues, which shifts the conformational equilibrium toward a structure where the pore is more open to the viral interior. This causes the water density in the pore to change between the open and closed conformations. Using a combination of linear and 2D IR spectroscopies, the authors mapped the local hydration of pore-lining residues across the transmembrane domain and their response to the channel structural transition (Figure 9) and proposed a helix rotation mechanism underlying the gating properties of the protein.11 These experiments helped firmly establish 2D IR as one of the techniques of choice for understanding transmembrane protein structural dynamics. The first evaluation of spectral diffusion time scales in transmembrane proteins came from the work of Ghosh, Hochstrasser, and their co-workers110 who examined the correlation dynamics of a specific pore-lining residue in the M2 protein and found that while the FFCF shows no appreciable decay in the closed state, it decays on a time scale of ~1.3 ps in the open state (Figure 9). This result shined light on how the water structure in the channel changes from “icelike” to “liquidlike” in response to the conformational transition of the tetramer, a conclusion that has also been supported by MD simulations and demonstrated that conformational dynamics of a protein can be interpreted through the ultrafast relaxation of water associated with it. The authors subsequently extended this premise to investigate binding of anti-influenza drugs in the M2 tetramer9 and uncovered that the water in the channel becomes more liquidlike upon drug binding, thereby contributing a favorable entropic factor to the drug-binding thermodynamics. This experimental result was in close agreement with predications from MD simulations147 and served as the first experimental verification of drug docking mechanisms in the channel that had previously been suggested from theoretical investigations.
Figure 8.
Residue-specific 2D IR spectra of the transmembrane protein CD3-ζ. (A, top left) The proposed structure of the transmembrane domain. (B, right) Absolute-value 2D IR spectra of the isotopically labeled V53 residue and the unlabeled amide I band. (C, bottom left) The variation of 2D IR diagonal line widths across the transmembrane domain, exposing local hydration effects. Reproduced with permission from ref 12. Copyright 2006 National Academy of Sciences.
Figure 9.
2D IR spectroscopy of the M2 proton channel. As the channel undergoes a conformational transition from a closed to an open state, the water in the pore becomes more liquidlike, as reflected in the evolution of the slope (right). Manor et al. have also shown using linear and 2D IR spectroscopy that the diagonal line width, which is sensitive to hydration of pore-lining residues, reflects the conformational change. Adapted with permission from ref 11 (Copyright 2011 National Academy of Sciences.) and ref 110 (Copyright 2009 National Academy of Sciences.).
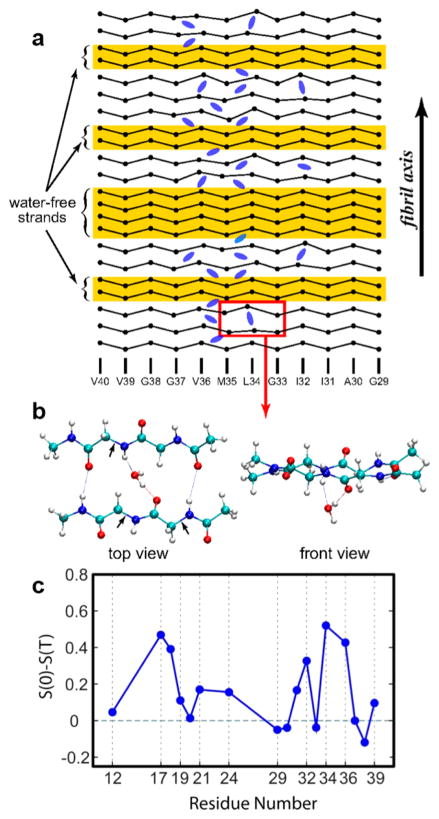
2D IR has also been utilized to locate kinetically or functionally confined water in proteins that have otherwise hydrophobic interiors. Kim, Hochstrasser, and their co-workers reported 2D IR experiments on isotopomers of β-amyloid (Aβ40) fibrils that accumulate as plaques in the brain tissue of Alzheimer’s patients.109,127 The structural parameters from these experiments were in excellent agreement with models of β-amyloid developed by Tycko and co-workers.152 Interestingly, it was observed that the 2D IR spectra of the residues in certain regions of the sequence exhibit an ultrafast decay (~1 ps) of the FFCF, which is typically seen in aqueous solutions. The variation of the slope of the 2D contours, shown in Figure 10, revealed that the fast dynamics is only associated with the apposed pairs 34, 36 and 17, 18, which led to the conclusion that water exists in these regions. This result was fundamentally important, as there had been little evidence for water in extended β-structures. While the exact structural implications of this observation were unclear at the time, more recent work153 has expanded on these experiments and studied fibrils under various conditions and different ages to confirm that structurally significant water molecules are present in the freshly formed fibrils and remain trapped within fibrils and mobile over 4 years. These results show that the interface between β-sheets in an amyloid fibril is not dry, and water trapping must be incorporated into structural models of amyloid fibrils.
Figure 10.
2D IR spectroscopy of β-amyloid (Aβ-40) revealed the existence of kinetically trapped water. (a) A pictorial representation of possible locations of water molecules inside Aβ40 fibrils. (b) Enlarged view of the region outlined in part a. The evolution of nodal slopes of specific residues, shown in part c, indicates the presence of water at certain interstrand locations. Adapted with permission from ref 109 (Copyright 2009 National Academy of Sciences.) and ref 103 (Copyright 2011 Elsevier.).
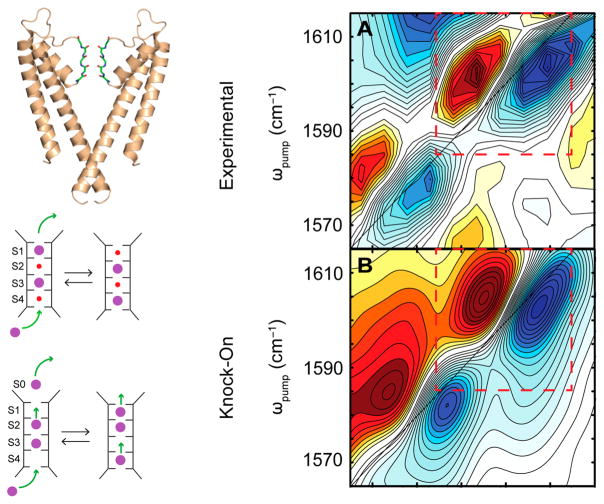
Very recently, 2D IR spectroscopy has been employed to expose ion configurations in the selectivity filter of a potassium channel, KcsA.154 Potassium channels play a vital role in cellular biology by regulating the membrane potential.155–158 The ultrafast time resolution of 2D IR allows one to capture snapshots of ion distributions in the channel that are too short-lived to be verified otherwise. Using 2D IR in combination with site-specific isotope labeling of amino acids in the ion channel, researchers were able to discriminate between proposed mechanisms of ion permeation.159 The left panel of Figure 11 shows the structure of the selectivity filter and the proposed mechanisms of ion transport. The right panel shows an experimental 2D IR spectrum along with a simulated spectrum for the proposed ion configuration. The 2D IR spectrum and the complementary MD simulations point toward a “knock-on” model, wherein the selectivity filter is simultaneously occupied by two K+ ions. Further analysis of the line shapes and frequencies revealed the presence of water in the filter, consistent with streaming potential measurements.
Figure 11.
Left panel: Structure of the potassium ion channel, KcsA, and schematic of the knock-on (top) and knock-off (bottom) mechanisms of ion transport. Right panel: (A) experimental 2D IR spectrum and (B) simulated 2D spectrum of the knock-on model. Reproduced with permission from ref 154. Copyright 2016 American Association for the Advancement of Science.
5.2. Dynamics Assessed Using Other Vibrational Modes
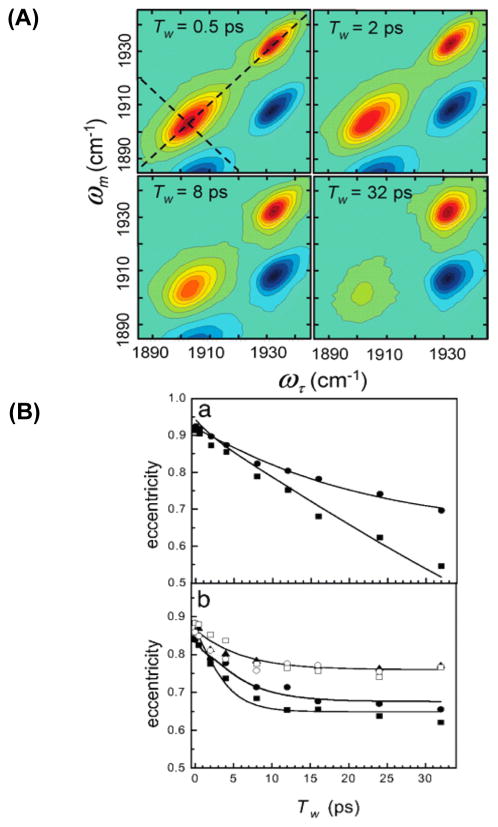
Fayer and co-workers were the first to use the carbon monoxide absorption at about 2000 cm−1 to study protein dynamics with 2D IR. By exploiting the binding of these molecules to heme proteins, they were able to study dynamics local to the binding pocket. Building on previous three-pulse photon echo experiments, 160 the first 2D IR measurements were performed on horseradish peroxidase (HRP).161 Since the heme-bound CO is in the vicinity of the catalytic active site, the time dependence of the CO vibrational frequency can be used as a probe of local active site dynamics. Figure 12A shows the 2D IR spectra of HRP, and Figure 12B shows a comparison between the decay of the eccentricities of the 2D IR line shape (proportional to the FFCF). Upon substrate binding, the nature and dynamics of the active site change dramatically. The authors suggested that the drastic change in dynamics could be evidence that the enzyme uses the dynamics to restrict motion of residues that catalyze the reaction and thus contribute to the decrease in reaction activation energy. Similar experiments on the neuroglobin protein were performed and the results were compared to the structural dynamics of myoglobin mutants.
Figure 12.
(A) 2D IR spectra of free HRP as a function of increasing waiting time. The dashed lines illustrate the diagonal and antidiagonal slices through the data for calculating the eccentricity parameter, a measure of the FFCF. (B) A comparison of HRP dynamics in the free and substrate-bound states. (a) Time-dependent eccentricities of the blue (circles) and red (squares) states of free HRP. (b) Eccentricities of HRP ligated with 2-NHA (filled squares), BHA (filled circles), BZA (open squares), BZH (open circles), and NMBZA (triangles). The solid lines were obtained by simultaneously fitting the linear and 2D IR data to determine the FFCFs. Reproduced from ref 161. with permission. Copyright 2007 National Academy of Sciences.
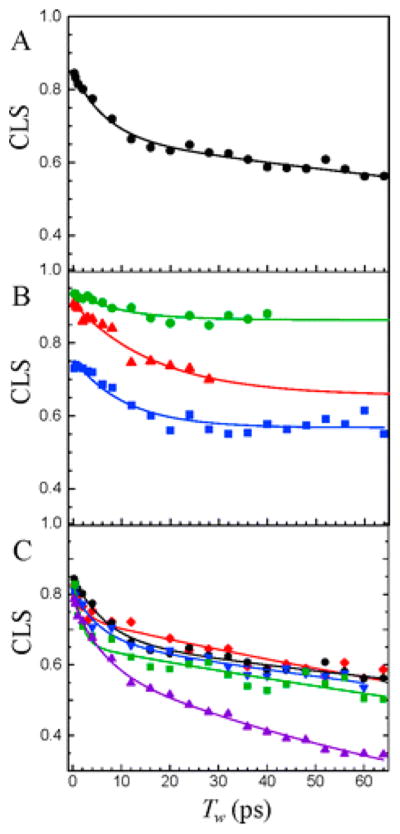
The Fayer group has made significant advances in unraveling the ultrafast dynamics of proteins in the cytochrome family. The first experiments studied the dynamics of folded and unfolded forms of cytochrome c.162 Significant spectral diffusion was observed in both the folded and denatured forms of the protein. However, the denatured form retained a residual inhomogeneous component absent in the native experiments. This led them to conclude that there was a larger distribution of conformations in the unfolded state and that these were not completely sampled on the time scale of the 2D IR experiment. Further experiments by Thielges et al. probed the effect of substrate binding on the dynamics of the protein active site.163 The dynamical parameters extracted from the decay of the FFCF were used to correlate the enzyme’s specificity toward particular substrates. Figure 13 show some of these FFCF decays. This data was particularly intriguing, as it provided evidence that the so-called “lock-and-key” mechanism of enzyme activity was too simplistic and knowledge of dynamics is imperative for a complete understanding of catalysis.
Figure 13.
CLS decay curves and corresponding exponential fits for (A) cyt P450cam–CO bound with its natural substrate camphor. The two time scales seen in the decays are evident. (B) The 1939 cm−1 (red), 1952 cm−1 (green), and 1963 cm−1 (blue) bands of substrate-free cyt P450cam–CO. The fits have been extended for two of the bands as an aid to the eye for comparing to the other curves. (C) The different substrate complexes: camphor (black), camphane (blue), adamantane (green), norcamphor (purple), and norbornane (red). Reproduced with permission from ref 163. Copyright 2011 American Chemical Society.
In addition to ultrafast frequency correlation dynamics, in the past decade 2D IR spectroscopy has also been employed to study picosecond equilibrium kinetics.164–166 In the event that there are chemically distinct species present in equilibrium, interconverting through bond rotations or solvent rearrangement, cross-peaks appear in 2D IR spectra on the time scales of this chemical exchange.165 For example, for an equilibrium given by A ↔ B, where A and B are chemically distinct species with different vibrational frequencies, cross-peaks arise due to population exchange between the species during the population period T. As mentioned in section 2, in 2D IR, the first pulse excites a coherence in A, and the second pulse generates a population in A. The emissive coherence created by the third pulse is put into B if there is a transfer of population from A to B prior to the arrival of the third pulse, leading to a cross-peak:
| (21) |
| (22) |
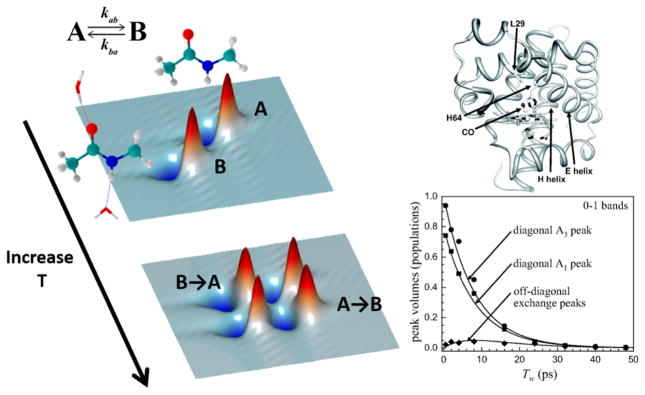
In fact, similar interpretations can be applied to the ultrafast dynamics of liquids: the distribution of frequencies can be thought of as a distribution of solvation environments that evolve into each other on a picosecond time scale. Thus, spectral diffusion observed in 2D IR might be interpreted as exchange among a large number of solvent–solute configurations. Woutersen, Hamm, and their co-workers reported the very first observation of chemical exchange using 2D IR for NMA in methanol, where they measured hydrogen-bond lifetimes through cross-peak dynamics between solvated and unsolvated amide moieties.166 This approach was later expanded and elaborated by Kim and Hochstrasser, who measured hydrogen-bond making and breaking between acetonitrile and methanol,167 and Fayer and co-workers, who applied this technique to study a diverse range of problems, ranging from the complex formation of phenol and benzene164 to observing single bond rotations.168 Since these early reports, there have been a number of applications of chemical exchange 2D IR spectroscopy to examine picosecond conformation transitions in proteins. Bagchi et al. reported picosecond exchange between two conformations of the tryptophan dipeptide in D2O,169 and theoretical analysis indicated that the two states differ with respect to accessibility of the amide group to water, which is restricted in one of the conformations due to rotation of the side chain indole ring. Similar observations have been recently reported for the histidine dipeptide,170 where protonation of the imidazole side chain was shown to regulate water accessibility to the amide backbone. The first observation of conformational exchange in proteins was reported by Ishikawa, Fayer, and their co-workers,171 who investigated conformational switching between the A1 and A3 substates of a myoglobin mutant (Figure 14). Analysis of the cross-peak evolution revealed a time scale of ~50 ps for the conformational transition and served to demonstrate that protein structural dynamics can indeed occur on ultrafast time scales. Bagchi et al. expanded this to include the T67R/S92D double mutant, which has peroxidase catalytic activity.172 MD simulations have also reproduced these experimental results within reasonable accuracy, and the molecular picture that emerges from theory is that the primary structural change between A1 and A3 conformations involves lateral movement of the backbone of His64, which pushes the δ-nitrogen of the imidazole side chain back and forth between two distances from the CO ligand.
Figure 14.
Left: Schematic representation of chemical exchange 2D IR spectroscopy. Interconversion of two chemically distinct species in equilibrium is manifested as cross-peaks that grow in with the waiting time. The species exchanging can range from different solvation states of an amide unit in a protein to different protein conformations. Right: The PDB structure of the L29I myoglobin mutant (top) and the waiting time dependence of diagonal peaks corresponding to the A1 and A3 states and the cross-peak between them (bottom). The cross-peak kinetics reveal a conformational exchange on the time scale of −50 ps. Adapted with permission from ref 171. Copyright 2008 National Academy of Sciences.
5.3. Non-Natural Metal Carbonyl Probes
Protein dynamics have been shown to be strongly coupled to hydration shell water and bulk solvent dynamics.173 Additionally, several biophysical chemists have proposed that solvating water can serve as an “entropy sink” to assist in the catalysis of enzymatic reactions.174 For these reasons, the structure and dynamics of so-called “biological water” are of fundamental and practical importance in developing a complete understanding of biological catalysis. Transition-metal carbonyl molecules have received significant attention in efforts to develop non-natural probes of protein structure and dynamics. Due to their large transition dipole strengths and long vibrational lifetimes, they serve as attractive candidates to study the dynamics of proteins over longer time scales compared to the amide vibration, which exhibits a shorter lifetime and weaker dipole moments. Metal carbonyl probes also allow for low concentration studies to disentangle the role of macromolecular crowding in protein folding and hydration. Additionally, the metal carbonyl absorptions appear in relatively uncongested spectral regions and generally avoids the complications of water absorption when studying the amide I mode.
Kubarych and co-workers first showed that the vibrational lifetimes of metal carbonyl oscillators serve as sensitive probes of hydration.113 By measuring the vibrational relaxation of a carbon monoxide releasing molecule (CORM) in polar solvents and comparing the time scale of relaxation in water, the metal carbonyl was observed to experience orders of magnitude faster relaxation. Additionally, the authors observed the vibrational dynamics to be dependent on H2O vs D2O, which indicates that the metal carbonyl is sensitive to the hydrogen-bond-switching events in water. Concurrently, Woys et al. reported a method to site-specifically label proteins with differing alkyl chain lengths to probe electrostatics and hydration, in a manner similar to EPR spectroscopic probes.175
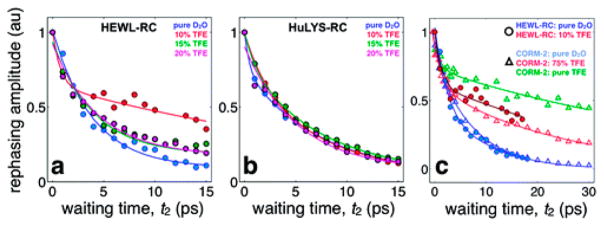
Using the concepts from the previous study, the Kubarych group was able to label a single residue in hen egg white lysozyme (HEWL) and human lysozyme Hu-Lys to study the differences in solvation in the lysozyme protein.176 These two proteins are structurally similar, consisting of an ordered and unstructured domain. In HEWL, the lone histidine residue appears in the structured region while in Hu-Lys, the label was in the random coil region of the protein.177 By comparing the lifetimes of the non-natural probe in H2O and D2O shown in Figure 15, the authors concluded that the structured region of the protein in HEWL, which showed no isotope dependence, was primarily hydrated by constrained water. While in Hu-Lys, in which the disordered random coil was probed, was hydrated by primarily bulklike water. The vast difference in lifetime dynamics was attributed to Hu-Lys resisting solvent exchange with 2,2,2-trifluorethanol (TFE) while the structured region of the HEWL was destabilized by the polar organic solvation. These observed differences were explained in terms of the local protein structure seen by the water. For the HEWL complex, the probe was covalently bound in a region with an extended protein surface that served as a mimic of macromolecular solvation. In contrast, the Hu-Lys probe was located in a protrusion and the water solvates this region much like it would a small molecule, and bulklike water dynamics can be preserved.
Figure 15.
Vibrational relaxation for HEWL-RC (a) and HuLys-RC (b) in D2O/TFE mixtures ranging from 0% to 20% TFE v/v. The addition of small amounts of TFE results in a large increase in the vibrational lifetime of HEWL-RC, followed by a monotonic decrease upon further addition. The increase in lifetime at low concentrations is the result of preferential solvation, and the subsequent decrease in lifetime is the result of the onset of partial protein destabilization. In contrast, HuLys-RC shows no sensitivity to TFE, suggesting that this region of the protein resists solvent exchange with TFE and remains hydrated. (c) A comparison of the cosolvent-dependent relaxation for HEWL-RC (cirlces) and CORM-2 (triangles) shows that at 10% TFE HEWL-RC indicates a local solvation environment with nearly no water, with a relaxation time scale similar to that of other metal carbonyls in alcohol environments. Reproduced with permission from ref 176. Copyright 2012 American Chemical Society.
Although the metal carbonyl probe molecule is most sensitive to the picosecond dynamics of the solvent and local side-chain dynamics, it can still probe the large-scale motions of the protein through offsets in the FFCF. As stated above, the FFCF must decay to zero at long times. Dynamical heterogeneity on time scales longer than those accessible in a 2D IR experiment often manifests as offsets in the FFCF. In other words, there is a component of the FFCF that has a correlation time of infinity (see eq 19). Using the same labeling scheme of their HEWL metal carbonyl labeling, King and Kubarych extracted the value of the FFCF at t2 = ∞ to measure the coupling between hydration dynamics and larger-scale protein motions.178 By measuring the decay of the FFCF in glycerol–D2O mixtures, the time scale of the local hydration dynamics can be compared to the “static” heterogeneity. Figure 16a shows the decay of the FFCF of the metal carbonyl-labeled HEWL for several different solvent mixtures. Despite observing no evidence of protein dehydration, the drastic differences in the FFCF decay were attributed to the coupling of low-frequency protein motions (~10 cm−1) to changes in the environment. This is a particularly elegant example of how non-natural carbonyl probes can be used to probe both solvation dynamics and the long-time scale motions that may be catalytically relevant.
Figure 16.
(A) FFCF of HEWL-RC in pure D2O, highlighting the initial decay due to hydration dynamics and the static offset of the correlation function corresponding to the protein dynamics. (B) Correlation functions for each solvent composition, ranging from pure D2O to 80% glycerol by volume. From the data, it is clear that there is a marked slowing in the hydration dynamics as well as in the protein dynamics (C). Adapted from ref 10. Copyright 2013 Nature Publishing Group. (D) Hydration and protein dynamics of HEWL-RC in crowding conditions plotted as a function of protein–protein distance. The protein–protein distance is defined as the average surface-to-surface distance between proteins using a spherical approximation, which can be estimated for each concentration. Assuming a homogeneous mixture, the average surface-to-surface distance between proteins can be estimated, revealing that the transition occurs at a protein–protein distance of 30–40 Å. Adapted with permission from ref 178 (Copyright 2012 American Chemical Society.) and ref 184 (Copyright 2014 American Chemical Society.).
The hydrophobic effect is ubiquitous in chemistry and biology.179,180 2D IR spectroscopy has historically been an experimental tool of choice8,31,181–183 to study water structure and dynamics. Site-specific labeling of metal carbonyls can provide useful information on the dynamics of the water solvating the protein. King et al. used this to study the differences in protein solvation in dilute and crowded environments.184 Using 2D IR, the researchers observed evidence of a water-jamming transition. In other words, water behaves vastly differently when it solvates dilute proteins compared to an environment with many macromolecular crowders. These measurements established the existence of collective dynamics of water on the order of 30–40 Å from the protein surface (see Figure 16).
Non-natural labeling of proteins with metal carbonyls will open the door to future experiments beyond solvation and protein hydration. Recent experiments by Ross et al. have used 2D IR and metal carbonyls to probe the active site electrostatics and dynamics of a de novo enzyme.185 Peran and co-workers have demonstrated a method to incorporate 2D IR spectroscopic probes that are sensitive to solvation and electrostatic environments.186 Both of these experiments have shown that 2D IR spectroscopy of metal carbonyl-labeled proteins will help to solve problems in protein structure and protein design. Transition-metal carbonyls also hold promise for live cell imaging, analogous to the successful fluorescent probes ubiquitous in biological imaging. Because of their strong absorption cross section, they can be used at low concentrations that are biologically relevant. One can imagine future experiments that can map water content and water dynamics in tissues.
5.4. Other Non-Natural Probes of Ultrafast Dynamics
In addition to transition-metal carbonyls, the nitrile stretch has also received attention as a minimally perturbative probe of site-specific protein electrostatics.187–196 Although the nitrile group has a smaller absorption cross section than metal carbonyls, it is less invasive and benefits from extensive theoretical work on the impact of electrostatics on the vibrational frequency.197–201 Additionally, the nitrile group can be easily incorporated into proteins through site-directed mutagenesis of a cyanophenylalanine residue.196 2D IR experiments on small molecules have also revealed evidence for real-time observation of hydrogen-bond making and breaking,202 which make it a promising probe of hydrogen bonding in proteins and enzymes.
Fang et al. were the first to use a nitrile probe to study the nonnucleoside HIV-1 reverse transcriptase (RT) inhibitor TMC 278 or rilpivirine.203 They measured the spectral diffusion of the cyano moieties on the two arms of the inhibitor. For the cyanovinyl arm of the inhibitor, the FFCF decayed on a time scale of ~7 ps, which was attributed to backbone and side chain motions in the hydrophobic binding pocket. While the nitrile modes in this study were not a part of the enzyme but rather the inhibitor, this study nevertheless served as a validation for nitrile probes at biologically relevant concentrations. Urbanek et al. also used the nitrile stretching vibration to study the villin HP35 protein.204 In this experiment, two distinct populations of nitrile probes were revealed and their exchange rates determined to be tens of picoseconds. Chung. et al. have also investigated the villin headpiece using cyano phenylalanine vibrations.205,206 While they did not observe the two states reported by Urbanek and co-workers, their work exposed different dynamics in the folded and unfolded protein: the unfolded peptide exhibited ~2-fold faster correlation decay compared to the folded state, which suggests a change in solvent accessibility upon unfolding. This work further validated the usefulness of the spectral diffusion time scales accessible from 2D IR as markers of protein conformation. Additional experiments with a doubly mutated (lysine → norleucine) peptide revealed that the mutations play a significant role in stabilizing the hydrophobic core, as mirrored in the slower spectral diffusion of the nitrile moiety.192 The Hochstrasser group also continued to look at the dynamics of the HIV transcriptase inhibitor by studying the dynamics of rilpivirine bound to two clinically important double mutants of reverse transcriptase.10 MD simulations predicted the presence of water in the binding pocket, which was confirmed by X-ray structures and borne out by 2D IR spectral dynamics. Thus, this work vindicated that the 2D IR approach can be used to uncover structural and mechanistic features in proteins independent of other structural biology methods. Bagchi et al. used a cyanophenylalanine amino acid residue in a ribonuclease complex to compare the fast protein dynamics of bound versus free form of a small segment of the peptide.207 This experiment showed that the structural dynamics of the free peptide are much slower than when it is incorporated in the protein complex. The authors were also able to confirm their results with MD simulations. More recently, Gai and coworkers have utilized 2D IR to understand the stabilizing effects of the osmolyte trimethylamine N-oxide (TMAO).208 Their studies found that the stabilizing effect of TMAO stems from weakening of hydrogen bonds between the protein backbone/side chain and water, which is reflected in the spectral diffusion of cyanophenylalanine-containing peptides. Furthermore, the static component of the correlation function (see eq 19) increases steadily upon addition of TMAO, indicating slower conformational fluctuations of the backbone.
In addition to nitriles, azide vibrations have also garnered much interest as alternatives to amide vibrations.209–213 Much like metal carbonyls and nitriles, the azide stretch is located in a spectral region free of water absorption and has a relatively strong IR cross section.210 The first applications of azide vibrations as probes of protein environment came in 1998 through the work of Lim et al., who studied frequency correlation dynamics of azide ions in carbonic anhydrase and hemoglobin using stimulated infrared photon echoes.214 In the past decade, Cheatum and co-workers have made significant progress in utilizing the azide stretch as a probe of picosecond protein dynamics. Bandaria et al. utilized the azide stretch to study the dynamics of the protein formate dehydrogenase in the presence of catalytically relevant ligands.212,215 The authors found evidence for a fairly narrow distribution of conformational states when bound to a ligand, and this was interpreted as further evidence for a static transition state. This is particularly exciting work, because it may help solve the long-standing controversy of the role of protein dynamics in catalysis.216 Further experiments will help deconvolute what protein fluctuations, if any, are catalytically important. Moreover, Tucker et al. have also demonstrated the utility of azide modes for studying nucleic acide structure and dynamics through azido modified nucleic acids.217 The NO stretch is another vibration that appears in a background free window in the mid-IR region, and very recently has started being used as a site-specific probe in proteins for 2D IR experiments. Hunt and co-workers have shown that the NO stretch can probe dynamics at an enzyme site218 and Cheng et al. have also used this vibrational mode to study the structural dynamics of nitric oxide transporter proteins.219
5.5. Structure and Vibrational Dynamics of Nucleic Acids
The vibrational dynamics that are revealed by 2D IR can also be useful for studying biomolecular assemblies other than proteins. Important examples of such biomolecular species that are a fundamental component of the cellular environment are nucleic acid and membranes. Both nucleic acids, particularly DNA, and membranes have witnessed increased attention from ultrafast infrared spectroscopy in the past decade. The backbone phosphate vibrations and the NH2 and carbonyl modes of the DNA bases offer the same advantages as amides in proteins: label-free vibrational spectroscopy. Similar to its sensitivity to protein structure, 2D IR spectroscopy is also sensitive to the structure of DNA. The structural sensitivity comes from the measured couplings. Krummel et al. measured the first 2D IR spectrum of DNA and showed that intrastrand carbonyl couplings are important to interpreting DNA vibrational spectra.220 The same researchers also showed that the 2D IR spectra of DNA molecules can be described by a local mode description, very similar to the procedure outlined above that uses coupling models to map protein structure from a local mode Hamiltonian.221 This work has laid the groundwork for further studies using 2D-SFG, a surface-sensitive variant of 2D IR to study single-stranded DNA monolayers.222
Elsasser and co-workers have made significant progress in understanding the structure of DNA base pairs in thin films. Using 2D IR they studied both guanine–cytosine (G–C)223 and adenine–thymine (A–T)224 base pairs. They observed significant inhomogeneous broadening, indicating that even in paired bases there is a rather large structural distribution. Additionally, they did not observe significant spectral diffusion, indicating that the residual molecules bound to the DNA in dehydrated films had limited structural flexibility. These studies focused on the NH and NH2 stretching regions of the spectrum to elucidate the structure and vibrational dynamics of the thin films.
Recent work by Tokmakoff and co-workers has used 2D IR spectroscopy to study the coupling and anharmonic character of the DNA vibrational modes.225 They found that there was significant coupling and delocalization of the vibrational modes. They also found that the experimental spectra only achieved reasonable match with DFT calculations when including water molecules at the solvating hydrogen-bonding sites. This has helped build a connection between the vibrational spectrum and the molecular structure of DNA. Peng et al. have used this information to study tautomerization in an anti-HIV drug.226 They found that this tautomerization and protonation are important to understanding the high rate of mutations and base-pairing promiscuity in the particular therapeutic drug studied.
The dynamical parameters furnished by 2D IR are equally fascinating and provide a fundamental understanding of structural dynamics in DNA. Spectral dynamics of both AT and GC oligomers have been studied at different levels of hydration to shine light on DNA–water interactions223,227 and hydrogen-bond dynamics, which play a pivotal role in DNA structure. The advances in pump–probe and 2D IR spectroscopy have been reviewed recently by Elsaesser and coworkers, 13 who have used 2D IR to expose the unique properties of water near DNA through vibrational dynamics of the O–H stretch and N–H stretch vibrations on the bases. The picture that emerges from a combination of different studies is that the dynamics of water associated with DNA is slower than the bulk and strongly depends on the hydration level.224,228 At low hydration levels, the backbone–water interactions lead to a “frozen” water structure, evidenced by little spectral diffusion, as illustrated in Figure 17. In more hydrated DNA (~92%), the O–H stretch shows picosecond spectral diffusion, indicating that the water shell next to the backbone is more bulklike. This is observed in both poly-AT and poly-GC oligomers and can therefore be interpreted as a property of DNA in general. This is an interesting conclusion, as similar observations regarding properties of water in transmembrane proteins have also been made. Another way of probing water near nucleic acids is through the backbone phosphate vibrations. Very recent work229,230 has utilized this approach to reveal that for both low and high hydration, the FFCF bimodally decays on a fast (~300 fs) and a slow (~10 ps) time scale. The fast time scale is consistent with those observed when the relaxation of water was directly studied and, therefore, is in accordance with the proposed model of water deceleration near DNA. The longer time scale can be attributed to backbone structural disorder, akin to slow backbone fluctuations in peptides.
Figure 17.
2D IR spectroscopy of nucleic acid–water interactions. Top: 2D spectra of hydrated DNA (92% relative humidity) measured with pump and probe pulses perpendicularly polarized at different waiting times. The solid black lines represent the center lines described in section 3. Bottom: Evolution of the center line slope (CLS) with the waiting time. CLSs of neat water are also shown as white circles. The results are compared with predictions from MD simulations, shown as solid and dashed lines [Cp(t) with and C(t) without resonant energy transfer between the water O–H vibrations]. Reproduced with permission from ref 227. Copyright 2011 American Chemical Society.
6. NANOSECOND–MILLISECOND DYNAMICS PROBES WITH NONEQUILIBRIUM 2D IR
Significant theoretical and experimental progress has been made in the protein-folding field through analytical theory, simulations, and experiments,231–237 yet questions remain regarding the nonequilibrium dynamics of proteins, such as the structural basis for the kinetics of folding and misfolding. The vibrational coherences that contribute to the third-order polarization in 2D IR experiments dephase on a picosecond time scale, which puts a limitation on the effective time window over which 2D IR can be used to observe protein dynamics.36,38 A major parameter behind the dephasing of vibrational coherences in solution is the vibrational lifetime.36 With the exception of metal carbonyls and some recently designed vibrational probes that have significantly longer vibrational lifetimes,113,238 most vibrational transitions, particularly those inherent to a protein, such as amides, relax on a time scale of ~1 ps.49 In recent years there has been effort to incorporate these “unnatural” vibrational probes into proteins and other biological systems,196 which was discussed in the previous section. However, there exist other time-resolved or transient vibrational spectroscopies, such as temperature-jump239–242 and pH-jump,243–246 that can access time scales more relevant to protein structural dynamics. The past decade has seen significant effort to couple and incorporate 2D IR into these experimental approaches to extend and utilize the capabilities of 2D IR to processes not observable in the traditional pump–probe form of the experiment.
The fundamental approach common to all these experiments has been to follow the kinetic evolution of protein conformational changes through 2D IR observables of the quasi-equilibrium distributions generated following a triggering event. The 2D IR approach combined with isotope-selective labeling permits the tracking of conformational changes by obtaining structural constraints, such as coupling constants or FFCF time scales, as a function of time following the trigger event. Hamm and co-workers presented the very first applications of transient 2D IR toward investigating nonequilibrium protein structural evolution.247 In their experiments, the conformational change is induced using an azobenzene photoswitch incorporated into the backbone of a cyclic octapeptide. The photoswitch could be reversibly converted between the cis and trans conformations using different excitation wavelengths, which altered the backbone conformation: the cis → trans transformation caused the structural equilibrium to shift from a broad ensemble of structures to a narrow well-defined backbone conformation. While the main conformational change of the backbone was over in under ~20 ps, subsequent equilibration continues for times >16 ns, which had been revealed earlier through ultrafast transient infrared experiments. The incorporation of 2D IR allowed for investigation of the response homogeneous and inhomogeneous line widths over the peptide structural evolution. It was observed that the homogeneous component of the amide I line width decreased during the course of the conformational transition, which was tentatively attributed to the change in the sampling rate of the potential energy surface. Transient cross-peaks that could potentially provide structural parameters were also observed in the experiments, though these features were not explored in detail. Soon after, Tokmakoff and co-workers presented an alternate approach toward extending 2D IR to the nanosecond time scales through integration with temperature-jump methods.248 They studied the backbone conformational changes during the thermal unfolding of ubiquitin using equilibrium 2D IR and transient dispersed vibrational echo spectroscopy, which is essentially the projection of 2D IR spectra onto the monochromator frequency axis. The transient experiments revealed nonexponential relaxation kinetics that can be separated into fast and slow time scales. Spectral simulations identified this observation to arise from unfolding of the less stable strands III–V of the β-sheet before unfolding of the hairpin. It should be noted that a temperature-jump experiment measures the evolution of one thermal distribution of structures into another. This differs from a photo release experiment, where a narrow, constrained distribution evolves into a thermal distribution.
These early results provided a glimpse of the wealth of structural information that can be uncovered by the combination of 2D IR with existing transient vibrational spectroscopies, the significance and importance of which were firmly established by Hamm and co-workers in 2006, who studied the real time weakening of the intramolecular hydrogen bonds in a photolyzable, constrained, four-residue β-turn (Figure 18) and the resultant opening of the turn on an ultrafast time scale.249 In these experiments, the conformational change was induced using photodissociation of a disulfide-bridged tetrapeptide, wherein a triggering UV or visible pulse is followed by a pulse pair consisting of infrared pump and probe pulses separated by picosecond time scales. 2D IR reports on relative positions and orientations of vibrational groups by mapping vibrational couplings through cross-peaks; the unique structural capabilities of a transient 2D IR experiment were clearly demonstrated by Hamm and co-workers in the aforementioned report, where they deciphered hydrogen bond dynamics through transient cross-peak kinetics as the β-turn unravels over nanoseconds (Figure 18). In 2012, Tokmakoff and co-workers reported the design of an improved 2D IR spectrometer integrated with a temperature-jump apparatus capable of performing transient temperature-jump 2D IR measurements, which was tested on diglycine and Trpzip2.250,251 The measurements on diglycine indicated that transient amide 2D IR spectra are sensitive to <10 ns changes in local H-bonds. The results with Trpzip2 revealed two distinguishable time scales for the disordering kinetics: on the <10 ns time scale, H-bonds are broken, causing the β-hairpin to loosen, and on the ~1 μs time scale, the peptide disorders. The authors subsequently expanded this approach to study three isotopologues of Trpzip2. The introduction of isotope labeling allowed site-specific probing of local β-sheet conformations. The experiments identified three distinct conformational ensembles: a folded state with a type I′ β-turn, a misfolded state with a bulged turn, and a disordered state. The transient 2D IR spectra, shown in Figure 19, evidenced the heterogeneous folding mechanism of Trpzip2, wherein a thermal unfolding process is not simply a transition from a single native conformation to a denatured state but, instead, is characterized by a shift of the relative populations within a heterogeneous ensemble. Concurrently, Tucker and co-workers reported the picosecond–nanosecond reorganization dynamics of a short helix close to equilibrium using transient 2D IR.22 The experimental approach employed was similar in essence to that of Hamm and co-workers. An initial distribution of kinked alanine-rich α-helices was designed using a photolabile tetrazine bridge (Figure 20). The bridge causes the structure to be slightly perturbed from the native α-helix equilibrium conformation near these residues. Upon excitation with a picosecond UV pulse, the bridge is released, resulting in the helix evolving into the equilibrium distribution of α-helix conformations, as evidenced by the evolution of the 2D IR diagonal line widths (Figure 20). The transient 2D IR spectra of the isotopically labeled residues were modeled using a transition dipole coupling model to yield coupling constants, which revealed angular constraints. The decay rates of the angle between the dipoles and distance autocorrelations obtained from supporting MD simulations provided evidence that the helical reorganization conforms to linear response theory. Very recently, Baiz and co-workers have employed temperature-jump 2D IR and spectral simulations based on Markov state models to study the unfolding and subsequent equilibration of a ribosomal protein.252 The consistency of theory and experiments furthers 2D IR as a useful tool for the study of protein folding.
Figure 18.
Transient 2D IR of a cyclic tetrapeptide. Top: Structure of the cyclic disulfide-bridged tetrapeptide. Bottom: Transient (a) linear and (b) 2D IR spectra 3 and 100 ps after photolysis. The transient cross-peaks are indicated as ‘TC”. (c) Slices through 2D IR spectra along the dashed lines shown in part b clearly illustrate the evolution of the transient cross-peak. Reproduced with permission from ref 249. Copyright 2006 Nature Publishing Group.
Figure 19.
Transient 2D IR spectra of Trpzip2 isotopologues (top row, unlabeled; middle row, double isotope labeled at T3 and T10 carbonyls; bottom row, isotope labeled at K8 carbonyl) following a temperature jump. (A) 2D IR spectra at T = 150 fs at thermal equilibrium. (B, C) Transient 2D IR basis spectra showing the spectral changes on nanosecond and microsecond time scales. Loss of diagonal peaks is observed as blue above and red below the diagonal line. Contours of the equilibrium and transient spectra are overlaid together. Reproduced with permission from ref 251. Copyright 2013 National Academy of Sciences.
Figure 20.
Reorganization of a perturbed helix probed by 2D IR. Left: A schematic outline of the experimental principle. The helix is generated in a near-equilibrium, and the kinked conformation is generated by a tetrzine bridge in the backbone. The bridge can be photolyzed using UV light, following which 2D IR spectra reveal the backbone reorganization. Right: 2D IR diagonal widths as a function of the delay between the UV and the 2D IR pulse sequence, reflecting the backbone conformational rearrangement. Reproduced with permission from ref 22. Copyright 2013 National Academy of Sciences.
7. STUDYING KINETICALLY EVOLVING PROTEINS USING 2D IR
Protein dynamics occurs on a large range of time scales from tens of picoseconds to seconds.1,253 The longer time scales are related to formation of tertiary and quaternary structures. Since its development, the utility of 2D IR in biomedical applications, particularly for studying protein structural dynamics, has increased steadily. The major successes of 2D-IR-based techniques at discerning structural and dynamical evolution of proteins over picoseconds to microseconds have been reviewed in the prior sections. These advances naturally raised the question: can 2D IR investigate the formation and reorganization of tertiary structures in real time, as they form? An important example of a class of problems that could benefit from development of fast 2D IR spectroscopy is the aggregation and self-assembly of short peptides into amyloid fibrils and other nanostructures, which are at the heart a number of diseases.254–256 The biophysical techniques commonly employed to investigate amyloid kinetics, such as FTIR,257 circular dichroism,258 and fluorescence spectroscopies,259 do not offer the same structural insights as 2D IR. Unlike the approaches described in the previous section, where 2D IR is augmented with a triggering mechanism to study dynamics in a quasiequilibrium, understanding aggregation mechanisms of self-assembling peptides requires characterization of protein structures evolving over seconds to minutes, which necessitates acquisition of 2D IR spectra orders of magnitude faster than the kinetic process under examination.
The traditional implementations of 2D IR utilized motorized stages to scan the delay between pulses, which was not only time-consuming but also prone to phase distortions from stage inaccuracies. The data acquisition can be accelerated by implementing 2D IR in the pump–probe geometry, where an interferometer scans the delay between two collinear pump pulses, leading to simultaneous collection of rephasing and nonrephasing signals, thereby making scan times shorter. In 2006, Zanni and co-workers reported a mid-IR implementation of acousto-optic pulse shaping.260,261 Warren and co-workers had first presented acousto-optic pulse shaping and its application to 2D visible spectroscopy.262 The pump pulse pairs in 2D IR is particularly well-suited for pulse shaper technology, as pulse shapers eliminate the need for slow and inaccurate mechanical stages, allowing electronic control of the pulse delays and phases.133 In 2D IR experiments with biological samples, scattered light is one of the main sources of spectral distortion, being particularly relevant for large macromolecular aggregates such as amyloids. Pulse shaping enables shot-to-shot modulation of the absolute phases and relative timing of the pump pulses, thus allowing removal of scattered light through phase cycling, similar to NMR spectroscopy. Furthermore, the 2D interferogram can also be acquired in the rotating frame, which leads to shorter data collection times. All of this leads to spectral acquisition times on the order of seconds, which enables aggregation kinetics to be measured in real-time. It should be noted that shot-to-shot phase modulation and phase cycling can also be implemented by other phase control devices, such as a photoelastic modulator or wobbling Brewster windows, as demonstrated by Hamm and co-workers.263 However, pulse-shaper-based 2D spectrometers, in addition to other capabilities as outlined above, are also now commercially available and are emerging as the preferred method for studying fast structural dynamics in proteins.
In 2007, Shim and co-workers reported the first application of mid-IR pulse shaping to amyloid proteins through comparison of different pulse sequences and shapes on 2D IR spectra of the 37-residue human islet amyloid polypeptide (hIAPP) or amylin, a protein implicated in type II diabetes (Figure 21).14 This work firmly established the importance of automated control of phase and delay control and demonstrated the capabilities possible with pulse shaping. Soon after, Strasfeld and co-workers reported the first implementation of rapid-scan 2D IR to follow the fiber formation kinetics of hIAPP.23 Two distinct features in the 2D-IR spectra were identified that allowed tracking of the random coil and β-sheet populations over the aggregation process (Figure 22). The β-sheet signatures were mirrored by the spectral intensity of a doublet at ~1620 cm−1, whereas the random coil populations were best characterized by a cross-peak feature, which demonstrates the inherent advantage of the technique over linear spectroscopies, where isolating cross-peak features is not possible. Concurrent fluorescence measurements further corroborated the accuracy and applicability of this rapid-scan 2D IR technique. The authors also suggested that transient structures could be present during the lag phase, which was not investigated in this work. Similar to equilibrium measurements, the structural detail available from rapid-scan 2D IR can be furthered by incorporating isotopic substitutions, which was utilized by Shim and co-workers to track the development of secondary structures for six residues during the aggregation of amylin.28 As shown in Figure 23, site-specific kinetics revealed that the peptides initially develop well-ordered structure in the region of the chain that is close to the ordered loop of the fibrils, followed by formation of the two parallel β-sheets, with the N-terminal β-sheet possibly forming before the C-terminal sheet. The importance of these experiments laid in the fact that these demonstrated the usefulness of ultrafast vibrational spectroscopy in providing unprecedented structural resolution during the aggregation of a peptide in real time, which has always been a challenging problem in biophysics. Middleton and co-workers exploited these structural capabilities of rapid scan 2D IR and isotope labeling to study the complexation of human amylin with a known inhibitor, rat amylin.264 The experiments revealed unexpected structural dynamics, which were also evidenced by electron microscopy: 8 h after mixing, rat amylin blocks the N-terminal β-sheet instead of the C-terminal one, and 24 h after mixing, rat amylin forms its own β-sheet on the outside of the human fibrils. This was unprecedented, as rat amylin is not known to form amyloid aggregates, and underlined the complexity associated with rational design of inhibitors. Additionally, this work also showed the applicability of 2D IR and infrared spectroscopy in general toward drug/inhibitor design. Moran et al. applied this rapid-scan 2D IR approach to study the eye lens protein γD-crystallin to reveal that the C-terminal domain forms β-sheets, whereas the N-terminal domain becomes extremely disordered but lies in close proximity to the β-sheets, which led to a structural model of the fibrils formed by the crystalline protein.30 The fibrillation was induced by acidification, and in essence, this experiment represented a long time scale version of the triggered 2D IR approaches described in the previous section. Recently, Buchanan and co-workers revisited the question of intermediate structures during the lag phase of amylin with the rapid scan approach to show that a transient oligomeric parallel β-sheet intermediate forms during the lag phase in a region that is a partially disordered loop in the fully formed fibril.26 The existence of this intermediate was verified using a set of macrocyclic peptides homologous to segments of hIAPP that can recognize β-sheets through hydrogen bonding. Identification of this intermediate provided an explanation for structural evolutions during the lag phase and helped reconcile many previous fragment studies of amylin. Figure 24 shows the energy landscape for fibril formation determined from these experiments. The advantages afforded by the integration of a structurally sensitive technique like 2D IR to protein kinetics were further demonstrated by Dunkelberger and co-workers, who reported the effects of deamidation on the aggregation kinetics of amylin.265 While neither TEM nor CD spectroscopy revealed a change in structure upon deamidation, 2D IR revealed not only accelerated kinetics but also structural changes for the fibrils formed from deamidated amylin. Although the rapid-scan 2D IR technology so far has seen applications primarily in the study of amyloid aggregation, it is a promising approach that has broad potential and can be applied to a wider range of biophysical problems, some of which are discussed in section 9.
Figure 21.
Most common pulse sequences used in 2D IR spectroscopy. (a) Traditional three-pulse heterodyned photon echo pulse sequence. (b) The collinear pump–probe sequence used in mid-IR pulse shaping, where the pump beam is shaped in the frequency domain to generate a pulse pair with electronically controlled delays and phases. (c) 2D IR spectra of amylin acquired with pulse-shaped 2D IR. Pulse shaping allowed for removal scatter, which is a significant deterrent for biological samples. Reproduced with permission from ref 14. Copyright 2007 National Academy of Sciences.
Figure 22.
Real-time evolution of 2D IR spectra with hIAPP aggregation. (Left) 2D IR spectra at times of 1 min (top) and 314 min (bottom) over the course of the aggregation process clearly reflect the aggregation. (Right) Top: Slices through 2D spectra at wpump = 1618 cm−1 reveal spectral markers that track random coil and β-sheet populations. Bottom: Evolution of random coil and β-sheet populations as obtained from 2D IR slices. Reproduced with permission from ref 23. Copyright 2008 American Chemical Society.
Figure 23.
2D IR spectra of isotopically labeled hIAPP exposes residue-specific kinetics. (A) 2D IR spectra Ala-25 at t = 5 min. (B–D) Difference 2D IR spectra at t = 31, 66, and 205 min, calculated by subtracting the t = 5 min spectrum. The red squares mark the labeled A25 transition, while the black rectangles denote the unlabeled amide band. The two spectral features observed in the label region are marked with blue and green arrows. The magenta and red arrows indicate the cross-peak between the labeled Ala-25 reidue and the unlabeled main band amide. Reproduced with permission from ref 28. Copyright 2009 National Academy of Sciences.
Figure 24.
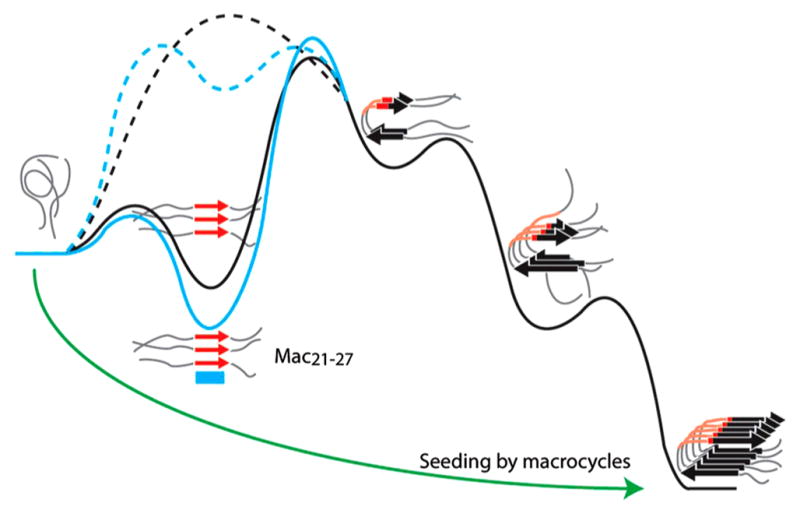
Rapid-scan 2D IR reveals a transient β-sheet intermediate during hIAPP aggregation. The FGAIL segment (residues 23–27) is shown in red. Macrocyclic inhibitors (Mac21–27) can bind to and stabilize the intermediate FGAIL β-sheet (cyan), thus increasing the free energy barrier. Some macrocycles seed fibril growth and circumvent the barrier (green arrow). Aggregation is inhibited by mutations such as I26P, which destabilize the intermediate (dashed black line). The addition of Mac21–27 can induce formation of the transient intermediate even for the mutated sequence (dashed cyan line). Reproduced with permission from ref 26. Copyright 2013 National Academy of Sciences.
8. SURFACE-SENSITIVE MULTIDIMENSIONAL SPECTROSCOPY OF BIOMOLECULES
An important subset of challenges in biophysics is structural dynamics on surfaces and interfaces. The structure of peptides and proteins on biological interfaces, such as cell membranes, and membrane–protein interactions are fundamentally important in biology. There is a separate review on new 2D spectroscopic surface techniques in this Special Issue; hence, we briefly highlight experiments here related to proteins. Structural information can be obtained from techniques such as ATR-FTIR266 or vibrational sum-frequency generation (SFG) spectroscopy,267,268 which can all achieve monolayer sensitivity. 269 SFG is a second-order spectroscopy in which a resonant mid-IR pulse combines with a nonresonant visible pulse to produce a signal at the sum of the two frequencies and is one of the most common techniques for studying surfaces and interfaces. However, similar to FTIR and ATR, SFG is a one-dimensional technique and has the same limitations in not being able to access dynamical and structural parameters directly. The limitations of SFG spectroscopy have been circumvented through the recent development of a novel technique called 2D SFG spectroscopy, which incorporates a pair of infrared pump pulses in a conventional SFG experiment, thereby adding an extra frequency dimension, analogous to 2D IR.222,270–275 2D SFG thus offers the best of both worlds: the surface sensitivity of SFG and the capabilities of 2D IR to extract structural and dynamical parameters.
Infrared pump-SFG probe experiments were developed as early as 2008272,276 and using a narrow-band pump pulse, akin to the early designs of 2D IR, enabled implementation of the very first 2D SFG experimental designs. The first experimental demonstration of heterodyned 2D SFG spectroscopy came in 2011 from Xiong and co-workers, who implemented a 2D SFG experiment by integrating a pump pulse pair with a broadband SFG spectrometer through mid-IR pulse shaping.270 The authors tested this technique by investigating carbon monoxide (CO) adsorbed on a polycrystalline Pt surface. Soon after, Laaser and co-workers reported the very first heterodyned 2D SFG (HD 2D SFG) measurement of the structure of a surface-bound peptide.274 The authors investigated a self-assembled monolayer of a cysteine-terminated 20-residue peptide on gold surfaces. The experimentally measured anharmonic shifts, 2D line shapes, nodal line slopes, and vibrational lifetimes clearly point to a helical structure on gold. Furthermore, comparisons with complementary 2D IR spectra suggest that the peptide structure is very similar between bulk solution and on surfaces and does not change significantly upon adsorption. Vibrational modes that are isotropically distributed across the interface are not SFG active and do not appear in either 1D SFG or along the diagonal in 2D SFG spectra. However, cross-peaks can still appear to SFG-forbidden modes.273 This occurs because an SFG-inactive mode is still pumped by the mid-IR pulses and so can emit a signal if it is coupled to an SFG-active mode. Cross-peaks between the helical amide I modes and a lower-frequency, SFG-inactive random coil vibration revealed that the peptide still has structurally disordered components, underscoring the advantages of 2D SFG over conventional SFG experiments. This was further exploited by Ho and co-workers, who studied the structure of single-stranded DNA monolayers of varying chain lengths on gold.222 Intra- and interbase couplings lead to distinct cross-peaks in 2D IR and 2D SFG spectra, which serve as constraints toward structural determination, similar to 2D IR. In contrast to previous investigations, the authors conclusively showed that DNA oligomers of 10, 15, and 25 bases have similar well-ordered structures, and the degree of ordering increases with oligomer length. On gold surfaces, surface selection rules dictate that only vibrational modes with a nonzero projection normal to the surface primarily contribute to the SFG signal. This was utilized by Ghosh and co-workers to reveal the orientation of an amyloidogenic peptide, FGAIL, on self-assembled monolayers of thiomercaptobenzoic acid (MBA) on gold.275 The experimental and simulated 2D SFG spectra point to a linear configuration of the peptide on the surface. Furthermore, cross-peaks between the carboxylic acid mode of the MBA and the a+ mode of the β-sheets suggested a surface-mediated mechanism for the aggregation of FGAIL.
9. CONCLUDING REMARKS
In this review, we have attempted to follow the development and applications of 2D IR spectroscopy toward addressing structural dynamics in proteins. The first demonstrations of 2D IR came about in 1998,49,277 and its strengths toward solving protein structures were quickly identified and utilized for investigating protein structure. Unlike linear infrared spectroscopies, 2D IR provides evidence of molecular coupling directly through existence of cross-peaks. Molecular couplings are of paramount importance for interpreting protein infrared spectra: the characteristic secondary structure resonances stem from delocalization of vibrational excitation through extensively coupled backbone amide modes.121 Cross-peaks in 2D IR allow for evaluating these couplings, leading to angles between dipoles, which in turn serve as structural constraints.36 This approach is further expanded by isotopic substitution of amide modes, which allows investigation of local vibrations spectrally isolated from other vibrations, leading to residue-specific coupling constants and structural parameters. This unique capability of 2D IR was exploited in early work with proteins, wherein 2D IR was applied to explore structural parameters in assemblies ranging from small peptides to larger transmembrane proteins.12,110,119,135,278 These experiments firmly established 2D IR as a viable technique complementary to the more common structural tools, such as NMR and X-ray spectroscopies.
In addition to vibrational frequencies and couplings, 2D IR also reflects the fluctuations of the frequencies. The frequency fluctuations and loss of frequency correlation, commonly termed “spectral diffusion”, is mirrored in the 2D peak shapes and their evolution with time. In a protein environment, the frequency correlations decay on a multitude of time scales, each corresponding to a physical and or structural process that affects the vibrational frequency distribution a certain way. The frequency fluctuation can also pertain to population transfer between states, wherein two distinct conformers are exchanging over a picosecond time scale.171 With its ultrafast time resolution, 2D IR has been proven invaluable at exposing these picosecond structural motions in proteins. The ultrafast dynamics also originate from motions of water molecules that associate with protein secondary structures, and understanding this biological water is pivotal to deciphering the structure–function relationship of protein assemblies, as has been demonstrated on many occasions with 2D IR.103 In essence, 2D IR allows one to isolate protein conformations thorough their dynamical signatures, and time-resolved 2D IR thus provides more than just relaxation time scales. This dynamical aspect of 2D IR particularly benefits from incorporation of so-called “non-natural” vibrational probes. While amide modes offer a structurally nonperturbative way to gain insight into residue level dynamics, the interpretation of amide spectra and elucidation of relaxation parameters from isotope-labeled amide modes in the presence of side chain vibrations can be challenging.279 Non-natural probes, such as azides280 and metal carbonyls,113,175 allow access to local information in a protein through spectral isolation from protein vibrations. This approach has been proven very useful in the past decade and successfully applied toward investigating dynamics in biological milieu.
Proteins undergo structural transitions over multitudes of time scales, and a traditional 2D IR measurement can only access tens to hundreds of picoseconds of the dynamical landscape, as the third-order signal in 2D IR is limited by the vibrational lifetime. However, the past decade has seen development of “hybrid” approaches, where 2D IR is augmented with another biophysical technique, such as temperature jump251 or visible excitation.281 In these experiments, a protein conformational transition is triggered, and the structural rearrangement is followed using 2D IR. These approaches extend the range of 2D IR out to microseconds and lends the structural capabilities of 2D IR to linear-spectroscopy-based techniques. One of the major ground-breaking developments in ultrafast infrared spectroscopy in the past decade has been mid-IR pulse shaping. Pulse-shaper-based spectrometers are becoming increasingly popular and allow acquisition of distortion-free 2D IR spectra in a few seconds. This paved the way for experiments where peptide self-assembly processes, such as amyloid formation, can be monitored in realtime. 23,28,260 This “rapid-scan” 2D IR approach enables mapping of site-specific couplings and their kinetics over the aggregation of small peptides into fibrils.
Finally, we would like to provide some perspective on the exciting directions in which 2D IR is currently headed. Advances in laser and detector technologies are impacting 2D IR spectroscopy, as are new biochemical methods. Regarding the technology, ultrafast laser technology is rapidly evolving: most 2D IR experiments now employ a 1 kHz source, but more robust, high-power 100 kHz sources are becoming available. High repetition rates promise not only to reduce the acquisition times of 2D spectra, which can probe faster aggregation kinetics, but also improve the spectral quality, as has been recently demonstrated.282 Infrared focal plane array detectors are now commercially available that enable new experiments and improve the quality of 2D IR spectra.80 Another exciting direction is ultrafast infrared microscopy. Vibrational hyper-spectral imaging modalities, such as FTIR, SFG, and Raman microscopy, have seen a surge in popularity in recent years due to the label-free contrast they can provide over conventional fluorescence-based techniques.283–286 Viability of both pointmapping46,287 and wide-field47 variants of 2D IR microscopy have now been demonstrated, enabling images to be created from many thousands of spatially resolved 2D IR spectra. 2D IR imaging provides higher contrast than FTIR imaging and will be useful for studying spatially heterogeneous samples, like tissues. Recent advances in dual-frequency, or two-color, 2D IR spectroscopy promise to explore more complicated couplings that could lead to more precise structure determination.288–291 The sensitivity of 2D IR spectroscopy is also improving via technological and scientific advances.292,293 Surface-enhanced 2D IR has been recently demonstrated using an ATR optical geometry.294–296 Additionally, the combination of 2D IR with plasmonic nanostructures297,298 promises to expand the technique’s impact by probing even smaller sample volumes and opening the door to vibrational modes with weaker oscillator strengths.
New advances in biochemical techniques are also broadening the range of protein systems that can be studied. Nonsense suppression techniques allow non-natural amino acids to be incorporated site-specifically into proteins. Cell-free protein expression enables new isotope-labeling schemes.81 Native chemical and express protein ligation strategies allow for pieces of proteins to be labeled.
This review covers many examples of 2D IR applications to biomolecules and especially proteins. What scientific problems are good targets for 2D IR spectroscopy that make it a technique that a biochemist or molecular biologist should consider in their research? In our opinion, there are several situations that make 2D IR spectroscopy a good tool for biophysics. The structural resolution of 2D IR spectroscopy is independent of the size of the system, unlike NMR spectroscopy, in which molecules must quickly rotate to get high-resolution spectra. Proteins do not need to crystallize for 2D IR spectra. Biomolecules undergoing structural changes can be difficult to map with other techniques, unless they fall within the time resolution of that technique. The time resolution of 2D IR spectroscopy is so fast that proteins can evolve on sub-millisecond time scales or even over the course of hours and still be probed. An example of a nearly perfect application of 2D IR spectroscopy is to amyloid aggregation, because the scientific problem involves assembles that are too large for high-resolution NMR, do not crystallize, and are evolving in time—all of the worst problems for standard biophysical tools. The ultrafast time resolution of 2D IR spectroscopy also has an interesting consequence for interrogating structures. The time resolution is so fast that the structures of a protein or biomolecule are essentially fixed in space, except for small side chain motions and water dynamics. A 2D IR spectrum is like an instantaneous snapshot of the protein structural distribution. That fact is useful, not because the femtosecond dynamics of proteins are important (they are probably not in almost all situations), but because it allows one to straightforwardly connect 2D IR spectroscopy with atomic structures via molecular dynamics simulations. A molecular dynamics trajectory only needs to be a ~100 ps in duration in order to compute a 2D IR spectrum. As a result, molecular structures can be tested against experiment by generating an appropriate MD simulation, or a long trajectory containing many structures can be evaluated piecemeal. An example is our recent work on the potassium ion channel, KcsA,154 in which two models of ion permeation were tested against experiment. Only one survived.
Of course, 2D IR spectroscopy has drawbacks. The biggest being that its structural resolution is poor unless isotope labeling or non-natural amino acids are used. That fact is why much of this review has been devoted to examples containing methods of labeling individual amino acids or ligating proteins to isotope-label domains. As a result, the sophistication of questions that can be addressed with 2D IR spectroscopy is in many ways coupled to the sophistication of the biochemistry for the protein at hand. Now is an exciting time, because there are so many new methods for mutating, incorporating non-natural amino acids, expressing (such as with cell-free), and semisynthesizing proteins. We predict, that as the communities of 2D IR spectroscopists, molecular biologists, and biochemists understand one another’s capabilities in more detail, the level of scientific sophistication of biological questions addressed with 2D IR spectroscopy will continue to rise.
Acknowledgments
Research described in this review was supported by the National Institute of General Medical Sciences of the National Institutes of Health (NIH) under award number R01GM102387, NIH NIDDK 79895, and the National Science Foundation under award CHE-1266422.
Biographies
Ayanjeet Ghosh was born in Kolkata, India. He completed his doctoral degree from the University of Pennsylvania under the tutelage of Prof. Robin M. Hochstrasser in 2012, studying transmembrane proteins with 2D IR spectroscopy. He worked as a postdoctoral researcher with Prof. Martin Zanni at the University of Wisconsin—Madison studying 2D SFG spectroscopy and the development of linear and 2D IR microscopy. He is presently working with Prof. Rohit Bhargava at the University of Illinois, Urbana–Champaign on applying vibrational imaging toward cancer diagnosis.
Joshua Ostrander was born in Kalamazoo, MI, and received his undergraduate degree from Indiana Wesleyan University in chemistry. He is currently a Ph.D. student in the lab of Prof. Martin Zanni at the University of Wisconsin—Madison. His research is focused on the development and application of nonlinear infrared microscopy.
Martin Zanni attended the University of Rochester for his Bachelor’s degrees and the University of California at Berkeley for his Ph.D. He was a postdoctoral researcher at the University of Pennsylvania with Robin Hochstrasser. He is currently the Meloche Bascom Professor of Chemistry at the University of Wisconsin—Madison. His research interests include the study of amyloid formation and excitonic energy transfer in electronic materials, all studied with multidimensional spectroscopy.
Footnotes
ORCID
Joshua S. Ostrander: 0000-0002-6338-6639
Martin T. Zanni: 0000-0001-7191-9768
The authors declare the following competing financial interest(s): M.T.Z. is a co-owner of PhaseTech Spectroscopy, which manufactures mid-IR pulse shapers and 2D IR spectrometers.
References
- 1.Henzler-Wildman K, Kern D. Dynamic Personalities of Proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 2.Hammes-Schiffer S, Benkovic SJ. Relating Protein Motion to Catalysis. Annu Rev Biochem. 2006;75:519–541. doi: 10.1146/annurev.biochem.75.103004.142800. [DOI] [PubMed] [Google Scholar]
- 3.Hanoian P, Liu CT, Hammes-Schiffer S, Benkovic S. Perspectives on Electrostatics and Conformational Motions in Enzyme Catalysis. Acc Chem Res. 2015;48:482–489. doi: 10.1021/ar500390e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Eaton WA, Muñoz V, Hagen SJ, Jas GS, Lapidus LJ, Henry ER, Hofrichter J. Fast Kinetics and Mechanisms in Protein Folding. Annu Rev Biophys Biomol Struct. 2000;29:327–359. doi: 10.1146/annurev.biophys.29.1.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fersht A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. 1. WH Freeman; 1998. [Google Scholar]
- 6.Thielges MC, Fayer MD. Protein Dynamics Studied with Ultrafast Two-Dimensional Infrared Vibrational Echo Spectroscopy. Acc Chem Res. 2012;45:1866–1874. doi: 10.1021/ar200275k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Roberts ST, Ramasesha K, Tokmakoff A. Structural Rearrangements in Water Viewed Through Two-Dimensional Infrared Spectroscopy. Acc Chem Res. 2009;42:1239–1249. doi: 10.1021/ar900088g. [DOI] [PubMed] [Google Scholar]
- 8.Fayer MD. Dynamics of Water Interacting with Interfaces, Molecules, and Ions. Acc Chem Res. 2012;45:3–14. doi: 10.1021/ar2000088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ghosh A, Wang J, Moroz YS, Korendovych IV, Zanni M, DeGrado WF, Gai F, Hochstrasser RM. 2D IR Spectroscopy Reveals the Role of Water in the Binding of Channel-Blocking Drugs to the Influenza M2 Channel. J Chem Phys. 2014;140:235105. doi: 10.1063/1.4881188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kuroda DG, Bauman JD, Challa JR, Patel D, Troxler T, Das K, Arnold E, Hochstrasser RM. Snapshot of the Equilibrium Dynamics of a Drug Bound to HIV-1 Reverse Transcriptase. Nat Chem. 2013;5:174–181. doi: 10.1038/nchem.1559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Manor J, Mukherjee P, Lin YS, Leonov H, Skinner JL, Zanni MT, Arkin IT. Gating Mechanism of the Influenza A M2 Channel Revealed by 1D and 2D IR Spectroscopies. Structure. 2009;17:247–254. doi: 10.1016/j.str.2008.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mukherjee P, Kass I, Arkin I, Zanni MT. Picosecond Dynamics of a Membrane Protein Revealed by 2D IR. Proc Natl Acad Sci U S A. 2006;103:3528–3533. doi: 10.1073/pnas.0508833103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Szyc L, Yang M, Nibbering ETJ, Elsaesser T. Ultrafast Vibrational Dynamics and Local Interactions of Hydrated DNA. Angew Chem, Int Ed. 2010;49:3598–3610. doi: 10.1002/anie.200905693. [DOI] [PubMed] [Google Scholar]
- 14.Shim SH, Strasfeld DB, Ling YL, Zanni MT. Automated 2D IR Spectroscopy Using a Mid-IR Pulse Shaper and Application of This Technology to the Human Islet Amyloid Polypeptide. Proc Natl Acad Sci U S A. 2007;104:14197–14202. doi: 10.1073/pnas.0700804104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fenn EE, Fayer MD. Extracting 2D IR Frequency-Frequency Correlation Functions from Two Component Systems. J Chem Phys. 2011;135:074502. doi: 10.1063/1.3625278. [DOI] [PubMed] [Google Scholar]
- 16.Roberts ST, Loparo JJ, Tokmakoff A. Characterization of Spectral Diffusion from Two-Dimensional Line Shapes. J Chem Phys. 2006;125:084502. doi: 10.1063/1.2232271. [DOI] [PubMed] [Google Scholar]
- 17.Kubo R. A Stochastic Theory of Line Shape. Adv Chem Phys Stoch Process Chem Phys. 1969;15:101. [Google Scholar]
- 18.Culyba EK, Price JL, Hanson SR, Dhar A, Wong CH, Gruebele M, Powers ET, Kelly JW. Protein Native-State Stabilization by Placing Aromatic Side Chains in N-Glycosylated Reverse Turns. Science. 2011;331:571–575. doi: 10.1126/science.1198461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tycko R. Physical and Structural Basis for Polymorphism in Amyloid Fibrils. Protein Sci. 2014;23:1528–1539. doi: 10.1002/pro.2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Peng CS, Baiz CR, Tokmakoff A. Direct Observation of Ground-State Lactam-Lactim Tautomerization Using Temperature-Jump Transient 2D IR Spectroscopy. Proc Natl Acad Sci U S A. 2013;110:9243–9248. doi: 10.1073/pnas.1303235110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cervetto V, Hamm P, Helbing J. Transient 2D-IR Spectroscopy of Thiopeptide Isomerization. J Phys Chem B. 2008;112:8398–8405. doi: 10.1021/jp801166q. [DOI] [PubMed] [Google Scholar]
- 22.Tucker MJ, Abdo M, Courter JR, Chen J, Brown SP, Smith AB, Hochstrasser RM. Nonequilibrium Dynamics of Helix Reorganization Observed by Transient 2D IR Spectroscopy. Proc Natl Acad Sci U S A. 2013;110:17314–17319. doi: 10.1073/pnas.1311876110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Strasfeld DB, Ling YL, Shim SH, Zanni MT. Tracking Fiber Formation in Human Islet Amyloid Polypeptide with Automated 2D-IR Spectroscopy. J Am Chem Soc. 2008;130:6698–6699. doi: 10.1021/ja801483n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Grechko M, Zanni MT. Quantification of Transition Dipole Strengths Using 1D and 2D Spectroscopy for the Identification of Molecular Structures via Exciton Delocalization: Application to α-Helices. J Chem Phys. 2012;137:184202. doi: 10.1063/1.4764861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dunkelberger EB, Grechko M, Zanni MT. Transition Dipoles from 1D and 2D Infrared Spectroscopy Help Reveal the Secondary Structures of Proteins: Application to Amyloids. J Phys Chem B. 2015;119:14065–14075. doi: 10.1021/acs.jpcb.5b07706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Buchanan LE, Dunkelberger EB, Tran HQ, Cheng PN, Chiu CC, Cao P, Raleigh DP, de Pablo JJ, Nowick JS, Zanni MT. Mechanism of IAPP Amyloid Fibril Formation Involves an Intermediate with a Transient -Sheet. Proc Natl Acad Sci U S A. 2013;110:19285–19290. doi: 10.1073/pnas.1314481110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Middleton CT, Woys AM, Mukherjee SS, Zanni MT. Residue-Specific Structural Kinetics of Proteins through the Union of Isotope Labeling, Mid-IR Pulse Shaping, and Coherent 2D IR Spectroscopy. Methods. 2010;52:12–22. doi: 10.1016/j.ymeth.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shim SH, Gupta R, Ling YL, Strasfeld DB, Raleigh DP, Zanni MT. Two-Dimensional IR Spectroscopy and Isotope Labeling Defines the Pathway of Amyloid Formation with Residue-Specific Resolution. Proc Natl Acad Sci U S A. 2009;106:6614–6619. doi: 10.1073/pnas.0805957106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Petty SA, Adalsteinsson T, Decatur SM. Correlations among Morphology, β-Sheet Stability, and Molecular Structure in Prion Peptide Aggregates. Biochemistry. 2005;44:4720–4726. doi: 10.1021/bi047445a. [DOI] [PubMed] [Google Scholar]
- 30.Moran SD, Woys AM, Buchanan LE, Bixby E, Decatur SM, Zanni MT. Two-Dimensional IR Spectroscopy and Segmental 13C Labeling Reveals the Domain Structure of Human γD-Crystallin Amyloid Fibrils. Proc Natl Acad Sci U S A. 2012;109:3329–3334. doi: 10.1073/pnas.1117704109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fecko CJ, Eaves JD, Loparo JJ, Tokmakoff A, Geissler PL. Ultrafast Hydrogen-Bond Dynamics in the Infrared Spectroscopy of Water. Science. 2003;301:1698–1702. doi: 10.1126/science.1087251. [DOI] [PubMed] [Google Scholar]
- 32.Stirnemann G, Laage D. Direct Evidence of Angular Jumps During Water Reorientation Through Two-Dimensional Infrared Anisotropy. J Phys Chem Lett. 2010;1:1511–1516. [Google Scholar]
- 33.Asbury JB, Steinel T, Stromberg C, Gaffney KJ, Piletic IR, Goun A, Fayer MD. Hydrogen Bond Dynamics Probed with Ultrafast Infrared Heterodyne-Detected Multidimensional Vibrational Stimulated Echoes. Phys Rev Lett. 2003;91:237402. doi: 10.1103/PhysRevLett.91.237402. [DOI] [PubMed] [Google Scholar]
- 34.Anna JM, Baiz CR, Ross MR, McCanne R, Kubarych KJ. Ultrafast Equilibrium and Non-Equilibrium Chemical Reaction Dynamics Probed with Multidimensional Infrared Spectroscopy. Int Rev Phys Chem. 2012;31:367–419. [Google Scholar]
- 35.Kuroda DG, Hochstrasser RM. Two-Dimensional Infrared Spectral Signature and Hydration of the Oxalate Dianion. J Chem Phys. 2011;135:204502. doi: 10.1063/1.3658461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hamm P, Zanni MT. Concepts and Methods of 2D Infrared Spectroscopy. 1. Cambridge University Press; New York: 2011. [Google Scholar]
- 37.Mukamel S. Principles of Nonlinear Optical Spectroscopy. 1. Oxford University Press; New York: 1995. [Google Scholar]
- 38.Cho M. Two-Dimensional Optical Spectroscopy. 1. CRC Press; Boca Raton, FL: 2009. [Google Scholar]
- 39.Fayer MD, editor. Ultrafast Infrared Vibrational Spectroscopy. CRC Press; Boca Raton, FL: 2013. [Google Scholar]
- 40.Khalil M, Demirdöven N, Tokmakoff A. Coherent 2D IR Spectroscopy: Molecular Structure and Dynamics in Solution. J Phys Chem A. 2003;107:5258–5279. [Google Scholar]
- 41.Abella ID, Kurnit NA, Hartmann SR. Photon Echoes. Phys Rev. 1966;141:391–406. [Google Scholar]
- 42.Hochstrasser RM. Dynamical Models for Two-Dimensional Infrared Spectroscopy of Peptides. Adv Chem Phys. 2005;132:1–56. [Google Scholar]
- 43.De AK, Monahan D, Dawlaty JM, Fleming GR. Two-Dimensional Fluorescence-Detected Coherent Spectroscopy with Absolute Phasing by Confocal Imaging of a Dynamic Grating and 27-Step Phase-Cycling. J Chem Phys. 2014;140:194201. doi: 10.1063/1.4874697. [DOI] [PubMed] [Google Scholar]
- 44.Fulmer EC, Mukherjee P, Krummel AT, Zanni MT. A Pulse Sequence for Directly Measuring the Anharmonicities of Coupled Vibrations: Two-Quantum Two-Dimensional Infrared Spectroscopy. J Chem Phys. 2004;120:8067–8078. doi: 10.1063/1.1649725. [DOI] [PubMed] [Google Scholar]
- 45.Saurabh P, Mukamel S. Two-Dimensional Infrared Spectroscopy of Vibrational Polaritons of Molecules in an Optical Cavity. J Chem Phys. 2016;144:124115. doi: 10.1063/1.4944492. [DOI] [PubMed] [Google Scholar]
- 46.Baiz CR, Schach D, Tokmakoff A. Ultrafast 2D IR Microscopy. Opt Express. 2014;22:18724–18735. doi: 10.1364/OE.22.018724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ostrander JS, Serrano AL, Ghosh A, Zanni MT. Spatially Resolved Two-Dimensional Infrared Spectroscopy via Wide-Field Microscopy. ACS Photonics. 2016;3:1315–1323. doi: 10.1021/acsphotonics.6b00297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.DeFlores LP, Nicodemus RA, Tokmakoff A. Two-Dimensional Fourier Transform Spectroscopy in the Pump-Probe Geometry. Opt Lett. 2007;32:2966. doi: 10.1364/ol.32.002966. [DOI] [PubMed] [Google Scholar]
- 49.Hamm P, Lim M, Hochstrasser RM. Structure of the Amide I Band of Peptides Measured by Femtosecond Nonlinear-Infrared Spectroscopy. J Phys Chem B. 1998;102:6123–6138. [Google Scholar]
- 50.Gallagher Faeder SM, Jonas DM. Two-Dimensional Electronic Correlation and Relaxation Spectra: Theory and Model Calculations. J Phys Chem A. 1999;103:10489–10505. [Google Scholar]
- 51.Rock W, Li YL, Pagano P, Cheatum CM. 2D IR Spectroscopy Using Four-Wave Mixing, Pulse Shaping, and IR Upconversion: A Quantitative Comparison. J Phys Chem A. 2013;117:6073–6083. doi: 10.1021/jp312817t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Baiz CR, Kubarych KJ, Geva E, Sibert EL. Local-Mode Approach to Modeling Multidimensional Infrared Spectra of Metal Carbonyls. J Phys Chem A. 2011;115:5354–5363. doi: 10.1021/jp201641h. [DOI] [PubMed] [Google Scholar]
- 53.Davydov AS. Theory of Molecular Excitons. Plenum; New York: 1971. [Google Scholar]
- 54.Hamm P, Lim M, DeGrado WF, Hochstrasser RM. The Two-Dimensional IR Nonlinear Spectroscopy of a Cyclic Penta-Peptide in Relation to Its Three-Dimensional Structure. Proc Natl Acad Sci U S A. 1999;96:2036–2041. doi: 10.1073/pnas.96.5.2036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Torii H, Tasumi M. Vibrational Structure and Temperature Dependence of the Electronic Absorption (11Bu ← 11Ag) of All-Trans-β-Carotene. J Phys Chem. 1990;94:227–231. [Google Scholar]
- 56.Barth A. Infrared Spectroscopy of Proteins. Biochim Biophys Acta, Bioenerg. 2007;1767:1073–1101. doi: 10.1016/j.bbabio.2007.06.004. [DOI] [PubMed] [Google Scholar]
- 57.Zhuang W, Abramavicius D, Mukamel S. Dissecting Coherent Vibrational Spectra of Small Proteins into Secondary Structural Elements by Sensitivity Analysis. Proc Natl Acad Sci U S A. 2005;102:7443–7448. doi: 10.1073/pnas.0408781102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Moran A, Mukamel S. The Origin of Vibrational Mode Couplings in Various Secondary Structural Motifs of Polypeptides. Proc Natl Acad Sci U S A. 2004;101:506–510. doi: 10.1073/pnas.2533089100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mukamel S, Abramavicius D. Many-Body Approaches for Simulating Coherent Nonlinear Spectroscopies of Electronic and Vibrational Excitons. Chem Rev. 2004;104:2073–2098. doi: 10.1021/cr020681b. [DOI] [PubMed] [Google Scholar]
- 60.Mukamel S. Multidimensional Femtosecond Correlation Spectroscopies of Electronic and Vibrational Excitations. Annu Rev Phys Chem. 2000;51:691–729. doi: 10.1146/annurev.physchem.51.1.691. [DOI] [PubMed] [Google Scholar]
- 61.la Cour Jansen T, Dijkstra AG, Watson TM, Hirst JD, Knoester J. Modeling the Amide I Bands of Small Peptides. J Chem Phys. 2006;125:044312. doi: 10.1063/1.2218516. [DOI] [PubMed] [Google Scholar]
- 62.la Cour Jansen T, Knoester J. A Transferable Electrostatic Map for Solvation Effects on Amide I Vibrations and Its Application to Linear and Two-Dimensional Spectroscopy. J Chem Phys. 2006;124:044502. doi: 10.1063/1.2148409. [DOI] [PubMed] [Google Scholar]
- 63.Hamm P, Woutersen S. Coupling of the Amide I Modes of the Glycine Dipeptide. Bull Chem Soc Jpn. 2002;75:985–988. [Google Scholar]
- 64.Krimm S, Bandekar J. Vibrational Spectroscopy and Conformation of Peptides, Polypeptides, and Proteins. Adv Protein Chem. 1986;38:181–364. doi: 10.1016/s0065-3233(08)60528-8. [DOI] [PubMed] [Google Scholar]
- 65.Cho M. Coherent Two-Dimensional Optical Spectroscopy. Chem Rev. 2008;108:1331–1418. doi: 10.1021/cr078377b. [DOI] [PubMed] [Google Scholar]
- 66.Lee C, Cho M. Local Amide I Mode Frequencies And Coupling Constants in Multiple-Stranded Antiparallel β-Sheet Polypeptides. J Phys Chem B. 2004;108:20397–20407. [Google Scholar]
- 67.Ling YL, Strasfeld DB, Shim S, Raleigh DP, Zanni MT. Two-Dimensional Infrared Spectroscopy Provides Evidence of an Intermediate in the Membrane-Catalyzed Assembly of Diabetic Amyloid. J Phys Chem B. 2009;113:2498–2505. doi: 10.1021/jp810261x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Demirdöven N, Cheatum CM, Chung HS, Khalil M, Knoester J, Tokmakoff A. Two-Dimensional Infrared Spectroscopy of Antiparallel β-Sheet Secondary Structure. J Am Chem Soc. 2004;126:7981–7990. doi: 10.1021/ja049811j. [DOI] [PubMed] [Google Scholar]
- 69.Knapp EW. Lineshapes of Molecular Aggregates, Exchange Narrowing and Intersite Correlation. Chem Phys. 1984;85:73–82. [Google Scholar]
- 70.Didraga C, Knoester J. Exchange Narrowing in Circular and Cylindrical Molecular Aggregates: Degenerate versus Nondegenerate States. Chem Phys. 2002;275:307–318. [Google Scholar]
- 71.King JT, Baiz CR, Kubarych KJ. Solvent-Dependent Spectral Diffusion in a Hydrogen Bonded “Vibrational Aggregate. J Phys Chem A. 2010;114:10590–10604. doi: 10.1021/jp106142u. [DOI] [PubMed] [Google Scholar]
- 72.Ge NH, Zanni MT, Hochstrasser RM. Effects of Vibrational Frequency Correlations on Two-Dimensional Infrared Spectra. J Phys Chem A. 2002;106:962–972. [Google Scholar]
- 73.Mehlenbacher RD, McDonough TJ, Grechko M, Wu MY, Arnold MS, Zanni MT. Energy Transfer Pathways in Semiconducting Carbon Nanotubes Revealed Using Two-Dimensional White-Light Spectroscopy. Nat Commun. 2015;6:6732. doi: 10.1038/ncomms7732. [DOI] [PubMed] [Google Scholar]
- 74.Mehlenbacher RD, Wu M, Grechko M, Laaser JE, Arnold MS, Zanni MT. Photoexcitation Dynamics of Coupled Semiconducting Carbon Nanotube Thin Films. Nano Lett. 2013;13:1495–1501. doi: 10.1021/nl304591w. [DOI] [PubMed] [Google Scholar]
- 75.Kuroda DG, Hochstrasser RM. Polarization Anisotropy Effects for Degenerate Vibrational Levels. Ultrafast Infrared Vib Spectrosc. 2013:169–202. [Google Scholar]
- 76.Kramer PL, Nishida J, Fayer MD. Separation of Experimental 2D IR Frequency-Frequency Correlation Functions into Structural and Reorientation-Induced Contributions. J Chem Phys. 2015;143:124505. doi: 10.1063/1.4931402. [DOI] [PubMed] [Google Scholar]
- 77.Golonzka O, Tokmakoff A. Polarization-Selective Third-Order Spectroscopy of Coupled Vibronic States. J Chem Phys. 2001;115:297–309. [Google Scholar]
- 78.Zanni MT, Ge NH, Kim YS, Hochstrasser RM. Two-Dimensional IR Spectroscopy Can Be Designed to Eliminate the Diagonal Peaks and Expose Only the Crosspeaks Needed for Structure Determination. Proc Natl Acad Sci U S A. 2001;98:11265–11270. doi: 10.1073/pnas.201412998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Ramasesha K, Roberts ST, Nicodemus RA, Mandal A, Tokmakoff A. Ultrafast 2D IR Anisotropy of Water Reveals Reorientation during Hydrogen-Bond Switching. J Chem Phys. 2011;135:054509. doi: 10.1063/1.3623008. [DOI] [PubMed] [Google Scholar]
- 80.Ghosh A, Serrano AL, Oudenhoven TA, Ostrander JS, Eklund EC, Blair AF, Zanni MT. Experimental Implementations of 2D IR Spectroscopy through a Horizontal Pulse Shaper Design and a Focal Plane Array Detector. Opt Lett. 2016;41:524–527. doi: 10.1364/OL.41.000524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Liu XM, Sonar S, Lee CP, Coleman M, RajBhandary UL, Rothschild KJ. Site-Directed Isotope Labeling and FTIR Spectroscopy: Assignment of Tyrosine Bands in the bR → M Difference Spectrum of Bacteriorhodopsin. Biophys Chem. 1995;56:63–70. doi: 10.1016/0301-4622(95)00016-q. [DOI] [PubMed] [Google Scholar]
- 82.Arkin IT. Isotope-Edited IR Spectroscopy for the Study of Membrane Proteins. Curr Opin Chem Biol. 2006;10:394–401. doi: 10.1016/j.cbpa.2006.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Torres J, Kukol A, Goodman JM, Arkin IT. Site-Specific Examination of Secondary Structure and Orientation Determination in Membrane Proteins: The Peptidic 13C=18O Group as a Novel Infrared Probe. Biopolymers. 2001;59:396–401. doi: 10.1002/1097-0282(200111)59:6<396::AID-BIP1044>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 84.Seyfried MS, Lauber BS, Luedtke NW. Multiple-Turnover Isotopic Labeling of Fmoc- and Boc-Protected Amino Acids with Oxygen Isotopes. Org Lett. 2010;12:104–106. doi: 10.1021/ol902519g. [DOI] [PubMed] [Google Scholar]
- 85.Woys AM, Almeida AM, Wang L, Chiu CC, McGovern M, de Pablo JJ, Skinner JL, Gellman SH, Zanni MT. Parallel β-Sheet Vibrational Couplings Revealed by 2D IR Spectroscopy of an Isotopically Labeled Macrocycle: Quantitative Benchmark for the Interpretation of Amyloid and Protein Infrared Spectra. J Am Chem Soc. 2012;134:19118–19128. doi: 10.1021/ja3074962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Remorino A, Korendovych IV, Wu Y, DeGrado WF, Hochstrasser RM. Residue-Specific Vibrational Echoes Yield 3D Structures of a Transmembrane Helix Dimer. Science. 2011;332:1206–1209. doi: 10.1126/science.1202997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Remorino A, Hochstrasser RM. Three-Dimensional Structures by Two-Dimensional Vibrational Spectroscopy. Acc Chem Res. 2012;45:1896–1905. doi: 10.1021/ar3000025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Woys AM, Lin YS, Reddy AS, Xiong W, De Pablo JJ, Skinner JL, Zanni MT. 2D IR Line Shapes Probe Ovispirin Peptide Conformation and Depth in Lipid Bilayers. J Am Chem Soc. 2010;132:2832–2838. doi: 10.1021/ja9101776. [DOI] [PubMed] [Google Scholar]
- 89.Peuker S, Andersson H, Gustavsson E, Maiti KS, Kania R, Karim A, Niebling S, Pedersen A, Erdelyi M, Westenhoff S. Efficient Isotope Editing of Proteins for Site-Directed Vibrational Spectroscopy. J Am Chem Soc. 2016;138:2312–2318. doi: 10.1021/jacs.5b12680. [DOI] [PubMed] [Google Scholar]
- 90.De Marco L, Thämer M, Reppert M, Tokmakoff A. Direct Observation of Intermolecular Interactions Mediated by Hydrogen Bonding. J Chem Phys. 2014;141:034502. doi: 10.1063/1.4885145. [DOI] [PubMed] [Google Scholar]
- 91.Schmidt JR, Corcelli SA, Skinner JL. Ultrafast Vibrational Spectroscopy of Water and Aqueous N-Methylacetamide: Comparison of Different Electronic Structure/molecular Dynamics Approaches. J Chem Phys. 2004;121:8887–8896. doi: 10.1063/1.1791632. [DOI] [PubMed] [Google Scholar]
- 92.Hamm P, Lim M, Hochstrasser RM. Non-Markovian Dynamics of the Vibrations of Ions in Water from Femtosecond Infrared Three-Pulse Photon Echoes. Phys Rev Lett. 1998;81:5326–5329. [Google Scholar]
- 93.Yang S, Cho M. Thermal Denaturation of Polyalanine Peptide in Water by Molecular Dynamics Simulations and Theoretical Prediction of Infrared Spectra: Helix-Coil Transition Kinetics. J Phys Chem B. 2007;111:605–617. doi: 10.1021/jp0649091. [DOI] [PubMed] [Google Scholar]
- 94.Lin YS, Shorb JM, Mukherjee P, Zanni MT, Skinner JL. Empirical Amide I Vibrational Frequency Map: Application to 2D-IR Line Shapes for Isotope-Edited Membrane Peptide Bundles. J Phys Chem B. 2009;113:592–602. doi: 10.1021/jp807528q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Bakker HJ, Skinner JL. Vibrational Spectroscopy as a Probe of Structure and Dynamics in Liquid Water. Chem Rev. 2010;110:1498–1517. doi: 10.1021/cr9001879. [DOI] [PubMed] [Google Scholar]
- 96.Wang L, Middleton CT, Zanni MT, Skinner JL. Development and Validation of Transferable Amide I Vibrational Frequency Maps for Peptides. J Phys Chem B. 2011;115:3713–3724. doi: 10.1021/jp200745r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Hayashi T, Zhuang W, Mukamel S. Electrostatic DFT Map for the Complete Vibrational Amide Band of NMA. J Phys Chem A. 2005;109:9747–9759. doi: 10.1021/jp052324l. [DOI] [PubMed] [Google Scholar]
- 98.Hayashi T, Mukamel S. Two-Dimensional Vibrational Lineshapes of Amide III, II, I and A Bands in a Helical Peptide. J Mol Liq. 2008;141:149–154. doi: 10.1016/j.molliq.2008.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Falvo C, Zhuang W, Kim YS, Axelsen PH, Hochstrasser RM, Mukamel S. Frequency Distribution of the Amide-I Vibration Sorted by Residues in Amyloid Fibrils Revealed by 2D-IR Measurements and Simulations. J Phys Chem B. 2012;116:3322–3330. doi: 10.1021/jp2096423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Van Der Vegte CP, Dijkstra AG, Knoester J, Jansen TLC. Calculating Two-Dimensional Spectra with the Mixed Quantum-Classical Ehrenfest Method. J Phys Chem A. 2013;117:5970–5980. doi: 10.1021/jp311668r. [DOI] [PubMed] [Google Scholar]
- 101.Jansen TLC, Knoester J. Waiting Time Dynamics in Two-Dimensional Infrared Spectroscopy. Acc Chem Res. 2009;42:1405–1411. doi: 10.1021/ar900025a. [DOI] [PubMed] [Google Scholar]
- 102.Schmidt JR, Sundlass N, Skinner JL. Line Shapes and Photon Echoes within a Generalized Kubo Model. Chem Phys Lett. 2003;378:559–566. [Google Scholar]
- 103.Ghosh A, Hochstrasser RM. A Peptide’s Perspective of Water Dynamics. Chem Phys. 2011;390:1–13. doi: 10.1016/j.chemphys.2011.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Woutersen S, Pfister R, Hamm P, Mu YG, Kosov DS, Stock G. Peptide Conformational Heterogeneity Revealed from Nonlinear Vibrational Spectroscopy and Molecular-Dynamics Simulations. J Chem Phys. 2002;117:6833–6840. [Google Scholar]
- 105.Kwak K, Park S, Finkelstein IJ, Fayer MD. Frequency-Frequency Correlation Functions and Apodization in Two-Dimensional Infrared Vibrational Echo Spectroscopy: A New Approach. J Chem Phys. 2007;127:124503. doi: 10.1063/1.2772269. [DOI] [PubMed] [Google Scholar]
- 106.Kwak K, Rosenfeld DE, Fayer MD. Taking Apart the Two-Dimensional Infrared Vibrational Echo Spectra: More Information and Elimination of Distortions. J Chem Phys. 2008;128:204505. doi: 10.1063/1.2927906. [DOI] [PubMed] [Google Scholar]
- 107.Kwac K, Cho M. Two-Color Pump-Probe Spectroscopies of Two- and Three-Level Systems: 2-Dimensional Line Shapes and Solvation Dynamics. J Phys Chem A. 2003;107:5903–5912. [Google Scholar]
- 108.Kwac K, Cho MH. Molecular Dynamics Simulation Study of N-Methylacetamide in Water. II. Two-Dimensional Infrared Pump-Probe Spectra. J Chem Phys. 2003;119:2256–2263. [Google Scholar]
- 109.Kim YS, Liu L, Axelsen PH, Hochstrasser RM. 2D IR Provides Evidence for Mobile Water Molecules in β-Amyloid Fibrils. Proc Natl Acad Sci U S A. 2009;106:17751–17756. doi: 10.1073/pnas.0909888106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Ghosh A, Qiu J, DeGrado WF, Hochstrasser RM. Tidal Surge in the M2 Proton Channel, Sensed by 2D IR Spectroscopy. Proc Natl Acad Sci U S A. 2011;108:6115–6120. doi: 10.1073/pnas.1103027108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Lazonder K, Pshenichnikov MS, Wiersma DA. Easy Interpretation of Optical Two-Dimensional Correlation Spectra. Opt Lett. 2006;31:3354–3356. doi: 10.1364/ol.31.003354. [DOI] [PubMed] [Google Scholar]
- 112.deBoeij WP, Pshenichnikov MS, Wiersma DA. On the Relation between the Echo-Peak Shift and Brownian-Oscillator Correlation Function. Chem Phys Lett. 1996;253:53–60. [Google Scholar]
- 113.King JT, Ross MR, Kubarych KJ. Water-Assisted Vibrational Relaxation of a Metal Carbonyl Complex Studied with Ultrafast 2D-IR. J Phys Chem B. 2012;116:3754–3759. doi: 10.1021/jp2125747. [DOI] [PubMed] [Google Scholar]
- 114.Middleton CT, Buchanan LE, Dunkelberger EB, Zanni MT. Utilizing Lifetimes to Suppress Random Coil Features in 2D IR Spectra of Peptides. J Phys Chem Lett. 2011;2:2357–2361. doi: 10.1021/jz201024m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Peng JW. Exposing the Moving Parts of Proteins with NMR Spectroscopy. J Phys Chem Lett. 2012;3:1039–1051. doi: 10.1021/jz3002103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Matthews BW. X-ray Crystallographic Studies of Proteins. Annu Rev Phys Chem. 1976;27:493–493. [Google Scholar]
- 117.Cavanagh J, Fairbrother WJ, Palmer AG, III, Rance M, Skelton NJ. Protein NMR Spectroscopy. 2. Elsevier Inc; Burlington, MA: 2007. [Google Scholar]
- 118.Ishima R, Torchia D. Protein Dynamics from NMR. Nat Struct Mol Biol. 2000;76:145–152. doi: 10.1038/78963. [DOI] [PubMed] [Google Scholar]
- 119.Woutersen S, Hamm P. Structure Determination of Trialanine in Water Using Polarization Sensitive Two-Dimensional Vibrational Spectroscopy. J Phys Chem B. 2000;104:11316–11320. [Google Scholar]
- 120.Fang C, Wang J, Charnley AK, Barber-Armstrong W, Smith AB, III, Decatur SM, Hochstrasser RM. Two-Dimensional Infrared Measurements of the Coupling between Amide Modes of an α-Helix. Chem Phys Lett. 2003;382:586–592. [Google Scholar]
- 121.Fang C, Senes A, Cristian L, DeGrado WF, Hochstrasser RM. Amide Vibrations Are Delocalized across the Hydrophobic Interface of a Transmembrane Helix Dimer. Proc Natl Acad Sci U S A. 2006;103:16740–16745. doi: 10.1073/pnas.0608243103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Maekawa H, De Poli M, Moretto A, Toniolo C, Ge NH. Toward Detecting the Formation of a Single Helical Turn by 2D IR Cross Peaks between the Amide-I and -II Modes. J Phys Chem B. 2009;113:11775–11786. doi: 10.1021/jp9045879. [DOI] [PubMed] [Google Scholar]
- 123.Maekawa H, Toniolo C, Moretto A, Broxterman QB, Ge NH. Different Spectral Signatures of Octapeptide 310- and α-Helices Revealed by Two-Dimensional Infrared Spectroscopy. J Phys Chem B. 2006;110:5834–5837. doi: 10.1021/jp057472q. [DOI] [PubMed] [Google Scholar]
- 124.Maekawa H, Toniolo C, Broxterman QB, Ge N. Two-Dimensional Infrared Spectral Signatures of 310- and α-Helical Peptides. J Phys Chem B. 2007;111:3222–3235. doi: 10.1021/jp0674874. [DOI] [PubMed] [Google Scholar]
- 125.Maekawa H, Formaggio F, Toniolo C, Ge NH. Onset of 310-Helical Secondary Structure in Aib Oligopeptides Probed by Coherent 2D IR Spectroscopy. J Am Chem Soc. 2008;130:6556–6566. doi: 10.1021/ja8007165. [DOI] [PubMed] [Google Scholar]
- 126.Sengupta N, Maekawa H, Zhuang W, Toniolo C, Mukamel S, Tobias DJ, Ge NH. Sensitivity of 2D IR Spectra to Peptide Helicity: A Concerted Experimental and Simulation Study of an Octapeptide. J Phys Chem B. 2009;113:12037–12049. doi: 10.1021/jp901504r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Kim YS, Liu L, Axelsen PH, Hochstrasser RM. Two-Dimensional Infrared Spectra of Isotopically Diluted Amyloid Fibrils from Aβ40. Proc Natl Acad Sci U S A. 2008;105:7720–7725. doi: 10.1073/pnas.0802993105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Baiz CR, Reppert M, Tokmakoff A. An Introduction to Protein 2D IR Spectroscopy. Ultrafast Infrared Vib Spectrosc. 2013:361–403. [Google Scholar]
- 129.Lam AR, Moran SD, Preketes NK, Zhang TO, Zanni MT, Mukamel S. Study of the γd-Crystallin Protein Using Two-Dimensional Infrared (2DIR) Spectroscopy: Experiment and Simulation. J Phys Chem B. 2013;117:15436–15443. doi: 10.1021/jp405159v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Moran SD, Zhang TO, Decatur SM, Zanni MT. Amyloid Fiber Formation in Human γD-Crystallin Induced by UV–B Photodamage. Biochemistry. 2013;52:6169–6181. doi: 10.1021/bi4008353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Baiz CR, Tokmakoff A. Structural Disorder of Folded Proteins: Isotope-Edited 2D IR Spectroscopy and Markov State Modeling. Biophys J. 2015;108:1747–1757. doi: 10.1016/j.bpj.2014.12.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Skoff DR, Laaser JE, Mukherjee SS, Middleton CT, Zanni MT. Simplified and Economical 2D IR Spectrometer Design Using a Dual Acousto-Optic Modulator. Chem Phys. 2013;422:8–15. doi: 10.1016/j.chemphys.2012.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Shim SH, Zanni MT. How to Turn Your Pump-Probe Instrument into a Multidimensional Spectrometer: 2D IR and Vis Spectroscopies via Pulse Shaping. Phys Chem Chem Phys. 2009;11:748–761. doi: 10.1039/b813817f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Wang L, Middleton CT, Singh S, Reddy AS, Woys AM, Strasfeld DB, Marek P, Raleigh DP, de Pablo JJ, Zanni MT, et al. 2DIR Spectroscopy of Human Amylin Fibrils Reflects Stable β-Sheet Structure. J Am Chem Soc. 2011;133:16062–16071. doi: 10.1021/ja204035k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Zanni MT, Asplund MC, Hochstrasser RM. Two-Dimensional Heterodyned and Stimulated Infrared Photon Echoes of N-Methylacetamide-D. J Chem Phys. 2001;114:4579–4590. [Google Scholar]
- 136.Kim YS, Hochstrasser RM. Dynamics of Amide-I Modes of the Alanine Dipeptide in D2O. J Phys Chem B. 2005;109:6884–6891. doi: 10.1021/jp0449511. [DOI] [PubMed] [Google Scholar]
- 137.DeCamp MF, DeFlores L, McCracken JM, Tokmakoff A, Kwac K, Cho M. Amide I Vibrational Dynamics of N-Methylacetamide in Polar Solvents: The Role of Electrostatic Interactions. J Phys Chem B. 2005;109:11016–11026. doi: 10.1021/jp050257p. [DOI] [PubMed] [Google Scholar]
- 138.Bagchi S, Falvo C, Mukamel S, Hochstrasser RM. 2D-IR Experiments and Simulations of the Coupling between Amide-I and Ionizable Side Chains in Proteins: Application to the Villin Headpiece. J Phys Chem B. 2009;113:11260–11273. doi: 10.1021/jp900245s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Tokmakoff A. Shining Light on the Rapidly Evolving Structure of Water. Science. 2007;317:54–55. doi: 10.1126/science.1144515. [DOI] [PubMed] [Google Scholar]
- 140.Nishida J, Tamimi A, Fei H, Pullen S, Ott S, Cohen SM, Fayer MD. Structural Dynamics inside a Functionalized Metal-Organic Framework Probed by Ultrafast 2D IR Spectroscopy. Proc Natl Acad Sci U S A. 2014;111:18442–18447. doi: 10.1073/pnas.1422194112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Fang C, Hochstrasser RM. Two-Dimensional Infrared Spectra of the 13C-=18O Isotopomers of Alanine Residues in an α-Helix. J Phys Chem B. 2005;109:18652–18663. doi: 10.1021/jp052525p. [DOI] [PubMed] [Google Scholar]
- 142.Torres J, Briggs JAG, Arkin IT. Multiple Site-Specific Infrared Dichroism of {CD3-Zeta}, a Transmembrane Helix Bundle. J Mol Biol. 2002;316:365–374. doi: 10.1006/jmbi.2001.5267. [DOI] [PubMed] [Google Scholar]
- 143.Zea AH, Rodriguez PC, Culotta KS, Hernandez CP, DeSalvo J, Ochoa JB, Park HJ, Zabaleta J, Ochoa AC. L-Arginine Modulates CD3ζ Expression and T Cell Function in Activated Human T Lymphocytes. Cell Immunol. 2004;232:21–31. doi: 10.1016/j.cellimm.2005.01.004. [DOI] [PubMed] [Google Scholar]
- 144.Bezanilla F. How Membrane Proteins Sense Voltage. Nat Rev Mol Cell Biol. 2008;9:323–332. doi: 10.1038/nrm2376. [DOI] [PubMed] [Google Scholar]
- 145.Engel A, Gaub HE. Structure and Mechanics of Membrane Proteins. Annu Rev Biochem. 2008;77:127–148. doi: 10.1146/annurev.biochem.77.062706.154450. [DOI] [PubMed] [Google Scholar]
- 146.Rasaiah JC, Garde S, Hummer G. Water in Nonpolar Confinement: From Nanotubes to Proteins and beyond. Annu Rev Phys Chem. 2008;59:713–740. doi: 10.1146/annurev.physchem.59.032607.093815. [DOI] [PubMed] [Google Scholar]
- 147.Wang J, Ma CL, Fiorin G, Carnevale V, Wang T, Hu FH, Lamb RA, Pinto LH, Hong M, Kein ML, et al. Molecular Dynamics Simulation Directed Rational Design of Inhibitors Targeting Drug-Resistant Mutants of Influenza A Virus M2. J Am Chem Soc. 2011;133:12834–12841. doi: 10.1021/ja204969m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Wang J, Ma C, Balannik V, Pinto LH, Lamb RA, DeGrado WF. Exploring the Requirements for the Hydrophobic Scaffold and Polar Amine in Inhibitors of M2 from Influenza A Virus. ACS Med Chem Lett. 2011;2:307–312. doi: 10.1021/ml100297w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Törnroth-Horsefield S, Wang Y, Hedfalk K, Johanson U, Karlsson M, Tajkhorshid E, Neutze R, Kjellbom P. Structural Mechanism of Plant Aquaporin Gating. Nature. 2006;439:688–694. doi: 10.1038/nature04316. [DOI] [PubMed] [Google Scholar]
- 150.Pinto LH, Lamb RA. The M2 Proton Channels of Influenza A and B Viruses. J Biol Chem. 2006;281:8997–9000. doi: 10.1074/jbc.R500020200. [DOI] [PubMed] [Google Scholar]
- 151.Acharya R, Carnevale V, Fiorin G, Levine BG, Polishchuk AL, Balannik V, Samish I, Lamb RA, Pinto LH, DeGrado WF, et al. Structure and Mechanism of Proton Transport through the Transmembrane Tetrameric M2 Protein Bundle of the Influenza A Virus. Proc Natl Acad Sci U S A. 2010;107:15075–15080. doi: 10.1073/pnas.1007071107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. A Structural Model for Alzheimer’s β-Amyloid Fibrils Based on Experimental Constraints from Solid State NMR. Proc Natl Acad Sci U S A. 2002;99:16742–16747. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Ma JQ, Komatsu H, Kim YS, Liu L, Hochstrasser RM, Axelsen PH. Intrinsic Structural Heterogeneity and Long-Term Maturation of Amyloid β Peptide Fibrils. ACS Chem Neurosci. 2013;4:1236–1243. doi: 10.1021/cn400092v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Kratochvil HT, Carr JK, Matulef K, Annen AW, Li H, Maj M, Ostmeyer J, Serrano AL, Raghuraman H, Moran SD, et al. Instantaneous Ion Configurations in the K+ Ion Channel Selectivity Filter Revealed by 2D IR Spectroscopy. Science. 2016;353:1040–1044. doi: 10.1126/science.aag1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Doyle DA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnon R. The Structure of the Potassium Channel: Molecular Basis of K+ Conduction and Selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 156.Raghuraman H, Islam SM, Mukherjee S, Roux B, Perozo E. Dynamics Transitions at the Outer Vestibule of the KcsA Potassium Channel during Gating. Proc Natl Acad Sci U S A. 2014;111:1831–1836. doi: 10.1073/pnas.1314875111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Bernèche S, Roux B. Energetics of Ion Conduction through the K+ Channel. Nature. 2001;414:73–77. doi: 10.1038/35102067. [DOI] [PubMed] [Google Scholar]
- 158.Hille B. Ion Channels of Excitable Membranes. 3. Sinauer Associates; Sunderland, MA: 2001. [Google Scholar]
- 159.Kopfer DA, Song C, Gruene T, Sheldrick GM, Zachariae U, de Groot BL. Ion Permeation in K+ Channels Occurs by Direct Coulomb Knock-On. Science. 2014;346:352–355. doi: 10.1126/science.1254840. [DOI] [PubMed] [Google Scholar]
- 160.Merchant KA, Noid WG, Akiyama R, Finkelstein IJ, Goun A, McClain BL, Loring RF, Fayer MD. Myoglobin-CO Substrate Structures and Dynamics: Multidimensional Vibrational Echoes and Molecular Dynamics Simulations. J Am Chem Soc. 2003;125:13804–13818. doi: 10.1021/ja035654x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Finkelstein IJ, Ishikawa H, Kim S, Massari AM, Fayer MD. Substrate Binding and Protein Conformational Dynamics Measured by 2D-IR Vibrational Echo Spectroscopy. Proc Natl Acad Sci U S A. 2007;104:2637–2642. doi: 10.1073/pnas.0610027104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Kim S, Chung JK, Kwak K, Bowman SEJ, Bren KL, Bagchi B, Fayer MD. Native and Unfolded Cytochrome c-Comparison of Dynamics Using 2D-IR Vibrational Echo Spectroscopy. J Phys Chem B. 2008;112:10054–10063. doi: 10.1021/jp802246h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Thielges MC, Chung JK, Fayer MD. Protein Dynamics in Cytochrome P450 Molecular Recognition and Substrate Specificity Using 2D IR Vibrational Echo Spectroscopy. J Am Chem Soc. 2011;133:3995–4004. doi: 10.1021/ja109168h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Zheng J, Kwak K, Asbury J, Chen X, Piletic IR, Fayer MD. Ultrafast Dynamics of Solute-Solvent Complexation Observed at Thermal Equilibrium in Real Time. Science. 2005;309:1338–1343. doi: 10.1126/science.1116213. [DOI] [PubMed] [Google Scholar]
- 165.Fayer MD. Dynamics of Liquids, Molecules, and Proteins Measured with Ultrafast 2D IR Vibrational Echo Chemical Exchange Spectroscopy. Annu Rev Phys Chem. 2009;60:21–38. doi: 10.1146/annurev-physchem-073108-112712. [DOI] [PubMed] [Google Scholar]
- 166.Woutersen S, Mu Y, Stock G, Hamm P. Hydrogen-Bond Lifetime Measured by Time-Resolved 2D-IR Spectroscopy: N-Methylacetamide in Methanol. Chem Phys. 2001;266:137–147. [Google Scholar]
- 167.Kim YS, Hochstrasser RM. Chemical Exchange 2D IR of Hydrogen-Bond Making and Breaking. Proc Natl Acad Sci U S A. 2005;102:11185–11190. doi: 10.1073/pnas.0504865102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Zheng J, Kwak K, Xie J, Fayer MD. Ultrafast Carbon-Carbon Single-Bond Rotational Isomerization in Room-Temperature Solution. Science. 2006;313:1951–1955. doi: 10.1126/science.1132178. [DOI] [PubMed] [Google Scholar]
- 169.Bagchi S, Charnley AK, Smith AB, Hochstrasser RM. Equilibrium Exchange Processes of the Aqueous Tryptophan Dipeptide. J Phys Chem B. 2009;113:8412–8417. doi: 10.1021/jp811168x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Ghosh A, Tucker MJ, Gai F. 2D IR Spectroscopy of Histidine: Probing Side-Chain Structure and Dynamics via Backbone Amide Vibrations. J Phys Chem B. 2014;118:7799–7805. doi: 10.1021/jp411901m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Ishikawa H, Kwak K, Chung JK, Kim S, Fayer MD. Direct Observation of Fast Protein Conformational Switching. Proc Natl Acad Sci U S A. 2008;105:8619–8624. doi: 10.1073/pnas.0803764105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Bagchi S, Nebgen BT, Loring RF, Fayer MD. Dynamics of a Myoglobin Mutant Enzyme: 2D IR Vibrational Echo Experiments and Simulations. J Am Chem Soc. 2010;132:18367–18376. doi: 10.1021/ja108491t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Frauenfelder H, Chen G, Berendzen J, Fenimore PW, Jansson H, McMahon BH, Stroe IR, Swenson J, Young RD. A Unified Model of Protein Dynamics. Proc Natl Acad Sci U S A. 2009;106:5129–5134. doi: 10.1073/pnas.0900336106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Breiten B, Lockett MR, Sherman W, Fujita S, Al-Sayah M, Lange H, Bowers CM, Heroux A, Krilov G, Whitesides GM. Water Networks Contribute to Enthalpy/entropy Compensation in Protein-Ligand Binding. J Am Chem Soc. 2013;135:15579–15584. doi: 10.1021/ja4075776. [DOI] [PubMed] [Google Scholar]
- 175.Woys AM, Mukherjee SS, Skoff DR, Moran SD, Zanni MT. A Strongly Absorbing Class of Non-Natural Labels for Probing Protein Electrostatics and Solvation with FTIR and 2D IR Spectroscopies. J Phys Chem B. 2013;117:5009–5018. doi: 10.1021/jp402946c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.King JT, Arthur EJ, Brooks CL, Kubarych KJ. Site-Specific Hydration Dynamics of Globular Proteins and the Role of Constrained Water in Solvent Exchange with Amphiphilic Cosolvents. J Phys Chem B. 2012;116:5604–5611. doi: 10.1021/jp300835k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Santos-Silva T, Mukhopadhyay A, Seixas JD, Bernardes GJL, Romão CC, Romão MJ. CORM-3 Reactivity toward Proteins: The Crystal Structure of a Ru(II) Dicarbonyl–Lysozyme Complex. J Am Chem Soc. 2011;133:1192–1195. doi: 10.1021/ja108820s. [DOI] [PubMed] [Google Scholar]
- 178.King JT, Kubarych KJ. Site-Specific Coupling of Hydration Water and Protein Flexibility Studied in Solution with Ultrafast 2D-IR Spectroscopy. J Am Chem Soc. 2012;134:18705–18712. doi: 10.1021/ja307401r. [DOI] [PubMed] [Google Scholar]
- 179.Ball P. Water as an Active Constituent in Cell Biology. Chem Rev. 2008;108:74–108. doi: 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
- 180.Berne BJ, Weeks JD, Zhou R. Dewetting and Hydrophobic Interaction in Physical and Biological Systems. Annu Rev Phys Chem. 2009;60:85–103. doi: 10.1146/annurev.physchem.58.032806.104445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Bakulin AA, Liang C, la Cour Jansen T, Wiersma DA, Bakker HJ, Pshenichnikov MS. Hydrophobic Solvation: A 2D IR Spectroscopic Inquest. Acc Chem Res. 2009;42:1229–1238. doi: 10.1021/ar9000247. [DOI] [PubMed] [Google Scholar]
- 182.Elsaesser T, Szyc Ł, Yang M. Ultrafast Structural and Vibrational Dynamics of the Hydration Shell around DNA. EPJ Web Conf. 2013;41:06004. [Google Scholar]
- 183.Elsaesser T. Two-Dimensional Infrared Spectroscopy of Intermolecular Hydrogen Bonds in the Condensed Phase. Acc Chem Res. 2009;42:1220–1228. doi: 10.1021/ar900006u. [DOI] [PubMed] [Google Scholar]
- 184.King JT, Arthur EJ, Brooks CL, Kubarych KJ. Crowding Induced Collective Hydration of Biological Macromolecules over Extended Distances. J Am Chem Soc. 2014;136:188–194. doi: 10.1021/ja407858c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Ross MR, White AM, Yu F, King JT, Pecoraro VL, Kubarych KJ. Histidine Orientation Modulates the Structure and Dynamics of a de Novo Metalloenzyme Active Site. J Am Chem Soc. 2015;137:10164–10176. doi: 10.1021/jacs.5b02840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Peran I, Oudenhoven T, Woys AM, Watson MD, Zhang TO, Carrico I, Zanni MT, Raleigh DP. General Strategy for the Bioorthogonal Incorporation of Strongly Absorbing, Solvation-Sensitive Infrared Probes into Proteins. J Phys Chem B. 2014;118:7946–7953. doi: 10.1021/jp5008279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Boxer SG. Stark Realities. J Phys Chem B. 2009;113:2972–2983. doi: 10.1021/jp8067393. [DOI] [PubMed] [Google Scholar]
- 188.Bagchi S, Fried SD, Boxer SG. A Solvatochromic Model Calibrates Nitriles’ Vibrational Frequencies to Electrostatic Fields. J Am Chem Soc. 2012;134:10373–10376. doi: 10.1021/ja303895k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Tucker MJ, Getahun Z, Nanda V, DeGrado WF, Gai F. A New Method for Determining the Local Environment and Orientation of Individual Side Chains of Membrane-Binding Peptides. J Am Chem Soc. 2004;126:5078–5079. doi: 10.1021/ja032015d. [DOI] [PubMed] [Google Scholar]
- 190.Waegele MM, Tucker MJ, Gai F. 5-Cyanotryptophan as an Infrared Probe of Local Hydration Status of Proteins. Chem Phys Lett. 2009;478:249–253. doi: 10.1016/j.cplett.2009.07.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Horness RE, Basom EJ, Thielges MC. Site-Selective Characterization of Src Homology 3 Domain Molecular Recognition with Cyanophenylalanine Infrared Probes. Anal Methods. 2015;7:7234–7241. doi: 10.1039/C5AY00523J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Chung JK, Thielges MC, Fayer MD. Conformational Dynamics and Stability of HP35 Studied with 2D IR Vibrational Echoes. J Am Chem Soc. 2012;134:12118–12124. doi: 10.1021/ja303017d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Andrews SS, Boxer SG. Vibrational Stark Effects of Nitriles I. Methods and Experimental Results. J Phys Chem A. 2000;104:11853–11863. [Google Scholar]
- 194.Andrews SS, Boxer SG. Vibrational Stark Effects of Nitriles II. Physical Origins of Stark Effects from Experiment and Perturbation Models. J Phys Chem A. 2002;106:469–477. [Google Scholar]
- 195.Zhang W, Markiewicz BN, Doerksen RS, Smith AB, III, Gai F. C=N Stretching Vibration of 5-Cyanotryptophan as an Infrared Probe of Protein Local Environment: What Determines Its Frequency? Phys Chem Chem Phys. 2016;18:7027–7034. doi: 10.1039/c5cp04413h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Ma J, Pazos IM, Zhang W, Culik RM, Gai F. Site-Specific Infrared Probes of Proteins. Annu Rev Phys Chem. 2015;66:357–377. doi: 10.1146/annurev-physchem-040214-121802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197.Suydam IT, Snow CD, Pande VS, Boxer SG. Electric Fields at the Active Site of an Enzyme: Direct Comparison of Experiment with Theory. Science. 2006;313:200–204. doi: 10.1126/science.1127159. [DOI] [PubMed] [Google Scholar]
- 198.Oh KII, Choi JHH, Lee JHH, Han JBB, Lee H, Cho M. Nitrile and Thiocyanate IR Probes: Molecular Dynamics Simulation Studies. J Chem Phys. 2008;128:154504. doi: 10.1063/1.2904558. [DOI] [PubMed] [Google Scholar]
- 199.Błasiak B, Ritchie AW, Webb LJ, Cho M. Vibrational Solvatochromism of Nitrile Infrared Probes: Beyond Vibrational Stark Dipole Approach. Phys Chem Chem Phys. 2016;18:18094–18111. doi: 10.1039/c6cp01578f. [DOI] [PubMed] [Google Scholar]
- 200.Choi JH, Oh KI, Lee H, Lee C, Cho M. Nitrile and Thiocyanate IR Probes: Quantum Chemistry Calculation Studies and Multivariate Least-Square Fitting Analysis. J Chem Phys. 2008;128:134506. doi: 10.1063/1.2844787. [DOI] [PubMed] [Google Scholar]
- 201.Choi JH, Cho M. Vibrational Solvatochromism and Electrochromism of Infrared Probe Molecules Containing C≡O, C≡N, C=O, or C–F Vibrational Chromophore. J Chem Phys. 2011;134:154513. doi: 10.1063/1.3580776. [DOI] [PubMed] [Google Scholar]
- 202.Ghosh A, Remorino A, Tucker MJ, Hochstrasser RM. 2D IR Photon Echo Spectroscopy Reveals Hydrogen Bond Dynamics of Aromatic Nitriles. Chem Phys Lett. 2009;469:325–330. doi: 10.1016/j.cplett.2008.12.094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Fang C, Bauman JD, Das K, Remorino A, Arnold E, Hochstrasser RM. Two-Dimensional Infrared Spectra Reveal Relaxation of the Nonnucleoside Inhibitor TMC278 Complexed with HIV-1 Reverse Transcriptase. Proc Natl Acad Sci U S A. 2008;105:1472–1477. doi: 10.1073/pnas.0709320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 204.Urbanek DC, Vorobyev DY, Serrano AL, Gai F, Hochstrasser RM. The Two-Dimensional Vibrational Echo of a Nitrile Probe of the Villin HP35 Protein. J Phys Chem Lett. 2010;1:3311–3315. doi: 10.1021/jz101367d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Chung JK, Thielges MC, Fayer MD. Dynamics of the Folded and Unfolded Villin Headpiece (HP35) Measured with Ultrafast 2D IR Vibrational Echo Spectroscopy. Proc Natl Acad Sci U S A. 2011;108:3578–3583. doi: 10.1073/pnas.1100587108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 206.Chung JK, Thielges MC, Lynch SR, Fayer MD. Fast Dynamics of HP35 for Folded and Urea-Unfolded Conditions. J Phys Chem B. 2012;116:11024–11031. doi: 10.1021/jp304058x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 207.Bagchi S, Boxer SG, Fayer MD. Ribonuclease S Dynamics Measured Using a Nitrile Label with 2D IR Vibrational Echo Spectroscopy. J Phys Chem B. 2012;116:4034–4042. doi: 10.1021/jp2122856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 208.Ma J, Pazos IM, Gai F. Microscopic Insights into the Protein-Stabilizing Effect of Trimethylamine N-Oxide (TMAO) Proc Natl Acad Sci U S A. 2014;111:8476–8481. doi: 10.1073/pnas.1403224111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 209.Czurlok D, Torres-Alacan J, Vöhringer P. Ultrafast 2DIR Spectroscopy of Ferric Azide Precursors for High-Valent Iron. Vibrational Relaxation, Spectral Diffusion, and Dynamic Symmetry Breaking. J Chem Phys. 2015;142:212402. doi: 10.1063/1.4914154. [DOI] [PubMed] [Google Scholar]
- 210.Dutta S, Li YL, Rock W, Houtman JCD, Kohen A, Cheatum CM. 3-Picolyl Azide Adenine Dinucleotide As a Probe of Femtosecond To Picosecond Enzyme Dynamics. J Phys Chem B. 2012;116:542–548. doi: 10.1021/jp208677u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Kuo CH, Vorobyev DY, Chen JX, Hochstrasser RM. Correlation of the Vibrations of the Aqueous Azide Ion with the O-H Modes of Bound Water Molecules. J Phys Chem B. 2007;111:14028–14033. doi: 10.1021/jp076503+. [DOI] [PubMed] [Google Scholar]
- 212.Bandaria JN, Dutta S, Nydegger MW, Rock W, Kohen A, Cheatum CM. Characterizing the Dynamics of Functionally Relevant Complexes of Formate Dehydrogenase. Proc Natl Acad Sci U S A. 2010;107:17974–17979. doi: 10.1073/pnas.0912190107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213.Pagano P, Guo Q, Kohen A, Cheatum CM. Oscillatory Enzyme Dynamics Revealed by Two-Dimensional Infrared Spectroscopy. J Phys Chem Lett. 2016;7:2507–2511. doi: 10.1021/acs.jpclett.6b01154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 214.Lim M, Hamm P, Hochstrasser RM. Protein Fluctuations Are Sensed by Stimulated Infrared Echoes of the Vibrations of Carbon Monoxide and Azide Probes. Proc Natl Acad Sci U S A. 1998;95:15315–15320. doi: 10.1073/pnas.95.26.15315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 215.Bandaria JN, Dutta S, Hill SE, Kohen A, Cheatum CM. Fast Enzyme Dynamics at the Active Site of Formate Dehydrogenase. J Am Chem Soc. 2008;130:22–23. doi: 10.1021/ja077599o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216.Kamerlin SCL, Warshel A. At the Dawn of the 21st Century: Is Dynamics the Missing Link for Understanding Enzyme Catalysis. Proteins: Struct, Funct Genet. 2010;78:1339–1375. doi: 10.1002/prot.22654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217.Tucker MJ, Gai XS, Fenlon EE, Brewer SH, Hochstrasser RM. 2D IR Photon Echo of Azido-Probes for Biomolecular Dynamics. Phys Chem Chem Phys. 2011;13:2237–2241. doi: 10.1039/c0cp01625j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 218.Adamczyk K, Simpson N, Greetham GM, Gumiero A, Walsh Ma, Towrie M, Parker AW, Hunt NT. Ultrafast Infrared Spectroscopy Reveals Water-Mediated Coherent Dynamics in an Enzyme Active Site. Chem Sci. 2015;6:505–516. doi: 10.1039/c4sc02752c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Cheng M, Brookes JF, Montfort WR, Khalil M. pH-Dependent Picosecond Structural Dynamics in the Distal Pocket of Nitrophorin 4 Investigated by 2D IR Spectroscopy. J Phys Chem B. 2013;117:15804–15811. doi: 10.1021/jp407052a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 220.Krummel AT, Mukherjee P, Zanni MT. Inter and Intrastrand Vibrational Coupling in DNA Studied with Heterodyned 2D-IR Spectroscopy. J Phys Chem B. 2003;107:9165–9169. [Google Scholar]
- 221.Krummel AT, Zanni MT. DNA Vibrational Coupling Revealed with Two-Dimensional Infrared Spectroscopy: Insight into Why Vibrational Spectroscopy Is Sensitive to DNA Structure. J Phys Chem B. 2006;110:13991–14000. doi: 10.1021/jp062597w. [DOI] [PubMed] [Google Scholar]
- 222.Ho JJ, Skoff DR, Ghosh A, Zanni MT. Structural Characterization of Single-Stranded DNA Monolayers Using Two-Dimensional Sum Frequency Generation Spectroscopy. J Phys Chem B. 2015;119:10586–10596. doi: 10.1021/acs.jpcb.5b07078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223.Greve C, Elsaesser T. Ultrafast Two-Dimensional Infrared Spectroscopy of Guanine – Cytosine Base Pairs in DNA Oligomers. J Phys Chem B. 2013;117:14009–14017. doi: 10.1021/jp408229k. [DOI] [PubMed] [Google Scholar]
- 224.Yang M, Szyc Ł, Elsaesser T. Femtosecond Two-Dimensional Infrared Spectroscopy of Adenine-Thymine Base Pairs in DNA Oligomers. J Phys Chem B. 2011;115:1262–1267. doi: 10.1021/jp1090697. [DOI] [PubMed] [Google Scholar]
- 225.Peng CS, Jones KC, Tokmakoff A. Anharmonic Vibrational Modes of Nucleic Acid Bases Revealed by 2D IR Spectroscopy. J Am Chem Soc. 2011;133:15650–15660. doi: 10.1021/ja205636h. [DOI] [PubMed] [Google Scholar]
- 226.Peng CS, Fedeles BI, Singh V, Li D, Amariuta T, Essigmann JM, Tokmakoff A. Two-Dimensional IR Spectroscopy of the Anti-HIV Agent KP1212 Reveals Protonated and Neutral Tautomers That Influence pH-Dependent Mutagenicity. Proc Natl Acad Sci U S A. 2015;112:3229–3234. doi: 10.1073/pnas.1415974112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 227.Yang M, Szyc L, Elsaesser T. Decelerated Water Dynamics and Vibrational Couplings of Hydrated DNA Mapped by Two-Dimensional Infrared Spectroscopy. J Phys Chem B. 2011;115:13093–13100. doi: 10.1021/jp208166w. [DOI] [PubMed] [Google Scholar]
- 228.Yang M, Szyc Ł, Elsaesser T. Vibrational Dynamics of the Water Shell of DNA Studied by Femtosecond Two-Dimensional Infrared Spectroscopy. J Photochem Photobiol A. 2012;234:49–56. [Google Scholar]
- 229.Guchhait B, Liu Y, Siebert T, Elsaesser T. Ultrafast Vibrational Dynamics of the DNA Backbone at Different Hydration Levels Mapped by Two-Dimensional Infrared Spectroscopy. Struct Dyn. 2016;3:043202. doi: 10.1063/1.4936567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 230.Siebert T, Guchhait B, Liu Y, Costard R, Elsaesser T. Anharmonic Backbone Vibrations in Ultrafast Processes at the DNA–Water Interface. J Phys Chem B. 2015;119:9670–9677. doi: 10.1021/acs.jpcb.5b04499. [DOI] [PubMed] [Google Scholar]
- 231.Cellmer T, Buscaglia M, Henry ER, Hofrichter J, Eaton WA. Making Connections between Ultrafast Protein Folding Kinetics and Molecular Dynamics Simulations. Proc Natl Acad Sci U S A. 2011;108:6103–6108. doi: 10.1073/pnas.1019552108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232.Ferreiro DU, Hegler JA, Komives EA, Wolynes PG. On the Role of Frustration in the Energy Landscapes of Allosteric Proteins. Proc Natl Acad Sci U S A. 2011;108:3499–3503. doi: 10.1073/pnas.1018980108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233.Kolodny R, Pereyaslavets L, Samson AO, Levitt M. On the Universe of Protein Folds. Annu Rev Biophys. 2013;42:559–582. doi: 10.1146/annurev-biophys-083012-130432. [DOI] [PubMed] [Google Scholar]
- 234.Freddolino PL, Harrison CB, Liu YX, Schulten K. Challenges in Protein-Folding Simulations. Nat Phys. 2010;6:751–758. doi: 10.1038/nphys1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 235.Bowman GR, Beauchamp KA, Boxer G, Pande VS. Progress and Challenges in the Automated Construction of Markov State Models for Full Protein Systems. J Chem Phys. 2009;131:124101. doi: 10.1063/1.3216567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 236.Dobson CM. Protein Folding and Misfolding. Nature. 2003;426:884–890. doi: 10.1038/nature02261. [DOI] [PubMed] [Google Scholar]
- 237.Daggett V, Fersht A. Opinion: The Present View of the Mechanism of Protein Folding. Nat Rev Mol Cell Biol. 2003;4:497–502. doi: 10.1038/nrm1126. [DOI] [PubMed] [Google Scholar]
- 238.Maj M, Ahn C, Kossowska D, Park K, Kwak K, Han H, Cho M. β-Isocyanoalanine as an IR Probe: Comparison of Vibrational Dynamics between Isonitrile and Nitrile-Derivatized IR Probes. Phys Chem Chem Phys. 2015;17:11770–11778. doi: 10.1039/c5cp00454c. [DOI] [PubMed] [Google Scholar]
- 239.Gruebele M, Sabelko J, Ballew R, Ervin J. Laser Temperature Jump Induced Protein Refolding. Acc Chem Res. 1998;31:699–707. [Google Scholar]
- 240.Balakrishnan G, Hu Y, Bender GM, Getahun Z, DeGrado WF, Spiro TG. Enthalpic and Entropic Stages in α-Helical Peptide Unfolding, from Laser T-Jump/UV Raman Spectroscopy. J Am Chem Soc. 2007;129:12801–12808. doi: 10.1021/ja073366l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 241.Callender R. Probing Protein Dynamics Using Temperature Jump Relaxation Spectroscopy. Curr Opin Struct Biol. 2002;12:628–633. doi: 10.1016/s0959-440x(02)00370-6. [DOI] [PubMed] [Google Scholar]
- 242.Williams S, Causgrove TP, Gilmanshin R, Fang KS, Callender RH, Woodruff WH, Dyer RB. Fast Events in Protein Folding: Helix Melting and Formation in a Small Peptide. Biochemistry. 1996;35:691–697. doi: 10.1021/bi952217p. [DOI] [PubMed] [Google Scholar]
- 243.Sato S, Luisi DL, Raleigh DP. pH Jump Studies of the Folding of the Multidomain Ribosomal Protein L9: The Structural Organization of the N-Terminal Domain Does Not Affect the Anomalously Slow Folding of the C-Terminal Domain. Biochemistry. 2000;39:4955–4962. doi: 10.1021/bi992608u. [DOI] [PubMed] [Google Scholar]
- 244.Causgrove TP, Dyer RB. Nonequilibrium Protein Folding Dynamics: Laser-Induced pH-Jump Studies of the Helix-Coil Transition. Chem Phys. 2006;323:2–10. [Google Scholar]
- 245.Abbruzzetti S, Crema E, Masino L, Vecli A, Viappiani C, Small JR, Libertini LJ, Small EW. Fast Events in Protein Folding: Structural Volume Changes Accompanying the Early Events in the N– > I Transition of Apomyoglobin Induced by Ultrafast pH Jump. Biophys J. 2000;78:405–415. doi: 10.1016/S0006-3495(00)76603-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 246.Dyer RB, Gai F, Woodruff WH, Gilmanshin R, Callender RH. Infrared Studies of Fast Events in Protein Folding. Acc Chem Res. 1998;31:709–716. [Google Scholar]
- 247.Bredenbeck J, Helbing J, Behrendt R, Renner C, Moroder L, Wachtveitl J, Hamm P. Transient 2D-IR Spectroscopy: Snapshots of the Nonequilibrium Ensemble during the Picosecond Conformational Transition of a Small Peptide. J Phys Chem B. 2003;107:8654–8660. [Google Scholar]
- 248.Chung HS, Khalil M, Smith AW, Ganim Z, Tokmakoff A. Conformational Changes during the Nanosecond-to-Millisecond Unfolding of Ubiquitin. Proc Natl Acad Sci U S A. 2005;102:612–617. doi: 10.1073/pnas.0408646102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 249.Kolano C, Helbing J, Kozinski M, Sander W, Hamm P. Watching Hydrogen-Bond Dynamics in a β-Turn by Transient Two-Dimensional Infrared Spectroscopy. Nature. 2006;444:469–472. doi: 10.1038/nature05352. [DOI] [PubMed] [Google Scholar]
- 250.Jones KC, Ganim Z, Peng CS, Tokmakoff A. Transient Two-Dimensional Spectroscopy with Linear Absorption Corrections Applied to Temperature-Jump Two-Dimensional Infrared. J Opt Soc Am B. 2012;29:118–129. [Google Scholar]
- 251.Jones KC, Peng CS, Tokmakoff A. Folding of a Heterogeneous β-Hairpin Peptide from Temperature-Jump 2D IR Spectroscopy. Proc Natl Acad Sci U S A. 2013;110:2828–2833. doi: 10.1073/pnas.1211968110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 252.Baiz CR, Lin YS, Peng CS, Beauchamp KA, Voelz VA, Pande VS, Tokmakoff A. A Molecular Interpretation of 2D IR Protein Folding Experiments with Markov State Models. Biophys J. 2014;106:1359–1370. doi: 10.1016/j.bpj.2014.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 253.Henzler-Wildman Ka, Lei M, Thai V, Kerns SJ, Karplus M, Kern D. A Hierarchy of Timescales in Protein Dynamics Is Linked to Enzyme Catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 254.Koo EH, Lansbury PT, Kelly JW. Amyloid Diseases: Abnormal Protein Aggregation in Neurodegeneration. Proc Natl Acad Sci U S A. 1999;96:9989–9990. doi: 10.1073/pnas.96.18.9989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 255.Gilead S, Gazit E. The Role of the 14–20 Domain of the Islet Amyloid Polypeptide in Amyloid Formation. Exp Diabetes Res. 2008;2008:1–8. doi: 10.1155/2008/256954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256.Scherzinger E, Sittler A, Schweiger K, Heiser V, Lurz R, Hasenbank R, Bates GP, Lehrach H, Wanker EE. Self-Assembly of Polyglutamine-Containing Huntingtin Fragments into Amyloid-like Fibrils: Implications for Huntington’s Disease Pathology. Proc Natl Acad Sci U S A. 1999;96:4604–4609. doi: 10.1073/pnas.96.8.4604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 257.Zandomeneghi G, Krebs MRH, McCammon MG, Fändrich M. FTIR Reveals Structural Differences between Native β-Sheet Proteins and Amyloid Fibrils. Protein Sci. 2004;13:3314–3321. doi: 10.1110/ps.041024904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258.Greenfield NJ. Using Circular Dichroism Spectra to Estimate Protein Secondary Structure. Nat Protoc. 2007;1:2876–2890. doi: 10.1038/nprot.2006.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 259.Biancalana M, Koide S. Molecular Mechanism of Thioflavin-T Binding to Amyloid Fibrils. Biochim Biophys Acta, Proteins Proteomics. 2010;1804:1405–1412. doi: 10.1016/j.bbapap.2010.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 260.Shim SH, Strasfeld DB, Zanni MT. Generation and Characterization of Phase and Amplitude Shaped Femtosecond Mid-IR Pulses. Opt Express. 2006;14:13120–13130. doi: 10.1364/oe.14.013120. [DOI] [PubMed] [Google Scholar]
- 261.Shim SH, Strasfeld DB, Fulmer EC, Zanni MT. Femtosecond Pulse Shaping Directly in the Mid-IR Using Acousto-Optic Modulation. Opt Lett. 2006;31:838–840. doi: 10.1364/ol.31.000838. [DOI] [PubMed] [Google Scholar]
- 262.Tian P, Keusters D, Suzaki Y, Warren WS. Femtosecond Phase-Coherent Two-Dimensional Spectroscopy. Science. 2003;300:1553–1555. doi: 10.1126/science.1083433. [DOI] [PubMed] [Google Scholar]
- 263.Bloem R, Garrett-Roe S, Strzalka H, Hamm P, Donaldson P. Enhancing Signal Detection and Completely Eliminating Scattering Using Quasi-Phase-Cycling in 2D IR Experiments. Opt Express. 2010;18:27067–27078. doi: 10.1364/OE.18.027067. [DOI] [PubMed] [Google Scholar]
- 264.Middleton CT, Marek P, Cao P, Chiu CC, Singh S, Woys AM, de Pablo JJ, Raleigh DP, Zanni MT. Two-Dimensional Infrared Spectroscopy Reveals the Complex Behaviour of an Amyloid Fibril Inhibitor. Nat Chem. 2012;4:355–360. doi: 10.1038/nchem.1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 265.Dunkelberger EB, Buchanan LE, Marek P, Cao P, Raleigh DP, Zanni MT. Deamidation Accelerates Amyloid Formation and Alters Amylin Fiber Structure. J Am Chem Soc. 2012;134:12658–12667. doi: 10.1021/ja3039486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 266.Glassford SE, Byrne B, Kazarian SG. Recent Applications of ATR FTIR Spectroscopy and Imaging to Proteins. Biochim Biophys Acta, Proteins Proteomics. 2013;1834:2849–2858. doi: 10.1016/j.bbapap.2013.07.015. [DOI] [PubMed] [Google Scholar]
- 267.Chen Z, Shen YR, Somorjai GA. Studies of Polymer Surfaces by Sum Frequency Generation Vibrational Spectroscopy. Annu Rev Phys Chem. 2002;53:437–465. doi: 10.1146/annurev.physchem.53.091801.115126. [DOI] [PubMed] [Google Scholar]
- 268.Shen YR. The Principles of Nonlinear Optics. Wiley-Interscience; Hoboken, NJ: 2003. [Google Scholar]
- 269.Hunt JH, Guyot-Sionnest P, Shen YR. Observation of C-H Stretch Vibrations of Monolayers of Molecules Optical Sum-Frequency Generation. Chem Phys Lett. 1987;133:189–192. [Google Scholar]
- 270.Xiong W, Laaser JE, Mehlenbacher RD, Zanni MT. Adding a Dimension to the Infrared Spectra of Interfaces Using Heterodyne Detected 2D Sum-Frequency Generation (HD 2D SFG) Spectroscopy. Proc Natl Acad Sci U S A. 2011;108:20902–20907. doi: 10.1073/pnas.1115055108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 271.Bredenbeck J, Ghosh A, Nienhuys HK, Bonn M. Interface-Specific Ultrafast Two-Dimensional Vibrational Spectroscopy. Acc Chem Res. 2009;42:1332–1342. doi: 10.1021/ar900016c. [DOI] [PubMed] [Google Scholar]
- 272.Bredenbeck J, Ghosh A, Smits M, Bonn M. Ultrafast Two Dimensional-Infrared Spectroscopy of a Molecular Monolayer. J Am Chem Soc. 2008;130:2152–2153. doi: 10.1021/ja710099c. [DOI] [PubMed] [Google Scholar]
- 273.Laaser JE, Zanni MT. Extracting Structural Information from the Polarization Dependence of One- and Two-Dimensional Sum Frequency Generation Spectra. J Phys Chem A. 2013;117:5875–5890. doi: 10.1021/jp307721y. [DOI] [PubMed] [Google Scholar]
- 274.Laaser JE, Skoff DR, Ho J, Joo Y, Serrano AL, Steinkruger JD, Gopalan P, Gellman SH, Zanni MT. Two-Dimensional Sum-Frequency Generation (2D SFG) Reveals Structure and Dynamics of a Surface-Bound Peptide. J Am Chem Soc. 2014;136:956–962. doi: 10.1021/ja408682s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 275.Ghosh A, Ho JJ, Serrano AL, Skoff DR, Zhang TQ, Zanni MT. Two-Dimensional Sum-Frequency Generation (2D SFG) Spectroscopy: Summary of Principles and Its Application to Amyloid Fiber Monolayers. Faraday Discuss. 2015;177:493–505. doi: 10.1039/c4fd00173g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 276.Ghosh A, Smits M, Bredenbeck J, Dijkhuizen N, Bonn M. Femtosecond Time-Resolved and Two-Dimensional Vibrational Sum Frequency Spectroscopic Instrumentation to Study Structural Dynamics at Interfaces. Rev Sci Instrum. 2008;79:093907. doi: 10.1063/1.2982058. [DOI] [PubMed] [Google Scholar]
- 277.Hamm P, Lim M, Hochstrasser RM. Ultrafast Dynamics of Amide-I Vibrations. Biophys J. 1998;74:A332–A332. [Google Scholar]
- 278.Asplund MC, Zanni MT, Hochstrasser RM. Two-Dimensional Infrared Spectroscopy of Peptides by Phase-Controlled Femtosecond Vibrational Photon Echoes. Proc Natl Acad Sci U S A. 2000;97:8219–8224. doi: 10.1073/pnas.140227997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 279.Ghosh A, Tucker MJ, Hochstrasser RM. Identification of Arginine Residues in Peptides by 2D-IR Echo Spectroscopy. J Phys Chem A. 2011;115:9731–9738. doi: 10.1021/jp201794n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 280.Nydegger MW, Dutta S, Cheatum CM. Two-Dimensional Infrared Study of 3-Azidopyridine as a Potential Spectroscopic Reporter of Protonation State. J Chem Phys. 2010;133:134506. doi: 10.1063/1.3483688. [DOI] [PubMed] [Google Scholar]
- 281.Bredenbeck J, Helbing J, Hamm P. Labeling Vibrations by Light: Ultrafast Transient 2D-IR Spectroscopy Tracks Vibrational Modes during Photoinduced Charge Transfer. J Am Chem Soc. 2004;126:990–991. doi: 10.1021/ja0380190. [DOI] [PubMed] [Google Scholar]
- 282.Greetham GM, Donaldson PM, Nation C, Sazanovich IV, Clark IP, Shaw DJ, Parker AW, Towrie M. A 100 kHz Time-Resolved Multiple-Probe Femtosecond to Second Infrared Absorption Spectrometer. Appl Spectrosc. 2016;70:645–653. doi: 10.1177/0003702816631302. [DOI] [PubMed] [Google Scholar]
- 283.Chung CY, Boik J, Potma EO. Biomolecular Imaging with Coherent Nonlinear Vibrational Microscopy. Annu Rev Phys Chem. 2013;64:77–99. doi: 10.1146/annurev-physchem-040412-110103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 284.Bhargava R. Infrared Spectroscopic Imaging: The next Generation. Appl Spectrosc. 2012;66:1091–1120. doi: 10.1366/12-06801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 285.Volkmer A, Cheng JX, Xie XS. Vibrational Imaging with High Sensitivity via Epidetected Coherent Anti-Stokes Raman Scattering Microscopy. Phys Rev Lett. 2001;87:023901. [Google Scholar]
- 286.Serrano AL, Ghosh A, Ostrander JS, Zanni MT. Wide-Field FTIR Microscopy Using Mid-IR Pulse Shaping. Opt Express. 2015;23:17815–17827. doi: 10.1364/OE.23.017815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Fournier F, Guo R, Gardner EM, Donaldson PM, Loeffeld C, Gould IR, Willison KR, Klug DR. Biological and Biomedical Applications of Two-Dimensional Vibrational Spectroscopy: Proteomics, Imaging, and Structural Analysis. Acc Chem Res. 2009;42:1322–1331. doi: 10.1021/ar900074p. [DOI] [PubMed] [Google Scholar]
- 288.Rubtsov IV, Wang J, Hochstrasser RM. Vibrational Coupling between Amide-I and Amide-A Modes Revealed by Femtosecond Two Color Infrared Spectroscopy. J Phys Chem A. 2003;107:3384–3396. [Google Scholar]
- 289.Kurochkin DV, Naraharisetty SRG, Rubtsov IV. A Relaxation-Assisted 2D IR Spectroscopy Method. Proc Natl Acad Sci U S A. 2007;104:14209–14214. doi: 10.1073/pnas.0700560104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 290.Kasyanenko VM, Tesar SL, Rubtsov GI, Burin AL, Rubtsov IV. Structure Dependent Energy Transport: Relaxation-Assisted 2DIR Measurements and Theoretical Studies. J Phys Chem B. 2011;115:11063–11073. doi: 10.1021/jp2066315. [DOI] [PubMed] [Google Scholar]
- 291.Kurochkin DV, Naraharisetty SRG, Rubtsov IV. Dual-Frequency 2D IR on Interaction of Weak and Strong IR Modes. J Phys Chem A. 2005;109:10799–10802. doi: 10.1021/jp055811+. [DOI] [PubMed] [Google Scholar]
- 292.Yan C, Yuan R, Pfalzgraff WC, Nishida J, Wang L, Markland TE, Fayer MD. Unraveling the Dynamics and Structure of Functionalized Self-Assembled Monolayers on Gold Using 2D IR Spectroscopy and MD Simulations. Proc Natl Acad Sci U S A. 2016;113:4929–4934. doi: 10.1073/pnas.1603080113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 293.Rosenfeld DE, Gengeliczki Z, Smith BJ, Stack TDP, Fayer MD. Structural Dynamics of a Catalytic Monolayer Probed by Ultrafast 2D IR Vibrational Echoes. Science. 2011;334:634–639. doi: 10.1126/science.1211350. [DOI] [PubMed] [Google Scholar]
- 294.Kraack JP, Lotti D, Hamm P. 2D Attenuated Total Reflectance Infrared Spectroscopy Reveals Ultrafast Vibrational Dynamics of Organic Monolayers at Metal-Liquid Interfaces. J Chem Phys. 2015;142:212413. doi: 10.1063/1.4916915. [DOI] [PubMed] [Google Scholar]
- 295.Lotti D, Hamm P, Kraack JP. Surface-Sensitive Spectro-Electrochemistry Using Ultrafast 2D ATR IR Spectroscopy. J Phys Chem C. 2016;120:2883–2892. [Google Scholar]
- 296.Kraack JP, Kaech A, Hamm P. Surface Enhancement in Ultrafast 2D ATR IR Spectroscopy at the Metal-Liquid Interface. J Phys Chem C. 2016;120:3350–3359. [Google Scholar]
- 297.Selig O, Siffels R, Rezus YLA. Ultrasensitive Ultrafast Vibrational Spectroscopy Employing the Near Field of Gold Nanoantennas. Phys Rev Lett. 2015;114:233004. doi: 10.1103/PhysRevLett.114.233004. [DOI] [PubMed] [Google Scholar]
- 298.Donaldson PM, Hamm P. Gold Nanoparticle Capping Layers: Structure, Dynamics, and Surface Enhancement Measured Using 2D-IR Spectroscopy. Angew Chem, Int Ed. 2013;52:634–638. doi: 10.1002/anie.201204973. [DOI] [PubMed] [Google Scholar]