Surfactant-free shape control of gold nanoparticles enabled by unified theoretical framework of nanocrystal synthesis

Abstract

Gold nanoparticles have unique properties that are highly dependent on their shape and size. Synthetic methods that enable precise control over nanoparticle morphology currently require shape-directing agents such as surfactants or polymers that force growth in a particular direction by adsorbing to specific crystal facets. These auxiliary reagents passivate the nanoparticle surface, and thus decrease their performance in applications like catalysis and surface-enhanced Raman scattering (SERS). Here we report a surfactant- and polymer-free approach to achieving high-performance gold nanoparticles. We develop a theoretical framework to elucidate the growth mechanism of nanoparticles in surfactant-free media and apply it to identify strategies for shape-controlled synthesis. Using the results of our analyses, we designed a simple, green-chemistry synthesis of the four most commonly used morphologies: nanostars, nanospheres, nanorods, and nanoplates. The nanoparticles synthesized by this method outperform analogous particles with surfactant and polymer coatings in both catalysis and surface-enhanced Raman scattering.

Graphical Abstract

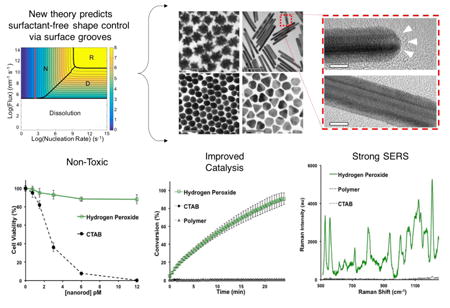
We present a new theoretical framework that identifies a surfactant-free route to controlling the shape of nanoparticles. We predict and confirm for the first time that gold nanorod formation in the absence of surfactants is driven by re-entrant groove defects on the end facets. Nanoparticles synthesized by our approach demonstrate excellent SERS and catalytic performance.

1. Introduction

Gold nanoparticles (AuNPs) exhibit exceptional chemical and physical properties applicable to diverse fields such as catalysis, sensing, photonics, and biomedical imaging and therapeutics^{[1, 2]}. The properties of AuNPs are strongly dictated by size, shape and local dielectric environment^{[1, 3]}. Synthetic methods have been developed to generate AuNPs with precisely controlled morphologies; however, these approaches rely upon shape-directing agents (SDAs) such as surfactants and polymers to selectively block the growth of certain facets^{[4, 5]}. Consequently, the nanoparticles synthesized by these methods have passivated, i.e. blocked, surfaces with weakened performance in applications like catalysis and SERS (Figure 1)^{[6, 7]}. Moreover, these unwanted surface ligands inhibit applications in the growing field of self-assembly by preventing the binding of desired molecules (e.g. cyclodextrins, DNA or cucurbiturils) and increasing the minimum achievable distance between constituent nanoparticles^[8].

Figure 1. Comparison of shape-controlled syntheses.

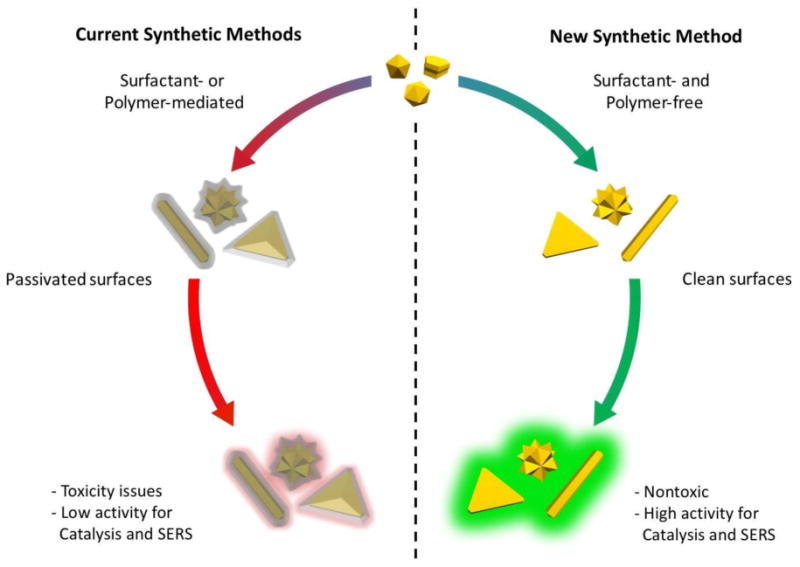
Conventional synthetic methods for shape-controlled nanoparticle formation use surface-blocking groups to drive growth in the direction of the least encumbered facets. This leaves the surface largely blocked by species such as surfactants or polymers that diminish the effectiveness of the nanoparticles for various applications. In contrast, the reactions free of surfactants and polymers generate nanoparticles with unblocked surfaces that are optimal for surface-dependent applications like catalysis and SERS.

In spite of the obvious limitations to nanoparticle performance, surfactant-mediated AuNP syntheses remain the gold standard because a viable alternative route to shape-controlled growth does not currently exist. Although some surfactant-free synthesis protocols are available, notably in the cases of nanostars and nanospheres, there is a lack of versatility in the shape control that can be achieved^{[9, 10]}. This is particularly true in the case of gold nanorods, which still require the use of the surfactant cetlytrimethylammonium bromide (CTAB). The complex interplay of thermodynamic and kinetic factors affecting nanoparticle morphology has obscured any clear directions to achieving a new synthetic method with the same degree of shape control as those empirically realized by SDAs. Herein, we present a new path to precisely controlling nanoparticle morphology without SDAs. We accomplish this in two steps: 1) we determine the growth mechanism of AuNPs in surfactant-free media and then 2) devise a strategy to manipulate this mechanism to enable synthesis of the most commonly used AuNP shapes.

In order to identify strategies for shape-controlled growth, we developed a theoretical framework that relates the observed crystal growth rate to the rate-limiting process controlling growth. Once the growth mechanism is known, rational approaches to manipulating the relative facet growth rates (i.e., controlling the shape) can be developed. We modeled crystal growth as proceeding by three distinct steps: nucleation of a monolayer, diffusion of growth units to a step front, and incorporation of growth units into binding sites at the step front (Figure 2a-d). In this regard, we have extended the classical theory of crystal growth by removing outdated mathematical simplifications, and by unifying the previously disparate theoretical approaches of nucleation-, diffusion-, and incorporation reaction-limited modelling ^{[11, 12]}. Our new theoretical framework uses literature values of diffusion activation energies and atomic vibrational frequencies at different lattice sites to holistically identify the ranges of nucleation rates and diffusional flux that correspond to nucleation-limited, diffusion-limited, and reaction-limited growth ^[13]. We note that our theoretical framework applies generally to other nanoparticle systems, but we apply it herein to the specific case of AuNPs.

Figure 2. Illustration and results of the theoretical framework.

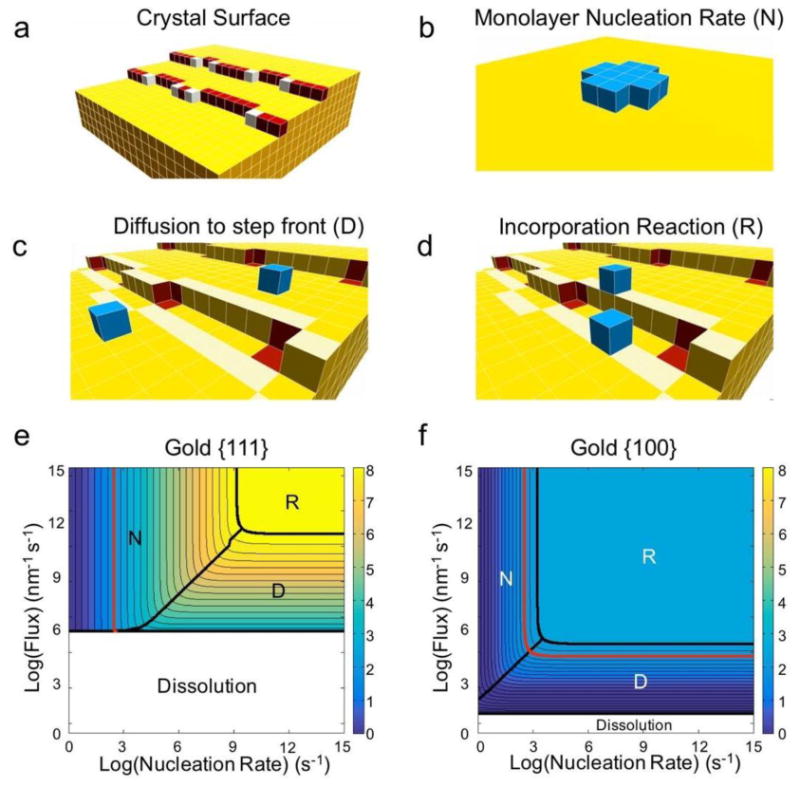
a, Schematic of a crystal facet. The surface is populated by terrace (yellow), step (red), and kink (white) sites. b-d, The three primary processes influencing the growth rate of a crystal facet. b, The monolayer nucleation rate (N) is the rate at which a critical nucleus (blue) – an island of growth units that will continue to grow rather than dissolve – forms on a facet (yellow). c, The “diffusion” rate can refer to different processes in different theories. Here, we define the rate of diffusion (D) specifically as the flux of growth units to the step front – the region of terrace sites that are one jump from step or kink sites (highlighted in light yellow). This definition separates growth unit diffusion from the incorporation reaction process. d, The incorporation “reaction” rate (R) as defined in our treatment is the net rate at which growth units in the step front (highlighted in light yellow) diffuse into kink binding sites (red). The delivery of growth units to kink binding sites is therefore divided into two regimes in our theory: diffusion of growth units to the step front, and incorporation reaction from the step front into the kink binding sites. e-f, Our theoretical framework produces contour plots of facet growth rates that highlight the rate-limiting growth process as a function of experimental conditions for (e) {111} and {f} {100} facets of gold nanoparticles. The red contour denotes the experimental growth rate at which secondary nucleation – the formation of new seeds – occurs. Polyhedra like rods and plates form below this rate.

2. Results and Discussion

The complete theoretical framework and all explicit calculations are given in the supporting information. In short, we calculate the expected time for a monolayer to form on a given facet and use that information to determine the asymptotic growth rate normal to each facet. This approach requires knowledge of the activation energies for hopping between adjacent surface sites, such that the rate at which atoms incorporate into binding sites can be calculated as a dependent variable using a continuous time Markov chain approach (supporting information). These activation energies have already been tabulated for many systems of interest, including gold. We treat the nucleation rate and flux (i.e., diffusion rate toward binding sites) as independent variables in order to identify the range of conditions wherein each process – nucleation, diffusion, or incorporation reaction – becomes rate-limiting. When the total facet growth rates are empirically known, we back-calculate the set of possible nucleation and diffusion rates. We then test these different values of nucleation and diffusion rates with a simple Monte Carlo simulation to see which of the possible values produces the experimentally observed (or desired) distribution of total facet growth rates, and by extension the observed distribution of final shapes.

Our theoretical results indicated that AuNP growth tends to be nucleation- or diffusion-limited at experimental growth rates (Figure 2e, f). Notably, the experimental range of growth rates characteristic to polyhedral particles (i.e., rods, plates, icosahedra, etc.) – that is, everything to the left of the red contour line in Figure 2e – falls primarily within the nucleation-limited regime for {111} facets. Under nucleation-limited growth, the facets which most strongly promote the nucleation of monolayers (i.e., facilitate clustering of atoms on the surface) grow the fastest. It is well known that monolayers form fastest on surfaces that exhibit surface defects, such as re-entrant grooves (Figure S1) that corral growth units into stable surface clusters ^{[12, 14]}. We therefore hypothesize that shape-controlled growth of AuNPs can be achieved by rationally distributing surface defects in the directions where fastest growth is desired.

The ideal reduction system for our proposed strategy is subject to many considerations. Recent theoretical investigations have revealed that the formation of surface defects on metal nanoparticles is a sensitive function of redox potential ^[15]. Moreover, the reduction rate of metal complexes can dictate the crystalline structure of the resulting nanoparticles, as has been experimentally observed in palladium ^[16]. For these reasons, we hypothesized that the reducing agent employed in surfactant-free syntheses would have to exhibit a finely tunable reduction potential ranging from oxidative to highly reductive values in order to enable shape-control. Additionally, the reducing agent should be small and not form particularly strong bonds with the nanoparticle, such that it does not passivate the surface. We found that hydrogen peroxide satisfied all of the desired criteria, as its reduction potential can be easily tuned by pH and its molecular interactions with gold surfaces are not sufficiently strong to result in passivation ^[17].

After testing various combinations of HAuCl₄, H₂O₂, NaOH, and 3.5 nm gold nanoparticle seeds, we identified protocols that generate the four most commonly used AuNP morphologies: nanostars, nanospheres, nanorods, and nanoplates (see Experimental Methods for details) (Figures 3 and S2). Nanostars and nanospheres formed under the fastest reduction kinetics (i.e., ≥ 1.35 × 10^-4 M s^-1) (Figures S3 and S4). Both morphologies demonstrate an intermediate state exhibiting protrusions from a central core. When the conditions are sufficiently reductive the protrusions are metastable and can be preserved indefinitely by dialysis to achieve nanostars (Figures S5 and S6). Slightly more oxidative conditions cause the protrusions to ripen, yielding nanospheres. Importantly, the symmetric development of protrusions mitigates any inherent anisotropy in the initial seed defect structure. When the reduction rate falls just below 7.26 × 10^-6 M s^-1, nanorods become the dominant anisotropic shape. Decreasing the reduction rate further to 9.34 × 10^-8 M s^-1 yields nanoplates as the primary product, and additional decreases in reduction kinetics generate heavily defected nanoparticles. The relationship between the growth regimes (e.g., nucleation-, diffusion-, and reaction-limited) and the observed morphologies is depicted in Figure 3d.

Figure 3. Shape-controlled synthesis of gold nanoparticles without surfactants.

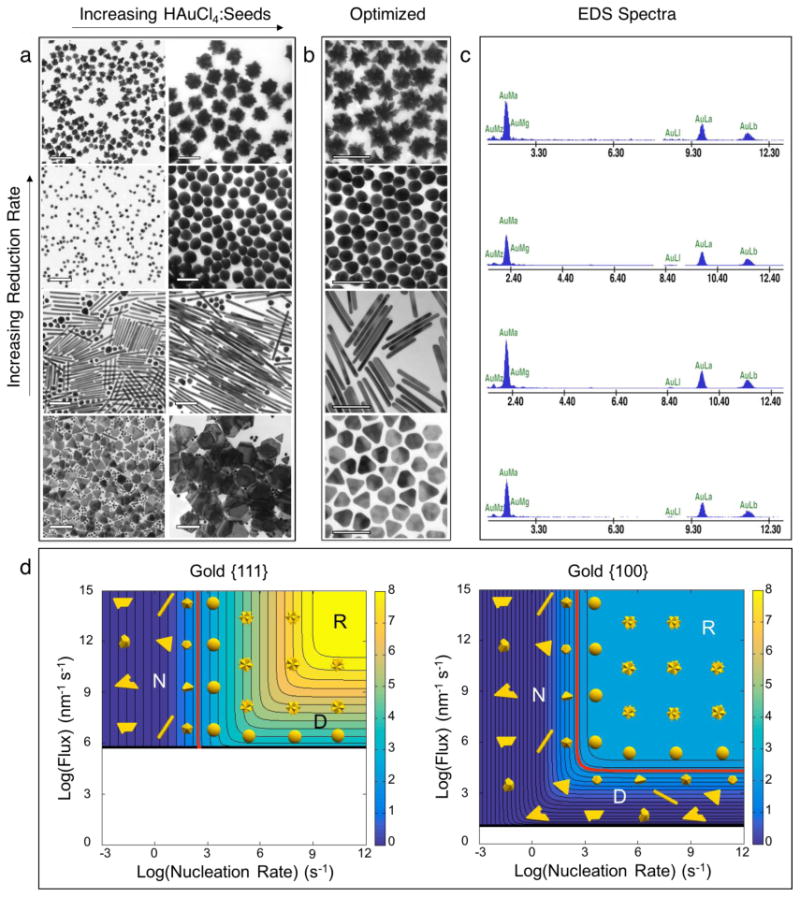
a, Synthesis of various morphologies from the same batch of 3.5 nm gold nanoparticle seeds. Nanostars form under the fastest rates of HAuCl₄ reduction, followed by nanospheres, nanorods, and nanoplates as the reduction rate decreases. The size of all shapes can be tuned by adjusting the HAuCl₄:Seeds ratio. b, Nanostars, nanospheres, nanorods, and nanoplates synthesized under optimized conditions. While nanostars and nanospheres form virtually quantitatively, the nanorods and nanoplates require post-synthetic separation. Scale bars for nanoplates in (a) are 500 nm; all other scale bars are 100 nm. c, Energy dispersive x-ray scattering (EDS) spectra of (top to bottom) nanostars, nanospheres, nanorods, and nanoplates. d, Crystal growth regimes for gold nanoparticles. The shapes observed experimentally are overlaid on the contour plots for {111} and {100} gold facets. When facet growth rates exceed approximately 100 nm/s the growth mechanism switches from lateral (monolayer-by-monolayer) to secondary nucleation (i.e. new seeds form during the reaction). This transition is highlighted in red on the contour plots. Regions where the contour lines are vertical represent nucleation-limited growth (N), and regions with horizontal contours represent diffusion-limited growth (D). The region above the highest rate contour is reaction-limited (R).

The formation of gold nanorods from this simple reaction is surprising, as they are the prototypical shape thought to require surfactants for synthesis ^{[5, 18]}. Although their yield (approximately 20%) was low with respect to the best surfactant-mediated synthesis, it is considerably higher than any other surfactant-free method previously reported^[10]. We note that the early surfactant-mediated approach (i.e., without Ag⁺) generated 4% yields of gold nanorods ^[19], so it is foreseeable that future optimizations of this method will achieve yields competitive with the current gold standard of surfactant-based syntheses. In the meantime, the present synthesis can be combined with purification techniques such as centrifugal split-flow thin cell (C-SPLITT) separation to obtain high-yield dispersions of nanorods (Figure S7) ^[20].

We investigated the nanorod formation mechanism both theoretically and experimentally. Selected area electron diffraction (SAED) analyses revealed an internal five-fold twin structure consistent with previously reported gold nanorods exhibiting slow-growing {100} side facets and fast-growing {111} end facets (Figure S8) ^[19]. Because the experimental growth rate of approximately 10 nm s^-1 from the {111} facets could possibly fall in either the nucleation- or diffusion-limited regimes, we performed more rigorous theoretical analyses using Monte Carlo statistical simulations of nucleation- and diffusion-limited growth (see Experimental Methods for details). Diffusion-limited growth was determined to be unstable with respect to realistic fluctuations in experimental conditions: a transient decrease in the flux of atoms to the nanoparticle would result in dissolution, and a transient increase would cause nanostar formation (Figure 4a). Nucleation-limited growth was found to be stable with respect to realistic fluctuations in experimental conditions (Figure 4b), making it the only viable rate-limiting step according to our theoretical framework.

Figure 4. Growth mechanism analysis for gold nanorods.

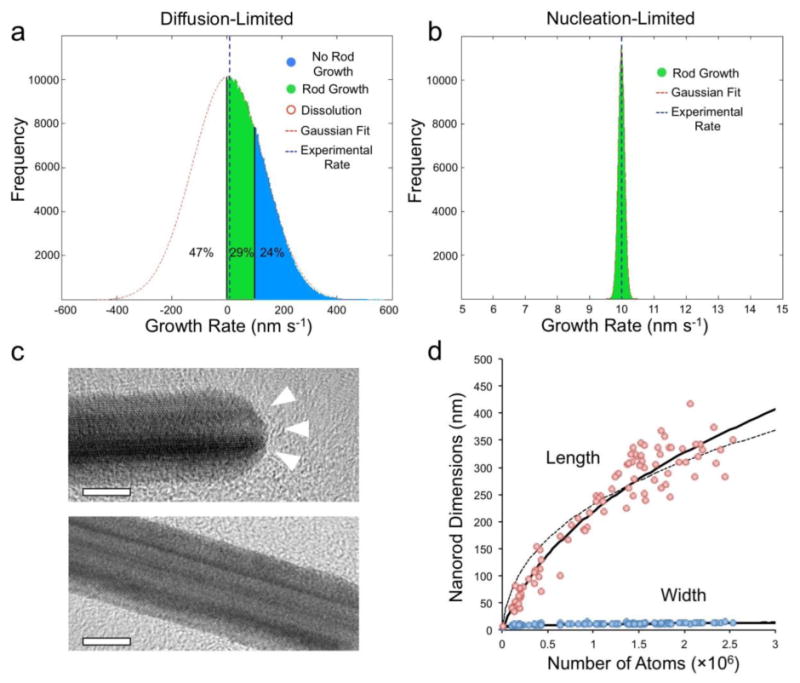
a, Simulated growth rate distribution of nanorods in the diffusion-limited regime. The diffusion-limited hypothesis yields a distribution of growth rates not observed experimentally, and incorrectly predicts that 47% of nanoparticles dissolve while 24% grow at a rate too fast to form nanorods. b, Simulated growth rate distribution of nanorods in nucleation-limited regime. The nucleation-limited hypothesis yields accurate predictions of distributions tightly centered about the experimentally observed growth rate. c, High-resolution transmission electron micrographs (HRTEM) of gold nanorods. The end facets exhibit re-entrant grooves, while the side facets are stepped, but relatively smooth by comparison. The grooves are known to catalyze monolayer nucleation, which explains the faster nucleation rate on the {111} facets. See Figure S1 for additional details about re-entrant grooves. d, Experimental length and width of nanoparticles fit to nucleation-limited growth. The curves are the best theoretical fits for anisotropic growth starting from a 4 nm seed (dashed line) and a 7.5 nm seed (solid line). The best fit to data occurs for a seed that begins growing into a rod once it reaches 7.5 nm in diameter.

Experimental corroboration of a nucleation-limited growth mechanism was provided by high-resolution transmission electron microscopy (HRTEM). Re-entrant grooves were discovered on the {111} end facets, but not on the {100} side facets (Figure 4c). The re-entrant grooves are known to increase monolayer nucleation rates, which explains why the end facets grow faster than the sides. Eucentric sample tilting was often required to resolve the grooved structures, but they were clearly and consistently observed. The need for high resolution imaging at the proper orientation may explain the lack of previous reports for these structures on metal nanorods. We fit the observed nanorod dimensions to a simple nucleation-limited growth model and found that the best fit to data occurs for a seed beginning anisotropic growth at a diameter of 7.5 nm and exhibiting a 76:1 ratio of {111} to {100} nucleation rates (Figure 4d). Interestingly, there was no particularly good fit to data for the 3.5 nm starting seed diameter, indicating that an active symmetry-breaking step – presumably the formation of re-entrant grooves – must occur for nanorods to grow in our synthesis. In other words, the 3.5 nm seeds grow spherically to a size of 7.5 nm, at which point grooves form on the {111} facets to induce anisotropic growth. Animations of nanorod growth at various ratios of {111} to {100} nucleation rates are provided in supplementary movies 1-4.

The preferential growth of nanoplates at slow reduction kinetics fits well with our theoretical model. SAED of nanoplates reveals the forbidden 1/13 {224} reflection (Figure S9) characteristic of parallel twin boundaries known to create re-entrant grooves on the nanoplate side facets ^{[14, 21]} which are typically {100}. Inspection of Figure 3d reveals that {100} facets grow under nucleation-limited growth at very slow nucleation rates, but then transition to diffusion-limited growth at higher nucleation rates. Note that only stars and spheres form to the right of the red contour line, so all other shapes are governed by nucleation-limited or diffusion-limited growth. The re-entrant grooves are known to have a strong catalytic effect for monolayer nucleation, but offer less preference when growth is limited by diffusion of growth units. This could explain why plates become considerably less anisotropic as reduction kinetics increase. The lack of nanorod formation at the lowest reduction kinetics appears to result from multiply twinned seeds attaining structural defects other than re-entrant grooves on {111} facets, such that the symmetry-breaking event that initiates nanorod growth does not occur.

3. Conclusion

Having obtained the four most commonly used gold nanoparticle morphologies from a single surfactant- and polymer-free method, we have established the utility of our unified theoretical framework (fully developed in the supplementary information) for designing shape-controlled nanoparticles. This marks an important step toward achieving metal nanoparticle syntheses completely tailored to specific applications because the non-passivated surfaces offer increased possibilities in surface chemistry design ^[7]. For example, the absence of surfactants and polymers makes the nanoparticle surfaces more accessible to molecules in solution thereby enhancing their performance in surface-area-dependent applications ^{[6, 7]}. Indeed, the catalytic efficiency and surface enhancement to Raman scattering of nanoparticles synthesized by our method demonstrated superior performance when compared to similar nanoparticles made with surfactant (CTAB) or polymer (thiolated polyethylene glycol) coatings (Figure S10). We anticipate that the theoretical and experimental findings presented herein will be broadly applicable in the design of improved nanoparticle syntheses and understanding of (nano)crystal growth mechanisms.

4. Experimental

Reagents

Hydrogen peroxide (TraceSELECT; Sigma Aldrich) and all other chemicals were ordered from Sigma-Aldrich with the highest purity available and used as received. In all cases 18.2 MΩcm water was used. Slide-A-Lyzer 2K Dialysis Cassettes G2 were ordered from Thermo Scientific and used in all dialysis experiments.

Preparation of 3.5 nm gold seeds

Briefly, 100 μL of 25 mM HAuCl₄ and 100 μL of 25 mM trisodium citrate were added to 9.8 mL of H₂O, then 300 μL of 100 mM ice-cold NaBH₄ was added to this solution under vigorous stirring. We also synthesized seeds using a modification of the above protocol wherein no trisodium citrate was added. In the absence of citrate the seeds should be immediately diluted 5 times with 18.2 MΩcm water to inhibit aggregation. The formation of seeds could be monitored by the immediate appearance of an orange-brown color. If the color turns purple or black the seeds have aggregated and should be discarded. Both the citrate-capped and non-citrate capped seeds generated all shapes reported herein with no ostensible differences. The following protocols are for the undiluted seeds, and should be modified to achieve equal seed concentration if diluted stocks are used.

Preparation of Nanoplates

150 μL of as-prepared 3 nm seeds were added to 9.85 mL of H₂O. 150 μL of 25.4 mM HAuCl₄ was added to the mixture and the reaction was initiated by the addition of 200 μL of 0.3% (v/v) H₂O₂ under stirring.

Preparation of Nanorods

600 μL of as-prepared 3 nm seeds were added to 9.40 mL of H₂O. 30 μL of 30% H₂O₂ was added to this mixture and the reaction was initiated by the addition of 300 μL of 25.4 mM HAuCl₄ under vigorous stirring. The best results were obtained by adding the HAuCl₄ in increments of 30 μL every 2 seconds. Faster addition can decrease selective growth of nanorods with respect to decahedra and icosahedra as seen in Figures 3 and S2.

Preparation of Nanospheres

30 μL of as-prepared 3 nm seeds were added to 9.97 mL of ice-cold H₂O. 150 μL of 25.4 mM HAuCl₄ was added to this mixture and the reaction was initiated by adding a solution of 15 μL 1 M NaOH dissolved in 1 mL of 0.3% H₂O₂. The balance between NaOH and seed concentration is very sensitive during sphere formation. When the synthesis begins with the appearance of a blue color, less NaOH should be used. When rods or other anisotropic polyhedra are observed in the products, more NaOH should be used. Addition of chloride or bromide before reduction of HAuCl₄ improves the symmetry of the spheres.

Preparation of Nanostars

30 μL of as-prepared 3 nm seeds were added to 9.97 mL of ice-cold H₂O. 150 μL of 25.4 mM HAuCl₄ was added to this mixture and the reaction was initiated by adding a solution of 50 μL 1 M NaOH dissolved in 1 mL of 0.3% H₂O₂. Some syntheses generate stars that transform more rapidly than others, but this can be controlled to an extent by consideration of the oxidation potential generated during HAuCl₄ reduction. In general, the amount of NaOH added should be the minimal amount necessary to generate stars, and increasing the pH beyond this point results in increasingly rapid transformation.

Dialysis

Immediately after the nanostars are synthesized they are added to a 2,000 Da molecular weight cut-off (MWCO) Slide-A-Lyzer dialysis cassette that is then placed into a large volume of H₂O and subjected to slow stirring. The dialysis water is replaced periodically until residual chemical species are removed. Our investigations did not reveal the presence of any impurities on the nanoparticle surface to suggest that cassette-derived particle stabilizing effects (e.g. membrane polymer leaching) occurred.

Catalysis

The catalytic reduction of resazurin to resorufin mediated by hydroxylamine in the presence versus absence of gold nanoparticles serves as an assay for their efficacy as catalysts. 1 μL of 5 mM resazurin was added to 100 μL of 33 pM gold nanoparticle mixtures (20% rods, 20% plates, and 60% spheres) and 150 mM hydroxylamine in 10 mM pH = 7.3 2-(N-morpholino)ethanesulfonic acid (MES) buffer. The fluorescence intensity at an excitation wavelength of 571 nm and emission wavelength of 584 nm was followed every ten minutes after reaction initiation. All experiments were performed in triplicate and measured under identical conditions.

Surface-Enhanced Raman Scattering

Surfactant-free (i.e., from the present synthetic methods), CTAB-coated, and polyethylene glycol (PEG)-SH-coated mixtures of 20% rods, 20% plates, and 60% spheres were compared for surface-enhanced Raman scattering (SERS) measurements of the common dye IR-792. 2.0 μL of 2 × 10^-5 M IR-792 was added to 100 μL of 0.50 nM aqueous nanoparticle samples and allowed to stir for 15 minutes at room temperature. SERS spectra were then recorded by a Raman spectrometer (Renishaw, Gloucestershire, UK) with 785 nm laser excitation at 3 mW/cm² for 1 s. No aggregation was present in any of the samples, ensuring that the SERS intensity was not complicated by the presence of aggregation-induced hotspots.

Monte Carlo Calculations

Expected distributions of nanorod growth rates from nucleation-limited and diffusion-limited hypotheses were generated in Matlab (see Supporting information for Matlab Scripts). Nucleation rate and flux (i.e. diffusion rate) were modeled as normally distributed random variables. The mean nucleation rate and flux were chosen to be the values that give the experimental growth rate (i.e. 10 nm/s from {111} facets) under nucleation-limited and diffusion limited hypotheses, respectively. The standard deviation was set to be 1% of the mean. The input distributions were randomly sampled 10⁶ times in order to generate the output facet growth rate distributions shown in Figure 4a,b.