Full body musculoskeletal model for muscle-driven simulation of human gait

Abstract

Objective

Musculoskeletal models provide a non-invasive means to study human movement and predict the effects of interventions on gait. Our goal was to create an open-source, three-dimensional musculoskeletal model with high-fidelity representations of the lower limb musculature of healthy young individuals that can be used to generate accurate simulations of gait.

Methods

Our model includes bony geometry for the full body, 37 degrees of freedom to define joint kinematics, Hill-type models of 80 muscle-tendon units actuating the lower limbs, and 17 ideal torque actuators driving the upper body. The model’s musculotendon parameters are derived from previous anatomical measurements of 21 cadaver specimens and magnetic resonance images of 24 young healthy subjects. We tested the model by evaluating its computational time and accuracy of simulations of healthy walking and running.

Results

Generating muscle-driven simulations of normal walking and running took approximately 10 minutes on a typical desktop computer. The differences between our muscle-generated and inverse dynamics joint moments were within 3% (RMSE) of the peak inverse dynamics joint moments in both walking and running, and our simulated muscle activity showed qualitative agreement with salient features from experimental electromyography data.

Conclusion

These results suggest that our model is suitable for generating muscle-driven simulations of healthy gait. We encourage other researchers to further validate and apply the model to study other motions of the lower-extremity.

Significance

The model is implemented in the open source software platform OpenSim. The model and data used to create and test the simulations are freely available at https://simtk.org/home/full_body/, allowing others to reproduce these results and create their own simulations.

I. INTRODUCTION

HUMAN movement involves complex interactions between the neuromuscular and skeletal systems. Understanding these interactions is necessary for designing treatments and devices to improve the gait of impaired individuals and to enhance performance of able-bodied individuals. While some components of human motion, such as body segment kinematics, ground reaction forces, and muscle activity can be measured or estimated using non-invasive tools including motion capture, force plates, and electromyography, more invasive means are necessary to measure muscle tension [1] and joint contact forces [2]. Biomechanical models provide an alternate, non-invasive method to calculate these quantities, and have revealed, for example, how muscles coordinate the swing phase of gait [3] and contribute to body weight support and propulsion [4], [5], and how muscle coordination impacts joint contact forces [6]. Researchers have systematically modified models and simulations of healthy gait to investigate how anomalies such as bony deformities [7] or muscle weakness [8], [9] change coordination and lead to pathological gait patterns. Understanding the roles of muscles in gait provides insights that can then be used to guide treatment planning; for example, simulations have been used to indicate if a hamstring lengthening surgery could improve crouch gait in children with cerebral palsy [10].

An important consideration in creating a musculoskeletal model to simulate and study human motion is determining a suitable trade-off between model complexity and simulation speed. Torque-driven models have been used in optimal control problems [11]; while these models provide valuable insights and are computationally fast, they are limited in their biological fidelity. At the other extreme, finite element simulations of muscle represent complex muscle geometry well, but are computationally expensive [12]. Between these extremes are muscle-driven models with Hill-type muscle actuators and three-dimensional skeletal geometry, such as the models developed by Delp et al. [13], Klein Horsman et al. [14], Arnold et al. [15], and Carbone et al. [16] (Table I).

TABLE I.

Lower limb musculoskeletal models

Model	Muscle architecture data sources	Software
Delp 1990 [13]	5 cadaver subjects [17], [18]	SIMM, OpenSim
Klein Horsman 2007 [14]	Single cadaver limb [14]	AnyBody, OpenSim
Arnold 2010 [15]	22 cadaver subjects [20]	SIMM, OpenSim
Carbone 2015 [16]	Single cadaver limb [16]	AnyBody
Our model	24 adult subjects [26], 22 cadaver subjects [20]	OpenSim

Previously published musculoskeletal models have been based on a variety of data sets describing skeletal geometry and muscle architecture. The models described above have been implemented in either OpenSim [27] or AnyBody [19].

Another important consideration is selecting appropriate experimental data to define the model’s parameters. The model created by Delp et al. has been used extensively to create muscle-driven simulations of gait and other lower-extremity motions, but the musculotendon parameters (e.g., optimal fiber length and pennation angle) are based on two studies of two and three cadavers [17], [18]. Klein Horsman et al. created a model with all parameters drawn from a single cadaver subject [14]. While this model is self-consistent, it is unclear how well this single subject represents other subjects. This model was recently updated by Carbone et al. [16] using a new dataset consisting of computed tomography and magnetic resonance images and implemented in the AnyBody Modeling System [19]; however, this model still reflects a single cadaver subject and thus may be unsuitable for scaling to a wide range of subjects. Arnold et al. [15] created a generic lower limb model using a comprehensive set of muscle architecture data collected by Ward et al. [20] from 21 cadaver subjects.

The model developed by Arnold et al. [15] has become widely used, but has two major drawbacks for use in muscle driven simulations. First, to represent musculoskeletal geometry accurately, the model makes extensive use of ellipsoidal wrapping surfaces [21]. Because there is no closed-form solution for how a muscle path wraps over an ellipsoidal surface, computing muscle paths is computationally expensive. This makes this model impractical for many muscle-driven forward simulations. Moreover, because the model by Arnold et al. [15], and other models [13], [16], [22], derive optimal muscle force values from measurements of muscle volume from elderly cadavers with significant muscle atrophy, the muscle force distribution in the models may not accurately represent the distribution in young healthy individuals [23]–[25]. Fortunately, Handsfield et al. [26] recently used magnetic resonance imaging (MRI) to measure muscle volumes of 24 young healthy subjects and found that (i) total lower limb muscle volume is correlated with a subject’s mass and height and (ii) the distribution of individual muscle volumes within the lower limb is well preserved between subjects.

Our goal was to build on the valuable data of Handsfield et al. to create a musculoskeletal model with high-fidelity representations of the lower limb musculature of healthy, young individuals suitable for simulating gait and that is computationally fast enough for use in muscle-driven simulations. We created a full-body model with muscle-actuated lower limbs and a torque-actuated upper body. Lower extremity muscle architecture was defined by combining the cadaver-based estimates of optimal muscle fiber lengths and pennation angles [20] with young adult MRI muscle volume data [26]. To test that our model met the fidelity and speed criteria, we generated muscle-driven simulations of walking and running using the open-source musculoskeletal simulation software, OpenSim [27]. We determined that our model met the fidelity criteria by comparing (i) the musculoskeletal geometry of our model to experimental data, (ii) our simulated muscle-generated joint moments to inverse dynamics joint moments, and (iii) our simulated muscle activity to electromyography (EMG) data. We determined that our model met the speed criteria by computing the time required to generate a simulation of a single gait cycle and ensuring that our model was as fast or faster than other frequently used models. This model was implemented in OpenSim [27], and is freely available for download at https://simtk.org/home/full_body/ along with all the data used to create the simulations.

II. METHODS

A. Rigid body geometry

The model’s bony geometry and dimensions reflect those of a 75 kg, 170 cm tall male [15], [28]. The model’s skeleton was built of 22 articulating rigid bodies— a pelvis and right and left femur, patella, tibia/fibula, talus, calcaneus (including the tarsal and metatarsal bones), and toes to represent the lower body, and a combined head and torso and right and left humerus, ulna, radius, and hand to represent the upper body (Fig. 1). The model had 20 degrees of freedom in the lower body (six describing the pelvis and seven per leg; described below) and 17 in the torso and upper body (three describing the lumbar joint and seven per arm). We aligned the coordinate system of each rigid body such that, when the model is in the anatomical position, the x direction pointed anteriorly, the y direction superiorly, and the z direction to the right. For further details about the location of each coordinate system with respect to bony landmarks, see Arnold et al. [15].

Fig. 1.

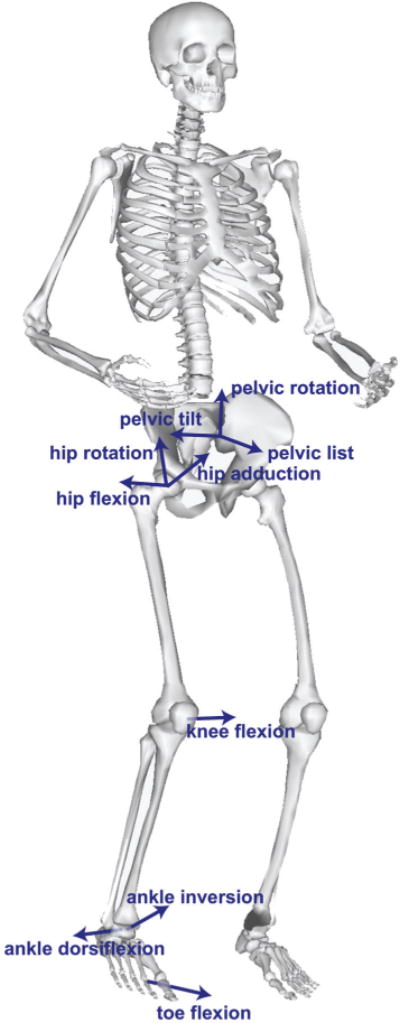
Rigid bodies and degrees of freedom in the model. The model was implemented in OpenSim with 22 rigid bodies representing the lower body (pelvis, and right and left femur, patella, tibia and fibula, talus, calcaneus (including the tarsal and metatarsal bones, and toes) and upper body (head and torso, and right and left humerus, ulna, radius, hand). There were seven degrees of freedom in each lower limb (labeled for the right limb), three rotational (labeled) and three translational (not labeled) degrees of freedom in the pelvis, and seventeen degrees of freedom in the upper body (not labeled).

The position of the pelvis origin with respect to the ground origin was represented using three independent translational degrees of freedom. The orientation of the pelvis relative to ground was determined using a pelvis-fixed ZXY rotation by angles representing pelvis tilt, list, and rotation, respectively. The model is oriented such that at zero degrees pelvic tilt, list, and rotation, the two anterior-superior iliac spines and pelvic tubercles are in the frontal (y–z) plane.

The femur articulated with the pelvis via a ball-and-socket joint. The orientation of the right femur relative to the pelvis was described by femur-fixed ZXY rotations of the femur by the hip flexion, adduction, and rotation angles, respectively, and similarly for the left hip. The hip joint range of motion was 30° extension to 120° flexion, 50° abduction to 30° adduction, and 40° external rotation to 40° internal rotation.

The knee joint was modeled as a single degree of freedom joint. The orientation of the right tibia with respect to the right femur was primarily determined by rotation of the tibia about the femur-fixed −Z axis by the knee flexion angle, and similarly for the left knee. The coupled rotation and translation of the tibia relative to the femur was parameterized by the knee flexion angle using the joint kinematic equations defined by Walker et al. [29], modified such that the joint reference frame on each body was coincident with anatomic approximations of the center of rotation. Similarly, patellar kinematics were parameterized by the knee flexion angle using the kinematics defined in Arnold et al. [15], modified such that the patella articulated with the femur. The knee flexion angle had a range of 0° to 120° flexion.

The ankle, subtalar, and metatarsophalangeal joints were each modeled as pin joints with coordinates representing ankle dorsiflexion, ankle inversion, and toe flexion angles respectively. The joint axes for these three joints were consistent with measurements made by Inman et al. [15], [30]. The ranges of motion were 40° plantarflexion to 30° dorsiflexion, 20° eversion to 20° inversion, and 30° toe extension to 30° toe flexion.

The ranges of motion for the lower body degrees of freedom were specified to be consistent with previously published models (e.g., [13] and [15]) and encompassed the walking and running motions simulated with our model. These limits, and any parameter of the model, can be changed to the user’s preference by editing the model file.

The head and torso were modeled as one rigid segment connected to the pelvis by a ball-and-socket joint. The orientation of the torso with respect to the pelvis was specified using torso-fixed ZXY rotations (lumbar extension, bending, and rotation, respectively). The humerus articulated with the torso by a ball-and-socket joint; the orientation of the right humerus with respect to the torso was given by humerus-fixed ZXY rotations (shoulder flexion, adduction, and rotation, respectively). The ulna connected to the humerus via a pin joint at the elbow. Pronation of the forearm was modeled by a pin joint connecting the radius and ulna. A two degree of freedom universal joint connected the hand to the radius; the orientation of the hand with respect to the radius was given by hand-fixed ZX rotations (wrist flexion, ulnar deviation, respectively). Because the upper body was provided primarily to track gross motion of the torso and upper extremities in gait, these joint descriptions did not capture detailed upper body joint kinematics, such as complex scapular motion or bending of the spine.

B. Muscle and torque actuators

The model was actuated by 80 muscle-tendon units in the lower body (40 per leg, listed in Table II, shown in Fig. 2a) and 17 torque actuators (one for each degree of freedom in the upper body). Each muscle-tendon unit was massless and had a line of action approximating the path of the anatomical muscle volume from origin to insertion. Muscles with large attachment areas (e.g., gluteus medius) were modeled as several independent units (Fig. 2b). The path of each muscle-tendon unit was specified using a set of body-fixed origin and insertion points and, when needed, additional path points and cylindrical wrapping surfaces that model physical constraints from bone and soft tissue (Fig. 2c). We did not model the patellar ligament directly, and instead defined the quadriceps lines of action to wrap over the patella and insert onto the tibia (Fig. 2d). Muscle paths were adapted from Arnold et al. [15] and all ellipsoidal wrapping surfaces were replaced with cylindrical wrapping surfaces. Because there is an analytic solution for how a muscle path wraps over a cylindrical surface [31], we expected this would improve simulation speed. We verified that we preserved the muscle geometry by comparing model moment arms of the major muscles crossing the hip, knee, and ankle to experimentally measured moment arms (Supplemental Fig. 1 and Supplemental Fig. 2) [12], [32]–[40].

TABLE II.

Musculotendon Parameters

Muscle	Abbreviation	Optimal force (N)	Optimal fiber length (cm)	Tendon slack length (cm)a	Pennation angle (°)
Adductor brevis	addbrev	626	10.3	3.5*	6.6
Adductor longus	addlong	917	10.8	13.2	7.9
Adductor magnusb
Adductor magnus (distal)	addmagDist	597	17.7	8.7*	11.2
Adductor magnus (ischial)	addmagIsch	597	15.6	21.6	9.6
Adductor magnus (middle)	addmagMid	597	13.8	4.7*	11.9
Adductor magnus (proximal)	addmagProx	597	10.6	4.0*	17.8
Biceps femoris long head	bflh	1313	9.8	32.5	10.1
Biceps femoris short head	bfsh	557	11.0	10.6*	15.1
Extensor digitorum longusc	edl	603	6.9	36.9	12.5
Extensor hallucis longusc	ehl	286	7.5	32.7	11.3
Flexor digitorum longus	fdl	423	4.5	37.9	12.9
Flexor hallucis longus	fhl	908	5.3	35.4	14.8
Gastrocnemius lateral head	gaslat	1575	5.9	37.6	12.0
Gastrocnemius medial head	gasmed	3116	5.1	39.9	9.5
Gluteus maximusb
Gluteus maximus (superior)	glmaxl	984	14.7	4.9*	20.3
Gluteus maximus (middle)	glmax2	1406	15.7	6.8*	21.0
Gluteus maximus (inferior)	glmax3	948	16.7	7.0*	21.9
Gluteus mediusb
Gluteus medius (anterior)	glmedl	1093	7.3	5.6*	18.1
Gluteus medius (middle)	glmed2	765	7.3	6.5*	18.1
Gluteus medius (posterior)	glmed3	871	7.3	4.5*	18.1
Gluteus minimusb
Gluteus minimus (anterior)	glminl	374	6.8	1.6*	10.0
Gluteus minimus (middle)	glmin2	395	5.6	2.6*	0.0
Gluteus minimus (posterior)	glmin3	447	3.8	5.1	1.0
Gracilis	grac	281	22.8	17.2*	9.9
Iliacus	iliacus	1021	10.7	9.6*	16.0
Peroneus brevisd	perbrev	521	4.5	14.8	11.8
Peroneus longusd	perlong	1115	5.1	33.2	14.2
Piriformis	piri	1030	2.6	11.5	10.0
Psoas	psoas	1427	11.7	10.0*	12.3
Rectus femoris	recfem	2192	7.6	44.9	12.4
Sartorius	sart	249	40.3	12.4*	1.5
Semimembranosus	semimem	2201	6.9	34.8	14.6
Semitendinosus	semiten	591	19.3	24.7	13.8
Soleus	soleus	6195	4.4	27.7	21.9
Tensor fascia latae	tfl	411	9.5	45.0	3.0
Tibialis anterior	tibant	1227	6.8	24.1	11.2
Tibialis posterior	tibpost	1730	3.8	28.1	13.0
Vastus intermedius	vasint	1697	9.9	20.2	3.6
Vastus lateralis	vaslat	5149	9.9	22.1	14.5
Vastus medialis	vasmed	2748	9.7	20.0	24.2

Musculotendon parameters. Muscle physiological cross sectional areas (PCSAs) were calculated from muscle volumes measured by Handsfield et al. [26] in healthy, young subjects. Optimal fiber lengths were measured by Ward et al. [20] in cadaver subjects. Pennation angle at optimal fiber length was calculated using pennation angle measurements in cadavers by Ward et al. and adjusted for fiber length using the constant-volume assumption made by Millard et al. Tendon slack length was set in the model to match normalized fiber length measurements reported by Ward et al.

^aTendons were modeled as rigid when the tendon slack length was less than the muscle optimal fiber length. Rigid tendons are indicated with a (*).

^bMuscle volume was only available for the whole muscle. Total muscle volume for each muscle was divided equally between the muscle-tendon units using the same volume distribution as in the model by Arnold et al. [15].

^cMuscle volume was only available for extensor digitorum longus, extensor hallucis longus, and peroneus tertius combined. Peroneus tertius was not included in our model. The total muscle volume was divided between extensor digitorum longus and extensor hallucis longus using the volume proportions used by Arnold et al. [15].

^dMuscle volume was only available for peroneus brevis and peroneus longus combined. The total muscle volume was divided between the two using the volume proportions used by Arnold et al. [15].

Fig. 2.

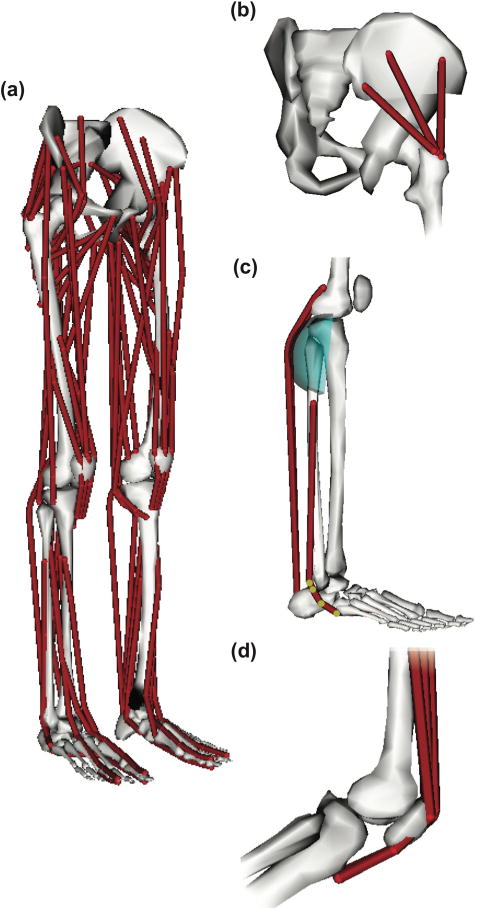
Muscles were modeled as massless linear actuators. (a) The model included 80 muscle-tendon units (40 per leg) actuating the lower limbs. (b) Muscles with broad attachment areas (e.g., gluteus medius) were modeled using multiple independent muscle-tendon units. (c) Muscle geometry was modeled using a set of body-fixed points (highlighted) and wrapping surfaces. (d) The force transmission mechanism between the quadriceps and patellar ligament was modeled implicitly by wrapping the quadriceps muscles over the patella and inserting the muscles directly to the tibia.

Each muscle-tendon unit was represented with the Hill-type muscle model [41] (Fig. 3a) described by Millard et al. [42]. The force-generating capacity of each muscle-tendon unit was specified using normalized fiber force-length-velocity and tendon force-length curves (Fig. 3b–d) scaled for each muscle by a set of experimentally determined values for muscle maximum isometric force, optimal fiber length, maximum fiber shortening velocity, pennation angle at optimal fiber length, and tendon slack length (Table II). The normalized active fiber force-length curve (Fig. 3c, solid line) was modified from the force-length curve published by Millard et al. [42] to account for the wider force-producing range of a whole muscle as opposed to a ingle muscle fiber [43]. The passive fiber force-length curve (Fig. 3c, dotted line), fiber force-velocity curve (Fig. 3d), and tendon force-strain curves (Fig. 3b) were taken directly from Millard et al. [42].

Fig. 3.

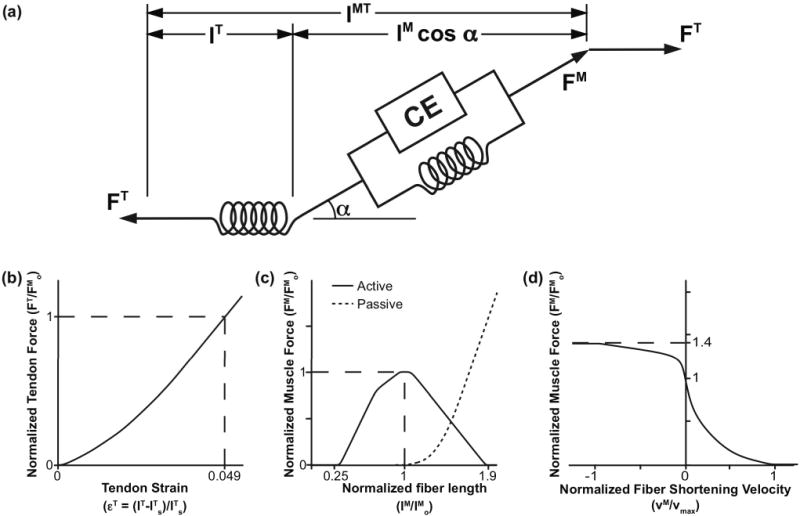
Computational model of muscle-tendon units. Muscles were represented as massless linear actuators with active and passive properties described by scalable generic force-length and force-velocity curves [42]. The generic curves were scaled by five muscle-specific parameters: maximum isometric force (F^M_o), tendon slack length (l^T_s), optimal fiber length (l^M_o), maximum fiber shortening velocity (v_max), and pennation angle at optimal fiber length (α_o). (a) The total muscle-tendon length (l^MT) was a function of the geometric pose of the model. The muscle fiber length (l^M), muscle pennation angle (α), and tendon length (l^T) were determined based on l^MT, muscle activation, and the force equilibrium constraints between the muscle fiber (F^M) and tendon (F^T). (b) Tendon was modeled as a passive series elastic element whose normalized force (F^T/F^M_o) was a function of tendon strain (ε^T). Tendon strain was calculated from the muscle-specific tendon slack length (l^T_s). We assumed a tendon strain (ε^T) of 4.9% [42] when the muscle developed maximum isometric force (F_o^m). (c) Muscle fiber was modeled as an active contractile element (CE) in parallel with a passive elastic element. Active isometric fiber force was a function of muscle activation (a) and fiber length normalized by optimal fiber length (l^M/l^M_o). Passive fiber force was a function of normalized fiber length (l^M/l^M_o) only. (d) Muscle active isometric fiber force was scaled based on fiber velocity (v^M) normalized by maximum shortening velocity (v_max) of the muscle. Total muscle force was calculated as the sum of active and passive fiber force.

The musculotendon parameters in the model were taken from cadaver studies by Ward et al. [20] and from MRI muscle volume data measured by Handsfield et al. [26]. For each muscle-tendon unit, the optimal fiber length was taken directly from the mean optimal fiber length calculated by Ward et al. To set the tendon slack length, the model was posed at 7° hip flexion, 2° hip abduction, 0° knee flexion, and 20° plantarflexion. These hip flexion, hip adduction, and knee flexion angles were chosen to match the average pose of the cadavers in the Ward et al. study [20]. The 20° plantarflexion angle was chosen to be consistent with the methods of Arnold et al. [15], since they found that setting tendon slack length with the model posed at the average cadaveric angle of 40° from Ward et al. [20] resulted in high passive forces in the ankle plantarflexors. After posing the model, the tendon slack length of the muscle-tendon unit was then set such that the normalized fiber length of the muscle-tendon unit, with 1% activation, matched the experimentally measured mean normalized fiber length reported by Ward et al. [20]. This method yielded unrealistically long fibers in the semimembranosus muscle-tendon unit when the hip was flexed and the knee fully extended, and thus large passive hip extension and knee flexion moments; because of this, we set the tendon slack length of the semimembranosus such that, when the model is posed as previously described and the muscle activation is set to 1%, the fiber length in our model matched the fiber length in the Arnold et al. model [15] instead of the fiber length reported in the Ward et al. data [20]. For any muscle-tendon unit whose tendon slack length was smaller than its optimal fiber length, we assumed tendon strain would be negligible in muscle force calculations and therefore modeled the tendon as rigid [41], [42]. This was done to increase the computational speed of our simulations [42], as stiff tendons increase the number of time steps required during numerical integration in forward simulations. Using this criterion, 17 of the 40 muscle-tendon units in each leg were modeled with a rigid tendon (Table II). This can be easily changed for any muscle by editing the model in OpenSim.

The pennation angle at optimal fiber length was calculated using the mean pennation angle measured by Ward et al. [20] and based on the constant muscle volume assumption used by Millard et al. in their muscle model [42]. Specifically, pennation angle at optimal fiber length, α_o, was calculated as

$${\alpha }_o={\sin }^{-1}({\stackrel{\sim }{l}}^m\sin \alpha ),$$ (1)

where α and ${\stackrel{\sim }{l}}^m$ are the pennation angle and normalized fiber length, respectively, measured by Ward et al. [20].

The optimal force for each muscle was calculated using MRI muscle volume data. The total muscle volume (V_total) of each lower limb was calculated based on our model’s mass (m) and height (h) using the relationship reported by Handsfield et al. [26] as shown in (2).

$$V_{\mathit{total}}={47\mathit{mh}+1285|}_{m=75\mathit{kg},h=1.70m}$$ (2)

Individual muscle volumes were calculated based on the mean lower limb muscle volume fraction (ϕ^m) for each muscle also reported in the Handsfield et al. study. From here, the muscle physiological cross-sectional area (PCSA) of each muscle was calculated as the muscle volume divided by the optimal fiber length $l_o^m$ of the muscle. Maximum isometric fiber force $F_o^m$ was assumed to be directly proportional to the muscle PCSA as in (3).

$$F_o^m={\sigma }_o^m\frac{{\varphi }^m{V}_{\mathit{total}}}{l_o^m}$$ (3)

Previously reported estimates of specific tension $({\sigma }_o^m)$ in mammalian muscle vary widely, from 15 N/cm² [44] to over 100 N/cm² [45]. We chose a specific tension of 60 N/cm², within this range. This specific tension resulted in our model generating higher passive joint torques at extreme joint angles compared to experimental data (Supplemental Fig. 3, (a), (d), (f)) and allowed our model to generate higher maximum isometric joint moments than those measured during maximum voluntary contraction trials (Supplemental Fig. 3, (b), (c), (e), (g)), but was necessary for our model to produce muscle-generated joint moments high enough to match those produced in dynamic motions such as running.

C. Model testing: sample simulations of gait

We first tested our model’s ability to simulate gait by using our model in OpenSim version 3.3 [27] to generate muscle-driven forward simulations of a single gait cycle of a 31-year-old male subject (height 182 cm, mass 85 kg) walking at self-selected speed and a 24-year-old male subject (height 178 cm, mass 73 kg) running at 4 m/s. Experimental data used to generate these simulations are described in the Appendix. To create these simulations, we first used the Scale Tool in OpenSim [27] to create a scaled version of the generic model that matched our subject anthropometry. We also used the mass-height-volume relationship for lower extremity muscle reported by Handsfield et al. [26] and described in equations (2) and (3) to scale the model maximum isometric muscle forces based on our subject’s mass and height. Joint kinematics for each motion were computed from motion capture data using the Inverse Kinematics tool in OpenSim. In this and future steps, we constrained the subtalar and metatarsal-phalangeal joints in the model to be 0° (neutral); this was done because the motion capture data used to generate these simulations were not of fine enough resolution to accurately capture movement in these degrees of freedom. For the same reason, we locked the wrist flexion and ulnar deviation degrees of freedom in the wrist. The Residual Reduction Algorithm (RRA) [27] was then used to generate a smoothed set of kinematics that reduced the dynamic inconsistency between the measured kinematic and kinetic data. These smoothed kinematics differed from the inverse kinematics results by less than 2° for all rotational degrees of freedom in the model (rotation) and 2 cm for pelvis translations at any time step and had a maximum RMS error of less than 1.75° (rotation) and 1 cm (pelvis translation) for both walking and running over the gait cycle. The smoothed kinematics were input into the Computed Muscle Control (CMC) algorithm [46], which uses forward simulation and a feedback controller that tracks the input kinematics to calculate muscle excitations, muscle activations, and muscle forces. CMC solves the muscle redundancy problem by computing muscle excitations (x_m) and excitations of the ideal torque actuators (x_d) that minimize the objective function J shown in (4).

$$J={\displaystyle {\sum }_{m=1}^{n_{\mathit{musc}.}}{x}_m^2}+{\displaystyle {\sum }_{d=1}^{n_{\mathit{DOF}}}{x}_d^2,}$$ (4)

We constrained the muscle excitations of the gastrocnemius medialis and lateralis muscles to be off in early to mid swing to improve numerical stability of our simulation and better match the recorded EMG signal.

We used the simulation results to compute, for each joint, the net muscle-generated joint moments (M^muscle) throughout the motion as the sum over all muscles of muscle moment arm (ma) multiplied by the muscle force (F^m) as in (5).

$$M^{\mathit{muscle}}={\displaystyle {\sum }_{i=1}^{n_{\mathit{musc}.}}m{a}_i·F_i^m}$$ (5)

Separately, we used inverse dynamics to compute the joint moments required to produce the smoothed gait kinematics. To generate the muscle-driven simulations, ideal torque actuators for each degree of freedom supplied small moments to account for the differences between the muscle-generated and inverse dynamics joint moments. We evaluated the simulation by verifying that the muscle-generated joint moments in the lower extremity accounted for at least 90% of the inverse dynamics joint moments at each instant in time [47], indicating that the muscles rather than these torque actuators were driving the motion. We also qualitatively compared the timing of the computed muscle activity to the subject’s recorded EMG data to determine if our simulations reproduced the major features of the experimental EMG (e.g., vasti activity in stance that is larger for running than for walking) [48]. Because muscle activity during maximum voluntary contraction was not available for both subjects, and because we sought only to compare timing of the simulated muscle activity with measured EMG activity, we normalized peak EMG activity for each muscle and condition to match the peak simulated muscle activity.

We next measured the average computation time required to generate muscle-driven simulations of single gait cycles of walking and running using our model and the CMC tool. To do this, we used our model with previously collected experimental data [48], [49] to automatically generate 80 muscle-driven simulations spanning 3 subjects, 8 speeds (4 walking, 4 running), and 3 to 6 gait cycles per subject/speed. These simulations were used only to verify robustness of the model within the OpenSim simulation pipeline and to calculate the average computation time required to generate muscle-driven simulations using our model, and as such, we did not carefully tune the RRA and CMC algorithm settings, nor did we carefully validate the simulation outputs.

Finally, we compared the simulation computation time of our model to two other commonly used OpenSim models [13], [15]. We used a version of the Delp model [13] modified to include arms [48] and the CMC tool to generate the simulation of the same subject running. The Arnold model [15] was prohibitively slow and not able to be used with the CMC tool to generate a muscle-driven simulation of gait. We instead used the Static Optimization tool [27] and, for the time periods where we were able to run a simulation with the Arnold model, computed the ratio of computation time required between the Arnold model and our model.

III. RESULTS

Computing dynamically consistent, smoothed joint kinematics from motion capture data using the Inverse Kinematics and RRA tools took less than 1 minute of computation time per gait cycle on one thread of a 2.6 GHz Intel Core i7 processor. The CMC computation time (i.e., the time to compute the pattern of coordinated muscle activity to drive a forward simulation that matches the smoothed kinematics) was greater. Computing muscle activations for one gait cycle of walking and running using the CMC tool took, on average, 14 and 9 minutes, respectively.

Generating the same running simulation using the Delp model and the CMC tool was 11% faster than using our model (8 minutes vs. 9 minutes). Computing the Static Optimization results using the Arnold model took 40% longer than using our model. It should be noted that Static Optimization does not run a forward simulation nor compute muscle-tendon equilibrium; we expect that adding these components would further increase the computational time required by the Arnold model compared to our model.

The muscle-driven simulations tracked the smoothed joint kinematics with a maximum coordinate RMS error of less than 1° (rotation) and 0.1 cm (pelvis translation) for walking, and 4° (rotation) and 0.2 cm (pelvis translation) for running. The RMS error between the inverse dynamics joint moments and the muscle-generated joint moments were 0.4 N-m, 1 N-m, and 0.3 N-m for hip, knee, and ankle flexion, respectively, for walking; and 3 N-m, 7 N-m, and 5 N-m for hip, knee, and ankle flexion, respectively, for running (Fig. 4). These RMS errors were less than 2% of the peak joint moments in walking, and less than 3% of the peak joint moments in running. Peak absolute differences between the inverse dynamics and muscle-generated joints moments were 1 N-m, 3 N-m, and 1 N-m for the hip, knee, and ankle flexion, respectively for walking; and 9 N-m, 26 N-m, and 14 N-m for the hip, knee, and ankle flexion, respectively for running. These peak differences were less than 6% of the peak joint moments in walking, and less than 11% of the peak joint moments in running.

Fig. 4.

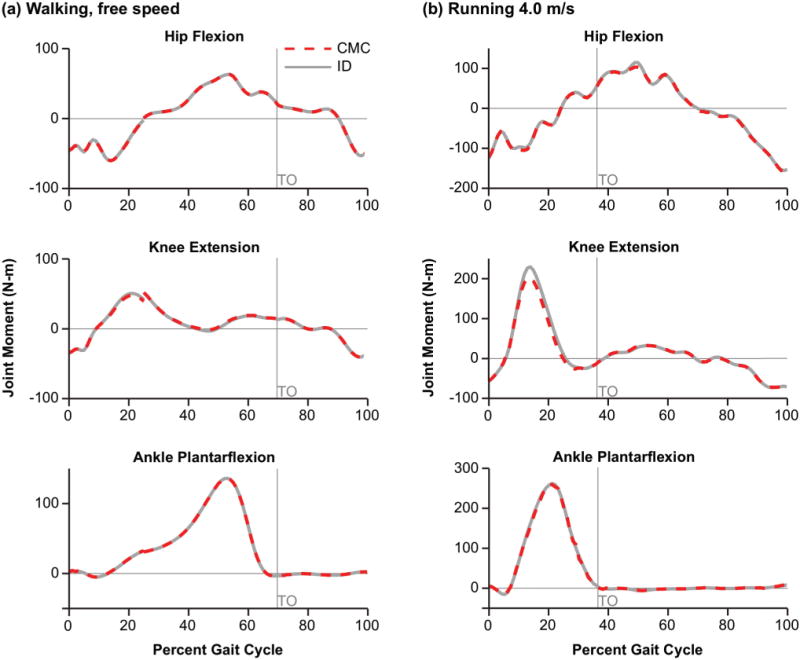
Joint moments for one gait cycle of walking and running. Joint moments for the hip, knee, and ankle joint during (a) walking and (b) running were computed using inverse dynamics (ID) and then compared to the net muscle-generated joint moments from the muscle-driven forward simulation (CMC). Toe-off (TO) is indicated with the gray vertical line.

The timing of the simulated muscle activations represented some of the major features of the measured EMG signals (Fig. 5). In walking, simulated activations and measured EMG signals both show hip extensor (gluteus medius and biceps femoris long head) and knee extensor (vastus lateralis) activity in early stance, plantarflexor (gastrocnemius and soleus) activity in late stance prior to toe-off, and tibialis anterior activity in early stance and swing, and hamstring (biceps femoris long head) activity in terminal swing prior to foot strike to brake the swing limb. Similarly, in running, we see gluteus maximus and gluteus medius simulated and EMG activity in stance, quadriceps (rectus femoris and vastus lateralis) activity in early stance, plantarflexor (gastrocnemius and soleus) activity in stance, increasing prior to toe-off, and tibialis anterior activity in early stance and swing. However, there are some notable differences between the simulated muscle activity and the EMG data. For example, in simulated walking, we saw activity for the gluteus maximus only in early stance, and activity for the gluteus medius throughout stance. This disagrees with the measured EMG signal which shows relatively constant gluteus maximus activity in gait and gluteus medius activity primarily in early stance. However, EMG activity in the gluteal muscles are susceptible to measurement error due to interference from other soft tissues. Our simulations results for the gluteal muscles agree with expected activity in stance published by Perry [50]. We also saw higher simulated activity in the tibialis anterior in swing compared to stance in both walking and running than we would expect given the EMG signal. This is likely to counteract the residual force in the plantarflexors after toe-off arising from the passive stretch of the plantarflexor fibers in the model.

Fig. 5.

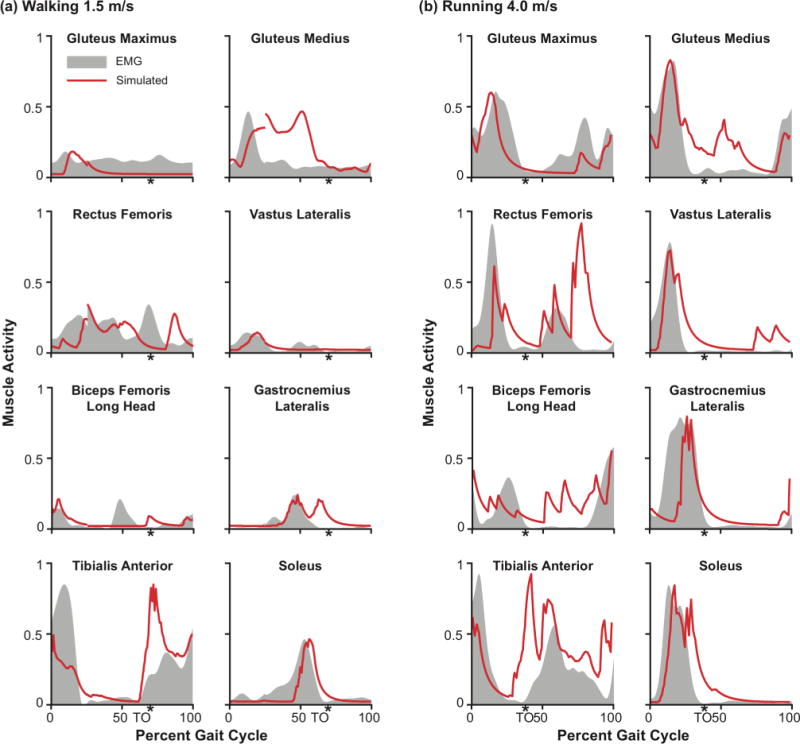
Computed muscle activations compared to measured EMG for the major lower extremity muscles during walking and running. Simulated muscle activity in (a) walking and (b) running for the gluteus maximus, gluteus minimus, rectus femoris, vastus lateralis, biceps femoris long head, gastrocnemius lateralis, tibialis anterior, and soleus are shown in red. The corresponding experimental EMG signals are shown by the gray shaded regions. The EMG signal for each muscle was normalized such that the peak EMG signal matched the peak simulated activity for that muscle during the gait cycle. Toe-off (TO) timing is indicated with a (*).

Finally, as expected, our simulated activity shows greater activity in running compared to walking. For example, we see greater gluteal and quadriceps activity in stance in running compared to walking, and greater activity in the plantarflexors (soleus and gastrocnemius) prior to toe-off in running compared to walking. Furthermore, although our simulated muscle activity was high, especially in running, we did not maximally activate any of these muscles; this is encouraging as it suggests that our model strength may be well tuned to saturate at higher, maximal activities such as high-speed sprinting or maximum height jumping.

IV. DISCUSSION

We created a full-body musculoskeletal model representative of a healthy young individual that can be used to create simulations of human walking and running. Our model can generate muscle-driven simulations of gait within a few minutes on a typical desktop computer. Using the CMC algorithm in OpenSim, we are able to compute muscle activations for a single gait cycle of walking and running in approximately 10 minutes on a single processor. We did not benchmark the time required to generate a muscle-driven simulation using the model by Arnold et al. [15] as this model was not able to be used to generate a muscle-driven simulation using CMC; however, the 10 minutes is comparable to the time required for a previous model by Delp et al. [13]. The simulations tracked smoothed experimental kinematics to within 4.0° and the muscle-generated joint moments differed from the inverse dynamics joint moments by less than 11% (peak) and 3% (RMSE) of the peak joint moment. The simulated muscle activity captures some of the salient features of experimental EMG data, though there are differences in timing and magnitude of some muscle activations when compared to EMG data. Obtaining simulated activations that faithfully match measured EMG of all muscles remains an important challenge in all studies involving muscle-driven simulations.

We believe that our model can be used to generate accurate simulations of normal walking and running gait because (i) our model muscle geometry compares well with experimental data (Supplemental Fig. 1 and Supplemental Fig. 2), (ii) our muscle architecture parameters, such as maximum isometric force and optimal fiber length are based on the most comprehensive available studies (Fig. 3, Table II) and are representative of a generic individual, (iii) our model can be used to generate muscle-driven simulations of gait without excessively relying on lower limb reserve torque actuators (Fig. 4), and (iv) the timing of our simulated muscle activity generally match well with experimentally measured EMG for the same motion for the major lower extremity muscles. In turn, our model can be used to calculate quantities such as muscle forces [3], muscle fiber velocities [49], joint forces [6], [51] and other variables that cannot be measured easily with an experiment but are helpful for understanding the biomechanics of movement. The model is freely available for download at https://simtk.org/home/full_body and is compatible with the open source software package OpenSim, allowing the model to be readily scaled to a variety of subjects and used for simulating gait and other lower extremity motions.

This model improves on past models by deriving its muscle strength parameters from MRI data collected from healthy young individuals [26] rather than elderly cadavers. Our model does, however, derive other muscle architecture parameters including optimal fiber length and fiber pennation angle using data collected from elderly cadavers [20]. While studies have shown that optimal muscle fiber lengths and pennation angles measured in elderly cadavers may be smaller than the corresponding values in healthy, young adults [52], there is no comprehensive and complete dataset measuring these muscle architecture values in a cohort of young adults.

Our model also includes a parameterization of the knee joint modified from previously published studies ([15], [29]) that better estimates both the anatomical center of rotation of the knee joint and the patellar force transmission mechanism between the femur and the tibia. This allows for estimation of knee joint contact forces which could not be done using previous models ([13], [15]). However, the calculation of joint contact forces in a model during a motion is sensitive to both the joint kinematic definition and the distribution of muscle forces crossing the joint in that motion ([6], [47]). Future work is necessary to validate both of these components.

Some limitations of our model should be noted. Our model does not contain representations of all lower limb muscles, nor does it include representations of ligaments or other soft tissues. Several small muscles crossing the hip, knee, and ankle, were left out if information about muscle volume and/or muscle fiber architecture were not included in the Handsfield et al. and Ward et al. studies [20], [26]. Per Handsfield et al., the muscles that were left out account for, on average, less than 4% of the total lower limb muscle volume.

Our model’s chosen musculotendon parameters represent an average individual based on experimental data from literature [20], [26]. However, there is variability in these data not captured in our model. Supplemental Table I enumerates the expected variability in our model parameters given the experimental data.

There are also limitations associated with our simplified modeling of muscle geometry and force generation. We model each muscle-tendon unit as a one-dimensional path representing the line of action; thus, we implicitly assume that as a muscle-tendon unit changes length, all fibers in the muscle change length equally. In reality, muscle fibers within a muscle are distributed over a range of lengths. Thus, our model likely overestimates both (i) the drop-off in the active force-generating capacity of muscle due to the overestimation of fiber length change (and consequently fiber velocity); and (ii) the passive fiber force developed by muscles as they are stretched beyond optimal fiber length [53].

The overestimation of fiber force-length-velocity effects can exaggerate the loss of active force-generating capacity of major muscles during dynamic activities and necessitate scaling model muscle forces by a high specific tension. For example, during late stance in running when the demand on the gastrocnemius is greatest, gastrocnemius fibers shorten from approximately 75% of optimal fiber length to 55% of optimal fiber length at a peak shortening velocity of 0.25 optimal fiber lengths per second [49]. These effects together permit the gastrocnemius, one of the largest contributors to forward propulsion in running [48], to produce at most 30% of its optimal force with maximal activation. For our model to produce forces sufficient to generate muscle-driven simulations of running, we scaled our muscle PCSAs with a specific tension of 60 N/cm², which is high but within the range of previously reported values [44], [45]. Solving the muscle force distribution problem using the same optimization objective as CMC but ignoring any muscle-tendon dynamics reduces the peak gastrocnemius activation in running from 79% to 27%. This suggests the need for a high specific tension can be partially attributed to simplifications in the modeling of muscle force generation. Other model simplifications (e.g., rigid body assumption [54] and joint kinematic models [55]) or muscle co-contraction resulting from the CMC algorithm [56] may also contribute to the need for a high specific tension, but likely play a smaller role.

The overestimation of passive fiber force developed by muscles stretched beyond optimal fiber length can also lead to compensatory muscle activity in simulations. While the passive component of our muscle-generated moments in gait are similar to previously published data (e.g., [57]), we observe high passive knee extension moments generated by the long quadriceps fibers during peak knee flexion in the swing phase of walking and running (Supplemental Fig. 4). We see compensatory hamstring activity during swing in simulations not observed in experimental EMG signals because the hamstrings activate to produce an active knee flexion moment that counteracts the passive knee extension moment generated by the quadriceps.

One way to correct for these effects (i.e., underestimation of active force and overestimation of passive force) is to better model the 3-dimensional structure of muscle and distribution of muscle fibers (e.g., using a finite-element model [12], or using a much larger number of muscle-tendon units to model a muscle [58]), but this increases the computational cost of a simulation.

Because we used a high specific tension, our model generates larger maximum isometric joint moments than those measured during maximum voluntary contraction (MVC) trials [59]–[67]. It should be noted, however, that humans generate higher muscle activations [68] and produce larger joint moments during dynamic activities like high-speed running than during MVC trials. For example, our subject produced a maximum ankle plantarflexion torque of 267 N-m while running (Fig. 4b), which is 53% higher than the maximum of 175 N-m reported by Sale et al. [67] during MVC trials and less than the 336 N-m mean peak ankle plantarflexion moment reported by Bezodis et al. [69] in similarly sized elite athletes running at roughly 10 m/s. In the past, the moment generating capacity of musculoskeletal models has been calibrated by comparison with MVC trials (e.g., [15], [70]); in the future, we suggest that the moment-generating capacity of musculoskeletal models be calibrated to the moments generated during dynamic maximum effort activities, like high speed running or maximum height jumping.

Our model geometry and simulations were tested within the defined range of motion for the joints: 40° plantarflexion to 30° dorsiflexion, 0° to 120° knee flexion, 30° hip extension to 120° hip flexion, 50° hip abduction to 30° hip adduction, 40° hip external rotation to 40° hip internal hip rotation. We did not test the validity of our moment arms or our muscle force-generating capacity outside these angle ranges. Sprinting or cycling may result in higher knee flexion angles, and the model geometry and fiber properties should be tested before being used in those applications. Furthermore, even within this range of motion, it is possible that some muscle-tendon paths may exhibit unexpected behavior (e.g., cross through bony geometry), especially at the hip joint. This is a general limitation of modeling complex, three-dimensional structures with one-dimensional muscle-tendon paths. We encourage users to test muscle-tendon paths within the kinematic space in which the model will be used in a particular study.

V. CONCLUSION

Muscle-driven simulations are valuable tools for understanding the role of muscles in healthy and pathological gait, and can produce useful insights for assistive device design [71] and surgical intervention analysis [10]. Testing a model in the context of its intended use is an important step in any study using musculoskeletal modeling. We have presented some testing and validation of the model, including successful simulations of walking and running, but comprehensive testing and sensitivity analysis by the community is needed [47]. The model is freely available for use in OpenSim for others to use and test. We encourage others to make refinements and share them with the community.

Appendix

Motion capture and EMG data for walking was collected as the subject walked over-ground at a self-selected walking speed. Marker positions of 41 retro-reflective markers were measured at 100 Hz using an eight-camera optical motion capture system (Motion Analysis Crop., Santa Rosa, CA, USA). We collected a static calibration trial and functional joint movement trials to calculate hip joint centers [72]; these were used in the OpenSim Scale Tool to create a scaled version of the generic model that matched subject anthropometry. Ground reaction forces and moments were measured at 2000 Hz using over-ground force plates (Bertec Corp., Columbus, OH, USA). Ground reaction forces were low pass filtered at 6 Hz with a 2^nd order critically damped filter [73]. EMG signals were recorded using wireless surface electrodes (Tringo, Delsys Inc., Boston, MA, USA) placed on 10 muscles: soleus, gastrocnemius lateralis, gastrocnemius medialis, tibialis anterior, biceps femoris long head, vastus medialis, vastus lateralis, rectus femoris, gluteus maximus, and gluteus medius. The raw EMG signal from each muscle was band-passed filtered between 50–500Hz, rectified, low-pass filtered at 7.5 Hz with a 4^th order Butterworth filter, and finally low-pass filtered at 15 Hz with a 4^th order critically damped filter [73]. Because the subject was walking over-ground, we did not have complete kinetic (ground reaction force) data for a full gait cycle from a right heel strike (RHS) to subsequent RHS. To simulate a full gait cycle, we used data from 25% of the first right gait cycle to 25% of the subsequent right gait cycle. We then realigned the simulation results to capture a full gait cycle starting at RHS. The Stanford University Institutional Review Board approved the experimental protocol and the subject gave informed consent to participate in the study.

Motion capture and EMG data for running was used from a previously published study by Hamner et al. [48]. The authors in this study collected motion capture data using 54 retro-reflective markers and collected ground reaction force data using a Bertec Corporation split-belt instrumented treadmill.