Grid Cell Responses in 1D Environments Assessed as Slices through a 2D Lattice

SUMMARY

Grid cells, defined by their striking periodic spatial responses in open 2D arenas, appear to respond differently on 1D tracks: the multiple response fields are not periodically arranged, peak amplitudes vary across fields, and the mean spacing between fields is larger than in 2D environments. We ask whether such 1D responses are consistent with the system’s 2D dynamics. Combining analytical and numerical methods, we show that the 1D responses of grid cells with stable 1D fields are consistent with a linear slice through a 2D triangular lattice. Further, the 1D responses of comodular cells are well described by parallel slices, and the offsets in the starting points of the 1D slices can predict the measured 2D relative spatial phase between the cells. From these results, we conclude that the 2D dynamics of these cells is preserved in 1D, suggesting a common computation during both types of navigation behavior.

In Brief

Grid cells exhibit striking periodic spatial responses in open fields, but their responses on 1D paths are non-periodic. Yoon et al. show that 1D responses are slices through a periodic lattice and provide evidence of a common computation in both cases.

INTRODUCTION

Over the course of navigation in real environments, animals traverse open fields and run along paths defined by natural trails and boundaries such as underground burrow systems, streams, and rock faces. If grid cells demarcate spatial coordinates in 2D open fields, as seems possible, it is important to learn whether they perform a similar function during navigation along stereotyped 1D paths.

Arena experiments in the lab mimic open field exploration, while 1D track experiments approximate runs along predefined paths. In arenas, individual grid cells of the mammalian entorhinal cortex exhibit spatially periodic tuning, in the form of increased firing at every vertex of a virtual triangular lattice overlaid on the floor of the enclosure (Hafting et al., 2005) (Figures 1A and 1B). As a population, cells from the same module (Stensola et al., 2012) exhibit essentially the same spatial firing patterns or spatial tuning curves, up to a global phase offset (Figure 1C). The offset in phase between cell pairs, also known as the relative phase, remains stable across time and environmental conditions (Fyhn et al., 2007; Yoon et al., 2013).

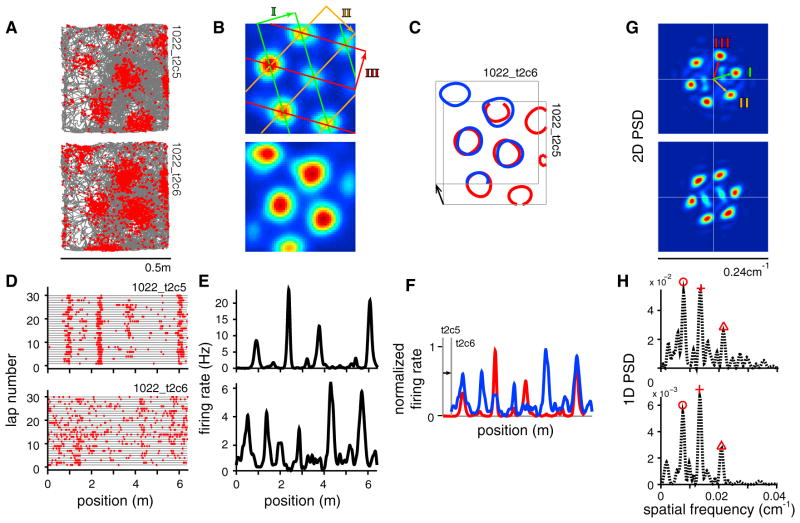
Figure 1. The Fourier Power Spectral Density Reveals Underlying Periodic Structure in 2D and 1D.

(A) Trajectory (gray) of an animal foraging in a square enclosure, with spike locations (red dots) for two comodular cells (top and bottom, respectively).

(B) Smoothed firing rate maps, with a decomposition of the triangular grid response into three 2D sinusoidal waves (three colors and the labels I, II, and III).

(C) Contour plot of the firing fields of cell 1 (red) overlaid on the fields of cell 2 (blue), after a rigid shift. Black arrow, relative phase.

(D and E) The same cell pair on a linear virtual track (D, trajectory and spikes; E, firing rates).

(F) Spatial tuning of cell 1 (red) overlaid on that of cell 2 (blue; after rigid shift).

(G) Fourier power spectral densities (PSDs) of the 2D responses. The peaks represent the three constituent planar sinusoidal waves (I–III as in B; see also Figure S1).

(H) PSDs of the 1D responses, with the highest three peaks marked by red symbols; note the similarity of the 1D PSDs.

Many grid cells also exhibit spatially specific responses when recorded on 1D tracks of various shapes (Derdikman et al., 2009; Yoganarasimha et al., 2011; Newman et al., 2014; Gupta et al., 2014; Lipton et al., 2007). On linear 1D tracks, the spatial tuning curves of grid cells consist of multiple firing fields with non-periodic spacing and a large range of field heights (Figures 1D and 1E). The average spacing between fields is typically several times larger than in the same cell’s 2D response, and the spatial tuning of different cells is not related by simple shifts (Figure 1F). At present, there is little understanding of the detailed structure of these 1D responses. In particular, it is unclear whether there is a relationship between the characteristic properties of 2D grid cell recordings—their hexagonal patterning, their similar tuning up to rigid shifts within a module—and the observed 1D responses. One wonders whether the cells continue to perform a similar underlying computation when the animals navigate in environments of dimension different than two (F.M. Kempf et al., 2012, Front. Comput. Neurosci., abstract; Yoganarasimha et al., 2011; Newman et al., 2014; Mathis et al., 2015; Hayman et al., 2011; Gupta et al., 2014; G. Ginosar et al., 2015, Soc. Neurosci., abstract). Here we seek to address this question by elucidating whether, and to what extent, the 1D responses of grid cells reflect the underlying structure of their population responses in 2D.

In this paper, we consider the hypothesis that grid cell responses on 1D linear tracks are generated by slicing linearly through an underlying 2D triangular lattice (Domnisoru et al., 2013; F.M. Kempf et al., 2012, Front. Comput. Neurosci., abstract). We begin by considering what this slice hypothesis predicts for the Fourier transform and power spectrum of an ideal 1D spatial response. We present analytical methods and numerical refinements for extracting the best slice and grid parameters from the Fourier transform of a general 1D spatial tuning curve. We then apply these methods to their 1D responses of grid cells with stable 1D and 2D fields and show that the resulting slices yield excellent fits to their 1D spatial responses. We further show that the 1D responses of comodular cell pairs (defined as simultaneously recorded cells deemed to be from the same module [Stensola et al., 2012], based on the similarity of their 2D responses) have similar power spectra despite the apparent dissimilarity in their spatial tuning and are therefore well fit by parallel slices through a triangular lattice. We next predict the 2D phase offsets between comodular cells based on their 1D responses and show that these closely match the recorded 2D phase offsets. Finally, while the 1D response can gradually reshape over the course of an experiment, this remapping can be interpreted as a drift in the slice parameters and slice drift appears to occur in tandem across cells from the same putative network, preserving cell-cell relationships. We conclude that the data strongly support the hypothesis that 1D responses can be generated by slicing through a regular underlying 2D triangular lattice. Finally, because the group relationships of comodular cells recorded on 1D tracks remained the same as the group relationships measured in 2D, we conclude that the network remains in the same dynamical regime during navigation in 1D and 2D environments.

RESULTS

The Fourier Power Spectral Density Reveals Underlying Periodic Structure

We find that the 1D tuning curves of simultaneously recorded grid cells (Domnisoru et al., 2013) exhibit a shared “fingerprint” that hints of an underlying periodic structure. To see this, first consider the 2D responses of these cells, in which this fingerprint—the power spectral density (PSD) of the spatial response—is easy to understand and interpret (Figure 1G). The periodic 2D response of a grid cell generates six discrete peaks forming a hexagon around the origin in the PSD (these peaks form part of a triangular lattice in spatial frequency space that is “dual” to the spatial triangular lattice, see Figure S1). Spatial phase information is lost in the PSD, thus co-modular cells, which exhibit the same spatial tuning parameters up to phase (Fyhn et al., 2007; Yoon et al., 2013), exhibit the same spectra (Figure 1G). Intriguingly, the PSDs of the 1D spatial responses of co-modular grid cells (determined to be co-modular on the basis of their 2D responses) also closely resemble each other (Figure 1H). We next explore this phenomenon and its possible implications for how 1D grid cell responses are generated.

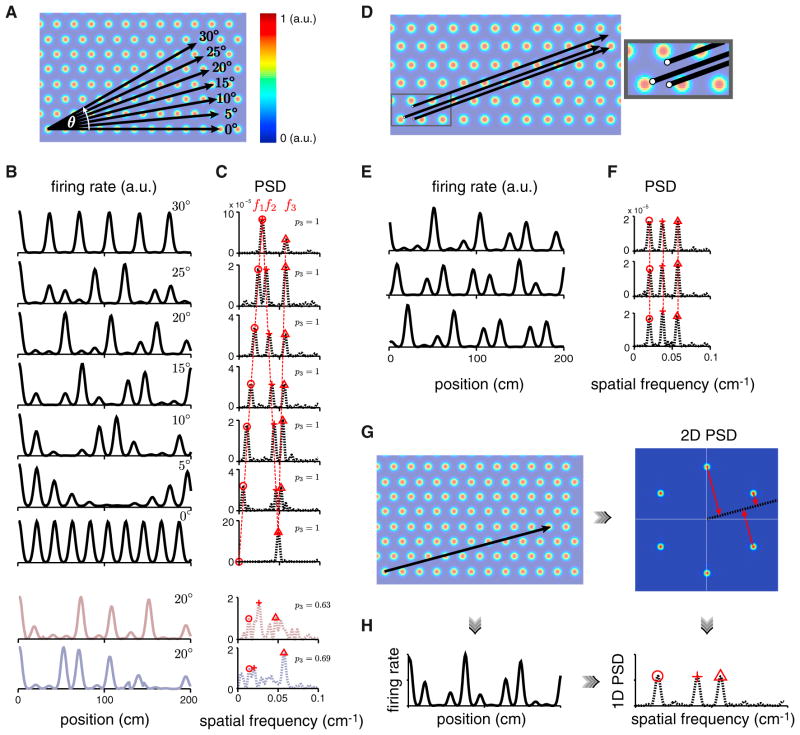
The PSD of a generic linear slice through an idealized 2D triangular lattice has exactly three dominant peaks of equal height (Figures 2A–2C). As the angle of the slice varies, the locations of these three peaks shift (Figures 2A–2C). These peak locations are independent of the origin (or spatial phase) of the linear slice for generic slices, thus parallel 1D lattice slices have nearly identical PSDs (Figures 2D–2F). Non-generic slices are those parallel to one of the primary lattice vectors (Figure 2B) or at the half-lattice angle of 30°; in these cases the PSD is predicted to exhibit only one or two major peaks, respectively (Figure 2C). Even in generic slices for which one would expect to see three PSD peaks, if the sampled slice segment is short (only 1–3 times the underlying period), finite length effects broaden the PSD peaks, potentially causing one or more of them to merge. In summary, linear slices through a 2D lattice should exhibit three or fewer major peaks in their PSDs, with most of the mass of the PSD residing in those peaks. We will quantify the fraction of the mass of a PSD that is concentrated in three or fewer peaks by a three peakiness score (p₃) (Experimental Procedures).

Figure 2. Features of the PSD for Linear Slices through a 2D Triangular Lattice.

(A and B) Different-angle slices (A, black) result in different 1D responses (B, black).

(C) The PSDs (dashed black) also differ, yet have commonalities: they are characterized by three main peaks (red symbols) (at θ = 0° and 30°, a pair of PSD peaks coalesce, for a total of two peaks). Two statistically matched random control tuning curves (reddish- and bluish-gray, B) with corresponding PSDs (C), for the 20° slice.

(D–F) Parallel linear slices with different starting points or phases (D) (inset: magnification of the starting points) exhibit different 1D responses (E) but identical PSDs (F).

(G) Linear slice through a 2D triangular lattice (left), the 2D PSD of the lattice with a slice through the origin at the same angle (black; right).

(H) Left: 1D response from the linear slice in (G, left). Right: PSD of the 1D response at left. This 1D PSD equals the projection (red arrows in G, right) of the 2D PSD onto the same linear slice (also see Figure S1).

Our frequency-space characterization provides a concise description of the particular heights, spacing, and ordering of firing fields in a lattice slice in terms of the constrained peak structure of the corresponding PSD. To illustrate the specific nature of these constraints, we compare lattice slices to two sets of statistically matched random controls: given a 1D response, we generate corresponding gap-randomized controls by randomly shuffling the order of the firing fields then assigning the fields new positions chosen randomly from a uniform distribution (Figure S2 and Experimental Procedures). We generate gap-shuffled controls by simply shuffling the gaps between fields (Figure S2 and Experimental Procedures). Examples of these two random controls and their PSDs can be seen in Figure 2B (reddish-gray and bluish-gray, respectively), with PSDs in Figure 2C. The tuning curves for both random controls can look very similar to slices, but generically their PSDs differ: they have variable numbers of PSD peaks and usually more than three (Figures 2C and S2; three-peakiness score p₃ = 0.63 for the gap-randomized and p₃ = 0.69 for the gap-shuffled controls, compared to p₃ = 1 for ideal lattice slices, Experimental Procedures). We will return to these controls to statistically test our conclusions throughout this work.

It is useful to note that the 1D PSD of a 1D slice through a 2D lattice is equivalent to a 1D projection of the 2D PSD of the 2D lattice onto a “slice line” taken at the same angle starting at the origin in frequency space (Figures 2G–2H and Experimental Procedures). This equivalence allows us to predict the PSD of a 1D slice at any angle by simply projecting the three closest-to-the-origin spectral peaks from the 2D PSD onto a line running through the origin at the desired angle (Figures 2G and 2H). Conversely, given the locations of two major PSD peaks from the 1D response, we can solve analytically for the angle of the slice (Figure S1 and Experimental Procedures). The slice angle obtained in this way is exact if the 1D slice extends to infinity.

Using similar techniques (Figure S1 and Experimental Procedures), we can infer the scale factor of a cell, which is the ratio of the inferred 2D lattice period underlying the 1D response to the recorded period in 2D enclosures. From the Fourier transform of the 1D response, we can furthermore deduce the starting point or 2D spatial phase of the slice (Figure 2D; Experimental Procedures). By taking the difference of the inferred 2D spatial phases for a pair of cells, we can predict their 2D relative phase. We can alternatively, and more directly, estimate the 2D relative phase for a cell pair through the Fourier transform of the cross-correlation of their 1D spatial responses (Experimental Procedures).

These four parameters, slice angle (θ), scale factor (α), and 2D phase (φ⃗), fully describe a linear slice that starts at the given phase within a unit cell in the canonical 2D grid and continues out to infinity at the given angle (like the schematic slices in Figure 2D). Once the scale factor has been determined, the length of the slice through the 2D grid is fully determined by the scale factor and the length of the track run by the animal.

Finite size effects induce uncertainty in the inferred slice parameters (Figures S3C–S3G), as does noise in the neural response (Figures S3H–S3L). In the presence of such uncertainty, supplementing the analytical estimates with numerical optimization can result in improved parameter estimates (Figures S3M–S3R and Experimental Procedures).

In summary, the mathematical duality between the spatial response domain and the Fourier spectral domain for slices through regular lattices allows us to determine, up to estimation uncertainty, whether the 1D spatial responses are consistent with an underlying 2D lattice and, if so, to infer the parameters of the slice relative to the lattice.

The Distribution of Gaps in a 1D Response Reveals Underlying Periodic Structure

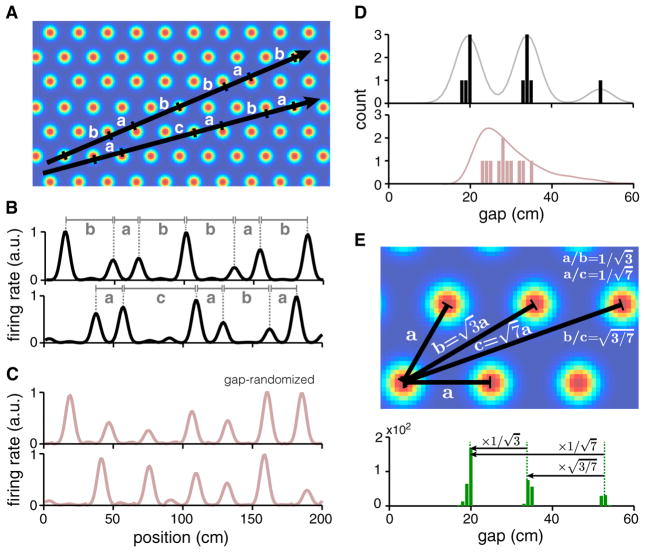
A second signature of lattice slices, complementary to the 1D PSD, is the distribution of the gaps between 1D firing fields. A linear slice through a 2D lattice cuts across several bumps, with a distinct sequence of gaps (spacing between bumps) depending on its angle (Figures 3A and 3B). The smallest gap occurs when the slice hits adjacent bumps in the 2D lattice; a larger gap occurs when the slice misses a 2D bump and hits the next-nearest bump, and so on. Thus, the set of possible gaps is restricted to the set of distances between a reference bump and all other bumps in the 2D lattice that can be reached by a straight line that does not cross any other bumps. (The bumps have some width, thus the slice can hit a bump “off-center.” Therefore, the actual measured distance between two bumps in a 1D slice will typically be slightly but systematically smaller than the analytically described gaps.) By contrast, the gaps in gap-randomized controls (Figure 3C) can be of arbitrary size; thus, the distribution of gaps is unimodal and smooth (Figure 3D, bottom), rather than multimodal with a few discrete peaks as predicted for slices (Figure 3D, top). (The gap-shuffled controls preserve the full gap distribution of the original data by construction.)

Figure 3. Distribution of Gaps in 1D Slices through a 2D Triangular Lattice.

(A and B) Linear slices (black) at different angles and spatial phases generate different sequences of inter-field distances or gaps (gaps delineated by horizontal lines with vertical ticks in A; equal gaps are marked by the same letter; only peaks with amplitudes above a threshold are considered in B).

(C) Matched random 1D responses (gap-randomized controls) for the responses in (B).

(D) Histogram of gaps for the slices in (B) (black) and the random controls in (C) (reddish-gray). Line: smoothed version of the histogram (gray) and a full gap distribution generated from 100 gap-randomized controls for each of the two slices in (A) and (B) (reddish-gray).

(E) Top: numeric values of the gaps are determined by the specific geometry of the 2D lattice (up to overall scaling by the lattice period), independent of slice angle and phase; gap ratios depend only on lattice geometry. Bottom: a histogram of gaps generated from pooling across 100 linear slices of the same length as in (B), with random angles and phases.

Up to an overall scale factor to account for the lattice period, the gaps in lattice slices are entirely specified by the geometry of the 2D lattice. Thus, the ratios between gaps will exhibit relationships characteristic of an underlying triangular lattice: $1/\sqrt{7}\approx 0.38;1/\sqrt{3}\approx 0.58;\sqrt{3/7}\approx 0.65$; and so on (Figure 3E), and will be the same across modules with different spatial tuning periods and orientations, and different slice angles, so long as the underlying grid geometry is the same.

The distribution of gaps collected by pooling across 100 slices of an idealized triangular lattice with varying angle and starting position (phase) is shown in Figure 3E (bottom; the lattice period is a = 20 cm). The gaps (Figure 3D, top) from the two slices of Figures 3A and 3B are simply samples from this gap distribution (Figure 3E), and a particular slice may sample only a subset of possible gaps from the lattice. To take an extreme example, a slice along one of the primary lattice vectors samples only the nearest-neighbor bump distances in the 2D lattice, thus the gap distribution consists of a single peak (Figure S4).

It is possible to extract gaps on a trial-by-trial basis from neural recordings and then pool the gap samples across trials. Even if the 1D firing field locations drift from trial to trial (Figure S4), the gaps in every trial will be drawn from the same small set governed by the 2D lattice geometry, assuming that all trials are linear (but possibly changing) slices through that lattice. Moreover, because gap ratios are independent of slice angle, grid period, and scale factor, it should be possible to pool gap ratios across modules. By contrast, PSDs depend on slice angle and cannot be similarly pooled. On the other hand, the gap analysis focuses on adjacent bumps, while the PSD contains information about relationships between all bumps, not just adjacent ones. Thus, gap analysis and PSDs provide complementary measures of a slice.

Grid Cell Responses on 1D Tracks Are Well Fit by Linear Slices through a Triangular Lattice

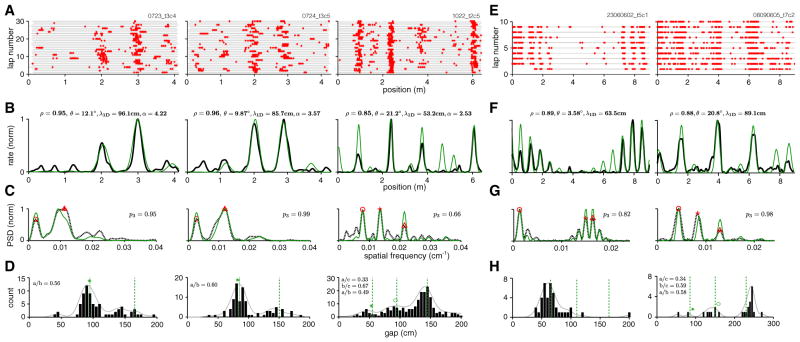
We applied the methods described above to the 1D virtual track responses of 25 neurons identified as well-isolated grid cells with stable 1D spatial responses from the experimental dataset (see Experimental Procedures). Examples of the 1D response are shown in Figure 4A (three cells from different experiments), with 30-trial firing rate averages in Figure 4B (black curves). The PSDs of the spatial tuning curves in Figure 4B (Figure 4C, black) exhibit three or fewer major peaks, with most of the PSD mass concentrated in these few peaks (p₃ = 0.95, 0.99, and 0.66, respectively), as expected for lattice slices.

Figure 4. 1D Spatial Tuning Curves Can Be Well Fit by Lattice Slices.

(A) Spike rasters of three cells on a linear virtual track (right: same cell as in Figure 1D, top; center, left: cells recorded from different animals on different dates [Domnisoru et al., 2013]).

(B–D) Smoothed trial-averaged rate (B, black), PSD (C, dashed black), and gap histogram (D, black bars; smoothed histogram indicated by solid gray line) for the same three cells. Gaps are computed from adjacent bursts per trial and pooled across trials. Red symbols in (C) indicate the PSD peaks used to generate the best-fit slice. The rate prediction from the slice is shown in (B, green), with fit quality (Pearson’s correlation coefficient between lattice slice prediction and neural tuning curve) and slice parameters noted at top. PSD of the slice (C, green). Green dashed line in (D): predicted peak locations for the gap distribution obtained by multiplying the ideal predicted gap ratios by the scale factor of the best-fit slice; green symbols: ideal gap ratios multiplied by the position of the actual rightmost peak in the gap distribution.

(E–H) The same as (A)–(D), for two cells from animals running on a long linear track (Brun et al., 2008).

Our Fourier-based slice analysis method (Experimental Procedures) returned slice parameters (inset values, Figure 4B) that produced the best fit (in the sense of Pearson’s correlation coefficient) to the measured 1D spatial tuning curve. For each neuron, the slice angle was confined (without loss of generality) to the interval [0°, 30°], the phase could fall anywhere within a predefined unit cell of the lattice, and the scale factor could take values between 1 and 8 (Experimental Procedures).

The 1D tuning curves predicted by the slice hypothesis (Figure 4B, green) provide excellent matches to the recorded 1D spatial tuning curves (average correlation value of 0.92 and average p value of 0.04 for these three cells). The best-slice PSDs, shown superimposed on the data PSDs (Figure 4C, green), are also very close to the data PSDs. The gap histogram obtained from pooling gaps between adjacent bursts across individual trials (Figure 4D; see Experimental Procedures) displays a small set of distinct peaks. Moreover, most gaps and gap ratios (inset numerical values, Figure 4D) are within 5% of the values predicted for a regular triangular lattice (Figure 3E). By contrast, for the gap-randomized controls, each gap ratio will be independently drawn from a smooth, broad unimodal distribution (Figure 3D, bottom).

We augment our virtual track recordings with data obtained by Brun and colleagues on a long linear 1D track (Brun et al., 2008; http://www.ntnu.edu/kavli/research/grid-cell-data). The track is punctuated by discrete visuospatial landmarks like doorways, and the spatial response statistics of a majority of cells change visibly roughly halfway into the track and persist to the track’s end. For this reason, we analyze responses on the first half of the linear track (Figure 4E).

Applying the same analysis as in Figures 4B–4D to two cells from Brun et al. (2008) yields striking agreement between their track responses and the linear slice hypothesis (Figure 4F, green; average slice correlation value of 0.89, and average p value of 5 × 10⁻⁴ for the cell pair; the p values, computed from the correlation coefficient and the number of above-threshold firing fields, are even more significant than for our virtual track data because of the greater track length and consequently larger number of fields).

Statistical Analysis of Slice Hypothesis across Linear Track Data

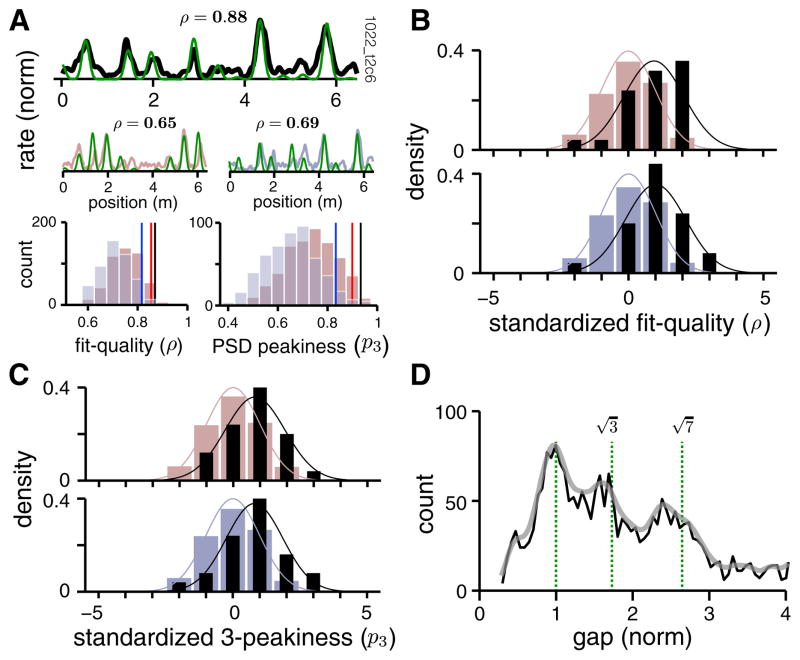
As we have seen, the 1D responses of some grid cells are extremely well fit by the slice hypothesis: the average fit correlation coefficients of the cells in Figure 4A are high (〈ρ〉 = 0.92), the PSD mass is largely concentrated in three or fewer peaks (〈p₃〉 = 0.87), and the gap distribution has peaks close to the predicted values for slices of triangular lattices.

To what extent is it generally true that the 1D responses of grid cells in our dataset can be well described by slices? To answer this question, we focus closely on dataset-wide statistical analyses of cells recorded on the virtual track, because there we possess 2D recordings, from which we can extract ground-truth information on whether the cells are grid cells, on their 2D periods, and their co-modularity.

We generate the best-fit slice for each cell in the dataset (e.g., Figure 5A, top row, green; fit in black), together with large samples of corresponding gap-randomized and gap-shuffled controls (one sample of each shown in Figure 5A, middle row, reddish-gray and bluish-gray, respectively) and their best-fit slices (green). We can now compare metrics of the cell against the metrics of its two random controls (Figure 5A, bottom row). Typically, the correlation coefficients between the data and a slice are well to the right of those for the two matched control distributions; the same is true for the three-peakiness scores (Figure 5A, bottom row). We standardize the correlation score and PSD three-peakiness score of each cell (by subtracting the mean and dividing by the SD of the distributions of these scores from matched controls, illustrated in Figure 5A, bottom row), so that the standardized scores reflect how many SDs away the data lies from the control distributions. Standardization allows us to collapse together results across all grid cells in the dataset. The resulting quality-of-fit distributions for the dataset are significantly to the right of both matched controls (Figure 5B; testing to see whether the data are drawn from a distribution with zero mean, as in the control distributions, yields p = 3 × 10⁻⁴; t = 4.28; df = 24 and 2 × 10⁻⁴; t = 4.49; df = 24, respectively, on a one-sample t test), as are the three-peakiness scores (Figure 5C; p = 1 × 10⁻³; t = 3.65; df = 24 and 8 × 10⁻⁴; t = 3.85; df = 24 respectively; one-sample t test). (The mean fit quality for non-standardized data is 0.786 and that for the controls is 0.729 [gap-randomized] and 0.730 [gap-shuffled]. The raw fit-quality distribution is also significantly to the right of both matched controls: p = 0.0039 for non-normalized fit quality of real data versus gap-randomized controls and p = 0.0046 versus gap-shuffled controls; one-sample t test.) Note that the controls are extremely conservative (not overly random), in that they preserve many higher-order statistics of the data; this is particularly true for the gap-shuffled controls on non-generic slice angles where the distribution of gaps is very narrow and thus the random controls closely resemble the original slice (see Figure S2); nevertheless, the slice hypothesis fits the data significantly better than it does the controls.

Figure 5. Statistical Validation of Slice Fits Compared to Chance.

In all spatial tuning plots, the slice prediction is given in green.

(A) Top: Cell firing rate (black). Middle: A gap-randomized (reddish-gray) and a gap-shuffled (bluish-gray) control sample of cell response above. Slice fit quality (ρ) noted above. Bottom left: quality of slice fit histogram for 500 gap-randomized control samples (reddish-gray), and for 500 gap-shuffled controls (bluish-gray). Red/blue vertical lines: 95% percentile level of the random/shuffle control fit score. Black line: slice fit value of the response at top. Bottom right: distribution of three-peakiness scores for the PSDs of random/shuffle controls (reddish- and bluish-gray histograms, respectively), compared to the score for the response at top (black vertical line). Red/blue vertical lines: 95% percentile level of the random/shuffle distributions.

(B) Top: distribution of fit-quality scores for all cells in the dataset (black), with each cell’s score standardized by the distribution for its matched gap-randomized controls (as in A); the randomized control distribution (reddish-gray) has zero mean and unit variance because of the standardization procedure. Bottom: the same as above, but the standardizing distributions are from gap-shuffled controls (bluish-gray); data in black as above. The difference in the means of the data and control histograms is highly significant (p values noted in text, one-sample t test).

(C) Same as (B), but the distribution quantifies the statistics of three-peakiness scores in the data PSDs compared to PSDs from both types of control.

(D) Aggregate gap distribution (black), pooled across all cells in the dataset, after the gaps in each cell’s response are normalized by the lattice period underlying the 1D response. Gray, smoothed version.

Finally, the combined histogram of gaps, normalized by the inferred period (scale factor times 2D grid period) for each cell and pooled across all cells in the dataset, yields a distribution with a small set of distinct peaks (Figure 5D). The peaks in the gap distribution lie very close to the predicted values for an underlying regular triangular lattice (see Figure 3E). The slight, systematic leftward shift in all the peaks relative to the prediction can be attributed to the fact that each firing field has a finite width, and so the measured spacing from field to field will be reduced by an amount proportional to the field width.

Lacking access to 2D data for cells recorded on 1D real tracks (Brun et al., 2008), we instead identified putative grid cells from their 1D responses alone using a modified version of criteria used in Domnisoru et al. (2013) (Experimental Procedures). An analysis of all passing cells (40 out of 97 cells, or 41%) yields excellent agreement with the preceding results: the 1D responses of putative grid cells are well fit by the slice hypothesis (average fit-quality of 0.72, close to that for virtual track data, Figure 6) and are better fit than are the statistically matched controls (Figures S5A–S5C); their gap distribution is consistent with slicing through a regular triangular lattice (Figure S5D); and slice parameters tend to cluster into groups, indicating the presence of comodular cells (Figure S5E).

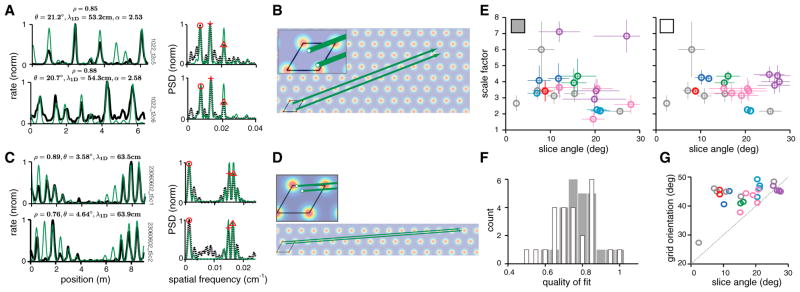
Figure 6. Comodular Cells Are Best Fit by Nearly Parallel Slices and Similar Scale Factors.

(A) Left: firing rates of a pair of comodular cells, recorded on a virtual track (black). Best-predicted firing rates from lattice slices, found separately for each cell (green). The slice angle θ, and scale factor α, are noted above. Right: PSD of the 1D response (black dashed) with the PSD of the predicted slice (green).

(B) The best-fit linear slices for the cell pair from (A), with the starting points of the slices magnified in the inset. The starting point of a slice defines the 2D spatial phase of the cell (with respect to the rhomboidal unit cell, black), as inferred from the 1D response.

(C and D) Same as (A) and (B), for a pair of putatively comodular cells recorded on a long linear track, data from Brun et al. (2008).

(E) Left: the best-fit slice parameters for all cells in the dataset, obtained for each cell individually. Cells classified as comodular are plotted in a common color and single (non-comodular) cells are colored in gray (12 groups, 25 cells). Crosshair: error bars, ± 1 SD (n = 100 bootstrap samples). Right: same as left, but the PSD peaks selected for the slice fits are chosen consistently for comodular cells (see Experimental Procedures). Slice parameters for comodular cells now cluster together.

(F) Histogram of fit-quality between measured 1D tuning and predicted slice fit, when fits are generated individually (as in E, left; gray histograms) and when they are obtained by imposing consistency across comodular cells (as in E, right; white histograms). Fit quality does not suffer in a way that is statistically significant when consistency is imposed (p values noted in text, paired t test).

(G) Grid orientation measured in 2D versus slice angle estimated from 1D responses of the same cells (same color codes as in E).

Cell-Cell Relationships: Pairs from the Same Module Are Well Fit by Parallel Slices

We next examine relationships in the 1D slice parameters of comodular cells. If the 1D responses of different cells from a module were generated by the coherent displacement (driven by animal motion) of an underlying 2D population pattern, we would expect their 1D tuning to correspond to parallel slices of the 2D population pattern with the same scale factor. As a consequence, their PSDs should also look similar (prediction in Figures 2D–2F). Indeed, the scale factors, slice angles, and PSDs of comodular cells can be very similar, as we can see for an example cell pair on the linear virtual track and another pair on a long linear track (Figures 6A–6D).

However, the best-fit slice parameters obtained individually for each cell in the dataset are not always very similar for comodular cells (Figure 6E, left). One reason for this discrepancy is the existence of an effective degeneracy in the solution for the best-fit slice of each cell, which arises because of data limitations. Because of response variability and the finite length of the track, there are sometimes two or three discrete good slice solutions for a cell (see Experimental Procedures). These solutions are not near each other in parameter space because the relationship between fit quality and slice parameters is non-convex—they tend to take the form of well-separated, similarly deep local optima in the solution landscape and correspond to a large step in slice angle and scale factor. Thus, there is an inherent uncertainty in estimating the best slice parameters, and cell responses actually generated from parallel slices may not yield similar parameters with our procedure if we choose different minima for each.

The question instead should be whether there exist parallel slice solutions for comodular cells that yield good fits. We refit cells using the same procedure, but after enforcing the constraint that a roughly consistent set of PSD peaks are selected across comodular cells to predict their slice parameters (Experimental Procedures and Figure S3). Not too surprisingly, the slice parameters for comodular cells are now well clustered (Figure 6E, right). Imposing constraints on a fit will generally worsen the quality of the fit, especially if the constraints are inconsistent with structure in the data. The mean quality-of-fit does decline when cell fits are fit consistently (Figure 6F, white histogram) than when individually optimized (Figure 6F, gray), but notably the drop is slight (the difference in means is not significant, p = 0.2; t = 1.30; df = 48; paired t test) and imposing consistency still produces slice fits that are much better than for the controls (p = 2 × 10⁻³; t = 3.72; df = 24 for average fit quality after imposing consistency versus matched gap-randomized controls and p = 1 × 10⁻³; t = 3.68; df = 24 versus gap-shuffled controls; one-sample t test). We conclude that the constraint is consistent with the underlying structure of the data: that is, comodular cells in 2D are well described by parallel grid slices through a common 2D grid. We will see below that a parallel slice description leads to accurate prediction of the 2D spatial tuning phase relationships between comodular cells on the basis of 1D track data.

Finally, the angles selected by the grid networks for generating 1D responses are well distributed relative to the underlying 2D lattice: there is no clustering around 0° or 30°, which would indicate roughly periodic 1D responses, and there is no other preferred slice angle for generating 1D responses (Figure 6G).

Cell-Cell Relationships: 2D Relative Phases Are Predicted by 1D Slice Fits

If the 2D response of grid cells is generated by rigidly translating an underlying population activity pattern according to animal movements, then the phase offset in the 2D spatial tuning of a pair of comodular cells (called their relative phase) should equal their phase offset with respect to the underlying population pattern. If the 1D response is generated in the same way, the same should be true, and the 2D phase offset between a pair of predicted 1D slices should equal the measured 2D relative phase. A stringent test of the slice hypothesis, then, is to ask whether a predicted 2D relative phase from fitting slices to the 1D tuning curves of grid cells on tracks agrees with the 2D relative phase measured in box environments.

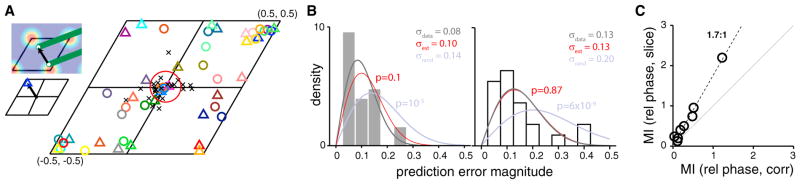
The predicted 2D relative phase from the slice analysis is the offset in the starting points of the two slices within a unit cell of the unit lattice (Figure 7A, inset; there is 12-fold degeneracy in the relative phase prediction intrinsic to the symmetry of the lattice, see Figure S6 and Experimental Procedures for how we obtain a unique solution and also apply similar procedures to generate fair controls). We generate 2D relative phase predictions from 1D track responses for all pairs of comodular cells (Experimental Procedures) and test them against the measured 2D relative phases obtained from 2D trajectories in boxes. We find very good agreement between the 2D relative phases predicted from the 1D slice analysis (under the consistency-imposed slice fits described above) and those measured in 2D (Figure 7B, left), up to the estimation uncertainty inherent to the prediction due to spiking variability (estimated by bootstrap sampling of spikes, Experimental Procedures): in other words, the predicted and measured 2D phases are not distinguishably different from one another (n = 25 total comodular pairs from the 3 comodular pairs, 2 comodular quadruples, and 1 comodular quintuple in the dataset).

Figure 7. Relationship of Relative Phase Predicted from 1D and Measured in 2D.

(A) Top inset: the offset in a pair of parallel slices, within a rhomboidal unit cell of the unit lattice, equals the predicted relative phase from the 1D slice analysis. Bottom inset: schematic of how the relative phase above is plotted as a symbol (blue triangle) within the unit cell. Main: relative phases predicted from 1D responses (colored triangles) and actual relative phases measured from 2D recordings (circles in matched colors). Shown are the best predictions from across 12 degenerate solutions per pair. Black “x” symbols: differences between the predicted and measured 2D relative phase values. Red circle: relative phase estimation uncertainty (expected error) obtained by bootstrap (Experimental Procedures).

(B) Left: Histogram of relative phase prediction error magnitudes for best pairwise slice fits (gray bars; Rayleigh distribution fit in black), inherent estimation uncertainty from bootstrap (Rayleigh distribution fit in red), and random prediction error magnitudes (Rayleigh fit in bluish-gray). Right: the same as left, but best fits constrained so that all pairs in a K-tuple of comodular cells were constrained a common solution domain from across the 12 possibilities (rather than a free choice per pair; Experimental Procedures and Figure S6). Left and right: p values that the slice prediction errors are from the same distribution as the estimation uncertainty (red), or the same distribution as random (bluish-gray).

(C) How much information (Shannon’s mutual information, abbreviated MI) the correlation coefficients between cell pairs’ 1D responses convey about their measured 2D relative phases (abscissa) versus the mutual information between measured 2D relative phases and the predicted values from slice analysis on the 1D responses (ordinate). The latter exceeds the former by a factor of 1.7.

The errors in predicted relative phase (predictions generated pairwise) are significantly smaller than if guessed at random (p = 10⁻⁵; χ = 4.62; df = 24 from a chi-square test; the errors in the random predictions are themselves not large because each random pair is also given the benefit of a 12-fold degeneracy in solutions, as noted above; see Figure S6 and Experimental Procedures). If the relative phase predictions for cells from a comodular K-tuple are generated by selecting a common solution domain out of the 12-fold degenerate domains across all (K choose 2) pairs (rather than allowing a different choice for each pair as above), the 2D relative phase prediction error barely increases. Importantly, the random predictions become worse because they are subject to the same constraint (see Figure S6 and Experimental Procedures), leading to a greater separation between the predicted relative phase errors and errors from random guessing (p = 6 × 10⁻⁹; χ = 2.26; df = 24 from a chi-square test).

The 1D slice analysis prediction of the phase offset between cells yields substantially more information about the 2D relative phase vector from 1D track data than can be obtained from the Pearson cross-correlation of the 1D responses (Figure 7C). The latter is a scalar measure that provides no information about 2D relative phase beyond its magnitude (On the other hand, if the goal is to predict only the magnitude of 2D relative phase from the 1D data, Pearson cross-correlation and slice analysis yield comparable results; Figure S6.)

Grid Expansion from 2D Real Environments to 1D Real and Virtual Environments

The spatial tuning period of grid cells expands ≈4-fold in going from 2D real open fields to 1D virtual tracks (Figure 6E). What factors contribute to this expansion? One factor is the move from real to virtual environments: the same cell, recorded first in 2D real open fields then in 2D virtual reality, undergoes a ≈2.5-fold expansion in its spatial tuning period (Aronov and Tank, 2014). Nevertheless, nearly 40% of the expansion in our results remains unexplained by this factor (note however that the virtual reality setup and mammalian species used in Aronov and Tank [2014] [rats] differed from those in the present experiments [mice], so under the same environmental transition, the expansion factor might differ in our setup). We hypothesize that even within real environments, the move from 2D to 1D induces a change in period. This possibility was already noted in Brun et al. (2008), but the 1D period estimation methods used, it was also observed, might overestimate the 1D period because of the propensity of grid cells to entirely “miss” fields, or fail to fire in a field. Thus, it remained unclear whether there is an expansion in going from 2D to 1D.

The slice hypothesis is not sensitive to missed fields: the PSD method and especially the gap distribution reveal the underlying grid period even with missed fields: missed fields will reduce the height of the gap distribution at the peak corresponding to the smallest gap, but so long as that peak is present, it provides a good estimate of period. Even without missed fields, inferring 2D parameters from 1D tracks using the slice hypothesis provides more information than gained by 1D correlation analyses (Figure S7A). Using the slice method, therefore, it is possible to more closely answer the question of 2D to 1D grid expansion. We estimate the 2D spatial tuning periods of cells based on their dorsoventral locations (Brun et al., 2008) (Figure S7B) and compare these to the inferred 2D lattice periods underlying 1D track runs (Figure S7C). The 2D lattice period during navigation on real 1D tracks expands by a factor of ≈2 (Figure S7D) relative to that for familiar 2D enclosures. With this finding, it is worth noting that the largest inferred underlying 2D grid period for the putative grid cells (those passing our gridness criteria) recorded on 1D tracks in Brun et al. (2008) is less than 1 m. Therefore the largest verified 2D grid period for grid cells anywhere along the DV axis is ≈1.3 m, as reported in Stensola et al. (2012).

To return to the question of expansion from 2D real environments to 1D virtual tracks, we conclude that both the 1D and virtual reality aspects of the environment independently contribute to the overall expansion (scale factor) we observe.

Shifting 1D Responses May Be Consistent with Drifting Slices

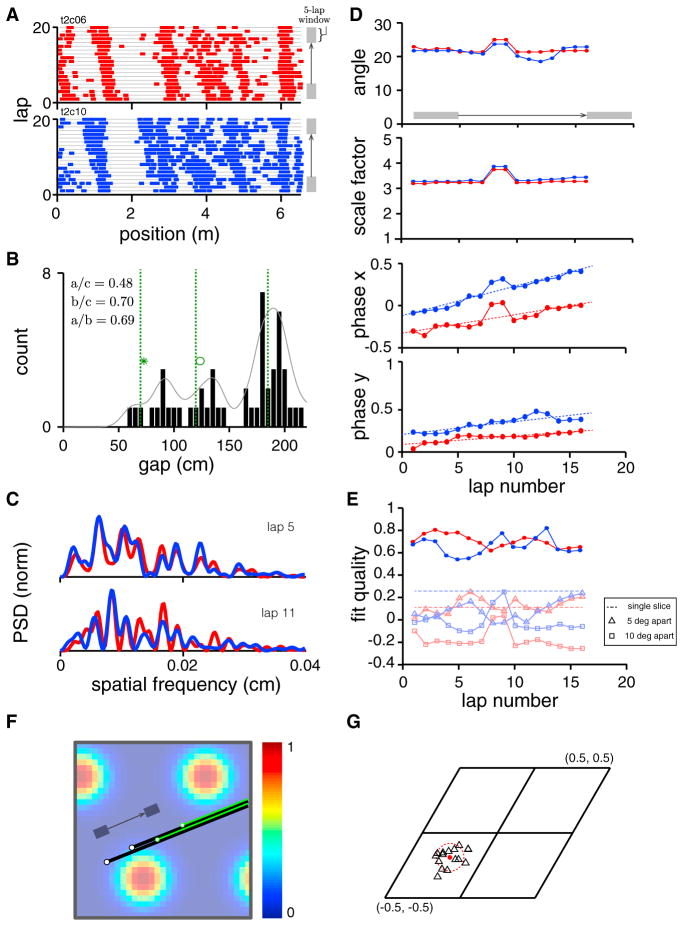
Occasionally, we observed systematic shifts across trials in the 1D spatial tuning of cells (Figure 8A). Averaging over trials in such cases yields a spatial tuning curve with broader firing bumps, extra bumps, and lower signal-to-noise ratio; indeed, this pair of cells was responsible for some of the worse relative phase predictions and slice fits in previous figures.

Figure 8. Relationship of Relative Phase Predicted from 1D and Measured in 2D.

(A) Spike rasters for a pair of comodular cells show field drift, field splitting, and field merging across trials.

(B) The gap histogram for the data in (A), pooled across both cells, contains three peaks. The three peaks are at the predicted values (green dashed lines; obtained from 200 randomly oriented and shifted slices through a triangular lattice), given the estimated slice period.

(C) Top: the PSDs of the two cells computed from a 5-trial block centered on lap 5. Bottom: the same, centered on lap 11. The across-cell PSDs for a given block of trials are more similar than the PSD of a given cell across trials.

(D) Slice parameter (slice angle, scale factor, and the two components of phase, respectively) evolution (estimated from 5-trial averages sliding one trial at a time). The best-fit slices have constant angle and scale factor, but the phase of the slice is drifting across trials. Since phase is a periodic variable, it is equivalent to plot it between [−0.5, 0.5] or equivalently, [0,1], as done in some plots here.

(E) The quality of fit for the slice hypothesis (red, blue cells) over the drifting trials. Light red/light blue: the quality of fit between the data and slices with angle 5 (triangle) or 10 (square) degrees from the best-fit slice. Dashed line: the quality of fit between a single data response by concatenating all individual trials and the best-fit linear slice.

(F) Depiction, on the 2D lattice, of the inferred drifting best-fit slices from (D). Black, green: best-fit slices from near the beginning and end of the block of trials, respectively.

(G) The estimated relative phase between cells across inferred slices over time (different black triangles) remains close to relative phase estimate obtained from 2D environments (red dot). The scatter in different time-resolved relative phase estimates is about equal to the inherent estimation uncertainty due to finite spike sampling (estimated by bootstrap), red dashed circle.

The single trial responses during drift, however, do not appear to differ statistically from trials in which there is little drift. While it is difficult in general to perform statistical tests and the PSD analysis to extract slice parameters on rapidly drifting responses, on cells with moderate drift (Figure 8A), we may average small sets of adjacent trials and perform a more temporally resolved analysis. Our aim is to determine whether the drifting response can still be described by the slice hypothesis locally in time, so that each small group of trials is well described as a slice, but more separated trials are described by slices with different parameters.

We first generate a gap histogram (Figure 8B), which we know should be invariant to changes in slice angle and phase, if the response is generated from a 2D lattice with invariant scale. Notice that the distribution has a few distinct peaks. The locations of the peaks (Figure 8B, green), scaled by the location of the third peak, closely coincide with the predicted ratios for a triangular lattice.

The PSDs of the two cells over small block of trials (5-trial averages; Figure 8C) are quite similar, even though the PSD of each cell changes considerably over trials. This indicates that the slice parameters of both cells are similar to each other locally in time, even as the slice parameters change over time. These PSDs tend to have more than three large peaks, an indication that, if the slice hypothesis is true, the slice has already drifted over the course of the 5-trial average (the PSD over a sum of drifting slices is the sum of the PSDs of those different slices).

Finally, we directly fit slices to 5-trial moving window average firing rates (with a 1-trial shift between windows) of the two cells (Figure 8D). We find that the best-fit slice solutions have a constant angle and scale-factor across trials (Figure 8D, rows 1–2). The main change across trials is in the 2D phases of the slices (Figure 8D, rows 3–4). Note that the quality of fit does not vary substantially over trials despite the drift in firing patterns (Figure 8E, dark red and blue) and remains reasonably high despite the smaller SNR in the 5-trial averaged firing rates (the SNR in the spatial responses from 30-trial averages over non-drifting responses is substantially higher), suggesting that the slice hypothesis is equally valid locally in time in this set of drifting trials as it is for cells that exhibit little drift. By way of control, slices 5° and 10° away from the optimal slice produce much poorer fit quality (Figure 8E, pale curves).

For visualization, we plot the moving slices directly on the underlying 2D lattice (Figure 8F). Note that the drift in slice parameters is largely coherent for both cells (the slices drift roughly in parallel with each other, Figure 8D). The predicted relative phase from the 1D responses, generated in this time-resolved way from slice fits, remains unchanged across trials up to the uncertainty inherent in the noisy spiking responses (Figure 8G, different black triangles for the moving 5-trial window averages; red dashed circle is the bootstrap estimation uncertainty from spikes), and all these estimates are close to the recorded relative phase from 2D environments (Figure 8G, red dot).

While the drift in slice parameters across trials for this pair is mostly confined to the slice phase, in other experiments the drift can be in angle or some combination of slice parameters (data not shown).

DISCUSSION

Summary of Findings

We characterized the responses of grid cells on 1D tracks by studying the Fourier transform of linear slices through a triangular lattice. In previous work, it was noted that spatially periodic 2D responses are characterized by their Fourier components, in particular a triangular bump pattern should have exactly three components of maximal amplitude, corresponding to plane waves at 60° angles (Krupic et al., 2012). We established that despite their aperiodic appearance, 1D slices through idealized 2D lattices have a 1D Fourier power spectrum which inherits this peaked structure, and their responses exhibit a characteristic gap distribution with gap ratios determined by the 2D lattice geometry. We further showed how to use the amplitude and phase of the Fourier components to analytically infer the parameters of the slice. The analysis of lattice slices via their Fourier properties arises in crystallography, as well as in the characterization of quasicrystals (Suck et al., 2013).

We applied these theoretical methods to 1D grid cell responses and demonstrated that their (non-periodic) spatial firing rates are well fit by slices through triangular lattices. Moreover, cells from the same module are well fit by parallel slices through the same triangular lattice and it is possible to predict the 2D relative phase of cells from slice fits of their 1D responses. These population-level findings have important implications for network mechanism during 1D navigation, as discussed below.

Together, our results provide the first direct evidence that the central defining property of grid cells—namely, a 2D lattice representation of space—is maintained on linear tracks, despite the specific 1D nature of the environment and running behavior. At the same time, the expansion of the spatial tuning period in 1D relative to 2D suggests that certain quantitative properties of the representation of space are environmentally dependent, similar to the stretching of grid cell tuning in rescaled 2D environments (Barry et al., 2007). (Since the scale factor can vary independently for the two spatial dimensions [Barry et al., 2007], one should not expect to predict the period of spatial tuning in the orthogonal direction on the basis of strict 1D experiments without further modeling of how environments determine scale.)

The PSD and gap characterization of 1D grid cells, and the ability to generate accurate slice fits, should allow for more accurate classification of entorhinal cells recorded in 1D experiments (Brun et al., 2008; Heys et al., 2014; Domnisoru et al., 2013; Hafting et al., 2008). In principle, responses on longer tracks provide more constraints on the parameters of a slice fit. At the same time, there may be a greater tendency toward remapping partway along longer tracks, complicating the slice analysis. It is possible that 1D tracks free of spatial landmarks could inhibit landmark-anchored remapping and thus permit parameter estimation and relatively rapid inference of cell-cell relationships like comodularity and 2D relative phase from short experiments involving <40 s of data (10 runs down an 8 m track at a running speed of 0.2 m/s).

Finally, our methods could be applied to characterize the structural characteristics of grid cell responses in three spatial dimensions (Hayman et al., 2011; G. Ginosar et al., 2014, Soc. Neurosci., abstract), by constructing 1D and 2D slices of the acquired 3D data then analyzing the resulting projections.

Mechanism: Implications for Recurrent Dynamics during 1D Navigation

Comodular grid cells with stable 1D responses retain the same cell-cell relationships as when they are recorded in 2D arenas: their relative spatial phase remains invariant across 1D and 2D despite the large change in the period of spatial tuning across all comodular cells. Thus, the instantaneous states of the neural population with stable 1D tuning are drawn from the same set of population states observed in 2D, even if the forward mapping from these instantaneous states to external spatial coordinates is stretched. In this sense, since the internal population states remain invariant across 2D and 1D navigation, we say that the system remains in fundamentally the same low-dimensional computational and dynamical regime that characterizes its 2D response (Yoon et al., 2013).

This finding aligns with a previous result and prediction (Burak and Fiete, 2009; Yoon et al., 2013) that non-unity scale factors in the spatial tuning of grid cells across environments are not due to a change in the population-level states and thus are expected to be caused by some change in the feed forward inputs to the system, including for instance visually derived spatial cues, border cells, or the effective strength of velocity inputs to the network. The effective strength of velocity input might be reduced in 1D environments either because of a reduced perception of speed or because of a down-regulation in the gain of the speed input to the system even for an unchanged speed percept.

Potential Exceptions to the Slice Hypothesis and Future Work

Single linear lattice slices cannot always describe the 1D responses of grid cells. As already noted, 1D response characteristics can sometimes change partway down a long track with landmarks (from our analysis of Brun et al., 2008): a frequently firing cell may become more sparse, the field spacings may go from more periodic to less, and so on. Similarly, in 1D tracks with hairpin turns and alternating linear segments, the grid cell responses across all segments run in one direction are nearly identical to each other (Derdikman et al., 2009). These kinds of effects might be explained within an expanded version of the slice hypothesis, according to which 1D track responses are piecewise compositions of different linear slice segments. Thus, a response remapping partway down a track would correspond to a change in the slice from that point onward. This is a topic for future empirical and theoretical tests.

A closely related observation is that grid cells can exhibit different spatial tuning in the outbound and return directions on a physical track (Brun et al., 2008), even when the spatial tuning in one run direction is consistent with the slice hypothesis (our analysis). An interesting question for future study is whether spatial tuning on the return journey is also well fit by a slice and, if so, how the two slices are related. If the slice hypothesis is a good description also of the return response, a shift in the grid cell slice parameters for different run directions or run contexts (Lipton et al., 2007) could explain the direction and context specificity of place cell tuning in similar experiments.

Spatial tuning curves obtained by averaging together blocks of trials tend to not be well fit by slices if there is a rapid drift in the spatial responses across trials. In such cases, it is possible that the single trial responses are generated by slicing a lattice, but the slice parameters shift rapidly across trials. Data limitations arising from the length and duration of an individual trial in the existing data means that further experiments and analysis will be required to properly resolve this question as well as to better characterize what drives the shift in slice parameters.

The ability of animals to solve starburst mazes (Olton and Samuelson, 1976) suggests that they can learn the geometrical relationships between 1D paths. To understand how animals use 2D coordinate frames when navigating along 1D trails, it will be interesting to study the selection of slice angles: supplied with two linear paths in a 2D arena starting from the same point but diverging at an angular separation angle δ, are the slice angles chosen by the animal along those paths consistent with δ and, if so, how does the slice angle difference converge to δ with experience?

A broader question related to 1D navigation is whether responses along nonlinear 1D tracks are based on corresponding nonlinear lattice slices. If grid cell activity is generated by a velocity input that shifts an underlying 2D population pattern around in tandem with animal motion (Burak and Fiete, 2009), we would expect the answer to be affirmative.

Indeed, according to existing analyses, grid cell responses on circular 1D tracks (Yoganarasimha et al., 2011; Newman et al., 2014) may be consistent with a circular slice through a 2D lattice, while remapped responses on the annular track may result from shifts in the phase of the circular slice (Neunuebel et al., 2013). Analytical Fourier parameter extraction is much more complex for circular tracks, but there are ways in which it can be generalized (K.Y. and E.L. Newman, unpublished data).

Finally, a suggestive but still anecdotal (because of the small sample size: n = 1 cell pair) observation from our analysis is that grid cells from the same animal but different grid modules can exhibit different 2D-to-1D scale factors and slice angles (Figure S8). If this result proves to be statistically significant when augmented by additional data and similar analyses, it would suggest that different grid cell modules (Stensola et al., 2012) are functionally independent.

EXPERIMENTAL PROCEDURES

Cell Selection

We analyzed units from Domnisoru et al. (2013) (real 2D arena and virtual linear track data for each cell) and Brun et al. (2008) (linear real tracks).

From Domnisoru et al. (2013), our starting sample consisted of 126 units (137 recorded; 126 passed the sorting criterion that no more than 0.25% of spikes in each unit were emitted with interspike intervals [ISIs] shorter than 1 ms [Domnisoru et al., 2013]). We applied the intersection of three criteria on spatial tuning (2D gridness, 1D stability across trials, 1D entropy to exclude cells with high background noise), then excluded duplicates based on similarity of tuning. The detailed methods are given in Supplemental Experimental Procedures. The final sample was 25 grid units (6 singles, 3 pairs, 2 quadruples, and 1 quintuple).

We identify putative grid cell responses in Brun et al. (2008) by adapting criteria from Domnisoru et al. (2013). Adjustments simplify the criteria slightly and account for the large difference in track length (Supplemental Experimental Procedures). We used only the first half of each run. Responses on opposite direction runs were treated as two independent spatial responses. We are left with 51 putative grid cells with 65 passing spatial responses, out of 97 recorded cells with 194 spatial responses. We applied slice fits to all passing responses with ≥3 fields on the half-track. (This condition is necessary for generating meaningful slice fits: two 1D fields are mathematically not enough of a constraint to specify a slice by any method. Excluded cells tend to be from the ventral end of the dorsolateral MEC.) This leaves 40 putative grid cells and 53 responses.

Trial Selection

Different cells were recorded for different numbers of trials and some cells showed substantial drift in their spatial tuning across trials. We adopted a trial-selection procedure to equalize the number of trials used per cell and obtain the most stable block of 30 trials for each cell, for Figures 1, 2, 3, 4, 5, 6, 7, and 8 (Supplemental Experimental Procedures). For comodular cells, we selected a common 30-trial block with the largest stability score averaged across cells.

Fourier Spectral Analysis for Inferring 2D Lattice Slice Parameters from a 1D Response: Theory

Consider a semi-infinite line in a 2D coordinate space, with line origin at c = (c₁, c₂) and angle θ relative to the x axis. Consider an equilateral triangular lattice firing rate profile with period λ and smooth bumps at the vertices, and consider how the rates will vary along the semi-infinite line. The Fourier transform of the firing rates along the semi-infinite line will have spectral peaks at the frequencies f₁(λ,θ) < f₂(λ,θ) < f₃(λ,θ), which satisfy:

$$f_1=\frac{1}{\lambda }\left(cos\theta -\frac{1}{\sqrt{3}}\text{sin}\theta \right),f_2=\frac{2sin\theta }{\lambda \sqrt{3}},$$

and f₃ = f₁ + f₂.

In addition, the phases of the Fourier transform, δ₁(c) and δ₂(c) at f₁ and f₂, relate to the offset (c₁, c₂) via

$${\delta }_1=\frac{1}{\lambda }\left(C_1+\frac{C_2}{\sqrt{3}}\right),{\delta }_2=\frac{4\pi C_2}{\lambda \sqrt{3}}.$$

The derivation is contained in Supplemental Experimental Procedures. From these relationships, it is straightforward to extract the slice parameters from the measured Fourier peak frequencies and their phases.

Fourier Spectral Analysis for Inferring 2D Lattice Slice Parameters from a 1D Response: Practice

For each cell recorded in 1D (or for each random control response), we compute the PSD of its response, identify the two highest PSD peaks, then apply the theory described above, equating the found peak locations with two of the analytically defined values of f₁, f₂, or f₃ from above (see Supplemental Experimental Procedures). We further numerically refined the analytical solution to optimize the fit (quantified by Pearson’s correlation coefficient, ρ) between the recorded 1D rate response and predicted rate from the slice theory (see Supplemental Experimental Procedures).

Imposing Consistency in the Slice Fits across Comodular Grid Cells

For a K-tuple of comodular cells, we imposed consistency in slice fits across the K cells as follows: first, compute the product of all K PSDs obtained from the spatial tuning curves of each cell. Select the spatial frequencies corresponding to the two highest peaks from the PSD product; call these q₁ and q₂. For each cell, we now pick the two peaks from their individual PSDs that lie closest to q₁, q₂. The rest of the procedure for finding the best slice for each cell is as described in Supplemental Experimental Procedures. This procedure corresponds to selecting the same local minimum in the solution landscape across all cells in the K-tuple.

When reporting relative phases between a pair of cells (or doing a K-tuple analysis for K comodular cells), the 2D period was set from 2D recordings to the average value along the two lattice vectors, and averaged across cells in the pair (or the K-tuple).

Measure for “Three-Peakiness” in PSD

To quantify to what extent a given PSD has a three-peaked structure as predicted for lattice slices (Figures 2C and 2F), we define a “three-peakiness score” (p₃): it is computed as the sum of the areas under the three largest peaks in the PSD, divided by the total area of the PSD, followed by a normalization step. The normalization step involves dividing the result by the same score for an ideal linear slice with parameters equal to the best-fit slice parameters—it leads to a score of p₃ = 1 for all ideal lattice slices. In general, the resulting three-peakiness score is high for a PSD with three or fewer major peaks and little area under the rest of the PSD curve.

Gap Analysis

We collected gap statistics for each cell as follows: per trial, we identified bursts of spikes (described next). A gap is the distance between the centers of mass of consecutive bursts. Per cell, we compile the combined histogram of all such gaps within and across all 30 selected trials (see above for Trial Selection).

To define a burst, we slide a small time-window of width w across a spike train. The window contains a burst if at least n_spk spikes occur in that window. We used n_spk = 3 and w = 0.1 s. When tabulating gaps, we ignored inter-burst distances smaller than the 2D grid period (counting these as gaps is the same as artifactually segmenting one burst into two, when a burst within one field contains a chance pause).

For any 1D responses that contain no spiking records (this includes random control responses, which are rates), we define gaps based on rates. We compute the inter-peak distances between all adjacent firing rate peaks of height >25% of the maximum firing rate (Figure 3C).

Generating Matched Random Control Data

For each spatial tuning curve, we generate two kinds of matched control: gap-randomized and gap-shuffled. For both types of control, we first define intervals in the spatial tuning curve as in-field (a threshold criterion for a firing field) and non-field (all regions not in-field); see Supplemental Experimental Procedures. To obtain a gap-randomized control sample, we randomize the ordering of in-field intervals and select gaps between in-field intervals at random (see Supplemental Experimental Procedures). This defines one gap-randomized sample for a given response. This procedure was used in Figure 5A (reddish-gray) to generate 100 random samples based on the response in Figure 5A (top). For Figures 5B and 5C (reddish-gray), we generated 100 random samples for each cell in our virtual track dataset; this pooled dataset was our full random sample.

To generate gap-shuffled controls, we tabulate the gaps between in-field intervals in the recorded response. We randomize the ordering of in-field intervals insert between fields a randomized ordering of the tabulated gaps (see Supplemental Experimental Procedures). The result of this procedure is to preserve the set of all gaps from the data in each random control sample. As described above, in Figure 5A (bluish-gray) we generated 100 random samples based on the response in Figure 5A (top). For Figures 5B and 5C (bluish-gray), we generated 100 random samples for each cell in our virtual track dataset.

Highlights.

• Grid cell responses on 1D tracks are well fit by slices through triangular lattices

• Cells from the same module are well fit by parallel slices through the same lattice

• Co-modular cells exhibit the same cell-cell relationships in 1D and 2D

• Thus, grid cells remain in a similar dynamical regime during 1D and 2D navigation