Abstract
Many important industrial separation processes based on adsorption operate close to saturation. In this regime, the underlying adsorption processes are mostly driven by entropic forces. At equilibrium, the entropy of adsorption is closely related to the enthalpy of adsorption. Thus, studying the behavior of the enthalpy of adsorption as a function of loading is fundamental to understanding separation processes. Unfortunately, close to saturation, the enthalpy of adsorption is hard to measure experimentally and hard to compute in simulations. In simulations, the enthalpy of adsorption is usually obtained from energy/particle fluctuations in the grand-canonical ensemble, but this methodology is hampered by vanishing insertions/deletions at high loading. To investigate the fundamental behavior of the enthalpy and entropy of adsorption at high loading, we develop a simplistic model of adsorption in a channel and show that at saturation the enthalpy of adsorption diverges to large positive values due to repulsive intermolecular interactions. However, there are many systems that can avoid repulsive intermolecular interactions and hence do not show this drastic increase in enthalpy of adsorption close to saturation. We find that the conventional grand-canonical Monte Carlo method is incapable of determining the enthalpy of adsorption from energy/particle fluctuations at high loading. Here, we show that by using the continuous fractional component Monte Carlo, the enthalpy of adsorption close to saturation conditions can be reliably obtained from the energy/particle fluctuations in the grand-canonical ensemble. The best method to study properties at saturation is the NVT energy (local-) slope methodology.
Introduction
In the chemical and petrochemical industries, pressure swing adsorption (PSA) and temperature swing adsorption (TSA) are very important separation technologies based on adsorption in nanoporous materials.1−6 In both of these processes, separation is mostly based on the difference in the adsorption equilibrium (determined by macroscopic state variables such as T and P) of the mixture components7 and is achieved by passing the mixture through a large column packed with adsorbent material. Ideally, PSA and TSA are isothermal processes, but in reality, they operate under almost adiabatic conditions.7 Adsorption is generally an exothermic process, and heat is produced as the mixture components are adsorbed. The differential enthalpy of adsorption Δh̅, or heat of adsorption Q = −Δh̅ (note that the heat of adsorption is path-dependent, whereas −Δh̅ is not; therefore, a better name is “differential enthalpy of desorption”8,9), is a quantitative measure of the strength of the adsorbates binding to the adsorbent, and it is therefore related to the temperature changes of the adsorbent during adsorption (an exothermic process) and desorption (an endothermic process). Many industrial separation processes based on adsorption work close to saturation conditions to operate cost efficiently.10−13 Because separations are driven by entropic forces in this regime,14−17 it is important to understand and study how entropy behaves in these systems to design a new generation of nanoporous materials for separations.18,19 Separations based on adsorption rely on the equilibrium loading differences of the mixture components. At equilibrium, the variation in the enthalpy of adsorption with loading is directly related to changes in the entropy of the system as adsorption occurs.20 Therefore, besides being an important parameter in the design and operation of equipment, the enthalpy of adsorption provides thermodynamic insight into the separation process. However, little is known about the behavior of the enthalpy of adsorption close to saturation conditions. Most of the experimental and molecular simulation studies have focused on the low loading regime,21−24 with the main reason for this being the complexity associated with studying systems close to saturation conditions.
The enthalpy of adsorption close to saturation is hard to measure experimentally and hard to compute in simulations. In experiments, the pressure range that can be explored for gas adsorption (before the adsorbate turns into a liquid) is limited by the vapor pressure, and in molecular simulations, the computation is restricted by currently available simulation methodologies. The most common ways to compute the enthalpy of adsorption in simulations are (1) the isosteric method,25,26 (2) the NVT method,27 (3) energy/particle fluctuations in the grand-canonical ensemble,28−30 (4) using the derivative of the energy as a function of loading in the grand-canonical ensemble,31 and (5) the energy slope method in the NVT ensemble.20 However, close to saturation, using any method in the grand-canonical ensemble (in particular the energy/particle fluctuations) does not work efficiently with conventional Monte Carlo methods.
In this work, we first develop a toy model to understand the limiting behavior of the enthalpy of adsorption at saturation. The theoretical model shows that repulsive interparticle interactions drive the enthalpy of adsorption to higher and higher (less favorable) values. Then, we show and explain why the conventional Monte Carlo method fails close to saturation conditions, and we present the Continuous Fractional Component Monte Carlo (CFCMC) algorithm as an alternative to obtain more reliable results for the enthalpy of adsorption close to saturation. Since this methodology is relatively new, before presenting our results we derive the framework for the computation of the enthalpy of adsorption in the CFCMC ensemble and the transformation of the measured values to the usual Boltzmann ensemble. We proceed by comparing both methods, conventional Monte Carlo and CFCMC, to the energy (local-) method of Poursaeidesfahani et al.32 and to a semianalytic approach using the n-site Langmuir–Freundlich isotherm model. Before presenting our conclusions, we discuss the findings in terms of the general behavior in zeolites and MOFs, with particular emphasis on the behavior at saturation and around inflections in isotherms because, as we will show, these are strongly related.
Analyzing the Limiting Behavior of the Enthalpy/Entropy of Adsorption Close to Saturation
Enthalpy of Adsorption from Isotherms
The differential enthalpy of adsorption Δh̅ is defined as the change in the total enthalpy of the system (in the gas phase; host and guest molecules) as a molecule is transferred from the gas phase to the adsorbed phase at constant temperature9
| 1 |
where H is the total enthalpy, Hsys refers to the enthalpy of the system (host and guest molecules), Hg refers to the enthalpy of a reference gas phase, n is the amount adsorbed or “loading”, V is the volume of the system, and T is the absolute temperature. Assuming that the gas phase behaves as an ideal gas and the adsorbent is rigid, it can be shown that the first term on the right-hand side of eq 1 is the isosteric enthalpy of adsorption Δhads and the second term is equal to RT, where R is the gas constant (8.314464919 J mol–1 K–1).32 Thus, the differential enthalpy of adsorption can be obtained from Δh̅ = Δhads + RT, where the isosteric enthalpy of adsorption is given by30,33
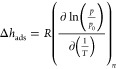 |
2 |
with p being the total pressure of the system and p0 being the pressure of the perfect gas reference state (commonly, p0 = 1 bar). Equation 2 is known as the Clausius–Clapeyron equation, and it relates the enthalpy of adsorption to the place where an adsorbed phase in equilibrium with a gas phase lies (at a given loading) on the pressure–temperature plane. It is often used experimentally to compute the enthalpy of adsorption from isotherm measurements at different temperatures, but of course it is also of use in simulations. The accuracy of the computed enthalpy of adsorption strongly depends on the quality of the measured/simulated isotherms.
The differential enthalpy of adsorption can also be obtained from9
 |
3 |
On the basis of eq 3, Myers and Monson developed expressions for
the excess enthalpy of adsorption Δh̅e and showed that this quantity diverges at the location
extremum,9 since in that case 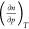 is exactly zero at that
point. In this
work, we are concerned with the absolute enthalpies
of adsorption, and for these, the term
is exactly zero at that
point. In this
work, we are concerned with the absolute enthalpies
of adsorption, and for these, the term 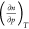 approaches zero but never reaches it. The
Langmuir model and the more general Langmuir–Freundlich isotherm
description do not shed any light on the behavior of the enthalpy
of adsorption at high loading. The Langmuir–Freundlich isotherm
is given by
approaches zero but never reaches it. The
Langmuir model and the more general Langmuir–Freundlich isotherm
description do not shed any light on the behavior of the enthalpy
of adsorption at high loading. The Langmuir–Freundlich isotherm
is given by
| 4 |
where n is the equilibrium loading, m is the saturation loading, p is the pressure, and c and ν are the Langmuir–Freundlich parameters for a given adsorbent–adsorbate and temperature. The temperature dependence of the parameters is often suggested to be9,34
| 5 |
The temperature-independent factor (1/p0) exp(A/R) is the entropic factor,9 and ν is the heterogeneity factor that describes the degree of heterogeneity. For ν = 1, the Langmuir–Freundlich isotherm reduces to the Langmuir isotherm. In this case, if we assume that m is temperature-independent, we can use eqs 2 and 4 to show that the differential enthalpy of adsorption is constant and given by parameter B. However, for most cases, the temperature dependence of the parameters is unclear a priori and no general behavior of the enthalpy of adsorption can be concluded. In fact, we will later show that parameters m and ν in the dual-site Langmuir model can increase but also decrease with temperature.
In adsorption in nanoporous materials, Langmuir isotherms are extremely rare (if not nonexistent), and the enthalpy of adsorption is never constant over the full loading domain. Assumptions of the Langmuir model include the following:35 (1) the adsorbent is structurally homogeneous, (2) monolayer adsorption, (2) the adsorbent has a finite capacity m, (3) all sites are identical and energetically equivalent, and (4) there is no interaction between molecules adsorbed on neighboring sites. The Langmuir–Freundlich model introduces heterogeneity into the model. Using the same procedure (eqs 2 and 4) for the Langmuir–Freundlich isotherm, including the temperature dependence of parameters m and ν (eq 4), we find that the enthalpy of adsorption in general diverges near saturation, but the limiting behavior at high loading/pressure depends on the specific temperature form of the parameters. Many models are proposed to alleviate these restrictions. For example, the BET model allows for multilayer adsorption. The Temkin–Pyzhev isotherm considers adsorbate interactions; it has the same functional form as eq 4, but coefficients c are assumed to be coverage-dependent, c = c(T,n). Because the parameters in these models are often fitting parameters, albeit with a physical underpinning, these models are of limited use to explore the high pressure/loading regime. We will therefore explore the high loading regime with explicit Monte Carlo simulations.
A sharp increase in the enthalpy of adsorption has experimentally already been reported for the adsorption of n-heptane on silicalite.36 These authors found an almost constant enthalpy of adsorption up to the point where the first saturation plateau was reached. At this point, the enthalpy of adsorption increased sharply. However, to the best of our knowledge, the behavior of the enthalpy of adsorption near saturation has never been explored theoretically or reported in simulations. To show that in general the enthalpy of adsorption sharply increases at saturation, we will develop a theoretical toy model. The analysis will reveal that this effect is driven by repulsive interparticle interactions and hence is very common. An analysis in zeolites will show that this behavior is common in channel-type structures with pores much larger than the dimension of the adsorbates. Other systems, like cage-type structures with strong local confinement, are able to avoid strongly repulsive interactions and hence do not show such a sharp increase in enthalpy of adsorption at saturation.
Theoretical Model
To study the enthalpy of adsorption close to saturation, we first develop a simple and generic model for the adsorption of Weeks–Chandler–Andersen-like (WCA) particles in a rigid cylindrical pore. In this simple model, the interaction of the particles with the pore is assumed to be attractive and set to −1 (in dimensionless units), and the interaction between particles is assumed to be repulsive and modeled with a WCA-like potential.37 We define the total potential for N molecules in the pore as
| 6 |
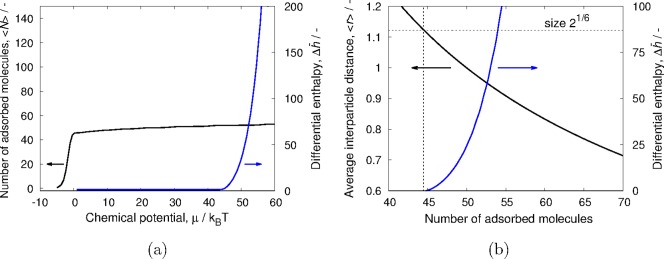
where r is taken as the distance between adsorbed particles and is given by the pore length divided by the number of adsorbed particles. For each number of molecules, only one system state is considered in which the interparticle distance r is the same for all neighboring particles. This corresponds to saturation conditions and low temperatures. For each chemical potential, the total loading is determined from the weighted average of all possible configurations. The enthalpy of adsorption is computed using the energy/particle fluctuations in the grand-canonical ensemble.28−30 In Figure 1a, we show the isotherm and differential enthalpy of adsorption for this system. At low loading, the enthalpy of adsorption is mainly determined by the interactions of the particles with the pore and is close to −1 (it is slightly larger than −1 because there is a small contribution from configurations where the particles just touch). As the number of particles inside the pore increases, the average distance between them decreases (Figure 1b). Since the WCA potential is purely repulsive, this eventually leads to unfavorable interactions between neighboring particles and a sharp increase in the enthalpy of adsorption. It is important to note that, for a repulsive soft potential, there is no theoretical maximum loading. If the chemical potential is sufficiently large, it is always possible to squeeze in an extra particle (Figure 2). However, this becomes increasingly difficult, as not only do the repulsive interactions become larger but the number of particles that simultaneously and collectively have to move also increases. The inset of Figure 2 shows how, upon adsorbing a new particle, all of the already adsorbed particles are equidistantly redistributed in the pore to minimize the energy penalty from overlapping. In this theoretical model, the collective motion is achieved by adjusting the interparticle distance r to the number of adsorbed particles, but in real systems, this can generate ergodicity problems as not all algorithms can reproduce the collective motion needed.
Figure 1.
(a) Adsorption isotherm and enthalpy of adsorption for a simple model of WCA particles adsorbing in a cylindrical pore and (b) average distance between neighboring WCA particles in the pore as a function of the number of adsorbed particles. A pore length of 50 dimensionless units was used.
Figure 2.
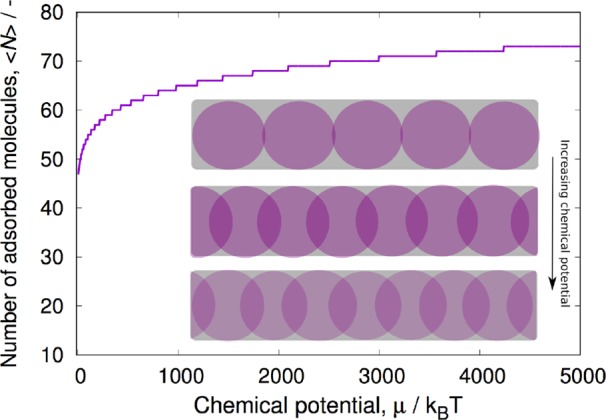
Adsorption isotherm of WCA particles in a cylindrical pore. Inset: schematic representation of adsorbed states. A pore length of 50 dimensionless units was used. It is always possible to adsorb a new particle if the chemical potential is high enough. This is visible as the “staircase” effect, where the “steps” become longer and longer, i.e., it takes progressively more pressure to push another particle in. Every time a new particle is adsorbed, the already adsorbed particles have to redistribute equidistantly to reduce the repulsive interactions. This requires the simultaneous collective motion of all adsorbed particles.
The previous analysis shows that, for this model, the enthalpy of adsorption diverges close to saturation due to repulsive interactions between the particles. In systems with more molecular details, the interaction of the particles with the adsorbent can also be repulsive (due to overlaps) and thus contribute to the rapid increase of the enthalpy of adsorption. At saturation, the confinement becomes increasingly tighter and the entropy of the system changes. In the next section, we explore state-of-the-art methods to compute the enthalpy of adsorption in simulations.
Methodology
Enthalpy of Adsorption in Simulations: Grand-Canonical Monte Carlo
In simulations, detailed information on the energetics of the system is available. The enthalpy of adsorption can also be obtained (under the same assumptions as for the Clausius–Clapeyron equation) as
| 7 |
where U refers to the total energy of the host and adsorbed molecules, ⟨Ug⟩ is the average energy of a single molecule in the gas phase, ⟨Uh⟩ is the average energy of the host system (in this work, it is taken as zero because the frameworks are rigid), and kB is Boltzmann’s constant. The first term on the right-hand side of eq 7 can be approximated by the difference in the energy of the system with N + 1 and N molecules in the NVT ensemble or using the energy/particle fluctuations in the grand-canonical ensemble.28−30 The NVT method is mostly used to estimate the enthalpy of adsorption at zero loading, but at higher loading, it becomes problematic because values U(N + 1) and U(N) can become significantly larger than their difference. However, the noise can almost be eliminated by using a continuous smooth fitting function through the energy-loading curve. We denote this methodology as the “energy-slope” method by Poursaeidesfahani et al.20 In that work, linear functions were used in separate loading regions. Here, we use a variant where the derivatives are determined by spline fitting and hence the derivatives are locally determined (we denote this the “energy local-slope method”). A similar approach has already been used by Vuong and Monson,31 albeit in the grand-canonical ensemble.
Using the energy/particle fluctuations in the grand-canonical ensemble,8,28−30 the change in the potential energy upon adsorption (eq 7) can be approximated by
| 8 |
where ⟨···⟩μ refers to averages in the grand-canonical ensemble. Therefore, the enthalpy of adsorption is given by
| 9 |
In the grand-canonical ensemble, the sampling of the phase space close to saturation conditions is hampered by the low acceptance probabilities of insertions and deletions of conventional Monte Carlo techniques, especially at low temperatures. To obtain reliable results of the enthalpy of adsorption close to saturation conditions at all temperatures, a method able to insert and delete particles under highly saturated conditions and that allows the system to adapt to the presence of new molecules (rearrangement of surrounding molecules) is needed. Methods based on the extended ensemble approach, in which the original ensemble is extended with intermediate molecular states,38−41 are very suitable for these conditions. Continuous fractional component Monte Carlo (CFCMC)42 is one of these methods. This method does not rely on the spontaneous formation of cavities, but it rather slowly creates them while the surrounding molecules adapt to it (Figure 3). In the next section, we will present, adapt, and test this method to compute the enthalpy of adsorption close to saturation. We will show that even for a simple system conventional Monte Carlo fails to capture the expected increase in the enthalpy of adsorption as we approach saturation. CFCMC is able to capture this behavior thanks to the collective and simultaneous rearrangement of molecules needed close to saturation conditions.
Figure 3.
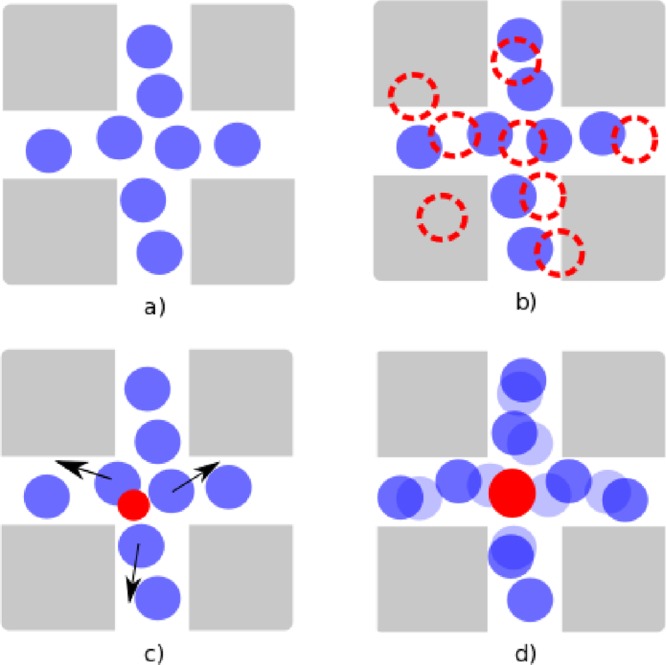
Schematic representation of the CFCMC algorithm. (a) System close to saturation (the host structure is represented in gray, and the adsorbed molecules are in blue). (b) Close to saturation, most attempts to insert a new molecule in a single step (dashed red circles) will result in an overlap with other molecules or with the host structure. (c) In CFCMC, insertions are facilitated by using a molecule with scaled interactions (a fractional molecule). Attempts to insert a fractional molecule have a higher probability of being accepted because the energy penalty due to overlaps is smaller. Once the fractional molecule is inserted, the surrounding molecules rearrange (black arrows) to minimize the repulsive interactions in the system. (d) For the fractional molecule to become a integer molecule, enough space has to be created. The configuration with N + 1 adsorbed molecules (dark blue) can be very different from the configuration with N adsorbed molecules (light blue). Close to saturation, inserting a molecule requires the collective motion of surrounding molecules.
CFCMC
In CFCMC,42−47 the insertion and deletion of molecules are facilitated by expanding the system with an additional molecule, from now on referred to as a fractional molecule. The interactions of the fractional molecule with the surroundings (Lennard-Jones and charge interactions) are scaled using a parameter λ
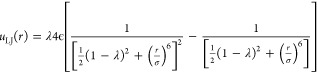 |
10 |
| 11 |
where ϵ0 is the dielectric constant in vacuum, r is the interatomic distance, q is the atomic charge, ϵ is the LJ strength parameter, and σ is the LJ size parameter. The modified potential used in this work to scale the intermolecular interactions (eq 11) was adopted from the original work on CFCMC by Shi and Maginn42 but is just one of many possibilities. Different forms can be used as long as the modified potential (1) remains finite when r → 0 for λ ≠ 1 and (2) has the correct behavior at the limits of λ = 0 and λ = 1, i.e., for λ = 0, there are no interactions, and for λ = 1, the conventional LJ and Coulombic interactions are recovered. Molecules are inserted and deleted by performing a random walk in λ space using λn = λo + Δλ, where λn is the value of λ in the new configuration, λo is the value of λ in the old configuration, and Δλ is chosen randomly between −Δλmax and Δλmax. Δλmax is adjusted to achieve roughly 50% acceptance. When λn ≥ 1, molecules are inserted, and when λn ≤ 0, molecules are deleted. Because λ space can be erratic, a biasing potential η(λ) is normally used to avoid getting trapped in local minima.42 In this work, the biasing potential is iteratively determined using the Wang–Landau method.48 When using a biasing potential, the average of a property x in the correct Boltzmann ensemble is
| 12 |
The procedure for insertion/deletion attempts using grand-canonical CFCMC method is
- insertion, λn ≥ 1
-
1.A new fractional molecule with λ = λn – 1 is randomly inserted
-
2.Acceptance rule:
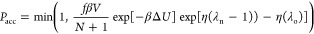
-
1.
- deletion, λn ≤ 0
-
1.The existing fractional molecule is deleted, and an existing molecule is randomly selected and converted into the fractional molecule with λ = 1 + λn
-
2.Acceptance rule:
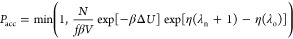
-
1.
where β = 1/(kBT), N is
the current number of adsorbed molecules,
ΔU is the difference in the energy between
the old and new configurations,42 and f is the fugacity of the system. The fugacity is related
to the chemical potential by μ = μIG0 + ln(βf), where 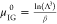 is the chemical potential of the reference
state (ideal gas).
is the chemical potential of the reference
state (ideal gas).
Derivation of the Enthalpy of Adsorption in CFCMC
As pointed out by Poursaeidesfahani et al.,32 it is not obvious how to deal with the fractional molecule when computing ensemble average properties. In ref (32), Poursaeidesfahani et al. showed that to compute the energy of a particle transfer in the Gibbs ensemble, the energy of the fractional molecule should not be taken into account and the total number of molecules should consider only integer molecules. Here, we will follow a similar derivation for the enthalpy of adsorption computed in the grand-canonical ensemble. The grand-canonical CFCMC partition function is given by49
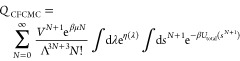 |
13 |
where Utotal is the total energy of the system and is the sum of the energy of the integer molecules plus the energy of the fractional molecule (Utotal = Uint + Ufrac), N + 1 is the total number molecules in the system (N = Nint), V is the volume, Λ is the thermal de Broglie wavelength, and the factor eη(λ) accounts for the biasing in λ space. In the grand-canonical CFCMC ensemble, the change in the potential energy upon adsorption (eq 8) can be approximated by
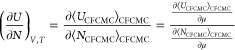 |
14 |
where UCFCMC and NCFCMC refer to the total energy and number of molecules obtained using the CFCMC algorithm and ⟨···⟩CFCMC refers to the ensemble average in the grand-canonical CFCMC ensemble.
In the most general case, UCFCMC and NCFCMC have the form
where f(λ,sN+1) and g(λ) are arbitrary functions related to the interaction energy and the “size” or degree of presence of the fractional molecule, respectively. Thus
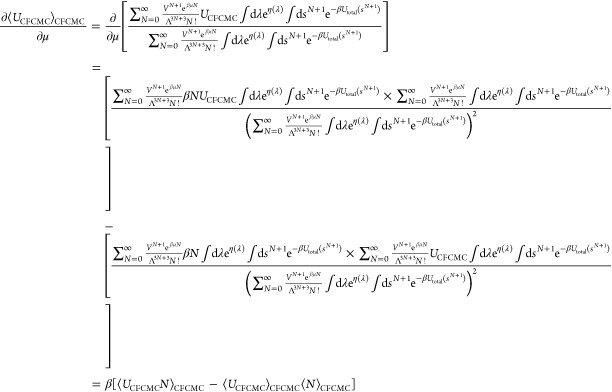 |
15 |
In the same way, one can show that
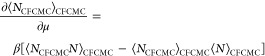 |
16 |
Therefore
| 17 |
It is convenient to set the functions f and g such that the computed enthalpy of adsorption is identical to the enthalpy of adsorption in the conventional grand-canonical ensemble
| 18 |
At the thermodynamic limit, the average of any property should be independent of the ensemble. This means that ⟨···⟩CFCMC ∼ ⟨···⟩μ for sufficiently large systems. The ensemble averages are equal only if f = 0 and g = 0. Therefore, the most trivial choice to guarantee the ensemble averages are equal is
| 19 |
Therefore, when computing the enthalpy of adsorption from the energy/particle fluctuations in the grand-canonical CFCMC ensemble, the energy of the fractional molecule should not be considered and the total number of molecules should be equal to the number of integer molecules. A similar derivation can be done for mixtures. In this case, the adsorption energy of component i in a mixture of j components is given by8
| 20 |
Converting Measured CFCMC Properties to the Normal Boltzmann Ensemble
To compute properties in the correct Boltzmann ensemble, the observable X should be computed using25
| 21 |
We can show that
| 22 |
| 23 |
| 24 |
Following the same procedure as above, for any property X
| 25 |
| 26 |
| 27 |
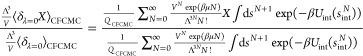 |
28 |
we notice that
 |
29 |
Equation 29 shows that to convert averages measure in grand-canonical CFCMC ensemble to averages in the grand-canonical ensemble properties should be measured at states where λ is small (ideally zero). This does not also imply that λ should be changed discretely, simply that the measurement should be done when λ = 0 to be 100% correct. However, the error of sampling at all λ values is small, and in practice, one can sample when λ is between 0 and a sufficiently small fractional number.
Results
Cylinder System
In the Theoretical Model section, we showed that the increasing confinement of the particles in a pore causes the enthalpy of adsorption to sharply increase. In this section, we will use the same model to show that in adsorption simulations, sufficient sampling is very important to predict the correct behavior of the enthalpy of adsorption close to saturation. In contrast to the Theoretical Model section, where the rearrangement of particles in the pore was done automatically by adjusting the interparticle distance, here we take a more realistic approach and simulate the adsorption process by performing Monte Carlo simulations in the grand-canonical ensemble. The chemical potential is imposed, and the number of particles in the pore is allowed to fluctuate until equilibrium is reached. Simulations were performed using (1) conventional grand-canonical Monte Carlo (GC) and (2) CFCMC. The Monte Carlo moves employed to reach equilibrium were (1) displacing the particles in the pore and (2) swapping particles in and out of the pore. Each of these moves had a 0.5 attempt probability. For the displacement, Δxmax = 0.2 was used. For the CFCMC method, the swapping of molecules was done by performing Monte Carlo moves in λ space with Δλmax = 0.2.
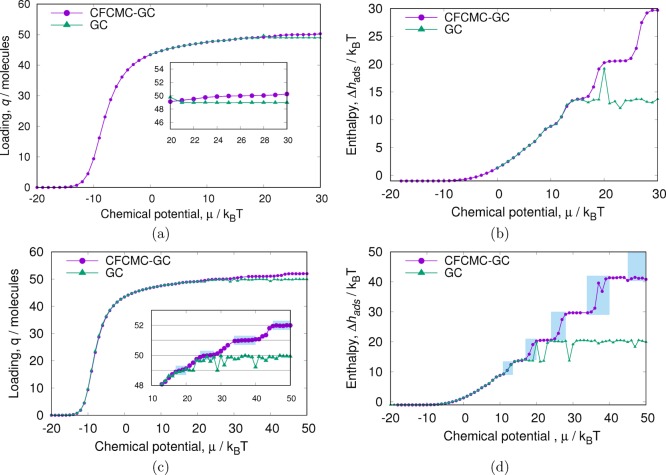
In Figure 4a, the isotherms obtained with both methods after 2 × 106 cycles are presented. Each Monte Carlo cycle consists of N = max(1000,Nads) Monte Carlo moves, where Nads is the amount of adsorbed particles in the system. The isotherms are identical up to a chemical potential of ∼20 kBT. After this point, CFCMC reaches states with more adsorbed particles than conventional GC. It is in principle always possible to push more particles inside the pore (the WCA potential is soft); however, with conventional GC, adsorbing more particles becomes increasingly difficult as it relies on the spontaneous formation of cavities for successful insertions. Insertions are done in a single step. With CFCMC, the stepwise insertions induce particle rearrangements in the pore, which reduce the energy penalty of insertion and thus enhance the probability of adsorbing a new particle.
Figure 4.
Grand-canonical simulations of WCA particles in a cylindrical pore. The pore length was set to 50 dimensionless units, and Δxmax = 0.2. For the CFCMC method, Δλmax = 0.2. Simulations (a) and (b) were run for 2 × 106 cycles, whereas (c) and (d) were run 5 times longer. After a chemical potential of around 20 kBT, the loading in conventional GC simulations reaches a plateau, whereas CFCMC simulations are able to place more particles in the pore. The enthalpy of adsorption was computed using the energy/particle fluctuations in the grand-canonical ensemble.
In Figure 4b, the enthalpy of adsorption for both methods is shown. Again, the results are in good agreement for low loading but differ close to saturation. With conventional GC, the enthalpy of adsorption reaches a plateau around 15 kBT, whereas the enthalpy of adsorption in the system simulated with CFCMC continues to go up as expected.
In Figure 4, panels c and d are the same as panels a and b, except that they have been run 5 times longer. The results for conventional GC improve a little, but it is clear that the conventional GC method has significant ergodicity problems at high loading. This problems seem to be of little importance in the isotherm (the saturation loading is underestimated only by ∼5%), but they have a profound effect on the behavior of the enthalpy of adsorption and thus on the design of new separation technologies. Small deviations in the isotherms’ saturation loading also have important repercussions when computing the enthalpy of adsorption using the Clausius–Clapeyron equation (eq 2).
A closer analysis of the probability of accepting swap moves (Figure 5) shows that CFCMC is capable of performing more swaps trial moves successfully and therefore of sampling phase space more efficiently. For CFCMC, an accepted swap is defined as an accepted move in λ space that results in a particle swap (i.e., accepted λ moves such that λn ≤ 0 or λn ≥ 1). For conventional GC, the probability of swapping particles has a maximum around a chemical potential of −10 kBT, after which it decreases very fast to almost zero. For CFCMC, the acceptance ratios are sufficiently high to ensure proper sampling at all chemical potentials.
Figure 5.
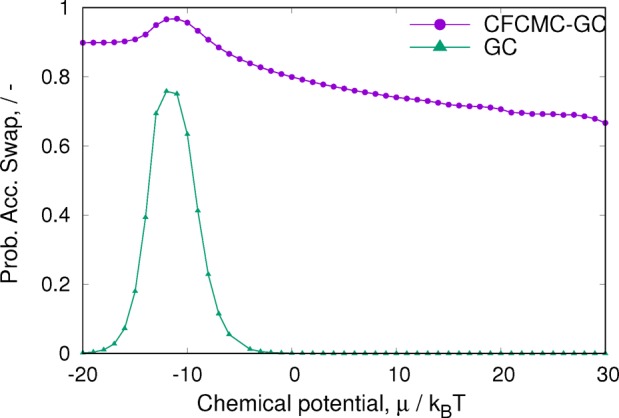
Grand-canonical simulations of WCA particles in a cylindrical pore. Simulations were run for 10 × 106 cycles, the pore size was set to 50, and Δxmax = 0.2. For the CFCMC simulations, Δλmax = 0.2.
In contrast to the model in the Theoretical Model section, here the increase in the enthalpy of adsorption has many different plateaus. In Figure 4, panels c (inset) and d, the same chemical potential intervals are highlited in blue. For every plateau in the isotherm, there is a corresponding “jump” in the enthalpy of adsorption. For isotherms, plateaus are caused by multilayer adsorption or saturation of different types of sites. The chemical potential at which the adsorption of different sites occurs depends on how repulsive the interactions of the sites are.50 Thus, the width of the plateaus is related to the difference in the amount of force required to insert particles in two energetically contiguous sites.51 This is also reflected in increasingly larger jumps in the values of the enthalpy of adsorption. In Figure 4d, for the last plateau in the isotherm (Figure 4c) there is no jump in the enthalpy of adsorption. This is because we have not reached the chemical potential for another particle insertion.
In this system, the repulsive sites arise from the overlap of the particles in the pore. In the Theoretical Model section, the particles were equidistantly placed in the pore. Thus, by definition, we can place up to 45 particles in the pore without any energy penalty (the WCA particles diameter is 21/6 ≈ 1.12). In Monte Carlo simulation, however, the distribution of particles in the pore is much more disordered, and overlaps are very likely to be present at lower chemical potentials.
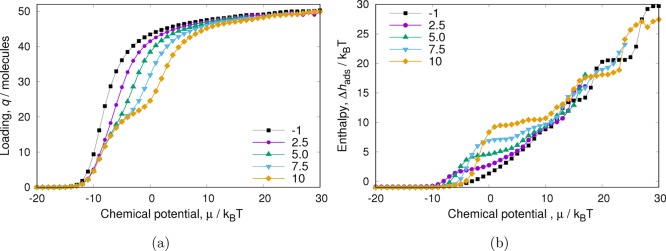
To investigate the influence of inflections in the isotherms, we changed the model system to include a second adsorption site by modifying the interaction of the particles with the pore in half of the pore. As defined in eq 6, the original interaction of the particle with the pore was set to −1. In Figure 6, we present the results of modifying the interaction potential of the particles with half of the pore to the following values: 2.5, 5.0, 7.5, and 10.0. By doing this, we effectively create a second (repulsive) adsorption site and induce an inflection in the isotherms. For adsorption to occur in the second repulsive site, force has to be applied (a higher chemical potential is required). In Figure 6a, this is reflected in a more pronounced inflection of the isotherm with increasing repulsive interactions. Figure 6b shows that increasing the repulsive interaction of the particles with the pore results in a steeper increase of the enthalpy of adsorption. Additionally, the increase in the difference of chemical potentials needed to fill up the sites is reflected in the appearance and widening of a plateau in the enthalpy of adsorption values. There is a close relationship between inflections and “pore saturation”. In both states, a lattice of adsorption sites is filled up. Note that adsorption sites are determined not only by the adsorbent (they are not just a location near the wall) but also by the other molecules. At higher loading, molecules can be “locked” in by other particles into their “sites”. As shown in Figure 6, for an inflection additional force is required to open up the accessibility of another lattice of sites (with less favorable interactions). At saturation, however, everything is basically filled up and the amount of force require to create new adsorption sites is unphysical. Here, particles are soft spheres, and it is always possible to force in another particle and induce structural rearrangement.
Figure 6.
Heat of adsorption of WCA particles in a pore with two different “adsorption sites”. For the first adsorption site, the interaction energy of the WCA particle with the pore is −1; for the second site, the interaction energy of the WCA particles with the pore is repulsive and either 2.5, 5.0, 7.5, or 10.0. The results correspond to simulations done using CFCMC. For conventional GC, the results look very similar, albeit with much larger fluctuations in the enthalpy of adsorption at high chemical potentials.
In all of the simulations, the pore was considered a rigid structure. Close to saturation, no large conformational changes are expected, but some structures can still have swelling. We expect swelling to be an important mechanism for the relaxation of some of the highly repulsive particle–particle interactions; thus, we expect that including flexibility could have a “washing-out” effect on the plateaus of the enthalpy of adsorption (Figures 4d and 6b). However, no conclusion on the effect of flexibility can be made in this study as we do not address this issue.
Zeolite Systems
To validate the obtained expressions for the enthalpy of adsorption in the CFCMC method, we computed and compared the enthalpy of adsorption of mixtures of CO2 and CH4 in a MFI-type zeolite at three different pressures and with different molarities using the Configurational Bias Monte Carlo52 (CBMC) and CFCMC methods at 300 K (Figure 7). The MFI-type zeolite (from now on referred to simply as MFI) was modeled as rigid with crystallographic positions taken from ref (53) and force field parameters taken from ref (54). Although at lower loadings the flexibility of the adsorbent could have some important effects on the enthalpy of adsorption, a rigid structure is a reasonable choice for this study as close to saturation most materials are in their open state and do not undergo any phase transition. Keeping the structure rigid has also the advantage of allowing different effects to be studied independently, in this case, the effect of particle interactions on the enthalpy of adsorption (which, by keeping the framework fixed, is not convoluted by small structural changes of the framework due to flexibility). The distribution of charges in the adsorbent was assumed to be uniform per type, i.e., all oxygen atoms have the same charge, and all silicon atoms have the same charge. An alternative newer approach would be to use the REPEAT55 method to obtain individual charges. The adsorbates were modeled using the TraPPE56,57 force field. In Figure 7, we show that there is excellent agreement between the methods in the obtained enthalpies of adsorption for the three pressures and all the mixture molarities.
Figure 7.
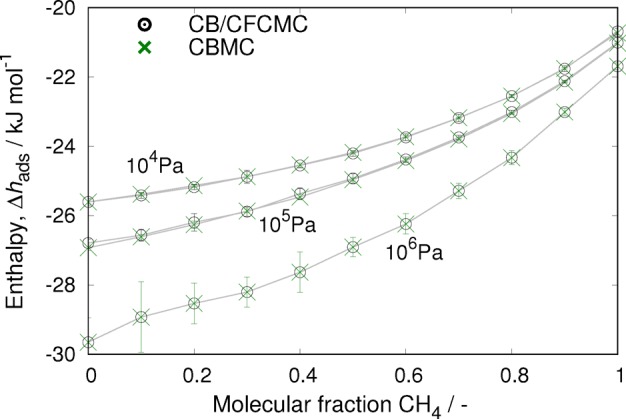
Enthalpy of adsorption for a mixture of CO2 and CH4 in MFI at different molarities at several pressures. The results obtained with CBMC and CFCMC are in excellent agreement.
Next, we explore the enthalpy of adsorption in a well-studied system: dibranched alkanes in MFI. The isotherm for dibranched alkanes in MFI can be nicely described by a dual-Langmuir isotherm15
| 30 |
The difference in the Gibbs free energy between the fluid phase and the adsorbed phase is given by ΔG = ΔH – TΔS. When equilibrium is reached (where an equal amount of adsorbates move from the fluid phase into the framework as from the framework into the fluid phase), ΔG = 0 and ΔH = TΔS.
Following Myers and Monson,9 adsorption may be decomposed into a two-step process: (1) isothermal, isobaric immersion of clean adsorbent in the compressed gas and (2) isothermal compression of the gas. The enthalpy and entropy differences can then be written as
| 31 |
| 32 |
where ΔHimm and ΔSimm are the enthalpy and entropy changes associated with isothermal immersion of the adsorbent from its clean state in vacuo (unadsorbed) to the equilibrium pressure of the bulk fluid, and ΔHcomp and ΔScomp are the enthalpy and entropy changes associated with isothermal compression of the outside gas from its perfect gas reference state to the equilibrium pressure of the bulk fluid.9
The grand potential Ω is the free energy change associated with the isothermal immersion of the clean adsorbent into the bulk phase. In the solution thermodynamics approach, the grand potential, also known as surface potential, is defined as Ω = μ – μs,9,30 where μ is the chemical potential of the solid adsorbent in the bulk phase and μs the chemical potential of the adsorbent in its clean state, which physically represents the minimum isothermal work necessary to clean (empty) the adsorbent. Using the following relationship9,30
| 33 |
where S is the entropy, dT is the change in temperature, ni is the adsorbed amount of component i, and dμi is the change in the chemical potential of component i, and assuming and isothermal process (dT = 0), Ω can be obtained by integrating from the clean state at zero pressure, where μ = μs and Ω = 0
| 34 |
Thus, for a dual-Langmuir behavior (eq 30)
| 35 |
where m1 and m2 are temperature-independent and c1 and c2 have the same temperature dependence as in eq 5
| 36 |
Therefore, the immersion functions for the dual-Langmuir model are given by
| 37 |
| 38 |
| 39 |
| 40 |
the compression functions by
| 41 |
| 42 |
| 43 |
| 44 |
and
| 45 |
| 46 |
In contrast to the single-Langmuir model, a dual model cannot
be
analytically inverted from a function p = f(n) to n = g(p). We want to plot the differential values, i.e., 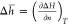 , where the differentiation is
with respect
to the total loading n. We resort to numerical differentiation
and plot the differential enthalpy, entropy, and Gibbs free energy
for 2-methylbutane in MFI in Figure 8. MFI possesses a 3D channel network consisting of
two types of channels: a “linear type” channel and a
“zig-zig” channel, and the channels cross at “intersections”.
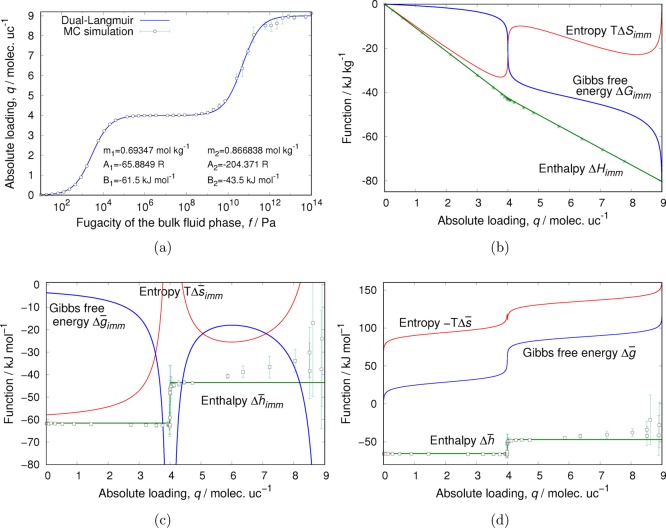
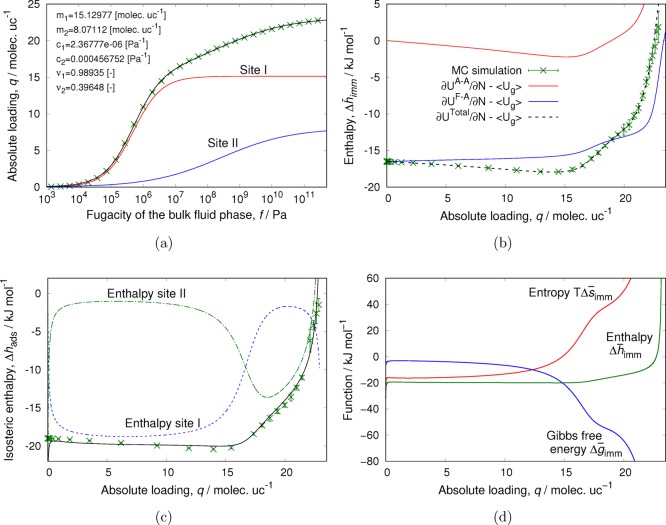
Enthalpies B1 and B2 (eq 38) have
been chosen to match the values obtained from the local-slope Monte
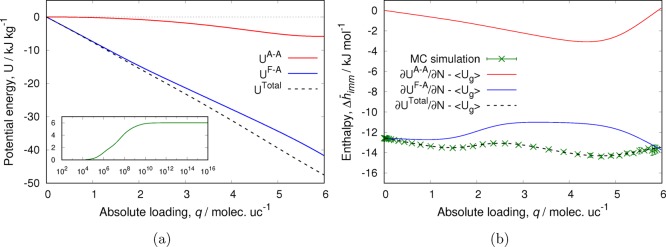
Carlo simulations (Figure 8b). As can be seen in Figure 8c, the constant enthalpy of adsorption matches very
well with the values obtained using the energy/particle fluctuations
up to 5 molec uc–1 and is in reasonable agreement
(considering the large fluctuations) for higher loading. This system
is one of the only cases that can be truly described as Langmuir behavior.
The dibranched molecules first fill the intersections, and the molecules
are adsorbing independently from each other. When the intersections
of the MFI are filled, the molecules start to occupy the channels
(the linear and zigzag channels) that connect the intersections. In
the channels, multiple molecules will fit, and due to adsorbate–adsorbate
interactions, the Langmuir assumptions break down. The adsorption
at the channels is energetically less favorable, but molecules are
pushed using force (i.e., high pressure is required). The channels
are about 18–19 kJ/mol less favorable than the intersections.
The switch between filling the intersection to filling the channels
leads to a large “inflection” in the isotherm since
additional force is required to push the adsorbates into the channels.
Entropically, adsorbates are confined more and more as a function
of loading. Molecules have more translational and rotational freedom
in the intersections than in the channels. Close to filling up a site
type, the differential immersion entropy shoots up to large positive
values (which happens at 4 molecules per unit cell for the intersections
and then at the saturation loading of 9 molecules per unit cell for
all of MFI). Something special happens at the inflection: before the
inflection, the adsorption lattice consisted of 4 sites per unit cell.
After the inflection, an additional 5 sites per unit cell become available.
As can be seen in Figure 8b,c, this has a large effect on the entropy term TΔS and the differential immersion entropy term TΔs̅imm.
, where the differentiation is
with respect
to the total loading n. We resort to numerical differentiation
and plot the differential enthalpy, entropy, and Gibbs free energy
for 2-methylbutane in MFI in Figure 8. MFI possesses a 3D channel network consisting of
two types of channels: a “linear type” channel and a
“zig-zig” channel, and the channels cross at “intersections”.
Enthalpies B1 and B2 (eq 38) have
been chosen to match the values obtained from the local-slope Monte
Carlo simulations (Figure 8b). As can be seen in Figure 8c, the constant enthalpy of adsorption matches very
well with the values obtained using the energy/particle fluctuations
up to 5 molec uc–1 and is in reasonable agreement
(considering the large fluctuations) for higher loading. This system
is one of the only cases that can be truly described as Langmuir behavior.
The dibranched molecules first fill the intersections, and the molecules
are adsorbing independently from each other. When the intersections
of the MFI are filled, the molecules start to occupy the channels
(the linear and zigzag channels) that connect the intersections. In
the channels, multiple molecules will fit, and due to adsorbate–adsorbate
interactions, the Langmuir assumptions break down. The adsorption
at the channels is energetically less favorable, but molecules are
pushed using force (i.e., high pressure is required). The channels
are about 18–19 kJ/mol less favorable than the intersections.
The switch between filling the intersection to filling the channels
leads to a large “inflection” in the isotherm since
additional force is required to push the adsorbates into the channels.
Entropically, adsorbates are confined more and more as a function
of loading. Molecules have more translational and rotational freedom
in the intersections than in the channels. Close to filling up a site
type, the differential immersion entropy shoots up to large positive
values (which happens at 4 molecules per unit cell for the intersections
and then at the saturation loading of 9 molecules per unit cell for
all of MFI). Something special happens at the inflection: before the
inflection, the adsorption lattice consisted of 4 sites per unit cell.
After the inflection, an additional 5 sites per unit cell become available.
As can be seen in Figure 8b,c, this has a large effect on the entropy term TΔS and the differential immersion entropy term TΔs̅imm.
Figure 8.
Enthalpy, entropy, and Gibbs free energy of adsorption of 2-methylbutane in MFI at 433 K as a function of loading: (a) isotherm with dual-Langmuir fit, (b) immersion values, (c) differential immersions, and (d) immersion + compression. The reference state is the adsorbent in vacuo, and the adsorbate is at its perfect gas reference pressure p0 = 1 bar. We should have Δg̅ = Δh̅ – TΔs̅ = RT ln(p/p0) and Δg̅ = 0 at 1 bar, which is indeed the case. The overline notation denotes a differential property with units of Joules per mole.
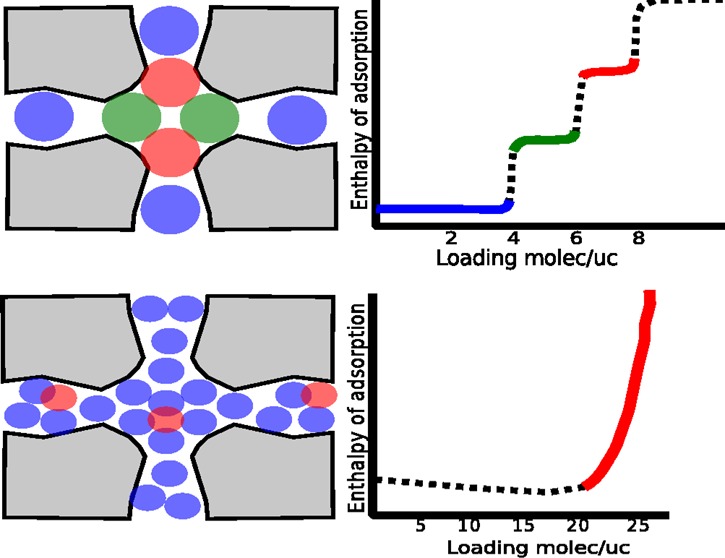
When the molecules are adsorbing into their well-defined adsorption sites up to saturation loading, then the assumptions of Langmuir-like models are satisfied and no divergence for the enthalpy is observed. There are many other systems that are also able to avoid repulsive adsorbate–adsorbate interactions. An example is the class of cage-like nanoporous materials where the cages are separated by “windows” that form free-energy barriers to diffusion. The inset in Figure 9a shows the isotherm of methane in CHA-type zeolite at 300 K. It reaches a saturation loading of 6 molecules per unit cell (which contains one cage) after a fugacity of 1010 Pa and remains flat up to at least 1016 Pa. In principle, the molecules in simulations are soft spheres, and one can always press in another molecule, but this would require an increase in pressure of many, many orders. In experiments, the saturation is limited by the highest pressure that is achievable by the apparatus and also by the stability of the material. In the energy local-slope methodology, the average energies as a function of loading in NVT simulations are computed, which has the advantage that no insertion/deletion of particles are required. The differential enthalpy can then be obtained by numerical differentiation, and as can be seen in the figure, the result is in excellent agreement with the fluctuation formula for the differential enthalpy using grand-canonical simulations. For both methods, we observe no divergence of the enthalpy close to or even at saturation. The energy slope methodology also has the advantage that the enthalpy can be easily decomposed into the framework–adsorbate and adsorbate–adsorbate contributions. We see that up to and including saturation strongly repulsive interactions can be avoided. In this picture, an integer amount of molecules fit in the cage and they all fit snugly without extensive repulsion. There is not really room for another molecule as this would require an increase of at least 6 orders in pressure (actually, much, much more than that).
Figure 9.
Adsorption of CH4 in CHA-type zeolite at 300 K: (a) total, framework–adsorbate, and adsorbate–adsorbate energies as a function of loading obtained from NVT MC simulations (inset: isotherm, loading in molecules per unit cell as a function of fugacity in Pa) and (b) enthalpy of adsorption computed from the fluctuation formula using grand-canonical MC simulations and derivatives of the energies of (a) with respect to loading. Using this energy decomposition, the enthalpy can be decomposed in the contribution from the framework–adsorbate and adsorbate–adsorbate interactions.
If the molecule is small in comparison to the channel, or when the cavities are large (e.g., MOFs), the adsorbates first adsorb at the surface. However, as the loading increases, a disordered fluid is formed in the pores. Molecules experience attractive interactions from the framework and also from other adsorbates. Pushing more molecules in inevitably leads to repulsive interactions and higher values for the enthalpy of adsorption. As an example, Figure 10 shows the results for adsorption of methane in a MFI-type zeolite at 300 K. The isotherm up to a fugacity of 1012 Pa can be decomposed using a dual-Langmuir–Freundlich model. The first contribution is close to being Langmuir (ν ≈ 1), but the second contribution captures the heterogeneous behavior. Both the energy-slope method and the dual-Langmuir–Freundlich are able to capture the behavior of the enthalpy of adsorption. The energy-slope method shows a slight downward trend at low loading, which is caused by attractive adsorbate–adsorbate interactions. However, at higher loading, the behavior becomes more and more repulsive and the enthalpy drastically increases in value. Using the dual-Langmuir–Freundlich model, we can analyze the contribution from the two different types of sites and also investigate the entropy and Gibbs free energy. We obtained the temperature dependence of the dual-Langmuir–Freundlich model by a Taylor expansion of the parameters around 300 K and fitting the first order to simulations of 285, 290, 295, 300, 305, 310, and 315 K. Using eqs 37–40 applied to the dual-Langmuir–Freundlich model, the expressions becomes too unwieldy to list, but we present here the numerical results. The c1 and c2 parameters for both sites have similar qualitative behavior as a function of temperature (decrease with increasing temperature), but m1 and m2 have opposite behavior as a function temperature (m1 decreases with temperature, but m1 increases with temperature), and so do ν1 and ν2. This is because of entropy. If two sites differ in energy, then, at low temperatures, the lowest site is filled up before the second site. However, at higher temperatures, the second site becomes accessible even before the “first” site is completely filled. Therefore, the temperature dependence of the n-site Langmuir–Freundlich model needs to be explicitly computed using simulation, as it would be difficult to theoretically derive it a priori. Another downside of the isotherm models is that n-site models cannot properly describe the low loading limit. For example, the parameter in the single-site Langmuir reduces to the Henry coefficient at low loading, but this is no longer true for multisite models. Perhaps the biggest objection to the Langmuir–Freundlich model is that, although it fits many isotherms in zeolites and MOFs well, the parameters have little physical basis as they lump the adsorbate–adsorbate interactions implicitly into the heterogeneity factor. Still, it is very useful to have analytical expressions for the isotherms.
Figure 10.
Adsorption of CH4 in MFI-type zeolite at 300 K: (a) dual-Langmuir–Freundlich isotherm fitted to grand-canonical MC simulation data and the two individual contributions of the sites, (b) enthalpy of adsorption from the (local-) energy slope method, showing the framework–adsorbate and adsorbate–adsorbate separately, (c) total enthalpy of adsorption and the individual contributions per site for the dual-Langmuir–Freundlich model using explicit simulation to obtain the temperature dependence of the model parameters, and (d) similar to (c) but showing the enthalpy, entropy, and Gibbs free energy as a function of loading.
Conclusions
Knowledge and understanding of variations in the enthalpy and entropy of adsorption as a function of loading can provide important information for the design of industrial separation processes. In simulations, the most common way to obtain the enthalpy of adsorption is from energy/particle fluctuations in the grand-canonical ensemble. With conventional Monte Carlo methods, this approach breaks down because of the difficulty of inserting and deleting molecules close to saturation conditions and also due to ergodicity problems. Here, we showed that by using the CFCMC algorithms the energy/particle fluctuations in the grand-canonical ensemble can be used to compute the enthalpy of adsorption close to saturation. The method dramatically enhances the probability of molecule insertions and deletions close to saturation. In terms of the accuracy and ease of use of the methodologies, we have the following order: NVT energy slope method > CFCMC fluctuation formula > GCMC fluctuation formula > isotherm models.
We find, in general, for the enthalpy of adsorption as a function of loading, that (1) if the added particle has only interactions with the framework, but not with other particles, then the differential enthalpy is constant as a function of loading; (2) if the added particle has favorable interactions with the framework and with other particles, then the differential enthalpy goes down; and (3) if the added particle has repulsive interactions with the framework and other particles, then the enthalpy goes up. Case (3) represents the limit of infinite pressure or loading. Case (1) over the full loading range is rare and corresponds to systems where there is a one-to-one correspondence between the adsorbate and an adsorption site and where the sites are far enough from each other to avoid repulsive interactions. Of course, with soft spheres one can always push in another particle, but this would require an increase in pressure of many, many orders of magnitude. Therefore, in practice, these system do not diverge to large positive enthalpy values at high loading. All other systems have less well-defined sites and more fluid-like behavior in the pores. Here, at high loading/pressure, the repulsive interactions causes the enthalpy to steeply increase close to saturation. At inflection points, we find a sudden change in entropy corresponding to opening up a new “lattice” of adsorption sites that was not accessible before the inflection.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b01193.
List of the parameters used in the equations and other terms (PDF)
This work was sponsored by NWO Exacte Wetenschappen (Physical Sciences) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organisation for Scientific Research, NWO). T.J.H.V. acknowledges NWO-CW (Chemical Sciences) for a VICI grant.
The authors declare no competing financial interest.
Supplementary Material
References
- Yang R. T.Gas Separation by Adsorption Process; Butterworth Publishers: USA, 1987. [Google Scholar]
- Crittenden B.; Thomas W. J.. Adsorption Technology and Design; Butterworth-Heinemann: Great Britain, 1998. [Google Scholar]
- Sicar S.Proceedings of the Third Pacific Basin Conference; Adsorption Science and Technology.: USA, 2003. [Google Scholar]
- Sircar S. Applications of Gas separation by Adsorption for the Future. Adsorpt. Sci. Technol. 2001, 19, 347–366. 10.1260/0263617011494222. [DOI] [Google Scholar]
- Sircar S.; Myers A. L. In Handbook of Zeolites Science and Technology; Auerbach S. M., Carrado K. A., Dutta P. K., Eds.; Marcel Dekker Inc.: USA, 2003; p 1063. [Google Scholar]
- Barea E.; Turra F.; Navarro J. L. R. In Metal-Organic Frameworks: Applications from Catalysis to Gas Storage; Farrusseng D., Ed.; Wiley-VCH: Germany, 2003; p 72. [Google Scholar]
- Ruthven D. M.; Farooq S.; Knaebel K. S.. Pressure Swing Adsorption; Wiley-VCH, 1994. [Google Scholar]
- Karavias F.; Myers A. L. Isosteric heats of multicomponent adsorption: thermodynamics and computer simulations. Langmuir 1991, 7, 3118. 10.1021/la00060a035. [DOI] [Google Scholar]
- Myers A. L.; Monson P. Adsorption in Porous Materials at High Pressure: Theory and Experiment. Langmuir 2002, 18, 10261–10273. 10.1021/la026399h. [DOI] [Google Scholar]
- Denayer J. F. M.; Vos D. D.; Leflaive P. In Metal-Organic Frameworks: Applications from Catalysis to Gas Storage; Farrusseng D., Ed.; Wiley-VCH: Germany, 2003. [Google Scholar]
- Denayer J. F. M.; van der Beken S.; De Meyer K. M. A.; Martens J. A.; Baron G. V. Chromatographic liquid phase separation of n-alkane mixtures using zeolites. Stud. Surf. Sci. Catal. 2004, 154, 1944–1949. 10.1016/S0167-2991(04)80731-6. [DOI] [Google Scholar]
- Chempath S.; Denayer J. F. M.; De Meyer K. M. A.; Baron G. V.; Snurr R. Q. Adsorption of Liquid-Phase Alkane Mixtures in Silicalite: Simulations and Experiment. Langmuir 2004, 20, 150–156. 10.1021/la035362+. [DOI] [PubMed] [Google Scholar]
- Daems I.; Baron G. V.; Punnathanam S.; Snurr R. Q.; Denayer J. F. M. Molecular Cage Nestling in the Liquid-Phase Adsorption of n-Alkanes in 5A Zeolite. J. Phys. Chem. C 2007, 111, 2191–2197. 10.1021/jp0668145. [DOI] [Google Scholar]
- Krishna R.; Smit B.; Vlugt T. J. H. Sorption-induced diffusion-selective separation of hydrocarbon isomers using silicalite. J. Phys. Chem. A 1998, 102, 7727–7730. 10.1021/jp982438f. [DOI] [Google Scholar]
- Vlugt T. J. H.; Krishna R.; Smit B. J. Phys. Chem. B 1999, 103, 1102–1118. 10.1021/jp982736c. [DOI] [Google Scholar]
- Krishna R. Perspective Separating mixtures by exploiting molecular packing effects in microporous materials. Phys. Chem. Chem. Phys. 2015, 17, 39–59. 10.1039/C4CP03939D. [DOI] [PubMed] [Google Scholar]
- Torres-Knoop A.; Dubbeldam D. Exploiting Large-Pore Metal-Organic Frameworks for Separations using Entropic Molecular Mechanisms. ChemPhysChem 2015, 16, 2046–2067. 10.1002/cphc.201500195. [DOI] [PubMed] [Google Scholar]
- Torres-Knoop A.; Heinen J.; Krishna R.; Dubbeldam D. Entropic Separation of Styrene/Ethylbenzene Mixtures by Exploitation of Subtle Differences in Molecular Configurations in Ordered Crystalline Nanoporous Adsorbents. Langmuir 2015, 31, 3771–3778. 10.1021/acs.langmuir.5b00363. [DOI] [PubMed] [Google Scholar]
- Torres-Knoop A.; Balestra S. R. G.; Krishna R.; Calero S.; Dubbeldam D. Entropic Separations of Mixtures of Aromatics by Selective Face-to-Face Molecular Stacking in One-Dimensional Channels of Metal-Organic Frameworks and Zeolites. ChemPhysChem 2015, 16, 532–535. 10.1002/cphc.201402819. [DOI] [PubMed] [Google Scholar]
- Poursaeidesfahani A.; Torres-Knoop A.; Rigutto M.; Nair N.; Dubbeldam D.; Vlugt T. J. H. Computation of the heat and entropy of adsorption in proximity of inflection points. J. Phys. Chem. C 2016, 120, 1727–1738. 10.1021/acs.jpcc.5b11606. [DOI] [Google Scholar]
- Siperstein F.; Gorte R. J.; Myers A. L. Measurment of Excess Functions of Binary Gas Mixtures Adsorbed in Zeolites by Adsorption Calorimetry. Adsorption 1999, 5, 169–176. 10.1023/A:1008973409819. [DOI] [Google Scholar]
- Ferreira A. F. P.; Mittelmeijer-Hazeleger M. C.; Bliek A. Adsorption and Differential Heats of Adsorption of Normal and Iso-butane on Zeolite MFI. Microporous Mesoporous Mater. 2006, 91, 47–52. 10.1016/j.micromeso.2005.11.012. [DOI] [Google Scholar]
- Whittaker P. B.; Wang X.; Regenauer-Lieb K.; Chua H. T. Predicting isosteric heats for gas adosrption. Phys. Chem. Chem. Phys. 2013, 15, 473. 10.1039/C2CP41756A. [DOI] [PubMed] [Google Scholar]
- Krishna R. Evaluation of Procedures for the Estimation of the Isosteric Heat of Adsorption in Microporous Materials. Chem. Eng. Sci. 2015, 123, 191–196. 10.1016/j.ces.2014.11.007. [DOI] [Google Scholar]
- Frenkel D.; Smit B.. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, 2002. [Google Scholar]
- Vlugt T. J. H.; García-Pérez E.; Dubbeldam D.; Ban S.; Calero S. Computing the heat of adsorption using molecular simulations: the effect of strong Coulombic interactions. J. Chem. Theory Comput. 2008, 4, 1107–1118. 10.1021/ct700342k. [DOI] [PubMed] [Google Scholar]
- Woods G. B.; Panagiotopoulos A. Z.; Rowlinson J. S. Adsorption of fluids in model zeolite cavities. Mol. Phys. 1988, 63, 49–63. 10.1080/00268978800100051. [DOI] [Google Scholar]
- Nicholson D.; Parsonage N. G.. Computer Simulation and the Statistical Mechanics of Adsorption; Academic Press: London, 1982. [Google Scholar]
- Chung Y. G.; Camp J.; Haranczyk M.; Sikora B. J.; Bury W.; Krungleviciute V.; Yildirim T.; Farha O. K.; Sholl D. S.; Snurr R. Q. Computation-Ready, Experimental Metal-Organic Frameworks: A Tool To Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mater. 2014, 26, 6185–6192. 10.1021/cm502594j. [DOI] [Google Scholar]
- Myers A. L. Thermodynamics of adsorption in porous materials. AIChE J. 2002, 48, 145–160. 10.1002/aic.690480115. [DOI] [Google Scholar]
- Vuong T.; Monson P. A. Monte Carlo simulation studies of heats of adsorption in heterogeneous solids. Langmuir 1996, 12, 5425–5432. 10.1021/la960325m. [DOI] [Google Scholar]
- Poursaeidesfahani A.; Torres-Knoop A.; Dubbeldam D.; Vlugt T. J. H. Direct Free Energy Calculation in the Continuous Fractional Component Ensemble. J. Chem. Theory Comput. 2016, 12, 1481–1490. 10.1021/acs.jctc.5b01230. [DOI] [PubMed] [Google Scholar]
- Do D. D.; Nicholson D.; Fan C. Development of equations for differential and integral enthalpy change of adsorption for simulation studies. Langmuir 2011, 27, 14290–9. 10.1021/la203531j. [DOI] [PubMed] [Google Scholar]
- Yang J.; Lee J.-H.; Lee C.-H.; Lee H. Hydrogen Separation by Two-bed PSA Process. Stud. Surf. Sci. Catal. 1997, 105, 1883–1890. 10.1016/S0167-2991(97)80656-8. [DOI] [Google Scholar]
- Shahbeig H.; Bagheri N.; Ghorbanian S.; Hallajisani A.; Poorkarimi S. A new adsorption isotherm model of aqueous solutions on granular activated carbon. World J. Modell. Simul. 1997, 9, 243–254. [Google Scholar]
- Eder F.; Lercher J. A. Alkane adsorption in molecular sieves: The contribution of ordering, intermolecualr interactions, and sorption on Bronsted acid site. Zeolites 1997, 18, 75–81. 10.1016/S0144-2449(96)00127-3. [DOI] [Google Scholar]
- Weeks J. D.; Chandler D.; Andersen H. C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. 10.1063/1.1674820. [DOI] [Google Scholar]
- Wilding N. B.; Müller M. Accurate measurements of the chemical potential of polymeric systems by Monte Carlo simulation. J. Chem. Phys. 1994, 101, 4324–4330. 10.1063/1.467482. [DOI] [Google Scholar]
- Kaminsky R. D. Monte Carlo evaluation of ensemble averages involving particle number variations in dense fluid systems. J. Chem. Phys. 1994, 101, 4986–4994. 10.1063/1.467421. [DOI] [Google Scholar]
- Escobedo F. A.; De Pablo J. J. Expanded Grand Canonical and Gibbs Ensemble Monte Carlo Simulation of Polymers. J. Chem. Phys. 1996, 105, 4391–4394. 10.1063/1.472257. [DOI] [Google Scholar]
- Escobedo F. A. Optimized expanded ensembles for simulations involving molecular insertions and deletions. II. Open systems. J. Chem. Phys. 2007, 127, 174104. 10.1063/1.2800321. [DOI] [PubMed] [Google Scholar]
- Shi W.; Maginn E. J. Continuous Fractional Component Monte Carlo: An adaptive biasing method for open system atomistic simulations. J. Chem. Theory Comput. 2007, 3, 1451–1463. 10.1021/ct7000039. [DOI] [PubMed] [Google Scholar]
- Shi W.; Maginn E. J. Improvement in Molecule Exchange Efficiency in Gibbs Ensemble Monte Carlo: Development and Implementation of the Continuous Fractional Component Move. J. Comput. Chem. 2008, 29, 2520–2530. 10.1002/jcc.20977. [DOI] [PubMed] [Google Scholar]
- Torres-Knoop A.; Burtch N. C.; Poursaeidesfahani A.; Balaji S. P.; Kools R.; Smit F.; Vlugt T. J. H.; Walton K. S.; Dubbeldam D. Optimization of Particle Transfers in the Gibbs Ensemble for Systems With Strong and Directional Interactions Using CBMC, CFCMC, and CB/CFCMC. J. Phys. Chem. C 2016, 120, 9148–9159. 10.1021/acs.jpcc.5b11607. [DOI] [Google Scholar]
- Ramdin M.; Chen Q.; Balaji S. P.; Vicent-Luna J. M.; Torres-Knoop A.; Dubbeldam D.; Calero S.; de Loos T. M.; Vlugt T. J. H. Solubilities of CO2, CH4, C2H6, and SO2 in Ionic Liquids and Selexol from Monte Carlo Simulations. J. Comput. Sci. 2016, 15, 74–80. 10.1016/j.jocs.2015.09.002. [DOI] [Google Scholar]
- Ramdin M.; Balaji S. P.; Torres-Knoop A.; Dubbeldam D.; de Loos T. W.; Vlugt T. J. H. Solubility of Natural Gas Species in Ionic Liquids and Commercial Solvents: Experiments and Monte Carlo Simulations. J. Chem. Eng. Data 2015, 60, 3039–3045. 10.1021/acs.jced.5b00469. [DOI] [Google Scholar]
- Ramdin M.; Balaji S. P.; Vicent-Luna J. M.; Torres-Knoop A.; Chen Q.; Dubbeldam D.; Calero S.; de Loos T.; Vlugt T. J. H. Computing bubble-points of CO2/CH4 gas mixtures in ionic liquids from Monte Carlo simulations. Fluid Phase Equilib. 2016, 418, 100–107. 10.1016/j.fluid.2015.09.041. [DOI] [Google Scholar]
- Wang F.; Landau D. P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. 10.1103/PhysRevLett.86.2050. [DOI] [PubMed] [Google Scholar]
- Torres-Knoop A.; Balaji S. P.; Vlugt T. J. H.; Dubbeldam D. A Comparison of Advanced Monte Carlo Methods for Open Systems: CFCMC vs. CBMC. J. Chem. Theory Comput. 2014, 10, 942–952. 10.1021/ct4009766. [DOI] [PubMed] [Google Scholar]
- Van Tassel P. R.; Davis H. T.; McCOrmick A. V. Lattice model for adsorption of small molecules in zeolite micropores. AIChE J. 1994, 40, 925–934. 10.1002/aic.690400603. [DOI] [Google Scholar]
- Smit B.; Krishna R. In Handbook of Zeolite Science and Technology; Auerbach S. M., Carrado K. A., Dutta P. K., Eds.; Mercel Dekker INC: USA, 2003; Chapter 9, pp 317–340. [Google Scholar]
- Siepmann J. I.; Frenkel D. Configurational Bias Monte-Carlo - A new sampling scheme for flexible chains. Mol. Phys. 1992, 75, 59–70. 10.1080/00268979200100061. [DOI] [Google Scholar]
- van Koningsveld H.; van Bekkum H.; Jansen J. C. On the location and disorder of the tetrapropylammonium (TPA) ion in zeolite ZSM-5 with improved framework accuracy. Acta Crystallogr., Sect. B: Struct. Sci. 1987, 43, 127–132. 10.1107/S0108768187098173. [DOI] [Google Scholar]
- Bai P.; Tsapatsis M.; Siepmann J. I. TraPPE-zeo: Transferable Potentials for Phase Equi- libria Force Field for All-Silica Zeolites. J. Phys. Chem. C 2013, 117, 24375–24387. 10.1021/jp4074224. [DOI] [Google Scholar]
- Campana C.; Mussard B.; Woo T. K. Electrostatic Potential Derived Atomic Charges for Periodic Systems Using a Modified Error Functional. J. Chem. Theory Comput. 2009, 5, 2866–2878. 10.1021/ct9003405. [DOI] [PubMed] [Google Scholar]
- Martin M. G.; Siepmann J. I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. 10.1021/jp972543+. [DOI] [Google Scholar]
- Potoff J. J.; Siepmann J. I. Vapor-liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 2001, 47, 1676–1682. 10.1002/aic.690470719. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.