Compressed Sensing CPMG with Group-Sparse Reconstruction for Myelin Water Imaging

Abstract

Purpose

Myelin content is a marker for nervous system pathology and is quantifiable by myelin water imaging using multi-echo CPMG sequence, which is inherently slow. One way to accelerate the scan is to utilize compressed sensing. However, reconstructing the images piecemeal by standard compressed sensing methods is not the optimal solution, because it only exploits intra-image spatial redundancy. It does not recognize that the different T2 weighted images are scans of the same anatomical volume and hence correlated. The purpose of this work is to test the feasibility of compressed sensed CPMG with group-sparsity promoting optimization for myelin water imaging.

Methods

Group-sparse reconstruction was performed at various simulated and actual undersampling factors for an electronic phantom, ex vivo rat spinal cord, and in vivo rat spinal cord. Normalized mean square error was used as the metric for comparison.

Results

For both simulated undersampling and the actual undersampling, the method was found to minimally impact myelin water fraction map quality (normalized mean square error < 0.25) when acceleration factor was below two.

Conclusion

Compressed sensed CPMG with group-sparse reconstruction is useful for achieving a shorter scan time than traditionally possible.

Introduction

Myelin water imaging (MWI) has been shown to measure myelin content in normal and diseased brain and spinal cord tissue (1,2). One way to generate myelin water map is to utilize multi-echo Carr Purcell Meiboom Gill (CPMG) sequence to obtain T2 decay curves from the tissue, and fit them for the T2 distribution (3). The results are used to generate myelin water fraction (MWF) map that correlates well to the amount of myelin measured by histology (1,2). However, while the standard CPMG yields very good MWF maps, it is inherently a slow sequence and reduction of scan time is beneficial to both cost and patient comfort.

Several studies have proposed pulse sequence based techniques and parallel imaging based methods for fast T2 imaging. For example, Mädler et al. (4) have demonstrated the use of gradient and spin echo based sequence for accelerated MWI acquisition by sampling the periphery of k-space using gradient echoes. More recent works (5,6) combine fast pulse sequences with parallel imaging methods to reduce the data acquisition time for T2 imaging. The multi-echo fast spin-echo sequence used in (5,6) samples the center of the k-space accurately with even echoes and the periphery with less accurate odd echoes to retain CPMG like sampling at the center of the k-space. For both (5,6) the parallel imaging reconstruction was performed using Compressed Sensing (CS) methods. The introduction of CS helped achieve higher acceleration factors than deemed possible by traditional parallel imaging alone. The difference between (5) and (6) is that while (5) addresses the problem of static imaging (static T2 map estimation), the objective of (6) is to address a dynamic imaging scenario where the T2 maps need to be computed over time.

In (7) a novel method was proposed to reconstruct T1 and/or T2 weighted images. A stack of multi-echo images can be assumed to lie in two coordinates – i) the spatial coordinate and ii) the parameter encoding coordinate. All prior studies in multi-echo reconstruction (4) – (6) only exploited the spatial redundancy of the images. Redundancy in the pixel domain led to sparsity in the transform domain; CS techniques could thus be used to exploit the spatial domain sparsity of these images during reconstruction. These studies only concentrated on the spatial coordinates. The novelty of (7) lies in the fact that they used a learned dictionary to sparsify along the parameter encoding coordinate. They showed that the learned dictionary can be used alone to sparsify the dataset of multi-echo images (sparsifying along the parameter encoding coordinate) or it can be used in conjunction with wavelet transform (sparsifying along both spatial and parameter encoding coordinates). They proposed a greedy algorithm to solve the reconstruction problem. The main shortcoming of this approach is the dictionary learning; it is a highly non-convex problem. Thus there are no convergence guarantees. Moreover the heuristic greedy algorithm based on Orthogonal Matching Pursuit that is used to solve the corresponding reconstruction problem lacks the strong theoretical guarantees of reconstruction via convex optimization (8).

Majumdar et al. have proposed a method for accelerating multiple acquisitions of the same anatomy in MR by utilizing both the intra-image spatial redundancy and inter-image correlation (9). For MWI using a CS CPMG sequence, time saving can be realized by jointly reconstructing all the echo-images simultaneously while enforcing group sparsity. This formulation makes echo-images reconstructed with high accuracy from significantly fewer k-space samples possible. Despite the non-linear nature of MWF map generation, the assumption is that if the series of individual T2-weighted echo-images can be reconstructed accurately, the resulting parametric map (i.e. the MWF map) will be accurate as well. We hypothesize that using CS multi-echo CPMG with group-sparse reconstruction will increase the acquisition efficiency of myelin water images.

Methods

Three fully sampled CPMG datasets served as baselines for simulated undersampling: a) a computer generated electronic phantom mimicking an idealized excised rat cervical spinal cord, b) a rat cervical spinal cord ex vivo, and c) rat lumbar spinal cord in vivo. A spinal cord sample from a previous study was used for the actual ex vivo CS CPMG acquisitions; and a 297 g female Sprague-Dawley rat was used for the actual in vivo CS CPMG acquisition.

Electronic Phantom

The electronic phantom is modelled after an excised rat cervical spinal cord sample constructed of idealized grey matter (GM), white matter (WM) and fixative solution. Only T2 relaxation was considered. The fixative was made of a single pool with T2 of 1,500 ms; the GM was made of a single pool with T2 of 24 ms; and the WM was made of two pools; 35% was assigned T2 of 12 ms and 65% with T2 of 28 ms. Proton densities were set at 34.4, 32.9, and 30.2 respectively. Data were generated at 25 μm isotropic resolution and down-sampled to 100μm × 100 μm by 1 mm to match the ex vivo baseline. The advantage of using synthetic data is that it is uncorrupted by noise; however its geometry and T2 distributions are simplistic.

Ex Vivo Imaging

Previous acquired data from paraformaldehyde fixed C4/5 spinal cord sample excised from female Sprague-Dawley rat was chosen for this study (10). The cord was scanned on a 7 T/30 cm bore animal MRI scanner (Bruker, Germany) using a single slice multi-echo CPMG sequence (11) with 256 × 256 matrix size, TE/TR = 6.738/1500 ms, 32 echoes, 2.56 cm field-of-view (FOV), 1 mm slice, number of averages (NA) = 2, 4, and 8, and the excitation pulse phase cycled between 0° and 180°.

In Vivo Imaging

Data from lumbar spine acquired using an actively decoupled phased array coils at T13/L1 level was chosen from a previous study. The same CPMG sequence used to acquire the ex vivo data was used here with slice thickness of 2.0 mm, 4.00 cm FOV, TE = 6.753 ms, and NA=6. Acquisition was respiratory triggered to minimized motion artefact, which resulted in total acquisition time of approximately 45 minutes.

Simulated Undersampling and Image Reconstruction

Undersampled k-space data in the phase encoding (PE) direction was generated from each data set for different acceleration factors (R = 1.33, 1.5, 1.6, 2, and 4, corresponding to 192, 170, 160, 128, and 64 PE lines). 33% of the read-out lines were placed around the centre of the k-space, and the rest randomly distributed in the periphery. Different sampling patterns were used for each echo to utilize the benefit of group-sparse optimization (9). Reconstruction was performed via group-sparse synthesis prior method using Spectral Projected Gradient for L1 (SPGL1) package (12). Daubechies 8 wavelet at three levels of decomposition (while the maximum levels of decomposition is log₂(size)-1, three levels work the best in practice) was used as the sparsifying transform. Zero-filled (ZF) reconstructions of equivalent PE lines at the central k-space were also performed.

CS CPMG Sequence

The single slice CPMG sequence was modified to acquire undersampled data using the same sampling scheme as in simulated undersampling. Gradient values were sorted such that PE jumps are minimized to reduce eddy current artifacts. Echo spacing was unaffected. CS CPMG data was acquired from uninjured ex vivo cord at various acceleration factors and number of averages (NA = 8 with R = 1, and 2; NA = 4 with R = 1, 1.33, 1.5, and 2; and NA = 2 with R = 1, 1.33, and 1.5). Actual in vivo CS CPMG experiment was performed using a actively decoupled surface coil, with NA = 6 and R = 1, and NA = 8 and R = 1.5.

Analyses

The data were processed with software procedures developed in-house using MATLAB R2009b (MathWorks Inc., Natick, MA). Regularized non-negative least square analysis (3) was used to calculate the continuous T2 distributions that has minimal energy within χ² misfit of 2% to 2.5%. MWF maps were generated by dividing the integral from 7.75–20 ms by the total integral of the T2 distribution for each voxel. Normalized mean square error (NMSE) was used as the metric for comparison. NMSE were generated from the spinal cord voxels for all T2-weighted echo-images, first T2-weighted echo-image, and the MWF map.

Results

Figure 1 shows the NMSE at various simulated undersampling for the three different baseline images as a function of PE lines used. The same trend in NMSE was observed in all three tested SNR levels (SNR = 786 at NA = 8, SNR = 585 at NA = 4, and SNR = 397 at NA = 2) in the ex vivo cord sample and matched those shown in Figure 1. The quality of CS reconstructed T2 images remained excellent while MWF map showed little degradation in quality with increased acceleration factor. The first and eighth T2-weighted echo image and MWF map, as well as the difference image to the baseline for each is shown in Figures 2–4 along with ZF reconstruction of equivalent PE at the central k-space. Interestingly, NMSE in the electronic phantom increased sharply when acceleration factor is increased beyond 2× as seen in Figure 2.

Figure 1. Normalized mean square error (NMSE) at various simulated undersampling for the three different baseline images as a function of number of phase encoding lines used.

NMSE was calculated from voxels in the spinal cord against the fully sampled baseline images (256 phase encodes) and plotted against the number of phase encoding lines used. NMSE was generated from the MWF map, all the T2 weighted echo-images, and the first T2 weighted echo-image. Insets show the first T2-weighted echo-image of each baseline.

Figure 2. Reconstruction results from simulated undersampling of the electronic phantom.

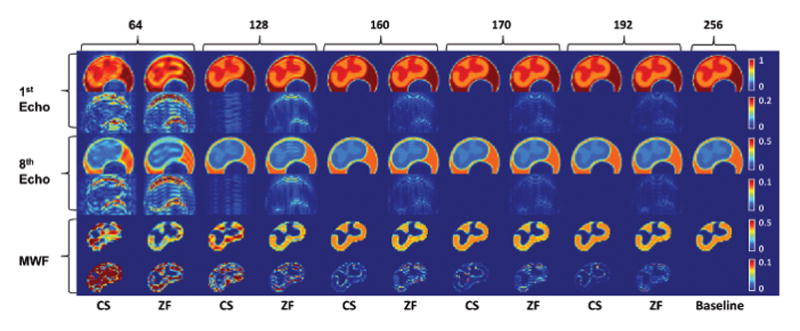
First and third row shows the first and eighth T2-weighted echo image, followed by the absolute difference map against the baseline T2-weighted echo image (far right column) in second and fourth row. Fifth row shows the generated myelin water fraction (MWF) map followed by the absolute difference map against the baseline MWF map (far right). Odd number columns are CS reconstructed images; even columns are zero-filled (ZF) reconstructions of equivalent phase encode lines at the central k-space. Numbers indicate the phase encode lines used. Far right column is the fully sampled baseline image.

Qualitatively, the MWF map quality in all three cases remained adequate when acceleration factor is under 2×. The enhancement in the cortical spinal tract in Figure 3 is clearly delineated. Especially in the case of the electronic phantom, majority of NMSE in MWF were contributed by GM/WM interface, where high wavelet coefficient corresponds to strong edge information. However, errors are smaller than non-CS images with equivalent PE at reduced FOV. While these regions are typically avoided in ROI analyses of WM tracts due to partial volume effect, the higher spatial resolution allows for more precise ROI definition. The trend in NMSE did not change when the GM/WM boundaries were excluded from our analyses. NMSE also did not vary significantly between WM tracts. The salt and pepper noise in the difference map seen in the non-synthetic baselines is a large contributor to NMSE in both the CS and ZF reconstruction. In the CS case, it is likely a result of the mixed l_2,1-minimization.

Figure 3. Reconstruction results from simulated undersampling of the ex vivo baseline.

First and third row shows the first and eighth T2-weighted echo image, followed by the absolute difference map against the baseline T2-weighted echo image (far right column) in second and fourth row. Fifth row shows the generated myelin water fraction (MWF) map followed by the absolute difference map against the baseline MWF map (far right). Odd number columns are CS reconstructed images; even columns are zero-filled reconstruction of equivalent phase encoding lines. Numbers indicate the phase encode lines used. Far right column is the fully sampled baseline image.

Figure 5 shows the result of the actual in vivo and ex vivo CS CPMG acquisition. The images do not appear to suffer from any eddy current artefacts. Again, the ex vivo MWF map quality remained very good when acceleration factor is under 2×. The in vivo CS CPMG MWF map quality was excellent and appears to have fewer artifacts when compared to the fully sampled data of equivalent acquisition time.

Figure 5. Myelin water fraction (MWF) map generated from actual compressed sensed CPMG data.

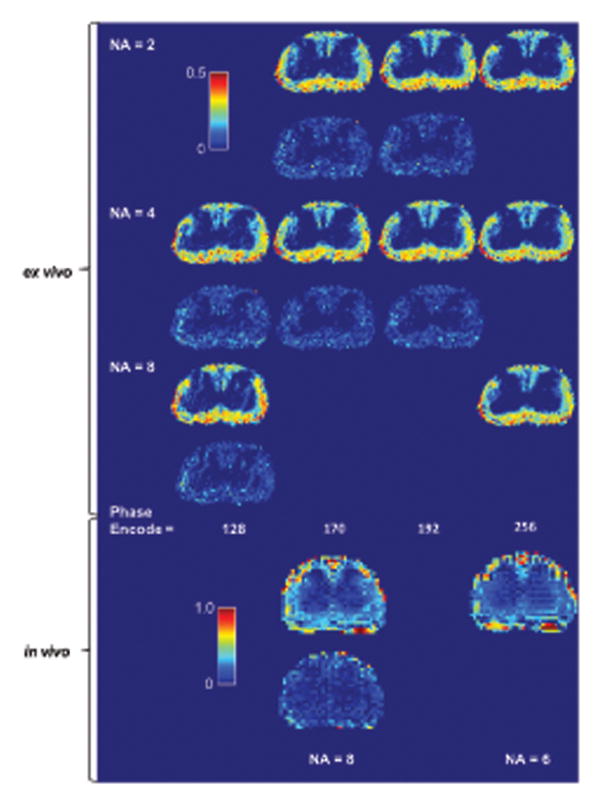
Odd number rows show the MWF map and even number rows show the absolute difference image against the baseline MWF map of the same average for ex vivo data and same acquisition time for ex vivo data. MWF quality remained adequate at 170 phase encode lines at two averages for the ex vivo data, which had a total acquisition time of 8 minutes. The in vivo CS MWF map appears to offer improved quality. Even averages were used due to the need for phase cycling.

Discussion

For accurate myelin water measurement, a SNR in the first echo-image of greater than 200 is normally required without filtering (13). As hardware and methods are refined, SNR per acquisition rises and fewer signal averages are needed. The protocol used in this study for ex vivo rat spinal cord imaging is capable of generating an SNR in the first echo-image of ~400 with two averages, which implies that one average should be sufficient if spurious signal generated by imperfect refocusing pulse is suppressed by the use of alternating descending crushers. However, at very high spatial resolution the required crusher strength to achieve 2π phase dispersion across the voxel is difficult to fulfill (14), especially for late echoes. Crushers are also unable to eliminate the signal from stimulated echoes that are in phase with the spin echoes (16). Lastly, the strong gradient pulses can also cause significant eddy currents. One solution is to use a two-step phase cycle, where the phase of the excitation 90° pulse is alternated between 0 and 180°, and the signal is alternatively added and subtracted. Such phase cycling effectively eliminates the spurious FID signal, but requires at least two averages. Thus CS CPMG is useful in achieving a shorter scan time than traditionally possible while retaining the use of phase cycling. This is demonstrated in the first row of Figure 5 where improvement in scan time can still be achieved using CS while dropping below 2× averages would incur significant artifacts in the later echoes. Furthermore, the quality of the in vivo CS CPMG data (Figure 5) suggests that time may be better spent on higher average CS acquisition rather than low average fully sampled acquisition.

The added flexibility in acquisition time by CS CPMG allows for larger coverage, higher resolution, and additional imaging methods in limited scan time. For ex vivo scenarios, scan time is typically the least important consideration, so CS CPMG is of little benefit. The in vivo situation presented here is the least favourable environment for MWI due to the small voxel size. In human brain where there is an excess of SNR, keyhole imaging have been demonstrated to accelerate MWI acquisitions (16). Given the same scenario, the technique presented in this paper could provide further improvements to MWI. Because patient comfort and cost are always concerns in the clinical setting, reduction of scan time is beneficial, especial since MWI has been applied successfully in clinical settings, such as in monitoring the demyelination process in multiple sclerosis (2).

While MWI has been successfully applied in excised rat spinal cord (1,17), the high SNR and spatial resolution requirements make it difficult to apply it in vivo. In order to achieve the high SNR in our setup, the geometric coverage was limited to a single 2.0 mm slice. Since the sequence is not capable of multi-slice acquisition, geometric efficiency can be improved by moving to a 3D based CPMG acquisition. With the intrinsically higher SNR efficiency per excitation, larger volume could be covered while retaining similar SNR to the 2D setup. However, the requirement for phase cycling remains, and is even more important in vivo due to B₁ field inhomogeneity. A 3D CS CPMG sequence would have the potential to improve image quality by allowing the use of phase cycling with minimal SNR loss when compared to a single signal average. It also allows sparse sampling in both PE directions.

In this study, each echo is phase encoded using a pair of PE gradients of opposite polarity around the echo signal, although the optimal solution is to use a single PE gradient pulse to encode all the echoes (11). Moving to other k-space trajectories, such as radial acquisition, can also improve image quality. Visual quality may be improved by moving to more sophisticated wavelet dictionary. When phase cycling is used, instead of signal averaging before CS reconstruction, the dataset can be formulated as a single CS reconstruction problem. Regardless, the Cartesian based sampling scheme and reconstruction method used in this paper is easy to implement on any scanners and applies equally well to other MWI methods, such as GRASE based MWI (4).

While the generated MWF maps consistently produce NMSE that is of an order of magnitude larger than the NMSE of the source T2 weighted echo images, the behaviour is typical of MWF map generation due to the noise sensitivity of MWF estimation (13). The NMSE in the T2 weighted echo images found here agrees with those demonstrated by Majumdar et al. in (18) and the NMSE in the MWF map follows the same trend, even with actual CS CPMG acquired data. Thus the original assumption that if the series of individual T2-weighted echo-images can be reconstructed accurately, then the MWF map generated from the data will be accurate as well is valid. This paper falls under the current techniques in estimating the parametric maps which consists of two steps – i) image reconstruction, ii) parameter estimation. Because each of the steps introduces estimation errors, there is less error in the reconstructed T2-weighted images than in the MWF maps. The former is corrupted only by reconstruction error but the latter is further corrupted by estimation error. One way to reduce these errors is to pose the parametric map estimation as a single step problem, i.e. directly estimate the map from the k-space samples without the intermediate step of image reconstruction. This is a non-linear least squares problem. When coupled with CS based sparsity techniques, this becomes an l₁-regularized non-linear least squares problem. There had been no known solution to the said problem until recently. Even the recent algorithms that exist are only applicable to explicit matrices and not to fast operators like Fourier transforms or wavelet transforms. In the future, as techniques in non-linear CS mature, solving the parametric maps directly from the measured samples may be a possibility.

The results here show that accurate reconstruction of the T2-weighted echo images from the CS accelerated CPMG sequence is possible and that the quality of the MWF maps generated are adequate, as long as the acceleration factor is less than two for practical SNR ranges.

Figure 4. Reconstruction results from simulated undersampling of the in vivo baseline.

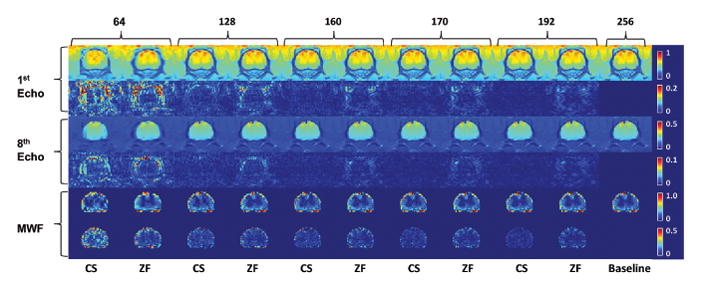
First and third row shows the first and eighth T2-weighted echo image, followed by the absolute difference map against the baseline T2-weighted echo image (far right column) in second and fourth row. Fifth row shows the generated myelin water fraction (MWF) map followed by the absolute difference map against the baseline MWF map (far right). Odd number columns are CS reconstructed images; even columns are zero-filled reconstruction of equivalent phase encoding lines. Numbers indicate the phase encode lines used. Far right column is the fully sampled baseline image.