Identifying Cell Subpopulations and Their Genetic Drivers from Single-Cell RNA-Seq Data Using a Biclustering Approach

Abstract

Single-cell RNA-Seq (scRNA-Seq) has attracted much attention recently because it allows unprecedented resolution into cellular activity; the technology, therefore, has been widely applied in studying cell heterogeneity such as the heterogeneity among embryonic cells at varied developmental stages or cells of different cancer types or subtypes. A pertinent question in such analyses is to identify cell subpopulations as well as their associated genetic drivers. Consequently, a multitude of approaches have been developed for clustering or biclustering analysis of scRNA-Seq data. In this article, we present a fast and simple iterative biclustering approach called “BiSNN-Walk” based on the existing SNN-Cliq algorithm. One of BiSNN-Walk's differentiating features is that it returns a ranked list of clusters, which may serve as an indicator of a cluster's reliability. Another important feature is that BiSNN-Walk ranks genes in a gene cluster according to their level of affiliation to the associated cell cluster, making the result more biologically interpretable. We also introduce an entropy-based measure for choosing a highly clusterable similarity matrix as our starting point among a wide selection to facilitate the efficient operation of our algorithm. We applied BiSNN-Walk to three large scRNA-Seq studies, where we demonstrated that BiSNN-Walk was able to retain and sometimes improve the cell clustering ability of SNN-Cliq. We were able to obtain biologically sensible gene clusters in terms of GO term enrichment. In addition, we saw that there was significant overlap in top characteristic genes for clusters corresponding to similar cell states, further demonstrating the fidelity of our gene clusters.

1. Introduction

Single-cell RNA-Seq (scRNA-Seq) has received much attention for allowing a deeper resolution into cellular biology. As an extension to the popular RNA-Seq technology, scRNA-Seq allows us to sequence cells that are rare in occurrence (e.g., embryonic cells) or simply hard to obtain (e.g., brain cells). In light of the rise of the technology, an increasing number of experiments have been conducted and yielded excellent results (Ramsköld et al., 2012; Yan et al., 2013; Deng et al., 2014; Wu et al., 2014). The unprecedented resolution into cell states provides hope for a better understanding of cell function and dysfunction (Eisenberg and Levanon, 2013), for which scRNA-Seq was bestowed the honor of “Method of the Year” by Nature in 2013 (Nawy, 2014).

Being a high-throughput technique, scRNA-Seq data pose interesting statistical problems. One such problem is to cluster cells into biological categories, for example, distinct developmental stages or cell types, to discover cell-based biologics. Compared to other clustering tasks, algorithms developed for scRNA-Seq data need to take into account the increased variation in data that comes with sequencing individual heterogeneous cells (e.g., Buettner et al., 2015; Xu and Su, 2015). To improve on existing algorithms, a natural extension is to simultaneously identify “biologically important” genes for each cell category while performing clustering. Under this setting of biclustering, it is reasonable to expect that the identified signature genes would not only aid clustering the cells by denoising the data but also help answer questions such as “what genes are heavily recruited in the 2-cell stage of mouse embryonic development?”

Since a gene may be involved in multiple cell conditions, the biclustering problem we consider allows for overlapping gene (rows) clusters but nonoverlapping cell (columns) clusters. For instance, it is reasonable to assume similar genes would drive 2-cell embryonic and 4-cell embryonic development due to their chronological proximity. Most existing biclustering algorithms such as block partitioning (Govaert and Nadif, 2008) are not suitable because they do not allow overlapping gene clusters. More flexible models such as the Cheng and Church model (Cheng and Church, 2000), which considers a bicluster as a submatrix with consistent column and/or row effects, are often too computationally expensive for the problems we consider (≈100 cells, >40,000 genes). Coupled two-way clustering (Getz et al., 2000) is a popular method that sequentially divides an initial cluster until a stable child cluster is found. However, since the method cannot self-correct, the quality of the child clusters may be entirely dictated by the quality of the initial cluster. In this article we introduce a fast, simple, self-correcting iterative biclustering method named “Biclustering using Shared-Nearest-Neighbor and Walktrap” (BiSNN-Walk for short, pronounced “bison walk”), in hope to address the above issues to some extent. BiSNN-Walk expands on the idea of clustering on Shared Nearest Neighbor network constructed from gene expression matrix proposed in Xu et al.'s SNN-Cliq algorithm (Xu and Su, 2015) by adding a gene clustering component to SNN-Cliq's cell clustering framework. We also introduce a simple entropy-based measure to guide our initial similarity matrix selection, which serves as a starting point for BiSNN-Walk. In our exploratory analyses, the entropy measure shows promise for gauging the “clusterability” of similarity matrices.

We applied BiSNN-Walk to three public single-cell RNA-Seq data sets and found that the algorithm not only maintained SNN-Cliq's clustering capability but also produced biologically interpretable results by establishing genes that are characteristic to those clusters.

The article is organized as follows: the Methods section will outline the algorithm and detail the key steps; the Results section will describe the three scRNA-Seq data sets used for validation, compare our cell clusters against SNN-Cliq, offer visual comparisons against selected biclustering algorithms, and finally evaluate the gene clusters via gene overlap and ontological term-enrichment analysis.

2. Methods

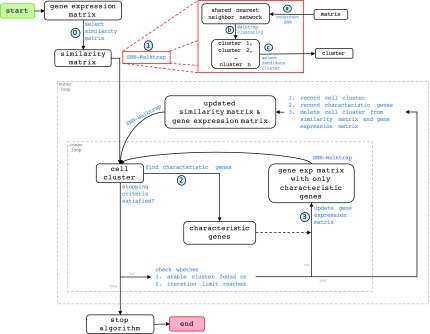
Figure 1 details the flow of BiSNN-Walk. In essence, the algorithm iterates between an inner loop and an outer loop.

FIG. 1.

BiSNN-Walk Algorithm Flowchart. Inputs and outputs are in rounded boxes, functions are in blue texts. The function SNN-Walktrap is a bit complicated, and its details are laid out in the red box. Steps with circled numbers are crucial steps that will be repeatedly referenced.

The inner loop cycles through three main steps: cell clustering “SNN-Walktrap,” gene finding, and expression matrix updating (Fig. 1, steps ①, ②, ③, respectively). We pass an initial similarity matrix into SNN-Walktrap to obtain a candidate cell cluster, which is used to find characteristic genes. Step ③ then produces a gene expression matrix containing only those characteristic genes. The reduced expression matrix is in turn used by SNN-Walktrap to obtain a new cell cluster. The process then iterates until either the cell cluster stabilizes or a preset iteration limit is reached. The inner loop will have produced one bicluster on termination.

The process then goes to the outer loop, where the cell cluster found by the inner loop is removed from the input matrices. The updated matrices are subsequently fed into the inner loop to obtain the next stable cluster. The process continues until stopping criteria (described in the Stopping Criteria section) are met. The following sections will detail several major steps.

2.1. Initial input: selecting a similarity matrix

The first step is to choose a similarity matrix to be used to obtain the initial cell cluster (Fig. 1, step ⓪). We consider an initial similarity matrix with high contrast to be ideal, that is, if correlation is used, the correlation between cells of the same type should concentrate tightly near 1, while that between different types should concentrate around near 0. In this study, we will examine four common types of similarity matrices: Euclidean distance, Spearman correlation, Pearson correlation, and the irreproducible discovery rate (IDR) matrix (Li et al., 2011). IDR measures the level of inconsistency between two cells' active genes; for example, two cells that have a similar set of active genes will generate a small IDR value and vice versa. The IDR stands apart from existing cell similarity measures, in that it does not resort to using all of the genes or a preselected set of “relevant genes.” The former is not desirable since a large portion of a cell's genetic profile consists of housekeeping and nonactive genes, which may lower a method's power to identify the relationship between two cells. The latter is not ideal either since the threshold for “active” genes will vary across cells. The use of IDR bypasses these difficulties. Our results (Supplementary Appendix G, Table 2) demonstrate that the IDR matrix consistently provides high-quality final clustering. An overview of IDR is provided in Supplementary Appendix F.

Table 2.

Collection Details of Mouse Embryonic Cells

Developmental stage	Hours after ovulation	No. of samples
Zygote	20–24	4
Early-2-cell	31–32	8
Mid-2-cell	39–40	12
Late-2-cell	46–48	10
4-Cell	54–56	14
8-Cell	68–70	48
16-Cell	76–78	58
Early-blastocyst	86–88	43
Mid-blastocyst	92–94	60
Late-blastocyst	100–102	30
C57 2-cell	NA‡	8
Liver	—	13
Fibroblast	—	10

To choose which similarity matrix to use, we propose a simple entropy-based measure.

Definition (entropy of a similarity matrix). Let x be the vector obtained from the upper triangle of the similarity matrix, we put the values of x into m equal sized bins, akin to what is done for histograms. Let 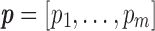denote the proportion of values that fall into each bin.^* The entropy for an m-bin configuration is calculated as

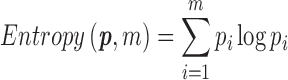This entropy can be interpreted as the amount of noise in a similarity matrix, and thus, a similarity matrix with a large amount of clustering information should have low entropy. Because entropy calculation depends on m, it is illustrative to compare entropy at several m's varying in an appropriate range. We found that the entropy measure performs as expected in simulation and provides good initial similarity matrix for real data. Please refer to Supplementary Appendix G for an in-depth exploration of the performance of the entropy measure.

2.2. Inner loop

SNN-Walktrap (Fig. 1, step ①) takes a matrix input (e.g., gene expression or similarity matrix) and returns a cell cluster. Overviews of SNN and Walktrap (Pons and Latapy, 2005) are presented in Supplementary Appendices C and D, respectively. Next (Fig. 1, step ②), we evaluate a gene's functional relevance to the cell cluster. Finally (Fig. 1, step ③), we use the identified characteristic genes to reduce potential impurities in the cell cluster. Figure 2 demonstrates this “purification” step at work. More details on step ① can be found in Supplementary Appendix A, and details for steps ② and ③ in Supplementary Appendix B.

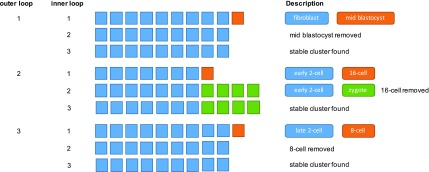
FIG. 2.

First 3 outer loops of BiSNN-Walk on mouse embryo data set. Outer loop 1 has three inner loops. On the first inner loop, our initial cluster contains nine fibroblast cells and one mid-blastocyst cell. Notice that on the second inner loop, the mid-blastocyst is removed from the cell, and we obtain the cleaned stable cluster on our third inner loop. The second outer loop also contains three inner loops. On the first inner loop, we obtain our initial cluster of seven early-2-cell-stage cells and one 16-cell-stage cell. On the second inner loop, the 16-cell-stage cell was removed, and the zygotes, which are much closer in developmental to early-2-cell stage, are added. On the third inner loop, we obtain the cleaned stable cluster. A similar self-correcting behavior can be seen in the third outer loop.

2.3. Stopping criteria

The algorithm stops if all Walktrap clusters obtained from Walktrap clustering are of size 2 or less or all candidates have zero transitivity, when further clustering is meaningless.

3. Results

We use three public data sets to evaluate our algorithm: Mouse Embryonic Cells (Deng et al., 2014), Human Embryonic Cells (Yan et al., 2013), and Human Cancer/Somatic Cells (Ramsköld et al., 2012). To ensure a level of uniformity of gene expression, we ran RNA short reads from each experiment through the standard ENCODE pipeline [ENCODE Consortium (2016)] using STAR for alignment (Dobin et al., 2013) and RSEM (RNA-Seq by Expectation Maximization) for transcript quantification (Li and Dewey, 2011). Gene expressions are normalized using transcript per million. The three data sets will be referred hereafter as “mouse,” “human embryo,” and “human cancer,” respectively. The expression matrices for mouse, human embryo, and human cancer are of sizes: 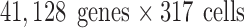, , 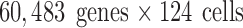and 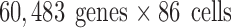, respectively; their collection summary can be found in Tables 2–4. Supplementary Appendix I contains brief descriptions of each experiment.

Table 3.

Collection Details of Human Embryonic Cells

Developmental stage	Hours (after fertilization)	No. of samples
Oocyte	4 (after retrieval)	3
Zygote	19	3
2-Cell	27	6
4-Cell	48	12
8-Cell	72	20
Morulae	96	16
Late-blastocyst	144	30
hESC	∼30 days	32

Table 4.

Collection Details of Human Somatic/Cancer Cells

Cell type	No. of samples
Universal human reference RNA	20
Brain	16
Prostate cancer cell line (PC3)	4
Bladder cancer cell line (T24)	4
Melanoma-derived circulating tumor cells (CTC)	6
Melanocytes	2
Melanoma cancer	7
Embryonic stem cells	8
Prostate cancer cells (picked from Petri dish)	7
Prostate cancer cells (isolated by EPCAM marker)	8

The run time of BiSNN-Walk is 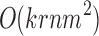, where k = number of clusters or number of outer loop iterations, n = number of genes, m = number of cells, and r = number of inner loop iterations. Since m and 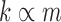are relatively small compared to n, n will dominate the run time. r is reflective of the quality of data—cleaner data will require less iterations. The minimum number of r is 2: one round to obtain an initial cluster and another round to verify that it is stable. Table 5 details BiSNN-Walk's outputs on the evaluation data sets.

Table 5.

BiSNN-Walk Output Information

	Time elapsed (s)	Average No. of inner loops	No. of clusters found (No. of real clusters)
Mouse	311	4	14 (13)
Human embryo	109	3.8	10 (9)
Human cancer	86	3.7	8 (11)

“Avg No. Inner Loops” is average number of inner loops called per round of outer loop, and can be interpreted as either the speed of convergence or quality of the data, as faster convergence is achieved with cleaner data.

3.1. Cell clustering results

3.1.1. Performance comparison versus SNN-Cliq

Adjusted Rand Index (ARI), a recommended metric to quantify agreement between clusters (Milligan and Cooper, 1986; Santos and Embrechts, 2009), was used to compare our clustering results against SNN-Cliq's. Please refer to Supplementary Appendix E for an overview of ARI. Direct comparison between the two clustering algorithms is not straightforward. First, SNN-Cliq requires the neighborhood parameter k and there is little guidance as to how to choose this parameter; we therefore obtained the SNN-Cliq clusters by varying k from 4 to 12 and considered the clustering result with the highest ARI; in other words, we purposely gave an advantage to SNN-Cliq's clustering result. In addition, neither BiSNN-Walk nor SNN-Cliq clustered all cells; therefore, we also used the number of clustered cells to gauge algorithm performance, with more cells clustered being more preferable.

From the results shown in Table 1, BiSNN-Walk is comparable to SNN-Cliq in terms of cell-clustering quality. For mouse data, ARI for SNN-Cliq is higher, but it only clustered about half of the cells. A major difficulty with this data set is distinguishing the three blastocyst stages. SNN-Cliq refused to cluster this stage almost entirely at optimal k parameter, which is why only 177 out of the 317 cells were clustered. In fact, if we force SNN-Cliq to cluster a similar number of cells (304/317) as BiSNN-Walk, SNN-Cliq's ARI drops down to 0.465, slightly lower than our result. For human cancer, SNN-Cliq has a much lower ARI even though the number of cells clustered is comparable. For human embryo, BiSNN-Walk has a slightly lower ARI, while the number of clustered cells is the same. Taking a closer look at the results, we found that BiSNN-Walk was not able to separate zygote, oocyte, and 2-cell-stage cells, whereas SNN-Cliq could. This problem does not appear if we had used Euclidean distance as an initial similarity matrix; in fact, in that case we actually have a slightly higher ARI than SNN-Cliq (0.798 vs. 0.796). This is yet another motivation for exploring the theoretical properties of our entropy-based measure so that we can select a more appropriate starting point.

Table 1.

Comparison Between Adjusted Rand Index of Final Clusters

	Mouse embryo	Human embryo	Human cancer
BiSNN-Walk	0.472 (311/317)	0.776 (124/124)	0.883 (82/86)
SNN-Cliq	0.574 (177/317)	0.796 (124/124)	0.661 (86/86)
GiniClust	0.098 (317/317)	0.379 (119/124)	0.870 (69/86)

Adjusted Rand Index are calculated against ground truth. Number in parentheses is (number of cells clustered/total number of cells).

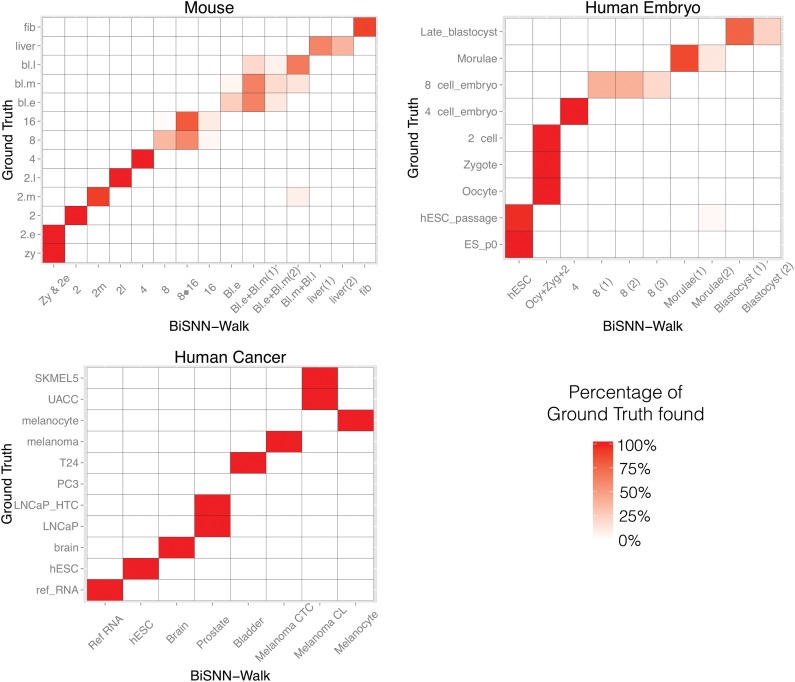
Figure 3 shows heatmaps of BiSNN-Walk clusters against ground truths. Both ground truth and BiSNN-Walk clusters are roughly ordered chronologically, and the visible diagonal block structure suggests strong concordance. As mentioned previously, it is difficult to separate 8- and 16-cell cells as well as the early-, mid-, and late-stage blastocysts; however, the diagonal structure of the heatmap indicates that developmental stages that are chronologically close are clustered together. Human embryo cell clusters are also ordered according to developmental stages. Similar to mouse data, the diagonal pattern is clearly visible, indicating that developmental stages are clustered by chronological proximity. Human cancer results are not ordered in any particular order, but as indicated by the diagonal structure and the high ARI score, most ground truth cell types are found perfectly. LNCaP cells (prostate cancer cell line cells) and LNCaP-HTC cells (prostate cancer cells isolated by EPCAM markers in Petri dish) could not be separated due to their close resemblance. SKMEL5 and UACC are two melanoma cell lines and could not be separated due to their similarity. The PC3 bladder cancer cell lines were not clustered because they were among the last four cells to be clustered, causing Walktrap to return two clusters of size 2, thus triggering the stopping condition.

FIG. 3.

BiSNN-Walk clusters compared to ground truths. x-Axis are the BiSNN-Walk clusters, and y-axis ground truth. The value in each grid represents the percentage of ground truth cluster that is in the BiSNN-Walk cluster. For example, in mouse data, the BiSNN-Walk cluster “Zy & 2e” contains all zygote and early-2-cell stage cells, thus the values in grids (“Zy & 2e,” “zy”) and (“Zy & 2e,” “2.e”) are both as follows. 1. The distinct diagonal pattern for all three data sets indicates that the ground truth was well recovered by BiSNN-Walk clusters.

3.1.2. Performance comparison versus selected algorithms

BiSNN-Walk is compared with GiniClust (Jiang et al., 2016), a recently published clustering algorithm specifically designed to handle scRNA-Seq data, and four general purpose biclustering algorithms: Plaid (Lazzeroni and Owen, 2002), (Cheng and Church, 2000), Xmotifs (Voggenreiter et al., 2012), and BiMax (Madeira and Oliveira, 2004). Please refer to Supplementary Appendix J for brief overviews of the algorithms.

To train each algorithm, we first find impactful tuning parameter(s) and explore a range of values where such parameters returned reasonable answers. We then pick candidate values from that range and perform an exhaustive search to choose the clustering most concordant with the ground truth (measured by Adjusted Rand Index). Again, we purposely gave an advantage to these methods for their parameter selections.

GiniClust returns nonoverlapping cell clusters, so we use ARI to measure its cell clustering performance. As the results in Table 1 show, BiSNN-Walk's clustering results surpass that of GiniClust's on all three data sets, as measured by ARI. GiniClust's performance on the developmental data sets, that is, mouse and human embryo, was unspectacular. It was able to cluster together cells that are roughly close in developmental stages but was not able to find the finer stages. This may be because GiniClust was designed to isolate small tight-knit rare cell types rather than general purpose biclustering. GiniClust's human cancer clusters were quite decent, although it only clustered 80% of the cells. Please find more detailed discussion on GiniClust results in Supplementary Appendix J.

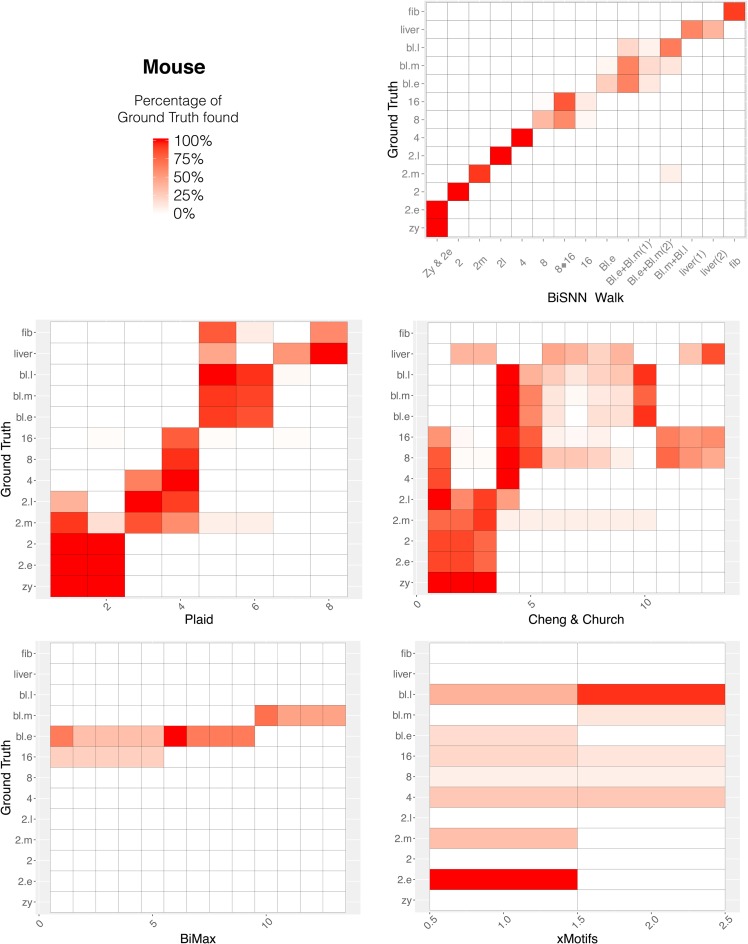
Because the other clustering algorithms allow overlapping cell clusters, ARI is not a suitable measure; thus, we will visually compare their results to BiSNN-Walk's. Figure 4 shows the cell clustering performance of each algorithm for the mouse data set. Among the four algorithms, only Plaid clusters showed a reasonable diagonal structure, indicating decent alignment with ground truth. A closer examination shows that the Plaid was able to cluster related cell stages together but did not have the specificity to obtain as fine a resolution as BiSNN-Walk clusters. Cell clustering results for other organisms show a similar theme and plots are shown in Supplementary Appendix J.

FIG. 4.

Cell clusters found by biclustering algorithm compared to ground truth for the mouse data set. x-Axis are the cell clusters found by indicated algorithm, ordered roughly by developmental stage. y-Axis is ground truth ordered by developmental stage. The value in each grid represents the percentage of ground truth cluster that is in each cell cluster. The lack of distinct diagonal patterns indicates that the cell clusters found by these algorithms were not homogenous.

3.2. Gene clustering results

One of the main features of our method is that it simultaneously clusters both cells and genes. We argue that our gene clusters indeed make sense using two methods of evaluation: gene overlap analysis and biological term-enrichment analysis.

In gene overlap analysis, we examine the overlap of top 100 characteristic genes of each cluster. Clusters that are more biologically similar should share more characteristic genes. For instance, mid-2-cell and late-2-cell stages should share more genetic drivers than, say, mid-2-cell and blastocyst stage. In enrichment analysis, we enrich the top 100 characteristic genes of each cluster and see whether the enriched terms make sense in the context of the cluster. For instance, for a cluster that contains mostly of brain cells, its characteristic genes should return neuron-related enriched terms. In other words, in gene overlap analysis, we check whether gene clusters make sense relative to each other, and in enrichment analysis, we verify whether the gene clusters are representative of their associated cell cluster.

3.2.1. Gene overlap analysis

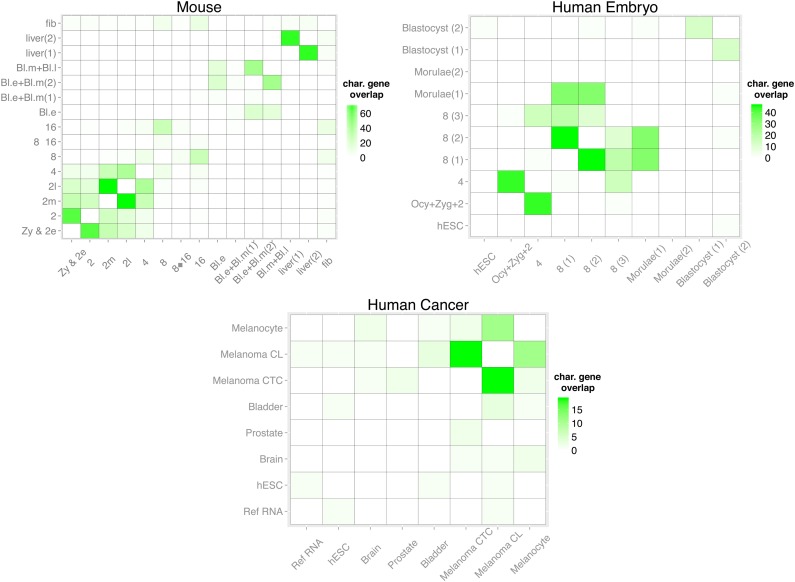
Figure 5 shows heatmaps of the overlap between top 100 characteristic genes between clusters. For mouse and human embryo data, the apparent block diagonal structure in Fig. 5 confirms the hypothesis that stages that are chronologically close will share more characteristic genes. For human cancer, as expected, we see very low overlap between clusters of different cell types except a somewhat elevated association between “Melanoma CTC” (circulating melanoma cells) and “Melanoma CL” (cancer line melanoma cells), which is reasonable, since they are of the same cell type. However the reason why we only see an overlap of 15 genes may be explained by previous observation that CTC profiles are quite distinct from those of cancer cell lines (Powell et al., 2012).

FIG. 5.

Overlap between top 100 characteristic genes. The color saturation indicates the number of overlapping genes between the top 100 characteristic genes of two clusters. Maximum value for each grid is therefore 100.

3.2.2. Biological enrichment analysis

To perform enrichment analysis, we took the top 100 characteristic genes for each cluster and checked whether enrichment terms make sense with respect to the types of cells in the cluster. GO term enrichment was used for human cancer data, whereas anatomy enrichment was performed on mouse data. Since anatomy enrichment is not available for human, no enrichment analysis was performed for human embryo. Selected enrichment results are shown in Tables 6 and 7, respectively. Enrichment was performed using InterMine's Python API (Smith et al., 2012).

Table 6.

Enriched Terms for Mouse Embryo Data Set

Cluster name	Cell types	Enriched terms
Zy & 2.e	Zygote early-2-cell	Germ cell of ovary
		Germ cell of gonad
		2-Cell stage conceptus
2	2-Cell	2-Cell stage conceptus
		1-Cell stage conceptus
2.m	Mid-2-cell	2-Cell stage conceptus
		1-Cell stage conceptus
		4-Cell stage conceptus
2.l	Late-2-cell	2-Cell stage conceptus
		1-Cell stage conceptus
4	4-Cell	2-Cell stage conceptus
8	8-Cell
8–16	8-Cell
	16-Cell
Bl.e	Early-blastocyst	embryo endoderm
	Mid-blastocyst	endoderm
Bl.e+Bl.m(1)	Early-blastocyst	primitive endoderm
	Mid-blastocyst	endoderm
	Late-blastocyst	early conceptus
Bl.e+Bl.m(2)	Early-blastocyst
	Mid-blastocyst
	Late-blastocyst
Bl.m+Bl.l	Late-blastocyst
	Mid-blastocyst
	Mid-2-cell
Liver(1)	Liver	Liver
		Liver lobe
		Liver and biliary system
Liver(2)	Liver	Liver
		Liver lobe
		Liver and biliary system
Fib	Fibroblast	Tendon
		Mesenchyme
		Bone

Cluster name is a nickname given to the reported cluster based on its cell type composition. Cell types lists the cell types found in the reported cluster. Enriched terms lists relevant ontological terms. As one can see, liver, fibroblast, and early developmental stages were well enriched. Early- and mid-blastocyst clusters also saw relevant enrichment. For Bl.e+Bl.m(2) and Bl.m+Bl.l clusters, significant terms were found, but were not reported since they did not seem relevant to the developmental stage. No significant terms were found for 8-cell and 16-cell clusters. Please refer to Supplementary Data for full list of enriched terms. EMAPA mouse development anatomy ontology database was used for enrichment.

Table 7.

Enriched Terms for Human Cancer Data Set

Cluster name	Cell types	Enriched terms
Ref_RNA	Reference RNA
hESC	Human embryonic stem cells	Stem cell population maintenance
		Somatic stem cell population maintenance
		Embryo development
Brain	Brain	Neuron part
		Axon part
		Synapse part
Prostate	LNCaP cell line cells
	LNCaP_HTC Petri dish extracted
Bladder	T24 bladder cancer cell line
Melanoma CTC	Circulating melanoma tumor cells
Melanoma CL	SKMEL5 melanoma cell line	Melanosome membrane
	UACC melanoma cell line
Melanocyte	Melanocyte	Melanosome membrane

Cluster name is a nickname given to the reported cluster based on its cell type composition. Cell types lists the cell types found in the reported cluster. Enriched terms lists relevant ontological terms. As one can see, four of the eight clusters saw relevant enrichment. Ref_RNA saw a wide mix of significant terms, as expected. Significantly enriched terms were returned for all clusters except Melanoma CTC, but were not reported since they did not seem relevant to the particular cell type. For the full list of enriched terms, please refer to Supplementary Data.

Mouse result shows highly relevant enriched terms for somatic cells (fibroblast, liver) and early embryonic cells (2-cell and 4-cell stage). Eight-cell to blastocyst cells were not enriched well because the clusters themselves are quite heterogeneous in the first place. Most of the human cancer cells have highly relevant enriched terms. No enrichment was found for prostate and bladder cancer clusters because none of the 82 prostate genes and 11 bladder-related genes was part of the gene expression in the first place.^† This indicates that these organs are poorly studied. The lack of enrichment in the “Melanoma CTC” cluster, as argued previously, is likely due to the genetic profile of CTCs exhibiting stark departure from Melanocyte and Melanoma cell line cells, both of which are significantly enriched with the term “melanosome.”

4. Discussion and Future Work

Clustering is an important tool for genetic analysis; however, finding important genes associated with those clusters is sometimes of more scientific interest. In this work, we presented a simple, fast, and self-correcting biclustering algorithm BiSNN-Walk, based on SNN-Cliq (Xu and Su, 2015). Results from applying BiSNN-Walk to three large scRNA-Seq studies showed that BiSNN-Walk is able to retain and even improve SNN-Cliq's clustering performance. Moreover, since BiSNN-Walk extracts cluster one at a time according to their “tightness” (measured by transitivity and conductance), the order in which the clusters is found can be reflective of their reliability. Being a biclustering algorithm, BiSNN-Walk also returns characteristic genes ranked by their relevance to the associated cell cluster. We have shown from multiple perspectives that BiSNN-Walk returns biologically sensible biclusters. We note that the clustering algorithm SNN-Walktrap can be replaced if a better method is available.

We used a simple entropy-based measure as a guidance to choose among initial similarity matrices. Using entropy as a surrogate for “clusterability” is a novel idea, and in our case it served well for choosing a highly clusterable similarity matrix as initial input. Further investigations on this idea are underway. Several other areas of the algorithm can be improved. The stopping criterion is currently too naive and should be further investigated and improved. The definition of characteristic genes is a bit ad hoc. Although it worked well in the three public data sets, a systematic way of tuning this parameter would greatly improve usability.

Acknowledgments

The authors thank Dr. Daniel Ramsköld for discussions about the data sets, Dr. Marcus Stoiber and Dr. Nathan Boley for guidance on processing of RNA-Seq data, and Dr. Ke Liu for pointing toward the Intermine project for ontological enrichment analysis. This work has been partially supported by NSF DMS-1160319 and NIH U01-HG007031.

Author Disclosure Statement

No competing financial interests exist.