Catch Bonds at T Cell Interfaces: Impact of Surface Reorganization and Membrane Fluctuations

Abstract

Catch bonds are characterized by average lifetimes that initially increase with increasing tensile force. Recently, they have been implicated in T cell activation, where small numbers of antigenic receptor-ligand bonds at a cell-cell interface can stimulate a T cell. Here, we use computational methods to investigate small numbers of bonds at the interface between two membranes. We characterize the time-dependent forces on the bonds in response to changes in the membrane shape and the organization of other surface molecules. We then determine the distributions of bond lifetimes using recent force-dependent lifetime data for T cell receptors bound to various ligands. Strong agonists, which exhibit catch bond behavior, are markedly more likely to remain intact than an antagonist whose average lifetime decreases with increasing force. Thermal fluctuations of the membrane shape enhance the decay of the average force on a bond, but also lead to fluctuations of the force. These fluctuations promote bond rupture, but the effect is buffered by catch bonds. When more than one bond is present, the bonds experience reduced average forces that depend on their relative positions, leading to changes in bond lifetimes. Our results highlight the importance of force-dependent binding kinetics when bonds experience time-dependent and fluctuating forces, as well as potential consequences of collective bond behavior relevant to T cell activation.

Introduction

Membrane-associated proteins experience a variety of forces at the interface between interacting cells. The forces can arise from sources including membrane undulations, cell motion, and active cytoskeletal processes (1). In the context of cell adhesion, there has been significant interest in protein-protein bonds known as catch bonds, which have average lifetimes that initially increase with an increasing tensile force (2, 3). This is in contrast to the more prevalent slip bond, which has an average lifetime that decreases with increasing force (4). Well-studied examples of catch bonds include adhesion proteins that mediate shear-enhanced adhesion, such as selectins in leukocytes (5) and FimH in Escherichia coli (6, 7, 8). Catch bonds are also involved in maintaining the integrity of multicellular tissues in cadherin-based adhesions (9, 10), and emerging evidence suggests that T cells use catch bonds in their search for antigens on the surfaces of other cells (11, 12).

T cells orchestrate the adaptive immune response and use the T cell receptor (TCR) complex to engage membrane-presented ligands on the surfaces of other cells as they scan for antigen. An outstanding question in immunology is how the T cell reliably distinguishes between self and foreign ligands while being sensitive to even a single antigenic ligand (13, 14, 15). A number of recent studies have shown that TCRs can exhibit catch-bond behavior when engaged with stimulatory ligands, which raises the intriguing question of whether the catch-bond behavior contributes to the T cell’s specific and sensitive response (11, 12, 16).

The TCR binds to peptide fragments presented by major histocompatability complex proteins (pMHC) on the surfaces of other cells. The binding kinetics between the TCR and pMHC are thought to largely control T cell activation (17, 18), yet kinetics are difficult to measure in situ (19, 20, 21). Work has begun to elucidate the importance of forces on the TCR at the T cell interface (22). For example, insight has been gained from experimental methods including optical tweezers (12, 23), biomembrane force probes (11, 24), atomic force microscopy (25), nanoparticle tension sensors (26), and traction force microscopy (27, 28). Some of these studies have directly measured TCR-pMHC binding times as a function of force, showing binding kinetics consistent with catch-bond behavior (11, 12, 24).

In this article, we focus on TCR lifetime data from Liu et al. (11), who measured the force-dependent average lifetime of OT1 TCRs bound to ligands of varying stimulatory strength. As shown in Fig. 1, they observed that stimulatory ligands (OVA and A2) exhibited catch-bond behavior whereas other ligands (E1 is shown here) exhibited slip-bond behavior. The off-rate of a slip bond is commonly described by the Bell model (4),

$$k_{\text{off}}^{\text{slip}}\left(f\right)=k_0{e}^{f/f_0},$$ (1)

where k₀ is the off-rate at zero applied force, f is the applied force on the receptor-ligand complex, and f₀ is the reference force. A number of simple mathematical models for catch-bond kinetics exist, with a common description being the two-pathway model (29),

$$k_{\text{off}}^{\text{catch}}\left(f\right)=k_c{e}^{-f/f_c}+k_s{e}^{f/f_s},$$ (2)

where c denotes catch-phase parameters and s denotes slip-phase parameters. The average lifetime of a bond is given by $k_{\text{off}}^{-1}$. Fig. 1 also includes fits of the data that were obtained using a nonlinear least-squares fitting procedure (parameters are tabulated in the Supporting Material).

Figure 1.

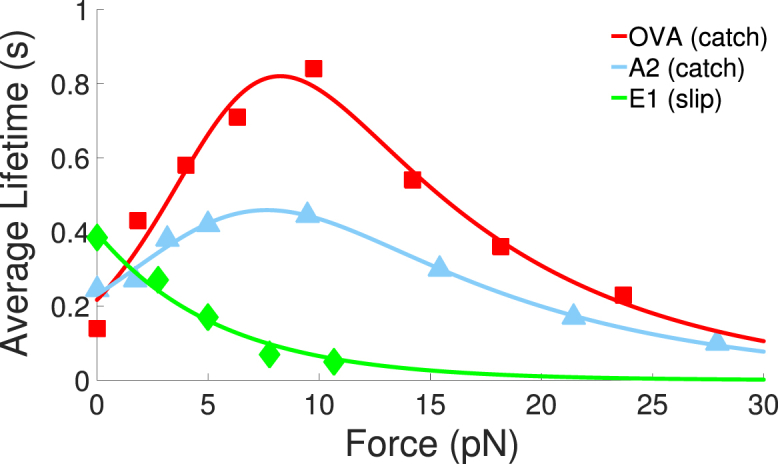
Force-dependent lifetime data (points) for the OT1 TCR bound to three different ligands. Data points are from Liu et al. (11). OVA and A2 exhibit catch-bond behavior. Solid lines are nonlinear least squares fits to the data using Eq. 1 for E1 and Eq. 2 for OVA and A2. To see this figure in color, go online.

It is interesting to consider the implications of catch-bond behavior in the context of antigen discrimination by T cells, as many factors influence the formation and dissociation of TCR-pMHC complexes at the T cell interface. For example, differences between the lengths of the TCR-pMHC complex and other key surface proteins have led to the kinetic-segregation model for TCR triggering, in which large proteins are excluded from regions near TCR-pMHC complexes (30, 31). This is due to the relatively short distance between membranes imposed by the TCR-pMHC complex (≈13 nm) that restricts access of longer molecules such as the transmembrane phosphatase CD45 (∼50 nm) (32). The exclusion of CD45 is proposed to locally alter the balance of kinase and phosphatase activity near the intracellular domain of the TCR complex (30). It is energetically unfavorable to bend membranes over short length scales, and the coupling of protein size exclusion to membrane bending mechanics can lead to deformations of the membrane, a large-scale reorganization of the membrane, and a time-dependent force on a single TCR-pMHC bond (32, 33, 34, 35).

Although experiments have studied the effects of a fixed force on TCR-pMHC bonds, it is unclear how small numbers of catch bonds at the cell-cell interface are influenced by dynamic forces resulting from membrane shape changes, reorganization of long surface molecules, and thermal fluctuations. In this work, we consider a computational framework that represents small numbers of bonds at the interface of a T cell and an antigen-presenting cell. We begin by introducing the framework and computational methods. We then explore the dynamic response to the formation of one or more fixed bonds, characterizing the resulting membrane reorganization, the time-dependent forces experienced by the bonds, and the resulting distribution of bond lifetimes. By using the data discussed above, we assess the influence of catch- versus slip-bond binding kinetics in the context of TCR binding.

Materials and Methods

Membrane dynamics

We consider a framework in which two apposed membranes are connected by one or more static intermembrane bonds. The membranes are modeled as continuum surfaces characterized by a bending rigidity that penalizes membrane deformations. The intermembrane bonds constrain the membranes to reside at a fixed distance apart at the location of the bonds. The membrane shape and distribution of long surface molecules evolve in time in response to the presence of bonds.

We consider a square domain and denote the position- and time-dependent distance between the membranes by z(x,y,t). The concentration of long surface molecules is denoted by C_SM(x,y,t) and the total energy of the system is

$$E\left[z,C_{\text{SM}}\right]=\iint dxdy\left(\frac{\kappa }{2}{\left({\nabla }^{2}z\right)}^2+C_{\text{SM}}{E}_p\right),$$ (3)

where κ is the membrane bending rigidity and E_p is the energy associated with compression of the long surface molecules (32, 33, 36). The total energy is composed of two parts: the first is the bending term of the Helfrich Hamiltonian in the limit of small deformations (37), which penalizes bending of the membrane. The second part penalizes the presence of long surface molecules if the local membrane separation differs from their natural length, z_p. The compressional energy takes the form E_p(x,y,t) = k_p(z_p – z)²/2. Position and time arguments are omitted for clarity.

We adopt a hybrid computational scheme to characterize the dynamics of the intermembrane distance profile (z) and the concentration profile of long surface molecules (C_SM): C_SM is governed by an advection-diffusion equation and the membrane adapts by mechanically equilibrating in response to the changing concentration profile. Given a membrane shape, the concentration of long surface molecules changes according to

$$\frac{\partial C_{\text{SM}}}{\partial t}=D{\nabla }^2{C}_{\text{SM}}+\frac{D}{k_{\text{B}}T}\nabla \cdot \left(C_{\text{SM}}\nabla E_p\right),$$ (4)

where D is the diffusion coefficient and k_BT is the thermal energy. Thus, the concentration of long surface molecules evolves in time in response to the shape of the membrane, which affects E_p. To solve the advection-diffusion equation, we employ an explicit forward-time difference method and spatially discretize the system, using central finite difference approximations with periodic boundary conditions. After each time step, we use Metropolis Monte Carlo computer simulations to generate a membrane configuration that is sampled from thermal equilibrium. Allard et al. (32) adopted a similar framework in which the equilibrated membrane separation profile was solved using a generalized Euler-Lagrange equation to minimize the energy. Using Monte Carlo methods allows one to account for thermal fluctuations in the membrane shape and provides flexibility in solving systems with various distributions of intermembrane bonds.

We initialize the system by assuming that one or more intermembrane bonds have formed and that long surface molecules are homogeneously distributed with concentration C_SM,0. Locations with bonds are pinned to their natural length (13 nm). We first equilibrate the intermembrane height profile given the presence of bonds and the uniform distribution of long surface molecules. The concentration profile of long surface molecules is propagated forward in time using the advection-diffusion equation, after which the membrane height profile is equilibrated. This process is then repeated to determine the time evolution of the system.

Parameters used in the model are summarized in Table 1. The system size is 510 nm × 510 nm, which is sufficiently large such that finite-size effects do not influence the results. The spatial discretization size is Δx = 10 nm, which is commensurate with the footprint of a single TCR complex within the T cell membrane (38). The time step is chosen to ensure stability of the numerical solutions of the advection-diffusion equation (Supporting Material) (39). To assess the effects of bending rigidity, we consider two values (κ = 12.15 and 40 k_BT) that span biologically relevant values (32, 40, 41, 42). The compressional stiffness, k_p = 0.1 pN/nm, is consistent with previous estimates (32) and is sufficiently large to drive segregation of long surface molecules away from TCR-pMHC bonds.

Table 1.

Model Variables and Parameters

Variable	Definition	Value	Units
CSM(x,y,t)	concentration of long SMs	—	[μm−2]
z(x,y,t)	intermembrane distance	—	[nm]
CSM,0	initial concentration of SMs	1000	[μm−2]
D	diffusion coefficient	0.01	[μm2/s]
κ	membrane bending rigidity	12.15, 40	[kBT]
kp	compressional stiffness of SMs	0.1	[pN/nm]
zp	natural length of SMs	50	[nm]
z0	TCR-pMHC complex height	13	[nm]
Δx	lattice spacing	10	[nm]
Δt	time step	7.5 × 10−4	[s]

SMs, surface molecules.

Monte Carlo simulations

Monte Carlo simulations are used to update the spatially discretized distance profile z(x,y,t). Trial configurations are generated by randomly choosing a lattice site and perturbing the distance by a uniformly sampled random variable between −0.05 and 0.05 nm. After calculating the resulting energy change (ΔE) using Eq. 3, the trial configuration is either accepted or rejected according to the Metropolis criterion: Energetically favorable (ΔE < 0) trial configurations are accepted; otherwise, the trial configuration is accepted with probability exp(−βΔE), where β = 1/k_BT. After bonds are placed between the two membranes, we run the initial equilibration for 10⁵ × 51² attempted configuration updates. After each update to C_SM, the membrane height profile is equilibrated for 5 × 10³ × 51² attempted updates. The number of steps required for equilibration is significantly smaller because the changes are more subtle after the initial binding event. For each set of conditions considered below, we run 10 independent trajectories.

In the results, we are interested in the effects of thermal fluctuations. As such, we also conduct simulations in which we let β → ∞ in the Metropolis criterion. For these simulations, any trial configuration with ΔE ≤ 0 is accepted and any energetically unfavorable trial configuration is rejected. Thus, the energy decreases monotonically. In results below, we refer to simulations “without thermal fluctuations” when β → ∞.

Bond tension and survival probability

The force experienced by a bond at time t is given by $f\left(t\right)={\partial E/\partial z|}_{\mathbf{x}={\mathbf{x}}_0}$, where x₀ denotes the position of the bond (32). We compute the derivative numerically by perturbing the intermembrane distance upward and downward from its constrained value of z₀ (43). Given the time-dependent tension on the bond, we calculate the distribution of rupture times. For every time step Δt, the probability that a bond ruptures is

$$p_{\text{rup}}\left(f\right)=1-e^{-k_{\text{off}}\left(f\right)\text{Δ}t},$$ (5)

where k_off(f) is the force-dependent dissociation rate. We report the calculated distributions in terms of the survival probability, S(t), which gives the probability that a bond has not ruptured by time t,

$$S\left(t\right)=\stackrel{N_t-1}{\prod _{i=0}}\text{exp}\left(-k_{\text{off}}\left(f\left(t_i\right)\right)\text{Δ}t\right).$$ (6)

Here N_t = t/Δt denotes the number of time intervals and f(t_i) is the force at time t_i.

Results

We begin by examining a system with a single bond. We characterize the membrane response to bond formation, the time-dependent bond tension and associated fluctuations, and the probability that the bond remains intact as a function of time. We then explore the impact of an additional bond as the distance between bonds is varied.

Bond formation drives membrane reorganization

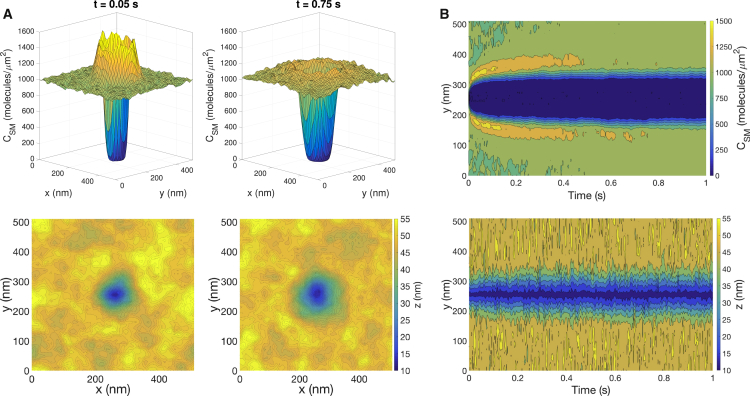
The formation of an intermembrane bond causes a response in the membrane shape (z) and in the distribution of long surface molecules (C_SM). Fig. 2 A shows snapshots of z and C_SM from a sample trajectory with a single bond at the center of the domain. Because the TCR-pMHC bond is shorter than the surrounding long surface molecules, there is an energetic penalty for molecules near the bond. This leads to a rapid expulsion of long surface molecules from the region near the bond, leading to a ring of high concentration that can be observed at t = 0.05 s. The size of the region in close apposition increases slightly between the two time points, and fluctuations in the distance profile are reflected in the nonuniform shape of this region and in the heterogeneity of z far from the bond.

Figure 2.

Characteristic response to the formation of a bond (with thermal fluctuations). (A) Shown are snapshots of the concentration of long surface molecules (top row) and the intermembrane distance (bottom row) with κ = 12.15 k_BT. Each column corresponds to a different time point. The bond is located at the center of the domain. (B) Kymographs of C_SM and z from a one-dimensional slice containing the bond are shown. To see this figure in color, go online.

To more completely characterize the time-dependence of z and C_SM, we consider a one-dimensional strip containing the bond and plot the time-dependence of z and C_SM along the strip as a kymograph (Fig. 2 B). For C_SM, there is a broadening of the region depleted in long surface molecules (i.e., the “depletion zone”) and an eventual dissipation of the high-concentration ring due to the diffusion of molecules from the ring into the region far from the bond. For z, one can see a slight broadening of the deformed region and the presence of fluctuations, although the shape of the deformation remains largely stable. Results for κ = 40 k_BT are qualitatively similar with a broader depletion zone, and analogous results from simulations in which thermal fluctuations are neglected are included in the Supporting Material. In this case, the membrane shape evolves to minimize energy at each time point. The results are qualitatively similar to Fig. 2, but the lack of thermal fluctuations in the membrane shape leads to smoother features.

The influence of bending rigidity and thermal fluctuations on membrane relaxation are more clearly observed in Fig. 3. Here, we plot the characteristic diameter of the depletion zone, d(t) = (4A_dep(t)/π)^1/2, where A_dep is the area of the membrane with C_SM ≤ 0.01 C_SM,0. For the two bending rigidities considered, the size of the depletion zone increases more rapidly for the case with thermal fluctuations, although the difference is more pronounced at the larger value of κ. Fig. 3 also demonstrates the effect of membrane bending rigidity on the size of the domain surrounding the bond. Because larger values of κ impose higher energetic penalties for bending, the intermembrane shape with κ = 40 k_BT adopts a locally flatter shape near the bond, and a larger footprint overall. This in turn leads to a larger region in which it is energetically unfavorable for long surface molecules to reside. Thus, increasing the membrane stiffness, κ, promotes the formation of a larger depletion zone. The size of the depletion zone is consistent with results from Allard et al. (32), in which a depletion zone of ≈80 nm formed with κ = 12.15 k_BT.

Figure 3.

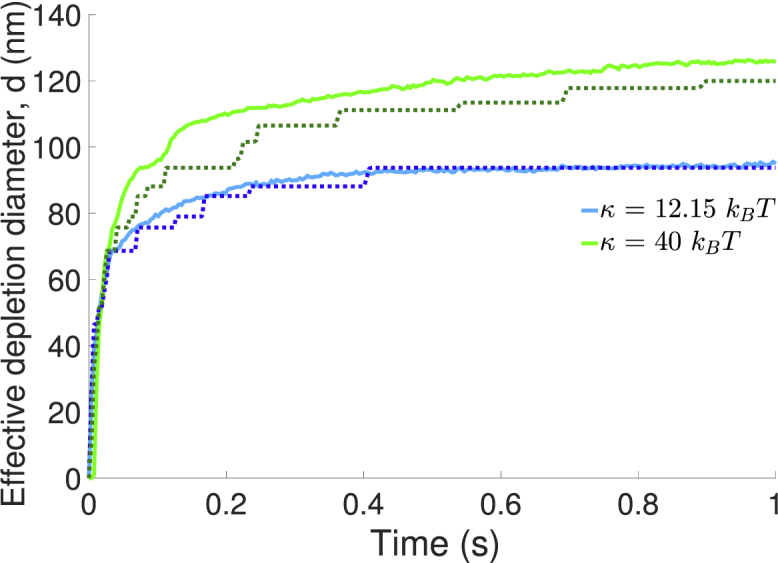
Time evolution of the effective diameter (d) of the depletion zone. Data is averaged over 10 independent trajectories for each condition. Simulations with thermal fluctuations (solid lines) lead to a more rapid expansion of the depletion zone than simulations without thermal fluctuations (dashed lines). Increasing the membrane stiffness, κ, promotes the formation of a larger depletion zone. To see this figure in color, go online.

Bonds experience a time-dependent tension with fluctuations driven by membrane shape fluctuations

When a bond forms, changes in membrane shape and surface organization alter the energy profile near the bond, which leads to a time-dependent force on the bond. As the system evolves toward more energetically favorable configurations, the average tension on the bond decreases. In Fig. 4, we compare the average tension experienced by a bond both with and without thermal fluctuations. Increasing the membrane bending rigidity (κ) leads to a larger average tension on the bond. The presence of thermal fluctuations leads to a smaller initial average force and a faster decay of the tension, which is consistent with the faster relaxation of the membrane discussed above. The difference is more pronounced at larger κ.

Figure 4.

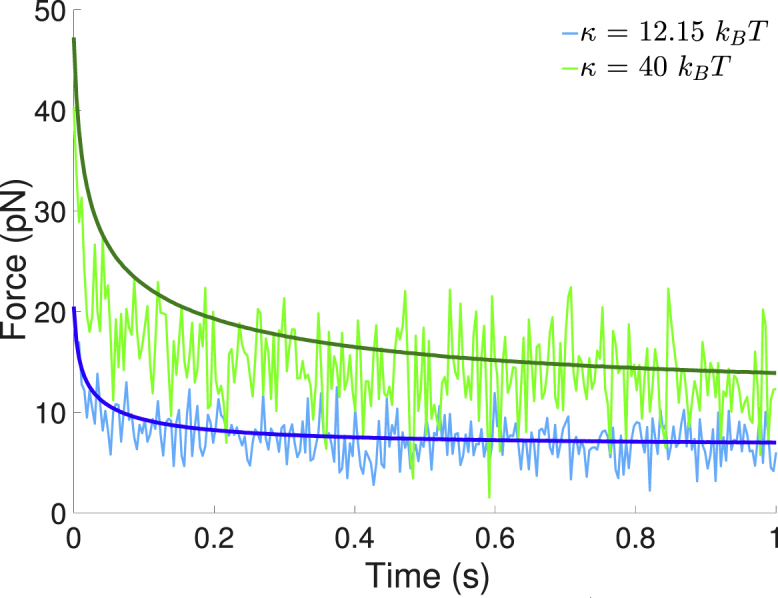
Average bond tension as a function of time. The average tension at each time point is calculated by averaging the tension from 10 independent simulation trajectories with κ = 12.15 k_BT (blue) and κ = 40 k_BT (green). The cases without fluctuations are shown in darker shades. To see this figure in color, go online.

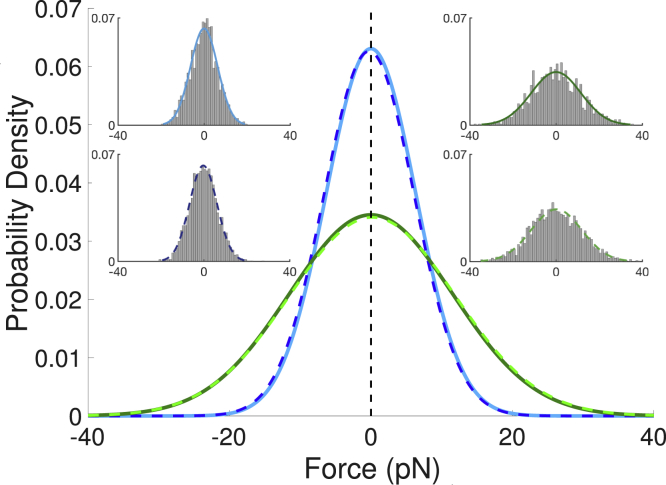
Comparing cases with and without thermal fluctuations, it is evident that membrane fluctuations lead to significant fluctuations in the force on the bond. To characterize the force fluctuations, we determine the distribution of forces for t > 0.5 s, as the depletion zone is almost completely formed during this time. For κ = 12.15 k_BT, the bond experiences a force of $7.07\pm 6.32$ pN (average ± SD); for κ = 40 k_BT, the bond experiences 13.5 ± 11.6 pN. The distribution of mean-centered forces is shown in Fig. 5, which demonstrates the broader range of fluctuations at the larger bending rigidity. By comparison, without fluctuations, the average force on the bond at t = 1 s is 6.99 pN for κ = 12.15 k_BT and 13.9 pN for κ = 40 k_BT. The forces at κ = 12.15 k_BT are smaller than those reported by Allard et al. (32), although they follow the same characteristic decrease over time and are within the range of forces obtained when parameters in their model were varied within biologically relevant regimes.

Figure 5.

Gaussian fits of the probability densities for the mean-centered forces obtained from simulations with and without long surface molecules present. Results are shown for κ = 12.15 k_BT (blue) and κ = 40 k_BT (green). Histograms of mean-centered force data are included as insets for cases with (solid) and without (dashed) long surface molecules. Each condition uses data from 10 trajectories, with forces for t > 0.5 s used when long surface molecules are present. To see this figure in color, go online.

The concentration of long surface molecules near the bond is small, suggesting that the fluctuations are a consequence of fluctuations in z near the bond. For comparison, we also consider a system with a single bond and no surface molecules. For such a system, there is no driving force for the membrane to deform. Thus, the average membrane separation should be 13 nm throughout the domain and the average force on the bond should be negligible because the membrane is locally flat on average. In our simulations, the mean force on the bond is ≈0 pN, as expected. We plot the distribution of forces in Fig. 5 along with the mean-centered forces from the cases with long surface molecules. The distributions are strikingly similar, which suggests that inherent shape fluctuations, independent of the surface molecules, drive the fluctuations in the force. It also underscores how a bond, even with zero average tension, can experience large forces due to shape fluctuations alone.

The physical picture that emerges from these results is that the evolving average shape of the membrane near the bond leads to a changing average tension on the bond. Fluctuations in z in the region surrounding the bond give rise to fluctuations in the bond tension with the characteristic size of the force fluctuations similar to the characteristic size at an undeformed interface.

Catch bonds enhance binding times

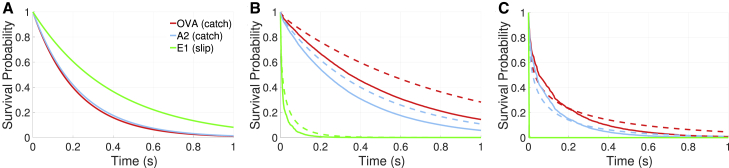
Given the forces characterized above, we now investigate their impact on the binding times of different ligands relevant to OT1 T cell activation. Fig. 6 shows the average survival probability as a function of time for the three ligands shown in Fig. 1. At zero applied force, the slip bond (E1) has the longest average lifetime, which is consistent with its survival probability being higher than the two stimulatory catch bonds (Fig. 6 A). When the slip bond experiences time-dependent forces, the bond ruptures more quickly (Fig. 6, B and C), with bonds breaking almost immediately at the higher bending rigidity. At the lower bending rigidity, the survival probability decays more rapidly with fluctuations. Because the time-dependence of the average force is similar both with and without fluctuations, fluctuations involving larger forces increase the likelihood of bond rupture and enhance the decay of S(t).

Figure 6.

Survival probabilities for different ligands. Each survival probability curve is calculated by averaging 10 independent survival curves. Different ligands (OVA, A2, and E1) are considered with (solid) and without (dashed) thermal fluctuations. (A) For survival probabilities with zero applied force, the slip bond (E1) exhibits the longest average lifetime. (B) Shown here are survival probabilities with κ = 12.15 k_BT. (C) Shown here are survival probabilities with κ = 40 k_BT. To see this figure in color, go online.

When forces are taken into account (Fig. 6, B and C), both catch bonds (OVA and A2) are far more likely to remain intact than E1. Furthermore, OVA, which is the more potent agonist, is more likely to remain intact than A2. At κ = 12.15 k_BT, the survival probabilities for catch bonds decay more quickly when thermal fluctuations are taken into account. At κ = 40 k_BT, the survival curves with fluctuations initially decay more slowly, but eventually fall below the curves without fluctuations. The initial decay is consistent with the average force plots (Fig. 4), where the difference in the average force is most pronounced at short times for κ = 40 k_BT. At longer times, when fluctuations are neglected, the average force decays to values close to the peak of the lifetime curve (Fig. 1). However, for the case with fluctuations, even though the average force leads to relatively long lifetimes, the fluctuations enhance the likelihood of bond rupture.

Thus, the physical picture that emerges is that thermal fluctuations lead to faster relaxation of the membrane and a more rapid decrease in the average force on a bond. This can have the effect of enhancing the survival probability of a bond at short times, as for the catch bonds with κ = 40 k_BT. However, if the average force on the bond is close to the force that maximizes the lifetime, the fluctuations lead to a smaller average lifetime.

The distance between bonds impacts bond tensions and survival probabilities

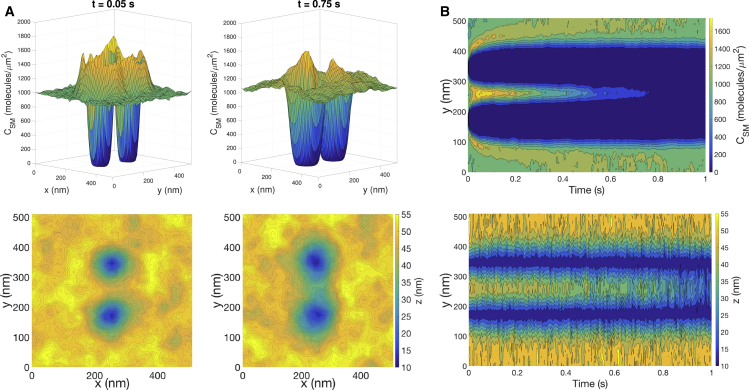
When a T cell interacts with another cell, multiple TCRs are likely to engage pMHC and mutually influence each other’s behavior. In this section, we investigate cooperative effects by introducing a second bond that is separated by a fixed distance (20, 40, 80, and 160 nm). As before, we characterize how the separation distance influences membrane organization, forces on the bonds, and survival times of the bonds. In a dynamic intermembrane environment, it is likely that TCR-pMHC mobility would lead to the bonds changing their positions to achieve more favorable energy configurations. We focus on fixed separations to carefully assess the resulting forces without complications of bond motion. The results give insight into trends related to bond tensions at different separation distances and are expected to provide a good approximation of the membrane dynamics at short timescales. Fig. 7 shows snapshots and kymographs of the surface molecule concentration and distance profile for two bonds separated by 160 nm. At this distance, a separate depletion zone forms around each bond at short times, but by 1 s, the depletion zones merge with each other. A single domain develops at shorter times for all cases in which the bonds are closer.

Figure 7.

Characteristic response to the formation of two bonds separated by 160 nm (with thermal fluctuations). (A) Shown are snapshots of C_SM (top row) and z (bottom row) with κ = 12.15 k_BT. Each column corresponds to a different time point. (B) Kymographs of C_SM and z from a one-dimensional slice containing both bonds are shown. To see this figure in color, go online.

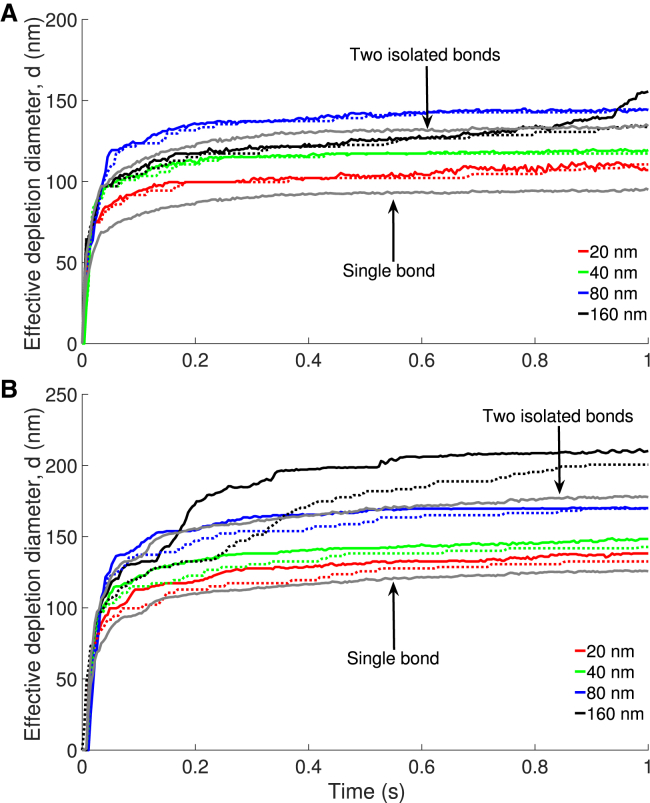
Fig. 8 shows the characteristic size of the depletion zone (d) at various distances between the bonds. As for a single bond, stiffer membranes lead to larger depletion zones. Additionally, thermal fluctuations expedite the formation of depletion zones at κ = 40 k_BT. With separations of 20, 40, and 80 nm, a single depletion zone forms at short times. It takes longer to form a single domain for the largest separation (160 nm), which is reflected by the depletion zone having a delayed second phase of growth that does not converge during the simulation. The drive to form a single domain is a consequence of the larger bending energy associated with having two minima in z rather than a single domain. If the separation between the two bonds is small, the intermembrane distance profile quickly adopts a single minimum and long surface molecules rapidly vacate the region between the bonds. As the distance between bonds increases, there is a smaller driving force to form a single depletion zone because the energetically unfavorable perimeter of the region grows. At sufficiently large bond separations, the domains would remain approximately independent. At small κ, the driving force to form a single domain is also smaller, and hence the long surface molecules persist for longer in the region between the bonds.

Figure 8.

Time evolution of the effective diameter (d) of the depletion zone for two bonds separated by different distances. Data is averaged over 10 independent trajectories for each condition. Results with (solid) and without (dashed) thermal fluctuations are shown for (A) κ = 12.15 k_BT and (B) κ = 40 k_BT. To see this figure in color, go online.

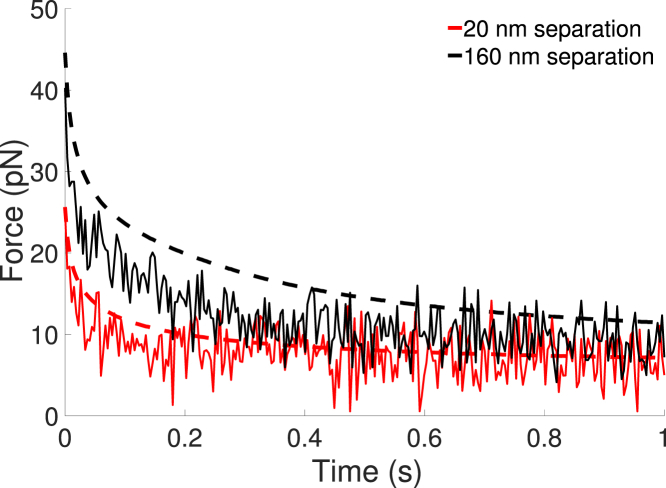
The distance between the bonds affects the time-dependent tension experienced by each bond in the system. Fig. 9 compares the average force on a bond given that a second bond is 20 or 160 nm away. The force is reduced when the bonds are close to one another, and the tension is similar to that of a single bond when the bonds are well separated. Table 2 shows the average force at long times on a bond for various separation distances. The average force increases as the separation distance increases. When two bonds are sufficiently close, they share the load associated with deforming the membrane, and each experiences a smaller force than a single, isolated bond.

Figure 9.

Average force on a bond when a second bond is a fixed distance away. Results with (solid) and without (dashed) thermal fluctuations are shown for κ = 40 k_BT. For each case, data is averaged over 10 independent trajectories. The average bond tension increases with increased separation. To see this figure in color, go online.

Table 2.

Average Force and SD on a Bond Given that a Second Bond Is Located a Fixed Distance Away

	κ = 12.15 kBT	κ = 40 kBT
Separation (nm)	〈f〉 ± σ (pN)	〈f〉 ± σ (pN)
20	3.43 ± 6.16	7.06 ± 11.38
	3.63	7.14
40	3.56 ± 6.24	7.23 ± 11.39
	3.79	7.38
80	3.78 ± 6.01	7.56 ± 11.74
	4.25	8.11
160	6.87 ± 6.34	9.67 ± 11.63
	7.16	11.42
Single bond	7.07 ± 6.32	13.46 ± 11.60
	6.99	13.90

The averages and SDs are calculated for t > 0.5 s. Forces reported without SDs are the average force at the final time point (1 s) of simulations without thermal fluctuations. 〈f〉, Average force; σ, SD.

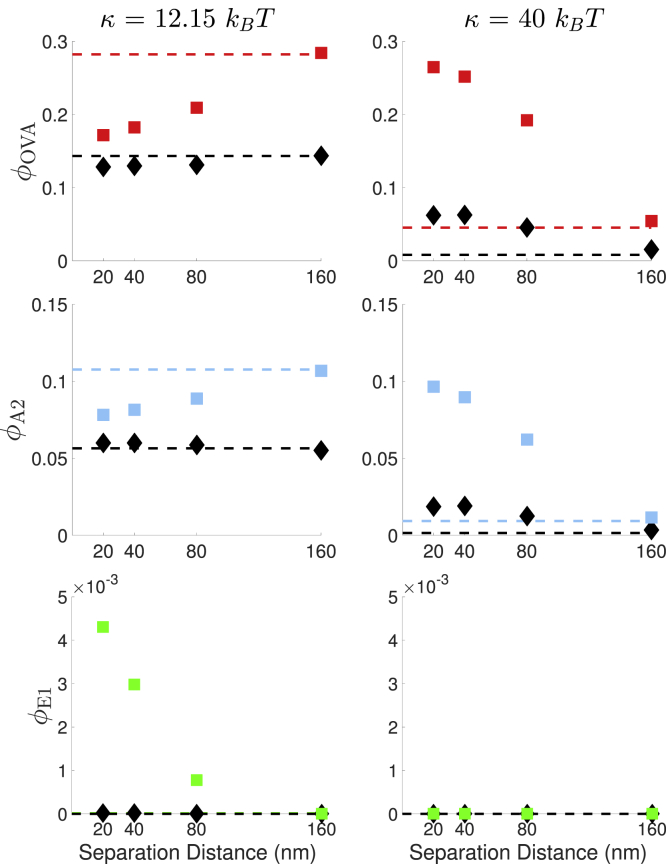
For each distance separating the two bonds, we characterize the average survival probability over time for a bond given that the other bond remains intact. Fig. 10 shows the fraction of bonds that remain after 1 s (denoted by ϕ) for each survival probability curve. Thermal fluctuations reduce ϕ for all cases considered, and the value of ϕ at the largest separation distance is similar to that of a single, isolated bond. At κ = 12.15 k_BT, load sharing between two catch bonds (at separation distances of 20, 40, and 80 nm) decreases the fraction bound in the absence of fluctuations but has minimal influence when fluctuations are present. This is because the average force when two bonds are close gives an effective lifetime that is similar to the zero-force case (shorter lifetime). However, fluctuations sample a broader distribution of lifetimes, weakening the dependence on the average force. At κ = 40 k_BT, load sharing between two catch bonds enhances the binding fraction both with and without fluctuations. This is because the average force at long times is close to the force that maximizes the lifetime of the bond. For all cases, the slip bond is significantly less likely to remain intact at 1 s.

Figure 10.

Fraction of bonds that remain at t = 1 (ϕ) as a function of bond separation distance. Rows correspond to different ligands (OVA, A2, and E1) and columns correspond to different values of κ. Results with (diamonds) and without (squares) fluctuations are shown. For comparison, the value of ϕ corresponding to a single bond is plotted as a horizontal line. It is similar to the value of ϕ for a bond when another is 160 nm away. For every condition tested, the catch bonds have a larger binding fraction than the slip bond. To see this figure in color, go online.

Discussion

The results above describe the time-dependent force experienced by bonds tethering two membranes when bond formation drives changes in membrane shape and organization of long surface molecules. Given recent experimental data that measured the average force-dependent lifetime of a TCR bound to various ligands (11), we characterized resulting bond-rupture distributions using the dynamically changing tension on the bond. For all of the cases we considered, the forces on the bonds lead to a higher survival probability of catch bonds (OVA and A2) compared with the slip bond (E1). This is in contrast to their behavior at zero force, when the slip bond remained intact longer on average. In this section, we further discuss features of the force fluctuations, the role of catch bonds in enhancing lifetimes and buffering fluctuations, and additional biological features such as collective effects when multiple bonds are present.

Features of force fluctuations

In Fig. 5, we showed that the mean-centered distribution of forces on a single bond was strikingly similar to the force distribution with no surface molecules present. This similarity holds despite the different average force experienced by the bonds in the two cases. Thus, even though the average shape of the membrane leads to a nonzero force on the bond when long surface molecules are present, the fluctuations in shape lead to the same distribution of fluctuations about the mean. The characteristic size of force fluctuations is also similar when multiple bonds are present (Table 2). We have assumed that the concentration of long surface molecules is governed by a deterministic advection-diffusion equation, which ignores fluctuations in local copy numbers of the molecules. However, because the long surface molecules are almost completely excluded from the region around the TCR-pMHC bond, fluctuations in the local concentration are expected to have a negligible influence on the bond tension.

It is interesting to view the survival probability curves in the context of the force fluctuations. Due to large fluctuations, the bonds occasionally experience forces far exceeding the average force. For large forces, the off-rate grows exponentially, k_off(f) ≈ k_s exp(f/f_s). Thus, a concern might be that large forces might effectively sever the bond due to the large off-rate. We tested the effect of the sampling time by recalculating the survival probability curves using the force at every other time point (doubling the sampling time). This has the effect of making fluctuations longer-lived, yet we find marginal changes in the survival probability curves. Thus, there is no evidence that outliers in the rupture probability significantly alter the survival curves. Additionally, this provides support for the assumption of mechanical equilibrium of the membrane, as fluctuations that stay correlated over longer times do not significantly change the survival probability curves.

Catch bonds buffer fluctuations

Our results suggest that catch bonds may buffer against thermal fluctuations when compared with slip bonds. For example, consider an average bond tension that is close to the force maximizing the bond lifetime. The slope of the lifetime curve is small (Fig. 1), and thus small fluctuations in the force do not significantly affect the off-rate. To further explore this, consider the effective off-rate given an average force (f_A) on a bond. Assuming a Gaussian distribution of fluctuations, we can write the ratio of the effective (average) off-rate to the off-rate evaluated at the average force as

$$\frac{{\langle k_{\text{off}}\left(f_A\right)\rangle }_f}{k_{\text{off}}\left(f_A\right)}=\frac{1}{k_{\text{off}}\left(f_A\right)\sqrt{2\pi {\sigma }^2}}{\int }_{-\infty }^{\infty }df{k}_{\text{off}}\left(f_A+f\right)\text{exp}\left(-\frac{f^2}{2{\sigma }^2}\right).$$ (7)

Using Eqs. 1 and 2 for k_off(f), we computed this quantity for the three different ligands using values of σ obtained from simulations. Fig. S3 shows the value of this ratio for a range of f_A. For all values of f_A, the ratio is largest for the slip bond. Thus, fluctuations increase the effective off-rate of the slip bond by the greatest factor, and the catch bonds suppress the effects of force fluctuations in comparison.

We can further evaluate the effective off-rate at large values of the force. In particular, for catch bonds with f_A ≫ f_c, averaging over the fluctuations gives

$$\frac{{\langle k_{\text{off}}\left(f_A\right)\rangle }_f}{k_{\text{off}}\left(f_A\right)}=\text{exp}\left(\frac{{\sigma }^2}{2f_s^2}\right).$$ (8)

Thus, the effective off-rate is larger than k_off(f_A), with broader distributions (larger σ) leading to higher effective off-rates. Note that the catch bonds have values of f_s approximately two times larger than the corresponding parameter (f₀) in the slip-bond model. For a given value of σ, the larger value of f_s suppresses the ratio for the catch bonds in comparison with the slip bond. From Fig. S3, it can be seen that this approximation is good when f ≳ 15 pN.

To investigate how the parameters in Eq. 2 influence bond dissociation, we consider the case of OVA and independently vary two of the four parameters at a time. Fig. S4 summarizes the survival probability of a single bond for four different combinations of parameters with κ = 12.15 k_BT. When the slip-phase reference force f_c ≲ 5 pN, bonds are likely to rupture before 1 s. Because the bonds commonly experience forces exceeding 5 pN, the slip-phase kinetics strongly influence the overall dissociation rate. For a given value of k_c, the survival fraction of the TCR-pMHC bond at 1 s is largely independent of the catch-phase reference force (f_c) when f_c ≳ 15 pN. Because most forces experienced by the bond are less than 15 pN, the catch-phase contribution to the off-rate does not decay significantly from k_c. Overall, these results suggest that the parameters for OVA reside close to a regime in which the force profile experienced by the bond significantly enhances the survival probability.

Additional bonds and other biological features

When a T cell interacts with an antigen-presenting cell, multiple TCRs are likely to interact with a variety of pMHCs, including many with endogenous peptides that are not stimulatory. In the previous section, we showed that a second bond reduced the average force on each bond when they were sufficiently close. To further explore cooperative binding effects, we added a third bond to the system and focused on a configuration in which the three bonds are colinear. Table 3 contains the average forces on the middle bond and the two other bonds, which we call “edge bonds”. It is interesting to note that when the receptors are close, the bond in the middle experiences a negative average force. The two edge bonds lead to an average configuration that, in the absence of the middle bond, would adopt a minimum intermembrane distance (z) smaller than the bond length (z₀). Including the middle bond forces the membrane to deviate upward, which leads to a compressive average force on the bond.

Table 3.

Average Force and SD on Edge Bonds and the Center Bond in a Configuration with Three Colinear Bonds

	Edge Bonds 〈f〉 ± σ (pN)	Center Bond 〈f〉 ± σ (pN)
20 nm separation	10.89 ± 11.31	−7.64 ± 10.81
40 nm separation	10.20 ± 11.68	− 4.58 ± 11.34
80 nm separation	10.06 ± 11.51	−0.46 ± 11.40

The separation distance is the distance between each edge bond and the center bond. The averages and SDs are calculated for t > 0.5 s. 〈f〉, Average force; σ, SD.

The case of three bonds highlights the importance of characterizing the dissociation kinetics of a bond under a compressive force. To our knowledge, there has been no extended study or discussion of catch bonds under compressive forces. In this work, we assumed that the off-rate was an even function of force, k_off(−f) = k_off(f). For comparison, we also considered the cases in which 1) negative forces were treated as equivalent to the zero-force case and 2) Eqs. 1 and 2 were evaluated without modification at negative values of the force. Resulting survival probabilities for the different cases are shown in Fig. S5. For a single bond, the assumption had relatively small effects, as most forces sampled were positive. However, for cases in which negative forces are common, more significant differences emerge. Because of the ambiguity regarding bonds under compressive force, we did not present survival curves for the cases without long surface molecules (〈f〉 = 0) or for the cases with three bonds (〈f〉 < 0 for the center bond). Experimental investigations of bonds under compressive force would be useful given the high likelihood that receptor-ligand bonds at intermembrane junctions experience both positive and negative forces. Such forces may arise due to membrane deformations, shape fluctuations, and active processes such as those mediated by the actin cytoskeleton.

It is useful to consider additional features of the T cell to contextualize the results of this article and to highlight potential areas for future theoretical development. The local bending rigidity of the T cell membrane is influenced by numerous factors including lipid content, the presence of the cortical actin cytoskeleton, and membrane structures such as microvilli (1, 44). We considered two values of the bending rigidity that span a biologically relevant range, observing that stiffer membranes result in larger forces on the TCR-pMHC bond. Hence, characterizing the local bending rigidity of the membrane is important for understanding forces on the TCR-pMHC bond. Forces on the bond can also arise from other sources such as actin-mediated processes and cell motion. Actin modulates the binding kinetics of TCR-pMHC bonds in situ and helps to regulate T cell activation, but many of the underlying mechanisms connecting actin to T cell activation remain unclear (45). At short times, actin and associated myosin motors may contribute additional forces to the TCR-pMHC bond in an additive manner by effectively pushing or pulling on the membrane near the TCR, thus shifting the average forces described in this work and modulating survival probabilities. Motion of T cells induced by external fluid flow also imposes forces on TCR-pMHC bonds. The motion impacts the entire T cell interface, where multiple TCR-pMHC bonds and adhesion complexes would likely share the load.

The results presented above assumed TCR-pMHC bonds had a fixed length (z₀ = 13 nm). Recent experimental studies have suggested that the TCR undergoes conformational transitions leading to large changes in the TCR-pMHC bond length (12, 46). In the Supporting Material, we demonstrate that a longer TCR-pMHC bond (z₀ = 22 nm ) decreases the average force on the bond (Fig. S6) and increases the survival probability of the bond (Fig. S7). Conformational changes of the TCR could be incorporated into the simulations by introducing a force-dependent length transition (from z₀ to z₀′) that would lead to a dynamic change in local membrane shape and a decreased force on the bond. In our simulations, we also assumed a fixed length of long surface molecules (z_p = 50 nm). Because the T cell interface contains many types and sizes of surface molecules, we also conducted simulations with z_p = 40 nm to assess the effects of surface molecule length. A decrease in the length of the long surface molecules leads to a smaller average force on the bond (Fig. S6) and an increase in the survival probability (Fig. S7). Multiple types of surface molecules could be introduced into the model by considering additional concentration fields associated with different values of z_p.

Conclusion

A growing body of work has revealed the importance of forces in T cell activation. Recent experiments measuring the force-dependent lifetimes of TCR-pMHC bonds have revealed the surprising finding that TCRs can behave as catch bonds when bound to stimulatory pMHCs. This is suggestive from a mechanistic standpoint, as force-dependent regulation of TCR-pMHC binding times provides a physical mechanism that could help T cells discriminate between self and foreign peptides.

Our approach provides a way to characterize the impact of surface molecule reorganization and membrane shape changes over times relevant to the earliest stage of T cell activation. We focused on immobile bonds to carefully characterize the time-dependent forces over a 1 s time period. In reality, TCR-pMHC bonds can diffuse and are influenced by the actin cytoskeleton, although actin-mediated forces initiated by TCR engagement are likely most relevant at later times (25). TCR-pMHC mobility is likely to promote the aggregation of bonds that are in close proximity, and both receptor mobility and actin-mediated forces will be interesting features to consider in future theoretical settings.

Our results indicate that agonist catch bonds are more likely to remain intact than an antagonist slip bond when the bonds experience a time-dependent and fluctuating force. After initial cell-cell contact, the presence of a single TCR-pMHC bond that is sufficiently long-lived could promote the formation of other TCR-pMHC bonds nearby, as the local intermembrane distance accommodates the bond formation. This could lead to an effective feedback and clustering mechanism in which the new bonds would reinforce the contact between the cells by sharing the load of deforming the membrane. Furthermore, the average time a bond remains intact is short enough to enable serial engagement of TCRs by antigenic pMHCs (47, 48, 49, 50), with binding likely to be promoted by fast in situ binding kinetics (19, 20). We anticipate that continued experimental progress and theoretical developments will lead to a better understanding of the mechanical modulation of TCR binding kinetics, which will enhance our understanding of how T cells act as specific and sensitive detectors of antigen.

Author Contributions

R.H.P. III and S.M.A. designed research. R.H.P. III performed research. Both authors analyzed data and wrote the manuscript.

Editor: Michael Dustin.