Abstract
We develop a new statistical mechanical model to predict the molecular crowding effects in ion-RNA interactions. By considering discrete distributions of the crowders, the model can treat the main crowder-induced effects, such as the competition with ions for RNA binding, changes of the electrostatic interaction due to crowder-induced changes in the dielectric environment, and changes in the nonpolar hydration state of the crowder-RNA system. To enhance the computational efficiency, we sample the crowder distribution using a hybrid approach: for crowders in the close vicinity of RNA surface, we sample their discrete distributions; for crowders in the bulk solvent away from the RNA surface, we use a continuous mean-field distribution for the crowders. Moreover, using the Tightly Bound Ion (TBI) model, the model accounts for ion fluctuation and correlation effects in the calculation for ion-RNA interactions. Applications of the model to a variety of simple RNA structures such as RNA helices show a crowder-induced increase in free energy and decrease in ion binding. Such crowding effects tend to contribute to the destabilization of RNA structure. Further analysis indicates that these effects are associated with the crowder-ion competition in RNA binding and the effective decrease in the dielectric constant. This simple ion effect model may serve as a useful framework for modeling more realistic crowders with larger, more complex RNA structures.
Graphical Abstract
Introduction
In vivo cellular environment is highly crowded.1, 2 The crowding agents can occupy up to 30% by volume fraction,3, 4 and can influence the cell chemical activity, physical structures and in vivo functions of biological molecules including RNAs.2, 4, 5 For example, crowders can increase the oligomerization and aggregation of proteins,2 diminish the diffusion of small molecules and macromolecules, and strongly restrict the mobility of larger particles and organelles.6, 7
Previous studies showed that crowding molecules can significantly affect RNA structure, folding stability, and dynamics.8–17 One of the important crowding effects is on the ion-RNA interactions. Crowding molecules (crowders) may influence the ion distribution around the RNA and ion-mediated RNA stability through three main effects: (a) crowder volume exclusion which causes competition with ions for RNA binding,2 (b) crowder-induced changes in the effective dielectric environment,8 and (c) changes in RNA hydration energy due to crowder-RNA binding.2
Because an RNA carries a significant amount of negative charges on the backbone, ion binding is critical for the stabilization of an RNA structure.18, 19 Most bound ions accumulate in the major and minor grooves (distance within 8 Å from the helix axis) and the surface region (10 to 15 Å from the axis). 20–23 The presence of crowders, which can occupy the space around RNA surface, may cause an exclusion of ions from RNA binding28 and hence lower the number of bound ions. Furthermore, crowders may have a lower effective dielectric constant than water, thus can enhance phosphate-phosphate repulsion and cation-RNA attraction, resulting in a change in the total electrostatic free energy. The above crowder-induced changes are dependent on the overall crowder volume fraction24 as well as the discrete spatial distribution of the crowders.
In addition to the effect on electrostatic interactions, crowders can also influence RNA folding through non-electrostatic effects. For example, the excluded volume of the crowders can impose a significant restriction on the conformational space of the RNA, especially for the unfolded state.2, 10 Such non-electrostatic effects, together with the electrostatic effects, can cause the shift in the equilibrium for the ion-RNA system and result in a new equilibrium for the ion-crowder-RNA system.
Recently, the crowding effect has received increasing attention both in theoretical and experimental studies.1, 2 Regarding the crowding effect in RNA folding, there have been two main conclusions about the crowding effects. First, it was found that crowders can stabilize the folded state of an RNA. For example, neutral cosolutes have been found to stabilize the tertiary structure of hammerhead ribozyme as indicated by the enhanced ribozyme activity.25 Consistent with the experimental findings, coarse-grained computer simulations showed that crowders can enhance pseudoknots stability relative to hairpins.26 Physically, this is because the volume exclusion from the crowder can reduce RNA conformational entropy, and the effect is more pronounced for the extended conformations than for the compact conformations, which causes a stabilization of the compact state.27 Second, it was found that crowders can induce destabilization of RNA secondary structure due to the preferential base-crowder (osmolyte) interaction in the unfolded state, where bases are solvent (osmolyte) accessible.28 In contrast, for tertiary structure, the competition between the favorable base-osmolyte (over water-osmolyte) contact and the unfavorable backbone-osmolyte (over water-osmolyte) contact can lead to a much more complicated, structure and ion-dependent crowding effects on RNA folding stability.28 These results highlight the necessity to develop a quantitative model for the various synergistic or competitive effects.
In parallel to experimental studies,29–37 several theories have been developed to model the crowding effect in ion-RNA interactions.2, 8, 38 For example, without considering the discrete crowder distributions and crowder excluded volume, a Poisson-Boltzmann equation-based model with an effective crowder volume has been developed to study the crowding effect on protein solubility.8 Molecular dynamics simulations have the advantage to explicitly account for the atomistic interactions between the crowders and the macromolecules (proteins and RNAs),38 however, the application of the method to treat crowding systems is limited by the exceedingly large sampling space of the crowder and ion distributions. We need a new approach for the sampling of discrete spatial distributions of the crowders and ions.
In this paper, we report a new model for predicting the crowding effect in ion-RNA electrostatic interactions. To efficiently sample the crowder distribution, we divide the space around the RNA according to the strength of crowding effect. For crowders in the region close to the RNA surface, whose excluded volume and dielectric effects may significantly affect ion-RNA interactions, we consider discrete distributions for the crowders. For crowders further away from the RNA surface, we account for the crowder’s electrostatic effect using a crowder volume fraction-dependent dielectric constant. Such a model allows us to treat ion-crowder competitions in RNA binding. Moreover, we can estimate the non-polar hydration energy of RNA from the change of solvent accessible surface area (SASA).
Crowding model for an ion-crowder-RNA system
We first sample crowder distributions, then for each crowder distribution, we sample ion distributions, from which we compute the electrostatic free energy and predict ion binding properties. Finally, ensemble average over all the possible crowder distributions gives the crowding effects in the ion-crowder-RNA system.
1. Sampling of the crowder distributions
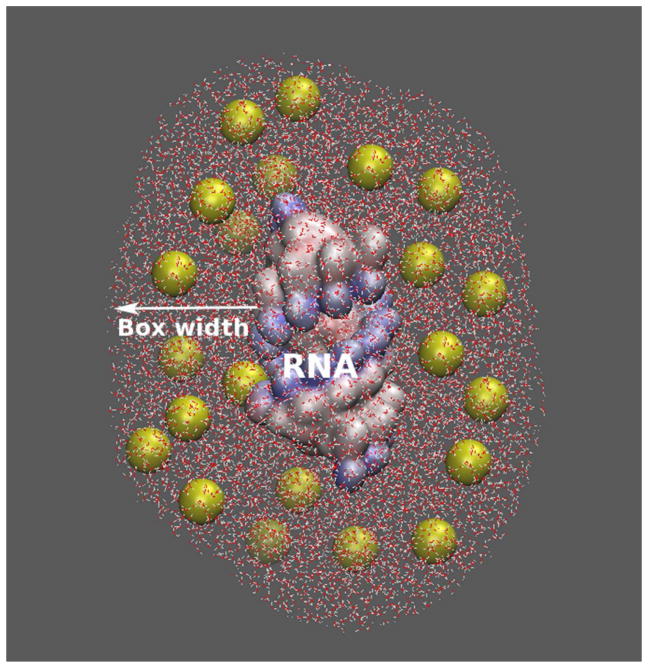
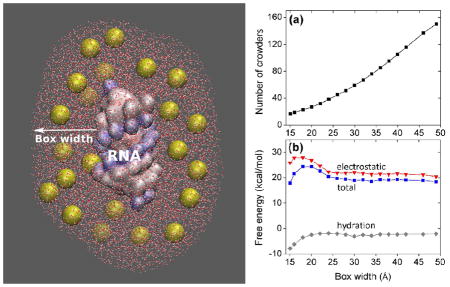
We use a 12-base pair (bp) RNA helix to illustrate the approach. In the experimental studies, polyethylene glycol (PEG) has been widely used to mimic crowding agent in biomolecular systems.29, 39, 40 A PEG polymer is quite flexible and its conformational state can be modelled with self-avoiding random walk. The “average structure” of PEG600 may be treated as a globular shape with radius of gyration equal to 7.0 Å.39, 40 The low electron density of PEG (compared to water) makes it useful for data collection and analysis. In addition, PEG molecular can be treated as an inert polymer, which has weak surface interactions with RNA. This property allows us to ignore specific chemical interactions between crowders and RNA. Following the experimental studies,29, 39, 40 we use PEG600 as the crowding agent. To further simplify the system, we simulate the crowders as spheres (see Figure 1) with dielectric constant εc of 20.0 and radius 7.0 Å (the radius of gyration for PEG600).24, 29, 40
Figure 1.
A schematic illustration of crowding molecules (yellow spheres) surrounding an RNA helix and a snapshot of discrete crowder distribution in the Inner Sampling Box (ISB).
In the sampling of discrete crowder distribution, in order to minimize the boundary effect, we set a large sampling box around the RNA (see Figure 1). For a box of 140 Å × 140 Å × 140 Å surrounding the 12-bp RNA helix, there are about 200 crowding spheres for a volume fraction fc equal to 20%. We randomly place the 200 spheres on the different grid sites using (uniform) Monte Carlo sampling. We model the crowders as hard spheres and disallow overlapping between crowders, ions, and RNA (due to the excluded volume effect). The sampling process leads to a large ensemble of crowder distributions. The complete sampling for the crowder distribution is prohibited by the exceedingly long computational time. To circumvent this problem, we develop a hybrid model, which accounts for discrete crowder distributions in the “important” region (near the RNA surface) and mean-field distributions in other regions (far away from the RNA).
Because the bound ions are distributed in the close vicinity of the RNA, crowders around the RNA surface (the “important region”) can have strong influence on ion-RNA interactions. Mathematically, we highlight such important regions using an “Inner Sampling Box” (ISB) around the RNA (see Figure 1). The boundary of the ISB is defined as the normal distance (“ISB width” or box width) measured from the RNA surface into the solution. Because the diameter of the crowder is assumed to be 14 Å, regardless of the RNA structure, the minimum ISB width should always larger than 14 Å. Our tests indicate that the results predicted by the model would be robust for the ISB width larger than a parameter that is weakly dependent on the RNA structure (see the section “Estimation of the optimal ISB width” below).
Inside the ISB, we sample discrete crowder distributions. Outside the ISB, we model the the crowder effects using uniform crowder distribution with an effective dielectric constant εeff:8
| (1) |
where εw (=78) is the dielectric constant of the crowder-free solution, εc (=20) is the dielectric constant of the crowder, and fc is the volume fraction of the crowder.
2. Ion-RNA electrostatic interaction model (for a given crowder distribution)
Ions, especially multivalent ions around the RNA, can involve high local concentration (~ several molar concentration) and can thus become strongly correlated. To account for the ion correlation and fluctuation effects, we use the previously developed Tightly Bound Ion (TBI) model.41–43 The basic idea of the TBI model is to consider correlated ion distributions by enumerating discrete, many-body ion distributions. Mathematically, this is achieved by distinguishing two different regions: the tightly bound (TB) and the diffusely bound (DB) regions, corresponding to the regions of ions with strong and weak Coulomb correlations, respectively. Depending on the ion concentration, the tightly bound (TB) region is usually a thin layer surrounding the RNA and the diffusely bound (DB) region covers the rest region (in the bulk solution away from the RNA surface). The correlation effect for monovalent ions (e.g., K+ and Na+) is negligible unless for very high ion concentrations (e.g., several molar concentration). In contrast, the correlation for multivalent ions (e.g., Mg2+) around the RNA surface can be strong even for submillimolar bulk concentrations. The diffuse ions are described by a continuous distribution determined by the Poisson-Boltzmann (PB) equation while the TB ions are treated with discrete ion distributions. To enumerate the distribution of the TB ions, TB ions are placed into the different ”cells” where each cell is a region around a phosphate. The ensemble of TB ion distributions is generated by the different ways to assign the TB ions to the different cells. We call each such ion distribution M as an “ion binding mode”.
The presence of the crowders can hinder the placement of the TB ions. Moreover, the crowders, as dielectric spheres, can influence the dielectric environment in the ISB. Therefore, the boundary of the TB region, the available ion binding modes, and the electrostatic energy for each ion binding model are all dependent on the crowder distribution C . For a given crowder distribution C and ion binding mode M, the electrostatic energy for the electric charges in the TB region can be computed as the sum of the self-energy, the polarization energy, and the Coulomb energy of the charges:41–43
| (2) |
| (3) |
| (4) |
| (5) |
where εin (~20) and εw (~78) are the dielectric constants of the RNA-crowder system and water, respectively, BP is the Born radius of backbone phosphate, Bi is the Born radius of the ion, and is the Born radius of an isolated ion far away from the RNA, qP and qj are the charges of phosphate and ion, respectively, rmn is the distance between the m-th and the n-th charges.
The electrostatic free energy for a given ion binding mode M is equal to the sum of the above free energy for the TB ions and the free energy for the diffuse ions and the interaction between the TB ions and the diffuse ions (solved from PB).41–43 Ensemble average over all the different modes M gives the mean electrostatic free energy for a given crowder distribution C:
The nonpolar solvation energy for a given crowder distribution C is calculated from the change of the solvent accessible surface area Δσ(C):44–46
where the surface tension coefficient λ is equal to 0.0054 kcal/(mol·Å2) and G0 is equal to 0.92 kcal/mol.47–49 The change in the solvent accessible surface area Δσ(C) for a given crowder distribution C is defined as:
| (6) |
where is the solvent accessible surface area of RNA-crowders complex, i.e., the crowder-RNA system, σRNA and are the surface areas of the separated RNA and crowders, respectively.
3. Ensemble average over crowder distributions
The ensemble average over the crowder distribution C gives the total mean free energies:
| (7) |
Here the P(C) is the probability function for the crowder distribution. The total free energy ΔGtot is the sum of the electric and the non-electric hydration energies:
| (8) |
4. Estimation of the optimal ISB width
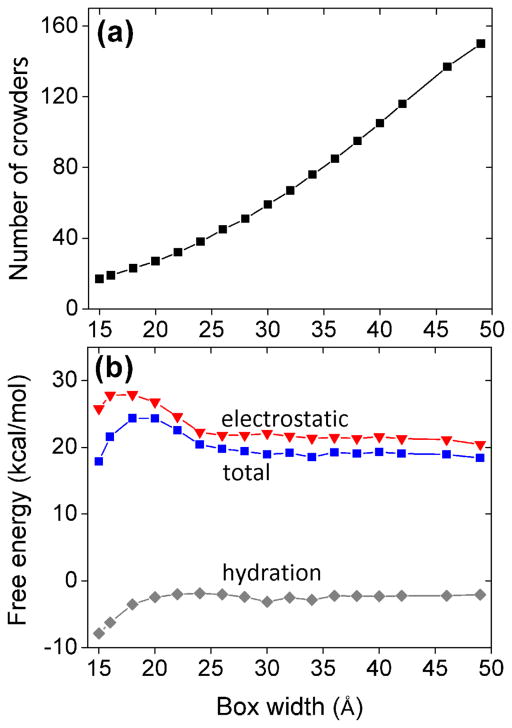
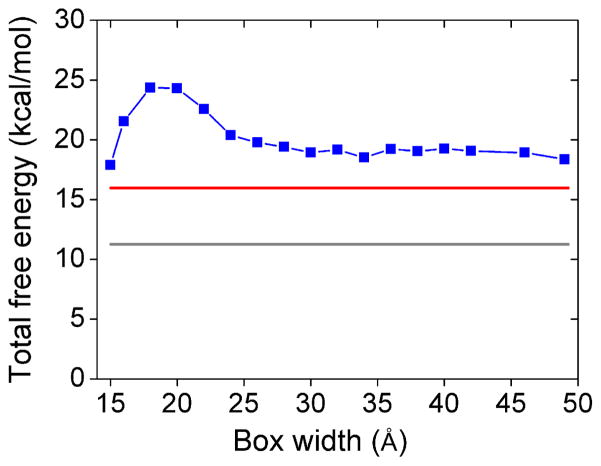
One of the important issues in the model is the selection of the ISB width. Ideally, to enhance the sampling efficiency, a smaller ISB is desirable. However, to ensure the robustness and accuracy of model, ideally the ISB should be large enough such that the theoretical predictions would be insensitive to the choice of the ISB width. Physically, such a robustness suggests that on the boundary, the effect of discrete crowder distribution can smoothly match that of the uniform continuous distribution. To find the optimal choices of the ISB width, we test the sensitivity of the electrostatic free energy to the ISB width (see Figure 2). For a 12-bp RNA helix in a solution at 25°C with 0.1M NaCl, 0.01M MgCl2, and 20% volume fraction of crowder, we find that for box width less than 20 Å, the free energy is sensitive to the box width, indicating a strong dependence of the dielectric and excluded volume effects on the discrete crowder distributions around the ISB boundary. As the box size increases, the crowding spheres on the ISB boundary is relatively distant from the RNA, thus, the crowding effect on ion-RNA interaction, which predominantly occurs around the RNA surface, is less sensitive to the discrete crowder distribution. Indeed, we find that the free energy converges to a stable result for large sampling boxes. In the test system, the diameter of the spheres is 14 Å. Thus, in order to minimize the boundary effect of the sampling box, we allow sufficient ISB space to accommodate at least two crowder spheres between the RNA surface and the boundary of the sampling box. This estimation sets an acceptable minimum box width of 28 Å. In our calculation, we choose box width 30 Å. For box width larger than 30 Å, the total free energy and the free energy components become stable against the variation of the box width (see Figure 3).
Figure 2.
The numbers of crowders inside the ISB and the free energy changes calculated with the different box widths. (a) The number of crowding spheres in the ISB for the different box widths. The results for calculated for a 12-bp RNA helix in a solution of crowders with (fixed) volume fraction (fc = .2) and ions with 0.1M NaCl and 0.01M MgCl2. (b) The predicted hydration energy ΔGsurface (gray), electrostatic energy ΔGele (red), and the total energy ΔGtot (blue) for the same system as in (a).
Figure 3.
The predicted total free energy ΔGtot of a 12-bp RNA helix structure as a function of the ISB box width in a solution with (blue) crowders (volume fraction fc = 20%) and (gray) no crowders (fc = 0). Also shown in the figure is the result (red) with a uniform dielectric constant εeff equal to 66.4 (Eq. 1) for the solution (without considering the discrete crowder distributions). For all the three cases, the solution contains 0.1M NaCl and 0.01M MgCl2.
We also examine the box width for the different volume fractions of the crowder. As shown in Figure S1, the total free energy increases quickly with the volume fraction and converges faster for larger volume fraction. For volume fractions 0.10 and 0.15, the ideal box widths are 40 Å and 32 Å, respectively. We further calculate the number of crowders in the ISB and find there must exist at least 50 crowders in the box (see Figure S2) in order for the predicted results to be stable.
Crowding effects on ion-RNA interaction
As a dielectric medium, a crowder is assumed to have a lower dielectric constant (εc = 20.0) than water (εw = 78.0). Therefore, crowders tend to lower the effective dielectric screening effect and hence strengthen the charge-charge interactions. As a result, crowders can enhance the backbone charge repulsion and cause an increase of the electrostatic energy. Moreover, crowders can further reduce ion binding, especially in the major/minor grooves, through crowder-ion volume exclusion. The major groove in RNA helix is narrow (typical width ~ 4–5 Å). For example, for a series of RNAs with the different sequence lengths, 12-bp RNA helix, BWYV pseudoknot (PDB ID: 437D), T2 pseudoknot (PDB ID: 2TPK) and yeast phenylalanine tRNA (PDB ID: 1TRA), our calculation shows a major groove width in the range from 4 Å to 7 Å. Therefore, crowders (radius = 7 Å) are too bulky to enter the major groove. However, crowders can be distributed around the groove entrance and to impede ion binding. As shown in Figure S3, crowders only appear around the RNA surface or in the bulk solution. The combination of the above two effects lead to an increase in the total free energy of the system. Such an crowding effect is confirmed by the computational results for a 12-bp helix (Figure 3). We find that for the 12-bp RNA helix with fc = 20% volume fraction of the crowders, the crowders cause an increase in the total free energy by 8.0 kcal/mol compared to the crowder-free system.8, 50
The effect of discrete crowder distribution
As a test, for the 12-bp helix in a solution of 20% volume fraction of crowder and 0.1 M NaCl and 10 mM MgCl2, we replace the discrete crowder distributions with the uniform crowder concentration and find a reduction of 3 kcal/mol in the crowder-induced free energy increase (see Figure 3). The result suggests the importance of considering the discrete positions of the crowders. Physically, only discrete crowder distributions can account for the crowder-ion volume exclusion and the crowder dielectric effect is sensitive to the discrete crowder distribution, especially in the close vicinity of RNA surface.
The effect of crowders on the free energy
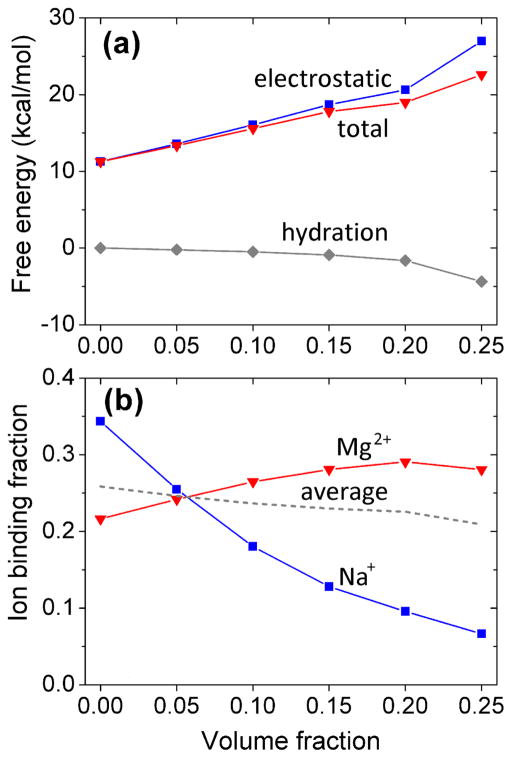
As shown in Figure 4, the electrostatic free energy ΔGele and the total free energy ΔGtot increase with the volume fraction fc of the crowder. In calculation, we choose 30 Å as the box width. The increase is mainly caused by the decrease in the overall effective dielectric constant and the displacement of bound ions by crowders. In the Generalized Born model (GB)-based calculation, the Born radii of the phosphates increase, resulting in an increase in the polarization energy as shown in our previous study.42 The hydration energy slowly decreases with fc because a larger number of crowders emerging around the RNA surface would enhance the decrease in the solvent accessible surface area Δσ (Eq. 6). These results suggest that a higher fc tends to contribute an destabilizing force to the RNA helices.28
Figure 4.
Free energies ΔGele and ΔGtot (a) and ion binding fraction (average number of bound ions per nucleotide) (b) as a function of the crowder volume fraction. The gray dashed line in (b) shows the result for the average net charge for the two types of bound ions per nucleotide. The predictions are for a 12-bp RNA helix in a crowded solution with 0.1M NaCl and 0.01M MgCl2.
The overall crowding effect on ion binding
Detailed analysis indicates that crowders have distinctive effects on monovalent Na+ ions and divalent Mg2+ ion binding (Figure 4b). For Na+ ion, we find a notable decrease in ion binding fraction from 0.34 for the crowder-free system (fc = 0) to 0.07 for the crowded system with fc = 0.25. Such a sharp drop in monovalent ion binding would reduce charge neutralization and weaken RNA stability. The reduction in Na+ ion binding is mainly caused by the volume exclusion from the crowders.
Accompanying the decrease in Na+ binding, for fc ≤ 0.2, Mg2+ ions, which have higher efficiency in ion binding than the monovalent Na+, show slight increase in ion binding from 0.22 in the crowder-free system (fc = 0) to 0.29 in the crowded system with fc = 0.20. The increase in Mg2+ binding may arise from the stronger ion-RNA attraction in a (low dielectric) crowder environment. Such an enhancement in electrostatic attraction is more pronounced for divalent Mg2+ ions than for monovalent Na+ ions. This different trends of ion binding for Na+ and Mg2+ suggest that Mg2+ ion may be more competitive than Na+ against the perturbations from the crowders.
As a result of the rapid decrease in Na+ ion binding (due to ion-crowder competition) and the relatively slow increase in Mg2+ ion binding (due to the crowder-induced dielectric change) (shown in Figure 4b), our calculation shows a crowder-induced net decrease in the effective charge of a nucleotide from −0.225 e (no crowder) to −0.325 e (20% crowder volume fraction). Here −e is the electronic charge.
Dependence of ion binding on crowder volume fraction
For a highly crowded system with fc > 0.20, the strong crowder-ion volume exclusion out competes the RNA-ion Coulomb attraction, resulting in an decrease in Mg2+ binding. For example, the number of crowders in the ISB can reach to 69 when the volume fraction reaches 0.25. The large amount crowder can occupy the positions around the RNA surface that could otherwise be occupied by Mg2+ ions. From our calculation and the above analysis, we can conclude that the crowder-modulated ion binding gives the maximum Mg2+ binding around fc = 0.20. For fc > 0.20, the combination of the decreasing Mg2+ and Na+ ion binding in the high fc regime results in a rapid increase in the free energy (see Figure 4b).
Effect of crowder size
The crowder size can also influence the ion-crowder volume exclusion and the spatial dielectric distribution of the system. For a polymeric crowder molecule, the radius mimic the radius of gyration of the chain. To the lowest order, the different crowding agents can be represented by their different sizes.
As shown in Figure S4, for the same volume fraction, the small size crowders can cause a much stronger crowding effect than the more bulky crowders. This is because small crowders can better fit in RNA grooves to exclude ions from binding to the RNA and to lower the effective dielectric constant. Moreover, the small crowders of radius 3–4 Å have the similar size as the (hydrated) ions and can therefore displace the bound ions more efficiently. These reasons combined together leads to a notable increase in the free energy with a reducing size of the crowders. In contrast, for bulky crowders larger than 8 Å, the free energy change with the crowder size is much weaker. Although small crowders cause larger free energy increase, we find that the optimal ISB width is around 30 Å for crowders with radius from 3.0 Å to 12.0 Å (see Figure S5).
Combining the crowder size and the volume fraction effects, we conclude that free energy of the RNA-ion-crowder solution increases with the volume fraction and the free energy increase is more pronounced for smaller crowders. The result suggests that smaller crowders are ideal candidates for controlling the crowder-mediated RNA-ion interactions.
Applications to the different RNA structures
In the preceding sections, for the purpose of the illustration, we have been focused on the simple RNA helix structure. In this section, to investigate the crowding effect for more general RNA structures, we compute the free energy and ion binding fractions for three representative RNAs: tRNA (76 nucleotides, PDB ID: 1TRA), a mRNA fragment (36 nucleotides, PDB ID: 2TPK), and the BWYV RNA (27 nucleotides, PDB ID: 437D).
Crowder-induced free energy change
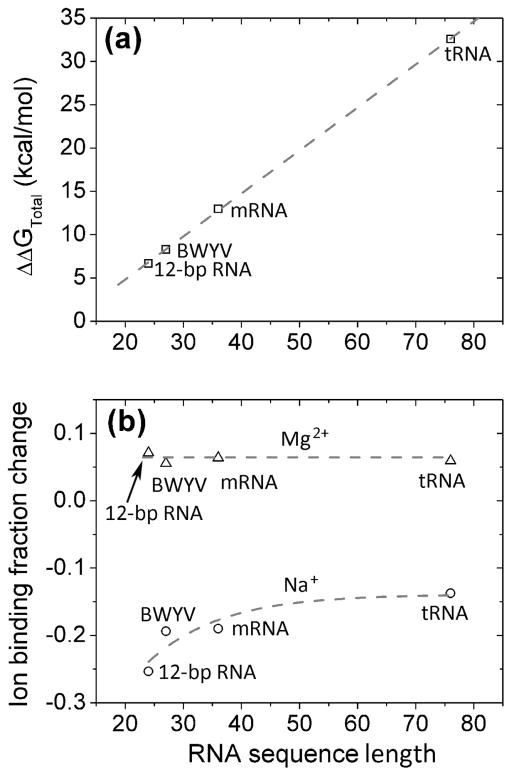
Similar to the results for the helix, Figure S6 shows that a box width larger than 30 Å can give reliable predictions for the energies. Moreover, as shown in Figure 5a, with the ISB width of 30 Å, the crowders cause a free energy increase (volume fraction fc = 0.2 vs. crowder-free system fc = 0). This conclusion is similar to that drawn from the helix. Figure 5a also shows that the crowder-induced total free energy change ΔΔGtot = ΔGtot (fc = 0.2) −. ΔGtot (fc = 0) scales roughly linearly with RNA sequence length NRNA: ΔΔGtot = 0.50·NRNA − 5.11 kcal/mol, equivalently, the crowder-induced energy change ΔΔGtot increases roughly 0.5 kcal/mol for each added nucleotide for crowder volume fraction of 0.2. Physically, the longer sequence corresponds to a larger number of phosphate charges on the RNA backbone, thus gives “amplified” crowding effects.
Figure 5.
Crowder-induced changes in (a) the total free energy ΔGtot and (b) the ion binding fraction for four representative RNAs: 12-bp RNA, BWYV (PDB ID: 437D), mRNA (PDB ID: 2TPK) and tRNA (PDB ID: 1TRA). The crowder-induced changes are calculated as the differences of the results between the crowded solution with volume fraction fc = 20% and the crowder-free system with fc = 0. In our calculations, we use ISB box width 30 Å. The gray dash line in (a) is the plot for the following equation: ΔΔGtotal = 0.50·lRNA − 5.11.
Crowder-induced changes in ion binding
The free energy increase of the crowder-induced system is related to the change in ion binding. Figure 5b shows the crowder-induced change in Na+ and Mg2+ binding fractions as a function of the RNA chain length. We find that monovalent ions (Na+) and divalent ions (Mg2+) show different behaviors. First, crowders cause a increase in Mg2+ binding and a decrease in Na+ binding. Second, the increase in the binding fraction for Mg2+ (about equal to 0.06 for the different sequence lengths tested) is much smaller than the decrease in the binding fraction for Na+. Such a Mg2+-Na+ difference in the crowding effect is more pronounced for shorter RNAs. Small size RNAs such as the 12-bp RNA in the test case involves greater decrease in the Na+ binding than the larger tRNA. Compared to the free energy changes in Figure 5a, the sequence length-dependence of the crowding effect on ion binding fractions in Figure 5b is less pronounced. This is because for longer sequences, the compact structure draws more bound ions and the stronger charge neutralization makes the change in the average number of bound ions per nucleotide less pronounced than the change of the total free energy. The crowder-induced overall net reduction of ion binding fraction results in the free energy increase.
As shown in Figure 5b, the reduction in Na+ ion binding fraction (i.e., the average number of the bound ions per nucleotide) caused by the crowders varies nonlinearly with the number of the nucleotides. As a result, the total number of bound ions for an RNA would decrease faster than the increase of the RNA sequence length. This behavior may be caused by the larger ratio between the crowder excluded volume and the RNA size for smaller RNAs, and hence the relatively stronger crowder excluded volume effects in ion-RNA interactions (for smaller RNAs). For Mg2+ ions, the excluded volume effect is damped by the crowder-induced enhancement in the ion-RNA Coulomb attraction, resulting in a nearly constant change (increase) in the ion binding fraction as a function of the RNA sequence length.
Crowding effect on Mg2+-purine riboswitch binding
Structural and thermodynamic experiments have shown that for a purine riboswitch RNA (PDB: 1Y26), ligand can enhance Mg2+ ion binding.51, 52 The ligand interacts with the purine riboswitch in two ways. First, a ligand can bind to the specific binding pocket in the three way junction region (specific binding). The specific binding may enhance the ion binding possibly through the ligand-induced RNA structural changes.51 Second, ligands can randomly distributed around the riboswitch and act as crowders. According to our analysis above, such nonspecific crowder distribution could impact ion binding through the dielectric environment changes around the RNA and the ligand-ion competition in RNA binding.
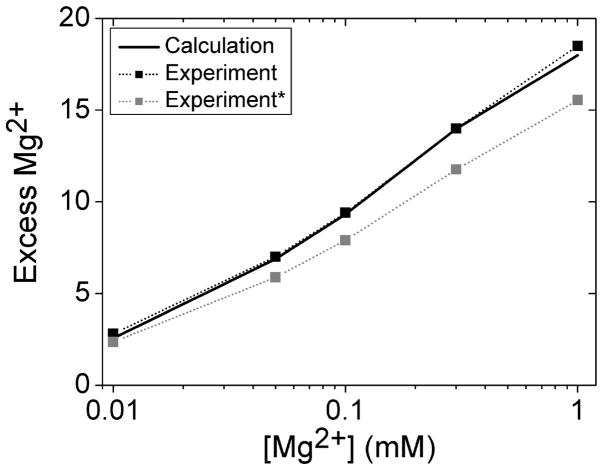
The crowding model developed here accounts for the nonspecific ligand binding effect. To discern the impact of the nonspecific and the specific ligand binding effects for the purine riboswitch system, we apply our model to calculate the impact of the ligands as crowders on the Mg2+-riboswitch interaction. We use the same solution condition as the one used in the experiment, which contains 250 μM DAP (2,6-diaminopurine).51 According to the size of the 3D structure of the DAP molecule, we use a sphere of radius 7 Å to represent the DAP crowder. As shown in Figure 6, the nonspecific distribution of the crowder causes negligible changes in Mg2+ ion binding for a solution with 250 μM DAP and 50 mM K+ at 20 °C. The result suggests that under crowder concentration as low as 250 μ;M , which corresponds to a low crowder volume fraction of fc=0.3%, the nonspecific crowding effect is outperformed by the specific ligand-RNA interaction. As a result, the enhanced Mg2+ ion binding is more likely from the specific ligand binding effect such as the ligand-induced structure change of the RNA.
Figure 6.
Comparison between our model prediction (solid black line) and the experimental data (black and gray squares connected by dotted lines) for the number of Mg2+ ions bound to a purine riboswitch (PDB ID: 1Y26) as a function of the bulk Mg2+ ion concentration in a solution with 250 μM DAP (2,6-diaminopurine) and 50 mM K+ background at 20°C.51 The black squares show the experimental data reported in Leipply & Draper (2011). The gray squares show the experimental data modified by a (80%) correction factor that might be necessary for the data (D.E. Draper, private communication).
Conclusions
Ion-RNA interactions are critical for RNA structure formation and folding stability. The ion-RNA interactions can be influenced by the crowders in the solution through a variety of effects such as the changes in the dielectric environment, the solvent accessible surface area and hydration energy, and the crowder-ion excluded volume repulsion. These crowding effects can be sensitive to discrete crowder distribution. Through explicit sampling of the discrete crowder distributions around RNA, we develop a new crowding model that can provide quantitative predictions for the crowding effect on ion-RNA interactions. To enhance the sampling efficiency, we develop a hybrid approach which samples discrete distributions for crowders in the most important region (around the close vicinity of the RNA) and use an effective uniform distribution for crowders that are distributed further away from the RNA. Consistent with the experimental findings, the model predicts a decrease and increase in ion binding for monovalent and divalent ions, respectively, and an increase in the free energy by the crowders.
The current model may serve as a starting framework for an ultimately more complete crowding for the ion effects for RNAs. The current model has several important limitations. For example, crowders are modelled as dielectric spheres in the model. Further development of the model should include the all-atom structures of the crowders. For a general all-atom nonspherical crowder molecule, sampling the rotational configuration of the crowders may require an additional step to further enhance the sampling efficiency. Moreover, the current model account for only the non-specific crowding effects. A future model should also include the possible specific (chemical) interactions between the crowder and the RNA.
Supplementary Material
Acknowledgments
This work was supported by the NIH Grant (No. R01-GM063732 to S-J. C), the China Scholarship Council Foundation (No. 201408420100 to T. Y), the National Natural Science Foundation of China (No. 11304123 to T. Y, No. 11547012 to Y. Z), and the Natural Science Foundation of Zhejiang Province (No. LY16A040009 to Y. Z).
Footnotes
Supporting Information Available
Figures S1 and S2 show the dependence of the free energy and the total crowder number on the crowder volume fraction. Figure S3 shows (schematically) the crowder and ion competition in RNA binding around RNA minor/major grooves. Figures S4 and S5 show the dependence of the total free energy on the volume fraction and the ISB box width for the different crowder sizes. Figure S6 shows the dependence of the total free energy on the ISB box width for four representative RNAs: tRNA, mRNA, BWYV, and 12-bp RNA.
References
- 1.Ellis RJ. Macromolecular Crowding: Obvious but Underappreciated. Trends in Biochem Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 2.Zhou HX, Rivas G, Minton AP. Macromolecular Crowding and Confinement: Biochemical, Biophysical, and Potential Physiological Consequences. Ann Rev Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Harada R, Sugita Y, Feig M. Protein Crowding Affects Hydration Structure and Dynamics. J Am Chem Soc. 2012;134:4842–4849. doi: 10.1021/ja211115q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thirumalai D, Klimov DK, Lorimer GH. Caging Helps Proteins Fold. Proc Natl Acad Sci U S A. 2003;100:11195–11197. doi: 10.1073/pnas.2035072100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Minton AP. Implications of Macromolecular Crowding for Protein Assembly. Curr Opin Struct Biol. 2000;10:34–39. doi: 10.1016/s0959-440x(99)00045-7. [DOI] [PubMed] [Google Scholar]
- 6.Dix JA, Verkman AS. Crowding Effects on Diffusion in Solution and Cells. Annu Rev Biophys. 2008;37:247–263. doi: 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
- 7.Luby-Phelps K. Cytoarchitecture and Physical Properties of Cytoplasm: Volume, Viscosity, Diffusion, Intracellular Surface Area. Int Rev Cytol. 1999;192:189–221. doi: 10.1016/s0074-7696(08)60527-6. [DOI] [PubMed] [Google Scholar]
- 8.Tjong H, Zhou HX. Prediction of Protein Solubility from Calculation of Transfer Free Energy. Biophys J. 2008;95:2601–2609. doi: 10.1529/biophysj.107.127746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Christiansen A, Wang Q, Samiotakis A, Cheung MS, Wittung-Stafshede P. Factors Defining Effects of Macromolecular Crowding on Protein Stability: An in Vitro/in Silico Case Study Using Cytochrome c. Biochemistry. 2010;49:6519–6530. doi: 10.1021/bi100578x. [DOI] [PubMed] [Google Scholar]
- 10.Cheung MS, Thirumalai D. Effects of Crowding and Confinement on the Structures of the Transition State Ensemble in Proteins. J Phys Chem B. 2007;111:8250–8257. doi: 10.1021/jp068201y. [DOI] [PubMed] [Google Scholar]
- 11.Martin J, Hartl FU. The Effects of Macromolecular Crowding on Chaperonin-mediated Protein Folding. Proc Natl Acad Sci U S A. 1997;94:1107–1112. doi: 10.1073/pnas.94.4.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rösgen J, Pettitt BM, Bolen DW. Protein Folding, Stability, and Solvation Structure in Osmolyte Solutions. Biophys J. 2005;89:2988–2997. doi: 10.1529/biophysj.105.067330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Homouz D, Stagg L, Wittung-Stafshede P, Cheung MS. Macromolecular Crowding Modulates Folding Mechanism of α/β Protein Apoflavodoxin. Biophys J. 2009;96:671–680. doi: 10.1016/j.bpj.2008.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang W, Xu WX, Levy Y, Trizac E, Wolynes PG. Confinement Effects on the Kinetics and Thermodynamics of Protein Dimerization. Proc Natl Acad Sci U S A. 2009;106:5517–5522. doi: 10.1073/pnas.0809649106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rosen J, Kim YC, Mittal J. Modest Protein-crowder Attractive Interactions Can Counteract Enhancement of Protein Association by Intermolecular Excluded Volume Interactions. J Phys Chem B. 2011;115:2683–2689. doi: 10.1021/jp200625k. [DOI] [PubMed] [Google Scholar]
- 16.McGuffee SR, Elcock AH. Atomically Detailed Simulations of Concentrated Protein Solutions: the Effects of Salt, pH, Point Mutations, and Protein Concentration in Simulations of 1000-molecule Systems. J Am Chem Soc. 2006;128:12098–12110. doi: 10.1021/ja0614058. [DOI] [PubMed] [Google Scholar]
- 17.White DA, Buell AK, Knowles TPJ, Welland ME, Dobson CM. Protein Aggregation in Crowded Environments. J Am Chem Soc. 2010;132:5170–5175. doi: 10.1021/ja909997e. [DOI] [PubMed] [Google Scholar]
- 18.Bai Y, Greenfeld M, Travers KJ, Chu VB, Lipfert J, Doniach S, Herschlag D. Quantitative and Comprehensive Decomposition of the Ion Atmosphere Around Nucleic Acids. J Am Chem Soc. 2007;129:14981–14988. doi: 10.1021/ja075020g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Grilley D, Soto AM, Draper DE. Direct Quantitation of Mg2+-RNA Interactions by Use of a Fluorescent Dye. Methods Enzymol. 2009;455:71–94. doi: 10.1016/S0076-6879(08)04203-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Robbins TJ, Ziebarth JD, Wang Y. Comparison of Monovalent and Divalent Ion Distributions Around a DNA Duplex with Molecular Dynamics Simulation and a Poisson-Boltzmann Approach. Biopolymers. 2014;101:834–848. doi: 10.1002/bip.22461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kirmizialtin S, Pabit SA, Meisburger SP, Pollack L, Elber R. RNA and Its Ionic Cloud: Solution Scattering Experiments and Atomically Detailed Simulations. Biophys J. 2012;102:819–828. doi: 10.1016/j.bpj.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Draper DE, Grilley D, Soto AM. Ions and RNA Folding. Annu Rev Biophys Biomol Struct. 2005;34:221–243. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 23.Bojovschi A, Liu MS, Sadus RJ. Mg2+ Coordinating Dynamics in Mg:ATP Fueled Motor Proteins. J Chem Phys. 2014;140:115102. doi: 10.1063/1.4867898. [DOI] [PubMed] [Google Scholar]
- 24.Mali CS, Chavan SD, Kanse KS, Kumbharkhane AC, Mehrotra SC. Dielectric Relaxation of Poly Ethylene Glycol-water Mixtures Using Time Domain Technique. Indian J Pure Appl Phys. 2007;45:476–481. [Google Scholar]
- 25.Nakano S, Karimata HT, Kitagawa Y, Sugimoto N. Facilitation of RNA Enzyme Activity in the Molecular Crowding Media of Cosolutes. J Am Chem Soc. 2009;131:16881–16888. doi: 10.1021/ja9066628. [DOI] [PubMed] [Google Scholar]
- 26.Denesyuk NA, Thirumalai D. Crowding Promotes the Switch from Hairpin to Pseudoknot Conformation in Human Telomerase RNA. J Am Chem Soc. 2011;133:11858–11861. doi: 10.1021/ja2035128. [DOI] [PubMed] [Google Scholar]
- 27.Hong J, Gierasch LM. Macromolecular Crowding Remodels the Energy Landscape of a Protein by Favoring a More Compact Unfolded State. J Am Chem Soc. 2010;132:10445–10452. doi: 10.1021/ja103166y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lambert D, Draper DE. Effects of Osmolytes on RNA Secondary and Tertiary Structure Stabilities and RNA-Mg2+ Interactions. J Mol Biol. 2007;370:993–1005. doi: 10.1016/j.jmb.2007.03.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spink CH, Chaires JB. Effects of Hydration, Ion Release, and Excluded Volume on the Melting of Triplex and Duplex DNA. Biochemistry. 1999;38:496–508. doi: 10.1021/bi9820154. [DOI] [PubMed] [Google Scholar]
- 30.Bonnet-Gonnet C, Leikin S, Chi S, Rau DC, Parsegiau VA. Measurement of Forces between Hydroxypropylcellulose Polymers: Temperature Favored Assembly and Salt Exclusion. J Phys Chem B. 2001;105:1877–1886. [Google Scholar]
- 31.Goobes B, Kahana N, Cohen O, Minsky A. Metabolic Buffering Exerted by Macromolecular Crowding on DNA–DNA Interactions: Origin and Physiological Significance. Biochemistry. 2003;42:2431–2440. doi: 10.1021/bi026775x. [DOI] [PubMed] [Google Scholar]
- 32.Nakano S, Karimata H, Ohmichi T, Kawakami J, Sugimoto N. The Effect of Molecular Crowding with Nucleotide Length and Cosolute Structure on DNA Duplex Stability. J Am Chem Soc. 2004;126:14330–14331. doi: 10.1021/ja0463029. [DOI] [PubMed] [Google Scholar]
- 33.Cheung MS, Klimov D, Thirumalai D. Molecular Crowding Enhances Native State Stability and Refolding Rates of Globular Proteins. Proc Natl Acad Sci U S A. 2005;29:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dhar A, Samiotakis A, Ebbinghaus S, Nienhaus L, Homouz D, Gruebele M, Cheung MS. Structure, Function, and Folding of Phosphoglycerate Kinase are Strongly Perturbed by Macromolecular Crowding. Proc Natl Acad Sci U S A. 2010;107:17586–17591. doi: 10.1073/pnas.1006760107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ando T, Skolnick J. Crowding and Hydrodynamic Interactions Likely Dominate in Vivo Macromolecular Motion. Proc Natl Acad Sci U S A. 2010;107:18457–18462. doi: 10.1073/pnas.1011354107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Blose JM, Pabit SA, Meisburger SP, Li L, Jones CD, Pollack L. Effects of a Protecting Osmolyte on the Ion Atmosphere Surrounding DNA Duplexes. Biochemistry. 2011;50:8540–8547. doi: 10.1021/bi200710m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Leduc C, Padberg-Gehle K, Varge V, Helbing D, Diez S, Howard J. Molecular Crowding Creates Traffic Jams of Kinesin Motors on Microtubules. Proc Natl Acad Sci U S A. 2012;109:6100–6105. doi: 10.1073/pnas.1107281109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Predeus AV, Gul S, Gopal SM, Feig M. Conformational Sampling of Peptides in the Presence of Protein Crowders from AA/CG-multiscale Simulations. J Phys Chem B. 2012;116:8610–8620. doi: 10.1021/jp300129u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hosek M, Tang JX. Polymer-Induced Bundling of F-actin and the Depletion Force. Phys Rev E. 2004;69:051907. doi: 10.1103/PhysRevE.69.051907. [DOI] [PubMed] [Google Scholar]
- 40.Soranno A, Koenig I, Borgia MB, Hofmann H, Zosel F, Nettels D, Schuler B. Single-Molecule Spectroscopy Reveals Polymer Effects of Disordered Proteins in Crowded Environments. Proc Natl Acad Sci U S A. 2014;111:4874–4879. doi: 10.1073/pnas.1322611111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tan ZJ, Chen SJ. Electrostatic Free Energy Landscapes for DNA Helix Bending. Biophys J. 2008;94:3137–3149. doi: 10.1529/biophysj.107.122366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.He Z, Chen SJ. Quantifying Coulombic and Solvent Polarization-mediated Forces Between DNA Helices. J Phys Chem B. 2013;117:7221–7227. doi: 10.1021/jp4010955. [DOI] [PubMed] [Google Scholar]
- 43.Zhu Y, He Z, Chen SJ. TBI Server: A Web Server for Predicting Ion Effects in RNA Folding. PLoS One. 2015;10:e0119705. doi: 10.1371/journal.pone.0119705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Simonson T, Brunger AT. Solvation Free Energies Estimated from Macroscopic Continuum Theory: An Accuracy Assessment. J Phys Chem. 1994;98:4683–4694. [Google Scholar]
- 45.Vallone B, Miele A, Vecchini P, Chiancone E, Brunori M. Free Energy of Burying Hydrophobic Residues in the Interface Between Protein Subunit. Proc Natl Acad Sci U S A. 1998;95:6103–6107. doi: 10.1073/pnas.95.11.6103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Raschke TM, Tsai J, Levitt M. Quantification of the Hydrophobic Interaction by Simulations of the Aggregation of Small Hydrophobic Solutes in Water. Proc Natl Acad Sci U S A. 2001;98:5965–5969. doi: 10.1073/pnas.111158498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sitkoff D, Sharp KA, Honig B. Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 48.Sanner MF, Olson AJ, Spehner J. Reduced Surfacesan Efficient Way to Compute Molecular Surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 49.Treesuwan W, Wittayanarakul K, Anthony NG, Huchet G, Alniss H, Hannongbua S, Khalaf AI, Suckling CJ, Parkinson JA, Mackay SP. A Detailed Binding Free Energy Study of 2 : 1 Ligand–DNA Complex Formation by Experiment and Simulation. Phys Chem Chem Phys. 2009;11:10682–10693. doi: 10.1039/b910574c. [DOI] [PubMed] [Google Scholar]
- 50.Kilburn D, Roh JH, Behrouzi R, Briber RM, Woodson SA. Crowders Perturb the Entropy of RNA Energy Landscapes to Favor Folding. J Am Chem Soc. 2013;135:10055–10063. doi: 10.1021/ja4030098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Leipply D, Draper DE. Effects of Mg2+ on the Free Energy Landscape for Folding a Purine Riboseitch RNA. Biochemistry. 2011;50:2790–2799. doi: 10.1021/bi101948k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lipfert J, Sim AYL, Herschlag D, Doniach S. Dissecting Electrostatic Screening, Specific Ion Binding, and Ligand Binding in an Energetic Model for Gycine Riboswitch Folding. RNA. 2010;16:708–719. doi: 10.1261/rna.1985110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.