An analytical solution for steady flow of a Quemada fluid in a circular tube

Abstract

An analytical solution is obtained for steady flow of Quemada-type fluids in a circular tube driven by a constant pressure gradient. Expressions are derived for velocity distribution and for volumetric flow rate as a function of pressure gradient or wall shear stress.

Introduction

Rheology of concentrated suspensions has been an active area of research for several decades. Numerous models have been formulated for fluids with internal structure; some of the models derived from first physical principles, while others formulated as empirical fits to experimental data. Quemada (1978 a, b) formulated a rheological model for concentrated suspensions based on physical arguments. The model introduces an intrinsic viscosity that, generally, is governed by a kinetic equation. In case of simple shear flow, the intrinsic viscosity becomes a function of local shear rate and concentration of suspended particles. Quemada's model is an extension of the well-known Casson's rheological model (Casson, 1959) with one additional rheological parameter; thus, it contains three rheological parameters. The principal difference between the two models is that Casson's model is characterized by a yield shear stress and, hence, the viscosity approaches infinity as shear rate approaches zero, whereas in Quemada's model viscosity assumes a large, but finite, value as shear rate goes to zero.

The Quemada model has been used extensively in recent years in applications to flow of blood (Quemada, 1978b, 1983; Lerche and Oelke, 1990; Cokelet and Goldsmith, 1991), microemulsions (Langevin, 1986), food pastes (Doublier et al., 1987), and coal slurries (Lapasin and Pricl, 1992), to name a few. It has been shown to be one of the most accurate hemorheological models; the model is in excellent agreement with experimental data (Easthope and Brooks, 1980). However, the practical applications of the model are significantly hampered by the lack of analytical expressions for velocity profiles and volumetric flow rate versus pressure gradient for simple “viscometric” flows. Of particular importance is the problem of steady fully developed flow in a circular tube driven by a constant pressure gradient. Solutions of this problem have been obtained numerically (Cokelet and Goldsmith, 1991).

This paper presents an exact analytical solution for steady fully developed flow of Quemada-type fluid in a circular tube. Closed-form expressions are derived for velocity profile and for volumetric flow rate as a function of pressure gradient or wall shear stress.

Formulation of the problem

A cylindrical coordinate system (r, θ, z) is chosen with the z-axis along the axis of the tube. Quemada's model (Quemada, 1978 a, b) for non-Newtonian shear viscosity can be formulated as follows. If H is the local concentration of suspended particles, and η_p is the viscosity of the suspending fluid, then the absolute value of the shear stress, τ = |τ_rz|, for a steady fully developed flow can be expressed in terms of the non-Newtonian shear viscosity, η, and the shear rate, γ̇ = |dν_z/dr|:

$$\tau =\eta \dot{\gamma },$$ (1)

where

$$\eta =\eta (k,H)=\frac{{\eta }_p}{{(1-\frac{1}{2}kH)}^2}$$ (2)

and k is an intrinsic viscosity. The intrinsic viscosity is expressed in terms of three Quemada parameters, k₀, k_∞, and γ_c:

$$k=\frac{k_0+k_{\infty }\sqrt{\dot{\gamma }/{\gamma }_c}}{1+\sqrt{\dot{\gamma }/{\gamma }_c}}.$$ (3)

Parameters k₀, k_∞, and γ_c are, generally, functions of particle concentration, H.

Equations (1 – 3) can be recast as

$$\sqrt{\tau }=(\sqrt{{\eta }_{\infty }}+\frac{\sqrt{{\tau }_0}}{\sqrt{\lambda }+\sqrt{\dot{\gamma }}})\sqrt{\dot{\gamma }},$$ (4)

where the new parameters τ₀, η_∞, and λ are expressed in terms of the Quemada parameters:

$${\tau }_0={\eta }_p{\gamma }_c\frac{{[\frac{1}{2}H(k_0-k_{\infty })]}^2}{{(1-\frac{1}{2}{k}_{\infty }H)}^4}$$ (5)

$${\eta }_{\infty }=\frac{{\eta }_p}{{(1-\frac{1}{2}{k}_{\infty }H)}^2}$$ (6)

$$\lambda ={\gamma }_c{\left[\frac{1-\frac{1}{2}{k}_{0}H}{1-\frac{1}{2}{k}_{\infty }H}\right]}^2.$$ (7)

When written in this form, the Quemada model reduces to the Casson model as λ → 0. In the Casson model, τ₀ is the yield shear stress and η_∞ is the asymptotic viscosity at large shear rates. At very small shear rates, γ̇ ≪ λ, Eq. (4) describes a Newtonian fluid with a viscosity

$${\eta }_0=\frac{{\eta }_p}{{(1-\frac{1}{2}{k}_{0}H)}^2}.$$ (8)

In the following analysis it would be convenient to use Eq. (4) as a representation of the Quemada model; note that Eqs. (1) – (3) and Eq. (4) are equivalent for steady shear flow. We consider steady fully developed flow of the Quemada fluid in a circular tube of radius R driven by a constant pressure gradient P = (p_in – p_out)/L, where p_in and p_out are the inlet and outlet pressures, respectively, and L is the tube length. Because the problem is axisymmetric and the flow is fully developed, only the axial velocity component, ν_z(r), is considered; the other two components are equal to zero. In the following section, expressions for shear rate, γ̇(r), velocity, ν_z(r), and volumetric flow rate, Q(P), are derived.

Solution

Writing the momentum equation in the z direction and integrating it, we find that shear stress is a linear function of r

$$\tau =\mathit{\text{Pr}}/2.$$ (9)

Thus, shear stress at the wall is τ_w = PR/2. It is convenient to introduce dimensionless variables and parameters:

$$\begin{array}{ccc}\xi =\frac{r}{R};& \alpha =\frac{\sqrt{{\tau }_0}+\sqrt{{\eta }_{\infty }\lambda }}{\sqrt{{\tau }_w}},& q=\frac{\sqrt{{\tau }_0}-\sqrt{{\eta }_{\infty }\lambda }}{\sqrt{{\tau }_0}+\sqrt{{\eta }_{\infty }\lambda }}.\end{array}$$ (10)

Note that 0 ≤ ξ ≤ 1, α ≥ 0, and −1 ≤ q ≤ 1. The extreme values of q correspond to Newtonian (q = −1) and Casson (q = 1) fluids, respectively.

Solving Eq. (4) to express γ̇ in terms of τ, and using Eq. (9), after simple algebraic transformations we express shear rate γ̇ in terms of dimensionless radial coordinate, ξ,

$$\dot{\gamma }=\frac{\mathit{\text{PR}}}{4{\eta }_{\infty }}[\xi -\alpha (1+q)\sqrt{\xi }+{\alpha }^2+(\sqrt{\xi }-\alpha )\cdot \sqrt{\xi -2\alpha q\sqrt{\xi }+{\alpha }^2}].$$ (11)

Substituting (11) into the equation dν_z/dr = −γ̇, and integrating this equation together with boundary condition ν_z(R) = 0, we obtain velocity profile; in dimensionless form

$$\begin{array}{c}\nu =\frac{{\nu }_z}{({\mathit{\text{PR}}}^2/4{\eta }_{\infty })}=\frac{1}{2}[{(1-\alpha q)}^4-{(\sqrt{\xi }-\alpha q)}^4]+\frac{2}{3}\alpha (2q-1)[{(1-\alpha q)}^3-{(\sqrt{\xi }-\alpha q)}^3]\\ +{\alpha }^2{(q-1)}^2[{(1-\alpha q)}^2-{(\sqrt{\xi }-\alpha q)}^2]-2{\alpha }^{3}q(q-1)(1-\sqrt{\xi })\\ +\frac{1}{2}\left\{\right[1+\frac{1}{3}\alpha (5q-4)]{(1-2\alpha q+{\alpha }^2)}^{3/2}-[\sqrt{\xi }+\frac{1}{3}\alpha (5q-4)\left]{(\xi -2\alpha q\sqrt{\xi }+{\alpha }^2)}^{3/2}\right\}\\ +\frac{1}{4}{\alpha }^2(q-1)(5q+1)[(1-\alpha q){(1-2\alpha q+{\alpha }^2)}^{1/2}-(\sqrt{\xi }-\alpha q){(\xi -2\alpha q\sqrt{\xi }+{\alpha }^2)}^{1/2}]\\ -\frac{1}{4}{\alpha }^4{(q-1)}^2(q+1)(5q=1)\\ ln\frac{{(1-2\alpha q+{\alpha }^2)}^{1/2}+1-\alpha q}{{(\xi -2\alpha q\sqrt{\xi }+{\alpha }^2)}^{1/2}+\sqrt{\xi }-\alpha q}.\end{array}$$ (12)

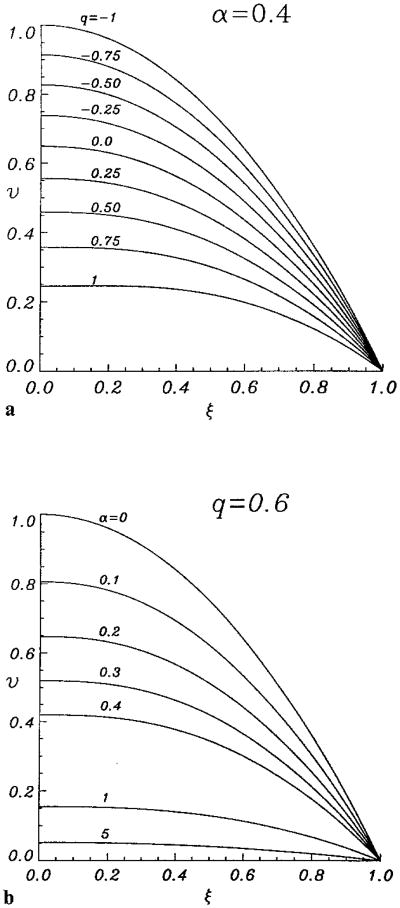
The normalizing factor, PR²/4η_∞, represents the maximum velocity of a Newtonian fluid with viscosity η_∞. When q → 1 (e.g., when λ → 0), Eq. (12) reduces to Casson's velocity profile. For q^→ – 1 or α → 0, Eq. (12) reduces to parabolic velocity profile. Figure 1 shows a family of velocity profiles for different values of parameters α and q. Note the parabolic profiles ν = 1 – ξ² for q = −1 and α = 0; the Casson profile corresponding to q = 1 has a flat core of radius ξ_c = α².

Fig. 1.

Normalized velocity profiles, ν = ν_z/(PR²/4η_∞), for steady fully-developed flow in a tube as a function of normalized radius, ξ = r/R, for a) α = 0.4 and different values of q, and b) q = 0.6 and different values of α. Cases α = 0 and q = −1 correspond to Poiseuille flow of a Newtonian fluid, case q = 1 corresponds to Casson flow

To express the volumetric flow rate, Q, in terms of the pressure gradient, P, we will use the relationship

$$Q=2\pi \underset{0}{\overset{R}{\int }}r{\nu }_{z}dr=\frac{\pi R^3}{{\tau }_w^3}\underset{0}{\overset{{\tau }_w}{\int }}{\tau }^{2}f(\tau )d\tau ,$$ (13)

where γ̇ = f(τ). Combining Eqs. (9) and (11) with Eq. (13) and integrating, we obtain, after somewhat lengthy transformations,

$$Q=\frac{\pi {\mathit{\text{PR}}}^4}{8{\eta }_{\infty }}F(\alpha ,q)$$ (14)

$$F=\frac{1}{2}[1-\frac{8}{7}\alpha (1+q)+\frac{4}{3}{\alpha }^2-{\alpha }^8{P}_7+(1+\sum _{n=1}^7{\alpha }^n{P}_n)\sqrt{1-2\alpha q+{\alpha }^2}{\alpha }^8{P}_{8}ln\frac{1-\alpha q+\sqrt{1-2\alpha q+{\alpha }^2}}{\alpha (1-q)}].$$ (15)

Here, P₁, P₂, …, P₈ are polynomials in powers of q:

$$\begin{array}{c}{P}_1=-\frac{1}{7}(q+8)\\ P_2=-\frac{1}{42}(13q^2-8q-7)\\ P_3=-\frac{1}{210}(143q^3-88q^2-113q+48)\\ P_4=-\frac{1}{840}(1287q^4-792q^3-1342q^2+632q+175)\\ P_5=-\frac{1}{840}(3003q^5-1848q^4-3894q^3+1944q^2+1011q-256)\\ P_6=-\frac{1}{1680}(15015q^6-9240q^5-23331q^4+12096q^3+9081q^2-3179q-525)\\ P_7=-\frac{1}{1680}(45045q^7-27720q^2-82005q^5+43680q^4+42819q^3-17304q^2-5619q+1024)\\ P_8=-\frac{1}{16}{(1-q)}^2(1+q)(429q^5+165q^4-330q^3-90q^2+45q+5).\end{array}$$ (16)

When q→ 1, Eq. (14) reduces to Casson's equation

$$Q=\frac{\pi {\mathit{\text{PR}}}^4}{8{\eta }_{\infty }}[1-\frac{16}{7}\alpha +\frac{4}{3}{\alpha }^2-\frac{1}{21}{\alpha }^8],$$ (17)

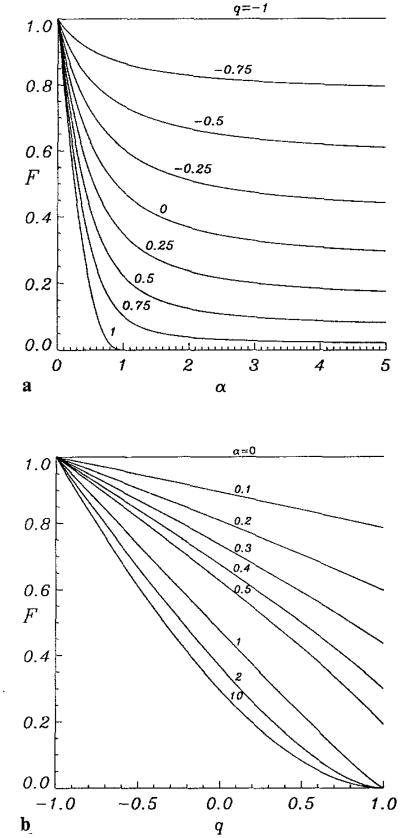
in which α = (τ₀/τ_w)^1/2, 0 ≤ α < 1; for α ≥ 1 there is no flow. Figure 2 shows F as a function of α and q. Note the monotonic decrease of F with increasing q and increasing α. This behavior for large values of α is not evident from Eq. (15) that contains positive powers of α. However, when the square root and the logarithmic terms are expanded in inverse powers of α, all positive powers of α cancel out; an asymptotic expression for function F for large α is

Fig. 2.

Function F(α, q), given by Eq. (15); a) versus α for several values of q; b) versus q for several values of α. F = 1 for α = 0 and for q = −1 (Newtonian fluid); F = 0 for q = 1 and α ≥ 1 (Casson fluid, τ ≤ τ₀)

$$F=\frac{1}{4}{(1-q)}^2+\frac{2}{9}{(1-q)}^2(1+q)\frac{1}{\alpha }+O\left(\frac{1}{{\alpha }^2}\right).$$ (18)

From (10) we have q = 1 – 2(η_∞/η₀)^1/2, thus F→ (1 – q)²/4 = η_∞/η₀, as α → ∞; here, viscosity η₀ is expressed by Eq. (8).

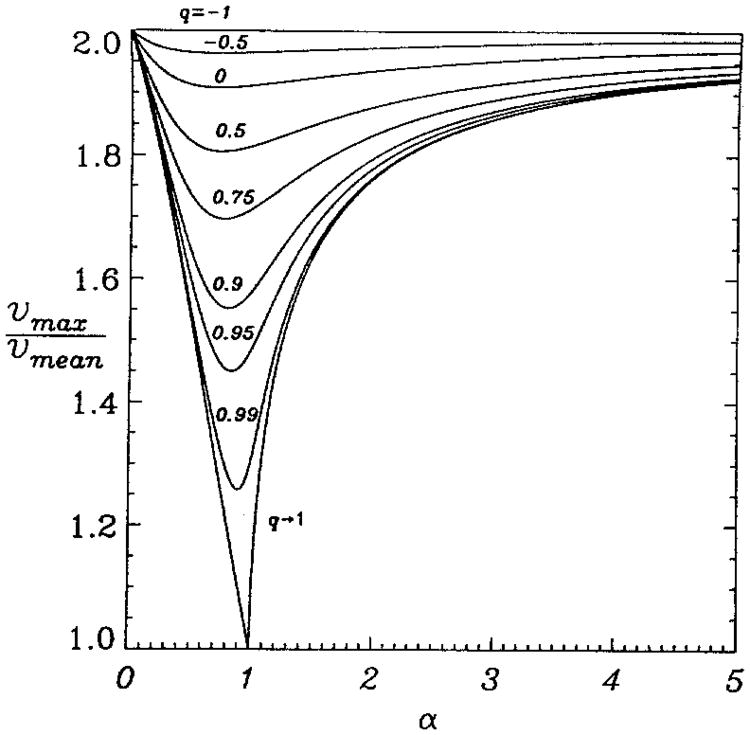
The ratio of maximum velocity, ν_max = ν_z|_{r = 0}, and mean velocity, ν_mean = Q/πR², characterizes the shape of velocity profile; the ratio can be expressed in terms of dimensionless variables ν_max/ν_mean = 2ν|_{ξ = 0}/F. This ratio is equal to 2 in the case of flow of a Newtonian fluid, and approaches 1 for flow of a Casson fluid when shear rate at the wall approaches zero (i.e., τ_w → τ₀ or α → 1). Note that in the latter case both the maximum velocity and mean velocity approach zero. Figure 3 depicts the velocity ratio as a function of α for different values of q. To better understand the asymptotic behavior of the velocity ratio as q → 1, we introduce a parameter ε = 1 – q, and using Eqs. (12) and (15), calculate the leading terms in the corresponding asymptotic expansions for small ε.

Fig. 3.

Maximum-to-mean velocity ratio, ν_max/ν_mean = 2ν|_{ξ = 0}/F, as a function of α for −1 ≤ q ≤ 1. Note the sensitive dependence of the function on q when q → 1. The limiting curves for q → 1 are obtained from Eqs. (19) for α ≤ 1 and Eqs. (20) for α > 1

For α ≤ 1

$$\begin{array}{c}\nu {|}_{\xi =0}=1-\frac{8}{3}\alpha +2{\alpha }^2-\frac{1}{3}{\alpha }^4+O(\epsilon )=\frac{1}{3}{(1-\alpha )}^3(3+\alpha )+O(\epsilon )\\ F=1-\frac{16}{7}\alpha +\frac{4}{3}{\alpha }^2-\frac{1}{21}{\alpha }^8+O(\epsilon )=\frac{1}{21}{(1-\alpha )}^3(21+15\alpha +10{\alpha }^2+6{\alpha }^3+3{\alpha }^4+{\alpha }^5)+O(\epsilon )\end{array}.$$ (19)

These leading terms correspond to a Casson fluid.

For α > 1

$$\begin{array}{c}\nu {|}_{\xi =0}=\frac{{\epsilon }^2}{2}[\frac{{\alpha }^2(-1-3\alpha +6{\alpha }^2)}{\alpha -1}-6{\alpha }^{4}ln\frac{\alpha }{\alpha -1}]+o({\epsilon }^2)\\ F=\frac{{\epsilon }^2}{2}[\frac{{\alpha }^2(-10-14\alpha -21{\alpha }^2-32{\alpha }^3-70{\alpha }^4-210{\alpha }^5+420{\alpha }^6)}{15(\alpha -1)}-28{\alpha }^{8}ln\frac{\alpha }{\alpha -1}]+o({\epsilon }^2).\end{array}$$ (20)

For α ≫ 1, expanding ν and F in (20) in powers of 1/α, we obtain

$$\begin{array}{c}\nu {|}_{\xi =0}=\frac{{\epsilon }^2}{4}(1+\frac{8}{5}\frac{1}{\alpha }+\dots )\\ F=\frac{{\epsilon }^2}{4}(1+\frac{16}{9}\frac{1}{\alpha }+\dots )\end{array}$$ (21)

in accordance with Eq. (18). In Fig. 3 the limiting curve corresponding to q → 1, α > 1 does not represent a physical solution, whereas the curve corresponding to q → 1, α ≤ 1 represents Casson's fluid.

Equations (12) and (15) can be extended to the case of two-phase flow with a core of suspension with a constant concentration of particles, described as a Quemada fluid, and a concentric layer of a Newtonian fluid adjacent to the walls.