MCTBI: a web server for predicting metal ion effects in RNA structures

Abstract

Metal ions play critical roles in RNA structure and function. However, web servers and software packages for predicting ion effects in RNA structures are notably scarce. Furthermore, the existing web servers and software packages mainly neglect ion correlation and fluctuation effects, which are potentially important for RNAs. We here report a new web server, the MCTBI server (http://rna.physics.missouri.edu/MCTBI), for the prediction of ion effects for RNA structures. This server is based on the recently developed MCTBI, a model that can account for ion correlation and fluctuation effects for nucleic acid structures and can provide improved predictions for the effects of metal ions, especially for multivalent ions such as Mg²⁺ effects, as shown by extensive theory-experiment test results. The MCTBI web server predicts metal ion binding fractions, the most probable bound ion distribution, the electrostatic free energy of the system, and the free energy components. The results provide mechanistic insights into the role of metal ions in RNA structure formation and folding stability, which is important for understanding RNA functions and the rational design of RNA structures.

INTRODUCTION

Nucleic acids (DNAs and RNAs) are highly charged polyanions. The folding of a compact three-dimensional structure requires metal ions (counterions) in the solution to neutralize the negative backbone charges on the RNA in order to promote folding and to stabilize a folded structure (Brion and Westhof 1997; Tinoco and Bustamante 1999; Li et al. 2008; Xu et al. 2016). In general, ions can bind to an RNA through site-specific and nonspecific associations (Cate and Doudna 1996; Draper et al. 2005; Lipfert et al. 2014; Petukh et al. 2015). Site-specific association (binding) is often accompanied with full or partial dehydration of the ions, which are trapped at specific sites (Misra and Draper 2001; Philips et al. 2012) such as specific pocket regions in the structure. The nonspecifically bound ions usually remain hydrated and form a mobile “ionic atmosphere” (Lipfert et al. 2014) (“ionic cloud”) (Kirmizialtin et al. 2012) to cover the RNA to neutralize most charges in RNA (Bai et al. 2007; Tan and Chen 2010). The depth of the “ionic atmosphere” can extend more than 20 Å away from the RNA surface (Hayes et al. 2012). Although unlike the site-specific bound ions, nonspecifically bound ions cannot interact with RNA through very close contact, the large number of the nonspecifically bound ions may play a dominant role in the overall electrostatic free energy for the global fold (Misra and Draper 1998). It is therefore important to predict the effects from the nonspecifically bound ions for RNA structures.

The accumulation of counterions around an RNA can cause a high local concentration of the counterions, which may result in the excluded volume and Coulomb correlations between the ions. As a result, the electric force on an ion is dependent not only on the coordinate of the ion but also on the positions of the other ions. Therefore, it is necessary to consider many-ion distributions. The effect is more significant for multivalent ions such as Mg²⁺ than monovalent ions due to the stronger Coulomb forces between the charges (Draper 2008; Grochowski and Trylska 2008; Wang et al. 2008). Indeed, previous computer simulations and experimental studies support the important role of the ion effect in RNA thermodynamic stability, cooperativity, and folding kinetics (Bai et al. 2007, 2008; Koculi et al. 2007; Chen 2008; Denesyuk and Thirumalai 2015).

Traditional polyelectrolyte theories such as the counterion condensation (CC) theory (Manning 1978; Hecht et al. 1995; Manning 2002) and the nonlinear Poisson–Boltzmann (NLPB) method (Zhou 1994; Misra and Draper 1999; Baker et al. 2001; Baker 2005; Tjong and Zhou 2006, 2007; Xiao et al. 2014) have been successful for predicting ion effects, especially the monovalent ion effects, for many biomolecular systems. However, these theories do not treat ion correlations (and the fluctuations), thus cannot always lead to accurate predictions. For example, experimental studies with different techniques such as “ion counting” (Grilley et al. 2006, 2007; Bai et al. 2007; Soto et al. 2007; Greenfeld and Herschlag 2009; Leipply and Draper 2011a,b; Gebala et al. 2015), small-angle X-ray scattering (Das et al. 2003; Bai et al. 2005, 2008; Qiu et al. 2007), and single-molecule optical trapping (Bizarro et al. 2012; Shi et al. 2016) have suggested that NLPB may underestimate the stabilizing effect from multivalent ions such as Mg²⁺ ions (Bai et al. 2007; Tan and Chen 2010).

Computer simulations can treat discrete ions and the ion correlation and fluctuation effects (Chen et al. 2009, 2012; Kirmizialtin and Elber 2010; Hayes et al. 2012, 2015; Yoo and Aksimentiev 2012; Fried et al. 2013; Mak and Henke 2013; Giambasu et al. 2014, 2015; Henke and Mak 2014; Denesyuk and Thirumalai 2015; Wu et al. 2015). However, a sampling of a large number of ions often demands exceedingly long computer time (Dong et al. 2008). Therefore, several analytical and semi-analytical models have been developed. For example, the three-dimensional interaction site model (3D-RISM), a method based on Ornstein and Zernike integral equation theory, can provide a direct solution to the 3D density distribution around the RNA by considering the correlation effect (Giambaşu et al. 2014, 2015). The generalized counterion condensation theory (Hayes et al. 2015) is another recently developed model that can treat the Mg²⁺-mediated correlation effect while taking into account the complicated structure of RNA.

The tightly bound ion (TBI) model (Tan and Chen 2005, 2006a,b, 2007, 2008, 2010; He and Chen 2012, 2013; He et al. 2014) is a statistical mechanics-based model that can treat both the correlation and the fluctuation effects. The basic idea of the model is to enumerate all the possible modes of many-ion distributions, and for each mode, evaluate the many-body total interaction energy. Extensive tests using experimental data showed that the TBI model can provide much improved predictions for ion-binding properties and ion-mediated RNA folding stability (Tan and Chen 2005, 2006a,b, 2007, 2008, 2010; He and Chen 2012, 2013; He et al. 2014). However, the applicability of the original TBI model is limited by two factors. First, enumeration of discrete ion distributions for large RNA structures (>100 nt) becomes infeasible due to the exceedingly long computer time. Even for small (<100 nt) RNAs, it may cost hours or even days to run the computation for an RNA structure in a given ion condition. Second, the coarse-grained ion distribution renders the inability of the model to provide detailed information about the spatial distribution (coordinates) for the bound ions.

Recently, inspired by the demands for the prediction and analysis of the metal ion effects at the atomic resolution for larger RNAs (>100 nt), we developed a new model, the Monte Carlo tightly bound ion (MCTBI) model (Sun and Chen 2016). The main advantages of this new model are the following (see Fig. 1). First, Monte Carlo sampling of the ion distributions combined with a parallelized algorithm leads to significantly enhanced computational efficiency. Second, unlike the original TBI model, the new model predicts the three-dimensional coordinates for the bound ions. In this article, we introduce a MCTBI-based web server (http://rna.physics.missouri.edu/MCTBI) for the prediction of metal ion effects for an RNA structure in a given ionic solution.

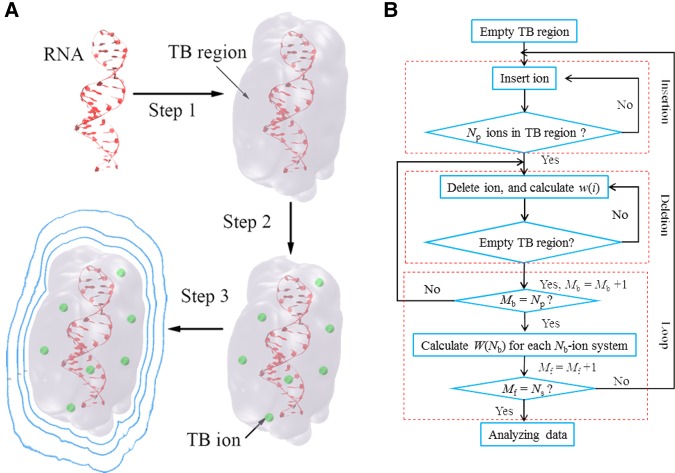
FIGURE 1.

(A) Three steps of the MCTBI computation. The blue solid lines present the electrostatic equipotential lines. (B) The flowchart of the “insertion–deletion” algorithm in a MCTBI computation.

RESULTS AND DISCUSSION

The MCTBI web server (http://rna.physics.missouri.edu/MCTBI) is a user friendly platform for the prediction and analysis of ion effects for nucleic acids. The current version of the server can treat mixed salt with divalent (Mg²⁺)/monovalent (Na⁺ or K⁺) ions with Cl^– (by default) as the co-ion. To avoid exceedingly long computational time, the server sets a default limit for the sequence length of 256 nt. In the following, using adenine-riboswitch (PDBID: 4TZX) (Zhang and Ferré-D'Amaré 2014) as an example, we illustrate the use of the MCTBI web server for predicting ion effects.

Input

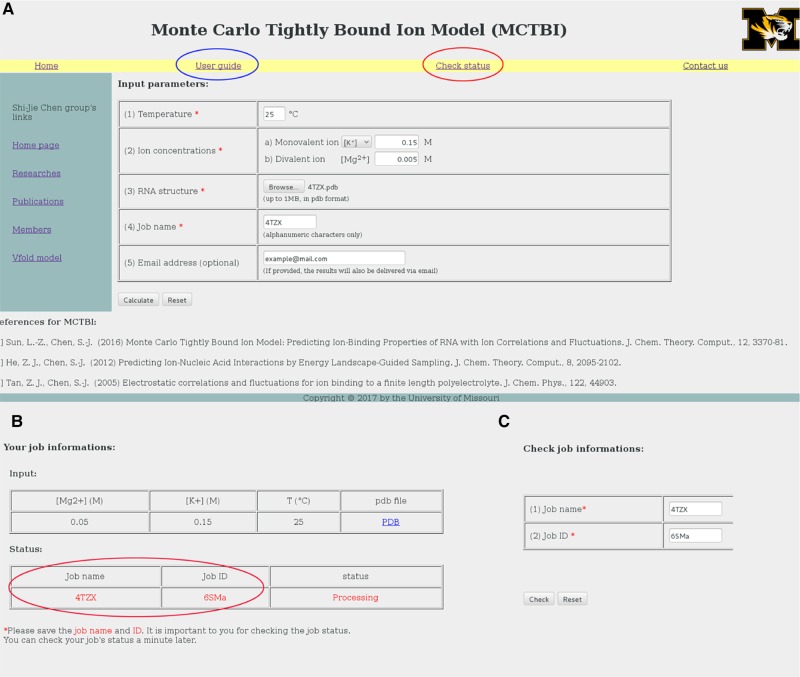
As shown in Figure 2A. the input parameters (labeled by red stars) are the following: (i) the temperature in Celsius, (ii) the bulk concentrations of the monovalent (Na⁺ or K⁺) and divalent (Mg²⁺) cations in the unit of M, (iii) the structure of RNA/DNA in PDB format, and (iv) the job name. The user can select Na⁺ or K⁺ as the monovalent ions. As an optional choice, the user can also input an email address for the delivery of the calculation results. The details of the input/upload data are described in the “User guide” web page (marked by a blue circle in Fig. 2A).

FIGURE 2.

The user interface of the MCTBI web server: The web pages for job submission (A), job information (B), and job status (C).

After the job is submitted, the server shows a web page (see Fig. 2B) that displays the basic information of the job, such as the input parameters and the job status. Each submitted job has a unique job ID (marked by red circle in Fig. 2B) as well as a job name (provided by the user). With the job name and ID, the “Check status” link shows the status of the submitted job: “processing” for a job waiting in the queue, “running” for an active job in calculation, and “done” for a completed job. See Figure 2A (marked by red circle) and the screenshot shown in Figure 2C.

Output

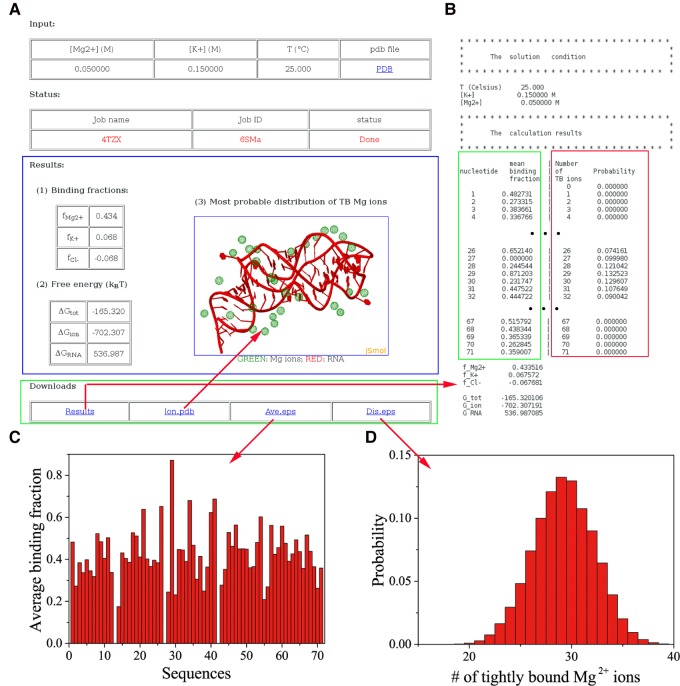
The user receives the output results in two ways. If the user chooses to provide the email address, a URL for the results is sent to the email address. Alternatively, the user can retrieve the data directly from the “Check” link (see Fig. 2C). As shown in the screenshot for the results page (marked by blue rectangle in Fig. 3A), the user can choose to download the results through the “Downloads” link (marked by green rectangle in Fig. 3A).

FIGURE 3.

(A) The web page that shows the results. (B) An example of the data text file, including the solution condition and calculation results. (C) The average binding fraction of TB Mg²⁺ ions for each nucleotide. (D) The probability distribution of the number of the TB Mg²⁺ ions.

The output “Results” web page shows the following items:

1. “Binding fractions”: defined as the average number of excess bound ions per nucleotide, denoted as f_Mg²⁺ for Mg²⁺, f_{Na⁺ (or K⁺)} for Na⁺ (or K⁺), and f_Cl– for Cl^–, respectively (see Equation S6 in the Supplemental Information). The predicted number of bound ions quantifies the ion-induced charge neutralization (Bai et al. 2007; Greenfeld and Herschlag 2009; Gebala et al. 2015).

2. “Free energy”: includes ΔG_tot for the total electrostatic free energy of the system, ΔG_RNA for the electrostatic interaction energy of the RNA, and ΔG_ion for the electrostatic free energy induced by the ions (see Equations S8–S10 in the Supplemental Information). We note that the binding fractions and the free energies involve integration over the whole solution box (the TB and DB regions), whose size is larger than six times of Debye length.

3. “The most probable distribution” of the TB Mg²⁺ ions. Although the TB region-like ionic layer could be observed in MD simulations (Hayes et al. 2012) and experiments (Das et al. 2003), the TB ions are not observed in RNA crystal structures. This is because TB ions are nonspecifically bound ions with strong ion–ion coupling. They are not site-bound ions. Although the TB ions are not directly shown in RNA crystal structures, as shown in the comparisons with mean-field (correlation-free) models such as NLPB (Tan and Chen 2005, 2006a,b, 2007, 2008, 2010; He and Chen 2013; He et al. 2014), the TB ion correlation and fluctuation effects may play an important role in ion-mediated folding stability. Therefore, the web server reported here may offer a reliable tool to predict the probable ion binding sites and the predicted most probable ion binding sites may serve as a reliable starting point for further refinement in the search for more accurate and precise binding sites. The result provides direct insights on how and where the ions bind to the RNA. The TB ions and the RNA structure are depicted through the JMol visualization applet. The coordinates of the ions can be downloaded as “Ion.pdb” in the “downloads” section.

4. The “downloads” section gives the raw data of the numerical calculations (see Fig. 3B for a screenshot). For example, the average binding fraction of the TB Mg²⁺ ions for each nucleotide in RNA (marked with green rectangle; see Eq. S12 in Supplemental Information) and the probability distribution of the number of TB Mg²⁺ ions (marked with a red rectangle; see Eq. S13 in Supplemental Information). The average binding fraction of the TB Mg²⁺ ions accounts for only the TB ions around every nucleotide and does not include the weakly correlated ions, while the “binding fraction” contains both the TB ions and the excess weakly correlated ions, including the excess monovalent ions. The server provides downloadable figures (Fig. 3C,D) for the results.

Application examples of the web server

Example 1: ion binding fractions for an rRNA fragment and its complex with the Bst-L11C protein

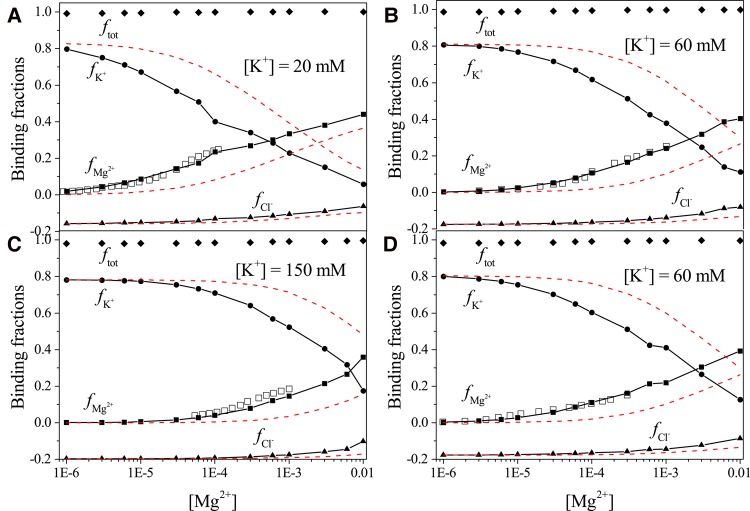
For a 58-nt fragment of rRNA and the RNA–protein (PDBID: 1HC8) (Conn et al. 2002) complex, the server-predicted binding fractions (see Fig. 4) show good agreement with the experimental data for various salt conditions. The server gives better results than NLPB (red dashed lines). Although both Mg²⁺ and K⁺ ions accumulate around the RNA/complex to form the “ion atmosphere,” they show competitive binding to RNA. With the increase in the bulk ion concentration [Mg²⁺], more Mg²⁺ ions bind to the RNA/complex due to the reduced entropic cost for Mg²⁺ ion binding, and in the meantime, less K⁺ ions bind to the RNA/complex. Compared with the K⁺ ions, due to the higher charge, Mg²⁺ ion binding can more effectively screen the Coulombic repulsion between the RNA/complex and Cl^– ions, resulting in an increase in the binding fraction f_Cl–. Furthermore, we find that the total binding fraction f_tot (see S7 in Supplemental Information) maintains a value nearly equal to one for the different ion conditions, indicating that the whole RNA/complex-ion system keeps nearly neutral.

FIGURE 4.

The [Mg²⁺]-dependence of the ion binding fraction for each ion species: for the 58-nt fragment RNA at [K⁺] = 20 mM, 60 mM, and 150 mM, respectively (A–C); for the RNA–protein complex at [K⁺] = 60 mM (D). The temperature for all the calculations is set at 25°C. Empty squares represent the experimental data from Grilley et al. (2007) and Leipply and Draper (2011b). The red dashed lines show the ion binding fractions calculated using the NLPB model.

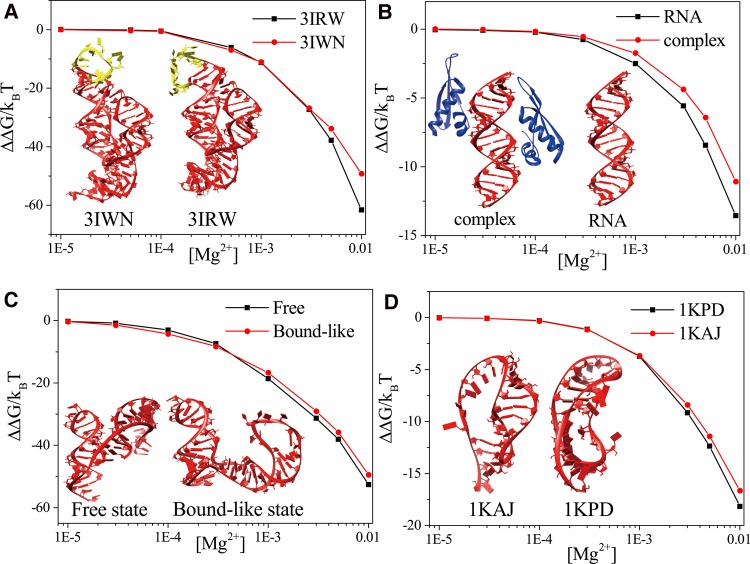
Example 2: Mg²⁺ ion-induced stabilization for c-di-GMP riboswitch

The c-di-GMP riboswitch is a gene-regulating RNA that can function as a second messenger signaling molecule. Two structures have been reported for the c-di-GMP riboswitch (PDBID: 3IWN and 3IRW) (Kulshina et al. 2009; Smith et al. 2009). A notable difference between the two structures is the position of the loop (labeled yellow in the inset of Fig. 5A): The loop in 3IWN involves larger bending than that in 3IRW. The difference may result from multiple factors such as the different mutations in the sequences, salt conditions, and the different crystal packing effects. Another difference in the two structures is that some specifically bound (dehydrated) Mg²⁺ ions are detected for 3IRW, but none for 3IWN. This example illustrates how to use the web server to analyze the different Mg²⁺ ion effects for the two structures. The server gives the Mg²⁺-induced electrostatic free energy:

$$\mathrm{\Delta \Delta }G=\mathrm{\Delta }{G}_{\mathrm{tot}}([{\text{Mg}}^{2+}])-\mathrm{\Delta }{G}_{\mathrm{tot}}(0).$$ (1)

FIGURE 5.

The [Mg²⁺]-dependence Mg²⁺-induced free energy for (A) two structures of the c-di-GMP riboswitch at [Na⁺] = 0.3 M, (B) the dsRNA-NF90 complex and dsRNA alone at [Na⁺] = 50 mM, (C) the free state and the bound-like state of the glutamine riboswitch at [K⁺] = 100 mM, and (D) the RNA pseudoknot and its mutant at [Na⁺] = 50 mM. The temperature in all the calculations is set at 25°C. The insets show the corresponding RNA structures.

Here ΔG_tot([Mg²⁺]) and ΔG_tot(0), the total free energies with Mg²⁺ and without Mg²⁺, can be directly calculated from the server. The result, as shown in Figure 5A, shows that at high [Mg²⁺], the Mg²⁺-induced stabilizing free energy ΔΔG is more significant for 3IRW than for 3IWN. In the 3IRW structure, the loop and the surrounding structure form a pocket that can capture TB Mg²⁺ ions (see Fig. S2A in the Supplemental Information) at high (Mg²⁺). In contrast, no TB Mg²⁺ ion is predicted to bind to the 3IWN loop region because the bending of the loop is too strong to form a pocket (also see Fig. S2A in the Supplemental Information). Therefore, compared with the structure of 3IWN, the 3IRW structure can attract more TB Mg²⁺ ions, as shown in Fig. S2B in the Supplemental Information, resulting in a stronger Mg²⁺ ion effect. For a solution with low [Mg²⁺], however, Mg²⁺ binding to the pocket region in 3IRW is diminished, and the two structures show nearly the same (low) number of TB Mg²⁺ ions (see Supplemental Fig. S2C,D). Therefore, for a dilute Mg²⁺ solution, the two structures show similar (weak) Mg²⁺ ion-induced stabilization effects.

Example 3: Mg²⁺ ion effect on protein–RNA binding

The RNA-binding proteins (RBPs) such as nuclear factors 90 and 45 (NF90 and NF45) have crucial roles in post-transcriptional control of RNAs. The server can be used to predict the ion effect in RNA–protein binding. Here, we apply the server to investigate the Mg²⁺ effects in the binding between NF90 and a double-stranded RNA (dsRNA) helix. With the dsRNA–NF90 complex (PDBID: 5DV7) (Jayachandran et al. 2016) and the dsRNA structure (the inset of Fig. 5B), the server gives the Mg²⁺ ion-induced free energies. As shown in Figure 5B, the effect of the Mg²⁺-induced stabilization is more pronounced for the dsRNA than the complex, resulting in an effective decrease in protein–RNA affinity.

Further, the average binding fraction predicted by the server (Fig. S3A in the Supplemental Information) shows that for most nucleotides, the average binding fraction decreases after the dsRNA–NF90 binding. However, some other nucleotides, such as A5, A12, and A29, marked in Supplemental Figure S3A, show an increased ion binding fraction. This phenomenon is the result of two competitive effects induced by the protein binding. On the one hand, the protein binding may displace some of the bound Mg²⁺ ions, leading to a decrease in the average binding fraction for nucleotides on the protein binding site (labeled green in Supplemental Fig. S3B–D). On the other hand, the presence of protein can effectively lower the dielectric constant and thus enhance ion–RNA attraction. As a result, nucleotides that are near but not directly bounded by the protein (labeled yellow in Supplemental Fig. S3B–D) can attract more Mg²⁺ ions.

Example 4: Mg²⁺-induced structure change for the glutamine riboswitch

The apo form of the glutamine riboswitch can adopt two states in the presence of Mg²⁺ ions ([Mg²⁺] = 5 mM) (Ren et al. 2015): a major free state (PDBID: 5DDO) (Ren et al. 2015) that is identical to the state in the absence of Mg²⁺ and a minor bound-like state that is similar to the state in the presence of ligand (PDBID: 5DDP) (Ren et al. 2015). Moreover, the dehydrated specifically bound ions could be detected in the presence of ligand. The structures of both states are presented in the inset of Figure 5C. Experimental studies indicated that in a solution of 5 mM Mg²⁺, Mg²⁺ ions help stabilize the major free state over the bound-like state. The result is consistent with the server-predicted Mg²⁺-induced free energies (see Fig. 5C).

The server-predicted TB ion binding probability (Supplemental Fig. S4A) shows that the free state attracts more TB ions than the bound state at high [Mg²⁺]. At dilute [Mg²⁺] (such as [Mg²⁺] = 0.1 mM), the situation is reversed so the Mg²⁺-induced free energy of the bound state is lower than that of the free state (Supplemental Fig. S4B). As a result, the bound state may become the major state at dilute [Mg²⁺]. Furthermore, as shown in Supplemental Figure S4C, the server-predicted most probable distribution of the TB Mg²⁺ ions for the bound state suggests that three of the TB ions are close to the specific binding sites of Mg²⁺ ions (labeled with blue spheres).

Example 5: Mg²⁺ ion binding properties for an RNA pseudoknot and its mutant

This example illustrates the application of the web server to investigate the binding properties of Mg²⁺ ions for an RNA pseudoknot (PDBID: 1KAJ) (Kang et al. 1996) and its mutant (PDBID: 1KPD) (Kang and Tinoco 1997). The structures are presented in Supplemental Figure S5A and the inset of Figure 5D. Compared with 1KAJ, the mutant structure 1KPD contains one more base pair and has a different tertiary structure. Because the mutant structure is more compact and thus has higher charge density, it attracts more Mg²⁺ ions, especially at high [Mg²⁺]. Indeed, the server gives a higher average binding fraction for most of the nucleotides in the mutant than the wild-type RNA. Consistent with the ion binding result, the server predicts a stronger Mg²⁺ ion-induced free energy decrease for 1KPD than for 1KAJ (Fig. 5D). However, the above situation of ion binding is reversed for some other nucleotides, such as A13 (marked in Supplemental Fig. S5B). To further investigate this phenomenon, we use the server to compute the most probable distributions of the TB Mg²⁺ ions for the two structures. The results show that there are three TB Mg²⁺ ions near A13 because the tertiary structure of 1KAJ forms several pockets nearby, while none of the TB Mg²⁺ ions is observed to bind near A13 in 1KPD.

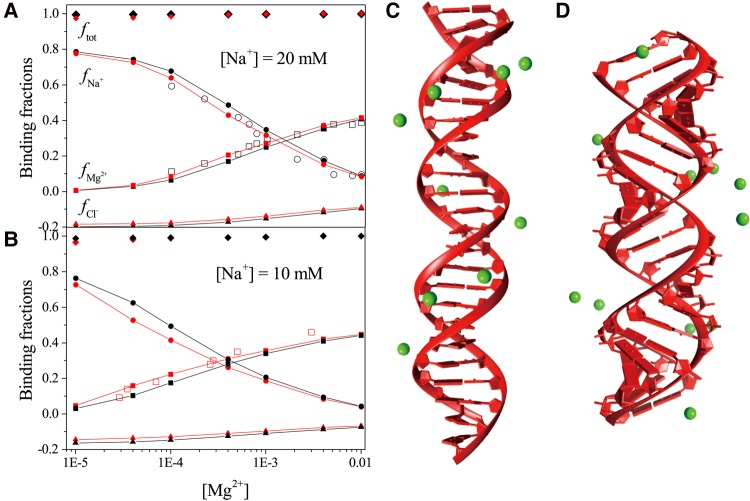
Example 6: comparisons of Mg²⁺ ion binding properties between A-form and B-form helices

In this example, the 24- and 40-bp B-form DNA (B-DNA) and A-form RNA (A-RNA) duplex structures are generated using the open source software X3DNA (Lu and Olson 2003). Figure 6A,B show that the server predictions for the ion binding fractions for 24-bp B-DNA (black lines in Fig. 6A) and 40-bp A-RNA (red lines in Fig. 6B) are in good agreement with the results of the “Ion Counting” experiments (Krakauer 1971; Bai et al. 2007). We also use the MCTBI server to calculate the ion binding fractions for the 24-bp A-RNA helix (see the red lines in Fig. 6A) and 40-bp B-DNA helix (see the black lines in Fig. 6B). Compared with the B-DNA, the A-RNA can attract more Mg²⁺ ions around it and result in less Na⁺ association and Cl^– depletion. The most probable TB ion distributions (Mg²⁺) for 24-bp B-DNA and A-RNA, as shown in Figure 6C,D, show that all the TB ions are aligned along the deep groove. However, because the deep groove of the A-RNA is narrower and deeper, which results in the higher charge density in the backbone, the attraction on Mg²⁺ ions is more pronounced.

FIGURE 6.

(A,B) The [Mg²⁺]-dependence of the ion binding fractions for each species for 24-bp A-RNA and B-DNA at [Na⁺] = 20 mM (A) and 40-bp A-RNA and B-DNA at [Na⁺] = 10 mM (B). The black and red lines belong to B-form DNA duplex and A-form RNA duplex, respectively. The empty scatters (circles and squares) represent the experimental results of the 24-bp B-form DNA duplex from Bai et al. (2007) and the 40-bp A-form RNA duplex from Krakauer (1971). (C,D) The most possible distributions of TB ions around the 24-bp B-DNA and A-RNA structures at [Mg²⁺] = 1 mM and [Na⁺] = 20 mM.

Summary and conclusion

The Mg²⁺ ion, as the essential metal ion for RNA folding, may involve significant ion–ion correlation and fluctuation effects. Extensive theory–experiment comparisons suggested the importance to account for such effects for the prediction of the ion effects in nucleic acid folding. By considering ion correlation and fluctuation effects, the MCTBI web server offers a user friendly web-based platform for the calculation of the ion binding properties, such as average ion binding fractions and the most probable bound ion distributions, and ion-mediated electrostatic free energies and the different free energy components. From these predicted results, users can gain novel insights into how and where metal ions would likely bind to the structure, how a structure is stabilized/destabilized through metal ion-mediated electrostatic interactions, and how metal ions induce switches between the different conformations.

However, as a caveat, it is important to point out that the current version of the web server is limited, as noted below. First, because the MCTBI model does not treat specific interactions and ion dehydration, the server cannot provide accurate, high-resolution predictions for site-specific ion binding and the formation of ion clusters (such as Mg²⁺–Mg²⁺ clusters and K⁺–Na⁺ clusters) (Serganov et al. 2008; Drozdzal et al. 2016). Second, the current model is focused only on ion correlation for multivalent ions, therefore, it cannot handle monovalent ion-mediated correlation, an important effect for many RNA systems (Bai et al. 2008; Gebala et al. 2015). Future development of the model and server would address the above two issues. The new model and web server should allow predictions for different metal ions such as Mn²⁺, Ba²⁺, and Ca²⁺.

MATERIALS AND METHODS

In the MCTBI model, an RNA structure is placed at a large solution box with mixed ions, including divalent ions (Mg²⁺), monovalent cations (Na⁺ or K⁺), and monovalent anions (Cl^–). The solution box size is larger than six Debye lengths in order to reduce the boundary effect (Tan and Chen 2005). The MCTBI model is focused on the nonspecifically bound ions and treats ions with full hydration, where divalent ions have two hydration shells (Pavlov et al. 1998), and monovalent ions keep one hydration shell. Because of the strong Coulombic attraction from the RNA, ions (especially cations) accumulate around the RNA, resulting in a region of high concentration and hence strong correlation for the ions (Tan and Chen 2005). In such a region, the ion correlation and fluctuation effects cannot be neglected, due to the strong mutual Coulomb and excluded volume couplings (Sun et al. 2017). Correspondingly, the ions around RNA can be classified into tightly bound (TB; strongly correlated, high concentration) ions, which are located in the strong correlation region, and the diffusely bound (DB; weakly correlated) ions, which are located away from the RNA surface. The TB region for a given RNA structure and ionic condition is usually a nonuniform thin layer surrounding the RNA surface. The rigorous demarcation of the TB and the DB regions can be found in previous publications (Tan and Chen 2005; He and Chen 2012; Sun and Chen 2016). In the MCTBI model, the TB ions and DB ions are treated as discrete particles (with the correlation effect) and continuum background (without the correlation effect), respectively.

Unlike multivalent ions, monovalent ions have a low charge and hence have a weak correlation effect. As a result, for monovalent ions, NLPB-based predictions, which ignore the correlation effect, can often give good agreements with experimental results (Bai et al. 2007, 2008). The weak correlation effect for monovalent ions allows us to treat all the monovalent ions as DB ions and define TB regions only for multivalent (such as Mg²⁺) ions. However, it is important to note that the model does not account for other potentially significant correlation effects involving monovalent ions/charges. Experimental studies showed that for monovalently charged particles, such as TMA⁺, F^–, and As(CH₃)₂O₂^–, in mixed salt solutions (Bai et al. 2008; Gebala et al. 2015), the correlation effect between monovalent ions (especially cation–anion pair correlation) cannot be neglected (Gebala et al. 2015). Furthermore, it is worth noting that because the MCTBI does not account for the ion dehydration effect, it cannot treat specific ion binding and the formation of metal ion core/cluster, which may involve significant ion dehydration.

For a given RNA structure, the MCTBI calculation follows three steps, as shown in Figure 1A. Below we briefly summarize the main points of the model. Further details can be found in Sun and Chen (2016).

1. We first run NLPB to estimate the ion distribution, from which we calculate the spatial distribution of ion correlation strength. For TB ions in the strong correlation region (or TB region), we sample discrete many-ion distributions and evaluate the electrostatic energy for each distribution. By considering the simultaneous distribution of all the TB ions, the model accounts for the correlation effect. For weakly correlated ions, we use NLPB to calculate the free energy.

2. For a given RNA structure with N_p nucleotides, the partition function of the whole system can calculated as the sum over all the ion distributions, which can be classified by the number of the TB ions N_b (Sun and Chen 2016):

   $$\begin{array}{rll}\hfill Z& \hfill =\hfill & \sum _{N_{\mathrm{b}}=0}^{N_{\mathrm{p}}}Z(N_{\mathrm{b}})\hfill \\ & \hfill =\hfill & \sum _{N_{\mathrm{b}}=0}^{N_{\mathrm{p}}}\left[Z_{\mathrm{id}}{(c_{2+}^0)}^{N_{\mathrm{b}}}\frac{W(N_{\mathrm{b}})}{N_{\mathrm{b}}!}{e}^{-\mathrm{\Delta }{G}_{\mathrm{non}-\mathrm{tb}}/k_{\mathrm{B}}T}\right]\hfill \end{array}$$ (2)

   Here, the number of the TB ions N_b is assumed to vary between zero and N_p. Z(N_b) and Z_id are the partition functions for the system with N_b TB ions and the ideal reference system without RNA polyanions, respectively. c₂₊⁰ denotes the bulk concentration of the divalent ion such as Mg²⁺. ΔG_non-tb denotes the free energy for the non-TB ions, including the electrostatic interaction energy between the DB ions, between DB ions and other charged particles, and between the charged atoms in RNA. The details about the free energy calculation can be found in the Supplemental Information (SI) and Sun and Chen (2016)
3. The calculation of the total statistical weight W(N_b) for a given number of the TB ions N_b involves the sampling of the TB ion distributions. To sample the ion distribution, we place the TB ions on the grid sites of a cubic lattice and each lattice site can be occupied by at most one ion. We generate the ion distributions by inserting ions one by one. The procedure gives W(N_b) as

   $$W(N_{\mathrm{b}})=\prod _{i=1}^{N_{\mathrm{b}}}w(i).$$ (3)

   Here the product ${\prod }_{i=1}^{N_{\mathrm{b}}}$ corresponds to the process of adding 1,2….Nb ions. w(i) is the statistical weight of the ith inserted ion, which is equal to the sum over all the available (vacant) sites for the (ith) ion:

   $$w(i)=\sum _{k=1}^{m_i}{e}^{-\mathrm{\Delta }{U}_i(k)/k_{\mathrm{B}}T}.$$ (4)

   Here m_idenotes the number of the available sites for placing the ith ion, ΔU_i(k) is the interaction energy between the ith ion at site k and the rest of the charged particles.
4. The MCTBI model uses a novel Monte Carlo insertion–deletion (MCID) algorithm to sample the TB ion distributions (see Fig. 1B for the flowchart of the MCID algorithm). First, ions are inserted such that the ith TB ion is placed at site k according to the following insertion probability:

   $$p_{\mathrm{f}}(i,k)=\frac{e^{-\mathrm{\Delta }{U}_i(k)/k_{\mathrm{B}}T}}{{\sum }_{k=1}^{m_i}{e}^{-\mathrm{\Delta }{U}_i(k)/k_{\mathrm{B}}T}}.$$ (5)

   The ions tend to occupy the low-energy sites. After all the TB ions are inserted, ions are removed such that the jth ion at site k is removed according to the following deletion probability:

   $$p_{\mathrm{b}}(j,k)=\frac{e^{\mathrm{\Delta }{U}_j(k)/k_{\mathrm{B}}T}}{{\sum }_k{e}^{\mathrm{\Delta }{U}_j(k)/k_{\mathrm{B}}T}}.$$ (6)

   High-energy ions are more likely to be removed. The above two-step sampling–resampling algorithm enhances the sampling of the important (low-energy) distributions.

In the MCTBI server, we use the simple open multiprocessing (OpenMP) application programming interface (API) to parallelize the MCID algorithm to enhance the computational efficiency (see Supplemental Information for the details).

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.