Structure-based control of complex networks with nonlinear dynamics

Significance

Many biological, technological, and social systems can be encoded as networks over which nonlinear dynamical processes such as cell signaling, information transmission, or opinion spreading take place. Despite many advances in network science, we do not know to what extent the network architecture shapes our ability to control these nonlinear systems. Here we extend a recently developed control framework that addresses this question and apply it to real networks of diverse types. Our results highlight the crucial role of a network’s feedback structure in determining robust control strategies, provide a dynamic-detail-independent benchmark for other control methods, and open up a promising research direction in the control of complex networks with nonlinear dynamics.

Abstract

What can we learn about controlling a system solely from its underlying network structure? Here we adapt a recently developed framework for control of networks governed by a broad class of nonlinear dynamics that includes the major dynamic models of biological, technological, and social processes. This feedback-based framework provides realizable node overrides that steer a system toward any of its natural long-term dynamic behaviors, regardless of the specific functional forms and system parameters. We use this framework on several real networks, identify the topological characteristics that underlie the predicted node overrides, and compare its predictions to those of structural controllability in control theory. Finally, we demonstrate this framework’s applicability in dynamic models of gene regulatory networks and identify nodes whose override is necessary for control in the general case but not in specific model instances.

Controlling the internal state of complex systems is of fundamental interest and enables applications in biological, technological, and social contexts. An informative abstraction of these systems is to represent the system’s elements as nodes and their interactions as edges of a network. Often asked questions related to control of a networked system are how difficult to control it is, and which network elements need to be controlled, and through which control actions, to drive the system toward a desired control objective (1–11). Among control frameworks, structure-based methods distinguish themselves due to their ability to draw dynamical conclusions based solely on network structure and a general assumption about the type of allowed dynamics. For example, structural controllability (SC), which assumes unspecified linear dynamics or linearized nonlinear dynamics, allows the identification of the minimal number of nodes whose receiving an external signal $u(t)$ drives the system into a state of interest (12, 13).

Despite its success and widespread application (14–18), SC may give an incomplete view of the network control properties of a system. In the case of systems with nonlinear dynamics, it provides sufficient conditions to control the system in the neighborhood of a trajectory or a steady state (refs. 1 and 18 and SI Appendix), and its definition of control (full control; from any initial to any final state) does not always match the meaning of control in biological, technological, and social systems, in which control tends to involve only naturally occurring system states (19). In addition to the approaches provided by nonlinear control theory (9–11, 18), new methods of network control have been proposed to incorporate the inherent nonlinear dynamics of real systems and relax the definition of full control (4, 6, 11, 18, 20). Only one of these methods, namely, feedback vertex set control (FC), can be reliably applied to large complex networks in which only the structure is well known and the functional form of the governing equations is not specified. This method, introduced by Mochizuki and coworkers in refs. 3 and 21, incorporates the nonlinearity of the dynamics and considers only the naturally occurring end states of the system (e.g., steady states and limit cycles) as desirable final states. In this work, we use FC on biological, technological, and social networks to predict the nodes whose override (by external control) can steer a network’s dynamics toward any of its natural long-term dynamic behaviors (its dynamical attractors). We identify the topological characteristics underlying the predicted node overrides, compare the obtained results with those of control theory’s SC (1, 12, 13), and identify the model-dependent and model-independent overrides it provides for network models with parameterized dynamics.

Structure-Based Network Control with Nonlinear Dynamics

Most real systems are driven by nonlinear dynamics in which a decay term prevents the system’s variables from increasing without bounds. The state of the system’s $N$ nodes at time $t$, characterized by source node variables $S_j(t)$ (for nodes with no incoming edges) and internal node variables $X_i(t)$, obeys the equations

$$d{X}_i/dt=F_i(X_i,X_{I_i},t),$$ [1]

$$d{S}_j/dt=G_j(t),$$ [2]

where $i=1,\mathrm{\dots },N-N_s$, $j=N-N_s+1,\mathrm{\dots },N$, and $N_s$ is the number of source nodes. The dynamics of each source node $j$ is independent of the internal node variables $X_i$ (by definition), is fully determined by $G_j(t)$, and does not include a decay term. In the simplest case, $G_j=0$ and $S_j$ will remain in its specified initial value. The dynamics of each internal node $i$ is governed by $F_i(X_i,X_{I_i},t)$, which captures the nonlinear response of node $i$ to its predecessor nodes $I_i$ (which can be source or internal nodes), and which includes decay in the dependence of $F_i$ on $X_i$ (SI Appendix). Functions of the form $F_i=f_i(X_{I_i})-{\alpha }_i(X_{I_i})X_i$, which satisfy these conditions, are used to describe the dynamics of birth–death processes (22, 23), epidemic processes (22, 24, 25), biochemical dynamics (26, 27), and gene regulation (26–29). As an example, $X_i(t)$ can denote the concentration of proteins involved in a signal transduction pathway, and $S_j(t)$ can denote the concentration of extracellular signals (molecules). In this case, $f_i$ can take the form of a Hill function [e.g., $f_i={\beta }_i{X}_k^2/(X_k^2+{\theta }^2)$ if $k$ is the only node in $I_i$] or of a mass action term (e.g., $f_i={\beta }_i{X}_k{X}_l$ if $k$ and $l$ are the only nodes in $I_i$). As an alternative example, $X_i(t)$ can denote the probability that an individual is infected in a contagion network, $S_j(t)$ can denote the influence of vaccination or prevention measures on certain individuals, and $F_i$ can take the form of a susceptible–infected–susceptible model term [e.g., $F_i={\beta }_i{X}_k(1-X_i)-{\alpha }_i{X}_i$ if $k$ is the only node in $I_i$]. (Note that these functions are just examples, and that the framework we describe is valid for any bounded dynamical process of the form of Eqs. 1 and 2 that occurs on the specified network structure.)

The dynamics described by Eqs. 1 and 2 are such that they possess some naturally occurring end states, or dynamical attractors. Dynamical attractors in biological, social, and technological systems represented by networks have been found to be identifiable with the stable patterns of activity of the system. For example, in gene regulatory networks, dynamical attractors correspond to cell fates (27–29); in opinion spreading dynamics on social networks, they correspond to opinion consensus states of groups of individuals (25); and, in disease or computer virus spreading, they correspond to the long-term (endemic) patterns of infected elements (24).

In many systems, there is adequate knowledge of the underlying wiring diagram but not of the specific functional forms and parameter values required to fully specify $F_i$ and $G_j$. Analyzing such systems requires the use of structure-based control methods such as FC. FC, developed by Mochizuki and coworkers (3, 21), is a mathematical formalization of the following idea: To drive the state of a network to any one of its naturally occurring end states (dynamical attractors), one needs to manipulate a set of nodes that intersects every feedback loop in the network–the feedback vertex set (FVS). This requirement encodes the importance of feedback loops in determining the dynamical attractors of the network, a fact that was recognized early on in the study of the dynamics of biological networks (30, 31). Mochizuki and coworkers (3, 21) mathematically proved that, for a network governed by the nonlinear dynamics of Eq. 1, the control action of forcing (overriding) the state variables of the FVS into the trajectory specified by a given dynamical attractor of Eq. 1 ensures that the network will asymptotically approach the desired dynamical attractor, regardless of the specific form of the functions $F_i$. Note that FC does not use a controller or driver signal, and instead considers node state override as its control action. [The general task of designing a controller with an attractor as the target state in a nonlinear system is a difficult and unsolved problem that depends strongly on the functions $F_i$, although several numerical algorithms for specific types of controllers have been proposed (refs. 4, 7, and 18 and SI Appendix).] This type of intervention is often used in biological systems, with examples such as genome editing or pharmacological treatment (19, 32), and in epidemic spreading networks, where vaccination is a node state override that prevents a node from being infected. When using node state overrides as the control action, controlling the FVS is sufficient to drive the system to any of its attractors for each form of $F_i$ and is necessary if this must hold for every $F_i$ (refs. 3 and 21 and SI Appendix). The problem of exactly identifying the minimal FVS is nondeterministic polynomial-time hard (NP-hard), but a variety of fast algorithms exist to find close-to-minimal solutions (SI Appendix).

In the structural theory of Mochizuki and coworkers (3, 21), every element is governed by Eq. 1. It is assumed that the source nodes converge to a unique state (or trajectory) and do not need independent control; thus they are iteratively removed from the network before applying FVS control. However, source nodes can denote external stimuli or boundary conditions the system is subject to; a different set of attractors may be available for each state of a source node. For example, in the parameterized biological models we consider, source nodes provide positional information for the cells and affect the patterning behaviors cells are capable of.

Here we adapt the structural theory of Mochizuki and coworkers (3, 21) to networks in which source nodes are governed by Eq. 2 (Fig. 1A and SI Appendix). Because the source nodes are unaffected by other nodes, one additionally needs to lock the source nodes of the network in the trajectory specified by the attractor. We emphasize that the treatment of source nodes is not merely cosmetic, because the state of a source node can affect the dynamical attractors available to the system. For example, steady states can merge, appear, or disappear depending on the presence or absence of an external stimulus represented by a source node (26, 33). In summary, control of the source nodes and of the FVS of a network guarantees that we can guide it from any initial state to any of its dynamical attractors (i.e., its natural long-term dynamic behaviors) regardless of the specific form of the functions. In the following, we refer to this attractor-based control method as FC (Fig. 1A), and to the group of nodes that need to be manipulated by FC as an FC node set.

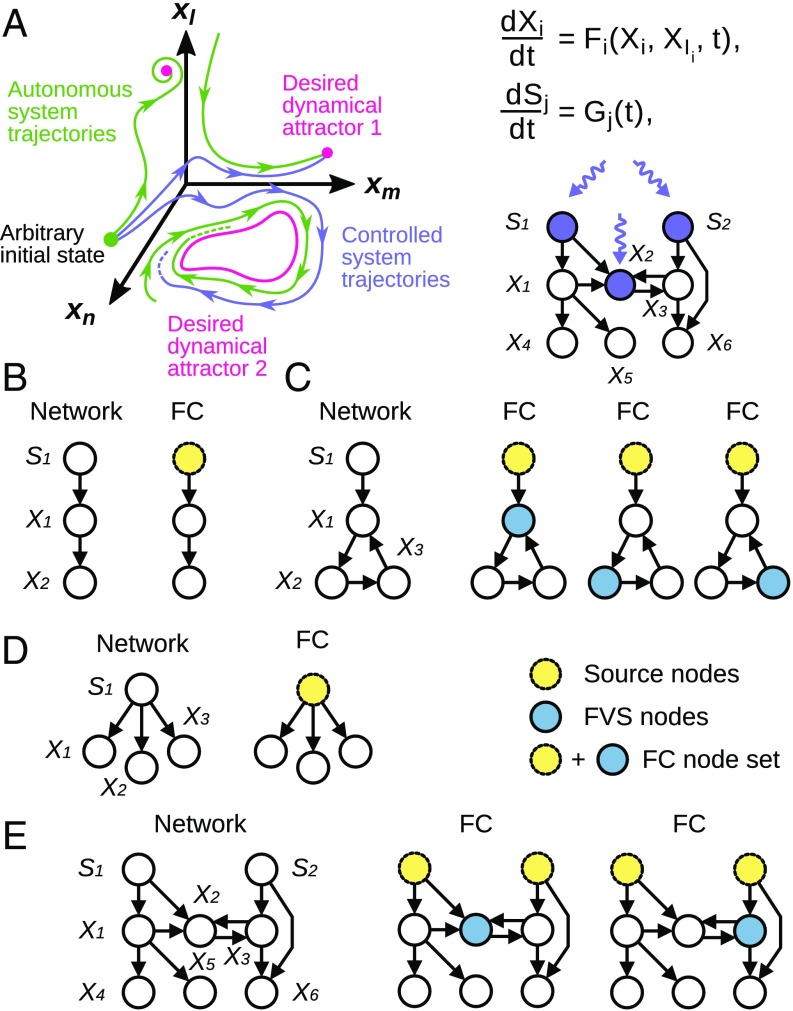
Fig. 1.

Structure-based network control with nonlinear dynamics. FC is a structure-based control method that can make conclusions about the long-term dynamics of a system using solely the network structure. (A) In FC, the objective is to drive the network from an arbitrary initial state to any desired dynamical attractor of the system (e.g., a steady state) by forcing (overriding) the state variables of certain nodes. (B–E) FC in simple networks. FC requires control of the source nodes (yellow nodes with dotted outlines) and of all cycles by control of the FVS (blue nodes with solid outlines).

To illustrate FC, consider the example networks in Fig. 1. In a linear chain of nodes (Fig. 1B, Left), the only node that needs to be controlled is the source node $S_1$. For Fig. 1C, a source node connected to a cycle, FC requires controlling the source node $S_1$ and any node $X_i$ in the cycle, the FVS in this network. Fig. 1D consists of a source node with three successor nodes, and FC requires controlling only the source node $S_1$, because there are no cycles in the network. In Fig. 1E, we show a more complicated network with a cycle and several source and sink nodes, and two minimal FC node sets. These examples illustrate an important feature of FC, namely, that it is determined by the cycle structure and the input layer of the network. SI Appendix, Fig. S1 illustrates FC in a network in which a specific form of the functions $F_i$ and $G_j$ is given.

Feedback Vertex Set Control of Real Networks

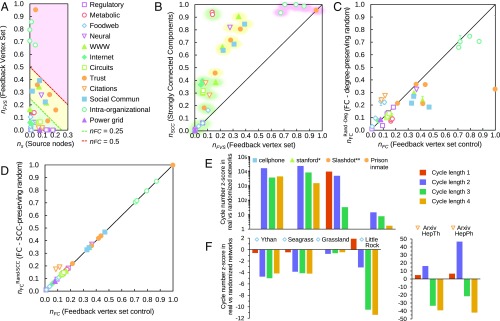
We applied FC to several real networks and the ratio of the minimal FC node set, $N_{FC}$, and the total number of nodes, $n_{FC}=N_{FC}/N$, was used to gauge how difficult it is to control these networks. The real networks are of diverse types (biological, technological, and social) and various sizes (from dozens to millions of elements), and have been repeatedly used as benchmarks to study SC (1, 18). The FC results are shown in SI Appendix, Table S1 and Fig. 2A, where the FVS and source node contributions of $n_{FC}$ are denoted by $n_{FVS}$ and $n_s$, respectively ($n_{FC}=n_{FVS}+n_s$). We observed that most types of biological networks (gene regulatory, metabolic, and food web networks) require control of a smaller fraction of nodes than social networks (trust, social communication, and intraorganizational networks); $n_{FC}$ is between 1% and 18% in biological networks vs. more than 21% in social networks. FC’s prediction that biological networks are easier to control than social networks matches recent experimental results in cellular reprogramming and large-scale social network experiments (19, 33, 34).

Fig. 2.

FC in real networks. (A) Scatter plot with the contribution of source nodes $n_s$ and the FVS $n_{FVS}$ to the fraction of control nodes in FC $n_{FC}$ for each real network in SI Appendix, Table S1. Each of the two lines in the scatter plot correspond to a fixed value of $n_{FC}$, because $n_{FC}=n_s+n_{FVS}$. The background color of the scatter plot indicates areas in which $n_{FC}$ takes a certain range of values: green for $n_{FC}<0.25$, yellow for $0.25<n_{FC}<0.5$, and pink for $n_{FC}>0.5$. (B) Scatter plot of the fraction of nodes in the FVS $n_{FVS}$ and the fraction of nodes in an SCC $n_{SCC}$ for each real network. The shading of the symbols corresponds to their position in A and reflects the relative size of their FC node set. (C and D) Scatter plot with the fraction of control nodes in FC for real networks ($n_{FC}$) and their (C) degree-preserving randomization ($n_{FC}^{Rand-Deg}$) or (D) SCC-preserving randomization ($n_{FC}^{Rand-SCC}$). Error bars denote the estimated SD of the randomized ensembles. (E and F) Cycle number z score for different cycle lengths in real versus degree-preserving randomized networks for the networks with (E) $n_{FC}>>n_{FC}^{Rand-Deg}$ and (F) $n_{FC}<<n_{FC}^{Rand-Deg}$.

To understand the topological properties underlying the diversity of the fraction of control nodes $n_{FC}$ among networks, we identify the nodes in a network that determine its cycle structure and thus the FVS contribution of the control nodes ($n_{FVS}$). Every node that is involved in a cycle must also be part of a strongly connected component (SCC), a group of nodes in a network in which there is a directed path between any pair of nodes. The concept of SCC is related to the bow tie structure of multiple empirical directed networks (35), in which most of the network belongs to a large SCC, its in-component (the nodes that can reach the SCC), or its out-component (the nodes that can be reached from the SCC).

Applying this reasoning to the studied real networks (SI Appendix, Table S1), we expect the networks in which the fraction of nodes that are part of an SCC is high to have a large FVS contribution $n_{FVS}$. As shown in Fig. 2B, the networks show a strong correlation between the relative size of their SCCs (denoted by $n_{SCC}$) and of their FVS (SI Appendix, Fig. S2A). For example, all of the networks with the largest FC node set size ($n_{FC}>0.5$, Fig. 2 A and B, pink shading; e.g., intraorganizational networks) have a large fraction of nodes in their SCCs ($n_{SCC}>0.93$). Similarly, networks with an intermediate FC node set size ($0.25<n_{FC}<0.5$, Fig. 2 A and B, yellow shading; e.g., social communication networks, and most trust and WWW networks) have an intermediate $n_{SCC}$ ($0.46<n_{SCC}<0.91$), and most of the networks with the smallest FC node set size ($n_{FC}<0.25$, Fig. 2 A and B, green shading; e.g., food webs, circuits, and gene regulatory networks) have correspondingly small SCCs ($n_{SCC}<0.4$).

Motivated by the observed remarkable agreement between the number of control nodes of real networks and their degree-preserving randomized versions in SC (1, 36), we study FC in similarly randomized networks (SI Appendix, Table S1 and SI Text). We find much weaker agreement (Fig. 2C): For most networks, the number of FC nodes is higher than the number of control nodes in randomized versions ($n_{FC}>n_{FC}^{Rand-Deg}$), with the notable exceptions of food web and citation networks, in which randomized networks require more control nodes ($n_{FC}<n_{FC}^{Rand-Deg}$) (Fig. 2 C and F). A closer look reveals that the cycle structure of the real networks—their cycles and SCCs—is responsible for the discrepancy of $n_{FC}$. Although the number of nodes in an SCC is similar or smaller compared with their degree-preserving randomized counterparts, real networks tend to have a more complicated cycle structure, evidenced by the overrepresentation of short cycles compared with the randomized networks (Fig. 2E), and reflected by the larger size of their FVS (SI Appendix, Table S1). The exceptions to this reasoning are food web and citation networks (Fig. 2F), which are known to have an acyclic (e.g., tree-like) or close-to-acyclic structure (37), and thus feature fewer cycles and fewer nodes in an SCC than randomized networks.

To verify that the cycle structure of real networks explains the observed FC node set size, we generated degree-preserving randomized versions of these networks that maintain their cycle structure, which we achieve by randomizing the directed acyclic part of the graph while keeping intact the SCCs (SI Appendix). The results show a remarkable agreement between the FC node set size of the networks and their randomized versions (Fig. 2D and SI Appendix, Table S1). Given that short cycles were found to correlate well with the discrepancy in FC node set size in real networks compared with randomized networks (SI Appendix, Table S1, and Fig. 2 E and F), we reasoned that preserving only the short-cycle structure of networks (in addition to their degree) might be sufficient to explain the FC node set size of real networks. To test this theory, we generated degree-preserving randomized versions of the networks that maintain their short-cycle structure (cycles of length 4 or less) (SI Appendix). SI Appendix, Fig. S2B and Table S1 show the resulting FC node set sizes, which have an excellent agreement with that of the real networks, the exceptions being the near-acyclic food web and citation networks, for which short cycles cannot capture their near-acyclic structure.

Taken together, these results show that the cycle structure of a network, specifically its SCCs and short cycles, determines the number of nodes that need to be overridden in FC.

Comparing Feedback Vertex Set Control and Structural Controllability

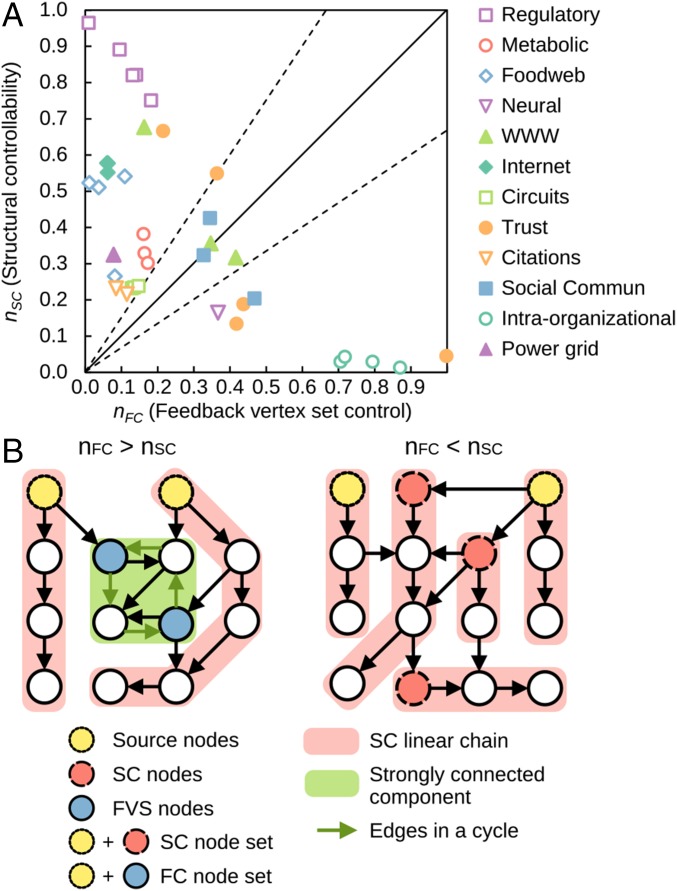
An interesting result from applying FC on real networks is that biological networks are easier to control than social networks, yet this prediction stands in contrast with those of SC on the same type of networks, in which the opposite result was obtained (1). This contradicting prediction is somewhat surprising, because both methods can be used to answer the question of how difficult to control a network is based solely on network structure, albeit each focuses on a different aspect of control (full control vs. attractor control), considers different underlying dynamics (linear vs. nonlinear), and uses different control actions (controller signal vs. node state override). To test whether this significant difference in the predictions of FC and SC is common among other networks, we compare their fraction of control nodes $n_{SC}$ and $n_{FC}$. As shown on Fig. 3A and SI Appendix, Table S1, $n_{SC}$ and $n_{FC}$ appear to be inversely related across several types of networks. For example, gene regulatory networks require between 75% and 96% of nodes in SC yet only require between 1% and 18% of nodes in FC. A similar $n_{SC}>>n_{FC}$ relationship is also seen in food web networks and internet networks, whereas the opposite relationship ($n_{SC}<<n_{FC}$) is seen in the social trust networks with low $n_{SC}$ and intraorganizational networks. This difference between methods warns practitioners against a naive application of SC or FC to control situations beyond their realm of applicability in terms of dynamics, control objective, or control action, as others have previously cautioned (8).

Fig. 3.

Comparing FC and SC. (A) Scatter plot with the fraction of control nodes in FC ($n_{FC}$) and SC ($n_{SC}$) for each real network in SI Appendix, Table S1. The bold line denotes the positions in the plot with $n_{SC}=n_{FC}$, and the dashed lines denote $n_{SC}=1.5\hspace{0.17em}{n}_{FC}$ and $n_{FC}=1.5\hspace{0.17em}{n}_{SC}$. (B) Examples of the effect of cycle structure in the FC and SC node set size. Control of the source nodes (yellow nodes with dotted outlines) is shared by SC and FC; in SC, every source node is the top node of a chain in a minimal group of nonintersecting linear chains of nodes (pink background) and directed cycles (green edges) that span the network. SC additionally requires controlling the top nodes in other chains (red nodes with dashed outlines) but requires no independent control of cycles. FC requires controlling all cycles by control of the FVS (blue nodes with solid outlines).

The difference in $n_{SC}$ and $n_{FC}$ can be attributed to the treatment of cycles in each of these methods: Cycles have to be controlled in FC but do not require independent control in SC. In SC, the nodes that must be directly controlled are each node at the top of a (minimal) group of nonintersecting linear chains of nodes and directed cycles that span the network; these cycles do not need to be directly controlled if there is a path to them from a linear chain of nodes.

To illustrate how the cycle structure influences the number of control nodes in FC and SC, consider the networks in Fig. 3B. The left-most network contains several cycles (green background) and requires more nodes to be manipulated in FC compared with SC ($n_{FC}>n_{SC}$). In FC, each of these cycles can be controlled through the nodes in the FVS (blue nodes); in SC, the cycles do not require independent control given that the whole network is spanned by the specified group of linear chains of nodes (pink background) and a directed cycle (green edges). The right-most network in Fig. 3B has $n_{FC}<n_{SC}$ because of the absence of cycles, which means FC only requires controlling the source nodes (yellow nodes), whereas SC requires additional nodes (red nodes) because of the group of nonintersecting linear chains. A detailed analysis in which the topological properties underlying SC and FC are jointly considered backs up the importance of the cycle structure in the differences between their results and points to other contributing factors (SI Appendix).

Feedback Vertex Set Control and Dynamic Models of Real Systems

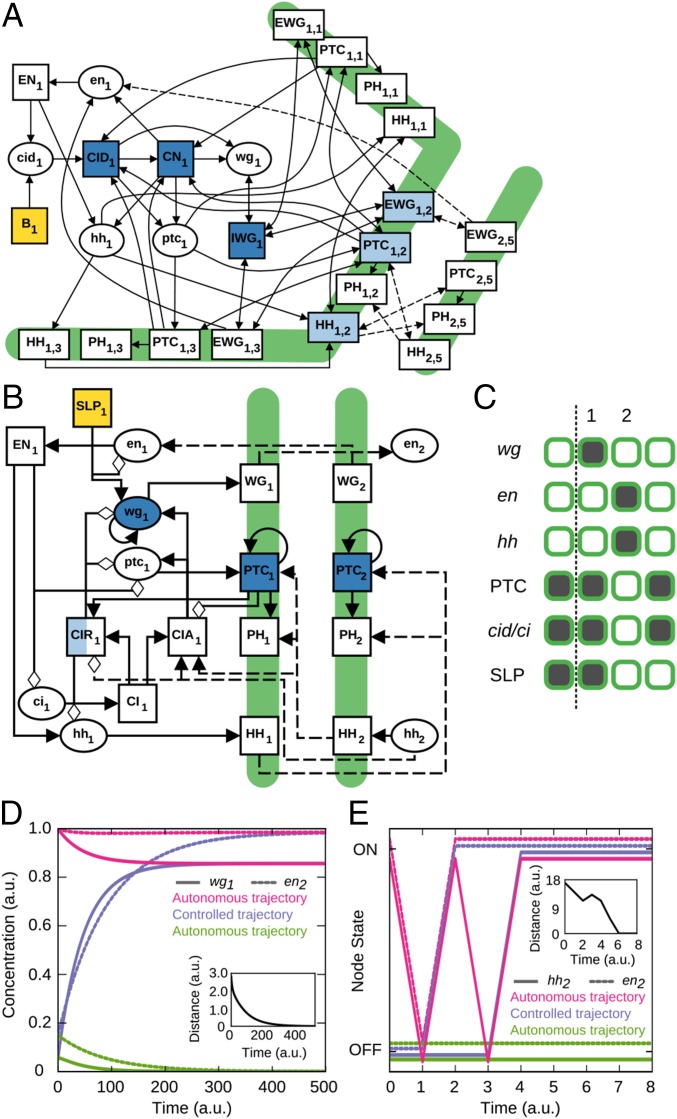
Validated dynamic models can be an excellent testing ground to assess control methods (4, 6, 8). Here we use two models for the gene regulatory network underlying the segmentation of the fruit fly (Drosophila melanogaster) during embryonic development: a differential equation (ODE) model by von Dassow et al. (28) (Fig. 4A) and a discrete (Boolean) model by Albert and Othmer (29) (Fig. 4B). Both models consider a group of four subsequent cells as a repeating unit, include intracellular and intercellular interactions among proteins and mRNAs, and recapitulate the observed (wild type) stable pattern of gene expression (Fig. 4 A–C and SI Appendix).

Fig. 4.

Control of the Drosophila segment polarity network models. (A and B) Networks corresponding to (A) the differential equation model and (B) the discrete model. Each image shows one cell of the four-cell parasegment together with the cell boundaries (thick green lines); the complete networks contain four cells in a symmetric completion of each image. Elliptical nodes denote mRNAs, and rectangular nodes denote proteins, which can be localized inside the cell or in the membrane (subscripts refer to the cell number and surface index). Intracellular interactions are drawn with solid lines, and intercellular interactions are dashed. In B, positive edges are drawn with black arrowheads, and negative edges are drawn with white diamonds. Yellow nodes are source nodes, blue nodes are FC nodes in every cell, and half white/half blue nodes are FC nodes in alternating cells. Dark blue nodes are sufficient for attractor control in the considered dynamic models. (C) Wild-type segment polarity gene product expression pattern in a Drosophila parasegment. The parasegment boundary (dotted line) is between the wg-expressing cells (cell 1) and en-expressing cells (cell 2). (D and E) The dynamics of (D) wg in the first cell (solid lines) and (E) hh in the second cell (solid lines), and en in the second cell (dotted lines) in the models. Pink lines and green lines represent autonomous trajectories that start from different initial conditions and converge to different steady states (the wild-type state and the unpatterned state, respectively). Blues lines represent the case when the system starts from the initial condition that autonomously evolves to the unpatterned state but, when applying FC, evolves into the wild-type steady state. (Insets) Evolution of the norm of the difference between the desired attractor and the controlled state trajectory using FC.

Using FC on these network models, we find $N_{FC}=52$ ($14$) for the ODE (discrete) model (Fig. 4 A–C and SI Appendix, Fig. S3, and SI Text). Both model networks have a large SCC and, thus, a significant FVS contribution to the FC node set; $n_{SCC}/n_{FVS}$ are 0.74/0.35 and 0.5/0.18, respectively, similar to the yellow-shaded networks in Fig. 2. In FC, locking the FC nodes into their trajectory in the wild-type attractor successfully steers the system to the wild-type attractor (Fig. 4 D and E and SI Appendix, Figs. S4 and S5 and SI Text). Thus, FC gives a control intervention that is directly applicable to dynamic models and that is directly linked to their long-term behavior.

FC gives a sufficiency condition about the ensemble of all models with a given network structure, and, consequently, a subset of the FC node set can often be sufficient for a given model and an attractor of interest (i.e., FC provides an upper limit for the size of the control node set). For the fruit fly gene regulatory models, we show that 16 (12) nodes are sufficient for the continuous (discrete) model, which is a 66% (14%) reduction (Fig. 4 A–C and SI Appendix, Figs. S4 and S5 and SI Text). Similar results were obtained by ref. 21, who found that five nodes (out of seven in the FVS) are sufficient for attractor-based control in a model of the mammalian circadian rhythm. The generality of these findings is supported by a recently developed control method in which controlling a subset of the cycles (and thus a subset of the FVS) in Boolean dynamic models was proven to be sufficient for attractor control (ref. 6 and SI Appendix, SI Text). This finding shows that FC provides a benchmark of attractor control node sets that are model independent, as well as an upper limit to model-dependent control sets.

Discussion

Network control methods have the general objective of identifying network elements that can drive a system toward a specified goal while satisfying a set of constraints. Different control methods answer complementary aspects of control in a complex network; which one to use depends on the specific question being asked, on the natural definition of control, and on the underlying dynamics in the system or discipline of interest. We argue that attractor-based control (and thus FC) is the appropriate choice of control for biological systems, for which a long history of dynamic modeling has established the correspondence of attractors with biological states of interest (27), but also in many social and technological contexts, as illustrated by opinion dynamics and the consensus state, and by epidemic processes and the endemic state (24, 25).

As we showed in this work, FC is directly applicable to systems in which only structural information is known, and also to systems in which a parameterized dynamic model is available, for which it provides realizable control strategies that are robust to changes in the parameters and functions. FC also provides a benchmark and a point of contact with the large body of work in network control methods that require the network structure and a dynamic model (4, 6, 8, 18, 20). The prescription of a directly realizable control action (even if a controller signal is not provided) has no analogue in control theory’s structure-based methods such as SC, wherein the existence of a controller signal is guaranteed but is yet to be determined. SC instead has the advantage of integrating controller signals into its framework, and being a well-developed concept in control and systems theory with connections to other notions of control in linear and nonlinear systems (9–11). Further work is needed to extend FC and address topics such as the level of control provided by a subset of nodes, the task of building a controller signal that can implement the node state overrides, and the difficulty of steering the system toward a desired state, concepts that are well-developed in control theory (9–11, 18). Taken together, our work opens up a research direction in the control of complex networks with nonlinear dynamics, connects the field of dynamic modeling with structure-based methodologies, and has promising theoretical and practical applications.