System-wide organization of actin cytoskeleton determines organelle transport in hypocotyl plant cells

Significance

In the crowded interior of a cell, diffusion alone is insufficient to master varying transport requirements for cell sustenance and growth. The dynamic actin cytoskeleton is an essential cellular component that provides transport and cytoplasmic streaming in plant cells, but little is known about its system-level organization. Here, we resolve key challenges in understanding system-level actin-based transport. We present an automated image-based, network-driven framework that accurately incorporates both actin cytoskeleton and organelle trafficking. We demonstrate that actin cytoskeleton network properties support efficient transport in both growing and elongated hypocotyl cells. We show that organelle transport can be predicted from the system-wide cellular organization of the actin cytoskeleton. Our framework can be readily applied to investigate cytoskeleton-based transport in other organisms.

Abstract

The actin cytoskeleton is an essential intracellular filamentous structure that underpins cellular transport and cytoplasmic streaming in plant cells. However, the system-level properties of actin-based cellular trafficking remain tenuous, largely due to the inability to quantify key features of the actin cytoskeleton. Here, we developed an automated image-based, network-driven framework to accurately segment and quantify actin cytoskeletal structures and Golgi transport. We show that the actin cytoskeleton in both growing and elongated hypocotyl cells has structural properties facilitating efficient transport. Our findings suggest that the erratic movement of Golgi is a stable cellular phenomenon that might optimize distribution efficiency of cell material. Moreover, we demonstrate that Golgi transport in hypocotyl cells can be accurately predicted from the actin network topology alone. Thus, our framework provides quantitative evidence for system-wide coordination of cellular transport in plant cells and can be readily applied to investigate cytoskeletal organization and transport in other organisms.

The cell interior is a heterogeneous and crowded space comprising a large range of molecules and organelles (1, 2). Because diffusion through this complex environment is not sufficient to match varying demands for cell maintenance and growth, intricate cellular transport schemes have evolved (3, 4). Transport of cellular components across large distances relies substantially on the cytoskeleton (4–7). Moreover, in plant cells, many organelles move rapidly due to actomyosin-based cytoplasmic streaming (8–10). For instance, Golgi transport relies on the actomyosin system, and an impaired actin cytoskeleton leads to Golgi aggregation and reduced secretion and endocytosis (10–12). Although many molecular features of actin-based transport in plant cells have been elucidated (13, 14), quantitative measures of the structure of the actin cytoskeleton, and how this structure relates to organelle transport, remain elusive. This is largely due to the difficulties in accurately segmenting the actin cytoskeleton and organelle movement, in particular in growing plant cells.

Theoretical models have been used to analyze the interplay between cytoplasmic streaming and actin organization, demonstrating the emergence of self-organized, rotational streaming patterns (3, 15). However, these studies neglected the discrete, filamentous structure of the cytoskeleton. Theoretical investigations that have considered discrete cytoskeletal structures revealed different regimes of transport, depending on the contribution from diffusion or motor-protein–driven transport along random networks of segments (16); the impact of motor-protein movements on cytoplasm in lattice networks (17); and the effect of length, orientation, and polarity of random filament segments on transport rates (18). The studies that do incorporate biological data have suggested that plant cytoskeletal networks, approximated as grids, may support efficient transport processes in hypocotyl cells (19, 20) and that organelle movement depends on local actin structures in root epidermal cells (10). A detailed study of leaf trichome growth demonstrated the importance of organized actin networks for efficient and targeted distribution of new cell wall material (21). However, a global, system-wide view of actin-based organelle transport remains elusive and is complicated by differences between cell types and developmental stages.

Here, we developed a network-based framework that accurately segments the actin cytoskeleton from three developmental stages of hypocotyl plant cells and combined it with an automated tracking of Golgi transport. This approach allowed us to analyze the four aspects of the actin cytoskeletal transport system, including its structure, design principles, dynamics, and control (22). We found that the actin cytoskeleton maintains properties that support efficient transport over time in growing, partially and fully elongated hypocotyl cells, despite rapid reorganization. We also show that Golgi wiggling behavior is reminiscent of optimized search strategies that might indicate efficient uptake and deposition of Golgi-related cell material. In addition, we demonstrated that features of Golgi transport can be predicted from properties of the system-wide organization of the actin cytoskeleton. Altogether, our framework opens up a systems perspective to dissect and understand the transport functionality of the actin cytoskeleton.

Results

A Pipeline to Extract and Represent the Actin Cytoskeleton as a Network.

Because the actin cytoskeleton is composed of discrete and interconnected filaments, it can be efficiently represented in a network-based framework (19, 23, 24) with nodes representing crossings or end points of actin filaments (AFs) and weighted edges capturing AF segments. We extracted network representations from partially elongated Arabidopsis thaliana (Arabidopsis) hypocotyl cells, around $3\hspace{0.17em}\mathrm{mm}$ from the apical hook, that expressed FABD-GFP, using spinning-disc confocal microscopy data (Fig. 1F for pipeline; Materials and Methods). To study actin-based transport at different cell developmental stages, we further analyzed fully elongated as well as growing hypocotyl cells, around $5\mathrm{mm}$ and $1\mathrm{mm}$ from the apical hook, respectively (Fig. S1 and below). The recorded images were corrected for drift and bleaching (Fig. 1A), manually cropped to the cellular region of interest, and filtered to enhance tube-like structures of the cytoskeleton with a parameter $v_{\mathrm{width}}$ (Fig. 1B). AFs were segmented by applying an adaptive median threshold of block size, $v_{\mathrm{thres}}$ (Fig. 1C). The binary images were skeletonized to obtain AF center lines and spurious fragments smaller than $v_{\mathrm{size}}$ pixels or below $v_{\mathrm{int}}$ of the average fragment intensity were removed (Fig. 1D). Networks were obtained by identifying the nodes, adding edges between pairs of nodes directly connected via the skeleton, and assigning edge weights reflecting features of AF segments, e.g., average thickness (Fig. 1E).

Fig. 1.

Automated extraction and validation of networks from actin cytoskeletal image data. (A) Grayscale confocal image of two partially elongated Arabidopsis hypocotyl cells after registration and background subtraction (“original + preprocessing”). The same cell was used as example throughout the paper. (B) Cytoskeleton image with improved signal-to-noise ratio after cropping of the largest cell and application of tubeness filter ($v_{\mathrm{width}}=1.8$; “filtering”). (C) Binary cytoskeleton image after application of adaptive median threshold ($v_{\mathrm{thres}}=101$; “thresholding”). (D) Skeletonized cytoskeletal structures after removal of spurious fragments of small size or low intensity ($v_{\mathrm{size}}=27\hspace{0.17em}\mathrm{pixels}$ and $v_{\mathrm{int}}=0.5$; “skeletonization + cleaning”). Positions of network nodes are marked by colored pixels (Inset). (E) Overlay of skeleton image and extracted cytoskeletal network with edges color coded by their capacity, reflecting average filament thickness (“network extraction”). Multiple filaments may contribute to an edge (compare Inset and star). Edges were added to connect the network (compare dotted lines and triangles). (F) Overview of automated pipeline for network-based representation of the actin cytoskeleton incorporating image processing (A–D), network extraction (E), and parameter gauging (G–K). (G) Overlay of synthetic filaments (blue) and automated segmentation (red) of a synthetic cytoskeleton image (gray). (H) Overlay of manual (blue) and automated (red) segmentation of a biological cytoskeleton image (gray). (I) Four image processing parameters were varied to determine their optimal values for $20$ images and $20$ images of synthetic and biological cytoskeletons, respectively, which were segmented manually for comparison (“parameter gauging”). Segmentation quality was measured by the average of the smallest distance, $d_{\mathrm{manu}\to \mathrm{auto}}$ (blue), from the pixels of the manual segmentation to those of the automated segmentation and vice versa, $d_{\mathrm{auto}\to \mathrm{manu}}$ (red). Shown are sections of the parameter space, averaged over all $40$ studied images, for fixed $\left(v_{\mathrm{width}},v_{\mathrm{int}}\right)=\left(1.8,101\right)$ and varying block size $v_{\mathrm{thres}}$ and size threshold $v_{\mathrm{size}}$. (J) Minimization of the Haussdorf distance $d_{\mathrm{HD}}=\frac{1}{2}\left(d_{\mathrm{manu}\to \mathrm{auto}}+d_{\mathrm{auto}\to \mathrm{manu}}\right)$ (purple) to avoid both over- and undersegmentation yielded $\left(v_{\mathrm{width}}^{\ast },v_{\mathrm{thres}}^{\ast },v_{\mathrm{size}}^{\ast },v_{\mathrm{int}}^{\ast }\right)=\left(1.8,101,27,0.50\right)\pm \left(0.2,8.0,8.9,0.06\right)$ (mean $\pm$ $\mathrm{SD}$). (K) Distribution of average distances between manual and automated segmentations for the optimal parameters with $d_{\mathrm{manu}\to \mathrm{auto}}=1.2\pm 0.9\hspace{0.17em}\mathrm{pixels}$, $d_{\mathrm{auto}\to \mathrm{manu}}=3.5\pm 3.2\hspace{0.17em}\mathrm{pixels}$, and $d_{\mathrm{HD}}=2.4\pm 2.1\hspace{0.17em}\mathrm{pixels}$, respectively.

Fig. S1.

Differences in actin architecture and Golgi transport between growing and fully elongated hypocotyl cells. Shown are results for fully elongated/growing cells of untreated hypocotyls (green/blue) and hypocotyls treated with the actin-disrupting drug LatB (orange/yellow). Please refer to SI Text for detailed explanations. (A) Overlay of cellular recording of actin cytoskeleton from fully elongated hypocotyl cell and extracted actin network with edge colors representing their capacities, i.e., average thicknesses. (B) Same overlay as before for growing hypocotyl cell showed reduced bundling and stronger branching of actin cytoskeleton compared with that for fully elongated hypocotyl cells. (C) Time series and box plots of the number of connected components after removal of edges with capacities below the $50\mathrm{t}\mathrm{h}$ percentile (fragmentation; Fig. 2) for a growing and a fully elongated hypocotyl cell under control conditions and after LatB treatment, respectively. (D) Ratios of different properties of networks extracted from three control and three LatB-treated cells for both growing and fully elongated hypocotyl cells (see Fig. 2 for details; independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant). Actin networks from growing and fully elongated cells differed with respect to the number of connected components and average edge capacity (bundling) but were similar with respect to their assortativity (heterogeneity). (E) Ratios of different properties of biological and randomized null model networks for both growing and fully elongated hypocotyl cells (see Fig. 2 for details). Compared with the null models, actin networks in both cells at both developmental stages exhibited properties that may support efficient transport. (F) Heat maps of Pearson correlation coefficients $c_P$ between different edge properties of actin and Golgi flow networks for control cells in fully elongated (Left) and growing (Right) hypocotyls (see Fig. 4 for details) showed strong agreement between the two developmental stages. (G) Heat maps of Pearson correlation coefficients $c_P$ between different edge properties of actin and Golgi flow networks for LatB-treated cells in fully elongated (Left) and growing (Right) hypocotyls (see Fig. 4 for details) showed strong agreement between the two developmental stages.

To test whether our network-based framework captured relevant biological features of the actin cytoskeleton, we compared our automated segmentations against synthetic images of known cytoskeleton-like structures (Fig. 1G) as well as manually segmented cytoskeleton images as a gold standard (Fig. 1H). Because the accuracy of the network representation relies on four parameters ($v_{\mathrm{width}}$, $v_{\mathrm{thres}}$, $v_{\mathrm{size}}$, and $v_{\mathrm{int}}$), we performed extensive gauging by varying these parameters in a wide range of values (Fig. 1 I and J) and identified those ensuring best agreement between manual and automated segmentations measured by the Haussdorf distance, i.e., the average minimum distance between pixels of the two segmentations (25, 26). Parameter gauging yielded an optimal average of $d_{\mathrm{HD}}=2.4\pm 2.1\hspace{0.17em}\mathrm{pixels}$ (Fig. 1 J and K; mean$\pm \mathrm{SD}$), comparable to contending approaches (SI Materials and Methods). Thus, whereas errors in the automated segmentation occur, our parameter optimization ensures an optimal compromise between over- and undersegmentation across different recordings.

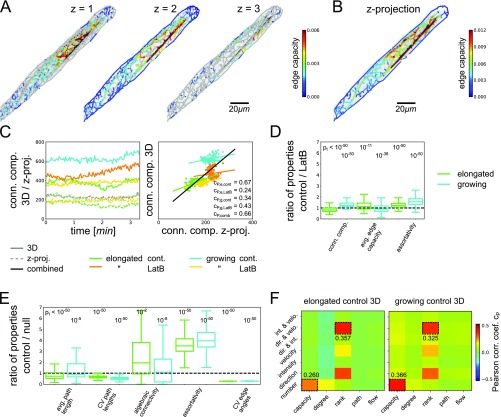
Our approach is directly applicable to 3D image data. However, our focus in the main text on 2D networks is justified by the cylindrical shell geometry of the cortical cytoskeleton (19, 27) as well as the size of the transported Golgi, which may bridge gaps between cortical AFs that are not resolved in 2D images (28–30). Moreover, we show that our findings remain valid for 3D image data (Fig. S2 and below). Thus, our approach yields an accurate and mathematically powerful network representation of the cytoskeleton in hypocotyl plant cells from image data.

Fig. S2.

Extension of analysis to 3D image data of actin cytoskeleton and Golgi. Shown are results for fully elongated/growing cells of untreated hypocotyls (green/blue) and hypocotyls treated with the actin-disrupting drug LatB (orange/yellow) and the combined data (black). Please refer to SI Text for detailed explanations. (A) Extracted 3D actin network and z slices of 3D image data ($1\mu \mathrm{m}$ spacing between z slices) from untreated, elongated hypocotyl cell showed localization of cortical actin cytoskeleton close to the plasma membrane with rare, thick cytoplasmic actin cables (edges in out-of-focus z slices are shown in gray). (B) Extracted 2D actin network and z-projected 3D image data from untreated, fully elongated hypocotyl cell showed good agreement with 3D counterpart (compare to A). (C, Left) Time series of number of connected components for 3D image data and corresponding 2D z projection of growing and fully elongated hypocotyl cells under control conditions and after LatB treatment, respectively. (C, Right) Scatter plot of network property for 3D and 2D networks extracted from the full and the z-projected image data, respectively, showed strong correlation ($c_P=0.66$ for the combined data). (D) Ratios of different properties of 3D networks extracted under control conditions and after LatB treatment from three growing and three fully elongated hypocotyl cells (see Fig. 2 for details; independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant). Results are in agreement with those from 2D networks (Fig. S1). (E) Ratios of different properties of 3D biological and randomized null model networks for both growing and fully elongated hypocotyl cells (see Fig. 2 for details). Results are in agreement with those from 2D networks (Fig. S1). (F) Heat maps of Pearson correlation coefficients $c_P$ between different edge properties of 3D actin and Golgi flow networks for fully elongated (Left) and growing (Right) cells under control conditions (see Fig. 4 for details). Results are in agreement with those from 2D networks (Fig. S1).

The Network Representations Capture Biologically Relevant Features of the Actin Cytoskeleton.

To ensure that our framework captured known changes in the actin cytoskeleton, we determined differences in cytoskeletal organization between partially elongated hypocotyl cells of plants treated with Latrunculin B (LatB; Fig. 2A), a drug that inhibits actin polymerization (31), and control cells (Fig. 2B; seven cells from seven different seedlings per treatment). To quantify actin network phenotypes, we computed the number of connected components after removal of edges with capacities below the $50\mathrm{t}\mathrm{h}$ percentile as a measure of fragmentation (Fig. 2D and ref. 32; mathematical definitions and interpretations of all studied network properties are given in Table S1). Fragmentation was lower in networks of control than of LatB-treated cells (Fig. 2E; independent two-sample $t$ test $P$ value $P_t<{10}^{-50}$), indicating that large connected patches of AFs were absent in LatB-treated cells, consistent with visual inspection. Similarly, the average edge capacity was higher in control than in LatB-treated cells ($P_t<{10}^{-38}$), reflecting a reduction in actin bundling in the LatB-treated cells. Finally, these findings were corroborated by the assortativity (32), which quantifies whether two adjacent nodes are of similar degree and reflects the network heterogeneity. We found stronger heterogeneity for control than for LatB-treated cells ($P_t<{10}^{-50}$), suggesting regions of bundled actin that are surrounded by AFs in the control cells.

Fig. 2.

Phenotyping of actin cytoskeleton using the extracted networks captures biological signals and reveals transport efficiency. Shown are results for partially elongated hypocotyl cells of plants treated with the actin-disrupting drug LatB (orange), untreated control plants (green), and ensembles of $20$ randomized networks (gray). (A) Cellular recording (Left) and extracted actin network (Right) of a LatB-treated cell with edge colors representing edge capacities. (B) Cellular recording (Left) and extracted actin network (Right) of an untreated control cell. (C) Artistic interpretation of the randomization procedure (Left) and a randomized network (Right) of the control cell (B) with occasional edge crossings (e.g., triangles). (D) Time series and box plots of the number of connected components after removal of edges with capacities below the $50\mathrm{t}\mathrm{h}$ percentile (“fragmentation”) for a control and a LatB-treated cell. (E) Ratios of different properties of networks extracted from seven control and seven LatB-treated cells. The number of connected components was lower and the average edge capacity (“bundling”) and the degree assortativity (“heterogeneity”) were higher for control than for LatB-treated cells (independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant). (F) Scatter plots of the arc length $a_F$ of the filament segments vs. the Euclidean length $a_E$ of the corresponding edges showed strong correlation for control and LatB-treated cells (Pearson correlation coefficient $c_P=0.998$ and $P$ value $P_P<{10}^{-50}$). F, Inset displays relative lengths $B=a_E^{-1}{a}_F$ (“bending”) with an average of $B=1.2\pm 0.2$ (mean $\pm$ $\mathrm{SD}$). (G) Distribution of edge angles, weighted by edge capacities, relative to the major cell axis showed a prevalence of AFs parallel to the cell axis in the control cells but not in LatB-treated cells. (H) Time series and box plots of the average path length (“reachability”) for one control cell and $20$ randomized networks of the first null model for each time step (mean $\pm$ $\mathrm{SD}$). (I) The extracted actin networks of the seven control cells showed significantly lower average path lengths, $\mathrm{CV}$ of the path lengths (“dispersal”), and $\mathrm{CV}$ of the edge angles (“contortion”) than their counterparts from the first null model. The algebraic connectivities (“robustness”) and assortativities (heterogeneity) of the actin networks were higher than expected from the first null model.

Table S1.

List of studied (edge) properties of actin and Golgi flow networks

Property	Symbol	Explanation/interpretation	Eq.
Actin network edge $e$
Euclidean edge length	$a_{e,E}$	Linear distance between end points of filament segment	—
Filament edge length	$a_{e,F}$	Arc length of filament segment	—
Filament bending	$a_{e,B}$	Ratio of filament and Euclidean edge lengths	S7
		Bending or convolutedness of filament segment
Edge weight	$a_{e,w}$	Total intensity along filament segment	—
Edge capacity	$a_{e,c}$	Average intensity per unit length along filament segment	S8
		Average thickness of actin bundles
Edge length	$a_{e,l}$	Inverse edge capacity used to compute shortest paths	S9
Edge angle	$a_{e,a}$	Angle between edge and major cell axis	S10
		Alignment of AFs and bundles
Edge degree	$a_{e,\mathrm{deg}}$	Total thickness of neighboring edges	S18
		Prevalence of surrounding AFs and bundles
Edge rank	$a_{e,\mathrm{rank}}$	Page rank of given edge	S19
		Probability that cargo is found at given filament segment when cargo randomly switches
		between filaments and preferably targets thicker bundles
Edge path betweenness	$a_{e,\mathrm{path}}$	No. of shortest paths through given edge	S20
		Importance of filament segment when cargo between any
		two nodes is transported preferably along thick bundles
Edge flow betweenness	$a_{e,\mathrm{flow}}$	total maximum flow through given edge	S21
		Importance of filament segment when bundle thickness limits the amount of cargo per edge and
		the cytoskeleton transports maximum amounts of cargo between any two nodes
Actin network
Conn. Comp.	$F$	No. of strongly connected patches of actin bundles	S11
		Fragmentation
Avg. edge capacity	$\mathrm{E}\left[a_c\right]$	Prevalence of thick actin bundles	S12
		Bundling
Assortativity	$A$	Degree of clustering or mixing of fine AFs and thick bundles	S13
		Heterogeneity
Avg. Shortest path length10.2	$\mathrm{E}\left[L\right]$	Average effective distance between any two nodes when thicker bundles transport cargo faster	S14
		Reachability
$\mathrm{CV}$ of shortest path lengths	$\mathrm{CV}\left[L\right]$	Variability of effective distances between any two nodes	S15
		Dispersal
Algebraic connectivity	$C$	Robustness of cargo transport against disruptions of AFs and bundles,	S16
		i.e., reliability and redundancy of transport routes
		Robustness
Edge angles	$\mathrm{CV}\left[a_a\right]$	Alignment of AFs and bundles with major cell axis	S17
		Contortion
Golgi flow network edge $e$
Number	$g_{e,n}$	No. of close-by Golgi	S23
Wiggling	$g_{e,w}$	Average relative angle of movement of close-by Golgi	S24
Intensity	$g_{e,i}$	Average intensity of close-by Golgi	S25
Direction	$g_{e,d}$	Average angle between edge and movement of close-by Golgi	S26
Velocity	$g_{e,v}$	Average velocity of close-by Golgi	S27
Combinations	e.g., $g_{e,d+v}$	Average velocity of close-by Golgi along edge direction	S28

Please refer to SI Text for detailed explanations. In the top section, shown are edge properties of actin networks that were used to compare networks across conditions and time and to predict organelle flow (see bottom section). Some edge properties are local (a_e,E to ae;a) whereas some consider the role of the edge in the network context (a_e,deg to a_e,flow). In the middle section, shown are properties of the actin network that were used for quantification of cytoskeletal phenotypes and assessment of transport efficiency. In the bottom section, shown are edge properties of the Golgi flow network derived from Golgi tracking data, taking into account numbers, intensities, velocities, and directions of Golgi as well as combinations thereof.

To further assess the filamentous structure of the actin cytoskeleton, we compared the arc length of filament segments to their Euclidean length and found a strong correlation (Fig. 2F; Pearson correlation coefficient $c_P=0.998$ and $P$ value $P_P<{10}^{-50}$). Consequently, filament bending, i.e., the ratio of the two lengths, was small, $B=1.2\pm 0.2$, in particular for long filament segments (Fig. 2F, Inset). This limited bending of longer filament segments is plausible because actin bundles, typically resulting in longer filament segments, exhibit greater stiffness compared with AFs (33, 34). Furthermore, we found that filament segments were preferentially oriented in parallel to the major cell axis in control cells, but not in LatB-treated cells (Fig. 2G). To demonstrate the robustness of our findings, we showed that the differences in network properties between control and treatment were not affected by removal of a random fraction of edges, simulating effects of erroneous network extraction (Fig. S3).

Fig. S3.

Inference of network design principles using two different null models and negative controls. Shown are differences between cytoskeletal networks from partially elongated control cells (green), cells treated with LatB (orange), combined data (black), and randomized null model networks (gray). (A) Box plots of the number $X$ of crossings per edge in the original actin networks with $X=0.04\pm 0.02$ (mean $\pm$ $\mathrm{SD}$) and networks derived from the first null model with $X=0.14\pm 0.11$. (B) Box plots of the ratio $r$ of the number of edges in the extracted actin networks and the corresponding first null model networks. By construction, the ratio is larger than $1$ and, across all studied actin networks, the number of edges in the first null model networks was increased by $r=1.12\pm 0.07$. (C) Box plots of the $\mathrm{NNI}$ that captures the spatial distribution of node positions in the extracted actin networks. Values below $1$ indicate a stronger spatial clustering compared with a random and uniform distribution of node positions and the observed NNI was $\mathrm{NNI}=0.83\pm 0.09$ across all extracted networks. (D) Example of an original extracted actin network with edge colors reflecting edge capacities. (E) Example of network obtained from our second null model, i.e., by shuffling of the edge properties. The structure of the randomized network is identical to that of the original network (D). (F) Box plots of the ratios of various network properties of the extracted networks and an ensemble of networks obtained from the second null model. The significance of the differences when considering the second null model remained unchanged compared with the differences found from using the first null model (independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant; Fig. 2I). (G) Analysis of biological significance of various network properties of the reconstructed actin network for LatB-treated cells, using the first null model. In contrast to the cytoskeletal networks of the untreated control cells, no significant differences were observed (all $P_t\ge 0.05$; Fig. 2I). (H) Analysis of various network properties using the second null model showed no biological significance of cytoskeletal network properties in LatB-treated cells (all $P_t\ge 0.05$; Fig. 2I). (I) Average numbers per connected components of actin networks after removal of increasing fractions of edges were consistently smaller for control than for LatB-treated cells. (J) Average path lengths of actin networks after removal of increasing fractions of edges were consistently smaller for biological than for null model networks.

Next, we compared cytoskeletal networks in hypocotyl cells at different developmental stages, i.e., in growing and fully elongated cells, and found notable differences (Fig. S1). In particular, in contrast to both partially and fully elongated hypocotyl cells, the actin cytoskeleton in untreated growing hypocotyl cells showed stronger fragmentation and weaker bundling than in their LatB-treated counterparts. These differences are in agreement with the more even distribution and more strongly branched structure of the actin cytoskeleton in growing hypocotyl cells (35, 36) (Fig. S1), as well as the continuous gradient in cell elongation rates along the hypocotyl in dark-grown Arabidopsis seedlings (37). Moreover, our findings from 2D image data were corroborated by analyses of 3D image data and networks (Fig. S2). Therefore, our results show that the extracted network representations of the actin cytoskeleton enable automated phenotyping of cytoskeletal structures.

The Actin Cytoskeleton Supports Efficient Transport.

A major function of the plant actin cytoskeleton is to mediate transport of a range of organelles and compartments. To assess the transport efficiency of actin networks in partially elongated hypocotyl cells, we computed a number of seminal network properties and compared them against ensembles of two types of randomized null model networks (each network was randomized $20$ times; Fig. 2C for first null model that shuffles node positions and edges and Fig. S3 for second null model that shuffles edge properties only). We determined the average path length (32), which reflects the reachability of a network, and compared it against an ensemble of networks from the first null model (Fig. 2H). We found that the average path length of the extracted networks was smaller than that of the null model networks (Fig. 2I; $P_t<{10}^{-50}$; Fig. S3 for analysis of robustness of this finding against removal of edges). This difference indicates that the actin cytoskeleton is tuned toward shorter path lengths. Similarly, the coefficients of variation ($\mathrm{CVs}$) of the shortest path lengths in the extracted networks were smaller than expected from the null model networks ($P_t<{10}^{-50}$), indicating that also fluctuations in the path length between any two nodes are maintained at a low level. Another classical transport-related network property is the algebraic connectivity (32), which reflects the redundancy of paths between any two nodes and thus captures the robustness of the transportation network against disruptions. The algebraic connectivity of the extracted networks was higher than expected by chance ($P_t<{10}^{-14}$). In contrast, the LatB-disrupted actin cytoskeletons did not show any significant differences in their transport-related network properties compared with the null model networks (Fig. S3). These findings support the hypothesis that transport efficiency is a biological design principle of the intact actin cytoskeleton (19).

To investigate the structural origin of this transport efficiency, we reconsidered the assortativity (32) of the cytoskeleton and found that it was higher in the extracted networks than expected by chance ($P_t<{10}^{-50}$). Similarly, we found that the $\mathrm{CV}$ of the angles between AF segments and the major cell axis was smaller in the extracted networks than expected by chance ($P_t<{10}^{-50}$). Together these findings suggest that the formation of connected patches of aligned actin bundles is a functionally relevant feature of the cytoskeleton.

To ensure that our results were robust, we used an additional and more restricted null model, which shuffles only edge properties. Whereas the first null model is more flexible, the second one excludes potential artifacts that could arise from an increased number of edge crossings or a more homogeneous distribution of node positions compared with the extracted networks (Fig. S3). Our findings from the first null model were consistently confirmed by the second one. Hence, differences in the studied network properties between extracted and null model networks are not an artifact of the randomization procedures.

Despite organizational differences of the actin cytoskeleton in hypocotyl cells at different developmental stages, the actin network in partially elongated as well as fully elongated and growing hypocotyl cells showed properties of efficient transport (Fig. S1). For example, both reachability and robustness of the actin networks were better than expected by chance. Again, our findings remained valid when studying actin networks extracted from 3D image data (Fig. S2).

A potential issue, shared by all current approaches that extract transport-related networks from image data, is the unknown edge directionality. Individual AFs usually allow unidirectional movement of motor proteins only, and actin bundles in root hairs and other tip growing cells are typically composed of parallel AFs (9, 38, 39). In contrast, our analyses of cytoskeletal transport capacity rely on the assumption of bidirectional transport along edges. Indeed, our data showed that $<50\%$ of actin edges exhibit predominantly unidirectional movement of close-by Golgi, irrespective of the actin bundle thickness (see Fig. 4 and Fig. S4), partially justifying the assumption of bidirectional transport. This deviation from the expected unidirectional movement along bundles of parallel AFs may be partially due to noise-induced tracking errors that may lead to apparent bidirectional movement, especially during phases of Golgi pausing (11, 40). Moreover, in the computation of edge directionality a given Golgi may be associated with multiple edges and neighboring actin bundles may exhibit different orientations (10, 21) (details in Fig. S4). Finally, given the low Reynolds numbers of the cytoplasm (1), cytoplasmic streaming may carry temporarily detached Golgi (41) irrespective of the underlying actin bundle or its orientation (Fig. S5). In summary, our analyses indicate that transport efficiency is a central design principle of the actin cytoskeleton in hypocotyl plant cells.

Fig. 4.

Analysis of cellular organization of actin cytoskeleton enables prediction of Golgi dynamics. Shown are results for partially elongated hypocotyl cells of plants treated with the actin-disrupting drug LatB (orange) and untreated control cells (green). (A) Overlay of cellular recording of actin cytoskeleton and extracted actin network. (B) Extracted actin network with edge colors representing their capacities, i.e., average thicknesses. (C) Extracted actin network with edge colors representing their edge ranks. (D) Overlay of cellular recording of Golgi and Golgi tracks throughout the recording. (E) Golgi flow network with edge colors representing the numbers of close-by Golgi, i.e., track segments with starting points within $8\hspace{0.17em}\mathrm{pixels}$ from a given edge. (F) Golgi flow network with edge colors representing the direction and velocity of close-by Golgi track segments (no Golgi were assigned to white edges, e.g., triangles). (G) Time series of Pearson correlation coefficients $c_P$ between Golgi track segment direction and velocity and actin edge rank (Upper) and exemplary scatter plots for one time point for a control and a LatB-treated cell, respectively (Lower; compare to open circles in Upper). (H) Heat maps of Pearson correlation coefficients $c_P$ between different edge properties of actin and Golgi flow networks for control (Left) and LatB-treated (Right) cells. For control cells and LatB-treated cells, there was a significant correlation between the actin edge capacity and the Golgi number (compare to I). Correlations between the actin edge rank and Golgi direction and velocity were significant for the control cells with $c_P=0.384$ but not for the LatB-treated cells with $c_P=-0.023$ (compare to G). (I) Scatter plots of the number of Golgi close to an edge and the respective edge capacity showed positive correlations with $c_P=0.347$ for control and $c_P=0.350$ for LatB-treated cells. The slope of a linear regression for the combined data was $s=51$ (black). (J) Heat map of coefficients of determination $R^2$ for multiple linear regressions of the Golgi flow network edge properties (first column) and the respective predictive power $P$ values $P_{t\prime }$ of the actin edge properties that were used as predictors (last five columns; one-sample two-sided $t$ test $P$ values $P_{t\prime }$ measure whether inclusion of the respective predictor improves the prediction) for the control cells. Coefficients of determination were highest for direction- and velocity-related Golgi properties ($R^2>0.7$). The actin capacity, degree, and rank were more reliable predictors ($P_{t\prime }<0.05$) than edge flow and path betweenness ($P_{t\prime }\ge 0.05$).

Fig. S4.

Directionality of actin edges, correlations of actin edge properties, and periodic actin networks. Shown are results for partially elongated hypocotyl cells of untreated control plants (green), cells of plants treated with the actin-disrupting drug LatB (orange), and the combined data (black). Please refer to SI Text for detailed explanations. (A) Overlay of cellular recording of Golgi and Golgi flow network with edge colors representing edge directionality, capturing the average angle between network edge and close-by Golgi track segments. (B) Distribution of edge directionality in dependence of capacity of the respective edge for control (Left) and LatB-treated (Right) cells, for a cutoff distance of $8\hspace{0.17em}\mathrm{pixels}$ between actin edge and Golgi. Edge directionality was not correlated with edge capacity; i.e., thicker edges did not imply stronger unidirectionality of transport. For the control cells, $46\%$ of the edges showed predominantly unidirectional transport with average angles below ${45}^{\circ }$ or above ${135}^{\circ }$. For the LatB-treated cells, $44\%$ of the edges showed predominantly unidirectional transport (see Fig. S6B for detailed explanation of the panels). (C) Distributions of edge directionalities for cutoff distances of $4\hspace{0.17em}\mathrm{pixels}$ (dashed lines) and $12\hspace{0.17em}\mathrm{pixels}$ (dotted lines) between actin edges and Golgi. Smaller cutoff distances yielded higher fractions of edges with predominantly unidirectional transport, i.e., with average angles below ${45}^{\circ }$ or above ${135}^{\circ }$ between actin edge and Golgi ($55\%$ for control and $52\%$ for LatB-treated cells). (D) Heat maps of the colinearity between the studied actin edge properties for the original, nonperiodic networks (Upper) and the periodic networks (Lower). The colinearities were averaged across all time points of all control cells (Left) or the minimum value was taken (Right). In all cases, the edge path and flow betweenness were strongly correlated. The edge capacity, degree, and rank were mutually correlated on average but the minimum colinearity revealed lower colinearity, especially for the periodic networks. (E) Scatter plots of edge flow betweenness vs. edge path betweenness showed strong correlations with Pearson correlation coefficients $c_P=0.97$ and $c_P=0.98$ for control and LatB-treated cells, respectively. (F) Box plots of the ratio $t$ of the number of edges in the extracted actin networks and the corresponding spanning trees. Across all studied networks there were $t=1.03\pm 0.02$ (mean $\pm$ $\mathrm{SD}$) times more edges in the actin networks than in the corresponding spanning trees. (G) Extracted actin network with cylindrical periodic boundary conditions. Edge colors represent their edge rank and gray edges indicate network edges added to implement periodic boundary conditions. Edge ranks in the periodic and nonperiodic networks generally differ (Fig. 4C and triangles). (H) Heat maps of Pearson correlation coefficients $c_P$ between different edge properties of periodic actin and Golgi flow networks for control (Left) and LatB-treated (Right) cells. In particular, some correlations involving the direction and velocity of Golgi were higher for the periodic than for the nonperiodic networks (Fig. 4H). (I) Heat map of coefficients of determination $R^2$ for multiple linear regressions of the Golgi flow network edge properties (first column) and the respective predictive power $P$ values $P_{t\prime }$ of the periodic actin edge properties used as predictors (last five columns) for the control cells. Analogous to the correlation-based analyses, the coefficients of determination especially of the direction- and velocity-related Golgi properties were higher for the periodic than for the nonperiodic networks (Fig. 4J). (J) Box plots of coefficients of determination for predictions of Golgi direction and velocity for actin network without and with periodic boundary conditions, respectively (independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant). The prediction quality for actin networks incorporating periodic boundary conditions was significantly higher than for networks without periodic boundary conditions for the control cells ($P_t<{10}^{-13}$), but not for the LatB-treated cells ($P_t\ge 0.05$).

Fig. S5.

Passive and active transport of Golgi and switching between filaments. Shown are Golgi dynamics in partially elongated hypocotyl cells of plants treated with the actin-disrupting drug LatB (orange) and untreated control plants (green). Please refer to SI Text for detailed explanations. (A) Scatter plots of actin bundling, measured by the average edge capacity and the average Golgi velocity, showed positive correlations (Pearson correlation $P$ values $P_P<0.05$) for control (green) and LatB-treated cells (orange) as well as the combined data (black). (B) Box plots of the fractions of Golgi in control and LatB-treated cells that stayed close to the same filament segment within one time step (referred to as “stay”), those that likely moved to a different segment of the same filament (“move”), and those that moved to a different, nonadjacent filament (“jump”). The fraction of stationary Golgi was higher for LatB-treated than for control cells (independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant). (C) Overlay of cellular recording of actin cytoskeleton from control cell and extracted actin network. (D) Section of overlay of an extracted actin network (green; compare to C) and its line graph (gray) that has a node for each edge in the original network and a link between nodes that represent adjacent edges. (E) Scatter plots of the length of the shortest path connecting the two edges that are closest to a given track segment’s start and end points and the associated maximal angle along the shortest path (compare to B). Track segments were assigned to the move or jump class if they moved to a different edge while the maximal angle along the corresponding shortest path between the two edges was below or above ${90}^{\circ }$, respectively. (F) Scatter plots of the length of the shortest path connecting the two edges that are closest to a given track segment’s start and end points and the associated Golgi velocity showed positive correlations for control and LatB-treated cells as well as the combined data ($c_P\approx 0.3$ and all $P_P<0.05$). (G) Scatter plots of the maximal angle along the shortest path connecting the two edges that are closest to a given track segment’s start and end points and the associated Golgi velocity showed moderate correlations for control and LatB-treated cells as well as the combined data ($c_P\approx 0.2$ and all $P_P<0.05$). (H) Heat maps of the distributions of pairwise angles, i.e., angles between two segments of two different Golgi tracks at a given time step, in dependence of the spatial separation of the two track segments (Right). Shown are distributions of pairwise angles for small spatial separations below $1\mu \mathrm{m}$ (H, Left and dashed lines in H, Right). In the control cells, there was a tendency toward parallel or antiparallel movement of Golgi (H, Upper Right) and for distances below $10\mu \mathrm{m}$, a large fraction of Golgi tracks showed parallel alignment (triangle). Nevertheless, even at small spatial separations below $1\mu \mathrm{m}$, a fraction of $45\%$ of Golgi pairs exhibited antiparallel movement with angles above ${90}^{\circ }$ (H, Upper Left). In the LatB-treated cells (H, Lower), no preferred alignment was observed, irrespective of the spatial separation of the track segments.

Automated Quantification of Golgi Movement.

To quantify actin-based cellular transport, we studied partially elongated hypocotyl cells dually labeled with FABD-GFP and tdTomato-CesA6 (tdT-CesA6), used as a proxy for Golgi movement (42, 43). We analyzed the flow of Golgi through automated tracking (44, 45) in image series from control and LatB-treated cells (Fig. 3 A and B). Golgi bodies moved with velocity $v=0.36\pm 0.26{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$ in control cells (Fig. 3C), which is higher than $v=0.04\pm 0.03{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$ in LatB-treated cells, consistent with previous studies (10, 11). The Golgi movement was predominantly parallel to the major cell axis in control cells but not in LatB-treated cells (Fig. 3D), correlating with the orientation of actin bundles (compare with Fig. 2G). Thus, our automated tracking captures known features of Golgi movement and may therefore be suitable for further, more detailed analyses of Golgi behavior.

Fig. 3.

Quantification of Golgi movement indicates stability and efficiency of wiggling behavior. Shown are Golgi dynamics in partially elongated hypocotyl cells of plants treated with the actin-disrupting drug LatB (orange) and untreated control plants (green). (A) Overlay of cellular recording of Golgi and Golgi tracks from a control cell. (B) Overlay of cellular recording of Golgi and Golgi tracks from a LatB-treated cell. (C) Distributions of Golgi velocities in LatB-treated cells, $v=0.04\pm 0.03{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$, and control cells, $v=0.36\pm 0.26{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$ (mean $\pm$ $\mathrm{SD}$). (D) Distributions of absolute angles for control and LatB-treated cells. (E) Schematic of different angles used to study movement of Golgi bodies. Shown are the absolute angle between a Golgi track segment and the major cell axis (dashed gray angle) and the relative angle between two consecutive segments of a given Golgi track (solid gray angle), as well as the pairwise angle between two segments of two different Golgi tracks at a given time step (dotted gray angle). (F) Distributions of relative angles were broad with $a={85}^{\circ }\pm {55}^{\circ }$ and $a={104}^{\circ }\pm {55}^{\circ }$ for control and LatB-treated cells, respectively (dashed lines). (G) Distributions of relative angles, averaged over a given track, showed unimodal distributions with peaks around ${85}^{\circ }$ and ${104}^{\circ }$ for control and LatB-treated cells, respectively (dashed lines). (H) Time series of relative angles, averaged over a given time step, for each of the studied control and LatB-treated cells (Left). All time series were stationary; i.e., they showed no increasing or decreasing trend (H, Upper Right; augmented Dickey–Fuller unit root-test $P$ values $P_{DF}<0.05$), except one (see triangle). The fluctuations of the time series were small (H, Lower Right; $\mathrm{CV}\left[a\right]=0.10\pm 0.03$). (I) Distributions of relative angles in dependence of distance of the track segments from the cytoskeleton (Left; circles show results for control cells; solid lines and shaded areas show mean $\pm$ $\mathrm{SD}$). Excess of Golgi at a given distance from the cytoskeleton for control and LatB-treated cells (I, Right; compare solid lines and triangle) is given by the difference between the frequency of actual Golgi and the frequency of Golgi distributed randomly and uniformly across the cell area (dashed black line). (J) Example of an original Golgi track (solid light green) and the corresponding straightened track (dashed dark green), where each new track segment represents a largely straight run of the Golgi with relative angles below ${90}^{\circ }$. (K) Distributions of segment lengths of straightened Golgi tracks followed truncated power laws with exponents $\alpha =3.60$ and $\alpha =4.48$ and bounds $l_{\min }=5.11$ and $l_{\min }=0.62$ for control and LatB-treated cells, respectively.

Golgi Bodies Exhibit Wiggling, Which Does Not Change Over Time or with Distance to the Actin Cytoskeleton.

The movement of Golgi bodies is characterized as saltatory or stop and go (11, 30), whereby Golgi switch between periods of directed movement and undirected “wiggling” behavior (Fig. 3E). Whereas it has been suggested that Golgi wiggling is not specific to individual Golgi bodies (10), it is yet unclear whether Golgi wiggling changes over time or depends on the distance of the Golgi from the actin cytoskeleton. To quantify these characteristics, we computed the angles between consecutive Golgi track segments (referred to as “relative angles”; Fig. 3E) and refer to movement with relative angles above ${90}^{\circ }$ as wiggling behavior (Fig. S6 shows another measure of wiggling). The observed distributions of relative angles across the studied cells were broad, demonstrating that both largely unidirectional movement and wiggling behavior were present (Fig. 3F). For LatB-treated cells, the average relative angle $a={104}^{\circ }\pm {55}^{\circ }$ was larger than for control cells with $a={85}^{\circ }\pm {55}^{\circ }$ and wiggling was thus more common. The distributions of relative angles averaged across a given track (Fig. 3G) peaked at around ${90}^{\circ }$ for both untreated and LatB-treated cells, showing that the majority of Golgi tracks contained both periods of directed movement and wiggling behavior. Hence, our findings confirm that wiggling behavior is not specific to individual Golgi.

Fig. S6.

Golgi wiggling in dependence of actin cytoskeleton and consistency across cells. Shown are results for partially and fully elongated/growing hypocotyl cells of untreated control plants (green/blue), cells of plants treated with the actin-disrupting drug LatB (orange/yellow), and the combined data (black). Please refer to SI Text for detailed explanations. (A) Overlay of cellular recording of Golgi and Golgi flow network with edge colors representing the average relative angle of close-by Golgi tracks, capturing the wiggling behavior of Golgi. (B) Distributions of average relative angles of close-by Golgi tracks per edge in dependence of capacity of the respective edge for control and LatB-treated cells. The average relative angles approached ${90}^{\circ }$ with increasing edge capacities (B, Right; dashed lines indicate averages and dotted lines are discussed below). The distributions of average relative angles exhibited peaks close to ${85}^{\circ }$ and ${104}^{\circ }$ for control and LatB-treated cells, respectively (B, Left; dashed lines, Fig. 3F). For the control cells, $25\%$ of the edges showed average relative angles below ${45}^{\circ }$, reflecting predominant directed movement of close-by Golgi, and $16\%$ showed average relative angles above ${135}^{\circ }$, reflecting predominant wiggling behavior of close-by Golgi. For LatB-treated cells, these fractions were roughly reversed with $15\%$ and $31\%$, respectively. (C) Heat map of relative angles and streaming coefficients (Eq. S6) of Golgi tracks as two measures of Golgi wiggling. Linear regression (white line) indicates a moderate but highly significant negative correlation between the two measures ($c_P=-0.323$ and $P_P<0.05$). (D) Scatter plots of Golgi diameter and average intensity estimated from the Golgi detection step (Materials and Methods) showed a strong positive correlation (Pearson correlation coefficients $c_P\approx 0.9$ and all $P$ values $P_P<0.05$). (E) Overlays of cellular recordings of Golgi and tracking results in fully elongated (green) and growing (blue) hypocotyl cells showed similar patterns of Golgi movement (see Fig. S1 for a detailed description of the recording details for the two developmental states). (F) Distributions of absolute angles for control and LatB-treated, growing and fully elongated cells, averaged across cells (solid lines and error bars indicate mean $\pm$ $\mathrm{SD}$), with small standard deviations indicating little cell-to-cell variability. (G) Golgi velocities varied between treatments but showed little variation across different cells (mean $\pm$ $\mathrm{SD}$) and between developmental stages. (H) Distributions of relative angles were affected by treatment but not by cell-to-cell variability (mean $\pm \mathrm{SD}$) or cell developmental stage. (I) Distributions of relative Golgi angles averaged across a given track were affected by treatment but were nearly identical across different cells (mean $\pm$ $\mathrm{SD}$) and across developmental stages. (J) Time series of relative angles, averaged over a given time step and across different cells (mean $\pm$ $\mathrm{SD}$), were stationary (Fig. 3) and showed little cell-to-cell variability. (K) The distributions of segment lengths of straightened Golgi tracks varied between cells only slightly and followed truncated power laws with similar exponents (mean $\pm$ $\mathrm{SD}$).

To test whether the prevalence of Golgi wiggling changes over time, we calculated the distribution of average relative angles over time (Fig. 3H, Left). We found that Golgi motility did not change during the course of the recordings (Fig. 3H, Upper Right). Moreover, the prevalence of Golgi wiggling showed only very minor fluctuations within and across time series (Fig. 3H, Lower Right; $\mathrm{CV}\left[a\right]=0.10\pm 0.03$), indicating that a constant fraction of Golgi exhibited wiggling behavior over time. Our data therefore suggest that Golgi wiggling is a common and stable cellular phenomenon. To study the effect of the distance between actin cytoskeleton and Golgi on wiggling, we computed the relative angles between consecutive track segments at a given distance from the cytoskeletal center line (Fig. 3I, Left). The frequency of Golgi was dependent on the distance to the AFs (Fig. 3I, Right), with high Golgi densities up to $2\mu \mathrm{m}$ from the AFs. Surprisingly, the prevalence of Golgi wiggling did not depend on the distance from the AFs (or on their thickness, Fig. S6). Moreover, although Golgi movement may vary substantially between cells, the features of Golgi movement studied here were highly consistent across cells (Fig. S6).

Movement Patterns of Golgi Resemble Search Strategies and Might Optimize Uptake and Delivery.

We note that the Golgi wiggling resembles the searching behavior of foraging animals (46, 47) or microbial motion (48) that has been suggested to optimize search efficiency. This type of motion is characterized by random reorientations (Fig. 3D) and step sizes $l$ that follow a power-law distribution $P\left(l\right)=\frac{\alpha -1}{l_{\min }}{\left(\frac{l}{l_{\min }}\right)}^{-\alpha }$. Because our image series provide snapshots with fixed time intervals, to quantify the distribution of Golgi step sizes, we considered track segments with relative angles below ${90}^{\circ }$ as one step and replaced them by a single segment capturing the net displacement (Fig. 3J). Indeed, the distributions of step sizes of these straightened tracks followed truncated power laws with exponents $\alpha =3.60$ and $\alpha =4.48$ for control and LatB-treated cells, respectively [Fig. 3K; in particular, truncated power laws yielded higher likelihoods than exponential distributions (49)]. These exponents are larger than those typically reported for foraging animals or bacteria, $1<\alpha <3$ (46–48), but might indicate search strategies in small areas with a limited number of targets (50) or in the presence of obstacles or preferred areas (51–53), e.g., other organelles or delivery sites. Again, these findings were highly consistent across cells (Fig. S6).

Despite obvious differences in mechanisms underlying Golgi movement and animal foraging there may be similar goals. Namely, it is plausible that Golgi-derived material may need to be exchanged between parts of the plasma membrane, the endoplasmatic reticulum (ER), and other compartments. Assuming that these sites are not globally coordinated by the cell, the switching of Golgi between directed movement and wiggling behavior may therefore provide an efficient search strategy. This is compatible with proposed models of Golgi movement (30), such as the “vacuum cleaner” model (Golgi move through the cell and pick up products from the ER) or the “recruitment” model (Golgi pause in the vicinity of active ER sites to facilitate trafficking). Our findings might therefore indicate a connection between Golgi wiggling and the optimization of uptake and delivery of Golgi-related material throughout the cell.

The Golgi search behavior is compatible with the movement of Golgi along the actin structures. Whereas, at a given time step, the majority of Golgi stayed at the same AF, some faster Golgi moved to different AFs (Fig. S5). Moreover, it remains unclear whether Golgi bodies are transported through the cell by direct interactions with motor proteins or indirectly via cytoplasmic streaming (54). By investigating the relative movement of different Golgi at a given time step (referred to as “pairwise angles”; Fig. 3E), we found substantial antiparallel movement of close-by Golgi (Fig. S5). Taking into account the low Reynolds numbers of the cytoplasm (1), this antiparallel movement contradicts the assumption of indirect, cytoplasmic-streaming–induced movement and instead supports myosin-based transport of a substantial fraction of Golgi bodies. In conclusion, our data suggest that switching of Golgi to adjacent AFs is myosin dependent, whereas switching to nonadjacent AFs is due to cytoplasmic streaming that may carry the Golgi over large distances.

Local and Global Actin Network Architecture May Be Used to Predict Direction and Velocity of Golgi Movement.

Our previous analyses assumed that the capacity of a given actin network edge, i.e., its average thickness, reflects its potential to transport cellular cargo (Fig. 2). To test this hypothesis, we studied the Golgi flow on two levels: First, we computed pairwise correlations between the properties of Golgi flow and actin structures, as modeled by our extracted networks. Second, we combined different edge properties of the actin networks to predict features of Golgi flow (e.g., direction and velocity), using a multiple–linear-regression approach. To this end, for the extracted actin networks (Fig. 4 A and B), we determined the local edge capacities and global edge properties that incorporate information about the importance of any given edge in the network context. Namely, we studied edge degree (measuring the total thickness of adjacent edges), the edge page rank (measuring the probability that cargo that randomly traverses the network is found at the given edge), the edge path betweenness (measuring the likelihood that the given edge lies on a shortest path through the network), and the edge flow betweenness [measuring the total maximum flow between any two nodes through the given edge (32); see Table S1 for mathematical definitions and explanations]. In parallel, from the Golgi tracks at each time step, we constructed an auxiliary Golgi flow network by copying the structure of the actin network and assigning new edge weights in the Golgi flow network according to various features of Golgi movement in the vicinity of the respective edge [e.g., the number of Golgi (Fig. 4E) or the direction and velocity of close-by Golgi (Fig. 4F)].

To investigate the relationship between actin structure and Golgi dynamics in partially elongated hypocotyl cells, we first computed the correlation between the determined edge properties of actin and Golgi flow networks. For instance, we studied the dependence of the Golgi direction and velocity on the actin edge rank. The correlation between the two properties varied over time and across cells (Fig. 4G). Across all studied partially elongated cells, this correlation was significant for control cells with $c_P=0.384$, whereas no significant correlation was found for the LatB-treated cells with $c_P=-0.023$. These findings are compatible with the severely reduced flow (Fig. 3C) and increased wiggling behavior of Golgi (Fig. 3F) in LatB-treated cells. We further evaluated the correlations between all pairs of edge properties, averaged across the studied cells and time points (Fig. 4H). Some pairs of properties, such as Golgi direction and velocity and actin edge rank discussed above, were correlated for the control cells ($|c_P|>0.2$) but not for the LatB-treated cells ($|c_P|\le 0.2$; Fig. 4G). Only the number of Golgi close to a given edge was correlated with the respective edge capacity and edge degree for both control and LatB-treated cells (Fig. 4I). These findings show that although the flow of Golgi is severely altered by the LatB treatment, Golgi still agglomerate in the vicinity of the actin stubs (Fig. 3I). However, for most pairs of actin and Golgi flow network edge properties, there was no or only weak correlation ($|c_P|\le 0.2$). Hence, whereas in particular, edge flow and path betweenness have been suggested to predict transport in real-world networks (55–57), they were not predictive of Golgi transport along the actin cytoskeleton in hypocotyl plant cells. This deviation may be due to different transport requirements in particular regions of the cell, especially during hypocotyl elongation growth (37, 58).

Because pairwise correlations were of moderate value, we then used multiple linear regression to see whether certain aspects of Golgi flow could be predicted from a combination of actin edge properties. Indeed, the number of Golgi close to an actin edge (Fig. 4K; coefficient of determination $R^2=0.704$) and the Golgi direction and velocity ($R^2=0.747$) were accurately predicted from the edge properties of the underlying actin cytoskeletal network. Moreover, edge capacity, edge degree, and edge rank of the actin network had higher predictive power (one-sample two-sided $t$ test $P$ values $P_{t\prime }<0.05$ for most Golgi flow properties) than the edge path and flow betweenness ($P_{t\prime }\ge 0.05$). As edge capacity and edge degree reflect (semi)local actin bundling, their observed high predictive power supports the finding that actin bundling is correlated with Golgi density and velocity (Fig. S5) (10). As indicated above, the edge rank measures the (global) importance of an edge in the network context and corresponds to the probability that cargo that randomly switches between adjacent filament segments is found at the given edge, whereby thicker filaments are frequented with higher probabilities. This assumption of random movement is compatible with the wiggling of Golgi (Fig. 3).

Interestingly, these correlations between actin structures and Golgi movement were very similar for growing and fully elongated hypocotyl cells (Fig. S1). Our results were confirmed by analysis of 3D data of actin cytoskeleton and Golgi (Fig. S2). Therefore, the system-wide organization of the actin cytoskeleton in hypocotyl cells shapes, and may be used to predict, the dynamic flow of Golgi.

Finally, we note that our imaging setup captured only the outer periclinal cell side, for both 2D and 3D data. Because 3D imaging of the complete, quickly rearranging plant cytoskeleton is not yet feasible, we modeled the cylindrical geometry of the cortical cytoskeleton by periodically extending the original, 2D extracted network. Whereas cytoskeletal structures on different cell sides generally differ (e.g., refs. 59 and 60 for actin and ref. 61 for microtubules), it is parsimonious and avoids an unbiological plane-like cytoskeletal geometry. Indeed, taking into account this cylindrical geometry moderately but significantly improved the predictive power of our regression-based analyses of Golgi movement (Fig. S4). Taken together, our data show that Golgi transport in hypocotyl cells is not merely determined by the local structure of the cortical cytoskeleton, but also depends on larger architectural contexts, as well as its cylindrical geometry.

SI Materials and Methods

Plant Material and Experimental Setup.

We used Arabidopsis Columbia-0 35S:FABD-GFP and pCesA6:tdT-CesA6 dual-labeled seedlings (12, 36) to study actin cytoskeleton and Golgi bodies. The seedlings were surface sterilized (ethanol), stratified for $2\mathrm{d}$ at $4^{\circ }\mathrm{C}$, and germinated on MS agar plates (1$\times$Murashige and Skoog salts, $8{\mathrm{L}}^{-1}\cdot \mathrm{g}$ agar, 1$\times$B5 vitamins, and $10.8{\mathrm{L}}^{-1}\cdot \mathrm{g}$ sugar). All plants were grown in the dark on vertical plates at ${21.8}^{\circ }\mathrm{C}$ for $3\mathrm{d}$. For drug treatment, seedlings were floated on distilled water containing $150\mathrm{nM}$ LatB and a set of control seedlings on pure water in six-well plates. The seedlings were incubated in the dark with gentle shaking for $4\mathrm{h}$ before imaging. To immobilize the seedlings and to avoid mechanical damage, they were mounted between a cover glass and a $1-\mathrm{mm}$-thick $1\%$ agar pad affixed on a circular coverslip. A spinning-disk confocal microscope was used to capture rapid changes and to minimize bleaching, yielding $512\times 512{\mathrm{pixels}}^2$ images with a spatial resolution of $0.133{\mathrm{pixel}}^{-1}\cdot \mu \mathrm{m}$ (64). Exposure times were $400\mathrm{ms}$ for FABD-GFP and $300\mathrm{ms}$ for tdT-CesA6 with a time interval of $2\mathrm{s}$ between subsequent actin and Golgi images, respectively. Cells were recorded for at least $100$ frames, i.e., about $3\min$. Only seedlings expressing both fluorescent markers were used for further analyses. For the results in the main text, seven recordings of different control and LatB-treated partially elongated hypocotyl cells from seven seedlings were analyzed, respectively.

For the comparison of actin-based Golgi transport across different developmental stages, i.e., between growing and elongated hypocotyl cells (Fig. S1), we used a slightly modified imaging setup yielding $1,024\times 1,024{\mathrm{pixels}}^2$ images with the same temporal resolution of $2\mathrm{s}$ between subsequent images, exposure times of $250\mathrm{ms}$, and a very similar spatial resolution of $0.129{\mathrm{pixel}}^{-1}\cdot \mu \mathrm{m}$. More specifically, seedlings were imaged using a CSU-W1 spinning-disk head (Yokogawa) mounted to an inverted Ti-E microscope (Nikon) equipped with a 100× oil-immersion objective (Apo TIRF, N.A. 1.49). Fluorescence detection was achieved using a deep-cooled iXon Ultra 888 EMCCD (Andor Technology). Both setups were controlled via PC using MetaMorph (Molecular Devices). We imaged growing and fully elongated hypocotyl cells around $1\mathrm{mm}$ and $5\mathrm{mm}$ below the apical hook, respectively, each with and without LatB treatment as described above. Additionally, 3D image stacks were obtained using the same settings with a spacing of $1\mu \mathrm{m}$ between three subsequent z slices (Fig. S2). For each of the described conditions, three cells were analyzed.

Image Preprocessing of Actin and Golgi Recordings.

We preprocessed the confocal recordings, using the image-processing package Fiji (45) (see Fig. 1A for illustration and mathbiol.mpimp-golm.mpg.de/CytoSeg/ for the open-source code and examples): We corrected the potential drift of the seedlings under the microscope by applying the Fiji-StackReg stack registration algorithm to the image series, which allows rigid body transformations, minimizes the mean square intensity difference between subsequent frames, and does not require any parameter selection (65). To enable simultaneous registration of the dual-labeled plant recordings, we merged actin and Golgi recordings from one cell as different color channels and split the channels after registration. We compensated photobleaching by normalizing the mean intensity of each frame. We improved the signal-to-noise ratio by using the Fiji-BackgroundSubtraction rolling ball filter with radius of $50\hspace{0.17em}\mathrm{pixels}$ (66). Moreover, for the data from the second imaging setup, the Fiji-Despeckle median filter was applied to reduce salt and pepper noise (45). For 3D image data, the rolling ball filter was applied to each z slice separately. To determine the cellular region of interest for each cell, we performed a maximum projection of the registered and concatenated actin and Golgi recordings and manually selected the largest cell as the region of interest for both actin and Golgi images. Moreover, to identify the major cell axis, we skeletonized the binary representation of the cellular region of interest and selected the pixels along $20\%$ and $80\%$ of the length of the resulting center line to compute the angle $\gamma$ of rotation of the cell (Fig. 2G).

Extraction of Actin Networks from Image Data.

From the preprocessed 2D and 3D image data, we represented the actin cytoskeleton as a network through a custom procedure that has been developed and implemented using Python (70) (see Fig. 1 B–E for illustration and mathbiol.mpimp-golm.mpg.de/CytoSeg/ for the open-source code and examples): First, to obtain the filamentous actin skeleton, we applied a 2D tubeness filter to each frame of the preprocessed actin images to enhance the signal of the filamentous structures of width $v_{\mathrm{width}}$ (67) (Fig. 1B) (for 3D images, the filters were applied to each z slice separately). Next, we obtained binary images by applying an adaptive median threshold with block size $v_{\mathrm{thres}}$ (68) (Fig. 1C). We determined the center lines of the actin structures by skeletonizing the thresholded image (69); i.e., the skeleton and the background are given in a binary representation by $1$ and $0$ pixels, respectively. Then, we removed all spurious connected components of less than $v_{\mathrm{size}}$ pixels in size as well as those whose average intensity in the original actin image was below $v_{\mathrm{int}}$ of the average component intensity (Fig. 1D). The image processing parameters $v_{\mathrm{width}}$, $v_{\mathrm{thres}}$, $v_{\mathrm{size}}$, and $v_{\mathrm{int}}$ were determined in a gauging step by comparison of automated segmentation to manually obtained gold standard segmentations (Fig. 1J).

Second, for each skeletonized, binary actin image, we identified the nodes of the network as crossings or endpoints of filaments by checking the $3\times 3\hspace{0.17em}{\mathrm{pixels}}^2$ neighborhood for each pixel and assigning a node if the center pixel was $1$ and the outer ring of the neighborhood contained exactly one or more than two connected $1$ pixels. By ignoring potential nodes with zero or two connected $1$ pixels in the outer neighborhood we excluded disconnected pixels and pixels in the middle of a filament, respectively. For 3D image data, we used a $3\times 3\times 3\hspace{0.17em}{\mathrm{pixels}}^2$ neighborhood to detect nodes. In cases where several nodes touched, we removed all except for the one whose position coincided with the center of mass of the touching node pixels. Components of the actin cytoskeleton without connection to any node were removed. Then, we labeled the node pixels and created an auxiliary image where the background was set to $-1$, the filaments were set to $0$, and the $N$ nodes were labeled sequentially from $1$ to $N$ (Fig. 1E).

Third, we constructed a weighted network by starting from an empty multigraph $G=(\mathcal{N},\mathcal{E})$ with $N=|\mathcal{N}|$ nodes at positions $x_n\in {ℝ}^2$, $n\in \mathcal{N}$, and initially $E=|\mathcal{E}|=0$ edges. We iteratively propagated the node labels to the eight neighboring pixels, given that these pixels were part of a filament, and aborted the iteration when no filament pixels were left. Then, for each two neighboring pixels with different labels, $n\ne m$, $n,m\in \mathcal{N}$, we added an edge $e=(n,m)$ to the multigraph $G$. To obtain further information about the edges, we computed different properties parallel to the propagation of node labels: We defined the arc length $a_{e,F}$ of an edge $e$ as the arc length of the corresponding filament segment. We computed it by creating another auxiliary image of zeros and, when propagating a node label, setting the value at the new position to the value of the old position of that array and adding ($\sqrt{3}$) $\sqrt{2}$ or $1$, depending on whether the propagation step was (space) diagonal or not. The arc length $a_{e,F}$ of an edge $e$ was then given by the sum of values of the two neighboring pixels that were used to create the edge. Similarly, we measured the weight $a_{e,w}$ of an edge by using another auxiliary image and propagating the intensity of the original actin image, filtered with a Gaussian kernel with a $\mathrm{SD}$ of $2\hspace{0.17em}\mathrm{pixels}$, along the filaments. Again, $a_{e,w}$ was given by the sum of the values of the two different neighboring, propagated node pixels. Due to the Gaussian filtering, $a_{e,w}$ is a measure for the summed intensity in the neighborhood of the filament and, by construction, increases with the length of the filament. We therefore derived the capacity $a_{e,c}$ of an edge as the ratio of its weight and arc length, $a_{e,c}=a_{e,F}^{-1}{a}_{e,w}$, $a_{e,F}\ge 1$ by construction. The edge capacity reflects the average thickness of the filament segment and was used as a measure for the average potential amount of cargo that may traverse the edge (Fig. 2). For the computation of shortest paths in the network, we further defined the length $a_{e,l}$ of an edge as the inverse of the capacity, $a_{e,l}=a_{e,c}^{-1}$. We normalized the edge capacities of a given network to one for better comparability. Additionally, we calculated the Euclidean edge length $a_{e,E}$ directly from the node positions and the bending of a filament segment was measured by the ratio of arc and Euclidean length, $a_{e,B}\equiv B=a_{e,E}^{-1}{a}_{e,F}$.

In general, the extracted network is a multigraph (e.g., two curved filaments may cross twice, leading to two edges between the same pair of nodes; Fig. 1E). For simplicity, we projected the multigraph onto a simple graph by summing the multiple-edge capacities $a_{e,c}$ and taking the minimum of the remaining multiple-edge properties. This is justified by our assumption of current-like flow along the filaments that is additive in $a_{e,c}$ and our calculation of shortest paths that favor the minimum $a_{e,l}$ in the case of multiple edges. Because the network is not guaranteed to be connected, we simplified analyses by adding edges of minimum total Euclidean length to obtain a connected network. Their edge weights were given by the average intensity of the Gaussian filtered image along a connecting line of pixels between its two respective nodes, similar to the original edges above (Fig. 1E). Network extraction procedures similar to ours are reviewed below.

Finally, we derived several higher-level edge properties that not only reflect the local structure of the cytoskeleton but also capture global features (Table S1). As a simple measure of the importance of an edge $e$ in the network context, we computed its degree $a_{e,\mathrm{deg}}$ in the line graph $LG$, i.e., the summed capacity of its adjacent edges (32). The line graph $LG$ of a graph $G$ has a node for each edge in $G$ and an edge between two nodes if the corresponding edges are adjacent in $G$ (32). Moreover, we derived the edge page rank $a_{e,\mathrm{rank}}$ of an edge $e$ in the line graph $LG$ (32), which quantifies the expected frequency of cargo at a given edge when the cargo is assumed to randomly switch between edges. To capture the importance of an edge $e$ with respect to shortest paths in the network context, we further derived the edge path betweenness $a_{e,\mathrm{path}}$, given by the number of shortest paths between all pairs of nodes that traverse $e$ (32). Finally, the edge current flow betweenness $a_{e,\mathrm{flow}}$ was computed as the sum of maximum flows through $e$ between all pairs of nodes (32).

Gauging of Network Extraction Parameters.

To ensure an accurate network representation of the actin cytoskeleton, we performed extensive gauging of the four imaging parameters $v_{\mathrm{width}}$, $v_{\mathrm{thres}}$, $v_{\mathrm{size}}$, and $v_{\mathrm{int}}$. To this end, we generated $20$ synthetic images of known, cytoskeleton-like structures and created manual segmentation of $20$ biological cytoskeleton images as a gold standard for comparison against the automated segmentation results. We note that the extraction of networks from the segmented center lines is deterministic, i.e., identical segmentations result in identical networks, and we therefore focused on comparing the segmented center lines.

First, for the manual segmentations, we randomly chose $20$ of the investigated actin cytoskeleton images. For these images, we performed the preprocessing steps described in Materials and Methods and manually segmented the center lines of the filaments (Fig. 1H).

Second, we created $20$ empty images of $100\times 500{\mathrm{pixels}}^2$ in size, comparable to the typical cellular region of interest. For each image, we created 10 auxiliary images by drawing two random points uniformly distributed over the image area, adding a line of unit intensity between these points, blurring the line with a Gaussian filter of random $\mathrm{SD}$ uniformly drawn from the interval $[0.5,1.5]$, and rescaling the average image intensity to one. We superimposed all 10 auxiliary images to obtain a cytoskeleton-like structure of filaments of different thicknesses. Finally, we added gamma-distributed noise such that both mean and $\mathrm{SD}$ of the synthetic image intensity were similar to those of the biological images (Fig. 1G). Whereas noise in digital camera images is typically a combination of Gaussian-distributed sensor noise, gamma-distributed speckle noise, and Poisson-distributed shot noise, we adhered to simple gamma-distributed noise for simplicity here, which was similar to that in the biological cytoskeleton images.

We then varied all four parameters in a wide range with 10 linear steps each, $v_{\mathrm{width}}\in \{0.4,\mathrm{\dots },2.2\}$, $v_{\mathrm{thres}}\in \{21,\mathrm{\dots },111\}$, $v_{\mathrm{size}}\in \{2,\mathrm{\dots },47\}$, and $v_{\mathrm{int}}\in \{0.1,\mathrm{\dots },1.9\}$ (Fig. 1 I and J) for all $40$ gauging images. As a measure of agreement between the segmentations, we used the average minimum Euclidean distance between two pixels from the manual to the automated segmentation, $d_{\mathrm{manu}\to \mathrm{auto}}$, and vice versa, $d_{\mathrm{auto}\to \mathrm{manu}}$. Small values for $d_{\mathrm{manu}\to \mathrm{auto}}$ typically favor parameters that detect only thick actin bundles (Fig. 1I, Left), whereas small values for $d_{\mathrm{auto}\to \mathrm{manu}}$ typically yield parameters that overestimate the prevalence of filamentous actin in the cell (Fig. 1I, Right). Therefore, we minimized the Haussdorf distance $d_{\mathrm{HD}}=\frac{1}{2}(d_{\mathrm{manu}\to \mathrm{auto}}+d_{\mathrm{auto}\to \mathrm{manu}})$ to obtain a compromise between over- and undersegmentation (Fig. 1J).

The optimal parameters and their confidence intervals were determined as follows: We randomly selected $40$ of the $40$ images, allowing duplicates; stored the parameters that minimized the average $d_{\mathrm{HD}}$; repeated the procedure $500$ times; and computed mean and $\mathrm{SD}$ for each of the stored parameters (Fig. 1K). Using these optimized parameters guaranteed small average distances between the pixels of manual and automated segmentations and, hence, accurate network representations of the cytoskeleton.

Review of Network Extraction Methods.

Finally, we review other, existing methods for the extraction of networks from different image sources and systems of interest. The first class of approaches typically relies on 2D image data and uses classical image segmentation for network extraction: From high-contrast dark-field microscopy images of leaves, venation networks were extracted in a supervised procedure (71). However, due to the high signal-to-noise ratio ($\mathrm{SNR}$), no filters to enhance the signal of the curvilinear veins were applied, as necessary for the cytoskeletal images. No edge weights capturing the thickness of the underlying structures were computed, but are essential for understanding the cytoskeleton. Moreover, only the largest connected component of the venation network was kept, which removes smaller, disconnected parts of the network that commonly occur in the cytoskeleton. Finally, although the supervised adjustment of extraction parameters increases flexibility, it requires manual input, thereby also introducing user bias.

Using a fully automated extraction procedure, photographic image series were used to extract networks formed by slime molds (72). Again, the high $\mathrm{SNR}$ did not necessitate enhancement of curvilinear structures. A background subtraction was performed by subtracting the first frame of the image series before the growth of the slime mold, which is not applicable to image data of the constantly rearranging cytoskeleton. The thickness of the veins was measured by counting the average number of pixels per unit vein length, which is reasonable for slime mold images. However, this measure ignores the underlying image intensity, which is a better estimator of thickness for cytoskeletal filaments and bundles whose diameter is typically well below the resolution limit of confocal microscopes (73). The parameters of the procedure were determined manually without gauging or comparison with a known gold standard. Although providing a user-friendly graphical user interface and efficient implementation for the extraction of networks from different systems and imaging sources, the NEFI software tool is confronted with the same challenges (74).

Our network extraction procedure was inspired by another, more sophisticated method for the extraction of fungal networks from photographs (75). Whereas there the curvilinear vein structures were enhanced using a contrast-independent phase-congruency filter (76), we used a faster and widely used tubeness filter for simplicity (67). As for the slime mold network above, the vein thickness was determined only based on the average pixel numbers per unit vein length and we extended the thickness computation by taking into account pixel intensities. Moreover, we adopted the gauging of the free image analysis parameters by computing the average smallest distances between the center lines of manually segmented gold standard images and automated segmentations. However, ref. 76 considered only one direction, $d_{\mathrm{manu}\to \mathrm{auto}}$, which clearly favors undersegmentation, i.e., an excess of pixels in the automated segmentation (Fig. 1I). Instead, we included the opposite direction and minimized the Haussdorf distance $d_{\mathrm{HD}}=\frac{1}{2}\left(d_{\mathrm{manu}\to \mathrm{auto}}+d_{\mathrm{auto}\to \mathrm{manu}}\right)$ in the gauging step to avoid both under- and oversegmentation (Fig. 1J) (25, 26). Thus, although the average smallest distance $d_{\mathrm{manu}\to \mathrm{auto}}\approx 1\mathrm{pixel}$ in refs. 75 and 76 was smaller than our $d_{\mathrm{HD}}\approx 3\hspace{0.17em}\mathrm{pixels}$, this is due to the poorer $\mathrm{SNR}$ of the original cytoskeletal images as well as the trade-off between under- and oversegmentation incorporated in $d_{\mathrm{HD}}$. Importantly, in contrast to most approaches presented above, our method is directly applicable to 3D image data (Fig. S2).

Another class of approaches for the detection of networks from image data does not rely on segmentation but encompasses tracing-, tracking-, or open contour-based approaches (26, 77, 78). Instead of (global) image segmentation, these approaches typically identify two or more points on the network and find a connecting path through the network by optimization of an (usually local) energy function. Because many of these approaches have been originally developed for the reconstruction of neural networks, they are directly suitable for the extraction of 3D network structures. However, because most existing approaches in this class require manual user input, we focus our discussion on SOAX, a software for quantification of 3D biopolymer networks (26). SOAX represents a recent and fully automated open contour-based approach whose strengths and limits are largely representative for the related approaches: Especially for large sets of 3D image data, SOAX is faster than segmentation-based approaches. Furthermore, we note that SOAX incorporates resampling of the 3D image data to compensate for the decrease in $\mathrm{SNR}$ toward the distant side of the cell (see Fig. S4 for discussion of periodic boundary conditions). However, whereas our highly time-resolved recordings of the cytoskeleton displayed low $\mathrm{SNR}\approx 1$, the image data studied in ref. 26 displayed high $\mathrm{SNR}\approx 3$, which rendered filters for the enhancement of curvilinear structures unnecessary. Nevertheless, such filters (67, 76) may be readily applied in open contour-based approaches as well. Moreover, ref. 26 used manual segmentations and careful parameter gauging to optimize the network extraction quality and found $d_{\mathrm{HD}}\approx 1\mathrm{pixel}$, which outperforms our approach, but benefited from higher $\mathrm{SNR}$. Finally, whereas our presented approach, including the image preprocessing, involves only $6$ parameters, SOAX uses more than $20$ parameters in total.

Despite the differences in the image segmentation procedures, which have been designed for different image sources and systems of interest, systematic gauging (Fig. 1) provides a means to adjust the free parameters of any of the above segmentation procedures. Whereas automated segmentation methods are steadily improving, a quantitative comparison with manual, expert-driven segmentations remains crucial.

Construction of Golgi Flow Networks from Tracking Data.

To automatically track the movement of Golgi through the cell in 2D and 3D, we used Fiji-TrackMate to detect the Golgi as particles of $5\hspace{0.17em}\mathrm{pixels}$ in radius and discarded those with quality values below the $80\mathrm{t}\mathrm{h}$ percentile (44, 45). We note that the used “difference of Gaussian”-based algorithm also detects smaller Golgi as well as Golgi up to $10\hspace{0.17em}\mathrm{pixels}$ in radius, which allows tracking even of agglomerated Golgi that may merge and split over time. We then linked the Golgi in different frames, using the linear assignment problem tracker with a maximum linkage distance of $24\hspace{0.17em}\mathrm{pixels}$, a maximum gap-closing distance of $24\hspace{0.17em}\mathrm{pixels}$, and a maximum frame gap number of $4$. The detection and tracking parameters were determined manually and whereas changes in the tracking parameters may alter the full Golgi tracks, the majority of our analyses focused on individual track segments that are more robust against changes in parameters. The chosen parameters enable tracking of Golgi with velocities up to $1.6{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$ and although maximum velocities of up to $7{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$ have been observed, typically only around $8\%$ of the Golgi exceed $1{\mathrm{s}}^{-1}\cdot \mu \mathrm{m}$ (10). The tracking results enable detailed analysis of Golgi dynamics, e.g., over time or under different conditions (Fig. 3 and Fig. S5).

Next, we constructed networks from the tracking data, referred to as Golgi flow networks, for comparison with their actin cytoskeleton counterparts (Fig. 4). For a given time step, we copied the nodes and edges of the actin network and computed the minimum distance $d_{t,e}$ between the edges $e$ and the center points $x_t$ of the tracking segments that originate in the respective time step. Each edge $e$ of the Golgi flow network was then assigned different weighting factors (Table S1): the number $g_{e,n}$ of track segments that are closer to the considered edge than a cutoff distance of $8\hspace{0.17em}\mathrm{pixels}$, the average intensity $g_{e,i}$ of close-by Golgi, the average velocity $g_{e,v}$ of close-by Golgi, the average angle $g_{e,d}$ between the edge and the close-by Golgi track segments, and combinations thereof. Whereas the distance threshold of $8\hspace{0.17em}\mathrm{pixels}$ may assign a given Golgi to multiple edges, smaller thresholds drastically reduce the number of Golgi assigned to each edge and do not allow computation of meaningful averages for the studied Golgi features.

A crucial step in the computation of several edge properties of the Golgi flow network involves the scalar product between a segment vector of a Golgi track and an actin network edge vector (i.e., the vector connecting the two edges’ nodes). Although the actin filaments may be curved, we showed that the bending of a filament segment is typically very small with $B=1.2\pm 0.2$ (Fig. 2E), justifying the assumption of straight edge vectors.

Randomization and Null Models of Actin Networks.

We investigated the structure of the actin networks, using a number of seminal and biologically relevant properties, such as assortativity and average path length (Fig. 2 and Table S1). Whereas some of these properties may be interpreted by themselves (like the sign of the assortativity that provides information about whether thick actin bundles are grouped together or whether they are intermingled with filaments), a suitable reference is needed to interpret others (like the average path length whose value depends, e.g., on the size of the network and the sum of edge weights).

Therefore, for any given actin network, we introduced two types of null models that randomize certain properties of the network while preserving relevant others (see Fig. S3 and mathbiol.mpimp-golm.mpg.de/CytoSeg/ for the open-source code and examples). From both null models we generated an ensemble of $R=20$ randomized networks for comparison with a given extracted network. For the first null model, the actin network was copied, its edges were divided into $21$ bins according to their Euclidean length $a_{e,E}$ (bins were given by $[\mathrm{0,10},\mathrm{\dots },\mathrm{190,200},\mathrm{\infty }]\hspace{0.17em}\mathrm{pixels}$), they were saved in a temporary list (their other properties, like the capacity $a_{e,c}$, remained unchanged), and they were removed from the network. All nodes were distributed randomly and uniformly across the cell area or volume for 2D and 3D data, respectively. Then, the longest edge in the temporary list was inserted between two random nodes whose discretized Euclidean distance matched the length bin of the edge. For each edge, $50$ pairs of matching nodes were tested and the edge was inserted such that the number of crossings with already placed edges was minimized. We repeated the procedure until all edges were added to the network. Because the randomized network may be disconnected, we connected it by adding edges of minimum total Euclidean length, as discussed for the original networks above. Although this procedure increased the number of edges by a factor of $r=1.12\pm 0.07$ with respect to the original extracted networks, the increase is small (Fig. S3). Whereas the randomized networks are not guaranteed to be planar, the number of edge crossings per edge is typically small, around $X=0.14\pm 0.11$ (Fig. S3). The obtained null model networks share several important features with the extracted cytoskeletal networks: Because the distribution of edge capacities is not changed, also their sum is preserved, reflecting the amount of filamentous actin in the cell. In addition, the distribution of edge lengths is identical to that of the actin cytoskeletal network.

We further used a second, more restricted model that does not increase the number of edges and edge crossings and does not randomize the node positions (Fig. S3). These null model networks were generated by shuffling only the edge properties of the original network (19, 20). The second null model, too, leaves the distribution of edge capacities unchanged.

Concluding Remarks

Although the molecular details of actin monomers and filaments as well as actin-associated proteins are relatively well studied, quantifying actin-based transport in a larger cellular context remains challenging. To address this gap, we introduced an accurate image-based network representation of the actin cytoskeleton to facilitate automated and unbiased quantification of cytoskeletal phenotypes and functions. We used this framework to establish that system-level properties of the actin cytoskeleton determine key features of Golgi transport in Arabidopsis hypocotyl cells.

Our approach of integrating cytoskeletal network structures with tracking data of organelles is directly transferable to various biological systems and functions: In plants, in addition to the analysis of different cell types, transport of mitochondria (4, 10) and photodamage avoidance movement of chloroplasts (62) represent interesting test grounds. In animals, it has been shown that cytoplasmic streaming in fruit fly oocytes (63) and transport of lysosomes in monkey kidney cells depend on microtubules (7). Although these are interesting local correlations of cytoskeletal features and organelle transport, we expect broader, system-level understanding of these processes by the application of interdisciplinary approaches such as ours. Our automated framework paves the way for quantitative assessment of the actin cytoskeleton and trafficking in, for example, large-scale chemical and genetic screens. Moreover, our findings indicate that network-based models could be used to predict potential exchange sites of Golgi-related material. Altogether, the presented combination of experimental imaging techniques and theoretical network-based analyses provides an important step toward a systems understanding and, ultimately, control of cytoskeleton-based transport.

Materials and Methods

Plant Material and Experimental Setup.

We used Arabidopsis Columbia-0 35S:FABD-GFP and pCesA6:tdT-CesA6 dual-labeled, 3-d-old, and dark-grown seedlings (12, 36) to study actin cytoskeleton and Golgi bodies (SI Materials and Methods and Movie S1). For drug and control treatment, seedlings were floated on distilled water with and without $150\hspace{0.17em}\mathrm{nM}$ LatB, respectively. Image series of partially elongated hypocotyl cells around $1\mathrm{mm}$ below the apical hook were captured using a spinning-disk confocal microscope with a spatial resolution of $0.133{\mathrm{pixel}}^{-1}\cdot \mu \mathrm{m}$ and a time interval of $2\mathrm{s}$ between subsequent 2D images (64). In a slightly modified imaging setup, both growing and fully elongated cells around $1\mathrm{mm}$ and $5\mathrm{mm}$ below the apical hook, respectively, were imaged for comparison. Additionally, 3D image stacks were obtained using the same setup with $1\mu \mathrm{m}$ between three subsequent z slices.

Extraction and Randomization of Actin Networks.

We corrected the potential drift of the seedlings using Fiji-StackReg rigid body stack registration (45, 65), compensated photobleaching by normalizing mean intensities, and improved the signal-to-noise ratio by using the Fiji-BackgroundSubtraction filter with a radius of $50\hspace{0.17em}\mathrm{pixels}$ (66) (SI Materials and Methods; see mathbiol.mpimp-golm.mpg.de/CytoSeg/ for open-source code and examples). To represent the actin cytoskeleton as a network in 2D and 3D, we enhanced filamentous structures of width $v_{\mathrm{width}}$ with a 2D tubeness filter (67), applied an adaptive median threshold with block size $v_{\mathrm{thres}}$ (68), skeletonized the resultant binary image (69), and removed all spurious connected components smaller than $v_{\mathrm{size}}$ pixels or with average intensities below $v_{\mathrm{int}}$ of the average component intensity. We identified the nodes of the network as crossings or endpoints of filaments. We added an edge between two nodes if they were directly connected by a skeleton line and assigned different edge weights such as its capacity, i.e., the average intensity along the respective filament per unit length. We gauged the four imaging parameters, using synthetic images of known cytoskeleton-like structures and manual segmentations of cytoskeleton images as a gold standard. To assess the biological relevance of the studied actin network properties, we used a first null model that distributes the nodes of the original network randomly and uniformly across the cell area (2D) or volume (3D) and shuffles edges such that their Euclidean length is preserved. A second null model shuffles only the edge properties of the original network (19).

Quantification of Golgi Movement.

We automatically tracked the movement of Golgi in 2D and 3D, using Fiji-TrackMate (SI Materials and Methods). We detected the Golgi as particles of around $5\hspace{0.17em}\mathrm{pixels}$ in radius (44, 45). We then linked the Golgi in different frames, using the linear assignment problem tracker with a maximum linkage distance of $24\hspace{0.17em}\mathrm{pixels}$, a maximum gap-closing distance of $24\hspace{0.17em}\mathrm{pixels}$, and a maximum frame gap number of $4$. To correlate actin structures with Golgi movement, we constructed auxiliary Golgi flow networks by copying the actin network. Each edge of the Golgi flow network was then assigned different weighting factors, e.g., the number of track segments within a cutoff distance of $8\hspace{0.17em}\mathrm{pixels}$ or the average velocity of close-by Golgi.

SI Text

Differences in Actin Architecture and Golgi Transport Between Growing and Fully Elongated Hypocotyl Cells.

To further assess the accuracy of our network extraction procedure, we analyzed and compared actin networks from hypocotyl cells at different developmental stages. In addition to partially elongated hypocotyl cells studied in the main text (Fig. S1A), we analyzed image data from growing and fully elongated hypocotyl cells around $1\mathrm{mm}$ and $5\mathrm{mm}$ below the apical hook, respectively (Fig. S1B). The slightly modified experimental setup captured larger sections of the cortical actin cytoskeleton and is described in detail in SI Materials and Methods. The actin structures at the two cell developmental stages showed clear differences, with a more uniform distribution of actin, fewer bundles, and more fine branches in growing hypocotyl cells (35, 36).

To quantify these structural differences, we computed the number of connected components after removal of edges with capacities below the $50\mathrm{t}\mathrm{h}$ percentile for an individual cell over time (“fragmentation”; Fig. S1C and Fig. 2). In particular, the actin networks in growing, untreated hypocotyl cells showed consistently larger fragmentation than in fully elongated cells. Combining the data of all three studied cells over the full imaging periods (Fig. S1D), we confirmed that the actin networks in growing, untreated hypocotyl cells were significantly more fragmented than in their LatB-treated counterparts, opposite to the results for fully elongated hypocotyl cells. Similarly, the average edge capacity (“bundling”) in growing, untreated hypocotyl cells was lower than in their LatB-treated counterparts, whereas the ratio was reversed for fully elongated hypocotyl cells. For the assortativity, no significant differences between growing and elongated hypocotyl cells were observed. These findings are in agreement with the finer and more branched structure of the actin cytoskeleton in growing hypocotyl cells (35, 36) in combination with the actin-disrupting effect of LatB, which especially affects fine AFs and leads to the formation of actin stubs (31). Moreover, these differences are compatible with the continuous gradient in cell elongation rates along the hypocotyl in dark-grown Arabidopsis seedlings (37).

However, no significant differences were observed regarding transport efficiency (Fig. S1E) or the correlations of actin edge properties and features of Golgi movement (Fig. S1 F and G). This indicates that despite differences in actin organization (and especially actin bundling), the cytoskeleton in hypocotyl cells may work as an efficient transportation network.

Extension of Analysis to 3D Image Data of Actin Cytoskeleton and Golgi.

Whereas the cytoskeleton is an inherently 3D structure, in the main text we focused on 2D image data and networks (Figs. 1–4). As explained in Results, this focus is justified by the thin cylindrical shell geometry of the cortical actin cytoskeleton (19, 27) (Fig. S2A, the confinement of finer actin meshes to the plasma membrane with only rare thick actin cables pervading the cell interior) and the size of the Golgi, which may bridge gaps between cortical AFs (28–30) (Fig. S6).

However, our approach is directly applicable to 3D image data (SI Materials and Methods). To test the validity of our 2D results, we therefore recorded 3D image data from growing and fully elongated hypocotyl cells under control conditions and after LatB treatment, respectively, and repeated our previous analyses. The extracted 3D networks confirmed the localization of the actin to the plasma membrane (Fig. S2A). For comparison, we further z projected the 3D image data by taking the average intensity across z slices and extracted 2D networks as before (Fig. S2B). For a given cell, the network properties of 3D and 2D networks generally differ (Fig. S2C, Left; time series of numbers of connected components after removal of edges with capacities below the $50\mathrm{t}\mathrm{h}$ percentile are shown for illustration), as expected for networks with different numbers of nodes and edges. However, we found a strong correlation between properties of 3D and 2D networks (Fig. S2C, Right; Pearson correlation coefficients $c_P=0.66$ for the combined data from different developmental stages and treatments).

Moreover, we computed various structural (Fig. S2D) and transport-related (Fig. S2E) properties of the 3D actin networks from growing and fully elongated hypocotyl cells as before. Our findings support those reported for the 2D analyses (Fig. S1). Similarly, the correlations between various edge properties of 3D actin and Golgi flow networks (Fig. S2F) confirmed our findings from 2D analyses (Fig. S1). In conclusion, our results suggest that the actin cytoskeleton at the outer periclinal side of hypocotyl plant cells can be approximated by a 2D network representation (Fig. S4).

Inference of Network Design Principles Using Two Different Null Models and Negative Controls.

We demonstrated that the actin cytoskeleton displays network properties supportive of efficient transport processes (Fig. 2). In particular, by proposing suitable null models, we showed that this transport efficiency arises from the specific organization of the cytoskeleton in biological cells, hence indicating an evolutionary basis. Here, we discuss and justify our proposed null models in more detail.

The first null model randomly and uniformly distributes the node positions across the cell and assigns the edges to new, randomly chosen pairs of nodes whose distance matches the Euclidean length of the respective edge, while keeping the number of edges crossings low (Fig. 2 H–J and Materials and Methods). This procedure is a modified version of the Erdős–Rényi model with hidden variables that has been used to identify structural features of various real-world networks (79). In our version, the hidden node variables are given by their positions and the probability of adding an edge between two nodes depends on their Euclidean distance and the fraction of edges from the original network of identical (binned) length that have not already been added to the null model network. Moreover, as an extension to the hidden variable model, for each added edge, we tried $50$ possible pairs of nodes and assigned the edge such that the number of intersections with already added edges was minimized.

This null model preserves the distribution of edge capacities, whose sum reflects the amount of filamentous actin in the cell. The null model further maintains the length distribution of filament segments. The null model as well as the extracted networks may exhibit crossing edges (Materials and Methods) whose frequency was measured by the crossing number,

$$X=E^{-1}\sum _{\underset{e\ne f}{e,f\in \mathcal{E}}}e\times f,$$ [S1]

where $e\times f=1$ if edges $e$ and $f$ cross and $0$ otherwise. Although the generated null model networks are in general not planar, their crossing number is small, with $X=0.14\pm 0.11$ crossings per edge (Fig. S3A; mean $\pm$ $\mathrm{SD}$). We note that whereas the extracted actin skeleton is planar by construction (all filament crossings are nodes; Fig. 1D), the reconstructed actin network may exhibit crossing edges because the edges are modeled as straight lines between the nodes, so that $X=0.04\pm 0.02$ already for the original networks. Moreover, because the null model networks are generally not connected, we added edges of minimum total Euclidean length to connect the network. However, across all generated null model networks, the number of edges $E_{\mathrm{null}}$ of the null model networks exceeded the number of edges $E_{\mathrm{bio}.}$ of the corresponding extracted networks only by a factor $r=1.12\pm 0.07$ (Fig. S3B), where

$$r=\frac{E_{\mathrm{null}}}{E_{\mathrm{bio}.}}.$$ [S2]

Furthermore, in contrast to the nodes in the null model networks, the nodes of the extracted actin networks were typically not randomly and uniformly distributed across the cell. We quantified the spatial distribution of node positions, using the nearest-neighbor index ($\mathrm{NNI}$) (80),

$$\mathrm{NNI}=\frac{\frac{1}{N^2\left(N-1\right)}{\sum }_{n,m=1}^N{d}_{n,m}}{\frac{1}{2}{(\frac{A_{\mathrm{cell}}}{N})}^{1/2}},$$ [S3]

where $d_{n,m}=\parallel {𝐱}_n-{𝐱}_m\parallel$ is the Euclidean distance between nodes $n$ and $m$, $n,m\in \mathcal{N}$, $N=|\mathcal{N}|$, and $A_{\mathrm{cell}}$ is the area of the cellular region of interest. Averaged across all extracted networks, we found $\mathrm{NNI}=0.83\pm 0.09$ (Fig. S3C). This $\mathrm{NNI}$ below $1$ indicates a stronger spatial clustering of nodes than expected by chance. This clustering is consistent with the visible actin-free regions in the cells (Fig. 2A). In addition, the extraction procedure does not allow nodes at neighboring pixels, violating the assumption of a uniform distribution of nodes (Fig. 1 and Materials and Methods).

To overcome these shortcomings, we introduced a second, more restricted null model in which all node positions of the original extracted network (Fig. S3D) were kept and only edge properties were shuffled (Fig. S3E). This procedure has been previously used in refs. 19 and 20 with a similar purpose, i.e., to study the biological relevance of properties in a grid approximation of the cytoskeleton. The null model preserves the total amount of filamentous actin and further leaves the connectedness and planarity of the original network unchanged. All investigated properties of the extracted networks showed the same significant differences for the second null model as for the first null model (Fig. S3F and Fig. 2I; independent two-sample $t$ test $P$ values $P_t<0.05$ were considered significant). Namely, the average path length and the $\mathrm{CV}$ of the path lengths were smaller than expected by chance, whereas the algebraic connectivity and the assortativity were larger than expected by chance. By construction, the distribution of edge angles in the second null model networks was identical to that in the original networks, yielding a unit ratio of the $\mathrm{CV}$ of edge angles. In conclusion, our two different null models yielded consistent results and were able to capture biologically relevant signals.

Moreover, as a negative control, we assessed the biological relevance of transport-related properties of cytoskeletal networks extracted from recordings of LatB-treated cells (Fig. S3 G and H and Fig. 2). Indeed, none of the studied properties of the cytoskeletal networks of the LatB-treated cells showed significant differences for either of the two null models (all $P_t\ge 0.05$). This absence of deviations from transport-related properties of randomized networks in chemically perturbed cells further supports our claim that the used null models are suitable to uncover biological design principles.

Finally, we assessed the robustness of our findings against random removal of edges as a model for errors in the network extraction procedure. To this end, for a given network, we created an ensemble of $20$ distorted networks by removing a certain fraction up to $20\%$ of randomly selected edges and, if necessary, by adding edges of minimum total Euclidean length to reobtain connected networks (as before and for comparability with our previous computations; Materials and Methods). Whereas such removal of edges may change the network topology and hence various network properties, most of our analyses concerned differential behavior of the network properties between two scenarios (e.g., control vs. treatment; Fig. 2). For instance, the number of connected components for the network times series of control and LatB-treated cells changed only very moderately with the fraction of removed edges (Fig. S3I; all $P_t<0.05$). Similarly, we compared ensembles of distorted networks from the network time series of the control cells to the distorted versions of their randomized counterparts (Fig. S3J; all $P_t<0.05$). We found that the average path lengths of the biological networks were consistently smaller than those of the randomized networks, even when the fraction of removed edges was increased up to $20\%$. Therefore, we validated the robustness of our findings against edge removal (Fig. 2 E and I).

Directionality of Actin Edges, Correlations of Actin Edge Properties, and Periodic Actin Networks.

Our analyses of the transport capacity of the actin cytoskeleton rely on the assumption of undirected edges, i.e., edges that allow bidirectional transport (Fig. 2). To elucidate the biological plausibility of this assumption, we constructed an additional type of Golgi flow networks (Fig. 4) by weighting the edges according to the average angle between the respective edge and the close-by Golgi track segments (Fig. S4A). For an edge that allows predominantly unidirectional transport, this average angle is expected to be below ${45}^{\circ }$ or above ${135}^{\circ }$. For both control and LatB-treated cells, around $45\%$ of the edges showed such predominantly unidirectional transport (Fig. S4B, Left) and we found no correlation between the unidirectionality of transport of an edge and its capacity, i.e., its thickness (Fig. S4B, Right). The computation of edge directionalities relies on a maximum cutoff distance of $8\hspace{0.17em}\mathrm{pixels}$ between actin edge and Golgi (Table S1). Because the cutoff distance affects the number and identity of Golgi associated with an edge, we also recomputed edge directionalities for cutoff distances of $12\hspace{0.17em}\mathrm{pixels}$ and $4\hspace{0.17em}\mathrm{pixels}$, respectively (Fig. S4C). We found that smaller cutoff distances led to higher fractions of unidirectional edges. This is expected as Golgi farther away from an actin bundle, and potentially closer to another bundle, are more likely to move in different directions (Fig. S5). Averaging of multiple such Golgi may lead to apparent bidirectional movement along a given edge. However, because smaller cutoff distances reduced the number of edges that were associated with any Golgi and led to poorer statistics, we kept a cutoff distance of $8\hspace{0.17em}\mathrm{pixels}$ throughout the remainder of this article (see Fig. 3 for a discussion of edge directionality).

When investigating the flow of Golgi along the actin cytoskeleton, we considered several local and global edge properties of the actin network as regressors or predictors of the Golgi flow (Fig. 4 and Table S1). Across the studied networks, there were on average $E=218\pm 52$ edges (dependent variables) whose flow properties were predicted using sets of five different actin edge properties (predictors). Because the number of predictors was much smaller than the number of dependent variables, overfitting was not an issue. Moreover, the reliability of the multiple linear regression results might be affected by colinearity of the predictors, which may be quantified by the condition number $n$. Because the condition number diverges for colinear predictors, the median was used to exclude the effect of outliers. Across the studied network, the median of the condition number $n=16.93\pm 4.36$ (median $\pm$ absolute median deviation) was below $20$, suggesting that our findings were not severely affected by colinearities (81). Analyzing the colinearity of the predictors in more detail, we computed the colinearity of any two actin edge properties $x$ and $x\prime$ (Fig. S4D), via

$$C_{x,x\prime }=\frac{{\sum }_{e=1}^E{a}_{e,x}{a}_{e,x\prime }}{{\left({\sum }_{e=1}^E{a}_{e,x}{a}_{e,x}\right)}^{\frac{1}{2}}{\left({\sum }_{e=1}^E{a}_{e,x\prime }{a}_{e,x\prime }\right)}^{\frac{1}{2}}}.$$ [S4]

Some of the studied actin edge properties were strongly correlated, such as the edge path betweenness and the edge flow betweenness (Fig. S4E). Although these two properties generally measure different aspects of the importance of an edge in the network context, they are identical for tree-like networks of unit edge capacities and lengths. We therefore quantified how tree-like our studied actin networks were by computing the ratio of their number of edges $E$ and the number of edges $N-1$ in the corresponding spanning trees (Fig. S4F),

$$t=\frac{E}{N-1}.$$ [S5]

Because the original actin networks are connected by construction, the ratio is larger than $1$. Indeed, there were on average only $t=1.03\pm 0.02$ times more edges in the actin networks than in the corresponding spanning trees, thus explaining the strong correlation between edge path and flow betweenness.

Finally, we note that the 2D rendering of images captured only the outer periclinal part of the actin cytoskeleton. This restriction introduces boundaries and, hence, bias in the extracted network as the cortical actin cytoskeleton follows the near-cylindrical shape of the hypocotyl cells. Because imaging 3D time series of the complete actin cytoskeleton is intrinsically challenging, we modeled the cylindrical geometry of the cortical cytoskeleton by periodically extending the original, 2D extracted network (Fig. S4G and SI Materials and Methods; see Fig. S2 for 3D data and analyses of the outer periclinal side of the actin cytoskeleton). We refer to these networks as periodic and to the original ones without boundary conditions as nonperiodic.

To model the cylindrical geometry of the cortical cytoskeleton we assumed that the cytoskeleton at the back of the cell is identical to its imaged counterpart at the front (see Results for a discussion of this assumption). We implemented the boundary conditions for arbitrary cell shapes by augmenting the original network (see mathbiol.mpimp-golm.mpg.de/CytoSeg/ for the open-source code of the implementation of periodic boundary conditions): We started from the cellular region of interest and created an empty graph $JG$, termed jump network, with nodes and node positions given by the pixels bounding this region. We computed the angle $\gamma$ of the cell axis as described above. Next, we rotated the node positions by an angle of $-\gamma$ and rounded the new coordinates to integer numbers. We added an edge to $JG$ for each pair of nodes with the same $x$ or $y$ coordinates given that the connecting line was fully contained within the region of the cell. These links allow jumps parallel and perpendicular to the cell axis and were therefore assigned edge attributes $a_{e,J}=1\equiv a_{e,\parallel }$ for parallel jumps and $a_{e,J}={10}^{-3}\equiv a_{e,\perp }$ for perpendicular jumps. Furthermore, we added edges between all neighboring boundary nodes to the jump network $JG$. We then coupled the nodes of the original actin network $G$ to the nodes of jump network $JG$ if their Euclidean distance $a_{e,E}$ was smaller than a threshold value of $10\hspace{0.17em}\mathrm{pixels}$. Finally, we recomputed the shortest path lengths for all pairs of nodes of the original network, using a modified Dijkstra’s algorithm (82) that increases the auxiliary path lengths by an arbitrarily large number if more than one parallel or perpendicular jump has been executed. Finally, we connected all nodes of the original actin network that were connected by a shortest path of less than $10\hspace{0.17em}\mathrm{pixels}$ in length and involved one parallel and/or perpendicular jump. Thus, the augmented network displays periodic, cylindrical boundary conditions. The properties of the new edges that were needed to assess the organization of the cytoskeletal network were computed as follows: The Euclidean and the filament arc lengths $a_{e,E}$ and $a_{e,F}$ were given by the sums of edge lengths for the respective shortest path, whereby jumps were excluded. The edge weight $a_{e,w}$ was given by the total intensity of the Gaussian filtered actin image, summed along the connecting lines of the path, again excluding jumps. The edge capacity $a_{e,c}$ and length $a_{e,l}$ were derived from these properties as before. For the augmented network with periodic boundary conditions, we recomputed the edge betweenness properties $a_{e,\mathrm{deg}}$, $a_{e,\mathrm{rank}}$, $a_{e,\mathrm{path}}$, and $a_{e,\mathrm{flow}}$. The procedure can be readily applied to realize periodic, cylindrical boundary conditions for cellular networks of arbitrary shapes.

Then, we repeated our correlation- and regression-based analyses for the periodic networks (Fig. S4 H and I). For the control cells, Golgi velocity and direction were more accurately predicted by the global edge rank rather than other local and global edge measures of the actin network. These results are in agreement with those for the nonperiodic networks above. Intriguingly, the prediction of Golgi direction and velocity was further improved for the periodic networks compared with the nonperiodic ones (Fig. S4J; independent two-sample $t$ test $P$ values $P_t<0.05$). For the LatB-treated cells, no difference in the coefficients of determination ($P_t=0.114$) was observed between the periodic and nonperiodic networks.

Our periodic boundary conditions conform to parsimony by assuming identical actin structures at the two sides. Although the actin cytoskeleton at the distant periclinal side of the cell may differ from that at the outer periclinal side, e.g., due to different mechanical forces inside the hypocotyl (see Results for a discussion), 3D imaging will be necessary to resolve such differences. However, imaging with sufficient spatiotemporal resolution, and without substantial photobleaching, to accurately capture the fast dynamics of actin rearrangement and Golgi movement in distant parts of the cell introduces major limitations. In addition, absorption and scattering of light by plant cell features will result in images of reduced quality and may not resolve fine AFs. Therefore, our implementation of periodic boundary conditions appears reasonable until high-quality data of the complete cortical actin cytoskeleton become available.

Passive and Active Transport of Golgi and Switching Between Filaments.

Regions of bundled actin may lead to higher average velocities of Golgi movement in root epidermal cells (10). To test whether our network-based framework supports these findings in partially elongated hypocotyl cells, we computed the average Golgi velocity and compared it to the overall actin bundling in the cell (Fig. S5A), measured by the average edge capacity (Fig. 2E). Indeed, actin bundling showed a high correlation with Golgi velocities for both control and LatB-treated cells (Pearson correlation coefficients $c_P\approx 0.4$ and $P$ values $P_P<0.05$).

Reasons for this correlation are manifold: Thick bundles are typically surrounded by fewer AFs that might slow down the Golgi (10, 21) (Figs. 1 and 2I). The high rigidity of bundles increases the run length of motor proteins (83), which may be further extended through binding of multiple motor proteins (84). Furthermore, the varying orientations in an array of fine AFs have been suggested to counteract cooperative movement of cargo (10). Thus, the average velocity of Golgi in hypocotyl cells is determined by the prevalence of actin bundles. However, studying overall actin bundling and average Golgi velocities does not consider the identity of individual AFs and the potential movement of Golgi along and between filaments.

To further quantify the movement of Golgi along and between filaments we distinguished three classes (Fig. S5B): (i) Golgi that maintained positions along an edge in the actin network between consecutive time steps (around $80\%$ and $90\%$ of $n\approx 40,000$ and $n\approx 25,000$ Golgi track segments for control and LatB-treated cells, respectively); (ii) Golgi that moved to a different edge along a path with angles smaller than ${90}^{\circ }$ (around $10\%$ and $5\%$ for control and LatB-treated cells, respectively) (because individual AFs, and especially bundles, rarely exhibit strong bending (33, 85), the Golgi in this class likely moved along the same AF between the given time steps); and (iii) Golgi that moved to an altogether different AF (around $10\%$ and $5\%$ for control and LatB-treated cells, respectively). For the LatB-treated cells, the fraction of Golgi in the first class was higher than for the control cells ($P_t<{10}^{-50}$). This increase is compatible with the general reduction of Golgi movement in LatB-treated cells (Fig. 3C).

To obtain this classification of Golgi, we assigned the start and end points of each track segment to their nearest edge in the actin network that we refer to as start and end edges, respectively. From the original actin network (Fig. S6C, green), we constructed the line graph (Fig. S6D, gray), i.e., a graph that has a node for each edge in the original network and a link between nodes that represent adjacent edges (ref. 32 and Table S1). We computed the shortest paths from the start to the end edges through the line graph of the actin network. For a given shortest path, we calculated the path length and the maximal angle between any two adjacent edges along the path. We then classified different types of Golgi movement (Fig. S6E; the classes are referred to as “stay,” “move,” and “jump”), depending on the minimum number of edges traversed by the Golgi and the associated maximal angle between traversed edges of the cytoskeletal network. The frequencies of Golgi in these different classes showed stationary Golgi, Golgi likely moving along a given filament, and Golgi switching between different, nonadjacent filaments (Fig. S5B). A closer inspection further showed that $<1\%$ of Golgi track segments in the move class traversed more than $10$ edges of the actin network. This supports the assumption that most Golgi in this class did not switch to a different filament but moved along a single filament.

Next, we investigated the relationship between Golgi velocity and redistribution across AFs. Both the maximal angle along the shortest path from the start to the end edge and its path length were moderately correlated with the velocity of the respective Golgi (Fig. S6 F and G; $c_P\approx 0.3$ and $c_P\approx 0.2$, respectively, and all $P_P<0.05$). Thus, as expected, faster Golgi were more likely to reach different AFs.

Switching of cargo between different, intersecting filaments has been previously shown for organelles tracking along microtubules in animal cells (7). However, these studies focused on movement and switching of cargo at filament intersections and did not investigate switching of cargo to nonadjacent filaments.

Despite recent studies, it remains unclear whether Golgi bodies are transported through the cell by direct interactions with motor proteins or indirectly via cytoplasmic streaming (54). The two scenarios are reflected in the behavior of neighboring Golgi tracks. Movement of close-by Golgi tracks in the same direction is indicative of indirect bulk flow. In contrast, movement in opposite directions suggests direct actomyosin-based transport of Golgi. To distinguish these two cases, we measured the angles between any two segments of different Golgi tracks within the same time step (referred to as pairwise angles) in dependence of their spatial separation. For the LatB-treated cells, the frequency of a given pairwise angle of Golgi movement correlated with neither the angle nor the spatial separation of the two Golgi track segments (Fig. S5H, Lower Right). In contrast, the Golgi movement displayed mainly parallel or antiparallel trajectories in control cells (Fig. S5H, Upper Right), consistent with Golgi movement occurring preferentially along the major cell axis (Fig. 3D). Even for small distances below $1\mu \mathrm{m}$ between different Golgi, a substantial fraction of Golgi trajectories showed antiparallel movement at any given time (Fig. S5H, Upper and Lower Left; $45\%$ of $n\approx 5,000$ pairwise angles across the studied cells and imaging periods). As the low Reynolds numbers of the cytoplasm favor laminar streaming (1), this antiparallel movement of close-by Golgi contradicts the assumption of indirect, cytoplasmic-streaming–induced movement and instead supports myosin-based transport of a substantial fraction of Golgi bodies.

In conclusion, our data suggest that switching of Golgi to adjacent AFs is myosin dependent, whereas switching to nonadjacent AFs is due to cytoplasmic streaming that may carry the Golgi over large distances.

Golgi Wiggling in Dependence of Actin Cytoskeleton and Consistency Across Cells.

In our quantitative analysis of cellular transport dynamics, we combined automated tracking data of Golgi with automated extraction of actin cytoskeletal networks (Fig. 3). Here, we discuss two of these analyses in more detail: the investigation of Golgi wiggling in dependence of actin structures and the movement of Golgi along and between filaments. Moreover, we present results on the cell-to-cell variability of Golgi movement across different developmental stages.

We confirmed that the Golgi wiggling behavior is not Golgi specific (10) and showed further that the prevalence of Golgi wiggling behavior is stationary over the course of the recording period and does not depend on the distance from the actin cytoskeleton (Fig. 3 F–I). However, the actin cytoskeleton is composed of filaments and bundles of varying thickness and it has been suggested that arrays of fine actin filaments promote wiggling (10). To test this hypothesis in detail, we used our extracted, weighted network representation of the actin cytoskeleton. We constructed a Golgi flow network in which the edges of the actin network were assigned a measure of Golgi wiggling (Fig. S6A and Table S1). To this end, for each edge, we considered all Golgi in a vicinity of $8\hspace{0.17em}\mathrm{pixels}$ of the edge and computed their average relative angle of movement, where angles above ${90}^{\circ }$ were considered as wiggling behavior. For both control and LatB-treated cells, this average relative angle showed no significant correlation with the capacities of the actin edges, i.e., their average thickness (Fig. S6B). In particular, the average relative angles approached ${90}^{\circ }$ for larger edge capacities, which may be explained by the larger number of Golgi close to thicker edges (Fig. 4I; linear regression yielded a slope of $s=51$). Therefore, assuming that the relative angles were distributed randomly across Golgi tracks, the $\mathrm{SD}$ of average relative angle decreased and the expected average relative angle converged to ${90}^{\circ }$ (Fig. S6B, dotted black lines). These findings suggest that the thickness of close-by actin bundles does not influence the Golgi wiggling behavior. However, this is still compatible with the observation that arrays of fine actin filaments increase Golgi wiggling (10) because the thickness of individual filaments studied here does not capture the surrounding actin environment.

In addition to the relative angles of Golgi tracks, we studied the streaming coefficient as another measure of Golgi wiggling (10, 11). For a given track and time step $i$, we computed the streaming coefficient over a sliding window of four time steps via

$$c_i=\underset{\mathrm{net}\mathrm{velocity}}{\underbrace{\frac{\parallel {𝐱}_{i+2}-{𝐱}_{i-2}\parallel }{4\cdot 2\mathrm{s}}}}\cdot \underset{\mathrm{directionality}\mathrm{factor}}{\underbrace{\frac{\parallel {𝐱}_{i+2}-{𝐱}_{i-2}\parallel }{{\sum }_{j=-2}^1\parallel {𝐱}_{i+1+j}-{𝐱}_{i+j}\parallel }}},$$ [S6]

which is large for fast Golgi that move straight in one direction. Therefore, in contrast to the relative angle (Eq. S24), the streaming coefficient combines information about Golgi velocity and directionality. Nevertheless, across Golgi tracks of all studied cells, relative angle and streaming coefficient showed a moderate but highly significant negative correlation (Fig. S6C; $c_P=-0.323$ and $P_P<0.05$). This negative correlation is plausible because small relative angles imply straight movement and are furthermore often correlated with higher velocities (Fig. 3 C and F), leading to large streaming coefficients. This correlation suggests that using the streaming coefficient as a measure of Golgi wiggling leaves our findings on the persistence of Golgi wiggling largely unchanged.

We note that Golgi size is strongly correlated with the average Golgi intensity (Fig. S6D; Pearson correlation coefficients $c_P\approx 0.9$ and $P$ values $P_P<0.05$) so that Golgi intensity may be used as an estimator of Golgi size (Fig. 4).

Furthermore, we analyzed Golgi movement in hypocotyl cells at different developmental stages, i.e., in growing and fully elongated cells both in untreated control plants and after LatB treatment (Fig. S6E). A detailed description of the additional recordings is given in SI Materials and Methods and Fig. S1. Indeed, the studied features of Golgi movement were nearly identical for growing and fully elongated hypocotyl cells and affected only by the drug treatment (Fig. S6 F–K; compare control cells in green and blue and LatB-treated cells in orange and yellow). Moreover, although Golgi movement is generally highly variable over time and across cells, the low-level features of Golgi movement studied here were very consistent and uniform across cells (Fig. S6 F–K; compare solid lines and error bars indicating mean $\pm$ $\mathrm{SD}$). Thus, we are confident that our analyses capture genuine and biologically relevant features of actin-based Golgi transport in hypocotyl plant cells.

List of Studied (Edge) Properties of Actin and Golgi Flow Networks.

After extracting the actin cytoskeletal networks from image data, we computed various seminal properties to quantify cytoskeletal phenotypes and evaluate transport efficiency (Fig. 2). The actin cytoskeleton at a given time is represented by a weighted, undirected network $G=(\mathcal{N},\mathcal{E})$ of $N=|\mathcal{N}|$ nodes with positions ${𝐱}_n\in {ℝ}^2$ or ${ℝ}^3$, $n\in \mathcal{N}$, and $E=|\mathcal{E}|$ edges with weightings $a_e$, $e=(n,m)\equiv (m,n)\in \mathcal{E}$. We considered different weightings of the actin edges (Table S1): The Euclidean length $a_{e,E}$ of an edge $e$ is the Euclidean distance between its two nodes and its filament length $a_{e,F}$ is given by the arc length of the curvilinear filament segment (Materials and Methods). In addition, we derived the filament bending as the ratio of filament and Euclidean length,

$$a_{e,B}\equiv B=a_{e,E}^{-1}{a}_{e,F},$$ [S7]

which is close to one for straight filaments (compare to the definition of convolutedness in ref. 85). The edge weight $a_{e,w}$ is the intensity of the image summed along the filament segment. The edge capacity,

$$a_{e,c}=a_{e,F}^{-1}{a}_{e,w},$$ [S8]

captures the average weight per unit length of the filament segment and reflects the average thickness of a filament segment. The edge length,

$$a_{e,l}=a_{e,c}^{-1},$$ [S9]

is given by the inverse capacity. Moreover, we quantified the alignment of filament segments by the angle between the respective edge and the cell axis vector ${𝐱}_{\mathrm{cell}}$,

$$a_{e\equiv (n,m),a}=\arccos \left(\frac{\left({𝐱}_n-{𝐱}_m\right){𝐱}_{\mathrm{cell}}}{\parallel {𝐱}_n-{𝐱}_m\parallel \parallel {𝐱}_{\mathrm{cell}}\parallel }\right).$$ [S10]

The organization of the extracted networks was quantified by various seminal network properties (Table S1): To study the fragmentation of a given network, we removed all edges with capacities below the $50\mathrm{t}\mathrm{h}$ percentile and computed the number of connected components,

$$F,$$ [S11]

which is lower for more strongly connected networks. As a measure of actin bundling across the cell, we computed the average edge capacity,

$$\mathrm{E}\left[a_c\right]=E^{-1}\sum _{e\in \mathcal{E}}{a}_{e,c}.$$ [S12]

As a measure of heterogeneity of the actin distribution, we calculated the assortativity,

$$A=\frac{1}{2E}\sum _{n\in \mathcal{N}}\sum _{m\in \mathcal{N}}\left(a_{(n,m),c}-\frac{d_n{d}_m}{2E}\right)d_n{d}_m,$$ [S13]

which is positive if nodes are preferentially connected to nodes of similar degrees $d_n={\sum }_{m=1}^N{a}_{(n,m),c}$, hence detecting regions of spatially clustered bundling of the actin cytoskeleton.

Moreover, the average shortest path length was computed as a standard measure of transport efficiency,

$$\mathrm{E}\left[L\right]=\frac{1}{2N\left(N-1\right)}\sum _{n\in \mathcal{N}}\sum _{\begin{array}{c}\hfill m\in \mathcal{N}\hfill \\ \hfill m>n\hfill \end{array}}{L}_{n,m},$$ [S14]

where $L_{n,m}={\min }_{\mathcal{P}\in {\mathcal{P}}_{n,m}}{\sum }_{e\in \mathcal{P}}{a}_{e,l}$ and ${\mathcal{P}}_{n,m}$ is the set of all paths from node $n$ to $m$ (32). The dispersal of the transport efficiency was measured by the $\mathrm{CV}$ of the shortest path lengths,

$$\mathrm{CV}\left[L\right]=\frac{\mathrm{SD}\left[L\right]}{\mathrm{E}\left[L\right]}.$$ [S15]

The robustness of the transportation network against disruptions was evaluated by the algebraic connectivity,

$$C={\lambda }_2,$$ [S16]

which is the second smallest eigenvalue of the graph Laplacian ${\mathcal{L}}_G=D_G-A_G$ and is zero for a disconnected network (32). Here, $D_G$ is the diagonal matrix of the capacity-weighted node degrees and $A_G$ is the capacity-weighted connectivity matrix of $G$. Finally, the alignment of filament segments in the cell was measured using the $\mathrm{CV}$ of edge angles,

$$\mathrm{CV}\left[a_a\right]=\frac{\mathrm{SD}\left[a_a\right]}{\mathrm{E}\left[a_a\right]}.$$ [S17]

To correlate the flow of organelles with the structure of the actin network, we derived two networks with identical structure and different edge weightings that we refer to as actin and Golgi flow networks, respectively (Fig. 4 and Table S1). As a (local) edge property of the actin network we studied the capacity $a_{e,c}$. Moreover, we investigated the (global) importance of a given edge in the actin network context, using several betweenness measures. First, we introduced the edge degree as a (semilocal) measure of actin organization,

$$a_{e,\mathrm{deg}}=\sum _{\begin{array}{c}\hfill f\in \mathcal{E}\hfill \\ \hfill e\sim f\hfill \end{array}}{a}_{f,c},$$ [S18]

where $e\sim f$ indicates adjacent edges. This measure may be conveniently computed in the line graph $LG$ of $G$, whereby each node in $LG$ represents an edge in $G$ and two nodes in $LG$ are adjacent if the corresponding edge shares a node in $G$ (32). In the line graph $LG$, the edge degree $a_{e,\mathrm{deg}}$ simply corresponds to the capacity-weighted degree of the node $e$. Analogously, we computed another famous (global) property of an edge $e$ in the line graph $LG$ with capacity-weighted connectivity matrix $A_{LG}$, i.e., its page rank

$$a_{e,\mathrm{rank}}=\alpha \sum _{f\in \mathcal{E}}{A}_{LG,e,f}{D}_{LG,e,f}^{-1}{a}_{f,\mathrm{rank}}+1,$$ [S19]

where $D_{LG}$ is the diagonal matrix of capacity-weighted node degrees of the line graph and classically $\alpha =0.85$ (32). Moreover, we computed the shortest path edge betweenness that counts the number of shortest paths between any two nodes in the network that pass through a given edge,

$$a_{e,\mathrm{path}}=\sum _{\begin{array}{c}\hfill n,m\in \mathcal{N}\hfill \\ \hfill n\ne m\hfill \end{array}}\{\begin{array}{cc}1\hfill & ,\mathrm{if}e\in {\mathcal{P}}_{n,m}^{\mathrm{shortest}}\hfill \\ 0\hfill & ,\mathrm{otherwise},\hfill \end{array}$$ [S20]

where ${\mathcal{P}}_{n,m}^{\mathrm{shortest}}$ is the shortest path (in terms of the edge length $a_{e,l}$) between nodes $n$ and $m$. Similarly, we computed the maximum current flow edge betweenness that is the maximum flow (in terms of the edge capacity $a_{e,c}$) across an edge summed over all pairs of nodes that are treated as unit sinks and sources of the flow, respectively,

$$a_{e,\mathrm{flow}}=\sum _{\begin{array}{c}\hfill n,m\in \mathcal{N}\hfill \\ \hfill n\ne m\hfill \end{array}}{\mathcal{F}}_{n,m,e},$$ [S21]

where ${\mathcal{F}}_{n,m,e}$ is the maximum flow between nodes $n$ and $m$ across edge $e$.

The studied edge properties of the introduced Golgi flow network considered the movement of Golgi close to an edge (Table S1). At a given time, the center points of Golgi track segments are given by ${𝐲}_{t\equiv (u,v)}=2^{-1}({𝐱}_u+{𝐱}_v)$, $t\in \mathcal{T}$, where ${𝐱}_u$ and ${𝐱}_v$ denote the endpoints of the track segment $t\equiv (u,v)$. The minimum distance between the track segments’ center point ${𝐲}_t$ and an edge $e$ was computed as

$$d_{t,e\equiv (n,m)}=\underset{\lambda \in \left[\mathrm{0,1}\right]}{\min }\parallel {𝐲}_t-\left({𝐱}_n+\lambda \left({𝐱}_m-{𝐱}_n\right)\right)\parallel .$$ [S22]

Then, as a first simple measure of Golgi flow, we computed the number of close-by Golgi,

$$g_{e,n}=\sum _{t\in \mathcal{T}}\mathrm{\Theta }\left(d_{\mathrm{thres}}-d_{t,e}\right),$$ [S23]

where $d_{\mathrm{thres}}=8\hspace{0.17em}\mathrm{pixels}$ throughout this article and $\mathrm{\Theta }(d)=1$ if $d\ge 0$ and $\mathrm{\Theta }(d)=0$ otherwise is the step function. To measure the wiggling behavior of Golgi, we computed the angle between consecutive track segments,

$$g_{e,w}=g_{e,n}^{-1}\sum _{t\in \mathcal{T}}\mathrm{\Theta }\left(d_{\mathrm{thres}}-d_{t,e}\right){\omega }_t,$$ [S24]

where ${\omega }_{t\equiv (u,v)}=\arccos \left(\frac{\left({𝐲}_u-{𝐲}_v\right)\cdot \left({𝐲}_{u\prime }-{𝐲}_{v\prime }\right)}{\parallel {𝐲}_u-{𝐲}_v\parallel \parallel {𝐲}_{u\prime }-{𝐲}_{v\prime }\parallel }\right)$ and ${𝐲}_{u\prime }$ and ${𝐲}_{v\prime }$ are the endpoints of the track segment in the next time step. If there was no next track segment in the track, we set ${\omega }_t=0$. Moreover, the average intensity ${\iota }_t$ of the Golgi was used as a measure for their size (Fig. S6),

$$g_{e,i}=g_{e,n}^{-1}\sum _{t\in \mathcal{T}}\mathrm{\Theta }\left(d_{\mathrm{thres}}-d_{t,e}\right){\iota }_t.$$ [S25]

The directionality of the Golgi track segments with respect to the respective actin edges was computed as

$$g_{e,d}=g_{e,n}^{-1}\sum _{t\in \mathcal{T}}\mathrm{\Theta }\left(d_{\mathrm{thres}}-d_{t,e}\right){\delta }_{t,e},$$ [S26]

where ${\delta }_{t\equiv (u,v),e\equiv (n,m)}=\frac{\left({𝐱}_n-{𝐱}_m\right)\cdot \left({𝐲}_u-{𝐲}_v\right)}{\parallel {𝐱}_n-{𝐱}_m\parallel \parallel {𝐲}_u-{𝐲}_v\parallel }$. The average Golgi velocity in the vicinity of an edge was calculated as

$$g_{e,v}=g_{e,n}^{-1}\sum _{t\in \mathcal{T}}\mathrm{\Theta }\left(d_{\mathrm{thres}}-d_{t,e}\right){\nu }_t,$$ [S27]

where ${\nu }_{t\equiv (u,v)}=\parallel {𝐲}_u-{𝐲}_v\parallel$. Finally, combinations of these edge properties (${\iota }_t$, ${\delta }_{t,e}$, ${\nu }_t$) were calculated using their products, e.g.,

$$g_{e,d+v}=g_{e,n}^{-1}\sum _{t\in \mathcal{T}}\mathrm{\Theta }\left(d_{\mathrm{thres}}-d_{t,e}\right){\delta }_{t,e}\cdot {\nu }_t,$$ [S28]

for the combined Golgi direction and velocity.