Abstract
While slowly turning the ends of a single molecule of DNA at constant applied force, a discontinuity was recently observed at the supercoiling transition, when a small plectoneme is suddenly formed. This can be understood as an abrupt transition into a state in which stretched and plectonemic DNA coexist. We argue that there should be discontinuities in both the extension and the torque at the transition, and provide experimental evidence for both. To predict the sizes of these discontinuities and how they change with the overall length of DNA, we organize a theory for the coexisting plectonemic state in terms of four length-independent parameters. We also test plectoneme theories, including our own elastic rod simulation, finding discrepancies with experiment that can be understood in terms of the four coexisting state parameters.
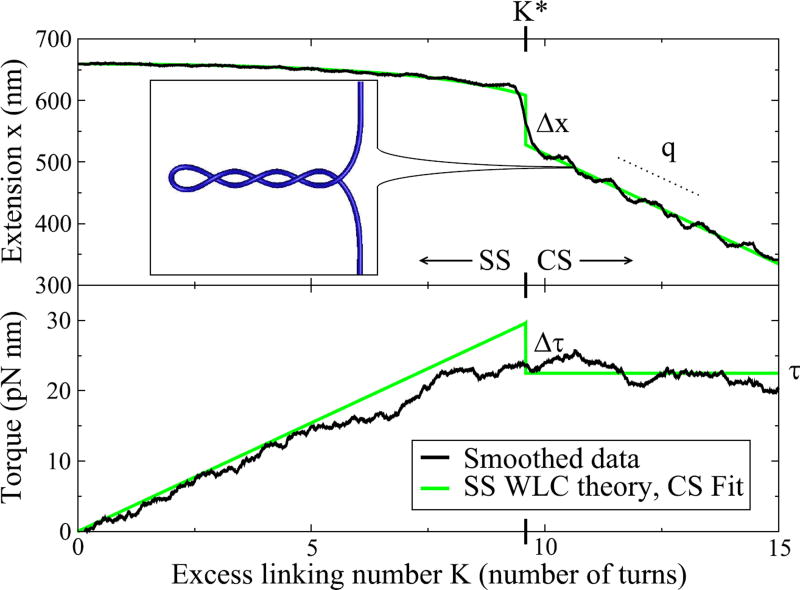
A recent experiment performed by Forth et al. [1] has shown a novel effect in DNA supercoiling: a discontinuity in the transition from stretched to partially-supercoiled DNA (see Fig. 1). Using an optical trap, as the two ends of a single molecule of DNA are pulled with a constant force and slowly twisted, there is a sudden jump in the distance between the two ends when a supercoiled structure known as a plectoneme (inset of Fig. 1) is formed.
FIG. 1.
Extension and torque as a function of linking number K, for L = 2.2 kbp at F = 2 pN. Black lines show data from Ref. [1], smoothed using a “boxcar” average of nearby points, with window size 1/4 turn for the extension data and 4 turns for the torque data. The light blue lines show worm-like chain (WLC) predictions below the transition [in the unsupercoiled “stretched” state (SS)], and fits to the data after the transition [in the “coexisting” state (CS) with both plectonemic and stretched DNA], linear for the extension and constant for the torque. The size of the torque jump, not directly visible in the smoothed data, is implied by the torque for the WLC, the CS fit, and the transition linking number K* in the extension data. Inset: Simulated DNA showing the CS of a plectoneme and straight DNA, ignoring thermal fluctuations. The ends of the DNA are held with fixed orientation and pulled with a constant force F, here 2 pN.
Below the transition, the DNA is in a fluctuating “stretched” state (SS), which is described nicely by the well-known worm-like chain (WLC) theory [2]. Above the transition, the situation is well-described as phase coexistence between usual stretched DNA and a plectoneme, which can store more of the added turns (linking number) as ‘writhe’ [3]. As linking number increases, a linearly-increasing fraction of DNA becomes part of the plectoneme. In this coexisting state (CS), the extension decreases linearly with linking number, and the torque remains constant.
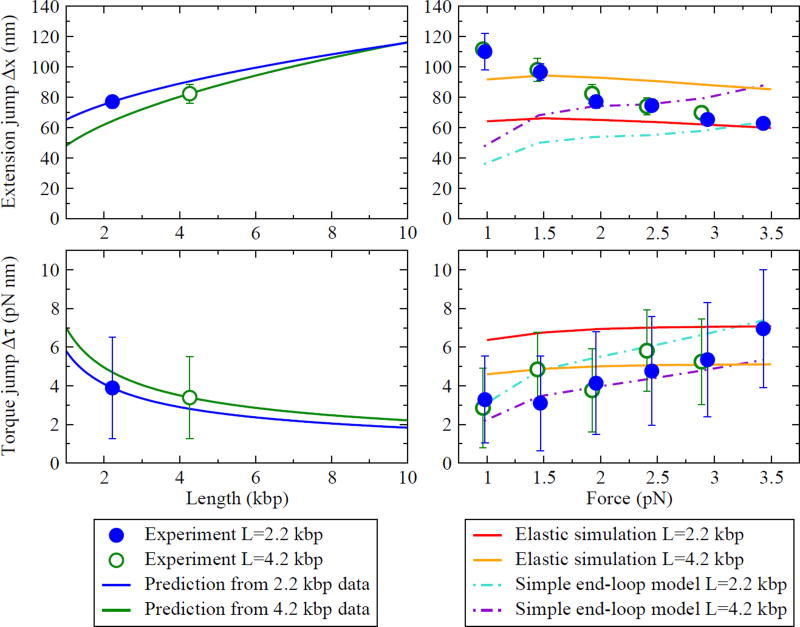
At the transition between the SS and CS, Forth et al. observed a discontinuity in the extension [1]. Attempting to model this transition, we were led to explore two puzzling aspects of the data. First, two overall DNA lengths were tested (2.2 kbp and 4.2 kbp) and found to have the same size extension jump Δx (circles in Fig. 4). There is not, however, any simple physical argument to suggest that the size of the jump should be independent of length. Second, the torque was also directly measured, and no discontinuity Δτ was observed in the filtered torque data (see Fig. 1). Interpreting the extension jump as an abrupt transition, however, we expect that there should also be a jump in the torque.
FIG. 4.
(Left) Predicted length-dependence of the extension and torque jumps at F = 2 pN. Using the CS parameters extracted from the experiment, Eqs. (11)–(12) predict the L-dependence of Δx and Δτ. The circles show experimentally-measured values [with the torque jump here calculated from K* using Eq. (11)]. The lines show the predictions from data collected at two different overall DNA lengths L. (Right) Force-dependence of the extension and torque jumps, and predictions from two models. The Marko model does not include discontinuities at the transition. The elastic rod simulation and the simple end-loop model produce discontinuities of the correct order of magnitude, but neither fits the data well. Discrepancies can be attributed to misestimates of the four CS parameters in Fig. 3.
Here we aim, then, to use models of plectonemic DNA supercoiling to predict the magnitudes of these discontinuities, Δx and Δτ. We will first show that models of the CS can be specified by four force-dependent but length-independent parameters. We will then write Δx and Δτ in terms of these parameters, thus determining their expected length-dependence. We will find that we expect Δx in general to vary with length, and based on measured values, this length dependence should be detectable with further experiments. We will also see that, by time-averaging near the transition, a torque jump of the predicted size can be experimentally detected. Finally, we will use our formulation to test various models of plectonemes, finding that there is currently no model that fits all the data.
What determines where the transition occurs? Forth et al. showed that the DNA hops between two states at the transition, spending equal time in each state under thermal fluctuations [1]. This demonstrates that the two states are stable and that they have the same free energy at the critical linking number K* (where our free energy is defined by the ensemble with constant applied force and linking number). We will therefore need models for the free energy ℱ and extension x of both the SS and CS.
The properties of stretched, unsupercoiled DNA are well-established. At small enough forces and torques that avoid both melting and supercoiling, DNA acts as a torsional spring with twist elastic constant C [11]: , where K is the added linking number, L is the overall (basepair) length of DNA, and C is measured to be 89 ± 3 nm×kT, with the thermal energy kT = 4.09 pN nm for this experiment (at 23.5°C). Differentiating with respect to K gives the torque: . The extension of unsupercoiled DNA is shortened by thermal fluctuations, and in the relevant force regime is approximately given by xSS = ξ(τSS)L, where [4]
| (1) |
B = 43±3 nm×kT is the DNA’s bending elastic constant, and F is the force applied to the ends of the DNA.
Since supercoiling theories must include contact forces, they are less amenable to traditional theoretical methods. Current approaches range from describing the plectoneme as a simple helix [5–7] to using a more phenomenological approach [3]. For any theory of super-coiling, however, we find that we can simply describe the properties of the CS by using scaling properties to usefully parameterize the dependence on K and L.
First, as expected for a situation in which two phases of DNA coexist at constant F and L, experiments suggest that both ℱCS and xCS are linear functions of added linking number K. We also expect ℱCS and xCS to be linear in L: Since the CS has both constant force and torque, adding length will add stretched DNA with free energy and extension linear in L. As shown below, these scaling properties allow us to specify ℱCS and xCS with four force-dependent values: their slopes with respect to K (τ and q), along with K = L = 0 offsets (ℱ0 and x0). A theory of the CS must then predict these four values.
To show this, we first write down the linear scaling of the free energy and extension with linking number. For any δK that does not take the system out of the CS,
| (2) |
| (3) |
where q is the slope of extension versus linking number in the CS. Next, to find the scaling with increasing L, we imagine adding a piece of stretched DNA of length δL at the coexisting torque (keeping the system in a stable CS). This also adds an amount of linking number that scales with δL,
| (4) |
which we will have to unwind to get back to the original K. First adding the piece of stretched DNA, we find
| (5) |
We then unwind to find the dependence on L only, obtaining
| (6) |
Similarly for the extension, we have [using ξ(τ) from Eq. (1)]
| (7) |
which upon unwinding becomes
| (8) |
Combining Eqs. (2) and (3) with Eqs. (6) and (8), we can write the free energy and extension of the CS as linear in K and L, each with a slope and an intercept:
| (9) |
| (10) |
Note that C and ξ(τ) are known from experiments on stretched DNA, leaving the four anticipated force-dependent, length-independent quantities to be described by a theory of supercoiling: τ, q, ℱ0, and x0.
Finally, we connect these four parameters to the experimental observables. Easiest are τ and q, which are directly measured. Next, the linking number K* at the transition is found by equating the CS free energy with that of the SS: ℱCS(K*, L) = ℱSS(K*, L) implies
| (11) |
where Δτ is the jump in the torque at the transition.
Lastly, inserting K* from Eq. (11) into Eq. (10), we find the change in extension at the transition:
| (12) |
We conclude that four force-dependent values are enough to specify the behavior of the CS. The slope of the extension curve q and the coexisting torque τ describes the helical plectoneme phase and how it coexists with the stretched phase. The intercepts ℱ0 and x0 describe the extra free energy and extension necessary to form the interface between the phases—the end loop and tails of the plectoneme.[12]
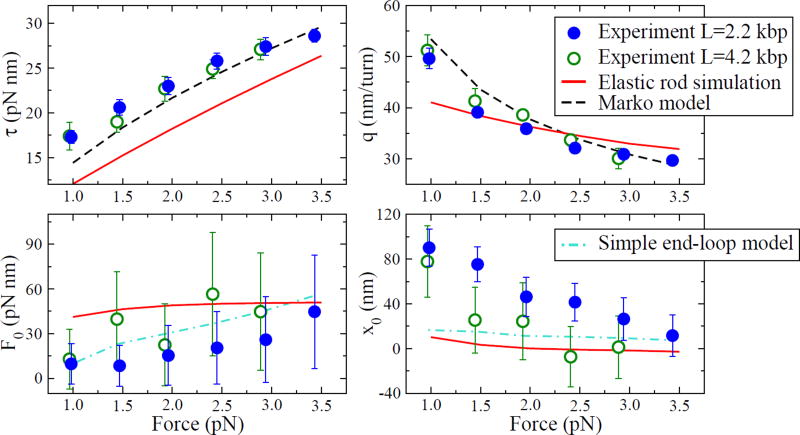
Given experimental data (τ, q, K*, and Δx), we can solve for the four CS parameters. The results from Ref. [1] are shown as circles in Fig. 3 for the two overall DNA lengths tested. Note that, neglecting sequence dependence or other differences between the two DNA molecules tested, the results should be independent of L. However, x0 for the two lengths do not agree within experimental error bars at some forces. The difference between the two lengths could be due to sequence dependence, since the elastic properties of DNA are known to vary for different sequences.
FIG. 3.
The four parameters describing the CS, as a function of applied force. The circles represent values calculated from experimental data taken at two different overall DNA lengths L. The coexisting torque τ and the slope of extension versus linking number q describe the coexistence of the plectoneme helix and the stretched phase. The values ℱ0 and x0 describe the extra free energy and extension necessary to form the end loop and tails of the plectoneme. All four values should be independent of length—we suspect the discrepancy in x0 between the two measured lengths could be due to sequence-dependence. Model predictions for our simulation and Marko’s model [3] are shown as solid and dashed lines, respectively. The simple end-loop model uses average τ and q values from the experiment to predict ℱ0 and x0, shown as dot-dashed lines.
With this data, and independent of any explicit plectoneme model, we can also predict the length-dependence of the discontinuities, as shown in Fig. 4. We expect that this length-dependence should be detectable with further experiments.
Note that here we are solving for the experimental size of the torque jump using the observed K* and τ using Eq. (11). We also find direct evidence of Δτ in the data by averaging over the torque separately in the SS and CS near the transition (see Fig. 2). With data taken at F = 2 pN and L = 2.2 kbp, we find Δτ = 2.9 ± 0.7 pN nm, in good agreement with the prediction from K* (3.9 ± 2.6 pN nm; see Fig. 4).
FIG. 2.
Hopping between the SS and CS near the supercoiling transition, for the same conditions as Fig. 1. As linking number K is slowly increased near K*, thermal fluctuations induce hopping between states with (CS) and without (SS) a plectoneme. Averaging over these two states gives a direct way of measuring the torque jump: we first separate the data into SS (black) and CS (red) by setting a threshold for the extension, and then average each set of data near the transition, producing the black and red bars on the right side of the figure. Using multiple traces gives an average torque jump of Δτ = 2.93 ± 0.68 pN nm for L = 2.2 kbp at F = 2 pN.
We can now test various plectoneme models by calculating their predictions for the four CS parameters, which in turn give predictions for the experimental observables. The results are shown as lines in Fig. 3 and Fig. 4.
First, we test a phenomenological model recently proposed by John Marko [3]. The plectoneme is modeled as a phase with zero extension and an effective twist stiffness, P, that is smaller than the twist stiffness C of stretched DNA. Shown as dashed lines in Fig. 3, the Marko model predicts the coexisting torque and extension slope well, with P as the only fit parameter (we use P=26 nm). However, the Marko model (along with all other models that include only terms in the free energy proportional to L) produces ℱ0 = 0 and x0 = 0.
In order to have a discontinuous transition, we must include the effects of the end loop and tails of the plectoneme. To accomplish this, we use an explicit simulation of an elastic rod, with bend and twist elastic constants set to the known values for DNA. We must also include repulsion between nearby segments to keep the rod from passing through itself. Physically, this repulsion has two causes: screened Coulomb interaction of the charged strands and the loss of entropy due to limited fluctuations of the DNA in the plectoneme. We use the repulsion free energy given in Ref. [6], which is derived for the helical part of a plectoneme. Since we also include straight parts of the DNA that should not have the same entropic interaction, we cut off the entropic potential at a distance of 2B/kT, where the argument for the form of the potential breaks down [6].
We find that the simulation does form plectonemes (see inset of Fig. 1), and we can extract the four CS parameters, shown as solid lines in Fig. 3. Since ℱ0 and x0 are nonzero, we find discontinuities in the extension and torque at the transition; their magnitudes are plotted versus external force in Fig. 4. We note that while the simulation predicts the correct qualitative behavior, including discontinuities, it does not fit the experimental observables quantitatively. This can be traced back to poor fits to the four CS parameters in Fig. 3.
Since the parts of the CS behavior that describe the shape of the helical part of the plectoneme (τ and q) are more well-understood than those that describe the endloop and tails (ℱ0 and x0), a simple model of the end-loop giving ℱ0 and x0 in terms of τ and q could be useful. The simplest such model would assume that creating a plectoneme requires an additional circular loop of DNA. Minimizing the total free energy for this simple end-loop model gives
| (13) |
| (14) |
where Wrloop is the writhe taken up by the loop. For a perfect loop, Wrloop = 1, and Wrloop < 1 for a loop with two ends not at the same location. We chose Wrloop = 0.8 as a reasonable best fit to the data. Using the experimentally measured values for τ and q, the predictions are shown as dot-dashed lines in Fig. 3 and Fig. 4.
The largest discrepancy between the plectoneme models and experiment is at low applied force, where all the models severely underestimate x0. Via Eq. (12), this leads to an underestimate of the extension jump at low forces. We do expect fluctuations and entropic effects to become more important at these lower forces, and our rough treatment of entropic effects may be causing this discrepancy [13]. A more sophisticated model that includes fluctuations explicitly would be a useful next step.
Recent experiments have shown that bending with a radius of curvature less than about 4 nm can cause DNA minicircles to kink [8]. In our simulations, the minimum radius of curvature (at the tip of the plectoneme) ranged from 6.1 nm at F=1 pN to 3.3 nm at F=3.5 pN. Kinking and other corrections to simple elastic bending may therefore be important. Even so, including kinking in our simple end-loop model appears to produce a smaller x0, taking us further from the experimental values.
We have shown that four length-independent parameters can usefully describe any theory of the CS. We find that the extension and torque jumps at the transition should be length-dependent, in a potentially measurable way. Finally, current plectoneme models do not fit the data well, and the poor estimates of the size of the extension jump can largely be attributed to an underestimate of the extra extension x0 absorbed by the plectoneme, especially at low forces.
Acknowledgments
BCD was supported by NSF Grant DMR-0705167. MDW wishes to acknowledge support from NIH (GM059849), NSF (MCB-0820293), and the Cornell Nanobiotechnology Center.
References
- 1.Forth S, Deufel C, Sheinin MY, Daniels B, Sethna JP, Wang MD. Phys. Rev. Lett. 2008;100:148301. doi: 10.1103/PhysRevLett.100.148301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Marko JF, Siggia ED. Macromolecules. 1995;28:8759. [Google Scholar]
- 3.Marko JF. Phys. Rev. E. 2007;76:021926. doi: 10.1103/PhysRevE.76.021926. [DOI] [PubMed] [Google Scholar]
- 4.Moroz JD, Nelson PC. Macromolecules. 1998;31:6333. [Google Scholar]
- 5.Clauvelin N, Audoly B, Neukirch S. Macromolecules. 2008;41:4479. [Google Scholar]
- 6.Marko JF, Siggia ED. Phys. Rev. E. 1995;52:2912. doi: 10.1103/physreve.52.2912. [DOI] [PubMed] [Google Scholar]
- 7.Neukirch S. Phys. Rev. Lett. 2004;93:198107. doi: 10.1103/PhysRevLett.93.198107. [DOI] [PubMed] [Google Scholar]
- 8.Du Q, Kotlyar A, Vologodskii A. Nucleic Acids Res. 2008;36:1120. doi: 10.1093/nar/gkm1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moroz JD, Nelson P. Proc. Natl. Acad. Sci. USA. 1997;94:14418. doi: 10.1073/pnas.94.26.14418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fain B, Rudnick J, Ostlund S. Phys. Rev. E. 1997;55:7364. [Google Scholar]
- 11.As described in Ref. [9], C is renormalized to a smaller value by bending fluctuations. We use C calculated from the torque measured in the experiment, which gives its renormalized value.
- 12.Note, however, that this analysis does not assume any specific model for the supercoiling, or even whether the supercoiling produces plectonemes. We only assume that the supercoiled state is localized enough that the ends of the DNA behave like the usual stretched state.
- 13.A hint as to what is wrong here may come also from the unexpectedly slow hopping between the SS and CS at the transition, which has a frequency on the order of 1 Hz (see Fig. 2). If the saddle configuration between the two states is of the form found in Ref. [10], this corresponds to barrier energies of about 5 kT. This is much too low to account for the slow hopping; assuming an attempt rate of 109 Hz, we would expect a barrier of 20 kT.