3D single-molecule tracking enables direct hybridization kinetics measurement in solution

Abstract

Single-molecule measurements of DNA hybridization kinetics are mostly performed on a surface or inside a trap. Here we demonstrate a time-resolved, 3D single-molecule tracking (3D-SMT) method that allows us to follow a freely diffusing ssDNA molecule in solution for hundreds of milliseconds or even seconds and observe multiple annealing and melting events taking place on the same molecule. This is achieved by combining confocal-feedback 3D-SMT with time-domain fluorescence lifetime measurement, where fluorescence lifetime serves as the indicator of hybridization. With sub-diffraction-limit spatial resolution in molecular tracking and 15-ms temporal resolution in monitoring the change of reporter’s lifetime, we have demonstrated a full characterization of annealing rate (k_on = 5.13×10⁶ M⁻¹s⁻¹), melting rate (k_off = 9.55 s⁻¹), and association constant (K_a = 0.54 μM⁻¹) of an 8-bp duplex model system diffusing at 4.8 μm²/s. As our method completely eliminates the photobleaching artifacts and diffusion interference, our k_on and k_off results well represent the real kinetics in solution. Our binding kinetics measurement can be carried out in a low signal-to-noise ratio condition (SNR ≈ 1.4) where ~130 recorded photons are sufficient for a lifetime estimation. Using a population-level analysis, we can characterize hybridization kinetics over a wide range (0.5–125 s⁻¹), even beyond the reciprocals of the lifetime monitoring temporal resolution and the average track duration.

Graphical abstract

Accurate knowledge of nucleic acid (NA) hybridization kinetics in its natural context is critical for understanding the fundamental regulatory functions of small NAs. However, the current kinetics measurement techniques are not live cell compatible. Surface plasmon resonance^{1, 2} and ensemble fluorescence quenching^3–5 are common techniques for annealing and melting kinetics measurements, but these methods require an externally imposed perturbation (such as rapid mixing⁴ or temperature jump⁶) followed by relaxation analysis, making them generally incompatible with live cell studies. In addition, not at the single-molecule level, these ensemble methods do not provide information about rare reaction intermediates⁷, minor reaction pathways⁸ or interaction hot spots⁹.

Recently, kinetics measurements have been carried out using single-molecule detection, which relies on either surface-based (e.g. DNA tethered to a surface^10–13) or confinement-based schemes (e.g. DNA confined in a vesicle¹⁴ or electrokinetically trapped in a microfluidic device¹⁵) to enable long-time observation of single molecules. While these single-molecule methods have revealed k_on and k_off at equilibrium, there are concerns about artifacts from the surfaces and the confinements in the experiments¹⁶. For instance, the stability of surface-tethered duplexes can be affected by their electrostatic interactions with the surface^{17, 18} and the hydrophobicity of the surface¹⁹. The entropic effects on surface-tethered ssDNA (i.e. reduction in conformational freedom) can also influence duplex stability as single-stranded hairpin formation is favored on the surface²⁰. Since these measurement conditions are not physiologically relevant, it is questionable whether those results faithfully reflect the true NA annealing and melting kinetics in solution. Therefore, a method that can directly probe the hybridization kinetics of freely diffusing NAs at the single-molecule level in solution is highly desired. Such a method will facilitate the kinetics studies of small NAs in their native conditions.

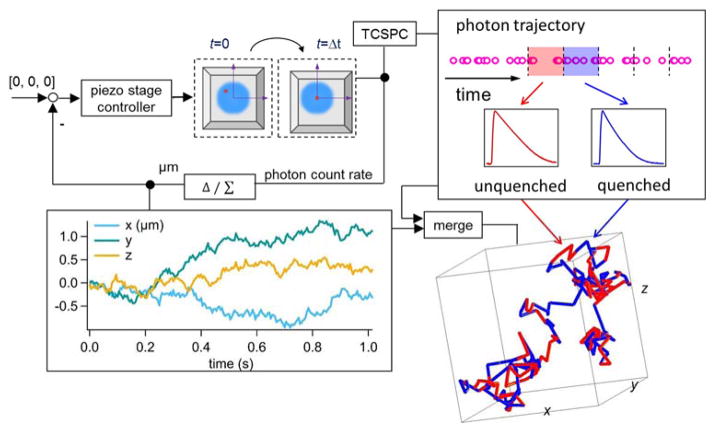
Here we demonstrate a time-resolved, 3D single-molecule tracking (3D-SMT) method that allows us to follow a freely diffusing ssDNA molecule in solution for hundreds of milliseconds to seconds and observe multiple annealing and melting events taking place on the same molecule. Without the need to tether the ssDNA molecule to a surface or to confine it in a trap, our technique is completely compatible with live cell studies. Confocal-feedback 3D-SMT microscopes (Supplemental Note S1) have been previously reported by us^21–23 and others^{24, 25}. In short, the 3D position of the molecule of interest is estimated by analyzing the fluorescence signals collected through four multimode optical fibers which serve as spatial filters (50-μm core diameter; each fiber is connected to a single-photon avalanche photodiode). These spatial filters are arranged in a way that the difference in signals collected by one pair of the optical fibers reveals the x position of the molecule, while the difference in signals collected by the other pair reveals the y position. As these two pairs of fibers are axially offset, the signal difference between the two pairs reveals the z position. Once the 3D position of the molecule is determined (at 5-ms temporal resolution), active feedback provided by an xyz piezo stage is employed to keep the molecule of interest at the center of the excitation focus (Fig. 1 top left). The 3D molecular trajectory is thus derived from the motion history of the xyz piezo stage.

Figure 1.

Schematic of our solution-based, spatiotemporally resolved single DNA annealing-melting kinetics measurement method. 3D single-molecule tracking is achieved by a confocal-feedback scheme (Top left). Active feedback provided by an xyz piezo stage is employed to keep the DNA molecule at the center of the excitation focus, where the motion history of the piezo stage represents the 3D trajectory of the tracked molecule (Bottom left). The time-tagged-time-resolved (TTTR) mode of the TCSPC module allows us to monitor the change of reporter’s fluorescence lifetime at 15-ms temporal resolution. In our DNA model system, the longer lifetime (from unquenched dye) represents the ssDNA state (red segment) while the shorter lifetime (from quenched dye) indicates the dsDNA state (blue segment) (Top right). The acquired single-molecule lifetime trace is mapped onto the molecule’s 3D trajectory, providing not only the temporal but also the spatial information of annealing-melting events that take place along this 1,015-ms trajectory (Bottom right).

Using a TCSPC (time-correlated single-photon counting) module, we can time tag the collected photons with 128-ps resolution and group them into consecutive time windows (Fig. 1 top right). After properly compensating the time delays among the four detection channels (Supplemental Note S2), a single fluorescent decay histogram can be built for each time window by accumulating photons collected in all four detectors. A maximum likelihood estimator²⁶ is then used to fit the decay histogram, generating a representative fluorescence lifetime for each time window (Supplemental Note S3). In our experiments, ~130 recorded photons (SNR ≈ 1.4, Supplemental Note S4) are sufficient for a lifetime estimation. This leads to a temporal resolution of 15 ms in monitoring the lifetime of the tracked molecule (emission rate of a single ATTO633 is about 7–9 kHz under 100 μW excitation at 640 nm). The resulting single-molecule lifetime trace can be merged with the molecule’s 3D trajectory (Fig. 1 bottom left) to provide spatiotemporally resolved binding/unbinding kinetic information of the tracked molecule, as long as the binding/unbinding event is accompanied by a change in reporter’s lifetime.

Fig. 1 bottom right panel shows such a merged 3D trajectory – a 5′-ATTO633-labeled 8-nt ssDNA (reporter strand-1 in Table 1) freely diffusing in 70 wt % glycerol solution and transiently hybridizing with the complementary strands. The trajectory is color coded with two distinct fluorescence lifetimes. The longer lifetime (from unquenched ATTO633) corresponds to the ssDNA state, whereas the shorter lifetime (from quenched ATTO633) indicates the dsDNA state. Multiple annealing-melting events can be clearly observed along this merged 1-second trajectory.

Table 1.

Comparison of annealing and melting rates of two reporter strands at different Tris-HCl and glycerol concentration

reporter	sequence (5′ to 3′)	Tris-HCl buffer	glycerol conc.	kon (106M−1s−1)	koff (s−1)
reporter strand-1	ATTO633-TGGGCGGG	20 mM	70%	5.13±0.40	9.55±0.64
		4 mM	70%	3.63±0.66	21.60±0.40
		20 mM	80%	0.45±0.05	10.99±2.0
reporter strand-2	ATTO633-TGATTGTG	20 mM	70%	5.65±0.56	15.71±1.98

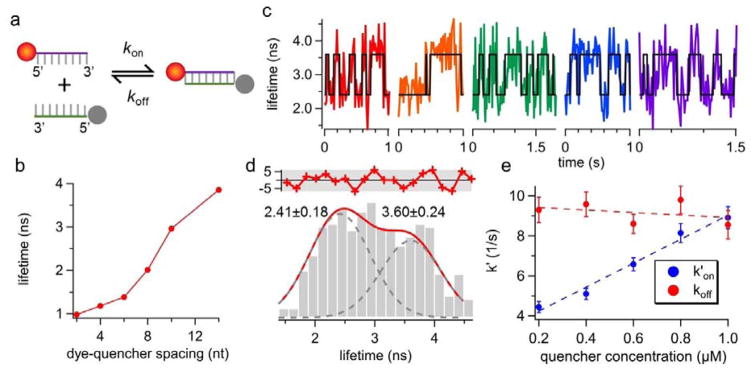
The goal of this work is to recover the annealing (k_on) and melting (k_off) rates of single DNA molecules from the fluorescence lifetime traces obtained in free solution. To enable tracking of one molecule at a time, the 5′-ATTO633-labeled reporter strand was kept at 50 pM throughout the experiments. The 5′-Iowa Black^® FQ-labeled quencher strand, on the other hand, was added to the solution at a much higher concentration (0.2–1 μM). Iowa Black^® FQ was selected as the dark quencher due to its absorption peak at 532 nm²⁸, which only partially quenched ATTO633 (emission peak at 653 nm) at the donor-quencher separation distance of 8 bp (Fig. 2a). Before landing on the 8-bp duplex model system, we first characterized the quenching efficiency of ATTO633-Iowa Black^® FQ pair at various donor-quencher separation distances (Fig. 2b and Supplemental Tables S1–S3). Our results indicated that 8 bp is an ideal donor-quencher separation distance for our FRET-based kinetics measurements, as at this distance reporter’s lifetime is ~50% reduced upon duplex formation. Because oxygen scavenging systems often lead to complex photophysics of dark quenchers (e.g. creating non-absorbing states of the quenchers) that induces donor blinking²⁹, no oxygen scavenging system was used in our experiments. We observed no quencher-induced ATTO633 blinking (Supplemental Fig. S5). Since molecules with large diffusivities are difficult to track for a long time, we slowed down the diffusion of DNA by running the tracking experiments in 70 wt % glycerol solution.

Figure 2.

(a) The reaction scheme of the donor-quencher system. The reporter strand is a 5′-ATTO633-labeled 8-nt ssDNA. The quencher strand is a 5′-Iowa Black^® FQ-labeled ssDNA that is complementary to the reporter. (b) The fluorescence lifetime of ATTO633 as a function of donor-quencher separation distance, measured from ensemble experiments. ATTO633’s lifetime drops from 4.16 ns (on ssDNA) to 2.01 ns (on dsDNA) when the dye-quencher distance is 8 bp. (c) Representative single-molecule lifetime traces of reporter strand-1 in 70 wt % glycerol solution at room temperature. The quencher strand concentration is 0.6 μM. Transient annealing and melting events are clearly manifested as the digital switch of fluorescence lifetime. (d) The lifetime histogram built from the lifetime traces in (c) also shows two states (3.60 ± 0.24 ns and 2.41 ± 0.18 ns, R² = 0.87). The red curve in the upper panel shows the residuals from the two-peak Gaussian fit. (e) Apparent annealing (k′_on) and melting (k_off) rates extracted by ebFRET²⁷. Dashed lines indicate linear fits. The annealing rate k_on, which is the slope of the linear fit of k′_on, is identified to be 5.13 ± 0.42 M⁻¹s⁻¹ whereas the melting rate k_off is calculated to be 9.55 ± 0.64 s⁻¹. Error bars represent standard deviations (SD) calculated from the SD of transition probabilities (Supplemental Note S6). R² for k_on fit is 0.98. The correlation coefficient between the quencher strand concentration and k_off is −0.35, and the p-value for testing the null hypothesis that k_off is independent of quencher concentration is 0.56 (≫0.05), indicating the null hypothesis is not rejected. Therefore, although k_off is slightly reduced at higher concentration of the quencher strand (a linear fit between them also shows negative slope), the dependence of k_off on quencher strand concentration is statistically insignificant.

Five representative lifetime traces of tracked single reporter strands are shown in Fig. 2c. The black lines indicate the binary-state (ssDNA or dsDNA) sequences identified by ebFRET²⁷, a MATLAB library that analyzes single-molecule FRET time traces using hidden Markov model (HMM). Digital switching between two lifetimes is only seen in the presence of quencher strands (Supplemental Fig. S1). The lifetime histogram built from these traces can be well fitted by two Gaussian-distributed peaks centered at 2.41 and 3.60 ns, respectively (Fig. 2d). The 3.60 ns lifetime, presumably given by the unquenched ATTO633 on reporter strand-1 in the single-molecule measurement, is substantially shorter than the 4.16 ns lifetime of the same strand measured in 20 mM Tris-HCl pH 8.0 buffer at the ensemble level (Supplemental Table S1). Three factors may contribute to this discrepancy. First, difference in the refractive indices of the buffers can give distinct lifetime measurement results, as suggested by the Strickler Berg equation^{30, 31}. Second, background fluorescence (lifetime < 600 ps) from Iowa Black^® FQ can bias the fitted lifetime towards a smaller value. Third, as ensemble measurements require a stable duplex at room temperature, locked nucleic acids (LNA) are incorporated in the duplexes for the ensemble lifetime characterization (Supplemental Table S3). LNA-modified duplexes can have a different donor-quencher orientation factor as compared with their DNA counterparts, which can possibly explain why the ensemble and single-molecule measurements on the 8-bp duplexes give two distinct lifetime values (2.01 and 2.41 ns in Fig. 2b and 2d).

To find out the annealing (k_on) and melting (k_off) rates of single DNA molecules freely diffusing in solution, we conducted 3D-SMT of reporter strands at five different quencher strand concentrations (from 0.2 to 1 μM). As shown in Fig. 2e, the apparent annealing rate (k′_on) recovered by ebFRET is proportional to the quencher strand concentration (k′_on = k_on · [quencher strand]), while the correlation of melting rate (k_off) with the quencher strand concentration is statistically insignificant (p-value 0.56). This result reflects the fact that the DNA annealing process is essentially a pseudo first-order reaction (since the quencher strand concentration is at least 4,000-fold higher than that of the reporter strand), whereas the melting is a zero-order reaction. We have successfully characterized k_on (5.13×10⁶ M⁻¹s⁻¹), k_off (9.55 s⁻¹), and K_a (0.54 μM⁻¹) of the 8-bp duplex model system diffusing at 4.8 μm²/s. It has been previously shown that k_on measured in a 3D solution is 3 to 4-fold higher than that measured on a 2D lipid film³². As expected, our kinetics values are 1.5 to 3-fold higher than chose measured by surface-based single-molecule techniques^10–12 (Supplemental Table S4).

A major challenge in SMT-based DNA hybridization kinetics measurement lies in the fact that the track duration (i.e. how long we can follow a single molecule, which is limited by photostability of the reporter, diffusivity of the tracked molecule, and SNR in the detection) can be shorter than the average dwelling time of the molecule in a certain state. Under this condition, most of the acquired single-molecule lifetime traces show no state transitions. The information content of these short traces is found insufficient for the conventional HMM algorithms (e.g. Hammy³³, vbFRET³⁴, QuB³⁵) to recover the transition rates between two states.

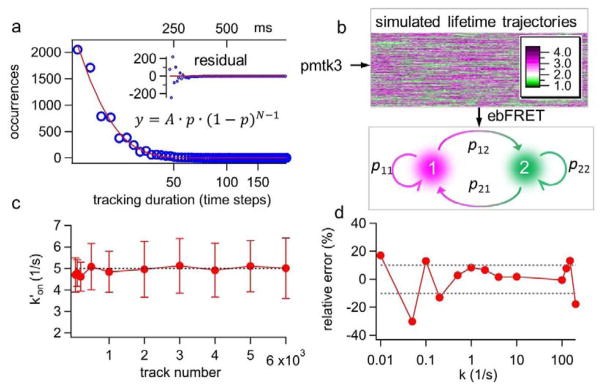
Here we show that the ebFRET algorithm provides an excellent solution to this challenge (Fig. 3 and Supplemental Note S5). The experimental track duration histogram can be modeled as a geometric distribution, showing the probability of 0.13 (p = 0.13) for losing track of a single molecule in the each 5-ms time step (Fig. 3a). Based on this experimentally derived probability (p = 0.13) and the preselected state transition rates (k′_on = 5 s⁻¹ and k_off = 10 s⁻¹), thousands of simulated lifetime traces were generated and fed to the ebFRET algorithm (Fig. 3b). Since ebFRET only generated a transition matrix, a conversion was carried out to turn the transition matrix (unitless) into the rates (s⁻¹) (Supplemental Note S6). In this test, the estimated k′_on was found to converge rapidly to the ground truth (5 s⁻¹) and the relative error was found less than 4% when 500 traces or more were used for analysis. The k_off result was similar (Supplemental Fig. S2). On the other hand, the estimated k′_on from the vbFRET algorithm did not converge to the true value even when more than 1,000 traces were used for analysis (Supplemental Fig. S3).

Figure 3.

(a) The experimental track durations are found to follow a geometric distribution (y) with p = 0.13, where p is the probability of losing track of the molecule in each time step; N is the number of time steps before the molecule is lost; and A is the proportional constant. (b) Based on the experimentally derived p value and the preset annealing-melting rates, we generate thousands of simulated lifetime traces of various durations using the MATLAB toolkit pmtk3. The lifetime traces are then processed by ebFRET to obtain the transition matrix, and hence to calculate k′_on and k_off (Supplemental Note S6). (c) Apparent annealing rate k′_on converges rapidly to the preset value (5 s⁻¹) when the number of lifetime traces used for ebFRET analysis is growing. The error bars are calculated from the standard deviations of the transition matrix, which are also the output parameters from ebFRET. (d) 2,000 simulated lifetime traces produced over a wide range of rates (here k′_on= k_off = k) are processed by ebFRET. The relative error of estimated k over the broad range of preset k values (0.01–100 s⁻¹) is shown.

In addition, ebFRET offers a broad dynamic range for rate estimation – ebFRET can recover k with less than 10% error when k is within 0.5–125 s⁻¹ and 2,000 lifetime traces are used for analysis (Fig. 3d). The dynamic range for vbFRET analysis is an order of magnitude smaller (Supplemental Fig. S4). We emphasize that 2,000 traces are a practical number as they can be collected experimentally within one hour. Our simulation results prove that the integrated 3D-SMT and ebFRET method can discern kinetics (0.5–125 s⁻¹) with average dwelling time shorter than the lifetime monitoring temporal resolution (15 ms) or longer than the average track duration (115 ms).

A number of buffer and strand conditions are known to affect the DNA annealing and melting rates, including salinity^{36, 37}, osmolyte concentration³⁸, and GC content. To further validate our method, we measured the kinetics of two model systems (GC content 87.5% vs. 37.5%) in buffers with different Tris-HCl and glycerol (an osmolyte) concentrations (Table 1). As expected, lowering the Tris-HCl concentration from 20 mM to 4 mM reduced the association constants K_a by 3.2 fold (from 0.54 to 0.17 μM⁻¹), which can be attributed to the decreased k_on and the increased k_off in the low-salt buffer. Depending on the salt and glycerol concentration, glycerol can either stabilize³⁹ or destabilize^40–42 DNA duplexes. Here we show the significant reduction in duplex stability (a 13-fold reduction in K_a) when the glycerol concentration was increased from 70 to 80 wt %. Clearly a large decrease in k_on (from 5.13 to 0.45×10⁶ M⁻¹s⁻¹) was responsible for the reduced K_a. On the other hand, lowering GC content decreased the duplex stability mainly through an increase in k_off, which is consistent with previous reports¹⁵.

Conclusion and Discussion

We have developed a single-molecule detection and analysis method that enables us to directly monitor individual DNA annealing and melting events occurring in the 3D space. By virtue of a population-level analysis, we can characterize DNA hybridization kinetics over a wide range, even beyond the reciprocals of the lifetime monitoring temporal resolution and the average track duration. In contrast to the traditional ensemble methods that rely on external perturbation and sequential relaxation analysis, our single-molecule approach can probe DNA kinetic properties at equilibrium. Although the transient binding rates can also be derived at equilibrium from fluorescence correlation spectroscopy (FCS, a pseudo single-molecule method)⁴³, the reaction time constant ((k_on + k_off)⁻¹) has to be quite different from the diffusion time constant in order for FCS to resolve the rate constants.

Previous single-molecule work has revealed that the transfer from a 3D solution to a 2D surface can substantially slow down the DNA hybridization kinetics, possibly due to the loss of freedom for surface-tethered DNA to explore its surroundings³². Therefore, compared with the surface-based detection schemes (Supplemental Table S4), our method is more suitable for examining DNA hybridization behavior in its native 3D environment. Additionally, in surface-based detection it is difficult to differentiate the event of reporter strand disassociation from surface from the event of reporter photobleaching, since both are shown as the disappearance of a bright spot in the TIRF image. On the contrary, in our method we record the annealing/melting event multiple times before the reporter bleaching finally occurs. Therefore, reporter bleaching does not bias our measurements.

While k_off is generally thought to be independent of the complementary strand concentration^{12, 15}, in our tracking-based kinetics measurement we have noticed that k_off is actually negative correlated (although not statistically significant) with quencher strand concentrations (Fig. 2e). This can be explained by the fact that at high quencher strand concentrations, there are on average more than 100 quencher strands at any time in the confocal volume, ready to form duplex with the reporter strand. When a duplex dissociates, the liberated reporter strand can rehybridize with a nearby quencher strand so quickly that the earlier melting event is missed by our system. In other words, multiple annealing-melting-annealing events may merge into an apparently longer annealing event, leading to a smaller measured k_off. To eliminate this artifact given by the high quencher strand concentration, an extrapolation of the k_off linear fit down to the low quencher concentration region is used as the melting rate. A similar trend of decreasing k_off at higher complementary strand concentrations has also been observed in surface-based detection¹¹, but it could be due to a different reason.

At this moment, our system can only probe rapid rates (0.5–125 s⁻¹) on the molecules diffusing at 4.8μm²/s. A homopolymer model^{12, 44} of DNA predicts that k_off grows approximately exponentially with the duplex length. For a 10-bp DNA duplex, k_off is about 0.11 s⁻¹. This translates to a mean dwelling time of 9 s in the dsDNA state, much longer than our current average track duration. That is why we focus on the kinetics study of 8-bp duplex models in this report. However, by improving the tracking algorithm⁴⁵ and enhancing reporter’s brightness and photostability, we can extend our capability to investigate the hybridization behaviors of the seed sequences (6–12 nt) on the small guided RNA⁴⁶.

In this study, 3D tracking only serves the purpose to extend the observation window. The solution is homogenous and hence the spatial information (i.e. the dynamic information) of the annealing/melting kinetic processes does not provide any functional insight of the tracked molecule. However, inside live cells, the nucleic acid annealing and melting kinetics can be intracellular location dependent⁴⁷. To observe kinetics in live cells, methods such as CellSqueeze⁴⁸- and Streptolysin O⁴⁹-based transient pore openings can be employed to deliver fluorescently labeled oligonucleotides into live cells. The fusion of spatial and temporal information on the nucleic acid’s kinetic and dynamic processes in complex biological environments can lead to new insight of regulatory functions of small nucleic acids. We emphasize that the investigation of kinetic properties of small nucleic acids in their native environments cannot be done by surface- or confinement-based single-molecule methods. Only 3D-SMT methods offer such an opportunity.