Abstract
Several methods have been proposed for automatic and objective monitoring of food intake, but their performance suffers in the presence of speech and motion artifacts. This work presents a novel sensor system and algorithms for detection and characterization of chewing bouts from a piezoelectric strain sensor placed on the temporalis muscle. The proposed data acquisition device was incorporated into the temple of eyeglasses. The system was tested by ten participants in two part experiments, one under controlled laboratory conditions and the other in unrestricted free-living. The proposed food intake recognition method first performed an energy-based segmentation to isolate candidate chewing segments (instead of using epochs of fixed duration commonly reported in research literature), with the subsequent classification of the segments by linear Support Vector Machine models. On participant level (combining data from both laboratory and free-living experiments), with 10-fold leave-one-out cross-validation, chewing were recognized with average F-score of 96.28% and the resultant area under the curve was 0.97, which are higher than any of the previously reported results. A multivariate regression model was used to estimate chew counts from segments classified as chewing with an average mean absolute error of 3.83% on participant level. These results suggest that the proposed system is able to identify chewing segments in the presence of speech and motion artifacts, as well as automatically and accurately quantify chewing behavior, both under controlled laboratory conditions and unrestricted free-living.
Index Terms: Food Intake Monitoring, Piezoelectric Strain Sensor, Segmentation, Chewing detection, Chewing behavior, Obesity, SVM
I. Introduction
Research suggests that changing the eating behavior might be helpful in reducing total energy intake in individuals. For example, the energy intake is proportional to the portion size, thus, reducing the portion size may lead to a decrease in total energy intake [1]–[3]. Reducing the bite rate (the number of bites of food per minute) may reduce the energy intake [4]. Other studies have shown that increasing or decreasing the rate of intake may impact the energy intake [5]–[10]. For example, results in [9] suggest that increasing number of chews per bite by 150% and 200% from the baseline may achieve a reduction of total mass intake by 9.5% and 14.8%, respectively. Authors in [10] claimed that the number of chews per 1 gram of food in obese individuals is lower compared to normal weight individuals while increasing the number of chews per bite in both obese and normal weight individuals reduced their total energy intake. The counts of chews and chewing rate can also be used for estimation of ingested mass and energy intake. In [11], individually calibrated models were proposed for estimation of the ingested mass and caloric energy intake from the chew counts. Chewing rate estimated from chewing sounds captured through a miniature microphone was proposed for estimating weight per bite for three different food types [12].
In many of these studies ([5]– [9]), chew counts were measured by manual counting either by the participants or the investigators. Manual chew counts can be inaccurate, pose participant’s burden and limit the applicability of the interventions targeting the modification of the chewing rate. Thus, there is a need for objective and automatic methods for quantification of the chewing behavior of individuals. In [11], chewing sounds were used for estimation of chewing sequences and chewing microstructure with a recall of 80%. However, acoustic-based approaches are susceptible to surrounding acoustic noise or speech. Semi-automatic chew counting methods based on wearable piezoelectric strain sensors have been proposed [12]–[15]. In [13], a piezoelectric strain sensor was used for quantification of sucking behavior of infants. Histogram-based peak detection was used to estimate the chew counts in adults instrumented with a piezoelectric strain sensor and a printed strain sensor, resulting in the mean absolute error of 8% [14]. An accelerometer-based method [20] achieved an absolute error of 13.8% for chew count estimation. Chew count estimation methods reported in the literature have been tested under controlled laboratory conditions; however, they are not evaluated in unrestricted daily living. Thus, objective and accurate chew count estimation in unrestricted free-living situations is largely an unsolved problem. Therefore, there is a need to develop methods which can automatically estimate chew counts with reliable accuracy both under controlled laboratory setting as well as in more natural unrestricted daily living.
Several wearable sensor systems have been reported for automatic and objective detection of food intake based on recognition of chewing, such as in-ear miniature microphones [16], [17], strain sensors [14], [18], accelerometers [20], and in-ear proximity sensors [19]. In [17], authors presented an earpiece with embedded miniature microphone for capturing chewing sounds of sedentary individuals in a quiet laboratory setting. A reference microphone was used for rejecting environmental sounds. Hidden Markov Model (HMM) trained with 16 features from the sensor signals were able to differentiate between chewing and non-chewing sequences with an average accuracy of 83%. One of the few studies conducted in unrestricted conditions of free living [18] used a piezoelectric strain sensor and a subject-independent classification model based on Artificial Neural Networks to achieve the food intake detection accuracy of 89% over the 24 hours of sensor wear. In [19], authors presented an earpiece with three orthogonally placed infrared proximity sensors for capturing the deformation of the ear canal during chewing. In free-living testing, the HMM based subject-independent classifier achieved an average accuracy of 82%.
A significant number of the systems for food intake detection described in the literature are either tested only under laboratory conditions or only considers food intake in the sedentary postures. People can eat while being sedentary or while performing low to moderate intensity physical activities such as walking (snacking/eating “on the go”) [18], [20]. Research also suggests that with changing lifestyles, the prevalence of the fast food and lack of lunch breaks at work, people are increasingly ‘eating on the go’ [21]. A recent study found that people who ‘eat/snack on the go’ are more susceptible to increase their food intake later in the day compared to those who do not [22]. Therefore, it may be of interest to detect and differentiate food consumption while sedentary and while low to moderately active (food intake during high-intensity activities is not common due to the high breathing rate).
Another common limitation of the current techniques for food intake monitoring is the use of the epoch-based classification to detect chewing ([16], [18], [19], [23]–[25]) and to compute the number of chews. With this approach, the sensor signal is split into short segments (epochs) which then are classified either as chewing or no chewing. The algorithms then count the number of chews in the epochs classified as chewing. Such approach is prone to accumulation of error as the epochs are not aligned with the boundaries of the chewing bouts, thus, accumulating the error from the classification stage and chew counting stage.
Main contributions of this paper are as follow: (i) Proposed is a novel wearable sensor system in the form of eyeglasses. Sensor (piezoelectric strain sensor) is placed on the temporalis muscle, compared to below the ear or in-ear sensors presented in the literature. The sensor system is specifically designed to detect eating while participants are performing low to moderate intensity activities so that the system’s performance is not hindered by the presence of motion artifacts (speech, walking, head motions, etc.). The sensor system is non-invasive, non-obtrusive and potentially socially acceptable. (ii) Instead of an epoch based approach, energy based segmentation (similar to voice activity detection [26]) is proposed to identify the boundaries of potential chewing bouts (of variable length) and chew count estimation. (iii) The presented system and related algorithms are tested in unrestricted free-living conditions to establish the feasibility of the system for detection of chewing segments and estimation of chew counts in free-living.
II. Methods and Material
A. Data Collection Protocol
Ten participants (8 males and 2 females) with an average age of 29.03±12.20 years and range of 19–41 years were recruited for the study. The average body mass index (BMI) was 27.87±5.51 kg/m2 with a range of 20.5–41.7 kg/m2. Recruited participants did not have any medical conditions which would impact their chewing. Each participant read and signed an informed consent form before the start of the experiment. The study was approved by the University of Alabama’s Institutional Review Board.
Experiments consisted of two parts, conducted on different days. The first part consisted of a laboratory visit where it was possible to monitor participants and accurately annotate their activities for developing the gold standard. The laboratory part included an initial quiet rest period of 5 minutes where participants used a computer or cellphone while sitting comfortably. The rest period was followed by a meal in which a slice of cheese pizza was consumed. Next, participants talked to the investigators for 5 minutes. Last two activities included walking on the treadmill and eating a granola bar while walking on a treadmill. Eating while walking was included to replicate snacking/eating ‘on the go.’ Normal walking speed for a human is in the range of 2.8 to 3.37 mph, depending on the age [26]. Thus, walking speed of 3 mph was chosen. Participant’s body movements were not restricted, and they were allowed to talk during all activities except for the quiet rest activity.
The second part of the study included another visit to the laboratory followed by a period of unrestricted free-living. This second visit was completed by 8 participants. During the laboratory portion, the participants were instrumented with the wearable sensor and asked to perform head movements (up and down and left and right motions), trunk movements, raising hands and transitions between sitting and standing to replicate conditions that may potentially generate motion artifacts in the sensor data. Each movement was repeated 5 times and the laboratory part lasted for about 15 minutes. This was followed by a period of unrestricted free-living testing where participants left the laboratory and were asked to follow their daily routine for up-to 3 hours. Participants were asked to have at least one meal/eating episode during the free-living portion of the study.
B. Sensor System and Annotation
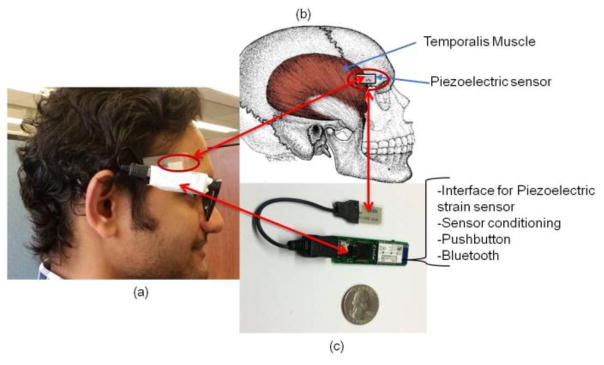
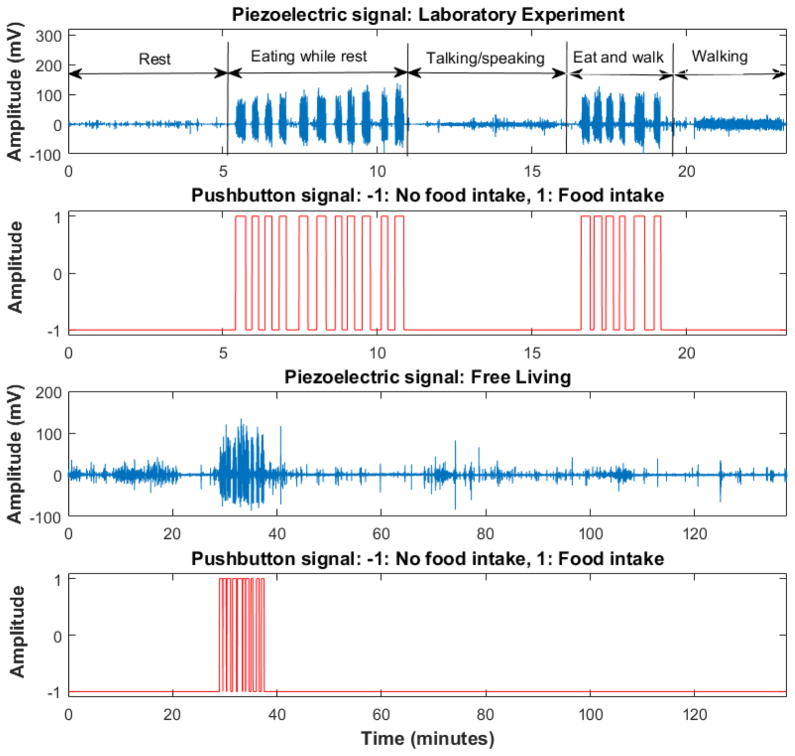
On both experiment days, participants were monitored using a portable, wearable sensor system. The wearable system consisted of a piezoelectric strain sensor and a data collection module which was connected to the temple of the eyeglasses. An off the shelf piezoelectric film sensor (LDT0-028K from Measurement Specialties Inc. VA) was placed on the temporalis muscle (attached via medical tape) for capturing jaw motion. Temporalis muscle (Fig. 1(b)) is part of the muscles that controls the jaw movements during chewing [27]. The selected sensor consists of Polyvinylidene fluoride (PVDF) polymer film with a thickness of 28 μm. The sensor’s sensitivity (10 mV per micro-strains) has been shown to be good enough to capture vibration due to chewing at the skin surface [43]. The data collection module consisted of circuitry for signal acquisition, signal conditioning, and data transmission. Sensor signals were sampled at 1000 Hz by a microprocessor (MSP430F2418, from Texas Instruments) with a 12-bit ADC. Onboard signal conditioning included the amplification of the sensor signal using an ultra-low power operational amplifier and the use of capacitors at the input, output and feedback stages to remove high-frequency RF noise and to eliminate high voltage spikes that may be created by accidental high-frequency excitation [33]. A pushbutton was used by the participants to mark the start and end of chewing bouts. On both experiment days (laboratory meal and free-living eating), participants also kept count of the number of chews for each chewing bout using a portable tally counter. Collected sensor signals were sent to an Android Smartphone via Bluetooth from the onboard RN-42 Bluetooth module. Data was logged on the Smartphone for further offline processing in MATLAB (Mathworks Inc.). Fig. 1(a) shows a participant wearing eyeglasses where the piezoelectric strain sensor is placed on the temporalis muscle and the data collection device is connected to the temple of the eyeglasses. Fig. 1(b) shows the location of the sensor placement on the temporalis muscle. Fig. 1(c) shows the data collection module and the piezoelectric strain sensor. Fig. 2 shows examples of the signals collected both in the controlled laboratory session as well as in free-living session. Pushbutton signals indicate eating episodes. Fig. 2(a) shows an example of the piezoelectric sensor signals and the corresponding pushbutton signal for the activities performed by participants in the laboratory session. Fig. 2(b) shows the signals during a free-living experiment. For each participant data from both visits (controlled laboratory and free-living experiments) were processed in the same way explained below.
Fig. 1.
(a) A participant wearing smart glasses. The wearable sensor system is connected to the temple of glasses. (b) Temporalis muscle is involved in controlling jaw movements during chewing and the sensor location on the muscle. (c) Data collection device which comprises of an interface for piezoelectric strain sensor signal, signal conditioning circuitry, Bluetooth and a microprocessor.
Fig. 2.
Sensor signals captured during laboratory session and during the free-living experiment. (a) The first row shows the activities performed by the participants in the laboratory session and the corresponding piezoelectric sensor signal. The second row shows the pushbutton signal. (b) Third row shows the piezoelectric strain sensor during free living experiment. Last row shows the pushbutton signal during the free-living experiment.
C. Signal Processing and Pattern Recognition Stages
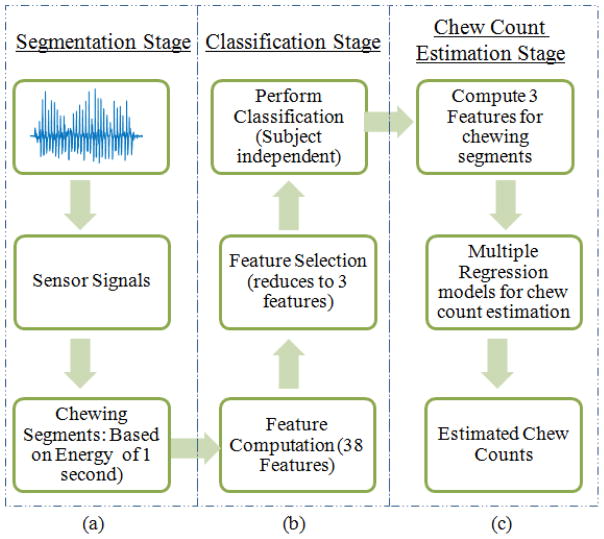
A novel three-stage algorithm is proposed for automatic detection and characterization of the chewing bouts. Since chewing bouts are of variable length, therefore using fixed length epochs might include partial chewing or non-chewing. Close observation of Fig. 2 indicates that chewing results in higher amplitudes in the piezoelectric sensor signal compared to other activities, both in laboratory session as well as in free living. Therefore, we suggest using short-time energy based segmentation to identify the boundaries of variable length, high energy segments, which can potentially be chewing. However, these high energy segments may or may not belong to chewing; therefore, a second classification stage is presented where a classifier differentiates chewing segments from other activities that may result in high-energy segments (e.g. talking or walking). For chew count estimation from the chewing segments recognized by the classifier, multivariate regression models were used. These three stages are depicted in Fig. 3. A detailed description of each stage is given below.
Fig. 3.
Three stages of the proposed algorithm. (a) In the segmentation stage short-time energy is used to isolate low and high energy segments. High energy segments are potential chewing segments. (b) Second stage is the classification stage, where features are computed from both potential chewing and non-chewing segments and subject independent classification is performed with selected features from a feature selection procedure. (c) Chew count estimation stage employs multiple regression models using features computed from segments classified as chewing to estimate chew counts.
D. Segmentation Stage
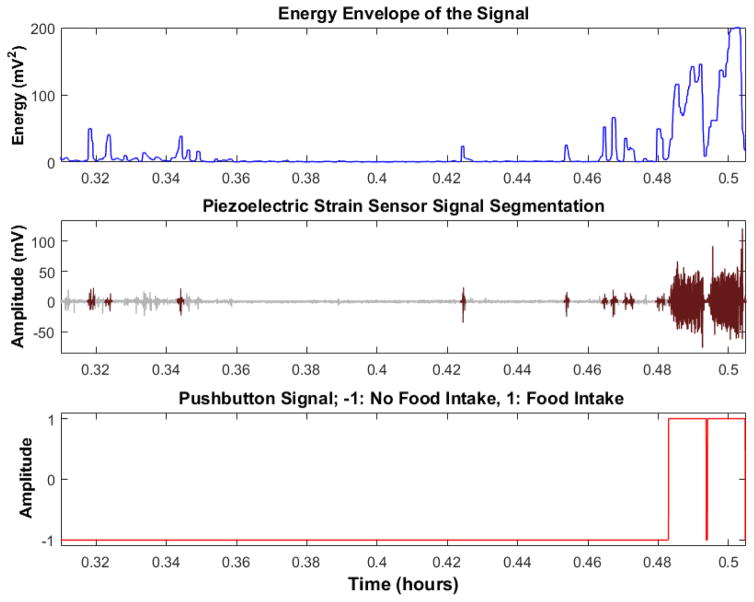
Energy envelope of the signal was computed using a sliding window (Hanning), to identify boundaries of the signal segments with high energy (potential chewing events). Since the sliding window is supposed to capture the energy of the chewing, located in the frequency band of 0.94–2.17 Hz [28], a window size of 1 second with an overlap of 0.5 seconds was used to compute the short-time energy. The short-time energy of each window was combined into a vector and a threshold (T) was dynamically estimated with the thresholding criterion presented in [29]. Successive windows for which the computed energies were higher than T were combined to form high energy segments that were considered as candidate chewing segments and successive windows with lower energies compared to T were combined to form low energy segments considered as non-candidate segments. Fig. 4 shows an example of the segmentation procedure. The first row shows the energy envelope computed from the signal whereas the second row shows the resultant segmentation of the sensor signal. White segments are low energy segments whereas the black segments are the high energy segments. Notice that some of the high energy segments do not belong to chewing (based on the pushbutton signal). In order to identify chewing segments, further processing using a classifier is needed.
Fig. 4.
A segment of chewing in free-living with corresponding pushbutton signal. The first row shows the energy envelope computed from the sensor signal. Second shows the results of the segmentation procedure. White segments indicate low energy segments whereas dark segments show high energy segments. The third row indicates the pushbutton used by the participants to mark chewing and non-chewing. There are some high energy segments which are not actual chewing.
E. Classification Stage: Feature Selection and Classification
High energy activity segments may or may not belong to chewing events (for example, such segments may be caused by walking or talking, Fig. 4). Therefore, a classifier was used to determine whether a given candidate segment belonged to chewing or not. However, for training and validation of the classification models, reference labels are required for each segment. In this case, each segment from the segmentation stage (candidate and non-candidate) was assigned a class label i.e. Ci ∈ {‘−1’,‘+1’} based on the pushbutton signals. From the data, it was observed that average overlap between the candidate segments (from the segmentation stage) and the pushbutton (indicating true chewing) was 80%. Therefore, a segment was labeled as chewing (Ci = +1) if the overlap between the segment and pushbutton (indicating eating) was at least 80% or more, otherwise it was labeled as a non-chewing (Ci = −1). These labels were used for training and validation of the classifier and for performance evaluation, in both laboratory and free-living experiments.
A number of supervised learning algorithms are available for the classification task, among which support vector machine (SVM), have shown excellent performance because of their generalization and speed. SVM models are robust and less prone to overfitting [30]. Linear SVM models find the minimum number of support vectors to define the separating hyperplane by the optimization of maximizing the margins. Hyperplane equation can be extracted from the SVM and used for fast classification. In this work, linear SVM models were trained using Classification Learner tool in MATLAB 2015 (from Mathworks Inc.). For training participant independent models, data from laboratory and free-living experiments was aggregated for each participant and the aggregated data was used for training models. Linear SVM models were trained using a leave-one-out cross-validation procedure where the SVM model was trained with data from 9 participants, and data from the remaining participant was used for testing the trained SVM model. This procedure was repeated 10 times such that each participant was used for testing once. F1 score was computed for each iteration as:
| (1) |
| (2) |
| (3) |
where TP, FP, and FN denote true positives, false positives, and false negatives, respectively.
For each sensor segment, a set of 38 time and frequency domain features (proposed in a previous study for piezoelectric strain sensor [18]) was computed. Using all computed features might be redundant for the given classification task, therefore, a feature selection procedure based on Fisher score [31] was used to obtain a subset of features more suitable for differentiation between chewing and no chewing. Fisher score is a filter-based feature selection algorithm that ranks features according to their discriminatory information, such that in the data space spanned by the selected features, the distance between data points in the different classes is as large as possible while the distance between data points in the same class is as small as possible. The feature selection procedure was performed in two steps. First, all 38 features were ranked using Fisher score algorithm. Second, 38 individual support vector machine (SVM) models were created, where the first SVM model was trained using only the highest ranked feature and the subsequent models were trained by adding one feature at a time to the feature set according to their ranking. Each model was evaluated in terms of its classification accuracy (F1 score) and the feature set achieving the maximum average F1 score was chosen to train the final model.
Final participant independent (group) linear SVM models were trained using leave-one-out cross-validation with selected features. Actual labels and predicted labels by the models for test participants were combined to plot the Receiver Operation Characteristic (ROC) curve and compute Area under the Curve (AUC) for each class. Both ROC and AUC were used as metrics for the comparison of classifiers performances.
F. Estimation Stage: Chew Counts
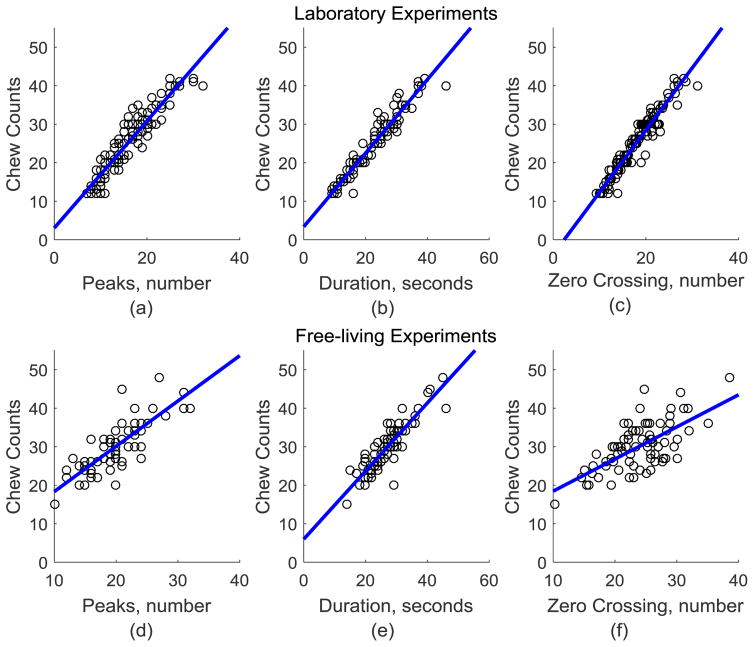
In this stage, the segments classified as chewing were further processed for estimation of chew counts. Three features were computed from each chewing segment i.e. number of peaks, duration, and number of zero crossings. Fig. 5 shows a scatter plot of the chew counts (from chewing segments marked by the pushbutton) against these three features. Fig. 5 suggests a linear relationship between the computed features and chew counts. Having more than one explanatory variable might improve the performance of the regression model. Therefore, a multivariate linear regression model was used.
Fig. 5.
Scatter plot of chew counts versus 3 features computed from piezoelectric strain sensor signal. Computed features were number of peak, duration and number of zero crossings (ZC) in a chewing sequence. First row shows the scatter plots for laboratory experiments. Blue line indicated the regression fit when only one variable is used. Each plot shows regression fit where dependent variable is the number of chew counts (a) Regression equation: y = 1.4*(No. of Peaks) + 3.1 (b) Regression equation: y = 0.96*(Duration) + 3.4 (b) Regression equation: y = 1.6*(ZC) + (−3.8). Second row shows linear regression models for data collected during free living. (d) Regression equation: y = 1.2*(No. of Peaks) + 6.6 (e) Regression equation: y = 0.88*(Duration) + 6. (f) Regression equation: y = 0.83*(ZC) + 10. Scatter plot suggests that there is a linear relationship between the number of chews and the three computed features.
G. Linear Regression for Chew Count Estimation
Linear regression is a predictive analysis technique used to model the relationship between a dependent variable and one or more explanatory variables [32]. General form of linear regression model is:
| (4) |
where, β0 is the called the intercept coefficient and βk is the coefficient of the kth explanatory variable and defines the effect of the kth variable on the output of the model. Here ε is called the error term and describes the variance in the data that cannot be explained by the model. The goodness of the fit of the regression model is given by the coefficient of determination, adjusted R2 (for multivariate regression model). Ten-fold leave-one-out cross-validation was used to train the regression models for chew count estimation. For training of the regression models, features were computed from chewing segments marked by the participants with a pushbutton. This was done because the actual chew counts were available for human marked chewing segments only. Total/cumulative human annotated chew counts for nth participant/experiment is represented by ACNT(n) (aggregate of laboratory and free-living experiments). For validation of the regression model, the chewing segments recognized by the classification stage were used. In the leave-one-out cross-validation, 9 participants were used for training of the model and the 10th participant was used for testing. Total estimated chew counts for the nth participant is represented by ECNT(n). The mean and mean absolute errors were computed as
| (5) |
| (6) |
where M=10 is the number of participants, Error mean (signed) error and |Error| is the mean absolute error (unsigned). For comparison, chew count errors were reported for chew counts in laboratory experiment meals, in free-living meals and aggregate chew counts of both laboratory and free-living meals.
III. Results
Fig. 2 shows examples of piezoelectric sensor signals for both laboratory experiments (Fig. 2(a)) and free-living experiments (Fig. 2(b)) with corresponding pushbutton signals to indicate chewing bouts. A total of 202 chewing bouts were marked by participants with the pushbutton during eating (both laboratory and free-living meals). Table I lists the number of chewing bouts in the laboratory session and free-living, marked by the participant. The segmentation stage resulted in a total of 1274 segments where 617 segments were high energy, and 657 segments were low energy. Distribution of high energy segments between the laboratory and free-living experiments is given in Table I. Fig. 4 shows an example of the segmentation procedure where the first row shows the energy envelope of the signal during a part of the free-living experiment. Second row shows the results of segmentation of the piezoelectric sensor signal, where higher energy segmetns are shown in darker colors. Next, for creating reference labels for the classifier, detected segments were compared to the pushbutton (as described in the Methods), where it was found that 1059 segments were non-chewing (marked as Ci = −1) and 215 segments were actual chewing segments (marked as Ci = 1). Distribution of chewing segments in the laboratory and free-living experiments is listed in Table I. These labels were used for training and evaluation of the classifiers.
Table I.
Chewing Bouts Marked By Participants, Results of the Segmentation Stage and Label Assignment for Classification Stage.
| Chewing Bouts marked with Pushbutton | |||
|---|---|---|---|
| Bouts | Laboratory | Free-living | Total |
| Chewing Bouts | 127 | 75 | 202 |
| Segmentation Stage (High energy segments) | |||
| Segments | Laboratory | Free-living | Total |
| High Energy | 130 | 487 | 617 |
| Label Assignment for training of the classifier | |||
| Laboratory | Free-living | Total | |
| Chewing Segments | 130 | 85 | 215 |
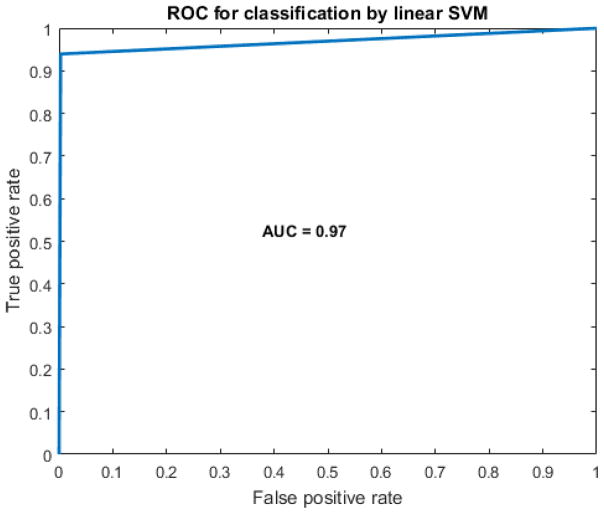
The candidate segments were further classified into chewing and non-chewing segments by linear SVM models. Classification results are reported for leave-one-out cross-validation, where data from both laboratory experiment and the free-living experiment was aggregated before training and validation of the classification models. The best model achieved the average F-score of 96.28 +/−5.91% (average precision and recall of 94.58 +/− 8.95% and 98.41+/−3.68%, respectively) on the aggregated dataset. Table II shows the confusion matrix where 13 chewing segments were misclassified as non-chewing segments. Fig. 6 shows the ROC of the classifier for the whole dataset. AUC of the group model was 0.97.
Table II.
Confusion matrix for linear SVM classification.
| Bouts | Non-Chewing | Chewing |
|---|---|---|
| Non-Chewing | 1056 | 3 |
| Chewing | 13 | 202 |
Fig. 6.
Receiver Operation Characteristics (ROC) curve for participant independent SVM models. AUC of 0.97.
The classification stage relied on the subset of features achieving the highest average F1 score (from the feature selection stage), which was achieved by using 3 features. Selected features were mean absolute value; root mean square (RMS) value; and median values of the signal from the piezoelectric sensor.
In the chew count estimation stage, for the aggregated dataset (both laboratory and free-living experiments), linear regression models estimated chew counts with a mean absolute error of 3.83% and standard deviation of 2.06%. Fig. 5 shows the individual scatter plots of features used in multivariate linear regression models for chew count estimation in both laboratory experiments and free-living experiments. These scatter plots show a linear relationship between these computed features and chew count estimation. Table III lists the coefficients of the multivariate linear regression model, fitted to the whole dataset. This model was able to achieve an R2 of 0.93 and adjusted R2 of 0.93. The corresponding p-values for each feature suggest that all features are signification to the model. Based on human counting, there was a total of 5541 chews across 10 participants whereas the sensor estimated total chew counts were 5651. Table IV shows the error estimation for each participant along with the total human chew counts and algorithm estimated chew counts. Error values are listed for laboratory experiment, free living experiments and aggregated chew counts for each participant. Free-living testing has slightly higher chew count estimation error (mean absolute value: 6.24%) compared to controlled laboratory experiments (mean absolute error: 3.43%). In Table IV, note that the last two participants did not complete the free-living experiments, hence, free-living results are reported for 8 participants.
Table III.
Coefficients of the multivariate linear regression fitted to the data. At 0.05 significance level, the results show that all predictors/features are significant.
| Estimate | SE | t-Stat | p-value | |
|---|---|---|---|---|
| Intercept | 1.47 | 0.54 | 2.75 | 0.006 |
| Number of Peaks | 0.28 | 0.08 | 3.49 | 0.0006 |
| Duration of chewing | 0.72 | 0.05 | 14.27 | 2.76e-32 |
| Number of zero Crossings | 0.15 | 0.05 | 2.86 | 0.0047 |
R2 = 0.93 and Adjusted R2 = 0.93, Root Mean Squared Error: 2.21
Table IV.
Self-reported and algorithm estimated chew counts. Errors for laboratory Experiment, Free living Experiment and total chews per participant
| Participant # | ACNT | ECNT | Error (%) | |Error| (%) | ACNT | ECNT | Error (%) | |Error| (%) | ACNT | ECNT | Error (%) | |Error| (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 283 | 274 | 3.18% | 3.18% | 258 | 272 | −5.43% | 5.43% | 541 | 546 | −0.92% | 0.92% |
| 2 | 423 | 414 | 2.13% | 2.13% | 356 | 341 | 4.21% | 4.21% | 779 | 755 | 3.08% | 3.08% |
| 3 | 203 | 212 | −4.43% | 4.43% | 240 | 250 | −4.17% | 4.17% | 443 | 462 | −4.29% | 4.29% |
| 4 | 307 | 300 | 2.28% | 2.28% | 329 | 324 | 1.52% | 1.52% | 636 | 624 | 1.89% | 1.89% |
| 5 | 291 | 285 | 2.06% | 2.06% | 336 | 389 | −15.8% | 15.77% | 627 | 674 | −7.50% | 7.50% |
| 6 | 344 | 356 | −3.49% | 3.49% | 316 | 293 | 7.28% | 7.28% | 660 | 649 | 1.67% | 1.67% |
| 7 | 338 | 351 | −3.85% | 3.85% | 200 | 210 | −5.00% | 5.00% | 538 | 561 | −4.28% | 4.28% |
| 8 | 299 | 306 | −2.34% | 2.34% | 229 | 244 | −6.55% | 6.55% | 528 | 550 | −4.17% | 4.17% |
| 9 | 414 | 431 | −4.11% | 4.11% | ||||||||
| 10 | 375 | 399 | −6.40% | 6.40% | ||||||||
|
| ||||||||||||
| Mean: | −1.50% | 3.43% | −2.99% | 6.24% | −2.50% | 3.83% | ||||||
| STD: | 3.52% | 1.36% | 7.22% | 4.22% | 3.68% | 2.06% | ||||||
where ACNT, where the annotated chew counts and ECNT where the algorithm estimated chew counts.
IV. Discussion
The focus of the proposed work was the automatic detection and characterization of the chewing bouts in the presence of motion artifacts caused by physical activity and speech. Many of the earlier studies have considered food intake detection when participants were sedentary [12], [17], [19], [23], [24], [33]–[36]. The design of this study accounts for the possibility of consuming food while moderately active (“snacking/eating on the go”). The desired functionality is achieved by two innovations. First is a novel sensor system that monitors the activity of the temporalis muscle as opposed to previously reported chewing sounds [16], [17] and jaw motion [18] monitoring. Second is a novel algorithm that identifies candidate chewing segments and classifies these variable length segments as opposed to splitting the signal into epochs of fixed length and classifying each epoch individually. Experiments were performed in both controlled laboratory settings as well as unrestricted free-living daily conditions to evaluate the performance of the system and to establish the viability of the proposed approach.
The sensor signals shown in Fig. 2 suggest that chewing segments have higher energy compared to non-chewing segments. This characteristic allows to segment the signal and identify the candidate chewing bouts using the energy envelope of the signal. The segmentation algorithm results in variable length segments compared to fixed size epoch based approach widely presented in the literature. This step was used to find the boundaries of potential chewing segments. However, these high energy segments may or may not be chewing (can be caused by other activities, such as walking). For example, the segmentation procedure resulted in a total of 617 high energy segments; however, only 215 segments out of them were actual chewing bouts. A possible reason is the excessive walking, especially in the free-living part of the experiments. Therefore, it was necessary to use a classifier to further verify whether a given high energy segment was indeed chewing or not.
Instead of using all computed features, a feature selection procedure was used to reduce feature dimensionality which resulted in the selection of three most prominent features, i.e. mean absolute value, RMS value and median values. Selected features suggest that amplitude based metrics of the signal can provide discriminatory information to the classifier. In the classification stage, participant independent linear SVM models were used to avoid participant dependent calibration which is necessary for the use of the trained models in the wider population.
For training and validation of the classification models as well as for chew count estimation regression methods, participant independent leave-one-subject-out cross-validation procedure was used. Cross-validation was performed on participant level to ensure that data from the validation participant is not present in the training set (compared to leave-one-sample out). This procedure ensures that there is no over-fitting of the model to the participants due to information leakage and also ensures the applicability of the models to a wider population. Further, classification results are reported on participant level by combining data from laboratory and free-living experiments. This was done to present results which are independent of experimental conditions (laboratory vs. free-living experiments) and participants. A similar approach was adopted for chew count estimation models i.e. separate models were not trained for laboratory and free-living experiments.
Results in Table II show that only 13 chewing segments were misclassified as non-chewing segments whereas only 3 of the non-chewing segments were misclassified. The classifier achieved an average F-score of 96.28% for leave-one-out cross-validation (participant level). Several sensor systems have been presented where the accuracy of food intake detection varies from 80% to 96% [18], [19], [24], [25], [34]. For most of these sensor systems, their ability to detect food intake was tested when the participants were sedentary. In comparison to state of the art for automatic detection of food intake, the proposed device presents a more accurate system tested under challenging conditions that include eating while being physically active as well as testing of the system in daily free-living conditions where participants followed their daily routine.
For estimation of chew counts, linear regression models were used since linear relationship was observed between the computed features and chew counts for chewing bouts (Fig. 6). Actual chew counts were available only for chewing bouts marked by participants using the pushbutton and not for chewing bouts identified by the classification model. Therefore, during the training of the regression models, features computed from chewing bouts marked by participants were used, but for the validation phase, the chewing segments identified by the classifier were used. For the same reasons, errors were computed for the cumulative chew counts over the whole experiment rather than for individual chewing bouts. Table III presents an example of the regression model, where slopes of the linear fit are positive which indicates that there is a positive relationship between the dependent variable (chew count estimation) and the explanatory variables. In the case of the multivariate regression model, adjusted R2 indicates that the model explains about 93% of the variation in the estimation of chew counts which shows a very good fit.
Several studies have utilized chew count for studying different aspects of eating e.g. studies which rely on modification of eating behavior by increasing the number of chews per bite or modifying the chewing rate [5]–[10]. Other studies have proposed the use of chew counts or chewing rate for estimation of mass per bite [12] or energy intake estimation in a meal [11]. In order to automate these systems/approaches, there is a need to developed methods for accurate estimation of chew counts. For current methods (both automatic and semi-automatic), the chew count estimation error varies between 8 – 20%, while tested in laboratory conditions [12]–[15], [37]. However, the segmentation and chew count estimation procedure proposed provides a better estimation of chew counts (overall error rate of 3.83%, aggregated over laboratory and free-living experiments), which should be in acceptable range for developing methods both for eating behavioral modification as well as energy estimation from chew counts/rate.
The wearable sensor system presented in this study combines all components into a single module which is connected to the temple of the eyeglasses, hence reducing the participant burden. There is a possibility of further miniaturizing the electronics to improve the user comfort. Further research is needed to study the social acceptability and user compliance with using the sensor system.
A possible limitation of this study is the exclusion of liquids, which were not included in the study since the main goal was to test the ability of the system for capturing chewing. Previous research suggests that during continuous intake of liquid, characteristic jaw motions similar to the ones produced by chewing are present which can be captured by the proposed device [23]. Further studies are required to test the ability of the proposed sensor system for detection of liquid intake. Another limitation of the current approach is the use of medical tape to attach the sensor to the temporalis muscle, which might impact the comfort and long-term use. Further research is needed to explore new methods of sensor attachment such as the inclusion of the sensor in the temple of the glasses. The study included both laboratory and free-living testing; however, there is a need to further test the device in long-term studies. The current study presented results for 10 participants as preliminary results; larger studies with a wide variety of food items will be conducted in future to test the system.
V. Conclusion
This work presents a novel wearable sensor system for detection and characterization of chewing bouts in the presence of motion artifacts originating from physical activity and speech. The proposed sensor relies on monitoring of the activity in the temporalis muscle to detect chewing. A multistage algorithm first identifies candidate chewing segments and then uses linear SVM models to classify chewing bouts with the average F1 score of 96.28%, in both controlled laboratory situations as well as unrestricted free living experiments. In the last stage, a multivariate linear regression model estimates the chew counts with the mean absolute error of 3.83% (aggregate error over laboratory and free-living experiments). The results suggest that the system is able to detect the presence of food intake and can accurately estimate chew counts in complex situations involving speech and physical activity as well as activities performed in daily living.
Acknowledgments
Research reported in this publication was supported by the National Institute of Diabetes and Digestive and Kidney Diseases (grants number: R01DK100796). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- 1.Rolls BJ, Roe LS, Meengs JS. The effect of large portion sizes on energy intake is sustained for 11 days. Obes Silver Spring Md. 2007 Jun;15(6):1535–1543. doi: 10.1038/oby.2007.182. [DOI] [PubMed] [Google Scholar]
- 2.Ello-Martin JA, Ledikwe JH, Rolls BJ. The influence of food portion size and energy density on energy intake: implications for weight management. Am J Clin Nutr. 2005 Jul;82(1):236S–241S. doi: 10.1093/ajcn/82.1.236S. [DOI] [PubMed] [Google Scholar]
- 3.Ledikwe JH, Ello-Martin JA, Rolls BJ. Portion Sizes and the Obesity Epidemic. J Nutr. 2005 Apr;135(4):905–909. doi: 10.1093/jn/135.4.905. [DOI] [PubMed] [Google Scholar]
- 4.Scisco JL, Muth ER, Dong Y, Hoover AW. Slowing biterate reduces energy intake: an application of the bite counter device. J Am Diet Assoc. 2011 Aug;111(8):1231–1235. doi: 10.1016/j.jada.2011.05.005. [DOI] [PubMed] [Google Scholar]
- 5.Zandian M, Ioakimidis I, Bergh C, Brodin U, Södersten P. Decelerated and linear eaters: Effect of eating rate on food intake and satiety. Physiol Behav. 2009 Feb;96(2):270–275. doi: 10.1016/j.physbeh.2008.10.011. [DOI] [PubMed] [Google Scholar]
- 6.Westerterp-Plantenga MS, Westerterp KR, Nicolson NA, Mordant A, Schoffelen PF, ten Hoor F. The shape of the cumulative food intake curve in humans, during basic and manipulated meals. Physiol Behav. 1990 Mar;47(3):569–576. doi: 10.1016/0031-9384(90)90128-q. [DOI] [PubMed] [Google Scholar]
- 7.Lepley C, Throckmorton G, Parker S, Buschang PH. Masticatory performance and chewing cycle kinematics-are they related? Angle Orthod. 2010 Mar;80(2):295–301. doi: 10.2319/061109-333.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Spiegel TA. Rate of intake, bites, and chews-the interpretation of lean-obese differences. Neurosci Biobehav Rev. 2000 Mar;24(2):229–237. doi: 10.1016/s0149-7634(99)00076-7. [DOI] [PubMed] [Google Scholar]
- 9.Zhu Y, Hollis JH. Increasing the number of chews before swallowing reduces meal size in normal-weight, overweight, and obese adults. J Acad Nutr Diet. 2014 Jun;114(6):926–931. doi: 10.1016/j.jand.2013.08.020. [DOI] [PubMed] [Google Scholar]
- 10.Li J, Zhang N, Hu L, Li Z, Li R, Li C, Wang S. Improvement in chewing activity reduces energy intake in one meal and modulates plasma gut hormone concentrations in obese and lean young Chinese men. Am J Clin Nutr. 2011 Sep;94(3):709–716. doi: 10.3945/ajcn.111.015164. [DOI] [PubMed] [Google Scholar]
- 11.Fontana JM, Higgins JA, Schuckers SC, Bellisle F, Pan Z, Melanson EL, Neuman MR, Sazonov E. Energy intake estimation from counts of chews and swallows. Appetite. 2015 Feb;85:14–21. doi: 10.1016/j.appet.2014.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Amft O, Kusserow M, Troster G. Bite Weight Prediction From Acoustic Recognition of Chewing. IEEE Trans Biomed Eng. 2009 Jun;56(6):1663–1672. doi: 10.1109/TBME.2009.2015873. [DOI] [PubMed] [Google Scholar]
- 13.Farooq M, Chandler-Laney PC, Hernandez-Reif M, Sazonov E. Monitoring of infant feeding behavior using a jaw motion sensor. J Healthc Eng. 2015;6(1):23–40. doi: 10.1260/2040-2295.6.1.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Farooq M, Sazonov E. Comparative testing of piezoelectric and printed strain sensors in characterization of chewing. 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC); 2015; pp. 7538–7541. [DOI] [PubMed] [Google Scholar]
- 15.Farooq M, Chandler-Laney P, Hernandez-Reif M, Sazonov E. A Wireless Sensor System for Quantification of Infant Feeding Behavior. Proceedings of the Conference on Wireless Health; New York, NY, USA. 2015; pp. 16:1–16:5. [Google Scholar]
- 16.Amft O. A wearable earpad sensor for chewing monitoring. 2010 IEEE Sensors. 2010:222–227. [Google Scholar]
- 17.Päßler S, Wolff M, Fischer W-J. Food intake monitoring: an acoustical approach to automated food intake activity detection and classification of consumed food. Physiol Meas. 2012;33(6):1073–1093. doi: 10.1088/0967-3334/33/6/1073. [DOI] [PubMed] [Google Scholar]
- 18.Fontana JM, Farooq M, Sazonov E. Automatic Ingestion Monitor: A Novel Wearable Device for Monitoring of Ingestive Behavior. IEEE Trans Biomed Eng. 2014 Jun;61(6):1772–1779. doi: 10.1109/TBME.2014.2306773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bedri A, Verlekar A, Thomaz E, Avva V, Starner T. Detecting Mastication: A Wearable Approach. Proceedings of the 2015 ACM on International Conference on Multimodal Interaction; New York, NY, USA. 2015; pp. 247–250. [Google Scholar]
- 20.Lee IM, Hsieh CC, Paffenbarger RS., Jr Exercise intensity and longevity in men: The Harvard Alumni Health Study. J Am Med Assoc. 1995;273(15):1179–1184. [PubMed] [Google Scholar]
- 21.Hajna S, Leblanc PJ, Faught BE, Merchant AT, Cairney J, Hay J, Liu J. Associations between family eating behaviours and body composition measures in peri-adolescents: results from a community-based study of school-aged children. Can J Public Health Rev Can Santé Publique. 2014 Feb;105(1):e15–21. doi: 10.17269/cjph.105.4150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ogden J, Oikonomou E, Alemany G. Distraction, restrained eating and disinhibition: An experimental study of food intake and the impact of ‘eating on the go,’. J Health Psychol. 2015 Aug;:1359105315595119. doi: 10.1177/1359105315595119. [DOI] [PubMed] [Google Scholar]
- 23.Wang S, Zhou G, Hu L, Chen Z, Chen Y. CARE: Chewing Activity Recognition Using Noninvasive Single Axis Accelerometer. Adjunct Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2015 ACM International Symposium on Wearable Computers; New York, NY, USA. 2015; pp. 109–112. [Google Scholar]
- 24.Kalantarian H, Alshurafa N, Le T, Sarrafzadeh M. Monitoring eating habits using a piezoelectric sensor-based necklace. Comput Biol Med. 2015 Mar;58:46–55. doi: 10.1016/j.compbiomed.2015.01.005. [DOI] [PubMed] [Google Scholar]
- 25.Alshurafa N, Kalantarian H, Pourhomayoun M, Liu JJ, Sarin S, Shahbazi B, Sarrafzadeh M. Recognition of Nutrition Intake Using Time-Frequency Decomposition in a Wearable Necklace Using a Piezoelectric Sensor. IEEE Sens J. 2015 Jul;15(7):3909–3916. [Google Scholar]
- 26.Ramírez J, Segura JC, Benítez C, de la Torre Á, Rubio A. Efficient voice activity detection algorithms using long-term speech information. Speech Commun. 2004 Apr;42(3–4):271–287. [Google Scholar]
- 27.Blanksma NG, van Eijden TMGJ. Electromyographic Heterogeneity in the Human Temporalis and Masseter Muscles during Static Biting, Open\ Close Excursions, and Chewing. J Dent Res. 1995 Jun;74(6):1318–1327. doi: 10.1177/00220345950740061201. [DOI] [PubMed] [Google Scholar]
- 28.Po JMC, Kieser JA, Gallo LM, Tésenyi AJ, Herbison P, Farella M. Time-frequency analysis of chewing activity in the natural environment. J Dent Res. 2011 Oct;90(10):1206–1210. doi: 10.1177/0022034511416669. [DOI] [PubMed] [Google Scholar]
- 29.Giannakopoulos T. A method for silence removal and segmentation of speech signals, implemented in Matlab. Univ Athens Athens. 2009 [Google Scholar]
- 30.Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;20(3):273–297. [Google Scholar]
- 31.Duda RO, Hart PE, Stork DG. Pattern Classification. 2. New York: John Wiley & Sons; 2001. [Google Scholar]
- 32.Rosner BA. Cengage Learning. 2006. Fundamentals Of Biostatistics. [Google Scholar]
- 33.Sazonov E, Fontana JM. A Sensor System for Automatic Detection of Food Intake Through Non-Invasive Monitoring of Chewing. IEEE Sens J. 2012;12(5):1340–1348. doi: 10.1109/JSEN.2011.2172411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Farooq M, Fontana JM, Sazonov E. A novel approach for food intake detection using electroglottography. Physiol Meas. 2014 May;35(5):739. doi: 10.1088/0967-3334/35/5/739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Biallas M, Andrushevich A, Kistler R, Klapproth A, Czuszynski K, Bujnowski A. Feasibility Study for Food Intake Tasks Recognition Based on Smart Glasses. J Med Imaging Health Inform. 2015 Dec;5(8):1688–1694. [Google Scholar]
- 36.Kong F. PhD Dissertation. Michigan Technological University; Houghton, MI: 2012. Automatic food intake assessment using camera phones. [Google Scholar]
- 37.Farooq M, Sazonov E. Automatic Measurement of Chew Count and Chewing Rate during Food Intake. Electronics. 2016 Sep;5(4):62. doi: 10.3390/electronics5040062. [DOI] [PMC free article] [PubMed] [Google Scholar]