Abstract
Skin cancer is the most common cancer in the United States with over 3.5M annual cases. Presently, visual inspection by a dermatologist has good sensitivity (> 90%) but poor specificity (< 10%), especially for melanoma, which leads to a high number of unnecessary biopsies. Here we use dynamic thermal imaging (DTI) to demonstrate a rapid, accurate and non-invasive imaging system for detection of skin cancer. In DTI, the lesion is cooled down and the thermal recovery is recorded using infrared imaging. The thermal recovery curves of the suspected lesions are then utilized in the context of continuous-time detection theory in order to define an optimal statistical decision rule such that the sensitivity of the algorithm is guaranteed to be at a maximum for every prescribed false-alarm probability. The proposed methodology was tested in a pilot study including 140 human subjects demonstrating a sensitivity in excess of 99% for a prescribed specificity in excess of 99% for detection of skin cancer. To the best of our knowledge, this is the highest reported accuracy for any non-invasive skin cancer diagnosis method.
OCIS codes: (040.1490) Cameras, (040.1880) Detection, (040.3060) Infrared, (110.2970) Image detection systems, (170.1610) Clinical applications, (170.3660) Light propagation in tissues, (170.3880) Medical and biological imaging, (170.4580) Optical diagnostics for medicine, (330.1880) Detection
1. Introduction
There is a higher incidence of skin cancer than the combined occurrence of breast, prostate, lung and colon cancers [1]. Melanoma, which accounts for an estimated 4% of skin cancer cases, is responsible for approximately 75% of all deaths from skin cancer. The total deaths in the United States due to melanomas and other types of skin cancer are estimated to be more than 12,000 for 2014 [2]. Currently, the detection of melanoma relies on a subjective ABCDE (Asymmetry, Border, Color, Diameter and Evolution) test performed visually by dermatologists, general practitioners (GP) or primary care physicians (PCP) [3]. However, the ABCDE test provides a qualitative guideline and it requires a trained specialist to actually distinguish malignant lesions from benign nevi. Moreover, the ABCDE approach has a relatively high false-alarm probability (0.35–0.44, i.e., a specificity in the range 56% to 65%) and moderate detection probability (0.47–0.89) [3–5]. Since a false negative (i.e., a patient with malignant condition that is declared to have benign condition) could lead to metastasis (spreading to other parts of the body) and death, excisional biopsies are routinely performed even on lesions that are non-cancerous. It was estimated that the number of biopsies undertaken in nine geographical areas of the US between 1986 and 2001 was close to 60 for every melanoma detected [6]. One of the critical barriers in early skin-cancer detection is the lack of reliable non-invasive techniques [7] that can detect the cancer at an early stage with high detection probability (i.e., the probability of correctly detecting a malignant lesion) and low false-alarm probability (i.e., the probability of declaring a benign lesion as malignant).
Non-invasive techniques for skin-cancer detection include multispectral (MS) imaging [8–10], digital dermatoscopy and videodermatoscopy (sequential digital dermatoscopy) [11, 12], reflectance-mode confocal microscopy [13], ultrasound [14, 15], laser Doppler perfusion imaging [16], and optical coherence tomography (OCT) [17, 18]. Each technology presents some restrictions and limitations to non-invasively detect skin cancer with high detection probability and low false-alarm probability. For example, on one hand MelaFind, which is a device approved by the Food and Drug Administration (FDA), presents a high-level of detection probability (> 95%) [19], but high false-alarm probability (> 90%) [20]. On the other hand, Vivosight Multi – Beam System, another FDA-approved device, achieves a detection probability between 79–94% and a false-alarm probability between 4–15% for non-melanoma skin cancer lesions [21], but the challenge is that the suspicious lesion must be probed several times before such an accuracy is achieved, which makes the acquisition time prohibitively high.
Here we report a method for statistical inference, which uses the technique of dynamic thermal imaging (DTI) and it demonstrates a rapid, accurate and non-invasive imaging system for detection of skin cancer. DTI has already demonstrated to have high potential for the skin cancer diagnosis [22, 23] and it is a technique in which a thermal stimulus is applied to the suspected lesion and the thermal recovery is captured as function of time using an infrared (IR) camera [24]. Even though several groups have reported that the thermal recovery curves (TRCs) of a skin-cancer lesion and the surrounding healthy skin is different [25–30], these methods only partially extracted the information present in the temporal evolution of the recovery process. More specifically, the existing DTI techniques have neglected the temporal statistical features inherent in the thermal recovery process. To fully extract the vital information present in the recovery process, which will enable us to make a reliable inference on the malignancy of lesion, two problems must be solved. First, the recovery process must be viewed as a random function of time and its temporal statistical properties, such as its temporal correlations, must be mathematically characterized. Second, such complete statistical understanding of the thermal recovery process must, in turn, be utilized in a statistical-inference framework that yields the optimal decision rule for classifying a lesion as malignant or benign. Both of these problems are formulated and solved in the present work. The mathematical method reported here optimally extracts all the temporal information present in the DTI time series, and subjects the extracted vital information to optimal statistical decision theory. A pilot study is also undertaken on 140 human subjects at the University of New Mexico (UNM) Dermatology clinic to demonstrate the effectiveness of the method. We have demonstrated > 99% sensitivity and > 90% specificity while showing excellent robustness to statistical variation in algorithm-training and patient data collection. To the best of our knowledge, this is by far the highest reported accuracy and robustness for any non-invasive method for detection of skin cancer.
This paper is organized as follows: In Section 2 we utilize the knowledge of the TRCs to postulate the classification of a lesion as benign or malignant as a continuous-time detection problem. We explain the parametric stochastic model for the TRCs and how we obtained an analytical form of the auto-covariance functions (ACF), which we use to solve the continuous-time detection problem. In Section 3 we study the inclusion of a reference signal to the detection problem, obtained locally from the very same patient under study. More precisely, for each hypothesis, we define a self-reference signal from the tissue that surrounds the suspicious lesions. In Section 4 we present the results over a sample of 140 patients and a robustness analysis of the methodology. In Section 5 we present the discussion and summarize our main conclusions.
2. Postulation and solution of the detection problem
2.1. Use of dynamic thermal imaging for skin cancer detection
Skin cancers, like all solid malignant tumours, require a blood supply in order to grow larger than a few millimeters in diameter [31, 32]. Tumours induce the growth of new capillary blood vessels by producing specific angiogenesis-promoting growth factors. New blood-vessel growth continues through the progression from precancerous skin lesions to full-blown skin cancer as depicted in Fig. 1. The presence of new blood vessels and the increased blood supply somehow change the thermal response of the tumor cells when a stimulus is applied.
Fig. 1.
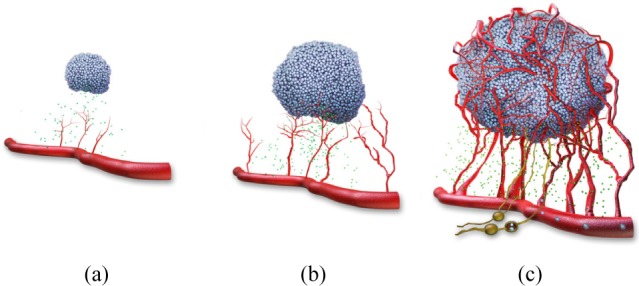
Tumor angiogenesis in cancer at different stages: (a) The tumor release growth factors that activate the growing cells generating blood vessel sprouts. (b) The blood vessels feed the tumor that growths thanks to cell proliferation. (c) The tumor becomes vascularized and it starts to metastasize through the blood stream (from webpage [33]).
Under this scenario, we assume that the patient condition is hidden within TRCs of suspicious lesions. Moreover, we assume that the malignancy of a lesion can be inferred only by monitoring the tissue of the mole. Later in Section 3, the proposed method is further generalized to include TRCs of the tissue that surrounds the suspicious lesion as a local reference. Such a local reference permits the compensation of any possible anomalous behaviour in the lesion thermal recovery, which, in turn, improves both the theoretical and empirical performance of the method.
In the next section we propose a physics-based stochastic model for the skin thermal recovery, which is later utilized in the context of continuous-time detection theory in order to define an optimal decision rule for classifying a lesion as malignant or benign. To the best of our knowledge, the TRCs have never been modeled as continuous-time random processes, and, as such, there is no known relationship between the tumor morphology or blood vessel development and the statistical properties of the TRCs. As a consequence, the model we propose in the next section can pave the way to future research in such a relationship in order to further improve the performance of the proposed method.
2.2. Physics-based stochastic model for the skin thermal recovery
Let us assume that the lesion boundary is defined by visual inspection over the mole region in a visible image. In Section 4.2 we explain how this is achieved. Since the area that defines the mole may contain malignant and benign tissue we need to look at the aggregated effect of the lesion TRC. The most natural and simple way to do such an aggregation is by computing the average TRC over all the pixels within the region that defines the mole.
In the transfer of heat in biological environments, Pennes bioheat equation [34] is generally considered as the most suitable method in all the bioheat models so far [35]. The Pennes bioheat equation is normally simplified as , where k, C and ρ are the coefficient of heat conduction of the skin, the thermal capacity of the skin and the tissue density, respectively. Here, s is the distribution function of internal temperature (refered in this work as the TRC) and qv represents the internal heat source of the body. Even though this model is the most appropriated for the purpose of this work, we want the mathematical model of the TRCs to be simple enough to ensure a feasible solution with the available information. As such, we assume that the physics of the problem is simply governed by a heat equation, where an effective difussion constant, , captures the cumulative effect of all the subcutaneous thermal processes originated by k, C, ρ and qv. We further assume that the model only will be affected by the variations on the depth of the lesion, x, due to the agregation of TRCs previously discussed. Therefore, the temperature of the skin sample is assumed to be modeled by the one-dimensional heat equation,
| (1) |
where T represents the acquisition time and H the bottom of the spatial domain. (To clarify, x = 0 represents the skin surface.) Using the appropiated boundary conditions [27], we have found that the temperature at the skin surface is
| (2) |
Here, TB is the body core temperature, TA is the air temperature, h∞ is the convective heat coefficient between the tissue and the air. The coefficients {Cn} are determined by the generalized Fourier-series expansion of the initial (internal) temperature distribution and μn are the solutions of the trigonometric equation tan μnH = kμn/h∞. Clearly, none of these parameters are known in a deterministic fashion; nevertheless, Eq. (2) gives us a mathematical structure to model the TRCs as a function of time. We address the inherent uncertainties of the model by considering each parameter within the model as a random variable. Therefore, the stochastic-process model for the TRCs is given by the temporal structure prescribed by the solution of a heat equation in Eq. (2) parameterized by, in principle, an infinite set of random variables. We have proved different initial temperature distributions across the skin layers to determine that two coefficients seem to be sufficient in the model because the generalized Fourier coefficients {Cn} decay rapidly as we increase the number of exponential functions in Eq. (2). This situation is particularly true for the case of initial temperature distributions with cubic and exponential functions, which, based on Wilson and Spence’s work [36], present the most feasible functions as initial conditions. Thus, the TRCs are modeled by the parameterized stochastic process given by
| (3) |
where j = 0, 1, representing the case when the TRC was measured from a benign and a malignant lesion, respectively, and N encapsules the noise inherent to the imaging process. In this work, we have assumed that N has zero-mean and it is statistically independent of the parameters Θj.
From the available subject data we have used in this work, the realizations of the random variables θj,1, θj,2 and θj,4, with j = 0, 1, follow a Gaussian distribution, which is an assumption we use later. The realizations of the random variables θj,3 and θj,5 also follow a Gaussian distribution, but their variances are at least two orders of magnitud lower than their mean value. In this work we have assumed that θj,3 and θj,5 area random variables, keeping in mind that their mean values are positive (0.01 and 0.12, respectively) and that their variances are very small (2.2 × 10−5, and 1.5 × 10−3, respectively). Comparing θj,3 and θj,5 variances with respect to the variances of the other three parameters, we notice that θj,1, θj,2 and θj,4 always dominate the behaviour of Eq. (3). An unexplored reasonable option is to also assume θj,3 and θj,5 as deterministic, which is one of the future lines of research we are exploring now.
The binary hypothesis-testing problem (also termed detection problem) of determining whether a measured TRC, say Y (t), is either from benign tissue (null hypothesis, H0) or malignant tissue (alternative hypothesis, H1) can be now formulated by the continuous-time binary detection problem
| (4a) |
| (4b) |
where T represents the TRCs acquisition time, and S(t; Θj), with j = 0, 1 is given in Eq. (3). The alternative hypothesis is assumed to include all the conditions classified as non-benign, including malignant melanomas (MM), basal-cell carcinoma (BCC) and squamous-cell carcinoma (SCC) cases.
The distributions and the correlations between the random vectors Θj = [θj,1…θj,5], j = 0, 1 must be determined, in principle, from patient data with known condition. It is possible, in principle, to utilize the vector of random parameters Θj to perform a statistical decision regarding the malignancy of the suspected lesions, but it will not be necessarily optimal. It can be optimal if exact extraction from the TRCs of these parameters is possible, but this is not the case here due to the noise inherent in infrared imaging. Thus, we solve the continuous-time detection problem in Eq. (4) by first constructing an analytical auto-covariance function of the TRC under each hypothesis (and hence account for the majority of the statistical correlation in the TRC), and then following Grenander’s approach [37] to perform the statistical decision.
2.3. Analytical form of the auto-covariance function
The auto-covariance function (ACF) of the stochastic processes S(t; Θj) is defined by Cj (t, u) = E [S(t; Θj)S(u; Θj)]−E [S(t; Θj)] E [S(u; Θj), where E [·] denotes the (ensemble) expectation operation. By expanding the first expression, the jth (j = 0, 1) ACF can be recast as
| (5) |
for (t, u) ∈ [0, T]2.
The first term in Eq. (5) is E[θj,12], which can be easily estimated from the patients with known diagnosis. Following Bohrnstedt and Goldberger ideas [38] we have found that the terms with three random variables can be expressed by
| (6) |
As mentioned earlier, it was observed from the available subject data that these random parameters follow a joint Gaussian distribution, i.e. , then E[θj,n] = μj,n, for j = 0, 1 and n = 1, 2, 3, 4, 5. Now, for a fixed t ∊ ℝ, E [exp (−θj,ℓt)] = exp also for j = 0, 1 but for ℓ = 3, 5. Moreover, the random variables given by the products of the form θj,n exp (−θj,ℓt) can be approximated to as a random variable that follows a Normal–log-Normal distribution [39–41]. In particular, from Chen’s work we know that the covariance of these products can be approximated by [39]
where ρn,ℓ is the estimated correlation coefficient between θj,n and ln(θj,ℓ). An important observation must be made at this point. Due to the positive mean and the small variance of the realizations of the random parameters θj,ℓ for j = 0, 1 and ℓ = 3, 5, the parameter ρn,ℓ can be calculated ensuring that it always takes the log of a positive random variable. Moreover, given the small variance of the random parameters θj,ℓ for j = 0, 1 and ℓ = 3, 5, they can be assumed to be deterministic (please refer to the previous section for more details), then the terms with three random variables are simplified to
which is a simplification we decided to not use in this work. A similar approach can be used to describe the expectation of four random variables under the observation that they follow a joint Gaussian distribution and a similar simplification can be done by assuming the parameters θj,ℓ for j = 0, 1 and ℓ= 3, 5 as deterministic; the details are not shown here.
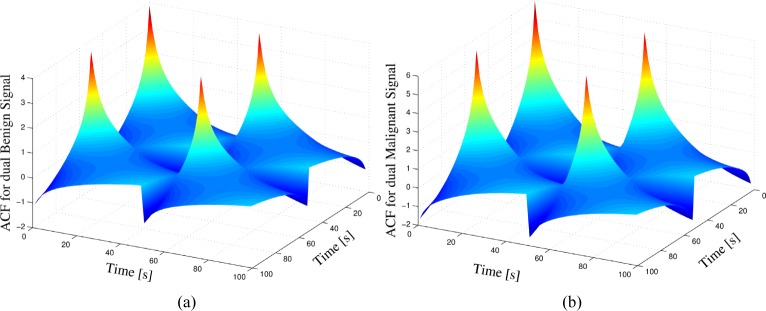
Assembling these results into Eq. (5) we observe that one can compute the ACF analytically by simply estimating pairwise moments of the random parameters of the TRCs. These moments are estimated from a collection of TRCs by assuming that each measured TRC is a realization of the random process of interest. The resulting ACF from the parameters of patients with known benign and malignant conditions are depicted in Fig. 2(a) and Fig. 2(b), respectively. More information on the patient data is detailed later in Section 4. In both cases, the acquisition time for each TRC was 100 seconds. By looking the ACFs from the left plane, as shown in Fig. 2(c) and Fig. 2(d), one can clearly note some of the differences between them. Thus, each ACF encapsules the different statistical correlations that describe the TRCs under each hypothesis and, therefore both can be used to statistically describe the detection problem under Grenander’s approach.
Fig. 2.
(a) Auto-covariance function for the null-hypothesis (H0) estimated from patient data with known benign condition. (b) Auto-covariance function for the alternative-hypothesis (H1) estimated from patient data with known malignant condition. In order to highlight their differences, (c) and (d) show the projection onto one of the left plane of the Auto-covariance function for the null-hypothesis and the alternative-hypothesis, respectively.
2.4. Mercer’s theorem and the Karhunen-Loève expansion of the thermal recovery curves
According to Mercer’s theorem [42], the jth ACF (j = 0, 1) can then be expanded by the absolutely-convergent series
| (7) |
where and are the eigenvalues and the corresponding orthonormal eigenfunctions of the jth ACF, Cj (·,·). The eigenvalues and eigenfunctions are the solutions of the integral equation
| (8) |
with , where δk,ℓ is the Kronecker delta. This equation is known as a Fredholm integral equation of the second kind. The expansion (7) is known as the Mercer’s theorem and it is the key enabling theorem to solve our problem. In this work we solve Eq. (8) numerically following a similar approach as the one presented by Chen et al. [43] in order to obtain two sets of eigenvalue-eigenfunction pairs (one for each hypothesis).
The two sets of eigenfunctions, namely and , are two complete sets because the corresponding ACFs, C0 and C1, are symmetric and positive definite [42, 44]. The completeness of these two sets allow us to represent (in the mean-square sense) any process with either of these sets. We choose to represent each signal with its own set; namely, for the jth hypothesis
| (9) |
where the expansion coefficients Sj,k are known as the Karhunen-Loève (KL) coefficients associated with the stochastic process S(t; Θj). The KL coefficients are computed as the projections of each process on its respective basis functions, namely
| (10) |
where E S(t; Θj) represents the mean of the corresponding random process S(t; Θj). One of the main properties related with the KL expansion for random processes is that the expansion coefficients have zero mean and are uncorrelated [42]. The KL expansion enables us to conveniently decouple randomness (compactly contained in the KL coefficients, Sj,k) and time-variations (embodied in the sequence of eigenfunctions, ϕj,k (t)) for the TRCs under each hypothesis. As such, the KL expansion enables us to equivalently view the continuous-time TRC stochastic signals S(t; Θj) for j = 0, 1, as sequences of uncorrelated random variables, namely the KL coefficients Sj,k, for j = 0, 1 and k = 1, 2,…. These two sequences of KL coefficients in effect constitute the set of statistical features that fully describe the TRC for each patient under each hypothesis. With such statistical equivalence between a TRC and its KL sequences, Grenander’s theorem [42] states that the solution obtained by employing optimal-inference theory (i.e., by invoking the likelihood-ratio function) to the KL coefficients to announce the hypothesis yields the optimal solution to the corresponding continuous-time hypothesis testing problem, which we casted originally in Eq. (4). Therefore, with this statistical equivalence we can recast the detection problem (4) as
| (11a) |
| (11b) |
The main challenge in solving Eq. (11) by optimal-inference theory is the need to know the probability density function of the KL coefficients under each hypothesis and for each k = 1, 2, … (in order to be able to describe the probability density function of the likelihood-ratio function, to be introduced later); this is extremely difficult in general, if not impossible [42]. An important exception to this difficulty is when the random processes S(t; Θj) are Gaussian, which is an assumption we adopt here given the dominance of the Gaussian parameters θj,n with j = 0, 1 and n = 1, 2, 4. Under this assumption and since the KL coefficients are always uncorrelated, they are also independent random variables, with ; thus, the original continuous-time detection problem becomes the discrete (but infinite) detection problem between two Gaussian distributions with different (diagonal) covariance matrices. Hence, for the observation process Y(t), we have the discrete detection problem
| (12a) |
| (12b) |
where the KL coefficients of the observation Y(t), namely Yj,k, j = 0, 1 are the KL expansion coefficients of Y(t) under the jth hypothesis, namely dt, j = 0, 1.
The discrete-time detection problem cast in Eq. (12) has a likelihood-ratio function defined by
| (13) |
where Y denotes , the vector that contains all the KL coefficients. The first restriction required to ensure the convergence of (13) is that λ1,k > λ0,k for k = 1, 2, …, and the convergence of the second term is ensured if (because the logarithm function is monotonic). The convergence in mean-square of each term within the summation can be proven by following the same procedure as in Poor [42] (pp. 305-306) by letting and λk = λj,k, for j = 0, 1 in Equation (VI.D.20); the details will not be shown here.
The test-statistic associated with (13) is obtained as usual by separating the terms that depend on the KL coefficients of the observation process and letting the remaining terms be absorbed by the threshold. After some algebra, we find that the test-statistic, Z is defined by
| (14) |
where the threshold η must be determined under an optimal prescribed decision rule (NP decision rule in our case) as we explain next.
It is worth mentioning that there is a practical limit in the number of eigenvalue-eigenfunction pairs one can reliably extract from the estimated ACFs. Nevertheless, the KL expansion offers the optimality-under-truncation property, i.e., the mean-square error resulting from a finite representation of the process is minimized [44]. Such a property allows us to still optimally represent our processes and our resulting test-statistic, when the most important eigenvalue-eigenfunction pairs are used.
2.5. Neyman-Pearson decision rule
In this section, we describe how to optimally define the threshold, η such that detection probability is maximized for a fixed, prescribed false-alarm probability. By detection probability we mean the probability of announcing H1 when H1 is true; in symbols PD = Pr(H1|H1) = Pr(L(Y) > η|H1). By false-alarm probability we mean the probability of announcing H1 when H0 is true; in symbols PF = Pr(H1|H0) = Pr(L(Y) > η|H0). It is clear that the definitions of PF and PD require us to know the distribution of either the likelihood ratio or the test-statistic, which is what we address next.
The KL coefficients under H0 are Y0,k = Y1,k = S0,k, k = 1, 2, …. As such, the test-statistic under H0, denoted here by Z0, is given by
| (15) |
Under the assumption of Gaussian random processes, the KL coefficients are also Gaussian, then the random variables , for k = 1, 2, … are χ2-distributed because the variance of the kth KL coefficient S0,k is precisely λ0,k. Moreover, since λ1,k > λ0,k, for k = 1, 2, …, the weights in the summation are positive. If we denote the χ2-distributed random variables by Xk, then (15) can be recast as
| (16) |
where ak = 2(1 − λ0,k/λ1,k) > 0 are the coefficients of a linear combination of χ2-distributed random variables. (The pdf for this linear combination is discussed later.) Similarly, if H1 is true, the test-statistic is given by
| (17) |
where bk = 2(λ1,k/λ0,k − 1) > 0 are the coefficients of another linear combination of χ2-distributed random variables.
In summary, the test-statistic under each hypothesis is a linear combination of χ2-distributed random variables, with a different set of positive coefficients for each hypothesis. For a finite number of KL coefficients (16) and (17) are quadratic forms of the Gaussian random variables, S0,k and S1,k, k = 1, 2, …, K. The distribution of quadratic forms of independent and identically-distributed Gaussian random variables with positive coefficients was studied by Pachares [45]. Pachares’ main result was that the cumulative distribution function (CDF) of any finite linear combination of independent χ2-distributed random variables with one degree of freedom, Xk, with positive coefficients c = [c1 c2 ⋯ cK ], i.e., the CDF of , is given by
| (18) |
where and is the kth moment of that can be computed from its cumulants. Thus, we compute the false-alarm probability by
| (19) |
where a = [a1 a2 ⋯ aK ] with ak = 2(1 − λ0,k/λ1,k). Similarly, the detection probability is computed by , where b = [b1 b2 ⋯ bK], with bk = 2(λ1,k/λ0,k − 1). Now, for a prescribed level of false-alarm, say α, the NP lemma tell us that the optimal threshold, η0, will be given by
| (20) |
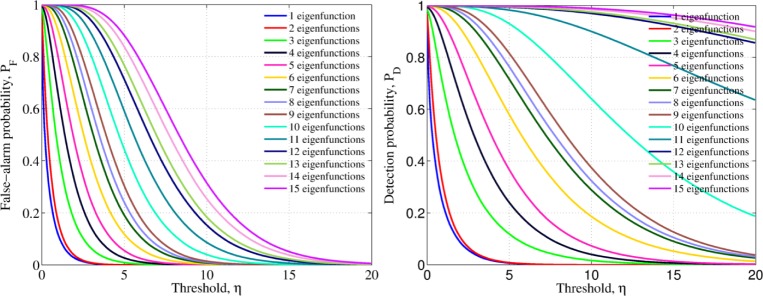
where G−1 represent the inverse of the CDF function (18). When using this optimum threshold, the detection probability PD = 1 − G(η0; b) is maximum amongst all the other possible test one may design. The complexity of implementing (18) makes the implementation of its inverse function an almost impossible task. Therefore, we numerically solve the equivalence by parameterizing the false-alarm and detection probabilities by the threshold, η. Figure 3 depicts the how the false-alarm and detection probabilities are parameterized by η for different number of used eigenfunctions.
Fig. 3.
False-alarm and detection probabilities parameterized by the threshold value, η, for different number of eigenfunctions used in the construction of the test-statistic (14)
Once the desired false-alarm probability is specified, say PF = α, the parameterized optimum threshold, η0 can be obtained from Fig. 3 and Eq. (20). Such an optimum threshold is later used to classify patient data by comparing the test-statistic of a patient with unknown diagnosis: if the test-statistic exceeds the optimum threshold then is classified as malignant. More details are given in the following section. With the parameterized false-alarm and detection probabilities, one can construct the so-called receiver-operating characteristic (ROC) curve, a standard measure of the decision-rule performance that depicts the direct relationship between the theoretical false-alarm probability and the corresponding (theoretical) detection probability. The ROC curve of a perfect classifier correspond to a line that achieves 100% detection (sensitivity) for any value of the false-alarm probability (i.e., PD = 1.0 for PF ∈ (0, 1)). We show the ROC curve corresponding to the parameterized probabilities in Fig. 4, where it can be noted that, as expected, as we include more eigenvalue-eigenfunction pairs, more features are extracted from the TRC and the theoretical performance is improved, plateauing at a level, around the twelfth pair.
Fig. 4.
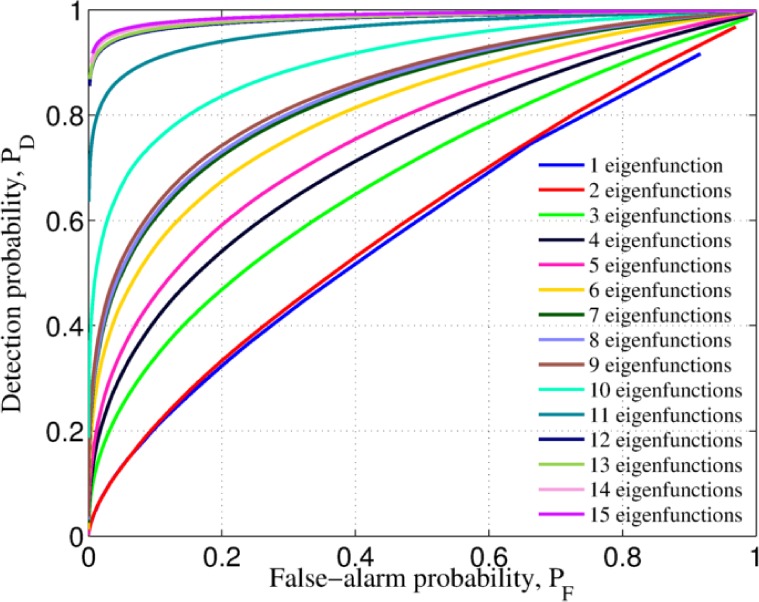
The theoretical receiver-operating characteristic (ROC) curve graphically shows the expected performance of the detector as we increase the number of eigenvalue-eigenfunction pairs. The larger the number of the pairs utilized to construct the test-statistic, the more statistical features utilized and the better the performance of the algorithm
2.6. Eigenvalue-eigenfunction pairs selection
Here we investigate the maximum number of reliable eigenvalue-eigenfunction pairs that can be extracted from estimated ACFs. In our study, we sorted the largest sixteen eigenvalues and examined the corresponding eigenfunctions for both hypotheses. It was observed that both eigenfunction sets are essentially the same under each hypothesis. However, as we require more eigenfunctions from the ACFs a slight phase difference begins to appear. Once the phase difference becomes notorious (e.g., for K > 10) the eigenfunctions lose their similarity, and as a consequence, the cross-orthogonality (among eigenfuctions corresponding to different hypothesis) is also lost. Our results indicated that after the twelfth eigenvalue, the eigenfunction start to become noisy. The source of this problem is estimation error in associated with the ACFs. It is expected that after having more patient data available with sufficient variability, higher K value can be considered.
To produce a systematic method for finding the highest reliable value for K, we first computed the Discrete Fourier transform (DFT) of each eigenfunction and for each hypothesis. It is observed that as the eigenvalue number is increased, the peak spectrum of each eigenfunction is slightly shifted and reduced in amplitude. The maximum K value can be determined by looking for abrupt changes in the peak of the spectrum of the set of eigenfunctions. In our example such abrupt drop occurs at K = 12.
2.7. Summary of the procedure for detecting malignancy of a suspicious lesion
To this end, we assume that the auto-covariance functions were correctly estimated from patient data with known condition (i.e., training patient data), and that the eigenvalues-eigenfunction pairs were also obtained and sorted based on the value of the corresponding eigenvalues. We denote the number of the stored (and sorted) pairs under each hypothesis by K. We also assume that the optimum threshold, η0 was already defined by means of the NP decision rule as described in the previous section.
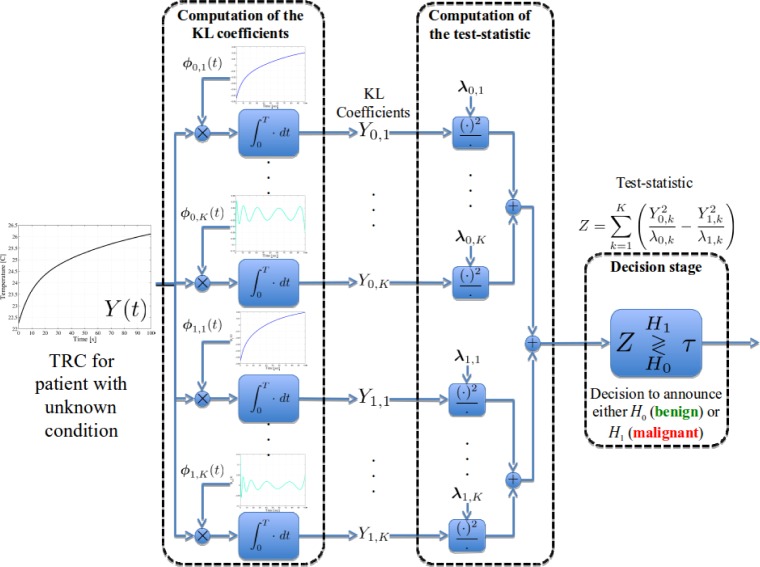
Let the aggregated TRC of the patient with unknown condition be denoted by Y (t). We first utilize the eigenfunctions to compute the KL coefficients under each hypothesis, i.e., , for j = 0, 1 and k = 1, 2, …, K. This computation is depicted graphically in Fig. 5 (left dashed block). We next utilize the KL coefficients and the corresponding eigenvalues to construct the test-statistic as defined in Eq. (14). Such a calculation is depicted in Fig. 5 (middle dashed block). The test-statistic is later compared with the optimum threshold, η0. This last step is termed the decision stage and it is depicted in Fig. 5 (right dashed block). By the extraction of the KL coefficients and the thresholding of the test-statistic by the optimally defined threshold, the detection problem is guaranteed to ensure the maximum achievable detection probability, and, as such, it presents an upper bound in the expected performance of the detector.
Fig. 5.
Block diagram of the detection stage of the proposed algorithm. The KL coefficients are computed by using the eigenfunctions of each hypothesis. These coefficients and the eigenvalues are used to compute the patient’s test-statistic, which is later compared with the optimum threshold to declare the malignancy
Next, we generalize the proposed approach to include a self-reference TRC of the very same patient under analysis. The idea is that the additional information introduced by this new TRC can compensate out anomalous behaviour of the lesion TRCs either improving the overall performance of the algorithm or achieving the same performance as with one TRC but requiring less eigenvalue-eigenfuncion pairs.
3. Generalization to a self-referenced approach
3.1. Theoretical rationale and generalized KL expansion for vector random processes
In this section, we study the inclusion of a reference signal to the detection problem, obtained locally from the very same patient under study. More precisely, for each hypothesis, we define a self-reference signal from the tissue that surrounds the suspicious lesions. The hope is that the by self-referencing the patient’s TRC, abnormal features from the lesion TRCs can be compensated out and, as a consequence, a reduced number of KL coefficients is required to correctly detect the malignant lesions.
For simplicity, we utilize one aggregated TRC of the lesion and one of the surrounding skin. As before, we define the lesion TRC as the average TRC over all the pixels within the lesion boundary. Similarly, we define the reference TRC as the average TRC over all the pixels outside the lesion boundary. The lesion boundary can be selected manually only by visual inspection by the practitioner that conducts the analysis or by a color-based image classifier.
Let us define then the new random process that describe the jth hypothesis as the vectorial random process
| (21) |
where S(t; ΘS,j) is the same aggregated TRC of the lesion used in the previous section and T(t; ΘT,j) is the aggregated TRC of the lesions’ surrounding skin. Therefore, including the reference signal from the surrounding tissue into the detection problem can be stated by the following continuous-time hypothesis-testing problem:
| (22a) |
| (22b) |
The ACF associated with each hypothesis is a 2 × 2 matrix [44] given by
| (23) |
In Fig. 6 we show the obtained estimations of the matrix ACFs for both hypotheses using the same patient dataset used in the previous section.
Fig. 6.
ACFs for the case of vectorial random processes: (a) Autocorrelation function for the null-hypothesis (H0) estimated from patient data with known benign condition. (b) Autocorrelation function for the alternative-hypothesis (H1) estimated from patient data with known malignant condition.
3.2. Karhunen-Loève expansion for vector processes
Once again, we wish to represent this matrix ACF as a linear combination of eigenvalues and eigenvectors as we did for the single-signal approach. Van Tress [44] and Oya et al. [46] stated that the optimal way to address this problem is by defining vector eigenfunctions, since it was proved by Kelly and Root [47] that the vector eigenfunction with scalar eigenvalue representation is a generalization of the KL expansion, and, as such, is optimal. Hence, let us assume that we have a complete set of vector eigenfunctions , j = 0, 1 to represent the vector random processes of the jth hypothesis, where each vector eigenfunction is defined by , and the corresponding vector random process of the jth hypothesis X(t; Θj) can be expanded over this vector eigenfunctions by
| (24) |
The corresponding expansion coefficients associated with this representation are given by
| (25) |
We want the projection coefficients to be uncorrelated, i.e., ; this is achieved when
| (26) |
which is the equivalent of the eigenvalue-eigenfunction integral equation for vector-valued processes. According to Van Tress [44] and Oya et al. [46] this representation satisfies the conditions for Mercer’s theorem; as a consequence
| (27) |
A useful property of this expansion is that the expansion coefficients are scalar, which is a property we exploit in the following section.
3.3. Solution of the dual-signal detection problem
The resulting vector eigenfunctions allow us to represent the dual TRC under each hypothesis with scalar expansion coefficients by
| (28) |
Since this series representation for vector random processes can be considered as a generalization of the KL expansion [44, 46], then the scalar expansion coefficients contain all the statistical features of the dual TRC, in a similar way that the KL coefficients contained the statistical temporal features in the single TRC approach. As a consequence, we can also solve the dual TRC problem by solving the statistical equivalent problem of detecting the malignancy of the lesion based on the expansion coefficients. In symbols, the dual TRC detection problem can be recast as
| (29a) |
| (29b) |
where, as before, we assume that the expansion coefficients are Gaussian as a consequence of assuming that the TRCs are Gaussian random processes. It can be easily shown that, the expansion coefficients have zero mean and are uncorrelated; therefore, they are also independent. It is clear now, that under the series expansion utilized in this approach, we have transformed the original dual TRC problem onto a new problem of scalar and independent coefficients, that follow a Gaussian distribution with variance equal to the corresponding eigenvalues. This is exactly the same form of problem that we already solved for the single TRC approach, and therefore, the mathematical structure of the likelihood ratio and the distribution of the test-statistic are the same. Moreover, we utilize the same structure of the NP decision rule, because the resulting test-statistic is a linear combination of χ2-distributed random variables (just as in the single-TRC approach) but with different eigenvalues, and, as a consequence, different coefficients for the CDFs defined in Eq. (18).
In the following sections, we evaluate the performance for the single- and the dual-TRC approach.
4. Results
In this section we demonstrate the efficacy and delimit the scope and robustness of the skin cancer detection algorithm by measuring its empirical performance. The metrics we utilize to evaluate the empirical performance of the algorithm are the empirical false-alarm and detection probabilities. The empirical false-alarm probability, PF,e, is defined as the ratio between the true-negatives (patients with benign condition as dictated by the biopsy that are declared as benign by the algorithm) and the total number of benign patients. The empirical detection probability, PD,e, is defined as the ratio between the true-positives (patients with malignant condition as dictated by the biopsy that are declared as malignant by the algorithm) and the total number of malignant patients.
A cohort study with 140 subjects was performed to investigate the proposed approaches. Fifty eight percent of the subjects were male and, from the biopsy result, out of the 140 subjects 82 had benign condition and 58 had malignant condition. Out of those 58 subjects with malignant condition, 6 were diagnosed with malignant-melanomas (MM), 42 with basal-cell carcinoma (BCC) and 10 with squamous-cell carcinoma (SCC). The subjects were diagnosed by means of excisional biopsies performed at the University of New Mexico (UNM) Dermatology Clinic, New Mexico, USA, and all patient data was acquired at the same center. The acquisition harware used in this setting is described next as well as the data pre-processing stages required to apply the proposed techniques.
4.1. Image acquisition hardware
We performed DTI with three components. The first component is a cooling unit that is used to impart the temperature stimulus to the lesion and the surrounding skin tissue. Two different cooling unit were used in our study. The first one was a a Ranque-Hilsch vortex tube that generates an oil-free, moisture-free, ultra-quiet air flow. It was later replaced by a commercially available air-conditioning (AC) unit due to its portability. It was observed that by properly modifying the time the cool air was applied to the skin, the imparted temperature was almost the same for both cooling units.
The second component is an infrared marker, which is used for correction of involuntary movement of the subject (i.e., image registration); the IR evolved from a canvas paper marker to a square piece of plastic with a square opening in the middle. Since the only purpose of the marker is to aid in the registration of the infrared sequence of frames, changing the material of the marker did not change the acquisition protocol.
The third component includes the imagers. The first imager is a commercial visible still camera that is used to capture a reference image before the DTI acquisition commences. The second and most important imager is a longwave infrared (LWIR) camera that is used to capture a sequence of frames of the thermal recovery of the skin after the cool stimulus is applied. The LWIR camera consists of a 320×256 focal-plane array (FPA) of quantum-well infrared photodetectors (QWIP) operating at 60K. The noise equivalent temperature difference (NEDT) of the FPA is 20mK and the QWIP camera is fitted with a 50mm, f/2 LWIR lens, yielding an approximate spatial resolution of 300 microns per pixel. The QWIP camera was chosen for our study because it has higher array uniformity, lower NETD and high spatial resolution as compared with other IR camera technologies [22, 48].
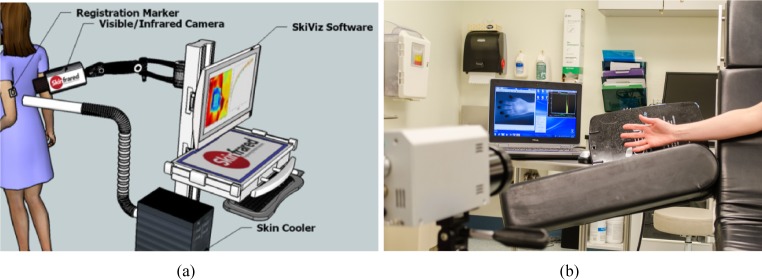
All the components of the acquisition hardware are pictorially represented in Fig. 7(a) whereas Fig. 7(b) shows the infrared imager as well as the acquisition software. Next we explain the imaging procedure.
Fig. 7.
Acquisition hardware utilized to acquire the patient datasets. (a) Prototype and (b) Infrared imager and aquisition software
4.2. Imaging procedure
After informed consent, each subject was escorted to a designated room in the UNM Dermatology Clinic to perform the imaging procedure. The temperature of the room was controlled to be between 20°C to 22°C to make sure that all the patients were exposed to the same temperature before applying the cooling stimulus to the area of interest. At the beginning of the procedure, the square registration marker was placed around the lesion with the lesion centered in the opening, as shown in Fig. 8(a). A visible image of the lesion was then taken with the digital camera for reference. After collection of the visible image, a 15 second infrared image sequence of the marked area was collected to serve as a baseline. Later, the subjectâĂŹs skin within the marker opening was cooled for 15 or 110 seconds, depending of the cooling unit used. After cooling, the exposed area was allowed to warm up naturally to ambient temperature. During the warm-up phase, thermal images of the skin were captured for a total of 2 minutes at a rate of 60 frames per second with the QWIP camera. All the thermal images were recorded using an uncompressed 14-bit format. The total time required to complete the entire imaging procedure was less than five minutes.
Fig. 8.
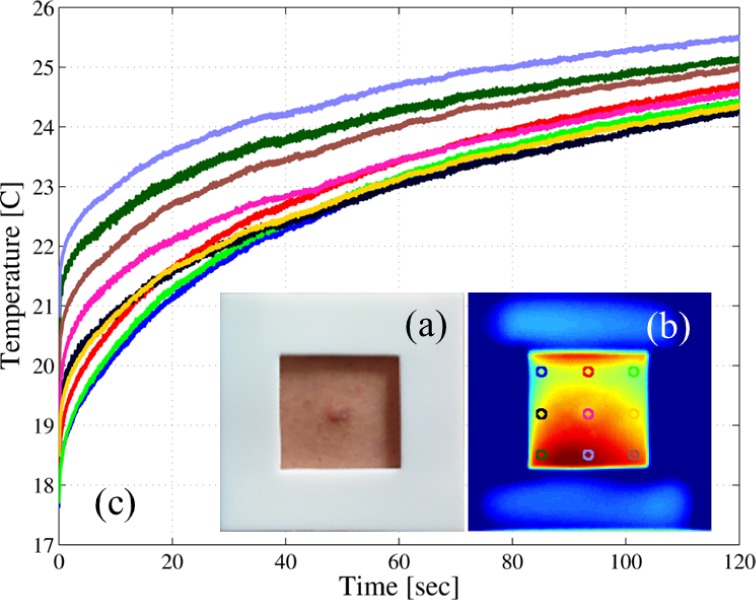
Example of a patient dataset: (a) example of one square plastic marker used in the data acquisition step; (b) first frame of the infrared sequence, note that the visible and this frame are spatially aligned; and (c) the thermal recovery curves (TRCs) for the labeled pixels in (b).
If the subject was scheduled for a biopsy, the biopsy was performed following the data collection by the attending dermatologist and sent to pathology for diagnosis. The biopsy results were delivered to us within the two weeks following the imaging procedure. Some patients were clinically diagnosed with a benign condition by the staff, and, therefore, no biopsy was performed. These patients are considered as control patients and are included in the set of benign patients.
4.2.1. Image registration
Since involuntary movements of the patients cannot be avoided, image registration must be performed over the infrared sequence of images. Moreover, to correctly reference the lesion location within the IR sequence (i.e., the mole, which not necessarily can be spotted in the IR sequence), the visible picture must also be spatially aligned with the IR sequence. Therefore, the visible image is considered as an additional frame for the purposes of the registration process.
The registration is conducted as follows. First, we use the Harris corner-detector algorithm [49] to automatically detect the four corners of the plastic marker amongst the entire sequence of frames. Second, by assuming rigid movement of the scene, we estimate an affine transformation matrix that maps such a movement between the corners of consecutive frames (one matrix is estimated for each pair of consecutive frames) [50]. Third, we utilize the inverse of each transformation matrix to align each frame with respect to the first frame of the sequence [51]. After registration, both the visible image and the entire IR sequence are spatially aligned, generating a three-dimensional (3D) array real numbers that we term the patient dataset. Figure 8(b) depicts the first IR frame after the cooling was removed of the same example case presented in Fig. 8(a); note that both the visible and the first IR frame are spatially aligned. The thermal recovery curves (TRCs) of the labeled pixels are shown in Fig. 8(c), where it can be noted that there is some non-uniformity in the cooling process that make these TRCs to start at different initial temperature.
4.2.2. Camera calibration
In order to have a temperature measurement of the skin surface as accurate as possible, the QWIP camera must be radiometrically calibrated. As in any FPA, the camera suffers of the nonuniform response of its detectors (a problem known in the literature as non-uniformity) and it is compensated by means of non-uniformity correction (NUC) tables performed and stored during the factory calibration process.
The radiometric calibration is achieved by means of the two-point calibration technique [52]. This calibration is performed by placing, in the field-of-view (FOV) of the camera, a uniform-intensity calibration device such as a black-body source at two distinct and known temperatures [53]. The gain and the bias of each detector are then calibrated across the array so that all detectors produce a radiometrically accurate and uniform readout at the two reference temperatures. The reference temperatures where chosen to be within the normal temperature of the skin, i.e., 25°C and 40°C. Examples of thermal recovery curves after the temperature calibration was performed were already shown in Fig. 8(c).
4.3. Clinical application, analysis and discussion
Recall we have 140 subjects, out of which 58 had a malignant condition (including melanoma, basal-cell and squamous-cell carcinoma) and 82 subjects had benign conditions. To reiterate, the subjects were diagnosed by means of excisional biopsies performed at the UNM Dermatology Clinic, New Mexico, USA.
By performing the training over different sizes and permutations of datasets from the 140 patients while testing the method on the remaining patients that where not used in the training, we found that at least 110 patients with known conditions and ten KL coefficients may be used to train the method in order to perfectly separate both benign and malignant conditions for the patient datasets used in the training stage. In order to assess the robustness of using a size of 110 patients in the training dataset and 10 KL coefficients, we repeated the training 200 times, each time with a distinct (but randomly selected) permutation of 110 patients from the totality of 140 patients. Each selection of the 200 training dataset permutations yielded a lesion classifier. We then tested the method by studying the performance of each of the 200 classifiers, namely, we used each classifier to determine the condition of each of the 30 remaining patients (outside of its training dataset). For the purpose of this study, we selected the theoretical false-alarm probability to be PF = 0.01. Since the eigenvalues were computed for each one of the trained classifiers, the corresponding optimal decision threshold varied for each classifier.
The empirical results demonstrate that the method achieves 100% accuracy (i.e., 100% sensitivity and 100% specificity) for 46% of the 200 training selections, which we term the highly reliable training data-sets, when we specify a theoretical false-alarm rate of 0.01. Moreover, the tested methodology achieves 100% sensitivity and 95% specificity (i.e., 5% false-alarm rate) for 76% of the 200 training datasets, and 100% sensitivity and 90% specificity for 93% of the 200 training datasets. These results demonstrate that by using highly reliable training datasets, the proposed technique is capable of correctly classifying both benign and malignant skin-cancer conditions with unprecedented accuracy. In addition, we have observed variability in the sensitivity (below 100%) within only 3% across all the 200 training datasets. Moreover, for different possible lesion boundaries (required to define the pixel-to-pixel averaged TRCs), we observed that the method presents a variability of 0.1% due to a change of 30% in the radius of the selected lesion, proving the robustness of the proposed method to variability in the selection of the lesion boundary by the operator or the medical practitioner performing the test.
After completing the above study, 11 new patient TRCs with known biopsy results were acquired: by means of biopsies 5 were diagnosed as malignant and 6 as benign. By testing the method on this new set of patients while using the same classifiers that were generated by the 200 training datasets from the previous study, we have correctly identified all malignant lesions and misclassified only one benign lesion for 76% of the original 200 classifiers. Moreover, we were able to correctly classify all new 11 lesions for 36% (71 classifiers) of the original 200 classifiers. Out of these 71 classifiers, 58 were from the “highly reliable dataset” identified in the earlier study (original set of 140 patients) as described in the previous paragraph, and 13 of the 71 were from the data set permutations that misclassified only one benign in the original set of patients. This observation shows consistency in the performance of the classifiers that were trained by the highly reliable datasets.
When the dual-TRC approach was utilized to classify the lesions we have observed that the mean theoretical performance over the same 200 permutations is improved with the help of the self-reference signal introduced as shown in Fig. 9. Here we utilize the area-under-the-ROC-curve (AUC) metric to compare the performance and it is defined as the computed area below the receiver-operating-characteristic (ROC) curve of the detector. (A perfect classifier, i.e., with 100% accuracy, will have an AUC of 1.) The most important characteristic of the proposed alternatives is that the detection is still performed over an scalar expansion coefficient, which has equivalent statistical features of the dual TRCs in a similar fashion as the KL coefficients characterized the single TRCs. The real difference in performance is observed in the empirical performance when 110 patients are utilized to train the algorithm. In this case, we observed that perfect classification of all malignant cases is achieved in all the permutations with only 5 eigenvalue-eigenfunction pairs per hypothesis when the highly reliable training datasets are utilized. (Again, this accuracy is achieved when the theoretical false-alarm rate is specified to be 0.01.) The same performance was achieved by the single-TRC approach with 110 training patients with exactly the double of the eigenvalue-eigenfunction pairs. It seems, therefore, that the inclusion of the reference signal can actually compensate some anomalous behaviour of the the lesion TRCs. Nevertheless, there some numerical issues when computing the eigenvalue-eigenfunction pairs that must be compensated in order to further validate this extension of the proposed methodology.
Fig. 9.
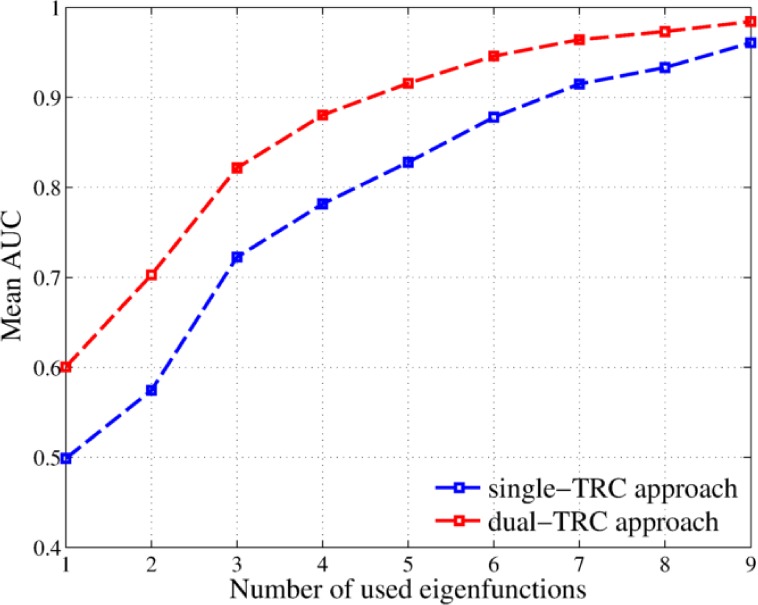
Comparison of the mean theoretical ROC curves over 200 permutations when 110 training are used to train the single-TRC algorithm (blue) and the dual-TRC algorithm (red). Comparison is made by using the mean AUC for different number of used eigenvalue-eigenfunction pairs, using 110 patients to train the algorithm.
In Table 1 we compare the results between the proposed algorithm (last row) and other methodologies previously discussed. The ABCDE test is only applied to melanomas, but it represents a classical approach to non-invasively detect skin cancer. Melafind achieves good performance in terms of sensitivity (high detection probability) but poor specificity (high false-alarm probability). Vivosight, on the other hand, achieves good sensitivity and specificity (i.e., high detection probability and low false-alarm probability). As it was aforementioned, the suspicious lesion must be probed several times before such an accuracy is achieved, which makes the acquisition time prohibitively high for clinical applications. The only approach found in the literature that utilized DTI with reported sensitivity and specificity is our previous work [30]. In that work, we performed classification by a distance-based classifier. To do so, we computed the aggregated TRCs inside and outside the suspicious lesions and then compared the normalized Euclidean norm of their distance. Malignant lesions were expected to have a bigger difference between these two curves, and, as such, have bigger values of their Euclidean distance. Even though this approach obtained good results, it did not extracted all the statistical information from the TRCs and neglected the order in the data, i.e., the temporal evolution of the TRCs; this explains why the method proposed here achieves better results than all other non-invasive techniques. Moreover, the rapid acquisition time and relatively fast processing are two other clear advantages of the proposed method as compared with other techniques for skin cancer detection.
Table 1.
Comparison between the proposed methodology and other non-invasive techniques
5. Conclusions
In order to construct a suitable stochastic model for the TRCs we have simplified the bioheat equation and solved it for properly established boundary conditions. We used this model to derive analytical auto-covariance functions for the proposed hypotheses whose parameters are estimated from patients with known conditions. An optimal statistical decision rule was then derived for which the sensitivity is guaranteed to be at a maximum for every prescribed false-alarm probability. The algorithm was trained using TRCs from 110 human subjects and tested on 30 human subjects with unknown diagnosis. All the malignant subjects were correctly identified (100% sensitivity) for a false-alarm probability below 1% (specificity > 99%). Robustness analysis was undertaken with various permutations of testing and training datasets, and under different selections of the lesion boundaries. The maximum variability in the sensitivity of the method was 3% and 0.1%, respectively, for 200 different random permutations in selecting the training set and different radii of the region that determine the lesion boundary.
The detection method exploits, in a probabilistic sense, the temporal evolution of the warming-up process, as obtained from the thermal-image sequence, in order to extract statistical features that can be utilized to discriminate a case of a benign lesion from a malignant lesion. The term evolution is emphasized to highlight the importance of the temporal order of the warming-up data obtained from the image sequence. This is why the performance is far better than that obtained when the Euclidean norm of the thermal-image sequence is used because the latter, unlike the proposed method, does not depend on the ordering of the images in the sequence [30].
The success of the proposed methodology relies on knowledge of the auto-covariance function of the warming-up process under each hypothesis, which has not been known (to the best of our knowledge) prior to this work. We have presented the construction of such auto-covariance function by parameterizing the warming-up process using a few random variables and by estimating (from patient-data with known conditions) the probability distribution for these random variables and their relevant correlation functions.
We have also introduced and discussed an approach to represent vector random processes that in the literature is treated as the vector generalization of the KL expansion. Using this representation we have solved the detection problem in which each hypothesis is characterized by a dual TRC. The approach followed has the property of using scalar expansion coefficients, equivalent to the KL coefficients for the scalar TRC approach. Hence, after the expansion is applied to the vector random processes, the dual-TRC detection problem becomes equivalent to the single-TRC detection problem. As a consequence, once the expansion coefficients are characterized, they contain most of the statistical information of both of the signals of each hypothesis, and the solution is trivial because all the properties and limitations discussed for the single TRC approach hold for this new alternative. We explored both the theoretical and empirical performance of the proposed alternative using the same training settings utilized to test the robustness of the single-TRC approach. By comparing the theoretical performance for different number of eigenvalue-eigenfunction pairs, the dual-TRC approach achieves the same performance as the single-TRC approach by requiring less eigenvalue-eigenfunction pairs. The empirical performance follows the same trend, allowing, for example, 100% detection of malignant patients using one half of the eigenvalue-eigenfunction pairs that the single-TRC approach required for the same training/testing setting.
To the best of our knowledge, this work reports the highest accuracy and robustness for any non-invasive method for detection of skin cancer. As a consequence, the method will be valuable in clinical applications where the accessibility to trained dermatologists is difficult. Moreover, the methodology is applicably to any continuous-time hypothesis testing problem for which an analytical parametric form of the auto-covariance function is obtainable.
Acknowledgments
The infrared camera utilized in this research was fabricated by QmagiQ and acquired by Skinfrared, LLC. Support from the UNM Dermatology Clinic staff is acknowledged. The authors also thank Pradeep Sen and the personnel of Skinfrared, LLC, especially Sanchita Krishna and Greg Von Winckel (formerly), for useful discussions. The authors want to thank the reviewers and the Journal Editor for their insightful suggestions and comments, which helped us to present a better manuscript.
Funding
Department of Energy NNSA (NA-22) (DE-NA0002494); National Science Foundation (NSF) (SBIR Phase I 1315372); Comisión Nacional de Investigación Científica y Tecnológica (CONICYT) Chile, (FONDECYT Iniciación 11150702)
References and links
- 1.Rogers H. W., Weinstock M. A., Harris A. R., Hinckley M. R., Feldman S. R., Fleischer A. B., Coldiron B. M., “Incidence estimate of nonmelanoma skin cancer in the United States, 2006,” Arch. Dermatol. 146, 283–287 (2010). 10.1001/archdermatol.2010.19 [DOI] [PubMed] [Google Scholar]
- 2.“American Cancer Society Cancer Facts & Figures 2014,” http://www.cancer.org/research/cancerfactsstatistics/cancerfactsfigures2014/. Last Accessed: November, 2015.
- 3.Abbasi N. R., Shaw H. M., Rigel D. S., Friedman R. J., McCarthy W., Osman I., Kopf A. W., Polsky D., “Early diagnosis of cutaneous melanoma: Revisiting the ABCDE criteria,” JAMA 292, 2771–2776 (2004). 10.1001/jama.292.22.2771 [DOI] [PubMed] [Google Scholar]
- 4.Thomas L., Tranchand P., Berard F., Secchi T., Colin C., Moulin G., “Semiological Value of ABCDE Criteria in the Diagnosis of Cutaneous Pigmented Tumors,” Dermatology 197, 11–17 (1998). 10.1159/000017969 [DOI] [PubMed] [Google Scholar]
- 5.Benellii C., Roscetti E., Pozzo V. D., “The dermoscopic (7FFM) versus the clinical (ABCDE) diagnosis of small diameter melanoma,” Eur. J. Dermatol. 10, 282–287 (2000). [PubMed] [Google Scholar]
- 6.Welch H. G., Woloshin S., Schwartz L. M., “Skin biopsy rates and incidence of melanoma: population based ecological study,” BMJ 331, 481 (2005). 10.1136/bmj.38516.649537.E0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mayer J. E., Swetter S. M., Fu T., Geller A. C., “Screening, early detection, education, and trends for melanoma: Current status (2007–2013) andÂfuture directions: Part II. Screening, education, and future directions,” Journal of the American Academy of Dermatology 71, 611 (2014). 10.1016/j.jaad.2014.05.045 [DOI] [PubMed] [Google Scholar]
- 8.Carrara M., Bono A., Bartoli C., Colombo A., Lualdi M., Santoro D. M. N., Tolomio E., Tomatis S., Tragni G., Santinami M., Marchesini R., “Multispectral imaging and artificial neural network: mimicking the management decision of the clinician facing pigmented skin lesions,” Phys. Med. Biol. 52, 2599–2613 (2007). 10.1088/0031-9155/52/9/018 [DOI] [PubMed] [Google Scholar]
- 9.Rigel D. S., Roy M., Yoo J., Cockerell C. J., Robinson J. K., White R., “Impact of guidance from a computer-aided multispectral digital skin lesion analysis device on decision to biopsy lesions clinically suggestive of melanoma,” Arch. Dermatol. 148, 541–543 (2012). 10.1001/archdermatol.2011.3388 [DOI] [PubMed] [Google Scholar]
- 10.Quinzan I., Sotoca J. M., Latorre-Carmona P., Pla F., Garcia-Sevilla P., Boldo E., “Band selection in spectral imaging for non-invasive melanoma diagnosis,” Biomed. Opt. Express 4, 514–519 (2013). 10.1364/BOE.4.000514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tromme L. S. I., Hammouch F., Legrand C., Marot L., Vereecken P., Theate I., van Eeckhout P., Richez P., Baurain J. F., Thomas L., Speybroeck N., “Availability of digital dermoscopy in daily practice dramatically reduces the number of excised melanocytic lesions: results from an observational study,” Br. J. Dermatol. 167, 778–786 (2012). 10.1111/j.1365-2133.2012.11042.x [DOI] [PubMed] [Google Scholar]
- 12.Saez A., Serrano C., Acha B., “Model-based classification methods of global patterns in dermoscopic images,” IEEE Trans. Med. Imaging 33, 1137–1147 (2014). 10.1109/TMI.2014.2305769 [DOI] [PubMed] [Google Scholar]
- 13.Pellacani G., Pace B. D., Reggiani C., Cesinaro A. M., Argenziano G., Zalaudek I., Soyer H. P., Longo C., “Distinct melanoma types based on reflectance confocal microscopy,” Experimental Dermatology 23, 414–418 (2014). 10.1111/exd.12417 [DOI] [PubMed] [Google Scholar]
- 14.Dancey A., Mahon B., Rayatt S., “A review of diagnostic imaging in melanoma,” J. Plast. Reconstr. Aesthet. Surg. 61, 1275–1283 (2008). 10.1016/j.bjps.2008.04.034 [DOI] [PubMed] [Google Scholar]
- 15.Kleinerman R., Whang T. B., Bard R. L., Marmur E. S., “Ultrasound in dermatology: Principles and applications,” J. American Academy of Dermatology 67, 478–487 (2012). 10.1016/j.jaad.2011.12.016 [DOI] [PubMed] [Google Scholar]
- 16.Hunger R. E., Torre R. D., Serov A., Hunziker T., “Assessment of melanocytic skin lesions with a high-definition laser doppler imaging system,” Skin Res. Technol. 18, 207–211 (2012). 10.1111/j.1600-0846.2011.00555.x [DOI] [PubMed] [Google Scholar]
- 17.Hamdoon Z., Jerjes W., Upile T., Hopper C., “Optical coherence tomography-guided photodynamic therapy for skin cancer: Case study,” Photodiagnosis Photodyn. Ther. 8, 49–52 (2011). 10.1016/j.pdpdt.2010.08.004 [DOI] [PubMed] [Google Scholar]
- 18.Themstrup L., Banzhaf C., Mogensen M., Jemec G., “Optical coherence tomography imaging of non-melanoma skin cancer undergoing photodynamic therapy reveals subclinical residual lesions,” Photodiagnosis Photodyn. Ther. 11, 7–12 (2014). 10.1016/j.pdpdt.2013.11.003 [DOI] [PubMed] [Google Scholar]
- 19.Wells R., Gutkowicz-Krusin D., Veledar E., Toledano A., Chen S. C., “Comparison of diagnostic and management sensitivity to melanoma between dermatologists and melafind: A pilot study,”, Arch. Dermatol. 148, 1083–1084 (2012). 10.1001/archdermatol.2012.946 [DOI] [PubMed] [Google Scholar]
- 20.Cukras A. R., “On the comparison of diagnosis and management of melanoma between dermatologists and melafind,” JAMA Dermatology 149, 622–623 (2013). 10.1001/jamadermatol.2013.3405 [DOI] [PubMed] [Google Scholar]
- 21.Nandanan D. M. S. N., Fisher J., Markowitz O., “Optical coherence tomography imaging of onychomycosis,” presented in 2014 at EADV, Florence. [Online]. Available: www.vivosight.com/clinical-presentations/
- 22.Lahiri B. B., Bagavathiappan S., Jayakuman T., Phillip J., “Medical applications of infrared thermography: A review,” Infrared Phys. Techn. 55, 221–235 (2012). 10.1016/j.infrared.2012.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Carlo A. D., “Thermography and the possibilities for its applications in clinical and experimental dermatology,” Bioengineering of the Skin 13, 329–338 (1995). [DOI] [PubMed] [Google Scholar]
- 24.Ambar M., Quantitative Dynamic Telethermometry in Medical Diagnosis and Management (CRC Press, Boca Raton, FL, 1994). [Google Scholar]
- 25.Buzug T. M., Schumann S., Pfaffmann L., Reinhold U., Ruhlmann J., Functional infrared imaging for skin-cancer screening, Conf. Proc. IEEE Eng. Med. Biol. Soc. 1:2766–2769 2006. [DOI] [PubMed] [Google Scholar]
- 26.Cetingul M. P., Herman C., “A heat transfer model of skin tissue for the detection of lesions: sensitivity analysis,” Phys. Med. Biol. 55, 5933–5951 (2010). 10.1088/0031-9155/55/19/020 [DOI] [PubMed] [Google Scholar]
- 27.Cetingul M. P., Herman C., “Quantification of the thermal signature of a melanoma lesion,” International Journal of Thermal Sciences 50, 421–431 (2011). 10.1016/j.ijthermalsci.2010.10.019 [DOI] [Google Scholar]
- 28.Cetingul M. P., Herman C., “The Assessment of Melanoma Risk Using the Dynamic Infrared Imaging Technique,” Journal of Thermal Science and Engineering Applications 3, 031006 (2011). 10.1115/1.4004424 [DOI] [Google Scholar]
- 29.Herman C., “The role of dynamic infrared imaging in melanoma diagnosis,” Expert Rev. Dermatol. 8, 177–184 (2013). 10.1586/edm.13.15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Godoy S. E., Ramirez D. A., Myers S. A., von Winckel G., Krishna S. S., Padilla R. S., Sen P., Krishna S., “Dynamic Infrared Imaging for Skin Cancer Screening,” Infrared Phys. Techn. 70, 147–152 (2015). 10.1016/j.infrared.2014.09.017 [DOI] [Google Scholar]
- 31.Nishida N., Yano H., Nishida T., Kamura T., Kojiro M., “Angiogenesis in Cancer,” Vascular Health and Risk Management 2, 213–219 (2006). 10.2147/vhrm.2006.2.3.213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.“The Angiogenesis Foundation webpage,” http://www.angio.org/. Last Accessed: December, 2014.
- 33.“Tumor Angiogenesis Infographic Colorectal Cancer webpage,” https://www.behance.net/gallery/11816509/Tumor-Angiogenesis-Infographic-Colorectal-Cancer. Last Accessed: December, 2014.
- 34.Pennes H., “Analysis of Tissue and Arterial Blood Temperature in the Resting Human Forearm,” J. Appl. Physiol. 1, 93–112 (1948). [DOI] [PubMed] [Google Scholar]
- 35.Shi G., Han F., Wang L., Liang C., Li K., “Q-r curve of thermal tomography and its clinical application on breast tumor diagnosis,” Biomed. Opt. Express 6, 1109–1123 (2015). 10.1364/BOE.6.001109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wilson S. B., Spence V. A., “A tissue heat transfer model for relating dynamic skin temperatures changes to physiological parameters,” Phys. Med. Biol. 33, 895–912 (1988). 10.1088/0031-9155/33/8/001 [DOI] [PubMed] [Google Scholar]
- 37.Grenander U., “Stochastic processes and statistical inference,” Arkiv för Matematik 1, 195–277 (1950). 10.1007/BF02590638 [DOI] [Google Scholar]
- 38.Bohrnstedt G. W., Goldberger A. S., “On the exact covariance of products of random variables,” J. Am. Stat. Assoc. 64, 1439–1442 (1969). 10.1080/01621459.1969.10501069 [DOI] [Google Scholar]
- 39.Chen D. G., “A bayesian model with a bivariate normal–lognormal prior distribution and a nonlinear mixed-effect model for a regional fish stock-recruitment meta-model,” in “Proceedings Am. Stat. Assoc.,” (2002). [Google Scholar]
- 40.Yang M., “Normal Log-normal Mixture: Leptokurtosis, Skewness and Applications,” Appl. Econ. Lett. 15, 737–742 (2008). 10.1080/13504850600749073 [DOI] [Google Scholar]
- 41.Zerovnik G., Trkov A., Kodeli I. A., “Correlated random sampling for multivariate normal and log-normal distributions,” Nucl. Instrum. Methods Phys. Res. A 690, 75–78 (2012). 10.1016/j.nima.2012.06.036 [DOI] [Google Scholar]
- 42.Poor H. V., An Introduction to Signal Detection and Estimation (Springer, 1994), chap. 6, pp. 263–326, 2nd ed. 10.1007/978-1-4757-2341-0_6 [DOI] [Google Scholar]
- 43.Chen M., Chen Z., Chen G., Approximate Solutions of Operator Equations, vol. 9 (World Scientific Publishing Co, 1997). 10.1142/3407 [DOI] [Google Scholar]
- 44.Trees H. L. V., Detection, Estimation and Modulation Theory, Part 1, 2nd ed. (John Wiley & Son, Inc, 2001). [Google Scholar]
- 45.Pachares J., “Note on the Distribution of a Definite Quadratic Form,” The Annals of Mathematical Statistics 26, 128–131 (1955). 10.1214/aoms/1177728601 [DOI] [Google Scholar]
- 46.Oya A., Navarro-Moreno J., Ruiz-Molina J., “A numerical solution for multichannel detection,” IEEE Trans. Commun. pp. 1734–1742 (2009). 10.1109/TCOMM.2009.06.070456 [DOI]
- 47.Kelly E. J., Root W. L., “A representation of vector-valued random processes,” J. Math. and Phys. 39, 211–216 (1960). 10.1002/sapm1960391211 [DOI] [Google Scholar]
- 48.Fauci M. A., Breiter R., Cabanski W., Fick W., Koch R., Ziegler J., Gunapala S. D., “Medical infrared imaging – differentiating facts from fiction, and the impact of high precision quantum well infrared photodetector camera systems, and other factors, in its reemergence,” Infrared Phys. Techn. 42, 337–344 (2001). 10.1016/S1350-4495(01)00093-7 [DOI] [Google Scholar]
- 49.Harris C., Stephens M., “A combined corner and edge detector,” in “In Proceedings of the Fourth Alvey Vision Conference,” (1988), pp. 147–151. [Google Scholar]
- 50.Chumchob N., Chen K., “A Robust Affine Image Registration Method,” Int. J. Numer. Anal. Model. 6, 311–334 (2009). [Google Scholar]
- 51.Goshtasby A. A., 2-D and 3-D Image Registration: for Medical, Remote Sensing, and Industrial Applications (Wiley Press, 2005). [Google Scholar]
- 52.Holst G. C., CCD Arrays, Cameras and Displays (SPIE Optical Eng. Press, 1996). [Google Scholar]
- 53.Godoy S. E., Pezoa J. E., Torres S. N., “Noise-cancellation-based nonuniformity correction algorithm for infrared focal-plane arrays,” Appl. Opt. 47, 5394–5399 (2008). 10.1364/AO.47.005394 [DOI] [PubMed] [Google Scholar]