MOSAIC: A Modular Single-Molecule Analysis Interface for Decoding Multistate Nanopore Data

Abstract

Biological and solid-state nanometer-scale pores are the basis for numerous emerging analytical technologies for use in precision medicine. We developed Modular Single-Molecule Analysis Interface (MOSAIC), an open source analysis software that improves the accuracy and throughput of nanopore-based measurements. Two key algorithms are implemented: ADEPT, which uses a physical model of the nanopore system to characterize short-lived events that do not reach their steady-state current, and CUSUM+, a version of the cumulative sum statistical method optimized for longer events that do. We show that ADEPT detects previously unreported conductance states that occur as double-stranded DNA translocates through a 2.4 nm solid-state nanopore and reveals new interactions between short single-stranded DNA and the vestibule of a biological pore. These findings demonstrate the utility of MOSAIC and the ADEPT algorithm, and offer a new tool that can improve the analysis of nanopore-based measurements.

Graphical Abstract

Protein and solid-state nanopores (Figure 1A) are the basis for single-molecule measurements of a variety of analytes including ions,^1,2 single-stranded RNA and DNA,^3–10 double-stranded DNA,^11,12 proteins,^13–19 synthetic polymers,^20–23 and metallic nanoparticles.^24,25 The method is conceptually simple. An electric potential applied across a nanopore that spans two electrically isolated chambers (filled with electrolyte solutions) results in an ionic current with a mean value 〈i₀〉 (Figure 1B). Single molecules that reversibly partition into the pore cause a series of pulses or current blockades (Figure 1B). The change in pore conductance is caused by the volume exclusion of mobile ions from the pore^20,21 and interactions between the ions and the analyte.^5,21,26 The change in conductance^{4,20,21,26,27} and the residence time of analytes in the pore^8,20,21 are used to estimate the analyte size,^20,21 effective charge,²¹ and dipole moment.²⁸

Figure 1.

(A) Schematic illustration of DNA translocation through a solid-state nanopore. An electric potential applied across the pore produces an ionic current. (B) The partitioning of DNA into the pore causes well-defined current reductions with different mean current blockade amplitudes (e.g., 〈i_a〉 and 〈i_b〉). (C) A single level event is characterized by the ratio of the mean currents for the occupied and fully open pore (〈i_a〉/〈i₀〉 and the level residence time (Δt). (D) A histogram illustrating the relative current blockade depth for two species obtained by analyzing the events. (E) Residence time distributions for the two blockade depth populations. The mean residence times are estimated from fits to the distributions.

Analyte-induced events appear as single or multiple conductance state levels, arising from changes in the analyte conformation or interactions in the pore^{9,11,20,21,27,29,30} (Figure 1C). Multiple conductance level events differ from the gating of ion channels, where the channel fluctuates between two states, open and closed.³¹ These fluctuations are well characterized using hidden Markov models^32–34 and kinetic simulations.^34,35 On the other hand, several analysis techniques have been applied to analyze nanopore-based single-molecule data including threshold detection,^4,21 slope- or area-based techniques, ^36,37 the cumulative sum (CUSUM) algorithm,³⁸ charge conservation,³⁹ and probabilistic machine-learning techniques. ^20,40 While these approaches are effective when the residence times of analytes in the nanopore are long (compared to the characteristic time constant of the system), they are not useful for characterizing short-lived events. To more accurately characterize short events, we developed a technique that models the ionic current response with an equivalent electrical circuit.^26,41 This algorithm, when applied to the interaction of a polydisperse mixture of a synthetic polymer with the Staphylococcus aureus α-hemolysin (αHL) nanopore, recovered 18-fold more events per unit time at high measurement bandwidth (B = 100 kHz), reduced the constraints on data acquisition by permitting polymers to be separated at lower bandwidth (B = 10 kHz), and improved the resolving power in the low mass regime (to polymers with molecular weight ≈ 370 g/mol).

Here, we describe Modular Single-Molecule Analysis Interface (MOSAIC), an improved data analysis tool for analyzing nanopore data. We implemented two algorithms in MOSAIC: ADEPT, the equivalent electrical circuit model described above,^26,41 and an improved version of CUSUM that is suitable for analyzing events with relatively long residence times in the pore. The software is extensible, and allows many commonly used data formats, signal conditioning, and data processing algorithms to be seamlessly integrated. Below, we demonstrate the features and utility of MOSAIC when applied to data measured with both biological and solid-state nanopores.

MATERIALS AND METHODS

Solid-State Nanopore Measurements

Solid-state nanopore data were reanalyzed from Briggs et al.⁴² Briefly, nanopores were fabricated in 50 μm × 50 μm, 10 nm thick low-stress silicon nitride (SiN_x) TEM windows (Norcada, Canada) via the controlled breakdown (CBD) method⁴⁷ in a 1 M NaCl buffer (pH 10, 10 mM NaHCO₃). Nanopore measurements of double-stranded DNA (dsDNA) were performed in 3.6 M LiCl, 10 mM HEPES (pH 8) using highly purified 50 base pair (bp) dsDNA fragments (NoLimits no. SM1421, Life Technologies). Data were low-pass filtered at 100 kHz with a hardware 4-pole Bessel filter (Axopatch 200B) and digitized using a National Instruments USB-6351 DAQ card (Austin, TX) at a sampling rate, F_s = 500 kHz.

Biological Nanopore Measurements

Nanopore measurements were performed using quartz capillaries with a (≈ 1 μm diameter) aperture on one end,^26,43,44 within a custom polycarbonate test cell with ≈ 200 μL volume (Electronic Biosciences, San Diego, CA). Analytes were dissolved in the working buffer and added directly into the capillary or to the external test cell.

For single-stranded DNA measurements, the quartz capillary was filled with a 10–20 μM solution of different length homopolymeric adenosine dA₂₀, dA₄₀, or dA₁₀₀ (Integrated DNA Technologies, Coralville, IA) dissolved in 1 M NaCl, 1× TE buffer (10 mM Tris, 1 mM EDTA in DNase-free water, titrated to pH 7.2 with 3 M HCl).

For poly(ethylene glycol) measurements (PEG), data from two previous studies that span a wide range of polymer sizes were combined.^22,26 In both cases, the capillary was filled with a solution containing a combination of polydisperse PEG (Fluka, Switzerland) and a highly purified calibration standard (Polypure, Oslo, Norway), dissolved in 4 M KCl (Sigma-Aldrich, St. Louis, MO), buffered with 10 mM Tris (Schwarz/Mann Biotech, Cleveland, OH) and titrated to pH 7.2 with 3 M citric acid. The two different solutions were as follows: (a) 20 μM PEG-600 (MW_avg = 600 g/mol), 40 μM PEG-400 (MW_avg = 400 g/mol) and 2 μM purified PEG-502 (M_w = 502 g/mol) or (b) 30 μM PEG-1000 (MW_avg = 1000 g/mol), 30 μM PEG-1500 (MW_avg = 1500 g/mol), and 1 μM purified PEG-1251 (M_w = 1251 g/mol).

Planar lipid bilayers were formed across the quartz capillary aperture using a 10 mg/mL solution of 1,2 diphytanolyl-sn-glycero-3-phosphatidylcholine (DPhyPC; Avanti Polar Lipids, Alabaster, AL) in n-decane (Sigma-Aldrich).²⁶ Subsequently, wild-type S. aureus α-Hemolysin (αHL) was introduced to the test cell by adding a solution containing either ≈250 ng of monomeric αHL (List Biological Laboratories, Campbell, CA) or ≈2.5 ng of purified preformed heptamers. To facilitate channel incorporation, the bilayer was thinned and enlarged by applying a transmembrane potential of ≈300 mV and a static back pressure within the capillary. Following the insertion of a single channel, the static pressure was reduced and the voltage decreased to the value used for the measurement to prevent further channel incorporation.

The potential was applied across the membrane by a pair of Ag/AgCl electrodes. Immediately prior to use, the electrode placed within in the capillary was prepared by abrading an Ag wire (Alfa Aesar) with 600 grit sandpaper and soaking it in bleach for ≈10 min. The external electrode in the test cell bath was a 2 mm Ag/AgCl disk electrode (E202, In Vivo Metric). Data were acquired with a custom high-impedance amplifier system (Electronic BioSciences, San Diego, CA) and conditioned with a low-pass antialiasing filter. The analog signal was digitized by a National Instruments PCI-6120 DAQ card with a sampling rate (F_s) of 1 MHz, further conditioned using a software-based 8-pole low pass Bessel filter with a cutoff frequency of 100 kHz and resampled at 500 kHz.

Data Processing and Analysis

Nanopore data were processed using a Python based program (MOSAIC) developed in-house. The software implements the ADEPT and CUSUM+ algorithms, which are described below. The compiled program and source code are freely available at https://pages.nist.gov/mosaic/. MOSAIC consists of a modular data processing pipeline which allows users to analyze ionic current data from single-molecule nanopore experiments. The software is designed using object-oriented principles, which ensures that modules remain interoperable. This also makes it straightforward to implement new features into the software, such as alternative analysis algorithms or custom data formats. In many cases, users can interact with MOSAIC using a front end graphical user interface.

Algorithms

MOSAIC consists of a pipeline with five modules: (i) load data, (ii) optional signal conditioning and filtering, (iii) event detection, (iv) event analysis, and (v) results storage. A detailed description of the software architecture is presented in the Supporting Information.

In this section, we discuss two algorithms implemented in MOSAIC: (i) CUSUM+, an improved version of the CUSUM algorithm³⁸ that provides robust statistical analysis of events which converge to a steady-state, and (ii) ADEPT, an implementation of a previously developed theory^26,41 that uses a physical model of the nanopore system to accurately characterize very short events that do not approach a steady-state ionic current.

Cumulative Sum Analysis (CUSUM+)

Cumulative Sum (CUSUM) is a commonly used method to detect step-like changes in time-series data⁴⁵ but was only recently implemented in nanopore analysis.³⁸ It assumes that the interaction of an analyte with the pore causes a series of instantaneous changes in the ionic current from its baseline value (defined as states and well-approximated by step functions⁴⁵), and the ionic current noise follows a known distribution (e.g., Gaussian). A statistical test identifies when the current level changes. The instantaneous log-likelihood ratios of sequential data points for both positive and negative step changes are calculated. The positive values of these ratios are independently summed and a negative log-likelihood resets the sum to zero. These form a two-sided decision function, which detects level changes that correspond to either an increase or decrease in the current level. A new state is identified when one of the decision functions exceeds a threshold determined automatically by the software. The locations of state changes are determined from the minima of related functions,⁴⁵ and the mean ionic current between sequential states is calculated and used to determine the local blockade depth, defined as ratio of the ionic current when the pore is occupied to that of the open pore (〈i〉/〈i₀〉, Figure 1C).

We implemented an improved version of the CUSUM algorithm in MOSAIC (CUSUM+), which is less sensitive to artifacts that can be falsely identified as a state change. This is achieved by specifying a minimum time between successive triggers (to exclude transients from the state change detection and blockade depth calculations) and by requiring that identified state levels differ by a minimum value (corresponding to a physically significant change). The efficiency is improved by eliminating or reducing redundant computations (e.g., maintaining running calculations of the mean and variance).

Adaptive Time-Series Analysis (ADEPT)

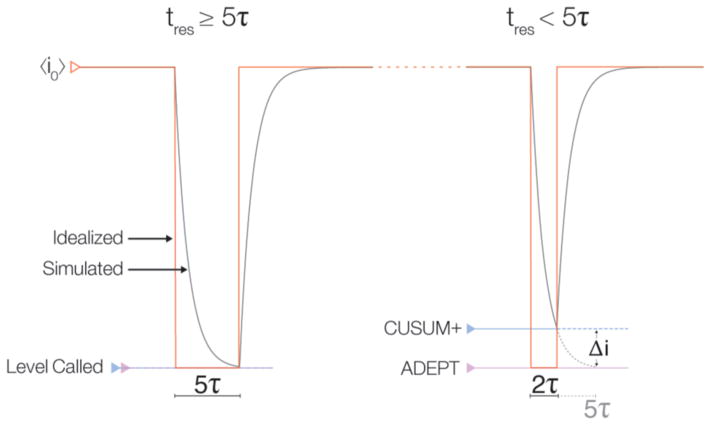
For very long events (>5τ, Figure 2 left), the blockade depth is easily estimated (e.g., with CUSUM+). However, that process fails for short-lived events (<5τ, Figure 2 right) that do not reach a steady-state mean value. In this case, the blockade depths are estimated by fitting the data to an electrical circuit model of the nanopore (implemented as ADEPT^26,41 in MOSAIC). The algorithm assumes a molecule partitioning into the nanopore instantaneously increases the nanopore resistance (R_p) by ΔR. However, the system capacitance causes the ionic current change to occur over a finite time. For a constant applied voltage, V_a, the predicted ionic current is i(t) = i₀ − β(1−e^−t/τ), where $i_0=\frac{V_{\mathrm{a}}}{R_{\mathrm{s}}+R_{\mathrm{p}}},\beta =\frac{V_{\mathrm{a}}\mathrm{\Delta }R}{(R_{\mathrm{s}}+R_{\mathrm{p}}+\mathrm{\Delta }R)(R_{\mathrm{s}}+R_{\mathrm{p}})}$, and $\tau =\frac{C_{\mathrm{m}}{R}_{\mathrm{s}}(R_{\mathrm{p}}+\mathrm{\Delta }R)}{R_{\mathrm{s}}+R_{\mathrm{p}}+\mathrm{\Delta }R}$. The difference between the time constants (τ) leading up to and following an event are much shorter than typical sampling rates (see the Supporting Information for the calculation). We therefore use a single fit parameter for τ, which reduces the degrees of freedom. There is an option to override this constraint.

Figure 2.

ADEPT and CUSUM+ analysis applied to a simulated nanopore measurement (gray). Two events with the same current blockade (red) but different residence times (t_res), with respect to the system characteristic relaxation time (τ) are shown. (Left) For a long event (t_res ≥ 5τ), the ionic current converges close to its steady-state value, and the current levels estimated by ADEPT and CUSUM+ are equivalent. (Right) For short events (e.g., t_res ≈ 2τ), the current does not reach the steady-state value of the idealized pulse (red). In this case, CUSUM+ and other algorithms used in nanopore analysis systematically underestimate the steady-state current (blue) by an amount Δi (gray; dashed). In contrast, the physical model underlying ADEPT allows the algorithm to accurately estimate an event’s steady-state current.

RESULTS AND DISCUSSION

Analysis of Short dsDNA Fragments Measured with SiN_x Nanopores

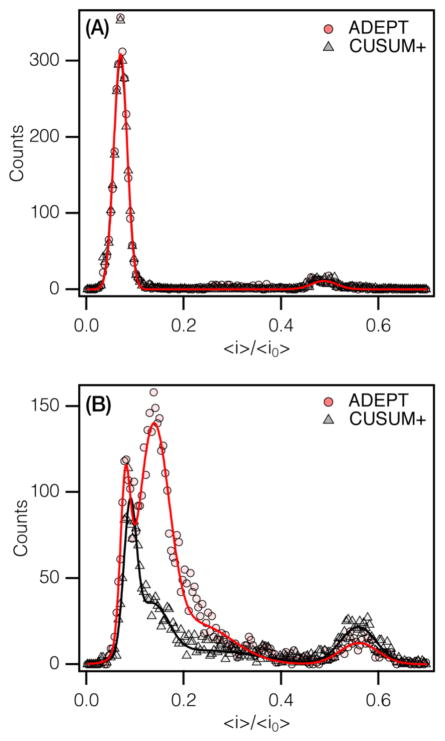
We compared the results of CUSUM+ and ADEPT on measurements of 50 base pair (bp) double-stranded DNA (dsDNA) translocating through a ≈2.4 nm diameter SiN_x nanopore (≈2800 events).⁴² At an applied potential of 400 mV, the mean residence time of dsDNA in the pore is ≈440 μs, more than an order of magnitude longer than the characteristic time constant of the system (τ = 10 μs; B = 100 kHz). Both algorithms produce two distinct peaks in the blockade depth histogram (〈i〉/〈i₀〉 = 0.070 ± 0.001 and 0.488 ± 0.004). Peak positions were obtained using an error-weighted Gaussian fit and are reported with an expanded uncertainty, k = 2 (see Supporting Information for a full listing of the analysis and fit parameters). The leftmost peak corresponds to DNA translocation, whereas the rightmost peak is likely due to the helical structure of dsDNA unwinding to transition from the B-form to the S-form dsDNA,^46,47 where the chain elongates by 1.7 fold because of the strong electric field gradient across the pore.⁴²

At 800 mV, the blockade depth histogram produced by ADEPT has two overlapping peaks (Figure 3B) consisting of a narrow peak (〈i〉/〈i₀〉 = 0.080 ± 0.002), the expected location for B-form dsDNA,⁴⁶ and a broader peak (〈i〉/〈i₀〉= 0.138 ± 0.002). The latter is comprised of short, single-level events, which likely result from transient interactions between the dsDNA and the access region outside the pore.⁴⁸ This was not accurately identified in our previous analysis⁴² (see below). A third, low amplitude, broad peak is visible at 〈i〉/〈i₀〉 = 0.226 ± 0.018. It is probable that this peak is associated with these access-region interactions. Alternatively, it is possible that these events could represent partial unwinding of the dsDNA secondary structure at forces below the B–S stretching transition threshold.⁴⁷ As seen in Figure 3B, CUSUM+ also detects the first peak, 〈i〉/〈i₀〉 = 0.090 ± 0.002 (albeit slightly shifted compared to the ADEPT value). However, it only characterizes ≈20% of the events in the second peak (〈i〉/〈i₀〉 = 0.134 ± 0.010) where the mean residence time of the events (〈t_res〉 = 47 ± 4 μs) is less than 5τ. In addition, CUSUM+ misses most of the events from the third peak detected with ADEPT. While CUSUM+ could be allowed to characterize events with lifetimes less than 5τ, it will underestimate the blockade depth ratios (see the Supporting Information, Figure S3). Both algorithms identify the fourth peak (〈i〉/〈i₀〉 ≈ 0.56), which arises from the stretching transition of dsDNA noted above (S-form of dsDNA^46,47). CUSUM+ recovers more events here than ADEPT, which utilizes a fitting routine that may not converge for some very long events (t_res > 25 ms; 50 000 points; F_s = 500 kHz). Clearly, the results would be improved if ADEPT is used for relatively short-lived events and CUSUM+ is used on events with residence times >5τ (Supporting Information, Figure S4). This functionality will be implemented in a future version of MOSAIC.

Figure 3.

Blockade depth histograms for a 50 base pair double-stranded DNA measured with a 2.4 nm diameter SiN_x nanopore.⁴² (A) At 400 mV, both CUSUM+ (gray), and ADEPT (red) are in excellent agreement. (B) At 800 mV, the mean residence time decreases to ≈36 μs (estimated from ADEPT analysis). The analyses by ADEPT and CUSUM+ are markedly different.

While both CUSUM+ and ADEPT produce comparable results for events with residence times >5τ, CUSUM+’s statistical approach is on average ≈10× faster than the Levenberg–Marquardt least-squares fitting used in ADEPT.⁴⁸ Therefore, CUSUM+ is preferred for events with mean residence times considerably longer than the recovery time of the system (≫5τ). Furthermore, the processing time per event for each algorithm scales linearly with the residence time, and therefore the number of data points in an event (see Supporting Information, Figure S5).

Analysis of Single-Stranded DNA Oligonucleotides with ADEPT

We use ADEPT to determine the blockade depth ratio histograms for three different length single-stranded DNA (ssDNA) homopolymers (dA₁₀₀, dA₄₀, and dA₂₀) entering an αHL nanopore from the cis side.⁴⁹ We consider events with up to 6 discrete states, with each state containing at least 5 data points (t_res > 10 μs, F_s = 500 kHz). Events are partitioned from the time series data with a thresholding algorithm that identifies when the current deviates by more than 5 standard deviations from the mean open channel current. A complete listing of the analysis parameters is shown in Supporting Information, Table S3.

The current blockades observed with poly(dA) appear as either one level (a shallow or deep blockade) or two levels (a shallow blockade followed by a deeper one^8,50,51). Approximately 60% of the events have two levels. As shown in the blockade depth ratio histograms for dA₁₀₀, dA₄₀, and dA₂₀ (Figure 4), these two observed levels are comprised of several different states. Figure 4A shows that the blockade depth histogram for dA₁₀₀ has three peaks, 〈i〉/〈i₀〉 = (0.11 ± 0.03), (0.15 ± 0.05), and (0.50 ± 0.05). The first two peaks (denoted 〈i〉/〈i₀〉_3′ and 〈i〉/〈i₀〉_5′) are consistent with the dependence of the blockade depth on the orientation of the leading end of the DNA (3′ vs 5′) entering the pore.^4,52,53 The location of these two peaks agrees with previous measurements of dA₁₀₀ where two highly overlapping peaks were observed at these locations.⁶ In contrast to earlier measurements we resolve the 3′ and 5′ events with a separation better than 3σ.

Figure 4.

Normalized blockade depth histograms for (A) dA₁₀₀, (B) dA₄₀, and (C) dA₂₀ single-stranded DNA interacting with the αHL nanopore estimated using the ADEPT algorithm. The applied potential is V = 140 mV and the polynucleotides are added to the cis side of the pore.⁴⁹

The differences between the 3′ and 5′ blockade depth peaks (Figure 4A, two leftmost peaks) are progressively more difficult to discern for the shorter polynucleotides (Figure 4B,C). The amplitude of the 5′ peak decreases substantially for dA₄₀ (Figure 4B) and is not resolved for dA₂₀ (Figure 4C). These results are likely due to the lower probability of the 5′-end entering the pore and the decreasing residence time of shorter ssDNA molecules.^4,53

Interestingly, the shallow blockade level (〈i〉/〈i₀〉 ≈ 0.5) is characterized by a single peak for dA₁₀₀ and dA₄₀ and two peaks for dA₂₀. Previous studies have either not reported this peak⁶ or only noted it for molecules as short as dA₅₀.⁵⁰ Furthermore, the sharp decrease in residence time associated with shorter polymers complicates their analysis and has thus far limited the analysis of polynucleotides as short as dA₂₀.

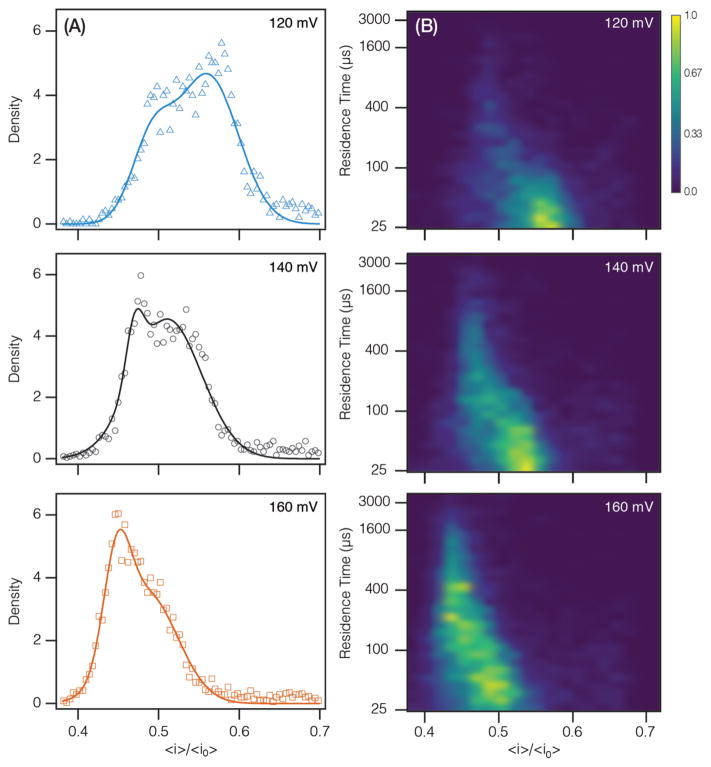
The algorithms within MOSAIC improve the characterization of short polynucleotides. Figure 5 shows the voltage-dependent behavior of the dA₂₀ shallow blockade peaks and their residence time distributions. The shallow blockade depth distributions are qualitatively different than those measured for longer polymers (Figure 4), as noted previously. Furthermore, we observe a change in the morphology of the peaks with increasing voltage as seen in Figure 5A. In particular, increasing the magnitude of the applied potential: (i) shifts the peaks to smaller 〈i〉/〈i₀〉 values, i.e., the polynucleotide blocks more current (Figure 5A), (ii) increases the residence times (Figure 5B) (in contrast to the mean residence time of the deep blockades in Figure 4 that are associated with translocation),^4,5 and (iii) increases the number of events observed per unit time (capture rate) (see the Supporting Information, Figure S7). Moreover, with increasing voltage, the shallow blockades were more likely to exhibit two states with the shallow blockade preceding a deep blockade.

Figure 5.

Voltage dependence of dA₂₀ shallow blockade depth and residence time. (a) The normalized blockade depth histogram as a function of voltage yields peaks with changing morphology. (B) Joint residence time-blockade depth distribution (log–linear) as a function of voltage. Z-scale (color) was normalized and smoothed using a Gaussian interpolation.

The above results strongly suggest that the shallow blockade peaks correspond to dA₂₀ interacting with the vestibule but not translocating through the pore. Furthermore, the observed increase in the residence time of the shallow blockade (Figure 5B) with voltage suggests that the change in the leftmost peak amplitude in Figure 5A is likely due to interactions between the analyte and different regions of the vestibule, rather than a loss of signal. Interestingly, of the three measured analytes (dA₁₀₀, dA₄₀, dA₂₀), this voltage-dependent change in peak structure was only observed with dA₂₀, indicating that the phenomenon may be length-dependent.^49,54

Example of Using MOSAIC: Single Molecule Mass Spectrometry with a Biological Nanopore

We show a typical analysis using MOSAIC’s graphical user interface. Specifically, we use both CUSUM+ and ADEPT to separate monomers in polydisperse PEG samples with an αHL nanopore.^{20–22,26,55,56} Previous studies showed that the blockade depth ratio (〈i〉/〈i₀〉) and mean residence time of these events scale monotonically with polymer size.

Analysis of the PEG data is set up using the GUI shown in Figure 6 and is configured using drop down menus. After selecting a data source (MOSAIC accepts most common electrophysiology data formats: Axon ABF, QUB QDF, as well as raw binary and comma separated value, CSV, data), a segment of the time series is displayed, which assists in determining the mean open channel current (<i₀>), noise (σ_i0) and threshold values for preliminary event identification.

Figure 6.

Graphical user interface (GUI) used to setup and run an analysis in MOSAIC. A main settings window is used to configure the analysis. The results of an analysis are displayed in real-time in the adjacent panels. Completed analysis can also be reexamined within the GUI by opening the saved database files.

A key feature of MOSAIC is the ability to integrate custom algorithms into the processing pipeline. Within the GUI, the user can select the analysis algorithm. The PEG data were analyzed independently using both the ADEPT and CUSUM+ algorithms. The blockade depth histogram of the events and the processing statistics are presented in real time. Fits of the physical model (ADEPT) or detected states (CUSUM+) of individual analyzed events are also displayed to monitor the progress and quality of the analysis. The results are stored in a SQLite database (or can be exported as a CSV file from within the GUI) for further analysis.

This example further illustrates the differences between the CUSUM+ and ADEPT algorithms. Only events that deviate from the open channel current baseline by at least 2.7σ were analyzed. Events shorter than 5τ were excluded from the CUSUM+ analysis (the default value when running CUSUM+ from the GUI). On the other hand, when using ADEPT, we excluded events shorter than 2.5τ (25 μs) to minimize fitting errors (set with the Advanced Settings dialogue in the GUI).

Both algorithms produce well-resolved peaks for PEGs larger than 17-mers (Figure 7 and Supporting Information, Figure S8). For smaller PEGs that have shorter mean residence times, CUSUM+ shows a single broad peak whereas ADEPT easily identifies additional individual species. Here, CUSUM+ recovers significantly fewer events than ADEPT because only a fraction of the total events (those with t_res > 5τ) are considered. This effect is particularly significant because it amounts to examining the tail of the exponentially distributed lifetimes.^20,21

Figure 7.

Comparison of ADEPT (gray) and CUSUM+ (blue) analyses of a polydisperse polyethylene glycol (PEG) solution measured with an αHL nanopore. Blockade depth histogram of events recovered by each algorithm show that the number of events recovered by CUSUM+ decreases sharply for small polymers (n < 20) that exhibit fast residence times (<5τ) in the pore.

The histograms in Figure 7 are fit to a sum of Lorentzian functions using Igor Pro 6.3 (Wavemetrics Inc., Portland, OR). To directly compare the blockade depth histograms, we use the peak positions from the ADEPT data set as initial guesses for a fit of the CUSUM+-derived blockade depth distribution (Figure 7, gray). As expected, for both algorithms, where the peaks are resolved, the peak positions are in good agreement. For PEGs (n < 17), the signal-to-noise ratio of the CUSUM+ peaks is lower than those recovered by ADEPT (Supporting Information, Figure S8), consistent with the lower number of events recovered by CUSUM+ in this region.

CONCLUSIONS

We developed a new open source platform for the analysis of single-molecule data (MOSAIC) and implemented two robust optimized algorithms (ADEPT and CUSUM+) for biological or solid-state nanopore measurements. When applied to dsDNA measurements with a 2.4 nm SiN_x nanopore, MOSAIC found previously undetected states most likely arising from the transient interactions between dsDNA and the access region of the solid-state pore. Additionally, when measuring short oligonucleotides poly(dA)_n, MOSAIC accurately analyzed events with residence times <5τ, thereby characterizing previously unreported interactions of dA₂₀ with the αHL nanopore. Such analysis can be used to provide greater insight into the underlying physics of analyte-nanopore interactions.