A Multi-Dimensional Functional Principal Components Analysis of EEG Data

Summary

The electroencephalography (EEG) data created in event-related potential (ERP) experiments have a complex high-dimensional structure. Each stimulus presentation, or trial, generates an ERP waveform which is an instance of functional data. The experiments are made up of sequences of multiple trials, resulting in longitudinal functional data and moreover, responses are recorded at multiple electrodes on the scalp, adding an electrode dimension. Traditional EEG analyses involve multiple simplifications of this structure to increase the signal-to-noise ratio, effectively collapsing the functional and longitudinal components by identifying key features of the ERPs and averaging them across trials. Motivated by an implicit learning paradigm used in autism research in which the functional, longitudinal and electrode components all have critical interpretations, we propose a multidimensional functional principal components analysis (MD-FPCA) technique which does not collapse any of the dimensions of the ERP data. The proposed decomposition is based on separation of the total variation into subject and subunit level variation which are further decomposed in a two-stage functional principal components analysis. The proposed methodology is shown to be useful for modeling longitudinal trends in the ERP functions, leading to novel insights into the learning patterns of children with Autism Spectrum Disorder (ASD) and their typically developing peers as well as comparisons between the two groups. Finite sample properties of MD-FPCA are further studied via extensive simulations.

1. Introduction

Electroencephalography (EEG) is a well-established noninvasive method for measuring spontaneous electrical activity across brain regions to identify neural function and cognitive states. Our motivating data is from a visual implicit learning study on young children with autism spectrum disorder (ASD) (Jeste et al., 2015). The experiment involved event-related potentials (ERP) in which EEG signals were time locked to the presentation of a continuous sequence of colored shapes (visual stimuli) recorded in age-matched 2 to 5 year old typically developing and ASD children (Figure 1(a)). The six colored shapes, grouped into three shape pairs, were presented in random order. Transitions within a shape pair were labeled ‘expected’ since they could be learned (shape ordering within a pair was fixed) and transitions between shape pairs were labeled ‘unexpected’ since they could not be predicted. The goal of the study was to characterize implicit learning, defined as the detection of regular patterns in one’s environment without a conscious awareness or intention to learn, by contrasting brain response to expected and unexpected transitions.

Figure 1.

(a) The sequence of shape pairs in the implicit learning study. Transitions within a shape pair are labelled ‘expected’ (square and cross are a shape pair, so that the cross always follows the square); transitions between shape pairs are labelled ‘unexpected’. (b) The ERP waveform containing the P3 and N1 phasic components from the implicit learning study.

The data created in typical ERP studies as the one described above are rich and multidimensional. Each stimulus, corresponding to the presentation of a single shape, referred to as a trial, results in an ERP function with paradigm-specific phasic components. The P3 peak and N1 dip phasic components typically studied in this paradigm and thought to be related to cognitive processes and early category recognition are given in Figure 1(b) (Jeste et al., 2015). Hence the experiment creates functional data (ERP curves) for each subject, collected longitudinally over trials (presentation of each shape) at multiple electrodes placed on the scalp. Due to the richness and multifaceted nature of the data along functional, longitudinal and electrode dimensions (repetitions over electrodes), typical practice involves multiple simplifications of the data before analysis. To increase the low signal-to-noise ratio (SNR) in raw ERP data, data are first collapsed in the longitudinal dimension, in which ERP functions observed over trials are averaged for each subject (Jeste et al., 2015; Gasser and Molinari, 1996). In addition, aside from a few works on functional mixed effects modeling for the analysis of ERP data (Bugli and Lambert, 2006; Davidson, 2009), the functional dimension is typically summarized by the amplitude (magnitude of the peak or dip) or latency (time when the peak or dip occurs) of the phasic components of the averaged ERP functions. Hence, once both functional and longitudinal dimensions have been collapsed into one-dimensional data summaries, a repeated measures ANOVA can be used for analysis.

In this paper we propose, for the first time in the literature, a longitudinal principal components decomposition for the EEG data, which we refer to as multi-dimensional functional principal components analysis (MD-FPCA). MD-FPCA embodies all three dimensions (functional, longitudinal and electrode) of the ERP data, preserving the full complexity without stringent assumptions or data reduction. In order to increase the SNR without collapsing the longitudinal dimension over trials, we adopt MAP-ERP, a meta-preprocessing step based on a moving average of the ERP functions over trials in a sliding window (Hasenstab et al., 2015). Capturing the longitudinal dimension is especially important in settings such as our motivating example, where patterns of learning correspond by definition to changes in ERP functions across trials. Previous studies in neuroscience and biomedical engineering have acknowledged that ERP function morphology may change over the course of a task. However, most prior work has focused on controlling for longitudinal trends (Gasser et al., 1983; Turetsky et al., 1989) rather than modeling them; the few works on modeling longitudinal trends have been limited to parametric forms (Rossi et al., 2007; De Silva et al., 2012). We will build our proposed MD-FPCA on data produced by the novel meta-preprocessing step, MAP-ERP, capturing the continuum of longitudinal dynamics.

The literature on functional data analysis (FDA) (Ramsay and Silverman, 2005) has grown rapidly over the past two decades, with a considerable fraction of the work involving applications to longitudinal data (James et al., 2000; Müller, 2008; Sentürk and Müller, 2010). More recently, there has been interest in analyzing multiple trajectories, with dependencies among the repeatedly measured functional data (Crainiceanu et al., 2009; Di et al., 2009; Kundu et al., 2016; Morris and Carrol, 2009; Morris et al., 2003; Zupinnikov et al., 2011). Functional principal components decompositions for multilevel or longitudinal functional processes have been a major modeling theme in the FDA literature. Di et al. (2009) suggested decomposing sources of functional variation in an additive fashion via multilevel ANOVA, which we refer to as the ANOVA functional principal components decomposition (ANOVA-FPCA). Greven et al. (2010) proposed a decomposition based on a functional random intercept and slope to capture longitudinal variations, which we refer to as linear FPCA (LFPCA). Chen and Müller (2012) suggested a double decomposition (DFPCA) to capture potential nonlinear and nonparametric longitudinal trends within repeatedly observed functional data; parsimonious extensions of DFPCA have recently been proposed by Park and Staicu (2015) and Chen et al. (2016). While ANOVA-FPCA models longitudinal repetitions as repeated measurements without a particular time ordering, similar to an ANOVA, LFPCA models longitudinal trends linearly, and DFPCA does not assume a parametric form. For spatially correlated functional data, Delicado et al. (2010) summarize limited works in three categories, analysis of geostatistical functional data (Baladandayuthapani et al., 2008; Giraldo et al., 2010; Zhou et al., 2010; Staicu et al., 2010; Liu et al., 2016) (mostly involving distance-based parametric correlation structures), point processes with associated functional data and functional areal data.

Our proposed MD-FPCA combines the flexible DFPCA modeling of longitudinal trends, especially important for modeling learning trajectories in the motivating implicit learning experiment, with the decomposition of the total variation into subject and electrode level components as in ANOVA-FPCA, to embody all the dimensions of the multidimensional ERP data. MD-FPCA induces correlation between the electrode repetitions via random effects and utilizes multilevel random effects for extensions that involve data from multiple scalp regions. Following the initial ANOVA decomposition of the total variation, the proposed MD-FPCA involves a two-stage functional principal components decomposition of the subject and electrode level variations across functional and longitudinal time, leading to highly interpretable components contributing to the principal surfaces in a multiplicative fashion. Hence, even though multiple decompositions have been proposed for longitudinally observed or spatially correlated functional data in the literature, MD-FPCA is the first decomposition proposed for repeatedly measured longitudinal functional data which is tailored to model the specific features of the EEG data produced in ERP studies.

The remainder of the paper is organized as follows. Section 2 introduces the proposed MD-FPCA approach, compares it with other recently proposed functional principal components decompositions for longitudinally observed functional data, and outlines the extension of the methodology to analysis of data from multiple scalp regions. Section 3 provides insights gained from the implicit learning application, including comparisons of learning patterns in ASD and TD groups, summarized via the longitudinal trends in ERP functions across the experiment. We study the performance of the proposed decomposition in extensive simulation studies summarized in Section 4 and conclude with a brief discussion in Section 5.

2. Multi-Dimensional Functional Principal Components Analysis (MD-FPCA)

2.1 The Proposed MD-FPCA Decomposition

Denote by X_ij(t|s) a multilevel square integrable random function observed across continuous functional time t, t ∈ $\mathcal{T}$, at longitudinal time s, s ∈ $\mathcal{S}$, for subunit j, j = 1, …, J, and subject i, i = 1, …, n. In applications to the EEG data, data collected over electrodes represent the subunits within subjects, functional time is the time scale of the ERP function and longitudinal time corresponds to trials. The notation, X_ij(t|s), for the multilevel longitudinal functional process is used to stress the two-stage nature of the Karhunen-Loève decompositions in MD-FPCA, where the first-stage expansions are conditional on a particular longitudinal time s, and second-stage decompositions describe the variations along longitudinal time s. The function X_ij(t|s) is decomposed using a multilevel random effects model at each longitudinal time s,

$$X_{ij}(t|s)=\mu (t,s)+{\eta }_j(t,s)+Z_i(t|s)+W_{ij}(t|s)+{\epsilon }_{ij}(t|s),$$ (1)

where μ(t, s) and η_j(t, s) are fixed functional effects that represent the overall mean function and subunit-specific shifts, respectively; Z_i(t|s) and W_ij(t|s) are the random subject- and subunit-specific deviations, respectively; and ε_ij(t|s) is measurement error with mean zero and variance ${\sigma }_s^2$. Denote the total variation of X_ij(t|s) at a fixed longitudinal time s by Σ_T (t, t^′|s) = cov{X_ij(t|s), X_ij(t^′|s)} and let ${\mathrm{\sum }^{\sim }}_T(t,t\prime |s)=\mathrm{cov}\{X_{ij}(t|s),X_{ij}(t\prime |s)\}-{\sigma }_s^2{1}_{\{t=t\prime \}}$ be the total variation without the measurement error with 1_{A} denoting the indicator function for event A. Assuming the subject and subunit-specific deviations, Z_i(t|s) and W_ij(t|s), are uncorrelated mean zero stochastic processes, (1) implies separation of the total variation ${\mathrm{\sum }^{\sim }}_T(t,t\prime |s)$ at each longitudinal time s into subject level ${\sum }^{(1)}(t,t\prime |s)=\mathrm{cov}\{X_{ij}(t|s),X_{i{j}^{\prime }}(t\prime |s)\}={\displaystyle {\sum }_k{\mathrm{\lambda }}_k^{(1)}(s)}{\varphi }_k^{(1)}(t|s){\varphi }_k^{(1)}(t\prime |s)$ and electrode level ${\sum }^{(2)}(t,t\prime |s)={\mathrm{\sum }^{\sim }}_T(t,t\prime |s)-{\sum }^{(1)}(t,t\prime |s)={\displaystyle {\sum }_p{\mathrm{\lambda }}_p^{(2)}(s)}{\varphi }_p^{(2)}(t|s){\varphi }_p^{(2)}(t\prime |s)$ variation. Note that Σ⁽¹⁾(t, t^′|s) captures variation between electrodes within a subject and Σ⁽²⁾(t, t^′|s) represents the remaining second level variance; we refer to these quantities as subject and electrode level variations, respectively, to build intuition that this separation is analogous to an ANOVA decomposition. In this formulation, ${\varphi }_k^{(1)}(t|s)$ and ${\varphi }_k^{(2)}(t|s)$ are the first and second level eigenfunctions, describing modes of variation across functional time t at each longitudinal time s, and ${\mathrm{\lambda }}_k^{(1)}(s)$ and ${\mathrm{\lambda }}_p^{(2)}(s)$ are the first and second level eigenvalues.

Note that while the terminology ‘level’ is used to refer to the separation of the variation into the subject and electrode components, ‘stage’ is going to be used to refer to the two subsequent functional principal components decompositions applied to the deviation/variance defined at each level, first conditional on a particular longitudinal time s, and second describing variations along s. The first-stage Karhunen-Loève decompositions for $Z_i(t|s)={\displaystyle {\sum }_k{\xi }_{ik}(s)}{\varphi }_k^{(1)}(t|s)$ and $W_{ij}(t|s)={\displaystyle {\sum }_p{\xi }_{\mathit{ijp}}(s)}{\varphi }_k^{(2)}(t|s)$ are carried out at each s, yielding

$$X_{ij}(t|s)=\mu (t,s)+{\eta }_j(t,s)+{\displaystyle \sum _{k=1}^{\infty }{\xi }_{ik}(s)}{\varphi }_k^{(1)}(t|s)+{\displaystyle \sum _{p=1}^{\infty }{\zeta }_{\mathit{ijp}}(s){\varphi }_p^{(2)}(t|s)+{\epsilon }_{ij}(t|s),}$$

where ξ_ik(s) and ζ_ijp(s) are the first and second level eigenscores, respectively, such that var $\{{\xi }_{ik}(s)\}={\mathrm{\lambda }}_k^{(1)}(s)$ and var $\{{\zeta }_{\mathit{ijp}}(s)\}={\mathrm{\lambda }}_p^{(2)}(s)$. In practice, the decompositions are truncated at only a small number of eigencomponents K and P (Web Appendix A). Note that the subunit repetitions within a subject, W_ij(t|s) and hence ζ_ijp(s), are assumed to be independent across j, since the subunit dependency is modeled by the subject-specific random component Z_i(t|s). Next, the second-stage Karhunen-Loève decompositions for the first and second level eigenscores, ${\xi }_{ik}(s)={{\displaystyle {\sum }_{k\prime =1}^{\infty }\xi \prime }}_{ikk\prime }{\psi }_{kk\prime }^{(1)}(s),{\zeta }_{\mathit{ijp}}(s)={\displaystyle {\sum }_{p\prime =1}^{\infty }{{\zeta }^{\prime }}_{\mathit{ijp}p\prime }{\psi }_{pp\prime }^{(2)}(s)}$, yield

$$X_{ij}(t|s)=\mu (t,s)+{\eta }_j(t,s)+{\displaystyle \sum _{k=1}^{\infty }{\displaystyle \sum _{k\prime =1}^{\infty }{\xi \prime }_{ikk\prime }}}{\psi }_{kk\prime }^{(1)}(s){\varphi }_k^{(1)}(t|s)+{\displaystyle \sum _{p=1}^{\infty }{\displaystyle \sum _{p\prime =1}^{\infty }{{\zeta }^{\prime }}_{\mathit{ijp}p\prime }}}{\psi }_{pp\prime }^{(2)}(s){\varphi }_p^{(2)}(t|s)+{\epsilon }_{ij}(t|s).$$ (2)

In (2), ${\xi \prime }_{ikk\prime }$ and ${{\zeta }^{\prime }}_{\mathit{ijp}p\prime }$ are the eigenscores, ${\mathrm{\lambda }}_{kk\prime }^{(1)}=\mathrm{var}({\xi \prime }_{ikk\prime })$ and ${\mathrm{\lambda }}_{pp\prime }^{(2)}=\mathrm{var}({{\zeta }^{\prime }}_{\mathit{ijp}p\prime })$ are the eigenvalues and ${\psi }_{kk\prime }^{(1)}(s)$ and ${\psi }_{pp\prime }^{(2)}(s)$ are the eigenfunctions describing the modes of variation across longitudinal time of the first-stage eigenscores.

We propose two decomposition summaries for MD-FPCA that are important in identifying the contributions of different sources to the total variation in the analysis of the multilevel stochastic process X_ij(t|s). While the first quantity, $\rho (s)=\{{\displaystyle {\sum }_k{\mathrm{\lambda }}_k^{(1)}(s)}\}/\{{\displaystyle {\sum }_k{\mathrm{\lambda }}_k^{(1)}(S)}+{\displaystyle {\sum }_p{\mathrm{\lambda }}_p^{(2)}(s)}\}$, summarizes the proportion of variability explained by the subject level (first level) variation in the first-stage of MD-FPCA conditional on longitudinal time s, the second summary measure, $\rho =\{{\displaystyle {\sum }_k{\displaystyle {\sum }_{k\prime }{\mathrm{\lambda }}_{kk\prime }^{(1)}}}\}/\{{\displaystyle {\sum }_k{\displaystyle {\sum }_{k\prime }{\mathrm{\lambda }}_{kk\prime }^{(1)}}}+{\displaystyle {\sum }_p{\displaystyle {\sum }_{p\prime }{\mathrm{\lambda }}_{pp\prime }^{(2)}}}\}$, captures the overall proportion of variability explained by the subject level variation in both stages of the MD-FPCA across longitudinal time s. The two summaries can be viewed as extensions of the intra-cluster correlation of the linear mixed effects framework to the decomposition of multilevel longitudinally observed functional processes. The intraclass correlations can also be interpreted as the average correlation between two subunits from the same subject, conditional on and across longitudinal time s, respectively. In applications to ERP data, repetitions over electrodes are considered subunits; within-subject correlations between these repetitions provide insight into the similarity of the trends across electrodes.

2.2 Comparison to other Karhunen-Loève Decompositions

We briefly review three recently proposed principal components decompositions for functional processes, which are special cases of the proposed MD-FPCA, and highlight differences of MD-FPCA from a multilevel two-dimensional Karhunen-Loève decomposition. The three special cases are given without additive measurement error for simplicity. The ANOVA-FPCA of Di et al. (2009),

$$X_{ij}(t)=\mu (t)+{\eta }_j(t)+Z_i(t)+W_{ij}(t)=\mu (t,s)+{\displaystyle \sum _{k=1}^{\infty }{\xi }_{ik}{\varphi }_k^{(1)}(t)+}{\displaystyle \sum _{p=1}^{\infty }{\zeta }_{\mathit{ijp}}{\varphi }_p^{(2)}(t),}$$ (3)

is a special case of MD-FPCA, where the decomposition does not have a longitudinal component. The repeatedly observed functional process X_ij(t) is decomposed into an overall mean μ(t), a visit-specific mean η_j(t), a subject-specific deviation from the visit-specific mean Z_i(t) and a subject-visit-specific deviation W_ij(t). Similar to MD-FPCA, Z_i(t) and W_ij(t), which are called the first and second level deviations, respectively, are expanded using Karhunen-Loève decompositions with first and second level eigenscores ξ_ik and ζ_ijp and eigenfunctions ${\varphi }_k^{(1)}(t)$ and ${\varphi }_p^{(2)}(t)$, respectively. Note that repetitions of the functional process are modeled without a particular time ordering, similar to an ANOVA.

In contrast, the linear FPCA (LFPCA) of Greven et al. (2010) models longitudinal trends in a repeatedly observed functional process linearly. The double FPCA (DFPCA) decomposition of Chen and Müller (2012),

$$X_i(t|s)=\mu (t,s)+Z_i(t|s)=\mu (t|s)+{\displaystyle \sum _{k=1}^{\infty }{\xi }_{ik}(s)}{\varphi }_k(t|s)=\mu (t,s)+{\displaystyle \sum _{k=1}^{\infty }{\displaystyle \sum _{p=1}^{\infty }{\zeta }_{\mathit{ikp}}{\psi }_{kp}(s){\varphi }_k(t|s),}}$$ (4)

does not assume a parametric form for the longitudinal time trend and thus can capture very flexible dynamics, similar to MD-FPCA. Note that the decomposition is for a longitudinally observed functional process that is not repeatedly observed, hence is a special case of MD-FPCA which considers the repeatedly observed longitudinal functional process X_ij(t|s) with subject-and subunit-specific deviations. In (4), X_i(t|s) is decomposed at a grid of longitudinal times s, yielding the mean function μ(t, s), eigenfunctions ϕ_k(t|s) and subject-specific random eigenscores ξ_ik(s) at the first-stage. The eigenscores at each longitudinal time s are then decomposed further at the second-stage to yield eigenscores ζ_ikp and eigenfunctions ψ_kp(s). Only decompositions LFPCA and DFPCA are suitable for situations in which interest centers on detecting changes in the ERP functions across longitudinal time. Moreover, in applications to the implicit learning paradigm, even LFPCA may be quite restrictive, since it requires these trends to be linear. Hence the proposed MD-FPCA combines the more flexible DFPCA to model longitudinal trends with ANOVA-FPCA to model repetitions over electrodes (the electrode dimension), enabling us to compare the nature of the implicit learning processes of children with ASD and their typically developing peers.

In comparing MD-FPCA to a multilevel two-dimensional Karhunen-Loève decomposition, note that the proposed MD-FPCA in (2) implies principal surfaces across both the functional and longitudinal domains,

$$X_{ij}(t|s)=\mu (t,s)+{\eta }_j(t,s)+{\displaystyle \sum _{k=1}^{\infty }{\displaystyle \sum _{k\prime =1}^{\infty }{\xi \prime }_{ikk\prime }{\phi }_{kk\prime }^{(1)}(t,s)}+{\displaystyle \sum _{p=1}^{\infty }{\displaystyle \sum _{p\prime =1}^{\infty }{{\zeta }^{\prime }}_{\mathit{ijp}p\prime }{\phi }_{pp\prime }^{(2)}(t,s)}+{\epsilon }_{ij}(t|s),}}$$ (5)

such that ${\phi }_{kk\prime }^{(1)}(t,s)={\varphi }_k^{(1)}(t|s){\psi }_{kk\prime }^{(1)}(s)$ is a product of the first- and second-stage eigenfunctions, describing the variation conditional on longitudinal time s and along longitudinal time s, respectively; similarly ${\phi }_{pp\prime }^{(2)}(t,s)={\psi }_{pp\prime }^{(2)}(s){\varphi }_p^{(2)}(t|s)$. However, the principal surfaces ${\phi }_{kk\prime }^{(1)}(t,s)$ and ${\phi }_{pp\prime }^{(2)}(t,s)$ in (5) are not the eigenfunctions of the unconditional subject and subunit level covariance operators. In other words, the proposed MD-FPCA is distinct from a multilevel two-dimensional Karhunen-Loève decomposition with eigenscores θ_ik and ν_ijp and two-dimensional orthogonal eigenfunctions ${\omega }_k^{(1)}(t,s)$ and ${\omega }_p^{(2)}(t,s)$,

$$X_{ij}(t,s)=\mu (t,s)+{\eta }_j(t,s)+{\displaystyle \sum _{k=1}^{\infty }{\theta }_{ik}{\omega }_k^{(1)}}(t,s)+{\displaystyle \sum _{p=1}^{\infty }{\nu }_{\mathit{ijp}}{\omega }_p^{(2)}(t,s)+{\epsilon }_{ij}(t,s)}.$$

For the multilevel two-dimensional Karhunen-Loève decomposition, the unconditional total covariance of X_ij(t, s) minus measurement error, ${\mathrm{\sum }^{\sim }}_T(t,s,t\prime ,s\prime )=\mathrm{cov}\{X_{ij}(t,s),X_{ij}(t\prime ,s\prime )\}-{\sigma }_s^2{1}_{\{t=t\prime ,s=s\prime \}}$, would be decomposed into subject ${\sum }^{(1)}(t,s,t\prime ,s\prime )=\mathrm{cov}\{X_{ij}(t,s),X_{i{j}^{\prime }}(t\prime ,s\prime )\}$ and subunit level ${\sum }^{(2)}(t,s,t\prime ,s\prime )={\mathrm{\sum }^{\sim }}_T(t,s,t\prime ,s\prime )-{\sum }^{(1)}(t,s,t\prime ,s\prime )$ covariances. Then the covariation at both the subject and subunit levels would be expanded with two-dimensional functional principal component expansions, ${\sum }^{(1)}(t,s,t\prime ,s\prime )={{\displaystyle {\sum }_k\tau }}_k^{(1)}{\omega }_k^{(1)}(t,s){\omega }_k^{(1)}(t\prime ,s\prime ),{\sum }^{(2)}(t,s,t\prime ,s\prime )={{\displaystyle {\sum }_p\tau }}_p^{(2)}{\omega }_p^{(2)}(t,s){\omega }_p^{(2)}(t\prime ,s\prime )$ with eigenvalues ${\tau }_k^{(1)}$ and ${\tau }_k^{(2)}$ and eigenfunctions ${\omega }_k^{(1)}(t,s)$ and ${\omega }_p^{(2)}(t,s)$.

A major advantage of the proposed MD-FPCA is that while the multilevel two-dimensional Karhunen-Loève decomposition would require decomposition and hence smoothing of multiple four-dimensional covariance surfaces at the subject and subunit levels, the proposed MD-FPCA involves decompositions of only two-dimensional covariance surfaces due to the two-stage structure, leading to ease in implementation and savings in computational costs. Conditioning on longitudinal time s at the first-stage lowers the dimension of the covariance surface considered at both stages of the proposed algorithm. A second major advantage, as will be demonstrated in our application to the implicit learning study, is in interpretations of the decomposition components. The two-stage structure leads to additional decomposition components, such as the first- and second-stage eigenfunctions, which help with the interpretation of complex variation patterns in higher dimensions.

2.3 Extension to Data From Multiple Scalp Regions

In applications to the ERP data from the implicit learning paradigm, we consider four electrodes in the right frontal region of the scalp where maximal condition differentiation is detected. Motivated by the exchangeable correlation structure among electrodes within the same scalp region observed in the longitudinal functional ERP data, MD-FPCA models electrode repetitions by a random effect similar to an ANOVA approach. However MD-FPCA can be extended within the same ANOVA framework for analysis of data from multiple regions of interest on the scalp by an additional level of random effects at the scalp region level to account for differences between electrodes from different regions.

Denote by X_irj(t|s) a multilevel square integrable random function observed across continuous functional time $t,t\in \mathcal{T}$, at longitudinal time $s,s\in \mathcal{S}$, for electrode j, j = 1, …, J, within scalp region r, r = 1, …, R, and subject i, i = 1, …, n. Separating the total variation into variability at the subject, region and electrode levels at each longitudinal time s leads to

$$X_{\mathit{irj}}(t|s)=\mu (t,s)+{\eta }_r(t,s)+{\alpha }_{rj}(t,s)+Z_i(t|s)+W_{ir}(t|s)U_{\mathit{irj}}(t|s)+{\epsilon }_{\mathit{irj}}(t|s),$$ (6)

where μ(t, s), η_r(t, s) and α_rj(t, s) are the overall mean function, region- and electrode-specific shifts, respectively; Z_i(t|s), W_ir(t|s) and U_irj(t|s) are the random subject-, region- and electrode-specific deviations, respectively; and ε_irj(t|s) is measurement error with mean zero and variance ${\sigma }_s^2$. Denote the total variation of X_ij(t|s) at a fixed longitudinal time s by ${\sum }_T(t,t\prime |s)=\mathrm{cov}\{X_{\mathit{irj}}(t|s),X_{\mathit{irj}}(t\prime |s)\}$ and let ${\mathrm{\sum }^{\sim }}_T(t,t\prime |s)=\mathrm{cov}\{X_{\mathit{irj}}(t|s),X_{\mathit{irj}}(t\prime |s)\}-{\sigma }_s^2{1}_{\{t=t\prime \}}$. Decomposition (6) implies separation of the total variation ${\mathrm{\sum }^{\sim }}_T(t,t\prime |s)$ at each longitudinal time s into subject level ${\sum }^{(1)}(t,t\prime |s)=\mathrm{cov}\{X_{\mathit{irj}}(t|s),X_{i{r}^{\prime }{j}^{\prime }}(t\prime |s)\}={\sum }_k{\mathrm{\lambda }}_k^{(1)}(s){\varphi }_k^{(1)}(t|s){\varphi }_k^{(1)}(t\prime |s)$ region level ${\sum }^{(2)}(t,t\prime |s)=\mathrm{cov}\{X_{\mathit{irj}}(t|s),X_{ir{j}^{\prime }}(t\prime |s)\}={\displaystyle {\sum }_p{\mathrm{\lambda }}_p^{(2)}(s)}{\varphi }_p^{(2)}(t|s){\varphi }_p^{(2)}(t\prime |s)$ and electrode level ${\sum }^{(3)}(t,t\prime |s)={\mathrm{\sum }^{\sim }}_T(t,t\prime |s)-{\sum }^{(1)}(t,t\prime |s)-{\sum }^{(2)}(t,t\prime |s)={\displaystyle {\sum }_v{\mathrm{\lambda }}_v^{(3)}}(s){\varphi }_v^{(3)}(t|s){\varphi }_v^{(3)}(t\prime |s)$ variation. The second-stage Karhunen-Loève decompositions applied to the eigenscores ${\xi }_{ik}(s)={\displaystyle {\sum }_{k\prime =1}^{\infty }{\xi \prime }_{ikk\prime }{\psi }_{kk\prime }^{(1)}}(s),{\zeta }_{\mathit{irp}}(s)={\displaystyle {\sum }_{p\prime =1}^{\infty }{{\zeta }^{\prime }}_{\mathit{irp}p\prime }{\psi }_{pp\prime }^{(2)}}(s)$ and ${\beta }_{\mathit{irj}v}(s)={\displaystyle {\sum }_{v^{\prime }=1}^{\infty }{{\beta }^{\prime }}_{\mathit{irj}v{v}^{\prime }}{\psi }_{v{v}^{\prime }}^{(3)}(s)}$ from the first-stage Karhunen-Loève decompositions, $Z_i(t|s)={\displaystyle {\sum }_k{\xi }_{ik}(s)}{\varphi }_k^{(1)}(t|s),W_{ir}(t|s)={\displaystyle {\sum }_p{\zeta }_{\mathit{irp}}(s)}{\varphi }_p^{(2)}(t|s)$ and $U_{\mathit{irj}}(t|s)={\displaystyle {\sum }_v{\beta }_{\mathit{irj}v}(s)}{\varphi }_v^{(3)}(t|s)$, yield the extended MD-FPCA decomposition

$$\begin{array}{l}{X}_{ij}(t|s)=\mu (t,s)+{\eta }_r(t,s)+{\alpha }_{rj}(t,s)+{\displaystyle \sum _{k=1}^{\infty }{\displaystyle \sum _{k\prime =1}^{\infty }{\xi \prime }_{ikk\prime }}}{\psi }_{kk\prime }^{(1)}(s){\varphi }_k^{(1)}(t|s)\\ +{\displaystyle \sum _{p=1}^{\infty }{\displaystyle \sum _{p\prime =1}^{\infty }{{\zeta }^{\prime }}_{\mathit{irp}p\prime }{\psi }_{pp\prime }^{(2)}(s){\varphi }_p^{(2)}(t|s)}}+{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{v^{\prime }=1}^{\infty }{{\beta }^{\prime }}_{\mathit{irj}v{v}^{\prime }}{\psi }_{v{v}^{\prime }}^{(3)}(s){\varphi }_v^{(3)}}}(t|s)+{\epsilon }_{ij}(t|s).\end{array}$$

Similar to MD-FPCA, ${\xi \prime }_{ikk\prime }$, ${{\zeta }^{\prime }}_{\mathit{irp}p\prime }$ and ${{\beta }^{\prime }}_{\mathit{irj}v{v}^{\prime }}$ denote the second-stage eigenscores, ${\mathrm{\lambda }}_k^{(1)}(s)=\mathrm{var}\{{\xi }_{ik}(s)\},{\mathrm{\lambda }}_p^{(2)}(s)=\mathrm{var}\{{\zeta }_{\mathit{irp}}(s)\}$ and ${\mathrm{\lambda }}_v^{(3)}(s)=\mathrm{var}\{{\beta }_{\mathit{irj}v}(s)\}$ are the first-stage eigenvalues, ${\mathrm{\lambda }}_{kk\prime }^{(1)}=\mathrm{var}({\xi \prime }_{ikk\prime }),{\mathrm{\lambda }}_{pp\prime }^{(2)}=\mathrm{var}({{\zeta }^{\prime }}_{\mathit{ijp}p\prime }),{\mathrm{\lambda }}_{v{v}^{\prime }}^{(3)}=\mathrm{var}({{\beta }^{\prime }}_{\mathit{irj}v{v}^{\prime }})$ are the second-stage eigenvalues and ${\psi }_{kk\prime }^{(1)}(s),{\psi }_{pp\prime }^{(2)}(s)$ and ${\psi }_{v{v}^{\prime }}^{(3)}(s)$ are the second-stage eigenfunctions.

Note that the above outlined extension models correlations between electrodes within a scalp region and correlations between electrodes across different scalp regions as exchangeable. While in our experience, the first assumption is easier to verify for EEG data, the second assumption may be relaxed by modeling spatial correlations between electrodes across different scalp regions based on anatomical distances between the scalp regions. Distance-based correlations can be modeled by the addition of a spatial process to the expansion in (6) similar to the approach taken by (Staicu et al., 2010). Authors model multilevel functional data where spatial correlations are modeled at the lowest level of the hierarchy via a random spatial process. For EEG applications, the random spatial process would be added at the region level rather than the lowest level of the hierarchy which is the electrode level. This extension requires further developments and is identified as a topic for future research. Finally note that both the mean and the random effects structures can include additional terms such as diagnostic group (e.g. ASD, TD) or condition (e.g. expected, unexpected) for incorporation of different experiment specific factors into MD-FPCA. For illustration of the methodology, we model condition difference trajectories directly in applications to the implicit learning paradigm in the next section, where the diagnostic groups are modeled separately since we expect the ASD and TD groups to be different in mean trends as well as covariation.

3. Application to the Implicit Learning Study

3.1 Description of the Data Structure

In our motivating implicit learning study, EEG data are recorded on 37 ASD and 34 TD children for 120 trials per condition (expected and unexpected) for each subject at 128 electrodes. The EEG signals are sampled at 250Hz, producing 250 within-trial time points per waveform spanning 1000ms. The standard preprocessing steps of the data include artifact detection, bad channel replacement, referencing and baseline corrections. Next, the meta-preprocessing of Hasenstab et al. (2015) is applied to the data, following the preprocessing steps, to increase the SNR to a level at which P3 peak locations can be identified without collapsing the entire longitudinal dimension (via averaging the ERP curves over all trials). The meta-preprocessing step averages ERP functions separately for each subject, electrode and condition, in a moving window of 30 trials to identify the P3 peak location in the averaged ERPs (see Web Appendix B for more details). We capture the shape of the entire P3 peak from these averaged ERPs by examining a 140ms window around the P3 peak identified in the meta-preprocessing step (i.e. functional time domain around the P3 peak location is t ∈[-70ms, 70ms] in 4ms increments). The length of the functional time domain of 140ms is determined by scientific practice and our own observation of the length of the entire P3 peak across trials. Note that the ERP curves in the described functional domain are already aligned across subjects, trials and electrodes, since we consider a symmetric window around each P3 peak. Since the interest lies in condition differentiation characterizing implicit learning, we focus on ERP difference functions obtained by subtracting the meta-preprocessed ERP corresponding to the unexpected condition from the expected condition. For illustration of the proposed methods, MD-FPCA is applied to meta-preprocessed difference ERPs from four electrodes in the right frontal region of the scalp, observed in trials s ∈ [5, 60], where maximal condition differentiation is detected. Note that the longitudinal time domain starts at trial 5 to avoid boundary effects.

The proposed MD-FPCA algorithm is applied to the ASD and TD groups separately. Five subjects are removed as outliers prior to analysis. One of the removed subjects in the ASD group did not have available data until trial 20 and the remaining four subjects (two in each diagnostic group) had ERP difference functions more than 2 standard deviations away from their respective group means for most of the observations across both functional and longitudinal time domains. In addition, a single electrode is omitted from two subjects in the TD group due to highly nonhomogeneous trends compared to the other electrodes. The bandwidths of the mean functions and covariance smooths are selected using GCV and visual inspection of the one- and two-dimensional smooths. The selected bandwidths for the two-dimensional smoothing of the overall and subunit mean functions and total and within covariances in the first-stage decompositions are (30ms, 30 trials), (30ms, 30 trials), (15ms, 15ms), (15ms, 15ms) in the ASD group and (30ms, 30 trials), (30ms, 30 trials), (5ms, 5ms), (5ms, 5ms) in the TD group. The selected bandwidths for the mean functions and covariances in the second-stage decompositions are (15 trials, 15 trials), (5 trials, 5 trials) in the ASD group and (10 trials, 10 trials), (15 trials, 15 trials) in the TD group.

3.2 Data Analysis Results

Overall mean surface estimates μ(t, s) of ERP difference trajectories for both diagnostic groups are given in Figure 2 (a–b). The ASD mean surface displays a trend of positive concave condition differentiation across trials that is uniform across ERP time. The mean surface peaks around trial 35 where there is a slight differential increase around the P3 peak location (indexed by functional time t = 0). In contrast to the ASD mean surface, the TD group exhibits a trend of negative differentiation across trials with much smaller magnitude, including a prominent dip of negative differentiation around trial 25. Since the mean surfaces represent condition differentiation, the opposing mean trends between diagnostic groups imply that children with ASD have higher EEG values in the expected condition while those in the TD group have higher values in the unexpected condition. This is consistent with our previous findings in Hasenstab et al. (2015) and Hasenstab et al. (2016). Another difference between diagnostic groups is in the timing of maximal condition differentiation (trial 35 for ASD and trial 25 in TD). This implies that while both diagnostic groups differentiate between the conditions, implying implicit learning, the children in the TD group are learning at higher speeds. Finally, while the entire P3 peak trajectory is increasing until trial 35 in the ASD group, there is a narrower window around the P3 peak that is minimized at the time of maximal condition differentiation in TD youth. The electrode specific means have similar patterns to the overall mean surfaces and are deferred to Web Figures 2 and 3.

Figure 2.

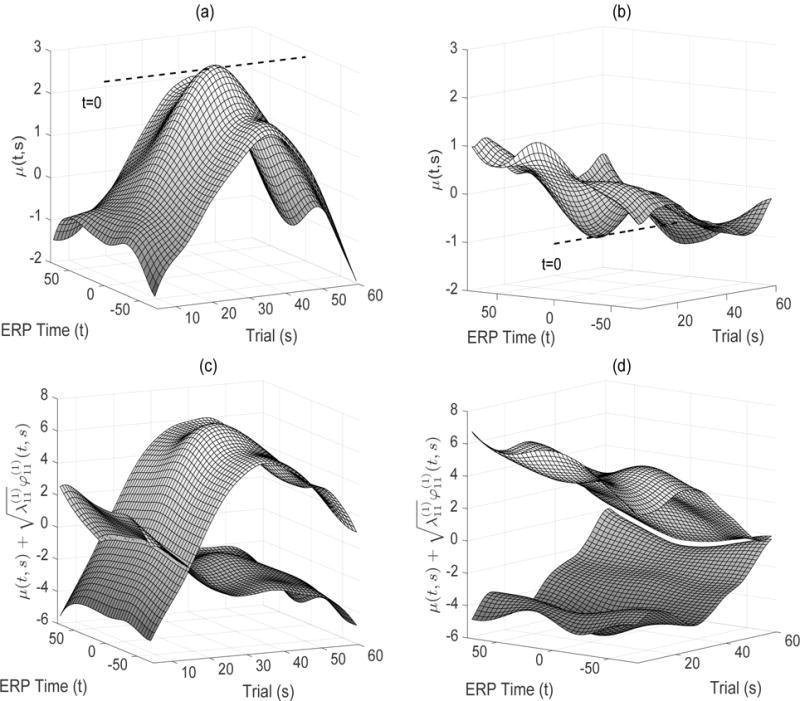
(a)–(b) Estimated mean surfaces, μ(t, s), for the ASD and TD groups, respectively. (c)–(d) Estimated surface intervals, $\mu (t,s)\pm \sqrt{{\mathrm{\lambda }}_{11}^{(1)}}{\phi }_{11}^{(1)}(t,s)$, for the ASD and TD groups, respectively.

Estimated leading subject level first-stage eigenfunctions ${\varphi }_k^{(1)}(t|s)$ and second-stage eigenfunctions ${\psi }_{kk\prime }^{(1)}(s)$ are given in Figures 3 and 4 for the ASD and TD groups, respectively. Recall that while the eigenfunctions ${\varphi }_k^{(1)}(t|s)$ display modes of variation in the functional dimension at a fixed longitudinal time s, the eigenfunctions ${\varphi }_{kk\prime }^{(1)}(s)$ display modes of variation of the first-stage eigenscores in the longitudinal dimension. The products of these two quantities create subject level principal surfaces ${\phi }_{kk\prime }^{(1)}(t,s)$ in (5) capturing the variation along both dimensions. Note that the model components ${\varphi }_k^{(1)}(t|s)$ and ${\varphi }_{kk\prime }^{(1)}(s)$ within themselves are quantities of interest and viewing them together provides an easily interpretable summary of the total variation conditional on and along longitudinal time.

Figure 3.

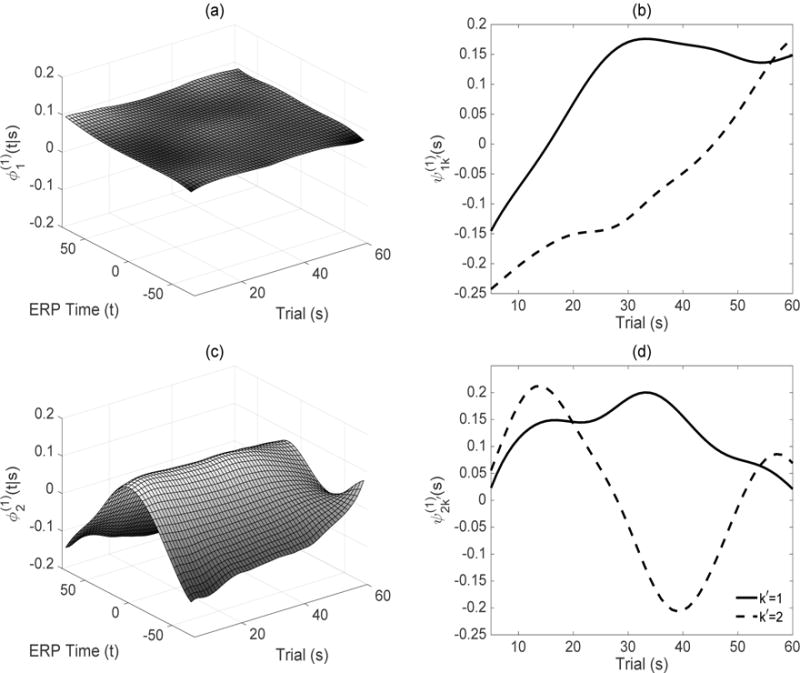
(a), (c) Estimated leading subject level first-stage eigenfunctions, $\{{\varphi }_k^{(1)}(t|s)\},k=1,2$, respectively, for the ASD group. (b), (d) Estimated leading subject level second-stage eigenfunctions, $\{{\psi }_{kk\prime }^{(1)}(s)\},k,k\prime =1,2$.

Figure 4.

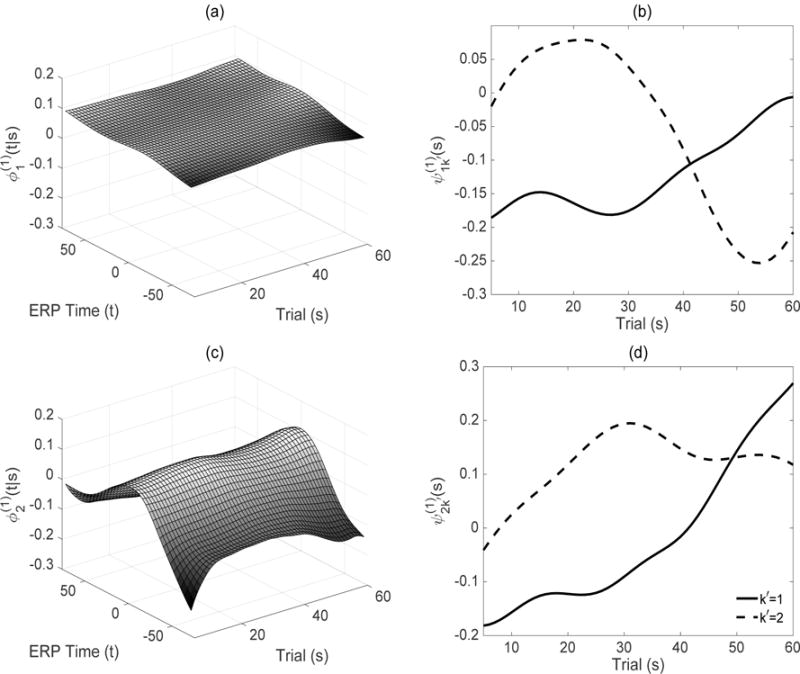
(a), (c) Estimated leading subject level first-stage eigenfunctions, $\{{\varphi }_k^{(1)}(t|s)\},k=1,2$, respectively, for the TD group. (b), (d) Estimated leading subject level second-secondstage eigenfunctions $\{{\psi }_{kk\prime }^{(1)}(s)\},k,k\prime =1,2$.

In the ASD group, the uniform variation across ERP time in the leading component ${\varphi }_1^{(1)}(t|s)$ (Figure 3 (a)), coupled with ${\psi }_{1k\prime }^{(1)}(s),k\prime =1,2$ (Figure 3 (b)) displaying variation along trials, indicate that majority of the variation is in the longitudinal/trial dimension at intermediate and later trials, k′ = 1 (solid, corresponding to 27% of total variation explained), and at the boundary trials, k′ = 2 (dashed, corresponding to 18.4% of variation explained). The resulting product principal surfaces and surface intervals $\mu (t,s)\pm \sqrt{{\mathrm{\lambda }}_{1k\prime }^{(1)}}{\phi }_{1k\prime }^{(1)}(t,s)$ for k′ = 1 and 2, leading to the same interpretations, are given in Web Figures 6–7, Figure 2 (c) and Web Figure 5 (a), respectively. The second component ${\varphi }_2^{(1)}(t|s)$ (Figure 3 (c)) of the subject level variation conditional on longitudinal time, captures a uniformly concave mode of variation in ERP time maximized at the P3 peak location t = 0. Estimated ${\psi }_{21}^{(1)}(s)$ (Figure 3 (d)) (solid, 1.8%), capturing modes of variation in the trial direction, indicates that the variation around the P3 peak is maximized at trial 35, the trial of maximum positive condition differentiation in the overall mean surface in the ASD group. There is additional variation in the boundary and intermediate trials in component ${\psi }_{22}^{(1)}(s)$ (Figure 3 (d)) (dashed, 1%).

As in the flat contour of the ASD leading eigenfunction, the leading component ${\varphi }_1^{(1)}(t|s)$ (Figure 4 (a)) for the TD group is also fairly flat with majority of the variation still in the longitudinal/trial dimension at the early and intermediate trials as captured by ${\psi }_{11}^{(1)}(s)$ (Figure 4 (b)) (solid, 36.9%) and later trials as captured by ${\psi }_{12}^{(1)}(s)$ (Figure 4 (b)) (dashed, 18.6%). (See Figure 2 (d) and Web Figure 5 (b) for surface intervals $\mu (t,s)\pm \sqrt{{\mathrm{\lambda }}_{1k\prime }^{(1)}}{\phi }_{1k\prime }^{(1)}(t,s)$ k′ = 1 and 2, respectively.) The estimated ${\varphi }_2^{(1)}(t|s)$ (Figure 4 (c)) captures leftover variation around the peak location and in the boundaries of the functional/ERP time domain, with variation in the trial direction maximized at boundary trials as reflected in ${\psi }_{21}^{(1)}(s)$ (Figure 4 (d)) (solid, 1.3%) and intermediate trials as reflected in ${\psi }_{22}^{(1)}(s)$ (Figure 4 (d)) (dashed, 0.9%). In summary, while the majority of the variation is in the longitudinal/trial dimension for both ASD and TD groups, most of the variation is observed at intermediate and later trials in the ASD group and at early and intermediate trials in the TD group. For interpretations on the electrode level variation and subject-specific eigenscores, see Web Appendix C.

The number of principal components at both stages of the MD-FPCA fit are selected to explain at least 90% of the variation. The breakdown of the total variation explained by each component of the subject and electrode level decompositions are given in Table 1 for the ASD and TD groups. While two components are selected in the first-stage decompositions uniformly across levels and diagnostic groups, three to four components are needed in the second-stage decompositions. The variability explained by the subject level variation in both stages of the MD-FPCA across longitudinal time (ρ) is estimated to be 62% and 72%, respectively, in the ASD and TD groups. This indicates that the longitudinal functional trajectories observed at the four electrodes in the right frontal region within a subject behave similarly, as expected, and the majority of the total variation is explained at the subject level for both diagnostic groups. Nevertheless, the similarity among electrodes seems to be larger in the TD group, although the difference between diagnostic groups is not found to be significant (90% percentile CI’s for ρ for ASD and TD groups are (0.53, 0.71) and (0.67, 0.82), respectively, based on a bootstrap procedure on the meta-preprocessing and MD-FPCA using 200 data sets sampled with replacement from subjects). Figure 5 (a–b) display the estimated proportion of variability ρ(s) explained at the subject level in the first-stage of MD-FPCA for the ASD and TD groups, respectively. The average estimated ρ(s) values again are higher in the TD group, where locations (along s) of maximum condition differentiation (trials 20 to 30) correspond to higher estimated ρ(s) values in both groups. The similarity among electrodes within a subject seems to get stronger as the children start differentiating between the conditions, especially in the TD group.

Table 1.

The number of principal components at both stages of the MD-FPCA fit selected to explain at least 90% of the variation.

Level 1					Level 2
	ASD		TD			ASD		TD
	k = 1	k = 2	k = 1	k = 2		p = 1	p = 2	p = 1	p = 2
k′ = 1	.270	.018	.369	.013	p′ = 1	.217	.006	.118	.007
k′ = 2	.184	.010	.186	.009	p′ = 2	.085	.004	.074	.005
k′ = 3	.133	.005	.141	.002	p′ = 3	.062	.002	.055	.003
k′ = 4	/	.004	/	/	p′ = 4	/	/	.014	.001

Figure 5.

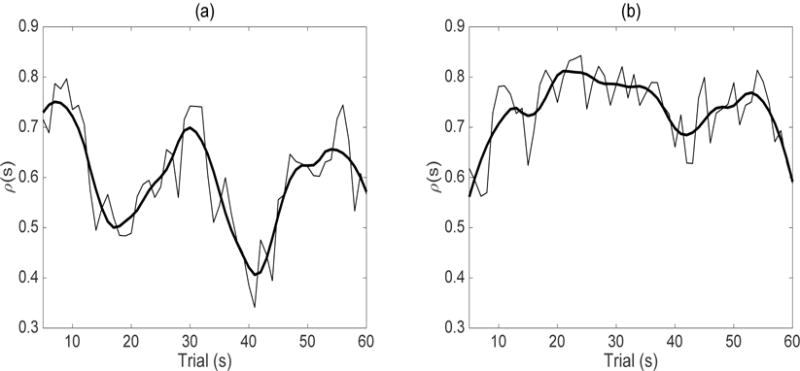
(a)–(b) Estimated proportion of variability explained at the subject level in the first-stage of MD-FPCA for the ASD and TD groups, respectively. The thin black line corresponds to the raw proportion of variability explained while the thick line corresponds to its smooth.

To conclude, we briefly highlight the additional insights gained by utilizing all the dimensions of the data in the analysis without collapsing across longitudinal, functional or electrode repetitions. Note that the analysis of the longitudinal functional condition differentiation trajectories averaged over the electrodes, collapsing the electrode dimension, can be carried out by DFPCA of Chen and Müller (2012) which is a special case of MD-FPCA. Modeling the electrode dimension allowed us to study the electrode level variability, including comparisons to the variability at the subject level and the direction of the variation at the electrode level. More specifically, we learned that the majority of the variability was explained at the subject level in both groups (62% and 72% in ASD and TD, respectively). In addition, the proposed index ρ(s) provided a more detailed depiction of the proportion of total variability at the subject level as a function of longitudinal time.

Similarly, the analysis of the data collapsed over either the functional or longitudinal dimensions can be carried out by ANOVA-FPCA of Di et al. (2009), another special case of MD-FPCA. Not collapsing the longitudinal dimension (enabled by the meta-preprocessing and MD-FPCA) revealed critical information in the application to the implicit learning study. We were able to characterize the entire learning process as well as its speed in addition to comparisons between groups. There is exploratory evidence that the TD group starts differentiating between the two conditions of the experiment earlier (trial 25) than the ASD group (trial 35). Modeling the P3 waveform instead of just the P3 peak amplitude (see our previous work (Hasenstab et al., 2015, 2016)) allowed us to compare the variation in the longitudinal and functional dimensions. Variations/changes over longitudinal time (trials) explain more of the total variation in the data than variation in the functional dimension. We also observed that longitudinal changes in the P3 waveform morphology were different between the two groups. While the entire P3 peak trajectory increased until trial 35 in the ASD group, the TD group showed condition differentiation in a much narrower functional time window around the P3 peak at the time of maximal condition differentiation.

4. Simulation

We study the finite sample properties of MD-FPCA through extensive simulations outlined in Web Appendix D. MD-FPCA recovers the true first- and second-stage model components for both small (N = 30) and moderate (N = 100) sample sizes, under varying SNRs (between 1 and 100) and sparsity levels in the longitudinal time domain, with up to 40% of data missing at random longitudinal time points per subject. The median relative squared errors (RSEs) for all model components decrease with a denser design, increasing sample size and a higher SNR with the exception of the RSEs of the second-stage eigenfunctions which do not change with increasing SNR. This may be due to the fact that these quantities do not directly depend on data observed with measurement error.

5. Discussion

The proposed MD-FPCA has been presented under general settings without stringent assumptions on the separability of the longitudinal, functional and electrode covariances. Note that under the additional assumptions that modes of variability in the functional dimension stay the same across longitudinal times and electrode locations, or that modes of variability in the longitudinal dimension stay the same across functional times and electrode locations, more parsimonious versions of MD-FPCA can be derived using the marginal and product FPCA ideas of Park and Staicu (2015) and Chen et al. (2016). These extensions would lead to a common set of eigenfunctions in functional time across longitudinal times and electrode locations and/or a common set of eigenfunctions in longitudinal time across functional time and electrode locations. Finally, while we focused on modeling the P3 peak curves in the current application, MD-FPCA can be extended to model the entire ERP waveform in the functional dimension. This extension would require warping of the ERP waveforms after meta-preprocessing according to data features (e.g. N1, P3) while simultaneously carrying out the multi-dimensional functional principal components decompositions.