Abstract
Neuroinflammation due to glial activation has been linked to many CNS diseases. We developed a computational model of a microglial cytokine interaction network to study the regulatory mechanisms of microglia-mediated neuroinflammation. We established a literature-based cytokine network, including TNFα, TGFβ, and IL-10, and fitted a mathematical model to published data from LPS-treated microglia. The addition of a previously unreported TGFβ autoregulation loop to our model was required to account for experimental data. Global sensitivity analysis revealed that TGFβ- and IL-10-mediated inhibition of TNFα was critical for regulating network behavior. We assessed the sensitivity of the LPS-induced TNFα response profile to the initial TGFβ and IL-10 levels. The analysis showed two relatively shifted TNFα response profiles within separate domains of initial condition space. Further analysis revealed that TNFα exhibited adaptation to sustained LPS stimulation. We simulated the effects of functionally inhibiting TGFβ and IL-10 on TNFα adaptation. Our analysis showed that TGFβ and IL-10 knockouts (TGFβ KO and IL-10 KO) exert divergent effects on adaptation. TFGβ KO attenuated TNFα adaptation whereas IL-10 KO enhanced TNFα adaptation. We experimentally tested the hypothesis that IL-10 KO enhances TNFα adaptation in murine macrophages and found supporting evidence. These opposing effects could be explained by differential kinetics of negative feedback. Inhibition of IL-10 reduced early negative feedback that results in enhanced TNFα-mediated TGFβ expression. We propose that differential kinetics in parallel negative feedback loops constitute a novel mechanism underlying the complex and non-intuitive pro- versus anti-inflammatory effects of individual cytokine perturbations.
Introduction
Neuroinflammation is implicated in the pathophysiology of many disease conditions including Alzheimer’s disease, epilepsy, stroke, traumatic brain injury, and infection. Microglia are the resident macrophages of the central nervous system (CNS) and these cells are key regulators of immune functions of the brain such as responses to bacterial infection, injury, or neurodegeneration. 1 Following an injury or inflammatory stimulus, microglia often adopt a non-ramified morphology and release a number of pro- and anti-inflammatory substances including cytokines and chemokines.2–5 At the extreme end of this continuum, microglia acquire an ameboid phenotype that supports mobilization to the lesion site for phagocytosis of damaged cellular material or pathogen.6–8 Microglia also express receptors for many secreted factors such that autocrine and paracrine signaling coordinate the inflammatory microenvironment in CNS parenchyma following glial activation.9 The morphological and neurochemical effects of glial activation can lead dysregulation of synaptic physiology and intrinsic neuronal excitability,10–15 thus highlighting the important functional implications of microglial activation. Furthermore, given the well established role of microglia in the development and maintenance of synaptic function,16–18 acute infection- or injury-driven microglial inflammation during development exerts chronic deleterious effects on CNS functions.19–21
It is well known that neuroinflammation often entails a complex panoply of interactions amongst neurons, astrocytes, endothelial cells, and various immune cells.22,23 However, microglia-mediated coordination of the inflammatory microenvironment is integral to the regulation of neuroinflammation.24,25 Despite the critical role of microglia in CNS homeostasis, the mechanisms regulating microglial inflammation are not well understood. Microglial secretion of pro-inflammatory cytokines is often considered to be harmful, although prevention of microglial activation has been shown to yield pathological consequences. For instance, antibodies directed against tumor necrosis factor-α (TNFα) have been shown to exacerbate multiple sclerosis, and mutations in a TNFα receptor gene have been shown to be associated with this disease.26 Further, antiinflammatory cytokine interleukin-10 (IL-10) has been shown to produce inflammatory effects in the periphery.27 Hence, understanding how dynamic interactions amongst cytokines coordinate the inflammatory microenvironment is an outstanding goal in neuroinflammation research.
It is clear thatmicroglia both secrete and respond to a number of inflammatory cytokines.9 A expansive intracellular cytokine signaling network has been utilized in computational studies of microglia in Alzheimer’s disease.28,29 However, a comprehensive network of microglial cytokine/chemokine autocrine/paracrine inter-cellular interactions has not been assembled to our knowledge. The elucidation of this network structure is necessary for defining the roles of secreted cytokines in coordinating processes such as cellular adaptation. Cells often adapt to a sustained stimulus by responding briefly and then returning to baseline, and this adaptation is supported by signaling network architectures involving negative feedback.30 Bacterial toxin lipopolysaccharride (LPS) elicits TNFα release from cultured microglia followed by response adaptation in the continuous presence of the stimulus.31 TNFα has also been shown to stimulate negative feedback from IL-10 and transforming growth factor-β (TGFβ).31–33 While TNFα is an important component of the microglial innate immune response, its adaptation to LPS is likely to be equally important for restraining inflammation and preventing unnecessary tissue damage. However, the mechanistic basis for TNFα adaptation, and the relative contributions of feedback inhibitors such as TGFβ and IL-10 to adaptation, has not been established. Computational analyses have provided useful insight as to the mechanisms of adaptation.30,34 For instance, in a model of TLR-4-mediated NFκB responses to LPS, occlusion of an anti-inflammatory negative feedback loop was counter-intuitively shown to enhance adaptation.35 Such results highlight the value in studying the mutual influences of network structure and kinetics on system dynamics.36
Many investigations of cytokine signaling in microglia examined the pairwise interactions between two cytokines, or the effects of one cytokine on a set of others.37,38 More comprehensive examinations of microglial phenotypic properties under varied inflammatory conditions, accomplished using next generation sequencing technologies,39,40 were limited to studies of few time points. Hence, we do not currently understand how the interplay amongst secreted cytokines, to which microglia are responsive, is coordinated to render physiological response characteristics such as adaptation. Furthermore, defining the interactions of the microglial cytokine network, as has been accomplished for astroglia,41 is necessary but insufficient for providing insight as to the control mechanisms that govern the physiological responses of the integrated network and the coordination of such responses over time.
Computational modeling approaches have provided valuable insights into the mechanisms of peripheral and CNS inflammatory regulation. Such models vary according to level of analysis, cell type specificity, and model formulation. Levels of analysis include intracellular biochemical signaling,42 autocrine/paracrine regulation of cell signaling, intercellular interactions, 43 global tissue level inflammatory regulation,44,45 and various multiscale models incorporating integrated levels of analysis.46–49 Intracellular signaling models are generally cell type-specific, where cell types include microglia28,42,50 and peripheral macrophage,51,52 as well as other cell types.53,54 Modeling formalisms range from Boolean logic representations28 to differential equations42,51,54 and agent based models.46–48,55 We employed a novel computational approach to study microglial autocrine/paracrine cytokine interactions with a model characterized by differential equations. We focused on studying the LPS response in microglia. Simulations and analyses of our model revealed that TGFβ and IL-10 have distinguishable kinetics and opposing contributions to adaptation of TNFα responses to LPS.
Experimental and computational methods
Mathematical model of autocrine/paracrine cytokine signaling in microglia
We employed a variant of the classic S-systems model formulation, 56 based on the successful application of such an approach in recent models incorporating cytokine–cytokine interactions.57,58 We used the following formulation to simulate the expression dynamics of each cytokine,
| (1) |
| (2) |
where Cx = Cx(t) is the expression of cytokine x (TNFα, IL-1β, IL-6, TGFβ, IL-10, or CCL5) that is produced at rate kx upon activation by cytokine Ci at time = t − τd,ix. Thus, the delay term τd,ix is time between the activation of Ci and its subsequent activation of Cx. The activation of Cx depends on Ci according to a Hill function characterized by half-maximal activation constant Kix and cooperativity coefficient nix. Similarly, inhibitory cytokine Cj reduces Cx production with time delay τd,jx according to a decreasing sigmoidal function characterized by Kjx and njx. The degradation of Cx occurred with both concentration-dependent and concentration-independent components determined by rate constants γx and γss,x, respectively. The concentration-independent degradation term encompassed the initial value of cytokine x, which was set to Css,x = 0.1 for all cytokines, and a degradation constant that was set to maintain a constant steady state (eqn (2)) in the absence of stimulation.59 According to available data, LPS directly stimulates the production of all species in our model aside from TGFβ. Hence, LPS was included among the Ci terms for all species other than TGFβ.
The model was implemented in MATLAB 2013a (The Math- Works Inc., Natick, MA) using ode45 to integrate the differential equations. We found that ode15s gave approximately identical results. All parameter values appear in ESI† and code to implement the model is available on the modelDB database (http://senselab.med.yale.edu/modeldb/; accession number: 170029).60
Parameter estimation
We followed a procedure similar to our previous work61 (see ESI,† “Parameter estimation and model comparison” for further details). First, we initiated all coupling constants (Kix and Kjx) based on available data. We then fitted the entire model parameter set to normalized experimental waveforms because our primary interest was to recapitulate the relative experimental kinetics (Fig. 1). Furthermore, it was not possible to fit our model to cytokine concentrations, given the available data, so the model was set in arbitrary units. We constrained the fits such that all model outputs were of the same order of magnitude (Fig. S1, ESI†). The model includes a total of 93 parameters. We modeled cytokine interactions without explicitly incorporating mechanistic detail, hence, there is not an explicit relation between parameter values and biological mechanisms. In particular, our model is phenomenological and does not include details such as the dynamics of receptor–ligand interactions, intracellular signaling interactions, and gene expression regulation. Hence, it is not entirely appropriate to explicitly associate the model parameters with specific biological referents. Rather, each parameter aggregates a number of biological processes (e.g., cytokine production rate depends on transcription, translation, and post-translational modification). As described in the ESI,† we used numerical optimization to fit parameters based on minimization of summed square differences between model prediction and experimental data. We implemented a global sensitivity analysis prior to selecting a final parameter set and manually tuned the most sensitive parameters, as well as parameter associated with the most sensitive network interactions (see Fig. 2 and 4D).
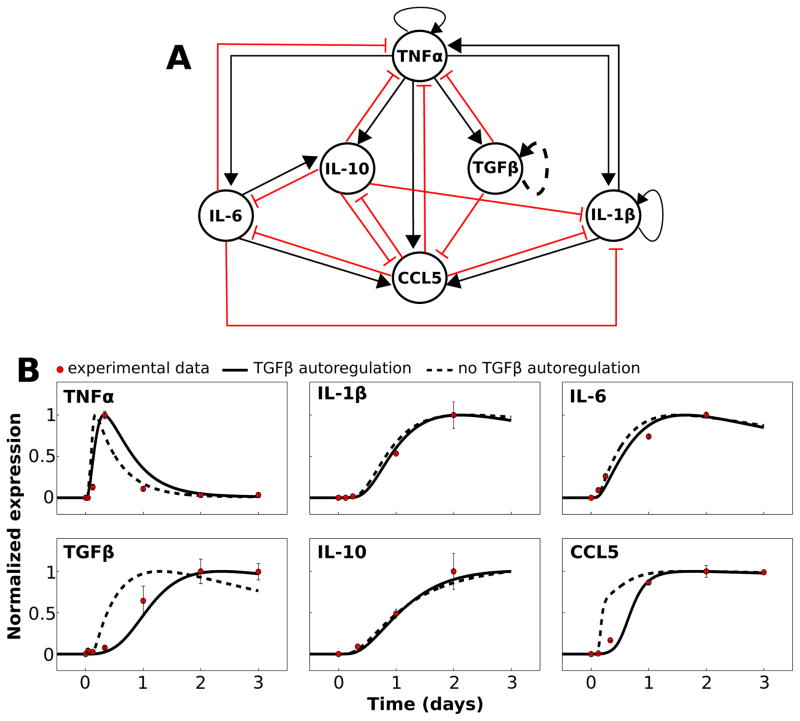
Fig. 1.
Network model and mathematical simulation of complex signaling dynamics involving pro- and anti-inflammatory cytokines. (A) The literature-based network model depicts activation and inhibition of cytokine production, respectively, with black arrows and red T-connectors. The dashed line representing the TGFβ autoregulation loop indicates that this interaction is hypothesized rather than demonstrated experimentally. All model species aside from TGFβ were activated by LPS in our simulations. (B) The results of our calibrated model are shown along with normalized experimental kinetic profiles. Simulations were performed in which a saturating stimulus of LPS = 1000 was applied at t = 0 and maintained throughout the simulation. Traces are shown with and without the TGFβ autoregulatory loop.
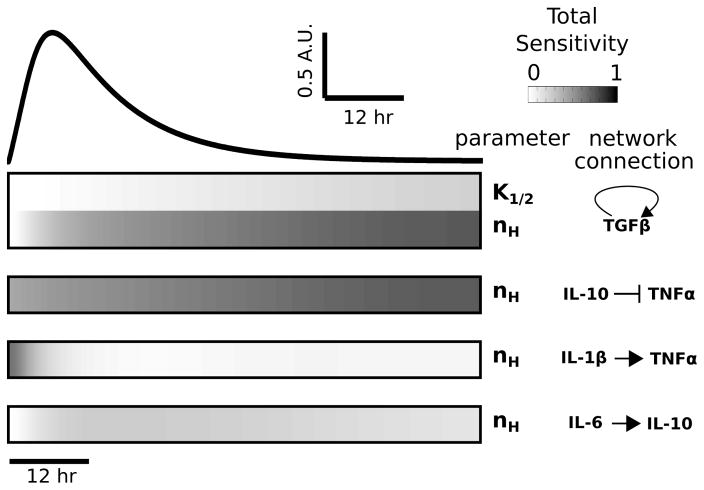
Fig. 2.
Global sensitivity analysis reveals that TNFα is highly sensitive to TGFβ and IL-10. Total sensitivity indices (ST) were computed for each parameter and data are shown for all parameters with ST > 0.2. The temporal profile of the LPS-induced TNFα response, for saturating stimulus (LPS = 1000), is shown above the sensitivity index heatmap. Sensitivity indices were computed at times corresponding to the simulated waveform. All identified parameters involve one of the following cytokines: IL-1β, TGFβ, IL-10, or IL-6.
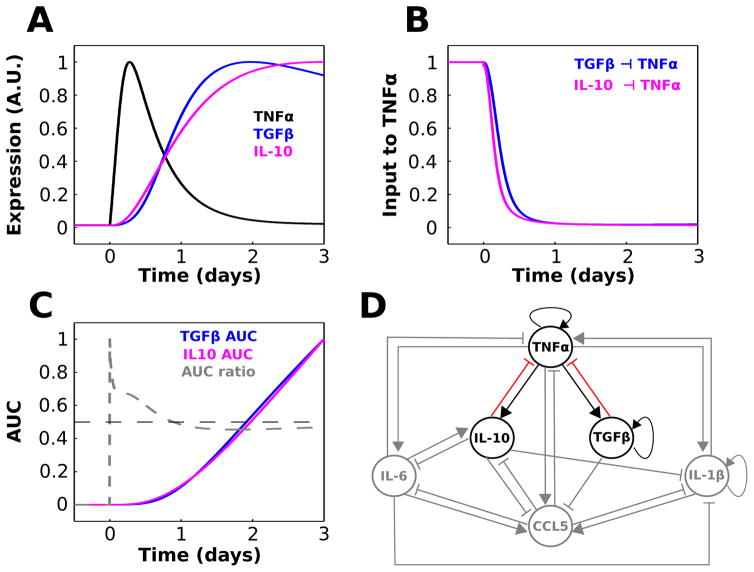
Fig. 4.
TGFβ and IL-10 provide temporally distinct feedback inhibition to TNFα. (A) Relative waveforms of TNFα, TGFβ, and IL-10 are plotted for comparison (LPS = 1000 starting at t = 0). (B) Normalized TGFβ and IL-10 contributions to the TNFα activation rate equation show that IL-10-mediated inhibition of TNFα precedes that of TGFβ. These quantities were computed as and . (C) Normalized area under the curve (AUC) was computed as a function of time for the TGFβ and IL-10 inputs to TNFα shown in panel A. The AUC ratio trace represents the fractional contribution of IL-10 relative to TGFβ: AUC ratio = AUCIL10/(AUCTGF + AUCIL10). (D) Cytokine interaction network where sensitive interactions that will be the focus of the remainder of the paper are highlighted.
Global sensitivity analysis
We implemented variance-based global sensitivity analysis as described previously.61,62 We used the high dimensional model reduction technique to decompose model output variance with respect to parameter variations imposed across 100 000 samples. This implementation of global sensitivity analysis is superior in evaluating parameter sensitivity in terms of parameter sampling63 and accurate performance on non-linear models.64 The total contribution of parameter θi to Cx, including effects due to first and higher order interactions, was given by
| (3) |
where E(·) is the expectation of the argument and V(Cx|θ~i) is the variance of Cx conditioned on all parameters other than θi. We determined the global parametric sensitivities of the TNFα response to LPS by numerically estimating STi for all model parameters according to a previously described algorithm.62 Two-fold variations were implemented for all parameters.61 See ESI† for further detail on sensitivity analyses and their implementation (“Sensitivity analyses”, Fig. S2 and S3).
Analysis of sensitivity to initial conditions
To assess the sensitivity of the LPS-mediated TNFα response to the initial conditions of anti-inflammatory cytokines TGFβ and IL-10, we varied their initial values from 0.01 to 20 and evaluated the effects on the TNFα response. In addition, we performed all of these anti-inflammatory variations over the same range of initial TNFα values (TNFα0). For these variations, we used 20 initial values from the aforementioned range, varied incrementally in log space. All combinations of TGFβ, IL-10, and TNFα initial values were considered, thus generating 8000 simulations. To assess TNFα sensitivity, we computed the normalized gradient of the LPS-induced TNFα response with respect to either TGFβ or IL-10 (see Results, eqn (5) and (6)). We computed these gradients over a range of time points and TNFα0 levels and plotted the data in a coordinate system defined by TGFβ0 and IL-100.
Experimental techniques and data analysis
Animals
All procedures were approved by the Animal Care Committee of the Research Institute of the McGill University Health Centre (RIMUHC). Male homozygote IL-10 KO mice (obtained from Dr Radzioch, RIMUHC) or C57BL/6 control mice (WT; Charles River Laboratories, CA) at 8 to 12 weeks of age were used to obtain bone marrow derived macrophages for cell culture.
Macrophage culture and treatment
Macrophages were generated as previously described.65 Briefly, mice were euthanized and their hind leg bones were removed. Bone marrow was flushed out, homogenized and red blood cells were hypotonically lysed. After washing, cells were cultured in RPMI media containing 10% fetal bovine serum (FBS; 10%. Invitrogen, CA), L-cell-conditioned media (10%; a source of M-CSF), penicillin/streptomycin, and vitamins solution (1%; Invitrogen, CA) for 7 days. Mature macrophages were re-plated at a density of 80 000 cells per well in 24-well plates and left to adhere overnight. Cells were treated with lipopolysaccharide (LPS; 100 ng mL−1) or vehicle control (PBS) in RPMI containing FBS (10%) for 6 and 18 h durations.
Following LPS treatment, cells were lysed and total RNA was extracted using the RNeasy Lipid Tissue Kit (Qiagen, CA). Reverse-transcription was performed with the Omniscript Reverse Transcription Kit (Qiagen, CA), and qPCR was performed using 1 μL of cDNA with Fast SYBR Green Master Mix (Applied Biosystems, CA) on a Step-One Plus qPCR machine (Applied Biosystems). Peptidylprolyl isomerase A (PPIA) was used as an internal control gene. TNF primer sequences for were as follows: forward: 5′-TTG CTC TGT GAA GGG AAT GG-3′; reverse: 5′-GGC TCT GAG GAG TAG ACA ATA AAG-3′.
Data analysis
We calculated TNFα expression following LPS application with standardization relative to PPIA. The effects of LPS on TNFα gene expression levels were computed as −ΔΔCt values:66
Statistical comparisons of LPS responses from WT versus IL-10 KO macrophages were performed using the two factor analysis of variance (ANOVA). The Tukey honestly significant difference (HSD) test was applied for multiple comparisons. The Mann– Whitney–Wilcoxon test was applied to check ANOVA results with a non-parametric test. Adaptation of the TNFα response to LPS from 6 to 18 h was computed as follows:
| (4) |
where represents the average gene expression change at time i. To compare adaptation between WT and KO genotypes, we used an ‘error propagation’ metric to estimate the standard deviation of adaptation:67
| (5) |
where A = Adaptation (eqn (3)) and SEMi is the standard error of the mean (i.e., ) at time i. Statistical analyses were completed using functions aov, TukeyHSD, and wilcox.test in the statistical programming language R.68
Results and discussion
Network structure and simulation of cytokine signaling in microglia
Our first goal was to establish a cytokine signaling network, based on microglial time-series data, that could be simulated with a mathematical model. Experimental data show the temporal profiles of cytokine release following the application of bacterial toxin lipopolysaccharide (LPS) to cultured microglia.69 We created a network including the following cytokines/chemokines: TNFα, TGFβ, IL-10, IL-6, IL-1β, and chemokine (C–Cmotif) ligand 5 (CCL5). These species were chosen as network nodes for the following reasons: (1) there exist time-series data documenting the microglial release profile following LPS application for all network species, (2) a wealth of data exist with characterizations of the interactions amongst these cytokines (e.g., the application of TGFβ to LPS treated microglial cultures attenuates TNFα release33), (3) these species are particularly relevant to our interest in CNS-mediated control over cardiovascular physiology, based on in vitro and in vivo data,70–72 and (4) these cytokines are of broad interest in neuroinflammation and neurodegenerative disease research.73–75
We distilled the results of our literature search into the interaction network shown in Fig. 1A. All species in the network other than TGFβ have been shown to be directly activated by LPS, while TGFβ activation following LPS treatment depends on TNFα.76 With one exception (see below), every edge in the network was derived from experimental data from microglia demonstrating an activating or inhibitory effect of the source node on the target (Table S1, ESI†). We assessed the topological properties of the network and found that TNFα exhibited connectivity features indicative of a prominent role in network control. TNFα had the highest in-degree, out-degree, and number of shortest path connections between other nodes. This suggests that TNFα is topologically situated to globally control the dynamics of the cytokine network, as expected based on experimental work.75,77–79
To examine the dynamic coordination of microglial cytokine signaling, we developed a mathematical model based on the network of microglial cytokine/chemokine signaling interactions (Fig. 1A). A modified S-systems model formulation permitted calibration to experimental data (Fig. 1B).56 A key assumption of our model formalism was that AND logical gating governs the combined effects of a group of cytokines on their target. For instance, if cytokines A and B both activate the production of cytokine C, cytokine C will only be produced if both A and B are active. In OR gating, if cytokines A and B both activate the production of cytokine C, cytokine C will be produced if either A and B is active. We attempted to implement OR gating, in which the sequence product operator was replaced by the summation operator in eqn (1), but the model could not be calibrated to data with this configuration (see ESI,† “OR gating model”). Hence, we hypothesize that AND gating characterizes the collective influences of a group of cytokines on their mutual target. We also assumed that the model rests at a steady-state state with arbitrarily low species levels in the absence of LPS. This assumption is consistent with data from cultured microglia in which cytokine expression is nearly undetectable in the absence of a perturbation,76 and data suggest that the brain in vivo contains low cytokine levels under baseline conditions relative to disease states or responses to inflammatory stimuli.80
While we did not find evidence in the published literature on microglia showing that TGFβ coordinates its own release, we hypothesize the existence of this autoregulatory loop because its inclusion in our mathematical model was necessary to recapitulate the time-series data. Without the positive feedback autoregulation loop for TGFβ, cytokine/chemokine data from experiments in which LPS was applied to cultured microglia could not be replicated by our model (Fig. 1B; see ESI,† “Experimental data used for parameter estimation” for further information). In particular, this autoregulation loop was necessary to obtain delayed and relatively slow LPS responses for TNFα, TGFβ, and CCL5. Supporting the plausibility of this hypothesized TGFβ autoregulatory loop, data from astrocytes (a CNS parenchymal cell-type involved in cytokine release with many functional similarities to microglia) show that TGFβ application stimulates TGFβ upregulation.41,81 TGFβ autoregulation has also been demonstrated in the CNS in vivo,82 and in other non-CNS cell types.83–85 Our model prediction of similar TGFβ autoregulation in microglia thereby yields a novel hypothesis for experimental evaluation. The final calibrated model recapitulated the relative experimental kinetics. These results suggest that our modeling formalism captures a complex set of interactions triggered by inflammatory stimulation by LPS.
In subsequent simulations, we found that our model with delay differential equations (DDEs, see Methods, eqn (1) and (2)) was computationally demanding to implement, and occasionally the model generated sharp deflections in the dynamic variables (see arrows in Fig. S1C; see also Fig. S10, ESI†). These sharp deflections were likely related to a numerical integration issue. However, DDEs did not provide a significant advantage, in terms of the model fit to data and model predictions, in comparison to ordinary differential equations (ODEs). To test whether we could obtain comparable results using ODEs, we set all time delay terms to zero (τd = 0 in eqn (1)) and verified that the resulting ODE model yielded qualitatively similar simulation results (Fig. S1C, ESI†). Thus, even though the DDE model provided a better fit to data, the performance of the ODE model was optimal for our model analyses (see ESI,† “Parameter estimation and model comparison”, Tables S2 and S3). The model fits appeared qualitatively similar and other simulation results were nearly identical for the ODE and DDE models. These results, along with others noted below, suggest that the DDE and ODE models are comparable. We examined the ODE model in the simulations and analyses presented below unless otherwise noted.
TNFα is sensitive to anti-inflammatory feedback inhibition
To determine the relative influences of model parameters on cytokine expression, we performed a global sensitivity analysis. 61,62 This analysis entailed the variation of all parameters in tandem followed by the decomposition of model output variance into the relative contributions of each parameter. Because our initial analysis of the cytokine network revealed that TNFα is topologically positioned to exert robust control over network dynamics, and given the well documented role of TNFα in neuroinflammatory disease states,75 we focused on the sensitivity of TNFα to themodel parameters. Our sensitivity analysis showed that the TNFα response to sustained LPS input was most sensitive to parameters associated with TGFβ production, IL-10 inhibition of TNFα, IL-1β activation of TNFα, and IL-6 activation of IL-10 (Fig. 2). All other parameters had a relatively insignificant impact (i.e., total sensitivity < 0.2) on the global variability of TNFα. Of all model parameters, 5.7% of the parameters exerted a prominent influence on the LPS-induced TNFα response, thereby indicating model robustness.
To enhance our confidence in model robustness and the absence of deleterious parameter uncertainty, we evaluated the first order sensitivity indices of each parameter and estimated the confidence bounds on the entire set of TNFα responses included in our global analysis. Furthermore, we conducted a local (i.e., single parameter) sensitivity analysis and found independent validation of the results from our global analysis. The results from these analyses were consistent with model robustness (see ESI,† “Sensitivity analyses”, Fig. S2 and S3). To further address whether multiple parameter sets could predict the experimental data equally well, we performed parameter estimation starting from 20 randomly selected initial parameter sets (ESI,† “Parameter variation analyses”). The results show that several distinct parameter fits describe the data comparably, though none of the fits were significantly better than the reference parameter set (see Fig. S4A and Table S2, ESI†). These findings are thoroughly described and discussed in the ESI† (Fig. S4 and S5).
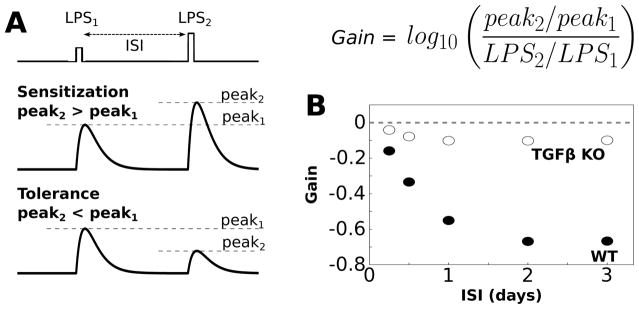
Endotoxin tolerance simulations support model validity
An important aspect of computational modeling is model validation using data that were not used for parameter estimation. Given that tolerance in the TNFα response to sequentially applied LPS stimuli has been experimentally observed in microglia, 86 we tested whether our model could recapitulate such endotoxin tolerance. Our results demonstrate that our model exhibits tolerance of the TNFα response to LPS over a range of inter-stimulus intervals (ISIs) and relative levels of the two LPS stimuli (Fig. 3B). To further examine the validity of our model, we tested whether TGFβ regulated endotoxin tolerance, as was observed experimentally for microglia.87 The relative effects of TGFβ were isolated by simulating a functional knockout (KO) of this cytokine (i.e., TGFβ KO). This KO condition simulates the effect of pharmacological antagonism or genetic mutation. We found that TGFβ KO enhanced response gain, thereby occluding tolerance (Fig. 3B). Our results supported the experimental finding that TGFβ enhanced tolerance of the TNFα response to LPS over a range of stimulus conditions. These results are consistent with model validity.
Fig. 3.
Simulations of endotoxin tolerance support model validity. (A) Tolerance is evaluated by applying two sequential LPS doses, separated by an interstimulus interval (ISI), where the first dose is smaller than the second dose (LPS1 = 500, LPS2 = 1000). In general sensitization occurs when the peak response to the second LPS dose is greater than the peak response to the first dose (gain>0, see equation). Tolerance occurs when the peak response to the second LPS dose is smaller than the peak response to the first dose (gain < 0). (B) Gain of the TNFα response to LPS was evaluated over a range of ISIs (2 h LPS pulse duration). For these simulations we set LPS = 0.1 during the ISI to maintain network coupling. Negative gain was observed for the wildtype condition for ISI > 6 h, thereby indicating tolerance. Simulated functional knockout (KO) of TGFβ resulted in the absence of negative gain, thereby eliciting sensitization.
TNFα is prominently inhibited by kinetically distinct TGFβ and IL-10 inputs
Our sensitivity analysis motivated us to further examine the relative influences of TGFβ and IL-10 on TNFα. In agreement with the sensitivity analysis, experimental data suggest that TGFβ and IL-10 are critical regulators of TNFα production in peripheral macrophages and microglia.88,89 Upon closer examination of the TGFβ and IL-10 response profiles during LPS stimulation, we found that IL-10 activation temporally preceded TGFβ activation (Fig. 4A). This temporal shift in the LPS-mediated activation of IL-10, relative to that of TGFβ, resulted in an accelerated inhibitory input to TNFα from IL-10 compared to TGFβ (Fig. 4). We evaluated the cumulative LPS-induced activation levels of TGFβ and IL-10 by computing area under the expression curve (AUC) over time, as well as the relative contribution of total IL-10 expression (Fig. 4C). The results showed that IL-10 expression contributed more than 50% of the combined inhibitory input to TNFα throughout the upstroke, peak, and approximately half of the adapting decay in the continuous presence of LPS. Similar findings were obtained for the DDE model (Fig. S6, ESI†). Our results were not surprising given similar experimental findings.31–33,90 These results suggest that while IL-10 and TGFβ jointly impose negative feedback on TNFα, the effects of IL-10 precede those of TGFβ and play a greater role in shaping the peak TNFα response to LPS. Based on the above results, we chose to further investigate the relative contributions of IL-10 and TGFβ to the regulation of TNFα. These interactions are highlighted in Fig. 4D.
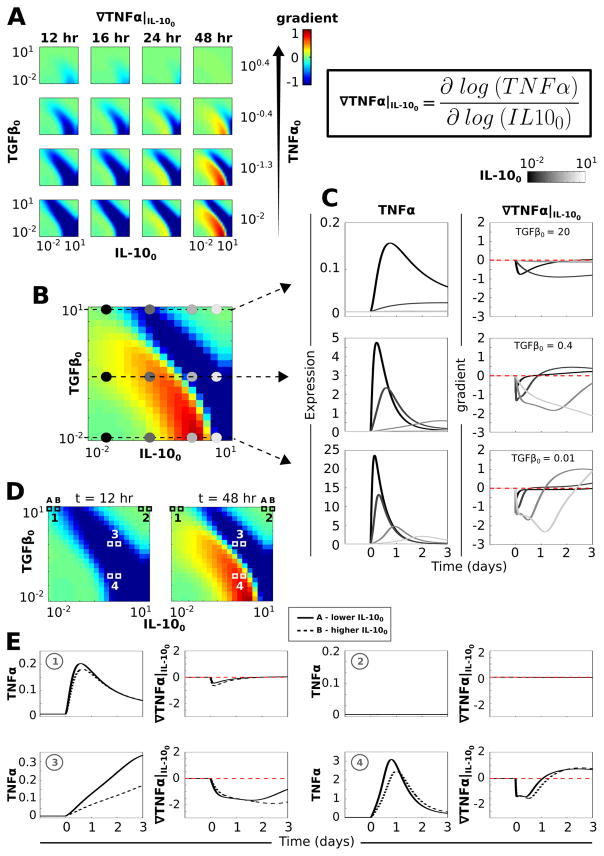
A separatrix distinguishes anti-inflammatory initial condition effects on TNFα gradients
Because TGFβ and IL-10 levels were believed to be particularly important for determining the TNFα response to LPS, we systematically evaluated the effects of initial TGFβ, IL-10, and TNFα levels on the effects of continuously applied LPS. This analysis allowed us to assess the dependence of the TNFα response on the configuration of anti-inflammatory initial conditions. We simulated the LPS response for a set of permutations in the initial conditions of TNFα, TGFβ, and IL-10. From these simulation results we computed the normalized TNFα gradients in the directions of both the TGFβ and IL-10 initial levels (i.e., TGFβ0 and IL-100):
| (6) |
| (7) |
These gradients elucidate the sensitivity of the LPS-induced TNFα response changes in the initial conditions of either TGFβ or IL-10. Further, these gradients showed how sensitivity to initial conditions varied depending on the relative baseline levels of TGFβ and IL-10. Our analysis entailed ∇TNF|TGF0 and ∇TNF|IL100 computations over a range of simulation times and TNFα0 values.
Our results revealed that the TNFα response to LPS declined with increases in the initial IL-10 level for particular pairings of the TGFβ and IL-10 initial expression levels (see blue bands in Fig. 5A). Combinations of the initial TGFβ and IL-10 levels along the diagonal of the TGFβ0–IL-100 space rendered decreases in the TNFα response to LPS for increases in initial IL-10 levels when TNFα0 was relatively low (Fig. 5A; see Fig. S7, ESI† for similar plots of the TNFα gradient with respect to the initial TGFβ level). In addition to the negative TNFα response gradients for increases in IL-100 observed for certain combinations of the TGFβ and IL-10 initial levels, positive gradients were observed for other initial condition permutations (see red bands in Fig. 5A). ∇TNF|IL100 > 0 occurred when increases in the initial IL-10 level led to increases in the TNFα response to LPS. The finding of such positive TNFα gradients with respect to IL-100 was surprising given that IL-10 inhibits TNFα expression and thus, increases in initial IL-10 levels would be expected to only reduce TNFα responses, as found for TGFβ (Fig. S7, ESI†). Hence, a separatrix defined by adjacent negative and positive gradients, extending along the negative diagonal of the TGFβ0– IL-100 space, was observed for low TNFα0 values at simulation times around t = 48 h of LPS stimulation (Fig. 5A and B).
Fig. 5.
A separatrix distinguishing TNFα response profiles exists in the TGFβ–IL-10 initial condition space. Simulations in which a saturating dose of LPS = 1000 was applied continuously starting at t = 0 were performed for range of TNFα, TGFβ, and IL-10 initial condition permutations. (A) The normalized TNFα gradient is plotted in the direction of the IL-10 initial condition (see equation in upper right). In each plot, the y-axis is defined by the TGFβ initial condition range and the x-axis is defined by the IL-10 initial condition range. Each column corresponds to a different time point at which the gradients were computed and each row corresponds to a different value of the initial TNFα level. (B) The plot shows the gradient for a low initial level of TNFα (TNFα0 = 0.01) at a late time point (t = 48 h). A separatrix cuts across the diagonal distinguishing negative versus positive gradients of the TNFα response to LPS with respect to increases in the initial IL-10 level. Colored circles denote the regions of initial condition space for which TNFα temporal profiles are shown in panel C. (C) Temporal profiles of TNFα (left) and ∇TNF|IL100 (right) are shown for TNFα0 = 0.01 at three levels of TGFβ0 and four levels of IL-100 as indicated in panel B. (D) Gradient plots for TNFα0 = 0.01 are shown at t = 12 h (left) and t = 48 h (right) along with numerical indicators of regions of TGFβ–IL-10 initial condition space examined in panel E. (E) Temporal profiles of TNFα and ∇TNF|IL100 are shown for each of two adjacent values of IL-100. This illustrates the correspondence between the temporal profile and computed gradient. Zone 1 in panel D is characterized by high TGFβ0 and low IL-100. Increasing IL-100 from 0.01 to 0.15 resulted in a TNFα peak reduction associated with a negative gradient at corresponding times. Zone 2 depicts the TNFα gradients observed for relatively high initial TGFβ and IL-10 levels. Under these conditions, TNFα is unresponsive to LPS and the TNFα gradients are approximately zero. For zones 3 and 4, we compare the TNFα response to LPS at two adjacent IL-100 levels (1.2 and 1.8) at TGFβ0 levels on either side of the separatrix observed at 48 h. The data for zone 3, in which the TGFβ0 and IL-100 levels are relatively high (both 1.2), the TNFα response over three days of LPS stimulation is monotonically increasing and the gradient as a function of IL-100 is negative. If TGFβ0 is lowered to 0.07 (zone 4), the same increase in IL-100 results in a temporal shift in the TNFα profile along with a peak reduction. Due to the temporal shift, the gradient shows a negative deflection followed by a trajectory reversal into the positive range, thereby instantiating the positive gradient range demarcating the separatrix.
The evaluation of sample traces showed that the TNFα response amplitude and gradient varied inversely with respect to both TGFβ0 and IL-100 (Fig. 5B and C). We specifically examined the LPS-mediated TNFα response for a series of initial IL-10 levels at three levels of initial TGFβ (Fig. 5B). For the highest initial level of TGFβ, increases in the initial amount of IL-10 resulted in decreases in the TNFα response amplitude, thereby producing the negative TNFα gradient with respect to IL-100 (Fig. 5C, top). At intermediate initial TGFβ levels, increased IL-100 resulted in reduced TNFα response amplitude along with a temporal shift in the response profile (Fig. 5C, middle). These temporal shifts in the TNFα response resulted in delays in both the response peaks and decays, the latter of which produced negative TNFα gradients with respect to initial IL-10 levels. Increasing IL-100 resulted in reduced kinetics of the LPS-mediated TNFα response. These responses were characterized by slower recovery from the peak and thus higher levels at late simulations times compared to the TNFα expression profile observed for lower initial IL-10 levels (Fig. 5C, middle). For the lowest TGFβ0 level, negative TNFα gradients were found for earlier time points and regions of TGFβ0–IL-100 space, whereas positive gradients were observed at relatively later simulation times (Fig. 5C, bottom). Similar to the case for intermediate TGFβ0 levels, increases in initial levels of IL-10 resulted in peak reductions and temporally right-shifted TNFα response profiles. This shift yielded both negative and positive gradients with respect to IL-100. In general, as TGFβ0 was reduced, the TNFα response was larger with a faster decay.
To further elucidate the basis for the separatrix observed at low initial TNFα levels (Fig. 5B), we examined adjacent temporal profiles of TNFα and ∇TNF|IL100 at select zones in TGFβ0–IL-100 space (Fig. 5D and E). For zone 1, the TNFα response to LPS was small due to high TGFβ0 and an incremental increase in IL-100 resulted in a modest peak reduction associated with a negative gradient at corresponding times (Fig. 5E). When both TGFβ0 and IL-100 were high (zone 2), TNFα was unresponsive to LPS and this unresponsiveness was insensitive to changes in IL-100. In contrast, zone 3 was characterized by negative gradients at all time points, due to the moderately high levels of both TGFβ0 and IL-100. In zone 4, the presence of negative gradients, temporally followed by positive gradients, resulted from the combined effects of reduced TNFα response amplitude and decrease in response kinetics (Fig. 5D and E). To further evaluate the effects of initial conditions on the network response, we performed a Lyapunov exponent analysis (see ESI,† “Lyapunov exponent analysis”). This analysis showed that regions of TGFβ0–IL-100 space with the highest sensitivities to initial conditions corresponded to the negative gradients observed with low TNFα0 in Fig. 5A (Fig. S8, ESI†). This suggests that ∇TNF|IL100 is indicative of global network sensitivity under such conditions. Overall, these results show that the cytokine network is sensitive to initial antiinflammatory conditions. For low TNFα levels, a single negative TNFα gradient with respect to initial IL-10 expression temporally precedes the instantiation of a separatrix defined by adjacent negative and positive gradients in TGFβ0–IL-100 space.
TGFβ and IL-10 exert divergent effects on the adaptation of TNFα to LPS
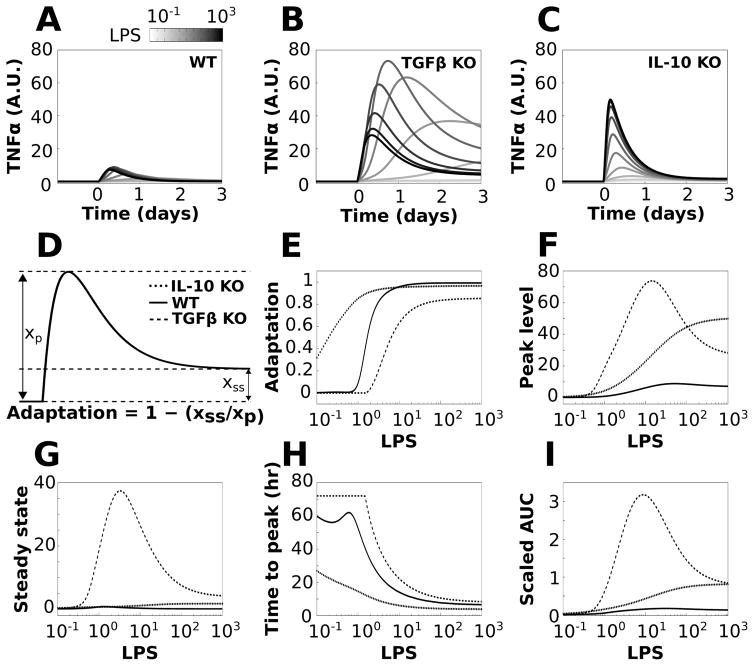
The preceding analyses identified TGFβ and IL-10 as critical regulators of TNFα and established that the effects of IL-10 on TNFα are instantiated before those of TGFβ. We next examined the relative effects of TGFβ and IL-10 on TNFα adaptation to sustained LPS stimulation. The relative effects of TGFβ and IL-10 were isolated by simulating the KO of each cytokine (i.e., TGFβ KO and IL-10 KO). We simulated the responses to sustained LPS stimuli, over a concentration range, in wildtype (WT) and KO phenotypes (Fig. 6A–C). We computed adaptation based on the relative levels of the peak TNFα response and the TNFα level at t = 3 days of LPS stimulation (termed steady state response, Fig. 6D):
| (8) |
Fig. 6.
TGFβ and IL-10 have divergent effects on TNFα adaptation. Simulations were performed for a range of LPS doses in which LPS was applied continuously starting at t = 0 for the duration of the simulation. The effects of knocking out TGFβ or IL-10 were simulated by removing these nodes from the network. The reference simulation is referred to as WT and the knockouts are referred to as TGFβ KO and IL-10 KO. (A–C) Sample TNFα responses to LPS are shown across the range of stimulation levels for the WT (A), TGFβ KO (B), and IL-10 KO (C) phenotypes. (D) Adaptation was computed using the ratio of steady state to peak TNFα responses to sustained LPS applications (see equation). (E) Adaptation was computed for LPS inputs ranging from 0.1 to 1000 in all three model phenotypes. (F) Plots of maximal TNFα values show that KO of either feedback inhibitor increased the peak response to LPS. (G) The TNFα steady state response shows that TGFβ knockout markedly increases the TNFα steady state, whereas IL-10 knockout has a relatively minor effect. (H) The time from the initiation of the LPS pulse to the peak TNFα response (ttp) is shown for the three conditions. (I) Plots show the total amount of TNFα produced following LPS application, assessed by the area under the TNFα curve (AUC).
For the WT phenotype, the degree of TNFα adaptation exhibited a sigmoidal dose–response profile (Fig. 6E). For IL-10 KO, we observed increased adaptation (left-shifted adaptation curve), whereas TGFβ KO produced a reduction in adaptation (right-shifted adaptation curve) (Fig. 6E). These results suggest that IL-10 reduces adaptation whereas TGFβ enhances adaptation. Both KO phenotypes produced relatively shallow dose–response adaptation curves in comparison to the WT phenotype. Further analyses showed that although KO of both TGFβ and IL-10 resulted in increased TNFα peak response levels, albeit to different degrees (Fig. 6F), the removal of TGFβ increased TNFα steady state values to a greater extent than observed for IL-10 KO (Fig. 6G). These findings suggest that TGFβ controls adaptation by reducing both the peak and steady state TNFα responses to LPS. In contrast, IL-10 reduces the TNFα peak but does not affect the steady state, and thus IL-10 reduces adaptation.
To further characterize the relative effects of TGFβ and IL-10 on the TNFα response to LPS, we assessed the time from stimulus initiation to peak response (ttp) and area under the expression curve (AUC) for the three phenotypic conditions. We found that TGFβ KO increased ttp while IL-10 KO decreased ttp (Fig. 6H). This suggests that TGFβ reduces ttp and thereby speeds up the peak TNFα response to LPS, whereas IL-10 delays the peak response. We examined the cumulative amounts of TNFα produced following the initiation of LPS stimulation by computing the TNFα integrals (AUCs) over time. The results showed that KO of either TGFβ or IL-10 resulted in AUC increases. The TGFβ KO phenotype resulted in a greater TNFα expression increase than that for IL-10 elimination at lower LPS levels, but the KO AUCs converged as LPS was increased. Similar findings for the effects of anti-inflammatory occlusion were obtained for the DDE model (Fig. S9, ESI†). These results suggest that TGFβ occlusion may result in particularly harmful inflammatory effects at low levels of inflammatory stimulation, whereas the effects of IL-10 elimination may be exacerbated as a function of stimulus intensity.
Because TGFβ appeared to enhance adaptation, we examined the TGFβ amplitude following an LPS stimulus in WT and IL-10 KO phenotypes (Fig. S10A, ESI†). The TNFα peak was smaller for the WT phenotype in comparison to IL-10 KO. However, peak TNFα expression was positively related to TGFβ in both phenotypes. This analysis showed that TGFβ was activated in proportion to the degree of LPS-induced TNFα activation, which was attenuated by IL-10. Similarly, IL-10 expression was positively related to TNFα for WT and TGFβ phenotypes (Fig. S10B, ESI†). Collectively, our data demonstrate that LPS-activated TNFα levels determine the amount of TGFβ produced. In turn, TGFβ determines the degree of tolerance. In contrast, IL-10 reduces the TNFα response and consequently the amount of TGFβ produced following the LPS stimulus. Overall, these novel simulation results indicate that antiinflammatory cytokines TGFβ and IL-10, which both provide feedback inhibition to TNFα, have surprisingly disparate effects on TNFα, related to temporal differences in expression and feedback regulation.
IL-10 attenuates TNFα adaptation to LPS in murine macrophages
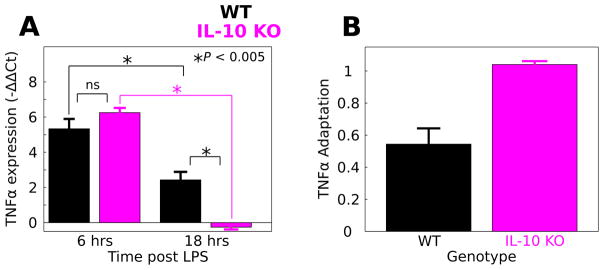
To experimentally test the hypothesis that IL-10 suppresses adaptation of the TNFα response to LPS, we compared the LPS responses of macrophages isolated from WT and IL-10 KO mice. We evaluated TNFα expression using qPCR at six and 18 hours after the initiation of continuously applied LPS (100 ng mL−1). We quantified the TNFα response to LPS by computing −ΔΔCt values (Fig. 7A, see Methods). To compare the LPS responses in WT versus IL-10 KO macrophages, we performed a two factor ANOVA to determine the effects of genotype (WT, IL-10 KO), LPS stimulus duration (6, 18 h) and the corresponding interaction. Our results showed significant effects of LPS duration (F = 137.7, P = 3.6 × 10−7), genotype (F = 5.0, P = 0.05), and a duration/genotype interaction (F = 20.9, P = 0.001). A post-hoc analysis revealed that the mean TNFα response was not different at six h post LPS application in WT (mean = 5.33, sd = 0.97, n = 3) compared to IL-10 KO (mean = 6.3, sd = 0.53, n = 4; P = 0.40). At 18 h, the TNFα expression responses were increased in WT (mean = 2.43, sd = 0.91, n = 4) compared to IL-10 KO (mean = −0.26, sd = 0.23, n = 3; P = 0.003). Additionally, we examined the difference between WT and IL-10 KO TNFα expression at 18 h using the Mann–Whitney–Wilcoxon test, a non-parametric test of similarity between distributions. The results provided support for time-dependent genotype difference (P = 0.057). These results show that although IL-10 KO does not affect the macrophage TNFα response to six h LPS, IL-10 KO results in a reduced TNFα to LPS following 18 h of stimulation.
Fig. 7.
IL-10 restrains TNFα adaptation to LPS in macrophages. LPS was applied continuously to macrophage cultures from WT and IL-10 KO mice and TNFα gene expression was evaluated at 6 and 18 h stimulus durations. (A) IL-10 KO mice responded similarly to LPS applied for 6 h (data are presented as mean ± SEM, * P < 0.005, ns – not significant). For 18 h of LPS stimulation, the IL-10 KO response was significantly attenuated relative to WT. (B) Adaptation was calculated for the WT and IL-10 KO macrophages based on the relative responses at 6 and 18 h (eqn (4)). Adaptation levels are shown along with corresponding estimates of standard deviation (eqn (5)). The analysis suggests that IL-10 KO enhances adaptation of the TNFα response to LPS in macrophages.
Our experimental data suggest that occluding IL-10-mediated negative feedback regulation of TNFα inhibits TNFα release following prolonged LPS application, though TNFα was not decreased by IL-10 KO at six h. This trend is consistent with IL- 10-mediated repression of TNFα adaptation to LPS. To test whether IL-10 KO influences TNFα adaptation to LPS, we computed the degree of adaptation between six and 18 h of LPS stimulation for WT and IL-10 KO macrophages (Fig. 7B). We found that adaptation was reduced in WT compared to the IL-10 KO (WT adaptation = 0.54, IL-10 KO adaptation = 1.04, see Methods eqn (3)). To evaluate the errors of these adaptation calculations, we applied an error propagation computation to estimate the respective standard deviations of WT versus KO adaptation (Methods eqn (4)). Based on these estimated deviations, we computed the adaptation values ± two times the standard deviations (adaptation ± 2 × sd): for the WT genotype this interval was (0.35, 0.74) whereas for the IL-10 KO genotype the interval was (1.00, 1.08). The adaptation ± 2 × sd intervals were non-overlapping and these intervals are likely to encompass the respective 95% confidence intervals ( ). Thus, our results provide convincing evidence that IL-10 KO increases adaptation of TNFα to LPS. Our experimental results support our computationally derived hypothesis that IL-10- mediated inhibition of TNFα has the counter-intuitive effect of suppressing adaptation to LPS.
Discussion
Our microglial cytokine network was established based on controlled cell culture experiments that demonstrated pairwise functional interactions between cytokines. Network inference approaches have shown utility in generating network structures from large data sets,91 but we chose to restrict our analysis to only interactions that have been experimentally validated. Data driven network structures can lack biological precision due to spurious correlations, inadequate pruning of indirect connections, and lack of information on edge sign (activation versus inhibition).92–94 Our approach of using mechanistic interaction data sets obviated the need for network discovery approaches.
In our modeling approach, we implemented a mathematical framework derived from the S-systems formalism.56 Similar adaptations of the S-systems model haven been useful in previous models involving cytokine signaling.57,58,95,96 A key assumption of our model was that the integrated effects of input cytokines on their target are governed by AND gating. While we do not have specific evidence validating this assumption for all connections in the network, both computational and experimental data indicate that AND gating is common in intracellular signaling networks involved in coordinating cytokine responses and production.97–100 Furthermore, incubation of macrophages with either TGFβ or IL-10 renders the cells almost completely refractory to LPS such that TNFα release is negligible,90 consistent with AND gating. Thus we hypothesize that such AND gating characterizes microglial cytokine interactions based on the congruence between our model and the available kinetic data.
Our network included an inhibitory effect of IL-6 on TNFα based on experimental data showing that IL-6 attenuates TNFα production by cultured microglia in response to LPS.31 However, it has been shown that IL-6 activates latent TGFβ,101 and this interaction was not included in our network model. We did not include this interaction because our sensitivity analyses indicated that the interaction between IL-6 and TNFα did not significantly contribute to our simulation results. Furthermore, a number of well documented molecular species that were not included in our model have been shown to influence the microglial phenotype.102 In particular, interferon-γ, nitric oxide, and superoxide have been shown to regulate microglial inflammation, 102 and these species have been shown to exert effects on TGFβ regulation in other immune cells.103,104 While we appreciate that these interactions may be important in the context of microglial LPS response, we chose not to include such interactions based on the dearth of microglia-specific data regarding these regulatory mechanisms, and the lack of time-series data necessary for parameter estimation.
A common feature of many systems biology models is that the inverse problem of parameter estimation is ill posed such that multiple non-unique solutions exist, thus rendering the problem underdetermined.105,106 This problem can be mitigated by using regularization techniques to facilitate error reduction in parameter estimation.107 However, the utilization of such techniques requires a priori criteria for penalizing certain parameter fits. It has been proposed that a priori information should not be used in solving inverse problems based on philosophical and mathematical arguments.108 While confidence in a model is enhanced by confidence in parameter estimates and parameter identifiability,109,110 it has been demonstrated that many models in systems biology and other areas of science have a spectrum unidentifiable parameters with exceedingly large confidence bounds.106,111 Even with very large data sets, such “sloppy” parameters can be prohibitively difficult to precisely estimate experimentally.106,110 While lack of parameter precision is a limitation inherent to situations in which the number of parameters exceeds the number of experimental data points, as in our case, approaches have been devised to mitigate problems associated with model parameter inidentifiability. Such alternative approaches include focusing on the robustness of model predictions106 and simulating a spectrum of parameter set phenotypes108,112 (see ESI,† “Parameter analysis discussion” for an expanded discussion). Our approach integrated the aforementioned perspectives by using sensitivity analysis to (1) focus manual parameter tuning of sensitive parameters, (2) thoroughly assess model output uncertainty, and (3) verify our model predictions for a population of optimized parameter sets. As detailed in the ESI,† we demonstrated that our model generates well constrained predictions. Thus, despite the limitation that our parameters are not ideally constrained, due to the lack of adequately sampled data, our predictions have very tight confidence bounds. The validity of our model is also supported by our findings of endotoxin tolerance and its dependence on TGFβ. Furthermore, we have performed Differential Lyapunov exponent analysis for TNFα trajectory to examine the maximal exponential rate of divergence of trajectories surrounding it. Our results indicate that the negative feedback loops imposed by IL-10 and TGFβ are more sensitive to perturbations in the initial state when the system is operating closer to the bifurcation point (Fig. 5B). Despite all the complexities in the network, the model preserves bifurcative characteristics of negative feedback loops as observed elsewhere.113 These results are consistant with our sensitivity analyses indicating model robustness. Finally, our model predictions regarding tolerance and adaptation were confirmed in 5/7 (>70%) of parameter the parameter sets estimated from random starting points (Fig. S5, ESI†).
Topological analysis of our cytokine interaction network suggested that TNFα is a critical control-point for the microglial LPS response. Global sensitivity analysis of our mathematical model showed that TGFβ and IL-10 are prominent feedback inhibitors of TNFα. Consistent with these analyses, TNFα has been implicated as a regulator of neuroinflammation in central infections77,78 and traumatic injuries2 as well as neurological, neurodegenerative, and psychiatric diseases.75,79 Assessment of TNFα sensitivity to the initial state of the network showed that the initial levels of TGFβ and IL-10 can exert opposing influences on TNFα. Increases in the initial levels of TGFβ could only lead to reductions of the TNFα response to LPS regardless of the initial IL-10 and TNFα levels. However, increases in the initial levels of IL-10 could elicit TNFα peak reductions and temporal shifts. These results indicate the instance of a separatrix depending on the initial states of TGFβ and IL-10. Based on our topological analysis of the network, and sensitivity analyses of the mathematical model, we focused our study on the roles of TGFβ and IL-10 in regulating TNFα dynamics. While we did not explicitly examine the contributions of IL-1β, IL-6, and CCL5 to network behavior in our simulations, their presence in the model shaped the network interactions we studied.
To further assess the functional implications of cytokine interaction dynamics, we studied the contributions of TGFβ and IL-10 to TNFα expression in the physiological context of adaptation to LPS. Surprisingly, TGFβ and IL-10 were found to have opposing effects on adaptation to LPS. These divergent effects appear to be related to the differences in the kinetics of the feedback inhibition. Experimental data from macrophages and microglia show that that IL-10 activation precedes that of TGFβ.31–33,90 IL-10 controls the amount of TGFβ produced by providing relatively fast negative feedback to TNFα and thereby coordinating its level of activation. In turn, TGFβ regulates the sustained level of TNFα. Based on our modeling predictions, we experimentally tested the hypothesis that IL-10 KO results in enhanced TNFα adaptation to sustained LPS in macrophages. Our data supported the mechanisms proposed based on our modeling work, thereby demonstrating that IL-10 occlusion enhances adaptation to LPS. However, we note that our model predicts a relatively augmented TNFα in the IL-10 condition. This was not observed in our experiment, however, we believe this is because we may not have sampled at the time of the peak response. Furthermore, the LPS response kinetics are likely to be different between WT and IL-10 KO conditions. Experiments are currently underway to address these possibilities. Nevertheless, our experimental results are consistent with enhanced adaptation following prolonged LPS exposure, whereas instance of peak modulation will be addressed in future experiments.
While recent evidence has shown microglia, under homeostatic conditions, express a unique gene profile,40,114 microglia and peripherally derived macrophages share the majority of genes involved in the inflammatory response. In a functional context, LPS tolerance of the TNFα to sequentially applied LPS doses has been observed in both macrophages115 and microglia. 86 Our model validation results were consistent with these findings. Furthermore, TGFβ was shown to mediate LPS tolerance in both macrophages115 and microglia,87 and our model recapitulated these results. Importantly, there is a wealth of data demonstrating that macrophages and microglia engage similar interactions amongst TNFα, TGF, and IL-10.87,89,90,115,116 Therefore, we believe the use of macrophages is highly relevant in this context and validates our unexpected finding that IL-10 reduces TNFα adaptation. This interpretation is consistent with the common use of bone marrow-derived cells as models of neuroinflammation, given the experimental accessibility of these cells.6,117,118 Furthermore, given the issues raised above modeling issues related to the sloppiness and inidentifiability of model parameters, our macrophage results support the generalizability of our findings to other myeloid cell types. Efforts are currently focused on modeling and experimentally testing the effects of IL-10 KO on adaptation and tolerance in microglia in vivo.
Our novel findings that TGFβ and IL-10 exert opposing effects on adaptation supports and extends the conclusions of several modeling studies. It has been shown that negative feedback loops with differential kinetics exert distinguishable influences in an oscillating network.119 In a model of peripheral immune response to LPS, it was shown that relatively slow versus fast anti-inflammatory activation led to sepsis.120 Faster anti-inflammatory activation was associated with restoration to health.120 In contrast, we found that the faster IL-10 response was associated with pro-inflammatory effects via indirect inhibition of TGFβ mediated indirectly by TNFα. An important distinction between our microglial model and peripheral infection models120 is that the peripheral models simulate cell to cell interactions, whereas our model is microglia-specific. As such, seemingly pro-inflammatory effects of adjustments to anti-inflammatory levels in peripheral models occur due to excessive reduction of the capacity of phagocytes to clear pathogens. This context is distinct from our study of autocrine/paracrine regulation of microglia via cytokine network dynamics.
Similarly, simulations with a computational model of NFκB dynamics showed that kinetically distinct negative feedback inhibitors (A20 and IκBα) exert differential influences on the TNFα response to LPS stimulation.35 A20 KO resulted in an enhanced TNFα response to LPS. Response adaptation was increased, as with our finding that IL-10 KO increased adaptation. Further, IκBα KO resulted in an increased A20 response, analogous to our finding that IL-10 KO resulted in increased TGFβ expression. However, the increased expression of A20 was insufficient for attenuating the LPS response in the NFκB model. The A20 anti-inflammatory response adapted rapidly compared to the sustained activation anti-inflammatory cytokines in our model, thus highlighting a key difference between the systems under study. Hence, while a number of previous studies document phenomena similar to our observations, in the contexts of multi-cellular interactions or isolated signaling pathways, our study provides novel insights into the roles of parallel negative feedback interactions involving cytokine signaling in microglia.
Conclusions
Our simulations and analyses show novel phenomena whereby TGFβ and IL-10 exert opposing influences on TNFα. While our focus on LPS response directly pertains to the microglial endotoxin response, microglial phenotypes associated with bacterial infection have been shown to resemble those associated with neurodegenerative diseases.121 In particular, LPS activates inflammatory signaling through interaction with tolllike receptor-4, which also activates sterile inflammation in hypoxic, ischaemic, and traumatic injuries.122–126 It is clear that macrophages and microglia exhibit a plethora of stimulus-specific phenotypic states,127,128 although the mechanisms underlying regulation of cytokine production share a common network regulatory basis in disparate inflammatory phenotypes. 127 Our study of microglial LPS responses may have broader implications regarding cytokine network interactions stimulated by other inflammatory ligands such as beta-amyloid and alpha-synuclein. Simulations and analysis of our model highlight novel hypotheses that can be addressed through experiments with cultured microglia using available tools for perturbing and measuring cytokines. Thus, our model of cytokine signaling in microglia offers utility in generating mechanistic hypotheses regarding the therapeutic applications of cytokine perturbations to treat conditions associated with neuroinflammation.
Supplementary Material
Acknowledgments
Thanks to Dr Lakshmi Kuttippurathu and Dan Cook for helpful discussion and advice. Thank you to the reviewers for thoughtful comments and suggestions for improvement. Thank you to Dr Radzioch (RIMUHC) for providing IL-10 KO mice. This study was supported by National Heart, Lung, and Blood Institute grant No. R01 HL111621 to RV and JSS; and Canadian Institute of Health Research grant (MOP-14828) to SD.
Footnotes
Electronic supplementary information (ESI) available. See DOI: 10.1039/c5mb00488h
References
- 1.Rock RB, Gekker G, Hu S, Sheng WS, Cheeran M, Lokensgard JR, Peterson PK. Clin Microbiol Rev. 2004;17:942–964. doi: 10.1128/CMR.17.4.942-964.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kroner A, Greenhalgh AD, Zarruk JG, Passos Dos Santos R, Gaestel M, David S. Neuron. 2014;83:1098–1116. doi: 10.1016/j.neuron.2014.07.027. [DOI] [PubMed] [Google Scholar]
- 3.Parakalan R, Jiang B, Nimmi B, Janani M, Jayapal M, Lu J, Tay SSW, Ling EA, Dheen ST. BMC Neurosci. 2012;13:64. doi: 10.1186/1471-2202-13-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.David S, Kroner A. Nat Rev Neurosci. 2011;12:388–399. doi: 10.1038/nrn3053. [DOI] [PubMed] [Google Scholar]
- 5.Kettenmann H, Hanisch UK, Noda M, Verkhratsky A. Physiol Rev. 2011;91:461–553. doi: 10.1152/physrev.00011.2010. [DOI] [PubMed] [Google Scholar]
- 6.Greenhalgh AD, David S. J Neurosci. 2014;34:6316–6322. doi: 10.1523/JNEUROSCI.4912-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nimmerjahn A, Kirchhoff F, Helmchen F. Science. 2005;308:1314–1318. doi: 10.1126/science.1110647. [DOI] [PubMed] [Google Scholar]
- 8.Olson JK, Miller SD. J Immunol. 2004;173:3916–3924. doi: 10.4049/jimmunol.173.6.3916. [DOI] [PubMed] [Google Scholar]
- 9.Hanisch UK. Glia. 2002;40:140–155. doi: 10.1002/glia.10161. [DOI] [PubMed] [Google Scholar]
- 10.Trapp BD, Wujek JR, Criste GA, Jalabi W, Yin X, Kidd GJ, Stohlman S, Ransohoff R. Glia. 2007;55:360–368. doi: 10.1002/glia.20462. [DOI] [PubMed] [Google Scholar]
- 11.Chen Z, Jalabi W, Hu W, Park HJ, Gale JT, Kidd GJ, Bernatowicz R, Gossman ZC, Chen JT, Dutta R, Trapp BD. Nat Commun. 2014;5:4486. doi: 10.1038/ncomms5486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Riazi K, Galic MA, Kuzmiski JB, Ho W, Sharkey KA, Pittman QJ. Proc Natl Acad Sci U S A. 2008;105:17151–17156. doi: 10.1073/pnas.0806682105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pickering M, Cumiskey D, O’Connor JJ. Exp Physiol. 2005;90:663–670. doi: 10.1113/expphysiol.2005.030734. [DOI] [PubMed] [Google Scholar]
- 14.Stellwagen D, Malenka RC. Nature. 2006;440:1054–1059. doi: 10.1038/nature04671. [DOI] [PubMed] [Google Scholar]
- 15.Pribiag H, Stellwagen D. J Neurosci. 2013;33:15879–15893. doi: 10.1523/JNEUROSCI.0530-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Paolicelli RC, Bolasco G, Pagani F, Maggi L, Scianni M, Panzanelli P, Giustetto M, Ferreira TA, Guiducci E, Dumas L, Ragozzino D, Gross CT. Science. 2011;333:1456–1458. doi: 10.1126/science.1202529. [DOI] [PubMed] [Google Scholar]
- 17.Parkhurst CN, Yang G, Ninan I, Savas JN, Yates JR, Lafaille JJ, Hempstead BL, Littman DR, Gan WB. Cell. 2013;155:1596–1609. doi: 10.1016/j.cell.2013.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schafer DP, Lehrman EK, Stevens B. Glia. 2013;61:24–36. doi: 10.1002/glia.22389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Williamson LL, Sholar PW, Mistry RS, Smith SH, Bilbo SD. J Neurosci. 2011;31:15511–15521. doi: 10.1523/JNEUROSCI.3688-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bilbo SD, Biedenkapp JC, Der-Avakian A, Watkins LR, Rudy JW, Maier SF. J Neurosci. 2005;25:8000–8009. doi: 10.1523/JNEUROSCI.1748-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hornig M, Weissenbock H, Horscroft N, Lipkin WI. Proc Natl Acad Sci U S A. 1999;96:12102–12107. doi: 10.1073/pnas.96.21.12102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Neher JJ, Brown GC. Biochem Soc Trans. 2007;35:1166–1167. doi: 10.1042/BST0351166. [DOI] [PubMed] [Google Scholar]
- 23.Barone FC, Feuerstein GZ. J Cereb Blood Flow Metab. 1999;19:819–834. doi: 10.1097/00004647-199908000-00001. [DOI] [PubMed] [Google Scholar]
- 24.Saijo K, Glass CK. Nat Rev Immunol. 2011;11:775–787. doi: 10.1038/nri3086. [DOI] [PubMed] [Google Scholar]
- 25.Welser-Alves JV, Milner R. Neurochem Int. 2013;63:47–53. doi: 10.1016/j.neuint.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gregory AP, Dendrou CA, Attfield KE, Haghikia A, Xifara DK, Butter F, Poschmann G, Kaur G, Lambert L, Leach OA, Prömel S, Punwani D, Felce JH, Davis SJ, Gold R, Nielsen FC, Siegel RM, Mann M, Bell JI, McVean G, Fugger L. Nature. 2012;488:508–511. doi: 10.1038/nature11307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mocellin S, Panelli MC, Wang E, Nagorsen D, Marincola FM. Trends Immunol. 2003;24:36–43. doi: 10.1016/s1471-4906(02)00009-1. [DOI] [PubMed] [Google Scholar]
- 28.Anastasio TJ. Mol BioSyst. 2015;11:434–453. doi: 10.1039/c4mb00457d. [DOI] [PubMed] [Google Scholar]
- 29.Anastasio TJ. Front Pharmacol. 2015;6:116. doi: 10.3389/fphar.2015.00116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ma W, Trusina A, El-Samad H, Lim WA, Tang C. Cell. 2009;138:760–773. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chao CC, Hu S, Sheng WS, Peterson PK. Dev Neurosci. 1995;17:97–105. doi: 10.1159/000111278. [DOI] [PubMed] [Google Scholar]
- 32.Sheng WS, Hu S, Kravitz FH, Peterson PK, Chao CC. Clin Diagn Lab Immunol. 1995;2:604–608. doi: 10.1128/cdli.2.5.604-608.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chao CC, Hu S, Sheng WS, Tsang M, Peterson PK. Clin Immunol Immunopathol. 1995;77:358–365. doi: 10.1006/clin.1995.1163. [DOI] [PubMed] [Google Scholar]
- 34.Behar M, Hao N, Dohlman HG, Elston TC. Biophys J. 2007;93:806–821. doi: 10.1529/biophysj.107.107516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.An GC, Faeder JR. Math Biosci. 2009;217:53–63. doi: 10.1016/j.mbs.2008.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Barzel B, Barabasi AL. Nat Phys. 2013;9:673–681. doi: 10.1038/nphys2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Minogue AM, Barrett JP, Lynch MA. J Neuroinflammation. 2012;9:126. doi: 10.1186/1742-2094-9-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hopp SC, Royer S, Brothers HM, Kaercher RM, D’Angelo H, Bardou I, Wenk GL. J Neuroimmunol. 2014;267:86–91. doi: 10.1016/j.jneuroim.2013.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang Y, Chen K, Sloan SA, Bennett ML, Scholze AR, O’Keeffe S, Phatnani HP, Guarnieri P, Caneda C, Ruderisch N, Deng S, Liddelow SA, Zhang C, Daneman R, Maniatis T, Barres BA, Wu JQ. J Neurosci. 2014;34:11929–11947. doi: 10.1523/JNEUROSCI.1860-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Butovsky O, Jedrychowski MP, Moore CS, Cialic R, Lanser AJ, Gabriely G, Koeglsperger T, Dake B, Wu PM, Doykan CE, Fanek Z, Liu L, Chen Z, Rothstein JD, Ransohoff RM, Gygi SP, Antel JP, Weiner HL. Nat Neurosci. 2014;17:131–143. doi: 10.1038/nn.3599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dong Y, Benveniste EN. Glia. 2001;36:180–190. doi: 10.1002/glia.1107. [DOI] [PubMed] [Google Scholar]
- 42.Sheppard PW, Sun X, Emery JF, Giffard RG, Khammash M. BMC Bioinf. 2011;12:276. doi: 10.1186/1471-2105-12-276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Puri IK, Li L. PLoS One. 2010;5:e15176. doi: 10.1371/journal.pone.0015176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rodriguez-Fernandez M, Grosman B, Yuraszeck TM, Helwig BG, Leon LR, Doyle FJ., III PLoS One. 2013;8:e73393. doi: 10.1371/journal.pone.0073393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Yiu HH, Graham AL, Stengel RF. PLoS One. 2012;7:e45027. doi: 10.1371/journal.pone.0045027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Marino S, Cilfone NA, Mattila JT, Linderman JJ, Flynn JL, Kirschner DE. Infect Immun. 2015;83:324–338. doi: 10.1128/IAI.02494-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cilfone NA, Perry CR, Kirschner DE, Linderman JJ. PLoS One. 2013;8:e68680. doi: 10.1371/journal.pone.0068680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ziraldo C, Mi Q, An G, Vodovotz Y. Adv Wound Care. 2013;2:527–537. doi: 10.1089/wound.2012.0416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nguyen TT, Calvano SE, Lowry SF, Androulakis IP. PLoS One. 2013;8:e55550. doi: 10.1371/journal.pone.0055550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sheppard PW, Sun X, Khammash M, Giffard RG. PLoS Comput Biol. 2014;10:e1003471. doi: 10.1371/journal.pcbi.1003471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Maiti S, Dai W, Alaniz R, Hahn J, Jayaraman A. Processes. 2014;3:1–18. [Google Scholar]
- 52.Caldwell AB, Cheng Z, Vargas JD, Birnbaum HA, Hoffmann A. Genes Dev. 2014;28:2120–2133. doi: 10.1101/gad.244749.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Moya C, Huang Z, Cheng P, Jayaraman A, Hahn J. IET Syst Biol. 2011;5:15. doi: 10.1049/iet-syb.2009.0060. [DOI] [PubMed] [Google Scholar]
- 54.Werner SL, Barken D, Hoffmann A. Science. 2005;309:1857–1861. doi: 10.1126/science.1113319. [DOI] [PubMed] [Google Scholar]
- 55.Correnti JM, Cook D, Aksamitiene E, Swarup A, Ogunnaike B, Vadigepalli R, Hoek JB. J Physiol. 2015;593:365–383. doi: 10.1113/jphysiol.2014.284109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Savageau MA. J Theor Biol. 1969;25:370–379. doi: 10.1016/s0022-5193(69)80027-5. [DOI] [PubMed] [Google Scholar]
- 57.Meyer-Hermann M, Figge MT, Straub RH. Arthritis Rheum. 2009;60:2585–2594. doi: 10.1002/art.24797. [DOI] [PubMed] [Google Scholar]
- 58.Valeyev NV, Hundhausen C, Umezawa Y, Kotov NV, Williams G, Clop A, Ainali C, Ouzounis C, Tsoka S, Nestle FO. PLoS Comput Biol. 2010;6:e1001024. doi: 10.1371/journal.pcbi.1001024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Furchtgott LA, Chow CC, Periwal V. Biophys J. 2009;96:3926–3935. doi: 10.1016/j.bpj.2009.01.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM. J Comput Neurosci. 2004;17:7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Miller GM, Ogunnaike BA, Schwaber JS, Vadigepalli R. BMC Syst Biol. 2010;4:171. doi: 10.1186/1752-0509-4-171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, Saisana M, Tarantola S. Global Sensitivity Analysis The Primer. Wiley-Interscience; Hoboken, NJ: 2008. [Google Scholar]
- 63.Tarantola S, Becker W, Zeitz D. Comput Phys Commun. 2012;183:1061–1072. [Google Scholar]
- 64.Yang J. Environ Modell Softw. 2011;26:444–457. [Google Scholar]
- 65.Longbrake EE, Lai W, Ankeny DP, Popovich PG. J Neurochem. 2007;102:1083–1094. doi: 10.1111/j.1471-4159.2007.04617.x. [DOI] [PubMed] [Google Scholar]
- 66.Livak KJ, Schmittgen TD. Methods. 2001;25:402–408. doi: 10.1006/meth.2001.1262. [DOI] [PubMed] [Google Scholar]
- 67.Tellinghuisen J. In: Methods in Cell Biology. Correia IJJ, William Detrich H, editors. Vol. 84. Academic Press; 2008. pp. 737–780. [Google Scholar]
- 68.R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2008. [Google Scholar]
- 69.Chao CC, Hu S, Close K, Choi CS, Molitor TW, Novick WJ, Peterson PK. J Infect Dis. 1992;166:847–853. doi: 10.1093/infdis/166.4.847. [DOI] [PubMed] [Google Scholar]
- 70.Agarwal D, Dange RB, Raizada MK, Francis J. Br J Pharmacol. 2013;169:860–874. doi: 10.1111/bph.12177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zubcevic J, Waki H, Raizada MK, Paton JFR. Hypertension. 2011;57:1026–1033. doi: 10.1161/HYPERTENSIONAHA.111.169748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wu KLH, Chan SHH, Chan JYH. J Neuroinflammation. 2012;9:212. doi: 10.1186/1742-2094-9-212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Heneka MT, Kummer MP, Latz E. Nat Rev Immunol. 2014;14:463–477. doi: 10.1038/nri3705. [DOI] [PubMed] [Google Scholar]
- 74.Whitney NP, Eidem TM, Peng H, Huang Y, Zheng JC. J Neurochem. 2009;108:1343–1359. doi: 10.1111/j.1471-4159.2009.05886.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.McCoy MK, Tansey MG. J Neuroinflammation. 2008;5:45. doi: 10.1186/1742-2094-5-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Chao CC, Hu S, Sheng WS, Tsang M, Peterson PK. Clin Immunol Immunopathol. 1995;77:358–365. doi: 10.1006/clin.1995.1163. [DOI] [PubMed] [Google Scholar]
- 77.Szretter KJ, Samuel MA, Gilfillan S, Fuchs A, Colonna M, Diamond MS. J Virol. 2009;83:9329–9338. doi: 10.1128/JVI.00836-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Chen CJ, Ou YC, Chang CY, Pan HC, Liao SL, Chen SY, Raung SL, Lai CY. Glia. 2012;60:487–501. doi: 10.1002/glia.22282. [DOI] [PubMed] [Google Scholar]
- 79.Park KM, Bowers WJ. Cell Signalling. 2010;22:977–983. doi: 10.1016/j.cellsig.2010.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Vitkovic L, Konsman JP, Bockaert J, Dantzer R, Homburger V, Jacque C. Mol Psychiatry. 2000;5:604–615. doi: 10.1038/sj.mp.4000813. [DOI] [PubMed] [Google Scholar]
- 81.Cambier S, Gline S, Mu D, Collins R, Araya J, Dolganov G, Einheber S, Boudreau N, Nishimura SL. Am J Pathol. 2005;166:1883–1894. doi: 10.1016/s0002-9440(10)62497-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Morgan TE, Rozovsky I, Sarkar DK, Young-Chan CS, Nichols NR, Laping NJ, Finch CE. Neuroscience. 2000;101:313–321. doi: 10.1016/s0306-4522(00)00387-0. [DOI] [PubMed] [Google Scholar]
- 83.Norgaard P, Spang-Thomsen M, Poulsen HS. Br J Cancer. 1996;73:1037–1043. doi: 10.1038/bjc.1996.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Joyce ME, Roberts AB, Sporn MB, Bolander ME. J Cell Biol. 1990;110:2195–2207. doi: 10.1083/jcb.110.6.2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Van Obberghen-Schilling E, Roche NS, Flanders KC, Sporn MB, Roberts AB. J Biol Chem. 1988;263:7741–7746. [PubMed] [Google Scholar]
- 86.Ajmone-Cat MA, Nicolini A, Minghetti L. J Neurochem. 2003;87:1193–1203. doi: 10.1046/j.1471-4159.2003.02087.x. [DOI] [PubMed] [Google Scholar]
- 87.Le Y, Iribarren P, Gong W, Cui Y, Zhang X, Wang JM. J Immunol. 2004;173:962–968. doi: 10.4049/jimmunol.173.2.962. [DOI] [PubMed] [Google Scholar]
- 88.Lodge PA, Sriram S. J Leukocyte Biol. 1996;60:502–508. doi: 10.1002/jlb.60.4.502. [DOI] [PubMed] [Google Scholar]
- 89.Bogdan C, Nathan C. Ann N Y Acad Sci. 1993;685:713–739. doi: 10.1111/j.1749-6632.1993.tb35934.x. [DOI] [PubMed] [Google Scholar]
- 90.Bogdan C, Paik J, Vodovotz Y, Nathan C. J Biol Chem. 1992;267:23301–23308. [PubMed] [Google Scholar]
- 91.Azhar N, Ziraldo C, Barclay D, Rudnick DA, Squires RH, Vodovotz Y for the Pediatric Acute Liver Failure Study Group. PLoS One. 2013;8:e78202. doi: 10.1371/journal.pone.0078202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Zoppoli P, Morganella S, Ceccarelli M. BMC Bioinf. 2010;11:154. doi: 10.1186/1471-2105-11-154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Janes KA, Lauffenburger DA. Curr Opin Chem Biol. 2006;10:73–80. doi: 10.1016/j.cbpa.2005.12.016. [DOI] [PubMed] [Google Scholar]
- 94.Kholodenko BN, Kiyatkin A, Bruggeman FJ, Sontag E, Westerhoff HV, Hoek JB. Proc Natl Acad Sci U S A. 2002;99:12841–12846. doi: 10.1073/pnas.192442699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Shao H, He Y, Li KCP, Zhou X. Mol BioSyst. 2013;9:398–406. doi: 10.1039/c2mb25370d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Ray JCJ, Wang J, Chan J, Kirschner DE. J Theor Biol. 2008;252:24–38. doi: 10.1016/j.jtbi.2008.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Bezbradica JS, Rosenstein RK, DeMarco RA, Brodsky I, Medzhitov R. Nat Immunol. 2014;15:333–342. doi: 10.1038/ni.2845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Saez-Rodriguez J, Alexopoulos LG, Epperlein J, Samaga R, Lauffenburger DA, Klamt S, Sorger PK. Mol Syst Biol. 2009;5:331. doi: 10.1038/msb.2009.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Cheng CS, Feldman KE, Lee J, Verma S, Huang DB, Huynh K, Chang M, Ponomarenko JV, Sun SC, Benedict CA, Ghosh G, Hoffmann A. Sci Signaling. 2011;4:ra11. doi: 10.1126/scisignal.2001501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Morris MK, Saez-Rodriguez J, Clarke DC, Sorger PK, Lauffenburger DA. PLoS Comput Biol. 2011;7:e1001099. doi: 10.1371/journal.pcbi.1001099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Villiger PM, Kusari AB, ten Dijke P, Lotz M. J Immunol. 1993;151:3337–3344. [PubMed] [Google Scholar]
- 102.Vincent VA, Tilders FJ, Van Dam AM. Mediators Inflammation. 1998;7:239–255. doi: 10.1080/09629359890929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Vodovotz Y, Chesler L, Chong H, Kim SJ, Simpson JT, DeGraff W, Cox GW, Roberts AB, Wink DA, Barcellos-Hoff MH. Cancer Res. 1999;59:2142–2149. [PubMed] [Google Scholar]
- 104.Vodovotz Y, Bogdan C, Paik J, Xie QW, Nathan C. J Exp Med. 1993;178:605–613. doi: 10.1084/jem.178.2.605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Klipp E, Liebermeister W, Wierling C, Kowald A, Lehrach H, Herwig R. Systems Biology. John Wiley & Sons; 2011. [Google Scholar]
- 106.Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. PLoS Comput Biol. 2007;3:1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Engl HW, Flamm C, Kügler P, Lu J, Müller S, Schuster P. Inverse Probl. 2009;25:123014. [Google Scholar]
- 108.Tarantola A. Nat Phys. 2006;2:492–494. [Google Scholar]
- 109.Dai W, Bansal L, Hahn J, Word D. AIChE J. 2014;60:181–192. [Google Scholar]
- 110.Raue A, Karlsson J, Saccomani MP, Jirstrand M, Timmer J. Bioinformatics. 2014;30:1440–1448. doi: 10.1093/bioinformatics/btu006. [DOI] [PubMed] [Google Scholar]
- 111.Machta BB, Chachra R, Transtrum MK, Sethna JP. Science. 2013;342:604–607. doi: 10.1126/science.1238723. [DOI] [PubMed] [Google Scholar]
- 112.Daun S, Rubin J, Vodovotz Y, Roy A, Parker R, Clermont G. J Theor Biol. 2008;253:843–853. doi: 10.1016/j.jtbi.2008.04.033. [DOI] [PubMed] [Google Scholar]
- 113.Cai S, Zhou P, Liu Z. Cogn Neurodyn. 2013;7:417–429. doi: 10.1007/s11571-012-9236-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Hickman SE, Kingery ND, Ohsumi TK, Borowsky ML, Wang L-c, Means TK, El Khoury J. Nat Neurosci. 2013;16:1896–1905. doi: 10.1038/nn.3554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Pan H, Ding E, Hu M, Lagoo AS, Datto MB, Lagoo-Deenadayalan SA. J Immunol. 2010;184:5502–5509. doi: 10.4049/jimmunol.0901601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Naiki Y, Michelsen KS, Zhang W, Chen S, Doherty TM, Arditi M. J Biol Chem. 2005;280:5491–5495. doi: 10.1074/jbc.C400503200. [DOI] [PubMed] [Google Scholar]
- 117.Vereyken EJF, Heijnen PDAM, Baron W, de Vries EHE, Dijkstra CD, Teunissen CE. J Neuroinflammation. 2011;8:58. doi: 10.1186/1742-2094-8-58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Wang W, Hu D, Xiong H. Glia. 2008;56:241–246. doi: 10.1002/glia.20609. [DOI] [PubMed] [Google Scholar]
- 119.Hoffmann A, Levchenko A, Scott ML, Baltimore D. Science. 2002;298:1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- 120.Reynolds A, Rubin J, Clermont G, Day J, Vodovotz Y, Bard Ermentrout G. J Theor Biol. 2006;242:220–236. doi: 10.1016/j.jtbi.2006.02.016. [DOI] [PubMed] [Google Scholar]
- 121.Amor S, Puentes F, Baker D, van der Valk P. Immunology. 2010;129:154–169. doi: 10.1111/j.1365-2567.2009.03225.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Bell MT, Puskas F, Agoston VA, Cleveland JC, Freeman KA, Gamboni F, Herson PS, Meng X, Smith PD, Weyant MJ, Fullerton DA, Reece TB. Circulation. 2013;128:S152–S156. doi: 10.1161/CIRCULATIONAHA.112.000024. [DOI] [PubMed] [Google Scholar]
- 123.Kilic U, Kilic E, Matter CM, Bassetti CL, Hermann DM. Neurobiol Dis. 2008;31:33–40. doi: 10.1016/j.nbd.2008.03.002. [DOI] [PubMed] [Google Scholar]
- 124.Tang SC, Arumugam TV, Xu X, Cheng A, Mughal MR, Jo DG, Lathia JD, Siler DA, Chigurupati S, Ouyang X, Magnus T, Camandola S, Mattson MP. Proc Natl Acad Sci U S A. 2007;104:13798–13803. doi: 10.1073/pnas.0702553104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Caso JR, Pradillo JM, Hurtado O, Lorenzo P, Moro MA, Lizasoain I. Circulation. 2007;115:1599–1608. doi: 10.1161/CIRCULATIONAHA.106.603431. [DOI] [PubMed] [Google Scholar]
- 126.Kigerl KA, Lai W, Rivest S, Hart RP, Satoskar AR, Popovich PG. J Neurochem. 2007;102:37–50. doi: 10.1111/j.1471-4159.2007.04524.x. [DOI] [PubMed] [Google Scholar]
- 127.Xue J, Schmidt SV, Sander J, Draffehn A, Krebs W, Quester I, De Nardo D, Gohel TD, Emde M, Schmidleithner L, Ganesan H, Nino-Castro A, Mallmann MR, Labzin L, Theis H, Kraut M, Beyer M, Latz E, Freeman TC, Ulas T, Schultze JL. Immunity. 2014;40:274–288. doi: 10.1016/j.immuni.2014.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Perry VH, Cunningham C, Holmes C. Nat Rev Immunol. 2007;7:161–167. doi: 10.1038/nri2015. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.