Understanding the molecular mechanism of pulse current charging for stable lithium-metal batteries

Pulse current charging stabilizes high-energy lithium-metal batteries.

Abstract

High energy and safe electrochemical storage are critical components in multiple emerging fields of technologies. Rechargeable lithium-metal batteries are considered to be promising alternatives for current lithium-ion batteries, leading to as much as a 10-fold improvement in anode storage capacity (from 372 to 3860 mAh g⁻¹). One of the major challenges for commercializing lithium-metal batteries is the reliability and safety issue, which is often associated with uneven lithium electrodeposition (lithium dendrites) during the charging stage of the battery cycling process. We report that stable lithium-metal batteries can be achieved by simply charging cells with square-wave pulse current. We investigated the effects of charging period and frequency as well as the mechanisms that govern this process at the molecular level. Molecular simulations were performed to study the diffusion and the solvation structure of lithium cations (Li⁺) in bulk electrolyte. The model predicts that loose association between cations and anions can enhance the transport of Li⁺ and eventually stabilize the lithium electrodeposition. We also performed galvanostatic measurements to evaluate the cycling behavior and cell lifetime under pulsed electric field and found that the cell lifetime can be more than doubled using certain pulse current waveforms. Both experimental and simulation results demonstrate that the effectiveness of pulse current charging on dendrite suppression can be optimized by choosing proper time- and frequency-dependent pulses. This work provides a molecular basis for understanding the mechanisms of pulse current charging to mitigating lithium dendrites and designing pulse current waveforms for stable lithium-metal batteries.

INTRODUCTION

Since the first commercial lithium-ion battery (LIB) appeared in the early 1990s, LIBs have been widely used in portable electronic devices and have recently been successfully applied in electric vehicles, unmanned aircraft, and large-scale deployment (1). However, the graphite anode of LIBs only has a theoretical specific capacity of 372 mAh g⁻¹. This inherent limitation makes it unlikely to meet the growing demand for high-energy storage (2, 3). Li metal is thought to be one of the most promising alternative anodes because of its step-change improvement in capacity (3860 mAh g⁻¹) and its low redox potential (−3.04 V versus the standard hydrogen potential electrode) (2, 4). In addition, lithium-metal anode is an essential component for lithium-sulfur and lithium-air batteries, which are currently under intensive research for next-generation high-energy lithium batteries (5–7). Unfortunately, many challenges need to be overcome before Li metal batteries become a reliable technology, the most serious of which are the poor cycling stability and safety issues (8).

During a typical charge step of cell cycling in lithium-metal batteries, lithium cations gain electrons on the anode surface and become metallic lithium. The reductive electrodeposition is usually nonuniform and hard to control because of the complicated surface chemistry and morphology of the anode. This heterogeneous nature of the electrodeposition or so-called Li dendrite becomes more marked during the subsequent cycles because of the uneven charge distribution along the rough surface. The growth of lithium dendrites is known as the source of battery failure. On the other hand, the electrolyte and the lithium metal could react irreversibly and form a solid electrolyte interface (SEI) on the metal surface to passivate the highly active Li metal and reduce further consumption of active materials. The fragile SEI could be ruptured during cycling because of the huge volume expansion of the anode. The instability of an SEI is another reason for the propensity of lithium to deposit in dendritic structures (9, 10). Once the fresh Li encounters the electrolyte, chemical reactions happen again and form a new SEI, leading to irreversible consumption of Li and electrolyte. As a consequence, the coulombic efficiency of Li metal batteries decreases, and the capacity fades quickly. The sharp dendrites on the surface of Li metal anode could pierce the separator and cause short circuit, generating heat or even igniting the organic solvents (11). In addition, the huge volume change of Li metal anode leads to internal stress and interface fluctuation (12). These problems have hindered the practical applications of rechargeable Li-metal–based batteries over the past 40 years.

Many experimental studies have emerged to regulate the Li metal anodes and stabilize the electrochemical behavior of lithium-metal batteries (13–20). In addition, the formation of lithium dendrites has been monitored at various length scales. Researchers have reported and theoretically predicted the conditions of dendrite nucleation and propagation. The dendrite growth is understood to be driven by the diffusion and electromigration of both Li ion and the counter ion under electric driving force. During charging, lithium cations and their counter ions transport in opposite directions and cause ion concentration gradient. At high current densities, the situation for the anions is more marked because they cannot form electrodes. Eventually, anions pile up near the anode and deplete near the cathode. This phenomenon is called “space charge,” which determines the onset time of lithium dendrites (21–25).

To fundamentally understand the mechanisms of electrolyte transport properties and suppress or even eliminate dendrite growth from the nucleation step, we report on the relaxation of ion concentration gradient via pulse current charging instead of common constant current charging and the stabilization of lithium-metal batteries via simply charging cells with square-wave pulse current (Fig. 1A). Pulse current charging was first used for lead acid battery to remove lead sulfate compound and extend battery lifetime (26). It was later used as an advanced charging technique for LIBs for the homogeneity of ion distribution between the two electrodes (27, 28). These reports showed that the pulse current charging could lower the impedance and temperature increment during the charging process and reduce side reactions compared to constant current charging. Only a few studies for the influence of pulse current charging in rechargeable lithium-metal batteries have been reported. To the best of our knowledge, the only experimental work for pulse current charging contains limited cycling information without appropriate simulation support (29). The underlying mechanism at the molecular level, which is essential for the rational design of pulse current charging, is also limited so far. Only two recent studies by Aryanfar et al. (30) and Mayers et al. (31) performed coarse-grained molecular simulations for lithium dendrite growth under pulse current charging. They both revealed a competition between the time scales for Li⁺ diffusion and reduction at the anode-SEI interface to understand the dendrite formation, and theoretically suggested that lithium dendrites could be inhibited by pulse charging with appropriate charging frequency.

Fig. 1. MD simulations of 1 M LiTFSI in PC solvent.

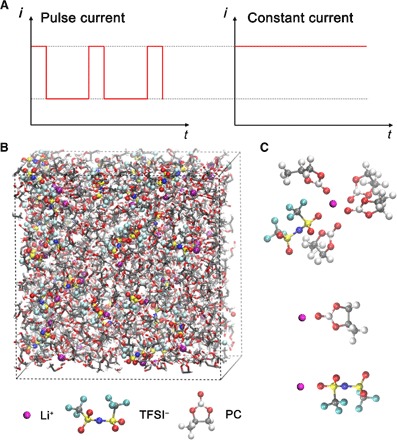
(A) Basic waveforms for pulse current and constant current. (B) Snapshot of the simulation box from MD simulations. Purple, red, blue, gray, yellow, teal, and white denote lithium, oxygen, nitrogen, carbon, sulfur, fluorine, and hydrogen atoms, respectively. (C) Representative configuration of solvation structures of Li⁺ from MD simulations. One lithium ion is associated with four PC molecules (one Li⁺ coordinates with four oxygen atoms in carbonyl groups) and one TFSI⁻ anion (one Li⁺ coordinates with two oxygen atoms in one TFSI⁻ anion).

To understand dendrite growth mechanism both theoretically and experimentally, we used rectangular cathodic pulses with various frequencies and rest time, and monitored their growth propensity by all-atom molecular dynamics (MD) simulations and voltage-time profiles. MD simulations were performed to examine the diffusivity of Li ions in an electrolyte under pulsed electric fields with different frequencies and strength. The solvation structures of Li ions were also considered to further understand the effectiveness of transport properties on dendrite growth. The model predicts that loose association between cations and anions can enhance the diffusion of Li⁺. We also evaluated the cycling behavior by galvanostatic cycling measurements and found that the cell lifetime can be more than doubled using certain pulse current waveforms. Both experimental and MD simulation results demonstrated that the effectiveness of pulse current charging can be optimized by choosing proper time- and frequency-dependent pulses. This work provides a molecular basis for understanding the mechanisms of pulse current charging for mitigating lithium dendrites and designing pulse current waveforms for stable performance in advanced lithium-metal batteries, such as high-energy lithium-sulfur and lithium-oxygen batteries.

RESULTS

Diffusion of Li⁺ in pulsed electric fields

Pulsed electric fields may affect both the diffusion and electrodeposition of Li⁺. Although it is still challenging to examine the electrodeposition of Li⁺ using classic all-atom MD at a large scale, it is, however, feasible to examine the diffusion of Li⁺ at the molecular level, which is the focus of this work. We abstract a local area in an electrolyte and analyze the microscopic motion of Li⁺ based on all-atom MD simulations. In all-atom models, the position and velocity of each individual atom are explicitly represented in the simulations, which allow high-resolution analysis of simulation trajectories. The simulation system is constructed with 51 Li⁺, 51 TFSI⁻ [bis(trifluoromethanesulfonyl)imide anion], and 600 PC (propylene carbonate) molecules, which gives a total of 8616 atoms and represents LiTFSI [lithium bis(trifluoromethanesulfonyl)imide]–PC solution with a concentration of 1.0 M lithium salt. The system is in a cubic box with a dimension of 43.88 Å in length (x), width (y), and height (z) (Fig. 1B). The self-diffusion coefficient D of Li⁺ can be computed from the mean square displacement (MSD) of MD trajectories based on the Einstein relation

$${\mathit{D}}^{\text{MSD}}=\underset{\mathit{t}\to \infty }{\text{lim}}\frac{\langle {|\overrightarrow{\mathit{r}}(\mathit{t})-\overrightarrow{\mathit{r}}(0)|}^2\rangle }{6\mathit{t}}$$ (1)

where $\overrightarrow{\mathit{r}}(\mathit{t})$ is the location of the center of mass of a specific ion at time t; the brackets indicate the ensemble average. Figure 2 shows that the diffusion coefficients of Li⁺ in all cases are sensitive to applied electric fields. Pulsed electric fields may significantly enhance the diffusion of Li⁺, which is larger than that in a static electric field or in the control case, where no electric field is applied. The pulsed electric field with a T_on/T_off ratio of 1:3 (T_on means the period of constant current charging or discharging, and T_off means the rest period followed by the constant current charging or discharging) is observed to offer the highest diffusion coefficient of Li⁺ among all the cases examined in this study. Moreover, in an electric field with a higher strength of 3 × 10⁶ V m⁻¹, a T_on/T_off ratio of 1:3 is also found to be the optimal condition for Li⁺ diffusion (fig. S1A). This observation suggests that an innate nature of LiTFSI-PC solution may determine the optimal pulse current waveform for achieving the highest diffusivity of Li⁺, which is independent of the strength of the electric field within a certain range. For instance, in electric field with an even higher strength, such as 3 × 10⁸ V m⁻¹, the diffusion coefficient was observed to be dominated by the strength of electric field (fig. S1B). This is consistent with a recent experimental study by Pei and co-workers (32), suggesting that high overpotentials are capable of effectively reducing the dendrite formation of lithium-metal batteries. Because the only intramolecular interactions of Li⁺ in the solutions are the ones with TFSI⁻ and PC, the solvation structures of Li⁺ and TFSI⁻ in PC solutions need to be examined for further insights.

Fig. 2. The impact of pulsed electric fields on the diffusivity of Li⁺.

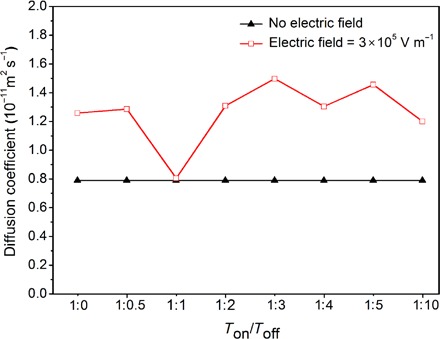
Diffusion coefficients of Li⁺ in 1 M LiTFSI/PC solutions under a static electric field with a strength of 3 × 10⁵ V m⁻¹, under a pulsed electric field with the same strength, and with no electric field. The T_on/T_off ratios of pulsed electric fields are 1:0.5, 1:1, 1:2, 1:3, 1:4, 1:5, and 1:10. For convenience, a static electric field is shown as the one with a T_on/T_off ratio of 1:0. The diffusion coefficient of Li⁺ is shown to be sensitive to the T_on/T_off ratio of the pulsed electric field with an optimal value at 1:3.

It should be noted that the diffusion coefficients of Li⁺ obtained from this work are similar to those from other MD studies using the OPLS-AA (optimized potentials for liquid simulations for all-atom) force field (33, 34), which are typically about one order of magnitude lower than the experimental findings measured with the pulse gradient spin echo nuclear magnetic resonance (35). Despite the difference in value, the diffusion coefficients derived from simulations were understood to qualitatively agree with those revealed by experiments (33).

Solvation structure of Li⁺ in PC solutions

As shown in the simulation snapshot (Fig. 1, B and C), Li⁺ may associate with TFSI⁻ and PC, leading to certain solvation structures. The structures can be described with the radial distribution function (RDF), which shows how density of atom j varies as a function of distance from a reference atom i (i in this case is Li⁺, and j could be either a PC molecule or TFSI⁻)

$${\mathit{g}}_{\mathit{i}\mathit{j}}(\mathit{r})=\frac{\langle {\mathit{N}}_{\mathit{i}\mathit{j}}(\mathit{r})/\mathit{V}(\mathit{r})\rangle }{{\mathrm{\rho }}_{\mathit{j}}}$$ (2)

where N_ij(r) is the ensemble averaged number of atoms j in a spherical shell of volume V(r) at a distance r from atom i, and ρ_j is the bulk density of atom j. The coordination numbers of the PC solvent molecules surrounding the solvation shell of the ions are calculated from the following integral

$$\mathit{n}(\mathit{R})=4\mathrm{\pi }{\mathrm{\rho }}_{\mathit{j}}{\displaystyle {\int }_0^{\mathit{R}}}{\mathit{r}}^2{\mathit{g}}_{\mathit{i}\mathit{j}}(\mathit{r})\mathit{d}\mathit{r}$$ (3)

where R is the minimum after the first peak in the RDF g_ij(r). The different coordination numbers may affect the dynamic properties of the Li⁺, such as their diffusivity (36).

Figure 3 (A and B) shows that the first peak in g(r) for Li⁺ appears at around 2.1 Å for both carbonyl oxygen atoms in PC and oxygen atoms in TFSI⁻. These results agree with previous reported studies of LiPF₆ in PC (37) and LiTFSI-acetamide systems (36). It also indicates that Li⁺ has strong solvation structures with PC molecules. This association is more obvious between Li⁺ and TFSI⁻ ion pairs because the peak intensity in Fig. 3B is stronger than that in Fig. 3A.

Fig. 3. The solvation structures of Li⁺ in PC solutions.

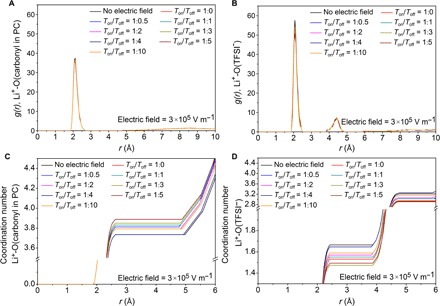
RDFs of (A) cation-solvent [Li⁺-O(carbonyl in PC)] and (B) cation-anion [Li⁺-O(TFSI⁻)] and the coordination numbers of (C) cation-solvent [Li⁺-O(carbonyl in PC)] and (D) cation-anion [Li⁺-O(TFSI⁻)] under conditions of no electric field, static electric field, and pulsed electric fields with a strength of 3 × 10⁵ V m⁻¹. The T_on/T_off ratios of pulsed electric fields are 1:0.5, 1:1, 1:2, 1:3, 1:4, 1:5, and 1:10. For convenience, the static electric field is shown as the one with a T_on/T_off ratio of 1:0. Pulse current charging can reduce the coordination number of TFSI⁻ around Li⁺ ions.

As shown in Fig. 3 (C and D), the coordination number of oxygen atoms around Li⁺ is approximately six, among which four are from PC and one or two are from TFSI⁻. Similar results have been previously reported with Raman intensity experiments (38) and classical MD simulations (39–41) that, when a static electric field is applied, the coordination number of TFSI⁻ around Li⁺ gets smaller. In addition, Fig. 3 (C and D) demonstrates that both coordination numbers of cation-solvent [Li⁺-O(carbonyl in PC)] and cation-anion [Li⁺-O(TFSI⁻)] can be affected by applying pulsed electric fields. When a pulsed electric field with a T_on/T_off ratio of 1:3 is used, Li⁺ has a relatively larger coordination number of PC and a smaller coordination number of TFSI⁻ compared with the control case where no electric field is applied, leading to a larger diffusivity of Li⁺ (Fig. 2). It is demonstrated that the pulse current charging affects the structural properties of the electrolyte, which decreases the coordination number of TFSI⁻ around Li⁺ ions. That is, the number of TFSI⁻ anions around Li⁺ is reduced, and the repulsion effect between Li⁺ and Li⁺ is promoted. As a result, the Li⁺ can transport easily, and the diffusion coefficient of Li⁺ is increased. This enhanced diffusion would reduce the cluster behavior of Li⁺ in the bulk electrolyte, promoting uniform distribution of ions and reducing ion concentration gradient.

Cycling behavior

Galvanostatic cycling measurements were used to mimic the real condition of battery cycling. Cells were cycled at 3 mA cm⁻² for 20 min in each half-cycle. Same symmetrical cells were cycled with pulse current at various T_on durations and T_on/T_off ratios (T_on/T_off = 1:0.5, 1:1, 1:2, 1:3, 1:5, and 1:10; T_on = 1, 5, and 10 s). All pulse waveforms are galvanostatic square-wave pulses. The current density and total capacity passed through in each half-cycle were kept the same for cells with and without pulse current. To obtain a quantitative measure of the relative performance of the two cells, we arbitrarily defined the cell lifetime as the time before peak voltage amplitude increases to 1 V. The voltage becomes unstable, and postmortem scanning electron microscopy (SEM) analysis of the lithium electrode from cells interrupted at 1 V also indicates that the voltage change coincides with the appearance of lithium dendrites on the electrode surface. Figure 4A reports the voltage-time profiles for cells without pulse current at 3 mA cm⁻², and it shows a gradual increase in hysteresis (overpotential between Li plating and stripping) as the number of cycles increases. It is interesting to notice that a sudden increase in voltage appears at the 20th cycle, and the voltage profile becomes unstable in the following cycles. The sudden increase is known as an indication for cell instability that the internal impedance changes as the lithium dendrite shoots out from the substrate. Figure 4B shows the voltage profile for cells with pulse current (T_on/T_off = 1:5; T_on = 1 s) at the same current density. The cell can be cycled for at least 54 cycles without sudden increase or drop in voltage. The cutoff lifetime for cells with pulse current is 48 cycles (192 hours), which is 2.4 times higher than that for cells with constant current cycling. Their detailed comparison in voltage at the 11th cycle can be found in Fig. 4 (C and D), which shows enlarged views of the rectangular areas corresponding to Fig. 4 (A and B, respectively). Cells under pulse current cycling exhibit a stable voltage response with small increase in hysteresis (about 0.8 V at the 11th cycle) compared to cells cycled without pulse current (about 1 V at the 11th cycle). Figure 4 (E and F) shows the details about the voltage response, current density, and T_on/T_off settings in Fig. 4 (C and D). Generally, when cycled with pulse current, the cell shows lower voltage hysteresis and great improvement in cycling stability and cell lifetime.

Fig. 4. The cycling behavior of cells with constant current or pulse current at a high current density of 3 mA cm⁻².

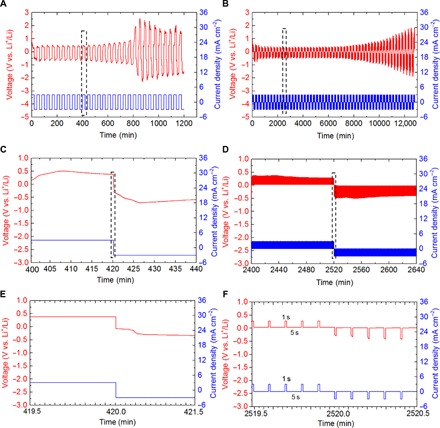
(A) Voltage-time and current-time profiles of Li/Li symmetrical cells cycled with constant current. (B) Voltage-time and current-time profiles of Li/Li symmetrical cells cycled with pulsed current (T_on/T_off = 1:5; T_on = 1 s). (C and D) Enlarged views of the dashed rectangular area in (A) and (B), respectively. (E and F) Enlarged views of the rectangular area in (C) and (D), respectively.

To demonstrate the growth of lithium dendrites after galvanostatic cycling, we used SEM to analyze the surface and cross-section morphologies of Li-metal electrodes before cycling and after being cycled with constant current or pulse current. Symmetric Li cells were cycled at a fixed current density of 3 mA cm⁻² with a string/plating capacity of 1 mAh cm⁻² for each half-cycle. Then, the cells were disassembled in an Ar-protected glove box, and the Li-metal electrodes were washed by PC and dried rigorously before SEM test. As shown in fig. S2A, the surface of a pristine Li-metal electrode is uniform in general except for some small manufactural defects. After being cycled eight times, lithium foil harvested from cells without using pulse current shows rough, fibrous, and irregular jaggy-shaped structures, as displayed in fig. S2B. These nonuniform and sharp structures of lithium could eventually become Li dendrites, penetrate the separator, and cause cell short circuit. Figure S2C displays the surface morphology of the Li electrode obtained from pulse current cycling and shows uniform microstructure compared with that of the Li-metal anode with constant current cycling. We also tracked the thickness of the Li electrode from cross-section SEM analysis to study the electrode volume change upon cycling. The thickness of the pristine Li electrode is around 420 μm. After eight cycles, the electrode thickness increases by 30 and 84 μm for cells with and without pulse current cycling, respectively. The smaller increment in electrode thickness indicates that the electrode structure is more compact using pulse current cycling and the electrode volume expansion is significantly reduced. The results are consistent with the findings in galvanostatic cycling measurements and suggest that fewer lithium dendritic structures form in cells with pulse current cycling. Cycling with pulsed current can increase the lithium coulombic efficiency and ultimately improve the cycling stability and cell lifetime.

To find the optimal conditions for dendrite suppression under pulse current cycling, we provide additional details about the effectiveness of pulse current cycling and statistically calculated the cell lifetime using galvanostatic measurements in Li/Li cells. The cell lifetime (T_c) is defined as the time when the amplitude of voltage exceeds 1 V. A high current density of 3 mA cm⁻² was implemented for practical rate capability. Figure 5 summarizes T_c as a function of T_on and frequency. The voltage of cells with constant current cycling exceeds 1 V at about the 20th cycle, whereas all cells with pulse current cycling show improvement in cell lifetime. It can also be seen in general that the cell lifetime increases with the increment of T_off at fixed T_on and increases when reducing the period of T_on at a fixed ratio of T_on/T_off. The optimal enhancement in cell lifetime appears when T_on/T_off = 1:5, indicating that more rest time between the two periods of charging is not necessary for longer cell lifetime. The results also show that the cell lifetime depends on the pulse frequency and high-frequency pulse cycling is more efficient in promoting uniform Li electrodeposition and extending the cell lifetime.

Fig. 5. Cell lifetime at various frequencies with fixed T_on.

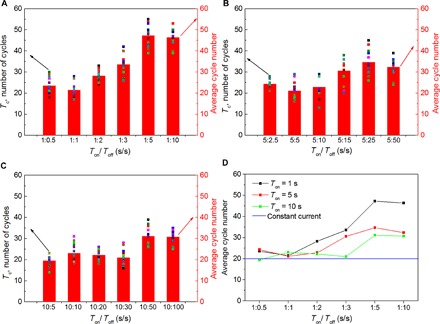
(A) Cell lifetime (T_c) of Li/Li symmetrical cells cycled with pulse current at various T_off with fixed T_on = 1 s. (B) Cell lifetime (T_c) of Li/Li symmetrical cells cycled with pulse current at various T_off with fixed T_on = 5 s. (C) Cell lifetime (T_c) of Li/Li symmetrical cells cycled with pulse current at various T_off with fixed T_on = 10 s. The cell lifetime is calculated when the amplitude of the voltage exceeds 1 V. Fourteen cells under each cycling condition are tested, and their cell lifetimes are displayed in filled square with different colors. The red column shows the average lifetime from the 14 points. (D) Average cell lifetime as a function of T_on/T_off ratios at fixed T_on of 1, 5, or 10 s.

DISCUSSION

Pulse current charging was demonstrated to be a promising method for stabilizing lithium-metal batteries compared with common constant current charging. We have used MD simulations to study the diffusion of Li⁺ at the molecular level. The results suggest the existence of an optimal ratio, T_on/T_off, for achieving the highest diffusion coefficient of Li⁺. We also analyzed the solvation of Li ions and revealed that a lower coordination number of TFSI⁻ near Li⁺ promotes the diffusivity of Li⁺. In pulsed electric fields, Li⁺ has an increased coordination number of PC and a reduced coordination number of TFSI⁻ compared to the control case where no electric field is applied. The simulation results indicate that the transport of Li⁺ in the bulk electrolytes and the underlying ion concentration gradient play a critical role in reducing dendrite formation and promoting stable cell cycling. A weaker association between Li cation and its counter ion is preferred. Electrochemical cycling performance was also evaluated for further evidence of the effectiveness of pulse current charging on cell stability. Consistent with the findings in MD simulations, all cells cycled with pulse current show enhanced cycling stability and lower hysteresis. Results from SEM analysis provide support of the cycling measurements and conclude that Li dendrites could be effectively hindered with pulse current and the volume expansion of the Li electrode can also be reduced. We found from both simulation and experimental results that the ratio of T_on/T_off is critical for stabilizing the cycling behavior, and pulse charging with T_on/T_off = 1:5 or T_on/T_off = 1:3 is an optimal condition examined in this study. Considering the difference in time scales and other factors, such as ion migration and electrodeposition of Li ions on electrode surface, it is reasonable that some results are unable to have a one-to-one correspondence between simulations and experiments. To further enhance the benefits brought by the pulse current charging, future studies could include finding an anion with a lower coordination number around Li⁺ to promote the Li diffusivity and eventually improve cycling stability and extend the lifetime of high-energy Li-metal batteries.

MATERIALS AND METHODS

Simulation details

The simulation system was constructed with 51 Li⁺, 51 TFSI⁻, and 600 PC molecules, which give a total of 8616 atoms and represent the LiTFSI solution with a concentration of 1.0 M lithium salt. The system is in a cubic box with a dimension of 43.88 Å in length (x), width (y), and height (z). The whole system, including Li⁺, TFSI⁻, and PC, were initially energy-minimized for 10,000 steps using the conjugate gradient algorithm to remove abnormally close contacts between molecules. Following the minimization, the system was heated from 50 to 300 K using a short MD run of 1 ns or 1.0 fs time steps and 50 K increments for every 100 ps until the system reached 300 K. After heating, an additional 1 ns or 1.0 fs MD steps were run to allow further isothermal equilibration of Li⁺ and TFSI⁻ in PC. The velocity Verlet method was used for the integration of the Newtonian equations in NPT (a simulation system that consists of a constant number of atoms at a constant pressure, in which the temperature of the system is controlled by using a thermostat) ensemble for equilibration. A pressure of 1 atm was used in all simulation cases. A cutoff of 1.2 and 1.0 nm was used for the Lennard-Jones and electrostatic terms, respectively. A neighbor searching was made up to this same distance from the central ion and was updated every five simulation steps. The electrostatic interactions beyond 1.0 nm were accounted for by the computationally efficient K-space method based on particle-particle particle-mesh (PPPM). It is important to use the PPPM method in the case of ionic systems, because electrostatic energy beyond the cutoff usually contributes a lot to the total electrostatic energy (42). The final configuration of the system has a density of ~1.329 g cm⁻³, which agrees with the experimentally determined density of PC solution of LiTFSI (1.3205 g cm⁻³, 1.11 M) (43).

For production runs, a series of 12-ns simulations at 300 K were carried out in the NVT (a simulation system that consists of a constant number of atoms at a constant volume, in which the temperature of the system is controlled by using a thermostat) ensemble using a Nosé-Hoover thermostat with a coupling constant of 0.1 ps. A pulsed or static electric field was applied to the system in the z direction. The strength of the static electric field was set at 3 × 10⁵ V m⁻¹. The pulsed electric field was implemented as a square wave, with the strength of the electric field during its “on” and “off” periods equal to 3 × 10⁵ and 0 V m⁻¹, respectively. A pulsed electric field with the strength of the electric field during its on and off periods equal to 3 × 10⁶ and 0 V m⁻¹, respectively, was also examined. The off duration of the pulsed electric field was set to be 0.01 ns. The on duration was set in a way so that the on/off value was 0.5, 1, 2, 3, 4, 5, and 10, respectively. Moreover, a simulation case with no applied electric fields was studied as a control. The simulation results were obtained by analyzing the last 4 ns trajectories of production runs.

The OPLS-AA force field (44, 45) was used. This force field has been widely used for biomolecules (46), hydrocarbon molecules (47, 48), and ionic liquids (49, 50). The basic functional form of potential energy in the OPLS-AA force field is defined as follows

$$\mathit{E}={\displaystyle \sum _{\mathit{i}}}{\mathit{K}}_{\mathit{b},\mathit{i}}{[{\mathit{r}}_{\mathit{i}}-{\mathit{r}}_{0,\mathit{i}}]}^2+{\displaystyle \sum _{\mathit{i}}}{\mathit{K}}_{\mathit{b},\mathit{i}}{[{\mathrm{\theta }}_{\mathit{i}}-{\mathrm{\theta }}_{0,\mathit{i}}]}^2+{\displaystyle \sum _{\mathit{i}}}[\frac{1}{2}{\mathit{V}}_{1,\mathit{i}}(1+\text{cos}({\mathrm{\varphi }}_{\mathit{i}}))+\frac{1}{2}{\mathit{V}}_{2,\mathit{i}}(1- \text{cos}(2{\mathrm{\varphi }}_{\mathit{i}}))+\frac{1}{2}{\mathit{V}}_{3,\mathit{i}}(1+ \text{cos}(3{\mathrm{\varphi }}_{\mathit{i}}))+\frac{1}{2}{\mathit{V}}_{4,\mathit{i}}(1- \text{cos}(4{\mathrm{\varphi }}_{\mathit{i}}))]+{\displaystyle \sum _{\mathit{i}}}{\displaystyle \sum _{\mathit{j}>\mathit{i}}}\{\frac{{\mathit{q}}_{\mathit{i}}{\mathit{q}}_{\mathit{j}}{\mathit{e}}^2}{{\mathit{r}}_{\mathit{i}\mathit{j}}}+4{\mathrm{\epsilon }}_{\mathit{i}\mathit{j}}[{\left(\frac{{\mathrm{\sigma }}_{\mathit{i}\mathit{j}}}{{\mathit{r}}_{\mathit{i}\mathit{j}}}\right)}^{12}-{\left(\frac{{\mathrm{\sigma }}_{\mathit{i}\mathit{j}}}{{\mathit{r}}_{\mathit{i}\mathit{j}}}\right)}^6\left]\right\}$$ (4)

The total energy E of the system is evaluated as the sum of individual energies for the harmonic bond stretching and angle bending terms, a Fourier series for torsional energetics, and Coulomb and 12-6 Lennard-Jones terms for the nonbonded interactions. K_b,i is the force constant, and r₀ and θ₀ represent the reference values. The Fourier coefficients V and the partial atomic charges q were fixed on each atom center. i and j represent all pairs of atoms (i < j). r_ij is the distance between atoms i and j. σ_ij and ε_ij represent the Lennard-Jones radii and potential well depths, respectively, which are obtained from parameters for each type of atom by using geometric combination rules ε_ij = (ε_iiε_jj)^1/2 and σ_ij = (σ_iiσ_jj)^1/2 (48). The Lennard-Jones parameters and partial charges for Li⁺ and PC were taken from the OPLS-AA parameterization (37, 49, 51). The bonded stretching, angle bending, dihedral torsion, and nonbonded parameters of TFSI⁻ anions were obtained from Canongia Lopes and Pádua (49). The partial charge of atoms in TFSI⁻ anions was calculated with the following protocol. First, geometry optimizations were carried out at the Hartree-Fock (HF) level by using a moderately sized polarized basis set at the 6-31G* level. The partial charges were computed by fitting the molecular electrostatic potential at the atomic centers. The effects of electron correlation and basis set extension of HF structures were considered by performing single-point calculations with second-order Møller-Plesset perturbation method MP2/cc-Pvdz and the correlation consistent polarized valence cc-pVTZ(-f) basis set. This MP2/cc-pVTZ(-f) //HF/6-31G(d) method is a common practice for OPLS-AA parameterization (50, 52, 53). The calculated restrained electrostatic potential charges for TFSI⁻ agree with other studies (49).

All MD simulations were performed with the LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) package on a 20-node Linux cluster (54). All quantum chemistry calculations were carried out with the Gaussian 09 package (55).

Electrochemical measurements

CR2032 coin cells were assembled in an argon-filled glove box. Bare Li metal was used as the reference and counter electrodes, and 1 M LiTFSI in PC was used as the electrolyte. Symmetrical lithium cells were galvanostatically cycled at 3 mA cm⁻² for 20 min in each half-cycle. The same symmetrical cells were cycled with pulse current charging and discharging at various T_on and T_on/T_off ratios (T_on/T_off = 1:0.5, 1:1, 1:2, 1:3, 1:5, and 1:10; T_on = 1, 5, and 10 s). T_on means the period of constant current charging or discharging, and T_off means the rest period followed by the constant current charging or discharging. The current density and total capacity in each half-cycle were kept the same for cells with and without using pulse current. Neware electrochemical testing system (CT4008) and Solartron Analytical Electrochemical Workstation were used for the electrochemical measurements.

SEM analysis

After galvanostatic cycling, the cells were carefully disassembled in a dry glove box filled with argon to obtain Li-metal electrodes. Then, Li-metal electrodes were gently washed with PC three times to remove residual lithium salts and fully dried under vacuum. To access the cross-section images of the Li-metal electrodes, the obtained lithium foils were cut with a sharp surgical knife blade and placed on a vertical sample holder. SEM analysis was conducted on a field-emission SEM (Hitachi SU8000 FE-SEM) at 5 kV.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1701246/DC1

fig. S1. The impact of pulsed electric fields on the diffusivity of Li⁺.

fig. S2. Surface and cross-section SEM images of Li-metal electrodes cycled with or without pulse current.

fig. S3. Cell lifetime at various T_on with fixed frequencies.

fig. S4. Voltage-time profiles of cells cycled with pulse current at fixed T_on = 1 s.

fig. S5. Voltage-time profiles of cells cycled with pulse current at fixed T_on/T_off = 1:5.