Modulation of Molecular Flux Using a Graphene Nanopore Capacitor

Abstract

Modulation of ionic current flowing through nanoscale pores is one of the fundamental biological processes. Inspired by nature, nanopores in synthetic solid-state membranes are being developed to enable rapid analysis of biological macromolecules and to serve as elements of nanofludic circuits. Here, we theoretically investigate ion and water transport through a graphene-insulator-graphene membrane containing a single, electrolyte-filled nanopore. By means of all-atom molecular dynamics simulations we show that the charge state of such a graphene nanopore capacitor can regulate both the selectivity and the magnitude of the nanopore ionic current. At a fixed transmembrane bias, the ionic current can be switched from being carried by an equal mixture of cations and anions to being carried almost exclusively by either cationic or anionic species, depending on the the sign of the charge assigned to both plates of the capacitor. Assigning the plates of the capacitor opposite sign charges can either increase the nanopore current or reduce it substantially, depending on the polarity of the bias driving the transmembrane current. Facilitated by dynamic inversion of the nanopore surface charge, such ionic current modulations are found to occur despite the physical dimensions of the nanopore being an order of magnitude larger than the screening length of the electrolyte. The ionic current rectification is accompanied by a pronounced electro-osmotic effect that can transport neutral molecules such as proteins and drugs across the solid-state membrane and thereby serve as an interface between electronic and chemical signals.

Graphical abstract

Introduction

Transport of ions across biological membranes is a process fundamental to the biology of all living organisms.¹ For instance, the very survival of a biological cell depends on its ability to control the concentrations of ionic species within the cell, a control realized by a diverse families of membrane proteins, which include molecular pumps,¹ transporters² and ion channels.³ Crystallographic studies of membrane proteins^4–6 permit the intricate mechanisms of ion transport regulation to be understood at the molecular level.^7–9 From an engineering standpoint, however, the function of ion channels can be simply described as controlling the ion flux,^10–12 which includes control over the direction of ion transport (ion current rectification) and over the type of ions are that being transported (ion selectivity).

With an eye on potential applications in nanoscale engineering, synthetic nanopore systems have been developed to mimic the function of biological ion channels.^13,14 Nanoporous polymer^{15– 17} and solid-state^18–20 membranes have been fabricated to display diode-like behavior.^21,22 Combinations of these diodic elements comprise the basic units of nanofluidic electronics such as logic-gates^23,24 or externally coupled circuitry²⁵ potentially useful in lab-on-a-chip technologies. Among possible applications of such rectifying and ion selective nanoporous membranes are systems for the separation of molecular species^26–29 or larger-scale filtration.^30,31 In sensing applications, transient fluctuations of the nanopore ionic current indicates the passage of biomolecules through the nanopore,³² which has been used to identify the passage of DNA,^33–35 proteins,^36–39 and synthetic structures such as nanoparticles.^40,41

The primary method of controlling the molecular flux through both biological and synthetic ion channels is steric exclusion: molecules larger than the smallest cross-section of the nanopore cannot pass through it. Charge exclusion is another common mechanism, where the passage of a particular molecule is opposed by a large electrostatic barrier from fixed charges on the nanopore. The directionality of the ionic transport, or current rectification, typically arises from the asymmetric distribution of the surface charges,^22,42 which can be caused, for example, by the shape of the nanopore²¹ or preferential binding of ions to the nanopore surface.⁴³

The mechanism of nanopore ionic current regulation often derives from the properties of the membrane that contains the nanopore. In biological nanopores, the surface charge distribution is determined by the locations of the charged amino acids and thus cannot be easily adjusted beyond small-scale structural rearrangement such as in ion channel gating. Nanopores in synthetic membranes such as polymer,⁴⁴ thick solid-state,^45–47 and atomically thin material membranes^28,48 can be manufactured purposefully with custom geometries,^49,50 chemical functionalizations,⁵¹ and charge distributions. In polymer membranes, the ionic current is rectified due to the differential binding of ions to the interior of the nanopore,^16,52 while in glass nanocapallaries, the negative surface charge and the narrow pore dimensions can lead to a depletion or enhancement of ions inside different regions in the nanopore, a so-called concentration polarization, which produces current and electro-osmotic flow rectification.⁵³ Recent experimental investigations suggest that a single layer graphene membrane can carry a negative surface charge in solution, causing ion selective transport through nanopores with diameters as large as 5.0 nm at high salt concentrations.⁵⁴ In the case of nanopores in semiconductor or metallic membranes, the nanopore surface charge can be externally controlled via electrical bias,^22,55 making it possible to change the ionic conductivity of a nanopore without altering its geometry.

In this work, we report molecular dynamics (MD) simulations of a graphene nanopore capacitor made by stacking a layer of insulator between two graphene membranes. Our simulations show that charging the graphene plates can either increase or decrease the overall ionic current, make the ionic current selective to cations or anions, and control the direction of the electro-osmotic flow. Analysis of our MD trajectories explains why local adjustment of the nanopore surface potential can affect the overall ionic current despite an order of magnitude mismatch between the diameter of the nanopore (~3 nm) and the Debye length of the electrolyte solution (~3 Å).

Methods

Protocols of MD Simulations

All MD simulations were performed using the program NAMD,⁵⁶ a 2 fs integration time step, and 2-2-6 multiple time-stepping. Parameters for carbon atoms in the graphene membrane, modeled as type CA atoms, and ions were taken from the CHARMM36 parameter set with the CMAP corrections.⁵⁷ Silica parameters were taken from a custom force field⁵⁸ and a TIP3P model was used for water.⁵⁹ All simulations employed a 10–12 Å cutoff for van der Walls and short-range electrostatic forces, the particle mesh Ewald (PME) method for long-range electrostatics⁶⁰ computed over a 1.1 Å grid and periodic boundary conditions. Simulations in the NPT (constant number of particles N, pressure P, temperature T) ensemble were performed using a Lowe-Andersen thermostat,⁶¹ and Nosé-Hoover Langeivn piston pressure control⁶² set at 295 K and 1 atm, respectively. Visualization and analysis were performed using VMD.⁶³

All Atom Models of a Graphene Nanopore Capacitor

Atomic-scale models of the silica membrane was built by first using the Inorganic Builder plugin⁶⁴ of VMD⁶³ to create a rectangular volume of crystalline silicon dioxide. Following that, the silicon dioxide membrane was annealed in vacuum by first heating the system to 7000 K for 40 ps, then reducing the temperature to 5000 K for 40 ps, 2000 K for 1 ns, and finally, to 300 K for 1 ns to create an amorphous silica membrane.⁵⁸ During the annealing procedure, G-SMD⁶⁵ forces were applied to expel atoms from an hourglass shaped pore region and confine atoms to a 6 nm rectangular volume arranged normal to the z-axis.⁶⁴ The annealing simulations were performed using the BKS force field⁶⁶ under periodic boundary conditions in the x and y-dimensions. The resulting membrane had dimensions of 8.0 × 8.0 × 6.0 nm and was periodic along the xy-plane. The nanopore had an hourglass shape and was 1.0 nm in radius at its narrowest part and 1.75 nm in radius at either surface of the membrane.

To create the stacked graphene-silica-graphene nanostructure, the two sheets of graphene were generated using the Inorganic Builder plugin. Each graphene sheet was 8.0 × 8.0 nm and periodic along the xy-plane. Next, carbon atoms were removed from the centers of each sheet to create a circular pore with a radius of 1.75 nm. Following that, the graphene sheets were placed at the top and at the bottom of the amorphous silica membrane such that the nanopores in the graphene sheets were concentric with the nanopore in the silica membrane. No bonds were added between the graphene and silica atoms. From this point, graphene and silica atoms were restrained to their positions with a spring constant of 5 kcal mol⁻¹ Å⁻² in all further simulations. The different charged states of the graphene nanopore capacitor were modeled by assigning the same partial charge to each carbon atom of a graphene layer to produce the target surface charge density.⁵⁵ In the baseline (uncharged) state of the capacitor, each and every carbon atom of graphene was electrically neutral. Next, the systems were solvated using the Solvate Plugin of VMD. Finally, K⁺and Cl⁻ ions were added to produce an electrically neutral 1.1 M solution of KCl using the Autoionize plugin of VMD. Each of the final systems measured 8.0 × 8.0 × 14.2 nm³ and contained approximately 96,000 atoms.

Upon assembly, each system was first equilibrated in the NPT ensemble for 12.5 ns. To induce ionic current, the systems were simulated in the presence of a uniform electric field applied to all atoms along the z-direction. The voltage bias produced by such field is^67,68 V = −L_zE_z, where L_z is the length of the unit cell along the z-axis. All simulations of the ionic current were performed in the NVT (constant number of particles N, pressure P, and temperature T) ensemble.

Calculation of Ionic Current

The ionic current calculations were carried out inside the nanopore volume defined as −l/2 ≤ z ≤ l/2, where l = 5.4 nm. The instantaneous ionic current I(t) was calculated as

$$I(t)=\frac{1}{\mathrm{\Delta }\mathit{\text{tl}}}\sum _i^N{q}_i({\zeta }_i(t+\mathrm{\Delta }t)-{\zeta }_i(t)),$$ (1)

where

$${\zeta }_i(t)=\{\begin{array}{c}{z}_i(t),|z_i(t)|<l/2\hfill \\ -l/2,z_i(t)<-l/2\hfill \\ l/2,z_i(t)>l/2\hfill \end{array}$$ (2)

and i indicates the sum over all ions within the volume of interest, Δt = 9.6 ps, the time between two consecutive frames in the MD trajectory, ξ_i is the z-coordinate of the ith ion atom defined by Eq. 1, and q_i is the charge of ion i. The average ionic current was computed by summing the instantaneous ionic currents from each frame of a trajectory and dividing by the total number of frames. To estimate the error, the trajectory was block averaged over intervals of 1.0 ns; the standard error was computed as $\sigma /\sqrt{n}$, where σ is the standard deviation of the block-averaged ionic current values and n is the number of blocks. All average ionic current values and error estimates were obtained from the analysis of the last 15 ns fragment of the respective 25 ns-long MD trajectories.

Calculation of the Water Flow Rate

The calculations of the water flow rate were performed by analyzing displacements of water molecules inside the nanopore volume (−l/2 ≤ z ≤ l/2, l = 5.4 nm). The instantaneous current of water molecules (molecules / seconds) was computed as

$$w(t)=\frac{1}{\mathrm{\Delta }\mathit{\text{tl}}}\sum _i^{N(t)}({\zeta }_i(t+\mathrm{\Delta }t)-{\zeta }_i(t)),$$ (3)

where N(t) is the total number of water molecules in the volume of interest at a time t, ξ_i is the z-coordinate of the ith water molecule defined by Eq. 3, and Δt = 9.6 ps is the time between two consecutive frames in the MD trajectory. The average rate of water flow was calculated by averaging the instantaneous water currents over the last 15 ns fragment of the respective MD trajectory. The error was estimated by averaging the instantaneous water flow rate over 1.0 ns trajectory blocks and computing the standard error of the block-averaged values.

Calculation of Concentration Profiles

The concentration of ions in a cylindrical bin centered at the pore axis, c_j was computed as c _j = n_j/(hπr²), where j denotes the ion species, n_j is the number of ions of j species, h =0.5 nm is height of the bin along the z axis and r = 0.5 nm is the radius of the bin. The concentration profiles were computed by averaging c_j over the last 15 ns of the respective MD trajectory.

Calculation of Electrostatic Potential

To visualize the electrostatic potential in our systems, we averaged the instantaneous distributions of the electrostatic potential over the MD trajectory using a previously described method⁶⁹ implemented in the PMEpot Plugin of VMD. Each atom of the system was approximated by a spherical Gaussian

$${\rho }_i(\mathbf{r})=q_i{\left(\frac{\beta }{\sqrt{\pi }}\right)}^3{e}^{-\beta |\mathbf{r}-{\mathbf{r}}_i{|}^2},$$ (4)

where β was the Gaussians’ width. The instantaneous distribution of the electrostatic potential corresponding to the instantaneous charge configuration was obtained by solving the Poisson equation

$${\nabla }^2\varphi (\mathbf{r})=4\pi \sum _i{\rho }_i(\mathbf{r}).$$ (5)

To obtain the average distribution of the potential in a given MD simulation, instantaneous distributions of the potential were averaged over the entire MD trajectory. Three-dimensional (3D) electrostatic potential maps were obtained by averaging the last 15 ns fragments of MD trajectories; β= 0.1 A⁻¹ was used for these calculations. One-dimensional profiles of the electrostatic potential through the nanopores were obtained by taking values from the 3D profiles along the z-coordinate, which is also the nanopore axis in our coordinate system.

Calculations of the 2D Current Density

To visualize the flow of the K⁺ and Cl⁻ ions, the volume of the simulations systems was divided into 0.3 × 0.3 × 0.5 nm grid elements on which the local averages of the K⁺ and Cl⁻ density and ionic flux were calculated with a sampling frequency of 480 ps. The local current in each grid element was calculated as:⁷⁰

$${\mathit{I}}_j=\sum _j{q}_j\times f_{j,k},$$ (6)

where j denotes a particular ion species (K⁺ or Cl⁻), q_j denotes the ion charge, k the x, y or z-directions, and f _j,k the flux of ionic species j along the k-coordinate. Next, the 3D density and ionic flux data was averaged along an azimuthal coordinate in a cylindrical coordinate system to obtain the mean density and the mean flux in the r-z plane. Velocities were obtained by dividing the average ionic flux by the density of the ion species in each bin. The resulting 2D density and ion velocity maps were made symmetric about the z-axis by making the mirror image mapping of values from r → −r. Contourf and Streamplot functions in the python matplotlib library were used to generate the density and velocity plots.

Results & Discussion

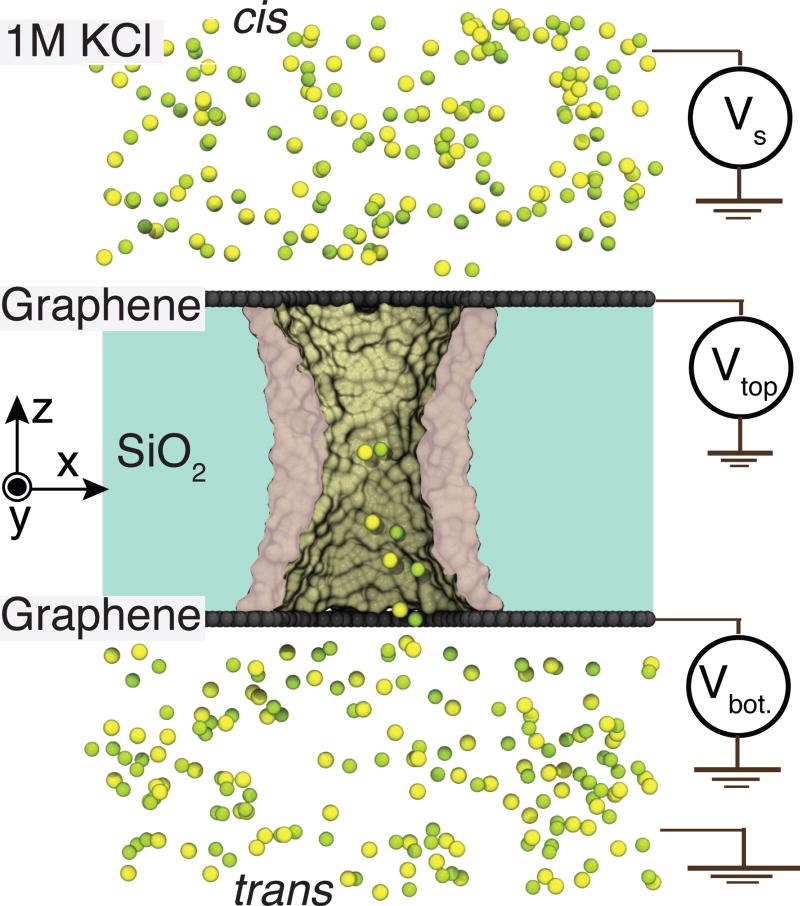
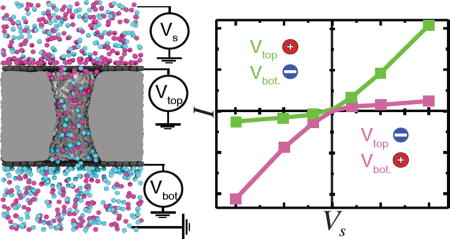
Figure 1 schematically illustrates the graphene nanopore capacitor system considered in this work. The key element of the system is an electrolyte-filled hourglass nanopore in a graphene-insulator-graphene membrane. Such stacked graphene membranes have been experimentally manufactured by combining chemical vapor deposition, graphene transfer and atomic layer deposition techniques;⁷¹ nanometer diameter pores have been drilled through such membranes using an electron field-emission gun.⁵⁰ We assume that the electric potential of each of the graphene sheets with respect to one of the electrolyte compartments (the trans compartment in our setup) can be independently controlled via two voltage sources. An additional voltage source can generate an electric potential difference (the transmembrane bias V_s) between the two electrolyte-filled compartments, causing the ionic current to flow through the nanopore. Below we investigate how charging of the graphene sheets affects the nanopore ionic current.

Figure 1.

Schematic of a graphene nanopore capacitor system considered in this work. A layer of insulating silica membrane (light gray) is sandwiched between two layers of graphene (dark gray), forming a parallel plate capacitor. An hourglass nanopore spans the stacked graphene-silica-graphene membrane connecting the two (cis and trans) electrolyte-filled compartments. The inner surface (green) of the silica nanopore is shown in a cut-away representation; potassium and chloride ions are shown as yellow and green van der Waals spheres, respectively. An electric potential V_s biases the solution at the one side of the membrane (cis) relative to the solution at the other (trans) side, which is grounded. The graphene membranes are electrically biased relative to the trans side with a potential differences V_top and V_bottom. The potential differences V_top and V_bottom are modeled implicitly by assigning partial charges to the atoms of the corresponding graphene membranes to achieve the target charge densities σ_top and σ_bottom.⁵⁵

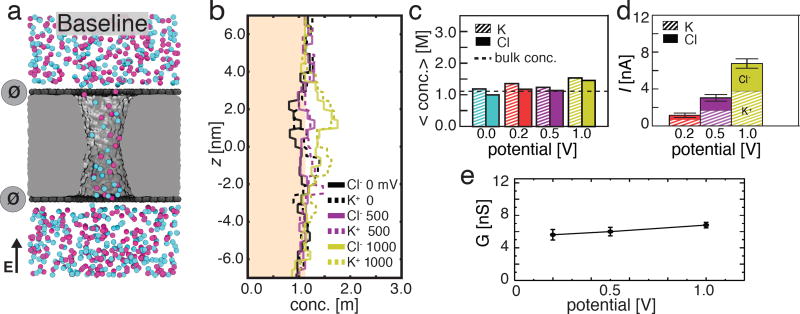
First, we consider a baseline state of the nanopore capacitor where both graphene sheets are electrically neutral (V_top = V_bottom = 0). For this purpose, we built an all-atom model of the graphene nanopore capacitor submerged in a 1.1 M solution of KCl, see Methods for details. Following energy minimization and equilibration at constant pressure, the system was simulated under a constant electric field that produced ionic current through the nanopore.⁶⁸ In such applied field simulations, the electric field magnitude, E, relates to the transmembrane bias, V, as V = −EL_z,^67–69 where L_z is the length of the simulation system along the direction of the applied field (the z axis in our case); the ionic current can be determined by summing up the instantaneous displacements of ions, see Methods for details.

Figure 2a illustrates a typical microscopic configuration realized during the ionic current simulations. K⁺ and Cl⁻ ions are dispersed throughout the nanopore volume, which is confirmed by the plots of the local ion concentrations along the nanopore axis, Fig. 2b. At zero transmembrane bias, the average concentration of K⁺ ions in the pore is similar to that in the bulk whereas the the concentration of Cl⁻ ions is slightly reduced, Fig. 2c. Such mild cation selectivity is likely caused by the negative charge of oxygen atoms that predominantly comprise the outer layer of our annealed silica membrane;⁴³ the entire silica membrane is electrically neutral. Supporting Information Movie 1 illustrates an MD trajectory of this system at a transmembrane bias of 200 mV. The average concentration of both ion types slightly increases with the transmembrane bias, Fig. 2b and Fig. 2c, causing a slightly superlinear dependence of the nanopore current, I, on voltage, Fig. 2d. The magnitudes of the currents carried by K⁺ and Cl⁻ ions are not equal: the current of K⁺ ions constitutes approximately 60% of the total ionic current. The nanopore conductance, G = I(V)/V, increases slightly with the transmembrane bias, Fig. 2e, as prescribed by the current versus voltage plot.

Figure 2.

Ionic conductivity of uncharged (baseline) graphene nanopore capacitor. (a) Representative configuration of ions in an uncharged nanopore capacitor. The nanopore capacitor is shown in a cut-away representation, purple and light blue spheres represent Cl⁻ and K⁺ ions, respectively. The top and bottom graphene layers are electrically neutral (σ_top = σ_bottom = 0 e nm⁻²), which is schematically indicated by the dark grey circles. The particular molecular configuration shown corresponds to a transmembrane bias of 200 mV. (b) The average concentration of Cl⁻ (solid) and K⁺ (dashed) ions along the pore axis at 0 mV (black), 500 mV (purple), and 1 V (yellow) transmembrane bias (the profiles at 200 mV are omitted for clarity). The shaded region indicates concentrations below the bulk concentration of 1.1 M. The concentration profiles were obtained by averaging over 0.5 nm-radius disks centered at the pore axis and over the last 15 ns of the respective 25 ns MD trajectory. (c) The total average concentration of K⁺ (striped) and Cl⁻ (solid) ions inside the nanopore at transmembrane biases of 0 mV (blue), 200 mV (red), 500 mV (purple), and 1000 mV (yellow). The average concentrations were obtained by averaging the concentration profiles from panel b within the region of |z| < 2.0 nm where z =0 nm is at the center of the nanopore. (d) The average ionic current (total height of each bar) and the currents carried by K⁺ (striped) and Cl⁻ (solid) species at 200 mV (red), 500 mV (purple), and 1 V (yellow) transmembrane bias. Error bars indicate the standard error of the mean value. (e) The simulated conductance of the uncharged nanopore capacitor versus the transmembrane bias.

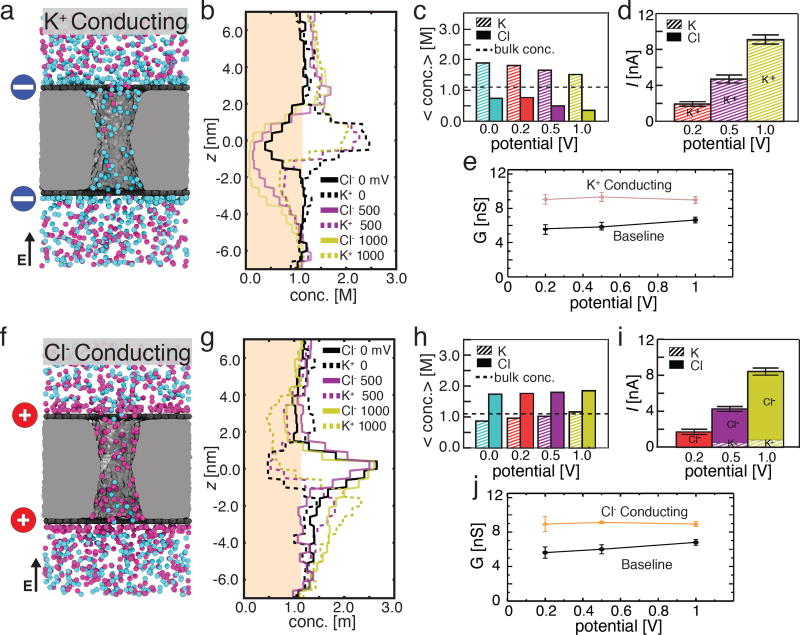
Next, we examine the system where both top and bottom graphene layers carry the same negative charge of −2.0 e nm⁻². Note that a free-standing graphene membrane may carry a net negative charge, which could be attributed to partial oxidation of graphene or adsorption of contaminant material;⁵⁴ the charge densities considered in our work are well within the range of experimental estimates.⁵⁴ The microscopic model of the negatively charged capacitor system, Fig. 3a, was built starting from the baseline system by assigning the same partial charge to all carbon atoms of the graphene layers, producing the target surface charge densities σ_top = σ_bottom = −2.0 e nm⁻²; additional K⁺ ions were added to the system to make it electrically neutral. After energy minimization and equilibration, the system was simulated at several transmembrane biases. In all simulations of this negatively charged nanopore capacitor system, K⁺ ions were observed to form a boundary layer near the charged graphene sheets. Supporting Information Movie 2 illustrates an MD trajectory of this system at a transmembrane bias of 200 mV. Within the nanopore, the concentration of K⁺ ions exceeds the bulk concentration whereas the concentration of Cl⁻ ions is reduced, Fig. 3b and Fig. 3c. The average concentration of both ion types in the nanopore decreases as the transmembrane bias increases, Fig. 3c, whereas the difference in the nanopore concentration of K⁺ and Cl⁻ ions increases. The total ionic current increases approximately linearly with the transmembrane bias, Fig. 3d. K⁺ ions carry 94, 98, and 98% of the total ionic current at transmembrane biases of 200 mV, 500 mV and 1.0 V, respectively, indicating that ionic current through the negatively charged nanopore capacitor system is highly selective to cations. Hereafter we will refer to the negatively charged state of the nanopore capacitor system as K⁺ conducting. The overall conductance of the nanopore capacitor system in the cation conducting state is larger than that in the baseline state regardless of the transmembrane bias, Fig. 3e, which is explained by the increased concentration of ions in the nanopore volume (compare Fig. 2c and Fig. 3c).

Figure 3.

Selective ionic transport in charged nanopore capacitor systems. (a) Representative configuration of ions in a nanopore capacitor system that has both graphene plates negatively charged to σ_bottom = σ_top = −2.0 e nm⁻². The particular molecular configuration shown corresponds to a transmembrane bias of 200 mV. Blue circles schematically indicate the negative charge of the graphene plates. (b) The average concentration of Cl⁻ (solid) and K⁺ (dashed) ions along the pore axis at 0 mV (black), 500 mV (purple), and 1 V (yellow) transmembrane bias (the profiles at 200 mV are omitted for clarity). The shaded region indicates a concentration below the bulk concentration of 1.1 M. (c) The total average concentration of K⁺ (striped) and Cl⁻ (solid) ions inside the nanopore at transmembrane biases of 0 mV (blue), 200 mV (red), 500 mV (purple), and 1000 mV (yellow). The average concentrations and the concentration profiles were obtained as described in the caption to Figure 2c,d. (d) The average ionic current (total height of each bar) and the currents carried by K⁺ (striped) and Cl⁻ (solid) species at 200 mV (red), 500 mV (purple), and 1 V (yellow) transmembrane bias. Error bars indicate the standard error of the mean. (e) The simulated conductance of the positively charged nanopore capacitor versus the transmembrane bias. Data for the baseline (uncharged) capacitor are shown for comparison. (f–j). Same as panels a–e but for the nanopore capacitor system that has both graphene plates positively charged to σ_bottom = σ_top = +2.0 e nm⁻². Red circles schematically indicate the positive charge of the graphene plates.

The ion conductivity properties of the positively charged nanopore capacitor (σ_top = σ_bottom = 2.0 e nm⁻², Fig. 3f) mirror that of the negatively charged one with the roles of the cation and anion reversed, see Supporting Information Movie 3. K⁺ ions are depleted from the nanopore volume whereas the concentration of Cl⁻ exceeds the bulk value, Fig. 3g and Fig. 3h. Cl⁻ ions dominate the ionic current, Fig. 3i, and make up 91%, 88%, and 92% of the total ionic current at transmembrane biases of 200 mV, 500 mV and 1.0 V, respectively, indicating that the positively charged system is selective to anions. Consequently, we refer to the positively charged state of the graphene nanopore capacitor as Cl⁻ conducting. As in the case of the K⁺ conducting state, the overall nanopore conductance is increased with respect to the baseline state, Fig. 3j; the magnitudes of the currents in the K⁺ and Cl⁻ conducting states are within the error at each transmembrane bias. The key difference, however, between the K⁺ and Cl⁻ conducting states is the relative contribution of anions and cations to the total current, which is more pronounced for the K⁺ conducting state. We attribute such breakage of symmetry to the inherent negative charge of the outer shell of the silica surface and the electro-osmotic effect (described below).

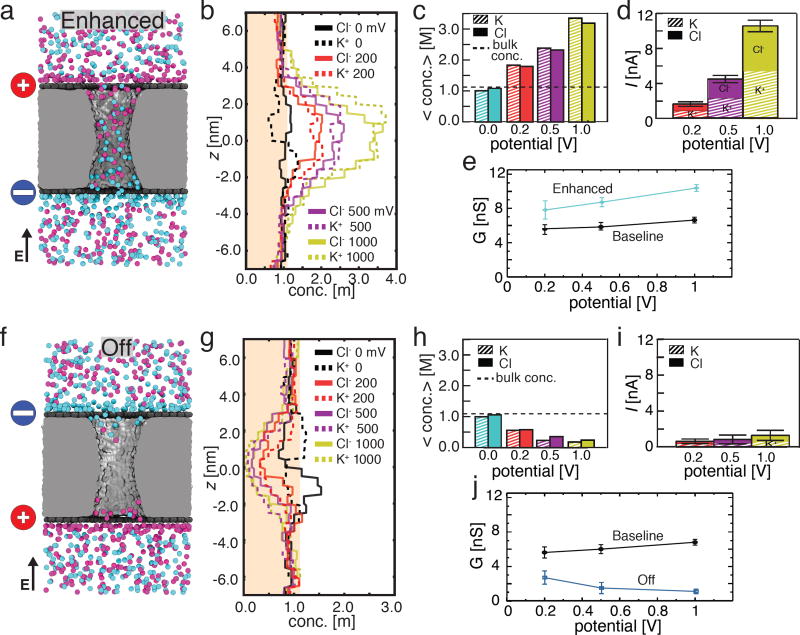
Next, we examine the case of an overall electrically neutral graphene capacitor that contains oppositely charged graphene plates. The response of such a system to the transmembrane bias can be expected to depend on the direction of the bias with respect to the direction of the electric field produced by the charged plates. Here we first consider the case when both fields are parallel, which, in our setup, corresponds to the top and bottom graphene sheets carrying the charges of σ_top = 2.0 e nm⁻² and σ_bottom = −2.0 e nm⁻² and the cis compartment being positively biased with respect to the trans one, Fig. 4a. The microscopic model of such a system was built starting from the baseline state model by changing the charge of the carbon atoms comprising the graphene plates; no additional ions were added as changing the charge of the graphene sheets did not change the overall charge of the system. With no transmembrane bias applied, Cl⁻ and K⁺ ions form boundary layers near the oppositely charged graphene sheets and are also present in approximately equal amounts within the nanopore volume, Fig. 4b, c, although individual ion concentration profiles vary along the nanopore axis, Fig. 4b. The nanopore concentration of both ion types increases with the transmembrane bias, Fig. 4c, leading to larger than baseline total currents, Fig. 4d. The currents carried by K⁺ and Cl⁻ ions are approximately equal at all biases. The nanopore conductance increases with the bias and is considerably greater than the baseline current, Fig. 4e. Hereafter we refer to this conductance state of the nanopore capacitor as an Enhanced state. Supporting Information Movie 4 illustrates the MD trajectory of this system at a transmembrane bias of 200 mV.

Figure 4.

Enhancement and reduction of ionic current by oppositely charged graphene plates. (a) Representative configuration of ions in a nanopore capacitor system that has oppositely charged graphene plates: σ_top = +2.0 e nm⁻² and σ_bottom = −2.0 e nm⁻²; the direction of the transmembrane bias aligns with the direction of electric field produced by the charged graphene sheets. The particular molecular configuration shown corresponds to a transmembrane bias of 200 mV. The vertical arrow indicated the direction of the electric field produced by the transmembrane bias. (b) The average concentration of Cl⁻ (solid) and K⁺ (dashed) ions along the pore axis at 0 mV (black), 200 mV (red), 500 mV (purple), and 1 V (yellow) transmembrane bias. The shaded region indicates a concentration below the bulk concentration of 1.1 M. (c) The total average concentration of K⁺ (striped) and Cl⁻ (solid) ions inside the nanopore at transmembrane biases of 0 mV (blue), 200 mV (red), 500 mV (purple), and 1000 mV (yellow). The average concentrations and the concentration profiles were obtained as described in the caption to Figure 2c,d. (d) The average ionic current (total height of each bar) and the currents carried by K⁺ (striped) and Cl⁻ (solid) species at 200 mV (red), 500 mV (purple), and 1 V (yellow) transmembrane bias. Error bars indicate the standard error of the mean. (e) The simulated conductance of the nanopore capacitor system versus the transmembrane bias. Data for the baseline (uncharged) capacitor are shown for comparison.(f–j). Same as panels a–e but for the opposite arrangement of the charged graphene plates: σ_top = −2.0 e nm⁻² and σ_bottom = +2.0 e nm⁻². In this system, the direction of the transmembrane bias is opposite to that of the electric field produced by the charged graphene sheets.

Reversing the polarity of the nanopore capacitor charge (σ_top = −2.0 e nm⁻², σ_bottom = 2.0 e nm⁻², Fig. 4f) in the absence of the transmembrane bias produced the expected redistribution of ions with the roles of K⁺ and Cl⁻ reversed, Fig. 4g. Increasing the transmembrane bias, however, was observed to reduce the concentration of ions within the nanopores, Fig. 4h, opposite to the effect observed for the reversed charge polarity, Fig. 4c. Consequently, the ionic current through the nanopore, Fig. 4i was considerably reduced in comparison to the baseline current; the nanopore conductance reduced with the bias, Fig. 4j. Hereafter we refer to this conductance state of the nanopore capacitor as an Off state. Supporting Information Movie 5 illustrates the MD trajectory of this system at a transmembrane bias of 200 mV.

Repeating the simulations of the nanopore capacitor system at negative transmembrane biases yielded the current-voltage (I–V) dependence of the system at the five charged states considered in this work, Fig. 5a,b. The baseline, K⁺ conducting and Cl⁻ conducting states exhibits linear I–V curves, Fig. 5a. Such a highly symmetric response to the direction of the applied bias can be expected given the symmetric distribution of charges in these three charged states of the system. In contrast, the ionic current flowing through the nanopore capacitor system containing oppositely charged graphene sheets highly depends on the direction of the bias, which is reflected by a highly rectifying I–V curves, Fig. 5b. In these two systems, the conductance state of the nanopore capacitor changes from Enhanced to Off depending on whether the transmembrane bias is aligned with or counteracts the electric field produced by the charged plates of the capacitor. Note that the behavior of the system remains symmetric with respect to simultaneous change of the transmembrane bias and the polarity of the charge at the capacitor’s plates.

Figure 5.

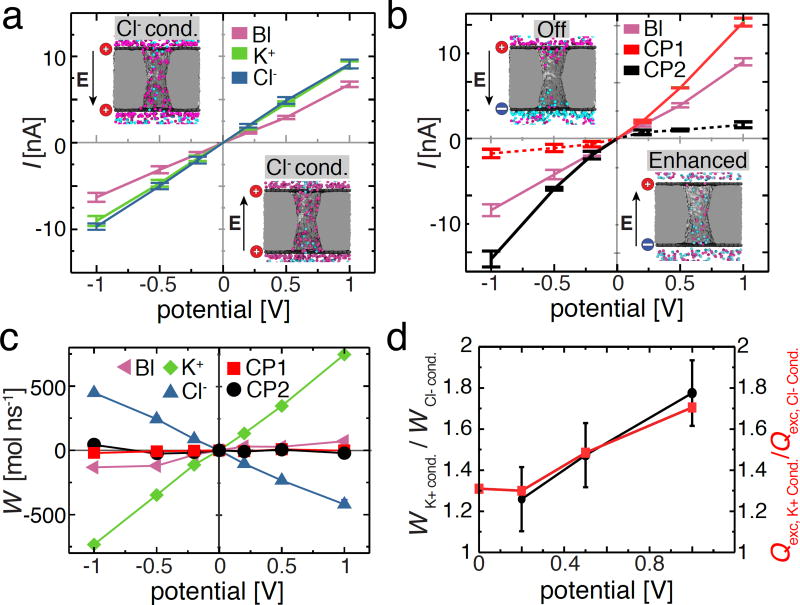
Rectification of ion and water flux by a charged nanopore capacitor. (a) Current–voltage dependence of the neutral (baseline, labeled as ‘Bl’, magenta), negatively charged (K⁺ conducting, green), and positively charged (Cl⁻ conducting, blue) nanopore capacitor system. The embedded images illustrate two representative configurations of ions inside the positively charged nanopore capacitor system (σ_top = σ_bottom = 2.0 e nm⁻²) for the two polarities of the 200 mV transmembrane bias. (b) Current voltage dependence of the electrically neutral nanopore capacitor system for the following three charge states of the plates: both plates are neutral (baseline, magenta, same as in panel a), σ_top = +2.0 e nm⁻² and σ_bottom = −2.0 e nm⁻²(CP1, red) and σ_top = −2.0 e nm⁻² and σ_bottom = +2.0 e nm⁻², (CP2, black). The dashed and solid red or black lines indicate the Off and Enhanced conductance states of the nanopore capacitor, respectively. The embedded images illustrate two representative configurations of ions inside the CP1 system for the two polarities of the 200 mV transmembrane bias. (c) Water flux, W, through the nanopore capacitor systems for the five charge states of the capacitor’s plate. A positive water flux represents the net movement of water molecules from trans to cis chamber. The water flux was computed by summing up instantaneous displacements of water molecules within the nanopore volume, see Methods for details. (d) The ratio of the water flux magnitudes (left) or of the excess ion numbers (right) for the K⁺ conducting and Cl⁻ conducting states. The excess number of ions, Q_exc, was computed as the absolute magnitude of the charge of all ions confined within the |z| < 2.0 nm volume of the nanopore averaged over the last 15 ns of the respective MD trajectory.

The fixed charge at the nanopore walls is compensated by counterions that, subject to a transmembrane bias, move through the nanopore volume, producing the ionic current. When the nanopore volume contains unequal amounts of cations and anions, the electric field-driven motion of ions produces a net flow of water known as the electro-osmotic effect.^72–74 Fig. 5c illustrates the net water flux through the five charged states of the nanopore capacitor for transmembrane biases from the 1000 mV range. The electro-osmotic effect is small in the case of the electrically neutral nanopore capacitor systems, where both plates are either electrically neutral (baseline) or carry opposite charges (CP1 and CP2), which is in agreement with the mild selectivity of the ionic current in these systems, Fig. 2d and Fig. 4d,i. As expected, prominent electro-osmotic effects are observed for K⁺ and Cl⁻ conducting states, reflecting the high selectivity of the ionic current, Fig. 3d,i. Interestingly, at a given transmembrane bias, the magnitude of the water flux is considerably smaller in the Cl⁻ conducting state than in the K⁺ conducting state, Fig. 5c; the ratio of the water flux magnitudes closely match the ratio of the excess number of ions in the nanopore volume in the respective states, Fig. 5d. We attribute this asymmetry of the electro-osmotic effect to the mild cation selectivity of the silica nanopore, which produces a slight imbalance in the K⁺/Cl⁻ ionic makeup even in the absence of the transmembrane bias or the charge at the capacitor’s plates, Fig. 2b–d. The difference in the magnitude of the electro-osmotic effect explains the difference in the ion selectivity of the K⁺ and Cl⁻ conducting states, Fig. 3d,i: the higher water flux in the K⁺ conducting state makes it more difficult for Cl⁻ ions to enter the nanopore in comparison to K⁺ ions entering the nanopore in the Cl⁻ conducting state. Such a behavior can be clearly seen in the animations of the MD trajectories, Supporting Information Movies 2 and 3.

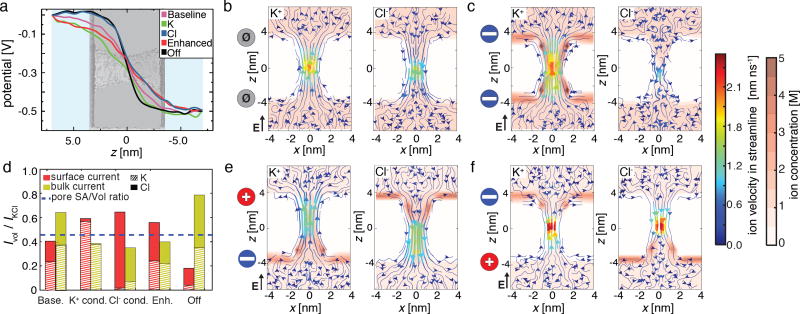
Our simulations have shown that the charge of the nanopore capacitor’s plates can affect both the selectivity and the overall magnitude of the nanopore current. At first look, such a behavior could be explained by the charge plates of the capacitor presenting an electrostatic barrier to ion permeation through the nanopore. This explanation, however, is not correct because the Debye length in our electrolyte solution is only 0.3 nm, a length considerably smaller than the nanopore dimensions. Hence, the electrostatic field produced by the charge of the capacitor’s plates should not affect the motion of ions in electrolyte if the ions are located more than 0.3 nm away from the plates. To illustrate this fact, we plot in Fig. 6a the profiles of the electrostatic potential along the nanopore axis: the electrostatic potentials smoothly decay within the nanopore volume regardless of the charge state of the capacitor plates and exhibits no barriers.

Figure 6.

Molecular mechanism of ionic current modulation by a graphene nanopore capacitor. (a) Profiles of the electrostatic potential along the nanopore axis for the five conductance states of the nanopore capacitor. The background image showing the outline of the nanopore capacitor is aligned with the z coordinate. Each electrostatic profile was obtained by averaging instantaneous distributions of the electrostatic potentials over the frames of the respective MD trajectory (see Methods). All potentials shown were obtained from the simulations performed under a transmembrane bias of 500 mV. (b) Local density (red color scale) and local velocity (streamlines) of K⁺ (left) and Cl⁻ (right) ions in the baseline state of the nanopore capacitor, which is schematically indicated by the dark grey circles, at a 200 mV transmembrane bias. The maps show the x − z cross section of the corresponding three-dimensional density and velocity fields. The maps were obtained by averaging over the corresponding MD trajectories and radially with respect to the nanopore axis. The solid-state membrane is not shown for clarity. (c) Same as panel b but for the K⁺ conducting state of the nanopore capacitor. The blue circles schematically indicate the negative charge of the graphene sheets. (d) The relative contribution of the surface and bulk currents to the total ionic current for the five conductance states of the graphene nanopore capacitor. The horizontal dashed line indicates the ratio of the volume of the solution located within 0.6 nm from the nanopore surface to the entire volume of the nanopore. (e,f) Same as panel b but for the Enhanced and Off states of the nanopore capacitor. The red and blue circles indicate the charge (positive or negative, respectively) of the graphene layers.

So, what is the mechanism of ionic current modulation by the nanopore capacitor? First, we examine the difference in the local currents of K⁺ and Cl⁻ ions between the baseline, Fig. 6b and the K⁺ conducting, Fig. 6c, states. In the K⁺ conducting state, K⁺ ions form a boundary layer near the negatively charged graphene sheets, as described previously. Close inspection of the ion density distributions reveals that K⁺ ions also form a boundary layer along the entire inner surface of the silica nanopore, which is reminiscent of the effect theoretically predicted for doped silicon membranes.⁷⁵ Thus, although counterions do screen the charge of the graphene plates in the electrolyte solution, the charge screening does not occur within the silica membrane and hence the negative electrostatic potential extends to the nanopore surface, where it attracts K⁺ ions; the K⁺ ions screen the potential within the electrolyte-filled volume of the nanopore. To illustrate the importance of the surface effect, we plot in Fig. 6d the contribution of surface current to the overall nanopore current. For the baseline system, the surface currents are slightly lower than the value prescribed by the ratio of the boundary layer volume to the volume of the entire nanopore, which is explained by the reduction of ion mobility in proximity of the nanopore surface.⁷⁶ In contrast, surface currents constitute the majority of the overall current in the K⁺ conducting state. The same mechanism explains the ion selectivity of the Cl⁻ conducting state of the system, Fig. 6d.

In the case of the Enhanced and Off conducting states, K⁺ and Cl⁻ ions also form boundary layers near the graphene capacitor plates and along the nanopore surface, Fig. 6,d,e. In contrast to the K⁺ and Cl⁻ conducting states, however, ions of a particular type form a boundary layer that extends along the nanopore surface only to the center of the membrane. Thus, in both Enhanced and Off states, one half of the nanopore surface is coated with K⁺ ions and the other half with Cl⁻. When the direction of the transmembrane bias aligns with the direction of the electric field generated by the plates’ charges (Enhanced state), ions enter the nanopore from the side where their surface concentration is enhanced, producing higher than baseline current, see Supporting Movie 4. In the opposite (Off) case, ions enter from the side where their concentration is depleted, which reduces the current below the baseline value, see Supporting Movie 5.

Conclusions

In summary, we have shown that the charge state of a graphene nanopore capacitor can regulate both selectivity and magnitude of the nanopore ionic current. Such combination of a graphene capacitor with a solid-state nanopore offers a means to couple electronic processes in conventional solid-state circuits (of which graphene is poised to become commonplace) to elements of nanofluidic electronics, where electrical current is carried by ions dissolved in solution. The coupling, however, is not limited to ionic current, as selective ionic current is accompanied by a strong electro-osmotic effect that can drive neutral or mildly charged biomolecules through the pore, transforming a change of the electrostatic potential into a chemical signal. One could envision a system where a nanopore capacitor acts as an injector of biomolecular species regulated by a conventional solid-state circuit.

In contrast to previously described ion current rectifiers and/or nanofluidic electrical diodes, the system described in our work can operate at high ion concentrations. In our system, the mechanism of the ionic current regulation relies on modulation of the surface currents, similar to an ion selectivity mechanism suggested for atomically thin, single layer graphene membranes.⁵⁴ The main difference, however, is that, in our system, charging the surface layer of the graphene-dielectricgraphene membrane alters the effective charge of the pore lumen that in turn modulates surface currents along the full length of the nanopore. This mechanism differs substantially from the electrostatic^21,77,78 or concentration polarization^53,79,80 mechanisms that regulate ionic current through nanopores in thick dielectric membranes. We would like to note that the microscopic model of the nanopore surface used in our work does not allow for prolonged direct binding of ions,⁴³ which is known to produce an ion species-dependent rectification effect.^16,81 Electrostatic regulation of ion binding by graphene charging can thus offer yet another route to diversifying functional response of a graphene nanopore capacitor system.