Abstract
The presence of carbonates in inclusions in diamonds coming from depths exceeding 670 km are obvious evidence that carbonates exist in the Earth’s lower mantle. However, their range of stability, crystal structures and the thermodynamic conditions of the decarbonation processes remain poorly constrained. Here we investigate the behaviour of pure iron carbonate at pressures over 100 GPa and temperatures over 2,500 K using single-crystal X-ray diffraction and Mössbauer spectroscopy in laser-heated diamond anvil cells. On heating to temperatures of the Earth’s geotherm at pressures to ∼50 GPa FeCO3 partially dissociates to form various iron oxides. At higher pressures FeCO3 forms two new structures—tetrairon(III) orthocarbonate Fe43+C3O12, and diiron(II) diiron(III) tetracarbonate Fe22+Fe23+C4O13, both phases containing CO4 tetrahedra. Fe4C4O13 is stable at conditions along the entire geotherm to depths of at least 2,500 km, thus demonstrating that self-oxidation-reduction reactions can preserve carbonates in the Earth’s lower mantle.
Carbonates are shown to exist in the lower mantle as seen in diamond inclusions, but thermodynamic constraints are poorly understood. Here, the authors synthesise two new iron carbonate compounds and find that self-oxidation-reduction reactions can preserve carbonates in the mantle.
Plate tectonics drives subduction of carbonate-bearing oceanic plates, that are responsible for recycling carbon from the surface down to the deepest regions of our planet. Indeed, geophysical, geochemical and petrological evidence1,2,3,4 suggest that sufficiently cold and/or fast subducting slabs can penetrate the transition zone and the Earth’s lower mantle, possibly even reaching the core–mantle boundary. Subducting plates are the major source of carbon influx inside the Earth5. Observation of carbonate inclusions in super-deep diamonds of lower mantle origin is evidence for their existence at depths greater than 700 km (refs 6, 7, 8). Untangling the behaviour of carbonates at extreme conditions, that is, determining their stability regions and properties, is a key to understanding the deep carbon cycle.
There are two major mechanisms that could affect carbonate phase stability and carbon oxidation state in the Earth’s interior—chemical reaction(s) with surrounding minerals or transformations (including self-oxidation-reduction) of carbonates themselves at specific pressures and temperatures. Previous studies on the Ca, Mg, Fe-bearing carbonates have established that they all undergo several high-pressure high-temperature (HPHT) phase transitions without decomposing in the pressure range up to 140 GPa and restricted temperatures9,10,11,12,13. Investigations of the stability of MgCO3 in the transition zone and upper part of the lower mantle as a function of oxygen fugacity demonstrated that carbon is expected to occur as diamond and carbides in the bulk mantle (when homogenously distributed) rather than carbonates14. However, in subducting slabs carbonates are expected to be stable due to the more oxidizing conditions compared to the surrounding mantle15, which may preserve them to the bottom of the lower mantle. The presence of iron is crucial to the fate of high-temperature carbonates13,16. Iron can radically change the thermodynamic stability of carbonate phases, thereby preserving them from breaking down. This behaviour may be a direct consequence of pressure-induced spin crossover17,18,19,20,21, which has been observed to occur at ∼43 GPa at room temperature to over 50 GPa at ∼1,200 K (ref. 22) for the endmember FeCO3. The presence of Fe-bearing carbonates in the lower mantle is supported by experimental evidence12,13. Iron plays a fundamental role in the redox state of the mantle23 due to its ability to exist in multiple valence states, and its abundance in the mantle is sufficient to govern the redox state of other elements, carbon in particular.
Interest in the high-pressure behaviour of carbonates has been enhanced by recent reports of novel compounds containing tetrahedral CO44− groups instead of the triangular planar CO32− groups that occur at ambient pressure9,12,24,25. Theoretical predictions indicate potential analogues between CO4-bearing carbonates and silicates25, but so far experimental information about structures of high-pressure carbonates are too limited (and indeed controversial) to speculate about their crystal chemistry.
In this study, we performed an experimental investigation of the high-pressure high-temperature behaviour of synthetic iron carbonate (FeCO3). Experimental conditions of our work cover the entire mantle and reveal two novel compounds containing tetrahedral CO4 groups, as well as the complex role of ferrous and ferric iron in stabilizing carbonates at extreme conditions. Our single-crystal X-ray diffraction data unambiguously establish the existence of at least one carbonate with a unique structural type (not known for silicates or other tetrahedral anion-bearing compounds), and demonstrate that the conditions in the Earth’s lower mantle do not lead to full decomposition of Fe-based carbonates due to self-oxidation-reduction reaction(s).
Results
Synthesis and structures of CO4-bearing Fe-carbonates
Synthesis of FeCO3 single crystals and their characterization at ambient conditions was described by Cerantola et al.20. HPHT experiments were performed in laser-heated diamond anvil cells (DACs) (see Methods section for details). We employed single-crystal X-ray diffraction as the primary method for sample characterization, and powder X-ray diffraction when analysis of single-crystal data were not possible. We used energy-domain Mössbauer spectroscopy (synchrotron Mössbauer source, SMS; see Methods section for details) as a complementary method of phase analysis and to determine the iron oxidation state.
Tetrairon(III) Orthocarbonate Fe4 3+C3O12
We observed appearance of the new sharp spots in the diffraction pattern after laser heating of FeCO3 single crystals at 1,750(100) K at 74(1) GPa (Fig. 1, Supplementary Table 1). Single-crystal X-ray diffraction (for example, Supplementary Fig. 1) data were collected on a temperature-quenched sample (Supplementary Tables 2 and 3). Reflections of one of the phases were indexed in a hexagonal unit cell (space group R3c, #161). After the integration procedure the resulting data set contained 327 reflections with I>2σ (I). Structure solution using direct methods identified the phase as a novel iron carbonate with stoichiometry Fe4C3O12. Charge balance considerations show that all iron is ferric. Each carbon atom is surrounded by four oxygen atoms (C–O distances ∼1.31–1.40 Å at 74 GPa), forming isolated (that is, not linked to each other) tetrahedra (Fig. 2a,b). Thus, the new compound is referred to as tetrairon(III) orthocarbonate.
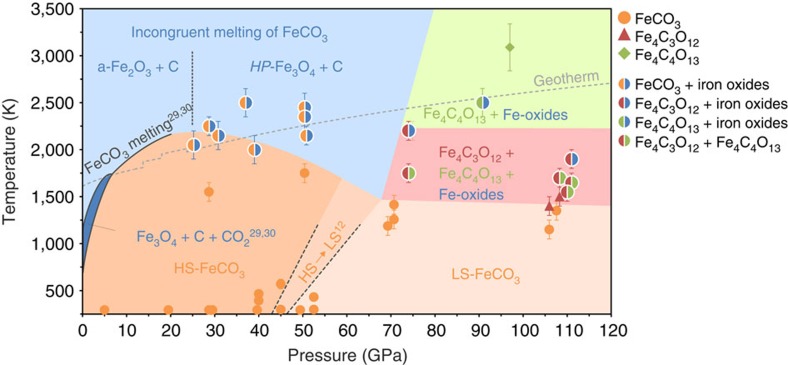
Figure 1. Stability diagram of FeCO3 at high P-T.
Symbols and phase regions identified in experiments: magnesite-structured FeCO3 (orange dots), oxide(s) and recrystallized FeCO3 (orange-blue dots), tetrairon(III) orthocarbonate Fe4C3O12 (red triangles), diiron(II) diiron(III) tetracarbonate Fe4C4O13+Fe4C3O12 (red-green dots), Fe4C4O12+oxides (red-blue dots), Fe4C4O13+oxides (green-blue dots), FeCO3 decomposition to Fe3O4+C+CO2 (refs 29, 30; dark blue area), high- and low- spin FeCO3 (dark and light orange area, respectively), incongruent melting of FeCO3 (light blue area), and formation of HP-carbonates Fe4C3O12 and Fe4C4O13 (red and green areas). The grey dashed curve is the expected mantle geotherm59. The black solid lines are from refs 29, 30. Black dashed lines indicate the region delimiting the spin transition in magnesio-siderite at HPHT from Liu et al.13. The vertical dashed black line separates the regions in which the formation of α-Fe2O3 and HP-Fe3O4 was observed upon incongruent melting of FeCO3.
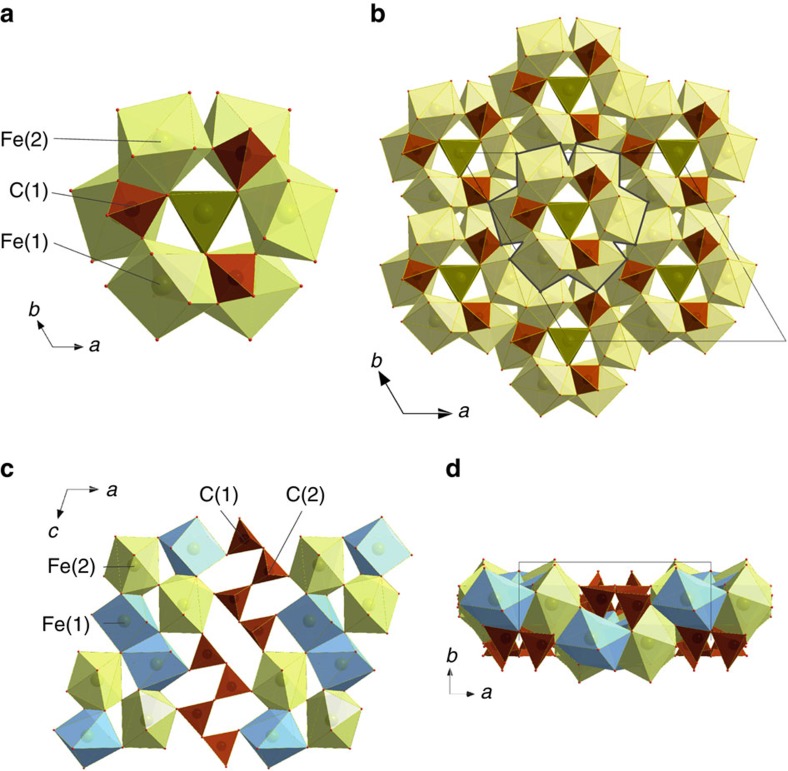
Figure 2. Crystal structures of high-pressure carbonates.
(a,b) Tetrairon(III) orthocarbonate Fe4C3O12 and (c,d) diiron(II) diiron(III) tetracarbonate Fe4C4O13, at ambient temperature and 74(1) and 97(2) GPa, respectively. In a, three FeO8 bicapped prisms (light green) and three CO4− tetrahedra (brown) form a ring with threefold symmetry by corner and edge sharing. The rings form layers that are stacked along the c axis. FeO6-prisms (dark green) are connected by triangular bases and located in the channels created by the rings. In b the overall structure of the orthocarbonate is displayed along the c-axis. In c FeO8 bicapped prisms (light green) are connected in a 3D framework by dimers of edge-shared FeO7 monocapped prisms (blue) and zigzag-shaped C4O1310−chains (brown) shown along the b axis. In d the tetracarbonate structure is displayed along the c axis.
There are two structurally distinct iron positions in the phase: the Fe(1) atom is situated on a threefold axis, while Fe(2) occupies a general position (Supplementary Table 2). Fe(1) is surrounded by nine oxygen atoms where three of the oxygen atoms are much further away than the other six (∼2.30 Å versus ∼1.94 and 1.97 Å at 74(1) GPa); hence this polyhedron can be considered to be a regular trigonal prism (Fig. 2a). The Fe(2) atom is located in a bicapped trigonal prism coordinated by oxygen. The individual (and average) Fe–O distances in both of the iron polyhedra in Fe4C3O12 are longer than in low-spin iron(III)-bearing oxides and compounds (∼1.8 Å) at corresponding pressures, which suggests that the phase contains high-spin iron. Although a precise characterization of the pure phase using Mössbauer spectroscopy is difficult due to the presence of other iron compounds (particularly iron oxides, see below) in the laser-heated samples, the available information supports the presence of iron in the high-spin state (see Supplementary Fig. 2, Supplementary Table 4 and Supplementary Note 1).
The threefold symmetry ring formed by corner- and edge-shared CO4− tetrahedra and three Fe(2)O8-bicapped prisms is a notable characteristic of the tetrairon orthocarbonate structure (Fig. 2a). The rings form layers that are stacked along the c axis (where each subsequent layer is rotated by 120° with respect to the original one, Fig. 2a). The trigonal Fe(1)O6-prisms are connected via triangular bases that are located in the channels formed by stacked rings. We are not aware of any other compounds that form the same structure.
Diiron(II) Diiron(III) Tetracarbonate Fe2 2+Fe2 3+C4O13
Laser heating of FeCO3 at temperatures above 1,750(100) K at pressures above 74(1) GPa resulted in formation of not only Fe4C3O12 and iron oxides (see below), but also a monoclinic phase (space group C2/c, #15; Supplementary Tables 1 and 2). Single-crystal X-ray diffraction data were collected on temperature-quenched samples at different pressures, where the best results were obtained for the experiment at 97(2) GPa (Fig. 1, Supplementary Tables 1 and 2). The chemical composition derived from the structure solution is Fe4C4O13, or more specifically Fe2+2Fe3+2C4O13. Each carbon atom is tetrahedrally coordinated by four oxygen atoms (C–O distances ∼1.27–1.39 Å at 97(2) GPa), and four CO4 groups are linked in truncated chains (Fig. 2b, Supplementary Fig. 4b). Thus, we refer to the new compound as diiron(II) diiron(III) tetracarbonate.
The atomic arrangement of the structure is based on corner-linked infinite layers of Fe(2)O8-bicapped prisms connected in a three-dimensional (3D) framework by dimers of edge-shared Fe(1)O7 monocapped prisms and zigzag-shaped C4O1310− chains (Fig. 2b). The average Fe–O distances in Fe(1)O7 and Fe(2)O8 polyhedra are similar to one another (∼1.96 Å and ∼2.02 Å, respectively, at 97(2) GPa) and longer than expected for low-spin ferric or ferrous iron26. Similarity in the sizes of iron polyhedra may indicate that Fe cations are in a mixed valence state (intermediate between +2 and +3) as proposed for high-pressure iron oxides26,27.
Fe4C4O13 is isostructural with recently reported Mg1.6Fe2.4C4O13 (ref. 24) obtained by annealing Mg-bearing natural siderite at 141 GPa and 2,650 K. Indeed there is an entire family of tetrasilicates containing four-member Si4O1310− groups (ref. 28 and references therein), as well as germanates, vanadates and arsenates.
FeCO3 behaviour at high pressures and high temperatures
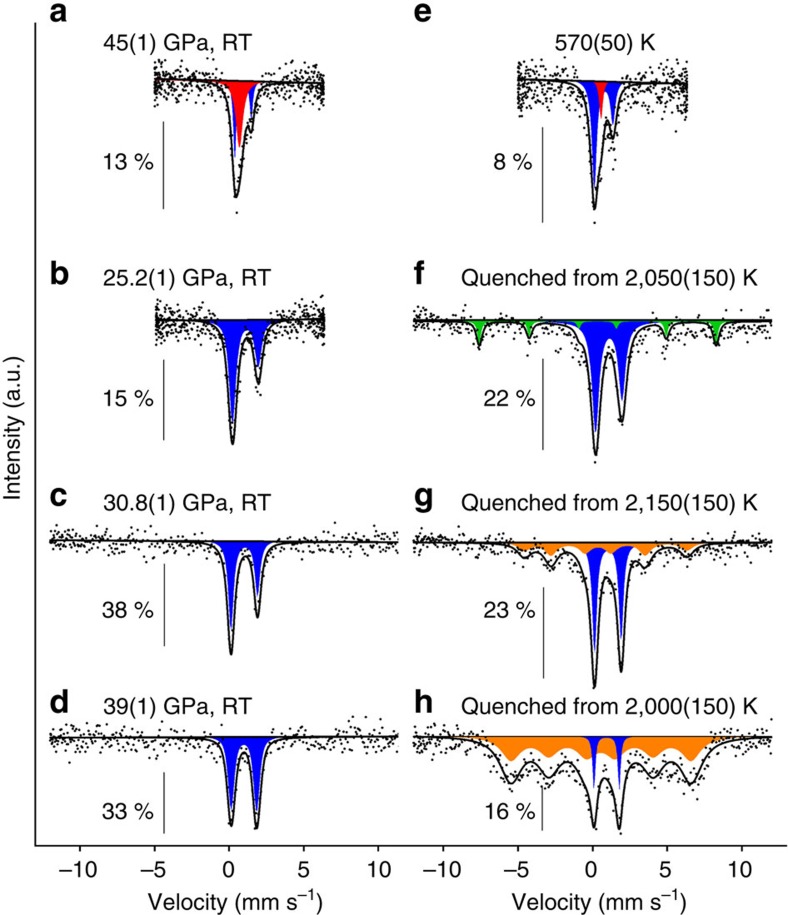
Recent studies of FeCO3 at pressures up to 20 GPa (refs 29, 30) have shown that while it melts above ∼6 GPa, below this pressure the phase dissociates to the mixture Fe3O4+C+CO2 before melting. Heating FeCO3 single crystals at 28.7(1) GPa and 1,550(100) K does not result in any phase or structural changes or destruction of the single crystal (Fig. 3b). Heating the same sample at higher temperatures (2,250(100) K) causes complete recrystallization of the material (Fig. 3c), thus indicating melting. Mössbauer spectra of the samples quenched from the molten state show unambiguously the presence of FeCO3 as well as iron oxides: α-Fe2O3 (hematite) at pressures below ∼25 GPa and HP-Fe3O4 (ref. 26) above ∼31 GPa (Figs 1 and 4b,c,f,g; Supplementary Tables 1,4 and 5).
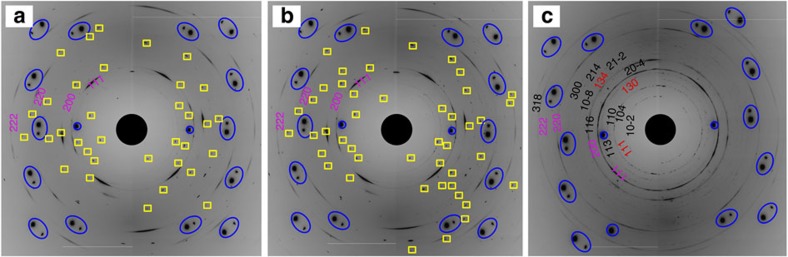
Figure 3. Selected 2D diffraction images of FeCO3 before and after heating.
Single-crystal diffraction images were collected at 28.7(1) GPa at (a) ambient temperature before heating, (b) after heating at 1,550(100) K and (c) 2,250(100) K. Melting and recrystallization of starting material is evidenced by the appearance of FeCO3 powder diffraction rings after heating to the highest temperature. Appearance of diffraction lines of HP-Fe3O4 indicates incongruent melting of FeCO3. Blue ellipsoids indicate diamond diffraction spots from the diamond anvils and yellow squares mark the single-crystal diffraction spots of FeCO3. Numbers designate hkl-indices of diffraction lines belonging to FeCO3 (black), neon pressure transmitting medium (magenta) and HP-Fe3O4 (red).
Figure 4. Selected synchrotron Mössbauer spectra from high P-T treatment of FeCO3.
(a–d) Spectra collected at the indicated pressures at room temperature before heating; (e–h) Spectra collected during or after heating at the indicated temperatures. Subspectra are shaded as follows: blue doublet—high-spin ferrous iron, red singlet—low-spin ferrous iron; green sextet—α-Fe2O3 and orange sextet—HP-Fe3O4 (Supplementary Fig. 5). Note that in a the intensity (amount) of high-spin ferrous iron increases with increasing temperature. The appearance of HP-Fe3O4 in g and h is the result of progressive decomposition of FeCO3 upon melting at high pressure. Continuous lines are fitted with the full transmission integral (Methods section). Percentages on the left of each spectrum indicate the relative absorption.
We observed a similar behaviour for FeCO3 upon heating to ∼51 GPa (Fig. 1, Supplementary Tables 1 and 5). However, while the degree of carbonate decomposition appears to increase at increasing temperature (at a given pressure) and increasing pressure (at a given temperature), we cannot quantify the process based on our existing data. Nevertheless it is clear that all experiments performed below ∼51 GPa produced only partial decomposition of the carbonate. Even heating above ∼2,450 K for up to one hour always showed diffraction lines of recrystallized FeCO3 and/or its presence in SMS spectra. However, we cannot exclude that heating at sufficiently high temperature (and for a sufficiently long time) could result in complete breakdown of FeCO3.
Fe2+ in FeCO3 is known17,18,19,20,21 to undergo spin crossover from high to low spin at about 40 GPa. Although the goal of this work was not to investigate the pressure–temperature dependence of spin crossover, Mössbauer spectroscopy (SMS) was able to show the temperature effect on the spin state at different pressures (examples of spectra are given in Fig. 4). The corresponding data points are shown on Fig. 1 and are reasonably consistent with the data reported by Lin et al.21 and Liu et al.22 for magnesio-siderite Mg0.35Fe0.65CO3.
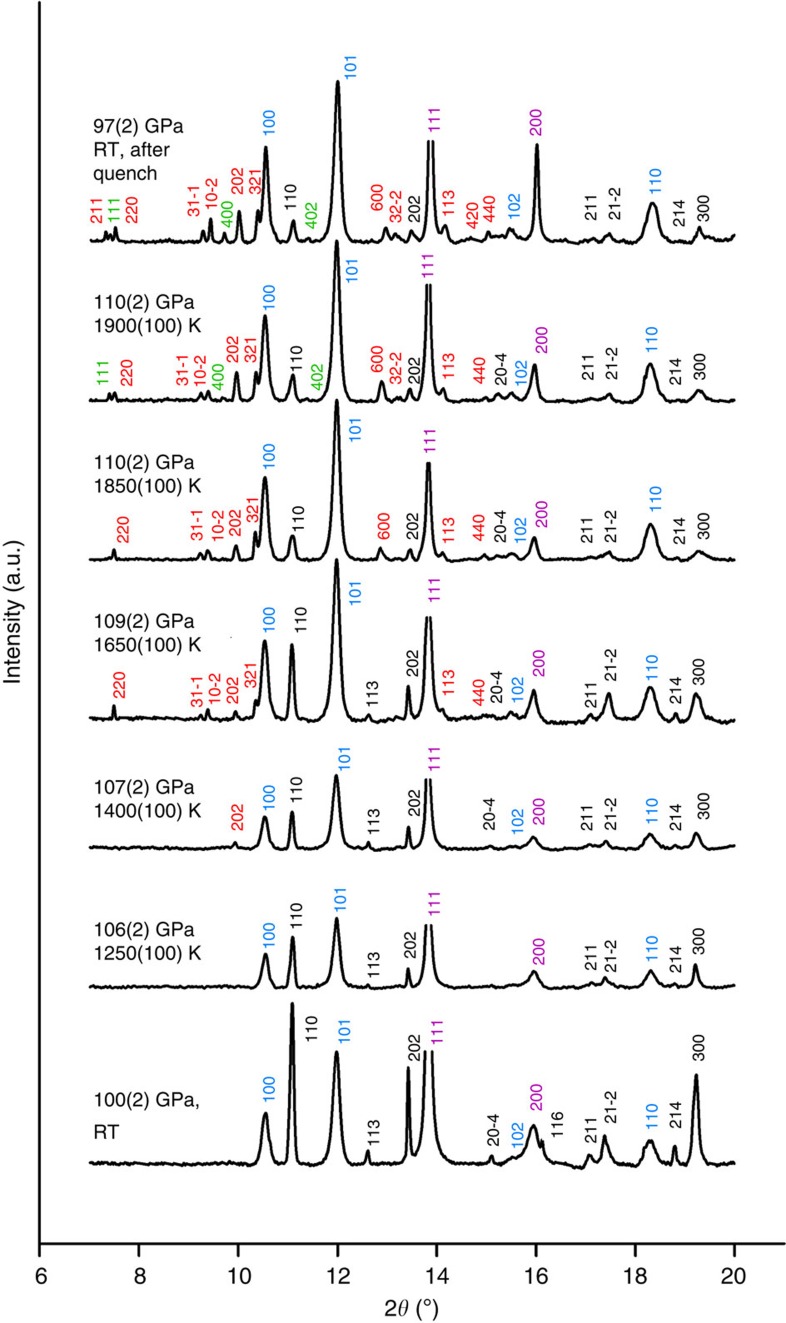
Heating FeCO3 at 74(1) GPa and 1,750(100) K resulted in the formation of multi-domains of both tetrairon orthocarbonate Fe4C3O12 and diiron(II) diiron(III) tetracarbonate, Fe4C4O13 (Fig. 1). The result is reproducible: the simultaneous appearance of both phases was observed at the same pressure and temperature on heating of different crystals in different loadings (Supplementary Table 1). The observations may (a) indicate non-equilibrium conditions in laser-heated DACs, (b) be a consequence of complex redox chemical reactions that form both phases simultaneously or (c) be a result of successive transformations between carbonate phases that are so closely located in P-T space that they cannot be distinguished. Indeed the results of further experiments at higher pressures (103–110 GPa) suggests that scenario (c) is the most plausible. Heating a FeCO3 single crystal to 1,400(100) K at 110(2) GPa resulted in the formation of hexagonal tetrairon orthocarbonate Fe4C3O12 (Figs 1 and 5). Monoclinic diiron(II) diiron(III) tetracarbonate, Fe4C4O13 appeared only after laser heating above 1,650(100) K (Figs 1 and 5). The highest temperature at which Fe4C4O13 was observed is 3,088(250) K at 97(2) GPa (Fig. 1).
Figure 5. Selected integrated X-ray diffraction patterns collected on heating of FeCO3 near or above 100 GPa.
Patterns are labelled with the pressure and temperature during data collection. Indices of different phases are coloured as follows: FeCO3 starting material (black), Ne (magenta), Re (light blue), tetrairon(III) orthocarbonate Fe4C3O12 (red) and diiron(II) diiron(III) tetracarbonate Fe4C4O13 (green). Neon was used both as a quasi-hydrostatic pressure medium and a pressure standard (Methods section). Data were collected at ID09a at ESRF with an X-ray wavelength of 0.4126 Å.
Close examination of X-ray diffraction patterns containing diiron(II) diiron(III) tetracarbonate, Fe4C4O13 reveal the presence of further reflections which do not belong in any obvious way to the previously identified carbonates. While in some cases it was not possible to identify phase(s) unambiguously due to close overlapping of reflections and/or their low amount, for most data points we were able to determine lattice parameters and even refine structure(s). In all cases, the appearance of Fe4C4O13 upon heating at pressures above ∼74 GPa was associated with the formation of orthorhombic (space group Cmcm) CaIrO3-structured η-Fe2O3 (ref. 26) and/or orthorhombic (space group Bbmm) CaTi2O4-type structured HP-Fe3O4 phase26,31 (Fig. 1, Supplementary Tables 1 and 5). Additionally, in several experiments after heating at different pressures but at temperatures above ∼2,200 K, we observed monoclinic (space group C2/m) Fe5O7 (ref. 26).
Samples recovered after experiments at pressures above ∼30 GPa at temperatures higher than ∼1,800 K show strong broad features in Raman spectra that are typical for nano-diamond32 and sometimes a band at 1,330 cm−1 that is characteristic for diamond (Supplementary Fig. 3), even though in situ X-ray measurements were not able to detect the presence of diamond (or any other carbon phases) after laser heating of FeCO3 crystals. The formation of diamond upon heating of FeCO3 at high pressures and temperatures has been unambiguously documented in previous studies12,29,30.
Discussion
The increase of carbon co-ordination number from three (CO3 triangles) to four (CO4 tetrahedra) under compression is the obvious consequence of rules known for decades33. Numerous theoretical studies have predicted the formation of CO4-bearing carbonates at pressures ranging from over 80 GPa to 150 GPa34,35,36,37 depending on chemical composition and computational methods. Different configurations, from isolated tetrahedra to pyroxene-like chains, were anticipated for compounds with carbon tetra-co-ordinated by oxygen. In general, theoretical analysis of possible carbonates with condensed CO4 groups suggests that there should be analogues with silicates, but expected variations of C–O–C angles are much smaller than for Si–O–Si angles in silicates36,38.
We are not aware of dedicated theoretical studies of pure iron CO4-bearing carbonates. However, the predicted36 structure of Mg-carbonate containing three-membered rings C3O96− made of CO4 tetrahedra was used to index peaks in powder diffraction data of HPHT Fe- and Fe/Mg carbonates12,16. The same structural model has been used to interpret infrared spectra of magnesiosiderite39. However, important structural details predicted by theory36 and obtained by powder X-ray diffraction experiments12,16 are not in agreement (even reported space groups are different). Moreover, it is not obvious how reliable structural information can be extracted based on LeBail fits with large unit cells13 or from powder X-ray diffraction of complex mixtures of different phases: for example, α-Fe2O3 (hematite) was one of the phases reported to co-exist with carbonates at 88 GPa (ref. 12) while it is well documented by now26 that above ∼50 GPa iron(III) oxide adopts different structures.
The average interatomic C–O distance in the CO32− ion in magnesite-structured FeCO3, MnCO3, and CoCO3 (refs 17, 40) extrapolated to 75 GPa is ∼1.24 Å, and is ∼1.26 Å9 in dolomite-III. In iron ortho- and tetracarbonates the average C–O distance is ∼1.35 Å, where the larger value is consistent with the increase of coordination number on transformation and quantitatively similar to borates (the typical difference in ionic radius of B3+ in triangular BO3 and BO4 tetrahedra is ∼0.1 Å)33. Notably, the average O–O distance (2.20(2) Å) in the CO44− group in iron orthocarbonate at ∼74 GPa is, for example, almost the same as in magnesite-structured Fe, Mn and Co carbonates (∼2.15 Å) and in dolomite-III (∼2.17 Å) (refs 17, 40). This observation indicates that is not the size of the carbon cation, but rather the oxygen–oxygen contacts that define the size of CO4 tetrahedra.
The shapes of CO4 tetrahedra in HP-carbonates are far from ideal. The polyhedron is especially distorted in tetrairon orthocarbonate Fe4C3O12 with dissimilar individual C–O distances (varying from 1.254 to 1.385 Å at 103.7(2) GPa) and O–C–O angles (varying from 98 to 115° with bond angle variance of 61.4 degree2, see Supplementary Note 2 for definition and reference). While orthosilicates display a great variety of geometries, such distortion of SiO4 units is not unusual and garnets in particular show bond angle variances in the same range (57 degree2 for pyrope, for example, ref. 41).
In tetracarbonate there are two non-equivalent CO4-tetrahedra, two ‘outer’ and two ‘inner’ that form four-membered C4O1310− truncated chains (Fig. 2c,d). In both Mg-bearing24 and pure iron tetracarbonate the ‘inner’ tetrahedra are significantly more distorted than the ‘outer’: the bond angle variances are 35.9 degree2 compared to 13.1 degree2 for pure iron tetracarbonate at 97(2) GPa, and 146.2 compared to 19.0 degree2 for the Mg-bearing phase at 135 GPa (ref. 24). Indeed the same tendency is observed in tetrasilicates (ref. 28 and references therein). Moreover, the Si–O–Si angles in tetrasilicates are ∼122° and 125–143° (for ‘outer’-‘inner’ and ‘inner’-‘inner’ tetrahedra, respectively28), while for tetracarbonates the corresponding C–O–C angles are ∼113° and 122–125°. Thus, the analogous structural behaviour of silicates and CO4-based carbonates is obvious: based on experimental observations there is no reason that ‘high-pressure’ carbonate structures should be more limited than those of silicates. Moreover, iron(III) orthocarbonate, Fe4C3O12, with its unique structure is an example of the diversity of atomic arrangements that are possible in high-pressure CO4-bearing carbonates.
Heating FeCO3 above 1,750(100) K at pressures to at least ∼50 GPa (Fig. 1) resulted in partial decomposition of the material with formation of iron oxides (α-Fe2O3 below ∼25 GPa and high-pressure orthorhombic HP-Fe3O4 at higher pressure). These observations are in agreement with results obtained in large volume apparatus: for example, according to Kang et al.30, FeCO3 partially decomposes on melting according to the following reaction:
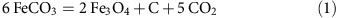 |
Formation of tetrairon(III) orthocarbonate, Fe4C3O12, at pressures above ∼74 GPa (Fig. 1) may be described by the simple equation:
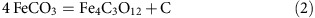 |
According to equation (2) and known equations of state of FeCO3 (with low-spin Fe2+) and diamond17,42 the gain in volume on decomposition of FeCO3 is ∼4%. Thus, redox reaction (2) may be driven by a volumetric effect.
Diiron(II) diiron(III) tetracarbonate, Fe4C4O13, appears on heating of FeCO3 above ∼74 GPa, but at temperatures significantly higher than needed to form tetrairon(III) orthocarbonate (Fig. 1). The experiment at ∼110 (Fig. 5) GPa indeed demonstrates that tetracarbonate forms after further heating of already synthesized orthocarbonate. Thus, we can conclude that tetracarbonate is a product of the chemical evolution of orthocarbonate. Some schemes that may lead to formation of tetracarbonate are the following:
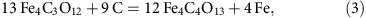 |
or
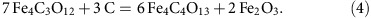 |
Equations (3) and (4) suggest that carbon (as a decomposition product of FeCO3 according to equation (2) or as diamond from the anvils) reduces Fe3+. However, this process is unlikely because carbon (diamond) cannot reduce iron at pressures above ∼25 GPa (refs 15, 26). Moreover, we did not observe evidence of pure iron or its alloys (or carbides) in reaction products, which adds to the arguments against reaction (3).
Another process which could lead to formation of tetrairon tetracarbonate is
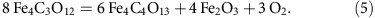 |
In this case iron is reduced by oxygen. The same phenomenon was observed in studies of iron(III) oxide at pressures above ∼70 GPa (ref. 26). Moreover, together with iron tetracarbonate we observed (Fig. 1, Supplementary Tables 1 and 5) CaIrO3-structured η-Fe2O3 and possible products of its further decomposition24,26: monoclinic (space group C2/m) Fe5O7, monoclinic (space group C2/m) Fe13O19 and orthorhombic (space group Bbmm) CaTi2O4-type structured HP-Fe3O4 phases. These observations support the schematic process described by equation (5) and imply that the presence of iron oxides among products of HPHT treatment of iron carbonate(s) above 74(1) GPa is not a signature of their full breakdown, but rather an indication of the intrinsic process of formation of CO4-bearing phase(s) containing iron in different oxidation states.
While only reaction (5) explicitly depends on oxygen fugacity, all other processes described above may be affected by different redox conditions (and could play a role in buffering reactions in more complex processes involving iron-bearing carbonates). In view of the recently reported26,43 fundamental changes in the chemical behaviour of the iron-oxygen system at pressures above ∼70 GPa and high temperatures, our results are also calling for detail investigations of redox processes in the lowermost part of Earth’s lower mantle and core–mantle boundary.
Heating magnesio-siderite (Fe0.65Mg0.35)CO3 at pressures of ∼50(1) GPa and 1400(100) K resulted13 in formation of a new phase which Liu et al.13 called ‘siderite II’ and described as orthorhombic. The same phase was reported13 at pressures up to ∼120 GPa and temperatures up to 2,200 K. Liu et al.13 provided us with the powder X-ray diffraction pattern collected at 90 GPa after heating at 2,200 K. We fit this data using the Rietveld method (as implemented in the GSAS package) using the model of hexagonal tetrairon orthocarbonate Fe4C3O12 (Supplementary Fig. 4). The good quality of the fit (Supplementary Fig. 4) unambiguously confirms that ‘siderite II’ has the structure of tetrairon orthocarbonate. The quality of the powder X-ray diffraction data does not allow the occupancy of cation positions to be refined so we do not know how much magnesium is incorporated in the phase. However, the absence of reflections of any other phases (apart from the gold standard and Ne pressure transmitting medium) suggests that at least 35% of magnesium may be incorporated in the structure of orthocarbonate.
Single-crystal X-ray diffraction data on iron-bearing carbonates subjected to high pressures and high temperatures are very limited. Studies of ankerite9 up to about 60 GPa reveal the formation of a phase with non-planar CO32− groups as a tendency to increase the co-ordination number of carbon. Magnesium-siderite exposed to pressures and temperatures corresponding to the top of the Earth’s D″ layer (135 GPa and 2,650 K) was shown24 to transform to iron(II)-bearing dimagnesium diiron(III) tetracarbonate Mg1.6Fe2.4C4O13. It contains tetrahedrally coordinated carbon units, corner-shared in truncated C4O1310− chains, and up until the present work it was the only unambiguously proven case of carbonate with CO4 groups.
In the case of tetrairon orthocarbonate, incorporation of magnesium may significantly expand its pressure–temperature stability field at the expense of the diiron diiron tetracarbonate phase. It may mean that Mg, Fe-orthocarbonate might remain stable along the geotherm.
Modern estimates indicate the concentration of carbon in altered oceanic crust to be in the range of 500–600 p.p.m. (ref. 5 and references therein). A recent study concludes that between none and almost all of the carbonates in subducting slabs are subducted into the mantle5. The most plausible scenario however is that a relatively small amount of carbon is recycled into the convecting mantle based on a careful re-evaluation of carbon fluxes in subduction zones, where carbon is preferentially stored in the lithospheric mantle and the crust5. Our experiments clearly show that along an average subducting slab temperature profile44 (Fig. 1), Fe-carbonates will not melt during subduction. Still, recent reports4 suggest that the majority of slab geotherms intersect a deep depression along the melting curve of carbonated oceanic crust at depths of ∼300–700 kilometres, creating a barrier to direct carbonate recycling into the deep mantle. Nevertheless, a portion of the subducted carbonates can still be recycled in the convecting mantle, not taking part in hydrothermal alteration reactions, partial melting and formation of carbonatitic magmas and ‘premature’ carbon degassing processes. For instance, cold subducting slabs44,45 (Fig. 1) could stabilize carbonates down to mid lower mantle depths, favouring Fe-partitioning into carbonates13 due to Fe2+ high- to low-spin crossover, which starts in carbonates at much shallower depths than in other Fe2+-bearing minerals46,47. In this case, the average composition of carbonates in the Earth’s lower mantle could be significantly enriched towards the ‘FeCO3’ component. While self-redox reactions involving iron may potentially destabilise Fe-bearing carbonates, our experiments demonstrate that at pressures above ∼70 GPa (corresponding to a depth of ∼2,000 km), iron carbonates drastically change their structures, forming CO4-bearing compounds, and may persist to temperatures above 3,000 K in the 100 GPa range (that is, exist above the mantle geotherm). Thus, based on our experimental observations we conclude that CO4-based carbonates may be carriers of carbon in the lower mantle.
Methods
Sample preparation
Single crystals of 57FeCO3 were grown from 57FeCO3 powder at 18 GPa and 1,600 °C in a 1,200-t Sumitomo press at Bayerisches Geoinstitut (Bayreuth, Germany). 57FeCO3 powder was synthesized using 57Fe-oxalate (57FeC2O4) as a precursor, which in turn was obtained via chemical reactions starting from 57Fe-metal (see ref. 20 for more details). Mössbauer spectroscopy and single-crystal diffraction data confirm that synthetic samples are free of ferric iron.
Single crystals with an average size of 0.015 × 0.015 × 0.005 mm3 were pre-selected on a three-circle Bruker diffractometer equipped with a SMART APEX CCD detector and a high-brilliance Rigaku rotating anode (Rotor Flex FR-D, Mo-Kα radiation) with Osmic focusing X-ray optics.
Selected crystals together with small ruby chips (for pressure estimation) were loaded into BX90-type DACs48 and European Synchrotron Radiation Facility (ESRF) high-pressure membrane cells. Diamonds with culet sizes of 250 μm and 120 μm in diameter were used to generate pressures up to ∼75 GPa and ∼110 GPa, respectively. Neon was used as a pressure transmitting medium and was loaded at Bayerisches Geoinstitut and/or at ESRF.
X-ray diffraction
The single-crystal X-ray diffraction experiments were conducted on the ID09a beamline at ESRF, Grenoble, France (MAR555 detector, λ=0.4126 Å); on the ID27 beamline at ESRF (PerkinElmer flat panel detector, λ=0.3738 Å); and on the 13-IDD beamline at the advanced photon source (APS), Chicago, USA (MAR165 CCD detector, λ=0.3344 Å). The X-ray spot size was dependent on beamline settings and varied from, for example, 3 × 2.5 μm2 (13-IDD) to 10 × 10 μm2 (ID09a), where typically a smaller beam was used for laser heating experiments. A portable double-sided laser heating system49 was used for experiments on ID09a (ESRF) to collect in situ single-crystal X-ray diffraction data, while a state-of-the art stationary double-sided laser heating setup at IDD-13 (APS) was used to collect temperature-quenched single-crystal X-ray diffraction data. Crystals (as a rule about 10 μm in diameter) were completely immersed in laser radiation and there was no measurable temperature gradient within the samples. In the case of prolonged heating experiments the temperature variation during the heating did not exceed ±100 K. Pressures were calculated from the positions of the X-ray diffraction lines of Ne (ref. 50). X-ray diffraction images were collected during continuous rotation of DACs typically from −38° to +38° on ω; while data collection experiments were performed by narrow 0.5–1° scanning of the same ω range.
Integrated patterns (Fig. 5) from powder XRD experiments were processed using Fit2d (ref. 51) and indexed using the Rietveld method implemented in the GSAS and EXPUI packages52,53.
XRD data analysis
Integration of the reflection intensities and absorption corrections were performed using CrysAlisPro software54. Diffraction images were converted to the native CrysAlisPro format ‘ESPERANTO’. An instrument model was refined to calibrate the diffractometer. For this purpose we performed data collection on standard samples. Calibration of the instrument model for Fit2D software51 was done using powder standards, that is, LaB6 (NIST SRM 660a) or CeO2 (NIST SRM 674b) and for CrysAlisPro software we used a standard orthoenstatite calibration single crystal ((Mg1.93,Fe0.06)(Si1.93,Al0.06)O6, Pbca, a=8.8117(2), b=5.18320(10), c=18.2391(3) Å, already mounted in a DAC. The peak hunting of the experimental data set was performed using the smart peak hunting option in CrysAlisPro for images collected with MAR165 (13=IDD beamline at APS and ID27 beamline at ESRF) and Perkin Elmer (ID27 beamline at ESRF) detectors. For images collected with a MAR555 detector (ID09a) we utilized the traditional peak hunting procedure. To obtain the unit cell parameters of the measured phases(s) we proceeded with the automatic indexing of the peaks. The best performance of the automatic indexing method can be achieved on a small set of reflections (∼20–30) belonging only to a single crystal. One has to manually select those reflections that build a 3D lattice in the reciprocal space. The obtained unit cell was then refined against the whole batch of reflections and the UB matrix was derived. Once the unit cell parameters were defined, we proceeded with the data reduction that is necessary to extract the reflection intensities from the experimental images. By default, after data reduction, CrysAlisPro applies frame scaling, absorption corrections and searches for the space group analysing the systematic absences. This operation requires the following integration parameters: correct data ranges, DAC’s opening angle, integration box size, reflection profile fitting mode (2D or 3D) and background evaluation mode. If the reflection profiles were split over several frames, the 3D profile fitting was used, the 2D option otherwise. Data from laser-heated samples (noisy data) required the smart background option to be used. Data reduction output files (including intensity and resolution statistics) were inspected manually to check for consistency between intensities of equivalent reflections. Indicators of the XRD data quality are Rσ, F2obs/σint(F2obs) and Rint and a form of frame-by-frame scaling coefficients (frame scaling curve). The Rint value indicates the overall quality of the data collection and if it is higher than 10% an accurate structural refinement will not be possible. Processes of elaboration of phases are nowadays automated, and there are a number of techniques implemented in different structure solution programs such as direct methods, Patterson synthesis, heavy-atom method, charge flipping and so on. Here, the structures were solved by the direct method and refined in the isotropic (and anisotropic for iron atoms) approximation by full matrix least-squares refinements using SHELXS and SHELXL software55, respectively. The atomic co-ordinates were calculated using an inverse Fourier transform for the structure factor Fhkl of the specific (for each phase) diffracted waves. Once we obtained the initial structural model we refined it against the experimental data by least-squares minimization of adjustable parameters. At the first stage, missing atoms were found from the reconstruction of residual electron density maps, their position, and when applicable, atomic occupancies were refined.
High-pressure data normally suffer from overlapping with parasite diffractions, mostly created by diamonds and crystallized pressure media. Those overlapping reflection were omitted from the refinement.
Note that all information given here can be found illustrated in https://epub.uni-bayreuth.de/2124/.
SMS spectroscopy
Energy-domain Mössbauer spectroscopy measurements were carried out at the nuclear resonance beamline ID18 (ref. 56) at ESRF using the SMS. The SMS is based on a nuclear resonant monochromator employing pure nuclear reflections of an iron borate (57FeBO3) crystal. The source provides 57Fe resonant radiation at 14.4 keV within a bandwidth of 15 neV which is tunable in energy over a range of ∼±0.6 μeV (ref. 56). The beam of γ-radiation emitted by the SMS was focused to a 10 μm × 15 μm spot size, fully within the size of the Fe-carbonate crystals. During each laser heating experiment we measured the Mössbauer spectrum of the sample before and after heating. We did not measure the Mössbauer spectrum of the sample during heating with exception of the experiments performed in the spin crossover pressure range, in between ∼40 and ∼50 GPa (Fig. 1 and Supplementary Table 1). The small cross section of the beam and its high intensity allow for rapid collection of Mössbauer data57. The collection time for one FeCO3 spectrum before heating was ∼20 min, whereas after heating (depending on the sample composition) the collection time varied from 30 min to 6 h (the latter for the new HP-carbonates). The velocity scales of all Mössbauer spectra were calibrated relative to 25 μm-thick α-Fe foil, and all spectra were fitted using the software package MossA (ref. 58). Lorentzian lines were used to fit all Mössbauer spectra and a linear function was applied to model the background. All spectra were fit using the full transmission integral to avoid distortion of the area ratios due to the high loading of 57Fe in our samples. In this way we were able to obtain an accurate determination of iron distribution in the different investigated samples such as the high spin and low spin abundance and site population in HP-carbonates.
Data availability
The X-ray crystallographic co-ordinates for structures reported in this article have been deposited at the Inorganic Crystal Structure Database (ICSD) under deposition number CSD 432930-432931. These data can be obtained free of charge from FIZ Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: (+49)7247-808-666; e-mail: crysdata@fiz-karlsruhe.de) through the hyperlink: https://www.fiz-karlsruhe.de/en/leistungen/kristallographie/kristallstrukturdepot/order-form-request-for-deposited-data.html
Additional information
How to cite this article: Cerantola, V. et al. Stability of iron-bearing carbonates in the deep Earth’s interior. Nat. Commun. 8, 15960 doi: 10.1038/ncomms15960 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Acknowledgments
We thank G. Aprilis, D. Vasiukov, I. Chuvashova, A. Pakhomova and N. Solopova for assistance with HPHT experiments at ESRF. We acknowledge the helpful collaboration of J. Liu & J.-F. Lin and the technical assistance of S. Linhardt and S. Übelhack. L.D. and C.M. thank the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) and the Federal Ministry of Education and Research (BMBF, Germany) for funding. M.B. thanks the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST "MISIS" (No. K2-2016-013). We acknowledge the ESRF for provision of beam time at ID09a, ID18, ID27 and the Sample Environment Service-HP lab for the technical support of their loan pool diamond anvil cells. Portions of this work were performed at GeoSoilEnviroCARS (sector 13), APS, Argonne National Laboratory. GeoSoilEnviroCARS is supported by the National Science Foundation-Earth Sciences (EAR-1128799) and Department of Energy-GeoSciences (DE-FG02-94ER14466). This research used resources of the APS, a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357.
Footnotes
The authors declare no competing financial interests.
Author contributions L.D., C.M. and V.C. proposed the research, did the project planning and provided the sample. E.B. and L.I. selected the single-crystals. V.C., L.D., L.I., I. Yu. K. and J.J. prepared the high-pressure experimental set-ups. V.C., L.D., E.B., M.M., L.I., M.B., V.S., S.P., M.H., C.P., V.B.P. and M.M. conducted the HPHT single-crystal X-ray diffraction experiments. V.C., L.D., C.M., I.K., A.I.C. and R.R. conducted the SMS experiments. E.B., L.D. and M.M. analysed the X-ray single-crystal diffraction data. V.C. and L.D. analysed the X-Ray powder diffraction data. V.C., C.M. and L.D. analysed the Mössbauer data. V.C., L.D. and C.M. interpreted the results and wrote the manuscript with contributions of all authors. V.C. wrote the Methods section.
References
- Christensen U. R. The influence of trench migration on slab penetration into the lower mantle. Earth Planet. Sci. Lett. 140, 27–39 (1996). [Google Scholar]
- Fukao Y., Widiyantoro S. & Obayashi M. Stagnant slabs in the upper and lower mantle transition region. Rev. Geophys. 39, 291–323 (2001). [Google Scholar]
- Walter M. J. et al. Deep mantle cycling of oceanic crust: evidence from diamonds and their mineral inclusions. Science 334, 54–57 (2011). [DOI] [PubMed] [Google Scholar]
- Thomson A. R. et al. Slab melting as a barrier to deep carbon subduction. Nature 529, 76–79 (2015). [DOI] [PubMed] [Google Scholar]
- Kelemen P. B. & Manning C. E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl Acad. Sci. USA 112, E3997–E4006 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenker F. E. et al. Carbonates from the lower part of transition zone or even lower mantle. Earth Planet. Sci. Lett. 260, 1–9 (2007). [Google Scholar]
- Thomson A. R. et al. Origin of sub-lithospheric diamonds from the Juina-5 kimberlite (Brazil): constraints from carbon isotopes and inclusions compositions. Contrib. Mineral. Petrol. 168, 6 (2014). [Google Scholar]
- Kaminsky F. Mineralogy of the lower mantle: a review of ‘superdeep' mineral inclusions in diamond. Earth Sci. Rev. 110, 127–147 (2012). [Google Scholar]
- Merlini M. et al. Structures of dolomite at ultrahigh pressure and their influence on the deep carbon cycle. Proc. Natl Acad. Sci. USA 109, 13509–13514 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ono S., Kikegawa T. & Ohishi Y. High-pressure transition of CaCO3. Am. Mineral. 92, 1246–1249 (2007). [Google Scholar]
- Isshiki M. et al. Stability of magnesite and its high-pressure form in the lowermost mantle. Nature 427, 60–63 (2004). [DOI] [PubMed] [Google Scholar]
- Boulard E. et al. Experimental investigation of the stability of Fe-rich carbonates in the lower mantle. J. Geophys. Res. 117, B02208 (2012). [Google Scholar]
- Liu J., Lin J.-F. & Prakapenka V. High-pressure orthorhombic ferromagnesite as a potential deep-mantle carbon carrier. Sci. Rep. 5, 7640 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stagno V. et al. The stability of magnesite in the transition zone and the lower mantle as function of oxygen fugacity. Geophys. Res. Lett. 38, L19309 (2011). [Google Scholar]
- Rohrbach A. & Schmidt M. W. Redox freezing and melting in the Earth's deep mantle resulting from carbon-iron redox coupling. Nature 472, 209–212 (2011). [DOI] [PubMed] [Google Scholar]
- Boulard E. et al. New host for carbon in the deep Earth. Proc. Natl Acad. Sci. USA 108, 5184–5187 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavina B. et al. Siderite at lower mantle conditions and the effects of the pressure-induced spin-pairing transition. Geophys. Res. Lett. 36, L2330 (2009). [Google Scholar]
- Lobanov S. S., Goncharov A. F. & Litasov K. D. Optical properties of siderite (FeCO3) across the spin transition: crossover to iron-rich carbonates in the lower mantle. Am. Mineral. 100, 1059–1064 (2015). [Google Scholar]
- Lobanov S. S., Holtgrewe N. & Goncharov A. F. Reduced radiative conductivity of low spin FeO6-octahedra in FeCO3 at high pressure and temperature. Earth Planet. Sci. Lett. 449, 20–25 (2016). [Google Scholar]
- Cerantola V. et al. High-pressure spectroscopic study of siderite (FeCO3) with focus on spin crossover. Am. Mineral. 100, 2670–2681 (2015). [Google Scholar]
- Lin J.-F. et al. Vibrational and elastic properties of ferromagnesite across the electronic spin-pairing transition of iron. Am. Mineral. 97, 583–591 (2012). [Google Scholar]
- Liu J. et al. Thermal equation of state and spin transition of magnesiosiderite at high pressure and temperature. Am. Mineral. 99, 84–93 (2014). [Google Scholar]
- McCammon C. The paradox of mantle redox. Science 308, 807–808 (2005). [DOI] [PubMed] [Google Scholar]
- Merlini M. et al. The crystal structures of Mg2Fe2C4O13, with tetrahedrally coordinated carbon, and Fe13O19, synthesized at deep mantle conditions. Am. Mineral. 100, 2001–2004 (2015). [Google Scholar]
- Lasaga A. & Gibbs G. V. Applications of quantum mechanical potential surfaces to mineral physics calculations. Phys. Chem. Minerals 14, 107–117 (1987). [Google Scholar]
- Bykova E. et al. Structural complexity of simple Fe2O3 at high pressures and temperatures. Nat. Commun. 7, 10661 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ovsyannikov S. et al. Charge-ordering transition in iron oxide Fe4O5 involving competing dimer and trimer formation. Nat. Chem. 8, 501–508 (2016). [DOI] [PubMed] [Google Scholar]
- Wierzbicka-Wieczorek M., Kolitsch U. & Tillmanns E. Ba2Gd2(Si4O13): a silicate with finite Si4O13 chains. Acta Cryst. C 66, i29–i32 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao R. et al. Experimental determination of siderite stability at high pressure. Am. Mineral. 98, 1565–1572 (2013). [Google Scholar]
- Kang N. et al. Melting of siderite to 20 GPa and thermodynamic properties of FeCO3-melt. Chem. Geol. 400, 34–43 (2015). [Google Scholar]
- Dubrovinsky L. S. et al. The structure of the metallic high-pressure Fe3O4 polymorph: experimental and theoretical study. J. Phys. Condens. Matter 15, 7697–7706 (2003). [Google Scholar]
- Solopova N. A. et al. Melting and decomposition of MgCO3 at pressures up to 84 GPa. Phys. Chem. Miner 42, 73–81 (2014). [Google Scholar]
- Müler U. Inorganic Structural Chemistry Wiley (2007). [Google Scholar]
- Oganov A. R., Glass C. W. & Ono S. High-pressure phases of CaCO3: Crystal structure prediction and experiment. Earth Planet. Sci. Lett. 241, 95–103 (2006). [Google Scholar]
- Skorodumova N. V., Belonoshko A. B., Huang L., Ahuja R. & Johansson B. Stability of the MgCO3 structures underlower mantle conditions. Am. Mineral. 90, 1008–1012 (2005). [Google Scholar]
- Oganov A. R., Ono S., Ma Y. M., Glass C. W. & Garcia A. Novel high-pressure structures of MgCO3, CaCO3 and CO2 and their role in earth’s lower mantle. Earth Planet. Sci. Lett. 273, 38–47 (2008). [Google Scholar]
- Bouibes A. & Zaoui A. High-pressure polymorphs of ZnCO3: evolutionary crystal structure prediction. Sci. Rep. 4, 5172 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oganov A. R. et al. Structure, bonding, and mineralogy of carbon at extreme conditions. Rev. Mineral. Geochem. 75, 47–77 (2013). [Google Scholar]
- Boulard E., Pan D., Galli G., Liu Z. & Mao W. Tetrahedrally coordinated carbonates in Earth’s lower mantle. Nat. Commun. 6, 631 (2015). [DOI] [PubMed] [Google Scholar]
- Merlini M., Hanfland M. & Gemmi M. The MnCO3-II high-pressure polymorph of rhodocrosite. Am. Mineral. 100, 2625–2630 (2015). [Google Scholar]
- Nakatsuka A. et al. Static disorders of atoms and experimental determination of Debye temperature in pyrope: low- and high-temperature single-crystal X-ray diffraction study. Am. Mineral. 96, 1593–1605 (2011). [Google Scholar]
- Dewaele A., Datchi F., Loubeyre P. & Mezouar M. High pressure–high temperature equations of state of neon and diamond. Phys. Rev. B 77, 094106 (2011). [Google Scholar]
- Hu Q. et al. FeO2 and FeOOH under deep lower-mantle conditions and Earth’s oxygen–hydrogen cycles. Nature 534, 241–244 (2016). [DOI] [PubMed] [Google Scholar]
- Syracuse E. M. et al. The global range of subduction zone thermal models. Phys. Earth Planet. Inter. 183, 73–90 (2010). [Google Scholar]
- Komabayashi T., Omori S., Hirose K. & Maruyama S. On the slab temperature in the deep lower mantle. AGU, Spring Meeting, abstract #DI11B-02, 2009AGUSMDI11B..02K (2009).
- Kantor I. Y. U. et al. Spin crossover in (Mg,Fe)O: a Mössbauer effect study with an alternative interpretation of x-ray emission spectroscopy data. Phys. Rev. B 73, 100101 (2006). [Google Scholar]
- Kupenko I. et al. Oxidation state of the lower mantle: in situ observations of the iron electronic configuration in bridgmanite at extreme conditions. Earth Planet. Sci. Lett. 423, 78–86 (2015). [Google Scholar]
- Kantor I. et al. BX90: a new diamond anvil cell design for X-ray diffraction and optical measurements. Rev. Sci. Instrum. 83, 125102 (2012). [DOI] [PubMed] [Google Scholar]
- Kupenko I. et al. Portable double-sided laser-heating system for Mössbauer spectroscopy and X-ray diffraction experiments at synchrotron facilities with diamond anvil cells. Rev. Sci. Instrum. 83, 124501 (2012). [DOI] [PubMed] [Google Scholar]
- Fei Y. et al. Toward an internally consistent pressure scale. Proc. Natl Acad. Sci. USA 104, 9182 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammersley A. P. FIT2D: An Introduction and Overview. ESRF Internal Report ESRF Internal Report, ESRF97HA02T (1997).
- Larson A. C. & Von Dreele R. B. General Structure Analysis System (GSAS). Los Alamos National Laboratory Report, LAUR 86-748 (2000).
- Toby B. H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 34, 210–213 (2001). [Google Scholar]
- CrysAlisPro Software system. Version 1.171.37.35. (Agilent Technologies Ltd, Yarnton, Oxfordshire, England, 2014).
- Sheldrick G. M. A short history of SHELX. Acta Crystallogr. A 64, 112–122 (2008). [DOI] [PubMed] [Google Scholar]
- Rüffer R. & Chumakov A. I. Nuclear-resonance beamline at ESRF. Hyperfine Interact. 97, 589–604 (1996). [Google Scholar]
- Potapkin V. et al. The 57Fe synchrotron Mössbauer source at the ESRF. J. Synchrotron Radiat. 19, 559–569 (2012). [DOI] [PubMed] [Google Scholar]
- Prescher C., McCammon C. & Dubrovinsky L. MossA: a program for analyzing energy-domain Mössbauer spectra from conventional and synchrotron sources. J. Appl. Crystallogr. 45, 329–331 (2012). [Google Scholar]
- Katsura T., Yoneda A., Yamazaki D., Yoshino T. & Ito E. Adiabatic temperature profile in the mantle. Phys. Earth Planet. Inter. 183, 212–218 (2010). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The X-ray crystallographic co-ordinates for structures reported in this article have been deposited at the Inorganic Crystal Structure Database (ICSD) under deposition number CSD 432930-432931. These data can be obtained free of charge from FIZ Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: (+49)7247-808-666; e-mail: crysdata@fiz-karlsruhe.de) through the hyperlink: https://www.fiz-karlsruhe.de/en/leistungen/kristallographie/kristallstrukturdepot/order-form-request-for-deposited-data.html