Variable selection for zero-inflated and overdispersed data with application to health care demand in Germany

Abstract

In health services and outcome research, count outcomes are frequently encountered and often have a large proportion of zeros. The zero-inflated negative binomial (ZINB) regression model has important applications for this type of data. With many possible candidate risk factors, this paper proposes new variable selection methods for the ZINB model. We consider maximum likelihood function plus a penalty including the least absolute shrinkage and selection operator (LASSO), smoothly clipped absolute deviation (SCAD) and minimax concave penalty (MCP). An EM (expectation-maximization) algorithm is proposed for estimating the model parameters and conducting variable selection simultaneously. This algorithm consists of estimating penalized weighted negative binomial models and penalized logistic models via the coordinated descent algorithm. Furthermore, statistical properties including the standard error formulae are provided. A simulation study shows that the new algorithm not only has more accurate or at least comparable estimation, also is more robust than the traditional stepwise variable selection. The proposed methods are applied to analyze the health care demand in Germany using an open-source R package mpath.

1 Introduction

In health services and outcome research, investigators are frequently interested in study outcomes such as visits to a physician in an office or hospital, to an emergency room, and number of inhospital stays (Deb and Trivedi, 1997; Riphahn et al., 2003). These are examples of count data in which the observations can take only the non-negative integer values. Poisson and negative binomial (NB) regression are commonly used to develop predictive models for count data. Because of high frequency of zero values in empirical data, these models may fail to describe the data adequately. In health care demand data, the population may consist of no-demanding healthy individuals who never need to visit the doctor, and usual-demanding and less healthy individuals who may or may not visit the doctor, depending on the health status and other factors. Thus, due to heterogeneous data, there are extra zeros that a single model is not designed to model. To take into account the extra zero observations, the zero-inflated Poisson (ZIP) and NB model (ZINB) have been applied. For instance, see Lambert (1992); Garay et al. (2011). The zero-inflated count model assumes a latent mixture model consisting of a count component and a degenerated zero component which has a unit point mass at zero. The count component can be modeled as a Poisson or NB distribution. For the Poisson distribution, the variance is assumed to be equal to the mean, which may be violated in real data. In contrast, the NB distribution has less constraint than the Poisson distribution. Therefore, the ZINB model is more appropriate to incorporate extra over dispersion not accounted for through zero-inflation by the Poisson model. The ZINB model characterizes the study population into two groups as the no-demanding group corresponding to the zero component, and the usual-demanding group for the count component. For zero-inflated data, alternative models including the hurdle model have been proposed, see Min and Agresti (2005); Alfò and Maruotti (2010). The hurdle model may be considered as a two-stage modeling process. The first stage determines whether the outcome is above or equal to zero. In the second stage, a truncated Poisson or NB model is applied to fit the positive counts. A zero can be produced by only one process in hurdle models, which is contrast to zero-inflated models which assume that a zero can be produced by two different processes.

Zero-inflated count regression may be used to predict health care demand with demographics, social status and other clinical risk factors. For the zero component, the risk factors have effect on probability that an individual has zero-demanding. For the count component, the risk factors have effect on the count outcome, given that the individual is in a usual-demanding group. Among many potential risk factors, researchers are often interested in identifying a small subset. A parsimonious model often offers better interpretation, which will be demonstrated in this paper when analyzing health care demand data. In statistical literature, variable selection is one of the most active research areas. Penalized regression with a variety of penalty function is a popular choice, see, the least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996), smoothly clipped absolute deviation (SCAD) (Fan and Li, 2001) and minimax concave penalty (MCP) (Zhang, 2010). In penalized regression algorithms, a coefficient below some threshold value is set to zero and otherwise will be shrunk towards zero. The LASSO is a convex penalty function which has computational advantages than non-convex penalties MCP and SCAD. The LASSO, however, introduces bias when shrinking large coefficients towards zero. The MCP and SCAD are successful to reduce the bias and have an additional oracle property under some conditions. Namely, the MCP and SCAD performs like there is a prior knowledge on whether a variable has zero or non-zero coefficient.

However, there is a lack of methods in selecting variables in a zero-inflated and overdispersed count data framework, and recent research has focused on penalized ZIP models (Buu et al., 2011; Tang et al., 2014;Wang et al., 2014a). In the current paper, we extend the work in Wang et al. (2014a) to the penalized ZINB model and propose an EM (expectation-maximization) algorithm for the penalties LASSO, MCP and SCAD, respectively. The ZINB model can incorporate additional overdispersion, thereby potentially fitting much better than a ZIP model in real data analysis. Indeed, the penalized ZIP is a special case of the current paper. Our major contribution is that we develop variable selection methods for zero-inflated and overdispersed count data through the penalized ZINB model and implement the EM algorithm into open-source statistical software.

The rest of the paper is organized as follows. Section 2 introduces a penalized ZINB model, and presents statistical properties and estimation methods. A simulation study is conducted in Section 3 to evaluate the proposed methods and compare with competing methods. In Section 4, the proposed methods are applied to a data set of health care demand collected in Germany. In Section 5, software and reproducible research are described. A discussion is provided in Section 6. Some technical details are in the Appendix.

2 Penalized ZINB regression model

In this section, we present new methodologies for penalized ZINB regression models, theoretical properties of estimates, an EM algorithm to estimate parameters, and standard error formulae of estimators.

2.1 Variable selection of ZINB regression model

Consider a ZINB regression model. Assume Y_i, i = 1, …, n has a probability function

$$Pr(Y_i=y_i)=\{\begin{array}{ll}{p}_i+(1-p_i){(\frac{\theta }{{\mu }_i+\theta })}^{\theta },\hfill & \text{if}{y}_i=0\hfill \\ (1-p_i)\frac{\mathrm{\Gamma }(\theta +y_i)}{\mathrm{\Gamma }(y_i+1)\mathrm{\Gamma }(\theta )}{(\frac{{\mu }_i}{{\mu }_i+\theta })}^{y_i}{(\frac{\theta }{{\mu }_i+\theta })}^{\theta },\hfill & \text{if}{y}_i>0,\hfill \end{array}$$

where 0 ≤ p_i ≤ 1,μ_i ≥ 0 and 1/θ is the positive overdispersion parameter. The mean and variance are (1 − p_i)μ_i and $(1-p_i)({\mu }_i+{\mu }_i^2/\theta +p_i{\mu }_i^2)$, respectively. Because the variance can only be larger than the mean, underdispersion cannot be modeled adequately in a ZINB model. When underdispersion occurs, the fitting of a ZINB model typically generates zero-inflated Poisson with a large value of θ. On the other hand, if the data are generated by a ZINB model but are fitted by a NB model, a downward biased estimator of θ is expected to fit the overdispersion. The model is reduced to the NB distribution if p_i = 0. In ZINB regression, assume length q₁ predictor vector x_i and length q₂ vector v_i are associated with μ_i and p_i, respectively. Let $log({\mu }_i)=x_i^T\beta$ and $log(\frac{p_i}{1-p_i})=v_i^T\zeta$ where β = (β₀,β₁, …, β_q1) and ζ = (ζ₀,ζ₁, …, ζ_q2 ) are unknown parameters. Here β₀ and ζ₀ are intercepts. For n independent random samples, let ϕ = (β ^T, θ, ζ ^T )^T, the log-likelihood function is given by

$$\ell (\varphi )=\sum _{y_i=0}log\left[p_i+(1-p_i){(\frac{\theta }{{\mu }_i+\theta })}^{\theta }\right]+\sum _{y_i>0}log\left[(1-p_i)\frac{\mathrm{\Gamma }(\theta +y_i)}{\mathrm{\Gamma }(y_i+1)\mathrm{\Gamma }(\theta )}{(\frac{{\mu }_i}{{\mu }_i+\theta })}^{y_i}{(\frac{\theta }{{\mu }_i+\theta })}^{\theta }\right],$$

where ${\mu }_i=exp(x_i^T\beta )$ and $p_i=\frac{exp(v_i^T\zeta )}{1+exp(v_i^T\zeta )}$.

For variable selection, consider a penalized ZINB model:

$$p\ell (\varphi )=\ell (\varphi )-p(\beta ,\zeta ),$$

where the nonnegative penalty function is given by

$$p(\beta ,\zeta )=n\sum _{j=1}^{q_1}p({\lambda }_{NB};\mid {\beta }_j\mid )+n\sum _{k=1}^{q_2}p({\lambda }_{BI};\mid {\zeta }_k\mid ),$$

with tuning parameters λ_NB and λ_BI determined by data-driven methods. Since intercepts and scaling parameter θ are always included in the model, they are not penalized. The following three penalty functions are investigated:

1. the LASSO penalty (Tibshirani, 1996), for λ ≥ 0, p(λ ; |ξ|) =λ |ξ |.

2. the MCP penalty (Zhang, 2010), for λ ≥ 0 and γ > 1, the derivative of p(λ ;ξ ) with respect to ξ is given by p′(λ ;ξ ) = (λ –ξ/γ )I(ξ ≤γλ), where I(·) is an indicator function.

3. the SCAD penalty (Fan and Li, 2001) $p^{\prime }(\lambda ,\xi )=\lambda \left\{I(\xi <\lambda )+\frac{{(\gamma \lambda -\xi )}_{+}}{(\gamma -1)\lambda }I(\xi >\lambda )\right\}$ for λ ≥ 0 and γ > 2, where t₊ denotes the positive part of t.

The oracle properties of penalized ZINB models can be established, see Appendices A and B. These results are direct applications of the respective theorems in Fan and Li (2001). Therefore, if λ_NB,n → 0,λ_BI,n →0, $\sqrt{n}{\lambda }_{NB,n}\to \infty$ and $\sqrt{n}{\lambda }_{BI,n}\to \infty$, then the ZINB-MCP and ZINB-SCAD estimators hold the oracle property: with probability tending to 1, the estimate of coefficients without an effect is 0, and the estimate for coefficients with an effect has an asymptotic normal distribution with mean being the true value of nonzero coefficient and variance being the submatrix of the Fisher information matrix corresponding to the nonzero coefficients.

2.2 The EM algorithm

Let z_i = 1 if Y_i is from the zero state and z_i = 0 if Y_i is from the NB state. Since z = (z₁, …, z_n)^T is not observable, it is often treated as missing data. The EM algorithm is particularly attractive to missing data problems. If complete data (Y_i, z_i) are available, the complete-data penalized log-likelihood function is given by

$$p{\ell }_c(\varphi )=\sum _{i=1}^n\{(z_i{v}_i\zeta -log(1+exp(v_i\zeta ))+(1-z_i)log(f(y_i;\beta ,\theta ))\}-p(\beta ,\zeta ),$$

where $f(y_i;\beta ,\theta )=\frac{\mathrm{\Gamma }(\theta +y_i)}{\mathrm{\Gamma }(y_i+1)\mathrm{\Gamma }(\theta )}{(\frac{{\mu }_i}{{\mu }_i+\theta })}^{y_i}{(\frac{\theta }{{\mu }_i+\theta })}^{\theta }$, with ${\mu }_i=exp(x_i^T\beta )$. The EM algorithm computes the expectation of the complete-data log-likelihood, which is linear in z. Thus, the E-step simplifies to update z by its conditional expectation given the observed data and previous parameter estimates. Specifically, the conditional expectation of z at iteration m is provided by

$${\widehat{z}}_i^{(m)}=\{\begin{array}{ll}{\left(1+exp(-v_i{\widehat{\zeta }}^{(m)}){\left[\frac{{\widehat{\theta }}^{(m)}}{exp(x_i{\widehat{\beta }}^{(m)})+{\widehat{\theta }}^{(m)}}\right]}^{{\widehat{\theta }}^{(m)}}\right)}^{-1},\hfill & \text{if}{y}_i=0\hfill \\ 0,\hfill & \text{if}{y}_i>0.\hfill \end{array}$$

Therefore, the expectation of the complete-data log-likelihood can be calculated:

$$Q(\varphi \mid {\widehat{\varphi }}^{(m)})=E(p{\ell }_c(\varphi \mid y,z)\mid y,{\widehat{\varphi }}^{(m)})=Q_1(\beta ,\theta \mid {\widehat{\varphi }}^{(m)}+Q_2(\zeta \mid {\widehat{\varphi }}^{(m)}),$$

where

$$\begin{array}{l}{Q}_1(\beta ,\theta \mid {\widehat{\varphi }}^{(m)}=\sum _{i=1}^n(1-{\widehat{z}}_i^{(m)})logf(y_i,\beta ,\theta )-n\sum _{j=1}^{q_1}p({\lambda }_{NB},\mid {\beta }_j\mid )\\ Q_2(\zeta \mid {\widehat{\varphi }}^{(m)})=\sum _{i=1}^n{\widehat{z}}_i^{(m)}{v}_i\zeta -log(1+exp(v_i\zeta ))-n\sum _{k=1}^{q_2}p({\lambda }_{BI},\mid {\zeta }_k\mid )\end{array}$$

Next, the EM algorithm updates the estimates by maximizing Q(ϕ | ϕ̂^(m)), which is handy since (β, θ ) and ζ are in two disjoint terms. The first term, Q₁(β, θ | ϕ̂^(m) is a weighted penalized NB log-likelihood function and the second term Q₂(ζ | ϕ̂^(m)) is a penalized logistic log-likelihood function. The coordinate descent algorithm has been proposed to optimize generalized linear models (Friedman et al., 2010; Breheny and Huang, 2011; Wang et al., 2014b). The EM iterations are repeated for the E-step and M-step until convergency.

In Wang et al. (2014a), the coordinate descent algorithm adaptively rescales a shrinkage parameter for the nonconcave MCP and SCAD penalties (Breheny and Huang, 2011). While this strategy may help select tuning parameters, the EM algorithm can be substantially slow to converge for the penalized ZINB model. This is because the adaptive rescaling violates the non-decreasing property of the EM algorithm and estimating the dispersion parameter θ further complicates the algorithm. In this paper, the proposed algorithm avoids the adaptive rescaling, leading to much improved computing efficiency.

2.3 Selection of tuning parameters

The penalty parameters (λ_NB,λ_BI) can be determined based on the BIC (Schwarz, 1978):

$$\text{BIC}=-2\ell (\widehat{\varphi };{\lambda }_{NB},{\lambda }_{BI})+log(n)\text{df},$$

where ϕ̂ are the estimated parameters, (λ_NB,λ_BI) are tuning parameters, and ℓ(·) is the log-likelihood function. The degrees of freedom are given by df = Σ_j=0,…,q1 1{β _j ≠ 0}+Σ_k=0,…,q2 1{ζ_k ≠ 0}+1, which includes the degree of freedom for the scaling parameter θ. We first construct a solution path based on the paired shrinkage parameters. To begin with, the algorithm generates two decreasing sequences ${\lambda }_{NB}^{(1)}>{\lambda }_{NB}^{(2)}\dots >{\lambda }_{NB}^{(M)}$ and ${\lambda }_{BI}^{(1)}>{\lambda }_{BI}^{(2)}\dots >{\lambda }_{BI}^{(M)}$. Then, we pair the sequences: $({\lambda }_{NB}^{(1)},{\lambda }_{BI}^{(1)}),\dots ,({\lambda }_{NB}^{(M)},{\lambda }_{BI}^{(M)})$. In principle, large values ( ${\lambda }_{NB}^{(1)},{\lambda }_{BI}^{(1)}$) can be chosen such that all the coefficients are zeros except the intercepts. A refined method suggests that the smallest values ( ${\lambda }_{NB}^{(1)},{\lambda }_{BI}^{(1)}$) can be calculated from data for the LASSO penalty (Wang et al., 2014a). For other penalties, we follow the same strategy.

2.4 Standard error formula

Wang et al. (2014a) used the computational demanding bootstrap procedure to estimate standard errors for the penalized ZIP model. In this paper, we establish standard error formulae for the penalized ZINB models. A sandwich formula can be used as an estimator of the covariance of the non-zero estimates ϕ₁ = (β₁,ζ₁) (Fan and Li, 2001; Fan and Peng, 2004):

$$\widehat{cov}({\varphi }_1)={\{{\nabla }^2\ell ({\widehat{\varphi }}_1)+n\mathrm{\sum }({\widehat{\varphi }}_1;{\lambda }_{NB},{\lambda }_{BI})\}}^{-1}\widehat{cov}\nabla ({\varphi }_1){\{{\nabla }^2\ell ({\widehat{\varphi }}_1)+n\mathrm{\sum }({\widehat{\varphi }}_1;{\lambda }_{NB},{\lambda }_{BI})\}}^{-1},$$ (1)

where

$$\begin{array}{ll}\hfill \widehat{cov}\nabla ({\varphi }_1)& =\frac{1}{n}\sum _{i=1}^n{\nabla }_i({\varphi }_i){\nabla }_i{({\varphi }_i)}^{\top }-\left\{\frac{1}{n}\sum _{i=1}^n{\nabla }_i({\varphi }_1)\right\}{\left\{\frac{1}{n}\sum _{i=1}^n{\nabla }_i({\varphi }_1)\right\}}^{\top },\hfill \\ \hfill \nabla \ell ({\varphi }_1)& =\frac{\partial \ell ({\varphi }_1)}{\partial {\varphi }_1},{\nabla }^2\ell ({\varphi }_1)=\frac{{\partial }^2\ell ({\varphi }_1)}{\partial {\varphi }_1\partial {\varphi }_1^{\top }},\hfill \end{array}$$

where Σ(·) is defined in Appendix B. For the ZINB regression model, the elements of ∇²ℓ(ϕ₁) are provided in Appendix C. It is worth noting that most of the results in Appendix C are different from Garay et al. (2011). Indeed there is a mistake in the log-likelihood function presented in that paper.

3 A simulation study

We investigate performance of the proposed methods with sample size n = 300,100 and 20 predictors in both count and zero components (q₁ = q₂ = 20) in the simulation study. The predictor variables were randomly drawn from multivariate normal distributions N₂₀(0,Σ), where Σ has elements ρ ^|i−j|(i, j =1, …, 20). The correlation among predictor variables was fixed at ρ = 0.4 and 0.8, respectively. The predictor variables are the same for the count and zero components. We set θ = 2 or 10 for the scaling parameter of the NB distribution. There were 100 replications for each set of parameters described below. These parameters were chosen to have a different number of effective predictors and different levels of zero inflation.

1. In example 1, set the parameters

   β = (1.10, 0, 0, 0, −0.36, 0, 0, 0, 0, 0, 0, 0, 0, −0.32, 0, 0, 0, 0, 0, 0, 0)

   ζ = (0.30, −0.48, 0, 0, 0, 0.4, 0, 0, 0, 0, 0.44, 0, 0.44, 0, 0, 0, 0, 0, 0, 0, 0).

   The zero inflation is about 55%.

2. In example 2, we kept all elements of β in example 1 and only changed the first element of ζ from 0.30 to −1.20, which has about 25% zero inflation.

3. In example 3, we remained all elements of β in example 1 and changed the first element of ζ from 0.30 to −0.35, leading to about 43% zero inflation.

4. In example 4, we doubled the number of ineffective predictors from the above examples, and the parameters were set to obtain about 29% zero inflation:

   β =(1.50, 0, 0, 0, −0.22, 0, 0, 0, −0.25, 0, 0.20, 0, 0.30, −0.32, 0, 0, 0, 0.20, 0, 0, 0)

   ζ =(−1.05, 0, 0.45, 0, −0.3, 0, 0, 0, 0, 0, −0.33, 0, −0.39, 0, 0, 0.3, 0, 0, 0, 0.36, 0).

5. In example 5, the parameters were set to obtain about 21% zero inflation:

   β = (2.20, 0, 0, 0, −0.72, 0, 0, 0, 0, 0, 0, 0, 0, −0.64, 0, 0, 0, 0, 0, 0, 0)

   ζ = (−2, −0.96, 0, 0, 0, 0.8, 0, 0, 0, 0, 0.88, 0, 0.88, 0, 0, 0, 0, 0, 0, 0, 0).

   The effective predictors were dichotomized at median values, and ineffective variables remained continuous.

Statistical methods evaluated are penalized NB regression, penalized ZINB regression, a backward stepwise elimination (BE) procedure for significance levels α = 0.1573,0.05,0.01 following Sauerbrei et al. (2008), and an oracle ZINB model assuming the true non-zero coefficients are known. In a BE(α) procedure, insignificant variables are removed from a full ZINB model (including all predictor variables in the NB and zero component), then a model is refit with the remaining predictors. This procedure is repeated until all variables are significant based on the α level. Estimation accuracy is measured by ratio of mean squared error of parameters (MSE) between a specific model and the full ZINB model. To evaluate performance of variable selection, we calculated sensitivity (proportion of correctly identified number of non-zero coefficients) and specificity (proportion of correctly identified number of zero coefficients). To compare prediction accuracy, we generated the same number of test observations as the training data from each model, and computed the log-likelihood values using the parameters estimated from the training data. Finally, we evaluated accuracy of the proposed standard error formulae.

Estimation and variable selection results are summarized in Tables 1–4 and the Supporting Information, where bold fonts indicate the best values among the competitive models (excluding the oracle models). We first focus on the results with n = 300,ρ = 0.4 and θ = 2. It is clear that the penalized zero-inflated NB models have better performance than their counterparts which ignore zero-inflation. The estimates of ZINB models have smaller MSEs, larger sensitivity and specificity, and have more accurate scaling parameter θ̂. Due to zero-inflation, a smaller estimate of θ was typically obtained in the NB models in an effort to capture this extra variability. Within the penalized ZINB models, the LASSO estimates can be less accurate in the NB component but are more comparable in the zero component; however, there is no universal winner on variable selection. The BE procedure is sensitive to the choice of the significance level α. For a large α value, the BE procedure keeps more predictor variables with increased sensitivity. For a small α value, more variables are eliminated to increase specificity. It would be interesting to determine an optimal value of α so that there is a trade-off between sensitivity and specificity. However, it appears that even a small change of α value can select variables quite differently. In comparison, the penalized ZINB models provide comparable solutions to the BE procedure, if not better. Specifically, in example 1, excluding the oracle model, ZINB-MCP has the most accurate parameter estimation with smallest MSEs in both the NB and zero components. Reducing zero-inflation as in examples 2 and 3, variable selection was more accurate in the NB component. In example 4 and 5, ZINB-MCP and ZINB-SCAD are highly competitive to existing methods. In all examples, ZINB-MCP and ZINB-SCAD have good performance on variable selection in the NB components. Effective predictors are correctly selected most of the time, ranging from 85%–96% of sensitivity while variables having no effect are correctly eliminated in a high probability (more than 96%).

Table 1.

Simulation results with example 1, ρ = 0.4,θ = 2,n = 300. Median and robust standard deviations (in parentheses) of the MSE ratio between the penalized model and full model, and the estimated θ. Mean and standard deviations of sensitivity and specificity.

Method	MSE	Sensitivity	Specificity	θ̂
NB component
NB-LASSO	2.529 (1.434)	0.559 (0.427)	0.895 (0.123)	0.277 (0.067)
NB-MCP	3.514 (2.149)	0.713 (0.355)	0.869 (0.093)	0.309 (0.059)
NB-SCAD	3.434 (1.991)	0.644 (0.392)	0.854 (0.129)	0.304 (0.067)
ZINB-LASSO	0.243 (0.202)	0.862 (0.278)	0.924 (0.087)	2.229 (0.784)
ZINB-MCP	0.1 (0.133)	0.846 (0.243)	0.974 (0.048)	2.286 (0.868)
ZINB-SCAD	0.167 (0.214)	0.856 (0.239)	0.958 (0.056)	2.119 (0.881)
BE(0.1573)	0.614 (0.279)	0.956 (0.161)	0.748 (0.129)	3.138 (1.46)
BE(0.05)	0.404 (0.353)	0.918 (0.201)	0.879 (0.113)	2.666 (1.136)
BE(0.01)	0.177 (0.235)	0.824 (0.273)	0.968 (0.053)	2.207 (0.86)
ZINB-ORACLE	0.042 (0.042)	1 (0)	1 (0)	2.127 (0.759)
Zero component
ZINB-LASSO	0.381 (0.343)	0.614 (0.306)	0.973 (0.043)
ZINB-MCP	0.327 (0.282)	0.745 (0.201)	0.938 (0.09)
ZINB-SCAD	0.382 (0.316)	0.59 (0.234)	0.981 (0.036)
BE(0.1573)	0.607 (0.24)	0.83 (0.174)	0.788 (0.134)
BE(0.05)	0.406 (0.319)	0.731 (0.212)	0.922 (0.085)
BE(0.01)	0.403 (0.308)	0.58 (0.241)	0.987 (0.029)
ZINB-ORACLE	0.119 (0.091)	1 (0)	1 (0)

Table 4.

Mean and standard deviations (in parentheses) of the predictive log-likelihood values with ρ = 0.4,θ = 2,n = 300.

	example 1	example 2	example 3	example 4	example 5
NB-LASSO	−452.5 (28.3)	−608.2 (20.1)	−533.4 (26)	−705.2 (26.1)	−712.5 (18.5)
NB-MCP	−450.5 (27.9)	−606.4 (19.8)	−532.3 (25.6)	−701.2 (24.4)	−710.5 (18.6)
NB-SCAD	−453.1 (28.7)	−606.9 (20)	−533.2 (25.7)	−702.1 (25.2)	−711 (18.8)
ZINB-LASSO	−438 (29.3)	−601.4 (22.4)	−519.8 (26.8)	−691.5 (26.6)	−695.5 (20.4)
ZINB-MCP	−435.4 (29.4)	−607.4 (49.5)	−516.6 (27.1)	−689.4 (24.7)	−696.4 (20.7)
ZINB-SCAD	−437.1 (28.9)	−605 (50.9)	−519 (26.7)	−689.8 (24.7)	−693.7 (21)
BE(0.1573)	−453.3 (35)	−616.3 (29.2)	−529.8 (30.6)	−692.8 (26.3)	−705.9 (23.2)
BE(0.05)	−444.7 (31.9)	−605 (26)	−520.8 (29)	−689.2 (25.1)	−698.7 (22.4)
BE(0.01)	−438.5 (29.7)	−601.7 (23.2)	−519.1 (27.2)	−689.5 (24.3)	−695.8 (19.9)
ZINB-ORACLE	−425.3 (27.1)	−591.9 (22.2)	−508.6 (26.3)	−675.8 (23)	−686 (19.3)

Determining predictors in zero components is more difficult than determining predictors in the count components (Buu et al., 2011; Wang et al., 2014a; Jochmann, 2013). Sensitivities for the zero components are typically lower than the corresponding sensitivities for the NB components. As argued in Jochmann (2013), this is to be anticipated since the data generally are not very informative about the hidden components of the observations.

Table 4 reports the predictive log-likelihood values. The penalized ZINB models have better prediction than the penalized NB models, and are better or comparable to the BE procedure. ZINB-MCP has the most accurate prediction in example 1 and 3 and ZINB-LASSO is the best in example 2. In examples 4 and 5, ZINB-MCP and ZINB-SCAD have best prediction or are comparable to BE.

With increased correlation from ρ =0.4 to 0.8, variable selection becomes more challenging. In general, sensitivity and specificity are decreased in all variable selection methods. However, the penalized ZINB models have the smallest MSEs in all examples with n=300. With increased scaling parameter from θ =2 to 10, the variance of the ZINB model decreases. As expected, variable selection methods have improved performances while the penalized ZINB models have the smallest or nearly the smallest MSEs. When the sample size decreases from n=300 to n=100, the performance of the variable selection methods becomes worse. Similar conclusions hold for ZIP models with small sample sizes (Buu et al., 2011; Wang et al., 2014a). It should be pointed out that the ZINB model is more complex than the ZIP model. Therefore, variable selection of ZINB models may perform inferior to the ZIP models with comparable sample sizes.

Next we evaluate the standard error formulae. For non-zero coefficient estimates with example 1, we computed the median absolute deviation divided by 0.6745, denoted by SD in Table 5. The SD can be treated as the true standard error. The median of estimated standard errors using formula (1), denoted by SE, and the median absolute deviation of estimated standard errors divided by 0.6745 in the parentheses (std(SE)), are used to compare with SD. Due to space limitation, only a handful coefficients are displayed for example 1 while similar conclusions hold in other examples. The standard error formulae performs reasonably well as the differences between SD and SE are within twice std(SE). While the estimated standard error can underestimate the true SD (Hunter and Li, 2005), it is less severe when compared with the robust standard errors for the oracle estimators.

Table 5.

Standard deviations of estimators with example 1, ρ = 0.4,θ = 2,n = 300.

	β̂4		β̂13		ζ̂1
	SD	SE	SD	SE	SD	SE
	ZINB-LASSO	0.119	0.089 (0.022)	0.113	0.089 (0.021)	0.143	0.13 (0.01)
ZINB-MCP	0.1	0.086 (0.023)	0.096	0.085 (0.023)	0.227	0.168 (0.029)
ZINB-SCAD	0.127	0.086 (0.024)	0.109	0.085 (0.021)	0.226	0.168 (0.035)
ZINB-ORACLE	0.131	0.087 (0.019)	0.123	0.085 (0.023)	0.259	0.166 (0.034)

The proposed algorithm for fitting penalized ZINB appears to be stable, which is contrast to the BE procedure. In a typical algorithm to fit the ZINB model, the Newton-Raphson method requires to invert the Hessian matrix. The inverted Hessian can be numerically unstable and the solution may diverge. For instance, when estimating the full ZINB model in example 2 with ρ = 0.4,θ = 2,n = 300, the Newton-Raphson method failed in 41 out of 141 (30%) simulated data sets. As a consequence, the BE procedure could not be implemented for the 41 data sets. For the remaining 100 data sets, even though the full ZINB model was successfully estimated, the BE procedure still failed five times. Such a phenomenon is not unique to example 2, and can be more severe when the number of predictor increases, or the sample size decreases.

4 Health care demand

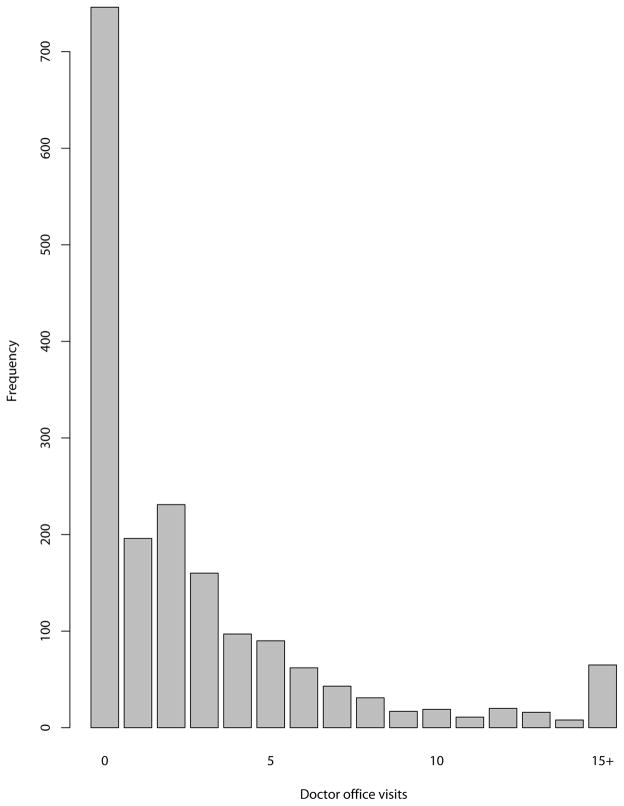
Riphahn et al. (2003) utilized a part of the German Socioeconomic Panel (GSOEP) data set to analyze the number of doctor visits and the number of hospital visits. The original data have twelve annual waves from 1984 to 1995 for a representative sample of German households, which provide broad information on the health care utilization, current employment status, and the insurance arrangements under which subjects are protected. The German health insurance system provides almost complete coverage of the population. Those low-income individuals are required to have health insurance by a law except for civil servants and the self-employed, who along with high-income persons can choose to remain uninsured, to sign up one of the mandatory health insurances, a private insurance, or a combination of two. Consequently, the employment characteristics were thought to be linked with health care demand. The data set contains number of doctor office visits for 1,812 West German men aged 25 to 65 years in the last three months of 1994. As shown in Figure 1, many doctor office visits are zeros, which can be difficult to fit with a Poisson or NB model.

Figure 1.

Empirical distribution of number of doctor office visits

We focus on zero-inflated models and alternative models may be found in Riphahn et al. (2003); Jochmann (2013). The predictor variables are illustrated in Table 6. This data set was recently analyzed using a Bayesian variable selection procedure (Jochmann, 2013). Following Jochmann (2013), instead of the original variable age and its square, we study more complex effect of age. Namely, we include the linear spline variables age30 to age60 and their interaction terms with the health satisfaction health (for instance health:age30). We estimate the following three models: the full ZINB model, models selected by the BE procedure and the penalized ZINB models. Other penalized count data regression models were evaluated and discussed below, although not included in Table 7. Among α = 0.1573,0.05,0.01, BE(0.01) produces the most parsimonious model with the smallest BIC value. The results are given in Table 7.

Table 6.

Variable descriptions

Variable	Description
health	health satisfaction, 0 (low) – 10 (high)
handicap	1 if handicapped, 0 otherwise
hdegree	degree of handicap in percentage points
married	1 if married, 0 otherwise
schooling	years of schooling
hhincome	household monthly net income, in German marks/1000
children	1 if children under 16 in the household, 0 otherwise
self	1 if self employed, 0 otherwise
civil	1 if civil servant, 0 otherwise
bluec	1 if blue collar employee, 0 otherwise
employed	1 if employed, 0 otherwise
public	1 if public health insurance, 0 otherwise
addon	1 if add-on insurance, 0 otherwise
age30	1 if age >= 30
age35	1 if age >= 35
age40	1 if age >= 40
age45	1 if age >= 45
age50	1 if age >= 50
age55	1 if age >= 55
age60	1 if age >= 60

Table 7.

ZINB models on doctor office visits. The estimated coefficients with standard errors in parentheses, log-likelihood (logLik), log-likelihood by cross-validation (logLik-CV), BIC and AIC values.

	ZINB	BE(0.01)	ZINB-LASSO	ZINB-MCP	ZINB-SCAD
NB component
(Intercept)	2.41(0.32)	2.57(0.12)	2.31(0.15)	2.49(0.12)	2.10(0.15)
health	−0.16(0.03)	−0.20(0.02)	−0.17(0.02)	−0.20(0.02)	−0.19(0.02)
handicap	0.27(0.22)	0.30(0.09)	0.16(0.10)	0.23(0.10)	0.26(0.10)
hdegree	−0.002(0.005)
married	−0.15(0.11)
schooling	−0.005(0.01)
hhincome	0.004(0.02)
children	0.02(0.09)
self	−0.36(0.19)	−0.37(0.13)		−0.37(0.12)
civil	−0.27(0.16)	−0.34(0.12)		−0.33(0.12)
bluec	0.10(0.10)
employed	−0.09(0.11)
public	−0.01(0.14)		0.06(0.09)		0.31(0.09)
addon	0.36(0.30)
age30	0.09(0.35)
age35	−0.25(0.35)
age40	0.05(0.36)
age45	0.72(0.43)
age50	0.20(0.41)		0.04(0.10)		0.22(0.07)
age55	−0.52(0.33)		0.10(0.11)	0.21(0.09)
age60	0.40(0.33)
health:age30	−0.01(0.05)
health:age35	0.04(0.05)
health:age40	−0.02(0.06)
health:age45	−0.10(0.07)
health:age50	−0.02(0.06)
health:age55	0.13(0.06)
health:age60	−0.10(0.06)
θ̂	1.38(0.12)	1.27(0.11)	1.37(0.13)	1.27(0.13)	1.25(0.13)
Zero component
(Intercept)	−2.31(0.99)	−2.98(0.38)	−2.70(0.29)	−3.35(0.41)	−3.62(0.41)
health	0.23(0.10)	0.30(0.04)	0.25(0.03)	0.32(0.05)	0.34(0.04)
handicap	−0.33(0.79)
hdegree	−0.002(0.02)
married	−0.40(0.27)
schooling	0.02(0.04)
hhincome	−0.04(0.04)
children	0.51(0.25)		0.20(0.15)	0.43(0.18)	0.52(0.18)
self	−0.25(0.65)
civil	0.02(0.42)
bluec	0.02(0.24)
employed	−0.08(0.32)
public	−0.23(0.39)
addon	0.30(0.53)
age30	−1.68(1.32)
age35	0.90(1.41)
age40	−0.65(1.33)
age45	3.00(1.05)				−0.33(0.20)
age50	−2.96(1.35)	−1.00(0.28)	−0.40(0.18)	−0.67(0.25)
age55	0.34(1.36)
age60	−2.34(2.76)
health:age30	0.23(0.16)
health:age35	−0.11(0.17)
health:age40	0.12(0.17)
health:age45	−0.41(0.14)
health:age50	0.25(0.17)
health:age55	0.11(0.18)
health:age60	0.20(0.35)
Summary
logLik	−3625.9	−3656.3	−3664.5	−3648.8	−3654.7
BIC	7679.5	7380	7411.6	7380.2	7384.3
AIC	7365.9	7330.5	7351.1	7319.7	7329.3
logLik-CV	−370.6	−368.7	−368.5	−368.0	−368.7

The results indicate more utilization of health care from the publicly issued than from privately issued. The mean doctor visits are 2.74 and 1.90, respectively. ZINB-LASSO and ZINB-SCAD generated positive coefficient estimates for variable public in the NB component, consistent with Riphahn et al. (2003); Jochmann (2013). The data show higher health care utilization for the aged and handicapped. ZINB-LASSO and ZINB-MCP both have positive coefficients on age55 in the NB component. However, the estimate for the full ZINB model is −0.52, which needs caution when interpreting the results. Notice that BE(0.01) is not able to select public or an age variable. For self, the ZINB-MCP and BE(0.01) estimates are −0.37, close to the estimate −0.356 in (Riphahn et al., 2003). Accordingly, the estimate suggests that a self-employed individual visits doctor about 31% less often than not self-employed, which confirms incentive effects in the health care demand. Those self-employed were lack of any financial compensation when visiting a doctor. In the ZINB-MCP model, age55 and age50 are chosen in the NB and zero components, respectively. Thus, males being 50 or older are more likely to see a doctor, and conditional on that males over 55 years old have more repeat doctor visits. The LASSO estimators also generate similar conclusions. In the zero component, the penalized methods all indicate a negative effect of having children on the demand of health care. The presence of children is less likely to increase the chance to see a physician (Riphahn et al., 2003). However, children was eliminated by BE(0.01). As expected, people with high health satisfaction are unlikely to see a doctor and have low demand on health care. The results also suggest that interaction between health status and age is not correlated with doctor office visits. The results from penalized ZINB models are similar to those in Jochmann (2013). The five variables selected by the NB component in the ZINB-MCP correspond to the top five inclusion probabilities by a Bayesian analysis (Jochmann, 2013). Similarly, the three variables selected by the zero component in the ZINB-MCP correspond to the top three inclusion probabilities. However, the penalized model has sparse representation, which is different from the Bayesian model selection. For instance, the interaction terms are not selected by the ZINB-MCP while two interaction terms were selected by the Bayesian procedure despite relatively small inclusion probabilities. In this case, it can be subjective when making a cut-off point of inclusion probability.

In the sequel, we focus on the ZINB-MCP method which has similar BIC value compared with BE(0.01), and largest log-likelihood value and smallest AIC value. The log-likelihood values from the reduced models are similar based on 10-fold cross validation, and larger than that from the full ZINB model, indicating better prediction with parsimonious models. Between ZINB-MCP and BE(0.01), we compare the predicted probabilities from the two methods. The Vuong test (Vuong, 1989; Greene, 1994) has a p-value < 0.001 in favor of the penalized model. Between ZINB-MCP and NB-MCP, the Vuong test has a p-value 0.01 preferring the zero-inflated model again. When comparing to the full ZINB model, a likelihood ratio test returns a p-value 0.48 (chi-square statistic 45.8 with degrees of freedom 46), which suggests that there is no statistically significant difference between the reduced and full ZINB models. One would question if a simpler ZIP model can fit the data as well as the ZINB model. To see this, we also fit penalized ZIP models. The ZIP-LASSO, ZIP-MCP and ZIP-SCAD have BIC 9012.6, 8944.2 and 8958.2, respectively, and log-likelihood −4405, −4400.8 and −4411.6, respectively. The penalized ZIP models have substantial large values of BIC and small values of log-likelihood, leading to poorer fitting compared with the penalized ZINB models. Overall, the analysis provides evidence that the ZINB-MCP model fits the data best. Furthermore, using the variable selected by the ZINB-MCP, we evaluated traditional maximum likelihood estimates (not shown) which are very close to those by ZINB-MCP in Table 7. Thus, this is an example that although the MCP penalty shrinks estimates, the bias can be reduced.

5 Software

To facilitate public usage, the proposed algorithm has been implemented in the free software mpath (Wang, 2014) available at http://CRAN.R-project.org/package=mpath. Using penalty scaling parameters, the software allows different penalties for each of the variables in count and zero components. Thus, the adaptive LASSO (Zou, 2006) can be implemented with the penalty rescaling. The elastic net penalty (Zou and Hastie, 2005) has also been included in the package. We provided a package vignette for analyzing the German health care demand, which may be invoked by the following R codes:

• R> library(“mpath”)

• R> vignette(“german”, package = “mpath”)

6 Discussion

Variable selection for mixture models is a challenging problem particularly when the sample size is small to modest while the number of predictors is large. This paper investigates the performance of an EM algorithm for variable selection in a ZINB model. An alternative algorithm may take Taylor approximation of the log-likelihood function. However, this approach requires to invert the Hessian matrix, which can be numerically unstable for complex models (Buu et al., 2011). Indeed, even with the non-penalized ZINB model, the local approximation can fail, thus the traditional stepwise variable selection can encounter a failure. The simulation study supports that the proposed algorithm does not suffer such deficiency, thus is more reliable than the stepwise variable selection for the ZINB regression models. In addition, the new algorithm can be potentially useful even with high-dimensional variables. The developed methods can be applied in many studies including but not limited to health care utilization and service.

The current paper is concerned with cross-sectional data only, whilst panel data often arise in empirical applications. This represents a limitation of the proposed model. Variable selection for zero-inflated panel data demands new, different methods, but is beyond the scope of our development.

Table 2.

Simulation results with example 4, ρ = 0.4,θ = 2,n = 300. Median and robust standard deviations (in parentheses) of the MSE ratio between the penalized model and full model, and the estimated θ. Mean and standard deviations of sensitivity and specificity.

Method	MSE	Sensitivity	Specificity	θ̂
NB component
NB-LASSO	2.291 (1.043)	0.638 (0.338)	0.893 (0.108)	0.628 (0.1)
NB-MCP	2.445 (1.088)	0.743 (0.248)	0.922 (0.076)	0.671 (0.092)
NB-SCAD	2.558 (1.172)	0.748 (0.278)	0.877 (0.096)	0.663 (0.084)
ZINB-LASSO	0.856 (0.489)	0.87 (0.243)	0.863 (0.112)	2.329 (0.544)
ZINB-MCP	0.548 (0.372)	0.859 (0.185)	0.965 (0.06)	2.345 (0.558)
ZINB-SCAD	0.584 (0.37)	0.889 (0.165)	0.935 (0.085)	2.384 (0.57)
BE(0.1573)	0.719 (0.29)	0.956 (0.099)	0.809 (0.121)	2.51 (0.549)
BE(0.05)	0.592 (0.336)	0.916 (0.125)	0.923 (0.092)	2.39 (0.577)
BE(0.01)	0.538 (0.411)	0.841 (0.172)	0.98 (0.043)	2.301 (0.533)
ZINB-ORACLE	0.232 (0.147)	1 (0)	1 (0)	2.352 (0.506)
Zero component
ZINB-LASSO	0.519 (0.405)	0.454 (0.252)	0.948 (0.077)
ZINB-MCP	0.635 (0.276)	0.733 (0.184)	0.777 (0.176)
ZINB-SCAD	0.619 (0.349)	0.429 (0.215)	0.962 (0.053)
BE(0.1573)	0.676 (0.252)	0.719 (0.179)	0.797 (0.123)
BE(0.05)	0.602 (0.299)	0.533 (0.19)	0.927 (0.08)
BE(0.01)	0.655 (0.434)	0.292 (0.192)	0.984 (0.033)
ZINB-ORACLE	0.177 (0.125)	1 (0)	1 (0)

Table 3.

Simulation results with example 5, ρ = 0.4,θ = 2,n = 300. Median and robust standard deviations (in parentheses) of the MSE ratio between the penalized model and full model, and the estimated θ. Mean and standard deviations of sensitivity and specificity.

Method	MSE	Sensitivity	Specificity	θ̂
NB component
NB-LASSO	2.114 (1.391)	0.967 (0.146)	0.921 (0.079)	0.681 (0.072)
NB-MCP	0.98 (0.57)	0.961 (0.154)	0.949 (0.062)	0.705 (0.079)
NB-SCAD	1.063 (0.908)	0.967 (0.146)	0.914 (0.082)	0.706 (0.078)
ZINB-LASSO	0.665 (0.48)	0.989 (0.074)	0.947 (0.062)	2.247 (0.311)
ZINB-MCP	0.158 (0.16)	0.972 (0.115)	0.99 (0.025)	2.189 (0.352)
ZINB-SCAD	0.131 (0.12)	0.983 (0.09)	0.987 (0.028)	2.167 (0.362)
BE(0.1573)	0.615 (0.278)	0.994 (0.053)	0.795 (0.111)	2.429 (0.44)
BE(0.05)	0.292 (0.256)	0.994 (0.053)	0.928 (0.078)	2.306 (0.43)
BE(0.01)	0.168 (0.14)	0.989 (0.075)	0.984 (0.026)	2.252 (0.344)
ZINB-ORACLE	0.103 (0.094)	1 (0)	1 (0)	2.171 (0.31)
Zero component
ZINB-LASSO	1.189 (0.989)	0.642 (0.273)	0.947 (0.07)
ZINB-MCP	0.706 (0.423)	0.853 (0.191)	0.787 (0.165)
ZINB-SCAD	0.87 (0.807)	0.611 (0.252)	0.96 (0.057)
BE(0.1573)	0.734 (0.428)	0.823 (0.189)	0.798 (0.132)
BE(0.05)	0.73 (0.634)	0.697 (0.243)	0.929 (0.085)
BE(0.01)	1.09 (0.965)	0.455 (0.24)	0.985 (0.034)
ZINB-ORACLE	0.219 (0.214)	1 (0)	1 (0)

Appendix A Regularity conditions

The oracle property of ZINB with MCP or SCAD may be developed based on the following regularity conditions, which also lead to asymptotic normality of the non-penalized maximum likelihood estimate of the ZINB model. Let u_i = (x_i,y_i), i = 1,…,n be independent and identically distributed from the ZINB model. The regularity conditions are as follows:

1. There exists an open subset ω of Ω containing the true parameter point ϕ₀ such that for almost all u_i, ℓ(ϕ,u_i) admits all third derivatives ∂³ℓ(ϕ,u_i)/∂ϕ _j∂ϕ_k∂ϕ_l for all ϕ ∈ ω.

2. The first and second partial derivatives of ℓ(ϕ,u_i) satisfy the equations

   $$E\left[\frac{\partial \ell (\varphi ,u_i)}{\partial {\varphi }_j}\right]=0\text{for}j=1,\dots ,d,$$
   and

   $$E\left[-\frac{{\partial }^2\ell (\varphi ,u_i)}{\partial {\varphi }_j\partial {\varphi }_k}\right]=E\left[\frac{\partial \ell (\varphi ,u_i)}{\partial {\varphi }_j}\frac{\partial \ell (\varphi ,u_i)}{\partial {\varphi }_k}\right]=I_{jk}(\varphi )\text{for}j,k=1,\dots ,d.$$

3. The Fisher information matrix I(ϕ ) is finite and positive definite for all ϕ ∈ ω.

4. There exist functions M_jkl such that

   $$\left|\frac{{\partial }^3}{\partial {\varphi }_j\partial {\varphi }_k\partial {\varphi }_l}\ell (\varphi ,u_i)\right|\le M_{\mathit{jkl}}(u_i)\text{for}\text{all}\varphi \in \omega ,$$

   where m_jkl = E_ϕ0 [M_jkl(u_i)] < ∞ for all j,k, l.

Appendix B Oracle properties of the MCP and SCAD estimates

Assume true parameter vector ϕ₀ has elements (β _j0,ζ_k0), j = 0,1,…,q₁,k = 0,1, …,q₂. Decompose ${\varphi }_0={({\varphi }_{10}^{\top },{\varphi }_{20}^{\top })}^{\top }$ and assume ϕ₂₀ contains all zero coefficients.

Theorem B.1

Let u₁,,u_n be independent and identically distributed, each with a probability distribution satisfying regularity conditions (a)–(d) in Appendix A. If

$$max\{\mid p^{″}({\lambda }_{NB,n};\mid {\beta }_{j0}\mid )\mid ,\mid p^{″}({\lambda }_{BI,n};\mid {\zeta }_{k0}\mid )\mid :{\beta }_{j0}\ne 0,{\zeta }_{k0}\ne 0\}\to 0,$$

then there exists a local maximizer ϕ̂ of pℓ(ϕ ) such that

$$\Vert \widehat{\varphi }-{\varphi }_0\Vert =O_p(n^{-1/2}+a_n),$$

where || · || is the Euclidean norm and

$$a_n=max\{\mid p^{\prime }({\lambda }_{NB,n};\mid {\beta }_{j0}\mid )\mid ,\mid p^{\prime }({\lambda }_{BI,n};\mid {\zeta }_{k0}\mid )\mid :{\beta }_{j0}\ne 0,{\zeta }_{k0}\ne 0\}.$$

Theorem B.2

Let u₁,,u_n be independent and identically distributed, each with a probability distribution satisfying conditions (a)–(d) in Appendix A. Assume that the penalty function satisfies

$$\underset{n\to \infty }{liminf}\underset{\beta \to 0+}{liminf}{p}_{{\lambda }_{NB,n}}^{\prime }(\beta )/{\lambda }_{NB,n}>0,\underset{n\to \infty }{liminf}\underset{\zeta \to 0+}{liminf}{p}_{{\lambda }_{BI,n}}^{\prime }(\zeta )/{\lambda }_{BI,n}>0.$$

If λ_NB,n → 0, $\sqrt{n}{\lambda }_{NB,n}\to \infty$,λ_BI,n → 0, $\sqrt{n}{\lambda }_{BI,n}\to \infty$ as n → ∞, then with probability tending to 1, the root-n consistent local maximizers ϕ̂ in Theorem 1 must satisfy:

1. Sparsity: ϕ̂₂ = 0.

2. Asymptotic normality:

   $$\sqrt{n}\{I_1({\varphi }_{10})+\mathrm{\sum }\}({\widehat{\varphi }}_1-{\varphi }_{10})+\sqrt{n}b\to N(0,I_1({\varphi }_{10}))$$
   in distribution, where I₁(ϕ₁₀) = I₁(ϕ₁₀,0), the Fisher information knowing ϕ₂ = 0, and

   $$\begin{array}{ll}\mathrm{\sum }\hfill & =\mathit{diag}\{0,p_{{\lambda }_{NB,n}}^{″}(\mid {\beta }_{10}\mid ),\dots ,p_{{\lambda }_{NB,n}}^{″}(\mid {\beta }_{s0}\mid ),0,p_{{\lambda }_{BI,n}}^{″}(\mid {\zeta }_{10}\mid ),\dots ,p_{{\lambda }_{BI,n}}^{″}(\mid {\zeta }_{t0}\mid )\},\hfill \\ b\hfill & =\left(0,p_{{\lambda }_{NB,n}}^{\prime }(\mid {\beta }_{10}\mid )\mathit{sgn}({\beta }_{10}),\dots ,p_{{\lambda }_{NB,n}}^{\prime }(\mid {\beta }_{s0}\mid )\mathit{sgn}({\beta }_{s0}),0,p_{{\lambda }_{BI,n}}^{\prime }(\mid {\zeta }_{10}\mid )\mathit{sgn}({\zeta }_{10}),\dots ,p_{{\lambda }_{BI,n}}^{\prime }(\mid {\zeta }_{t0}\mid )\mathit{sgn}({\zeta }_{t0})\right),\hfill \end{array}$$

   where s and t are the numbers of non-zero components (excluding intercepts) in β₁₀ and ζ₁₀, respectively.

Appendix C Elements of Hessian matrix

Let ${\mu }_i=exp(x_i^{\top }\beta ),{\xi }_i=exp(v_i^{\top }\gamma )$, p_i = ξ_i/(1+ξ_i), r_i = θ/(θ +μ_i), s_i = μ_i/(θ + μ_i), $t_i=r_i^{\theta }$,h_i = ξ_i +t_i. For ease of notation, the subscript i is suppressed in the sequel. Furthermore, Ψ′(·) denotes the trigamma function.

$$\begin{array}{l}{I}_{\theta ,\theta }=\sum _{y_i=0}\{t{\theta }^3{(log(r))}^2\xi +2tlog(r)\mu \xi (log(r)+1){\theta }^2\\ +{\mu }^2\xi t\left(2log(r)+1+{(log(r))}^2\right)\theta +{\mu }^2\xi t+{\mu }^2{t}^2\}\frac{1}{\theta {(\theta +\mu )}^2{h}^2}\\ +\sum _{y_i>0}\left\{{\mathrm{\Psi }}^{\prime }(y_i+\theta )-{\mathrm{\Psi }}^{\prime }(\theta )+\frac{s}{\theta }+\frac{y_i+\theta }{{(\theta +\mu )}^2}-\frac{1}{\theta +\mu }\right\},\\ I_{{\beta }_j,{\beta }_k}=\sum _{y_i=0}-\frac{{\theta }^2\mu (-t\mu \xi +\xi t+t^2)}{{((\theta +\mu )h)}^2}{x}_{ij}{x}_{ik}+\sum _{y_i>0}-\frac{\theta \mu (\theta +y_i)}{{(\theta +\mu )}^2}{x}_{ij}{x}_{ik},\\ I_{{\beta }_j,{\zeta }_k}=\sum _{y_i=0}\frac{\theta ts\xi x_{ij}{v}_{ik}}{h^2},\\ I_{{\beta }_j,\theta }=\sum _{y_i=0}\frac{-x_{ij}\{{\theta }^{2}tlog(r)\xi +\theta tlog(r)\mu \xi +t\theta \mu \xi +t\mu \xi +t^2\mu \}\mu }{{((\theta +\mu )h)}^2}+\sum _{y_i>0}\frac{-\mu (-y_i+\mu )x_{ij}}{{(\theta +\mu )}^2},\\ I_{{\zeta }_j,{\zeta }_k}=\sum _{y_i=0}{v}_{ij}{v}_{ik}\left(-p+p^2+\frac{\xi }{h}-{(\frac{\xi }{h})}^2\right)+\sum _{y_i>0}-p(1-p)v_{ij}{v}_{ik},\\ I_{{\zeta }_k,\theta }=\sum _{y_i=0}-\frac{1}{h^2}t(log(r)+s)\xi v_{ik}.\end{array}$$