The 3D Pelvic Inclination Correction System (PICS): A universally applicable coordinate system for isovolumetric imaging measurements, tested in women with pelvic organ prolapse (POP)

Abstract

In pelvic organ prolapse (POP), the organs are pushed downward along the lines of gravity, so measurements along this longitudinal body axis are desirable. We propose a universally applicable 3D coordinate system that corrects for changes in pelvic inclination and that allows the localization of any point in the pelvis at rest or under dynamic conditions on magnetic resonance images (MRI) of pelvic floor disorders in a scanner- and software independent manner.

The proposed 3D coordinate system called 3D Pelvic Inclination Correction System (PICS) is constructed utilizing four bony landmark points, with the origin set at the inferior pubic point, and three additional points at the sacrum (sacrococcygeal joint) and both ischial spines, which are clearly visible on MRI images. The feasibility and applicability of the moving frame was evaluated using MRI datasets from five women with pelvic organ prolapse, three undergoing static MRI and two undergoing dynamic MRI of the pelvic floor in a supine position.

The construction of the coordinate system was performed utilizing the selected landmarks, with an initial implementation completed in MATLAB. In all cases the selected landmarks were clearly visible, with the construction of the 3D PICS and measurement of pelvic organ positions performed without difficulty. The resulting distance from the organ position to the horizontal PICS plane was compared to a traditional measure based on standard measurements in 2D slices. The two approaches demonstrated good agreement in each of the cases.

The developed approach makes quantitative assessment of pelvic organ position in a physiologically relevant 3D coordinate system possible independent of pelvic movement relative to the scanner. It allows the accurate study of the physiologic range of organ location along the body axis (“up or down”) as well as defects of the pelvic sidewall or birth-related pelvic floor injuries outside the midsagittal plane, not possible before in a 2D reference line system. Measures in 3D can be monitored over time and may reveal pathology before bothersome symptoms appear, as well as allowing comparison of outcomes between different patient pools after different surgical approaches.

1. Introduction

Reference systems are widely used in medicine to classify physiologic and pathologic conditions. Each is specifically to be relevant for the joint or body part of interest and the questions to be asked (Wu and Cavanagh, 1995). The pelvic organs are complex, three-dimensional structures, dispersed in space within the bony pelvis.

Pelvic organ prolapse (POP) is a downward displacement of pelvic organs along the axis of gravity. POP is common and seen in 50% or more of parous women and often occurs along with micturition and defecation disorders, as well as sexual dysfunction (Nygaard et al., 2008) with a lifetime risk of necessary surgery in 5–19% (Haya et al., 2015).

Clinically, POP is currently quantified by gynecologic examination with the pelvic organ prolapse quantification system (POP-Q). Two limitations exist with this system. First the reference plane (hymen) descends with the organs in case of prolapse (Bump et al., 1996; Hall et al., 1996; Haya et al., 2015) so that true descent relative to the bony pelvis is not assessed and, second, it can only assess what is visible or palpable during examination.

With advances in soft tissue imaging technology such as magnetic resonance imaging (MRI), pelvic organs and structures can be visualized and studied with an accuracy impossible to achieve by clinical examination. It also allows measurements of organ position to be made relative to the bony pelvis. However, there is as yet no standardized reference system for measurement of pelvic organ positions in anatomic 3D space, needed for quantification of physiologic or pathologic conditions such as POP (Broekhuis et al., 2009b).

To date, at least five midsagittal pelvic reference lines for MRI have been employed to quantify prolapse in a two-dimensional (2D) plane (Broekhuis et al., 2009a). The lack of consensus in different pelvic floor disciplines such as radiology, urogynecology, urology and proctology, regarding which reference line should be used and how these relate to one other, makes the comparison of data from different collectives difficult (Agildere et al., 2003; Comiter et al., 1999; Fauconnier et al., 2008; Goodrich et al., 1993; Gousse et al., 2000; Gufler et al., 1999; Hodroff et al., 2002; Lienemann et al., 1997; Lienemann et al., 2004; Singh et al., 2001; Unterweger et al., 2001; Yang et al., 1991). In addition, these lines are either oblique to the body axis (so that measurements of how “high or low” cannot be made), or are based on scanner coordinate systems that do not account for pelvic orientation or pelvic movement during dynamic scans that involve Valsalva maneuvers, for example.

Reference lines drawn on individual slices of MRI or CT only allow measurements in a 2D plane, but not in a three-dimensional (3D) space. These traditional reference lines are based on landmarks in the midsagittal pelvic plane as captured by the MR scanner. In reality, prolapse points of interest are not all contained in the midsagittal plane. The important structures of support (Kim et al., 2014), including the pelvic floor muscle and the pelvic ligaments, originate from lateral structures. Those structures include laterally - the posterior surface of the superior pubic ramus; posteriorly - the inner surface of the spine of the ischium; and between these two points, from the obturator fascia. Other problems with calculating solely on a single plane include patient obliquity/rotation within the scanner, and changes in pelvic orientation with effort such as valsalva or defecation.

There is an unmet need for a 3D coordinate system that determines the position of any single point in the pelvis along the body axis within a normalized reference space. Coordinate systems for localization of structures in the 3D space have been proposed for stereotactic neurosurgery (Kall et al., 1994; Kall et al., 1985; Vannier et al., 1984). The International Society of Biomechanics (ISB) proposed a general reporting standard for joint kinematics in 2002. For the hip, the anterior and posterior superior iliac spine and the femoral condyle build a pelvic coordinate system with the center of rotation in the hip joint (Wu et al., 2002) and in orthopedic surgery different pelvic rotation axes have been described for the anatomic referencing of the cup orientation in total hip arthroplasty (Tannast et al., 2005).

Based on the Pelvis Inclination Correction System (PICS) line, which corrects for movement of the pelvis in the midsagittal plane (Betschart et al., 2013), we propose a standardized 3D coordinate system for evaluating the pelvic anatomy in the 3D space.

2. Materials and Methods

2.1 Characteristics of the 3D Pelvic Inclination Correction System (PICS)– a moving frame, attached to the pelvis

The proposed 3D coordinate system is independent of the patients’ pelvic position in the MR scanner, the size and shape of pelvis, the pre- or post-surgical condition, or the degree of prolapse (Fig. 1).

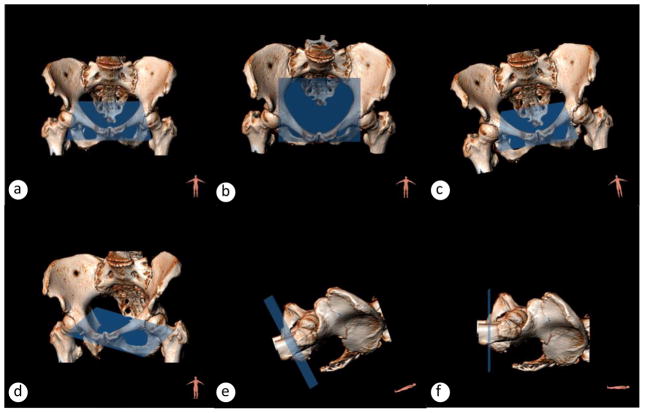
Fig. 1.

3D orientation in a scanner is characterized through three movements: azimuth, elevation and tilt. Blue area is the plane x/z in the local coordinate system that follows the movements of the pelvis. (a) standing position, (b) anteriorly flexed pelvis, for example scoliosis or defecation/defecography, (c) tilted pelvis, for example uneven legs, (d) twisted pelvis, for example cushion under one back side, (e) half-lying pelvis, (f) supine pelvis. The blue area reflects the horizontal plane of the 3D PICS coordinate system that is in average 34° below SCIPP line (Betschart et al., 2013). Bony pelvis registered with CT and MRI 3Dsoftware 3viseon 3.5TM.

The 3D Pelvic Inclination Correction System (PICS) will allow the measurement of any point, volume or surface within the pelvis. It is a rigid 3D coordinate system that follows the movements of the bony pelvis. In such a system, the calculation of not only the height of the organ along the body axis in relation to the standing horizontal plane, but the precise position of the organ within the pelvis will be possible. In order to achieve this, a transformation from the scanner’s coordinate system to a pelvic coordinate system is necessary (Fig. 2).

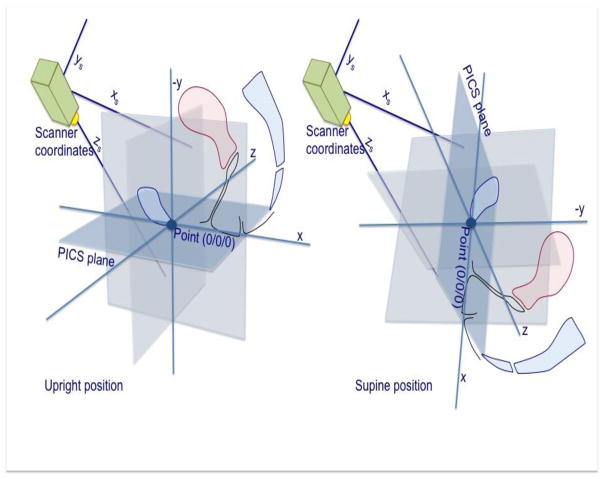
Fig. 2.

The principle of the 3D Pelvic Inclination Correction System (PICS): a scanner based local coordinate system is transformed into a pelvic 3D-coordinate system serving as a moving frame in supine or standing position.

There are a several additional conditions that should be fulfilled by the 3D coordinate system. It should measure the location of structures relative to a normalized horizontal plane perpendicular to the line of the body axis (y-axis). The definition of the 3D coordinate system should also be possible through easily identifiable, precisely localized structures that span the whole pelvis. Points that fulfill these requirements include the inferior pubic point, the sacrococcygeal articulation, and the ischial spines (Broekhuis et al., 2009a). The creation of the coordinate system and investigation of relative organ positions must be possible under circumstances including rest, strain, or defecation, allowing direct comparison between these conditions, and between patients. Finally, the computation shall be applicable to any 3D medical image data set and any 3D image analysis software capable of selecting landmark points relative to an external point of origin in the scanner; for scans with possible movement between series, the bony landmark reference points have to be set once for each image set, for example once in rest and once in strain; the position of the pelvis may change between acquisitions or between images of a dynamic maneuver such as Valsalva. The average angle from the sacrococcygeal to inferior pubic point line (SCIPP) in standing posture is 34° from the horizontal plane (Betschart et al., 2013; Broekhuis et al., 2009a) (Fig 1 and 3). Therefore, establishing the plane 34° below and parallel to the line between the ischial spines establishes the horizontal line to which the body axis is perpendicular.

Fig. 3.

The PICS line is drawn 34° below the SCIPP line and passing through the inferior pubic point. This angle is based on average values measured from our previous research subjects (n=149) between the SCIPP line and the longitudinal body axis established by scanner bed at rest (Betschart et al., 2013). The PICS line keeps a fixed relationship to the bony SCIPP line at any pelvic position. PICS Pelvic Inclination Correction System; SCIPP SacroCoccygeal Inferior Pubic Point.

The transformation of the pelvic organ locations from the scanner coordinate system to a new standardized reference system fulfilling the requirements defined above can be performed with vector and matrix geometry as described in the following section.

3. Theory/Calculation

The construction of the reference frame within the pelvis begins with the selection of four landmark points. The points required along the midline are the inferior pubic point at the lower border of the symphysis (A) and the sacrococcygeal point (B) (Fig. 4a). Laterally, the left and right ischial spine points (I_R and I_L) are chosen on each side of the pelvis to define the horizontal plane (Fig. 4b). Finally, the scanner coordinates of the organ of interest (Fig. 4c) are noted. We choose the inferior pubic point (Point A) as the origin of our rigid coordinate system. This pelvic landmark is always well visible and is independent of the intrinsic coordinate system of the imaging device.

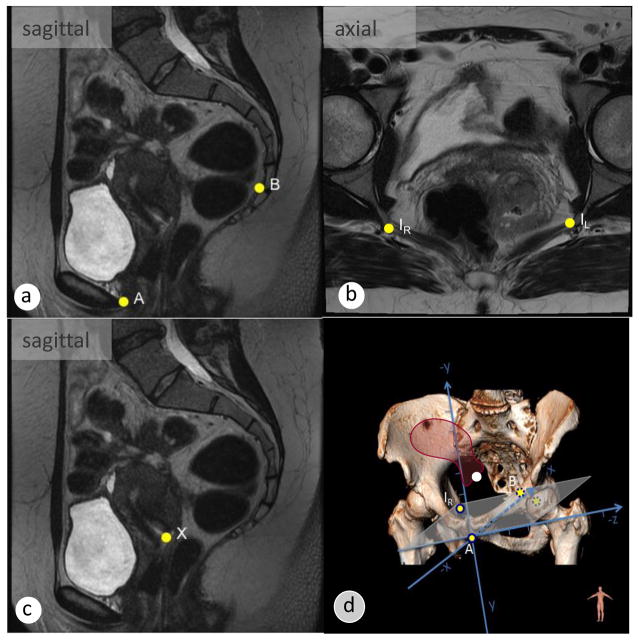
Fig. 4.

The definition of bony landmark points is required to set up the 3D coordinate system. Consistent bony landmark points include (yellow dots): (a) midsagittal slice: point A, inferior pubic point; B, anterior border of the sacrococcygeal point; (b) axial slice: I1=I_R, right ischial spines; I2=I_L, left ischial spine; (c) the cervical os is marked with point X; (d) a rigid coordinate system is set up to calculate the coordinates of point X (cervix, white dot), expressed as coordinates (x/y/z) in reference to the origin at the inferior pubic point. The height of the organ corresponds to the value of the coordinate y.

Each of the selected points is described using the scanner coordinates in a row vector, as shown below.

$$\widehat{x}=[xyz]$$ (1)

Three perpendicular axes are then constructed from the positions of the anatomical landmarks in the scanner coordinate system in order to define the standardized pelvic coordinate system. Three vectors are constructed: The vector û is drawn from the inferior pubic point (A) to the sacrococcygeal point (B). It is converted to a unit vector (with length 1) by dividing by its own length (Fig. 5a).

Fig. 5.

Construction of the PICS coordinate system. (a) Vector u is defined between point A and B. The direction of vector i is defined between positions I_L and I_R, and placed at the origin (point A). It is not necessarily perpendicular to vector u. (b) Vector v is given by the cross product of vectors u and i, perpendicular to the plane in which vectors u and i lie. (c) Vector w is calculated as the cross product of u and v, giving a vector in the ui plane perpendicular to u and v. The vectors u, v and w are 90° to one another. (d) The vectors u and v are rotated 34° around the w vector, resulting in vector u′ and v′.

$$\widehat{u}=\frac{B-A}{\Vert B-A\Vert }$$ (2)

A second vector î is then drawn from the left (I_L) to the right (I_R) ischial spine points, and also converted to a unit vector, as below (Fig. 5a) This aligns the coordinate system with the lateral axis of the pelvic bones.

$$\widehat{\iota }=\frac{I_R-I_L}{\Vert I_R-I_L\Vert }$$ (3)

In order to have a valid 3D Cartesian coordinate system, we need three different vectors that are 90 degrees from each other. Assuming for a moment that û is directed roughly in an anatomic sagittal plane (being constructed from two midline points) and that is approximately perpendicular to that sagittal plane (being constructed from two points which are far from the midline and roughly mirrored across the midline), we can determine a third direction for our system, v̂, which is perpendicular to the other two, by using the mathematic cross product (Fig. 5b):

$$\widehat{v}=\widehat{\iota }\times \widehat{u}$$ (4)

Lastly, we correct for our assumption that û and î are at 90 degrees by replacing î with a new vector, ŵ. ŵ is again constructed from û and v̂ using cross products to guarantee perpendicularity (Fig. 5c):

$$\widehat{w}=\widehat{u}\times \widehat{v}$$ (5)

These three unit vectors (û, v̂, ŵ) represent the orientation of the anatomic coordinate system, with each vector perpendicular to the others, a trait called ‘orthonormality’ which prevents distortion when converting between coordinate systems. In concept, in this initial system, û represents the vector from pubis to sacrum, ŵ from left to right, and v̂ from pelvic inlet to outlet.

$$R_{\mathit{Init}}=[\begin{array}{ccc}{\widehat{u}}^{\prime }& {\widehat{v}}^{\prime }& {\widehat{w}}^{\prime }\end{array}]$$ (6)

In order to align this with the longitudinal body axis standing position, it must be rotated in the sagittal plane; a rotation of 34° around the ŵ (left-right) axis will adjust for pelvic tilt and aligns the axes as shown in Fig 5d (Betschart et al., 2013).

$$R_{\mathit{Rot}}=R_{34°\widehat{w}}\times R_{\mathit{Init}}$$ (7)

Finally, we construct a transformation matrix from the rotated axes and the origin (point A).

$$T_{\mathit{PICS}}=\left[\begin{array}{cc}{R}_{\mathit{Rot}}& A^{\prime }\\ 0& 1\end{array}\right]$$ (8)

This can be applied to any point from the original scanner system, and will transform that point into our standardized system. To do this, the transformation matrix is inverted and the selected point multiplied, as so:

$$P_{\mathit{PICS}}={T_{\mathit{PICS}}}^{-1}\times P$$ (9)

Thus resulting in the transformation of the organ position from scanner coordinates into the standardized coordinate system that goes along with the clinically used POP-Q system.

Because we have constructed the system by pelvic landmarks and corrected it by 34°, we can say that it represents the concept of the pelvis as it should appear when standing: the x-axis points front to back, representing the sacrococcygeal inferior pubic point (SCIPP) after it is rotated 34° in the sagittal plane. As such, it provides a horizontal plane similar to the H-line, but with correction for changes in pelvic inclination within the scanner (Lienemann et al., 2004). This is necessary because the SCIPP line is neither vertical nor horizontal relative the action of gravity that is the critical factor in understanding prolapse. The y-axis points caudally in the direction of the vertical body axis (the direction gravity would pull when standing), and the z-axis points laterally from the anatomic left to the right (Fig. 4d). We could choose any units for our standardized system, but have chosen millimeters for convenience when describing pelvic anatomy.

Subsequently, in the constructed coordinate system each location on the pelvis can be represented by three coordinates, describing the distances in millimeters from the point of origin (point A, the inferior pubic point). As an example, the point 46/-60/-5 is in its standardized position posterior (46mm), cranial (60mm), and left (5mm) from point A. The height of this point is 60mm (y-value) above the horizontal PICS plane. Furthermore, no matter how the pelvis moves within the scanner, the new coordinates of this location will not change (Fig. 4d). This produces data that can be compared from one scan to another, or even one patient to another.

3.1 Validation of the Approach

MRI image datasets of five women with pelvic organ prolapse, three undergoing static MRI and two undergoing dynamic MRI of the pelvic floor were obtained. Patients gave their informed consent in the general consent for health-related personal data research of the University Hospital Zurich V1.2 05.05.2015. These datasets provided a suitable setting for the development and evaluation of the approach.

Both static and dynamic pelvic floor MRIs were performed on a 3T MRI scanner (Skyra, Siemens, Erlangen, Germany). The reference points of the static MRI were measured on a T2-weighted 2D turbo-spin echo sequence acquired in the sagittal and axial plane (repetition time (TR) 6034 ms, echo time (TE) 98 ms; slice thickness, 3; gap, 1; flip angle, 90°; matrix sagittal, 256 × 192, transverse, 256 × 224). The reference points of the dynamic MRI were measured on a 2D TrueFisp sequence acquired in the midsagittal plane (TR 1002 ms, TE 2.36 ms; flip angle, 40°; single slab slice thickness, 10 mm; matrix, 320 × 288) and on a 2D T2-weighted turbo spin echo sequence (TR 6610 ms, TE 91 ms; flip angle, 124°; slice thickness, 3; gap, 1; matrix 320 × 272) acquired in the transverse plane. The MRI datasets were transferred and uploaded in the OsiriX 8.0.2 medical imaging viewer and editor program where the point measurements (A, B, I_R, I_L and X, Figure 6) were done and resulted in a scanner based x/y/z coordinate for each point. The selected coordinates were then exported to MATLAB for coordinate system construction and analysis. Additional 2D measurements of the organ distance from the PICS line were taken for comparison with the results obtained with the 3D approach (Figure 6g).

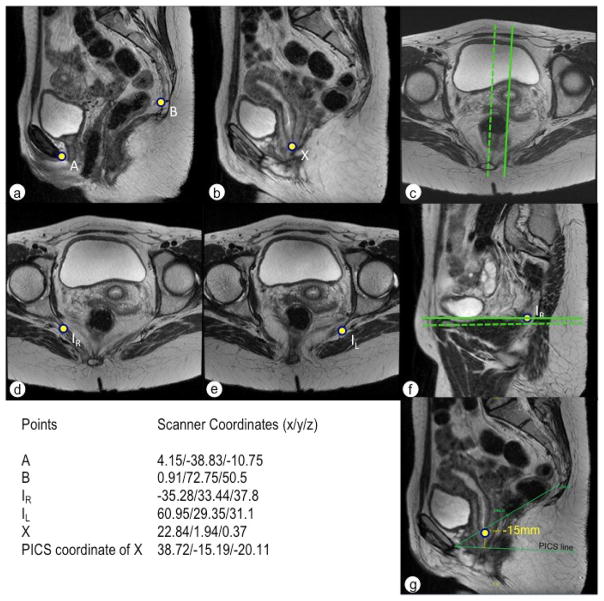
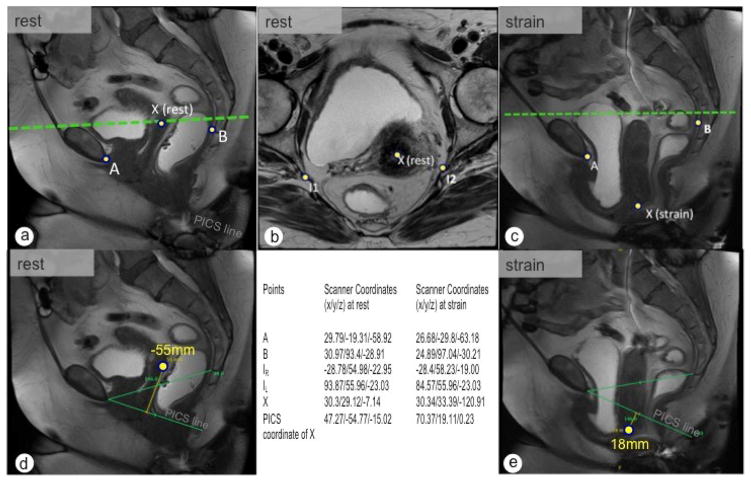
Fig. 6.

(a, b) extraction of the scanner coordinates in two different sagittal planes, as the cervix is 2cm left positioned from the midsagittal plane. Coordinates are shown in the table. (c) the dotted line marks the midsagittal plane of the placement of points A and B. The line represents the plane through the cervix approximately 2 cm (z=−20.11mm) to the left. (d) right ischial spine, (e) left ischial spine, (f) dotted line corresponds to the plane of the right ischial spine, straight line to the left ischial spine. (g) control check in the 2D system, where the PICS line is drawn 34° below the SCIPP line and the cervix point is measured perpendicularly to the PICS line yielding to a value of −15mm, corresponding to the value calculated using the 3D PICS.

For validation also test-retest intra-observer repeatability and test-retest inter-observer reproducibility of the point measurements and the 3D PICS system were assessed in five subjects by two examiners (CB and CR).

4. Results

The selection of the defined landmarks and construction of the reference coordinate system with measurement of organ position was successfully completed in all five patients, with measurements performed under both rest and strain conditions illustrated in one example patient (Fig. 7).

Fig. 7.

Dynamic MRI for the assessment of change of the uterus position between rest (a, b) and strain (c). In (d) and (e) are the standard measurement to the PICS line demonstrated. In rest (d) the cervix point is located −55mm above the PICS line (PICS y-value is −54.77). At strain (e) the cervix is located 18mm below the PICS line, corresponding to a calculated y value in the PICS of 19.11mm. The green dotted line represents the height of the ischial spines.

The point placement and coordinates of the bony landmarks and the cervix of a 29-year-old Gravida II, Para I at rest are shown in Fig. 6. Clinically the woman has a uterine descent to the hymen (Pelvic Organ Prolapse System Stage 2, POP-Q II). The inferior pubic point, the sacrococcygeal point and the ischial spines are well visible, as demonstrated in Fig. 6. The ischial spines show a difference of height to the scanner origin of 6.7mm (Fig 6f). Control measurements completed in single 2D slices revealed a distance of −15 mm from the cervix to the PICS line; the developed pelvis positioning coordinate system returned a distance of −15.19 mm (y-value) above the PICS horizontal plane.

The second example patient was a 65-year-old woman with a cystocele and uterine descent (Pelvic Organ Prolapse System Stage 3, POP-Q III) undergoing defecography MRI for stool outlet symptoms. The cervical location at rest and maximum Valsalva was registered on dynamic MRI (Fig. 7). Significant changes in the coordinates of the bony landmark points during maximum Valsalva were also observed (Fig. 7c). At rest, 2D control measurements revealed an organ to PICS line distance of −55 mm, with a value of −54.77 mm above the PICS horizontal plane observed when utilizing the 3D technique. At strain an organ to PICS line distance of 18 mm was observed, with an organ position 19.11 mm below the PICS horizontal plane calculated by the 3D technique.

The intra-observer repeatability and the test-retest inter-observer reproducibility were analyzed for input and output parameters. Input measurements of points A (x/y/z), B (x/y/z), I_R (x/y/z), I_L (x/y/z) and X (x/y/z) demonstrated an excellent intra-observer repeatability with an intra-class correlation coefficient (ICC) of 0.994, 1.00, and 1.00 (A), 0.994, 1.00, and 1.00 (B), 0.998, 0.999, and 1.00 (I_R), 0.999, 0.996, and 1.00 (I_L) 1.00, 1.00, and 1.00 (X) for the x-, y-, and z-coordinate, respectively. The inter-observer reproducibility of points A (x/y/z), B (x/y/z), I_R (x/y/z), I_L (x/y/z) and X (x/y/z) showed an excellent ICC of 0.997, 1.00, and 1.00 (A), 0.994, 0.987, and 0.993 (B), 0.986, 0.985, and 1.00 (I_R), 0.998, 0.999, and 1.00 (I_L), and 0.995, 0.973, and 0.999 (X) for the x-, y-, and z-coordinate, respectively. The MATLAB calculated output measurements of the cervix point 3D PICS (x/y/z) demonstrated accordingly a very good intra-observer repeatability with an intra-class correlation coefficient (ICC) of 0.984, 0.999, and 0.830 for the x-, y-, and z-coordinate, respectively and a very good inter-observer reproducibility of 0.814, 0.991, and 0.831 for the x-, y-, and z-coordinate, too. Further applications and structure measurements like ligaments or muscles have to be tested in clinical studies.

5. Discussion

The 3D PICS coordinate system allows physicians to quantify the position of any pelvic organ, as well as the location and magnitude of muscular or ligamentous defects lying in- and outside the midsagittal plane. This system takes into account different positions of the pelvis within the scanner and adjusts for movement between scans such as that which can happen with abdominal muscle contraction in Valsalva or simulated defecation. A further advantage is the possible comparison of pelvic floor structures between different scans, including between different subjects. This potentially represents a first step toward the goal of developing a normative human pelvis atlas from a population of MRI datasets of normal subjects (Li et al., 2003).

The developed technique will also allow improvements in understanding of the clinical or surgical situation in 3D, when compared to the limited information provided by measurements on (only midline) 2D image slices.

There exist multiple software tools capable of the analysis and display of medical image data that could implement a 3D coordinate system, allowing the computation of coordinates from a scanner dependent external reference point. Some of these include the Harvard free-download software 3D Slicer^®, the NIH developed ImageJ^®, the Dutch software 3D Viseon^® and the Swiss software OsiriX^®.

5.1 Limitations of the evaluation

There are several points to consider with respect to the developed technique. The accuracy of the approach depends on the accuracy of the localized landmarks and target points, with the accuracy of the target point placement dependent on the slice thickness and resolution of the MR images. The anatomical landmarks themselves are precisely defined and easily located. However, user error during the landmark selection will affect the overall accuracy. Thus during landmark selection, especially if the point placement is undertaken from two different planes and series such as rest and strain, it is recommended to double-check the point placement on one plane with the corresponding orthogonal plane, i.e. point placement on the axial slice should be checked on the corresponding sagittal plane. In addition, it is currently difficult to acquire a wide enough field of view in today’s dynamic MR images to cover both the midsagittal plane and the ischial spines, requiring registration of dynamic data to a static reference series.

Further limitations are the lack of comparisons with other pelvic reference line systems and the lack of longitudinal studies like pre- and postpartum or pre- and postoperative comparisons.

5.2 Future

In the future, we anticipate that data obtained from the proposed rigid 3D coordinate system will lead to clinically relevant advances in overall understanding of pelvic anatomy. Moreover, the 3D PICS will provide a valuable measurement system to solve questions of organ location and will contribute to the validation of clinical data. This will advance the study of the physiologic ranges of organ location as well establishing, for 9 example, how often women with disease fall outside of the normal range. This can be used in evaluation of birth trauma related pelvic floor injuries before the threshold of a clinically relevant prolapse is obvious. The approach will also allow the evaluation of surgical outcomes through the quantitative comparison of pelvic organs in pre- and postoperative image data.

Pelvic organ prolapse is a complex spatial problem that often results from birth injury. It is and will continue to be a major public health concern. Recent studies estimate an approximate doubling of pelvic floor disorders from 2010 to 2050 in the United States, from 18 million to 28.4 million, a situation expected to be mirrored in other Western countries (Wu et al., 2009). This unprecedented demographic change will add to the individual significance and impact of pelvic floor disorders requiring suitable diagnostic tools (York, 2013).

The acceptance and utilization of a standardized method for the measurement and presentation of pelvic organ measurements is vital to improving understanding of POP and other disorders of the pelvic organs; we assume that a normogram of organ height on MR images could also help to improve the specificity of oncologic radiotherapy, including brachytherapy, or diagnosing pelvic tumor extent though this has to be proven by clinical studies (Mazeron et al., 2016; Nguyen et al., 2017). For this kind of investigation all series of images have to be in the same coordinate system. An example can be taken from pulmonology, where a normative human lung atlas has already been developed from computed tomography data sets. This atlas system allows the computation of average transformation to register individual subjects to the template subject. In a next step the human lung atlas could be used for detection and quantification of early signs of lung pathology (Li et al., 2003, 2012).

Future work should aim towards the automation of the approach based on work currently underway towards the automatic recognition of specific pelvic organs or structures, without requiring user interaction (Onal et al., 2014a; Onal et al., 2014b). This might additionally provide quantitative and sensitive measures of structural changes in POP, aging and connective tissue disorders of the pelvis in a longitudinal study setting.

In order to aid research in the field, we are making a prototype of our new measurement technique available as a demo application online at https://3D-PICS.projects.healthcare, for use by radiologists, physicians, surgeons and researchers within the field.

6. Conclusion

Pelvic organ prolapse (POP), a major health concern, is a downward displacement along the axis of gravity of the organs of the pelvis. For reliable pelvic measurements we have proposed, implemented and evaluated a standardized 3D coordinate system called the 3D Pelvic Inclination Correction System (PICS) for evaluating the pelvic anatomy in 3D space. The approach relies on the selection of easily identifiable landmarks for the construction of the standardized coordinate system, meant to represent the pelvis as if the patient were standing. The PICS makes meaningful 3D quantitative assessment of pelvic anatomy possible. It allows the accurate study of the physiologic range of organ location as well as defects on the pelvic sidewall, or birth-related pelvic floor injuries. We expect it to aid in understanding of the anatomy and pathology of prolapse and comparison of outcomes between different surgical collectives.

Highlights.

• MRI reference lines currently available measure pelvic organ (POP) in the midsagittal plane. However. POP and its causes (ligament or muscle defects) are complex spatial problems.

• With four bony landmark points and a vector trigonometry application the first pelvic 3D coordinate system is constructed.

• The 3D Pelvic Inclination Correction System (PICS) allows the study of physiologic and pathologic range of organ location.

• It can be evaluated at various points in time, such as pre- and postoperatively or pre- and postpartum.

Biographies

Caecilia Reiner, MD completed here specialist training in Radiology in 2010 with board-certification in 2011. For her subspeciality training she did a research fellowship from 2011 to 2012 at the Abdominal Imaging Division at Duke Medical Center (Duke University, North Carolina). Since 2012 she is working as a staff radiologist and since 2014 as Assistant Professor at the Institute of Diagnostic and Interventional Radiology at the University Hospital Zurich. She is responsible for Abdominal Imaging in the Department and her research interests include magnetic resonance imaging of the liver including functional imaging and magnetic resonance imaging of the pelvic floor.

Tom Williamson received his Bachelor of Engineering (Biomedical) at Swinburne University, Australia in 2008, subsequently receiving his MSc and PhD in Biomedical Engineering from the University of Bern, Switzerland in 2011 and 2015, respectively. His expertise includes the development of surgical robotics and high precision instrument guidance, as well as the utilization of technological approaches for the improvement of surgical procedures and understanding of clinical situations. His major experience has been directed towards the application of surgical navigation technology and robotics for otologic microsurgery, with ongoing research extending into the fields of neurosurgery, obstetrics/gynaecology, angiology and visceral surgery.

Thomas Winklehner works since 2010 as a project manager in research and industry. He focuses on healthcare, as he has acquired wide experience in this area during his studies and work.

Thomas earned a PhD degree in computer science from the University of Zurich, graduating in 2011.

He currently lives in Bremgarten, Berne, with his wife and children.

Sean Lisse, MD began his career in computer science and artificial intelligence, later transitioning into medicine. He graduated from the University of Michigan Medical school in 2014, and is currently completing his residency in diagnostic radiology at Yale University. His research interests include pelvic floor anatomy and imaging, computer aided image registration, and fusion of different imaging modalities.

Daniel Fink, MD MBA is Professor and Chairman of the Department of Gynecology at the University Hospital of Zurich. He completed his medical training at the University of Zurich, spending two years as a Fellow at the University of California San Diego as well as a year as Associate Professor at the University of New South Wales, Sydney. He also holds an Executive MBA from the University of St. Gallen. Daniel Fink’s field of expertise covers all aspects of gynecologic oncology with a particular interest in the pelvic floor.

John O. L. DeLancey, MD is the Norman F. Miller Professor of Gynecology at the University of Michigan and Director of Pelvic Floor Research. He is a member of the Institute of Medicine and has been President of the American Urogynecologic Society and the Society of Gynecologic Surgeons. He has published over 230 scientific studies. Dr. DeLancey made important discoveries about the fundamental biomechanics of pelvic floor disorders, the factors leading to birth-related pelvic floor injury, and the mechanisms of urinary incontinence. His medical expertise has been recognized by selection for Who’s Who in Medicine and Best Doctors in America.

Cornelia Betschart, MD completed her specialist training in Obstetrics and Gynecology in 2006. For her subspecialty training in Urogynecology she did a Research Fellow Ship from 2011–2013 at the University of Michigan (John DeLancey). She is a board-certified Urogynecologist since 2016 and vice-president of the Swiss Urogynecological Association. Since 2008 she works as a Gynecologist at the University of Zurich and is co-responsible for the Urogynecology Department in the function of Assistant Professor and Lecturer. Her research interests include pelvic floor anatomy and imaging, urogynecological surgery, and phytotherapeutical treatments for chronic bladder conditions.

9. Appendix 1: PICS MATLAB Implementation

%% Minimal PICS MATLAB Implementation
%   Inputs:
%   a: Inferior Pubic Poin``t
%   b: Saccrococcygeal Point
%   i1: Right Ischial Spine
%   i2: Left Ischial Spine
%
% Outputs:
% organ_position: Position of organ in PICS coordinate system
%%
function organ_position = PICS(a, b, iR, iL, x)
       u = (b-a)/norm(b-a);
       i1i2 = (iR-iL)/norm(iR-iL);
       v = cross(iRiL,u);
       v = v/norm(v);
       z = cross(u,v);
       z = z/norm(z);
       cs = [u’,v’,z’];
       rotmat = vrrotvec2mat([cs(:,3)’ 34*pi/180]);
       cs_rot = rotmat*cs;
       transform = [cs_rot, a’; 0 0 0 1];
       organ_position = transform\[x 1]’;
       tmp = organ_position(3);
       organ_position(3) = organ_position(1);
       organ_position(1) = tmp;
end