Atmospheric brown clouds: Impacts on South Asian climate and hydrological cycle

Abstract

South Asian emissions of fossil fuel SO₂ and black carbon increased≈6-fold since 1930, resulting in large atmospheric concentrations of black carbon and other aerosols. This period also witnessed strong negative trends of surface solar radiation, surface evaporation, and summer monsoon rainfall. These changes over India were accompanied by an increase in atmospheric stability and a decrease in sea surface temperature gradients in the Northern Indian Ocean. We conducted an ensemble of coupled ocean-atmosphere simulations from 1930 to 2000 to understand the role of atmospheric brown clouds in the observed trends. The simulations adopt the aerosol radiative forcing from the Indian Ocean experiment observations and also account for global increases in greenhouse gases and sulfate aerosols. The simulated decreases in surface solar radiation, changes in surface and atmospheric temperatures over land and sea, and decreases in monsoon rainfall are similar to the observed trends. We also show that greenhouse gases and sulfates, by themselves, do not account for the magnitude or even the sign in many instances, of the observed trends. Thus, our simulations suggest that absorbing aerosols in atmospheric brown clouds may have played a major role in the observed regional climate and hydrological cycle changes and have masked as much as 50% of the surface warming due to the global increase in greenhouse gases. The simulations also raise the possibility that, if current trends in emissions continue, the subcontinent may experience a doubling of the drought frequency in the coming decades.

Atmospheric brown clouds (ABCs) are basically layers of air pollution consisting of aerosols such as black carbon (BC), organic carbon, and dust that absorb and scatter solar radiation (1). ABCs also contain other anthropogenic aerosols such as sulfates, nitrates, and fly ash, which primarily scatter solar radiation. The absorption of solar radiation by ABCs contributes to atmospheric solar heating. The absorption together with the scattering leads to a large reduction of UV and visible wavelength solar radiation at the surface (2), alternately referred to as dimming (3). In addition, aerosols nucleate more cloud drops that enhance scattering of solar radiation and contribute to additional dimming (4). The nucleation of clouds by aerosols also reduces the precipitation efficiency of clouds (5). The ABC radiative forcing can reduce rainfall through several mechanisms as described below.

ABC radiative forcing can cool the surface (4–8), stabilize the atmosphere (9, 10), and reduce evaporation (6, 7) and rainfall (6, 7, 11). Because aerosols have short lifetimes of a week or two, they are concentrated close to their sources in the Northern Hemisphere and thus cool the Northern Hemisphere oceans relative to the Southern Hemisphere oceans. This aerosol-imposed cooling of northern tropical oceans has been shown (8) to weaken the summertime meridional overturning circulation (also called Hadley cell or intertropical convergence zone circulation) and reduce rainfall in northern Africa. Lastly, absorbing aerosols alter the spatial gradient in the atmospheric solar heating, and in East and South Asia this alteration has been shown (9, 10) to perturb the spatial distribution of monsoonal rainfall, with more rains in some regions and less in others.

Several studies have pointed out the impacts of anthropogenic sulfate aerosols on rainfall (11–13). Only recently have we become aware that absorbing aerosols, particularly BC, can potentially play a major role in the global scale reduction of rainfall (6, 7).

As shown in this work, all of the above effects of aerosols are manifest over South Asia and the Northern Indian Ocean (NIO). During the long dry season extending from October to May, anthropogenic BC and other manmade aerosols are transported long distances and envelope most of South Asia and NIO in a 3-km-thick brownish layer (14). This brown cloud of aerosols reduces solar radiation at the surface by ≈10% and nearly doubles the atmospheric solar heating (6, 14). In this work, we investigate the impact of the ABC radiative forcing on the observed regional climate trends during the 20th century. The findings described here are based on comparison of 20th-century trends simulated by a coupled ocean-atmosphere climate model with observed trends. We find that the simulated climate impacts of just the greenhouse gases (GHGs) or sulfates are inadequate, and in many instances even inconsistent, with the observed trends. It is only when we include realistic ABC forcing that the simulated trends over India and NIO are similar to the observed changes.

The earlier modeling studies (9, 10) of the South Asian brown clouds provided interesting results about the connections between aerosols and rainfall but made several limiting assumptions. The earlier studies were conducted with prescribed sea surface temperatures (SSTs) and thus did not account for the response of the SSTs to aerosol forcing. They also did not account for the seasonal variation of the forcing, and both of these were major factors in the simulated climate changes. More importantly, the earlier studies were equilibrium simulations with ABC forcing held fixed at current values and, thus, could not examine the impact of the haze on the 20th-century climate trends. It was the comparison of the simulated with the observed trends that provided crucial new insights into the role of ABCs. Thus, the present study revisits the issue with a more comprehensive approach.

Methods

The simulations reported here were conducted with the coupled ocean-atmosphere model developed at the National Center for Atmospheric Research, referred to as the parallel climate model (PCM) (15, 16). The PCM consists of a dynamical ocean general circulation model (GCM) that is coupled to an atmospheric GCM. It has been run from the year 1850 until 2050 with observed increases of GHGs (16) and sulfate aerosols until 1998 and fixed at 1998 levels beyond 1998 (referred to as GHGs+SO4_1998). A second case, GHGs+SO4_2050, adopts a business-as-usual scenario for increases in GHGs and sulfates until 2050 (16). The model accounts for only the direct effects of sulfates. Five ensemble runs of 200 years per run are available for each of the two cases. The results from these two cases have been published elsewhere (16).

We ran three different ABC cases. The first, ABC_1998, adds to the GHGs+SO4_1998 case the ABC forcing from 1930 until 1998, after which the forcing due to GHGs, SO₄, and ABC were held fixed at 1998 levels. The ABC forcing for the South Asian region and the tropical Indian Ocean was determined for 1999 from satellite, aircraft, and surface observations during the Indian Ocean experiment (14) and subsequently extended to the 1995–1999 period (6). For the dry season from October to May, the 1995–1999 Indian Ocean experiment data for ABC forcing was incorporated in the PCM. For the wet season from June to September, observational data were not available, and we adopted the aerosol assimilation model of Chin et al. (17), which matches Indian Ocean experiment results for the March to May period. We include both the direct and the indirect forcing (see ref. 14 for details) of the aerosols. Details of the aerosol forcing as adopted in the PCM are given in ref. 10, and pertinent details from ref. 10 also are summarized in Supporting Text, which is published as supporting information on the PNAS web site.

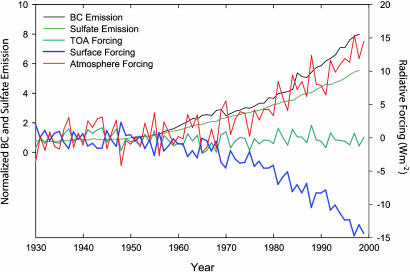
We scaled the 1995–1999 values of the ABC forcing to the emission history of SO₂ (18) and BC (19) for India (see Fig. 1) and extrapolated it back in time to estimate the time history of the forcing from 1930 (Fig. 1). The aerosols emissions before 1930 were very small (18, 19) for the South Asian region, and to save computational time, we started the PCM runs from 1930 onward. The results are not sensitive to the absolute values of the emission because we are scaling the emission to its value for 1995–1999. We could have scaled it to some fraction of SO₂ and BC emissions, but the scaling factors for SO₂ and BC are nearly the same because in Fig. 1 they are both due to fossil fuel combustion. For example, both SO₂ and fossil fuel BC increased ≈6-fold since the 1930s (Fig. 1), which is due to the nearly 4-fold increase in population since the 1930s and the accompanying industrialization The BC emission history shown in Fig. 1 does not include biomass burning or biofuel cooking source because we have no good basis for estimating the historical changes in these sources (19). Had we scaled these emission sources to population history, we would have arrived at scaling factors similar to those shown in Fig. 1, i.e., negligible impact of biomass and biofuel BC before 1930. However we do not expect our scaling factors to be impacted significantly, because as discussed in Novakov et al. (19), BC from fossil fuel combustion seem to be the major source of BC over the region of interest (see also ref. 14).

Fig. 1.

Time series of emissions and forcing terms. Published estimates of the emission of SO₂ (18) and BC (19) are normalized with their 1950 values. The changes, due to the ABCs, in the net (down minus up) solar fluxes at the surface (surface forcing), at top of the atmosphere (top-of-the-atmosphere forcing), and net solar heating of the atmosphere are taken from climate model (PCM) simulations for the ABC_1998 case. The forcing is for annual mean conditions and is the average for all of South Asia and NIO (0° to 30°N and 60°E to 100°E). The interannual variations in the forcing are due to variations in cloudiness.

The primary advantage of our approach of incorporating the aerosol forcing derived from observations is that it guarantees more accurate representation of the forcing. Its weakness is that it cannot account for potential feedbacks between the forcing and the response, such as changes in circulation resulting from the forcing altering the aerosol concentrations.

To get statistically significant results, we ran five independent simulations of 120 years each, with differing initial conditions. The second case, ABC_2050, allows for increases in GHGs and SO₄ (as in ref. 16) and extrapolates the ABC forcing, assuming a business-as-usual scenario to 2050. For this extrapolation, we obtained a linear fit to the 1990–1998 forcing trend (Fig. 1), assumed the same trend until 2050, and ran the model until 2050. To isolate ABC effects, we ran a third case, ABC_2050_1, in which ABC forcing was allowed to increase until 2050 as in ABC_2050, but the GHGs and SO₄ were held fixed at 1998 values. We conducted only one simulation each of ABC_2050 and ABC_2050_1. The signals for these two cases were sufficiently large that they did not require five ensemble simulations.

Results

The ABCs over the South Asian region have the following eight major regional climate impacts.

Aerosol Forcing. The ABC decreases the surface solar radiation flux (surface forcing), enhances the solar heating of the troposphere (atmospheric forcing), and alters the net (incoming minus reflected) solar flux at the top of the atmosphere (top-of-the-atmosphere forcing). The simulated time series of the three forcing terms are shown in Fig. 1 along with the changes in SO₂ and BC emissions. These results were obtained from the ABC_1998 simulations and thus include cloudiness changes. However, the cloudiness changes during 1930–2000 in the model were negligible, consistent with the negligible trends in observed cloudiness over NIO and India (20). The net solar forcing at top of the atmosphere is within ±1 W·m^–2 throughout the time period, whereas the surface forcing (and atmospheric forcing) is of the order of –10 (+10) W·m^–2 to –15 (+15) W·m^–2 in the 1990s. The regional, latitudinal, and seasonal variations of the forcing are large and are shown in Figs. 8–11, which are published as supporting information on the PNAS web site. The surface forcing ranges from near 0 W·m^–2 south of 10°S to approximately –25 W·m^–2 in northern Bay of Bengal (see Fig. 8 for annual mean values for 1995–1999). Peak surface forcing values ranging from –30 to –20 W·m^–2 occur from January to May (Fig. 10).

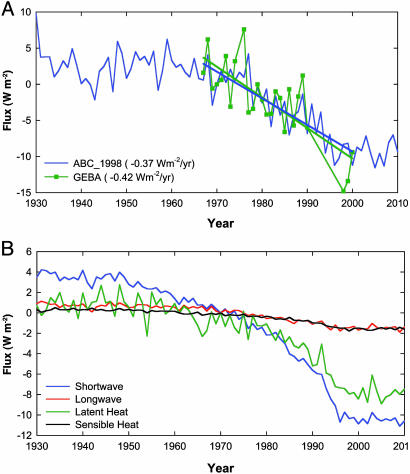
Dimming. A critical test of the simulation is a comparison of the computed dimming with observations. Fig. 2 compares the Global Energy Budget Archive surface solar radiation data set (21) for India with that from ABC_1998. Of the 24 Indian Global Energy Budget Archive stations, only 10 had nearly continuous observations for the 1960–2000 period, and fortunately these 10 stations, as shown below, were distributed over northern, southern, eastern, and western India as follows: Ahmedabad (72.63°E, 23.07°N), Bhaunagar (72.18°E, 21.75°N), Goa (73.82°E, 15.48°N), Chennai (80.18°E, 13.00°N), Nagpur (79.05°E, 21.10°N), New Delhi (77.20°E, 28.58°N), Pune (73.85°E, 18.53°N), Shillong (91.88°E, 25.57°N), Trivandrum (76.95°E, 8.48°N), and Vishakhapatnam (83.23°E, 17.72°N). These 10 stations were included in the results shown in Fig. 2. Both the observed and the simulated trends are in excellent agreement and reveal that the rate of the observed dimming for 1960–2000 is approximately –0.42 W·m^–2 per year to be compared with the simulated value of approximately –0.37 (±0.12) W·m^–2 per year. The corresponding values for the 1960–1990 period (when the Global Energy Budget Archive record was more continuous) were, respectively, –0.29 and –0.25 W·m^–2 per year. The uncertainty estimates for the simulated trends and the confidence intervals for the observed trends described here and elsewhere in the text are given in the figure legends. The uncertainties for the simulations were obtained by estimating the trend for each run of the five-member ensemble and calculating the 2σ of the five trend mean. For the 1930–2000 period, the simulated dimming is ≈8% (±2%).

Fig. 2.

Time series of surface heat budget terms. (A) Simulated (blue) and observed (green) annual mean solar fluxes for India at the surface. The fluxes are for average cloud conditions. The simulations are averaged over 5°N to 25°N and from 70°E to 90°E. The observed values are from 10 surface stations distributed between eastern, western, northern, and southern India. The trend in Global Energy Budget Archive is –0.42 W·m^–2 per year (±0.15; 95% confidence level), and the trend in the ABC_1998 run is –0.37 W·m^–2 per year (±0.12) (2SD of the trends from the five runs of the ensemble). (B) The simulated annual mean surface heat budget for the Indian Ocean from 10°S to 30°N and from 60°E to 100°E.

Reduction in Surface Evaporation. A reduction in surface solar radiation can lead to a reduction in surface evaporation (6, 7, 13) because ≈50–85% of the radiative heating at the surface is balanced by evaporation (22). The simulated evaporation decreased from both the land and the adjacent NIO (Fig. 2B and see also Fig. 12, which is published as supporting information on the PNAS web site) with the largest decreases occurring over the NIO (Fig. 12). Approximately 70% of the reduction in NIO solar radiation is balanced by a reduction in evaporation (Fig. 2B). Peak reductions (–10%) in evaporation occurred during January to April when the reduction in surface solar radiation was largest, but moderate decreases (–5%) persisted through June and early July. There are no data over the oceans (that are reliable for long-term trend analysis) to verify the reduction in evaporation, but observations for land surface (23) support the large reduction in evaporation in all seasons including the monsoon. As explained later, the evaporation decrease in the model was caused by a decrease in the temperature and humidity gradient between the surface and the boundary layer. The simulated link between reduction in solar radiation and reduction in evaporation is similar to that yielded by other model studies (7, 24).

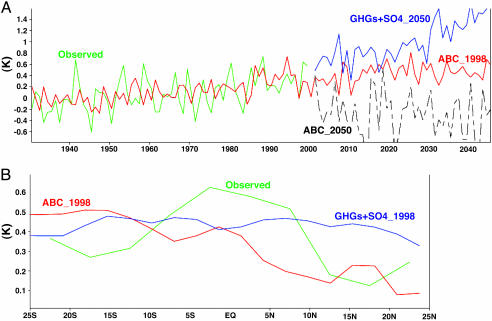
Surface Cooling Effect. ABCs exerted the largest surface-cooling effect during the dry season from October to May, and we examine this period first. The simulated temperature trends for the dry season are in excellent agreement with the observed trends (Fig. 3A). The simulated temperature change values shown in Fig. 3A are ensemble means of the five independent simulations, and, hence, the interannual variability shown in the figure for the simulations appears smaller than the observed variability. The 1930–2000 warming trend for GHGs+SO4_1998 is 0.76 (±0.1) K, whereas it is only 0.37 (±0.1) K for ABC_1998. For the annual mean, the 1930–2000 surface temperature trends for GHGs_1998, GHGs+SO4_1998, and ABC_1998 are, respectively, 0.8 (±0.1), 0.67 (±0.1), and 0.45 (±0.05) K. The observed trend of 0.44 K (±0.08 K is the 95% confidence interval) is in agreement with ABC_1998 simulations. Thus, ABC has a strong cooling effect on the surface, as we would expect from the negative surface forcing (Fig. 2). With just GHGs+SO4 beyond 1998, the annual mean 1930–2050 warming trend is 1.5 K (Fig. 3A), whereas the addition of ABCs nearly balances the surface warming of GHGs with a near-zero trend.

Fig. 3.

Simulated and observed surface temperature changes (K). (A) The dry season (October to May) temperature changes from observations (green) and from various cases of model simulations. (B) SST trend during 1930–2000 for the Indian Ocean (averaged between 60°E to 100°E) as a function of latitude for the premonsoon season of March to June. The uncertainty of the model trend, as estimated from five different ensemble member runs, is <0.1 K between 10°S and 20°N and <0.2 K outside, whereas the observed trend range at the 95% confidence level is ±0.2 K. For PCM, air temperature at 2 m above the sea surface was used. Observed temperature trends were obtained from the Jones Climatic Research Unit (CRU) data set (archived at the Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, Oak Ridge, TN).

Weakening of Latitudinal SST Gradients. Latitudinal gradients in SST play an important role in the monsoon dynamics and the tropical climate (8, 25). The ABCs introduce a hemispherical and latitudinal asymmetry in the radiative forcing, with more reduction in surface solar radiation over the NIO compared to the SIO and larger reduction over the Arabian Sea and Bay of Bengal compared with the equatorial Indian Ocean (6, 14) (Fig. 8). This spatial heating pattern drives a similar pattern in the simulated SST trends (Fig. 3B). We focused on the SSTs during March to June when the weakening effect was strongest in the simulations. The normal climatological SSTs during these months increase from ≈301 K at the equator to ≈303Kat ≈20°N (average of Arabian Sea and Bay of Bengal). The observed trends (Fig. 3B) reveal that since the 1950s, this gradient has weakened by ≈0.5 K, which is 25% of the climatological gradient. The simulated trends for ABC_1998 also reveal such a weakening (Fig. 3B), whereas GHGs+SO4_1998 shows (Fig. 2B) that GHGs are not responsible for this weakening. The simulated SST trend is positive at all latitudes because of the forcing due to GHGs. However, the NIO warms less than the SIO because of the ABC-induced surface cooling (see ABC_1998 curve in Fig. 3B). Comparing the ABC simulations with the observed trends, the equatorial Indian Ocean warms ≈0.4 K more than that at 20°N in the ABC_1998 simulations, very close to the 0.5 K equatorial warming (relative to 20°N) in the observations. Thus, according to our simulations, the SST change pattern caused by the ABC forcing is similar to the observed weakening of the SST gradient. It should be noted that, although the negative forcing at the surface is very small during June and July, the weakening effect on SST gradients persists through June and the first half of July because of the large thermal inertia of the oceans. The smaller warming of NIO also is supported by ocean heat content data (26), which showed that, whereas the global ocean as well as SIO heat content increased significantly since the 1950s, the increase in the NIO heat content was relatively smaller.

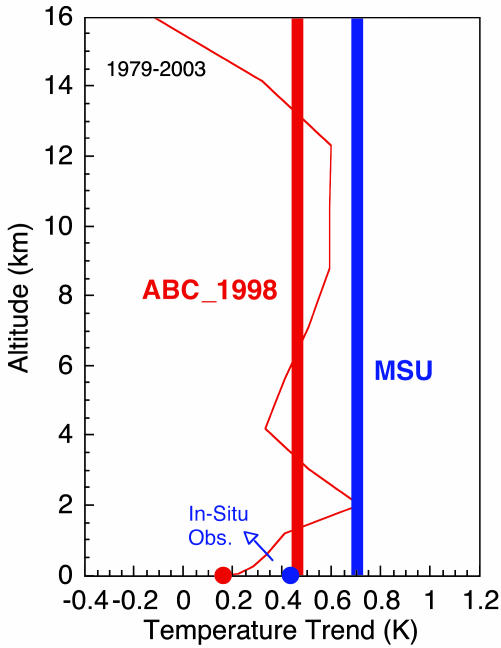
Stabilization of the Troposphere. In the tropics, within the first 5 km above the surface, the temperature drops with altitude sufficiently steeply, approximately –5 to –6 K/km, that the atmosphere is unstable to moist convection. This instability coupled with low-level moisture convergence triggers deep convection and rainfall. The ABC solar heating inhibits this instability by a differential warming of the atmosphere with respect to the surface (Figs. 4 and 12). The solar heating due to ABC is largely confined to the first 4 km (Fig. 11). This extra heating adds to the GHG warming of the lower troposphere, while, at the surface, the ABC cooling is competing with the GHG warming. A critical test of the simulation is to examine whether the observations support this ABC-induced stabilizing effect. We focus on the 1979–2003 period (Fig. 4) when the space-borne microwave sounding unit (MSU) observations are available (27). The MSU data does not yield a vertical profile of the temperature but instead provides an integrated measure of the temperature within the troposphere and lower stratosphere. The vertical average temperature of the troposphere for this period is derived by a linear combination of the MSU channels 2 and 4 brightness temperatures (27), which have an effective weighting function with near-zero contribution from the stratosphere. Fig. 4 shows the total annual mean temperature trends for 1979–2003 averaged over the India region. There are two versions of the MSU data, and we adopted the version that is referred to as MSU RSS data (27). To compare with the MSU trend, the simulated vertical trend profile shown in Fig. 4 is integrated with the effective MSU weighting function. The MSU-derived tropospheric temperature trend from 1979 to 2003 (blue bar in Fig. 4) is ≈0.7 K (with a 95% confidence interval of ≈0.2 K), whereas the ABC_1998 trend (red bar) is 0.46 (±0.2) K. The trend in the mean tropospheric stability (difference between atmospheric temperature trend and surface-air temperature trend) is +0.27 K (with a 95% confidence interval of 0.2 K) for the observations and is +0.3 (±0.2) K for ABC_1998. However, without ABCs, the change in the stability estimated by the GHGs+SO4 case is only 0.09 K. The observed and the ABC_1998 trend differences for the dry season are larger than the annual mean values by ≈50%, whereas for the GHGs+SO4 case the dry season trend is near zero, which clearly suggests that the ABC forcing is the major reason for the observed increase in the tropospheric stability. The critical parameter for convection is the instability of the lower troposphere, and Fig. 4 shows that from 1979 to 2003, the temperature at 2 km increased by ≈0.55 K relative to the surface, which is equivalent to decreasing the convective instability (measured in terms of the vertical gradient of equivalent potential temperature) of this region by as much as 15%.

Fig. 4.

Vertical profile of the simulated temperature trend by ABC_1998 (red curve) for the 1979–2003 period. The values are averaged over all of India. The blue vertical bar is the observed vertically averaged trend from MSU, and the red bar is the vertically averaged trend simulated by ABC_1998. The red bar was obtained by integrating the simulated vertical profile (red curve) with the MSU weighting function (27). The uncertainty in the simulated trend varies from 0.15 to 0.25 K depending on altitude. The mean uncertainty for the vertically averaged trend (red bar) is ≈0.2 K. The 95% confidence interval for the MSU observed trend is ≈0.2 K.

The increase in the low-level stability inhibits convection and vertical transport of moisture, accompanied by an increase in boundary-layer humidity and a decrease aloft (Fig. 13, which is published as supporting information on the PNAS web site). The increase in stability, together with the increase in boundary-layer humidity, leads to a decrease in evaporation (Figs. 2B and 12). The corresponding decrease in latent heat flux from the surface largely balances the dimming at the surface (Fig. 2B). Thus, the dimming accompanied by a corresponding increase in atmospheric solar heating (Figs. 1, 8, and 9) is the ultimate source of the decrease in evaporation.

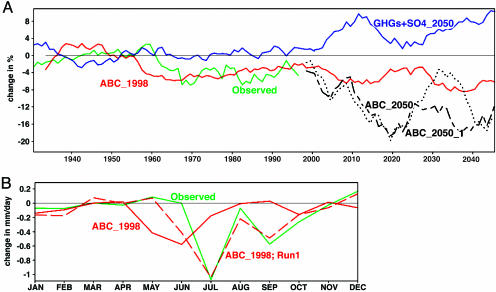
Decrease in Monsoon Rainfall. The rainfall during the summer monsoon season of June to September is the major source of precipitation for India and other parts of South Asia. The India-averaged June to September rainfall decreased after the 1950s (Fig. 5A) in both the observations and the ABC_1998 simulations. Conversely, the GHGs+SO4 case showed no trend until 2000 and a positive trend after 2000. Fig. 5A shows the rainfall anomaly as percent deviation from the 1930–1960 average. The simulated rainfall reduction of ≈5% (±3%) from 1930 to 2000 (the ABC_1998 curves in Fig. 5A) is consistent with trends in the Indian rainfall data (28). Both the model and the observations reveal an interdecadal variability of ≈2–3%. For example, examine the fluctuation during 2000–2050 for the ABC_1998 curve when ABCs and GHGs+SO₄ were fixed at the 1998 value. The model with just the GHGs and sulfates (GHS+SO4_1998 case; data not shown) estimates an equilibrium precipitation increase of ≈3–5%. Thus, the drying effect of ABC, i.e., the difference between the ABC_1998 and the GHG+SO4_1998 cases, is ≈8–10%. Most, if not all, of the rainfall reduction in the model since the 1950s is due to ABCs and not natural variability. In fact, none of the model cases that neglected the ABC forcing simulated the decrease witnessed after the 1950s. For example, with just the GHGs and SO₄, the precipitation anomaly after 2000 is consistently above the 1930–1960 mean.

Fig. 5.

Rainfall trends. (A) Time series of observed and simulated summer (June to September) rainfall for India from observations and PCM simulations. The results are the percent deviation of the rainfall from the 1930–1960 average. Observed rainfall data were obtained from ref. 28. The data are smoothed by an 11-year running mean averaging procedure. (B) Trend for 1930–2000 in monthly mean rainfall for India. The uncertainty of the model trend, as estimated from five realizations, is ≈0.4 mm/day from May to July and <0.2 mm/day in the other months. For the observed trend, the 95% confidence level is ±0.9 mm/day (wet season) down to ±0.2 mm/day (January–March).

The difference between the GHGs+SO4 and ABC simulations begins to deviate significantly after 2000. With no further increase in ABC beyond 1998, the decreases in rainfall equilibrate to approximately –5% to –8% of the 1930–1960 average. However, when ABC is allowed to increase beyond 1998 and with GHGs and SO₄ held constant at 1998 values (the ABC_2050_1 case), the average precipitation decreases by as much as 15–20%. Even when GHGs and SO₄ are allowed to increase with ABC (the ABC_2050 case), the ABC effect dominates, with a large decrease in rainfall, but the interdecadal fluctuations are larger, too. For example, the decrease in the 2020s is approximately –18%, whereas it is only approximately –4% for the 2030s, reverting back to a large decrease again in the 2040s. The cause of such large fluctuations may in part be due to the competing effects of GHGs and ABCs and in part due to the fact that we have only one run for this case and not the average of five ensemble runs.

Another important feature of the observed decrease is that it peaks in July (Fig. 5B), but the five-member ensemble mean of the model simulated decrease was in June. However, one of the five ABC runs (ABC_1998_Run 1 curve in Fig. 5B) was able to simulate better the decrease in July rainfall, and the amplitude of the decrease was also closer to the observed changes. It is interesting that, for this run, the decrease in evaporation and the SST gradients continued into July, whereas for the other four ensemble runs, these decreases weakened after June.

The largest reduction in monsoon rainfall occurs in the central Indian peninsula, somewhat similar to the observed decrease (see Fig. 14, which is published as supporting information on the PNAS web site). The peak decreases for 1930–2000 are as high as 1–2 mm/day. The spatial patterns between the observations and simulations differ somewhat, which is anticipated given the coarse resolution of the model (≈300 × 300 km) and due to the fact that the simulated trend is an average of five simulations of the ensemble compared with one realization of the observed trend.

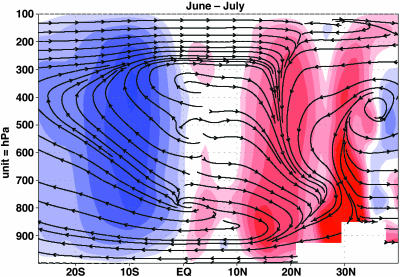
The normal circulation during the summer monsoon has warm and humid air rising over most regions north of the equator bringing rainfall to South Asia with a compensatory sinking branch south of the equator (25). This Hadley-type circulation decreased in intensity for the ABC_1998 simulation (Fig. 6), whereas such a decrease was not seen in the GHGs+SO4 case. The change in the June and July circulation due to ABCs for 1985–2000 was obtained by differencing the circulation for the ABC_1998 case with that for the GHGs+SO4 case. Fig. 6 shows a reverse circulation with rising branch south of ≈15°S and sinking north of 5°N covering most of South Asia and the adjacent NIO. There is some observational support for this reversal. The National Center for Environment Prediction's forecast meteorological fields also reveal a similar 45-year downward trend in the meridional circulation over India and NIO, but the reliability of the National Center for Environment Prediction fields for trend analysis is largely unknown. The increase in rising motions south of the equator, accompanied by a corresponding subsidence in the NIO, in effect leads to a southward shift of the monsoon circulation, similar to that obtained by the model studies of Rotstayn and Lohmann (8) for the Atlantic Ocean. In their model study, the weakening of the meridional circulation and the southward shift of rainfall was caused by the indirect effects of sulfate aerosols over the Atlantic. They deduced that the primary reason for the southward shift is a larger SST reduction in the northern Atlantic Ocean than the southern ocean, due to a larger perturbation of the negative aerosol forcing in the northern ocean. This result is similar to the finding of this study in which the larger negative forcing of ABCs at the surface over South Asia and the NIO suppressed the GHGs warming of SST more in the NIO (Fig. 3B) than in the SIO and weakened the SST gradient.

Fig. 6.

Change in the meridional circulation due to the ABC from 1985 to 2000 for June and July. The fields have been averaged from 60°E to 100°E, essentially covering the entire Indian Ocean and the South Asian region. The changes were obtained by differencing the 1985–2000 averaged streamlines: ABC_1998_GHGs+SO4_1998. The red shade indicates a region with increased sinking motions, and the blue shade indicates regions with increased rising motions.

The resulting deceleration of the summer monsoonal circulation, the decrease in evaporation, and the increase in stability are the primary mechanisms for the reduction in the summer monsoon rainfall. We arrived at this conclusion through a series of sensitivity studies with prescribed SST version of the GCM. We ran three simulations as follows: (i) the control case in which we ran the model without ABC forcing and the SST was prescribed to be climatological values (from observations); (ii) we ran the model without the ABC forcing but with the imposed SST trends obtained from the ABC_1998 case; and (iii) the SST was prescribed as in the control case, but we introduced the ABC forcing. The second case mimics the weakening of the SST gradients by the ABC forcing, whereas the third case accounts for the effects of the ABC forcing on evaporation and atmospheric stability. The second and the third cases were able to account for most (≈75%) of the simulated (by ABC_1998) weakening of the monsoonal circulation and rainfall, and the two cases had about the same effect on the rainfall reduction.

It is interesting to note that ABCs had the reverse effect on the wintertime circulation (see Fig. 15, which is published as supporting information on the PNAS web site). ABCs led to an increase in the upward motions over India. The increase in the rising motion is due to the direct soot heating of the lower atmosphere. In the low latitudes, because of the weaker Coriolis force, regionally concentrated atmospheric radiative heating is balanced primarily by adiabatic cooling due to rising motions (25). Conversely, during June and July, the soot heating decreases substantially. However, because of the large thermal inertia of the ocean and the 30- to 60-day response time of the atmosphere to radiative–convective perturbations (29), the effects of ABCs on the SST gradient, the atmospheric stability, and evaporation linger on few months longer into July.

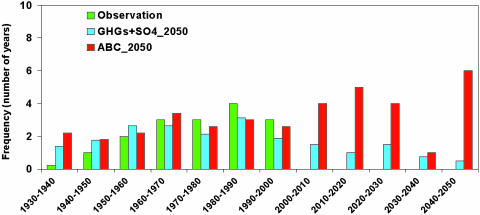
ABC-Induced Droughts. When the summer precipitation decreases (from the climatological average) by >10%, a drought is declared in India (30). Fig. 7 shows this drought frequency as number of years of drought for each decade, where we have taken the 1930–1960 average rainfall as the climatological average. There is a large interdecadal variability in the frequency. From 1930 to 2000, the frequency in both observations and model simulations ranges mostly from 1 to 3 years of drought per decade. Only once during this period does the frequency reach 4 years (see that observed for 1980–1990). However, if ABC is allowed to increase beyond 1998, the frequency is consistently >4 years (with the exception of one decade) and for the decade of 2040, 6 years suffer a drought.

Fig. 7.

Simulated and observed frequency of droughts per decade. Drought is defined to occur when the summer rainfall decrease exceeds 10% of the climatological average, defined here as the average summer rainfall for 1930–1960.

The monsoon system poses formidable modeling challenges (30, 31), and most, if not all global ocean–atmosphere models have difficulty in simulating the South Asian monsoon rainfall (9, 25, 31). The monsoon simulations by the PCM and by the prescribed SST version of the GCM used in this study are discussed in detail by Meehl and Arblaster (figures 2 and 5 and text in ref. 32). The rainfall maxima south of India and over eastern India, Bangladesh, and Bay of Bengal are well simulated by both versions of the model (PCM and prescribed SST GCM). PCM simulated deficient rainfall in western Indian peninsula and excess rainfall over the Himalayas when compared with observations. As shown by Meehl and Arblaster (32), the area-averaged seasonal monsoon index of June–July–August monsoon rainfall (averaged over 5°N to 40°N and 60°E to 100°E) is 5.3 mm/day for observations, 4.7 mm/day for PCM, and 6.9 mm/day for the prescribed SST version of the GCM. For just the Indian subcontinent, the monsoon rainfall for the two versions of the model are, respectively, 35% below and 30% above the observed rainfall.

Our confidence in the PCM trends is derived from the close agreement between the observed and simulated trends in the surface temperature over India and NIO, in the latitudinal gradients in the NIO SSTs, in the tropospheric stability over India, and in the monsoon rainfall trends and the drought frequencies. Furthermore, although the PCM-simulated area average monsoon rainfall is smaller than the prescribed SST version of the GCM by ≈35% (32), the two versions of the GCM responded similarly in the predicted decrease in rainfall when we impose the ABC-induced SST changes simulated by ABC_1998 on the prescribed SST GCM. This similarity is reassuring because it indicates that the present findings are not sensitive to the mean climate of the GCM. Lastly, the sensitivity of the PCM monsoon rainfall to radiative forcing is similar to that of other models. For example, several model studies (see references in ref. 32) have shown that increasing GHGs in the model increases the simulated monsoon rainfall, and the PCM simulations also reveal similar sensitivity (refs. 25 and 32; see also Fig. 5).

Discussion

We used Indian Ocean experiment field observations in conjunction with satellite data and an aerosol assimilation model to simulate the radiative forcing of ABCs since 1930. The simulated dimming trend of –0.37 W·m^–2 per year from 1960 to 2000 compares well with the observed trend of –0.42 W·m^–2 per year due to the ABCs. The total ABC-induced dimming from 1930 to 2000 is –8% (Fig. 2). In the GCM, the dimming led to a decrease in evaporation from India and NIO, an important source of water vapor for the monsoon rainfall. The dimming, in the GCM, also led to a large surface cooling that offset as much as 50% of the warming due to GHGs during the 8-month dry season and helps explain the smaller surface warming trends observed over India and NIO (Fig. 3A). The simulated annual mean surface warming trend is 0.45 K from 1930 to 2000, which compares well with the observed warming trend of 0.44 K. ABCs nearly doubled the atmospheric solar heating rate since the 1930s, and we show that the resulting atmospheric warming can help explain the increase in tropospheric stability over South Asia, i.e., a differential warming of the troposphere with respect to the surface, as observed by space-borne MSU (Fig. 4). For the 1979–2003 period, the simulated and observed differential warming trends are, respectively, 0.30 and 0.27 K. ABCs also help explain the observed weakening of the climatological NIO SST (Fig. 3B). All of the above changes work in the same direction to weaken the monsoon circulation and decrease summer rainfall by ≈5% (Fig. 5). We also show that over South Asia, ABCs and GHGs have competing effects on all of the above trends and that the increases in GHGs by themselves are unable to explain the magnitude, and even the sign in some instances, of the observed trends. The South Asian ABCs also leave a global signal. ABCs contribute a slight cooling of approximately –0.04 K (±0.02) during 1950–2000 and a decrease of ≈1% (±0.5%) in global mean land-average rainfall.

The uncertainties in the imposed South Asian aerosol radiative forcing are of the order of ±15% for the 1990s (14) with probably greater uncertainties for the earlier decades due to uncertainties in aerosol emissions history. Furthermore, the ABC aerosol forcing in the rest of the tropics has not been determined from observations, and the present as well as earlier studies (4, 7, 8) are largely relying on model estimates. Given the significance of the present findings, it is of great importance to undertake field observations of the forcing over East Asia, Africa, and South America.

Some remaining issues with respect to monsoon rainfall will be addressed here as follows. (i) Increase in aerosols can nucleate copious amounts of small droplets, which can inhibit the formation of larger raindrops and decrease precipitation efficiency (33). This microphysical effect can suppress rainfall in polluted regions (5) and add to the rainfall decreases simulated in the present study. (ii) There has been a steady increase of drought frequency from the 1930s, which peaked in the 1980s (Fig. 7), with decrease in average rainfall after the 1960s. The drought frequency abated during the 1990s (30), but the decadal rainfall was still less than normal. During 2001–2004, two droughts have already occurred, and the average rainfall for this decade so far is 9% below normal. These negative trends lead us to speculate whether the ABC is indeed appearing to show its impact as guided by our modeling results, even though there may be other causes such as El Niño–Southern Oscillation–monsoon (32, 34) interactions or natural variations in other slowly varying boundary conditions such as land-surface moisture, Eurasian snow cover, and others (34). ABCs have such a large effect on the monsoon primarily because the forcing simultaneously impacts many components of the monsoon system, including the solar heating of the surface–atmosphere system, the SST gradient, the convective instability of the troposphere, evaporation, and the Hadley circulation, which are factors that have fundamental influences on the monsoon rainfall (25, 30, 31, 34).

The increase in atmospheric stability and the reduction in rainfall are important aspects of the air pollution impacts on climate. Both these effects can enhance the lifetime of aerosols because increases in low-level inversion (see Fig. 4) can increase the persistence of brownish haze layers, and reduction in rainfall can decrease the washout of aerosols. Such feedback effects should be included in future studies to understand the full impact of the ABCs on South Asia. Of particular concern is the reduction in monsoon rainfall in India because in South Asia there is a strong positive correlation between food production and precipitation amount (35). In addition, availability of fresh water is a major issue for the future (36). Even with the forcing fixed at 1998 values, the rainfall decrease in India continues to worsen beyond 1998 (Fig. 3B). The impact of the ABC on monsoon rainfall, in conjunction with the health impacts of air pollution (37), provides a strong rationale for reducing air pollution in the developing nations. However, a sudden reduction in air pollution without a concomitant reduction in global GHGs also can accelerate the warming in South Asia because, according to the present simulations, ABCs have masked as much as 50% of the surface warming due to GHGs.