How Does Mg²⁺ Modulate the RNA Folding Mechanism: A Case Study of the G:C W:W Trans Basepair

Abstract

Reverse Watson-Crick G:C basepairs (G:C W:W Trans) occur frequently in different functional RNAs. This is one of the few basepairs whose gas-phase-optimized isolated geometry is inconsistent with the corresponding experimental geometry. Several earlier studies indicate that through post-transcriptional modification, direct protonation, or coordination with Mg²⁺, accumulation of positive charge near N7 of guanine can stabilize the experimental geometry. Interestingly, recent studies reveal significant variation in the position of putatively bound Mg²⁺. This, in conjunction with recently raised doubts regarding some of the Mg²⁺ assignments near the imino nitrogen of guanine, is suggestive of the existence of multiple Mg²⁺ binding modes for this basepair. Our detailed investigation of Mg²⁺-bound G:C W:W Trans pairs occurring in high-resolution RNA crystal structures shows that they are found in 14 different contexts, eight of which display Mg²⁺ binding at the Hoogsteen edge of guanine. Further examination of occurrences in these eight contexts led to the characterization of three different Mg²⁺ binding modes: 1) direct binding via N7 coordination, 2) direct binding via O6 coordination, and 3) binding via hydrogen-bonding interaction with the first-shell water molecules. In the crystal structures, the latter two modes are associated with a buckled and propeller-twisted geometry of the basepair. Interestingly, respective optimized geometries of these different Mg²⁺ binding modes (optimized using six different DFT functionals) are consistent with their corresponding experimental geometries. Subsequent interaction energy calculations at the MP2 level, and decomposition of its components, suggest that for G:C W:W Trans , Mg²⁺ binding can fine tune the basepair geometries without compromising with their stability. Our results, therefore, underline the importance of the mode of binding of Mg²⁺ ions in shaping RNA structure, folding and function.

Introduction

Consequent to the discovery of its enzymatic roles (1, 2), RNA has been found to be associated with numerous biophysical processes (3). To execute these cellular processes, including regulation of gene expression and protein synthesis, RNA molecules are required to be folded in functionally competent structures that display a diverse repertoire of noncanonical basepairs (4). The unique geometry and stability of these noncanonical basepairs shape up the characteristic features of different structural motifs in RNA (5, 6). Hence, recognizing the role of different noncanonical basepairs is important for developing a comprehensive understanding of the sequence-structure-function relationship in RNA.

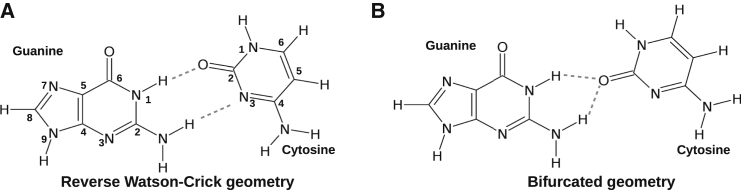
In this context, quantum-mechanics-based theoretical studies of the intrinsic properties of these basepairs have achieved remarkable success (7, 8). This was possible because in most of the cases, minimum-energy geometries of the isolated basepairs obtained in the gas phase are very much consistent with their geometry as observed within the crystal environment (experimental geometry) (9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19). Naturally, those noncanonical basepairs whose minimum-energy structures are significantly different from their experimental geometry become the subject of interest. Identifying the physicochemical factors that stabilize these “away-from-equilibrium” local geometries within the crystal environment constitutes an important problem. On the one hand, it provides insight into RNA’s structural dynamics, and on the other, it provides a testbed for designing nucleic-acid-based nanodevices with switching potential. One classical example of such a noncanonical basepair is the Levitt basepair (20), the conserved interaction between G15 and C48 residues in tRNA. This crucial tertiary interaction is located at the elbow of the L-shaped structure of cytosolic tRNAs and mediates the interaction between the D and V arms. Within the crystal structure, the G15-C48 interaction is found to be present in reverse Watson-Crick geometry (RWC), stabilized by two hydrogen bonds. However, on isolated geometry optimization in the gas phase, it converges to a bifurcated geometry (Fig. 1), stabilized by two bifurcated hydrogen bonds (21). This bifurcated geometry can be classified as G-C Ww/Bs trans, according to the Leontis and Westhof nomenclature extended for bifurcated geometries (5, 22). However, in this work, to annotate the basepairing interactions, we have followed a nomenclature slightly different from the Leontis and Westhof nomenclature. If edge X of base A interacts with edge Y of base B in cis (or trans) orientation, the interaction is annotated as A:B X:Y Cis (or A:B X:Y Trans). Therefore, the crystal geometry of the Levitt basepair is annotated as G:C W:W Trans.

Figure 1.

Schematic representation of the (A) RWC and (B) bifurcated geometries of the Levitt basepair. Hydrogen bonds are shown as dashed lines.

Analyzing tRNA crystal structures, Oliva et al. (23) have identified that positive charge buildup at the Hoogsteen edge of guanine (at position N7), in the form of coordination with Mg²⁺ ion or post-transcriptional archaeosine modification, stabilizes the RWC geometry of the Levitt basepair. Binding of other divalent cations like Mn²⁺ and Co²⁺ at the N7 position of guanine also has a similar effect on the RWC geometry of G:C W:W Trans pair (24). However, occurrence of G:C W:W Trans basepairs is not limited to G15-C48 of tRNA; rather, they occur recurrently in 23S rRNAs (25). They are also present in class II preQ1 riboswitches and participate in the recognition mechanism (26). Chawla and co-workers have analyzed all such occurrences of the G:C W:W Trans pair in high-resolution RNA crystal structures and have found that two-thirds of the total occurrences of G:C W:W Trans are involved in higher-order interactions (e.g., base triples, base quartets, interaction with ordered surrounding water molecules and interaction with phosphate backbone) that stabilize its RWC geometry (25). In our earlier work, we have shown that direct protonation at the N7 position of guanine is sufficient to stabilize the RWC geometry (27). Note that protonation of nucleobases is thermodynamically unfavorable, since the pK_a1 values of adenine ($\sim$ 4.1), guanine ($\sim$ 3.2) and cytosine ($\sim$ 4.4) are usually 2–3 units away from neutrality (28, 29). However, the importance of charged nucleobases in modulating structure (30, 31, 32, 33) and function (28, 34, 35) of nucleic acids is well documented in contemporary literature. Note that such nucleobase protonation remains “invisible” even in the high-resolution x-ray crystal structures and can only be inferred through circumstantial evidence. Our quantum mechanics (QM) studies (36) suggest that the charge redistribution caused by N7 protonation in guanine is qualitatively equivalent to that caused by the coordination of N7 with Mg²⁺ ions (23). It is therefore hypothesized that guanine N7 protonation may act as a stabilizing factor for those instances of G:C W:W Trans pairs that do not show post-transcriptional modification or metal ion coordination at guanine’s Hoogsteen edge or do not take part in higher-order interactions (27).

The importance of Mg²⁺ in tRNA folding has been known for a long time (37, 38, 39), and recent studies (40, 41) have also highlighted its role in stabilizing essentially all large RNAs, including transition states of some ribozymes (42, 43). Several recent theoretical studies have focused on understanding the Mg²⁺ binding architecture and its exact role in RNA’s structure and function (44, 45, 46, 47, 48). However, proper care should be exercised while drawing conclusions based on these studies, as the difference in electron density maps alone cannot distinguish between Na⁺, H₂O, and Mg²⁺ (44). For example, a very recent article by Leonarski et al. (49) has suggested that Mg²⁺ ions assigned near imino nitrogens are often suspect. The results of that study, in conjunction with an earlier report by Zheng et al. (44) on magnesium-binding architectures in RNA crystal structures, suggest that Mg²⁺ coordination with nucleobases takes place via different binding modes in RNA. At the same time, among all the nucleobase atoms, the propensity of Mg²⁺ binding is significantly high for O6 of guanine (44, 49). Further, water molecules in the first coordination shell of Mg²⁺ are highly polarized and have specific roles in mediating Mg²⁺-RNA interactions (44, 50). We have already said that charge redistribution in guanine caused by protonation at N7 can stabilize the RWC geometry of G:C W:W Trans pairs. In principle, interaction of the highly acidic first-shell water molecules (pK_a of Mg²⁺ (H₂O)₆ = 11.4, pK_a of Na⁺(H₂O)_6–8 = 14.4, pK_a of H₂O_bulk = 15.7 (51)) with N7 of guanine should cause similar charge redistribution and therefore can act as a stabilizing factor for the RWC geometry.

It may be noted that only Mg²⁺ binding to the N7 of guanine has been studied in the context of the G:C W:W Trans geometry. Therefore, it is necessary to investigate the effect of other binding modes of Mg²⁺ with the Hoogsteen edge of guanine and understand their influence on G:C W:W Trans basepairing. In this work, we have analyzed high-resolution crystal structures of RNA to identify instances of G:C W:W Trans pairs in which Mg²⁺ interacts with the Hoogsteen edge of guanine via different binding modes, such as 1) direct binding at N7, 2) direct binding at O6, 3) simultaneous binding at both N7 and O6, and 4) interaction via hydrogen bonding with the water molecules of the first coordination shell. We also have presented a molecular-level understanding of the chemistry of such interactions and their impact on the geometry and stability of G:C W:W Trans basepairs on the basis of density functional theory (DFT) calculations.

Materials and Methods

We have curated all the RNA x-ray crystal structures (a total of 1873 structures) that have a resolution of <3.5 Å and are available in the Protein Data Bank (PDB) server in September, 2015. We have also curated all the solution NMR structures containing RNA fragments (a total of 591 structures) available in the PDB server in September, 2015. We will refer to this set of 2464 structures as the “large data set” in the following text. To have an unbiased statistics of structural features, we have also considered two nonredundant sets of RNA crystal structures. One is provided by the Nucleic Acid Database (NDB) (52) and the other is provided by the HD-RNAS (53). We have applied a resolution cutoff of 3.5 Å and shortlisted 838 structures available in version 1.89 of the NDB database. This set of 838 structures will be referred to as the “NDB data set” in this article. The representative structures present in HD-RNAS are decided upon after taking into account length, R-factor, resolution, and sequence similarity. We have further shortlisted 167 RNA crystal structures after applying a resolution cutoff of 3.5 Å and length cutoff of 30 nucleotides to exclude the small synthetic RNA constructs. We will refer to this set of 167 structures as the “HD-RNAS data set.” All the PDB identities of the crystal structures of the corresponding data sets are listed in the Supporting Material.

For a given RNA crystal structure, first we have shortlisted all the guanine residues that have one or more Mg²⁺ ions within 6.5 Å of their respective Hoogsteen edge carbonyl oxygen (O6) and/or imino nitrogen (N7) atoms. These shortlisted Mg²⁺-nucleobase pairs can further be categorized into two classes depending on the mode of interaction between Mg²⁺ and nucleobase atoms (O6/N7): 1) direct interaction, or 2) water-mediated interaction. We have taken the ideal bond lengths of Mg-O and Mg-N bonds as 2.08 and 2.20 Å, respectively. These are the mean distances observed in the Cambridge Structural Database (54) and are also considered in earlier literature (44). With a buffer length of 0.5 Å, if the Mg-O6 distance is found to be $\le$ 2.70 Å and/or the Mg-N7 distance is found to be ≤2.58 Å, we have considered the corresponding Mg²⁺-nucleobase interaction as a direct interaction. On the other hand, we have considered it to be a water-mediated interaction if a water molecule (O_W) is found between the Mg²⁺ and the nucleobase atom in such a way that 1) it is directly bound to Mg²⁺ (i.e., the Mg²⁺-O_W distance is ≤2.70 Å), and 2) there is a possibility of a hydrogen-bonding interaction between the water molecule and the nucleobase atom, i.e., the O_W-O6/N7 distance is ≤3.8 Å, a reasonable cutoff for the hydrogen-bond donor-acceptor distance for biological systems (55, 56). This algorithm is pictorially depicted in Fig. S1.

Next, we analyzed the given RNA crystal structure with the BPFIND software (57) and identified whether or not the Mg²⁺-bound nucleobases are part of any G:C W:W Trans-type basepairing interaction. BPFIND is a well-accepted (58, 59, 60) precursor atom-based algorithm that identifies two nucleobases as a basepair if there are at least two conventional hydrogen bonds (N-H$\cdots$ N, N-H$\cdots$ O, O-H$\cdots$ N, O-H$\cdots$ O, C-H$\cdots$ N, or C-H$\cdots$ O) present between them. We have applied the following cutoffs to detect only “good” basepairing interactions: 1) a cutoff distance of 3.8 Å between the acceptor and donor atoms; 2) a cutoff angle of 120.0° for checking planarity of precursor atoms and linearity of the hydrogen bonds; and 3) a cutoff “E-value” of 1.8 to signify the overall distortion and maintain a good basepairing geometry.

We have extracted the coordinates of nucleobases and Mg atoms from the crystal structures and modeled the Mg²⁺ coordinated G:C W:W Trans basepairs by adding hydrogen atoms and waters (at the first coordination shell of Mg²⁺) manually using GaussView (61) software. As per common practice (62), we have substituted the sugar moiety by a methyl group to reduce the computational cost without compromising the accuracy of the results. All the basepairs and the corresponding monomers are geometry optimized at six different DFT functionals. The first one is B3LYP (63, 64, 65), as it is arguably the most popular hybrid GGA functional (20% HF exchange) implemented in studying basepairing systems (25, 66, 67, 68). Its long-range-corrected version, CAM-B3LYP (69), and its dispersion-corrected version, B3LYP-D3(BJ), have also been considered. In B3LYP-D3(BJ), the dispersion correction has been added explicitly by Grimme’s method (third order) with Becke-Johnson damping (70, 71). Another hybrid GGA functional used in this work is PBE0 (72) (25% Hartree-Fock (HF) exchange), where all the parameters (except those in the underlying local spin-density approximation) are physical constants. PBE0 has been successfully implemented earlier in studying various hydrogen bonded systems including metal-basepair interactions (73, 74). Apart from these four hybrid-GGA functionals, we have selected two hybrid meta-GGA functionals, M05-2X (75) (52% HF exchange) and M06-2X (76) (54% HF exchange). They are specially parameterized to consider dispersion interactions and are used regularly in the literature to study similar systems (77, 78, 79, 80, 81, 82, 83). Hessian calculations were performed for all the optimized geometries to confirm that they are not associated with any imaginary frequencies.

Interaction energy of these systems (at the DFT level) has been calculated as $E_{\text{DFT}}^{\text{int}}$ = E(Mg²⁺-bound basepair) − E(Mg²⁺-bound guanine) − E(cytosine) + BSSE, where E(X) represents the electronic energy corresponding to the optimized geometry of isolated X and the basis-set superposition error (BSSE) is calculated using the counterpoise method (84). All the DFT calculations have been performed using the 6-311++G(d,p) basis set for Mg and the 6-31++G(2d,2p) basis set for other atoms (85). We have verified that at the B3LYP level, the optimized geometries and their corresponding interaction energies obtained with this choice of basis-set combination is consistent with that obtained with a split-valance triple-ζ basis augmented with 1) one set of a d-type and one set of a p-type polarization function for all nonhydrogen atoms, and 2) one set of a p-type and one set of a d-type polarization function for hydrogen atoms, also including s-p diffused orbitals for nonhydrogen atoms, i.e., 6-311++G(2df,2pd) (Figs. S4 and S5). Our choice of basis sets, therefore, reduces the computational cost without compromising reliability. For the B3LYP-optimized geometries we have also calculated the BSSE-corrected interaction energy at the MP2 level and denoted it as E^int. Further, we have studied the solvent screening of the electrostatic component of the interaction energy using the conductor-like polarizable continuum model (CPCM) (86, 87), with water as solvent (ε = 78.4), and denoted it as $E_{\text{sol}}^{\text{int}}$. Note that CPCM uses the united-atom topological model to define the atomic radii and is found to be appropriate for polar liquids (88). All MP2 calculations have been performed using the aug-cc-pVTZ basis set for Mg and the aug-cc-pVDZ basis set for other atoms (89). Kitaura-Morokuma decomposition analysis (90) was performed using the GAMESS-US package (91) to study the partitioning of the two-body intermolecular interaction energies into electrostatic, polarization, charge transfer, and higher-order coupling terms, within the HF approximation. To study the charge distribution of a system, we have performed Natural Population Analysis (92, 93) using the NBO package (94) implemented in the Gaussian 09 package. All other QM calculations are also done using the Gaussian 09 package (95).

NUPARM package (96, 97) has been used to characterize the geometry of optimized basepairs on the basis of three translational (shear, stretch, and stagger) and three rotational (buckle, propeller twist, and opening) parameters. Structural alignment was performed using VMD (98). We have developed a Python-based program to detect Mg²⁺-coordinated basepairs in RNA crystal structures.

Results and Discussion

Context analysis of G:C W:W Trans basepairs in RNA crystal structures

Two nonredundant data sets of RNA crystal structures analyzed in this work, HD-RNAS and NDB, contain 116 and 86 instances of G:C W:W Trans, respectively. However, a total number of 2101 instances of G:C W:W Trans have been detected in the large set of RNA crystal structures. We have analyzed the context of occurrence of these instances and found that G:C W:W Trans occurs in 14 different contexts, of which eight show Mg²⁺ coordination at the Hoogsteen edge of guanine (Table 1). Apart from the well-studied Levitt pair (context 1), Mg²⁺ coordinated G:C W:W Trans is observed in 23S rRNA of Escherichia coli (context 2d and context 10), 23S rRNA of Thermus thermophilus (context 4b, context 5), 23S rRNA of Haloarcula marismortui (context 3c), 23S rRNA (context 2e) and 5.8S rRNA (context 13) of Saccharomyces cerevisiae. A detailed picture of the occurrence contexts is given in the Supporting Material (Fig. S2), which shows that Mg²⁺ coordinated G:C W:W Trans pairs are involved in various structural motifs such as kissing loop, internal loop, junction loop, and also in mediating loop-loop interactions.

Table 1.

Context of Occurrence of G:C W:W Trans Basepair in the Large Set of RNA Crystal Structures

	RNA Type	Species	Basepair	Mg2+ Coordination	Occ. Freq	E Value		Context of Occurrence
						$\overline{E}$	SD
1.	tRNA	various species	15G:48C	yes	396	0.67	0.34	Levitt basepair
2.	(a) 23S rRNA	Deinococcus radiodurans	2508G:2454C		15	1.01	0.55	kissing loop in domain V
	(b) 23S rRNA	T. thermophilus	2541G:2487C		19	0.64	0.24
	(c) 23S rRNA	H. marismortui	2564G:2510C		65	0.90	0.27
	(d) 23S rRNA	E. coli	2529G:2475C	yes	177	0.77	0.32
	(e) 25S rRNA	S. cerevisiae	2898G:2844C	yes	34	0.55	0.15
3.	(a) 23S rRNA	D. radiodurans	1809G:1791C		7	0.89	0.21	internal loop in domain IV
	(b) 23S rRNA	T. thermophilus	1817G:1800C		209	0.80	0.17
	(c) 23S rRNA	H. marismortui	1873G:1856C	yes	65	0.54	0.10
4.	(a) 23S rRNA	D. radiodurans	2484G:2589C		7	0.86	0.28	5-way junction loop in domain V
	(b) 23S rRNA	T. thermophilus	(a) 2505G:2610C	yes	199	0.73	0.25	5-way junction loop connecting domain 0 and domain V
			(b) 2517G:2622C		22	0.62	0.13
5.	23S rRNA	T. thermophilus	1271G:1615C	yes	212	0.62	0.20	connecting a junction loop (gua) and a hairpin loop (cyt) in domain III
6.	23S rRNA	T. thermophilus	(a) 1929G:1925C		205	0.50	0.20	4-way junction loop in domain IV
			(b) 1951G:1947C
7.	23S rRNA	T. thermophilus	430G:234C		173	0.45	0.14	connecting two junction loops in domain I
8.	(a) 23S rRNA	H. marismortui	1190G:1186C		60	0.83	0.26	3-way junction loop in domain II
	(b) 25S rRNA	S. cerevisiae	1261G:1257C		34	0.58	0.36
9.	23S rRNA	H. marismortui	1683G:1377C		65	0.36	0.09	connecting 2 junction loops within domain III
10.	23S rRNA	E. coli	1360G:2214C	yes	53	0.92	0.33	kissing loop interaction connecting domain III and domain V
11.	(a) 23S rRNA	D. radiodurans	1284G:1631C		20	0.92	0.34	helix-helix interaction between domain III (gua) and domain 0 (cyt)
	(b) 23S rRNA	T. thermophilus	1318G:1662C		20	0.56	0.11
12.	23S rRNA	T. thermophilus	1847G:1830C		20	0.69	0.11	bulge-helix interaction in domain IV
13.	5.8S rRNA	S. cerevisiae	39G:106C	yes	17	1.00	0.11	loop-loop interaction (a part of bifurcated triple)
14.	18S r RNA	S. cerevisiae	720G:717C		7	1.60	0.20	hairpin loop in domain C

Average ($\overline{E}$) and standard deviation (SD) of the E-value (calculated by BPFIND software) have been reported for each context. Occ. Freq., frequency of occurrence.

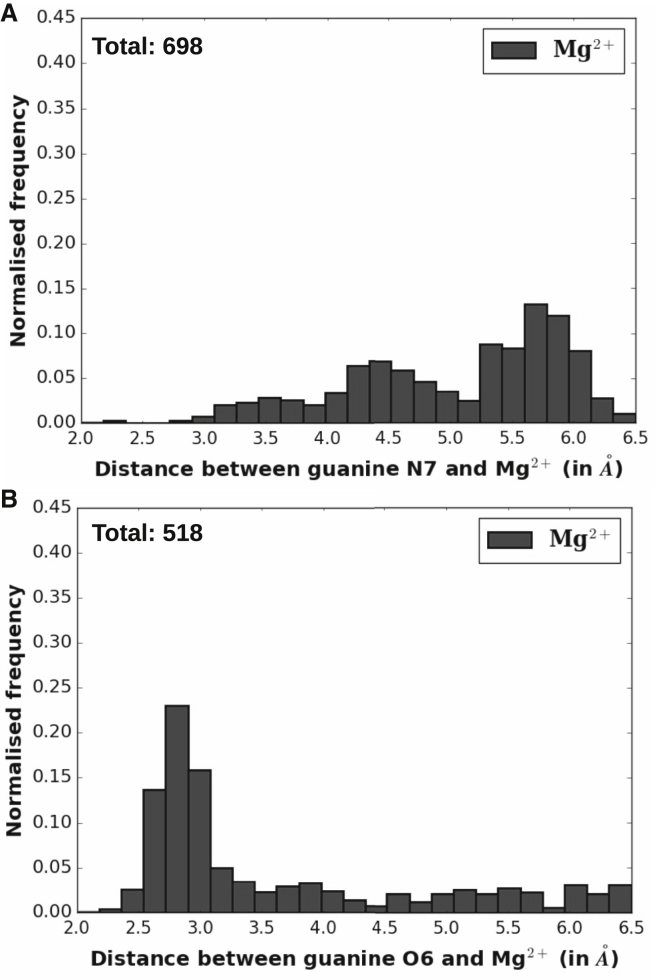
Analysis of the 2101 total instances of G:C W:W Trans basepairs shows that 36.2% (760 instances) have at least one Mg²⁺ within 6.5 Å of N7 and/or O6. This abundance of Mg²⁺ near G:C W:W Trans is remarkable, as the percentage is even higher than that for the Hoogsteen edge of canonical G:C W:W Cis pairs (32.2%). Among these 760 instances, the Mg²⁺ is found 242 times within 6.5 Å of N7, 62 times within 6.5 Å of O6, and 456 times within 6.5 Å of both N7 and O6. Thus, G:C W:W Trans pairs that have a Mg²⁺ within 6.5 Å of N7 (Fig. 2 A) is significantly greater than that for O6 (Fig. 2 B). Interestingly, however, the relative propensity of occurrences of Mg²⁺ within 3.0 Å of the base atom (i.e., close to the Mg-O/Mg-N covalent bond length) is remarkably higher for the O6 instances than for the N7 instances. In contrast, the frequency distribution of Mg-N7 distances has a high population at larger values (∼4.5 and ∼5.7 Å). These observations suggest a distinct preference for the direct coordination mode of Mg²⁺ binding for O6, whereas for N7, the preference seems to be strongly tilted toward water-mediated Mg²⁺ binding. To understand the implications of these new modes of Mg²⁺ binding to G:C W:W Trans basepairs, we have tried to detect all related instances in our RNA structure data sets.

Figure 2.

Distribution of the occurrence frequency (normalized) of G:C W:W Trans pairs that have at least one Mg²⁺ within 6.5 Å of the nucleobase atom (N7/O6) with respect to (A) the N7-Mg²⁺ distance and (B) the O6-Mg²⁺ distance.

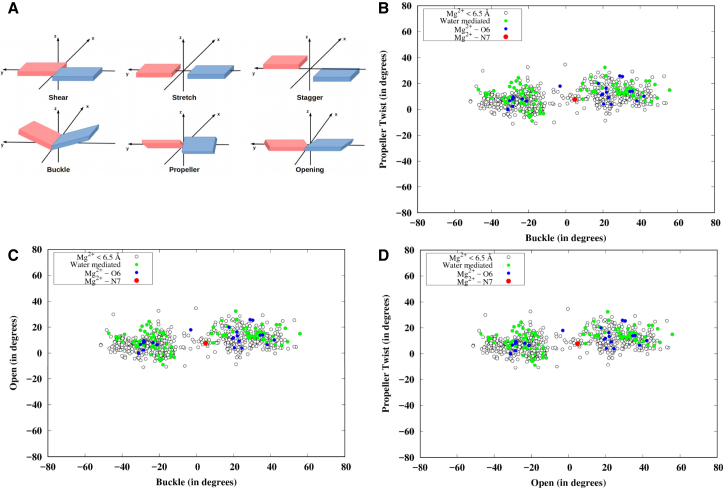
As seen above, our search space consists of the 760 instances involving Mg²⁺ detected within 6.5 Å of N7 and/or O6. Notably, definitive assignment of the two modes, based on interatomic distances and available coordinates of water, was possible for only ∼18% of the search space. This consisted of only one instance of direct Mg²⁺ binding at N7, 23 instances of direct Mg²⁺ binding at O6, and 112 instances of Mg²⁺ binding via the water molecules of the first coordination shell. To assess the tightness of direct and water-mediated Mg²⁺ binding in the two locations, we looked at their B-factors for these 136 instances. Although all the values were in general found to be on the higher side, they showed an interesting variation pattern. B-factors were higher for both the binding modes (direct and water mediated) when associated with N7 (average values are 68.6 and 78.5, respectively) than when associated with O6 (average values are 38.5 and 41.3, respectively), with the intermode variation also being higher for N7 instances than for O6 instances. We have also characterized the geometry of these Mg²⁺-bound G:C W:W Trans pairs by the three translational (shear, stretch, and stagger) and three rotational (buckle, propeller twist, and opening) parameters, as shown in Fig. 3 A. Distribution of these instances in the buckle-propeller-twist space (Fig. 3 B) shows that water-mediated Mg²⁺ binding at the Hoogsteen edge of guanine (green circles) and direct Mg²⁺ binding at O6 (blue circles) are usually associated with a nonplanar geometry characterized by high buckle and/or propeller-twist values. On the other hand, direct Mg²⁺ binding at N7 is associated with a relatively planar geometry (red circles). Distribution in the buckle-open (Fig. 3 C) and open-propeller-twist (Fig. 3 D) spaces shows no significant variation in the opening angle. However, data points corresponding to the water-mediated Mg²⁺ binding (green circles) and direct Mg²⁺ binding at O6 (blue circles) are distinctly clustered at the high buckle and propeller-twist values (both positive and negative) in Fig. 3, C and D, respectively. The planar geometry of G:C W:W Trans corresponding to direct Mg²⁺ binding at N7 is consistent with the optimized geometries reported in earlier QM-based studies (23, 24). Can the nonplanar geometries corresponding to the new Mg²⁺-binding modes also be explained on the basis of their ground-state electronic structures?

Figure 3.

(A) Definition of the three translational (shear, stretch, and stagger) and three rotational (buckle, propeller twist, and opening) parameters that define the mutual orientation of the two bases in a basepair. The distribution of all instances of G:C W:W Trans basepair detected in the larger set of RNA crystal structures having at least one Mg atom within 6.5 Å of N7 and/or O6 is shown for the (B) buckle-propeller-twist, (C) buckle-open, and (D) open-propeller-twist spaces. Solid circles represent the instances for which the exact binding mode of Mg²⁺ (red, direct coordination at N7; blue, direct coordination at O6; green, coordination via first-shell water molecules) can be identified in the crystal structures. Open circles represent instances where Mg²⁺ is present within 6.5 Å of N7/O6, but the exact binding mode cannot be identified. To see this figure in color, go online.

Influence of Mg²⁺ coordination on the geometry and charge distribution of guanine

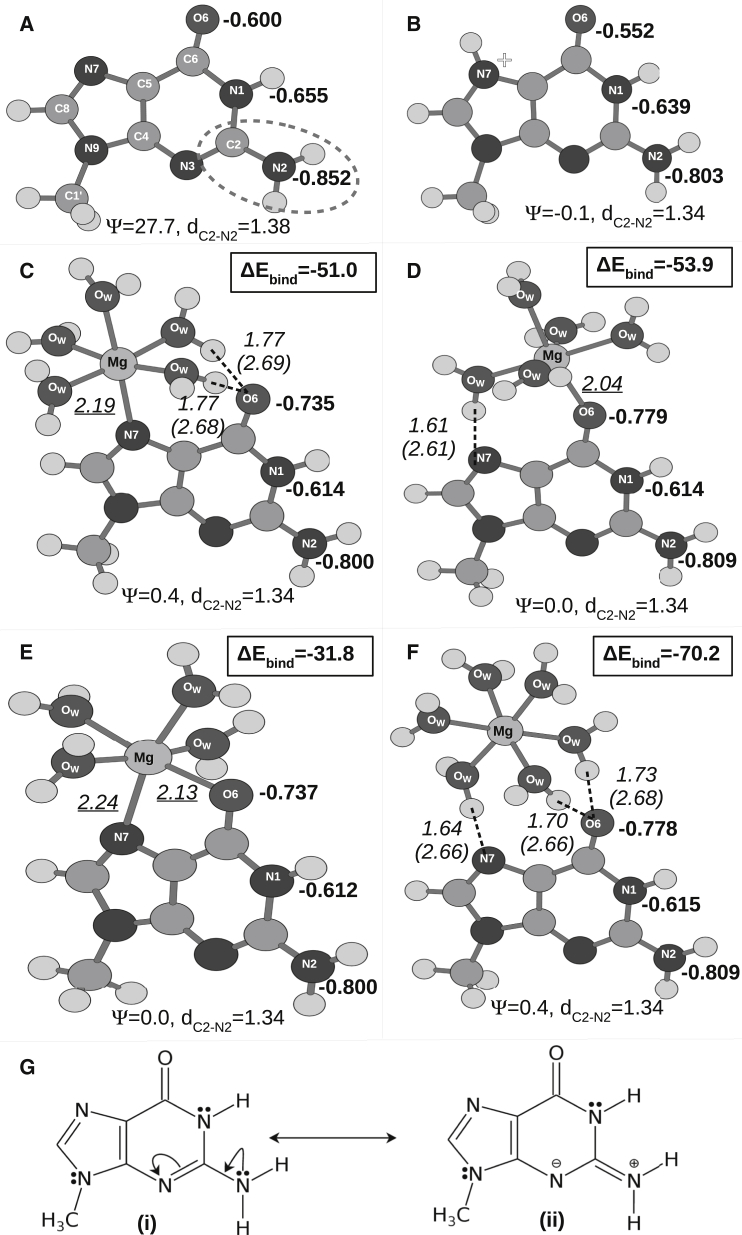
Apart from the three different Mg²⁺-binding modes observed in crystal structures (i.e., 1) direct Mg²⁺ binding at N7, 2) direct Mg²⁺ binding at O6, and 3) Mg²⁺ binding via first-shell water molecules), we have modeled one more mode of interaction: 4) direct binding of Mg²⁺ with both N7 and O6 simultaneously. The optimized geometry (at B3LYP) of Mg²⁺-bound guanine corresponding to these four different binding modes is shown in Fig. 4. Comparison with the optimized geometry of normal guanine (Fig. 4 A) reveals that the major change in the geometry takes place at the exocyclic amino group. In all four cases (Fig. 4, C–F), the change is characterized by depyramidalization of the amino group and shortening of the C2-N2 bond, which is indicative of a sp³$\to$sp² transition of N2’s hybridization state. This can be explained by the conjugation of the lone pair of the exocyclic amino group with the ring π system (Fig. 4 G). As discussed earlier for guanine N7 protonation (27), positive charge buildup at the Hoogsteen edge of guanine favors such charge delocalization by stabilizing the resonance canonical structure labeled (ii) in Fig. 4 G. Such Mg²⁺-binding-induced charge delocalization is also reflected in the reduced HOMO-LUMO gaps (ΔE_H-L) in Mg²⁺-bound systems. For example, at the B3LYP level, ΔE_H-L = 5.1 eV for normal guanine; 4.9 eV for direct Mg²⁺ binding at N7, O6, or both; and 4.8 eV for water-mediated Mg²⁺ binding.

Figure 4.

B3LYP optimized geometries of (A) normal guanine; (B) N7 protonated guanine; guanine with (C) direct Mg²⁺ binding at N7, (D) direct Mg²⁺ binding at O6, and (E) direct Mg²⁺ binding at both N7 and O6; and (F) Mg²⁺ binding at the Hoogsteen edge via the water molecules of its first coordination shell. The improper dihedral angle ψ measures the extent of pyramidalization of the amino group (see Fig. S3). ${\mathit{d}}_{C2-N2}$ represents the C2-N2 bond length. Hydrogen bonds are shown as dashed lines. For each hydrogen bond, the distance between hydrogen and the acceptor atom is reported in italic. Values in parentheses represent the distance between the hydrogen bond donor and acceptor atoms. Mg-N7/O6 distances are underlined. All interatomic distances are reported in Ångströms. Partial charges obtained from natural population analysis are reported (as a fraction of elemental charge (e)) for the hydrogen bond donor and acceptor atoms of the Watson-Crick edge (bold). ΔE_bind represents the binding energy (in kcal/mol, at the MP2 level) between the hydrated Mg²⁺ ion and guanine. (G) Conjugation of the lone pair of the exocyclic amino group with the ring π system is shown.

Mg²⁺-induced charge redistribution modulates the hydrogen-bonding potential of the hydrogen bond donor and acceptor sites of the Watson-Crick edge. On the basis of the NBO charges (q) shown in Fig. 4, it is evident that both N7 protonation and Mg²⁺ coordination reduce the electron density over the hydrogen bond donor sites (N1 and N2) and thus improve their hydrogen-bonding potential. To quantify this variation, let us introduce the parameter Δq = q(Mg²⁺ coordinate guanine) − q(normal guanine). Δq corresponding to N1 and N2 is similar for all four Mg²⁺ binding modes. However, the change in the hydrogen bond acceptor site (O6) is the opposite for N7 protonation and Mg²⁺ interaction. Across all four binding modes studied, Mg²⁺ interaction increases the electron density over O6, making it a stronger hydrogen bond acceptor. Interestingly, the four binding modes can be classified into two groups on the basis of their corresponding Δq values: group I, consisting of direct binding at N7 and at both N7 and O6 (Δq = 0.135 and 0.137 e, respectively (Fig. 4, C and E)); and group II, consisting of direct binding at O6 and water-mediated binding (Δq = 0.179 and 0.178 e, respectively (Fig. 4, D and F)). The same grouping is also valid for the extent of decrease in electron density over the hydrogen atoms of the Watson-Crick edge (Table S1). It is noteworthy that earlier works have considered the decrease in electron density over the amino hydrogens to be the key factor responsible for the stabilization of the RWC geometry on Mg²⁺ coordination, since it reduces the electrostatic repulsion between amino groups of guanine and cytosine (23). Therefore, on the basis of Mg²⁺-induced charge redistribution, we can expect that the influence of Mg²⁺ coordination on the G:C W:W Trans basepairing will be different for the two sets of conditions mentioned above, Group I and Group II.

An important observation is that stability of the hydrated Mg²⁺-guanine complex is highly dependent on the binding mode (Fig. 4, C–F). Water-mediated Mg²⁺ interaction is significantly stronger (E_bind = −70.2 kcal/mol) than any direct Mg²⁺ interaction mode. Due to restriction in the formation of the octahedral geometry, direct Mg²⁺ binding at both N7 and O6 (E_bind = −31.8 kcal/mol) is significantly weaker than for direct Mg²⁺ binding at N7 (E_bind = −51.0 kcal/mol) and O6 (E_bind = −53.9 kcal/mol). Here, E_bind for a (Mg²⁺, nH₂ O)-bound guanine has been calculated as E_bind = E(guanine bound to Mg²⁺, nH₂O) + (6 − n)E(H₂ O) − E(Mg²⁺, 6H₂O)- E(guanine), where E(X) corresponds to the ground state electronic energy of the species X.

Influence of different Mg²⁺ coordination modes on the geometry and stability of G:C W:W Trans pairs

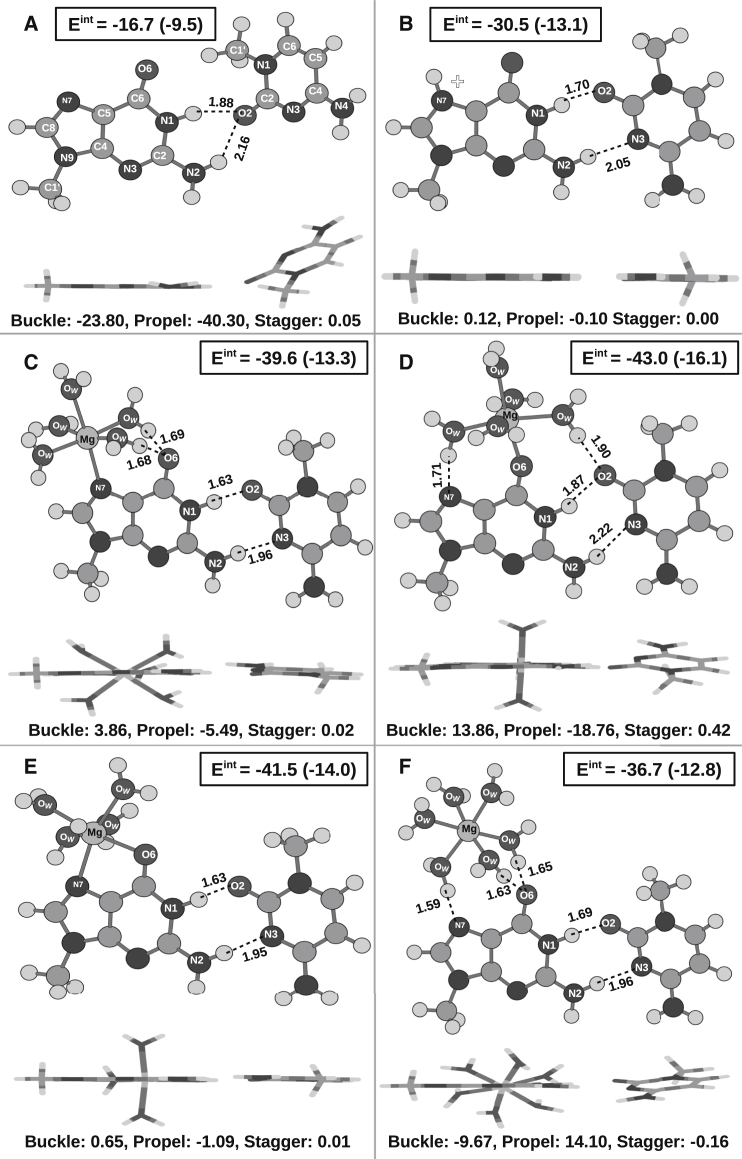
From the B3LYP-level optimized geometries shown in Fig. 5, it is clear that the RWC geometry of the G:C W:W trans pair is not favorable in the gas phase and converges to a bifurcated geometry on energy optimization (Fig. 5 A). Positive charge buildup at the Hoogsteen edge of guanine in the form of direct N7 protonation (Fig. 5 B), direct Mg²⁺ binding (Fig. 5, C–E), or water-mediated Mg²⁺ interaction (Fig. 5 F) stabilizes the RWC geometry. Fig. 5 also shows the BSSE-corrected interaction energy calculated at the MP2 level for the B3LYP optimized geometries. In general, the gas-phase interaction energy of these positively charged systems is dominated by the electrostatic component (the HF component of $E_{\text{MP}2}^{\text{int}}$ is >74% for all the systems, Table S2). We have therefore incorporated the effect of solvent screening on the interaction energy ($E_{\text{sol}}^{\text{int}}$) of the gas-phase optimized geometries. The $E_{\text{sol}}^{\text{int}}$ values shown in Fig. 5 suggest that the RWC geometry stabilized by positive charge buildup at the Hoogsteen edge is 3.3–6.6 kcal/mol stabler than for the bifurcated geometry. Among the three direct Mg²⁺-binding modes, direct binding at O6 results in the strongest pair (E^int = −43.0 kcal/mol and $E_{\text{sol}}^{\text{int}}$ = −16.1 kcal/mol), probably due to the extra hydrogen bond between one first-shell water and the O2 of cytosine. However, the interaction energy of G:C W:W Trans with water-mediated Mg²⁺ binding is lower than all three direct Mg²⁺ coordinated models. This relative order of stability of the G:C W:W Trans pairs corresponding to the four Mg²⁺-binding modes is consistent with the interaction energies calculated at all different DFT functionals except B3LYP-D3(BJ), where the dispersion interactions have been treated as an empirical correction term ($E_{\text{DFT}}^{\text{int}}$ in Fig. S6; Table 2). It is to be noted that optimized geometries of the G:C W:W Trans pair (except in the cases of direct Mg²⁺ binding at N7 and water-mediated Mg²⁺ binding) obtained at the B3LYP-D3(BJ) level are also not consistent with the other functionals (Table 2). Among the other five functionals, B3LYP-level calculations result in minimal interaction energy. Consideration of the long-range corrections in the CAM-B3LYP functional improves the interaction energy by up to 2.9 kcal/mol (for direct Mg²⁺ binding at O6). On the other hand, incorporation of dispersion interactions via a parameterized hybrid meta-GGA functional like M05-2X improves the interaction energy by 1.3 kcal/mol (for direct Mg²⁺ binding at N7) to 5.7 kcal/mol (for direct Mg²⁺ binding at O6). For M06-2X, the rise in interaction energies is even higher (up to 1 kcal/mol). However, except in the case of direct Mg²⁺ binding at O6, calculations performed at PBE0, the other hybrid GGA functional considered in this work, give the highest interaction energies (Fig. S6) and therefore are closer to the interaction energies calculated at the MP2 level (E^int values reported in Fig. 5). Our results therefore suggest that dispersion and long-range corrections are crucial for these systems, especially for direct Mg²⁺ binding at O6. At the same time, the method of incorporation of the dispersion interactions is also important.

Figure 5.

B3LYP optimized geometries of G:C W:W Trans pairs with (A) normal guanine, (B) N7 protonated guanine, and (C–F) Mg²⁺-bound guanine are shown. Different modes of Mg²⁺ binding are direct Mg²⁺ binding at (C) only N7, (D) only O6, and (E) both N7 and O6, and (F) binding via the water molecules of the first coordination shell. For each case, a lateral view of the optimized structure is also shown to highlight the extent of nonplanarity of the interaction. The same has been quantified by the buckle, propeller-twist, and stagger parameters. Hydrogen bonds are represented by dashed lines labeled with the distances (Å) between the hydrogen and the acceptor atom. BSSE-corrected interaction energies (E^int) calculated at the MP2 level have been reported in kcal/mol. E^int values calculated in the CPCM continuum solvent model are given in parentheses.

Table 2.

Basepair Geometry Parameters Corresponding to the Optimized Geometries of the G:C W:W Trans Basepair

	$E_{\text{DFT}}^{\text{int}}$	Buckle	Open	Propel	Stagger	Shear	Stretch
Normal Guanine
B3LYP	−14.7	−23.80	74.21	−40.30	0.05	−3.61	3.17
CAM-B3LYP	−17.2	21.87	74.87	38.73	−0.03	−3.63	3.13
B3LYP-D3(BJ)	−37.6	−156.68	15.64	−73.43	0.39	−1.27	2.90
PBE0	−16.0	−27.86	73.99	−42.54	0.05	−3.51	3.12
M05-2X	−17.7	−5.27	76.55	−4.35	0.23	−4.11	3.07
M06-2X	−17.5	−11.16	78.12	−5.21	0.32	−4.13	3.04
Direct Protonation at N7
B3LYP	−28.6	0.12	12.47	−0.10	0.00	−2.78	2.88
CAM-B3LYP	−30.4	0.28	12.79	−0.61	0.00	−2.80	2.86
B3LYP-D3(BJ)	−51.9	4.38	10.00	−16.16	0.03	−2.62	2.82
PBE0	−30.1	1.87	12.25	−3.83	0.01	−2.73	2.85
M05-2X	−30.8	−0.35	19.36	−0.23	0.00	−3.43	2.84
M06-2X	−30.4	−0.06	14.54	0.15	0.00	−3.10	2.84
Direct Mg2+ Coordination at N7
B3LYP	−32.3	3.86	12.70	−5.49	0.02	−2.64	2.85
CAM-B3LYP	−34.3	4.00	12.96	−5.77	0.02	−2.64	2.83
B3LYP-D3(BJ)	−73.9	4.44	11.42	−6.90	0.03	−2.55	2.82
PBE0	−35.4	6.36	12.52	−9.70	0.05	−2.58	2.82
M05-2X	−33.6	5.60	14.74	−9.12	0.05	−2.70	2.85
M06-2X	−34.6	11.82	12.88	−21.64	0.11	−2.56	2.80
Direct Mg2+ Coordination at O6
B3LYP	−34.1	13.86	11.55	−18.76	0.42	−1.8	3.03
CAM-B3LYP	−37.0	12.47	11.76	−18.34	0.36	−1.73	3.01
B3LYP-D3(BJ)	−29.6	10.83	3.39	−26.18	0.17	−2.18	2.89
PBE0	−37.0	13.11	11.63	−19.06	0.35	−1.76	2.99
M05-2X	−39.8	61.96	−3.4	−34.79	0.74	−0.19	2.96
M06-2X	−39.9	15.86	3.88	−37.43	0	−0.53	2.89
Mg2+ Coordination at Both N7 and O6
B3LYP	−34.1	0.65	8.51	−1.09	0.01	−2.68	2.77
CAM-B3LYP	−36.2	1.45	8.84	−2.33	0.02	−2.68	2.75
B3LYP-D3(BJ)	−46.8	10.74	6.1	−17.53	0.17	−2.54	2.72
PBE0	−37.1	3.55	8.46	−6.06	0.06	−2.63	2.74
M05-2X	−35.7	13.03	8.82	−23.63	0.22	−2.62	2.73
M06-2X	−36.8	8.15	8.67	−20.2	0.19	−2.58	2.73
Water-Mediated Mg2+ Coordination
B3LYP	−29.2	−9.67	10.88	14.10	−0.16	−2.61	2.88
CAM-B3LYP	−31.3	−9.51	11.29	13.74	−0.15	−2.61	2.86
B3LYP-D3(BJ)	−70.8	9.74	9.14	−17.58	0.17	−2.49	2.83
PBE0	−32.3	−11.55	10.52	17.62	−0.20	−2.55	2.84
M05-2X	−30.8	16.11	11.16	−22.90	0.22	−2.64	2.85
M06-2X	−31.8	7.39	11.82	−17.18	0.14	−2.61	2.85

Parameters were obtained using different DFT functionals for 1) normal, 2) N7 protonated, and (3–6) different modes of Mg²⁺ coordination. The BSSE-corrected interaction energy $\left(E_{\text{DFT}}^{\text{int}}\right)$ values corresponding to the optimized geometries of the basepair are given in kcal/mol.

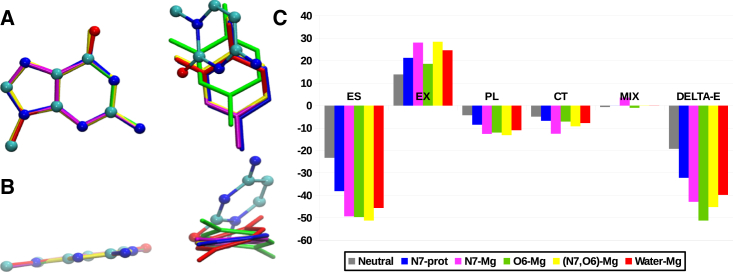
Interestingly, as expected from the Mg²⁺-coordination-induced charge redistribution in guanine, the optimized geometry of G:C W:W Trans with the Group I-type Mg²⁺ interaction is significantly different from that with the Group II-type Mg²⁺ interaction. For the latter group, the optimized geometry is nonplanar, having high buckle and propeller twist (Fig. 5, D and F), whereas the former results in a planar geometry (Fig. 5, C and E) similar to that for guanine N7 protonation (Fig. 5 B). The comparison is clearly depicted in Fig. 6, A and B, where the optimized geometries are structurally aligned with respect to the guanine residue. Optimized geometries corresponding to direct Mg²⁺ binding at O6 (green) and Mg²⁺ binding via first-shell water molecules (red) bend out of the plane, whereas optimized geometries corresponding to N7 protonation (blue), direct Mg²⁺ coordination at N7 (magenta), and direct Mg²⁺ coordination at both N7 and O6 (yellow) remain planar.

Figure 6.

(A) B3LYP optimized geometries of G:C W:W Trans pairs with normal (ball-and-stick format), N7 protonated (blue), and Mg²⁺-bound guanine are superposed with respect to the guanine residue. (B) Lateral view of the structural superposition in (A). Note the planar geometry for Mg²⁺ coordination at only N7 (magenta) and at both N7 and O6 (yellow), and the nonplanar geometry for Mg²⁺ coordination at only O6 (green) and water-mediated Mg²⁺ coordination (red). (C) Different components of the total interaction energy (ΔE) are shown. ES, electrostatic; EX, exchange repulsion; PL, polarization; CT, charge transfer; MIX, higher-order coupling. To see this figure in color, go online.

Nonplanarity of G:C W:W Trans on direct Mg²⁺ binding at O6 and Mg²⁺ binding via first-shell waters

It is important to note that the nonplanarity is inherent and not an artifact of the level of theory, as geometry optimization at all the six DFT functionals results in a buckled and propeller-twisted geometry for direct Mg²⁺ binding at O6 (case 1) and Mg²⁺ binding via first-coordination-shell water molecules (case 2) (Table 2). Interbase hydrogen-bonding distances corresponding to case 1 and case 2 are longer than that for the N7 protonated case. This indicates that the buckled and propeller-twisted geometry moves the bases away from each other. Again, for direct Mg²⁺ coordination at N7 (case 3) (Fig. 5 C) and at both N7 and O6 (case 4) (Fig. 5 E), the optimized geometries remain planar. The interbase hydrogen-bonding distances corresponding to case 3 and case 4 are shorter than that for the N7 protonated case. This indicates that the planar geometry brings the bases close to each other.

Decomposition of the interaction energies (Fig. 6 C) of the B3LYP optimized geometries show that in comparison to N7 protonation (blue bars), Mg²⁺ binding significantly increases the electrostatic component for all four cases. However, the corresponding charge-transfer components are relatively higher for case 3 (magenta bars) and case 4 (yellow bars). As a result, although the planar geometry of case 3 and case 4 brings the bases closer to each other, the subsequent increase in the exchange repulsion component gets compensated by the charge-transfer component. On the other hand, the charge-transfer component is relatively lower in case 1 (green bars) and case 2 (red bar). Therefore, these two systems tend to attain optimal stability by adopting a buckled and propeller-twisted geometry, which results in movement of the two bases away from each other, thus avoiding any consequent increase of the exchange repulsion component.

Table 2 shows that the optimized geometry corresponding to direct Mg²⁺ coordination at N7 is nonplanar only at the M06-2X level and can be considered as an outlier. However, optimized geometries corresponding to the two hybrid meta-GGA functionals (M05-2X and M06-2X) show relatively higher buckle and propeller twist for case 1 and case 2. Why do geometry optimizations at M05-2X and M06-2X tend to increase the nonplanarity of these basepairs? Note that the percentage of HF exchange energy incorporated into M05-2X (52%) and M06-2X (54%) is ∼2–2.7 times higher than that incorporated into the other two hybrid GGA functionals considered in this study, i.e., B3LYP (20%) and PBE0 (25%). However, understanding the correlation (if any) between the extent of nonplanarity in these systems and the percentage-of-HF-exchange-energy component incorporated into hybrid functionals requires further investigation and is beyond the scope of this work.

Consistency with the crystal structure

Optimized geometries associated with different Mg²⁺-binding modes, and their relative stabilities, are consistent with the corresponding trends observed in RNA crystal structures. As discussed in the previous section, the G:C W:W Trans pairs with Mg²⁺ binding at O6, both directly and with water mediation, are also associated with a buckled and propeller-twisted geometry in the crystal structure. Note that in the crystal structures, apart from the mode of Mg²⁺ binding, there are several other factors that determine the planarity of a basepairing interaction. However, in this particular case, the consistency between the crystal geometry and the optimized geometry is remarkable. It shows that Mg²⁺ can fine tune the geometry of basepairing interactions. The small difference between the interaction energy of G:C W:W Trans with 1) direct Mg²⁺ binding at N7 and 2) Mg²⁺ binding via first-shell waters (Δ$E_{\text{sol}}^{\text{int}}$ = 0.5 kcal/mol) further suggests that such Mg²⁺-binding-based geometric modulation can take place without changing the stability of the overall system. On the other hand, the resulting basepair due to direct Mg²⁺ coordination at O6 is ∼3 kcal/mol stronger than the above two cases and therefore is not likely to be influenced by such low energy conformational changes. Again, the relatively smaller values of the B-factor of the Mg atoms corresponding to direct Mg²⁺-O6 interactions (38.5) compared with that of Mg atoms associated with all other competing interactions is also suggestive of a less flexible G:C W:W Trans interaction on direct binding of Mg²⁺ at O6.

Conclusion

G:C W:W Trans basepairs occur frequently in 23S rRNA of all of the four species available in our data set. Occurrence of G:C W:W Trans is also observed in 5.8S rRNA of Saccharomyces cerevisiae and in tRNAs (the popular Levitt basepair) of various species. All of these occurrences can be classified into 14 contexts. Among them, Mg²⁺ binding at the Hoogsteen edge of guanine is observed in eight contexts, which are integrally associated with a variety of structural motifs including different types of loops and their interactions. Sensitivity of the geometry of these basepairs to the binding mode of Mg²⁺, as described in this work, may imply significant consequences of binding-mode variation for the functional role of those structural motifs. Such sensitivity toward Mg²⁺-binding modes need not be restricted to G:C W:W Trans pairs alone. In fact, binding of magnesium or other divalent ions to other noncanonical basepairs may also result in similar structural variations. Our results thus open up an additional avenue for researching the structural complexity and functional diversity of RNA molecules.

Author Contributions

A.M. and D.B. have designed the research, with A.H. carrying out background investigations leading to the problem definition. R.R. has implemented the bioinformatics search and analysis protocols. A.H. has carried out Q.M. calculations, and has performed subsequent analysis in conjunction with the bioinformatics results. All authors contributed to writing the article.

Editor: Tamar Schlick.